Effect of a Gaussian random external magnetic field with spatio temporal variation on compensation in Ising spin-1/2 trilayered square ferrimagnets

Abstract

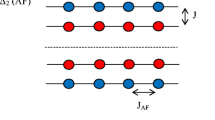
In this work, an extensive Metropolis Monte Carlo simulation is performed to investigate the steady-state magnetic and thermodynamic behaviour of a trilayered spin-1/2 Ising ferrimagnet with square monolayers, driven by external Gaussian random magnetic field with certain spatio-temporal variations. Such thin ferrimagnetic systems exhibit compensation phenomenon and thus are potentially interesting candidates for several technological applications. Here, two distinct theoretical atoms, A and B, make up the ABA and AAB types of configurations in which the like atoms (A–A and B–B) ferromagnetically interact and the unlike atoms (A–B) interact antiferromagnetically. Depending upon the strength of the spatio-temporally varying Gaussian random field, the compensation and critical points shift and steady-state magnetic behaviours change between the different distinct types of ferrimagnetic behaviours. The compensation phenomenon even vanishes after crossing a finite threshold of the standard deviation of the magnetic field for particular choices of the other controlling parameters. Consequently, in the Hamiltonian parameter space of both configurations, islands of ferrimagnetic phase without compensation appear within the phase area with compensation of field-free case. The areas of such islands grow with an increasing standard deviation of the external field, $\sigma$, obeying the scaling relation: $f(\sigma ,A(\sigma ))=\sigma ^{-b}A(\sigma )$ with $b_{ABA}=1.913\pm 0.137$ and $b_{AAB}=1.625\pm 0.066$. These values of exponents match within the statistical interval with those obtained with the uniform random magnetic field.

Appendices

Appendix

A: Characteristics of the external magnetic field

The local, Gaussian random external magnetic field values [of Eq. 1] at any site, at a time instant follow a Gaussian probability distribution. Box–Muller algorithm [43] is used to get such a distribution $G_{0}$ of standard deviation, $\sigma$ and zero mean:

$$\begin{aligned} G_{0}=\sigma \sqrt{-2 ln(U_{1})} cos(2\pi U_{2}) \end{aligned}$$

(12)

Here, $U_{1}$ and $U_{2}$ are two uniform random distributions between $\left[ 0,1\right]$.

A few additional characteristics are also added to the external field distribution [27]:

• (a) At different lattice sites, the values of the external field are uncorrelated at any time instant. Again at a lattice site, the values of the external field are uncorrelated for different time instants. So, $h_{m}(t)h_{n}(t^{\prime })=a(t)\text { }\delta _{mn}\text { }\delta (t-t^{\prime })$, where m, n are two different lattice sites and $t,t^{\prime }$ are two different time instants.

• (b) The following conditions are also satisfied:

  • (i) After the field is switched ON, the bulk average of the Gaussian field at a time instant, t, is zero:

    $$\begin{aligned} \sum _{m} h_{m}(t) =0 \end{aligned}$$

    . So,

    $$\begin{aligned} \sum _{m,n} h_{m}(t)h_{n}(t)\delta _{mn} =3L^{2}\sigma ^{2} \end{aligned}$$

    .

  • (ii) At the mth site, the temporal mean of the local field over the exposure interval, $\delta$, is zero: $\langle h_{m}(t)\rangle =\dfrac{1}{\delta }\int _{t_{0}}^{t_{0}+\delta } h_{m}(t)dt=0$.

At a few randomly chosen time instants within the exposure interval, the implementation of the desired field distribution is checked by the cumulative distribution function (CDF) [56], the kernel density estimate (KDE) [57, 58] and the histogram.

B: On compensation point and size of the system

We have mentioned that the system size in this study is fixed at $L=100$ in Sect. 3. The size of the system is a key factor in influencing the thermodynamic response in the context of a trilayered Ising system’s critical properties in a field-free environment, according to [22]. Due to the opposing magnetic moments of the sublayers, compensation happens when the net magnetisation of the system is zero. In [22], for $L\ge 60$, we have observed that the compensation point is immune to the linear system size in a field-free environment. But under the influence of a Gaussian random external field with spatio-temporal variation, we still need to find out whether the compensation point of the steady-state magnetisations depends on the linear system size. To address this issue, in this section, a few representative cases are discussed in Fig. 13. For both the configurations, ABA and AAB, the combination of moderate ferromagnetic–moderate antiferromagnetic coupling ratio is shown with $J_{AA}/J_{BB}=0.36$ and $J_{AA}/J_{BB}=-0.36$ and system sizes varied from $L=30$ to $L=100$. From these cases, we see the fluctuations in the values of compensation points have been confined to within $1\%$ across system sizes. For very few other randomly checked combinations of coupling strengths, the same feature is present. So, within the scope of available limited computational resources, using only the values of compensation temperatures for linear system sizes $L = 100$ does not compromise much on the accuracy for all the combinations of coupling strengths and standard deviation of the external Gaussian random magnetic field. That is a strong compendium in support of choosing $L=100$, in this study.

Fig. 13

Compensation temperatures versus linear system sizes of Ising trilayered square stacking of ABA type (a & b) and AAB type (c & d). The reported value of compensation temperature (L = 100) is confined within $1\%$ across all the sizes

C: On the transient behaviour

In this study, we have magnetic systems which are responding to time-dependent external fields and achieving steady state. So, we need to figure out the time interval the systems usually consume to die out the transient behaviours. A few selected examples are provided here which shows the reason behind the choice of transient time interval $(\Delta T)$ in Sect. 3. We can roughly estimate that $\Delta T \sim 50$ MCS, and that is why 250 MCS is consumed to reach the steady state (and record data) for surety.

Fig. 14

Transient behaviour of the trilayered systems: ABA (a & b) and AAB (c & d) for a few cases

D: Magnetic behaviour for $\sigma =1.00$

In this section, a small add-on is provided for better understanding of how magnetic order diminishes when the standard deviation is increased to $\sigma =1.00$ and dimensionless temperature, $T=0.01$. In the field-free environment, all the sublayers are perfectly ordered in such a nearly athermal condition. A few examples are provided in Fig. 15 where the external field affects the magnetic behaviour even in such low temperature. We understand now that when in-plane coupling strengths and corresponding cooperative energies are comparable to the steady-state spin-field energies, the corresponding sublayer magnetisations do not deviate much from equilibrium values. But when the spin-field term dominates, the steady-state sublayer magnetisation diminishes gradually as we increase the randomness of the external Gaussian random field. If the in-plane coupling strength is very weak, e.g. $J_{AA}/J_{BB}=0.04$ for the AAB configuration in Fig. 15(B), magnetic ordering in the steady state almost vanishes (steady-state sublayered magnetisation $\approx$ 0).

Fig. 15

Plots of magnetisations for square monolayers (sublattices) and total magnetisation of the bulk versus time in MCS, for the ABA and AAB configurations with $\sigma =1.00$. Here, $M_{t}(t)$: magnetisation of the top layer; $M_{m}(t)$: magnetisation of the mid-layer; $M_{b}(t)$: magnetisation of the bottom layer are all functions of time, t, in units of MCS. In these figures, Part: A describes the equilibrium (zero-field) and transient (field: ON) behaviour, whereas Part: B describes the steady-state behaviour (field: ON)