Abstract
Bismuth ferrite has been under intense research for many years as it can exhibit first- and second-order transitions where all the phases have distinct properties encapsulating various exciting phenomena. This work reports a computational study of bismuth ferrite and its varied phases using density functional theory with the implementation of Hubbard correction for increased accuracy. The proposed method is validated through Linear Response Theory using Quantum ESPRESSO. The phase transition and the mechanical properties are explored by calculating elastic tensors for different polymorphs. A negative Poisson's ratio for the tetragonal phase supporting its growth in compressive environments is predicted. The electronic properties of different phases of bismuth ferrite are explored, which helps in understanding properties such as charge transfer excitation, metal–insulator transition, ferroelectric nature based on lone pair charges and orbital hybridization. The phonon modes of different phases are also investigated.
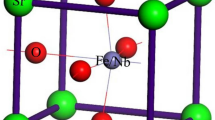
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Bismuth ferrite (BFO) is one of the promising multiferroic materials due to its unique properties such as high Curie and Neel temperatures, non toxicity, and hence has received intense research interest during the past decade. Most of the multiferroic materials belonged to either the perovskite (or distorted perovskite) family or the hexagonal family or boracites or fluorites [1]. The key features of BFO such as antiferromagnetic ordering, spontaneous polarization and antiferrodistortion are specific to the distorted rhombohedral structure [2, 3]. The effect of these properties individually or their coupling aids bismuth ferrite in potential application in many fields [4,5,6,7,8,9]. It was previously established that the stable phase of bismuth ferrite (BFO) is the rhombohedral R3c phase [10, 11]; however, reports on the other possible low-energy phases can also be found. One of the first well-known efforts was in 2006 [12], where it was shown that seven other phases could be computationally predicted. More recently, the investigations presented in references [13, 14] have elucidated the different possible low-energy phases with relatively large unit cells. Motivated in particular by these recent developments, the present work makes an effort to shed light on the structural, electronic, mechanical (elastic constants), and phonon modes of the phases, which are experimentally possible.
Usually, in an interface between a polar and a non-polar material, an electric field gets induced where the divergence is proportional to the density of charges at the interface. This can be energetically unfavourable, and a critical thickness is created, below which the net polarization is lost. However, if there exists a non-polar phase, it spontaneously transitions into other phases to reduce the electrostatic energy. This was demonstrated when BiFeO3 was interfaced with (La, Bi) FeO3, where the Pnma (orthorhombic) phase forms upon doping [13]. Similarly, cubic and tetragonal phases are experimentally possible with doping. The phase transitions are also possible with temperature and pressure [15,16,17], as listed in Table 1. Figure 1 shows the schematic representation of the different phases of bismuth ferrite investigated in the present study.
The parent rhombohedral phase faces many obstacles, such as leakage current and secondary phases, which blocks its complete utilization in potential applications hence making the study of non-rhombohedral phases essential, for example, though the rhombohedral phase exhibits a piezoelectric coefficient (d33) of 69 pm/V [18], it is far from usage in any commercial applications (without considering other properties such as dielectric constant and electromechanical coupling and hence, the figure of merit, which are also essential). However, with a similar d33, lead zirconate titanate (PZT) is commercially used [19]. The rhombohedral phase also falls short of ferroelectric applications, which is the primary objective for using bismuth ferrite. The conductivity and hence the loss of ferroelectric nature is caused by charge transfer excitations and oxygen vacancies [20]. On the other hand, the orthorhombic and tetragonal phases near the phase transition boundaries with the rhombohedral phase show enhanced mechanical, piezoelectric, and ferroelectric properties [21,22,23,24,25,26], which further confirms the need for the study of non-rhombohedral phases.
Significant applications of bismuth ferrite, which include memory devices, photovoltaic devices, and piezoelectric devices, are largely affected by leakage current and secondary phases. This work aims to find the root cause of these issues and possible solutions wherever necessary. In the following section on structural properties, we see how the rhombohedral phase, even though energetically favoured, is closely followed by the orthorhombic phase, which has minutely less formation energy than that of the rhombohedral phase. The source of leakage current can be found in the electronic properties, where Fe–O hybridization can lead to charge transfer mechanisms. Hence, the present work aims to solve issues related to multiple applications of bismuth ferrite.
The present work deals with the structural optimization of each phase computationally, and in the following sections, the functional properties are investigated through band structure and density of states (DOS). The usage of Hubbard correction is then verified through the Linear Response Theory [27]. Investigating mechanical properties through elastic constants is significant as the parent rhombohedral phase exhibits piezoelectric and ferroelastic properties. The phonon modes are also calculated. The following section elaborates on the technical details of each study.
2 Methods
We performed density functional theory calculation with GGA (generalized gradient approximation) exchange functional, namely, the PBE (Perdew–Burke–Ernzerhof), [54] with and without the Hubbard correction U = 0, 3, and 5 eV keeping J = 0 eV applied to the Fe atoms. The calculations are done using the Quantum ESPRESSO (QE) code [55], which uses the plane-wave basis set. All the calculations were done with spin-polarized conditions. Prior to the actual calculation, a two-step optimization of the input file was performed. The first step was to optimize the cutoff energy by fixing the K-point mesh. The second step involved using the optimized cutoff energy to find the appropriate K-point mesh. The fixed K-point mesh for SCF calculations was 5 × 5 × 5 for rhombohedral and cubic, 4 × 4 × 4 for orthorhombic, and 4 × 4 × 3 for tetragonal, and suitable denser K-point mesh was used for NSCF calculations. All the structures were relaxed and then the variable cell was relaxed with a pressure convergence threshold of 0.5 kBar, after which the equation-of-state formalism was used to find the cell volume with minimum energy for further calculation of DOS and band structure. The use of Hubbard correction was verified through Linear Response Theory within the QE code. Thermo_pw was used for the calculation of elastic constants (https://dalcorso.github.io/thermo_pw/). The atomic position represented with the Wyckoff positions is viewed in supporting information file.
3 Results and discussion
It is well known that the accuracy of DFT for structural and cohesive properties cannot be compared with that of electronic properties. However, the means to achieve accurate predictions are possible through the usage of large enough basis sets or hybrid functionals, which are both computationally demanding. A similar corrective approach to tackle the “electronic bandgap issue” is the DFT + U method, which is computationally much lighter than other alternatives. With the relatively better accuracy of GGA formulation, while computing the structural properties, it was chosen to use GGA + U formulation (the advantages of using GGA in other instances can be seen in [28,29,30]). The present work does not consider spin–orbit coupling as it has been shown in previous works that spin–orbit coupling has a minimal effect on the electronic properties in bismuth ferrite and hence has not been considered here [31].
3.1 Structural properties
The rhombohedral phase consists of two pseudocubic lattices derived from the distortion in the perovskite structure. The rhombohedral phase obtains a symmetry-breaking configuration through geometric distortions if it is possible to break the degeneracy of the electronic configuration known as the second-order Jahn–Teller effect (SOJTE). This distortion is seen through the shift in the Bi ions in the [111] pseudocubic direction powered by the stereochemical activity of 6s2 lone pair electrons of bismuth [11]. This results in the spontaneous polarization of the rhombohedral phase, which is the source of its ferroelectric nature. The lattice constant experimentally was found to be 5.643 Å, while the rhombohedral angle was around 59.348° [10]. The calculated lattice constant of the current work slowly converges to the experimental values with increasing Hubbard correction values as listed in Table 2.
The rhombohedral phase undergoes a first-order transition to the orthorhombic phase at certain temperatures and pressures. Due to the nature of the transition, it accompanies a discontinuous change in the first derivative of the free energy (polarization), making it non-polar, but conserves the antiferromagnetic ordering. The β-phase was shown to be orthorhombic by Arnold [32] amid confusions about it being non-orthorhombic [33,34,35].
The cubic phase appears due to the second-order transition from the orthorhombic phase, a metal–insulator band-type transition. To change from a valence band insulator (orthorhombic) to metal (cubic), there must be a change in the number of functional units and hence the number of electrons per unit cell. The disappearance of the rotation of the oxygen octahedron in the cubic phase powers the structural changes which drive the electronic modifications [2, 12, 15]. The tetragonal phase has been experimentally synthesized through strain engineering [36, 37]. According to [17], the tetragonal phase appears for a very short range of temperature between the orthorhombic and cubic phases. The significance of this phase lies in the fact that the tetragonal phase which is electrically polarizable exists between two non-polarizable phases. Theoretical calculations were also attempted by Ravindran et al. [12, 38, 39].
Table 2 shows the calculated structural parameters. The general trend is that with increasing the Hubbard correction, the lattice parameters increase mainly because of the on-site potential introduced to the iron atoms. In the cubic phase, a more significant effect of the Hubbard potential is seen, where there is a change of about 2% of the original lattice constant from U = 0 eV to U = 5 eV. The tetragonal phase also almost stabilizes after U = 3 eV, with only minor changes in the volume thereafter. The orthorhombic phase shows that with the increase in the U values, there is an elongation of the system with minor variations in the volume.
3.1.1 Phase stability
The rhombohedral R3c structure arises from cubic perovskite through two distortions. First the polar distortion where all the cations and the anions sublattice displace with respect to each other resulting in spontaneous electric polarization. Secondly, antiferrodistortive rotation of the FeO6 octahedra along the [111] direction. The simultaneous incorporation of both the displacements results in the transition of structure from Pm3̅m to R3c. Figure 2 shows the energy versus volume plots for all the phases.
The volume contraction from the rhombohedral to the orthorhombic phase can be interpreted as the α–β-phase transition [2]. The formation energy per atom was also calculated to further confirm that the rhombohedral phase is the stable ground-state phase.
The formation energy of bismuth ferrite (Table 3) was found through the equation given below
where Eform is the formation energy. The formation energy was found and tabulated in Table 3.
3.2 Electronic properties
(1) Band structure
Figure 3 shows the variation of the band structure with the implementation of the Hubbard correction in different phases. The band structure of the rhombohedral phase (Fig. 3b), at U = 0 eV, shows a small and finite bandgap, much less than the experimental values of 2.2–2.8 eV. With the introduction of the Hubbard potential, there is a displacement of the band structures to a deeper energy level. At U = 3 eV, both the valence and conduction bands are pushed to deeper levels giving a greater bandgap. When U = 5 eV is employed, we see a minor change in the band structure in the valence band, while the bands are reasonably pushed further into the conduction bands. There is a slight increase in the bandgap than the previous calculation of U = 3 eV.
With the α–β-phase transition, the orthorhombic phase (Fig. 3c) involves a bandgap, indicating that the transition from the rhombohedral phase to the orthorhombic phase is not a metal–insulator transition, but rather a first-order transition that leads to an emergence of the inversion centre in the structure, which neutralizes any spontaneous polarization. The band structure (Fig. 3c) shows a gradual increase in the bandgap with an increase in the Hubbard correction.
The cubic phase (Fig. 3a), which results from the β–Г transition, shows metallic behaviour confirming that the orthorhombic–cubic transition is a metal–insulator (MI) transition rather than a Mott insulator transition. The MI transition is a second-order transition due to semi-metal band overlap in the cubic phase, mainly due to its structure rather than a high-spin–low-spin transition [15]. Owing to its "metallic" nature, the variation in the Hubbard parameter does not affect the band structure; hence, there is an overlap of the valence and conduction bands for all values of U.
The tetragonal phase (Fig. 3d), which was wrongly assumed to be the β-phase, shows a similar bandgap as the orthorhombic phase of about 1 eV without the correction, while, with the introduction of the Hubbard parameter, the valence and the conduction bands are pushed to inner levels, thereby giving a higher bandgap.
Since it is well known that the band structure calculations are not the strong points of PBE exchange correlations, especially with Fe ions [48], the bandgap was also calculated using the hybrid potentials. The bandgaps determined through the hybrid potential (HSE, Heyd–Scuseria–Ernzerhof) are presented in Table 4. It should be noted that the bandgap values calculated from hybrid potentials match well with that of the literature (wherever available) but are a definite overestimate of the actual value.
(2) Density of states
Deeper insights into the electronic properties can be achieved through the density of states studies (Figs. 4, 5, 6, 7). The density of states (DOS) of the cubic phase (Fig. 4) confirms the band overlap between the conduction and valence levels. The states corresponding to the Bi 6s lone pair can be seen at − 12 eV (below the Fermi level) for U = 0 eV.
Nevertheless, spontaneous polarization is lost due to cubic lattice symmetry, making it paraelectric. With the introduction of the U values, we see that the Fe levels are pushed to deeper energies into the valence band. These "pushed" states aggregate approximately 8–10 eV below the Fermi level. Even though it appears that a virtual bandgap might have been created by the pushed Fe states, it must be noted that at all values of U, there remains a band overlap of either the Bi or O states from the valence to the conduction band, making it "metallic" in nature. These findings support the prediction that the orthorhombic–cubic transition corresponds to the metal–insulator transition. The difference in the spin-up and spin-down states suggests the presence of ferromagnetic nature, but keeping in mind at the temperature of synthesis, it may be difficult to sustain the ferromagnetic nature. However, there is the literature that suggests the cubic distortion into the rhombohedral phase through Ba doping can enhance ferromagnetism [49].
A small but finite bandgap exists in the orthorhombic phase (Fig. 6) when Hubbard parameter is not involved. With U = 3 eV, there is a minimal change in the DOS, but with the introduction of U = 5 eV, we see the aggregation of the pushed Fe states deeper into the valence band. It should also be noted that with the increasing U values, there is a reduction in Fe–O hybridization and an increase in Bi–O hybridization in both the valence and conduction bands. We hypothesize that this phase could have lower leakage current than the rhombohedral phase, which can aid specific material properties like the piezoelectric effect due to the variation in hybridization. Reports suggest orthogonal distortion into the rhombohedral phase or at the morphotropic phase boundary between the rhombohedral and orthorhombic phases; the material exhibits better piezoelectric, magnetic, and dielectric properties [23, 25, 50].
In the U = 0 eV plot for the rhombohedral phase (Fig. 5), the flatness of the valence band edge paves the way for equal probability for both the direct and indirect band transition [45, 51, 52]. The Bi 6s lone pair states observed approximately 10 eV below the Fermi level are the source of ferroelectricity in the rhombohedral phase. There is considerable hybridization between the Fe–O, both below and above the Fermi level. The iron states are pushed further into the valence band with the gradual increase in the Hubbard parameter. It should be noted that a hybridization exists between Fe–O about 0.5–0.6 eV above the conduction band edge due to the charge transfer excitation [20, 53]. This can be seen from the figure where there is an overlap between the Fe d and O p states at above 0.5 eV from the Fermi level (here, the Fermi level is closer to the conduction band edge).
The tetragonal phase (Fig. 7), which was initially believed to be the β-phase, has a relatively smaller bandgap at U = 0 eV than the orthorhombic phase. With increasing the Hubbard parameter, we see that the iron states move deeper into the valence band; hence, a small but definite bandgap would come into existence. Hybrid potential calculations confirmed that the tetragonal phase was not metallic. A more important observation would be that the lone pair Bi 6s states exist at approximately 10 eV from the Fermi level, similar to the rhombohedral phase. The non-centrosymmetric structure proves to be an advantage; hence, it retains the Bi 6s lone pair states as a source of ferroelectricity. With the introduction of the U values, we realize that there is a gradual reduction in the hybridization between the Fe–O states near the valence band. This reduced hybridization hints at a relatively lower leakage current when charge imbalance does occur (due to oxygen vacancies) than in the rhombohedral phase. Hence, the DOS suggests that this phase should show relatively better spontaneous polarization than the rhombohedral phase, providing the possible reasoning for the literature wherein greater spontaneous polarization is reported for the tetragonal phase than the rhombohedral phase [43, 44].
(3) Validating the use of the Hubbard parameter
The Hubbard correction is computationally lighter and an efficient alternative to HSE pseudopotentials and a large basis set if accuracy in the electronic properties is sought. However, the widespread practice of trying to match the experimental bandgap to fix the Hubbard correction can adversely affect the properties which are dependent on the band edges such as the charge carrier effective mass, optical absorption energies, and oxidation energies [31]. Hence, an automated code that correctly predicts the Hubbard parameter significantly reduces both time and effort, which can be invested elsewhere. One of the in-built codes of Quantum ESPRESSO does just that. The creators of the code have systematically discussed the formulation and working of the code in [27] and hence is not discussed here. The predicted values are presented in Table 5.
It should be noted that these values correspond to the input conditions; hence, the values are not universal. If the lattice contains antiferromagnetic Fe atoms, then the predicted Hubbard parameter remains the same except for the opposite spins for the Fe atoms with opposite magnetization. The values help us realize that for the structure and the input conditions chosen, the values of U up to and around 5 eV for the polymorphs are acceptable.
3.3 Elastic tensor
Elasticity is a material property that is mainly dependent on the arrangement and the strength of the bond between atoms. It should be noted that with the increase in symmetry of the lattice, the number of components required to define the tensor is reduced, cubic requires three, rhombohedral requires six (or seven), tetragonal requires six (or seven) and orthorhombic requires nine independent components. Experimentally, the elastic constants depend on the temperature, pressure (in the case of minerals) and the chemical components present. It should be noted that the elastic tensor calculated can vary with changes in the atomic positions; hence, the calculated elastic tensor depends on the position of the atoms, as reported in supporting information file.
Poisson's ratio of the tetragonal phase is negative, indicating a compressively deformed structure (supposedly obtained when the rhombohedral phase is compressed [54]). The calculated elastic tensors are given as follows:
The Zener anisotropy factor (A) gives the measure of microcracks and the degree of anisotropy in the cubic systems. It is given by the formula
where c11, c12, and c44 are the elements in the elastic tensor.
We can see that A > 1 and hence the cubic phase is elastically anisotropic. The elastic properties of the materials are listed in Table 6.
3.4 Raman study
The identification of different phases can be tedious as the X-ray diffraction plots of orthorhombic and tetragonal phases are very similar; hence, an analytical tool that is simple but robust to identify different phases would be the Raman study. It must be noted that the data of the rhombohedral phase are verified with the experimental results, while for other phases, it is reported as calculated, as there is a lack of experimental data available at the time of the work. The calculated phonon modes for each phase are viewed in supplementary file.
IR transitions are allowed if and only if the vibration symmetry is identical to the symmetry of x, y, and z of the respective point group of the molecule. Similarly, the selection rule for the Raman transition is that the vibration symmetry is similar to the symmetry of x2, y2 and the products of x, y, and z in the molecule's point group.
The analysis of the rhombohedral phase is as follows (supplementary file): The zone-centre optical phonon modes of R3c bismuth ferrite can be classified as 4A1 ⊕ 5A2 ⊕ 9E. The A1 modes are polarized along the z-axis, whereas the E modes are doubly degenerate along the x- and y-axes. The E and A1 modes are Raman and IR active, while the A2 modes are completely silent. The A2 modes were obtained at 109.4, 300.3, 309.0, 436.6, and 680.6 cm−1. The calculated modes match well with that of the one found in the literature [55]. The contribution of Bismuth towards these frequency modes can be up to the initial A1 mode of 145.9 cm−1, while oxygen contributes to modes higher than 252.4 cm−1 and the significant contribution of iron comes between 145 and 252 cm−1. This can be analytically supported by the fact that in IR modes, the main factor for the vibration depends on the reduced mass of the molecule; hence, Bi vibrates at lower frequencies, O vibrates at higher frequencies and iron vibrates at the intermediate frequency between the two ranges.
In the cubic form (supplementary file), the octahedron, when it vibrates in the T2u mode, is both Raman and IR inactive as it does not correspond to any of the symmetry of the lattice. The T1u mode has symmetry along (x, y, z) and hence is only IR active, not Raman active. In the tetragonal phase (supplementary file), the modes which correspond to A1 and E are both IR and Raman active, while the B1 mode (B1g mode) is only Raman active.
In the orthorhombic phase (supplementary file), the mutual exclusion principle holds due to the presence of the centre of symmetry, where a particular mode is either Raman active or IR active and not both simultaneously. All the u-modes except Au mode are IR active, while the g-modes are Raman active. The table reports a few modes of IR and Raman activity. The silent Au modes are seen at 118.8, 227.9, 243.7, 310.4, and 401.7 cm−1.
3.5 Magnetic moment
The magnetic moment of the iron atoms calculated for different phases are listed in Table 7. There was minimal magnetization of the O atoms due to Fe–O hybridization. The literature values are also reported for comparison in Table 8. The general trend in the magnetic moment is that it increases with the increase in the Hubbard correction values for all phases.
4 Conclusion
The complete structural, electronic, and mechanical properties of the polymorphs of bismuth ferrite, namely rhombohedral, orthorhombic, tetragonal, and cubic are reported. The simple PBE + U formalism was used and extensively validated by the implementation of linear response theory. The energy versus cell volume plot and formation energy calculation provide necessary and sufficient evidence to show that the ground phase is rhombohedral, and undergoes a volume contraction to become orthorhombic, confirming the α–β-phase transition. The electronic properties reveal that there is a considerable Fe–O hybridization in the rhombohedral phase which could aid the charge transfer excitations and leakage current. The lone pair electron states of the bismuth are the source of ferroelectricity in bismuth ferrite; hence, any disturbance to these states can also lead to loss of ferroelectric properties. We also see that tetragonal and orthorhombic phases can be possible alternatives to the rhombohedral phase in such applications. The cubic phases show metallic behaviour even with the implementation of Hubbard correction, confirming that the β–γ-phase transition is a metal–insulator transition. The investigation into the mechanical properties led to the calculation of elastic tensor and the calculation of elastic properties. In general, the Poisson's ratio is the relative increase in the lateral width concerning the increase in the axial length, which is dimensionless; the negative Poisson's ratio of the tetragonal phase can be correlated with the compressed nature of the lattice. The rhombohedral phase corresponds to the distortion of the two cubic lattices, due to which further increase in the lateral width might be smaller compared to the cubic and the orthorhombic phase. This could be the reason for the rhombohedral phase possessing a relatively smaller Poisson's ratio. Our work makes an effort to bridge the void present in the case of the experimentally available phases of bismuth ferrite, which can be essential for future works as potential applications are seen in multiple fields.
5 Supporting information
The atomic position represented with the Wyckoff positions is viewed in supporting information file.
Data availability statement
This manuscript has associated data in a data repository. [Authors’ comment: The data that support the findings of this study are available from the corresponding author [KKN] upon reasonable request.]
References
M. Fiebig, J. Phys. D. Appl. Phys. 38, R123 (2005)
G. Catalan, J.F. Scott, Adv. Mater. 21, 2463 (2009)
P. Fischer, M. Polomska, I. Sosnowska, M. Szymanski, J. Phys. C Solid State Phys. 13, 1931 (1980)
J.T. Heron, D.G. Schlom, R. Ramesh, Appl. Phys. Rev. 1, 021303 (2014)
C.S. Tu, Y.S. Jou, P.Y. Chen, C.S. Chen, Y.C. Hsu, K.C. Feng, R.R. Chien, V.H. Schmidt, S.C. Haw, A.C.S. Appl, Electron. Mater. 2, 3773 (2020)
X. Liu, J. Zhai, B. Shen, J. Mater. Chem. C 7, 5122 (2019)
M.R. Stan, M. Kabir, J. Lu, S. Wolf, in ISCAS 2012—2012 IEEE International Symposium on Circuits and Systems (2012), pp. 2525–2528
Y.V. Shaldin, S. Matyjasik, A.A. Bush, Crystallogr. Rep. 52, 123 (2007)
L.W. Martin, Y.H. Chu, R. Ramesh, Mater. Sci. Eng R Rep. 68, 89 (2010)
F. Kubel, H. Schmid, Acta Crystallogr. Sect. B Struct. Sci. 46, 698 (1990)
J. Wang, J.B. Neaton, H. Zheng, V. Nagarajan, S.B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D.G. Schlom, U.V. Waghmare, N.A. Spaldin, K.M. Rabe, M. Wuttig, R. Ramesh, Science (80-) 299, 1719 (2003)
P. Ravindran, R. Vidya, A. Kjekshus, H. Fjellvåg, O. Eriksson, Phys. Rev. B Condens. Matter Mater. Phys. 74, 224412 (2006)
B.F. Grosso, N.A. Spaldin, Phys. Rev. Mater. 5, 054403 (2021)
O. Diéguez, O.E. González-Vázquez, J.C. Wojdeł, J. Íñiguez, Phys. Rev. B Condens. Matter Mater. Phys. 83, 1 (2011)
S.A.T. Redfern, J.N. Walsh, S.M. Clark, G. Catalan, J.F. Scott (2009). https://doi.org/10.48550/arXiv.0901.3748
R. Palai, R.S. Katiyar, H. Schmid, P. Tissot, S.J. Clark, J. Robertson, S.A.T. Redfern, G. Catalan, J.F. Scott, Phys. Rev. B Condens. Matter Mater. Phys. 77, 1 (2008)
D.V. Karpinsky, E.A. Eliseev, F. Xue, M.V. Silibin, A. Franz, M.D. Glinchuk, I.O. Troyanchuk, S.A. Gavrilov, V. Gopalan, L.Q. Chen, A.N. Morozovska, Npj Comput. Mater. 3, 1 (2017)
A. Castro, M.A. Martins, L.P. Ferreira, M. Godinho, P.M. Vilarinho, P. Ferreira, J. Mater. Chem. C 7, 7788 (2019)
M.A. Fraga, H. Furlan, R.S. Pessoa, M. Massi, Microsyst. Technol. 20, 9 (2014)
T.D. Rao, T. Karthik, S. Asthana, J. Rare Earths 31, 370 (2013)
P.P. Biswas, S. Pal, V. Subramanian, P. Murugavel, Appl. Phys. Lett. 114, 173901 (2019)
G.A. Rossetti, A.G. Khachaturyan, G. Akcay, Y. Ni, J. Appl. Phys. 103, 114113 (2008)
Y. Heo, J.H. Lee, L. Xie, X. Pan, C.H. Yang, J. Seidel, NPG Asia Mater. 8, 1 (2016)
M.J. Han, Y.J. Wang, D.S. Ma, Y.L. Zhu, Y.L. Tang, Y. Liu, N.B. Zhang, J.Y. Ma, X.L. Ma, Acta Mater. 145, 220 (2018)
P. Kumar, C. Panda, M. Kar, Smart Mater. Struct. 24, 1 (2015)
D. Karpinsky, I. Troyanchuk, M. Silibin, S. Gavrilov, A. Roshchina, in Proceedings of 2017 IEEE Russian Young Researchers in Electrical and Electronic Engineering Conference ElConRus 2017, 1160 (2017)
I. Timrov, N. Marzari, M. Cococcioni, Phys. Rev. B 98, 085127 (2018)
C. Loschen, J. Carrasco, K.M. Neyman, F. Illas, Phys. Rev. B 75, 035115 (2007)
S.M. Griffin, N.A. Spaldin (2014). https://doi.org/10.48550/arXiv.1401.2277
B. Sun, P. Zhang, X.-G. Zhao, J. Chem. Phys. 128, 084705 (2008)
J.K. Shenton (2018). https://discovery.ucl.ac.uk/id/eprint/10057684/
D.C. Arnold, K.S. Knight, F.D. Morrison, P. Lightfoot, Phys. Rev. Lett. 102, 1 (2009)
H.D. Megaw, C.N.W. Darlington, Acta Crystallogr. Sect. A 31, 161 (1975)
I.A. Kornev, S. Lisenkov, R. Haumont, B. Dkhil, L. Bellaiche, Phys. Rev. Lett. 99, 227602 (2007)
R. Haumont, I.A. Kornev, S. Lisenkov, L. Bellaiche, J. Kreisel, B. Dkhil, Phys. Rev. B Condens. Matter Mater. Phys. 78, 1 (2008)
S.R. Burns, O. Paull, R. Bulanadi, C. Lau, D. Sando, J.M. Gregg, N. Valanoor, Phys. Rev. Mater. 5, 1 (2021)
P.S.S.R. Krishnan, J.A. Aguiar, Q.M. Ramasse, D.M. Kepaptsoglou, W.I. Liang, Y.H. Chu, N.D. Browning, P. Munroe, V. Nagarajan, J. Mater. Chem. C 3, 1835 (2015)
D. Ricinschi, K.Y. Yun, M. Okuyama, J. Phys. Condens. Matter 18, L97 (2006)
C. Ederer, N.A. Spaldin, Phys. Rev. B Condens. Matter Mater. Phys. 71, 1 (2005)
Y. Wang, J.E. Saal, P. Wu, J. Wang, S. Shang, Z.K. Liu, L.Q. Chen, Acta Mater. 59, 4229 (2011)
J. Kaczkowski, M. Pugaczowa-Michalska, A. Jezierski, Acta Phys. Pol., A 127, 266–268 (2015)
J.B. Neaton, C. Ederer, U.V. Waghmare, N.A. Spaldin, K.M. Rabe, Phys. Rev. B Condens. Matter Mater. Phys. 71, 1 (2005)
J. Kaczkowski, M. Pugaczowa-Michalska, I. Płowaś-Korus, Phys. Chem. Chem. Phys. 23, 8571 (2021)
E. Sagar, R. Mahesh, N. Pavan Kumar, P. Venugopal Reddy, J. Phys. Chem. Solids 110, 316 (2017)
S. Yang, G. Ma, L. Xu, C. Deng, X. Wang, RSC Adv. 9, 29238 (2019)
L. You, F. Zheng, L. Fang, Y. Zhou, L.Z. Tan, Z. Zhang, G. Ma, D. Schmidt, A. Rusydi, L. Wang, L. Chang, A.M. Rappe, J. Wang, Sci. Adv. 4, 1 (2018)
S.R. Basu, L.W. Martin, Y.H. Chu, M. Gajek, R. Ramesh, R.C. Rai, X. Xu, J.L. Musfeldt, Appl. Phys. Lett. 92, 091905 (2008)
Y. Meng, X.W. Liu, C.F. Huo, W.P. Guo, D.B. Cao, Q. Peng, A. Dearden, X. Gonze, Y. Yang, J. Wang, H. Jiao, Y. Li, X.D. Wen, J. Chem. Theory Comput. 12, 5132 (2016)
A.R. Makhdoom, S.M. Shah, T. Mahmood, M.J. Iqbal, M.J. Akhtar, M.A. Rafiq, J. Magn. Magn. Mater. 484, 286 (2019)
Y.Y. Liu, L. Yang, J.Y. Li, J. Appl. Phys. 113, 183524 (2013)
S.J. Clark, J. Robertson, Appl. Phys. Lett. 90, 132903 (2007)
A.R. Venkateswarlu, G.D. Varma, R. Nath, AIP Adv. 1, 042140 (2011)
S.R. Basu, L.W. Martin, Y.H. Chu, M. Gajek, R. Ramesh, R.C. Rai, X. Xu, J.L. Musfeldt, Appl. Phys. Lett. 92, 10 (2008)
A.J. Hatt, N.A. Spaldin, C. Ederer, Phys. Rev. B Condens. Matter Mater. Phys. 81, 054109 (2010)
P. Hermet, M. Goffinet, J. Kreisel, P. Ghosez, Phys. Rev. B Condens. Matter Mater. Phys. 75, 3 (2007)
I. Sosnowska, W. Schäfer, W. Kockelmann, K.H. Andersen, I.O. Troyanchuk, Appl. Phys. A Mater. Sci. Process. 74, 1040 (2002)
D.P. Kozlenko, A.A. Belik, A.V. Belushkin, E.V. Lukin, W.G. Marshall, B.N. Savenko, E. Takayama-Muromachi, Phys. Rev. B Condens. Matter Mater. Phys. 84, 1 (2011)
Acknowledgements
Srihari N.V. would like to acknowledge the financial support provided by Manipal Academy of Higher Education (MAHE), Manipal, India, through Dr. T.M.A. Pai PhD scholarship programme. Srihari N.V. would also like to acknowledge the support from Mr. Srinidhi N V. for providing the computational facility. The authors thank Andrea Dal Corso for resolving the multiple queries regarding Thermo_pw codes (https://dalcorso.github.io/thermo_pw/).
Funding
Open access funding provided by Manipal Academy of Higher Education, Manipal.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing financial interest.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Srihari, N.V., Nayak, S., Poornesh, P. et al. Variation in the electronic, mechanical, and structural properties among the polymorphs of bismuth ferrite: a first-principles approach. Eur. Phys. J. Plus 138, 465 (2023). https://doi.org/10.1140/epjp/s13360-023-04102-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-023-04102-1