1 Introduction

The presence of Dark Matter (DM) is one of the most plausible explanations for several astrophysical observations [1,2,3,4,5,6]. Results reported by the Planck mission [7] indicate that DM represents around 27% of the observed universe’s mass, according to the \(\varLambda\)CDM model.

One of the possible candidates of DM particles is Weakly Interacting Massive Particles (WIMPs), hypothetical particles assumed to be weakly interacting with the baryonic matter. Consequently, the detection of such particles at particle colliders is inferred by measuring the momentum imbalance in an event, as DM particles can cross a detector material without significant interactions.

At the LHC, searches for the possible production of DM particles are performed using events containing a visible particle which acts as a candle and large missing transverse momentum \((p\!\!\!/_{\textrm{T}})\). This visible particle could originate from initial or final state radiation (i.e., photon or gluon) or could be a W or Z gauge bosons. This topology is known in the literature as Mono-X strategy, where X acts as a visible particle that recoils against the dark sector particles. This idea has been used in searches for DM candidates produced alongside the Standard Model (SM) particles at the LHC, as Mono-(W/Z/jets) which were studied in [8, 9], Mono-\(\gamma\) and Mono-Higgs results were reported in [10] and [11], respectively. The same methodology has been extended to include searches for DM alongside new hypothetical, Beyond the Standard Model (BSM), particles [12], such as Mono-\({Z}^{\prime }\) in our present study [13, 14]. Such new heavy neutral \({Z}^{\prime }\) bosons are predicted in some theoretical extensions of the SM [15].

The results presented in this paper are complementary to those from the ATLAS collaboration performed at 13 TeV center-of-mass energy that was reported in [16]. They studied two simplified scenarios of the Mono-\({Z}^{\prime }\) model considering the hadronic decay of \({Z}^{\prime }\), while in our present work, we study the Effective Field Theory (EFT) formalism of the Mono-\({Z}^{\prime }\) model in addition to the simplified scenario considering the muonic decay of \({Z}^{\prime }\).

In the present work, we used the CMS open data and the corresponding Monte Carlo (MC) samples provided by the CMS open data project [17]. They correspond to LHC proton–proton (pp) collision at center-of-mass energy of 8 TeV and a total integrated luminosity of 11.6 \(\hbox {fb}^{-1}\). The status, performance and opportunities for the use of the open CMS data were reported in [18, 19].

In the next section, we introduce the theoretical model; in Sect. 3, we describe the CMS detector and the reconstruction techniques. The data samples are introduced in Sect. 4, including the MC simulation of the model signals, the MC simulation of the SM backgrounds and the CMS data sample. The method for the estimation of the contribution of each of the SM background channels is introduced in Sect. 5. The search strategy and the selection criteria are discussed in Sect. 6, followed by the estimation of systematic uncertainties in Sect. 7, and finally, the results including the statistical interpretation and the exclusion limits are introduced in Sect. 8.

2 The Mono-\({Z}^{\prime }\) model

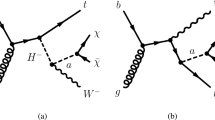
The model introduced in [13] assumes the production of DM candidate particles alongside a new \({Z}^{\prime }\) boson. We consider two scenarios: (i) dark-Higgsstrahlung from a Z’, with the dark Higgs decaying invisibly (dark Higgs, DH, scenario); (ii) the effective coupling between the SM and the DM fields. The Feynman diagrams for the mentioned processes are given in Fig. 1.

In the DH scenario, \({Z}^{\prime }\) is produced through \(q{\bar{q}}\) annihilation process in pp collisions; then, \({Z}^{\prime }\) radiates a dark sector Higgs (\(h_{\textrm{D}}\)) that decays into a pair of final state DM particles (\(\chi {\bar{\chi }}\)). The assumption used for setting masses for \({Z}^{\prime }\) and \(h_{\textrm{D}}\) is illustrated in Eq. (1):

$$\begin{aligned} M_{Z^{\prime }} = M_{h_{\textrm{D}}}, ~(\text {for} ~ M_{h_{\textrm{D}}} > 125~\text {GeV}). \end{aligned}$$
(1)

This mass assumption is know as “heavy dark sector” [13]. The free parameters of this simplified model are: the mass of the mediator \(Z^{\prime }\) boson, the mass of the \(M_{h_{\textrm{D}}}\), the coupling between the mediator and the SM fields (particularly quarks) \({g}_{\textrm{SM}}\), in addition to the coupling between the mediator and the DM field \({g}_{\textrm{DM}}\).

Fig. 1
figure 1

Feynman diagrams of the two scenarios assumed: a dark higgs, b light vector with inelastic effective field theory coupling

Full size image

The second scenario, which is known as the EFT scenario, reduces the interactions between the DM particles and the SM fields down to contact interaction as given in the following interaction term [13],

$$\begin{aligned} \frac{1}{2\varLambda ^{2}}{\bar{q}}\gamma ^{\mu }q({\bar{\chi }}_{2}\gamma ^{\mu }\gamma ^{5}\chi _{1}~+~{\bar{\chi }}_{1}\gamma ^{\mu }\gamma ^{5}\chi _{2}). \end{aligned}$$

In this scenario, the interaction between the SM fields and the DM fields is introduced by means of the effective coupling between them. The mediator is assumed to be very heavy (at the TeV scale), hence the interaction approaches a contact interaction. There are two assumed dark states (\(\chi _{1}\) and \(\chi _{2}\)), where \(\chi _{2}\) is heavy compared to the mass of \({Z}^{\prime }\), and the splitting between the two dark states is enough so that \(\chi _{2}\) can decay into \(\chi _{1} + Z^{\prime }\), and \(\chi _{1}\) is a final state stable dark fermion. The sets of masses for this scenario are given in Eq. (2) which has been introduced in [13].

$$\begin{aligned} M_{\chi _{2}} = M_{\chi _{1}} + M_{Z^{\prime }} + 25~\text {GeV},~ M_{\chi _{1}} = 5~\text {GeV}. \end{aligned}$$
(2)

The signature of the Mono-\({Z}^{\prime }\) process is dilepton or dijet, as products of the \({Z}^{\prime }\) decay, in addition to a missing transverse momentum that belongs to the DM candidates. The events analyzed in this work have the signature \(\mu ^{+}\mu ^{-} +p\!\!\!/_{\textrm{T}}\).

3 The CMS detector and reconstruction techniques

The Compact Muon Solenoid (CMS) is a general-purpose particle detector located at one of the four collision points of the LHC. A description of the detector and its performance with details can be found in [20]. The CMS can be divided into five main layers. The first layer surrounding the beam pipe is the tracker. The following layers, the electromagnetic and hadron calorimeters, play an essential role for the reconstruction of the missing transverse momentum, which is the signature of neutrinos or other exotic weakly interacting particles, e.g., DM candidates in our case. The superconducting solenoid is the \({4}\textrm{th}\) layer between the hadron calorimeter and the muon system. The last layer that envelopes the detector is the muon system, which covers the pseudorapidity range \(|\eta | < 2.4\).

We are interested in events containing dimuon and missing transverse momentum. The identification and reconstruction of muons described in [21], and the reconstruction of the missing transverse momentum \(p\!\!\!/_{\textrm{T}}\) described in [22]. Certain correctionsFootnote 1 must be applied while reconstructing the \(p\!\!\!/_{\textrm{T}}\), in order to improve data to MC agreement for all distributions related to missing transverse momentum as mentioned in [22], as the negative sum of the momenta of the particle flow (PF) objects. These corrections account for: inefficiencies in the tracker, the \(p_{\textrm{T}}\) threshold and the energy threshold in the tracker and calorimeters, respectively, and the nonlinear response of the calorimeters for hadrons [22]. The formula, that is used to calculate the \(p\!\!\!/_{\textrm{T}}\) after applying the mentioned corrections, is given in Eq. (3).

$$\begin{aligned} \vec {p\!\!\!/}_{\textrm{T}}^{~\text {corr}} = \vec {p\!\!\!/}_{\textrm{T}} - \sum _{\textrm{jets}} (\vec {p}_{\mathrm{T~jet}}^{~\text {corr}} - \vec {p}_{\mathrm{T ~jet}}), \end{aligned}$$
(3)

where \(\vec {p\!\!\!/}_{\textrm{T}}^{~\text {corr}}\) and \(\vec {p}_{\mathrm{T~jet}}^{~\text {corr}}\) refer to the corrected values considering the inefficiencies mentioned above. The equation indicates that the difference between the PF jet \(\vec {p}_{\textrm{T}}\) after and before applying the correction, must be subtracted from the reconstructed \(\vec {p\!\!\!/}_{\textrm{T}}\) in order to make correct balancing.

4 Data and Monte Carlo samples

4.1 The samples of the model signals

The simulated signal event samples for DH and EFT scenarios were produced privately using the matrix element event generator MadGraph5_aMC@NLO v2.6.7 [26]. The generation process and the calculation of the signal cross section are done at next-to-leading order (NLO), based on the Universal FeynRules Output UFO provided by the authorsFootnote 2 of [13]. This generator is interfaced with PYTHIA v.6.4.26 for the modeling of the parton showers [27]. The NNPDF2.3QED NLO set, which is available via the LHAPDF6 library [28], is used for the parton distribution functions (PDF) [29]. The full simulation for the CMS detector, The High Level Trigger (HLT) menu used for 2012 run-I data and the reconstruction process have been implemented within the standard CMSSW framework: the simulation of the detector response to the particles is performed with GEANT4 [30], the step of HLT and the reconstruction processes was done with the release CMSSW_5_3_32 [25], which is the relevant version for 2012 the CMS open data. The effect of pile-up was simulated by overlaying MC generated minimum bias events [31]. The selection process is performed accounting for the requirements of the experimental set up of the CMS detector during the LHC run-I at \(\sqrt{s}=8\) TeV, and these requirements will be introduced and discussed in the preselection of events at Sect. 6.

For the DH scenario, the Mono-\({Z}^{\prime }\) samples were generated with mediator masses between 150 and 700 GeV (higher values of the mediator have not been studied due to the dramatic drop in their cross section measurements, consequently the statistical analysis could not be done properly), with the \(g_{\textrm{DM}}\) coupling value set to \(g_{\textrm{DM}}\) = 1 [13, 16]. Following the experimental constraints from dijet resonance searches by CMS collaboration at the LHC with 8 TeV center of mass energy [32], and from [13] in particular those for the mediator mass range below about 500 GeV studied in this analysis, the \(g_{\textrm{SM}}\) coupling value was set to 0.25. The cross section measurements multiplied by the \(Z^{\prime } \rightarrow \mu ^{+}\mu ^{-} +p\!\!\!/_{\textrm{T}}\) branching ratios for the DH scenario are listed in Table 1, for two choices of the coupling \((g_{\textrm{SM}})\) 0.1 and 0.25. They vary with the change of both of the mediator and dark higgs masses and do not depend on the choice of dark matter mass. The cross section times branching ratio decreases by factor 10 for \(g_{\textrm{SM}}\) = 0.1. Hence, this analysis does not have sensitivity to it.

Table 1 Cross section measurements times branching ratios in pb, for the DH scenario, calculated at different values of the mass of \(M_{Z'}\), assuming the heavy dark sector set of masses with the DM mass \((M_{\chi })\) = 5 GeV at 8 TeV center of mass energy, and the coupling constant (\(g_{\textrm{DM}}\)) is taken to be 1.0. The values are illustrated for two choices of the coupling (\(g_{\textrm{SM}}\)) 0.1 and 0.25
Full size table

For the EFT, the cutoff scale (\(\varLambda\)) is the main parameter of the model. The EFT production cross section measurements times branching ratios as a function of \(\varLambda\), for a fixed mass point of \({Z}^{\prime }\) (\(M_{Z^{\prime }}\) = 450 GeV) and center of mass energy \(\sqrt{s} = 8\) TeV, are listed in Table 2.

Table 2 EFT production cross section measurements times branching ratios as a function of the scenario cutoff scale of the EFT(\(\varLambda\)), for a fixed mass point of \({Z}^{\prime }\) (\(M_{Z^{\prime }}\) = 450 GeV) and center of mass energy \(\sqrt{s} = 8\) TeV
Full size table

The decay widths for each of the \({Z}^{\prime }\) and the \(h_{\textrm{D}}\) for the DH scenario, or \({Z}^{\prime }\) and \(\chi _{2}\) for the EFT case, that increase with the particles’ masses, are calculated at each mass value within MadGraph5 [33]. For the \(Z^{\prime }\) resonance, the decay width ranges from 4.47 to 24.28 GeV over the scanned range of masses, i.e., between 150 and 700 GeV, with a width of 8.97 GeV at the used benchmark mass point for the EFT interpretation.

4.2 The SM backgrounds samples

The most significant SM backgrounds are: the top quark pairs production (\(t {\bar{t}}\)), the electroweak diboson production (WW, WZ, ZZ) and the Drell-Yan (DY) process. In the presented study, we have used the CMS open MC samples generated by the CMS collaboration to construct the SM backgrounds. These samples are available via the CERN open data portal [34]. The used samples are listed in Table 3. The process for the production of a single top quark alongside W boson is ignored in this analysis, basically because it is not included in the list of CMS open MC samples. The cross section measurements of the MC samples used in this analysis, at next-to-leading order (NLO) or next-to-next-to-leading order (NNLO), are indicated in Table 3. The cross section of the \(t{\bar{t}}\) process was calculated using the parton-level Monte Carlo program MCFM [35], and the rest of the samples’ cross sections was taken from [18]. The Drell-Yan and ZZ processes have been generated with POWHEGBox v1.0 MC program [36, 37] interfaced to Pythia v.6.4.26 parton shower model [27]. Other MC background samples (WW and WZ) were modeled with MadGraph5_aMC@NLO v5.1.3.30 [38] event generator interfaced to Pythia v.6.4.26. The CT10 parton distribution functions (PDFs) [39] and the Z2* PYTHIA6 tune [40, 41] have been used. Finally, the response of the CMS detector to the particles is simulated by GEANT4 [30].

Table 3 Monte Carlo samples used to build the SM backgrounds with the corresponding cross sections times the branching ratios, the dataset name for each sample, as appear on the open data portal, are also stated. These samples are generated for proton–proton collision at \(\sqrt{s}= 8\) TeV
Full size table

4.3 The CMS open data samples

The CMS open experimental data samples, used in this analysis, are based on pp collision at \(\sqrt{s}\) = 8 TeV during the LHC run-I and recorded by the CMS detector in 2012. We used the two open data runs (run-B and run-C) corresponding to a total integrated luminosity of 11.6 \(\hbox {fb}^{-1}\) [19]. The data were triggered by the high level trigger HLT_Mu40_eta2p1 which is a single muon trigger. This trigger was unprescaled for the full 2012 dataset and aim to collect events with at least one muon candidate within \(|\eta |<\) 2.1 and \(\text {p}_{\text {T}} > 40\) GeV. The efficiency of this trigger varies as a function of \(\eta\), resulting in an efficiency for triggering on a dimuon system that varies between 97% and 100% [47]. The events have been taken from the list of the validated runs (known as the good runs list), for the primary sets of 2012 data provided by the open data project [48], at which all the CMS sub-detectors were working stably. The samples, their dataset names and the corresponding integrated luminosity (\({\mathcal {L}}\)), are listed in Table 4.

Table 4 Used CMS-2012 open data samples collected by CMS experiment during the LHC run-I at 8 TeV center of mass energy and the corresponding integrated luminosity
Full size table

5 Backgrounds estimation

There are many background processes that include dimuons with missing transverse momentum in the final state and can mimic event topology in our search for new physics. The first type is the SM processes produced during pp collisions, the second is the jets contamination, and the third is the cosmic muons background.

The contribution of the SM background processes, that are considered in the present study, has been estimated from Monte Carlo simulation, following the same method as in Ref. [47]. The Monte Carlo samples of the SM backgrounds, which are listed in Table 3, are normalized to their corresponding cross sections. The jet background arises from the misidentification of jets as muons, where a jet passes the muons selection criteria. This background consists of two processes: W+jet and QCD multijet. The misidentification of single and multijet backgrounds in data is usually estimated from data using a data driven method which is explained in [47]. Above the Z peak, for the invariant mass of dimuon system \(M_{\mu \mu }>\) 120 GeV, the jets misidentification was found to be 150 events which represents about \(0.15\%\) of the total SM backgrounds (98,596 events) estimated in this region [47], which can have a very tiny effect on our results. For this reason, we neglect QCD and W+jets backgrounds estimated from data.

The last background source comes from cosmic muons that cross the detector layers and pass near the interaction point; this background can be suppressed by constraining the vertex position and the impact parameter associated with the reconstructed muon. A selection is applied such that the muon transverse impact parameter, with respect to the primary vertex, must be less than 0.2 cm. For cosmic muons that pass in-time with a collision event, and pass the vertex position and the impact parameter cuts, the angle between the reconstructed dimuons is restricted to be below \(\pi - 0.02\) rad. The mentioned cuts are applied in the identification of muons in the 2012-analysis [47, 51]. The cosmic muons contribution to our background found to be less than 0.1 events and can be also neglected [47].

6 Event selection

The aim of the selection is to pick out events containing dimuon in addition to missing transverse momentum. This selection is divided into two steps: the first one is the preselection which is presented in Table 5 (i), and the second step is the tight selection introduced in Table 5 (ii). The detailed definition of these cuts will be explained in this section.

6.1 Event preselection

The preselection is based on the high transverse momentum \((p_{\textrm{T}})\) muon identification (ID), which has been optimized for the response of CMS muon detector to muons with high transverse momentum. It is designed to reach the best reconstruction of the muon track parameters for high \(p_T\) muons (i.e., \(p_T > 200\) GeV) without relying on external information on the event. With this ID, the muon momentum resolution of the inner tracker has been improved, so that the muon identification efficiency is improved to be uniformly high as a function of muon p and \(p_T\). The high \(p_T\) muon ID [51] was applied in 2012 data analysis, used for the search for new physics with events containing dimuon resonance [47]. This preselection also includes cuts related to the trigger requirements (HLT_ Mu40_eta2p1). The \(p_T\) threshold of this trigger is 40 GeV within \(|\eta |<2.1\). Each event must have exactly two oppositely charged muons with \(p^{\mu }_{\textrm{T}} > 45\) GeV, \(|\eta ^{\mu }| < 2.1\) each, and one of these two muons should pass the single muon trigger previously mentioned. In addition, the invariant mass of the dimuon must be above 80 GeV, as we are looking for a resonance in the high mass regime. The preselection cuts are listed in Table 5(i).

The dimuon invariant mass distribution, after the application of the preselection, is shown in Fig. 2. The CMS data are represented by black dots with vertical bars (accounts for statistical error), the DY background is represented by the green histogram, the gray histogram represents the \(t {\bar{t}} + jet\) background, and the electroweak diboson backgrounds (WW, WZ and ZZ) are added together and represented by the blue histogram. Signals attributed to DH model, at different values of the mediator’s mass \(M_{Z^{\prime }}\), are overlaid. The lower band shows the ratio between the CMS data and the expected SM background, with an illustration of the total uncertainty related to the prediction of this background processes (which will be discussed in Sect. 7). In the rest of this paper, all figures follow the same plotting style and keys. Figure 3 shows the distribution of the missing transverse momentum \(p\!\!\!/^{\textrm{corr}}_{\textrm{T}}\), after the application of the preselection of events, the CMS data, the expected SM background. Examples of signal for the DH scenario at \(M_{Z^{\prime }} = 450\) GeV and the EFT scenario at \(M_{Z^{\prime }} = 450\) GeV and \(\varLambda = 2\) TeV are included.

Fig. 2
figure 2

Distribution of the dimuon invariant mass; after applying preselection of events (listed in Table 5), for the CMS data, the expected SM backgrounds and signal contributions for selected \({Z}^{\prime }\) masses in the DH model. The lower band shows the data-to-simulation ratio with an illustration of the total uncertainty in the estimation of the expected background (shaded region)

Full size image
Fig. 3
figure 3

The missing transverse momentum distibution is illustrated after the preselection (listed in Table 5), for the estimated SM background, the CMS open data and for a DH model signal produced at \(M_{Z^{\prime }} = 450\) GeV, and an EFT model signal produced at \(\varLambda = 2\) TeV. The data-to-simulation ratio with the total uncertainty in the estimated background (shaded region) is presented in the lower band of the figure. Signals distributions have been normalized to the product of the cross section times the muonic decay of \({Z^{\prime }} \) branching fraction

Full size image

Figures 2 and 3 show that the CMS data are in a good agreement with the Monte Carlo simulation of the expected SM processes within the total uncertainty. Moreover, the Mono-\({Z}^{\prime }\) model signals are totally submerged by the SM background. This problem has been successfully handled by applying extra cuts which will be discussed in the following subsection.

6.2 Event selection

The events selection is a combination between the preselection cuts introduced in Table 5(i) and extra tighter cuts, presented in Table 5(ii), based on four variables. The first variable is related to the dimuon invariant mass, which we restrict to a small range around the mass of the \({Z}^{\prime }\), such that \((0.9 \times M_{Z^{\prime }})< M_{\mu ^{+}\mu ^{-}} < (M_{Z^{\prime }} + 25)\). The aim of this cut is to suppress the Drell-Yan events. The second is the difference in the azimuthal angle between the dimuon and the missing transverse momentum vector (\(\varDelta \phi _{\mu ^{+}\mu ^{-},\vec {p\!\!\!/}_{\textrm{T}}^{\text {corr}}}\)), which is required to be greater than 2.6 rad. The third is the relative difference between the \(p_{\textrm{T}}\) of dimuon and the missing transverse momentum (\(|p_{\textrm{T}}^{\mu ^{+}\mu ^{-}} - p\!\!\!/_{\textrm{T}}^{\text {corr}}|/p_{\textrm{T}}^{\mu ^{+}\mu ^{-}}\)), it has been selected to be less than 0.6. Finally, a very tight cut on the value of \(p\!\!\!/_{\textrm{T}}^{\text {corr}}\) (i.e., \(p\!\!\!/_{\textrm{T}}^{\text {corr}}>\) 100 GeV) was applied in order to suppress DY, ZZ, W+jets and the QCD multijet contributions.

Table 5 Summary of the preselection cuts (i) and the cut-based final events selection (i + ii) applied in the analysis
Full size table

In Fig. 4, we have investigated the product of the signal acceptance (A) and total selection efficiency (\(\epsilon _{\textrm{total}}\)) for the dark Higgs simplified model after the full event selection as a function of the mediator mass (\(M_{Z^{\prime }}\)). This product is defined as the number of signal events satisfying the full set of selection criteria summarized in Table 5, divided by the total number of generated signal events. For mediator masses below \(M_{Z^{\prime }} = 300\) GeV, the cut on \(p\!\!\!/_{\textrm{T}}^{\text {corr}}\) in addition to the narrow mass window play the main role in the efficiency loss. While above 300 GeV, the cut which is based on narrow mass window is the main reason behind the seen loss in the efficiency.

Fig. 4
figure 4

Product of acceptance (A) and total efficiency (\(\epsilon _{\textrm{total}}\)), defined as the number of signal events passing the full set of selection criteria summarized in Table 5, divided by the total number of generated signal events, for the dark Higgs simplified model, shown in dependence on the mediator mass \(M_{Z^{\prime }}\)

Full size image

7 Systematic uncertainties

Several sources of theoretical and experimental systematic uncertainties are considered in this analysis and affect the results. We start with the experimental systematic uncertainties. The uncertainty related to the luminosity of the CMS-2012 data is estimated to be 2.6% [52]. The uncertainty that arises from the determination of the muon detector acceptance and from the muon reconstruction efficiency (\(A\times \epsilon\)) has been found to be 3% [47]. The transverse muon momentum resolution uncertainty was 5%, while the misalignment in the detector geometry has an impact of 5% on the transverse momentum scale uncertainty per TeV [47]. Regarding the systematic uncertainties on the measurements of missing transverse momentum \({p\!\!\!/}_{\textrm{T}}^{~\text {corr}}\), the uncertainty in the energy scale of low energy particles which is known as unclustered energy was found to be 10%, while 2–10% for jet energy scale and 6–15% for jet energy resolution [22]. Finally, the theoretical sources of the systematics are related to the uncertainties in the PDF choice. For the Drell-Yan cross section calculation, this uncertainty can be represented as a function of the dimuon invariant mass as \((2.67+3.03\times 10^{-3}M_{\mu ^{+}\mu ^{-}}+2.38\times 10^{-6}M_{\mu ^{+}\mu ^{-}}^{2})\%\) (in GeV) [47], while PDF uncertainties for the WW and WZ processes were 5% and 6%, respectively [53]. The summary of these sources of uncertainties and the corresponding values are indicated in Table 6.

Table 6 Sources of systematic uncertainties considered in the presented analysis and their values in percentage
Full size table

8 Results

The assumed masses of DM particles are much heavier than the SM neutrinos, specially for the heavy dark sector set of masses applied in this analysis and introduced in Sect. 2. Consequently, the distribution of the missing transverse momentum attributed to any DM signal is expected to be characterized by longer tail than the corresponding distribution from the SM neutrinos, which could be a good discriminator between the two hypotheses. The \(p\!\!\!/^{\textrm{corr}}_{\textrm{T}}\) distribution, after applying the criteria of the events selection summarized in Table 5, for each of the CMS data, the SM background channels and the mono-\({Z}^{\prime }\) signals, is shown in Fig. 5. A significant reduction in the SM backgrounds is achieved by applying the cuts introduced in the events selection; moreover, the distribution shows that the CMS data are in a good agreement with the SM simulated processes within the total uncertainty. The two stray points in the \(p\!\!\!/^{\textrm{corr}}_{\textrm{T}}\) distribution (above 250 GeV) can be explained in terms of the statistical fluctuations. We have found that these events are in an agreement with the expected background within 1.43 \(\sigma\) significance.

The number of events passing the criteria of the events selection, for each of the CMS data, the SM background channels, a DH signal (with coupling constants \(g_{\textrm{DM}} = 1.0\) and \(g_{\textrm{SM}} = 0.25\)), is listed in Table 7 for several \(Z^{\prime }\) mass points, and integrated luminosity of 11.6 \(\hbox {fb}^{-1}\). The total uncertainty, including the statistical and systematic components, is also indicated, and this summation has been done using a quadrature formula. The contribution of DY background is negligible due to strong cut on the missing transverse momentum applied in this analysis (i.e., \(p\!\!\!/^{\textrm{corr}}_{\textrm{T}}>\) 100 GeV).

In view of the small statistics which we observe in each mass bin, after applying the final analysis selection, we performed a single bin fit for \(p\!\!\!/^{\textrm{corr}}_{\textrm{T}}>\) 100 GeV as explained in the following section.

Fig. 5
figure 5

Distribution of the missing transverse momentum, after applying the event selection (listed in Table 5); for the CMS data, the expected SM backgrounds, a DH model signal produced at \(M_{Z^{\prime }} = 450\) GeV, and an EFT model signal produced at \(\varLambda = 2\) TeV. The lower band shows the data-to-simulation ratio with an illustration of the total uncertainty in the estimation of the background (shaded region). Signals are normalized to the product of the cross section times the branching ratio of the muonic decay of \({Z}^{\prime }\)

Full size image
Table 7 A number of events satisfying the criteria of the events selection are illustrated for several \(Z^{\prime }\) mass points, for each SM background, the DH model signals and the CMS open data; corresponding to a 11.6 \(\hbox {fb}^{-1}\) integrated luminosity and the coupling constants \(g_{\textrm{DM}} = 1.0\), \(g_{\textrm{SM}} = 0.25\). The total Uncertainty, including the statistical and systematic components, is indicated
Full size table

8.1 Statistical interpretation

A statistical test based on a single-bin likelihood function description, with the use of the modified frequentist construction CLs [54, 55] used in the asymptotic approximation [56], has been employed for making statistical interpretation of the results, i.e., setting limits on the model. The SM background-only hypothesis has been tested against the Mono-\({Z}^{\prime }\) signal hypothesis. The signal hypothesis is excluded at a probability value equal to 0.05, corresponding to a significance of 2\(\sigma\); the p value could be defined as the probability that the incompatibility of the data with the SM background-only hypothesis is a manifestation of the systematic uncertainty. The confidence intervals (fluctuations about the median) are calculated within 1\(\sigma\) or 2\(\sigma\), corresponding to confidence levels of 68% or 95%, respectively.

8.2 Exclusion limits

The cross section times the branching ratio \(Br(Z' \rightarrow \mu \mu )\) limits for the simplified model (DH) is shown in Fig. 6, with the heavy dark sector set of masses, the muonic decay of the \({Z}^{\prime }\) and coupling values of \(g_{\textrm{SM}} = 0.25\) and \(g_{\textrm{DM}} = 1.0\). The red dotted line represents the dark Higgs model at a fixed dark matter mass (\(M_{\chi } = 5\) GeV).

The observed and expected upper limits at 95% CL on the DM production cross section normalized to the predicted cross section, as a function of the model cutoff (\(\varLambda\)), are shown in Fig. 7 for the EFT scenario with \(M_{Z^{\prime }} = 450\) GeV. The red horizontal dotted line represents the unity axis at which \(\sigma = \sigma _{th}\).

Considering the DH scenario, we exclude the production of \({Z}^{\prime }\) with masses below 357 GeV for the expected median and 367 GeV for the observed data. Since the cross section measurements multiplied by the \(Z^{\prime } \rightarrow \mu ^{+}\mu ^{-}\) branching ratios for the DH scenario, which are listed in Table 1, are varied only with the change of both of the mediator and dark higgs masses and do not depend on the choice of dark matter mass [13], so that the expected and observed limits on \(M_{Z^{\prime }}\) will not change with the change of the DM mass. For the EFT scenario, we also exclude the cutoff scale of the model below 2780 GeV for the expected median, and below 2890 GeV for the observed data. The introduced limits have been set at 95% CL.

Fig. 6
figure 6

95% CL upper limits on the cross section times the branching ratio (expected and observed), as a function of the mediator’s mass (\(M_{Z^{\prime }}\)), regarding the DH scenario, with the heavy dark sector set of masses and the muonic decay of the \({Z}^{\prime }\). The red dotted line represents the dark Higgs model at a fixed dark matter mass (\(M_{\chi } = 5\) GeV)

Full size image
Fig. 7
figure 7

95% CL upper limits on the signal strength (expected and observed), plotted against the cutoff scale of the EFT approach (\(\varLambda\)), at \(M_{Z'}= 450\) GeV. The red horizontal dotted line represents the case \(\sigma / \sigma _{\text {th}} = 1\)

Full size image

9 Summary

A study of the production of DM particles (WIMPs) at the LHC has been performed. The production of DM particles alongside a new heavy gauge boson (\(Z^{\prime }\)) has been studied based on the Mono-\(Z^{\prime }\) model. Two scenarios of the model were considered, which are: a simplified model so called the dark Higgs and the light vector with effective field theory coupling. The study has been performed for the muonic decay of the \(Z^{\prime }\) boson.

In this analysis, we used the CMS open experimental data samples collected by the CMS detector for the proton–proton collisions at a center of mass energy of 8 TeV in 2012 during Run-I of the LHC, which correspond to an integrated luminosity of 11.6 \(\hbox {fb}^{-1}\). The SM expected backgrounds for our signals events were built using the CMS open Monte Carlo samples generated by the CMS collaboration.

The analyzed data were found in good agreement with the simulated SM backgrounds within the total uncertainty including the statistical and systematic components. Thus, no evidence for the existence of WIMPs was found. 95% CL upper limits were set on some of the model free parameters; for the DH scenario with coupling values of \(g_{\textrm{SM}}\) = 0.25, \(g_{\textrm{DM}}\) = 1.0, the \({Z}^{\prime }\) boson masses below 357 GeV for the expected median and 367 GeV for the observed data have been excluded. Finally, the ranges below 2780 GeV for the expected median, and below 2890 GeV for the observed data, were also excluded for the cutoff scale (\(\varLambda\)) of the EFT scenario, with \(M_{Z^{\prime }} = 450\) GeV.