Search for dark matter produced in association with a single top quark and an energetic W boson in $\sqrt{s}=$ 13 TeV $pp$ collisions with the ATLAS detector

Abstract

This paper presents a search for dark matter, $\chi$, using events with a single top quark and an energetic W boson. The analysis is based on proton–proton collision data collected with the ATLAS experiment at $\sqrt{s}=$ 13 TeV during LHC Run 2 (2015–2018), corresponding to an integrated luminosity of 139 fb$^{-1}$. The search considers final states with zero or one charged lepton (electron or muon), at least one b-jet and large missing transverse momentum. In addition, a result from a previous search considering two-charged-lepton final states is included in the interpretation of the results. The data are found to be in good agreement with the Standard Model predictions and the results are interpreted in terms of 95% confidence-level exclusion limits in the context of a class of dark matter models involving an extended two-Higgs-doublet sector together with a pseudoscalar mediator particle. The search is particularly sensitive to on-shell production of the charged Higgs boson state, $H^{\pm }$, arising from the two-Higgs-doublet mixing, and its semi-invisible decays via the mediator particle, a: $H^{\pm } \rightarrow W^\pm a (\rightarrow \chi \chi )$. Signal models with $H^{\pm }$ masses up to 1.5 TeV and a masses up to 350 GeV are excluded assuming a $\tan \beta$ value of 1. For masses of a of 150 (250) GeV, $\tan \beta$ values up to 2 are excluded for $H^{\pm }$ masses between 200 (400) GeV and 1.5 TeV. Signals with $\tan \beta$ values between 20 and 30 are excluded for $H^{\pm }$ masses between 500 and 800 GeV.

1 Introduction

The existence of non-luminous matter, referred to as dark matter (DM), is strongly suggested by a wide variety of astrophysical and cosmological measurements [1, 2]. Despite the strong evidence supporting the presence of DM, which accounts for 26% of the energy content of the universe [3, 4], its nature and properties remain largely unknown and constitute one of the most important unanswered questions in modern physics. Assuming that its main component is a weakly interacting massive particle (WIMP or $\chi$) [5], DM produced in proton–proton collisions does not interact with the ATLAS detector and it can be detected only if produced in association with Standard Model (SM) particles. This leads to signatures with missing transverse momentum ($\vec {p}_{\textrm{T}}^{\textrm{miss}}$, its modulus denoted by $E_{\textrm{T}}^{\textrm{miss}}$).

The signal model considered in this search belongs to a class of simplified models for DM searches at the Large Hadron Collider (LHC). It involves an extended two-Higgs-doublet sector (2HDM) [6,7,8,9,10,11,12,13,14], together with an additional pseudoscalar mediator (a) that couples to a fermionic DM candidate. This 2HDM$+a$ model [10, 15] represents the simplest ultraviolet-complete and renormalisable framework for investigating the broad phenomenology predicted by spin-0 mediator-based DM models [15,16,17,18,19,20,21,22,23,24,25,26,27].

The 2HDM$+a$ model offers a rich phenomenology [28,29,30,31,32,33], with a variety of final states that might arise depending on the production and decay modes of the various bosons composing the Higgs sector, as investigated in Refs. [15, 34,35,36,37,38]. A recent analysis performed by the ATLAS Collaboration [39] has considered topologies characterised by the presence of $E_{\textrm{T}}^{\textrm{miss}}$ and a single top quark in the context of 2HDM$+a$ models. That search allowed masses of the additional charged Higgs bosons, $H^{\pm }$, from 400 $\text {GeV}$ to 1.1 $\text {TeV}$ to be excluded at a 95% confidence level (CL) for different values of the a-boson mass and for low values ($< 2$) of $\tan \beta$ (the ratio of the vacuum expectation values of the two Higgs doublets), which significantly affects the phenomenology of the 2HDM$+a$ model. Values of the a-boson mass up to 330 $\text {GeV}$ are also excluded at 95% CL for $\tan \beta = 1$ and an $H^{\pm }$ mass of 800 $\text {GeV}$. CMS has also performed a search for these topologies [40], where the results are interpreted in the context of a different set of simplified models.

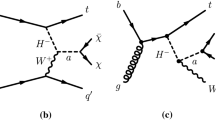
As in the case of the SM single top-quark production, the associated production of DM with a single top quark has three production modes at leading order (LO): t-channel production, s-channel production and associated production with a $W$ boson (tW). In the 2HDM$+a$ model, the dominant production mode for single-top-quark final states is the $tW$+DM channel, through the diagrams depicted in Fig. 1. On-shell production of charged Higgs bosons dominates the $tW$+DM production mode when $H^{\pm }\rightarrow W^{\pm } a$ decays are kinematically allowed and the $H^{\pm }$ mass is a few hundred $\text {GeV}$. Furthermore, the cross-section for this inclusive $tW$+DM production mode has a local minimum at $\tan \beta \approx 5$ and two local maxima at low $\tan \beta$ ($< 2$) and $\tan \beta \in [20,30]$ [28]. The aim of the search presented in this paper is to extend the current results obtained by ATLAS for the 2HDM$+a$ model by improving the sensitivity to single top-quark production in association with dark matter in the $tW$+DM process. The focus is to improve upon the current ATLAS limits at low $\tan \beta$ and to provide, for the first time, sensitivity to signal benchmarks probing the $tW$+DM cross-section maximum at high $\tan \beta$ values.

Fig. 1

Representative diagrams of $tW$+DM production from the 2HDM$+a$ model considered in this analysis. Charge-conjugate diagrams are considered as well

This paper presents a dedicated search for associated production of a single top quark, a $W$ boson and DM particles, based on 139 fb$^{-1}$ of proton–proton (pp) collisions at a centre-of-mass energy $\sqrt{s}= 13$ $\text {TeV}$ produced at the LHC and collected by the ATLAS detector (see Sect. 2) between 2015 and 2018. Due to the similarity of the experimental signature to $t\bar{t}$ production, the analysis is also sensitive to DM produced in association with two top quarks ($t\bar{t}$+DM). This final state is not considered in the optimization of the analysis, but its contribution is added to the $tW$+DM signal, according to the prediction of the 2HDM$+a$ model, when interpreting the final result. The analysis relies on Monte Carlo (MC) simulations, described in Sect. 3, which aid in the estimation of the SM background and DM signals. This search improves upon previous results [39] by targeting final states with an energetic W boson decaying hadronically or leptonically and characterised by the presence of exactly zero or one lepton ($\ell =e, \mu$). The hadronic decays of the $W$ boson are identified by requiring the presence of at least one high-$p_{\text {T}}$ large-radius jet consistent with originating from the hadronization of a resonant di-quark pair. In addition, at least one jet arising from the fragmentation of b-hadrons (b-jet) is required as a signature of the additional presence of a top quark, while large $E_{\textrm{T}}^{\textrm{miss}}$ is required as a sign of the production of DM particles. The identification of these objects, as well as the event reconstruction, is described in Sect. 4. Section 5 presents the selection of events in the one- or zero-lepton analysis channels, and also the method used to combine these two channels with the dilepton analysis described in Ref. [39]. Their combination maximises the sensitivity to $tW$+DM processes and further tightens previous constraints for 2HDM$+a$ models using the $tW$+DM channel. Systematic uncertainties are described in Sect. 6, followed by the experimental results and their interpretation in the context of the 2HDM$+a$ model in Sect. 7. Finally, Sect. 8 is devoted to the conclusions.

2 The ATLAS detector

The ATLAS detector [41] is a multipurpose particle detector with a forward–backward symmetric cylindrical geometry and nearly 4$\pi$ coverage in solid angle.¹ The inner tracking detector (ID) consists of pixel and microstrip silicon detectors covering the pseudorapidity region $|\eta |<2.5$, surrounded by a transition radiation tracker which enhances electron identification in the region $|\eta |<2.0$. An inner pixel layer, the insertable B-layer [42, 43], was added at a mean radius of 3.3 cm during the period between Run 1 and Run 2 of the LHC. The inner detector is surrounded by a thin superconducting solenoid providing an axial 2 T magnetic field and by a fine-granularity lead/liquid-argon (LAr) electromagnetic calorimeter covering $|\eta |<3.2$. A steel/scintillator-tile calorimeter provides hadronic coverage in the central pseudorapidity range ($|\eta |<1.7$). The endcap ($1.5<|\eta |<3.2$) and forward ($3.1<|\eta |<4.9$) regions of the hadron calorimeter are made of LAr active layers with either copper or tungsten as the absorber material. A muon spectrometer with an air-core toroid magnet system surrounds the calorimeters. Three layers of high-precision tracking chambers provide coverage in the range $|\eta |<2.7$, while dedicated fast chambers allow triggering in the region $|\eta |<2.4$. The ATLAS trigger system consists of a hardware-based level-1 trigger followed by a software-based high-level trigger [44]. An extensive software suite [45] is used in the reconstruction and analysis of real and simulated data, in detector operations, and in the trigger and data acquisition systems of the experiment.

3 Data and simulated events

The dataset used in the analysis corresponds to an integrated luminosity of 139 fb$^{-1}$ of pp collisions at a centre-of-mass energy of 13 $\text {TeV}$ recorded by the ATLAS detector with stable beam conditions. The uncertainty in the integrated luminosity is 1.7% [46], obtained using the LUCID-2 detector [47] for the primary luminosity measurements. The number of interactions in the same and temporally adjacent bunch crossings (pile-up) is 33.7 on average across all data-taking years. All detector subsystems are required to be operational for this dataset [48]. Candidate events were recorded using a combined set of triggers based on the presence of $E_{\textrm{T}}^{\textrm{miss}}$ or charged leptons ($\ell = e, \mu$). The $E_{\textrm{T}}^{\textrm{miss}}$ trigger [49] is fully efficient for events with reconstructed $E_{\textrm{T}}^{\textrm{miss}} > 250~\text {GeV}$ and is used for the zero-lepton and one-lepton analysis channels. Triggers based on single leptons [50, 51] are used to define auxiliary selections that aid in the estimation of the SM background processes. These selections require the presence of a muon or electron with transverse momentum, $p_{\text {T}}$ (or transverse energy $E_{\text {T}}$ for electrons), above certain thresholds, and impose data quality and lepton identification and isolation requirements.

Table 1 List of MC generators and the PDF sets used to simulate the different SM background processes. Diboson includes WW, WZ and ZZ production. Information is also given on the generator used to simulate the parton-shower and hadronization step and the underlying-event set of tuned parameters. The last column presents the perturbative QCD highest-order accuracy (NLO, next-to-next-to-leading order (NNLO), and next-to-next-to-leading logarithm (NNLL)) achieved in the calculation of the cross-section later used to normalizate of the different samples. Samples using Pythia 8 used NNPDF 2.3lo set of PDFs [59] for the parton-shower and hadronization step. Diboson cross-sections are directly taken from Sherpa

Dedicated MC simulated samples are used to model the SM and signal processes and to estimate their expected yields. The 2HDM$+a$ model considered in this paper assumes a type-II [52, 53] coupling structure of the Higgs sector, and has a CP-conserving potential and a softly broken $Z_2$ symmetry [52]. The additional pseudoscalar mediator of the model couples to DM particles and to the SM, and mixes with the pseudoscalar partner of the SM Higgs boson. The most important parameters that determine the phenomenology of the model are the masses of the CP-even (h and H), CP-odd (a and A) and charged ($H^\pm$) bosons; the mass of the DM particle ($\chi$); the three quartic couplings between the scalar doublets and the a boson ($\lambda _{P1}, \lambda _{P2}$ and $\lambda _3$) and the coupling between the a boson and the DM particle ($g_\chi$); the ratio of the vacuum expectation values (VEVs) of the two Higgs doublets ($\tan \beta$); and the mixing angles of the CP-even and CP-odd weak eigenstates, denoted by $\alpha$ and $\theta$, respectively. The alignment limit ($\cos (\beta -\alpha ) = 0$) and the decoupling limit are assumed. Thus the lightest CP-even mass eigenstate, h, can be identified as the SM Higgs boson with couplings predicted by the SM. The electroweak vacuum expectation value is set to $246~\text {GeV}$. The mixing angle $\theta$ is fixed at $\sin \theta =1/\sqrt{2}$, yielding full mixing between the a and A bosons and the largest cross-section for the processes of interest. To further reduce the parameter space, unitary couplings between the a-boson mediator and the DM particle $\chi$ ($g_\chi = 1$) are considered, with the DM particle mass set to $m_\chi =10\;\text {GeV}$. This has a negligible effect on the kinematic properties in the final states of interest, as long as $a\rightarrow \chi \chi$ is kinematically allowed. Following the prescriptions in Ref. [15], the masses of the heavy CP-even Higgs boson, H, and charged bosons, $H^\pm$, are set equal to the mass of the heavy CP-odd partner, A, and the three quartic couplings are set to a value of 3 for compatibility with constraints from electroweak precision measurements [10] and to ensure the stability of the Higgs potential for most of the parameter space of interest.²

The signal MC samples include tW production in association with DM particles. They were generated using LO matrix elements calculated by the MadGraph5_aMC@NLO [2.7.3] [54] generator interfaced to Pythia [8.244] [55], which used parameter values set to the A14 tune [56] to model parton showering (PS), hadronization and the underlying event. The five-flavour scheme NNPDF 3.0nlo [57] set of parton distribution functions (PDFs) was used. Signal cross-sections are calculated at LO accuracy in QCD. Additional simulated samples are used for $t\bar{t}$+DM processes. They were generated using LO matrix elements with up to one extra parton calculated by MadGraph5_aMC@NLO [2.6.7] interfaced to Pythia [8.244], with the same PDF set and tune as used for the tW processes. In this case, signal cross-sections are calculated at next-to-leading-order (NLO) accuracy using the same version of MadGraph5_aMC@NLO as suggested in Ref. [23]. The top-quark decays in all signal samples were simulated using MadSpin [58]. The final results are presented as a function of the $(m_a, m_{H^{\pm }})$ parameters while setting $\tan \beta$ to unity, or varying the $(m_{H^{\pm }}, \tan \beta )$ parameters while setting $m_a$ to 250 $\text {GeV}$ or 150 $\text {GeV}$.

The SM background processes were simulated using various MC event generators, accurate to NLO in perturbation theory, depending on the process. All background processes are normalised to the best available theoretical calculation of their respective cross-sections. The event generators, the accuracy of theoretical cross-sections, the underlying-event set of tuned parameters, and the PDF sets used in simulating the SM background processes most relevant for this analysis are summarised in Table 1. Note that the NNPDF 2.3lo PDF sets [59] were used for the parton-shower and hadronization steps in samples using Pythia 8.

For all samples, except those generated using Sherpa [60,61,62,63,64,65], the EvtGen [1.2.0] [66] program was used to simulate the properties of the b- and c-hadron decays. All generated events were then processed using the ATLAS simulation infrastructure [67] and $\textsc {Geant4}$ [68], which models the response of the various ATLAS subdetectors with high precision. In some cases, a faster simulation based on a parameterization of the calorimeter response, and on $\textsc {Geant4}$ for the other detector subsystems [67], was used. Subsequently, simulated events are reconstructed after including a realistic modelling of pile-up interactions, with pile-up profiles matching the ones in data. These profiles were obtained by overlaying each hard-scatter event with minimum-bias events simulated using the soft QCD processes of Pythia [8.186] [69] with the NNPDF 2.3lo set of PDFs [59] and the A3 tune [70].

4 Object identification and event reconstruction

All collision events considered in this paper are required to have at least one reconstructed interaction vertex with a minimum of two associated tracks each having $p_{\text {T}} >500$ $\text {MeV}$. In events with multiple vertices, the one with the highest sum of squared transverse momenta of associated tracks is chosen as the primary vertex [83]. Minimal quality criteria are applied to reject events with detector noise [48], non-collision backgrounds or events with jets failing basic cleaning requirements [84].

Electrons (e), muons ($\mu$) and jets are considered with two levels of quality requirements: baseline and signal. The baseline requirements have looser identification criteria. For each event, the missing transverse momentum [85] $\vec {p}_{\textrm{T}}^{\textrm{miss}}$, with magnitude $E_{\text {T}}^{\text {miss}}$, is calculated as the negative vector sum of the transverse momenta of all baseline reconstructed objects and the ‘soft term’. The soft term includes all tracks associated with the primary vertex but not matched to any reconstructed lepton or jet. Tracks not associated with the primary vertex are not considered in the $\vec {p}_{\textrm{T}}^{\textrm{miss}}$ calculation, improving the $\vec {p}_{\textrm{T}}^{\textrm{miss}}$ resolution by reducing the effect of pile-up. A quality criterion for the matching of topological cell clusters [86] in the electromagnetic calorimeter to electrons is also imposed in events containing electrons with $|\eta | \in [1.37,1.52]$ in data recorded during 2015 and 2016. Baseline reconstructed physics objects are also used when resolving possible reconstruction ambiguities (overlap removal). The details of the object prioritization and requirements in this procedure can be found in Ref. [87].

Electron candidates are reconstructed from energy deposits in the electromagnetic calorimeter that are matched to charged-particle tracks in the inner detector [88]. Baseline quality criteria include $p_{\text {T}} >4.5$ $\text {GeV}$, $|\eta |<2.47$ and satisfying the ‘LooseAndBLayer’ likelihood identification³ operating point [88]. The longitudinal impact parameter, $z_0$, relative to the primary vertex is required to satisfy $|z_0\sin \theta | <0.5$ mm. Signal-quality electrons are required to also satisfy $p_{\text {T}} >20$ $\text {GeV}$ and the ‘Medium’ likelihood identification criterion. The significance of the transverse impact parameter, $d_0$, must satisfy $|d_0/ \sigma (d_0)|<5$ for these electrons. Signal electrons with $p_{\text {T}} < 200$ $\text {GeV}$ are also required to be isolated⁴ from other activity in the detector by satisfying the ‘Loose’ isolation working point, while those with larger $p_{\text {T}}$ are required to pass the ‘HighPtCaloOnly’ isolation working point, as described in Ref. [89].

Muon candidates are reconstructed from matching tracks in the inner detector and muon spectrometer [90]. Requirements for baseline-quality muons include $p_{\text {T}} >4$ $\text {GeV}$, $|\eta |<2.7$ and satisfying the ‘Medium’ identification criterion⁵ [90]. Like the electrons, their longitudinal impact parameter relative to the primary vertex is required to satisfy $|z_0\sin \theta | <0.5$ mm. Signal-quality muons must satisfy $p_{\text {T}}$ $>20$ $\text {GeV}$ and a requirement on their transverse impact parameter significance of $\left| d_0/ \sigma (d_0)\right| <3$. Furthermore, they are required to be isolated based on the ‘Loose’ isolation criterion [90], which relies on variables calculated from energy deposits within a cone around the muon. The angular width of this cone depends on the $p_{\text {T}}$ of the muon, decreasing at higher $p_{\text {T}}$.

Jets are reconstructed using the anti-$k_t$ algorithm [91, 92] with a radius parameter $R=0.4$ and particle-flow objects (PFO) as inputs. PFOs combine information from the inner detector and calorimeter to reconstruct the energy and path of charged particles and neutral particles as described in Ref. [93]. Jet energy scale corrections, derived from MC simulation and data, are used to calibrate the average energies of jet candidates to the scale of their constituent particles [94]. To further reduce the effect of pile-up interactions, a jet-vertex-tagger (JVT) algorithm is used to identify jets originating from the primary vertex using track information [95]. Jets with $|\eta |<2.4$ and $p_{\text {T}} <60$ $\text {GeV}$ are required to satisfy the ‘Tight’ working point of this tagger, which corresponds to a JVT score of at least 0.5. In addition, jets with $|\eta |> 2.5$ and $p_{\text {T}} <50$ $\text {GeV}$ are required to pass a ‘Tight’ forward-JVT requirement [96], which corresponds to a forward-JVT score of less than 0.4 and a jet-timing requirement of less than 10 ns. Baseline-quality jets are selected in the region $|\eta |<4.5$ and must have a $p_{\text {T}} >20$ $\text {GeV}$. Signal-quality jets are required to fulfil $|\eta |<2.5$ and $p_{\text {T}} >30$ $\text {GeV}$.

Jets containing b-hadrons are identified as arising from b-quarks (‘b-tagged’ jets or $b\text {-jets}$) using a multivariate algorithm (DL1r) [97]. These b-tagged jets are reconstructed in the region $|\eta |<2.5$ and require $p_{\text {T}} >30$ $\text {GeV}$. The b-tagging working point used in this analysis provides an efficiency of 77% for $b\text {-jets}$ in simulated $t\bar{t}$ events.

A second category of jets is reconstructed by applying the anti-$k_t$ algorithm with radius parameter $R=1.0$ to a collection of noise-suppressed topological calorimeter-cell clusters calibrated using ‘local hadronic cell weighting’ [86] to correct for the non-compensating response of the ATLAS calorimeter. These jets are referred to as large-R jets to distinguish them from the $R=0.4$ version, also called small-R jets or simply ‘jets’. Large-R jets [98] are trimmed to remove pile-up and underlying-event effects. This trimming, extensively described in Ref. [99], is a grooming technique in which the original constituents of the jets are reclustered using the $k_t$ algorithm [100] with a radius parameter, $R_{\textrm{sub}}$, to produce a collection of subjets. These subjets are then discarded if they have less than a specific fraction, $f_{\textrm{cut}}$, of the $p_{\text {T}}$ of the original jet. The trimming parameters used are $R_{\textrm{sub}} = 0.2$ and $f_{\textrm{cut}}=0.05$. The jet energy scale and resolution and the mass scale and resolution of these large-R jets are then corrected via a calibration procedure described in Refs. [101, 102]. Large-R jets are required to have a $p_{\text {T}}\ > 200$ $\text {GeV}$ and $|\eta |<2.0$. To avoid reconstruction ambiguities between large-R jets and leptons, those large-R jets overlapping with signal leptons are removed. Ambiguities between large-R and baseline jets are not removed, as large-R jets are only used to construct higher-level quantities in order to identify hadronically decaying W bosons in the event. A set of $W$-tagging identification criteria [103] are applied to these large-R jets to identify those with topologies consistent with the decay of energetic hadronically decaying $W$ bosons. These identification criteria are only used for jets with a mass between 40 $\text {GeV}$ and 600 $\text {GeV}$ and a $p_{\text {T}} < 2.5$ $\text {TeV}$ and are based on the mass of the large R-jet, the number of inner-detector tracks associated with the jet and the $D_2$ variable [104]. This latter variable uses jet substructure energy correlations to identify deposits consistent with 2-prong particle decays against QCD quark and gluon initiated jets.

To compensate for remaining differences between data and simulation in trigger, particle identification and reconstruction efficiencies, correction factors are derived and applied to the samples of simulated events [89, 90, 105, 106].

5 Analysis strategy

This analysis complements and extends a previous search performed by the ATLAS Collaboration [39], by targeting final states with an energetic W boson and characterised by the presence of exactly zero or one lepton, referred to as the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels, respectively.

Top-quark decays contain a $W$ boson, and hence $tW$+DM signals contain two $W$ bosons in the decay chain. The ${{\textrm{tW}} _\mathrm {{0L}}}$ channel selects $tW$+DM events where both bosons in the event decay hadronically, while the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel selects events where one of them decays hadronically and the other decays leptonically. Both selections require high jet multiplicity and significant $E_{\text {T}}^{\text {miss}}$ from two DM particles escaping detection. In both channels, the $W$ boson arising from the decay of the massive $H^\pm$ boson is often produced with relatively high $p_{\text {T}}$, thus being significantly boosted. When this $W$ boson decays hadronically, it is reconstructed as a single large-R jet and W-tagged using the procedure described in Sect. 4. The one-lepton channel described in Ref. [39] is extended to include such boosted $W$-boson events. It is constructed to be statistically independent of the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel so that all signal regions (SRs) in this paper can be statistically combined. The ${{\textrm{tW}} _\mathrm {{2L}}}$ analysis channel in Ref. [39] targets $tW$+DM events with two opposite-sign leptons and is statistically independent of the SRs presented in this paper. As a consequence, this channel can be combined with ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ to derive the final results.

The relative importance of SM background processes varies across the different SRs. However, the most important can be broadly classified by the presence of genuine $E_{\text {T}}^{\text {miss}}$ produced by non-interacting particles, e.g. neutrinos, or $E_{\text {T}}^{\text {miss}}$ associated with the presence of particles that are either misidentified, mismeasured or outside the kinematic acceptance of the detector. Examples of backgrounds containing genuine $E_{\text {T}}^{\text {miss}}$, which constitute a significant part of the SM background yields in their respective channels, are the $Z$+jets background in the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, where the $Z$ boson decays into two neutrinos; and $W$+jets production in the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, where a lepton and neutrino are present in the decay. Other backgrounds such as $t\bar{t}$ or $W$+jets (in the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel) are examples of backgrounds that have high $E_{\text {T}}^{\text {miss}}$ due to leptons in the event which either escape detection or are misidentified as jets. Due to this, both make a large contribution in the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. Contributions from $t\bar{t}Z$ and single top-quark production, in particular the associated production of a top quark with a W boson, are also significant. The estimation of these five dominant SM backgrounds ($Z$+jets, $W$+jets, $t\bar{t}$, $t\bar{t}Z$ and single top quark) is aided by the use of six dedicated control regions (CRs), which are designed to be orthogonal to the SRs and are used to constrain six background normalization parameters in a phase space as close as possible to that of the SRs. The background normalizations are derived in common regions for the two analysis channels, with the exception of the $t\bar{t}$ background. Because $t\bar{t}$ has different compositions in the two channels, separate control regions and normalization parameters are used for ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. The validity of the background estimation strategy is confirmed in specific validation regions (VRs) adapted for each defined SR. The potential signal contamination in the CRs and VRs is found to be small: < 2.5% and < 10% of the total SM expectation for all analysis channels, respectively.

The strategy for the statistical analysis and combinations performed in this paper closely follows the one used in Ref. [39], and relies on a profile likelihood fit [107], with the systematic uncertainties, described in Sect. 6, introduced as nuisance parameters constrained by a Gaussian distribution. Following the definition of Ref. [39], the fit is performed using two configurations: background-only and exclusion fit set-ups. In the background-only configuration the fit is used to estimate the reliability of the background prediction in the VRs. It is performed using all ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ CRs in a simultaneous fit and assuming no contribution from ‘beyond-the-SM’ (BSM) physics processes. The six normalization factors of the SM backgrounds are hence determined in all the control regions simultaneously. The normalization factors determined in this set-up are applied to the VRs in order to verify that the background predictions agree with the data. The background-only fit configuration is also used to estimate the model-independent limits in Sect. 7, by extrapolating the background prediction of this fit to the SRs and estimating upper limits on the event yields of a general BSM signal in inclusive (i.e. single-bin) SRs. In this way, exact knowledge of BSM signal correlations across bins is not needed to estimate the result. Additionally, this configuration is also used to quantify the significance of possible data deviations from SM predictions. In the exclusion fit set-up, all CRs and SRs are fit simultaneously in order to test a BSM signal plus SM background hypothesis against a SM-only hypothesis. Unlike the model-independent configuration, these SRs are multi-bin regions that profit of the shape of benchmark signals to enhance the sensitivity to the 2HDM+a model in different areas of the parameter space. All correlations between CRs and SRs are taken into account by the common background normalization parameters and systematic uncertainty nuisance parameters. This configuration is used to place limits on the production cross-section at a given point in the parameter space of the 2HDM$+a$ model.

5.1 Signal regions

An optimization procedure is followed to derive the event selection criteria for the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. It follows a two-step process, using a varying set of kinematic variables. First, a manual, coarse optimization is carried out, seeking to maximise the sensitivity of the event selection to a set of benchmark signal models. Then a random grid search algorithm [108] is used to fine-tune the coarse selection criteria.

The ${{\textrm{tW}} _\mathrm {{0L}}}$ channel selection criteria are summarised in Table 2. Following the signal topology, this channel selects events with exactly zero leptons, at least four jets and at least one large-R jet which is consistent with the hadronic decay of a $W$ boson ($W$-tagged). Exactly one jet with $p_{\text {T}} >50\;\text {GeV}$ is required to be b-tagged. Further requirements are placed on the $W$-boson candidate and the b-jet to suppress events where they both originate from the decay of the same top quark, as it is assumed that the boosted W boson in the signal topology arises from the decay of the charged Higgs boson. These requirements involve a large angular separation between the $W$-tagged large-R jet and the leading (highest-$p_{\text {T}}$) b-tagged jet ($\Delta R_{W \text {-tagged},\textrm{b}_{1}}$) and an invariant mass of their combined four-vector ($m_{W \text {-tagged},\textrm{b}_{1}}$) larger than the top-quark mass.

Table 2 Summary of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ signal region selections. The ${{\textrm{tW}} _\mathrm {{0L}}}$ signal region and the ${{\textrm{tW}} _\mathrm {{1L}}}$ region searching for hadronic top decays ($\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$) are further split into bins of $E_{\text {T}}^{\text {miss}}$ to increase the sensitivity for different signal model parameters as described in the text. The signal region seeking leptonic top decays ($\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$) is used inclusively

Requirements on $E_{\text {T}}^{\text {miss}}$ and its object-based significance, $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ [109], are used to enhance the selection of events with invisible particles in the final state. As the momentum of the DM particles in the signal strongly depends on the mass difference between the a-boson mediator and the $H^{\pm }$ boson, the signal region is further split into five bins in $E_{\text {T}}^{\text {miss}}$ to maximise the sensivity of this analysis throughout the full considered parameter space. These five bins are defined with $E_{\text {T}}^{\text {miss}}$ intervals [250, 330] $\text {GeV}$, [330, 400] $\text {GeV}$, [400, 500] $\text {GeV}$, [500, 600] $\text {GeV}$ and $\ge 600$ $\text {GeV}$, referred to, respectively, as $\textrm{SR}^{\textrm{bin1}}_{{{\textrm{tW}} _\mathrm {{0L}}}}$–$\textrm{SR}^{\textrm{bin5}}_{{{\textrm{tW}} _\mathrm {{0L}}}}$. Inclusive signal regions, defined with $E_{\text {T}}^{\text {miss}}$ $\ge$ 250, 330, 400, 500 and 600 $\text {GeV}$, are also defined in this analysis as ‘discovery regions’. These single-bin overlapping SRs can be used to estimate either the significance of an excess or an upper limit on the signal yield with less stringent assumptions about the kinematic properties of the signal. The minimum azimuthal angle between $E_{\text {T}}^{\text {miss}}$ and the leading four jets, $\min [\Delta \phi ({\textrm{jet}}_{1-4},E_{\text {T}}^{\text {miss}})]$, is used to suppress fake $E_{\text {T}}^{\text {miss}}$ arising from mismeasured jets. The transverse mass variable constructed from the leading $b\text {-jet}$ of the event and the $\vec {p}_{\textrm{T}}^{\textrm{miss}}$, $m_{\textrm{T}}({\mathrm {b_{1}}},E_{\text {T}}^{\text {miss}})$, [110] is used to suppress events from semileptonic $t\bar{t}$ decays, which exhibit an endpoint in $m_{\textrm{T}}({\mathrm {b_{1}}},E_{\text {T}}^{\text {miss}})$ when the $E_{\text {T}}^{\text {miss}}$ in the event arises entirely from a missed W boson.

The ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, also summarised in Table 2, selects events with exactly one lepton and exactly one b-tagged jet with $p_{\text {T}} >50\;\text {GeV}$. As in the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, requirements in $E_{\text {T}}^{\text {miss}}$, $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ and $\min [\Delta \phi ({\textrm{jet}}_{1-4},E_{\text {T}}^{\text {miss}})]$ are used to enhance the selection of events with invisible particles and suppress events with fake $E_{\text {T}}^{\text {miss}}$. The one-lepton channel was explored previously in Ref. [39] and strategies used in the previous paper are now extended with ideas presented in Refs. [28, 111] and further enhanced by the use of W-tagging techniques.

Fig. 2

Schema of the definitions of the different regions corresponding to (left) the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel in $N^{J; R=1.0}_{W \text {-tagged}}$ and the number of leptons ($N_{\ell }$) and (right) the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel in $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$ and . Orthogonality between the different regions observed to overlap is ensured by the inversion of some selection cuts in variables that aren’t depicted in this figure. $m_{W \text {-tagged},\textrm{b}_{1}}$ and $\Delta R_{W \text {-tagged},\textrm{b}_{1}}$ are inverted to ensure the orthogonality of the ${{\textrm{tW}} _\mathrm {{0L}}}$ signal and validation regions. The $t\bar{t}$ validation regions and the ${{\textrm{tW}} _\mathrm {{1L}}}$ regions are independent thanks to the inversion of the selection cuts on $am_{\textrm{T2}}$. Finally, $m_{W}^{\textrm{had}}$ ensures the orthogonality of the $W \text {+\,jets}$ control and validation regions

In the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, events are selected with a boosted hadronically decaying W boson from the $H^{\pm }$ boson decays and a leptonically decaying W-boson from the top quark decays. These events are selected for the $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ region. The complementary set of events, where the W boson from the $H^{\pm }$ boson decays leptonically and the W boson from the top quark decays hadronically, are selected for the $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ region. A new variable, called , is used to guarantee that $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ are statistically independent. It is constructed as the invariant mass of the leading b-jet ($\textrm{b}_{1}$) and the highest-$p_{\text {T}}$ jet that is not b-tagged (). Signal events with the top quark decaying hadronically exhibit an endpoint in slightly below the top-quark mass, while events with a leptonically decaying top quark extend beyond this endpoint [28].

Following the previous analysis [39], the $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ regions exploit both the transverse mass of the lepton and the $E_{\text {T}}^{\text {miss}}$, $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$, and the asymmetric stranverse mass [112,113,114,115,116], $am_{\textrm{T2}}$, to suppress the background from semileptonic and dileptonic $t\bar{t}$ decays, respectively. The latter is constructed to have an endpoint at the top-quark mass for dileptonic $t\bar{t}$ events where one of the leptons is outside the acceptance or misidentified. In addition, the $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ region requires at least one $W$-tagged large-R jet, while $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ uses the variable $m_{W}^{\textrm{had}}$ [39, 116]. Here, $m_{W}^{\textrm{had}}$ uses a variable-radius jet reconstruction algorithm with standard jet inputs to identify the hadronically decaying W bosons in the event even when their momentum is not high enough to be reconstructed within a large-R jet. As in the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, binning the SRs in $E_{\text {T}}^{\text {miss}}$ is the optimal strategy to maximise the sensitivity throughout the full model parameter space. However, due to the low event yield in $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$, this strategy is implemented only in the $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ region. Five different bins are then defined with $E_{\text {T}}^{\text {miss}}$ intervals [250, 300] $\text {GeV}$, [300, 350] $\text {GeV}$, [350, 400] $\text {GeV}$, [400, 450] $\text {GeV}$ and $\ge 450$ $\text {GeV}$, referred to as $\textrm{SR}^{\mathrm {had.top \ bin1}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$–$\textrm{SR}^{\mathrm {had.top \ bin5}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$. Similarly, inclusive ‘discovery’ SRs are defined with $E_{\text {T}}^{\text {miss}}$ $\ge$ 250, 300, 350, 400 and 450 $\text {GeV}$.

5.2 Background estimation and validation

Control regions are designed to support the estimation of the dominant backgrounds. In the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, the three most important backgrounds are $Z \text {\,+\,jets}$, $t\bar{t}$ and $W \text {+\,jets}$. In the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, the most important backgrounds are $t\bar{t}$ and $t\bar{t}Z$ in $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $t\bar{t}$ and $W \text {+\,jets}$ in $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$. All background processes, with the exception of $t\bar{t}$, are estimated in common CRs and with common normalization parameters for the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. Figure 2 schematically depicts the requirements imposed on the main analysis observables in the CRs (and VRs) in order to ensure orthogonality to the SRs and low signal contamination, as well as high purity in the targeted background, in each region.

The composition of the $t\bar{t}$ background in the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels is very different. In the former, the background is dominated by semileptonic $t\bar{t}$ decays, while in the latter, dileptonic $t\bar{t}$ decays dominate. In both cases, these backgrounds satisfy the selection criteria because one lepton is misidentified as a jet or falls outside of the detector fiducial area. Due to the difference in composition, two control regions are defined in order to normalise the $t\bar{t}$ background for the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. The ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$ CR is enriched in semileptonic $t\bar{t}$ events by requiring exactly one lepton, low $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$, low $am_{\textrm{T2}}$ and dropping the $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ requirement. Requirements similar to those in the ${{\textrm{tW}} _\mathrm {{0L}}}$ SRs are also imposed on the presence of a W-tagged large-R jet and on $\Delta R_{W \text {-tagged},\textrm{b}_{1}}$ and $m_{W \text {-tagged},\textrm{b}_{1}}$ to ensure that this control region scans a topology similar to that in the SRs. The ${{\textrm{tW}} _\mathrm {{1L}}}$ $t\bar{t}$ CR is enriched in dileptonic $t\bar{t}$ events by inverting the constraints on $am_{\textrm{T2}}$ and $p_{\textrm{T}}^{\textrm{b}_{2}}$. Since this region is used to estimate the $t\bar{t}$ background in both ${{\textrm{tW}} _\mathrm {{1L}}}$ SRs, if a variable has different requirements in the two SRs, the requirement is either dropped in the CR or chosen to be the looser one.

The $Z \text {\,+\,jets}$ background, dominated in the ${{\textrm{tW}} _\mathrm {{0L}}}$ signal region by $Z (\rightarrow \nu \nu )$+jets, is estimated by selecting a large high-purity sample of events with two same-flavour opposite-sign (SF-OS) leptons, as presented in Fig. 2. The leptons from the Z-boson decay are treated as invisible particles and added to the $E_{\text {T}}^{\text {miss}}$ of the event, now denoted by $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$, to mimic the behaviour of the $Z \text {\,+\,jets}$ background in the ${{\textrm{tW}} _\mathrm {{0L}}}$ SR, where this background is dominant. The CR is defined by following the selection criteria of the ${{\textrm{tW}} _\mathrm {{0L}}}$ SR, but variables built with $E_{\text {T}}^{\text {miss}}$ in the SR are built with $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$ instead. The $W \text {+\,jets}$ background is estimated in a CR selecting events with exactly one lepton and $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$ in the $W$-boson mass range [40, 100] $\text {GeV}$ (as presented in Fig. 2), high $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ and low $m_{W}^{\textrm{had}}$ to ensure high acceptance for $W \text {+\,jets}$ events.

Table 3 Summary of $W \text {+\,jets}$, $Z \text {\,+\,jets}$, and both $t\bar{t}$ control regions. All variables used in $Z \text {\,+\,jets}$ CR are calculated using a corrected version of the $E_{\text {T}}^{\text {miss}}$, denoted by $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$, treating all leptons in the event as invisible. ‘SF-OS’ indicates that the selected leptons are required to have the same flavour and opposite-sign electric charges, such that they are compatible with the decay of a Z boson

Table 4 Summary of the single-top-quark and $t\bar{t}Z$ control regions. ‘SF’ and ‘OS’ indicate that the two leptons are required to have the same flavour and opposite-sign electric charges, respectively. For the $t\bar{t}Z$ CR, the leptons treated as invisible in $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$ are the SF-OS pair with invariant mass closest to the Z-boson mass

The estimation of the $t\bar{t}Z$ background is performed in a selection requiring exactly three leptons as described in Ref. [87]. A $Z$-boson candidate is reconstructed from the SF-OS lepton pair with invariant mass closest to the $Z$-boson mass. The resulting lepton pair is treated as invisible. The contribution from jets misidentified as leptons in this control region is estimated using MC samples and amounts to less than $10\%$ [87].

Finally, to correctly estimate the single-top-quark background and, therefore, to reduce the systematic uncertainties arising from its modelling, a dedicated CR with two leptons and high $E_{\text {T}}^{\text {miss}}$ is constructed. Most $Z \text {\,+\,jets}$ events are removed by requiring $m_{\ell \ell }$ to be outside of the $Z$-boson mass range i.e. $\notin [71, 111]$ $\text {GeV}$. Events with a leptonically decaying $W$ boson are selected by means of a low $m_{\text {T2}}$ requirement built using both leptons in the event and $E_{\text {T}}^{\text {miss}}$. The variables $m_{b\ell }^\text {min}$ and $m_{b\ell }^{t}$ [39, 117] are built by combining the leptons and jets in the event and present an endpoint in the range 153–170 $\text {GeV}$, close to the mass of the top quark. They are highly efficient in separating the single-top-quark, $t\bar{t}$ and $t\bar{t}Z$ backgrounds and are used to increase this CR’s purity in single-top-quark events.

A summary of all control region definitions can be found in Tables 3 and 4. Normalization factors for all of the aforementioned SM backgrounds are fitted simultaneously in these regions using the background-only fit configuration. Their values are $\mu _{t\bar{t}}^{{{\textrm{tW}} _\mathrm {{0L}}}} = 1.00 \pm 0.12$, $\mu _{t\bar{t}}^{{{\textrm{tW}} _\mathrm {{1L}}}} = 0.92 \pm 0.06$, $\mu _{Z \text {\,+\,jets}} = 0.98 \pm 0.07$, $\mu _{W \text {+\,jets}}=1.08 \pm 0.09$, $\mu _{\textrm{single top}} = 0.43 \pm 0.13$ and $\mu _{t\bar{t}Z} = 1.18 \pm 0.19$. There is a large discrepancy between the fitted value of the single-top normalization parameter and the Monte Carlo predicted value. This discrepancy is driven by the dominant contribution of the tW process to the single-top channel and related to the modelling of the interference between single-resonant and double-resonant top-quark production. It is found that the default scheme used to model this interference (diagram removal [118]) and the alternative scheme used to estimate the associated uncertainty (diagram subtraction, see Sect. 6 for details) bracket the observed number of events in the single-top CR data, with a large difference between the two predictions. The single-top CR allows $\mu _{\textrm{single top}}$ to be constrained by data independently of the choice of default interference scheme. Residual shape differences between the two schemes are assigned as systematic uncertainties as described in Sect. 6.

Figure 3 shows the post-fit $E_{\text {T}}^{\text {miss}}$ and $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$ distributions for all CRs, where good agreement between data and fitted predictions can be observed.

Fig. 3

The post-fit $E_{\text {T}}^{\text {miss}}$ and $E_{\textrm{T,}\ell \ell }^{\textrm{miss}}$ distributions in the a $Z \text {\,+\,jets}$, b ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$, c ${{\textrm{tW}} _\mathrm {{1L}}}$ $t\bar{t}$, d $W \text {+\,jets}$, e single-top, and f $t\bar{t}Z$ control regions. The last bin in the histogram includes the overflow events. The bottom panel shows the ratio of data to total SM background. The uncertainties shown are the sum of the statistical and post-fit systematic uncertainties as detailed in Sect. 6. The fit set-up corresponds to the background-only fit configuration. The ‘Others’ category includes contributions from rare processes such as tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH

Validation regions are defined in order to verify that the background estimation strategy is robust. One or more VRs are designed to validate each background estimate from the CRs. The ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$ background estimate is validated using a selection with zero reconstructed leptons. In order to ensure orthogonality to the SRs and a high $t\bar{t}$ background purity, the $m_{W \text {-tagged},\textrm{b}_{1}}$ and $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ selection requirements are inverted. A similar strategy is used for the $Z \text {\,+\,jets}$ and $W \text {+\,jets}$ VRs, where the normalization factors are extrapolated from two-lepton and one-lepton control regions to a zero-lepton selection. However, since the definition of a $W \text {+\,jets}$-enriched region using an event selection with no leptons poses a challenge due to its similarity to $Z \text {\,+\,jets}$, a combined $V\text {+\,jets}$ validation region is defined for $W \text {+\,jets}$ and $Z \text {\,+\,jets}$ with the goal of high acceptance for the sum of the two processes. In the $V\text {+\,jets}$ validation region, the selection requirement on $\Delta R_{W \text {-tagged},\textrm{b}_{1}}$ is also inverted to be orthogonal to the signal region, but the $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$ selection requirement is kept the same, as this ensures orthogonality to the ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$ VR. Furthermore, in order to decrease statistical uncertainties, the $N^{J; R=1.0}_{W \text {-tagged}}$ selection requirement is relaxed, as shown in Fig. 2, and requirements on $\min [\Delta \phi (\mathrm {j^{all}},E_{\text {T}}^{\text {miss}})]$ and $\Delta R_\textrm{j1,j2}$ are imposed to increase the $Z \text {\,+\,jets}$ and $W \text {+\,jets}$ purity.

Table 5 Summary of the ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$ and the $V\text {+\,jets}$ validation regions

To validate the $t\bar{t}$ prediction in the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, one validation region per SR is constructed. In both VRs, low $am_{\textrm{T2}}$ is required, both to ensure orthogonality to the signal regions and to enhance the $t\bar{t}$ fraction. To increase the acceptance in the regions, the $W$-tagging requirement is dropped in the $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ $t\bar{t}$ validation region and the $m_{W}^{\textrm{had}}$ requirement is dropped in the $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ $t\bar{t}$ validation region. The $W \text {+\,jets}$ VR is kinematically close to $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$. The acceptance of $W \text {+\,jets}$ events is increased by constraining $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$ to be in the $W$-boson mass range and demanding high $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$. The resulting region has large $t\bar{t}$ and single-top-quark contributions and can be considered a simultaneous validation region for all three backgrounds. Good agreement between data and the $t\bar{t}Z$ background predicted by its CR was reported in Ref. [87], so no dedicated $t\bar{t}Z$ VR is considered in this analysis.

Table 6 Summary of the ${{\textrm{tW}} _\mathrm {{1L}}}$ $t\bar{t}$, $W \text {+\,jets}$ and single-top-quark validation regions

Finally, the single-top-quark prediction is validated in a one-lepton region. The single-top-quark acceptance is enhanced by applying a low $m_{\textrm{T}}(\ell ,E_{\text {T}}^{\text {miss}})$ requirement. The $t\bar{t}$ events are suppressed by demanding high $am_{\textrm{T2}}$ and $\mathcal {S}_{E_{\text {T}}^{\text {miss}}}$. The $W \text {+\,jets}$ contribution is reduced by selecting events with high sub-leading b-jet transverse momentum.

A summary of all validation regions can be found in Tables 5 and 6. Figure 4 shows the post-fit $E_{\text {T}}^{\text {miss}}$ distribution in each VR. In addition, observed data and predicted background yields in all control and validation regions are presented in Fig. 5, together with the ratio of their difference to the estimated background uncertainty. Good agreement between data and the expected background predictions can be observed in both figures, thus validating the background estimation strategy of the analysis.

5.3 Statistical combination

The SRs of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels are constructed to be statistically independent and they are combined to derive the final results in Sect. 7. The CRs are constructed to be in common for the two channels, with the exception of the $t\bar{t}$ CRs which are disjoint and the $t\bar{t}$ background is estimated in each channel with a separate normalization parameter. These two channels are also statistically independent of the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel in Ref. [87]. For this reason the results are also derived using the statistical combination of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels with the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel, in order to provide the most stringent constraints on the model considered in this paper. The dominant SM background in the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel is $t\bar{t}Z$ production and it is estimated in Ref. [87] using a CR which is a subset of the $t\bar{t}Z$ CR in this paper. In the combination of the three channels, the $t\bar{t}Z$ background is estimated using a common normalization parameter fitted in the common ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ CR (Sect. 5.2). As the $t\bar{t}Z$ CR in this paper has less contamination from diboson processes than the ${{\textrm{tW}} _\mathrm {{2L}}}$ $t\bar{t}Z$ CR, the diboson CR of Ref. [87], which provides an estimate of the diboson processes in the $t\bar{t}Z$ CR, is not used. All other SM backgrounds in the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel are estimated directly from the MC simulation, as in Ref. [87]. These CR orthogonalization choices impact the final ${{\textrm{tW}} _\mathrm {{2L}}}$ background estimate by up to 10–15% because the normalization factor for the $t\bar{t}Z$ background in this channel changes from $0.8\pm 0.2$ to $1.2\pm 0.2$.

Fig. 4

The post-fit $E_{\text {T}}^{\text {miss}}$ distributions in the a ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$, b ${{\textrm{tW}} _\mathrm {{0L}}}$ $V\text {+\,jets}$, c $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ $t\bar{t}$, d $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ $t\bar{t}$, e $W \text {+\,jets}$ and f single-top-quark validation regions. The last bin in the histogram includes the overflow events. The bottom panel shows the ratio of data to the total SM background. The uncertainties shown are the sum of the statistical and post-fit systematic uncertainties as detailed in Sect. 6. The fit set-up corresponds to the background-only fit configuration. The ‘Others’ category includes contributions from rare processes such as tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH

Fig. 5

Summary of all control and validation regions comparing the post-fit predicted SM background with the observed number of events. The normalization parameters were extracted from the control regions. The fit set-up corresponds to the background-only fit configuration. Statistical and systematic uncertainties are included in the shaded region of the top panel as detailed in Sect. 6. The bottom panel shows the statistical significance [119] of the excesses and deficits of data relative to the predicted SM background

Fig. 6

Relative uncertainties (in percent) in the total background yield in each signal region of the two analysis channels, including the contributions from the different sources of uncertainty. The ‘Detector’ category contains all detector-related systematic uncertainties. The ‘Background normalization’ represents the uncertainty in the fitted normalization factors, including the available data event counts in the CRs. Individual uncertainties can be correlated, and do not necessarily add up in quadrature to the total background uncertainty. The fit configuration used to estimate these uncertainties corresponds to the background-only fit explained in Sect. 7

6 Systematic uncertainties

This analysis considers several sources of uncertainty, of both experimental and theoretical nature, that affect the prediction of the SM background and the DM signal in all channels. Figure 6 provides an overview of the size of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ systematic uncertainties, estimated in a combined fit of the two channels.

The uncertainties related to the limited measurement precision of reconstructed objects, the estimate of the dataset luminosity and the modelling of the pile-up are broadly referred to as ‘detector systematic uncertainties’. The dominant contributions to these uncertainties arise from the small-R jet energy scale and resolution and the large-R jet $W$-tagging. The small-R jet energy scale and resolution uncertainties have a large impact on the high $E_{\text {T}}^{\text {miss}}$ bins of the $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ region, respectively. In addition, small-R jet energy resolution uncertainties are the source of the second-largest experimental uncertainty in the ${{\textrm{tW}} _\mathrm {{0L}}}$ SRs. The $W$-tagging uncertainties dominate across the ${{\textrm{tW}} _\mathrm {{0L}}}$ SRs, being the dominant experimental uncertainty in this channel. The uncertainties associated with trigger requirements, pile-up modelling, lepton reconstruction and energy measurements have a small or negligible impact on the final results. The lepton, photon and jet-related uncertainties are propagated to the calculation of the $E_{\textrm{T}}^{\textrm{miss}}$, along with additional uncertainties due to the energy scale and resolution of the soft term. These $E_{\text {T}}^{\text {miss}}$ soft-term uncertainties are found to be small or negligible. Finally, as mentioned in Sect. 3, a 1.7% uncertainty in the combined 2015–2018 integrated luminosity is included.

Table 7 Event yields showing the observed data and the background-only fit SM predictions in the ${{\textrm{tW}} _\mathrm {{0L}}}$ signal regions. Signal regions are defined according to the five $E_{\text {T}}^{\text {miss}}$ bins presented in Sect. 5.1 for the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, corresponding to increasing $E_{\text {T}}^{\text {miss}}$ values in bins 1–5. SM predictions are decomposed into the main backgrounds of the analysis. Smaller backgrounds (tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH events) are grouped together and labelled as ‘Others’. The quoted uncertainties in the fitted SM background include both the statistical and systematic uncertainties

Table 8 Event yields showing the observed data and the background-only fit SM predictions in the ${{\textrm{tW}} _\mathrm {{1L}}}$ signal regions. Bin numbers for SR$^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ refer to the five $E_{\text {T}}^{\text {miss}}$ bins presented in Sect. 5.1 for the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel, corresponding to increasing $E_{\text {T}}^{\text {miss}}$ values in bins 1–5. SM predictions are decomposed into the main backgrounds of the analysis. Smaller backgrounds (tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH events) are grouped together and labelled as ‘Others’. The quoted uncertainties in the fitted SM background include both the statistical and systematic uncertainties

Theoretical uncertainties are estimated for the modelling of SM background processes in the MC simulation. Their theoretical cross-section uncertainties are also taken into account. Modelling uncertainties are important for both channels. In the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, single-top-quark uncertainties are dominant in the bins of the SRs with highest $E_{\text {T}}^{\text {miss}}$ requirements, while $Z$+jets theory uncertainties contribute significantly in the lowest $E_{\text {T}}^{\text {miss}}$ bins. The $t\bar{t}$ and $W$+jets uncertainties are the dominant ones in the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel. The $Z$+jets and $W$+jets modelling uncertainties are evaluated by varying the CKKW-L scale for matching of the matrix element and parton shower, and the resummation, renormalization and factorization scales independently by factors of 0.5 and 2. The $t\bar{t}$ and single-top-quark uncertainties from the renormalization and factorization scales and initial- and final-state radiation parameters are evaluated similarly. In addition, uncertainties due to our choices of hard-scattering generator and parton-shower and hadronization models are estimated for these two processes. The impact of the latter is evaluated by comparing the nominal simulated sample with a sample generated using the same matrix element generator, Powheg Box, interfaced to an alternative shower generator, Herwig [7] [120, 121]. This sample uses the H7UE set of tuned parameters [121]. To assess the uncertainty due to the choice of hard-scattering generator and matching scheme, an alternative generator set-up using MadGraph5_aMC@NLO [54] interfaced to Pythia [8] [55] is employed. An additional uncertainty is considered for the single-top-quark tW channel: the impact of interference between single-resonant and double-resonant top-quark production on the implementation of the W-boson lineshape in the generator is estimated by comparing the nominal sample generated using the diagram removal method with samples using the alternative diagram subtraction method [118]. For the $t\bar{t}Z$ background, uncertainties related to the choice of renormalization and factorization scales are assessed by varying the corresponding event generator parameters by factors of 0.5 and 2 from their nominal values. Overall, the total SM uncertainties vary from 11% to 42% across the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ signal regions.

Fig. 7

Comparison of the background-only fit SM predictions extrapolated to all SRs with the observed data. The normalization of the backgrounds is obtained from the fit to the CRs. The upper panel shows the observed number of events and the predicted background yields. The ‘Others’ category includes contributions from rare processes such as tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH. All uncertainties defined in Sect. 6 are included in the uncertainty band. The bottom panel shows the statistical significance [119] of the excesses and deficits of data events relative to the predicted SM background

Detector and modelling uncertainties are also evaluated for the DM signal processes. Detector uncertainties are found to have an impact of 9–43% on the expected signal yields across the $m_a$–$m_{H^{\pm }}$ and $m_a$–$\tan \beta$ planes for the signal regions of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ analysis channels. The largest uncertainties are found to be concentrated in the highest $E_{\text {T}}^{\text {miss}}$ bins of the SRs for both channels. In all SRs, the dominant experimental uncertainties affecting signal yields are found to be the uncertainties associated with the jet energy scale and resolution and with $W$-tagging, as observed for the SM processes. These uncertainties are assumed to be fully correlated with those affecting the SM background. Modelling uncertainties include renormalization and factorization scale uncertainties and uncertainties related to the modelling of the parton shower. For the signal regions of the ${{\textrm{tW}} _\mathrm {{0L}}}$ (${{\textrm{tW}} _\mathrm {{1L}}}$) analysis channel, the average value of these modelling uncertainties lies between 3% and 30% (3% and 24%) across the $m_a$–$m_{H^{\pm }}$ and $m_a$–$\tan \beta$ planes, but can reach 50% for certain benchmark signals in the highest $E_{\text {T}}^{\text {miss}}$ regions of the channel.

The effects of the various sources of systematic uncertainty on the signal and background estimates are introduced in the likelihood fit (see Sect. 5) through nuisance parameters (NPs) that affect the expectation values of the Poisson terms for each CR and SR bin. The probability density function of each nuisance parameter is described by a Gaussian distribution whose standard deviation corresponds to a specific experimental or theoretical modelling uncertainty. The preferred value of each nuisance parameter is determined as part of the likelihood fit and none of them is significantly altered or constrained by the fit. The uncertainties arising from the total number of data events in the CRs are also included in the fit for each region. Since the number of CRs matches the number of fitted background normalization parameters, the systematic uncertainties are not constrained in the background-only fit of this analysis.

All uncertainties arising from the same source, including background and signal modelling uncertainties, are treated as correlated across the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels. For the statistical combination of the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels with the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel, a simplified approach which considers uncorrelated experimental and theoretical systematic uncertainties is adopted. This is supported by the large differences between the definitions of the physics objects, the selection and quality criteria, and uncertainty schemes which were used in the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel and the analyses described in this paper. Only the modelling uncertainties for the DM signal are treated as correlated across all channels.

Fig. 8

Representative distributions of a $E_{\text {T}}^{\text {miss}}$, b $m_{W \text {-tagged},\textrm{b}_{1}}$, c $m_{\textrm{T}}({\mathrm {b_{1}}},E_{\text {T}}^{\text {miss}})$, and d the number of W-tagged large-R jets in the ${{\textrm{tW}} _\mathrm {{0L}}}$ signal region. Observed data are compared with the SM background predictions extrapolated from the background-only fit. The ‘Others’ category includes contributions from rare processes such as tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH. The expected distributions for representative scenarios with different $m_a$, $m_{H^{\pm }}$, and $\tan \beta$ are shown for illustrative purposes. All signal theory cross-sections ($\sigma _{\textrm{th}}$) have been multiplied by three for better visibility. The overflow events, where present, are included in the last bin. The lower panels show the ratio of data to the background prediction. The hatched error bands indicate the combined experimental, theoretical and MC statistical uncertainties of these background predictions. The arrows, when present, indicate the value of the SR requirement on the quantity presented on the x-axis

Fig. 9

Representative distributions of a $E_{\text {T}}^{\text {miss}}$ and b in $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$, as well as c the number of W-tagged large-R jets and d in $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$. Observed data are compared with the SM background predictions extrapolated from the background-only fit. The ‘Others’ category includes contributions from rare processes such as tWZ, tZ, triboson, ttt, $t{\bar{t}}t{\bar{t}}$, ttW and ttH. The expected distributions for representative scenarios with different $m_a$, $m_{H^{\pm }}$, and $\tan \beta$ values are shown for illustrative purposes. All signal theory cross-sections ($\sigma _{\textrm{th}}$) have been multiplied by three for better visibility. The overflow events, where present, are included in the last bin. The lower panels show the ratio of data to the background prediction. The hatched error bands indicate the combined experimental, theoretical and MC statistical uncertainties of these background predictions. The arrows, when present, indicate the value of the SR requirement on the quantity presented on the x-axis

7 Results

The expected and observed numbers of events in the ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ SRs are shown in Tables 7 and 8, respectively, together with the SM prediction breakdown for the background processes. The expected yields are derived using the background-only fit configuration. All systematic and statistical uncertainties described in Sect. 6 are included in the predictions. A graphical representation of the tables is given in Fig. 7, where the bottom panel shows the statistical significance [119] of the difference between the observation and prediction. No significant deviation of the observed data from the SM prediction is found. The largest difference appears in $\textrm{SR}^{\textrm{bin4}}_{{{\textrm{tW}} _\mathrm {{0L}}}}$, corresponding to $500< E_{\text {T}}^{\text {miss}} < 600$ $\text {GeV}$, and amounts to a data event deficit of around $2.5\sigma$ considering statistical and systematic uncertainties of the SM prediction. Since the data and predictions agree well in the bins below and above, this deficit is considered to be a statistical fluctuation.

Figure 8 shows the observed data and the SM prediction in the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel for the $E_{\text {T}}^{\text {miss}}$ distribution in the SR using the binning of the final fit. In the same figure, the W-tagged jet multiplicity, the $m_{W \text {-tagged},\textrm{b}_{1}}$ observable and the $m_{\textrm{T}}({\mathrm {b_{1}}},E_{\text {T}}^{\text {miss}})$ observable are shown in a region that contains all SR requirements with the exception of the one on the variable shown in the plot. Small local deficits are seen in the $m_{W \text {-tagged},\textrm{b}_{1}}$ variable around 480 $\text {GeV}$, although no significant trend is observed in any of the distributions and overall, given the uncertainties, there is good agreement between data and predictions.

Figure 9 shows the observed data and the SM prediction in $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ of the ${{\textrm{tW}} _\mathrm {{1L}}}$ channel. Panel (a) shows the $E_{\text {T}}^{\text {miss}}$ distribution in $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$, using the same bins as in the final fit. In the other panels, the W-tagged jet multiplicity in $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and the observable in both $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ are shown. In all cases, all SR requirements except the one on the shown quantity are applied. Similarly to the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel, no significant trend is observed in the distributions and overall there is good agreement between data and prediction. In addition, Fig. 9c, d show that $N^{J; R=1.0}_{W \text {-tagged}}$ and are powerful discriminating variables for rejecting $t\bar{t}$ and $W \text {+\,jets}$ backgrounds for the considered signal benchmark models.

7.1 Model-independent exclusion upper limits

Model-independent upper limits exclude the presence of a larger generic signal independently for each discovery region considered in this analysis. These limits are evaluated by extrapolating the SM background predictions obtained from the background-only fit configuration to the single-bin inclusive SR. Table 9 presents the results of this evaluation, provided in the form of CL$_\textrm{B}$ representing the probability of the predicted SM background to fluctuate to at least the observed number of events. In addition, 95% CL upper limits are set on the observed ($S^{95}_\textrm{obs}$) and expected ($S^{95}_\textrm{exp}$) numbers of BSM events as well as on the visible cross-section ($\sigma ^{}_\text {vis}$) for all discovery regions.

Table 9 The first column presents the name of the treated discovery region. The next two columns present the observed number of data events and expected SM contribution from the background-only fit in the model-independent regions. The fourth and fifth columns present the 95% CL upper limits on the visible cross-section ($\langle \epsilon \sigma \rangle _{\textrm{obs}}^{95}$) and on the observed number of signal events ($S_{\textrm{obs}}^{95}$), respectively. The sixth column ($S_{\textrm{exp}}^{95}$) shows the 95% CL upper limit on the expected number of signal events, given the expected number of background events and $\pm 1\sigma$ excursions of the expectation. The last two columns indicate the CL$_{\text {B}}$ value, i.e. the confidence level observed for the background-only hypothesis, and the discovery p-value ($p(s = 0)$). These values are calculated using an asymptotic calculator based on a one-sided profile likelihood. Therefore, the p-values corresponding to regions with deficits are capped at 0.5

7.2 Exclusion limits for the 2HDM$+a$ model

The ${{\textrm{tW}} _\mathrm {{0L}}}$ and ${{\textrm{tW}} _\mathrm {{1L}}}$ channels are statistically combined with the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel of Ref. [39] as described in Sects. 5 and 6, in order to provide the most stringent constraints for 2HDM$+a$ models using the $tW$+DM channel.

Exclusion limits on the 2HDM$+a$ model are derived as a function of the parameters $m_a$, $m_{H^{\pm }}$, and $\tan \beta$ in a combined likelihood fit to the events in all CRs and SRs of the three channels and are shown in Fig. 10. The results are presented as a function of $(m_a, m_{H^{\pm }})$ assuming $\tan \beta = 1$ and as a function of $( m_{H^{\pm }}, \tan \beta )$ assuming $m_a = 150\;\text {GeV}$ or $m_a = 250\;\text {GeV}$. Values of $\tan \beta$ up to 30 are considered in order to probe the local maximum at $\tan \beta \in [20,30]$, as explained in Section 1. The 1$\sigma$ uncertainty bands are shown as shaded areas around the expected limit contour of the statistical combination. The typical acceptance, i.e. percentage of events passing the selection requirements defined in Sect. 5, times detector efficiency for the $tW$+DM benchmark signals is 0.02–1.2% for the inclusive ${{\textrm{tW}} _\mathrm {{0L}}}$ SRs, 0.001–0.4% for $\textrm{SR}^{\mathrm {lep.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ and 0.04–1.1% for the $\textrm{SR}^{\mathrm {had.top}}_{{{\textrm{tW}} _\mathrm {{1L}}}}$ bins. Figure 10 also shows the sensitivity of each individual channel in both the $(m_a, m_{H^{\pm }})$ and $( m_{H^{\pm }}, \tan \beta )$ planes. For the fits in the individual channels, the non-$t\bar{t}$ background estimates in the signal regions are derived using all control regions defined in Section  5.2, including the common $t\bar{t}Z$ region for the ${{\textrm{tW}} _\mathrm {{2L}}}$ channel. For the $t\bar{t}$ process, the ${{\textrm{tW}} _\mathrm {{0L}}}$ fit uses the ${{\textrm{tW}} _\mathrm {{0L}}}$ $t\bar{t}$ CR, while the ${{\textrm{tW}} _\mathrm {{1L}}}$ $t\bar{t}$ CR is used in the ${{\textrm{tW}} _\mathrm {{1L}}}$ fit. The left panels in Fig. 10 consider only the $tW$+DM process as signal for the interpretation of the results, while the right panels in the same figure consider the contributions of both the $tW$+DM and $t\bar{t}$+DM processes as predicted by the 2HDM$+a$ model.

The introduction of the ${{\textrm{tW}} _\mathrm {{0L}}}$ channel and the statistical combination performed in this paper extend the sensitivity towards large $H^\pm$ boson masses. Exclusion limits are placed in the high $\tan \beta$ parameter space for the first time in this final state. Signal models assuming $H^{\pm }$ boson masses up to 1.5 $\text {TeV}$ and a-boson masses up to 350 $\text {GeV}$ can be excluded at 95% CL for $\tan \beta = 1$. For an a-boson mass of 150 (250) $\text {GeV}$, $\tan \beta$ values up to 2 are excluded for $H^{\pm }$ masses between 300 (400) $\text {GeV}$ and 1.5 $\text {TeV}$. Signals with $\tan \beta$ values between 20 and 30 are also excluded for $H^{\pm }$ masses between 500 and 800 $\text {GeV}$ (900 $\text {GeV}$) and a a-boson mass of 150 (250) $\text {GeV}$. If $t\bar{t}$+DM contributions are considered together with $tW$+DM, a-boson masses up to 250 $\text {GeV}$ can be excluded at 95% CL for an $H^\pm$ mass of 1.5 $\text {TeV}$ assuming $\tan \beta =1$. For low $H^\pm$ boson masses, the lower limit on $m_a$ is 20–40 $\text {GeV}$ higher than when considering only the $tW$+DM contribution at the same $\tan \beta$ value. Assuming an $m_a$ value of 150 $\text {GeV}$ or 250 $\text {GeV}$, $H^\pm$ boson masses below 400 $\text {GeV}$ can be excluded for $\tan \beta$ values lower than 1. No additional constraints are observed at $\tan \beta$ > 10 when adding the $t\bar{t}$+DM contribution to the $tW$+DM contribution since, as discussed in Refs. [15, 34], the $t\bar{t}$+DM cross-section in the 2HDM+a model is proportional to $1/\tan ^2\beta$ and is expected to be subdominant at high $\tan \beta$ values.

Fig. 10

The expected and observed exclusion contours as a function of a, b $(m_a, m_{H^{\pm }})$, c, d $( m_{H^{\pm }}, \tan \beta )$ assuming $m_a = 150\;\text {GeV}$ and e, f $( m_{H^{\pm }}, \tan \beta )$ assuming $m_a = 250\;\text {GeV}$. The individual ${{\textrm{tW}} _\mathrm {{0L}}}$ (green line), ${{\textrm{tW}} _\mathrm {{1L}}}$ (red line) and ${{\textrm{tW}} _\mathrm {{2L}}}$ (orange line) analysis channels are shown together with their statistical combination (blue line). Only $tW$+DM contributions are considered in a, c and e, while b, d and f consider $tW$+DM and $t\bar{t}$+DM contributions. Experimental and theoretical systematic uncertainties, as described in Sect. 6, are applied to background and signal samples and illustrated by the $\pm 1$ standard-deviation yellow band and the blue dashed contour lines, respectively, for the statistical combination

8 Conclusions

A search for dark matter in final states with a single top quark and an energetic $W$ boson using 139 fb$^{-1}$ of pp collisions delivered by the LHC at a centre-of-mass energy of 13 $\text {TeV}$ and collected by the ATLAS detector is presented. The search focuses on a two-Higgs-doublet model together with an additional pseudoscalar mediator, a, which decays into dark-matter particles. Final states which include either zero or one charged lepton (electron or muon) and a significant amount of missing transverse momentum are considered. No significant excess relative to Standard Model predictions was found and 95% confidence-level limits are set on the 2HDM$+a$ signal models considered. These limits exclude a-boson mediator masses up to 350 $\text {GeV}$ and $H^{\pm }$ boson masses up to 1.5 $\text {TeV}$ for $\tan \beta = 1$ in comparison with the current 1.3 $\text {TeV}$ bound, and are the most stringent limits on $tW$+DM signal models obtained so far at the LHC. This analysis also provides the first limits for a 2HDM$+a$ signal model assuming $\tan \beta \ge 10$ and using the single-top-quark production signature.