A fast Fibonacci wavelet-based numerical algorithm for the solution of HIV-infected $\textrm{CD4}^{+}\,\textrm{T}$ cells model

Abstract

In this article, we present a novel approach under the Fibonacci wavelet and collocation technique which is computationally efficient to obtain the solution of the model of $\textrm{CD4}^{+} \textrm{T}$ cells of HIV infection. A system of nonlinear ordinary differential equations represents this mathematical model. We have approximated unknown functions and their derivatives using the operational matrix of integration of Fibonacci wavelets to transform this model into a set of algebraic equations and then simplified using a suitable method. It is anticipated that the proposed approach would be more efficient and suitable for solving a variety of nonlinear ordinary and partial differential equations representing the model of medical, radiation, and surgical oncology, and drug targeting systems that occur in medical science and engineering. Tables and graphs are included to show how the suggested wavelet method provides enhanced accuracy for a wide range of problems. Relative data and computations are performed over MATLAB software.

1 Introduction

Several issues in daily living may be modeled mathematically. For instance, we developed a model to explain biological elements like a human immunodeficiency virus infection (HIV). Viruses may enter any live cell in a variety of ways, infect nearly the whole host cell, and evade immune detection. Separating viruses quickly and effectively is the eradication. As pathogens connect to pattern-recognition receptors (PRRs), which trigger innate immune cell antiviral activities, natural immunity responses are triggered. This provides a crucial first break on viral replication. Adaptive immunological responses trigger the immune system’s development of effector cells. Perelson created a biological model of HIV infection in 1989 [1]. This model is a representation of the virus propagation and includes three variables: The quantity of uncontaminated cells, infected cells, and free virus particles. Leukocytes, also known as $\textrm{CD4}^{+}\,\textrm{T}$ cells, are fundamental components of the human immune systems (HIS), which work to combat illnesses. Recent studies show that numerical approximation becomes a great tool to handle different phenomena in neuroscience and technology such as entropy optimization of hemodynamic peristaltic pumping [2], dynamism of a hybrid Casson nanofluid [3], and interaction between compressibility and particulate suspension [4].

1.1 International report on HIV

The primary reason to take into account the HIV infection model is because AIDS has an impact on our health-related difficulties and challenges. Around the world, there were 37.9 million people living with HIV, 23.3 million people receiving anti-HIV medication, and 1.7 million people who had only recently contracted the disease, according to the UNAIDS 2018 report. In 2018, about 1 million people had been passed away from illnesses linked to AIDS [5]. It was also predicted that there will be roughly 38.4 million HIV-positive people in the globe in 2021. There were 36.7 million adults and 1.7 million children (aged 15 and under). Moreover, there were $54 \%$ of women and girls in 2021. AIDS-related diseases claimed the lives of almost 650,000 people worldwide. The most affected nations by HIV are also plagued by other infectious illnesses, food shortages, and other critical issues. Throughout the last few decades, a large number of researchers have worked in a deep on infection of HIV and tried to find out the ways to prevent its infections in people. The modeling of HIV dynamics and its therapies, are of particular interest to those working in the field of biomathematics. We may examine the impact of infection on society and the governing factors via the use of a mathematical model. It is critical to developing models that depict HIV because of the numerous malignancies that have been associated with the presence of HIV. Numerical approaches are required to examine such a model. This motivates us to use wavelet methods to examine this model.

Consider the following system of nonlinear ordinary differential equations of the form:

$$\begin{aligned} \left. \begin{array}{l} \frac{\textrm{d}X}{\textrm{d} \alpha }=a-b X+c X\left( 1-\frac{X+Y}{X_{\max }}\right) -\eta Z X \\ \frac{\textrm{d} Y}{\textrm{d} \alpha }=\eta Z X-e Y \\ \frac{\textrm{d} Z}{\textrm{d} \alpha }=l e Y-\zeta Z \end{array}\right\} \end{aligned}$$

(1)

Which describes the biological model of HIV infection of the $\textrm{CD4}^{+}\textrm{T}$ cells under the initial conditions $X(0)=0.1, Y(0)=0$, and $Z(0)=0.1$.

Where the parameters of this model represent,

$$\begin{aligned} \begin{aligned} X(\alpha ) =\,&\text { Amount of assistant}\,\textrm{T}\,\text {cells in blood at}\;\alpha ,\\ Y(\alpha ) =\,&\text { Infected amount of assistant}\,\textrm{T}\,\text {cells by HIV in blood},\\ Z(\alpha ) =\,&\text { Concentration susceptible free HIV particles in the blood},\\ a=\,&\text { Producing rate of assistant}\,\textrm{T}\,\text {cells which are not infected }\\ b=\,&\text {Rate of uninfected assistant}\,\textrm{T}\,\text {cells at natural turnover }\\ e=\,&\text { Death rate of uninfected assistant}\,\textrm{T}\,\text {cells }\\ \zeta =\,&\text {Free virus particles at natural turnover }\\ \eta Z X =\,&\text { HIV infection of healthy assistant}\,\textrm{T}\,\text {cells}\\ X_{\max } =\,&\text { Maximum assistant}\,\textrm{T}\,\text {cells in the body}\\ \left( 1-\frac{X+Y}{X_{\textrm{max}}}\right) =\,&\text { Logistic development of the healthy } \textrm{CD4}^{+}\,\textrm{T}\,\text {cells}.\\ \end{aligned} \end{aligned}$$

In addition to the above notations, some particular values of the following parameters are also assumed as part of the model described above. Let the infection rate is denoted by a real number k in the infected human body and the values of the parameters occurred in this system as $a=0.1$, $b=0.02, e=0.3, c=3, \zeta =2.4, \eta =0.0027, X_{{\text {max}}}=1500, l=9$. At the initial stage of infection of T cells, not all the $\textrm{CD4}^{+} \textrm{T}$ cells are completely infected but some of them are still unaffected and also some of the infected cells are not capable to produce virus particles. $\eta$ is the rate at which the virus particle infects uninfected T cells, and $\eta ZX$ denotes the resulting amount of uninfected cells at that moment. Therefore, this total amount of infected cells is represented as a loss term in (1). Bursting or lytics may be the reason for the death of the infected T cells irrespective of the natural death and some of them may help to produce the virus particles. The death rate of infected T cells due to lytic is denoted by e. Further,$X_{\textrm{max}}$ denotes the maximum number of T cells and the term $1-\frac{X+Y}{X_{\textrm{max}}}$ acts as logistic growth of the T cells. This term is introduced to make sure that the total number of infected and uninfected helper T cells.

Numerous numerical methods have been introduced to tackle the model of HIV-infected $\textrm{CD4}^{+}\,\textrm{T}$ cells. For instance, the operational matrix of Bessel polynomials [6], technique based on differential transform [1], homotopy method for HIV infection model [7], LADM approach for HIV infection model [8], LSCA for HIV infection model [9], MDTM for fractional HIV infection model [10], MVIM for HIV infection model [11], SLCM for HIV infection model [12], BCM for HIV infection model [13], etc.

1.2 Wavelets in numerical analysis

Recently, wavelet algorithms have been developed by a number of researchers to solve various kinds of linear and nonlinear ordinary and partial differential equations (PDEs). Multiresolution analysis, density, orthogonality, and compact support are the main features of the wavelets. Wavelet-based numerical approaches are widely used to solve differential equations due to their simplicity and accuracy. Numerous mathematicians studied the Fibonacci wavelets to handle the differential and integral equations [14] in order to gain advantages from the local property. Both nonlinear Hunter–Saxton equations [15] and time-fractional telegraph equations [16] have seen extensive use of Fibonacci wavelets in numerical solutions. However, when we looked at the literature, we found that there was not much information on utilizing the Fibonacci wavelets to solve the model of HIV-infected $\textrm{CD4}^{+} \textrm{T}$ cells. This gave us the idea to introduce a numerical approach based on the Fibonacci wavelets for solving a system of differential equations representing the HIV-infected $\textrm{CD4}^{+}\,\textrm{T}$ cells.

Wavelet basis-based several approximation techniques also handle the other real-life application-based models of mathematical form such as Sunil et al. [17] applied the Hermite wavelet operational matrix of integration to the fractional model of COVID-19 disease, Sara et al. [18] applied the Legurre wavelets fractional predator–prey population model, SG Venkatesh et al. [19] used Legendre wavelet, and A Beler [20] used Legurre wavelet to handle HIV infection model recently. Also, we found some articles based on wavelets like BWM (Bernoulli wavelet method) [21], numerical solution using Haar wavelet [22,23,24], MTF equations using Hermite [25], etc.

1.3 Features

• Discontinuity is a big problem in the mathematical models to study the natural behavior of any problems but the proposed scheme is best suitable to handle such kind of issues.

• Window concept is used to work at the point of sharp edges and discontinuity to get more information about these types of phenomena.

The main objective of this paper is to provide and discuss a Fibonacci wavelet collocation method (FWCM) to know about the numerical and geometrical behavior of the nonlinear mathematical model with the help of the Fibonacci wavelet basis. The R-K method, Haar wavelet method, Laplace Adomian decomposition method (LADM), LADM-Pade, the homotopy analysis approach, differential transform method, multistep Adomian decomposition method, modified variational iteration method, Runge–Kutta, and other semi-analytic techniques are only a few of the methods that have been previously described to handle this mathematical model. The outcomes of the Fibonacci wavelets are also analyzed with number of these existing techniques. Even if the aforementioned strategies were precise and efficient, FWCM provides a solution with a higher degree of precision. The findings in this paper are novel and unpublished in the literature. Using this approach, complicated numerical methods are eliminated, and valuable information on the model’s numerical behavior is produced. The suggested method also solves the problem with numerical computation. The correctness and competence of the suggested method are demonstrated by contrasting our approach with the published work.

Following is an overview of this article: We explain the characteristics of the Fibonacci wavelets and the approximation of a function using the Fibonacci wavelet basis in Sect. 2. Section 3 presents a fundamental concept for generating the operational matrix of integration, while Sect. 4 provides convergence analysis of the method. In Sect. 5, we discuss how to use the Fibonacci wavelets and approximation of a function to represent FWCM based solution of the mathematical model. By applying the Fibonacci wavelet method described in this article is applied to the HIV-infected $\textrm{CD4}^{+}\,\textrm{T}$ cells model and outcomes are compared in Sect. 6 as well. In Sect. 7, an overall conclusion is drawn.

2 Fibonacci wavelets and function approximation

Wavelets are the family of functions generated by the translation and dilation of a given function recognized as the mother wavelet. When the translation and dilation parameters x and y vary continuously, we obtain the following family of continuous wavelets:

$$\begin{aligned} \varphi _{x, y}(\alpha )=|x|^{-1 / 2} \varphi \left( \frac{\alpha -y}{x}\right) , \quad \forall x, y \in {\mathbb {R}}, x \ne 0. \end{aligned}$$

(2)

If we choose $x=x_0^{-\theta }, y=\omega x_0^{-\theta } y_0, x_0>1, y_0>1$, and $\omega$ and $\theta$ are positive integers, the discrete wavelet family is introduced as,

$$\begin{aligned} \varphi _{\theta , \omega }(\alpha )=\left| x_0\right| ^{\frac{\theta }{2}} \varphi \left( x_0^\theta \alpha -\omega y_0\right) , \end{aligned}$$

where $\varphi _{\theta , \omega }(\alpha )$ is the wavelet basis in $L^2({\mathbb {R}})$. Further wavelets family $\varphi _{\theta , \omega }(\alpha )$ represents an orthonormal basis for the fixed values of $x_{0}=2$ and $y_{0}=1$.

2.1 Fibonacci wavelets

Fibonacci wavelets $\varphi _{\omega , r}(\alpha )=\varphi (\theta , {\widehat{\omega }}, r, \alpha )$ have four arguments; ${\hat{\omega }}=\omega -1, \omega =1,2,3, \ldots , 2^{\theta -1}$ for $\theta \in {\mathbb {N}}$. Variable r is defined to be the degree of Fibonacci polynomials, and $\alpha$ is the normalized time parameter. These wavelets are defined on [0, 1](see [26,27,28]). Therefore,

$$\begin{aligned} \varphi _{\omega , r}(\alpha )= {\left\{ \begin{array}{ll}\frac{2^{\frac{\theta -1}{2}}}{\sqrt{C_r}} F_r\left( 2^{\theta -1} \alpha -{\hat{\omega }}\right) , &\quad \frac{{\hat{\omega }}}{2^{\theta -1}} \le \alpha <\frac{{\hat{\omega }}+1}{2^{\theta -1}}, \\ 0, &\quad \text { Otherwise }\end{array}\right. } \end{aligned}$$

(3)

with

$$\begin{aligned} C_r=\int _0^1\left( F_r(\alpha )\right) ^2 \textrm{d} \alpha . \end{aligned}$$

Here, $r=$ $0,1, \ldots , \mu -1,$ is the degree of the well-known Fibonacci polynomial $F_r(\alpha )$ and the positive integer $\theta$ indicates the maximum resolution level while $\omega =1,2, \ldots , 2^{\theta -1}$ is for the translation parameter.

The solution of the following recurrence equation gives Fibonacci polynomials. So for every $\alpha \in {\mathbb {R}}^{+}$:

$$\begin{aligned} F_{r+2}(\alpha )=\alpha F_{r+1}(\alpha )+F_r(\alpha ), \quad \forall r \ge 0, \end{aligned}$$

with

$$\begin{aligned} F_0(\alpha )=1, F_1(\alpha )=\alpha . \end{aligned}$$

Moreover, the following confined formula may also be used to define them:

$$\begin{aligned} F_{r-1}(\alpha )=\frac{a^r-b^r}{a-b}, \quad \forall r \ge 1, \end{aligned}$$

where a and b are such that they are satisfying the equation $\left( \lambda ^2-\alpha \lambda -1\right) =0$ of the recursion when solved for $\lambda$. Furthermore, polynomial expansion of the Fibonacci wavelets can also be written as [28]:

$$\begin{aligned} F_r(\alpha )=\sum _{i=0}^{\frac{r}{2}}\left( \begin{array}{c} r-i \\ i \end{array}\right) \alpha ^{r-2 i}, \quad \forall r \ge 0, \end{aligned}$$

3 Operational integration matrix

Following is the family of the Fibonacci wavelet basis at $\theta =1$:

$$\begin{aligned} \begin{aligned}&\varphi _{1,0}(\alpha )=1, \\&\varphi _{1,1}(\alpha )=\sqrt{3} \alpha \\&\varphi _{1,2}(\alpha )=\frac{1}{2} \sqrt{\frac{15}{7}}\left( 1+\alpha ^2\right) , \\&\varphi _{1,3}(\alpha )=\sqrt{\frac{105}{239}} \alpha \left( 2+\alpha ^2\right) \\&\varphi _{1,4}(\alpha )=3 \sqrt{\frac{35}{1943}}\left( 1+3 \alpha ^2+\alpha ^4\right) \text {, } \\&\varphi _{1,5}(\alpha )=\frac{3}{4} \sqrt{\frac{385}{2582}} \alpha \left( 3+4 \alpha ^2+\alpha ^4\right) \\&\varphi _{1,6}(\alpha )=3 \sqrt{\frac{5005}{1268209}}\left( 1+6 \alpha ^2+5 \alpha ^4+\alpha ^6\right) , \\&\varphi _{1,7}(\alpha )=3 \sqrt{\frac{5005}{2827883}} \alpha \left( 4+10 \alpha ^2+6 \alpha ^4+\alpha ^6\right) \text {, } \\&\varphi _{1,8}(\alpha )=\frac{3}{2} \sqrt{\frac{85085}{28195421}}\left( 1+10 \alpha ^2+15 \alpha ^4+7 \alpha ^6+\alpha ^8\right) , \\&\varphi _{1,9}(\alpha ) =3 \sqrt{\frac{1616615}{5016284989}} \alpha \left( 5+20 \alpha ^2+21 \alpha ^4+8 \alpha ^6+\alpha ^8\right) , \\&\varphi _{1,10}(\alpha ) =3 \sqrt{\frac{1616615}{11941544471}} \left( 1+15 \alpha ^2+35 \alpha ^4+28 \alpha ^6+9 \alpha ^8+\alpha ^{10}\right) \text {, } \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} \begin{array}{r} \varphi _{10}(\alpha )=\left[ \varphi _{1,0}(\alpha ), \varphi _{1,1}(\alpha ), \varphi _{1,2}(\alpha ), \varphi _{1,3}(\alpha ), \varphi _{1,4}(\alpha ),\varphi _{1,5}(\alpha ), \varphi _{1,6}(\alpha ), \varphi _{1,7}(\alpha ), \varphi _{1,8}(\alpha ), \varphi _{1,9}(\alpha )\right] ^T. \end{array} \end{aligned}$$

Now integrate each member of the aforementioned vector with respect to $\alpha$ limit from 0 to $\alpha$ and then express them as a linear combination of Fibonacci wavelet basis we get;

$$\begin{aligned} \begin{aligned}&\int _0^\alpha \varphi _{1,0}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} 0&\frac{1}{\sqrt{3}}&0&0&0&0&0&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,1}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} -\frac{\sqrt{3}}{2}&0&\sqrt{\frac{7}{5}}&0&0&0&0&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,2}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} 0&\frac{\sqrt{5}}{6 \sqrt{7}}&0&\frac{\sqrt{239}}{42}&0&0&0&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,3}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} -\frac{\sqrt{105}}{2 \sqrt{239}}&0&\frac{7}{2 \sqrt{239}}&0&-\frac{\sqrt{1943}}{4 \sqrt{717}}&0&0&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,4}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} 0&0&0&\frac{\sqrt{717}}{5 \sqrt{1943}}&0&\frac{4\sqrt{2582}}{5 \sqrt{21373}}&0&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,5}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} \frac{\sqrt{385}}{4 \sqrt{2582}}&0&0&0&\frac{\sqrt{21373}}{24 \sqrt{2582}}&0&\frac{\sqrt{1268209}}{24 \sqrt{33566}}&0&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,6}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} 0&0&0&0&0&\frac{4 \sqrt{33566}}{7 \sqrt{1268209}}&0&\frac{\sqrt{2827883}}{7 \sqrt{1268209}}&0&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,7}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} -\frac{3 \sqrt{5005}}{4 \sqrt{2827883}}&0&0&0&0&0&\frac{\sqrt{1268209}}{8 \sqrt{2827883}}&0&\frac{\sqrt{28195421}}{4 \sqrt{48074011}}&0 \end{array}\right] \varphi _{10}(\alpha ), \\&\int _0^\alpha \varphi _{1,8}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} 0&0&0&0&0&0&0&\frac{\sqrt{48074011}}{18 \sqrt{28195421}}&0&\frac{\sqrt{5016284989}}{18 \sqrt{535712999}} \end{array}\right] \varphi _{10}(\alpha ),\\&\int _0^\alpha \varphi _{1,9}(\alpha ) \textrm{d} \alpha =\left[ \begin{array}{llllllllll} -3 \sqrt{\frac{323323}{25081424945}}&0&0&0&0&0&0&0&\frac{\sqrt{535712999}}{5 \sqrt{5016284989}}&0\end{array}\right] \varphi _{10}(\alpha ),\\ \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \int _0^\alpha \varphi (\alpha ) \textrm{d} \alpha =P_{10 \times 10} \varphi _{10}(\alpha )+{\overline{P}}(\alpha ), \end{aligned}$$

(4)

where

$$\begin{aligned} P_{10 \times 10} = \left[ \begin{array}{cccccccccc} 0 &{}\quad \frac{1}{\sqrt{3}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -\frac{\sqrt{3}}{2} &{}\quad 0 &{}\quad \sqrt{\frac{7}{5}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \frac{\sqrt{5}}{6 \sqrt{7}} &{}\quad 0 &{}\quad \frac{\sqrt{239}}{42} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -\frac{\sqrt{105}}{2 \sqrt{239}} &{}\quad 0 &{}\quad \frac{7}{2 \sqrt{239}} &{}\quad 0 &{}\quad \frac{\sqrt{1943}}{4 \sqrt{717}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sqrt{717}}{5 \sqrt{1943}} &{}\quad 0 &{}\quad \frac{4 \sqrt{2582}}{5 \sqrt{21373}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -\frac{\sqrt{385}}{4 \sqrt{2582}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sqrt{21373}}{24 \sqrt{2582}} &{}\quad 0 &{}\quad \frac{\sqrt{1268209}}{24 \sqrt{33566}} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{4 \sqrt{33566}}{7 \sqrt{1268209}} &{}\quad 0 &{}\quad \frac{\sqrt{2827883}}{7 \sqrt{1268209}} &{}\quad 0 &{}\quad 0\\ -\frac{3 \sqrt{5005}}{4 \sqrt{2827883}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sqrt{1268209}}{8 \sqrt{2827883}} &{}\quad 0 &{}\quad \frac{\sqrt{28195421}}{4 \sqrt{48074011}} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sqrt{48074011}}{18 \sqrt{28195421}} &{}\quad 0 &{}\quad \frac{\sqrt{5016284989}}{18 \sqrt{535712999}}\\ -3 \sqrt{\frac{323323}{25081424945}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\sqrt{535712999}}{5 \sqrt{5016284989}} &{}\quad 0 \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} {\overline{P}}(\alpha )=\left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \frac{\sqrt{11941544471}}{10 \sqrt{5016284989}} \varphi _{1,10}(\alpha ) \end{array}\right] \end{aligned}$$

Similarly, we can obtain the same operational matrices for multiple values of $\mu$ and $\theta$.

4 Convergence analysis

Theorem 1

Let H be a Hilbert space and W be a closed and finite dimensional subspace of H such that ${\text {dim}} W<\infty$ and $\left\{ w_1, w_2, \ldots , w_n\right\}$ is any basis for W. Let h be an arbitrary element in H and $h_0$ be the unique best approximation to h out of W. Then, [25]

$$\begin{aligned} \left\| h-h_{0}\right\| _{2}=\overline{G_{h}}.\\ \end{aligned}$$

where ${\overline{G}}_{h}=\left( \frac{{\tilde{Z}}\left( h, w_{1}, w_{2}, \ldots , w_{n}\right) }{{\tilde{Z}}\left( h, w_{1}, w_{2}, \ldots , w_{n}\right) }\right) ^{\frac{1}{2}} { and } {\tilde{Z}}$ is introduced in as follows [25]:

$$\begin{aligned} {\tilde{Z}}\left( h, w_{1}, w_{2}, \ldots w_{n}\right) =\left| \begin{array}{cccc} \langle h, h\rangle &{}\quad \left\langle h, w_{1}\right\rangle &{}\quad \ldots &{}\quad \left\langle h, w_{n}\right\rangle \\ \left\langle w_{1}, h\right\rangle &{}\quad \left\langle w_{1}, w_{1}\right\rangle &{}\quad \ldots &{}\quad \left\langle w_{1}, w_{n}\right\rangle \\ \ldots &{}\quad \ldots &{}\quad \ldots &{}\quad \ldots \\ \left\langle w_{n}, h\right\rangle &{}\quad \left\langle w_{n}, w_{1}\right\rangle &{}\quad \ldots &{}\quad \left\langle w_{n}, w_{n}\right\rangle \end{array}\right| . \end{aligned}$$

(5)

Theorem 2

Suppose $y \in L^{2}[0,1], y:[0,1] \rightarrow {\mathbb {R}}$, and ${\overline{I}}={\text {span}}\left\{ \varphi _{1,0}(\alpha ), \varphi _{1,1}(\alpha ), \ldots , \varphi _{2^{\theta -1}, \mu -1}(\alpha )\right\}$. If $C^{T} \varphi (\alpha )$ is the best approximation of y out of ${\overline{I}}$, and we use Eq. (4) for approximation of integration y, then the error bound is given by:

$$\begin{aligned} \left\| \int _{0}^{\alpha } y\left( \alpha ^{\prime }\right) d \alpha ^{\prime }-C^{T} P \varphi (\alpha )\right\| _{2} \le G_{y}+\gamma _{y}. \end{aligned}$$

(6)

Where,

$$\begin{aligned} \gamma _{y}=\frac{\mu _{1}}{2^{\theta -1} \mu } \sum _{\omega =1}^{2^{\theta -1}}\left| c_{\omega , \mu -1}\right| , \text { with } \mu _{1}=\max _{\alpha \in [0,1]}\left| \varphi _{\omega , \mu -1}\right| , \omega =1, \ldots , 2^{\theta -1}. \end{aligned}$$

Theorem 3

Let $L^{2}[0,1]$ be the Hilbert space generated by the Fibonacci wavelet basis. Let $U(\alpha )$ be the continuous bounded function in $L^{2}[0,1]$. Then, the Fibonacci wavelet expansion of $U(\alpha )$ converges to it.

$$\begin{aligned} \begin{aligned} U(\alpha )=\sum _{i=1}^{\infty } \sum _{j=0}^{\infty } d_{i, j} \varphi _{i, j}(\alpha ). \end{aligned} \end{aligned}$$

(7)

where, $d_{i, j}=\langle U(\alpha ), \varphi _{i, j}(\alpha ) \rangle$, and $\langle ,\rangle$ represents inner product and $\varphi _{i, j}(\alpha )$ are orthogonal functions on [0, 1]. Now,

$$\begin{aligned} d_{{i,j}} & = \int_{0}^{1} U (\alpha )\varphi _{{i,j}} (\alpha ){\text{d}}\alpha \\ d_{{i,j}} & = \int_{0}^{1} U (\alpha )\frac{{2^{{\frac{{\theta - 1}}{2}}} }}{{\sqrt {C_{r} } }}F_{r} \left( {2^{{\theta - 1}} \alpha - \omega + 1} \right) \times \varphi _{{i,j}} (\alpha ){\text{d}}\alpha \\ \end{aligned}$$

where $I=\left[ \frac{\omega -1}{2^{\theta -1}}, \frac{\omega }{2^{\theta -1}}\right]$ and $C_r=\int _0^1\left( F_r(\alpha )\right) ^2 \textrm{d} \alpha$.

Put $2^{\theta -1} \alpha -\omega +1=\vartheta$ then,

$$\begin{aligned} d_{{i,j}} & = \frac{{2^{{\frac{{\theta - 1}}{2}}} }}{{\sqrt {C_{r} } }}\int_{0}^{1} U \left( {\frac{{\vartheta - 1 + \omega }}{{2^{{\theta - 1}} }}} \right)F_{r} (\vartheta )\frac{{{\text{d}}\vartheta }}{{2^{{\theta - 1}} }}, \\ d_{{i,j}} & = {\mkern 1mu} \frac{{2^{{ - \left( {\frac{{\theta - 1}}{2}} \right)}} }}{{\sqrt {C_{r} } }}\left[ {\int_{0}^{1} U \left( {\frac{{\vartheta - 1 + \omega }}{{2^{{\theta - 1}} }},\alpha } \right)F_{r} (\vartheta ){\text{d}}\vartheta } \right]. \\ \end{aligned}$$

Now using the generalized form of mean value theorem to integrals,

$$\begin{aligned} d_{i, j}= \frac{2^{-\left( \frac{\theta -1}{2}\right) }}{\sqrt{C_r}} U\left( \frac{\xi -1+\omega }{2^{\theta -1}}\right) \times \left[ \int _0^1 F_r(\vartheta ) \textrm{d} \vartheta \right] , \end{aligned}$$

where $\xi \in (0,1)$ and choose $\int _0^1 F_r(\vartheta ) \textrm{d} \vartheta =\varepsilon$, then

$$\begin{aligned} d_{i, j}=\frac{\varepsilon 2^{-\left( \frac{\theta -1}{2}\right) }}{\sqrt{C_r}} U\left( \frac{\xi -1+\omega }{2^{\theta -1}}\right) , \forall \xi \in (0,1). \end{aligned}$$

Therefore,

$$\begin{aligned} \left| d_{i, j}\right| =\left| \frac{\varepsilon 2^{-\left( \frac{\theta -1}{2}\right) }}{\sqrt{C_r}}\right| \left| U\left( \frac{\xi -1+\omega }{2^{\theta -1}}\right) \right| , \end{aligned}$$

Since U is bounded by M,

$$\begin{aligned} \left| d_{i, j}\right| \le \frac{|\varepsilon |\left| 2^{-\left( \frac{\theta -1}{2}\right) }\right| M}{\left| \sqrt{C_r}\right| }. \end{aligned}$$

Which implies that the series expansion of $\displaystyle { U(\alpha )}$ converges uniformly as the series $\displaystyle {\sum \nolimits _{i=1}^{\infty } \sum \nolimits _{j=0}^{\infty } d_{i, j}}$ is absolutely convergent .

5 Methodology

In this section, we would like to give a methodology in order to find an approximate solution for the HIV infection model of $\textrm{CD4}^{+}\,\textrm{T}$ cells based on the Fibonacci wavelets. Assume that,

$$\begin{aligned} \frac{\textrm{d} X}{\textrm{d} \alpha }= & {} R^{T} \varphi (\alpha ) \end{aligned}$$

(8)

$$\begin{aligned} \frac{\textrm{d} Y}{\textrm{d} \alpha }= & {} S^{T} \varphi (\alpha ) \end{aligned}$$

(9)

$$\begin{aligned} \frac{\textrm{d} Z}{\textrm{d} \alpha }= & {} T^{T} \varphi (\alpha ) \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned} \text { where, } R^{T}&=\left[ r_{1,0}, \ldots r_{1, \mu -1}, r_{2,0}, \ldots r_{2, \mu -1}, r_{2^{\theta -1}, 0}, \ldots r_{2^{\theta -1}, \mu -1}\right] , \\ S^{T}&=\left[ s_{1,0}, \ldots s_{1, \mu -1}, s_{2,0}, \ldots s_{2, \mu -1}, s_{2^{\theta -1}, 0}, \ldots s_{2^{\theta -1}, \mu -1}\right] ,\\ T^{T}&=\left[ t_{1,0}, \ldots t_{1, \mu -1}, t_{2,0}, \ldots t_{2, \mu -1}, t_{2^{\theta -1}, 0}, \ldots t_{2^{\theta -1}, \mu -1}\right] ,\\ \text { and, } \varphi (\alpha )&=\left[ \varphi _{1,0}(\alpha ), \ldots \varphi _{1, \mu -1}(\alpha ), \varphi _{2,0}(\alpha ), \ldots \varphi _{2, \mu -1}(\alpha ), \varphi _{2^{\theta -1}, 0}(\alpha ), \ldots \varphi _{2^{\theta -1}, \mu -1}(\alpha )\right] . \end{aligned} \end{aligned}$$

Integrate (8), (9), and (10) concerning ‘$\alpha$’ from ‘0’ to ‘$\alpha$.’ We get

$$\begin{aligned} \begin{aligned}&X(\alpha )=X(0)+\int _{0}^{\alpha } R^{\textrm{T}} \varphi (\alpha ) \textrm{d} \alpha \\&Y(\alpha )=Y(0)+\int _{0}^{\alpha } S^{\textrm{T}} \varphi (\alpha ) \textrm{d} \alpha \\&Z(\alpha )=Z(0)+\int _{0}^{\alpha } T^{\textrm{T}} \varphi (\alpha ) \textrm{d} \alpha \end{aligned} \end{aligned}$$

Similarly, express the initial conditions using $\varphi (\alpha )$ in terms of known vectors D, E, and F. Therefore use (4) to obtain;

$$\begin{aligned} \left. \begin{array}{l} X(\alpha )=D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )] \\ Y(\alpha )=E^{T} \varphi (\alpha )+S^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )] \\ Z(\alpha )=F^{T} \varphi (\alpha )+T^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )] \end{array}\right\} . \end{aligned}$$

(11)

Now, substitute equations (8), (9), (10), and (11) in (1). We get,

$$\begin{aligned} \left. \begin{array}{c} R^{T} \varphi (\alpha )-a+b\left( D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) -c\left( D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) \\ \left( \frac{1}{X_{\max }}\right) \left( X_{\text {max }}-D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]+E^{T} \varphi (\alpha )+S^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) \cdot \\ +\eta \left( F^{T} \varphi (\alpha )+C^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) \left( D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) =0 \\ S^{T} \varphi (\alpha )+\eta \left( F^{T} \varphi (\alpha )+T^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) \left( D^{T} \varphi (\alpha )+R^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) \\ +e\left( E^{T} \varphi (\alpha )+S^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) =0. \\ T^{T} \varphi (\alpha )-l e\left( E^{T} \varphi (\alpha )+S^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) +\zeta \left( F^{T} \varphi (\alpha )+T^{T}[P \varphi (\alpha )+{\overline{P}}(\alpha )]\right) =0 \cdot \end{array}\right\} \end{aligned}$$

(12)

Hence using the grid points $\alpha _{i}=\frac{2 i-1}{2 \mu }, \quad i=1,2, \ldots , \mu$ collocate each equation in (12) to get a system of $3\mu$ number of nonlinear algebraic equations as:

$$\begin{aligned} \left. \begin{array}{c} R^{T} \varphi \left( \alpha _{i}\right) =a-b\left( D^{T} \varphi \left( \alpha _{i}\right) +R^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) +c\left( D^{T} \varphi \left( \alpha _{i}\right) +R^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \\ \left( \frac{1}{X_{{\text {max}}}}\right) \left( X_{{\text {max}}}-D^{T} \varphi \left( \alpha _{i}\right) +R^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] +E^{T} \varphi \left( \alpha _{i}\right) +S^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \cdot \\ -\eta \left( F^{T} \varphi \left( \alpha _{i}\right) +T^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \left( D^{T} \varphi \left( \alpha _{i}\right) +R^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \\ -e\left( E^{T} \varphi \left( \alpha _{i}\right) +S^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) . \\ S^{T} \varphi \left( \alpha _{i}\right) =-k\left( F^{T} \varphi \left( \alpha _{i}\right) +T^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \left( D^{T} \varphi \left( \alpha _{i}\right) +R^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \\ T^{T} \varphi \left( \alpha _{i}\right) =l e \left( E^{T} \varphi \left( \alpha _{i}\right) +S^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) -\zeta \left( F^{T} \varphi \left( \alpha _{i}\right) +T^{T}\left[ P \varphi \left( \alpha _{i}\right) +{\overline{P}}\left( \alpha _{i}\right) \right] \right) \cdot \end{array}\right\} . \end{aligned}$$

(13)

This system of $3\mu$ number of algebraic equations can be solved using fsolve command in MATLAB. Finally, substitute these values of the Fibonacci wavelet coefficients into (11) to get the Fibonacci wavelet solution (FWCM) of the discussed HIV infection model of $CD4{+}T$ cells.

6 Application

Take into account the following HIV infection biological model of $\textrm{CD4}^{+}\,\textrm{T}$ cells of the form.

$$\begin{aligned} \left. \begin{array}{c} \frac{\textrm{d}X}{\textrm{d} \alpha }=a-b X+c X\left( 1-\frac{X+Y}{X_{\max }}\right) -\eta Z X \\ \frac{\textrm{d} Y}{\textrm{d} \alpha }=\eta Z X-e Y \\ \frac{\textrm{d} Z}{\textrm{d} \alpha }=l e Y-\zeta Z \end{array}\right\} \end{aligned}$$

(14)

subject to the initial conditions $Y(0)=0, X(0)=0.1$ and $Z(0)=0.1$. For the values of the parameters of the HIV model given as $a=0.1, b=0.02, e=0.3, c=3, \zeta =2.4, \eta =0.0027, X_{{\text {max}}}=1500, l=9$, we applied the Fibonacci wavelets collocation method at different values of the $\mu =6,\quad 10$ and the obtained solutions are expressed below in terms of the Fibonacci wavelets.

$$\begin{aligned} \begin{aligned} X_{6}(\alpha )=\,&0.1+0.391226041063660 \alpha +0.658675023106998 \alpha ^2+0.277893133979247\alpha ^{3} \\&+1.177134783080766 \alpha ^{4}-0.645872371310166 \alpha ^{5}+0.636436216615935 \alpha ^{6}.\\ Y_{6}(\alpha )=\,&2.691834469996492 10^{-05} \alpha +1.752070565382036 ^{-05} \alpha ^{2}-9.114423829265501 \times 10^{-6} \alpha ^{3} \\&7.074026118122498 \times 10^{-6} \alpha ^{4}-3.139734237876142 \times 10^{-6} \alpha ^{5}+7.587217980409271 \times 10^{-7} \alpha ^{6}. \\ Z_{6}(\alpha )=\,&0.1-0.239930028644941 \alpha +0.287163848461543 \alpha ^{2}-0.225793198594894 \alpha ^{3} \\&0.125350273263879 \alpha ^{4}-0.046066809677993 \alpha ^{5}+0.008375606938865 \alpha ^{6}. \end{aligned} \end{aligned}$$

Similarly, the solution of the technique described in this paper for $\mu =10$ obtained as;

$$\begin{aligned} \begin{aligned} X_{10}(\alpha )=\,&0.1+0.397957486097656 \alpha +0.592843121911826 \alpha ^{2}+0.589916822894210 \alpha ^{3} \\&+0.434584659490634 \alpha ^{4}+0.276885379242344 \alpha ^{5}+0.100629706589874 \alpha ^{6} \\&+0.091218024363554 \alpha ^{7}-1.385994299865041 \times 10^{-4}\alpha ^{8} +0.009271277144194 \alpha ^{9}\\&+ 0.005588219574928 \alpha ^{10}. \\ Y_{10}(\alpha )=\,&2.700009620232397 \times 10^{-5} \alpha +1.727414215387677 \times 10^{-5} \alpha ^{2}\\&-8.405040841816345 \times 10^{-6} \alpha ^{3}+6.197272282093506 \times 10^{-6}\alpha ^{4}\\&-2.955361856777003 \times 10^{-6}\alpha ^{5}+1.389187262533337 \times 10^{-6}\alpha ^{6}\\&- 6.298772685137824 \times 10^{-7} \alpha ^{7}+2.454884456803799 \times 10^{-7} \alpha ^{8}.\\&-4.658120499988379 \times 10^{-10} \alpha ^{9} \\ Z_{10}(\alpha )=\,&0.1-0.239999906162426 \alpha +0.288034579883702 \alpha ^{2}-0.230396282041108 \alpha ^{3} \\&+0.138150334553266 \alpha ^{4}-0.066046831447757 \alpha ^{5}+0.025878619729596 \alpha ^{6} \\&-0.008160119735072 \alpha ^{7}+0.001863453186237 \alpha ^{8}-0.000225897923658 \alpha ^{9}. \end{aligned} \end{aligned}$$

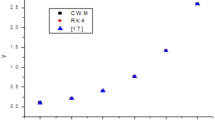
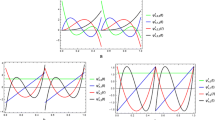
Tables 1, 2, and 3 represent a value comparison of the Fibonacci wavelet solution for $X(\alpha ), Y(\alpha )$, and $Z(\alpha )$, respectively, while Tables 4, 5, and 6 show error variations in FWCM and a comparison of the absolute error with some other existing method’s absolute errors, i.e., Haar method, LADM [29] for $X(\alpha ), Y(\alpha )$ and $Z(\alpha )$, respectively. Table 2 shows that the FWCM solution is accurate up to 9–10 digits, which is a good accuracy for a small number of grid points. It is also clear that error can be reduced by increasing the number of collocation points $(\mu )$ and size of the operational matrix of integration. Figures 1, 2, and 3 represent a graphical comparison of the Fibonacci wavelet solution for $X(\alpha ), Y(\alpha )$ and $Z(\alpha )$, respectively, while Figures 4, 5 and 6 show error variations in FWCM and in several other existing method’s solutions for $X(\alpha ), Y(\alpha )$ and $Z(\alpha )$, respectively. In Table 4, FWCM solution is compared with the homotopy perturbation method (HPTM) [30], the Legendre wavelet method (LWM) [19], orthonormal Bernstein collocation method (OBCM) [31], and quasilinearization method (QL) [32] (Figs. 7, 8, 9, 10, 11, 12; Table 7).

Table 1 Comparison of the FWCM with several other existing methods for X

Fig. 1

Approximate solution using Fibonacci wavelets for X

Table 2 Comparison of the FWCM with several other existing methods for Y

Fig. 2

Approximate solution using Fibonacci wavelets for X

Table 3 Comparison of the FWCM with several other existing methods for Z

Fig. 3

Approximate solution using Fibonacci wavelets for Z

Table 4 Comparison of the FWCM solution with some other existing method solution

Table 5 Error variation for X and at different values of $\mu$

Fig. 4

Absolute error for X

Table 6 Error variation for Y at different values of $\mu$

Fig. 5

Absolute error for Y

Table 7 Error variation for Z at different values of $\mu$

Fig. 6

Absolute error for Z

Fig. 7

Comparison of FWCM solution for different values of a for X

Fig. 8

Comparison of FWCM solution for different values of a for Y

Fig. 9

Comparison of FWCM solution for different values of a for Z

Fig. 10

Comparison of FWCM solution for different values of b for X

Fig. 11

Comparison of FWCM solution for different values of b for Y

Fig. 12

Comparison of FWCM solution for different values of b for Z

6.1 Figure observations

• (i) Increment in the quantity of death of free virus particles results in decrement in the quantity of number of infected cells. Hence, $\zeta$ is inversely proportional to both $Y(\alpha )$ and $Z(\alpha )$.

• (ii) Since infected T cells directly increase the production rate of free virus particles, therefore, l is directly proportional to $Y(\alpha )$ and $Z(\alpha )$.

• (iii) Rapid infection occurs if it is due to free virus particles. Hence, Y and Z are directly proportional to $\eta$.

• (iv) Increment in the death rate of the uninfected T cells results in decrement in the quantity of infected cells and number of free virus particles because $X(\alpha )$ decreases. Hence, all the modules are inversely proportional to b.

• (v) Increment in the production rate of the uninfected T cells result in increment in the quantity of uninfected cells and number of free virus particles. Therefore, this change will also increase the value of $Y(\alpha )$. Hence, $X(\alpha )$, $Y(\alpha )$, and $Z(\alpha )$ are directly proportional to a.

7 Conclusion

In this research, a numerical technique based on the Fibonacci wavelets and collocation approach is explored and applied for the solution of the HIV-infected $CD4+T$ cells mathematical model. This method delivers superior results with lower processing costs compare than several other existing methods in the literature. As a result, the recommended method is very effective and can be applied to several mathematical models like treatment of cancer, drug targeting systems, and biotherapy. Last but not least, we provide the following conclusions of our investigation:

• In comparison with the analytical solution, the current technique offers more precision.

• This methodology is simple to implement in computer programs, and we may expand it to higher orders by making a little change to the current approach.

• The suggested approach is also quite easy to apply, and the numerical results obtained indicate that it is very effective for solving the aforementioned mathematical models numerically as well as for solving additional systems of differential equations.

• Theoretical discussions are used to describe Fibonacci wavelet properties and their convergent analysis.

• From the analysis above, it can be summarized that we can only reduce the free virus particles and number of infected cells by changing the values of the parameters which directly decreases Y and Z without changing the quantity of healthy cells to a great extent.