Scattershot multiboson correlation sampling with random photonic inner-mode multiplexing

Abstract

Multiphoton interference is an essential phenomenon at the very heart not only of fundamental quantum optics and applications in quantum information processing and sensing but also of demonstrations of quantum computational supremacy in boson sampling experiments relying only on linear optical interferometers. However, scalable boson sampling experiments with either photon number states or squeezed states are challenged by the need to generate a large number of photons with fixed temporal and frequency spectra from one experimental run to another. Unfortunately, even the well-established standard multiplexing techniques employed to generate photons with fixed spectral properties are affected by the detrimental effects of losses, spectral distorsions and reduction in purity. Here, we employ sampling correlation measurements in the photonic inner modes, time and frequency, at the interferometer input and output to ensure the occurrence of multiphoton interference even with pure states of input photons with random spectral overlap from one sample to another. Indeed, by introducing a random multiplexing technique where photons are generated with random inner-mode parameters, it is possible to substantially enhance the probability to successfully generate samples and overcome the typical drawbacks in standard multiplexing. We also demonstrate the classical hardness of the resulting problem of scattershot multiboson correlation sampling based on this technique. Therefore, these results not only shed new light in the computational complexity of multiboson interference but also allow us to enhance the experimental scalability of boson sampling schemes. Furthermore, this research provides a new exciting route toward future demonstrations of quantum computational supremacy with scalable experimental resources as well as future applications in quantum information processing and sensing beyond boson sampling.

1 Introduction

Multiphoton interference is a fundamental phenomenon in quantum optics with numerous applications spanning from quantum foundations [1,2,3,4] to quantum information and sensing technologies [5,6,7,8,9].

Recently, the introduction of the boson sampling problem by Aaronson and Arkhipov (AABS) [10] and the following experimental realizations [11,12,13,14,15,16,17] have provided the potential to achieve quantum computational supremacy without the need of a general-purpose quantum computer. Indeed, AABS simply consists of the task of sampling from the probability distribution of all the possible ways of detecting N interfering photons at the output of a linear interferometer (described by a unitary matrix $\mathcal {U}$ chosen randomly with respect to the Haar measure) after being injected in N out of $M\sim N^2$ distinct fixed input ports [10].

A first enhancement in the scalability of boson sampling experiments was given by the introduction of Scattershot Boson Sampling (SBS) [16, 18, 19], where a fixed number N of identical single photons are postselected in a random set of N input ports by employing $M\sim N^2$ heralded spontaneous parametric downconversion (SPDC) sources. The recent introduction of the Gaussian boson sampling (GBS) problem, based on the use of nonheralded sources of squeezed states and therefore depending on matrix Hafnians instead of matrix permanents, has triggered interesting but still open questions on its computational hardness [20,21,22,23,24,25].

More recently, a variation in SBS with a random number of input photons and only a linear number of heralded SPDC sources was introduced by additionally sampling at the interferometer input over all the possible input states of N or more occupied input ports [26]. This has allowed to achieve a probability of generating input samples which increases instead of decreasing with N, differently from SBS and GBS with a fixed number of postselected photons.

However, all these boson sampling schemes suffer from the experimental challenge to generate a large number of input photons which are identical in their inner-mode properties in order to do not affect the computational hardness of the problem [4, 27,28,29]. Indeed, N photons emitted by different sources or by the same source at different times can differ in their frequency and temporal spectra, especially for $N > 50$ as required to achieve quantum computational supremacy [30]. This is indeed the case not only for single-photon emitters, such as diamond color centers [31], single molecules [32] and quantum dots [33, 34] in boson sampling experiments with single photons but also for sources of squeezed light employed in GBS experiments [22, 24, 35].

The experimental requirement for identical input photons in multiphoton interference experiments has been eased by introducing a sampling process called multiboson correlation sampling (MBCS) [36]. Here, the input photons can differ in their inner mode parameters, e.g., frequencies or injection times, and correlation measurements resolving the correspondent conjugate parameters are performed at the output [36,37,38,39]. This differs from AABS where the sampling measurements at the interferometer output do not resolve the photonic inner degrees of freedom and, therefore, full multi-photon indistinguishability at the detectors can only be observed only for photons identical in all their parameters, including both their frequencies and injection times [4]. The advent of very fast single-photon detectors and high-precision single-photon spectrometers [3, 4, 40,41,42,43,44,45,46] has already made possible the realization of MBCS experiments [47, 48].

Unfortunately, even for MBCS schemes with non-identical input photons, a key experimental challenge is still the need to generate a large number of input photons which states, although they may differ from each other, are not allowed to change between consecutive runs of the experiments.

One possible approach is the use of multiplexing to approximately generate SPDC states $\vert \psi \rangle =\otimes _{i=1}^{k} [ \sqrt{1-\gamma ^2} \sum _{n_i=0}^{\infty } \gamma ^{n_i} \vert n_i,n_i \rangle ]$, with $\gamma =tanh \, r$, of k “multiplexed” modes with $n_i\ge 0$ photons and the same squeezing parameter r [40, 49,50,51,52]. Indeed, by increasing the number k of inner modes in which each single photon can be generated by SPDC sources it is ideally possible to enhance the probability of single photon generation, while keeping the ratio between one photon pair events and two pair events constant. Only $k=13$ inner modes with the optimal value $\gamma = \gamma _{\text {opt}} = 1/\sqrt{2}$ are already enough to reach, in principle, a probability $p=1-\bigl (1-\gamma _{\text {opt}}^2(1-\gamma _{\text {opt}}^2) \bigr )^k \cong 98 \%$ for single-photon generation with a substantial enhancement with respect to the probability of $25 \%$ when no multiplexing is employed [52].

Another promising approach based on demultiplexing of single photons emitted by a single quantum dot was also demonstrated experimentally [17].

However, unfortunately, current multiplexing and demultiplexing techniques in the photonic inner modes, such as time and frequency [17, 40, 49,50,51,52], are threatened, especially for large photon numbers N, by the effect of losses, possible spectral distorsions and reduction in purity. This is due to the need of additional optical elements such as switches, delay lines, storage cavities or phase modulators which are employed to generate photons with both fixed frequency and temporal properties, limiting also the range of exploitable multiplexed modes to scale up the probability in single-photon generation [40, 51, 52]. Furthermore, for high values of squeezing parameters photon-number resolved detectors are required to ensure single-photon emissions.

Therefore, important questions remain to be addressed for future experiments at the intersection between quantum optics and quantum computational complexity. Can classical hardness be achieved by employing single photons whose inner-mode properties change randomly from one sample to another? Can the generation of input photons with random inner-mode properties be turned from an experimental drawback to a resource for more scalable boson sampling realizations while only using a linear number of sources? Can one take also advantage of multi-photon emission in multiplexing techniques without recurring to photon-number resolving detectors?

In this paper, we demonstrate the quantum computational complexity beyond any classical capabilities of quantum linear optics networks even with pure states of input photons which differ randomly in either their central frequencies or injection times from one experimental run to another. Remarkably, we also show how, in this case, a substantial scaling up of experimental implementations of boson sampling is achievable with the current technology.

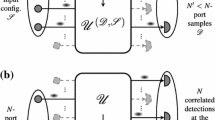
In particular, we introduce a novel technique, random inner-mode multiplexing, which employs heralding SPDC measurements to sample at the interferometer input over either the central times (Fig. 1a) or the central frequencies (Fig. 2a) of the input heralded photons. Further, by sampling at the output in the respective conjugate parameters, instead of “classically” average over such information, it is possible to restore multiphoton indistinguishability at the detectors (see Fig. 1b and 2b, respectively). The emergence of full multiphoton interference even with input photons with random spectral overlap is at the very heart of the classical hardness of this problem, named here scattershot multiboson correlation sampling (SMBCS), even in the approximate case. Indeed, full quantum interference occurs at each experimental run for all possible injection times (frequencies) heralded at the input and all detected frequencies (times) at the output, even if these values vary randomly in consecutive measurements.

By allowing the input photons to have either random central times or frequencies, losses, as well as possible spectral distortions and reduction in purity, due to additional optical elements needed to generate single photons in fixed inner modes are also avoided. This allows to scale up SMBCS experiments to larger photon numbers in comparison to boson sampling, SBS, and MBCS experiments where the input photons are generated in fixed inner modes. Furthermore, no filtering for particular detection times or frequencies is necessary, since this technique takes advantage of all the possible measurement outcomes in the photonic inner modes.

Let us consider, in general, N single photons injected into a set $\mathcal {S}$ of N input ports of an arbitrary passive, linear optical network with a total of $M\sim N^2$ input and output ports. Contrary to conventional boson sampling models, we allow these photons to have normalized spectra $\xi (\omega -\omega _s) {\text {e}}^{\textrm{i}\omega t_s}$ with either different central frequencies $\omega _s$ or different central times $t_s$, with $s \in \mathcal {S}$, where $\xi (\omega -\omega _s)$ is a positive function with maximum at $\omega = \omega _s$ describing the photonic wave packets. The overall input state can be written as the product state

$$\begin{aligned} \vert \mathcal {S} \rangle :={\bigotimes _{s\in \mathcal {S}}} \vert 1;\omega _s,t_{s} \rangle _{s} {\bigotimes _{s \notin \mathcal {S}}} \vert 0 \rangle _{s} \end{aligned}$$

(1)

of $M-N$ vacuum states in the unoccupied ports and N single photon states

$$\begin{aligned} \vert 1;\omega _s,t_{s} \rangle _{s} :=\int _{0}^{\infty } d \omega \, \xi (\omega -\omega _s) {\text {e}}^{+\textrm{i}\omega t_{s}} \hat{a}_{s}^{\dagger }(\omega ) \vert 0 \rangle _{s}. \end{aligned}$$

(2)

2 Scattershot multiboson correlation sampling (SMBCS) with input photons injected at random times

We consider first the case where the N input photons in Eq. (2) are generated with the same frequency ($\omega _s=\omega _0\ \forall s\in \mathcal {S}$) but at random different times $\{t_s\}$ from one sample to another by employing the random time multiplexing (RTM) technique in Fig. 1a. Here, the input photons are the signal photons of pulsed SPDC sources heralded at random times by time-resolved detections of the idler photons. Remarkably, by allowing random input times, this RTM technique is not affected by any losses associated with the optics required in boson sampling experiments based on standard time-multiplexing to generate the photons at fixed times (e.g., multiple delay lines and optical switchers) [49, 50], enhancing therefore substantially the experimental scalability to higher photon numbers.

Multiphoton interference at the interferometer output can be obtained by “erasing” any random time distinguishability via frequency-resolved measurements as depicted in Fig. 1b. For photonic wave packets of a given bandwidth $\Delta \omega$, for example of Gaussian or rectangular shape, this is ensured for small enough frequency resolution $\delta \omega$ according to the conditions

$$\begin{aligned} \delta \omega \ll \left|t_{s}-t_{s'} \right|^{-1} \ \forall s,s'\in \mathcal {S} \quad \text {and} \quad \delta \omega \ll \Delta \omega . \end{aligned}$$

(3)

This includes the case where the input photons exhibit no overlap in their temporal spectra.

We can now define the “Scattershot Multiboson Correlation Sampling” (SMBCS) problem with input photons injected at random input times as the task of generating an overall sample $[(\mathcal {D}, \{\omega _d\}_{d \in \mathcal {D}}),(\mathcal {S},\{t_{s}\}_{s \in \mathcal {S}})]$ determined by an input sample $(\mathcal {S},\{t_{s}\}_{s \in \mathcal {S}})$ of N input ports $\mathcal {S}$ occupied with single photons with random injection times $\{t_s\}$ in addition to the output sample $(\mathcal {D}, \{\omega _d\}_{d \in \mathcal {D}})$ of N detectors $\mathcal {D}$ detecting the N photons at random frequencies $\{\omega _d\}$.

Indeed, defining the annihilation operators $\hat{a}_d =\sum _{s\in \mathcal {S}}\mathcal {U}_{ds}\hat{a}_s$ at the detectors and the permanent ${{\,\textrm{perm}\,}}\mathcal {A} :=\sum _{\sigma \in \Sigma _N} \prod _{i=1}^{N} \mathcal {A}_{i\sigma (i)}$ of a matrix $\mathcal {A}$ as the sum over all possible permutations $\sigma$ from the symmetric group $\Sigma _N$ of order N, we find in appendix the value of the probability of generating a sample $[(\mathcal {D},\{\omega _d\}_{d \in \mathcal {D}}),(\mathcal {S},\{t_{s}\}_{s \in \mathcal {S}})]$ in the detected frequency intervals $I(\{\omega _d\}):=\bigotimes _{d\in \mathcal {D}}[\omega _d -\delta \omega /2, \omega _d +\delta \omega /2]$:

$$\begin{aligned} \begin{aligned} P^{(\mathcal {D}, \mathcal {S})}_{\{\omega _{d}\},\{t_s\}}&= \int\limits_{I(\{\omega _d\})}\prod _{d\in \mathcal {D}}d \omega _d\, \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle \\&= \int\limits_{I(\{\omega _d\})}\prod _{d\in \mathcal {D}}d \omega _d\, \Big [ \prod _{d \in \mathcal {D}} \xi (\omega _d-\omega _0) \Big ]\; \left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _d t_s} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2 \\&= \delta \omega ^{N} \Big [ \prod _{d \in \mathcal {D}} \xi ^2(\omega _d-\omega _0)\Big ]\ \left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _d t_s} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2, \end{aligned} \end{aligned}$$

(4)

where we used the condition (3) in the last equality.

The N! permutations which are coherently added in the matrix permanents defining Eq. (4) correspond to all possible multiphoton paths which bijectively connect the output ports $\mathcal {D}$ with the input ports $\mathcal {S}$. Evidently such multiphoton interference arises from the interfering terms in the squared modulus of each permanent dependent from the oscillating phase factors ${\text {e}}^{\textrm{i}\omega _d t_s}$ of the single-photon amplitudes associated with the detection of each photon s emitted at central time $t_s$ and detected with frequency $\omega _d$ at the output port d. Therefore, such interference is not affected by the random overlap between the photonic wave packets $\xi (\omega -\omega _0) {\text {e}}^{+\textrm{i}\omega t_{s}}$ emitted at random times $t_s$ as in the case of measurements not resolving any photonic degrees of freedom [4, 37]. Indeed, even in the case of negligible overlap between any pair of photons s and $s'$ (i.e., $\mid t_{s'}- t_{s}\mid \gg 1/\Delta \omega$) N-photon interference can be observed as in Eq. (4) if condition (3) is satisfied, as shown experimentally in Ref. [48]. In fact, in such a condition the frequency-resolved measurements “erase” at the detectors any distinguishability in time between the photons. In other words, at each measurement the detectors are not able to distinguish the detected photons in their emission times since they resolve with enough precision the conjugate parameter to time which is the frequency. Therefore, N-photon interference occurs at any possible set of detected frequencies corresponding to an N-photon detection sample without the need of postselecting particular events. Furthermore, the associated probability in Eq. (4) manifests quantum beats as a function of the relative values of the detected frequencies from one sample to another with a visibility which is independent of the photonic emission times. On the other hand, the squared moduli $\xi ^2(\omega _d-\omega _0)$ of the photonic amplitudes, corresponding to the single-photon spectral probability distributions, determine the modulation of such N-photon interference from one frequency sample to another. In particular, for photons of equal rectangular spectral shapes, such a modulation assumes the constant value $\Big [ \prod _{d \in \mathcal {D}} \xi ^2(\omega _d-\omega _0) \Big ] = \Delta \omega ^{-N}$ for N-photon events within the bandwidth $\Delta \omega$ around the central frequency $\omega _0$, while no events occur outside such bandwidth.

Differently, for measurements not resolving the photonic frequencies (i.e., not satisfying the condition (3)) a “classical average” of the N-photon sample probabilities occurs over all the possible photonic frequencies, i.e., an indefinite integration in the frequency domain in the second equality of Eq. (4). In such a case, the observance of N-photon interference would become dependent from the random overlap between the photonic wave packets [4]. Therefore, frequency-resolved measurements have key role in the occurrence of multiphoton interference for each N-photon detection event even if in this technique the photonic wave packets are not identical, but they randomly overlap in time.

We also emphasize that, as in all boson sampling schemes, the experimental task here is not to retrieve the probability for each sample but to experimentally sample from the probability distribution associated with all the possible time-resolved outcomes at the input and frequency-resolved outcomes at the output of the boson sampling interferometric network in Fig. 1a.

In order to give evidence of the classical hardness of SMBCS, we recall that, for Haar random unitary matrices U of size M, the elements $\mathcal {U}_{ds}$ of any submatrices of U of size $N \ll M$ are independent and identically distributed (i.i.d.) Gaussian random variables with a standard normal distribution $\mathcal {N}(0; 1)_{\mathcal {C}}$ with mean 0 and variance 1 [10]. Therefore, the same is valid for the entries $\mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _d t_s}$ of the $N\times N$ submatrices in Eq. (4), independently of the values of $t_s$ and $\omega _d$, since the additional phase factors ${\text {e}}^{\textrm{i}\omega _d t_s}$ only rotate the elements $\mathcal {U}_{ds}$ in the complex plane and the distribution $\mathcal {N}(0; 1)_{\mathcal {C}}$ is symmetric around the origin [36]. Permanents of matrices with i.i.d. Gaussian random entries as in Eq. (4) are strongly believed to be classically hard to estimate [10], implying that approximate SMBCS with random input injection times is at least as classically hard as approximate AABS [36]. Indeed, for any fixed set of injection times approximate SMBCS reduces to approximate MBCS, which has been already shown to be at least as classically hard as approximate AABS [36]. Since approximate SMBCS can be thought as sampling over any approximate MBCS experimental settings for random photonic injection times, such a problem is therefore at least as hard as approximate MBCS. Indeed, given k possible “multiplexed” injected times, the SMBCS problem has additionally the “bonus” that the number of possible samples is $k^N$ times larger in comparison to MBCS experiments with photons injected at fixed times.

Furthermore, the dramatic reduction in losses in the RTM technique enables to scale up boson sampling experiments by avoiding the need to generate photons at fixed times via standard time multiplexing [49, 50]. In addition, by increasing the pulsed pump laser repetition rate $f_{\text {p}}$ or by decreasing the frequency resolution $\delta \omega$ of the detectors it is possible to substantially increase the maximum number of pulses $k \ll f_{\text {p}}/\delta \omega$, therefore enhancing the single-photon generation probability. One may also extend this technique to the use of a cw pump laser which would lead to a maximum number of RTM time bins $k \ll (\delta t \delta \omega )^{-1}$ determined by the time resolution $\delta t$ and the frequency resolution $\delta \omega$ of the detectors.

3 Scattershot multi-boson correlation sampling (SMBCS) with input photons of random colors

We consider now the case where the N input photons in Eq. (2) are injected into the interferometer at the same time $t_s=t_0$ but can have random colors (generally, $\omega _s \ne \omega _{s'}$ if $s \ne s'$), by using the technique of random frequency multiplexing (RFM) in Fig. 2a. Here, SPDC sources are used to generate single photons at random, but known, central frequencies through frequency-resolved heralding with a single-photon spectrometer [40]. This technique differs from the standard frequency multiplexing technique introduced in Ref. [40], where a phase modulator is used to shift the random frequencies of the heralded single photons to a fixed value. Indeed, the RFM technique allows us to sample from all the possible random frequencies of the input photons, which we can assume for simplicity to occur equally likely. Additionally, at the interferometer output in Fig. 2b a sampling process occurs both in the output ports and the detections times the photons are detected at with detector integration times

$$\begin{aligned} \delta t \ll \left|\omega _s - \omega _{s'} \right|^{-1} \ \forall s, s' \in \mathcal {S}\text {\quad and\quad } \delta t \ll 1/\Delta \omega \end{aligned}$$

(5)

to ensure multiphoton indistinguishability. Indeed, this condition corresponds to Eq. (3) by interchanging the conjugate variables frequency and time.

Fig. 1

SMBCS implementation with input photons injected at random times. a Random time multiplexing: Using time-resolved heralding of the idler photons emitted by an SPDC source pumped by a train of laser pulses, N signal photons are generated in random but known time slots at each different sample. b Multiphoton interferometer based on frequency-resolved correlation measurements: N single photons, generated as in panel a, are injected into a passive linear network and detected using frequency-resolving detectors

We can now define SMBCS with input photons of random colors as the task of generating an overall sample $[(\mathcal {D}, \{t_d\}_{d \in \mathcal {D}}),(\mathcal {S},\{\omega _{s}\}_{s \in \mathcal {S}})]$ determined by input sample $(\mathcal {S},\{\omega _{s}\}_{s \in \mathcal {S}})$ of N input ports $\mathcal {S}$ occupied with single photons of random central frequencies $\{\omega _s\}$ in addition to the output sample $(\mathcal {D}, \{t_d\}_{d \in \mathcal {D}})$ of N detectors $\mathcal {D}$ detecting the N photons at random detection times $\{t_d\}$.

Indeed, by interchanging now the conjugate parameters times and frequencies in Eq. (4), the probability

$$\begin{aligned} P^{(\mathcal {D},\mathcal {S})}_{\{t_d\},\{\omega _s\}}\propto \left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _s t_d} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2 \end{aligned}$$

(6)

of generating the sample $[(\mathcal {D}, \{t_d\}_{d \in \mathcal {D}}),(\mathcal {S},\{\omega _{s}\}_{s \in \mathcal {S}})]$ is defined again by permanents of matrices with i.i.d. Gaussian random entries [36]. Analogously to the previous case, this implies that approximating SMBCS with input photons of random colors is at least as classically hard as approximate AABS and MBCS [36]. Again, this computational hardness is intimately connected with the N-photon interference arising from the interfering terms in the squared modulus of the matrix permanents in Eq. (6) dependent from the oscillating phase factors ${\text {e}}^{\textrm{i}\omega _s t_d}$ associated with the detection of a photon of central frequency $\omega _s$ at detection time $t_d$ [4, 36]. Analogously to the previous case, such interference is not affected by the overlap between the photonic wave packets $\xi (\omega -\omega _s) {\text {e}}^{+\textrm{i}\omega t_{0}}$ at random central frequencies since measurements in the conjugate parameter, i.e., detection time, are performed with a precision satisfying Eq. (5).

Furthermore, the RFM technique allows to avoid the losses connected with the need in standard frequency multiplexing of phase modulators to shift the photons heralded at a random frequency to a fixed frequency, enabling a scaling up of boson sampling experiments to higher photon numbers [40].

In addition, while in standard frequency multiplexing the maximum number $k_{max}$ of central frequencies is limited by the maximum frequency shift allowed by the phase modulators, in RFM $k_{max}$ is only limited by the detector resolution according to Eq. (5). As an example, given a frequency resolution of ${1}\textrm{GHz}$ c of ${10}\textrm{ps}$, it is possible to sample already over $k \sim 10$ different central frequencies.

Fig. 2

SMBCS implementation with input photons of random colors. a Random frequency multiplexing: Using frequency-resolved heralding of the idler photons emitted by a pulsed SPDC source, N signal photons are generated at random but known central frequencies at each different sample. b Multiphoton interferometer based on time-resolved correlation measurements: N single photons, generated as in panel a, are injected into a passive linear network and detected using time-resolving detectors

4 SMBCS with more than one single photon per input channel

So far we have considered SMBCS with one single photon in only one of the k multiplexed modes at each of the N input channels. We exploit now the case where $n_s \ge 1$ single photons, each in a different multiplexed mode, are allowed to be injected at each input channel $s \in \mathcal {S}$, leading to an input spatial sample $\mathcal {S'}$ of $N'\ge N$ occupied input channels where each channel s is counted $n_s$ times. In such a case, one can define the SMBCS samples $[(\mathcal {D}', \{t_{d'}\}_{d' \in \mathcal {D'}}),(\mathcal {S'},\{\omega _{s'}\}_{s' \in \mathcal {S'}})]$, for input photons with random colors, and $[(\mathcal {D}',\{\omega _{d'}\}_{d' \in \mathcal {D}'}),(\mathcal {S'},\{t_{s'}\}_{s' \in \mathcal {S'}})]$, for input photons at random times, which are detected in a random set $\mathcal {D}'$ of $N'$ distinct output channels by resolving the corresponding conjugate parameters. The corresponding detection probabilities $P^{(\mathcal {D'},\mathcal {S'})}_{\{t_{d'}\},\{\omega _{s'}\}}$ and $P^{(\mathcal {D'}, \mathcal {S'})}_{\{\omega _{d'}\},\{t_{s'}\}}$ for such samples in Eqs. (6) and (4), respectively, depend now on permanents of $N' \times N'$ matrices with $n_s$ columns for each input channel $s\in \mathcal {S}$, containing the same single-photon interferometer transition amplitudes $\mathcal {U}_{d's}$ but different phase factors associated with different $n_s$ input injection times or frequencies. Since the N sources produce at least one photons, such matrices contain at least $N\times N$ entries which are i.i.d. Gaussian random variables, which is again a strong evidence that such a problem is at least as classical hard as AABS and MBCS [10, 36]. Additionally, by considering additional samples where more than one single photon can be injected per channel the number of possible samples further increases exponentially with the number of multiplexed modes.

Since the total number $N'$ of photons is always proportional to the number N of independent sources, the number of interferometer channels still scales as $M \sim N^{\prime 2}$ for large values of N as in the case of single photon emissions. Therefore, in such a case photons are still likely to scatter separately toward different output channels instead of bunching in the same channel [10]. The likely absence of more than one photons at any of the output channels avoids the need of photon number resolving detectors. This also allows us to distinguish events where one of the multiplexed input modes is occupied with more than one photon if single photons are detected in more than N output channels without again employing photon-number resolving detectors as in standard multiplexing techniques.

Furthermore, the possibility of taking into advantage sampling events with more than N single photons has the potential to enhance the robustness of SMBCS to losses.

5 Discussion

We have introduced and shown the classical hardness even in the approximate case of the so-called scattershot multiboson correlation sampling (SMBCS) problem employing a linear interferometer with input photons which, differently from previous schemes, do not need to be generated with fixed frequencies or injection times from one experimental run to another.

Indeed, SMBCS relies on sampling over either the random central frequencies or injection times of the input photons generated by using the newly introduced random inner-mode multiplexing (RIMM) technique (Figs. 2 and 1). Remarkably, this technique also overcomes two main drawbacks in standard multiplexing techniques imposed by the need of tuning the SPDC generated photons to fixed inner-mode parameters from one experimental run to another: losses associated with the necessary auxiliary optics; limitation in the range of exploitable multiplexed frequencies or time of emissions.

Therefore, SMBCS allows both a scaling up in experimental realizations and an exponential increase in the number of samples with the number of multiplexed modes with respect to current schemes where the input single photons are required to have fixed inner modes at each experimental run.

Interestingly, the RIMM technique can be applied in general to schemes with input photons with any random inner mode parameters in addition to the central frequencies and injection times considered here, e.g., transverse momentum or orbital angular momentum. Indeed, by resolving at the interferometer output the correspondent photonic conjugate parameters, multi-photon indistinguishability is retrieved independently of the input inner modes from one experimental run to another.

One can further take advantage of an additional number of samples, again exponential with the number of multiplexed modes, by allowing more than one mode per channel to be occupied with single photons and without requiring photon-number resolving detectors. This motivates an interesting question: Would it be possible to demonstrate SMBCS quantum computational supremacy by keeping the number of sources fixed independently of N or even using a single source with N injected single photons in N different multiplexed modes in a single input port? Another interesting aspect concerns the effect of cross talk in the linear optical network, which could become less negligible at the increasing of the density of waveguide elements when integrated photonic circuits are employed. Although several techniques have been already developed to reduce such cross talk [53,54,55], it would be interesting to explore if the ability to consider in SMBCS also samples of photons with different temporal and frequency spectra both at the input and output of the interferometer can further reduce it with respect to standard boson sampling with identical photons. Further studies of SMBCS interferometers in these scenarios will surely be the focus of future works.

Finally, these results not only can be exploited to enhance the scalability of any boson sampling scheme with either photon number states or squeezed states with a fixed or random number of detected photons [19, 20, 26], but can also inspire new platforms for applications in quantum sensing and information processing beyond boson sampling, where experimental losses are minimized and the quantum information stored in the spectra of experimentally non-identical photons is exploited in its fullness [4, 56].

Appendix: Frequency correlations of N photons

The detection of a photon in output port $d \in \mathcal {D}$ and at frequency $\omega _d$ can be described by the application of the annihilation operator $\hat{a}_d(\omega _d)$ to the output state of the interferometer. Therefore, the probability density to measure the outcome $(\mathcal {D},\{\omega _d\})$ is given by the correlation function

$$\begin{aligned} \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle \end{aligned}$$

(S1)

evaluated for the input state (Eqs. (1) and (2) in the main paper)

$$\begin{aligned} \vert \mathcal {S} \rangle :={\bigotimes _{s\in \mathcal {S}}} \vert 1;\omega _s,t_{s} \rangle _{s} {\bigotimes _{s \notin \mathcal {S}}} \vert 0 \rangle _{s} \end{aligned}$$

(S2)

with

$$\begin{aligned} \vert 1;\omega _s,t_{s} \rangle _{s} :=\int\limits_{0}^{\infty } d \omega \, \xi (\omega -\omega _s) {\text {e}}^{+\textrm{i}\omega t_{s}} \hat{a}_{s}^{\dagger }(\omega ) \vert 0 \rangle _{s}. \end{aligned}$$

(S3)

Naturally, the structure of this correlation function strongly depends on the passive, linear optical network. Its effect can be described as a linear transformation which connects the output mode operators $\hat{a}_{d}(\omega )$ with the input mode operators $\hat{a}_{s}(\omega )$ via the single-photon transition amplitudes $\mathcal {U}_{ds}$. Since the unoccupied input ports $s\not \in \mathcal {S}$ do not contribute to the correlations, we can for given $\mathcal {S}$ and $\mathcal {D}$ effectively write

$$\begin{aligned} \hat{a}_d(\omega _d) = \sum _{s\in \mathcal {S}}\mathcal {U}_{ds} \hat{a}_s(\omega _d). \end{aligned}$$

(S4)

The probability to detect the N photons in the input state in Eq. (S2) at the output ports $\mathcal {D}$ and in the detected frequency intervals $I(\{\omega _d\}):=\bigotimes _{d\in \mathcal {D}}[\omega _d -\delta \omega /2, \omega _d +\delta \omega /2]$ consequently is

$$\begin{aligned} P^{(\mathcal {D}, \mathcal {S})}_{\{\omega _{d}\},\{t_s\}} = \int _{I(\{\omega _d\})}\prod _{d\in \mathcal {D}}d \omega _d\,\left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle . \end{aligned}$$

(S5)

Using the notation $\Vert \vert \psi \rangle \Vert :=\left\langle \psi |\psi \right\rangle$ and Eq. (S4), we can rewrite the correlation function, Eq. (S1), as

$$\begin{aligned} \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle = \left\| \prod _{d \in \mathcal {D}} \hat{a}_d(\omega _d) \vert \mathcal {S} \rangle \right\| ^2 = \left\| \prod _{d\in \mathcal {D}} \sum _{s_d \in \mathcal {S}} \mathcal {U}_{ds_d} \hat{a}_{s_d}(\omega _d) \vert \mathcal {S} \rangle \right\| ^2 = \Biggl \Vert \sum _{\{s_d\}\in \mathcal {S}^{N}} \prod _{d \in \mathcal {D}} \mathcal {U}_{d s_d} \hat{a}_{s_d}(\omega _d) \vert \mathcal {S} \rangle \Biggr \Vert ^2. \end{aligned}$$

(S6)

This expression can be further simplified by noting that due to the structure of the state $\vert \mathcal {S} \rangle$, Eq. (S2), only those terms contribute, in which each of the N annihilation operators $\hat{a}_{s}(\omega )$, $s\in \mathcal {S}$, appears exactly once. Denoting the set of all permutations of N elements, the symmetric group of order N, as $\Sigma _N$ and recalling Eq. (S2), the correlation function becomes

$$\begin{aligned} \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle = \left\| \sum _{\sigma \in \Sigma _N} \prod _{d \in \mathcal {D}} \mathcal {U}_{d \sigma (d)} \hat{a}_{\sigma (d)}(\omega _d) \vert \mathcal {S} \rangle \right\| ^2 = \left\| \sum _{\sigma \in \Sigma _N} \prod _{d \in \mathcal {D}} \mathcal {U}_{d \sigma (d)} \hat{a}_{\sigma (d)}(\omega _d) \vert 1;\omega _{\sigma (d)},t_{\sigma (d)}] \rangle _{\sigma (d)} \right\| ^2. \end{aligned}$$

(S7)

With the help of the definition of the single-photon states $\vert 1;\omega _s,t_s \rangle$ in Eq. (S3), and recalling the definition $perm \mathcal {A} = \sum _{\sigma \in \Sigma _N} \prod _{i=1}^{N} \mathcal {A}_{i\sigma (i)}$ of the permanent of an $N\times N$ matrix with elements $\mathcal {A}_{ij}$, this can be simplified to

$$\begin{aligned} \begin{aligned} \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle&= \left\| \sum _{\sigma \in \Sigma _N} \prod _{d \in \mathcal {D}} \mathcal {U}_{d \sigma (d)} \xi (\omega _d-\omega _{\sigma (d)}) {\text {e}}^{\textrm{i}\omega _d t_{\sigma (d)}}\vert 0 \rangle \right\| ^2 = \left| \sum _{\sigma \in \Sigma _N} \prod _{d \in \mathcal {D}} \mathcal {U}_{d \sigma (d)} \xi (\omega _d-\omega _{\sigma (d)}) {\text {e}}^{\textrm{i}\omega _d t_{\sigma (d)}}\right| ^2 \\&= \left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} \xi (\omega _d-\omega _s) {\text {e}}^{\textrm{i}\omega _d t_s} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2, \end{aligned} , \end{aligned}$$

(S8)

which, by considering photons with frequency spectra of width $\Delta \omega$ and identical central frequencies $\omega _s=\omega _0 \ \forall s\in \mathcal {S}$, reduces to

$$\begin{aligned} \begin{aligned} \left\langle \mathcal {S}\left| {\prod _{d \in \mathcal {D}}} \hat{a}^{\dagger }_{d}(\omega _d) {\prod _{d \in \mathcal {D}}} \hat{a}_d(\omega _d)\right| \mathcal {S}\right\rangle = \Big [ \prod _{d \in \mathcal {D}} \xi (\omega _d-\omega _0) \Big ]\; \left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _d t_s} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2. \end{aligned} \end{aligned}$$

(S9)

Then, under the conditions

$$\begin{aligned} \delta \omega \left|t_{s}-t_{s'} \right| \ll 1 \ \forall s,s'\in \mathcal {S} \quad \text {and} \quad \delta \omega \ll \Delta \omega \end{aligned}$$

(S10)

from Eq. (5), which ensure that the detectors do not “classically average” over the correlations, the probability in Eq. (S5) takes the form

$$\begin{aligned} P^{(\mathcal {D}, \mathcal {S})}_{\{\omega _{d}\},\{t_s\}} = \ \delta \omega ^{N} \Big [ \prod _{d \in \mathcal {D}} \xi (\omega _d-\omega _0) \Big ]\;\left|{{\,\textrm{perm}\,}}\Big ( \big [ \mathcal {U}_{ds} {\text {e}}^{\textrm{i}\omega _d t_s} \big ]_{\begin{array}{c} d\in \mathcal {D}\\ s\in \mathcal {S} \end{array}} \Big ) \right|^2. \end{aligned}$$

(S11)