Abstract
Given the limited medical resources in most cholera endemic countries, in this paper, a nonlinear fractional SVIR-B (Susceptible-Vaccinated-Infected-Recovered, Bacterial) cholera epidemic model with imperfect vaccination and saturated treatment is proposed and investigated. The model performs well-posed in both epidemiologically and mathematically, especially, we demonstrate the positivity and boundedness of all solutions using the generalized mean value theorem. The control reproduction number \(R_{vt}\) is derived using the next generation matrix method and both local and global stability analyses for the disease-free equilibrium is performed by analyzing the characteristic equation and using Lyapunov functional. Then, the existence and stability of endemic equilibria are further addressed. Sufficient conditions for the existence of backward bifurcation and Hopf bifurcation are also derived. Subsequently, an optimal control problem with vaccination, media coverage, treatment, and sanitation as control strategies is proposed and analyzed, providing a rationale for cholera control and prevention. In addition, several numerical examples are employed to illustrate our theoretical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cholera is a highly contagious acute watery dehydrating diarrheal disease caused by Vibrio cholerae and commonly transmitted by contaminated water and food [1]. Vibrio cholerae not only causes secretory diarrhea but also may be accompanied by serious complications such as renal failure and acute pulmonary edema, which can cause diarrhea, dehydration, and even death within a few hours. The mortality rate of cholera exceeded 50\(\%\) if left untreated [2]. According to the World Health Organization (WHO), cholera causes about 1.3 million to 4 million cases, and 21,000 to 143,000 deaths annually worldwide [3]. Since 2022, cholera outbreaks have occurred in multiple countries including Cameroon and South Sudan and Pakistan, among others, which has caused nearly 100 deaths and more than 6,000 infections in Cameroon (Cameroon Ministry of Public Health). This disease poses still a threat to public health, especially in developing and underdeveloped countries with high population densities.
Mathematical models have evolved into an effective tool for analyzing the spread of various infectious diseases dynamics and providing useful information, especially in terms of prediction. In recent years, various mathematical models have already been proposed to investigate the complex dynamic behavior of cholera. In 1979, Capasso and Paveri-Fontana [4] used two differential equations describing the number of the infected individuals and the concentration of the aquatic pathogenic bacteria to study the spread of the 1973 cholera in the Mediterranean region. Codeço [5] subsequently extended the basic model of Capasso and Paveri-Fontana by adding a compartment of susceptible individuals. Then, they discussed on the role of aquatic reservoirs in the persistence of endemic cholera, as well as derived minimum conditions for epidemic and endemic cholera. Hartley et al. [6] considered two classes of bacterial concentrations: less-infective stage and hyper-infective stage, and combined with a regular SIR (Susceptible-Infectious-Recovered) type model to construct a new high-dimensional dynamic model. It was shown that incorporating the hyper-infectious stage of Vibrio cholerae into the model can better fit observed data. Also, the study suggested that the reduction in the hyper-infectious form of Vibrio cholerae may contribute to reduce the scale of the epidemic effort. Several studies have demonstrated that cholera is largely transmitted not only through the fecal-oral route, but also through human-to-human contact. For this, Mukandavire et al. [7] proposed a mathematical model consisting of multiple transmission pathways to estimate the reproduction number for the 2008-2009 Zimbabwe cholera outbreak. In [8], Tien and Earn constructed a water-borne disease model with the dual transmission pathways using bilinear incidence rates. In the same way, Wang and Cao [9] also constructed cholera model that incorporate the dual transmission pathways, nonlinear incidence and removal rates to study the global dynamical properties of cholera. These works have made significant contributions to advancing the study of cholera dynamic.
Access to safe and sustainable water and sanitation is crucial for effective prevention and control of cholera transmission [3]. However, one in three humans worldwide still lack access to safe drinking water according to WHO and UNICEF (United Nations International Children’s Emergency Fund) [10]. Current strategies for cholera prevention and control mainly include oral cholera vaccine, treatment, and sanitation, and so on. To this end, many researchers have constructed and studied cholera models containing some control strategies. Wang and Chairat [11] analyzed the effects of vaccination, therapeutic treatment, and water sanitation on the cholera outbreaks with the help of a mathematical model in Mukandavire et al. [7]. Zhou et al. [12] considered the impact of imperfect vaccination on the global results dynamics of cholera. Posny et al. [13] combined three types control strategies (vaccination, treatment, and sanitation) with multiple transmission pathways to analyze the transmission of cholera. Lemos-Paião et al. [14] presented SIQRB model to control the transmission of cholera via quarantine treatment. Tian et al. [15] studied a cholera model that considers not only environment-to-human transmission but also waning vaccine-induced immunity as well, and several reasonable optimal control strategies were suggested. In addition, considering that cholera affects mainly the developing and underdeveloped countries with limited treatment facilities, Sharma and Singh [1] developed and studied a new cholera model with vaccination and saturated treatment function.
Clearly, all the above-mentioned works are based on classical integer-order derivatives. However, to some extent, the integer-order model cannot fully account for the natural behavior of the disease [16]. The main reason is that the local operator of the integer-order calculus does not carry any information about the learning and memory mechanisms of the population that influences disease transmission. Conversely, the non-local operator of the fractional-order calculus can expound the global characteristics of disease transmission process, and the derived results are more general nature. In fact, Cole [17] deduced that biological cell membranes possess fractional-order conductivity, so the model of the biological systems are supposed to partition in groups of non-integer order. Currently, there is considerable research on the applications of the fractional-order derivatives in describing different various diseases, such as malaria [18], dengue fever [16], Ebola [19], Covid-19 [20], HIV-AIDS [21], measles [22], cholera [23, 24], and so on.
Motivated by [12] and subsequent works, such as Tian et al. [15] studied some cholera models with imperfect vaccination, and Sharma and Singh [1] studied a cholera model with perfect vaccination and saturated treatment. Currently, there has been comparatively little work on the dynamic behavior of cholera with both imperfect vaccination and saturated treatment functions, to our knowledge. As a result, this paper focuses on the investigation of a fractional-order SVIR-B cholera model with imperfect vaccination and saturated treatment.
The remainder of this paper is structured as follows. In Sect. 2, we formulate a fractional SVIR-B cholera model and discuss the basic properties of its solutions. In Sect. 3, we present a detailed study on the dynamic behavior of the proposed model including the existence of equilibria, the basic reproductive number, the stability analysis and the bifurcation analysis. After that, in Sect. 4, an optimal control problem established and investigated. Numerical simulations are given in Sect. 5. At last, the conclusions are summarized in Sect. 6.
2 Model formulation and basic properties
2.1 Model formulation
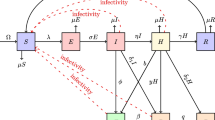
In this paper, we first propose a fractional SVIR-B model for cholera transmission, as depicted in Fig. 1. To better understand the proposed model, some descriptions or assumptions are concisely listed here.
-
(i)
Human population is described by SVIR type model, that is, the total human population N is divided into four mutually compartments subclasses: susceptible S, vaccinated V, infected I, and the recovered R. Then, a class of bacterial concentration (V. cholerae) is be considered and denoted by B.
-
(ii)
New recruitment (including birth, travel, etc.) is assumed to enter the population at a constant rate \(\varLambda\), with a fraction \(\rho\) is regarded as under vaccination control and directly enters the vaccinated class. Besides, the natural death rate of all individuals \(\mu\) and the death rate due to disease of infected individuals \(\epsilon\) are also considered.
-
(iii)
Cholera transmission is discussed only through environment-to-human pathway. More specifically, susceptible individuals are infected by ingesting environmental V. cholerae, and the infection rate is \(\beta B/K+B\), where \(\beta\) and K denote the ingestion rate of the bacteria through contaminated sources and the half saturation constant of the bacteria population, respectively.
-
(iv)
Assuming that vaccine is imperfect, individuals who received vaccines may become infected through contact contaminated sources, thus, \(\sigma\) denotes the vaccine efficacy, in which \(\sigma =0\) indicates that the vaccine is completely effective, while \(\sigma =1\) indicates that the vaccine is completely ineffective. In addition, it is assume that susceptible individuals enter the vaccinated compartment at a constant rate \(\phi\) through inoculation, and the vaccine protection wears off at a constant rate \(\eta\) over time.
-
(v)
An infectious individual can become recovered in two main ways: the natural recovery without treatment and treatment. In general, the untreated self-cure rate \(\gamma\) is less than the treated cure rate r. As the number of patients could exceed the capacity of the health system, a saturated treatment rate can be applied to characterize this saturation effect, and \(\alpha\) is half saturation constant.
-
(vi)
Assume that the growth rate of V. cholera concentration is proportional to the infected individual I, i.e., each infected individual promoted the increase in V. cholerae concentration at the rate of \(\theta\). Further, V. cholerae is assumed to decay at a rate constant \(\xi\).
The flow diagram of the model (1)
As mentioned above, the cholera model can be described as follows:
with initial conditions
where all the parameters are assumed to be non-negative, and \({}_0^{C}{\mathscr {D}}_t^q\) denotes the Caputo fractional derivative (CFD) of order \(q\in (0,1]\) for function f(t) such that [25]
in which \({}_{0}I_t^{q}f(t)=\frac{1}{{\varGamma ( q)}}\int _{0}^t \left( {t - z } \right) ^{q-1} f(z){\textrm{d}}z\) represents the Riemann-Liouville integral, and \(\varGamma (z)=\int _{0}^\infty t^{z-1}e^{-t}{\textrm{d}}t\) is the Gamma function.
2.2 Basic properties
In the following analyses, we shall demonstrate that the model performs well-posed in both epidemiologically and mathematically.
Theorem 1
For the given initial conditions (2), the solutions of system (1) are positive and bounded for all \(t\ge 0\).
Proof
For the proof of the positivity of the solutions, we proceed by contradiction. Assume that S(t) first reaches and crosses the t-axis at time \({\bar{t}}\), it follows that \(S\left( {\bar{t}}\right) =0\) and other state variables are greater than or equal to zero for \(t\in \left[ 0,{\bar{t}}\right]\). Then, recall from the first equation of system (1), it is not difficult to observe that
Using the generalized mean value theorem, S(t) is a non-decreasing function on \(t\in (0,{\bar{t}}]\), which contradicts \(S(t)=0\) for \(t={\bar{t}}\). Hence, \(S(t)\ge 0\) for all \(t\ge 0\). The bounds for other state variables can be obtained similarly.
Then, the boundedness of the solutions are performed in two parts: the human population and bacterial population. For the human population, the first four equations of system (1) are summed to give
Applying the Laplace transform of the above inequality, one has
that can be written as
applying the inverse of the Laplace transform on inequality (6) gives
where \({E_{a,b}}\left( z \right) = \sum \nolimits _{k = 0}^\infty {\frac{{{z^k}}}{{\varGamma \left( {ak + b} \right) }}}\) is Mittag-Leffler function with parameters a and b. It is clear that \(N(0)\le \varLambda /\mu\) when \(t=0\). Then, \(N(t)\le \varLambda /\mu\) can be derived from \(E_{q,1}(-\mu t^q)\ge 0\). From the first equation of system (1), one has
the following analysis process is similar to N(t), thus, one has \(S(t)\le \varLambda \left[ \mu (1-\rho )+\eta \right] /\mu (\mu +\phi +\eta )\). Similarly, from the second equation of system (1), it is easy to obtain \(V(t)\le \varLambda (\mu \rho +\phi )/\mu (\mu +\phi +\eta )\). Next, for the bacterial population, it follows that
thus, one has \(B(t)\le \varLambda \theta /\mu \delta\). Based on analysis and discussion described above, the solutions of the system (1) remain positive and bounded. Hence, system (1) is both mathematically and epidemiologically well-posed. As such, the feasible region for system (1) is given by
The proof is completed.□
3 Analysis of the model
As the variable R(t) does not appear in the other equations of system (1), for brevity, we omit the fourth equation and consider the subsystem of system (1), that is
with initial conditions \(S\left( 0 \right) \ge 0, V\left( 0 \right) \ge 0, I\left( 0 \right) \ge 0\) and \(B(0) \ge 0\) in \(\varXi\).
3.1 Disease-free equilibrium and the control reproduction number
The disease-free equilibrium of system (11) is given by
In the epidemiology, the basic reproduction number \(R_0\) is a essential concept to characterize sustainability threshold, which depends on pathogen and host population, defined as the expected number of secondary infections caused by introducing a single infected individual into otherwise susceptible population in the absence of control measures [26]. Since system (11) involves two control measures, therefore we refer the basic reproduction number as the control reproduction number \(R_{vt}\), which can be calculated using the next-generation matrix method [27].
Let \(Z=[I,B]^T\) denote a vector of infectious variables, then
with the next-generation matrices
which leads to
then, \(R_{vt}\) is determined by the spectral radius of the next-generation matrices
where \(\mathbb {{\varvec{\rho }}}\) is the largest magnitude eigenvalues.
-
(i)
If the vaccine is completely ineffective, and new recruitment are susceptible, i.e., \(\sigma =1\) and \(\rho =0\) or \(\phi =0\) and \(\rho =0\), system (11) becomes an SI-B type model with a single treatment control measure, then the treatment reproduction number is
$$\begin{aligned} R_t=\frac{\varLambda \theta \beta }{\mu \delta K(\mu +\epsilon +\gamma +r)}. \end{aligned}$$(14) -
(ii)
If there is no treatment control measure only with vaccination, i.e., \(r=0\), then the vaccination reproduction number is
$$\begin{aligned} R_v=\frac{\varLambda \theta \beta \left[ (1-\rho )\mu +\eta +\phi \sigma +\rho \sigma \mu \right] }{\mu \delta K(\mu +\epsilon +\gamma )(\mu +\eta +\phi )}. \end{aligned}$$(15) -
(iii)
If there is in the absence of control measures, then the basic reproduction number is
$$\begin{aligned} R_0=\frac{\varLambda \theta \beta }{\mu \delta K(\mu +\epsilon +\gamma )}. \end{aligned}$$(16)
According to the above analysis, the following the relationships hold
which indicates \(R_{vt}<\min \{R_t, R_v\}\).
Also,
which indicates \(R_0>\max \left\{ R_t,R_v\right\}\). It is clear that \(R_0>\max \left\{ R_t,R_v\right\}>\min \{R_t, R_v\}>R_{vt}\), implying that the more control measures are carried out, the less likely the disease spreads among the host population.
After that, we shall discuss the stability of disease-free equilibrium \(E_0\), and state the results in the form of theorems and prove them.
Theorem 2
The disease-free equilibrium \(E_0\) is locally asymptotically stable if \(R_{vt}<1\) and unstable if \(R_{vt}>1\).
Proof
The Jacobian matrix of system (11) evaluated at \(E_0\) is given as:
with the characteristic equation
where \(\nu _1=\mu +\epsilon +\gamma\) and \(\nu _2=\mu +\eta +\phi\). According to Ahmed et al. [28], the Routh-Hurwitz conditions are necessary and sufficient for the Matignon criterion \(\left| {\arg \left( {eig\left( J \right) } \right) } \right| = \left| {\arg \left( {{\lambda _s}} \right) } \right| > {q\pi }/{2}\). It is obvious that, if \(R_{vt}<1\), then all eigenvalues have negative real parts, which implies that \(E_0\) is locally asymptotically stable. But if \(R_{vt}>1\), then there is a positive real eigenvalue, which is not satisfied the Matignon criterion. This finishes the proof. \(\square\)□
Theorem 3
If \(R_{v}<1\), then the disease-free equilibrium \(E_0\) is globally asymptotically stable.
Proof
It is clearly that \(R_v<1\), then \(R_{vt}<1\). Consider the following Lyapunov function
where \(\nu _1\) is defined in Eq. (18). Then, taking on Caputo fractional-order derivative on both sides, one has
It obvious that \({{}_0^{C}{\mathscr {D}}_t^\theta }{L_1}<0\) if \(R_v<1\). Moreover, \(E_0\) is the largest invariant compact set in \(\varXi\). Hence, using LaSalle invariance principle [29], the disease-free equilibrium \(E_0\) is globally asymptotically stable when \(R_v<1\). The proof is completed.□
3.2 Existence of endemic equilibria and its stability
Let the right-hand terms of system (11) be equal to zero resulting in the endemic equilibria, after simplification, one can obtain
and B satisfies the following cubic equation
with
where \(\nu _3=\mu +\eta +\sigma \phi\). That is, there exists a one-to-one correspondence between the endemic equilibria and the positive real roots of \({\mathcal {Q}}(B)\). It can be observed that the coefficient \(a_3\) is always positive and the sign of \(a_0\) is determined by \(R_{vt}\).
Next, the existence and stability of endemic equilibria are discussed in two cases.
3.2.1 Case I: Treatment conditions with ample medical resources, i.e., \(\alpha =0\).
In this case, \(a_3=0\), and \({\mathcal {Q}}(B)\) can be then simplified as
with
-
(i)
If \(R_{vt}>1\), in this case, \(a_0<0\), then Eq. (20) has a unique positive real root.
-
(ii)
If \(R_{vt}<1\), in this case, \(a_0>0\), then \(a_1>0\). For the proof of \(a_1>0\), we will proceed by contradiction. Assume that \(a_1<0\) when \(R_{vt}<1\), in terms of the expression of \(R_{vt}<1\), one has
$$\begin{aligned} \varLambda \theta \beta \left[ (1-\rho )\mu +\eta +\phi \sigma +\rho \sigma \mu \right] <\mu \delta K(\nu _1+r)\nu _2, \end{aligned}$$then
$$\begin{aligned} \varLambda \theta \beta <\delta K(\nu _1+r)\nu _2. \end{aligned}$$(21)Besides, combining the expression of \(R_{t}\) with \(a_1<0\), one has
$$\begin{aligned} \theta \delta (\nu _1+r)K[\mu \nu _2(2-R_{vt})+\beta \nu _3+\beta \sigma \mu ]< \theta \delta (\nu _1+r)K\beta \sigma \mu R_{t}, \end{aligned}$$then
$$\begin{aligned} \delta K(\nu _1+r)[\mu \nu _2(2-R_{vt})+\sigma \beta \nu _2+\beta (\mu + \eta -\sigma \eta )]<\sigma \varLambda \beta ^2\theta , \end{aligned}$$this implies,
$$\begin{aligned} \delta K(\nu _1+r)\nu _2<\varLambda \beta \theta , \end{aligned}$$(22)which contradicts to the inequality (21), and thus \(a_1>0\) when \(R_{vt}<1\). Then, in this case, Eq. (20) has no positive real root. We can thus conclude the following result.
Theorem 4
Assume \(\alpha =0\). Then, system (11) has a unique endemic equilibrium when \(R_{vt}>1\), and no endemic equilibrium when \(R_{vt}<1\).
Then, the stability analysis of the endemic equilibrium \({\bar{E}}=({\bar{S}},{\bar{V}},{\bar{I}},{\bar{B}})\) will be performed in detail below.
Theorem 5
Assume \(\alpha =0\). Then, the endemic equilibrium \({\bar{E}}\) is locally asymptotically stable if \(R_{vt} > 1\).
Proof
The Jacobian matrix of system (11) at \({\bar{E}}\) is given by
giving the following characteristic equation
where
In the following, for simplicity, some notation are defined as:
Besides, the relationships \(\frac{\beta ({\bar{S}}+\sigma {\bar{V}})}{K+{\bar{B}}}=\frac{(\nu _1+r)\delta }{\theta }=\frac{A_0\delta }{\theta }\) and \(0<\sigma <1\) will be used in the following steps. Details of the specific analyses are provided below.
Step 1. The first step is to demonstrate \(b_0>0\). The process is briefly described as follows.
Step 2. The second step is to demonstrate \(b_2b_3-b_1>0\). Then,
Step 3. The last step is to demonstrate \(b_1b_2b_3-b_0b_3^2-b_1^2>0\). A direct calculation shows that
It obvious that all eigenvalues of the characteristic equation (23) have negative real parts, which means that \({\bar{E}}\) is locally asymptotically stable. This completes the proof.□
Then, to prove the global stability of \({\bar{E}}\), in particular, the following lemma is stated.
Lemma 1
[30] Let \(z(t)\in {\mathbb {R}}_+\) be a continuous and derivative function. Then,
Theorem 6
Assume \(\alpha =0\). Then, the unique endemic equilibrium \({\bar{E}}\) is globally asymptotically stable provided \(R_{vt}>1\).
Proof
To prove this, the Lyapunov function is defined as follows
where \(\varPsi \left( z\right) =z-1-\ln \left( z\right)\). It is clear that \(\varPsi (z)\ge 0\) for all \(z\in \left( 0,+\infty \right)\) and \(\varPsi (z)=0\) if and only if \(z=1\). Computing Caputo fractional derivative on both sides, and using Lemma 1, it follows that
From system (11), it is easy to see that \({\bar{E}}\) (\(\alpha =0\)) satisfies the following relations
As a consequence, we directly get that
Denote \({\mathfrak {h}}_1(t)=1-\frac{{\bar{S}}}{S(t)}-\frac{S(t)}{{\bar{S}}}\frac{{\bar{V}}}{V(t)}+\frac{{\bar{V}}}{V(t)}\) and \({\mathfrak {h}}_2(t)=1+\frac{{\bar{S}}}{S(t)}-\frac{{\bar{S}}}{S(t)}\frac{V(t)}{{\bar{V}}}-\frac{{\bar{V}}}{V(t)}\), then
which implies that \({\mathfrak {h}}_1(t)\) and \({\mathfrak {h}}_2(t)\) satisfy the following three cases
-
i)
\({\mathfrak {h}}_1(t)\le 0\) and \({\mathfrak {h}}_2(t)\le 0\);
-
ii)
\({\mathfrak {h}}_1(t)\ge 0\) and \({\mathfrak {h}}_2(t)\le 0\) and \(|{\mathfrak {h}}_2(t)|\ge |{\mathfrak {h}}_1(t)|\);
-
iii)
\({\mathfrak {h}}_1(t)\le 0\) and \({\mathfrak {h}}_2(t)\ge 0\) and \(|{\mathfrak {h}}_1(t)|\ge |{\mathfrak {h}}_2(t)|\).
For item i), it obvious that \({{}_0^{C}{\mathscr {D}}_t^q}{L_2}\le 0.\)
For item ii), we have \(\phi {\bar{S}}=\frac{\sigma \beta {\bar{V}}{\bar{B}}}{K+{\bar{B}}}+\left( \mu +\eta \right) {\bar{V}}-\rho \varLambda \Longrightarrow \phi {\bar{S}}<\frac{\sigma \beta {\bar{V}}{\bar{B}}}{K+{\bar{B}}}+\left( \mu +\eta \right) {\bar{V}}\), thus, inequality (26) can be further simplified as
For item iii), we have \(\eta {\bar{V}}=\left( \mu +\phi \right) {\bar{S}}+\frac{\beta {\bar{S}}{\bar{B}}}{K+{\bar{B}}}-(1-\rho )\varLambda \Longrightarrow \eta {\bar{V}}<\frac{\beta {\bar{S}}{\bar{B}}}{K+{\bar{B}}}+\left( \mu +\phi \right) {\bar{S}}\), after further simplification,
Thus, it is easy to observe that \({{}_0^{C}{\mathscr {D}}_t^q}{L_2}\le 0\) in all three cases. In addition, we can also verify that \({{}_0^{C}{\mathscr {D}}_t^q}{L_2}(t)=0\) if and only if \(S(t)={\bar{S}},V(t)={\bar{V}},I(t)={\bar{I}},B(t)={\bar{B}}.\) It follows that the largest invariant compact set in \(\left\{ \left( S,V,I,B\right) \in \varXi : {{}_0^{C}{\mathscr {D}}_t^q}{L_2}(t)\le 0 \right\}\) is \({\bar{E}}\). As consequence, the globally asymptotically stable of \({\bar{E}}\) has been shown via the Lasalle invariance principle [29]. This finishes the proof.□
Remark 1
For \(q=1,\alpha =0\), in [12], applying the second compound matrix techniques and autonomous convergence theorems, the authors of that study derived the condition for the global stability of endemic equilibrium as follows
where \(\chi >0\) is a constant. However, in the present study, the endemic equilibrium is globally asymptotically stable without any additional restrictions for \(\alpha =0\). In addition, we also analyzed the locally asymptotically stable of the endemic equilibrium, which is no studies in the literature [12].
3.2.2 Case II: Treatment conditions with limited medical resources, i.e., \(\alpha >0\).
In this case, the coefficients \(a_2\) and \(a_1\) change their sign according to different parameter values, and thus, \({\mathcal {Q}}(B)\) may have multiple positive real roots. In terms of Descartes’ rules of signs, we can get the number of all the possible positive real roots of \({\mathcal {Q}}(B)\) (defined in Eq. (19)), as shown in Table 1.
Theorem 7
Assume \(\alpha >0\).
-
(i)
When \(a_2>0,a_1>0\) or \(a_2>0,a_1<0\) or \(a_2<0,a_1<0\), then system (11) consists of a unique a endemic equilibrium \({\tilde{E}}_1\) for \(R_{vt}>1\).
-
(ii)
When \(a_2>0,a_1<0\) or \(a_2<0,a_1>0\) or \(a_2<0,a_3<0\), then system (11) consists maximum two endemic equilibria \({\tilde{E}}_2\) and \({\tilde{E}}_3\) for \(R_{vt}<1\).
-
(iii)
When \(a_2<0,a_1>0\), then system (11) consist maximum three endemic equilibria \({\tilde{E}}_4\), \({\tilde{E}}_5\) and \({\tilde{E}}_6\) for \(R_{vt}>1\).
Notably, item (ii) of Theorem 7 indicates that the system may exist two endemic equilibria provided \(R_{vt}<1\), which normally suggests the existence of backward bifurcation (i.e., a stable disease-free equilibrium coexists with a stable endemic equilibrium). At this time, \(R_{vt}<1\) is necessary but no longer sufficient for disease elimination. In addition, item (iii) of Theorem 7 indicates the system may have multiple endemic equilibria when \(R_{vt}>1\), implying that system may exhibit capable of more complex behavior, such as periodic oscillations and bifurcations. From this, the limited treatment conditions result in the system becomes substantially more complex. The possible existence of bifurcation phenomena will be elaborated later in the next subsection.
Next, we shall discuss the local stability of the endemic equilibria for system (11) under the conditions of limited treatment. Let \({{\tilde{E}}}=\left( {{\tilde{S}}},{{\tilde{V}}}, {{\tilde{I}}},{{\tilde{B}}}\right)\) denote an endemic equilibrium of system (11). Then, the Jacobian matrix at \({{\tilde{E}}}\) is given by
with the characteristics equation of \(J_{{{\tilde{E}}}}\) is
where
Denote
Theorem 8
Assume \(\alpha >0\).
-
(i)
The necessary and sufficient condition for the endemic equilibrium \({{\tilde{E}}}\), to be locally asymptotically stable is that the roots of the characteristic equation (27) satisfy \(\left| {\arg \left( {{\lambda _s}} \right) } \right| > \frac{q\pi }{2}\).
-
(ii)
A sufficient condition for the endemic equilibrium \({{\tilde{E}}}\), to be locally asymptotically stable is \({\varDelta _i}>0, i=1,2,3\).
-
(iii)
The necessary condition for the the endemic equilibrium \({{\tilde{E}}}\), to be locally asymptotically stable is \(c_0>0\).
Remark 2
Note that, the analytical results of Theorem 8 do not give more specific conditions about the stability of the endemic equilibrium. Currently, there are explicit criteria for the stability of fractional-order systems of 3rd-order and below (reviewed in [28]), but it is very difficult to give an explicit criteria for 4th-order and above.
3.3 Bifurcations analysis
As is well known, characterizing the types of bifurcations that the system may undergo is instructive for the disease control. In the following, we shall discuss the possible existence of bifurcations for the present model.
3.3.1 Backward and forward bifurcations
As mentioned before, we note that \(R_{vt}=1\) is equivalent to
according to Theorem 2, the disease-free equilibrium \(E_0\) is locally asymptotically stable if \(\beta <{\hat{\beta }}\) and unstable if \(\beta >{\hat{\beta }}\). Hence, \(\beta ={\hat{\beta }}\) is a bifurcation value. Then, taking \(\beta\) as the bifurcation parameter, we investigate the possibility of backward bifurcation, which should be noted herein that is similar to that presented in [31] but for the case of integer-order derivative. Hence, we shall go through the major outlines of it.
Theorem 9
If \(R_{vt}<1\), then
then system (11) exhibits a backward bifurcation at \(R_{vt}=1\). If the inequality holds reversed, then the system exhibits a forward bifurcation at \(R_{vt}=1\).
Proof
The Jacobian matrix of the system (11) at \(E_0\) and \({\hat{\beta }}\) is expressed as
with the eigenvalues are given by
it follows that \({J_{{(E_0,{\hat{\beta }})}}}\) have a simple zero eigenvalue and the rest of eigenvalues have negative real parts, which indicates \(E_0\) is a nonhyperbolic equilibrium when \(\beta ={\hat{\beta }}\).
Step 1. Calculate the eigenvectors of \({J_{{(E_0,{\hat{\beta }})}}}\) associated with \(\lambda _1=0\). The right eigenvector \({\varvec{w}}=\left( w_1,w_2,w_3,w_4\right) ^T\) is derived from \({J_{{(E_0,{\hat{\beta }})}}}\cdot {\varvec{w}}=0\), thus,
Also, the left eigenvector \({\varvec{v}}=\left( v_1,v_2,v_3,v_4\right)\) is derived from \({\varvec{v}}\cdot {J_{{(E_0,{\hat{\beta }})}}}=0\), and such that the property \({\varvec{v}}\cdot {\varvec{w}}=1\), thus
Step 2. Calculate bifurcation coefficients a and b. Then, the coefficients a and b are given by
where \(f_k\)’s denote the right-hand side of system (11) and \(x_i\) denote the corresponding state variables, i.e., \((x_1,x_2,x_3,x_4)=(S,V,I,B)\). It follows that the coefficients a and b are simplified to
then,
Clearly, the coefficient b is always positive, and the sign of coefficient a determines the direction of bifurcation for the system at \(R_{vt}=1\). Thus, system (11) may exhibit a backward bifurcation at \(R_{vt}=1\) if \(a>0\), i.e., inequality (30) holds, and if \(a<0\), i.e., inequality (30) is reversed, bifurcation is forward. \(\square\)□
Remark 3
When \(\alpha =0\), inequality (30) holds reversed, and the system exhibits a forward bifurcation, which coincides with the preceding analysis. At this point, the control reproduction number \(R_{vt}\) is usually a necessary and sufficient condition for disease elimination.
3.3.2 Existence of periodic solutions through Hopf bifurcation
Recall from Sec. 3.2 that system (11) with adequate treatment condition has a unique endemic equilibrium when \(R_{vt}>1\), whereas the system with limited treatment condition may exist multiple endemic equilibria at this point. This implies that the system may exhibit the complex behavior, such as periodic oscillations arising from the Hopf bifurcation. At present, there have been many studies on Hopf bifurcations of fractional-order systems. Some literature can be found in [32,33,34,35].
Let us consider \(\alpha\) as the bifurcation parameter when \(R_{vt}>1\), that is, \({{\tilde{E}}}\) is locally asymptotically stable when \(\alpha <{\tilde{\alpha }}\) and unstable when \(\alpha >{\tilde{\alpha }}\). At \(\alpha ={{\tilde{\alpha }}}\), the equilibrium \({{\tilde{E}}}\) loses its stability, at which point it begins periodic oscillations. Indeed, there exists a simple Hopf bifurcation as long as Eq. (27) satisfies the following conditions
-
(i)
Eq. (27) admits a pair of purely imaginary eigenvalues and the other eigenvalues have negative real parts;
-
(ii)
\({{\frac{{{\textrm{d}}\left[ {{\mathop {\textrm{Re}}\nolimits } \left( \lambda \right) } \right] }}{{{\textrm{d}}\alpha }}} \bigg |_{\alpha = {\tilde{\alpha }} }} > 0\).
For item (i), according to the literature [36], the coefficients of characteristics equation (27) are required to satisfy the following conditions
-
(a)
\(c_0>0,c_1>0\) and \(c_1c_2-c_0c_3>0\);
-
(b)
\(\varDelta _3=0\), which is defined in Eq. (28).
Next, we shall derive the transversely condition (ii). Differentiate Eq. (27) with respect to \(\alpha\), one has
which gives
Assume that \(\lambda =\pm iw\) is a pair of purely imaginary root of Eq. (27) corresponding to \({\tilde{\alpha }}\). Substituting \(\lambda =iw\) into the above equation, one has
where
Clearly, if
holds, then \({\left. {\frac{{{\textrm{d}}\left( {{{\textrm{Re}}}\left( \lambda \right) } \right) }}{{{\textrm{d}}\alpha }}} \right| _{\alpha = {\tilde{\alpha }}}}>0\). In what follows, we summarize this results.
Theorem 10
Assume that \(({\textbf{H}})\) is true, system (11) may occur a periodic oscillations at \({{\tilde{E}}}\) when \(\alpha ={\tilde{\alpha }}\).
4 Optimal control problem
In this section, we aim to control cholera transmission by minimizing the number of infected individuals and reducing the V. cholerae concentration in environment, as well as to reduce the cost associated with such control measures. As such, we extend system (1) and formulate a corresponding the control problem by considering the several control measures such as vaccination, media coverage, treatment, and sanitation. These control measures are discussed in details below.
-
(i)
Vaccination to susceptible individuals: in system (1), the inoculation proportion of susceptible individuals is assumed to be constant \(\phi\) throughout. Herein, vaccination rate \(\phi\) is treated as a control variable and indicated with \(u_1(t)\).
-
(ii)
Contact rate reduced through media coverage: it is well-known that media coverage can improve people awareness of prevention of infectious diseases, which decreases the opportunity and probability of contact transmission. Thus, we introduce control variable \(u_2(t)\) to denote the reduced contact rate through media coverage.
-
(iii)
Revaccination to vaccinated individuals: cholera vaccines efficacy and effectiveness can wear off with time, thus, vaccinated individuals could be vaccinated again for the booster immunization. The control variable \(u_3(t)\) is another kind of vaccination strategy used to control for rate of loss vaccine immunity.
-
(iv)
Treatment to infected individuals: despite the constrained medical resources in the community, government may invest more medical resources when the disease large-scale outbreaks. Introducing new control variable \(u_4(t)\) denotes intensive treatment for the infected individuals, that is, increase \(\gamma\) and decrease saturation constant \(\alpha\).
-
(v)
Contaminated water treatment: the control variable \(u_5(t)\) denotes water sanitation leads to the death rate of vibrios.
Thus, under these control measures, we consider the following fractional optimal control problem:
subject to the fractional control system
with the nonnegative initial conditions (2). Among them, \({\mathcal {J}}(\cdot )\) is the objective function of fractional control system (32), \(\kappa _i\), \(i=1,2,3,4,5\) denotes proportional weights associated with the cost of that corresponding control measures. Besides, control variable \(U=\left( u_1,u_2,u_3,u_4, u_5\right)\) comes from the following admissible set of control functions:
where \(t_f\) denotes the final time of control measures. For notational convenience, we rewrite Eq. (32) in the matrix form, that is
where \(X = {\left( {S,V,I,R,B} \right) ^T}\) and \(G=\left( g_S, g_V, g_I, g_R, g_B\right) ^T\).
Remark 4
In the objective function (31), we use quadratic terms expression to account for the nonlinear costs that may occur at high intervention levels. Although this is not necessary, it is currently one of the most common way to penalize the use of controls.
4.1 Existence of optimal control solution
Theorem 11
There exists an optimal control solution \(U^*=(u_1^*,u_2^*,u_3^*,u_4^*,u_5^*)\in \aleph\) that minimizes the objective functional in Eq. (31).
Proof
The existence of optimal control solution can be verified using the result of Fleming and Rishel theorem [37]. Namely, the optimal control problem (31)-(32) is required to satisfy the three conditions. The first condition is to prove the set of control and corresponding state variables are non-negative and non-empty. Clearly, the solution of system (32) is bounded, and its proof is similar to that of Theorem 1. Also, the right-hand side functions of system (32) satisfies the Lipschitz condition with respect to the state variables. From Picard-Lindelöf theorem [38], the first condition holds. Then, the second condition is to demonstrate that the control set \(\aleph\) is closed convex and the integrand of the objective functional in Eq. (31) is also convex with respect to control variable U. This condition is obviously holds. The final condition is to prove that there exists a continuous function g(U) satisfying the integrand of objection functional is greater than or equal to g(U), and \(g(U)/|U|\rightarrow \infty\) whenever \(|U|\rightarrow \infty\). Thus, let \(g(U)=\frac{\kappa }{2}\sum \nolimits _{i = 1}^5 {u_i^2}\) where \(\kappa =\min \left\{ \kappa _1,\kappa _2,\kappa _3,\kappa _4,\kappa _2,\kappa _5\right\}\), then
besides, g(U) is continuous and satisfy \(g(U)/|U|\rightarrow \infty\) as \(|U|\rightarrow \infty\). Thus, three conditions for existence of optimal control solution is satisfied. The proof is finished.□
4.2 Characterization of optimal control solution
According to Pontryagin’s maximum principle [39], and using the results described in [40], if \(U^*\in \aleph\) is optimal solution for the objective functional (31), then there exists an adjoint vector \(\lambda (t)=(\lambda _S(t),\lambda _V(t),\lambda _I(t),\lambda _R(t),\lambda _B(t)) \in {\mathbb {R}}_+^5\) satisfies:
-
(i)
the control system
$$\begin{aligned} {}_0^{C}{\mathscr {D}}_t^q S={\frac{\partial \mathcal{H}}{{\partial \lambda _S}}},~~{}_0^{C}{\mathscr {D}}_t^q V={\frac{\partial \mathcal{H}}{{\partial \lambda _V}}},~~~{}_0^{C}{\mathscr {D}}_t^q I={\frac{\partial \mathcal{H}}{{\partial \lambda _I}}},~~~ {}_0^{C}{\mathscr {D}}_t^q R={\frac{\partial \mathcal{H}}{{\partial \lambda _R}}},~~~{}_0^{C}{\mathscr {D}}_t^q B={\frac{\partial \mathcal{H}}{{\partial \lambda _B}}}; \end{aligned}$$(34) -
(ii)
the adjoint system
$$\begin{aligned} {}_t^{C}{\mathscr {D}}_{t_f}^q \lambda _S={\frac{\partial \mathcal{H}}{{\partial S}}},~~{}_t^{C}{\mathscr {D}}_{t_f}^q \lambda _V={\frac{\partial \mathcal{H}}{{\partial V}}},~~~{}_t^{C}{\mathscr {D}}_{t_f}^q \lambda _I={\frac{\partial \mathcal{H}}{{\partial I}}},~~~{}_t^{C}{\mathscr {D}}_{t_f}^q \lambda _R={\frac{\partial \mathcal{H}}{{\partial R}}},~~~{}_t^{C}{\mathscr {D}}_{t_f}^q \lambda _B={\frac{\partial \mathcal{H}}{{\partial B}}}; \end{aligned}$$(35) -
(iii)
the stationary condition
$$\begin{aligned} {\frac{\partial \mathcal{H}}{{\partial u_1}}}=0,~~~{\frac{\partial \mathcal{H}}{{\partial u_2}}}=0,~~~{\frac{\partial \mathcal{H}}{{\partial u_3}}}=0,~~~{\frac{\partial \mathcal{H}}{{\partial u_4}}}=0,~~~{\frac{\partial \mathcal{H}}{{\partial u_5}}}=0; \end{aligned}$$(36) -
(iv)
the transversality conditions
$$\begin{aligned} \lambda _S(t_f)=0,~~~\lambda _V(t_f)=0,~~~\lambda _I(t_f)=0,~~~\lambda _R(t_f)=0 ~~\text {and}~~\lambda _B(t_f)=0; \end{aligned}$$(37)
in which the Hamiltonian function is defined as
Remark 5
Eqs. (34)-(37) give a set of necessary conditions for optimal control problem (31)-(32). Compared with classical optimal control problems, the derived equations include the left and the right fractional derivatives.
Remark 6
It should be mentioned here that the adjoint system is derived from Riemann-Liouville fractional derivative (RLFD), that is, \({}_t{\mathscr {D}}_{t_f}^q \lambda _X={\frac{\partial \mathcal{H}}{{\partial X}}}, X=(S,V,I,R,B),\) where \({}_t{\mathscr {D}}_{t_f}^q\) represents right RLFD. Then, with the help of the relation between the right RLFD and CFD, the right RLFD is replaced with right CFD, shown in Eq. (35).
Theorem 12
Let \((S^*,V^*,I^*,R^*,B^*)\) be optimal state variables set related to optimal control solution \(U^*=(u_1^*,u_2^*,u_3^*,u_4^*,u_5^*)\) which minimizes the objective function for the optimal control problem (31)-(32), then there exists an adjoint variable \(\lambda =(\lambda _S,\lambda _V,\lambda _I,\lambda _R,\lambda _B)\) satisfying
with \(t'=t_f-t\), and the transversality conditions
Furthermore, the optimal control \(U^*\) is given by
where \({{\bar{u}}}_4\) is non-negative root of the equation \(\kappa _4u_4(1+\alpha u_4I^*)^2+(\lambda _R-\lambda _I)(1-\alpha r I^*)I^*=0\).
Remark 7
Generally, the numerical methods of fractional-order differential equations are mostly based on left fractional derivatives. For subsequent simulation convenience, the adjoint system (35) is rewritten as Eq. (38) by using equivalence relation \({}_t^C{\mathscr {D}}_{t_f}^q\lambda (t)={}_0^C{\mathscr {D}}_{t}^q\lambda (t_f-t)\) when \(q\in (0,1]\) (see [41,42,43] and references cited therein).
5 Simulations and discussions
To confirm the theoretical results, in this section, some numerical simulations are performed with MATLAB and Simulink. The simulation parameters are given in Table 2, in which specific r-value and \(\alpha\)-value are presented in Examples.
5.1 The dynamical behavior of the fractional cholera model
First, the disease-free equilibrium is calculated as \(E_0=(1824.8175,7299.2701,0,0)\) using the values for the parameters in Table 2. Then, the simulations of system (11) are performed with different parameter values r and \(\alpha\).
Example 1
Setting \(\alpha =0\), one can see in Fig. 2a that the system exhibits a forward bifurcation. First, setting \(r=1\) and \(q=0.98\) which results in \(R_{vt}=0.2093<1\), it follows that \(E_0\) is globally asymptotically stable from Theorem 3, as shown in Fig. 2b, c. Next, setting \(r=0.02\) and \(q=0.98\), it is easy to show that \(R_{vt}=5.4617>1\) and thus, the system has a locally asymptotically stable endemic equilibrium \(\bar{E}\), as predicted by Theorem 5 (see Fig. 2d, e). In addition, Fig. 2f shows the curves related to the infected individuals under different q-values. It is observed that the curves are stretched to the right as the decrease in q-value, owing to the increase in the memory effect of the system as q-value decreases, and thus the infection grows slowly, implying that the disease may take longer to be eradicated.
a Existence of forward bifurcation for \(\alpha =0\). b, c When \(R_{vt}=0.2093\), there are no endemic equilibria and \(E_0\) is globally asymptotic stable. d, e When \(R_{vt}=5.4617\), there is a unique equilibrium and \(\bar{E}\) is locally asymptotically stable. f When \(R_{vt}=5.4617\), all the trajectories converge to \(\bar{I}\) under different q-values
Example 2
Setting \(\alpha =5>0\), in this case, two endemic equilibria appear for \(R_{vt}<1\) shown in Fig. 3a. First, it is clear to see that \(\varDelta _1\) curve is drawn below the x-axis when \(R_{vt}<1\) from Fig 3b implying that the endemic equilibrium \({\tilde{E}}_2\) always unstable regardless of whichever q-value is taken from (0, 1]. For the other one endemic equilibrium \({\tilde{E}}_3\) when \(R_{vt}<1\), in particular, we separately discuss two cases.
-
(i)
For \(q=1\) in which reflects the integer-order derivative, it can be seen from Fig. 3c, d that this endemic equilibrium is also unstable as Routh-Hurwitz criterion is not met. As a result, both of the endemic equilibria are unstable for integer-order system, which differs from the usual backward bifurcation. At this point, the disease will die out when \(R_{vt}<1\).
-
(ii)
For \(q\in (0,1)\) in which reflects the fractional-order derivative, we take \(r=0.2\), then the endemic equilibrium \({\tilde{E}}_3\) is calculated as (171.7711, 760.8082, 21.4782, 6508.5595) and the corresponding eigenvalues are \(\lambda =[-0.350713797995747,-0.0106210224628660,0.000245239638796110 + 0.00300145540583674i,0.000245239638796110 - 0.00300145540583674i]\), it follows that the endemic equilibrium is locally asymptotically stable if \(q\in \bar{q}(0,0.9481)\). It is clear from Fig. 3e that under the identical initial conditions, the disease will become endemic when \(q\in \bar{q}\), and will die out when \(q\notin \bar{q}\). In this case, the fractional system exhibits usual backward bifurcation phenomenon, providing further evidence that the stability domain of fractional-order system is always larger than that of integer-order.
In addition, there is an unique endemic equilibrium \(\tilde{E_1}\) when \(R_{vt}>1\) from Fig. 3a. We find that the stability of \(\tilde{E_1}\) also depend on the value q when \(1<R_{vt}<1.2533\) from Fig. 3f, g, however, \(\tilde{E_1}\) becomes stable when \(R_{vt}>1.2533\). Fig. 3h, i show that \(\tilde{E_1}\) is locally asymptotically stable when \(r=0.02\) with different values of q.
a Existence of bifurcation for \(\alpha =5\). b Waveform plot of \(\varDelta _1\) (\({\tilde{E}}_2\)). c, d Waveform plot of \(\varDelta _i, i=1,2,3\) (\({\tilde{E}}_3\)). (e) When \(R_{vt}<1\), the behavior of the infected population under different q-values and identical initial conditions. f, g Waveform plot of \(\varDelta _i, i=1,2,3\) (\({\tilde{E}}_1\)). h, i When \(R_{vt} = 5.4617\), \({\tilde{E}}_1\) is locally asymptotically stable with different q-values
5.2 Numerical scheme and simulations for fractional optimal control problem
In this subsection, we present the numerical results for the fractional optimal control problem proposed in Sect. 4 by utilizing the Forward-Backward Sweep Method (FBSM) using Fractional Euler Method (FEM) in Ref [41]. Herein, we highlighted again the main steps of this algorithm.
- Step 0.:
-
Set the parameter values and initial conditions;
- Step 1.:
-
Divide the interval \([0, t_f]\) into N equal subintervals with length \(h=\frac{t_f}{N}\) and \(t_k=kh, k=0,1,2,...,N\);
- Step 2.:
-
Compute \(U(t_k)\) based on the formula as follows
$$\begin{aligned} \begin{aligned} u_1(t_k)&= \min \left\{ {\max \left\{ {0,\frac{{({\lambda _S(t_k)} - {\lambda _V(t_k)}){S(t_k)}}}{{{\kappa _1}}}} \right\} ,{{u_{1\max }}}} \right\} ,\\ u_2(t_k)&= \min \left\{ {\max \left\{ {0,\frac{{ {\left( {{\lambda _I(t_k)}\! -\! {\lambda _S(t_k)}} \right) \beta {S(t_k)}B(t_k)\! +\! \left( {{\lambda _I(t_k)} \!- \!{\lambda _V(t_k)}} \right) \sigma \beta {V(t_k)}} {B(t_k)}}}{{{\kappa _2}\left( {K\! +\! {B(t_k)}} \right) }}} \right\} ,{u_{2\max }}} \right\} ,\\ u_3(t_k)&= \min \left\{ {\max \left\{ {0,\frac{{\left( {{\lambda _S(t_k)} - {\lambda _V(t_k)}} \right) \eta V(t_k)}}{{{\kappa _3}}}} \right\} ,{u_{3\max }}} \right\} ,\\ u_4(t_k)&= \min \left\{ {\max \left\{ {0,{{{\bar{u}}}_4(t_k)}} \right\} ,{u_{4\max }}} \right\} , \\ u_5(t_k)&= \min \left\{ {\max \left\{ {0,\frac{{{\lambda _B(t_k)}{B(t_k)}}}{{{\kappa _5}}}} \right\} ,{u_{5\max }}} \right\} , \end{aligned} \end{aligned}$$in which the initial value of control \(U(t_0)\) can be determined by the initial conditions (2) and transversality conditions (39). The remaining values of \(U(t_k)\) can be obtained from the looping by solve the state and adjoint equations as in the next steps;
- Step 3.:
-
Solve the state system (33) forward-in-time by means of the FEM with initial conditions (2) to obtain the new starting point, that is
$$\begin{aligned} X({t_k})= X({t_0}) + \frac{{{h^q}}}{{\varGamma (q + 1)}}\sum \limits _{j = 0}^{k - 1} {{a_{j,k}}} G(t_j,X(t_j),U(t_j)), \end{aligned}$$where \(a_{j,k}=(k-j)^q-(k-1-j)^q\).
- Step 4.:
-
Solve the adjoint equation (38) forward-in-time by applying the FEM subject to terminal conditions and the values of the controls and state variables. For the sake of brevity, results are given as the matrix form as follows
$$\begin{aligned} \lambda _X(t_f-t_{N-k-1})=\frac{h^q}{\varGamma (q+1)}\sum \limits _{j = 0}^{k }a_{j,k+1}\frac{{\partial H}}{{\partial X}}\Big ( {{t_f} - {t_{N - j}},X\left( {{t_f} - {t_{N - j}}} \right) ,U\left( {{t_f} - {t_{N - j}}} \right) ,\lambda \left( {{t_f} - {t_{N - j}}} \right) } \Big ). \end{aligned}$$ - Step 5.:
-
Update control \(U(t_k)\) for \(k=1,2,...,N\) by entering the new state and adjoint values from Step 3 and Step 4 into Step 2;
- Step 6.:
-
Check convergence. If the results of the current iteration are significantly closer to the last iteration, output the current values as the optimal solutions. If the results are not close, return to Step 3.
Next, we apply the above numerical scheme to illustrate the effectiveness of suggested control measures on the transmission of cholera. For illustration purposes, we choose initial conditions \(S(0)=6000,V(0)=300,I(0)=1700,R(0)=3000, B(0)=300,000\) together with the parameter values in Table 2. Other parameter values are set to \(r=0.02,\alpha =5, q=0.98,\kappa _1=15,\kappa _2=10,\kappa _3=5,\kappa _4=10,\kappa _5=15,t_f=182\) and \(u_{1\max }=0.6,u_{2\max }=0.7,u_{3\max }=0.5,u_{4\max }=0.6,u_{5\max }=1\).
Subsequently, the above steps of numerical scheme are performed, the optimal control solutions are given in Fig. 4. It can be observed that during the first 40 days of cholera outbreak, the vaccination strategy \(u_1(t)\) remained at its highest level followed by a rapid fall to zero, whereby saving vaccination costs. Similarly, the treatment strategy \(u_4(t)\) is also canceled gradually after 90 days. Meanwhile, we find that revaccination strategy \(u_3(t)\) has a positive effect on control cholera outbreak, but it is not necessary. Thus, considering the relevant costs, this control strategy is not recommended. Relatively speaking, media coverage strategy \(u_2(t)\) and the sanitation strategy \(u_5(t)\) have been widely used throughout the disease control period.
In order to explain the effectiveness of the control strategies more intuitively, we compare the number of infectious individuals and bacterial concentration under three separate models, i.e., SI-B model without any control strategy, SVIR-B model (1), and optimal control model (32), where the simplest SI-B subsystem is given by
Then, simulate data are also compared with real data on the cholera outbreak that occurred in the Department of Artibonite, Haiti, from 1st November 2010 to 1st May 2011. As observed from Fig. 5, the implement of control measures could significantly reduce the number of infectious individuals and bacterial concentration. Besides, we also observe that both of them have slight rise toward end due to the rapid decay of control functions near final time.
In addition, the changes of the control variables under different q-value are given in Fig. 6. Clearly, the maximum levels of the controls increase as q-value decreases, in other words, the maximum levels of the controls can be reduced by decreasing the memory effect.
6 Conclusion
In this paper, we have addressed a fractional SVIR-B epidemic model with imperfect vaccination and saturated treatment to describe the transmission dynamics of cholera epidemic. First, some fundamental properties of the given model were investigated, such as the positivity and boundedness of solutions, the expression of the control reproduction number \(R_{vt}\), the existence and stability of equilibria, as well as the existence of bifurcations. Analytical study demonstrates that the model exhibits a rich and complex dynamics behavior due to saturated treatment. More specifically, the saturated treatment may cause the existence of backward bifurcation, which is important from an epidemiological point of view since it is probably not sufficient to eliminate cholera when the control reproduction number is reduced to less than unity. At this point, the initial size of the infected population determines whether cholera is eradicated. Also, the saturated treatment may result in the occurrence of Hopf bifurcation when \(R_{vt}>1\), which implies that cholera persist periodically within the population. As a result, the absence of ample medical resources makes it difficult to effectively control cholera. This recommends that it is necessary to deploy relatively ample medical resources during the large-scale cholera outbreak make \(R_{vt}\) lower than unity so that the system will be disease free in the sense of the disease-free equilibrium because it is globally asymptotically stable.
Subsequently, in order to control and reduce the spread of cholera as soon as possible, an optimal control problem is proposed by incorporating the different types of control strategies, such as vaccination, media coverage, treatment, and sanitation. Then, applying the fractional optimal control theory, the existence of optimal control pair was demonstrated, and the optimal control solution was characterized.
Lastly, to facilitate the understanding of theoretical results, some numerical simulations are performed. From the numerical simulations, it has been seen that although the integer-order model and fractional-order model possess the identical steady-state value, the fractional-order model requires a longer period of time to converge to the steady-state value. This suggests that cholera needs longer time to be eliminated as q-value approaches 0 (increasing memory). Then, the transmission intensity of the cholera will decrease as q-value decreases. Moreover, an interesting observation from our numerical simulation is that the integer-order model may have two unstable endemic equilibria when \(R_{vt}<1\), which differs from usual backward bifurcation. Nevertheless, it may be a usual backward bifurcation phenomenon in the corresponding fractional-order model, providing further evidence that the fractional-order system’s stability domain is clearly larger than that of integer-order. Another interesting result found is that the maximum levels of the controls increase as q-value decreases. Overall, in order to predict and control the development of disease more accurately, it is necessary to make a more in-depth analysis of the order q-value to ensure that the best value is chosen.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.]
References
S. Sharma, F. Singh, Bifurcation and stability analysis of a cholera model with vaccination and saturated treatment. Chaos Solit. Fractals 146, 110,912 (2021)
J.N. Zuckerman, L. Rombo, A. Fisch, The true burden and risk of cholera: implications for prevention and control. Lancet Infect. Dis. 7(8), 521–530 (2007)
World Health Organization. Cholera (2021). https://www.who.int/news-room/fact-sheets/detail/cholera
V. Capasso, S. Paveri-Fontana, A mathematical model for the 1973 cholera epidemic in the European Mediterranean region. Revue d’épidémiologie et de Santé Publiqué 27(2), 121–132 (1979)
C.T. Codeço, Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 1(1), 1–14 (2001)
D.M. Hartley, J.G. Morris Jr., D.L. Smith, Hyperinfectivity: a critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 3(1), e7 (2006)
Z. Mukandavire, S. Liao, J. Wang, H. Gaff, D.L. Smith, J.G. Morris, Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc. Nat. Acad. Sci. India Sect. B-Biol. Sci. 108(21), 8767–8772 (2011)
J.H. Tien, D.J. Earn, Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 72(6), 1506–1533 (2010)
Y. Wang, J. Cao, Global stability of general cholera models with nonlinear incidence and removal rates. J. Frankl. Inst.-Eng. Appl. Math. 352(6), 2464–2485 (2015)
United Nations International Children’s Emergency Fund, World Health Organization. 1 in 3 people globally do not have access to safe drinking water (2019). https://www.who.int/news/item/18-06-2019-1-in-3-people-globally-do-not-have-access-to-safe-drinking-water-unicef-who
J. Wang, C. Modnak, Modeling cholera dynamics with controls. Can. Appl. Math. Q. 19(3), 255–273 (2011)
X. Zhou, J. Cui, Z. Zhang, Global results for a cholera model with imperfect vaccination. J. Frankl. Inst.-Eng. Appl. Math. 349(3), 770–791 (2012)
D. Posny, J. Wang, Z. Mukandavire, C. Modnak, Analyzing transmission dynamics of cholera with public health interventions. Math. Biosci. 264, 38–53 (2015)
A.P. Lemos-Paião, C.J. Silva, D.F. Torres, An epidemic model for cholera with optimal control treatment. J. Comput. Appl. Math. 318, 168–180 (2017)
X. Tian, R. Xu, J. Lin, Mathematical analysis of a cholera infection model with vaccination strategy. Appl. Math. Comput. 361, 517–535 (2019)
N. Hamdan, A. Kilicman, A fractional order SIR epidemic model for dengue transmission. Chaos, Solit. Fractals 114, 55–62 (2018)
K.S. Cole, In Cold Spring Harbor symposia on quantitative biology, (Cold Spring Harbor Laboratory Press, 1933), vol. 1, pp. 107–116
X. Cui, D. Xue, F. Pan, Dynamic analysis and optimal control for a fractional-order delayed SIR epidemic model with saturated treatment. Eur. Phys. J. Plus 137(5), 1–18 (2022)
H. Singh, Analysis for fractional dynamics of Ebola virus model. Chaos, Solit. Fractals 138, 109,992 (2020)
Z. Lu, Y. Yu, Y. Chen, G. Ren, C. Xu, S. Wang, Z. Yin, A fractional-order SEIHDR model for COVID-19 with inter-city networked coupling effects. Nonlinear Dyn. 101(3), 1717–1730 (2020)
A. Boukhouima, E.M. Lotfi, M. Mahrouf, S. Rosa, D.F. Torres, N. Yousfi, Stability analysis and optimal control of a fractional HIV-AIDS epidemic model with memory and general incidence rate. Eur. Phys. J. Plus 136(1), 1–20 (2021)
S. Kumar, R. Kumar, M. Osman, B. Samet, A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer. Meth. Part Differ. Equ. 37(2), 1250–1268 (2021)
T. Nguiwa, G.G. Kolaye, M. Justin, D. Moussa, G. Betchewe, A. Mohamadou, Dynamic study of SIAISQVR-B fractional-order cholera model with control strategies in Cameroon Far North Region. Chaos, Solit. Fractals 144, 110,702 (2021)
D. Baleanu, F.A. Ghassabzade, J.J. Nieto, A. Jajarmi, On a new and generalized fractional model for a real cholera outbreak. Alex. Eng. J. 61(11), 9175–9186 (2022)
I. Podlubny, Fractional differential equations, vol. 198 (Academic Press Inc, San Diego, CA, 1999)
C. Sun, W. Yang, Global results for an SIRS model with vaccination and isolation. Nonlinear Anal. RealWorld Appl. 11(5), 4223–4237 (2010)
P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)
E. Ahmed, A. El-Sayed, H.A. El-Saka, On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rosler, Chua and Chen systems. Phys. Lett. A 358, 1–4 (2006)
J.P. La Salle, The stability of dynamical systems, vol. 25 (SIAM, Philadelphia, 1976)
C. Vargas-De-León, Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 24(1–3), 75–85 (2015)
C. Castillo-Chavez, B. Song, Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 1(2), 361 (2004)
B. Tao, M. Xiao, Q. Sun, J. Cao, Hopf bifurcation analysis of a delayed fractional-order genetic regulatory network model. Neurocomputing 275, 677–686 (2018)
C. Huang, J. Cao, M. Xiao, Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos, Solit. Fractals 87, 19–29 (2016)
C. Huang, J. Cao, M. Xiao, A. Alsaedi, T. Hayat, Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 292, 210–227 (2017)
M. Xiao, G. Jiang, J. Cao, W. Zheng, Local bifurcation analysis of a delayed fractional-order dynamic model of dual congestion control algorithms. IEEE/CAA J. Autom. Sinica 4(2), 361–369 (2016)
W.M. Liu, Criterion of Hopf bifurcations without using eigenvalues. J. Math. Anal. Appl. 182(1), 250–256 (1994)
W.H. Fleming, R.W. Rishel, Deterministic and stochastic optimal control, vol. 1 (Springer Science & Business Media, 2012)
E.A. Coddington, N. Levinson, Theory of ordinary differential equations (Tata McGraw-Hill Education, 1955)
L. Pontryagin, V. Boltyanskii, R. Gamkrelidze, E. Mishchenko, The mathematical theory of optimal processes, gordon and bs publishers, eds (Gordon and Breach Science Publishers, 1986)
D. Baleanu, K. Diethelm, E. Scalas, J.J. Trujillo, Fractional calculus: models and numerical methods, vol. 3 (World Scientific Publishing Co. Pte. Ltd, 2012)
I. Ameen, D. Baleanu, H.M. Ali, An efficient algorithm for solving the fractional optimal control of SIRV epidemic model with a combination of vaccination and treatment. Chaos, Solit. Fractals 137, 109,892 (2020)
H.M. Ali, I.G. Ameen, Optimal control strategies of a fractional order model for Zika virus infection involving various transmissions. Chaos, Solit. Fractals 146, 110,864 (2021)
H. Kheiri, M. Jafari, Fractional optimal control of an HIV/AIDS epidemic model with random testing and contact tracing. J. Appl. Math. Comput. 60(1), 387–411 (2019)
X. Zhou, X. Shi, M. Wei, Dynamical behavior and optimal control of a stochastic mathematical model for cholera. Chaos, Solit. Fractals 156, 111,854 (2022)
A. Mwasa, J.M. Tchuenche, Mathematical analysis of a cholera model with public health interventions. Biosystems 105(3), 190–200 (2011)
C. Modnak, A model of cholera transmission with hyperinfectivity and its optimal vaccination control. Int. J. Biomath. 10(06), 1750,084 (2017)
Acknowledgments
The work is supported by National Nature Science Foundation under Grant No. 61673094.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Cui, X., Xue, D. & Pan, F. A fractional SVIR-B epidemic model for Cholera with imperfect vaccination and saturated treatment. Eur. Phys. J. Plus 137, 1361 (2022). https://doi.org/10.1140/epjp/s13360-022-03564-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-022-03564-z