1 Introduction

The recent technological progress has ushered a new era for observational cosmology, the so-called Precision Cosmology [1] allowing for significant advances in our understanding of the Universe. Yet, most of the Universe matter–energy composition remains elusive. It is a fact that about 25% of matter content consists of an enigmatic substance—the dark matter (DM) [2]—the existence of which is established by astrophysical observations at large scales. Possibly, even more mysterious is the dark energy (DE) component (roughly 70%), which is invoked to account for the current accelerating expansion of the Universe. In spite of strong evidence from Supernova SNIa observations, baryon acoustic oscillations and gravitational waves, a complete explanation for the origin of DE is an open issue [3, 4]. Undoubtedly, this reveals the necessity of novel physics to be solved.

So far, several theoretical approaches to DE problem have been developed in the literature. The possibility that DE could be modeled by the cosmological constant acting as source of the vacuum energy was first considered as a natural way out of the DE puzzle. Nevertheless, this scenario seems to clash with our field-theoretical understanding of the quantum properties of vacuum. Alternative explanations were later offered by modified gravity theories based on the introduction of either geometric terms or extra degrees of freedom in the Einstein–Hilbert action (see [5,6,7,8,9,10,11] for reviews). Among these theories, the Brans–Dicke (BD) gravity is an extension of general relativity built upon the replacement of the gravitational coupling constant G by the inverse of a varying scalar field \(\phi\) [12]. The first motivation for this choice was to achieve a theory more in agreement with the Mach’s principle than GR [13, 14]. While being able to describe the accelerating expansion of the current Universe, this model predicts a value for the BD (\(\omega\)) parameter that is lower than the observational limit [15, 16], thus requiring to use different DE sources [17,18,19,20,21,22,23,24,25,26] to be reconciled with phenomenology.

In this respect, a useful paradigm is given by the holographic dark energy (HDE) [4, 27,28,29,30,31,32,33]. In the primary formulation, such an approach provides a precise quantitative analysis of DE, originating from the holographic principle with Bekenstein–Hawking (BH) entropy and the Hubble horizon as its IR cutoff. However, the shortcomings in describing the history of a flat Friedmann–Robertson–Walker (FRW) Universe have motivated some tentative changes of this model. For instance, HDE has been employed to solve the DE problem in the BD framework [18,19,20,21,22,23,24,25] by considering different IR cutoffs [24, 32, 33] or suitable interactions with DM [34].

On the other hand, modified HDE models based on deformations of the entropy area law have been proposed in [35,36,37,38,39,40,41,42,43,44], while still keeping the Hubble radius as IR cutoff. Due to the complex (and mostly unknown) thermostatistical properties of gravity systems, various deformed entropies have been adopted [45,46,47], all of which recovering BH entropy in a certain limit. In this context, a promising framework is provided by the Barrow holographic dark energy (BHDE) [38], which relies on a quantum gravitational deformation of BH area law in the form [47]

$$\begin{aligned} S_\Delta \,=\,\left( \frac{A}{A_0}\right) ^{1+\Delta /2}\,, \end{aligned}$$
(1)

where A is the standard horizon area and \(A_0\) the Planck area. Quantum gravity effects are parameterized by the Barrow exponent \(0\le \Delta \le 1\), with \(\Delta =0\) giving the BH limit, while \(\Delta =1\) corresponding to the maximal entropy deformation. It is worth mentioning that cosmological constraints on \(\Delta\) have been inferred in [48,49,50,51,52,53,54,55,56,57]. The possibility for a running \(\Delta\) has also been discussed in [58].

BHDE is inspired by similar generalizations of HDE based on Tsallis [35,36,37] and Kaniadakis [40] entropies. At a first glance, it appears as a proper model to trace the evolution of the Universe in the standard cosmological framework. Just as Tsallis holographic dark energy, however, BHDE suffers from instability problems. Thus, according to the dynamic behavior of HDE and its modified entropy-based extensions, it could be more appropriate to study the cosmological features of BHDE in extended frameworks and, in particular, in the BD dynamic framework [23, 34]. In [24], the authors have shown that the non-interacting HDE with the Hubble radius as IR cutoff cannot explain the current accelerated expansion of Universe in the BD theory. While in a similar analysis, it has been shown that the Tsallis and Kaniadakis holographic dark energy, due to the generalized entropy, with the Hubble cutoff in the BD gravity, can lead the accelerated Universe phase, even in the absence of interaction between two dark sectors [59, 60].

Starting from the above premises, in what follows we examine the implications of using BHDE to model dark energy in BD cosmology. To this goal, we resort to the holographic principle with Eq. (1) as horizon entropy and the Hubble radius as cutoff. In the next section, we extract the BHDE density in the BD gravity and investigate the evolution of its cosmological parameters for a spatially flat Universe in the non-interacting case. The same study is developed in Sect. 3 for the sign-changeable and linear interacting models. Stability analysis is investigated in Sect. 4. Conclusions and outlook are finally summarized in Sect. 5.

2 Non-interacting Barrow holographic dark energy in the Brans–Dicke cosmology

Throughout this work, we consider a homogeneous and isotropic Friedman–Robertson–Walker (FRW) geometry with metric

$$\begin{aligned} \textrm{d}s^2=-\textrm{d}t^2+a^2(t)\left( \frac{\textrm{d}r^2}{1-kr^2}+r^2\textrm{d}\Omega ^2\right) , \end{aligned}$$
(2)

where \(k=0,1,-1\) represent a flat, closed and open maximally symmetric space, respectively.

The Brans–Dicke field equations for a spatially flat FRW Universe which is filled by pressureless DM and DE are [20,21,22,23,24]

$$\begin{aligned} & \frac{3}{4\omega }\phi ^2H^2-\frac{\dot{\phi }^2}{2}+\frac{3}{2\omega }H\dot{\phi }\,\phi =\rho _M+\rho _\Lambda , \end{aligned}$$
(3)
$$\begin{aligned} & \quad \frac{-\phi ^2}{4\omega }\left( \frac{2\ddot{a}}{a}+H^2\right) -\frac{1}{\omega }H\dot{\phi }\,\phi -\frac{1}{2\omega }\ddot{\phi }\,\phi -\frac{\dot{\phi }^2}{2}\left( 1+\frac{1}{\omega }\right) =p_\Lambda , \end{aligned}$$
(4)

The scalar field evolution equation is

$$\begin{aligned} \ddot{\phi }+3H\dot{\phi }-\frac{3}{2\omega }\left( \frac{\ddot{a}}{a}+H^2\right) \phi =0. \end{aligned}$$
(5)

where \(\omega\) is the BD parameter and \(\phi ^2=\omega /(2\pi G_{\textrm{eff}})\) is the BD scalar field, with \(G_{\textrm{eff}}\) being the effective gravitational constant. Also, \(H=\dot{a}/a\) is the Hubble parameter and \(\rho _m\), \(\rho _\Lambda\) and \(p_\Lambda\) are the pressureless DM density, DE density and pressure of DE, respectively. Following [20,21,22,23,24], we consider the BD field as a power law of the scale factor, \(\phi \propto a^n\). Then, we have

$$\begin{aligned} \dot{\phi } & = nH\phi , \end{aligned}$$
(6)
$$\begin{aligned} \ddot{\phi } & = n^2H^2\phi +n\dot{H}\phi . \end{aligned}$$
(7)

where dot denotes derivative with respect to the cosmic time. The energy conservation equations for non-interacting DE and matter are

$$\begin{aligned} \dot{\rho }_D+3H\left( 1+\omega _D\right) \rho _D=0, \end{aligned}$$
(8)

and

$$\begin{aligned} \dot{\rho }_m+3H\rho _m=0, \end{aligned}$$
(9)

where \(\omega _D=\frac{p_D}{\rho _D}\) denotes the equation of state (EoS) parameter of DE. With the definition of the critical energy density, \(\rho _{cr}=\frac{3\phi ^2H^2}{4\omega }\), the dimensionless density parameters can be written as

$$\begin{aligned} \Omega _m=\frac{\rho _m}{\rho _{cr}} & = \frac{4\omega \rho _m}{3\phi ^2H^2}, \end{aligned}$$
(10)
$$\begin{aligned} \Omega _D=\frac{\rho _D}{\rho _{cr}} & = \frac{4\omega \rho _D}{3\phi ^2H^2}. \end{aligned}$$
(11)

Using the above definitions (10) and  (11), one can rewrite the Friedman Eq. (3) as follows:

$$\begin{aligned} \Omega _m+\Omega _D=1+ 2n-\frac{2\omega n^2}{3}. \end{aligned}$$
(12)

Here, by using the holographic principle with the generalized Barrow entropy (1), we can construct the Barrow holographic dark energy (BHDE) in the BD gravity, in which the apparent horizon in the flat Universe is considered as the IR cutoff \((L=H^{-1})\), as follows:

$$\begin{aligned} \rho _D=B\phi ^{2+\Delta }H^{2-\Delta }. \end{aligned}$$
(13)

Here, B is an unknown constant. In the limit of Einstein gravity, where \(G_{\textrm{eff}} \rightarrow G\), the BD scalar field becomes trivial (\(\phi ^2=\frac{\omega }{2\pi G}=4\omega M_p^2\)) and the BHDE in standard cosmology can be recovered [61]. Also for \(\Delta \rightarrow 0\) and \(G_{\textrm{eff}} \rightarrow G\), Eq. (13) reduces to the energy density of the original HDE in standard cosmology [24].

Taking the time derivative of Eq. (13), we have

$$\begin{aligned} \dot{\rho }_D=\left( 2+\Delta \right) nH\rho _D+\left( 2-\Delta \right) \frac{\dot{H}}{H}\rho _D. \end{aligned}$$
(14)

By differentiating Eq. (3) and combining the result with Eqs. (9), (10), (11),  (6) and (14), we obtain

$$\begin{aligned} \frac{{\dot{H}}}{{H^{2} }}{\text{ }} & = \left[ { - \frac{{9\Omega _{m}^{0} H_{0}^{2} \phi _{0}^{2} }}{{4\omega \phi ^{2} H^{2} }} + (2\omega n^{2} - 6n - 3)\frac{n}{{2\omega }} + nB(2 + \Delta )\left( {\frac{\phi }{H}} \right)^{\Delta } } \right] \\ & \quad \times \left[ {B(\Delta - 2)\left( {\frac{\phi }{H}} \right)^{\Delta } + \frac{3}{{2\omega }} - n^{2} + \frac{{3n}}{\omega }} \right]^{{ - 1}} , \\ \end{aligned}$$
(15)

where the zero-subscript represents present time. Using Eqs. (8) and (14), we find the EoS parameter for the BHDE model in the BD gravity as

$$\begin{aligned} \omega _D=-1-\frac{\left( 2+\Delta \right) n}{3}+\frac{\Delta -2}{3}\frac{\dot{H}}{H^2}. \end{aligned}$$
(16)

For \(\Delta = 0\) and \(n=0\), this equation coincides with the original HDE in the BD gravity [24]. Also in the limiting case \(n=0\) \((\omega \rightarrow \infty )\), the EoS parameter for BHDE in standard cosmology is restored [61].

In the following, using the accelerating parameter relation \(q=-1-\frac{\dot{H}}{H^2}\) and Eq. (15), the deceleration parameter can be extracted as

$$\begin{aligned} q & = - 1 + \left[ {\frac{{9\Omega _{m}^{0} H_{0}^{2} \phi _{0}^{2} }}{{4\omega \phi ^{2} H^{2} }} - \left( {2\omega n^{2} - 6n - 3} \right)\frac{n}{{2\omega }} - nB\left( {2 + \Delta } \right)\left( {\frac{\phi }{H}} \right)^{\Delta } } \right] \\ & \qquad \times \left[ {B\left( {\Delta - 2} \right)\left( {\frac{\phi }{H}} \right)^{\Delta } + \frac{3}{{2\omega }} - n^{2} + \frac{{3n}}{\omega }} \right]^{{ - 1}} \\ \end{aligned}$$
(17)

2.1 Cosmological evolution

In Fig. 1, we plot the evolution of cosmological parameters of the BHDE model by using a numerical solution of the Hubble differential Eq. (15) for \(H_0=70.9, \Omega _m=0.3, \omega =1000\) and \(n=0.05\) as the initial condition. In the first panel of this figure, we have \(\Omega _D\rightarrow 0\) at the early time (DM dominated phase), while at the late time the DE dominates \(\Omega _D\rightarrow 1\), in agreement with cosmological observations [62,63,64]. In the second panel of Fig. 1, we show the behavior of the deceleration parameter q(z). In contrast to standard HDE, we can see that non-interacting BHDE with the Hubble radius as IR cutoff can explain the current acceleration phase. We can see that the Universe undergoes a phase transition from deceleration to acceleration around \(z\approx 0.6\).

Furthermore, as it can be seen from the third panel, the EoS parameter is always in the quintessence regime (\(\omega _D>-1\)) and, at the late time \((z\rightarrow -1)\), it tends to the cosmological constant (\(\omega _D\rightarrow -1\)).

Finally, we plot the behavior of the total EoS parameter \(\omega _{\textrm{eff}}(z)\) in the last panel of Fig. 1. We can see that the total EoS parameter can suitably describe the Universe history, as the pressureless DM is dominant \((\omega _{\textrm{eff}}\rightarrow 0)\) at early times (\(z\rightarrow \infty\)), then it enters the quintessence regime at the present epoch and finally, by decreasing values of the model parameters, tends to a value very close to \(-1\) at late times (\(z\rightarrow -1\)).

Fig. 1
figure 1

Evolution of the \(\Omega _D(z)\), \(\omega _D(z)\), \(\omega _{\textrm{eff}}(z)\) and q(z) parameters for non-interacting BHDE in the BD gravity

Full size image

3 Interacting BHDE model

Let us now assume that dark components interact with each other and one can grow at the expense of the other. The mutual interaction between two dark components is initially proposed to solve the coincidence problem [65, 66]. Although some observations confirm the mutual interaction between dark matter and dark energy [67], since the nature of DM and DE is still unknown, the proposed different interaction models are purely phenomenological. So far, different models of interaction between the two dark components have been proposed in the literature works to study the dynamics of Universe (for details, one can look into [68,69,70,71,72,73,74,75,76,77] and references therein).

In the presence of interaction between two dark components, the conservation equations are

$$\begin{aligned} & \dot{\rho }_D+3H\left( 1+\omega _D\right) \rho _D=-Q, \end{aligned}$$
(18)
$$\begin{aligned} & \quad \dot{\rho }_m+3H\rho _m=Q, \end{aligned}$$
(19)

where Q represents the interaction term. Positive value of Q indicates that energy transfers from the BHDE to the DM, while for \(Q < 0\), the reverse scenario will occur. In the following, we consider the sign-changeable and linear models of interaction to investigate the cosmological evolution of BHDE in the BD gravity.

3.1 Sign-changeable interaction

Following [75, 76], we consider a sign-changeable interaction term as

$$\begin{aligned} Q=3b^2Hq\left( \rho _m+\rho _D\right) , \end{aligned}$$
(20)

where b is the coupling constant of interaction term and q is the deceleration parameter. Taking the time derivative of Eq. (3) and using Eqs. (6),  (14) and (19), we get

$$\begin{aligned} \frac{\dot{H}}{H^2} & = \left[ -\frac{9\Omega _m^0H_0^2\phi _0^2\left( 1+z\right) ^3}{4\omega \phi ^2 H^2}+\frac{3}{2\omega }\left( 2n-\frac{2\omega n^2}{3}-1\right) \right. \nonumber \\ & \left. \quad \times \left( n+\frac{3b^2}{2}\right) + nB\left( 2+\Delta \right) \left( \frac{\phi }{H}\right) ^\Delta \right] \nonumber \\ & \quad \times \left[ B\left( \Delta -2\right) \left( \frac{\phi }{H}\right) ^\Delta +\left( \frac{3}{2\omega }-n^2+\frac{3n}{\omega }\right) \left( 1+\frac{3b^2}{2}\right) \right] ^{-1}. \end{aligned}$$
(21)

Combining Eqs. (18) and (14), one can obtain the following expression for EoS parameter:

$$\begin{aligned} \omega _D & = -1-\frac{(2+\Delta )n}{3}+\frac{(\Delta -2)\dot{H}}{3H^2}\nonumber \\ & \quad + b^2\left( 1+\frac{\dot{H}}{H^2}\right) \left( \frac{1+2n-\frac{2\omega n^2}{3}}{\Omega _D}\right) . \end{aligned}$$
(22)

In the absence of interaction term \((b^2=0)\), these equations reduce to the corresponding relations of the previous section.

To investigate the effects of interaction term between dark sectors, we have plotted the behavior of \(\Omega _D\), the deceleration parameter q, the EoS parameter \(\omega _ D\) and the total EoS parameter \(\omega _{\textrm{eff}}\) against the redshift parameter z for the sign-changeable interacting BHDE in Fig. 2. Again, we see that at the early Universe \(\Omega _D\rightarrow 0\), and at the late time, the DE dominates, as expected. As it is clear from the second panel in Fig. 2, the deceleration parameter q transits from the decelerated phase \((q>0)\) at the earlier time, to current accelerated phase \((q<0)\). Also by increasing the values of \(\Delta , B\) and \(\phi _0\) and decreasing the value of \(b^2\), the transition occurs earlier (higher redshift). Interestingly, we found that, as in the non-interacting case, the EoS parameter of sign-changeable interacting BHDE cannot cross the phantom divide \((\omega _D=-1)\) at late time.

Fig. 2
figure 2

Evolution of the \(\Omega _D\), \(\omega _D\), q and \(\omega _{\textrm{eff}}\) versus redshift parameter z for sign-changeable interacting BHDE in the BD gravity. We have taken the \(H_0=70.9\), \(\omega _m=0.3\), \(n=0.005\) and \(\omega =1000\) as the initial conditions

Full size image

3.2 Linear interaction

In the following, we choose the linear interaction term given as [72, 73]

$$\begin{aligned} Q=H(\alpha \rho _m+\beta \rho _D), \end{aligned}$$
(23)

where \(\alpha\) and \(\beta\) are the coupling constants of interaction term. Taking the time derivative of Eq. (3) and using Eqs. (6),  (14), (19) and (23), we reach

$$\begin{aligned} \frac{\dot{H}}{H^2} & = \left[ B\left( \frac{\phi }{H}\right) ^\Delta (2n+\Delta n+\beta -\alpha ) \right. \nonumber \\ & \left. \quad - \frac{9\Omega _m^0H_0^2\phi _0^2\left( 1+z\right) ^3}{4\omega \phi ^2 H^2}+\frac{3}{2\omega }\left( 1+2n-\frac{2\omega n^2}{3}\right) \left( \frac{\alpha }{2}-n\right) \right] \nonumber \\ & \quad \times \left[ B(\Delta -2)\left( \frac{\phi }{H}\right) ^\Delta +\frac{3}{2\omega }-n^2+\frac{3n}{\omega }\right] ^{-1}. \end{aligned}$$
(24)

Substituting Eqs. (14) and (23) into Eq. (18), we find out

$$\begin{aligned} \omega _D & = -1-\frac{(2+\Delta )n}{3}+\frac{(\Delta -2)\dot{H}}{3H^2}\nonumber \\ & \quad - \frac{\alpha }{3\Omega }\left( 1+2n-\frac{2\omega n^2}{3}\right) +\frac{\alpha -\beta }{3}. \end{aligned}$$
(25)

The evolutions of \(\Omega _D\), \(\omega _D\), q and \(\omega _{\textrm{eff}}\) are plotted versus the redshift parameter z for the linear interacting BHDE in Fig. 3. It appears that the linear interacting BHDE, in the BD gravity, can describe the cosmological evolution of the Universe in a consistent way. Indeed, from the evolution of dimensionless BHDE density parameter \(\Omega _D(z)\) in Fig. 3, we observe that, at early times, \(\Omega _D\rightarrow 0\) and at late times \(\Omega _D\rightarrow 1\). The behavior of the deceleration parameter q(z) in Fig. 3 indicates that the Universe has a phase transition from deceleration to acceleration around \(0.3<z<0.8\), consistently with cosmological observations [62,63,64]. The evolution of the EoS parameter \(\omega _D(z)\) is shown in the third panel of Fig. 3. As we can observe, the EoS parameter successfully describes the cosmological evolution of the Universe and shows that the Universe is in the quintessence dominated phase (\(-1/3<\omega _D<-1\)) at the current epoch and will enter the phantom regime (\(\omega _D<-1\)) in the far future.

Fig. 3
figure 3

Evolution of the \(\Omega _D(z)\), \(\omega _D(z)\), q(z) and \(\omega _{\textrm{eff}}(z)\) for different values of \(\Delta , B,\phi _0, \alpha\) and \(\beta\) as mentioned in the caption, for linear interacting BHDE in the BD gravity. The initial conditions \(H_0=70.9\), \(\omega _m=0.3\), \(n=0.005\) and \(\omega =1000\) are adopted

Full size image

4 Stability analysis

We analyze now the stability of the obtained models against perturbations. So far, we have investigated the dynamical behavior of BHDE model. Now, we would like to see if there are small perturbations in the background, whether the disturbance grows or collapses. In the perturbation theory, the sign of the squared sound speed (\(v_s^2\)) determines classical stability or instability. For \(v_s^2>0\), the model is stable because the perturbation propagates on the background, while, for \(v_s^2<0\), the model is unstable since every small perturbation grows within the background.

The squared sound speed \(v_s^2\) is given by

$$\begin{aligned} v_s^2=\frac{\textrm{d}p}{\textrm{d}\rho _D}=\frac{\dot{p}}{\dot{\rho }_D}. \end{aligned}$$
(26)

By differentiating \(p_{D}\) with respect to the cosmic time, inserting the result in Eq. (26), and using Eq. (14), we have

$$\begin{aligned} v_s^2=\omega _D+\frac{\omega _D^\prime }{2\delta n+2(2-\delta )\frac{\dot{H}}{H^2}}, \end{aligned}$$
(27)

for the squared sound speed.

4.1 Non-interacting case

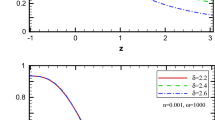
Taking the time derivative of Eq. (16) and using Eqs. (14), (15) and  (27), one can get \(v_s^2\) for the non-interacting BHDE with the Hubble cutoff. Since the analytic expression of \(v_s^2\) is rather cumbersome to exhibit, we shall limit to plot it in Fig. 4. As it is clear, from this figure, the non-interacting BHDE model in the BD gravity is unstable against small perturbations during the cosmic evolution, which is similar to the result obtained for BHDE in the standard model [61].

Fig. 4
figure 4

Evolution of the \(v_s^2(z)\) for non-interacting BHDE in the BD gravity. The initial conditions \(H_0=70.9\), \(\omega _m=0.3\), \(n=0.005\) and \(\omega =1000\) are adopted

Full size image

4.2 Interacting case

We now calculate the squared sound speed for the BHDE in the presence of sign-changeable and linear interaction terms, respectively. For the sign-changeable interacting case, by taking the time derivative of Eq. (22) and combining the result with Eqs. (13), (14), (21) and (27), we obtain \(v_s^2\). For the linear interacting case, we use time derivative of Eqs. (25) and (13), (14), (24) and (27) to get \(v_s^2\).

We plot \(v_s^2\) for the sign-changeable and linear interacting BHDE for BD gravity in Figs. 5 and 6, respectively. From Fig. 5, one can clearly see that the sign-changeable interacting BHDE in the BD cosmology evolves from an unstable configuration in the earliest stages of the Universe’s existence to a stable model in the present and far future. On the other hand, for the linear interacting BHDE the squared sound speed is always positive, which means that, in this case, the Universe is always stable, thus providing a good candidate to describe DE.

Fig. 5
figure 5

Evolution of the \(v_s^2(z)\) for sign-changeable interacting BHDE in the BD gravity. The initial conditions \(H_0=70.9\), \(\omega _m=0.3\), \(n=0.005\) and \(\omega =1000\) are adopted

Full size image
Fig. 6
figure 6

Evolution of the \(v_s^2(z)\) for linear interacting BHDE in the BD gravity. The initial conditions \(H_0=70.9\), \(\omega _m=0.3\), \(n=0.005\) and \(\omega =1000\) are adopted

Full size image

5 Concluding remarks

We considered the Barrow entropy to develop a holographic DE model within the framework of Brans–Dicke cosmology. To this goal, we assumed the Hubble horizon as the IR cutoff and studied the behavior of Barrow holographic dark energy for both interacting and non-interacting cases. We derived the equation governing the evolution of Hubble parameter and solved it numerically in order to study the evolution of corresponding cosmological parameters.

From the behavior of the deceleration parameter q, we inferred that, in contrast to the standard holographic dark energy, our model can explain the present accelerated phase of the Universe expansion, even in the absence of interactions between the dark sectors of cosmos (see [78] for a recent discussion on the inadequacy of standard HDE in explaining the accelerated expansion of the Universe consistently with observations). Furthermore, for the non-interacting case, the EoS parameter shows that BHDE model is always in the quintessence regime (\(\omega _D>-1\)) and, at the late time \((z\rightarrow -1)\), it tends to cosmological constant (\(\omega _D\rightarrow -1\)) (see Fig. 1). A similar behavior is exhibited in the sign-changeable interacting model, where the EoS parameter cannot cross the phantom divide at late times (see Fig. 2). On the other hand, in the presence of a linear interaction, the cosmological evolution of \(\omega _D\) shows that the Universe is in the quintessence dominated phase at the current epoch and will enter the phantom regime (\(\omega _D<-1\)) in the far future (see Fig. 3).

Finally, we performed a classical stability analysis using the squared sound speed. We found that the non-interacting BHDE model, in the BD gravity, is unstable against small perturbations during the cosmic evolution (see Fig. 4), similarly to the result obtained for BHDE in the standard model [61]. On the other hand, the sign-changeable interacting model can be stable only for certain values of the parameters (see Fig. 5), while the linear interacting model always predicts a stable Universe (see Fig. 6). This means that considering an interaction between the dark sectors provides a more reasonable scenario to trace the cosmological evolution in BHDE with BD gravity. This result can be achieved also in the framework of other interacting cosmological model [79].

Further aspects remain to be addressed. For instance, it is interesting to examine how our model gets modified in the more realistic scenario including also radiation fluid in the content of the Universe. However, since radiation effects are dominant in the early Universe only, we expect they do not spoil considerably our predictions for the current and future epochs. Additionally, we aim at investigating the correspondence between our model and HDE based on other extensions of Boltzmann–Gibbs entropy, such as Tsallis [59, 80,81,82,83] and Kaniadakis [60] holographic dark energy. Also, interesting results could be found by connecting BHDE and dark energy model based on Gurzadyan–Xue framework. This latter scenario has been recently addressed in [84], showing that a dark energy formula testable with observations can be obtained by reducing the Djorgovski–Gurzadyan integral equation [85] to a differential equation for the co-moving horizon. Finally, since our model relies on a phenomenological attempt to include quantum gravitational effects through the Barrow entropy, it is important to study whether our predictions reconcile with more fundamental candidate theories of quantum gravity, such as string theory or loop quantum gravity. Work along these directions is presently under investigation and will be presented elsewhere.