1 Introduction

Cohen et al.’s proposal [1] gives us an estimation for the upper bound of the energy density of quantum fields in the vacuum states. Shortly afterwards, it has been proposed that this bound may provide an explanation for dark energy (DE), a hypothesis called Holographic dark energy (HDE), is a promising approach to solve the dark energy problem, and its related topics [2,3,4,5,6,7,8,9,10]. Indeed, the HDE hypothesis helps us in finding the cosmological features of the vacuum energy. The mutual relation between the UV and IR cutoffs forms the backbone of HDE [9, 10]. Finally, it is worthwhile to mention here that any changes in the horizon entropy, including changes in (i) the entropy-area relation, (ii) the IR cutoff or even a combination of these ways, lead to new models for HDE [9,10,11,12,13].

The Brans–Dicke (BD) theory of gravity is an alternative to general relativity in which the gravitational constant G is not constant, and it is replaced with the inverse of a scalar field (\(\phi \)) [14]. Although the BD theory can provide a description for the current universe [15,16,17], its theoretical predictions for the w parameter has major difference with the observations [18,19,20]. In fact, the theoretical estimations for the value of w is much less than those are obtained from observations, a result encouraging physicists to use various dark energy sources in order to describe the current universe in the BD framework [18,19,20].

Motivated by the above arguments, the idea of HDE has also been employed to study the dark energy problem in the BD framework [21,22,23,24,25,26,27,28,29,30]. It has also been argued that since HDE is a dynamic model, one should use the dynamic frameworks, such as the BD theory, to study its cosmological features [25, 29]. It has been shown that the original HDE with the Hubble radius as IR cutoff cannot produce the cosmic acceleration in the BD theory [28], while for the event horizon as the IR cut-off, an accelerated universe is obtainable. Furthermore, it has been demonstrated that when an interaction between HDE and DM is taken into account, the phantom line is crossed in the BD cosmology [29]. The stability of interacting HDE with the GO cutoff in the BD theory has also been discussed in [30]. Observations also admit a sign-changeable interaction between the cosmos sectors [31,32,33]. Such interaction usually admits the cosmological models to experience a phantom phase [34].

Recently, using Tsallis generalized entropy [35], and by considering the Hubble horizon as the IR cutoff, in agreement with the thermodynamics considerations [11, 12], a new HDE model, called Tsallis holographic dark energy (THDE), has been introduced and studied in the standard cosmology framework [13]. At first glance, it is a proper model for the current universe in the standard cosmology framework [13, 36, 37], but, the same as the primary HDE based on the Bekenstein entropy [8], THDE is not stable [13, 36, 37]. More studies on the various cosmological features of the Tsallis generalized statistical mechanics can be found in Refs. [38,39,40,41]. It is also useful to note here that a non sign-changeable interaction between the cosmos sectors can not bring stability for this model [37].

Here, we are interested in studying the consequences of employing the THDE model in modeling dark energy in the BD cosmology. In our setup, the Hubble horizon as the IR cutoff is taken into account, and both the interacting and non-interacting cases are also investigated. In order to achieve this goal, we studied the non-interacting case in the next section. The situation in which there is a sing-changeable interaction between the cosmos sectors has also been addressed in Sect. 3. The fourth section includes our results about the classical stability of the obtained models against perturbations. The last section is devoted to concluding remarks.

2 Non-interacting Tsallis holographic dark energy in the Brans–Dicke cosmology

We consider a homogeneous and isotropic FRW universe described by the line element

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a^2(t)\left( \frac{\mathrm{d}r^2}{1-kr^2}+r^2\mathrm{d}\Omega ^2\right) , \end{aligned}$$
(1)

where \(k=0,1,-1\) represent a flat, closed and open universes, respectively. For the universe filled by a pressureless dark matter (DM) with energy density \(\rho _m\), and a DE candidate with energy density \(\rho _D\), the Brans–Dicke field equations are found as [27]

$$\begin{aligned}&\frac{3}{4\omega }\phi ^2\left( H^2+\frac{k}{a^2}\right) -\frac{\dot{\phi }^2}{2}+\frac{3}{2\omega }H\dot{\phi }\phi =\rho _M+\rho _D, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{-\phi ^2}{4\omega }\left( \frac{2\ddot{a}}{a}+H^2+\frac{k}{a^2}\right) -\frac{1}{\omega }H\dot{\phi }\phi \nonumber \\&\quad -\frac{1}{2\omega }\ddot{\phi }\phi -\frac{\dot{\phi }^2}{2}\Big (1+\frac{1}{\omega }\Big )=p_D, \end{aligned}$$
(3)
$$\begin{aligned}&\ddot{\phi }+3H\dot{\phi }-\frac{3}{2\omega }\left( \frac{\ddot{a}}{a}+H^2+\frac{k}{a^2}\right) \phi =0. \end{aligned}$$
(4)

where \(H=\dot{a}/a \) is the Hubble parameter and \(p_D\) represents the pressure of DE. Following [26], we assume that the BD field \(\phi \) can be described by a power function of the scale factor, namely \(\phi \propto a^n \). One can now get

$$\begin{aligned} \dot{\phi }=nH\phi , \end{aligned}$$
(5)

and hence

$$\begin{aligned} \ddot{\phi }=n^2H^2\phi +n\dot{H}\phi , \end{aligned}$$
(6)

where dot denotes derivative with respect to time.

Since the Tsallis generalized entropy-area relation is independent of the gravitational theory used to study the system [35], the energy density of Tsallis HDE (THDE) with the Hubble radius as the IR cutoff \((L=H^{-1})\), takes the following form

$$\begin{aligned} \rho _D=B\phi ^{2\delta }H^{4-2\delta }. \end{aligned}$$
(7)

Here, \(\phi ^2=\omega /(2\pi G_{eff})\), \(G_{eff}\) is the effective gravitational constant, and we used the holographic hypothesis [1,2,3, 13]. In the limiting case, where \( G_{eff} \) is reduced to G, the energy density of THDE in the standard cosmology is restored [13]. For the \( \delta =1 \) case, the above equation also yields the standard HDE density in the BD gravity [28]. The dimensionless density parameters are defined as

$$\begin{aligned} \Omega _m= & {} \frac{\rho _m}{\rho _{cr}}=\frac{4\omega \rho _m}{3\phi ^2H^2},\nonumber \\ \Omega _D= & {} \frac{\rho _D}{\rho _{cr}}= \frac{4B\omega }{3}\phi ^{2\delta -2}H^{2-2\delta },\nonumber \\ \Omega _\phi= & {} \frac{\rho _\phi }{\rho _{cr}}= 2n\Big (\frac{n\omega }{3}-1\Big ),\nonumber \\ \Omega _k= & {} \frac{k}{a^2H^2}. \end{aligned}$$
(8)
Fig. 1
figure 1

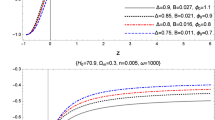
\(\Omega _D\) versus z. Here, we used \( \Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \(\Omega _{D0} = 0.73 \), \( n=0.001\) and \( \omega =1000 \) [19] as the initial conditions

Full size image

Here, we also assume that there is no energy exchange between the cosmos sectors, and hence, the energy conservation equations are as follows

$$\begin{aligned} \dot{\rho }_D+3H(1+\omega _D)\rho _D=0, \end{aligned}$$
(9)

and

$$\begin{aligned} \dot{\rho }_m+3H\rho _m=0, \end{aligned}$$
(10)

where \(\omega _D=\frac{p_D}{\rho _D}\) denotes the equation of state (EoS) parameter of dark energy. Taking the time derivative of Eq. (7), we have

$$\begin{aligned} \dot{\rho }_D=2H\rho _D\Big (n\delta +(2-\delta )\frac{\dot{H}}{H^2}\Big ), \end{aligned}$$
(11)

combined with relation \(\dot{\Omega }_D=H\Omega _D^\prime \) to obtain

$$\begin{aligned} \Omega _D^\prime =2(1-\delta )\Omega _D\Big (\frac{\dot{H}}{H^2}+n\Big ), \end{aligned}$$
(12)

where prime denotes derivative with respect to \(x=\ln a\). Now, combining the time derivative of Eq. (2) with Eqs. (5), (6), (10) and (11), one can easily get

$$\begin{aligned} \frac{\dot{H}}{H^2}= & {} \Big [3(\Omega _D-1)-\Omega _k +2n(\delta \Omega _D+\frac{2\omega n^2}{3}\nonumber \\&+n\omega -2n-\Omega _k-4)\Big ]\nonumber \\&\times \Big (2(\delta -2)\Omega _D-\frac{4n^2\omega }{3}+4n+2\Big )^{-1} \end{aligned}$$
(13)

Inserting Eq. (13) into (12), we also obtain the evolution of dimensionless THDE density as

$$\begin{aligned}&\Omega _D^\prime =2n(\delta -1)\Omega _D+\Omega _D(1-\delta )\nonumber \\&\quad \times \frac{\Big (3(\Omega _D-1)\,{-}\,\Omega _k\,{+}\,2n(\delta \Omega _D\,{+}\,n\omega {+}\frac{2\omega n^2}{3}\,{-}\,2n-\Omega _k\,{-}\,4)\Big )}{(\delta -2)\Omega _D-\frac{2n^2\omega }{3}+2n+1}.\nonumber \\ \end{aligned}$$
(14)

In the limiting case \( n=0 \) \( (\omega \rightarrow 0) \), Eq. (14) restores the result of the Einstein gravity [13]. The evolution of the dimensionless THDE density parameter \(\Omega _D\) against redshift z is shown in Fig. 1 for the \( \Omega _k=0 \) (the upper panel) and \( \Omega _{k0}=0.1 \) [42], where \(\Omega _{k0}\) is the current value of \(\Omega _k\), (the lower panel) cases whenever the initial condition \( \Omega _D(z=0)=0.73 \) has been considered. Additionally, \( n=0.001 \) and \(\omega =1000\) [19, 20] have also been used to plot Fig. 1, showing that in the early time \( (z\rightarrow \infty ) \) we have \( \Omega _D \rightarrow 0 \), while at the late time (where \( (z\rightarrow -1) \)) we have \( \Omega _D \rightarrow 1 \).

Combining Eqs. (9), (11) and (13) with each other, the EoS parameter is obtained as

$$\begin{aligned}&\omega _D=-1-\frac{2\delta n}{3}+(\delta -2)\nonumber \\&\quad \times \frac{3(\Omega _D-1)-\Omega _k+2n(\delta \Omega _D+n\omega +\frac{2\omega n^2}{3}-2n-\Omega _k-4)}{3(\delta -2)\Omega _D-2n^2\omega +6n+3}.\nonumber \\ \end{aligned}$$
(15)

It is easy to see that the EoS parameter for THDE in the standard cosmology is retrieved at the appropriate limit \( n=0 \) \( (\omega \rightarrow 0) \) [13]. The behavior of \( \omega _D \) against z has been plotted in Fig. 2, for both the \(\Omega _k=0 \) (upper panel) and \( \Omega _{k0}=0.1 \) [42] (lower panel) cases, whenever \( n=0.001 \) and \(\omega =1000\) [19]. From Fig. 2, one can clearly see that the THDE model with the Hubble cutoff in the BD gravity can lead to the accelerated expansion, even in the absence of an interaction between the two dark sectors of cosmos, and in addition, we have \(\omega _D(z\rightarrow -1)\rightarrow -1\) which implies that this model simulates the cosmological constant at future.

Fig. 2
figure 2

The evolution of the EoS parameter \(\omega _D\) versus redshift parameter z for the non-interacting THDE, where the different parameter values \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \( n=0.001 \) and \(\omega =1000\) [19] are adopted

Full size image
Fig. 3
figure 3

The evolution of the deceleration parameter q versus redshift parameter z for the non-interacting THDE, where the different parameter values \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \( n=0.001 \) and \(\omega =1000\) are adopted

Full size image

Using Eq. (13), we can also write

$$\begin{aligned} q= & {} -1-\frac{\dot{H}}{H^2}=-1\nonumber \\&-\frac{3(\Omega _D-1)-\Omega _k{+}2n(\delta \Omega _D+n\omega +\frac{2\omega n^2}{3}-2n-\Omega _k-4)}{2(\delta -2)\Omega _D-\frac{4n^2\omega }{3}+4n+2}.\nonumber \\ \end{aligned}$$
(16)

Once again, the respective relation in [13] can be obtained in the limiting case \( n=0 \). In the limiting case \( \delta =1 \), the obtained results in Eqs. (15) and (16) are reduced to their respective expressions for the original HDE in the BD gravity [28]. The evolution of q versus redshift parameter z for different values of the parameter \( \delta \) has also been plotted in Fig. 3 for the \(\Omega _k=0 \) (upper panel) and \( \Omega _{k0}=0.1 \) [42] (lower panel) cases, whenever \( n=0.001 \) and \(\omega =1000\) [19].

Our results show that the transition redshift (from the deceleration phase to an accelerated phase) lies in the interval \( 0.5<z<0.9 \), which is fully consistent with the recent observations [43,44,45]. Figures 1, 2 and 3 indicate that, for the assumed values of n and \(\omega \), (i) only the \(\delta =1.2\) case can produce acceptable behavior for the system quantities, including q, \(\omega _D\) and \(\Omega _D\), simultaneously in the flat FRW universe, and (ii) there are various values for \(\delta \) which lead to the proper behavior for the system quantities simultaneously in the non-flat universe.

Fig. 4
figure 4

The evolution of \(\Omega _D\) versus z for the interacting THDE in the BD gravity. Here, we considered \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \(\Omega _{D0} = 0.73\), \( n=0.005\) and \( \omega =10000\) [20] for the initial conditions

Full size image

3 Sign-changeable interacting THDE model

In the FRW background, filled with DE and DM interacting with each other, the total energy-momentum conservation law is decomposed into

$$\begin{aligned} \dot{\rho }_D+3H(1+\omega _D)\rho _D=-Q, \end{aligned}$$
(17)

and

$$\begin{aligned} \dot{\rho }_m+3H\rho _m=Q, \end{aligned}$$
(18)

where Q denotes the interaction term, and we assume that it has the \(Q=3b^2qH(\rho _m+\rho _D)\) form [31,32,33], in which \( b^2 \) is the coupling constant. Taking the time derivative of Eq. (2) and using Eqs. (5), (6), (11) and (18), we have

$$\begin{aligned} \frac{\dot{H}}{H^2}= & {} \Big [3\Omega _D-3(1+\Omega _k)(1+b^2)-2\Omega _k(n-1)\nonumber \\&+ 2n(\delta \Omega _D+\frac{2\omega n^2}{3}+(n\omega -3)(b^2+1)-2n-1)\Big ]\nonumber \\&\times \Big (2(\delta -2)\Omega _D-\frac{4n^2\omega }{3}+(3b^2+2)(2n+1)\nonumber \\&+ b^2\Big (3\Omega _k-2n^2\omega \Big )\Big )^{-1}, \end{aligned}$$
(19)

substituted into Eq. (12) to obtain

$$\begin{aligned} \Omega _D^\prime= & {} 2n(\delta -1)\Omega _D\nonumber \\&+\Big [\Omega _D(1-\delta )\Big (3\Omega _D-3(1+\Omega _k)(1+b^2)\nonumber \\&-2\Omega _k(n-1)+ 2n(\delta \Omega _D+n\omega +\frac{2\omega n^2}{3}\nonumber \\&+(n\omega -3)(b^2+1)-2n-1))\Big )\Big ]\nonumber \\&\times \Big ((\delta -2)\Omega _D-\frac{2n^2\omega }{3}+\left( \frac{3b^2}{2}+1\right) (2n+1)\nonumber \\&+ b^2(3\Omega _k-2n^2\omega )\Big )^{-1}. \end{aligned}$$
(20)

In the absence of interaction term \( (b^2=0) \), Eq. (20) is reduced to its respective relation in the previous section. The evolution of \(\Omega _D\) against redshift z for interacting THDE has been plotted in Fig. 4. As it is seen, we have \( \Omega _D \rightarrow 0 \) and \(\Omega _D \rightarrow 1\) at the \(z\rightarrow \infty \) (the early time) and \(z\rightarrow -1\) (the late time) limits, respectively. The Eos parameter \( \omega _D \) can also be derived by combining Eqs. (11) and (17) with Eq. (19) as

$$\begin{aligned} \omega _D= & {} -1-\frac{2\delta n}{3}+\frac{(2n-\frac{2\omega n^2}{3}+1)b^2}{\Omega _D}\nonumber \\&+\frac{(6n-2\omega n^2+3)b^2+2(\delta -2)\Omega _D}{6\Omega _D}\nonumber \\&\times \Big [3(\Omega _D-(1+\Omega _k)(1+b^2))-2\Omega _k(n-1)\nonumber \\&+2n(\delta \Omega _D+\frac{2\omega n^2}{3}+(n\omega -3)(b^2+1)-2n-1)\Big ]\nonumber \\&\times \Big (2(\delta -2)\Omega _D-\frac{4n^2\omega }{3}+(3b^2+2)(2n+1)\nonumber \\&+ b^2(3\Omega _k-2n^2\omega )2\omega \Big )^{-1}. \end{aligned}$$
(21)

We have also plotted the evolution of \( \omega _D \) versus z for the interacting THDE in Figs. 5 and 6 for \(n=0.05\) and \(\omega =1000\) [19]. From these figures, it is obvious that, depending on the values of \(\delta \), \(\Omega _k\) and \(b^2\), the phantom line can be crossed, and the cosmological constant model of DE (\(\omega _D\rightarrow -1\)) is obtainable at the \(z\rightarrow -1\) limit in both the flat (for \(0.5<\delta <1\) and \(b^2>0.1\)) and non-flat (for \(\delta >1\)) FRW universes. From Eq. (19), we also get

$$\begin{aligned} q= & {} -1-\Big [3(\Omega _D-(1+\Omega _k)(1+b^2))-2\Omega _k(n-1)\nonumber \\&+2n(\delta \Omega _D+\frac{2\omega n^2}{3}+(n\omega -3)(b^2+1)-2n-1)\Big ]\nonumber \\&\times \Big (2(\delta -2)\Omega _D-\frac{4n^2\omega }{3}+(3b^2+2)(2n+1)\nonumber \\&+b^2(3\Omega _k-2n^2\omega )2\omega \Big )^{-1}. \end{aligned}$$
(22)

It is obvious that, in the limiting case \( b^2=0 \), the respective relation in the previous section can be retrieved. The evolution of q versus z has been plotted in Figs. 6 and 7.

Fig. 5
figure 5

The evolution of \(\omega _D\) versus z for the interacting THDE, where \(\Omega _k=0 \) (upper panel), \(\Omega _{k0}=0.1\) (lower panel), \( \delta =0.6 \), \( n=0.05 \) and \(\omega =1000\) are adopted as the initial conditions

Full size image

From Figs. 6 and 7, it is clear that q starts from positive value at the earlier time, and takes the negative values later, and also, it has a zero at \( z\approx 0.6 \) [43,44,45]. Figures 4, 5, 6 and 7 indicate that, with the same set of the system parameters (\(\delta ,n,\omega ,b\)), acceptable and proper behavior for \(\omega _D\), q and \(\Omega _D\) is obtainable simultaneously only in the non-flat universe. In fact, as the non-interacting case, the non-flat universe can produce more better and acceptable results compared with the flat universe.

Fig. 6
figure 6

The evolution of \( \omega _D \) and q versus z for the interacting THDE in the non-flat BD cosmology. Here, we used \( \Omega _{k0}=0.1 \) , \( b^2=0.1 \), \( n=0.05 \) and \(\omega =1000\) as the initial conditions

Full size image
Fig. 7
figure 7

The evolution of q versus z for the interacting THDE. We considered \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \( \delta =0.6 \), \( n=0.05 \) and \(\omega =1000\) as the initial conditions

Full size image

4 Stability

In this section we would like to study the classical stability of the obtained models against perturbations. In the perturbation theory, an important quantity is the squared of the sound speed \( v_s^2 \). Stability or instability of a given perturbation in the background, can be specified by determining the sign of \( v_s^2 \). For \( v_s^2>0 \) the given perturbation propagates in the environment meaning that the model is stable against the perturbations.

The squared sound speed \( v_s^2 \) is given by

$$\begin{aligned} v_s^2=\frac{dp}{d\rho _D}=\frac{\dot{p}}{\dot{\rho }_D}. \end{aligned}$$
(23)

By differentiating of \( p_{D} \) with respect to time, inserting the result in Eq. (23), and using Eq. (11), we can finally get

$$\begin{aligned} v_s^2=\omega _D+\frac{\omega _D^\prime }{2\delta n+2(2-\delta )\frac{\dot{H}}{H^2}}. \end{aligned}$$
(24)
Fig. 8
figure 8

\(v_s^2\) versus z for the non-interacting THDE in the BD gravity, where \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \( n=0.001 \) and \(\omega =1000\) [19] are adopted

Full size image

4.1 Non-interacting case

Taking the time derivative of Eq. (15) and using Eqs. (11), (13), (14) and (24), one can obtain \( v_s^2 \) for the non-interacting THDE with the Hubble cutoff in the BD cosmology. Since this expression is too long, we shall not present it here, and only plot it in Fig. 8. This figure shows that, in the flat FRW universe, the non-interacting THDE model is classically stable (unstable) for \( 0<\delta <1 \) (\(\delta >1\)). In addition, the lower panel indicates that the model is classically unstable in the non-flat FRW universe.

4.2 Interacting case

By taking the time derivative of Eq. (21), and combining the result with Eqs. (7), (11), (19) and (24), we can obtain \(v_s^2\) for the interacting THDE. Again, since this expression is too long, we do not present it here, and it has been plotted in Figs. 9 and 10. As the upper panel of Fig. 9 shows, the model is classically stable in the flat universe, but the values chosen for \(\delta \), \(b^2\), n and \(\omega \) cannot produce proper behavior for q, \(\omega _D\) and \(\Omega _D\) simultaneously. In fact, in a flat FRW universe, the interacting THDE cannot produce stable and acceptable description for q, \(\omega _D\) and \(\Omega _D\) with the same set of (\(\delta ,n,\omega ,b\)) simultaneously. The same story is also obtained in the non-flat case. As it is obvious from Fig. 10 and the lower panel of Fig. 9, the model description of the cosmic evolution may be stable, depending on the value of \(\delta \). Indeed, although, the parameters leading to the stable description provide suitable behavior for q and \(\omega _D\), they cannot produce proper behavior for \(\Omega _D\).

Fig. 9
figure 9

\(v_s^2\) versus \(\Omega _D\) for the sign-changeable interacting THDE with the Hubble cutoff. Here, we used \(\Omega _k=0 \) (upper panel), \( \Omega _{k0}=0.1 \) (lower panel), \( \delta =0.6 \), \( n=0.05 \) and \(\omega =1000\) as the initial conditions

Full size image
Fig. 10
figure 10

\(v_s^2\) versus \(\Omega _D\) for the sign-changeable interacting THDE with the Hubble cutoff, where \( \Omega _{k0}=0.1 \) , \( b^2=0.1 \), \( n=0.05 \) and \(\omega =1000\) are adopted

Full size image

5 Concluding remarks

We studied the consequences of using THDE in order to model DE in the BD framework. For the flat universe and the non-interacting THDE, it has been obtained that, for the assumed initial conditions, only the \(\delta =1.2\) case can produce suitable behavior for q, \(\omega _D\) and \(\Omega _D\). For this case, we obtained \(\omega _D(z\rightarrow -1)\rightarrow -1\) addressing us that this model simulates cosmological constant at future. The classical stability analysis also shows that this model is not stable. If the interaction \(Q=3b^2qH(\rho _m+\rho _D)\) [31,32,33] is added to the system, then there is not a set of (\(\delta ,n,\omega ,b\)) leading to acceptable and proper behavior for q, \(\omega _D\) and \(\Omega _D\) simultaneously meaning that the system description is incomplete. It is also useful to mention here that this incomplete description can meet the classical stability requirement.

For the non-flat FRW universe, we found out that (i) for \(\delta >2\), the model can provide suitable descriptions for the cosmic evolution in both the interacting and non-interacting cases, (ii) these descriptions are not stable, and (iii) there are cases for which \(\omega _D(z\rightarrow -1)\rightarrow -1\) the same as the EoS of the cosmological constant (\(\omega _D=-1\)). In fact, the same as the flat universe, the sets of (\(\delta ,n,\omega ,b\)) leading to the stable cases cannot provide proper explanations for q, \(\omega _D\) and \(\Omega _D\) simultaneously and vice versa.