1 Introduction

During the last decades, the simple- and multi-scaling behavior of the river networks has been detected [1,2,3,4,5,6]. Such a behavior is observed at two different geomorphological scales known as basin (catchment), and channel (reach) scales [7]. At the catchment scale, the analysis deals with the dendritic, geomorphological structure of river networks. On the other hand, at the channel scale, the river’s behavior is related to the study of the uni- and multi-cursal characterization of the active channel networks [7,8,9].

The mechanism of formation of braided channels is very complex, and its characterization is not straightforward. In fact, one can focus on several features ranging from the fractal and multi-fractal scaling, to self-affine and self-similar properties [10,11,12,13,14].

Howard et al. [11] found strong correlations among dimensionless properties of braided streams, therefore highlighting the conservation of similarity-properties in streams with the same average number of width in channels of different sizes. A consequence is that the degree of braiding, defined as the average number of channels bisected by lines crossing the channel, increases with the product of discharge and slope, while it decreases with a higher variance in discharge [15].

Models based on Exner mass-balance equation also show that the main features that characterize braiding are bedload sediment transport and laterally unconstrained free-surface flow. Braided channel simulations for natural and laboratory gravel-bed rivers were compared in [15, 16], showing that the models remain statistically stable over time and, furthermore, their basic geometric statistics are in good agreement with real braided rivers. In [10] it is proved that the analogous formation mechanism of the braided channels is observed in streams with different flow regimes, scales, slopes, and bed material types. Moreover, it has been showed that a smaller part of a river, stretched differently along the mainstream and perpendicular directions, is statistically identical to the larger part [10]. Basing on samples with several braided river, Walsh and Hicks [14] examined the relation between the island length and width which are measured along the major and minor axes, and Hurst’s exponent. They deduced that, for islands, the behavior is generally isotropic or self-similar. Bassler et al. [17] compared the scaling properties of the braided vortex rivers with those of braided fluvial rivers, using a cellular model. They found that the vortex flow can make braided rivers strikingly similar to the aerial photographs of braided fluvial rivers (such as the Brahmaputra). De Bartolo et al. [8] investigated natural river networks and braided channels by using a fixed-mass multifractal analysis, highlighting a multi-scaling behavior. The spatial variability of braided channel networks is represented by the number of active channels or streams and their flows due to their unicursal nature. Therefore, the braided channels are river systems that show a multicursal behavior.

On the basis of the literature, a twofold behavior of the braided channels scaling process emerges, since they can be considered either simple or multi-scaling. In this framework, the purpose of our investigation is to address scaling processes through a direct stochastic scaling analysis, basing on a second-order stochastic theory, namely variance and mean, of the active channel fluctuations.

The novelty of this procedure consists in the use of the Taylor’s law [18] by a direct scaling of the active channel fluctuation exponents coupled with the fractal dimensions and the Hurst exponents. Unlike the standard direct scaling approaches used so far, our approach allows us to identify the theoretical distributions that best fit the measurements of the three examined rivers, i.e. Allaro, Precariti and Rakaia. Furthermore, this generalized procedure allows to determine the ranges in which the measures (active channel fluctuations) can be considered fractal or multifractal, namely simple or multi-scaling.

2 Methods

A braided river is a geomorphological system that, over some part of its length, flows in multiple, mobile channels across a gravel floodplain that remain relatively unmodified condition [19].

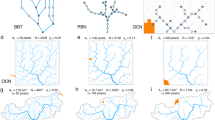
In particular, braided channels are characterized by a shift of bars during the flood events and by a number of active channels, here denoted by \(N_{\mathrm{ac}}\). For a given riverbed reach, this is defined as the number of intersections per transect occurring in a given spatial portion of the cartographic blue-line water channels (see Fig. 1a, b) [20].

Their evolution develops as follows: the initial stream, consisting in a sole active channel \(N_{\mathrm{ac}}=1\), widens and a sequence of islands is created (“island-braiding”). The elevation of the water free surface continually decreases, while the size of the islands (in plane view) increases. Thus, the flow around islands splits into pairs of other two streams (\(N_{\mathrm{ac}}=2\)). Likewise, other two streams produce “their own” islands and their own pair of other two streams (\(N_{\mathrm{ac}}=4\)) [21]. This sequence of branching processes (braiding) goes on until the equilibrium or a steady state regime is reached and, consequently, \(N_{\mathrm{ac}}\) changes along the reach [21].

Fig. 1
figure 1

Considered riverbed reach of the Precariti Fiumara (a). Example of subdivision into single transects of a riverbed reach of the Precariti Fiumara, about 1.5 km long (50 m spatial resolution between transects) (b). The black lines represent the orthogonal transects to the central axis (dashed grey line of the geometrical construction) of the braided channel skeleton

Full size image

Due to the uncertainty affecting such a process, braiding can be regarded as a stochastic process in space whose behaviour we wish to describe. Our purpose is to find a scaling law for spatial fluctuations of \(N_{\mathrm{ac}}\), thus generalizing previous studies [8, 10, 14, 17, 20]. The study relies upon the real data from three rivers: Allaro, Precariti and Rakaia. The first two, located in Calabria (Southern Italy) [20], and are of the type that is named Fiumara and are characterized by the high variability of the amount of water that flows in them throughout the seasons. The Rakaia River is one of the largest braided snow-fed river in New Zealand, with an unstable shingle bed [8].

2.1 Study site

The Allaro River flows into the Ionian Sea, an elongated bay of the Mediterranean Sea. Its main features are a drainage basin area of 130.1 \(\text {km}^{2}\), a mean elevation of 732 \(\text {m}\) asl, a main river course length of about 35.8 km, and a mean river slope at 2.85 \(\%\). The mean areal precipitation is 1394.43 \(\text {mm}\) and the mean flow is 2.76 \(\text {m}^{3}/\text {s}\). The Precariti River flows into the Ionian Sea, after a path length of about 24.0 \(\text {km}\). Its drainage area is 55.7 \(\text {km}^{2}\) and the mean elevation is 541 \(\text {m}\) asl. The Rakaia river flows into the Pacific Ocean, 50 \(\text {km}\) south of Christchurch, and it has a drainage area of about 2600 \(\text {km}^{2}\), with a length of about 150 \(\text {km}\). The mean flow is 203 \(\text {m}^{3}/\text {s}\) and the mean annual seven-day low flow of 87 \(\text {m}^{3}/\text {s}\) [22].

The two Calabrian rivers show quite elongated basins in a morphodynamic context characterized by noticeable seismicity and weathering processes responsible for huge soil erosion and landslide phenomena, enhanced by the typical discharge regime. The wide braided riverbeds mainly present a coarse-grained alluvium, shaped as elongated islands.

The Rakaia River is braided for much of its path, running through a wide shingle bed. Close to Mount Hutt, however, it is briefly confined to a narrow canyon known as the Rakaia Gorge.

The scaling analysis has been developed on peculiar braided reaches of the three rivers, with length 7.1 \(\text {km}\), 5.3 \(\text {km}\) and 19.9 \(\text {km}\) for the Allaro, the Precariti, and the Rakaia River. Allaro braided network data set was obtained from De Bartolo et al. [20]. Precariti is a new Fiumara data set here analyzed, while Rakaia was obtained from [14].

2.2 Taylor’s law approach

Taylor’s law approach is based on the empirical power relationship between the variance of a time series or a spatial sequence of measurements or counting (as in our case), and its corresponding mean. The quantity we are interested in is the fluctuation number of active channels \(N'_{\mathrm{ac}}\) in braided watercourses, that will be defined below.

According to [7, 23], in a fixed time process, the spatial sequence of \(N'_{\mathrm{ac}}\) can be regarded as a spatial stochastic process, indexed by the interval [0, L], where L represents the length of the braided channel reach under consideration. Sampling of the data is performed by dividing the whole interval [0, L] into equal sub-intervals of length \(\Delta s\), called the aggregation length. In our case, \(\Delta s\) takes values that are multiples of 1m, up to the whole length L, so defining a partition for each value taken.

For each partition, we introduce \(N_{\mathrm{ac}}^{*}\) the set of integer numbers such that \(1\le N_{\mathrm{ac}}^{*}\le N_m\), where \(N_{m}\) is the minimum of the maximum values that \(N_{\mathrm{ac}}\) takes upon all sub-intervals of the partition. We refer to unicursal reach whenever \(N^*_{\mathrm{ac}}=1\) and multicursal reach otherwise.

The hypothesis we want to validate is that the scaling of spatial series data can be assessed by grouping the data into aggregates of two, three and more measurements, calculating the mean and variance at each level of aggregation, and studying their statistical behavior in the framework of exponential probability distributions.

Thus, for any fixed \(\Delta s\) and \(N_{\mathrm{ac}}^{*}\), we define the number of fluctuating active channels

$$\begin{aligned} N_{\mathrm{ac}}^{'} := N_{\mathrm{ac}} - N_{\mathrm{ac}}^{*}, \end{aligned}$$
(1)

and we determine the mean \(\mu _{N_{\mathrm{ac}}^{'}}\) and variance \( \sigma ^{2} _{N_{\mathrm{ac}}^{'}}\) for each sequence of \(N'_{\mathrm{ac}}\) within each subinterval. Then, according to [18, 24, 25], we assume the Taylor power law

$$\begin{aligned} \sigma ^{2} _{N_{\mathrm{ac}}^{'}}= a \;\mu _{N_{\mathrm{ac}}^{'}}^b, \end{aligned}$$
(2)

with \( a \) and \( b \) two positive constants [26], named the dispersion parameter and the scaling exponent, respectively.

Taylor’s law is also a characteristic trait of a class of exponential probability distributions, known as Tweedie’s models, which exhibit a variance-mean relationship of the type (2) and are invariant under changes of scale. There are seven different Tweedie distributions, which vary according to the size of the exponent b. Two particular cases of Tweedie models will be briefly introduced in the next Section. They correspond to the Poisson distribution, when \(b=1\), and to the compound Poisson–Gamma distribution (PGD), when \(1<b<2\).

Part of the results of this article will validate the effectiveness of such models in describing the spatial distribution of braided channels of the rivers under considerations.

2.3 Background material

Distribution of real data of a stochastic process is often related to the fractal geometry. The idea is that, if the data is of fractal nature, then its behaviour is scaling-invariant and, therefore, it can be determined by aggregating the data as described above. Indeed, it is well known that [25, 27,28,29,30] the exponent b is related to the fractal dimension, D, and to the Hurst exponent, H, as:

$$\begin{aligned} b = 4 - 2 D, \qquad \qquad b = 2 H. \end{aligned}$$
(3)

When fractal structures manifest local variations in fractal dimension, they can be called multifractals [31, 32].

Now, focusing on our framework, the size of H provides the behavior of \(N_{\mathrm{ac}}^{'}\) along the reach, and that is often referred to as the index of dependence or index of long-range dependence [33].

In particular, whenever \(0.5< H < 1\) there is a sequence with long-term positive auto-correlation, meaning that a high value in the \(N_{\mathrm{ac}}^{'}\) sequence will be probably followed by another high value and that the values obtained considering a greater distance will also tend to be high [31]. In this first case, there is a positive correlation of the increments (regular increments of \(N_{\mathrm{ac}}^{'}\)): the process manifests a long range dependence and its behaviour is defined as persistent [27, 30, 34].

On the other hand, whenever \(0< H< 0.5\) it is expected a simple sequence with long-term switching between high and low values, meaning that a single high value will probably be followed by a low value and that the value after that will tend to be high. In this case, there is a negative correlation of the \(N_{\mathrm{ac}}^{'}\) increments with very irregular form, the process manifests a short range dependence and its behavior is referred as anti-persistent.

Finally, when \(H = 0.5\), the spatial process of the \(N_{\mathrm{ac}}^{'}\) per transects can be considered as a Brownian motion. Thus, \(H=0.5\) indicates a completely uncorrelated sequence and, hence, it is applicable to sequences for which the autocorrelations at small spatial lags can be positive or negative [31].

According to the literature, there is not, to the best of our knowledge (see, for example [11, 15, 30, 35, 36]), a procedure that, starting from a generic stochastic signal expressible by means of the Hurst exponent, indicates whether a posteriori this process is self-similar or self-affine. Certainly, this would help us (even if referred to other geomorphological indices [10, 11, 14, 15, 23, 35, 36]) to better evaluate, on the basis of the literature of braided systems, [10, 14, 36,37,38,39] the nature of these jumping processes. Therefore, in order to indicate whether the process is simple- or multi-scaling, we have to relate the Hurst index to the scaling exponent and the fractal dimension.

3 Results

3.1 Scaling analysis of the exponent b

According to the definitions provided in Sect. , we analyzed the spatial fluctuation \(N_{\mathrm{ac}}^{'}\) for the three river reach considered. Figure 2 sketches the trend of \(N_{\mathrm{ac}}\) as a function of the aggregation length, for the rivers Allaro (a), Precariti (b) and Rakaia (c).

Fig. 2
figure 2

Graphical representation of the sequences of the number of active channels \(N_{\mathrm{ac}}\): Allaro (a), Precariti (b) and Rakaia (c) braided river reaches

Full size image

The length L of each braided channel reach is partitioned in several spatial aggregation intervals, \(\Delta s\), whose length ranges between 5 m and 2000 m. The cutoff limit is \(\Delta s = 5\) m that corresponds to the feed function (equal to 0.5 mm) in a topographic map of scale 1:10000 (see Fig. 1). For further details we refer to Refs. [14, 20].

The mean and variance, calculated for any \(\Delta s\) between 5 m and 2000 m, are then represented in the log-log plane, from which two regimes of behaviour are inferred.

A deterministic regime characterizes the data in the interval \(5\, \text {m} \le \Delta s \le 60 \,\text {m}\), where Taylor’s law analysis does not apply. In fact, we obtain that the experimental data are fitted to the function

$$\begin{aligned} \sigma ^2 _{N_{\mathrm{ac}}^{'}}= \left\{ \begin{array}{ll} \displaystyle \delta \left| \sin \left( \pi \mu _{N_{\mathrm{ac}}^{'}} \right) \right| &{} \qquad \text {if} \;\; \sigma ^{2}_{N_{\mathrm{ac}}^{'}} < \delta , \\ &{} \\ \displaystyle \frac{1}{\sqrt{3}} &{} \qquad \text {if} \;\; \sigma ^{2} _{N_{\mathrm{ac}}^{'}}> \delta , \end{array} \right. \end{aligned}$$
(4)

with \(\delta \simeq 0.27\). Figure 3 sketches these behaviours for the three rivers under consideration, in correspondence of the spatial aggregation ranges \(\Delta s =45,\, 30,\, 30\) \(\text {m}\), with \(N_{\mathrm{ac}}^{*}=1\).

Fig. 3
figure 3

Fitting of experimental data for Allaro (a), Precariti (b) and Rakaia (c) corresponding to \(\Delta s= \) 45 m, 30 m, and 35 m, respectively. Circles represent the experimental data whose interpolating law is sinusoidal, while triangles are fitted to a constant [see Eq. (4)]. The panel d sketches the fitting of the measurement of Rakaia River (\(\Delta s=600\) m) to the power law (5). Each represented dataset corresponds to \(N_{\mathrm{ac}}^*=1\)

Full size image

On the other hand, as \(\Delta s\) exceeds 60 m, data follows statistical distributions that we wish to validate by means of Taylor’s law. Indeed, a typical distribution of the data is as shown in Fig. 3d, that suggests to fit the experimental data to the linear law

$$\begin{aligned} \log \sigma ^{2} _{N_{\mathrm{ac}}^{'}}=\log \textit{a}+b\log \mu _{N_{\mathrm{ac}}^{'}}, \end{aligned}$$
(5)

obtained from Eq. (2). Thus, we determine b for the three rivers under consideration by using the linear regression model, covering all ranges of aggregations between 5 \(\text {m}\) and 2000 \(\text {m}\) and considering all admissible values of \(N_{\mathrm{ac}}^{*}\). The results of this analysis is displayed in Fig. 4.

The goodness of fit is provided by the correlation coefficient \(r^2\), by applying the least squares method. Following the criterion given in [40], we will validate Taylor’s law only whenever \(r^2>0.8\). Thus, a direct inspection leads to consider only specific intervals of aggregation, and \(N_{\mathrm{ac}}^{*}=1\).

Table 1 shows, for the three rivers under consideration, the ranges of aggregation whose correlation coefficient is greater than 0.8, and the corresponding minimum, maximum and average values of the scaling exponent. It emerges that the Calabrian Fiumare, Allaro and Precariti, share the same behavior, with scaling exponent between 1 and 2, corresponding to the compound Poisson–Gamma distribution. On the contrary, for Rakaia, apart from a few negative values of the scaling exponent, most of the values of b range between 0 and 1. At \(\Delta s \simeq 60\) m, we obtain b approximately 1 that corresponds to the Poisson distribution.

On the other hand, for the case \(0< b < 1\) there are no scale invariant exponential dispersion models, so that this case will be treated within the framework of multifractal measures.

Fig. 4
figure 4

Scaling exponent b as a function of the aggregation length \(\Delta s\) for Allaro (a), Precariti (b) and Rakaia (c), for all admissible \(N_{\mathrm{ac}}^{*}\). The panel d displays a magnification of the trend of b in the range 60 m \( \le \Delta s \le 600 \) m and \(N_{\mathrm{ac}}^{*}=1\), for the three rivers under consideration

Full size image

3.2 Analysis of Tweedie distributions

We now determine how well the PGD for Allaro and Precariti, and the Poisson model for Rakaia, correspond to the respective empirical cumulative distribution functions.

The PGD is specified by three independent adjustable parameters \(\alpha \), \(\lambda \) and \(\theta \), to be fitted to the data, as

$$\begin{aligned} P\left( N^{'}_{\mathrm{ac}}; \theta , \lambda , \alpha \right) = c\left( N^{'}_{\mathrm{ac}}; \lambda \right) \exp \left[ \theta N^{'}_{\mathrm{ac}} - \lambda \kappa (\theta )\right] , \end{aligned}$$
(6)

with

$$\begin{aligned}c\left( N^{'}_{\mathrm{ac}}; \lambda \right) = \left\{ \begin{array}{l l l} \displaystyle \sum _{n=1}^\infty \frac{ \lambda ^n \kappa ^n (1/N^{'}_{\mathrm{ac}})}{N^{'}_{\mathrm{ac}} \Gamma (-\alpha n) n !} &{} \text {for} &{}N^{'}_{\mathrm{ac}}>0, \\ &{} &{} \\ \displaystyle 1 &{} \text {for} &{}N^{'}_{\mathrm{ac}}=0, \\ \end{array}\right. \qquad \qquad \kappa (\theta ) = \frac{\alpha -1}{\alpha } \left( \frac{\theta }{\alpha -1}\right) ^\alpha ,\end{aligned}$$

where \(\alpha \) is related to the dispersion parameter a and to the scaling exponent \(a=\lambda ^{1/(1-\alpha )}\) b and \(b = (\alpha - 2)/(\alpha - 1)\). We also define the cumulative density function related to the PGD as

$$\begin{aligned} F= \sum _{k=1}^{N'_{\mathrm{ac}}} P (k; \theta , \lambda , \alpha ), \end{aligned}$$
(7)
Table 1 Values of mean \({\overline{b}}\), maximum \(b_{\max }\) and minimum \(b_{\min }\) scaling exponent b in the spatial aggregation ranges \(\Delta s\) for the three analyzed rivers
Full size table

In view of the comparison between the theoretical and empirical CDFs, the maximum, minimum and mean values of \(\alpha \) were calculated (see Table 2) by implementing the method of moments.

Table 2 Average \({\overline{\alpha }}\), maximum \(\alpha _{\max }\) and minimum \(\alpha _{\min }\) values \(\alpha \) of the PGD within the interval \(60\;\text {m} \le \Delta s \le 600 \;\text {m}\), for Allaro and Precariti rivers
Full size table

In order to validate the consistency of the hypothesis of Tweedie distribution [41], the theoretical CDF (7) was then fitted to the empirical CDF. An example of this analysis, corresponding to \(\Delta s=571\) m for Precariti, is illustrated in Fig. 5a, where we can see, for each unitary class of \(N'_{\mathrm{ac}}\), a qualitative agreement between the empirical CDF (black dots) and theoretical CDF (grey dots). In particular, we found \(\alpha =-0.23\) that corresponds to \(b=1.81\).

As announced above, we expect the Rakaia River data to behave differently. In particular, for \(\Delta s\simeq 60\) m, where the scaling exponent is about 1, we expect the data to follow a Poisson distribution. That is a one-parameter distribution, where the unique parameter \(\lambda \) represents both the mean and the variance,

$$\begin{aligned} P_{ \lambda }\left( N'_{\mathrm{ac}};\lambda \right) =\frac{\lambda ^{N'_{\mathrm{ac}}}}{N_{\mathrm{ac}}^{'}!}\exp (-\lambda ). \end{aligned}$$
(8)

The related cumulative density function is

$$\begin{aligned} F_{\mathrm{\lambda }} = \sum _{k=1}^{N'_{\mathrm{ac}}} P_{\mathrm{\lambda }} (k; \lambda ). \end{aligned}$$
(9)

Once again, the theoretical CDF (9) has been fitted to the empirical CDFs. Figure 5b reveals the qualitative agreement between the theoretical Poisson distributions and the data, that is also supported by the probability-probability plot Fig. 5c. These qualitative agreements are corroborated by means of the Vaserstein [42] distances:

$$\begin{aligned} W_1 = \int ^\infty _0 \, dq \left| F_1(q)-F_2 (q)\right| , \qquad \quad W_2 = \int _{0}^{1}\,dq \left| F_1^{-1}(q)-F_2^{-1}(q)\right| ^{2}, \end{aligned}$$
(10)

where \(F_i\) (\(i=1,2\)) represent the cumulative density functions (7) and (9), respectively. From Fig. 6, it is seen that, for the Rakaia river, \(W_i\) increases with \(\Delta s\). For example, for \(\Delta s=300\) m, \(W_1\) and \(W_2\) are equal to 0.322 and 1.677, respectively. A similar behavior of the \(W_i\)-metric was found for the other rivers with, in particular, \(W_1\) and \(W_2\) laying within the ranges \(0.121\div 0.391\) and \(1.561\div 1.734\), for \(\Delta s\) equal to 60 and 600 m, respectively.

Thus, there is an overall deterioration in the agreement between theoretical models and data. This is a clear “scale effect” accounting for a physics that is negligible at the smallest \(\Delta s\)-values. Accounting for these “hidden” effects is left to future investigations.

Fig. 5
figure 5

Comparison between empirical and theoretical cumulative density functions, for Precariti (a), at \(\Delta s=571\) \(\text {m}\), and Rakaia (b), at \(\Delta s=60\) m. Panel c shows the probability-probability plot for Rakaia measurements, at \(\Delta s=60\) m

Full size image
Fig. 6
figure 6

Comparison between empirical and theoretical cumulative density functions, for Rakaia (a), at \(\Delta s=300\) \(\text {m}\). Panel b shows the probability-probability plot for Rakaia measurements, at \(\Delta s=300\) m

Full size image

4 Discussion

4.1 Fractal dimensions and Hurst exponents

For each reach braided river analyzed we have also investigated, on the base of Eq. (3) and the b scaling values, the fractal dimensions, D, and the Hurst exponents, H, of the variable \(N'_{\mathrm{ac}}\) as a function of the progressive spatial aggregations \(\Delta s\) in the range between 60 \(\text {m}\) and 600 \(\text {m}\), where essentially the correlation \(r^{2}\) is maximum. Figure 7 shows the development of the fractal dimensions D and Hurst exponents H for all rivers under consideration, for \(N^{*}_{\mathrm{ac}}=1\). The solid black lines represent the average trend of the variable D and H.

Specifically, it is possible to observe that, for the Allaro and Precariti (Fig. 7b, c) the fractal dimension D is roughly constant with a mean value \(\simeq 1.54\), for \(\Delta s\) between 60 \(\text {m}\) and 600 \(\text {m}\). Furthermore, our analysis restricts to \(\Delta s\) between 60 \(\text {m}\) and 200 \(\text {m}\) yields \(D=1.57\) in perfect agreement with [10, 43] for a cellular automata model (\(Q_{s}\) rules 4) for Hulahula, Aichilik, Brahmputra braided river simulation.

In any case, the values of the fractal dimension, D, for the Fiumaras Allaro and Precariti are very close to those provided in the works [10, 43] for self-affine properties of braided channels even if other different geomorphological descriptors were considered. This behaviour implies that, if a small part of the braided rivers is stretched differently in the direction of the river slope and in the perpendicular direction, then the stretched part looks statistically similar to the larger part of the braided river [43]. According to [43], this might indicates the presence of universal features in the underlying mechanisms responsible for the formation of the structure of braided river.

The correspondent Hurst index obtained for Allaro and Precariti is between 0.52 and 0.8 in agreement with [10, 43, 44], although the large difference in scale, slope and bed material (gravel to sands). Thus, in consideration of the values H that was found, there is a positive correlation of average, with regular increment of \(N'_{\mathrm{ac}}\) (persistent behavior) for Allaro and Precariti. There is also a negative correlation of average with irregular increment of \(N'_{\mathrm{ac}}\) (anti-persistent behavior) for Rakaia river network.

Fig. 7
figure 7

Fractal dimension D and Hurst exponent H as functions of the aggregation length \(\Delta s\). Panel a shows the trend of D, for \(N_{\mathrm{ac}}^*=1\), for the three rivers under consideration, with a magnification of the region 60 m \( \le \Delta s \le 600 \) m. The same data, compared to the relative interpolating curves, are reported in panels b, c and d for Allaro, Precariti and Rakaia, respectively

Full size image

However, for the Allaro and Precariti braided rivers, the average global trend of D can be considered monotone with a simple-scaling (monofractal) behaviour (see Fig. 7b, c).

A separate discussion concerns the analysis of fractal dimensions and Hurst exponents of the Rakaia braided river (see Fig. 7d). In this case, the trend of D, for 60 \(\text {m}\le \Delta s\le 600\) \(\text {m}\), shows a multi-scaling (multifractal) behaviour. Similar results were obtained by [8] for the multifractal analysis of the Ferro Fiumara also located in Calabria (Italy) with geomorphological properties similar to Rakaia and with generalized fractal dimensions between 1.5 and 1.82. These results can also be found in [44] for physical models of braided channels reproduced in the laboratory.

It is interesting to observe that the trend of H is monotonically decreasing. This behavior is provided by a smaller scaling exponent H, from 0.5 to 0, with a multifractal \(N'_{\mathrm{ac}}\) anti-persistent series [45].

It is also important to highlight that the results obtained for the Rakaia braided reach by the Taylor’s analysis are not directly comparable with the results obtained by [14] for other braided index like length, L, and width, W, of island or fluvial bars, because the obtained behaviour here is multifractal.

In short, our results obtained through the analysis of Taylor’s law are very similar to those in [10, 43, 44] and, in particular, the use of the scaling exponent show jumping processes from Poisson’s distribution to PGD with single and multifractal supports of measurements. It is interesting to note similar results are found in other branches, such as the theory of effective properties in the Stochastic Subsurface Hydrology [see, e.g. 46, 47, 48, 49] as well as the propagation of pollutants through randomly heterogeneous porous media [see, e.g. 50].

5 Conclusions

In this work we analyzed three braided channels (Allaro, Precariti and Rakaia) in order to directly recognize the simple- and the multi-scaling behavior of the fluctuation number of active channels per transect. Our new method is based on the Taylor’s power law [18] combined with the theory of exponential statistical distributions. The scaling exponent was investigated by considering several spatial aggregations \(\Delta s\).

The analysis highlighted a first range of spatial aggregations, \(5\; \text {m} \le \Delta s \le 60\; \text {m}\), with a surprising deterministic two-function behaviour. In the range \(60\; \text {m} < \Delta s \le 600\; \text {m}\) the dataset are fitted with the linear law, obtained from Taylor’s law. This analysis highlighted the common behavior of the Calabrian Fiumare, Allaro and Precariti, whose data distribution follows a compound Poisson–Gamma distribution. On the other hand, the Rakaia River shows for some aggregation values \(\Delta s \sim 60\) m a behavior in line with the Poisson distribution.

However, most of the aggregations of the Rakaia data carried a scaling exponent between 0 and 1, which means that they do not correspond to associated exponential distributions. For such aggregation intervals, we proposed a multi-fractal analysis and described their multi-scaling properties [8, 17]. This analysis, extended to the Calabrian Fiumare, confirmed the simple-scaling character of Taylor’s law [20]. These analyses can also be used to characterize other hydraulic and fluvial dynamics at the channel scale as manifestations of complex systems.