Introduction

River networks are endowed with a ubiquitous fractal signature, that is, the similarity between the parts and the whole1,2,3. The shape of river networks observed in Nature results from the interplay between chance (precipitation events, landslides and tectonic activity engendering local changes in landscape morphology) and necessity (the action of gravity and erosion driving network configurations towards optimal states)3,4. Indeed, the most probable river network configurations are those corresponding to a local minimum of energy dissipation5,6. The fractal character of river networks is subsumed by Horton’s laws on bifurcation, length and area ratios7, and by the power-law scaling of distributions of drainage areas and lengths8,9,10. These distinguishing features of river networks are relevant from a hydrological and geomorphological perspective as they control the hydrological response of a basin, its hydraulic geometry attributes and its sediment transport rates3,11,12.

Equally important, but hitherto often neglected, is the relevance of these river network properties from a biological perspective, and thus the adequate understanding of biological processes in river networks, such as biogeochemical cycling13,14 and the distribution of populations, species and pathogens15,16,17,18,19,20. Understanding how the spatial structure of landscapes influences community and ecosystem dynamics is a classic theme in ecology21,22,23,24. In this respect, river networks have recently attracted considerable interest by ecologists, due to their distinct dendritic structure25,26,27,28 and the outstanding relevance of riverine biodiversity, ecosystem functions, and their respective threats, at both local and global scales29,30. This spurred extensive research investigating how river connectivity affects biodiversity patterns31,32,33,34,35, genetic diversity36,37,38, dispersal39, and characteristics of a metapopulation (that is, a set of spatially structured populations of the same species connected by dispersal40), such as persistence41,42,43,44, stability and synchrony45,46,47,48.

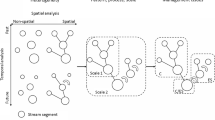
Systematic study of hydrological and ecological dynamics in rivers depends on a realistic representation of river network structures, and requires either the use of real river networks or the construction of synthetic network analogues. While the former is interesting for case-specific studies, only the latter allows generalisations and an analytical investigation of recurrent patterns. The use of synthetic analogues of river networks is especially interesting because it enables the generation of potentially infinite replicates of river networks sharing the same size and properties, which permits a proper assessment of ecological dynamics (and the uncertainty thereof) irrespective of the shape of a given river network. Several approaches have been used to approximate river networks in ecological studies. While some studies acknowledged possible shortcomings of certain network approximations25, the effects of inadequate network analogues on the ecological dynamics analyzed have not been systematically addressed (but see ref. 49). Specifically, a first group of studies25,33,34,36,37,43,45,50 modelled river networks as trees where all paths from the tree root to the source nodes (see Supplementary Note 1) have equal length; borrowing an analogy from computer science, these will hereafter be defined balanced binary trees (BBTs – Fig. 1a). A second group of studies35,38,46,47 considered a somewhat more realistic type of structures, where river network analogues were built as random assemblages of links of different lengths (e.g. following an exponential distribution46,51); these will hereafter be referred to as random branching networks (RBNs – Fig. 1b). Importantly, many of these studies35,38,45,46,47 claimed a property of such random networks, their branching probability p, to be a major driver of ecological processes such as richness patterns, genetic diversity and metapopulation stability. Finally, a third group31,32,41,42,44 exploited river network analogues derived following geomorphological principles, i.e. Optimal Channel Networks (OCNs - Fig. 1c–f). OCNs are spanning trees (see Supplementary Note 1) that correspond to a local minimum of a functional describing total energy expenditure across the network5,10,52. As such, the topological and scaling features of OCNs are indistinguishable from those of real river networks52.

Fig. 1: Examples of networks analyzed as river analogues.
figure 1

a a BBT network45. b a RBN network46. c A small OCN built on a 20 × 10 lattice and extracted with AT = 10 pixels. The river network is depicted in blue, while flow directions in the regions where AT < 10 pixels are drawn in grey. d–f An OCN built on a 200 × 200 lattice and extracted with three different values of AT. g–i A real river (Adige, Italy) extracted from a DEM (with pixel size l = 409.25 m) with three different values of AT; the catchment spans an area of 40,608 pixels. Network nodes are marked with grey dots in panels a, b and c (with filled dots corresponding to “branching" nodes, i.e. identifying the start of a link); the black solid lines in panels c–i depict the extent of the areas drained by the river networks. Orange areas (highlighted by arrows in panels d, g) depict the extent of the area (equal to AT) drained by an arbitrary headwater.

Full size image

Here, we show that, contrary to some statements and applications made in the literature, branching probability is not an inherent property of river networks and therefore does not allow distinguishing them according to their complexity level. Rather, p is a feature that depends on the scale at which a river network is observed. Here we use the term “scale invariance” to refer to a property or parameter that does not change with varying scale or resolution of the measured or observed parameter (e.g., the exponent of a power-law relationship). Conversely, we use the term “scale dependence” to refer to a property or parameter that varies depending on the scale or resolution of the measured or observed parameter. Next, we compare the topological and scaling features of BBTs, RBNs and OCNs with those of real rivers. Finally, we show that using purely random river network analogues such as BBTs and RBNs in ecological applications instead of OCNs leads to biased conclusions with respect to metapopulation stability and persistence, evaluated based on distributions of between-node distances and patch sizes. We therefore call for the use of OCNs as the only appropriate landscape model to investigate ecological processes in riverine environments. The outstanding suitability of OCNs to accurately depict hydrologic dynamics has been well-established in geosciences, yet not necessarily cascaded to other fields, and thus highlights, more in general, the need for a tighter integration of geosciences and biosciences in the study of the patterns of Nature.

Results and Discussion

Drainage area and branching ratio: a matter of scale

Geomorphological and ecological viewpoints on river networks generally differ owing to discordant definitions of the fundamental unit (the node) used to analyze them. From a geomorphological perspective, the determination of a river network entails the definition of an observational scale. Real river networks can be extracted from digital elevation models (DEMs) via algorithms for flow direction determination such as D8 (i.e., each pixel drains towards the lowest of its 8 nearest neighbors53). After the outlet location has been specified (and hence the upstream area A spanned by the river network), the first observational scale required is thus the pixel length l of the DEM, which defines the extent of a network node. A second scale is then needed to distinguish the portion of the drainage network effectively belonging to the channel network. The simplest but still widely used method53 defines channels as those pixels whose drainage area exceeds a threshold value AT. Hydrologically based criteria to determine the appropriate value for AT exist54; however, for the sake of simplicity, we here consider AT as a free parameter.

BBTs and RBNs are random constructs, and as such they do not satisfy the optimality criterion of minimizing total energy expenditure, which is the fundamental physical process shaping fluvial landscapes. Furthermore, neither of these networks is a spanning tree, which is a key attribute of real fluvial landforms10: in fact, in both BBTs and RBNs, the extent of the drained domain is not defined. As a result, the drainage area at an arbitrary network node cannot in principle be attributed, unless by using the number of upstream nodes as a proxy. This has practical implications from an ecological viewpoint because drainage area is the master variable controlling several attributes of a river, such as width, depth, discharge, or slope3,55, which in turn impact habitat characteristics and the ecology of organisms therein56.

In BBTs and RBNs, branching probability p has been defined35,38,45,46,47 as the probability that a network node is branching, i.e. connected to two upstream nodes. As such, the branching probability of a realized river network (be it a real river or a synthetic construct) could be evaluated as the ratio between the number of links NL constituting a network and the total number of network nodes N; if a unit distance between two adjacent nodes is assumed, the denominator equals the total network length. We note that the former definition of branching probability only holds in the context of the generation of a synthetic random network; it is in fact improper to refer to a “probability" when analyzing the properties of a realized river network. We clarify this aspect by introducing the concept of branching ratio pr for the latter definition (pr = NL/N). Moreover, in the case of BBTs, p and pr do not coincide (see Methods). Importantly, p and pr have no parallel in the literature on fluvial forms, nor do they refer to any of the well-studied measures of rivers’ fractal character.

The choice of different observational scales for the same drainage network results in different values of NL and N, and hence of pr. Remarkably, the very same drainage network can result in river networks that virtually assume any value of pr (ranging from 0 to 1) and N (up to the upper bound A) depending on the choice of AT and A (the latter corresponding to a given l value when measured in the number of pixels; Fig. 1d–i); networks with low AT/A ratios result in high N (Fig. 2a), while networks with low AT result in high pr (Fig. 2b). Furthermore, pr does not identify the inherent (i.e., scale-independent) branching character of a given river network in relation to other river networks. In fact, by extracting different river networks at various scales (i.e., various AT values) and assessing the rivers’ rank in terms of pr, one observes that rivers that look more “branching" (i.e., have higher pr) than others for a given AT value can become less “branching" for a different AT value (Fig. 3). We therefore conclude that branching probability is a non-descriptive property of a river network, which by no means describes its inherent branching character, and depends on the observational scale.

Fig. 2: Variation of N and pr as a function of observational scales for OCNs and real river networks.
figure 2

a Expected value of number of network nodes N as a function of threshold area AT and total drained area A (from Eq. (1)); the white dots indicate the values of AT and A used to generate the OCNs used in this analysis. b Expected value of branching ratio pr as a function of AT and A (from Eq. (1)); symbols as in a.

Full size image
Fig. 3: Values of branching ratio as a function of AT for the 50 real river networks analyzed in this study.
figure 3

a Natural values of pr in logarithmic scale. b z-normalized branching ratios (i.e., for each AT value, values of pr are normalized so that they have null mean and unit standard deviation), which better shows how rivers rank differently in terms of pr for different observation scales (i.e., AT). Lines connect dots relative to the same river. For visual purposes, rivers that rank first, second, second-to-last or last in at least one of the AT groups are displayed in colors; the other rivers are displayed in grey.

Full size image

Scaling is also crucial when looking at river networks from an ecological perspective. In this case, the relevant scale determining the dimension l of a node is the extent of habitat within which individuals (due to e.g. physical constrains) can be assigned to a single population57,58; the riverine connectivity and ensuing dispersal among these populations give rise to a metapopulation at the river network level. The specific spatial scale largely depends on the targeted species (e.g. being larger for fish than for aquatic insects), and it is conceivably much larger than (or, at least, it has no reason to be equal to) the pixel size of the DEM on which the river network is extracted. Since the evaluation of pr depends on the number of nodes N, which, in turn, is defined based on the scale length l, then the resulting pr derived from a random network would depend on the characteristics of the target taxa, which is inconsistent with the assumption of pr being a scale-invariant property of river networks.

Note also that using the ecological definition of l (i.e., spatial range of a local population) to discretize a real river network into N nodes, and from there calculate the branching ratio pr = NL/N, is problematic. Indeed, this would imply an elongation of all links shorter than l (which constitute a non-negligible fraction of the total links, under the assumption of exponential distribution of link lengths51), hence preventing a correct estimation of the connectivity patterns (i.e., distances between nodes) and the resulting ecological metrics of the river network (see section Ecological implications).

From an ecological perspective, it could be reasonable to consider AT as a parameter expressing how a particular taxon perceives the suitable landscape, rather than a value to be determined from geomorphological arguments: for instance, large fishes inhabit wide and deep river reaches, and do not access small headwaters56. In this case, imposing a large AT would result in a coarser, less branching network constituted by few main channels (Fig. 1f, i), which could mimic the potentially available habitat for such species. Conversely, aquatic insects inhabit also small headwaters17,59, therefore their perceived landscape would resemble the finely resolved networks of Fig. 1d, g, characterized by low AT and higher (apparent) pr.

Topology and scaling of river networks and random analogues

To verify the topological (i.e., Horton’s laws on bifurcation and length ratios) and scaling (i.e., probability distribution of drainage areas) relationships of the different network types, we extracted from DEMs 50 real river networks encompassing a wide range of drainage areas (Fig. 4), and we generated 50 OCNs, 50 RBNs and 50 BBTs of comparable size (see Methods).

Fig. 4: Location of real river basins used in the analysis.
figure 4

River basins are shown in dark grey; countries in light grey. Rivers' numbering is sorted in ascending order according to drainage area values.

Full size image

Typical values3,7,60 for the bifurcation ratio RB lie between 3 and 5, while length ratios (RL) range between 1.5 and 3.5. As expected, we observed that the real rivers and OCNs used in our analysis have RB and RL values within the aforementioned ranges (Fig. 5a, b). The same is true for RBNs, while the RB and RL values found for BBTs are lower than the typical ranges. This finding holds regardless of the scale (subsumed by AT) at which real river networks and OCNs are extracted (Supplementary Figs. 1 and 2). Remarkably, BBTs fail to satisfy Horton’s laws despite the statistical inevitability of such laws for any network argued by ref. 61. To this regard, we note that the networks analyzed by ref. 61 did not include constructs where all paths from the source nodes to the outlet have the same length, which is the defining feature of BBTs (Fig. 1a).

Fig. 5: Comparison of topological and scaling properties of the different networks.
figure 5

a Scaling of number of network links Nω as a function of stream order ω for the various network types (rivers and OCNs obtained with AT = 20 pixels; RBNs and BBTs derived accordingly - see Methods). b Mean link length Lω (in units of l) as a function of ω. Networks used are as in panel a. c Scaling of drainage areas: probability P[A ≥ a] to randomly sample a node with drainage area A ≥ a as a function of a. The displayed trend lines are fitted on the ensemble values for the 50 network replicates, by excluding nodes with drainage area larger than 2000 pixels (cutoff value marked with a black solid line). The scaling coefficients β reported correspond to the slopes of the fitted trend lines. Extended details on all panels are provided in the Supplementary Methods.

Full size image

While the power-law scaling of areas in OCNs (Fig. 5c) has an exponent β ≈ 0.45 that closely resembles the one found for the real rivers (β ≈ 0.46) and within the typically observed range8,10 β = 0.43 ± 0.02, drainage areas of RBNs scale as a power law with an exponent β ≈ 0.51, which departs from the observed range. Conversely, BBTs do not show any power-law scaling of areas. Scaling exponents of drainage areas fitted separately for each real river network yielded values in the range 0.36÷0.57 (Supplementary Table 1). In particular, we observed that these values tend to the expected range β = 0.43 ± 0.02 for increasing values of A, expressed in number of pixels (Supplementary Fig. 3), hence implying that highly resolved catchments are required in order to properly estimate β. Interestingly, the observed values of Horton ratios and scaling exponent β for RBNs are compatible with the values RB = 4, RL = 2, β = 0.5 predicted for Shreve’s random topology model3,60,62, which is actually equivalent to a RBN with infinite links.

Ecological implications

We compared the different network types via two metrics that express the ecological value of a landscape for a metapopulation: the coefficient of variation of a metapopulation CVM and the metapopulation capacity λM. The coefficient of variation of a metapopulation63 is a measure of metapopulation stability (a metapopulation being more stable the lower CVM is), while the metapopulation capacity42,64 expresses the potential for a metapopulation to persist in the long run (persistence being more likely the higher λM is). Both measures are among the most universal metrics describing dynamics of spatially fragmented populations24,40. In order to assess the impact of the two landscape features mostly affecting metapopulation dynamics, i.e. spatial connectivity and spatial distribution of habitat patches, we calculated these metrics for the four network types under two different scenarios: uniform (CVM,U, λM,U) and non-uniform (CVM,H, λM,H) spatial distribution of habitat patch sizes. In the first scenario, CVM,U and λM,U assess stability and persistence (respectively) of a metapopulation solely based on pairwise distances between network nodes; in the second scenario, CVM,H and λM,H depend on the interplay between pairwise distances and spatially heterogeneous habitat availability (namely, downstream nodes being larger than upstream ones).

We found that the values of CVM (be it derived with uniform (CVM,U) or nonuniform (CVM,H) distributions of patch sizes) obtained for OCNs match strikingly well those of real rivers (Fig. 6). These CVM values are consistently lower than those found for RBNs, while values of CVM for BBTs are even higher. Notably, this result holds for different values of AT (and hence different pr values) at which real rivers and OCNs are extracted (Fig. 6a–c; g–i), and for values of mean dispersal distance α (see Methods) spanning multiple orders of magnitude (Supplementary Figs. 4–7).

Fig. 6: Comparison of values of metapopulation metrics across river network types and observational scales (AT).
figure 6

a–c CVM,U. d–f λM,U. g–i CVM,H. j–l λM,H. Boxplot elements are as follows: center line, median; notches, \(\pm 1.58\cdot {{{{{{{\rm{IQR}}}}}}}}/\sqrt{50}\), where IQR is the interquartile range; box limits, upper and lower quartiles; whiskers, extending up to the most extreme data points that are within ±1.5 ⋅ IQR; circles, outliers. Metapopulation metric values were obtained by setting α = 100 l. Note that in Eq. (1), given A = 40, 000, AT = 20 results in E[N] ≈ 4574, E[pr] ≈ 0.228; AT = 100 yields E[N] ≈ 2231, E[pr] ≈ 0.098; AT = 500 results in E[N] ≈ 1088, E[pr] ≈ 0.042.

Full size image

For a constant α value, the CVM of real rivers, OCNs and RBNs decreases as the resolution at which the network is extracted increases (i.e., AT decreases; see Fig. 6 and Supplementary Figs. 4–7). This is expected63, since a decrease in AT corresponds to an increase in N (Fig. 2a), leading to a decrease in CVM. Indeed, a larger ecosystem, constituted of more patches, has the potential to include a larger (and more diverse) number of subpopulations, which increases stability at a metapopulation level through statistical averaging–a phenomenon widely known as the portfolio effect65. We also found that BBT networks do not generally follow the above-described pattern of decreasing CVM with increasing N; rather, the CVM of BBTs increases with N when the mean dispersal distance α is set to intermediate to high values (Fig. 6 and Supplementary Figs. 5–7), and only when α is very low (e.g. α = 10 l as in Supplementary Fig. 4) and a uniform patch-size distribution is assumed does CVM,U follow the expected decreasing trend with increasing N.

However, we need to warn against the conclusion that river networks with higher values of pr (and hence lower AT, see Fig. 2b) are inherently associated with higher metapopulation stability. Indeed, our result was obtained by changing the scale at which we observed the same river networks, and not by increasing the river networks’ size. If the number of network nodes (and, consequently, the branching ratio pr) is determined by the scale at which the landscape is observed, one cannot directly assume that any of such nodes is a node (or patch) in the ecological sense, i.e. the geographical span of a local population: the extent of such patches should be determined based on the mobility characteristics of the focus species, and should be independent of the scale at which the river network is observed. In contrast, we note that, if the same river network (with fixed A in km2) is extracted from DEMs at different resolutions (i.e., different values of l) but same AT (in km2), then the river network extracted at coarser resolution (larger l) will appear more branching (i.e., have larger pr). This is because the number of links NL and the total river length (in km) are primarily determined by AT and so would remain unchanged. Variation in the pixel size l will impact how the total river length is partitioned into nodes given the length resolution constraints imposed by l. Thus, the number of nodes N would be lower when extracted at coarser resolution (larger l). As pr = NL/N this means that pr will be artificially inflated for rivers extracted at coarser resolutions. This introduces an equivalent effect as selecting catchments with smaller A (in number of pixels) but constant ratio AT/A, which are located towards the bottom-left corner of Fig. 2a, b (i.e., parallel to the level curves AT/A). In this case, the apparent higher “branchiness” of the river network extracted at coarser resolution would result in higher values of CVM (i.e., lower metapopulation stability) because of a reduction in N.

We observed that metapopulation capacity λM values of OCNs (be it evaluated under uniform (λM,U) or non-uniform (λM,H) patch-size distribution assumption) are the closest to those of real rivers, while RBNs (and even more so BBTs) generally overestimate λM with respect to real rivers and OCNs (Fig. 6d–f; j–l). This result holds irrespective of the choice of AT and for intermediate to high values of α (Supplementary Figs. 5–7). When the mean dispersal distance is instead set to very low values (α = 10 l – Supplementary Fig. 4) and the river network is extracted at a high resolution (i.e., low AT), the metapopulation capacity of OCNs under assumption of uniform patch-size distribution (λM,U) is underestimated with respect to that of real rivers. A likely explanation for this apparent mismatch is that, for low values of AT, the number of nodes N tends to be somewhat higher for the extracted river networks used in this analysis than for OCNs (Supplementary Fig. 8), and the effect of the different dimensionality of real rivers and OCNs in the metapopulation capacity estimation tends to be more evident as the mean dispersal distance decreases. Interestingly, such mismatch is absent when a non-uniform patch size distribution is assumed, as λM,H values for OCNs match those for real rivers regardless of the mean dispersal distance value and the river network resolution (Fig. 6; Supplementary Figs. 4–7).

The OCN construct encapsulates both random and deterministic processes, the former related to the stochastic nature of the OCN generation algorithm, and the latter pertaining to the minimization of total energy expenditure that characterizes OCN configurations. As such, OCNs reproduce the aggregation patterns of real river networks. From an ecological viewpoint, this implies that both pairwise distances between nodes and the distribution of patch sizes (expressed as a function of drainage areas, or of a proxy thereof such as the number of nodes upstream) are much closer to those of real networks than is the case for fully random synthetic networks as BBTs and RBNs. In particular, BBTs and (to a lesser extent) RBNs tend to underestimate pairwise distances with respect to real rivers and OCNs, as documented by a comparison of mean pairwise distances across network types (Supplementary Fig. 9a–c). Our analysis shows that the connectivity structure of these random networks (subsumed by the matrix of pairwise distances) is too compact with respect to that of real rivers, which leads to an overestimation of the role of dispersal in increasing the ability of a metapopulation to persist in the long run, but also an increased likelihood of synchrony among the different local populations, which results in higher instability.

Comparison of patch size distributions among the network types expressed in terms of CVM,0 (i.e., the portion of CVM,H that uniquely depends on the distribution of patch sizes and not on pairwise distances) shows that, while for coarsely resolved networks (AT = 500) no clear differences in CVM,0 emerged, for highly resolved networks (AT = 20) BBTs heavily underestimate the CVM,0 of real rivers and OCNs, while RBNs slightly overestimate it (Supplementary Fig. 9d–f). As a result of the interplay of differences in distance matrices and patch size distributions, BBTs and (to a lesser extent) RBNs generally tend to overestimate the coefficient of variation of a metapopulation and the metapopulation capacity of real rivers and OCNs in both scenarios of uniform and non-uniform patch size distribution. The only exception to this trend occurs for the metapopulation capacity λM,H of very large BBTs (corresponding to AT = 20) in the case of very high dispersal distances (α = 1000 l – Supplementary Fig. 7): here, the patch-size effect (i.e., underestimation of CVM,0) predominates over the distance effect (i.e., overestimation of mean dij), resulting in an underestimation of λM,H with respect to real rivers and OCNs.

Our results were derived under a number of simplifying assumptions. In particular, we acknowledge that, while the distance matrix of a landscape and the distribution of patch sizes have in general important implications for metapopulation dynamics, other factors not considered here, such as Euclidean between-patch distance48, fat-tailed dispersal kernel66 and density-dependent dispersal67 could also play a relevant role in this respect. However, it needs to be noted that, especially with regards to the assessment of the Moran effect in metapopulation synchrony (i.e., increased synchrony in local fluvial populations that are geographically close but not flow-connected48), the use of OCNs allows integration of Euclidean distances in a metapopulation model, while this is not possible for RBNs and BBTs, where Euclidean distances are not defined. Moreover, if a larger degree of realism is required for a specific ecological modelling study, such as heterogeneity in abiotic factors (e.g. water temperature or flow rates), the use of OCNs as model landscapes allows a direct integration of these variables, as they can conveniently be expressed as functions of drainage area3,55. In contrast, this is not possible for RBNs or BBTs, because only OCNs verify the scaling of areas (Fig. 5c), while RBNs and BBTs lack a proper definition of drainage areas.

Our comparison of synthetic and real river networks showed that riverine metapopulations are more stable and less invasible than what would be predicted by random network analogues. Conversely, the use of OCNs as model landscapes allows capturing not only the scaling features of real rivers, but also drawing ecological conclusions that are in line with those that could be observed in real river networks. We thus support the use of OCNs as analogues of real river networks in theoretical and applied ecological modelling studies. While we found that BBTs are highly inaccurate in reproducing ecological metrics of real river networks and should be therefore discarded altogether in future modelling applications, RBNs show a certain degree of similarity with OCNs and real river networks in this respect; moreover, RBNs (as is the case for any random tree61) satisfy Horton’s laws on bifurcation and length ratios. A relevant advantage of RBNs over OCNs is that their generation algorithm is at least one order of magnitude faster49. Therefore, we acknowledge that RBNs could be considered as a suitable surrogate for real river networks as null models in cases where a large number of network replicates is required. To this end, we encourage researchers exploiting synthetic river networks (whether they be OCNs or RBNs) to always clarify the observational scales (that is, total area drained, size of a node, area drained by a headwater) subsumed by the synthetic network and which give rise to a certain complexity measure (i.e., branching ratio). Only in such a way could the predictions from these studies be compared with real river networks.

In conclusion, our results advocate a tighter integration between physical (geomorphology, hydrology) and biological (ecology) disciplines in the study of freshwater ecosystems, and particularly in the perspective of a mechanistic understanding of drivers of persistence and loss of biodiversity.

Methods

Generation of synthetic river networks

We generated 50 OCNs via the R-package OCNet68 on lattices of size 200 × 200 with a random positioning of the outlet pixel. All OCNs hence spanned an area A = 40, 000 pixels. Each of the 50 OCNs was extracted by imposing a threshold area AT equal to 20, 100 and 500 pixels. A threshold area value AT = 1 pixel was also applied in order to assess the scaling of drainage areas shown in Fig. 5c.

For each OCN and each AT value, we computed the respective number of nodes N and branching ratio pr = NL/N, and generated a corresponding random branching network (RBN) and balanced binary tree (BBT). Following ref. 46, RBNs were generated by randomly sampling network links with length following a geometric distribution with mean 1/pr, and such that the total network length be equal to N. The geometric distribution is the discrete equivalent of the exponential distribution, which approximates well the distribution of link lengths51. The network was then randomly assembled by imposing each link to have an outdegree (see Supplementary Note 1) of 1 (except possibly one link–the most downstream one) and an indegree (see Supplementary Note 1) of either 0 (source links) or 2 (links downstream of a confluence); moreover the network configuration had to be loopless. Details are provided in the Supplementary Methods.

BBTs were generated following ref. 45: the network was initialized with one node (the root), which was attributed to order 1. For all nodes belonging to a given order i, one or two upstream nodes were randomly assigned, the latter event occurring with probability p; all nodes thus generated belonged to order i + 1. The algorithm stopped when N nodes were allocated. Note that p is different (i.e., lower) than the branching ratio pr of the network, since all nodes lacking an upstream connection (i.e., the sources) are by construction the starting point of independent links, while this would be true only for a fraction p of them, if new nodes were added to the network by following the above-described algorithm. For these networks, we found p = pr/(2 − pr) (see Supplementary Methods for the derivation).

Extraction of real river networks

We extracted 50 real river networks from open-source digital elevation models retrieved via the R-package elevatr69. We selected catchments from different geographical areas: 25 in Europe and 25 in North America (Fig. 4). To guarantee a high similarity between extracted and actual river networks, catchments were essentially selected from regions with marked elevational gradients (i.e. the Alps, the North American Cordillera and the Appalachian Mountains). We chose catchments spanning a wide range (367 km2 – 57,949 km2) of drained areas (Supplementary Fig. 10a). To enable comparison between the extracted real rivers and the synthetic networks, we limited our search to catchments made up of 40,000 pixels ± 20% (Supplementary Fig. 10b). To do so, we used DEMs of different resolutions, by appropriately tuning the zoom option in the function get_elev_raster of elevatr. Note that the value in meters of the pixel side l varies both as a function of the zoom level and of latitude (Supplementary Table 2). Flow directions were derived via the D8 algorithm in a TauDEM routine53. The networks were finally extracted by imposing AT = 20, 100 or 500 pixels.

Relationships between the networks’ parameters

Ref. 68 evaluated how N and NL scale as a function of the two observational scales AT and A for four large OCNs. By rearranging those relationships, the expected values of N and pr for OCNs (and, in turn, real rivers) read, respectively:

$$E[N]\approx 0.435{A}_{{{{{{{{\rm{T}}}}}}}}}^{-0.446}A\,;\,\,\,\,\,E[{p}_{{{{{{{{\rm{r}}}}}}}}}]\approx 1.531{A}_{{{{{{{{\rm{T}}}}}}}}}^{-0.523}{A}^{-0.032}$$
(1)

where A, AT and N are expressed in the number of pixels, and pr is dimensionless. Note that the approximately equal sign in Eq. (1) highlights the fact that these relationships, being derived from a limited number of OCNs without exploring the full range of parameters involved in the OCN generation68, are to be intended as a first approximation. A graphical representation of these expressions is provided in Fig. 2a, b. Note that Eqs. (1) are valid as long as AT lies in the range of drainage area values for which the power-law scaling of the drainage area is verified68; for example, in the limiting case AT = 1, every pixel of the drainage domain belongs to the channel network, hence A = N and pr approaches 1.

Coefficient of variation of a metapopulation

In the general case, the coefficient of variation of a metapopulation made up of N nodes reads:

$$C{V}_{{{{{{{{\rm{M}}}}}}}}}=\frac{\sqrt{\mathop{\sum }\nolimits_{i = 1}^{N}{\sigma }_{i}^{2}+\mathop{\sum }\nolimits_{i = 1}^{N}\mathop{\sum }\nolimits_{j = 1,\,j\ne i}^{N}{C}_{ij}}}{\mathop{\sum }\nolimits_{i = 1}^{N}{\mu }_{i}},$$
(2)

where μi and σi are the mean and standard deviation of the local population abundance at node i, respectively, while Cij is the covariance between nodes i and j. We hypothesized that both mean and standard deviation of local population abundances scale linearly with the local habitat size Hi: μi = μHi, σi = σHi; without any loss of generality, we further assumed σ = μ. The covariance Cij was expressed via an exponential kernel: \({C}_{ij}={\sigma }_{i}{\sigma }_{j}\exp (-{d}_{ij}/\alpha )\), where dij is the along-stream distance between i and j, and α a parameter expressing the distance dependence of local population covariance. Note that dij > 0 also for pairs of nodes that are not flow-connected, as in a so-called tail-down exponential covariance model70, which has been used to describe the spatial covariance of any variable measured in streams, including ecological population counts70. Note also that dependence of population synchrony on along-stream distance has been widely observed in long-term fish population time series in European basins48. In the case of uniform patch size distribution, Hi = H does not depend on i, and Eq. (2) becomes:

$$C{V}_{{{{{{{{\rm{M}}}}}}}},{{{{{{{\rm{U}}}}}}}}}=\sqrt{\frac{1+\frac{1}{N}\mathop{\sum }\nolimits_{i = 1}^{N}\mathop{\sum }\nolimits_{j = 1,\,j\ne i}^{N}\exp (-{d}_{ij}/\alpha )}{N}}.$$
(3)

In the non-uniform patch-size distribution scenario, we assumed that local habitat size Hi is proportional to the river width, which is known to scale along a river as the square root of drainage area55. Given that drainage areas are not defined in BBTs and RBNs, to enable a fair comparison between the different network types we used the number Ui of nodes upstream of a node i as a proxy for drainage area; moreover, we normalized the local habitat size so that each network has a regional habitat availability of 1:

$${H}_{i}=\frac{{U}_{i}^{0.5}}{\mathop{\sum }\nolimits_{j = 1}^{N}{U}_{j}^{0.5}}.$$
(4)

In this case, Eq. (2) becomes:

$$C{V}_{{{{{{{{\rm{M}}}}}}}},{{{{{{{\rm{H}}}}}}}}}=\sqrt{\mathop{\sum }\nolimits_{i = 1}^{N}{H}_{i}^{2}+\mathop{\sum }\nolimits_{i = 1}^{N}\mathop{\sum }\nolimits_{j = 1,\,j\ne i}^{N}{H}_{i}{H}_{j}\exp (-{d}_{ij}/\alpha )}.$$
(5)

To assess the sensitivity of our results to variation of the mean dispersal length, we evaluated CVM,U and CVM,H for α equal to 10, 20, 100, 200 and 1000 pixel sizes l. Moreover, we evaluated CVM,H in the limit α → 0, which is equal to \(C{V}_{{{{{{{{\rm{M}}}}}}}},{{{{{{{\rm{0}}}}}}}}}=\sqrt{\mathop{\sum }\nolimits_{i = 1}^{N}{H}_{i}^{2}}\), as a measure of the role of patch size distribution on metapopulation stability.

Metapopulation capacity

We evaluated the metapopulation capacity64 as the maximum eigenvalue of a matrix M of order N with entries \({m}_{ij}={H}_{i}{H}_{j}\exp (-{d}_{ij}/\alpha )\) if i ≠ j and mii = 0. In particular, in the uniform patch-size distribution scenario, λM,U was evaluated by assuming42Hi = 1; in the non-uniform scenario, λM,H was calculated with Hi given by Eq. (4). As stated previously, α represents the mean dispersal distance (assuming an exponential kernel for the dispersal process). To assess the sensitivity of our results to variation of such parameter, we evaluated λM,U and λM,H for α equal to 10, 20, 100, 200 and 1000 pixel sizes l.