1 Introduction

A pandemic is an epidemic spread over a wide geographical area. The novel coronavirus, taxonomically known as SARS- CoV-2, first emerged in the Hubei province of China [1] in November, 2019. The World Health Organization declared it to be a pandemic on March 11, 2020. As per the reports from WHO [2], a total of 3972243 deaths have been registered as of June 28, 2021. According to the literature studies, this disease is transmitted through nasal discharge of saliva droplets [3] and is air borne as per the studies by [4, 5]. In India, the first case of COVID-19 was reported on January 30, 2020 [6], and in Nepal the first confirmed case was reported on January 23, 2020 [7]. Though both these countries have a huge difference in the number of COVID-19 cases, a similar pattern in the rise in cases is witnessed during the first and second wave of the pandemic. A pictorial representation is provided in Fig. 1, where the sudden rise in COVID-19 cases is showcased clearly.

COVID-19 has claimed several lives, and if no proper interventions are implemented, the pandemic could turn out to be a disaster. Though several interventions and other preventive measures [8] are recommended, its implementation needs to be of major priority. Social distancing and compulsory usage of face shields will contribute toward controlling the further spread of the virus [9, 10] majorly. A detailed work on the same is presented in [11, 12]. In [4], the authors have presented a detailed study on several non-pharmaceutical interventions and importance of social distancing in reducing the spread of infections. Apart from these, it is highly important to maintain hygiene and good sanitation, as lack of sanitation could accelerate the infections [13]. In addition to these measures, media information also plays an important role in making the citizens aware of various preventive measures, the do’s, and don’ts in case of positive results, etc. This does not add any additional cost and the information reaches the individuals sitting at home in terms of radio, television, social media websites, etc. In the works by [14] and [15], a detailed study on media impact as an alternate measure to control the wide spread of infections is presented. Adequate number of hospital beds and quarantine space is equally important to curb the further spread of infections. This is necessary to control the passage of virus to susceptible from identified infectives. If no proper medication, isolation, and hospital facilities are provided to these individuals, there are high chances of these individuals encountering susceptible population hence spreading the infection at alarming rate. A study by [16] stresses on importance of isolation as a public health measure to control the disease spread. According to [17], India had mere 5.3 beds per 10,000 population in the year 2017, and Nepal had 3 beds per 10,000 population in the year 2012. As per the present time, India had 1 bed per 2000 people before the pandemic hit it [18]. The reports by [19, 20] indicate the scarcity of basic medical facilities in Nepal, which is responsible for the lower hospitalization rate in the country. If these interventions are well implemented, the deaths could be controlled to a major extent.

Fig. 1
figure 1

First and Second Wave of COVID-19 in India and Nepal

Full size image

Till date, several works on COVID-19 have been published by researchers. Various works on combating of COVID-19, predictive analysis, lockdown effects on the disease spread, face masks efficacy, pharmaceutical intervention, and media impact on spread on COVID-19, etc., have been incorporated in different mathematical models to study the disease control. A majority of these works seek inspiration from the traditional SIR model [21]. In [22], a SUC compartmental model is discussed to estimate the unidentified infected in China, which differs from the SIR model in terms of the compartments U (unidentified infected population) and C (confirmed infectives, recovered and dead population), considering possibilities of many unreported cases. A brief review on various compartmental models is presented in [23], and a study on mathematical modeling with and without inclusion of interventions is presented in [24]. A detailed study on sensitivity and optimal control analysis for worst hit states of India with inclusion of compartments on quarantine and governmental measures is presented in [25]. In [26], the author worked on a mathematical model and performed statistical analysis to predict COVID-19 cases in India. A study based on lockdown effect is discussed in [27, 28]. In these studies, a detailed analysis based on different lockdown periods is laid out, where the former work is based on classical SIR model applied to different lockdown scenarios, the later has an additional treatment class with a piecewise treatment function, presenting both deterministic and stochastic analysis.

In [29], the authors have worked on SIR and fractal interpolation model, applying it on the COVID-19 data set of India and estimated the duration of second and third wave of COVID-19 in India. As per the study, the peak during the third wave could be achieved by October 2021, but these predictions are based on SIR model framework without inclusion of quarantine or lockdown and other intervention policies. On the other hand, a detailed explanation on SIR model with uncertainty is shown in [30], in which \(\alpha ~-\) path-based approach is used to calculate uncertain distribution of the solution, thereby presenting potential demand for medical resources and lockdown to combat the disease in Hubei, China. A detailed discussion on attainment of herd immunity in India is studied in [31] by working on COVID-19 infected population data of top fifteen counties and applying multifractal approach. In [32], the disease prevalence in Kerala and India is predicted using SIR model by incorporating quarantine and testing factors. The impacts of lockdown before and after rise in the cases are also quantified in the study. The studies by [33, 34] present results based on SIR model by providing estimations on recovery and infection rates and analysis based on effective reproduction number, respectively. In [35], the authors have worked on SIR model with a difference that the susceptible population does not decline monotonically. The study suggests that with appropriate restrictions, the disease spread could be controlled.

This study is based on mathematical modeling of COVID-19 and different analysis on it. In this work, we developed an epidemiological model with seven compartments, with inclusion of media factor in the nonlinear incidence term. We used Holling function [36] for inclusion of this decay factor. The population in the model is categorized to identified infected and unidentified infected. The proposed model in the study is different from the classical SIR model and the other SIR-related works discussed above in the sense that, in this model additional compartments namely exposed class which signifies incubation period, quarantine class and hospitalization class are included, along with identified and unidentified infected classes. However, the major difference is the media factor which is included in the nonlinear incidence term signifying disease transmission by using Holling function. In the model, testing and face mask factors are also incorporated. The aim is to determine the effective contact rate and the hospitalization rate of the identified infected for the two countries, Nepal and India. The focus is on improvement of the hospitalization facilities, so that the spread of infections from the detected infected population can be brought to decline. Section 2 gives a detailed information on the problem formulation followed by Sect. 3 in which stability of the equilibrium points and the basic reproduction number are discussed. The numerical simulations and analysis are presented in Sect. 4. The optimal control problem and simulation are discussed in detail in Sect. 5, where in the highlight is the control parameter relating to enhanced hospitalization and quarantine facilities. The work completes with conclusion in Sect. 6.

2 Problem formulation

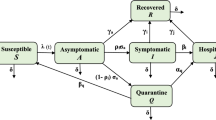
In this study, we develop an epidemiological model with 7 compartments. The compartments are Susceptible (S), Exposed (E), Infected unidentified \((I_{a})\), Infected identified \((I_{d})\), Quarantined (Q), Hospitalized (H) and Recovered (R). We consider that both the infected compartments involve individuals with no or mild symptoms and severe symptoms. Since here we have considered a detected set of infected population, we include a media factor (m) which is responsible for reduction in disease transmission via the detected infected individuals, since these detected infectives are aware of being infectious to others. Therefore, these individuals will be more careful toward following protocols. The information through media will make them more educated on the disease spread and control. We include natural births and deaths in this model. A schematic representation of the model is given in Fig. 2.

Fig. 2
figure 2

Schematic diagram of the epidemic model

Full size image

We make the following assumptions and frame the system of differential equations to get the desired model.

  1. 1.

    The disease transmission takes place when the susceptible encounters infected individuals. These infected individuals include both detected and undetected infectives. Let \(\beta \) be the effective contact rate at which the disease transmission takes place. Since media information is included in the study, there is a reduction in the disease transmission due to this media factors (m) which acts as a decay factor in the nonlinear incidence term denoting the disease transmission when the susceptible make effective contact with aware and identified infected \((I_{d})\) individuals. Hence, the force of infection is given by:

    $$\begin{aligned} \beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S \end{aligned}$$

    Here, \(\zeta \) is the modification parameter lying between 0 and 1 signifying reduction in disease transmission by identified infected population in comparison with unidentified infected population. This is due to the assumption that the identified infectives are treated to be aware and educated on the concerns related to the disease, thereby abiding by the protocols sincerely in comparison with the unaware infectives.

  2. 2.

    A fraction p of exposed individuals move to \(I_{a}\) and \((1-p)\) to \(I_{d}\) at a rate \(\delta \).

  3. 3.

    There is possibility for the unidentified infective to be detected and move to \(I_{d}\) class at rate \(\eta \).

  4. 4.

    The unidentified infectives with no symptoms or very mild symptoms might recover at a rate \(\gamma _{1}\) and move to the recovered class. It is also possible that few of these individuals in \(I_{a}\) might die before even getting detected.

  5. 5.

    The infectives in \(I_{d}\) who are asymptomatic or having mild symptoms are isolated or quarantined at a rate \(\xi \) and the ones with very severe symptoms are hospitalized at a rate \(\epsilon \).

  6. 6.

    It is possible that the quarantined individuals develop certain complications and are hospitalized at a rate \(\nu \).

  7. 7.

    The quarantined and hospitalized individuals recover at rates \(\gamma _{2}\) and \(\gamma _{3}\), respectively.

  8. 8.

    Since there are chances of the critically ill individuals to not recover even after hospitalization, these die at rate \(\mu _{2}\).

The model is framed into the following system of differential equations:

$$\begin{aligned} \frac{d S}{d t}= & {} \wedge -\beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S-\mu S \nonumber \\ \frac{d E}{d t}= & {} \beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S -(\mu +\delta )E\nonumber \\ \frac{d I_{a}}{dt}= & {} p\delta E-(\eta +\mu _{1}+\gamma _{1}+\mu )I_{a}\nonumber \\ \frac{d I_{d}}{d t}= & {} (1-p)\delta E+\eta I_{a}-(\xi +\epsilon +\mu )I_{d}\\ \frac{d Q}{d t}= & {} \xi I_{d}-(\gamma _{2}+\nu +\mu )Q\nonumber \\ \frac{d H}{d t}= & {} \epsilon I_{d}+\nu Q-(\gamma _{3}+\mu _{2}+\mu )H\nonumber \\ \frac{d R}{d t}= & {} \gamma _{1}I_{a}+\gamma _{2}Q+\gamma _{3}H-\mu R\nonumber \end{aligned}$$
(1)

3 Equilibria and stability

3.1 Disease-free equilibrium and reproduction number

The Disease-Free Equilibrium (DFE) is given by

$$\begin{aligned} E^{0}=\left( \frac{\wedge }{\mu },0,0,0,0,0,0\right) \end{aligned}$$

Basic reproduction number \(R_{0}\) is of major significance in epidemiological studies as it provides a complete overview on the disease transmission potential within a population. It is expected number of secondary cases arising from a single primary case in an otherwise susceptible population. Using Next Generation Matrix Method as explained in [37,38,39], we find the basic reproduction number \(R_{0}\) as follows:

$$\begin{aligned} {\mathcal {F}} = \begin{pmatrix} \beta \left( I_{a}+\frac{\zeta I_{d}}{(m+I_{d})}\right) S\\ 0 \\ 0 \end{pmatrix} \quad {\mathcal {V}} = \begin{pmatrix} (\delta +\mu )E\\ -p\delta E+(\eta +\mu _{1}+\gamma _{1}+\mu )I_{a} \\ -(1-p)\delta E-\eta I_{a}+(\xi +\epsilon +\mu )I_{d} \end{pmatrix} \end{aligned}$$

The two matrices F and V are Jacobian of \({\mathcal {F}}\) and \({\mathcal {V}}\), respectively, which depict new infections and transition terms, respectively.

$$\begin{aligned} F= \begin{pmatrix} 0&{}\quad \frac{\beta \wedge }{\mu }&{}\quad \frac{\beta \zeta \wedge }{\mu m}\\ 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{pmatrix} \quad V= \begin{pmatrix} \delta +\mu &{}\quad 0&{}\quad 0\\ -p\delta &{}\quad (\eta +\mu _{1}+\gamma _{1}+\mu )&{}\quad 0\\ -(1-p)\delta &{}\quad -\eta &{}\quad (\xi +\epsilon +\mu ) \end{pmatrix} \end{aligned}$$

From these we get,

$$\begin{aligned} FV^{-1} = \begin{pmatrix} a_{11}&{}\quad a_{12}&{}\quad a_{13}\\ 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} a_{11}= & {} \frac{\beta \wedge \delta }{(\eta +\mu _{1}+\gamma _{1}+\mu )(\mu +\delta )\mu } \left[ p+\frac{\zeta ((\eta +\mu _{1}+\gamma _{1}+\mu )(1-p)+p\eta )}{m(\xi +\epsilon +\mu )}\right] \\ a_{12}= & {} \frac{\beta \wedge }{\mu (\eta +\mu _{1}+\gamma _{1}+\mu )} +\frac{\beta \wedge \zeta \eta }{\mu m (\eta +\mu _{1}+\gamma _{1}+\mu )(\xi +\epsilon +\mu )} \\ a_{13}= & {} \frac{\beta \wedge \zeta }{\mu m (\xi +\epsilon +\mu )} \end{aligned}$$

The basic reproduction number is the largest eigenvalue of \(FV^{-1}\) which is \(a_{11}\)

$$\begin{aligned} \therefore R_{0}=\frac{\beta \wedge \delta }{(\eta +\mu _{1}+\gamma _{1}+\mu )(\mu +\delta )\mu } \left[ p+\frac{\zeta ((\eta +\mu _{1}+\gamma _{1}+\mu )(1-p)+p\eta )}{m(\xi +\epsilon +\mu )}\right] . \end{aligned}$$

Theorem 3.1

The Disease-Free Equilibrium \(E^{0}=\left( \frac{\wedge }{\mu },0,0,0,0,0,0\right) \) is locally asymptotically stable under certain restrictions when \(R_{0}<1\) and is unstable otherwise.

Proof

The proof begins with obtaining Jacobian matrix \(J_{E^{0}}\) of the system of equations (1) at the equilibrium point \(E^{0}\)

$$\begin{aligned} J_{E^{0}} = \begin{pmatrix} -\mu &{}0&{}-\beta \frac{\wedge }{\mu }&{}-\beta \frac{\wedge \zeta }{\mu m}&{}0&{}0&{}0\\ 0&{}-(\mu +\delta )&{}\beta \frac{\wedge }{\mu }&{}-\beta \frac{\wedge \zeta }{\mu m}&{}0&{}0&{}0\\ 0&{}p\delta &{}-(\eta +\mu _{1}+\gamma _{1}+\mu )&{}0&{}0&{}0&{}0\\ 0&{}(1-p)\delta &{}\eta &{}-(\xi +\epsilon +\mu )&{}0&{}0&{}0\\ 0&{}0&{}0&{}\xi &{}-(\gamma _{2}+\nu +\mu )&{}0&{}0\\ 0&{}0&{}0&{}\epsilon &{}\nu &{}-(\gamma _{3}+\mu _{2}+\mu )&{}0\\ 0&{}0&{}\gamma _{1}&{}0&{}\gamma _{2}&{}\gamma _{3}&{}-\mu \end{pmatrix} \end{aligned}$$

The characteristic polynomial \(|J_{E^{0}}-\lambda I|=0\) is given by:

$$\begin{aligned} (\lambda +a_{1})\times (\lambda + a_{4})\times (\lambda +\mu )^{2}\times (\lambda ^{3}+a_{5}\lambda ^{2}+a_{6}\lambda +a_{7}) \end{aligned}$$

where,

$$\begin{aligned} a_{1}= & {} \eta +\mu _{1}+\gamma _{1}+\mu , \quad a_{2}=\xi +\epsilon +\mu , \quad a_{3}=\gamma _{2}+\nu +\mu , \\ a_{4}= & {} \gamma _{3}+\mu _{2}+\mu , \quad a_{5}=a_{1}+a_{2}+\delta +\mu , \\ a_{6}= & {} a_{1}a_{2}+(a_{1}+a_{2})(\delta +\mu )-\delta p \beta \frac{\wedge }{\mu }-\beta \delta \frac{\wedge \zeta }{\mu m} (1-p)\\ a_{7}= & {} (a_{1}a_{2})(\delta +\mu )-a_{1}\beta \delta \frac{\wedge \zeta }{\mu m} (1-p)-\delta p \beta \frac{\wedge }{\mu }\left( a_{2}+\frac{\eta \zeta }{m}\right) . \end{aligned}$$

There are 7 eigenvalues, of which 4 are as follows \(-a_{3}<0,~-a_{4}<0,~-\mu <0\) with \(-\mu \) repeating twice. The remaining are the cube roots of the following

$$\begin{aligned} \lambda ^{3}+a_{5}\lambda ^{2}+a_{6}\lambda +a_{7}=0. \end{aligned}$$

By using Routh–Hurwitz Criteria, this Disease-Free Equilibrium is locally asymptotically stable if \(a_{5}\times a_{6}>a_{7}\) and \(a_{5}>0,~ a_{7}>0.\)

Clearly, \(a_{5}>0\), and when \(R_{0}<1\), we have

$$\begin{aligned} p\beta \frac{\wedge }{\mu }\delta \left( a_{2}-\frac{\zeta }{m}a_{1}+\frac{\eta \zeta }{m}\right) +\beta \delta \frac{\wedge \zeta }{\mu m}a_{1}<a_{1}a_{2}(\mu +\delta )\implies a_{7}>0. \end{aligned}$$

Therefore, along with the above two, if \(a_{5}\times a_{6}>a_{7}\), then \(E^{0}\) is locally asymptotically stable. \(\square \)

3.2 Endemic equilibrium

Theorem 3.2

A unique endemic equilibrium point \(EE_{1}=(S^{*},E^{*},I_{a}^{*},I_{d}^{*},Q^{*},H^{*},R^{*})\) for the model described by the system of equation (1) exists only when \(R_{0}>1.\)

The endemic equilibrium point has the following components:

$$\begin{aligned} R^{*}= & {} \frac{1}{\mu }\left( \gamma _{1} I_{a}^{*}+\gamma _{2} Q^{*}+\gamma _{3} H^{*}\right) , \quad H^{*}=\frac{1}{(\gamma _{3}+\mu _{2}+\mu )}\left( \epsilon I_{d}^{*}+\nu Q^{*}\right) , \\ Q^{*}= & {} \frac{\xi I_{d}^{*}}{(\gamma _{2}+\nu +\mu )} \quad I_{d}^{*}=\left[ \frac{(1-p)(\eta +\mu _{1}+\gamma _{1}+\mu )+p\eta }{p(\xi +\epsilon +\mu )}\right] I_{a}^{*}, \\ E^{*}= & {} \frac{(\eta +\mu _{1}+\gamma _{1}+\mu )I_{a}^{*}}{p \delta },\quad S^{*}=\frac{\wedge (m+B_{1} I_{a}^{*})}{\left( \beta ((m+\zeta B_{1})I_{a}^{*}+B_{1} {I_{a}^{*}}^{2})+\mu (m+B_{1} I_{a}^{*})\right) }, \end{aligned}$$

and \(I_{a}^{*}\) is obtained by solving the below quadratic equation in \(I_{a}\):

$$\begin{aligned} A {I_{a}}^{2}+B I_{a}+C=0 \end{aligned}$$

where,

$$\begin{aligned} A= & {} a_{1}(\mu +\delta ) B_{1} , \quad B=a_{1}(\mu +\delta )(\beta (m+\zeta B_{1})+B_{1}\mu )-\beta p \wedge \delta B_{1}\\ C= & {} a_{1}(\mu +\delta )\mu m(1-R_{0}) \end{aligned}$$

in which , \( a_{1}= \eta + \mu _{1} +\gamma _{1}+\mu \quad \text{ and } \quad B_{1}=\frac{(1-p)a_{1}+p\eta }{p(\xi +\epsilon +\mu )}. \)

Proof

Equating each equation of the model (1) to zero and solving the algebraic equations gives us \(EE_{1}\). To prove that the obtained equilibrium point is unique and positive, we prove that \(I_{a}^{*}\) is greater than zero when \(R_{0}>1\) and is unique.

From the equation \(A {I_{a}}^{2}+B I_{a}+C=0\), we have \( I_{a}=\frac{-B\pm \sqrt{(B^{2}-4AC)}}{2A}.\)

Clearly, A is positive. When \(R_{0}>1\), we have the following:

$$\begin{aligned} R_{0}> & {} 1\implies C<0\\&\Longrightarrow \frac{-B+ \sqrt{(B^{2}-4AC)}}{2A} > 0\quad and \quad \frac{-B- \sqrt{(B^{2}-4AC)}}{2A} <0. \end{aligned}$$

This implies for \(R_{0}>1\), there exists a unique endemic equilibrium point.

To complete the proof, we now show that for the case when \(R_{0}<1\), there exists no endemic equilibrium points. When \(R_{0}<1\) , it suggests the following,

$$\begin{aligned} R_{0}&<1\implies B>0 \quad and \quad C>0\\&\Longrightarrow -4AC<0 \quad \because \quad AC>0\\&\Longrightarrow If \quad B^{2}>4AC \quad then \quad B^{2}-4AC>0 \\&\Longrightarrow -B\pm \sqrt{ B^{2}-4AC}<0. \end{aligned}$$

If \(B^{2}-4AC<0\), then there exists no real roots of \(A I_{a}^{2} + B I_{a} + C =0\). Therefore, \(R_0<1\) implies non-existence of endemic equilibrium point. \(\square \)

Theorem 3.3

The Endemic Equilibrium given by \(EE_{1}\) which exists if \(R_{0}>1\) is locally asymptotically stable under certain restrictions and is unstable otherwise.

Proof

We begin with the proof by first determining the Jacobian matrix \(J_{EE_{1}}\) of the system (1) at the equilibrium point \(EE_{1}\),

$$\begin{aligned} J_{EE_{1}} = \begin{pmatrix} -(\beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) +\mu )&{}0&{}-\beta S^{*}&{}-\beta \zeta S^{*}\frac{m}{(m+I_{d}^{*})^{2}}&{}0&{}0&{}0\\ \beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) &{}-(\mu +\delta )&{}\beta S^{*}&{}\beta \zeta S^{*}\frac{m}{(m+I_{d}^{*})^{2}}&{}0&{}0&{}0\\ 0&{}p\delta &{}-a_{1}&{}0&{}0&{}0&{}0\\ 0&{}(1-p)\delta &{}\eta &{}-a_{2}&{}0&{}0&{}0\\ 0&{}0&{}0&{}\xi &{}-a_{3}&{}0&{}0\\ 0&{}0&{}0&{}\epsilon &{}\nu &{}-a_{4}&{}0\\ 0&{}0&{}\gamma _{1}&{}0&{}\gamma _{2}&{}\gamma _{3}&{}-\mu \end{pmatrix} \end{aligned}$$

The characteristic polynomial \(|J_{EE}-\lambda I|=0\) is given by:

$$\begin{aligned} (\lambda +a_{3})\times (\lambda + a_{4})\times (\lambda +\mu )\times (\lambda ^{4}+d_{1}\lambda ^{3}+d_{2}\lambda ^{2}+d_{3}\lambda +d_{4}) \end{aligned}$$

where,

$$\begin{aligned} d_{1}= & {} a_{1}+a_{2}+\beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) +\delta +2\mu ,\\ d_{2}= & {} \mu ^{2}+(a_{1}+a_{2})\left( 2\mu +\delta +\beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) \right) +a_{1}a_{2}\\&+\delta \mu +(\mu +\delta )\beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) \\&-\beta \zeta S^{*}\frac{m}{(m+I_{d}^{*})^{2}} \delta (1-p)-\beta \delta S^{*},\\ d_{3}= & {} (a_{1}+a_{2})\mu (\mu +\delta )+(a_{1}a_{2})(2\mu +\delta )\\&+\beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) ((a_{1}+a_{2})(\mu +\delta )+a_{1}a_{2})\\&-\beta \zeta S^{*}\frac{m}{(m+I_{d}^{*})^{2}}(\delta (a_{1}+\mu )(1-p)+\eta \delta p)-p\delta \beta S^{*}(a_{2}+\mu ),\\ d_{4}= & {} \beta I_{a}^{*}\left( 1+\frac{\zeta B_{1} }{m+B_{1}I_{a}^{*}}\right) (a_{1}a_{2})(\mu +\delta )+\mu (a_{1}a_{2})(\mu +\delta )-p a_{2}\beta \mu S^{*},\\&-\beta \zeta S^{*}\frac{m}{(m+I_{d}^{*})^{2}}(\delta \mu (a_{1}(1-p)+p\eta )). \end{aligned}$$

Therefore, the eigenvalues are as follows:

\(-a_{3}<0, ~-a_{4}<0, ~-\mu <0\). The remaining are the roots of the following

$$\begin{aligned} \lambda ^{4}+d_{1}\lambda ^{3}+d_{2}\lambda ^{2}+d_{3}\lambda +d_{4}=0. \end{aligned}$$

By using Routh–Hurwitz Criteria, this Disease-Free Equilibrium is locally asymptotically stable if

$$\begin{aligned} d_{1}>0, \quad d_{1}\times d_{2}-d_{3}>0, \quad d_{3}(d_{1}\times d_{2}-d_{3})-d_{1}^{2}\times d_{4}>0. \end{aligned}$$

\(\square \)

4 Numerical simulation

4.1 Fitting model to data

Data fitting involves fitting of the framed model to the data collected and analysis of the fit accuracy. A model which is fitted well provides more accurate results. In this study, we have worked with the data of India and its neighboring country Nepal, as these two share a similar demography and both these countries have diverse ethnicity and cultures. We collected the data of active COVID-19 cases for a period between July 1, 2020, and May 31, 2021, for Nepal [40], and between July 1, 2020, and May 15, 2021, for India [41]. We did the data fitting for the first and the second wave of COVID-19 in both these countries, along with predictions up to June 30, 2021. From the model simulation, we estimated the optimum values of the parameters \(\beta \) and \(\epsilon \) for which the best fit of the model to data was obtained. The remaining parameter values are listed in Table 1.

Table 1 Values of parameters for the model (1)
Full size table

Numerical simulation of the developed mathematical model is carried out in R software. Fitting of data is done by using the method of sum of least square [47], wherein the observed active cases are fitted with the model solution. The best fit is obtained by estimating the parameters \(\beta \) and \(\epsilon \) for the data set of India and Nepal for both the first and the second wave of COVID-19. The \(R_{0}\) value along with the estimated parameters is listed in Table 2.

Table 2 Estimated optimum parameter values and basic reproduction number
Full size table

Comparing the two countries in terms of the infection rate, we notice that the effective contact rate (\(\beta \)) is higher for India compared to Nepal and so is the basic reproduction number (\(R_{0}\)) in both the waves of the pandemic. As per [41], as on May 15, 2021, the total confirmed cases in India with more than 1352 million population is more than 24 million, and according to [40], the total confirmed cases in Nepal stand at more than 0.4 million, wherein the total population of the country is 29 million plus. We observe that the difference in the effective contact rate of these 2 countries is \(3.234\times 10^{-6}\) and \(1.7425\times 10^{-5}\) for the first and the second wave, respectively, which is a small difference. This could be justified with the fact that with such a large population the respective infections in these countries are quite smaller. We can also relate this to the fraction of confirmed COVID-19 cases, which is 0.013 and 0.018 for Nepal and India, respectively. Therefore, though individually these countries have a huge difference in the number of COVID-19 cases, but when compared with respect to the total population of each of these countries, the estimated infection rate suffices. It is also noticed that, India witnessed rise in COVID-19 cases during the second wave by much larger margin, in comparison with Nepal, hence during that period, the infection rate (\(\beta \)) and the basic reproduction number value obtained are largest.

In this numerical simulation, we also estimate the optimum hospitalization rate. We see that the hospitalization rate is better in the case of India as compared to Nepal. In comparison with the two waves in the respective countries, we note a rise in the hospitalization rate in each of these countries compared to that of the first wave due to major increase in the number of cases. Compared to the effective contact rate, in both the countries, the hospitalization rate is more. This also suggests if the hospitalization rate of the identified infectives is more, the possibilities of disease transmission from them will reduce to a major extent, hence reducing the infection rate through this set of infectious individuals. Fig. 3 represents the fitted model with the observed COVID-19 cases of the two countries for the first and the second wave, along with prediction till 30 June, 2021. From the plots, a declining curve is observed in both the countries for the next 30 to 40 days, which adheres with the data as per [40, 41].

Fig. 3
figure 3

Plots of fitted model with observed active cases of COVID-19 during the first wave for a India and b Nepal, and plots of the fitted model with observed COVID-19 cases with predictions during the second wave for c India and d Nepal. The red dotted line represents the observed data, and the green curve represents the model solution

Full size image

4.2 Sensitivity analysis

Sensitivity analysis plays a crucial role in determining the significance of various parameters in transmission of the disease. It helps in understanding the rise and fall in the reproduction number value with respect to certain parameters. A detailed study on the sensitivity for the dengue disease is presented in [48]. By means of sensitivity analysis, we can scrutinize parameters significant to the problem. Once these parameters are identified, various strategies can be implemented for obtaining optimum outcome.

The normalized forward sensitivity index of a variable with respect to a parameter is the ratio of the relative change in the variable to the relative change in the parameter. When the variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives. From [49], the normalized forward sensitivity index of \(R_{0}\), that depends differentiably on a parameter q, is defined by

$$\begin{aligned} r_{q}^{R_{0}}=\frac{\partial R_{0}}{\partial q}\times \frac{q}{R_{0}} \end{aligned}$$

Figure 4 depicts the Normalized Forward Sensitivity Indices of the basic reproduction number for (a) India and (b) Nepal. From both these figures, we note that the parameters \(\beta \), \(\zeta \), \(\wedge \), \(\delta \), p share positive indices with \(R_{0}\), whereas the parameters \(\eta ,~\xi ,~\epsilon ,~m,~\mu ,~\mu _{1},~\gamma _{1}\) have negative indices with \(R_{0}\). It can be clearly concluded from the figures that increase in the effective contact rate, and closer the value of the reduction parameter \(\zeta \) is toward 1, the faster will be the spread of the disease implying increase in \(R_{0}\). It can be also noted that the parameters m and \(\xi \) are negatively associated with \(R_{0}\), and it can be noticed that for the case of Nepal, increase in these 2 parameters has more impact in reduction in \(R_{0}\). In [50], an information of fake news and misleading information on COVID-19 spread in Nepal and other developing countries is laid out, which could suffice on the importance of right information reaching the population. Media factor plays a same role in case of India as well. Similarly, increase in the recovery rate of unidentified infected, hospitalization rate and detection rate will contribute in decreasing the infection spread, hence the basic reproduction number.

Fig. 4
figure 4

Normalized forward sensitivity indices of basic reproduction number with respect to certain parameters for a India and b Nepal

Full size image

A sensitivity analysis of the model (1) is performed using the approach of Latin Hypercube Sampling (LHS) and Partial Rank Correlation Coefficient (PRCC) method as in [51, 52] to assess the influence of model parameters on infected population, both identified and unidentified. We perform the analysis considering all the parameters to be uniformly distributed, and we consider the unidentified infected (\(I_{a}\)) and identified infected (\(I_{d}\)) as the response functions. The PRCC values which signifies mean strength help in identifying key parameters influencing \(I_{a}\) and \(I_{d}\), and its sign denotes correlation between the model parameters and the response function. Latin Hypercube Sampling is used to determine the PRCC values by means of stratified sampling with no replacement. Considering uniform distribution of the parameters, we run 500 simulation per LHS, setting the parameter values to deviate by \(\pm 25\%\) from their respective baseline values. Figure 5a and b denote the PRCC values for the response functions \(I_{a}\) and \(I_{d}\), respectively. From the figure, we note that the parameters \(\wedge ,~\beta ,~\delta ,~p\) share positive correlation with both unidentified and identified infectives. When compared the mean strength of the effective contact rate (\(\beta \)), movement rate from exposed to infected (\(\delta \)), and the fraction (p) with respect to \(I_{a}\) and \(I_{d}\), it is observed that the PRCC values of these parameters are greater for the former compared to the later. The parameters \(\xi ,~\epsilon ,~\gamma _{1}\) share negative correlation with both unidentified and identified infectives. The quarantine rate (\(\xi \)) is a significant parameter with respect to \(I_{d}\) as the response function, since if more identified infected are quarantined efficiently, their exposure to susceptible is nullified. The parameter m, which is the media factor, shares negative correlation with the identified infected, whereas a positive correlation with the unidentified infected, though the mean strength is very low. This is evident as the media information equated with the identified infected to be abiding by rules and not contributing toward disease spread. Similarly, the parameter \(\eta \) shares negative correlation with unidentified infected, and positive correlation with the identified infected, since higher detection rate implies more number of unidentified infectives moving to identified infected class. In all, this analysis emphasizes on the importance of better quarantine facility, enhanced treatment, better detection techniques and honest media information toward implementing improved interventions to curb the disease spread.

Fig. 5
figure 5

PRCC results showing sensitivity indices of the model parameters with a Unidentified Infected (\(I_{a}\)), and b Identified Infected (\(I_{d}\)). Baseline values of the parameters are as follows: \(\wedge =150\), \(\beta =0.000003\), \(\zeta =0.02\), \(m=1\), \(\delta =0.25\), \(p=0.15\), \(\eta =0.019\), \(\xi =0.07\), \(\epsilon =0.03\), \(\nu =0.004\), \(\mu _{1}=0.0001\), \(\mu _{2}=0.0002\), \(\gamma _{1}=0.2\), \(\gamma _{2}=0.1337\), \(\gamma _{3}=0.0714\), \(\mu =0.000425\)

Full size image

Figures 6, 7, 8, 9 and 10 represent the variation in \(R_{0}\) above and below 1, with respect to rise and fall of significant parameter values. Figure 4 shows that with the increase in effective contact rate(\(\beta \)), the disease transmission accelerates and with increase in hospitalization rate (\(\epsilon \)) of the identified infected population, the disease transmission slows down. Figure 7 shows that the increase in media information (m) in terms of spreading awareness on usage of face masks, hygiene, social distancing and home quarantining, etc., helps in reducing the passage of infection and hence lowers \(R_{0}\). Figure 8 depicts the reduction in the basic reproduction number with increase in the detection rate (\(\eta \)) and hospitalization rate (\(\epsilon \)). This is evident as more and more infected individuals are identified and hospitalized, the possibilities of those transmitting the disease to susceptible are reduced, since the possibilities of the susceptible getting exposed to them are reduced. Increased recovery rate of the unidentified infected implies smaller infectious period which in turn implies decreased probabilities of disease transmission from these individuals, hence implying reduction in number of secondary cases. This is depicted in Fig. 9. Figure 10 explains that with increase in effective contact rate (\(\beta \)) and increase in value of (\(\zeta \)), the \(R_{0}\) values increases. The \(\zeta \) is parameter which is responsible in reduction in infection rate through detected individuals with its value closer to zero implies reduction in disease transmission. \(\zeta \) multiplied with \(\beta \) gives the modified disease transmission rate of detected infected population. Hence, if the value of this reduction parameter is close to zero, i.e a very small value, then the overall infection rate reduces. On the contrary, increase in its value closer to 1 enhances the disease transmission and hence the number of secondary cases.

Fig. 6
figure 6

Contour Plot of Basic Reproduction Number with respect to effective contact rate (\(\beta \)) and hospitalization rate (\(\epsilon \)) for a India and b Nepal. The parameter values are as in Table 1

Full size image
Fig. 7
figure 7

Contour Plot of Basic Reproduction Number with respect to hospitalization rate (\(\epsilon \)) and media information (m) (decay factor) for a India and b Nepal. Parameter values: a \(\beta =5.888\times 10^{-6}\) and b \(\beta =2.654\times 10^{-6}\). The rest of the parameter values are as in Table 1

Full size image
Fig. 8
figure 8

Contour Plot of Basic Reproduction Number with respect to hospitalization rate (\(\epsilon \)) and detection rate (\(\eta \)) for a India and b Nepal. Parameter values: a \(\beta =5.888\times 10^{-6}\) and b \(\beta =2.654\times 10^{-6}\). The rest of the parameter values are as in Table 1

Full size image
Fig. 9
figure 9

Contour Plot of Basic Reproduction Number with respect to recovery rate of unidentified infected (\(\gamma _{1}\)) and effective contact rate (\(\beta \)) for a India and b Nepal. Parameter values: a \(\epsilon =0.03288\) and b \(\epsilon =0.02996\). The rest of the parameter values are as in Table 1

Full size image
Fig. 10
figure 10

Contour Plot of Basic Reproduction Number with respect to \(\zeta \) and effective contact rate (\(\beta \)) for a India and b Nepal. Parameter values: a \(\epsilon =0.03288\) and b \(\epsilon =0.02996\). The rest of the parameter values are as in Table 1

Full size image

4.3 Change in COVID-19 Prevalence with variation in parameters

In this section, we study the time series behavior of the developed mathematical model (1) for the total infected (\(I_{a}+I_{d}\)) and hospitalized population (H) with respect to parameter set : \(\eta ,~\epsilon \), \(\eta ,~\xi \), \(\nu ,~\epsilon \). We consider a time period of 800 days to depict the variation in these variables. Figure 11 showcases the fall in infected population with increase in the detection rate of the unidentified infectives (\(\eta \)) and the hospitalization rate of the identified infectives (\(\epsilon \)). This can be sufficed with the explanation that the more is the detection of the infectives and higher is the rate of hospitalization of these detected infectives based on the severity of conditions, lesser will be the infectives in open transmitting the disease to susceptible population.

A similar trend is observed in Fig. 12, wherein the change in total infected population is studied with rise in the values of parameter \(\eta \) and the quarantine rate of detected infectives. A similar reasoning applies in this case as well.

In Fig. 13, we witness the decrease in the number of hospitalized population with reduced hospitalization rate of identified infected and quarantined individuals. The non-availability of proper medical facilities and sufficient hospital beds leads to reduction in the hospitalization of the individuals in need of it, leading to the decrease in the hospitalized population.

Fig. 11
figure 11

Time series of the system of equations (1) depicting variation in Infected Population (\(I_{a}+I_{d}\)) with respect to \(\eta \) and \(\epsilon \) for a India and b Nepal

Full size image
Fig. 12
figure 12

Time series of the system of equations (1) depicting variation in Infected Population (\(I_{a}+I_{d}\)) with respect to \(\eta \) and \(\xi \) for a India and b Nepal

Full size image
Fig. 13
figure 13

Time series of the system of equations (1) depicting variation in Hospitalized Population (H) with respect to \(\nu \) and \(\epsilon \) for a India and b Nepal

Full size image

5 Optimal control

5.1 Optimal control problem

Dynamic optimization or optimal control is of major significance in fields of sciences, management, engineering and economics. Optimal control helps in identifying parameters which can control certain variables to produce the optimum result. In this section, we extend the system of equation (1) by adding 3 control parameters \(u_{1}\), \(u_{2}\), and \(u_{3}\) and develop the optimal control problem. The control \(u_{1}\) is included to reduce the transmission of disease. Though media information and awareness on the disease plays a major role, there are possibilities that certain precautions will not be followed by the unaware infective individuals. Hence, this control is equated to compulsory use of preventive face masks, gloves and sanitation. Since we have both undetected and detected infected population, if there are advances in the testing as well contact tracing, the detection rate could improve and hence help in identifying more infected individuals, from whom the passage of disease to susceptible is less compared to those from unidentified infectives. The control \(u_{2}\) is equated to this sort of improvement. In the system (2), \(\eta +u_{2}\) represent the enhanced detection rate. Control \(u_{3}\) is added to improve the quarantine and hospitalization rate of the identified infected population. This is necessary and will help in controlling the further spread of disease from this set of infectives, as the chances of them coming in contact with susceptible will be decreased majorly. \(\xi +u_{3}\) and \(\epsilon +u_{3}\) represent the improved quarantine and hospitalization rates. Hence, \(u_{3}\) can be equated to better medical facilities, with increase in number of beds, ventilators and mobile quarantine centers, etc. These three control functions are bounded and Lebesgue integrable on \([0,t_{f}]\), where \(t_{f}\) is the pre-fixed time interval length to which controls are applied. It is assumed that \(u_{1}\), \(u_{2}\), and \(u_{3}\) lie between 0 and 1, since if these 3 equal zero, it implies no efforts are placed in these controls. Similarly, maximum effort relates to these values being 1.

With the above assumptions, the following optimal control model is formulated:

$$\begin{aligned} \frac{d S}{d t}= & {} \wedge -\beta (1-u_{1}(t)) \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S-\mu S\nonumber \\ \frac{d E}{d t}= & {} \beta (1-u_{1}(t)) \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S -(\mu +\delta )E\nonumber \\ \frac{d I_{a}}{dt}= & {} p\delta E-(\eta +u_{2}(t))I_{a}-(\mu _{1}+\gamma _{1}+\mu )I_{a}\nonumber \\ \frac{d I_{d}}{d t}= & {} (1-p)\delta E+(\eta +u_{2}(t))I_{a}-(\xi +u_{3}(t))I_{d}-(\epsilon +u_{3}(t))I_{d}-\mu I_{d}\nonumber \\ \frac{d Q}{d t}= & {} (\xi +u_{3}(t))I_{d}-(\gamma _{2}+\nu +\mu )Q\nonumber \\ \frac{d H}{d t}= & {} (\epsilon +u_{3}(t))I_{d}+\nu Q-(\gamma _{3}+\mu _{2}+\mu )H\nonumber \\ \frac{d R}{d t}= & {} \gamma _{1}I_{a}+\gamma _{2}Q+\gamma _{3}H-\mu R \end{aligned}$$
(2)

The objective functional for the fixed \(t_{f}\) is given by

$$\begin{aligned} J=\int _{0}^{t_{f}}\left( C_{1}I_{a}+C_{2}I_{d}+C_{3}Q+C_{4}H+ \frac{1}{2}C_{5}u_{1}^{2}+\frac{1}{2}C_{6}u_{2}^{2}+\frac{1}{2}C_{7}u_{3}^{2}\right) dt \end{aligned}$$
(3)

where, \(C_{1},C_{2}, C_{3},C_{4},C_{5},C_{6}, C_{6}\ge 0\) are the weight constants.

Objective is to find the control parameters \(u_{1}*\), \(u_{2}*\), and \(u_{2}*\) such that

$$\begin{aligned} J(u_{1}*,u_{2}*,u_{3}*)=\min _{u_{1},u_{2},u_{3}\in \Omega _{1} } J(u_{1},u_{2},u_{3}) \end{aligned}$$

where, \(\Omega _{1}\) is the control set, defined as

$$\begin{aligned} \Omega _{1}=\left\{ u_{1},u_{2},u_{3}:measurable \quad and \quad 0\le u_{1},u_{2},u_{3}<1\right\} \quad and \quad t\in [0,t_{f}]. \end{aligned}$$

The Lagrangian of this problem is:

$$\begin{aligned} L(I_{a},I_{d},Q,H,u_{1},u_{2},u_{3})=C_{1}I_{a}+C_{2}I_{d}+C_{3}Q+C_{4}H+ \frac{1}{2}C_{5}u_{1}^{2}+\frac{1}{2}C_{6}u_{2}^{2}+\frac{1}{2}C_{7}u_{3}^{2}. \end{aligned}$$

The Hamiltonian \({\mathcal {H}}\) formed for our problem is :

$$\begin{aligned} {\mathcal {H}}= & {} L(I_{a},I_{d},Q,H,u_{1},u_{2},u_{3})+\lambda _{1}\frac{dS}{dt}+\lambda _{2}\frac{dE}{dt}+\lambda _{3}\frac{d I_{a}}{dt}\\&+\lambda _{4}\frac{d I_{d}}{dt}+\lambda _{5}\frac{dQ}{dt}+ \lambda _{6}\frac{dH}{dt}+\lambda _{7}\frac{dR}{dt} \end{aligned}$$

where \(\lambda _{i}'s\) are the adjoint variables (i = 1 to 7).

The adjoint variables are written in the form of differential equations as follows:

$$\begin{aligned} \frac{d\lambda _{1}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial S}=\lambda _{1}\mu +(\lambda _{1}-\lambda _{2})\beta (1-u_{1}(t)) \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) \nonumber \\ \frac{d\lambda _{2}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial E}=\lambda _{2}\mu +(\lambda _{2}-\lambda _{3})p\delta +(\lambda _{2}-\lambda _{4})(1-p)\delta \nonumber \\ \frac{d\lambda _{3}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial I_{a}}=-C_{1}+\lambda _{3}(\mu _{1}+\mu )+(\lambda _{1}-\lambda _{2})\beta (1-u_{1}(t))S+(\lambda _{3}-\lambda _{4})(\eta +u_{2}(t)) \nonumber \\&+(\lambda _{3}-\lambda _{7})\gamma _{1}\nonumber \\ \frac{d\lambda _{4}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial I_{d}}=-C_{2}+\lambda _{4}\mu +(\lambda _{1}-\lambda _{2})\beta (1-u_{1}(t))\frac{m\zeta S}{(m+I_{d})^2}+(\lambda _{4}-\lambda _{5})(\xi +u_{3}(t)) \nonumber \\&+(\lambda _{4}-\lambda _{6})(\epsilon +u_{3}(t))\nonumber \\ \frac{d\lambda _{5}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial Q}=-C_{3}+\lambda _{5}\mu +(\lambda _{5}-\lambda _{6})\nu +(\lambda _{5}-\lambda _{7})\gamma _{2}\nonumber \\ \frac{d\lambda _{6}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial H}=-C_{4}+\lambda _{6}(\mu +\mu _{2})+(\lambda _{6}-\lambda _{7})\gamma _{3}\nonumber \\ \frac{d\lambda _{7}}{dt}= & {} -\frac{\partial {\mathcal {H}}}{\partial R}=\lambda _{7}\mu . \end{aligned}$$
(4)

Let \({\widetilde{S}}\), \({\widetilde{E}}\), \(\widetilde{I_{a}}\), \(\widetilde{I_{d}}\), \({\widetilde{Q}}\), \({\widetilde{H}}\) and \({\widetilde{R}}\) be optimum values of S, E, \(I_{a}\),\(I_{d}\), Q, H and R, respectively. Let \(\widetilde{\lambda _{1}}\), \(\widetilde{\lambda _{2}}\),\(\widetilde{\lambda _{3}}\), \(\widetilde{\lambda _{4}}\), \(\widetilde{\lambda _{5}}\), \(\widetilde{\lambda _{6}}\), and \(\widetilde{\lambda _{7}}\) be solution of (3). By using [53,54,55], we state and prove the below theorem.

Theorem 5.1

There exists optimal controls \(u_{1}*\), \(u_{2}*\) and \(u_{3}*\) \(\in \) \(\Omega _{1}\) such that \(J(u_{1}*,u_{2}*,u_{3}*)\) \( = \min J(u_{1},u_{2},u_{3})\) subject to extended system of equations(2).

Proof

We use [53] to prove this theorem. In this case, we observe that the controls are non-negative. The necessary convexity of the objective functional in \((u_{1},~ u_{2},~u_{3})\) is satisfied for minimizing the problem. The set of control variable, \(u_{1},~ u_{2},~ u_{3} \in \Omega _{1}\) is convex and closed by definition. The state variables are bounded and the integrand of the functional \(C_{1}I_{a}+C_{2}I_{d}+C_{3}Q+C_{4}H+ \frac{1}{2}C_{5}u_{1}^{2}+\frac{1}{2}C_{6}u_{2}^{2}+\frac{1}{2}C_{7}u_{3}^{2}\) is convex on \(\Omega _{1}\). Since there exist optimal controls for minimizing the functional subject to systems (2) and (4), we use Pontryagin’s maximum principle [53] to derive the necessary conditions to find the optimal solutions in the following way:

Suppose (z, u) is an optimal solution of an optimal control problem, then this implies that there exists a non-trivial vector function \(\lambda =\lambda _{1},\lambda _{2},\dots ,\lambda _{n}\) satisfying the following:

$$\begin{aligned} \frac{dz}{dt}=\frac{\partial {\mathcal {H}}(t,z,u,\lambda )}{\partial \lambda }, \quad 0=\frac{\partial {\mathcal {H}}(t,z,u,\lambda )}{\partial \lambda }, \quad \frac{d\lambda }{dt}=\frac{\partial {\mathcal {H}}(t,z,u,\lambda )}{\partial \lambda } \end{aligned}$$

\(\square \)

Theorem 5.2

The optimal controls \(u_{1}*\), \(u_{2}*\), and \(u_{3}*\) which minimize J over the region \(\Omega _{1}\) are given by:

$$\begin{aligned} u_{1}*= & {} \min \left\{ 1, \max (0,\widetilde{u_{1}} \right\} \\ u_{2}*= & {} \min \left\{ 1, \max (0,\widetilde{u_{2}} \right\} \\ u_{3}*= & {} \min \left\{ 1, \max (0,\widetilde{u_{3}} \right\} \end{aligned}$$

where,

$$\begin{aligned} \widetilde{u_{1}}= & {} \frac{(\lambda _{2}-\lambda _{1})\beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S}{C_{5}}\\ \widetilde{u_{2}}= & {} \frac{(\lambda _{3}-\lambda _{4})I_{a}}{C_{6}}\\ \widetilde{u_{3}}= & {} \frac{(\lambda _{4}-\lambda _{5})I_{d}+(\lambda _{4}-\lambda _{6})I_{d}}{C_{7}} \end{aligned}$$

Proof

We prove this theorem by using [53, 54] and Theorem 5.1.

Using the optimally condition: \(\frac{\partial {\mathcal {H}}}{\partial u_{1}}=0\), \(\frac{\partial {\mathcal {H}}}{\partial u_{2}}=0\), and \(\frac{\partial {\mathcal {H}}}{\partial u_{3}}=0\), we get,

$$\begin{aligned} \frac{\partial {\mathcal {H}}}{\partial u_{1}}= & {} C_{5}u_{1}+(\lambda _{1}-\lambda _{2})\beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S=0\\ \implies u_{1}= & {} \frac{(\lambda _{2}-\lambda _{1})\beta \left( I_{a}+\frac{\zeta I_{d}}{m+I_{d}}\right) S}{C_{5}}=\widetilde{u_{1}}\\ \frac{\partial {\mathcal {H}}}{\partial u_{2}}= & {} C_{6}u_{2}+(\lambda _{4}-\lambda _{3})I_{a}=0\\ \implies u_{2}= & {} \frac{(\lambda _{3}-\lambda _{4})I_{a}}{C_{6}}=\widetilde{u_{2}}\\ \frac{\partial {\mathcal {H}}}{\partial u_{3}}= & {} C_{7}u_{3}+(\lambda _{5}-\lambda _{4})I_{d}+(\lambda _{6}-\lambda _{4})I_{d}=0\\ \implies u_{3}= & {} \frac{(\lambda _{4}-\lambda _{5})I_{d}+(\lambda _{4}-\lambda _{6})I_{d}}{C_{6}}=\widetilde{u_{3}} \end{aligned}$$

Again the lower bound is 0 and upper bound is 1 for the controls \(u_{1}\), \(u_{2}\) and \(u_{3}\). This suggests that \(u_{1}=u_{2}=u_{3}=0\) if \(\widetilde{u_{1}}<0\), \(\widetilde{u_{2}}<0\) and \(\widetilde{u_{3}}<0\), also \(u_{1}=u_{2}=u_{3}=1\) if \(\widetilde{u_{1}}>1\), \(\widetilde{u_{2}}>1\) and \(\widetilde{u_{3}}>1\), otherwise \(u_{1}=\widetilde{u_{1}}\), \(u_{2}=\widetilde{u_{2}}\) and \(u_{3}=\widetilde{u_{3}}\). Therefore, for these controls \(u_{1}*\), \(u_{2}*\) and \(u_{3}*\) we get optimum values of J. \(\square \)

Fig. 14
figure 14

Control Profiles of the control parameters a \(u_{1}\), b \(u_{2}\), and c \(u_{3}\)

Full size image
Fig. 15
figure 15

Control profiles of a \(u_{1}\) , b \(u_{2}\), and c \(u_{3}\) with variation in the costs of controls

Full size image
Fig. 16
figure 16

Variations of Infected Population (\(I_{a}+I_{d}\)) and Recovered Population (R) with and without control in (a,b) Nepal and (c,d)India

Full size image

5.2 Optimal control model simulation

To perform the optimal control simulation, we code in MATLAB by using certain parameter set which correspond to stability of endemic equilibrium point. We consider a time interval of 400 days to perform the simulation. The weight constants are \(C_{1}=1,~C_{2}=1,~ C_{3}=1,~ C_{4}=1,~ C_{5}=40, ~ C_{6}=45,~ C_{7}=45\). The extended system of equations (2) is solved by iterative method using forward and backward difference approximation [55]. Figure 14 depicts the control profile of \(u_{1}\), \(u_{2}\), and \(u_{3}\). From these figures, we can infer that the control profile \(u_{1}\) needs to be maintained at 1 for a longer duration compared to the other 2 controls. This control relates to reduction in disease transmission via social distancing, compulsory usage of face mask and sanitation. These measure are a bit difficult to be adhered to, and if these are applied by every individuals, the spread of the disease can be reduced drastically. From Fig. 14b, we notice that the control profile equating to enhanced detection by means of rapid testing moves from 0.15 to 0.95 within no time. It again drastically falls to 0.7 from where it can be controlled over a period of time. This is probably because, a detection rate is already included in the model, which is then related with media information associated with the detected infected. Hence, if the detected infected are very well aware of the situation, they will abide by the measures, media information on COVID-19 and this proportion of infected population will merely contribute in disease transmission. Figure 14c depicts that the control profile \(u_{3}\) is crucial in curbing the pandemic, since after detection of the infected if the infectives are not quarantined or hospitalized in a systematic manner, the chances of disease spreading from these individuals will rise.

Figure 15 depicts the variations in control profile with increase in the cost of these controls. We note that as the cost of these control parameters increases, the duration for these controls to be maintained at 1 reduces. This is due to the reason that as the cost of the equipment and advertisements to implement these controls increases, the likelihood of higher investment on those would reduce.

In Fig. 16, we visualize how the infected and recovered population are impacted by the control parameters. We do the optimal control simulation for Nepal and India.

NEPAL: Fig. 16a and b show the variation in infected population (\(I_{a}+I_{d}\)) and recovered population, respectively, with and without the 3 controls. We note that if all the three controls are applied, the number of infected population could be reduced drastically in Nepal. Figure 16b shows that with these controls the recovered population could be increased compared to when no controls are applied. As per [40], the total COVID-19 cases stand at 0.5 million plus, whereas the optimal control analysis suggests that systematic implementation of interventions encompassing the mentioned control parameters could have controlled the spread of infections to a major extent.

INDIA: Fig. 16c and d show the variation in infected population (\(I_{a}+I_{d}\)) and recovered population, respectively, with and without the 3 controls. In case of India, we note that there is difference in number of infected population of around 0.2 million, with and without the application of the 3 controls. As per ([41]), the recoveries are more than 20 million, however, with application of each of these controls it could be curbed further.

6 Conclusion

Compartmental epidemiological models aid in better understanding of disease spread and control. In this work, a 7 compartment epidemiological model is framed and solved. A detailed study on equilibria and stability analysis is presented in this work. We considered a 11 months data of observed active COVID-19 cases of India and Nepal and performed numerical simulation on it. We fitted the developed model to the data and estimated optimum parameter values of the effective contact rate and hospitalization rate of the identified infected which resulted in the best fit of the model. Predictions till June 30, 2021 were obtained using the second wave data for both the countries, and a declining trend was observed for both the countries for the next 30 to 40 days. We obtained higher effective contact rate for India in comparison with Nepal, which adheres as per the actual data reports [40, 41]. We obtain a smaller hospitalization rate for Nepal compared to India which is sufficed by news reports from [19, 20]. A detailed analysis on sensitivity is presented in this work by means of normalized forward sensitivity index of the basic reproduction number and PRCC with unidentified and identified infected as the response functions. We note that with increase in detection rate, hospitalization and quarantine rates, the infection spread can be controlled. Higher is the number of identified infectives getting quarantined and hospitalized, lower will be the probability of disease transmission from these individuals. Similarly, higher is the detection rate by means of testing and contact tracing, lower will be the disease spread. The inclusion of media information also plays a major role in controlling the disease spread. In addition to use of face masks and practice of social distancing, information through media will make the individuals aware on various aspects of the disease, be it the preventive measures to be undertaken before or after being infected, or the behavioral changes toward combating the spread of the virus. Valid and correct information will lead to increase in the number of aware individuals, irrespective of being infected or not, thereby taking necessary steps in terms of self-isolation, medication and abiding by other disease-related protocols. This is followed by the extension of proposed model to optimal control problem. In this case, a detailed study on control parameters related to social distancing, usage of face masks, rapid testing, and improved quarantine and medical facilities is discussed. A study on this leads to the conclusion that if interventions related to medical facilities, quarantine centers and rapid testing is implemented, the rising number of infections can be curbed majorly, further implying increased recoveries. A further study with inclusion of vaccination can be implemented in future. This could be further associated with age factor and the vaccine efficacy for different age groups. A detailed study, with various factors will help in getting a broader and deeper knowledge in COVID-19 study.