Predicting the Spread of COVID-19 Using $SIR$ Model Augmented to Incorporate Quarantine and Testing

Abstract

India imposed a nationwide lockdown from 25th March 2020 onwards to combat the spread of COVID-19 pandemic. To model the spread of a disease and to predict its future course, epidemiologists make use of compartmental models such as the $SIR$ model. In order to address some of the assumptions of the standard $SIR$ model, a new modified version of $SIR$ model is proposed in this paper that takes into account the percentage of infected individuals who are tested and quarantined. This approach helps overcome the assumption of homogenous mixing of population which is inherent to the conventional $SIR$ model. Using the available data of the number of COVID-19 positive cases reported in the state of Kerala, and in India till 26th April, 2020 and 12th May 2020, respectively, the parameter estimation problem is converted into an optimization problem with the help of a least squared cost function. The optimization problem is then solved using differential evolution optimizer. The impact of lockdown is quantified by comparing the rising trend in infections before and during the lockdown. Using the estimated set of parameters, the model predicts that in the state of Kerala, by using certain interventions the pandemic can be successfully controlled latest by the first week of July, whereas the ${R}_{0}$ value for India is still greater than 1, and hence lifting of lockdown from all regions of the country is not advisable.

Introduction

COrona VIrus Disease (COVID-19) has presented an out of the ordinary challenge before us. As of 12th May 2020, the disease has infected more than four million people globally and claimed the lives of almost three hundred thousand individuals (Situation report-113, 2020). COVID-19 is caused by the novel corona virus SARS-CoV-2 (Report of WHO 2020). Currently, there is no clinically proven medicine to treat this ailment (Sanders et al. 2020). Optimistic researchers suggest that a clinically proven and tested vaccine is at least 1–2 years away (Ferguson et al. 2020). As per WHO guidelines, the only way to combat and contain this pandemic is to maintain personal hygiene and observe strict social distancing measures (Ferguson et al. 2020). This strategy is widely adopted across the world and many countries have imposed nationwide lockdowns (Situation report-91 2020).

The first case in India was reported on 30th January 2020 (Situation report-3 2020). As of 12th May 2020, the cases have risen to more than seventy thousand in number (Ministry of Health & Family Welfare 2020). Government of India took an active step towards containing the spread of this disease by initially imposing a 21-day nationwide lockdown from 25th March 2020 and later extending it for 2 more weeks. This measure of abundant precaution has helped to suppress the frequency and magnitude of social contacts within the country (Situation report-91 2020). This quarantine period is also accompanied with continuous contact tracing of the increasing infected patients by local government authorities and functioning at war-footing of the health care system.

Epidemiology is a branch of medicine that deals with the incidence, distribution and possible control of diseases in a population. Epidemiological models such as the $SIR$ model are widely used to model the spread of diseases in a population. The standard $SIR$ model works with the assumption that there is continuous contact between the infected and susceptible population (Adamu et al. 2019). This assumption is violated in a scenario wherein restrictions such as quarantine and social distancing are enforced, in which case the portion of infected population which is quarantined will not be contributing in the spread of the disease. Several authors have made modifications to the existing SIR model to make more accurate predictions. Peng et al. (2020) has developed a 7-variable SEIR model, which was used to model the outbreak in China. Lopez et al. (2020), have used a model similar to Peng, to predict the outbreak in Italy and Spain. Stochastic models can also be used to make predictions, such as Aravind et al. (2020), where a stochastic model is used to predict the outbreak in India. In the same study, the ${R}_{0}$ value for India was estimated between 1.4 and 1.85.

In this paper, the growth characteristics of this disease using an augmented SIR model are discussed in detail. The standard $SIR$ model is tweaked to study the effect of testing by introducing categorization for quarantined and unquarantined individuals. The growth trend for pre-lockdown and post-lockdown scenarios is assessed and the necessary parameters of the $SIR$ model have been estimated separately for the state of Kerala and India, as the authors and their affiliated institution are located in the Indian state of Kerala.

The following section of this paper describes the standard $SIR$ model along with its assumption, and the proposal of the modified $SIR$ model is later presented. The methodology used in this study as well as the results and predictions for the state of Kerala and India are presented in the later sections.

Standard ${\varvec{S}}{\varvec{I}}{\varvec{R}}$ Model

The standard $SIR$ model divides the entire population into three compartments, namely, $S$: susceptible, $I$: infected, and $R$: removed or recovered (Adamu et al. 2019). A set of ordinary differential equations are then used to solve the disease dynamics and propagate the model.

The disease dynamics equations are,

$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \beta \cdot \frac{S \cdot I}{N},$$

(1)

$$\frac{{{\text{d}}I}}{{{\text{d}}t}} = \beta \cdot \frac{S \cdot I}{N} - \nu \cdot I,$$

(2)

$$\frac{{{\text{d}}R}}{{{\text{d}}t}} = \nu \cdot I,$$

(3)

where $S$ is the number of susceptible people in the population, i.e. number of people who are healthy but are likely to fall ill, $I$ is the number of people who are infected and infectious. Upon interacting with the susceptible population, these people are likely to infect them, $R$ is the number of people who have recovered or removed from considerations. This group consists of the number of people who were infected once upon a time, but have recovered and will neither get infected nor infect again, $N$ is the total number of people in the population.

The rate of change of infected population $\left(\frac{dI}{dt}\right)$ depends on two primary factors:

• 1. The number of people falling ill, and

• 2. The number of people recovering.

The number of people falling ill is dictated by the level of interactions between the infected and the susceptible population, and is related by the constant $\beta$, which stands for the rate of spread of infection by an infected person per day when he/she interacts with the susceptible population. The number of people recovering is dictated by the rate of recovery $\nu$.

Assumptions in the Standard ${\varvec{S}}{\varvec{I}}{\varvec{R}}$ Model

Despite its popular usage, the $SIR$ model makes several assumptions. Some important assumptions are:

• (1) It assumes that the total population does not change much with time, i.e. $\frac{dS }{dt}+ \frac{dI}{dt} + \frac{dR}{dt} = 0.$

• (2) The model assumes that each person in the population has the same health characteristics, i.e. same immunity, same immuno-response, etc.

• (3) Every person in the population interacts with one another.

• (4) All infected people are infectious and are spreading the disease among the susceptible population.

• (5) The natural history of the diseases, i.e. latency period, incubation period, etc., is not considered in this model.

Assumptions (3) and (4) can result in significant overestimation in the total number of cases. In order to address assumption 4, this paper presents a modified $SIR$ model that takes into account the effect of quarantining the infected people.

Modified SIR Model (${\varvec{S}}{\varvec{I}}{\varvec{R}}$ + Quarantine)

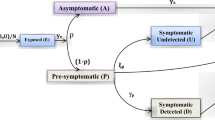
In order to accommodate the quarantine effect into the $SIR$ model, the infected population $(I)$, is broken into two sub-groups (shown in Fig. 1), namely,

Fig. 1

Categorization of infected individuals based on factor of testing

Quarantined: Consists of people who are infected and have been tested positive for the disease. Once they are quarantined, they no longer pose a risk to the susceptible population.

Unquarantined: Consists of people who are infected and have still not been tested for the diseases. This group is still interacting with the susceptible population and poses a risk to them.

The two groups can be correlated using the factor of testing $(ft)$ which stands for the fraction of infected people who are tested and quarantined. If $ft$ increases, then more infected people will get quarantined, and hence, the spread can be controlled as the bulk of infected people can no longer infect others. The modified $SIR$ equations are as such,

$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \frac{{\beta \cdot \left( {S \cdot UQ} \right)}}{N},$$

(4)

$$\frac{{{\text{d}}Q}}{{{\text{d}}t}} = {\text{ft}} \cdot \frac{{\beta \cdot \left( {S \cdot UQ} \right)}}{N} - v_{1} \cdot Q,$$

(5)

$$\frac{{{\text{d}}UQ}}{{{\text{d}}t}} = \left( {1 - {\text{f}}t} \right) \cdot \beta \cdot \frac{S \cdot UQ}{N} - \nu_{2} \cdot UQ,$$

(6)

$$\frac{{{\text{d}}R}}{{{\text{d}}t}} = v_{1} \cdot Q + \nu_{2} \cdot UQ$$

(7)

The rate of change of infected population, $\frac{dI}{dt}$ is broken into two parts, $\frac{dQ}{dt}$ and $\frac{dUQ}{dt}$ referring to the rate of change of quarantined population and unquarantined population, respectively. Separate recovery rates have been considered here for quarantined and unquarantined population owing to the fact that the quarantined population may be receiving better medical assistance at hospitals in the presence of professionals. However, due to lack of data, both the recovery rates are assumed to be same in this study, i.e. (ν = ${v}_{1}$  = ${v}_{2}$).

Basic Reproduction Ratios (${{\varvec{R}}}_{0}$ and ${{\varvec{R}}}_{\mathbf{e}\mathbf{f}\mathbf{f}}$)

The basic reproduction number ${R}_{0}$ and the effective reproduction number ${R}_{eff}$ are indicative of the number of secondary infections caused by a single infected person. In the standard SIR model, the basic reproduction number ${R}_{0}$ is defined as the ratio of the rate of spread and the rate of recovery, i.e. $\frac{\beta }{\nu }$. The equation for basic reproduction ratio can now be modified to

$$R_{{{\text{eff}}}} = \left( {1 - {\text{ft}}} \right) \cdot \frac{\beta }{\nu } \cdot \frac{S}{N}$$

(8)

During the beginning of an outbreak, $\frac{S}{N} \sim 1,$ hence the equation for ${R}_{0}$ can be written as

$$R_{0} = \left( {1 - {\text{ft}}} \right) \cdot \frac{\beta }{\nu }$$

(9)

This equation offers some very intuitive results. In order to control an outbreak of a disease, the basic reproductive number ${R}_{0}$ should be less than 1 (${R}_{0}< 1$), which can be achieved in three possible ways,

Increase in $ft$(factor of testing) If testing is ramped up and more number of infected people are tested, the number of unquarantined people will reduce, thereby controlling the spread of the disease among the susceptible population.

Reduction in $\beta$ (rate of spread) By employing social distancing measures and personal protective measures, such as wearing masks and regularly washing hands, the rate of spread can be controlled.

Increase in ν (rate of recovery) By ensuring the presence of sufficient amount of medicines and adequate healthcare equipment, the rate of recovery can be increased.

Effect of ${\varvec{\beta}}$ and ${\varvec{f}}{\varvec{t}}$ on the Spread of a Disease

The presence of factor of testing $(ft)$ in the SIR model greatly affects the dynamics of the model. Shown in Fig. 2a is the variation in the spread of a disease in a sample population of 10,000 people for different values of $ft$ while keeping the rate of spread per infected person per day $(\beta )$ and recovery ratio $(\nu )$ constant. The higher the value of ft, i.e. the higher the number of infected people who are quarantined, better controlled is the epidemic. If only 30% of all infected people are tested, the active cases can rise to 3000, which may be challenging for the health system to deal with. If testing is increased and 50% of all infected people are tested, the maximum number of active cases can be reduced to 1800. And if the testing is further increased to 80% of all infected people, the maximum number of active cases can be brought down to 500. This showcases the importance of testing in controlling a pandemic.

Fig. 2

a Growth of active cases with different $ft$ values keeping the rate of spread, $\beta$ and the recovery factor $(\nu )$ constant. $\beta\, =\,1.0$, $\nu\,=\,0.25$; b growth of active cases with different $\beta$ values keeping the factor of testing $(ft)$ and the recovery factor $(\nu )$ constant.$ft=0.4$, $\nu =0.25$

Figure 2b shows the variation in the spread of a disease in the same sample population of 10,000 people for different values of $\beta$ while keeping the factor of testing $(ft)$ and the recovery ratio $(\nu )$ constant. As explained earlier, $\beta$ is an indicator of the levels of interaction among a population, i.e. higher the value of $\beta$, the higher the levels of social interaction. If the interactions between the population are reduced, the spread of the disease can be controlled. For a $\beta$ value of 1.2, where each infected person spreads the disease to 1.2 people every day, the number of active cases can rise to beyond 3000. If with the help of social distancing measures, the value of $\beta$ is reduced to 0.8, the maximum number of active cases can be reduced to 1500. If the government poses stricter social distancing measures, and the value of $\beta$ is further brought down to 0.5, then the maximum number of active cases can be kept below 500.

Methodology

The parameters $\beta$ and $\nu$ are estimated from the available data on the number of positive cases (Crowd Source 2020 and Our world in data 2020). The above problem is then converted into a parameter estimation problem by formulating a cost function and using a differential evolution optimizer.

Formulation of Cost Function

Assume ${Y}_{D}$ to be the time series of the number of reported cases obtained from the data, and ${Y}_{M}$ to be the same parameter predicted by the model. The cost function can then be written as the sum of the squared difference of all data points as explained in Eq. 10:

$${\text{Cost}} = \sum\limits_{\forall T} {\frac{{\left( {Y_{{\text{D}}} - Y_{{\text{M}}} } \right)^{2} }}{2N}}$$

(10)

where $N$ is the total number of data points.

Differential Evolution

Differential evolution (DE) is an evolutionary heuristics-based optimization technique developed by Storn and Price in 1997. The method iteratively tries to improve the solution estimates by regularly creating new candidate solutions via combining existing ones according to a simple mathematical formula (Storn and Price 1997).

Platform

The simulations were carried out in Python 3.6© using the in-built differential evolution routine provided by the Scipy© package version 1.1.0.

Results and Predictions

Case Study: State of Kerala

By 26th April, Kerala had witnessed a total of 458 confirmed COVID-19 positive cases, with the highest rise seen on 28th March, 2020 after which a steady decline in the cases was observed. The technique presented in the above section was used to estimate the β and ft values before lockdown and during lockdown using data available till 26th April, 2020 and the following estimates were obtained.

As shown in Table 1, before the enforcement of lockdown on 25th March, 2020, the basic reproductive number $({R}_{0})$ in Kerala is estimated to be 1.9 with only 32% of all infected people tested. After the enforcement of lockdown, the R₀ appears to have reduced to 0.92 with testing improved to ~ 50%, which indicates a receding epidemic in Kerala.

As shown in Fig. 3, a significant match can be seen between the model predictions and the actual data, with a mean absolute percentage error of 13.9%. Given the current situation in Kerala, several different scenarios were simulated. In the following figures, the coloured region indicates a lockdown.

Fig. 3

Comparison between the actual data and model. a Comparison of the model with total number of confirmed cases; b comparison of the model with number of confirmed cases per day

Scenario 1: Lockdown Opened on 3rd May with Existing Testing Levels

If the lockdown is opened on 3rd May and the existing testing levels are maintained, then assuming a level of interaction similar to the pre-lockdown period, the number of cases in Kerala can be expected to increase (shown in Fig. 4).

Fig. 4

Number of new cases per day if the lockdown is opened in Kerala with the existing testing levels

Scenario 2: Lockdown Opened on 3rd May but Testing is Increased to 80%

If the government opens the lockdown on 3rd May, and at the same time increases the testing levels to 80%, then assuming the same level of interactions as the pre-lockdown period, the model predicts that Kerala will stop seeing new cases by 20th May, 2020 as shown in Fig. 5.

Fig. 5

Number of new cases per day if the lockdown is opened in Kerala with the testing levels increased to 80%

Scenario 3: Two-Month Lockdown with Testing Gradually Increased to 60%

Increasing testing levels rapidly can pose several logistical constraints, and thereby cannot be expected. Instead, if the government decides to opt for a 2-month long lockdown, while gradually increasing the testing to 60%, then assuming the same level of interactions as the pre-lockdown period, the model predicts that the pandemic can be completely controlled in Kerala by the first week of July (as shown in Fig. 6).

Fig. 6

Number of new cases per day if the lockdown is extended to two months while gradually increasing the testing levels to 60%

Scenario 4: Staggered Lockdown with Existing Levels of Testing

Having a long lockdown can severely affect the socio-economic activities of the state, therefore a possible option for the government can be to enforce intermittent or staggered lockdowns. Considered here is a scenario where the lockdown is opened on 3rd May for 1 week, after which a 20-day lockdown is re-imposed followed by another 1 week relief period and then another 20-day lockdown. In such a scenario, assuming the existing levels of testing, the model predicts that the cases in Kerala can be controlled by 26th June, 2020 (as shown in Fig. 7).

Fig. 7

Number of new cases per day in the case of an intermittent or staggered lockdown with existing testing levels

Scenario 5: Lockdown Opened on 3rd May with Social Distancing Measures

Another possible option for the government could be to open the lockdown on 3rd May, but with social distancing measures. Here, we have assumed that the level of interactions after the lockdown to be an average of the level of interactions before and during lockdown, i.e.:

$$\beta_{{{\text{AL}}}} = \frac{{\beta_{{{\text{BL}}}} + \beta_{{\text{L}}} }}{2} = 0.58,$$

where ${\beta }_{AL}$ is the rate of spread after the lockdown is lifted, ${\beta }_{BL}$ is the rate of spread before the lockdown was imposed, and ${\beta }_{L}$ is the rate of spread during the lockdown.

In such a scenario, assuming the present levels of testing, the model predicts that the number of cases in Kerala can be controlled by the first week of June (as shown in Fig. 8).

Fig. 8

Number of new cases per day in the case where the lockdown is lifted on 3rd May with adequate social distancing measures

Case Study: India

Unlike Kerala, the COVID-19-positive cases in India are still on the rise. As of 12th May, 2020, there are ~ 70,000 positive cases; hence removal of the lockdown is out of question. Figure 9 shows the comparison between the model’s prediction and actual data. Data till 12th May were used to estimate the parameters ${R}_{0}$ and $ft$ before and during lockdown. The estimated parameters, with a mean absolute percentage error of 26.3% are given below.

Fig. 9

Comparison of the model with total number of confirmed cases

As shown in Table 2, the R₀ value for India appears to have come down from 2.01 before lockdown to 1.44 during lockdown, but is still not low enough. The current estimates also indicate that India is testing 70% of its infected people. If this scenario continues, the model predicts that India can see at most 1.6 crore active cases by mid-September (shown in Fig. 10).

Table 1 β and ft values estimated for Kerala using data up to 26th April 2020

Table 2 ${R}_{0}$ and $ft$ values estimated for India using data up to 12th May 2020

Fig. 10

Number of active cases in the country if the current scenario continues

Conclusion

For the state of Kerala, the estimated values of $\beta$ and ft indicate that the pandemic is receding, and with a few careful decisions, it can be completely controlled. If the lockdown is lifted on 3rd May without any protective measures, the numbers will start rising again. In such a scenario, the following possible options can be explored in Kerala, namely,

• (1) Lift lockdown by rapidly increasing testing to 80%. In such a case, the spread can be controlled by May 20th.

• (2) Extend lockdown to 2 months while gradually increasing testing to 60%, in which case, the spread can be controlled by first week of July.

• (3) Intermittent or staggered lockdown while maintaining the current levels of testing, in which case, the spread can be controlled by 26th June.

• (4) Lifting the lockdown on 3rd May while ensuring adequate social distancing measures, in which case, the spread can be controlled by the first week of June.

In the case of India, estimates show that the $R_{0}$ value during lockdown has come down to 1.44 from 2.01 before lockdown. Although improved, the existing $R_{0}$ value is not low enough to call off the lockdown, hence removal of the country-wide lockdown must not be considered at present.