Diffusion and flow across shape-perturbed plasmodesmata nanopores in plants

Abstract

Plasmodesmata are slender nanochannels that link neighboring plant cells and enable the exchange of nutrients and signaling molecules. Recent experiments have demonstrated significant variability in the concentric pore shape. However, the impact of these geometric fluctuations on transport capacity is unknown. Here, we consider the effects on diffusion and advection of two ideal shape perturbations: a radial displacement of the entire central desmotubule and a harmonic variation in the cytoplasmic sleeve width along the length of the pore. We use Fick’s law and the lubrication approximation to determine the diffusive current and volumetric flow rate across the pore. Our results indicate that an off-center desmotubule always increases the pressure-driven flow rate. However, the diffusive current is only enhanced for particles comparable in size to the width of the channel. In contrast, harmonic variations in the cytoplasmic sleeve width along the length of the pore reduce both the diffusive current and the pressure-driven flow. The simple models presented here demonstrate that shape perturbations can significantly influence transport across plasmodesmata nanopores.

1 Introduction

Living organisms must confront the challenge of facilitating nutrient and signal exchange between proximal compartments [1]. Plants solve this problem, in part, using plasmodesmata (PD) nanopores [2]. PD are permanent channels that traverse the cell wall and directly link the cytoplasmic fluid of neighboring cells. Their shape is that of an approximately circular cylinder, and they are typically $L\approx 200{-}1000$ nm long and $2a\approx 25{-}50$ nm in diameter [3, 4]. The pores are open, that is the plasma membrane of adjacent cells meets inside the pore. The cortical endoplasmic reticulum permeates each PD, and the gap between the cylindrical desmotubule (diameter $2b\approx 20$ nm) and the membrane forms an annular cytoplasmic sleeve of width $h=a-b\approx 3{-}4\,\hbox {nm}$ in mature pores [5] through which water and solutes move (Fig. 1). See Table 1 for a summary of the geometric parameters.

The main transport impediment in plasmodesmata is associated with the open annular gap between the cell membrane and the central rod. The cytoplasmic sleeve width h defines the space available for molecular trafficking, governing the permeability and size exclusion limit of the pores. Current models stipulate that transport capacity is reduced as the gap h shrinks or the radius s of the diffusing molecule increases. Some, but not many, experiments have been carried out to test this proposition. Unexpectedly, [3] found that narrow, newly formed plasmodesmata with no visible cytoplasmic sleeve nonetheless enable fast small molecule diffusion and even non-selective macro-molecule trafficking between cells. This appears counterintuitive based on their morphology, and open questions related to the link between pore morphology and transport capacity remain.

Currently, PD-mediated transport is modeled as a purely diffusive or pressure-driven phenomenon (see, e.g., [6] and [7]), and the transport rates are derived from Fick’s law and basic solutions to the Navier–Stokes equation in the narrow cytoplasmic sleeve. These models are based on the assumption that the gap geometry is uniform across all pores. However, substantial variation in pore geometry has been observed [3]. Nevertheless, it is unclear if the possibility that the pore aperture might, occasionally, differ significantly from the steady-state size has an important impact on transport capacity.

In this paper, we therefore seek to quantify the impact of shape perturbations on plasmodesmata transport capacity. We begin by outlining two basic modes of geometric variation. Then, we quantify the impact on the cell–cell flux for diffusive and advective processes. The main finding—that an off-center desmotubule enhances transport—is discussed. Finally, future experiments are proposed.

Fig. 1

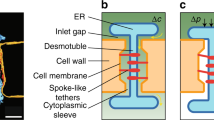
Shape fluctuations in plasmodesmata nanopores. a Electron tomography of a plasmodesma nanopore that links two plant cells. b Sketch of a plasmodesma. Transport occurs in the open region of width $h=a-b$ between the desmotubule rod (radius b) and cell membrane pore (radius a). A difference $\Delta c=c_1-c_2$ in the concentration c of signaling molecules (green dots) leads to a diffusive current I across the plasmodesmata. Likewise, a pressure difference $\Delta p=p_1-p_2$ leads to a fluid flow rate Q, which carries the particles across by advection. Side view (c) and top view (d) of an unperturbed desmotubule in the center of the cytoplasmic sleeve. We consider two modes of shape perturbation: In panel (e), the desmotubule is displaced a distance $h_0\delta$ from the center of the plasmodesmata, thus forming an eccentric channel. In panel (f), the radius of the desmotubule varies harmonically along the pore axis with amplitude $h_0\varepsilon$. Panel (a) adapted from [3] and reproduced with permission

Table 1 Geometric parameters relevant to diffusion and advection in plasmodesmata. See details and sources in the text

2 Results

2.1 Morphology of shape-perturbed plasmodesmata nanopores

Plasmodesmata are small channels that link adjacent plant cells (Fig. 1a–d). The cell wall, lined by the cell membrane, provides the outer channel boundary, while the cylindrical membranous desmotubule forms the inner channel wall. The coaxial structure is held in place by filamentous protein tethers that anchor the cell membrane and desmotubule surface. In the following, we denote the outer radius of the pore a, while the mean radius of the desmotubule is $b_0$. Molecular transport occurs in the cytoplasmic sleeve of average thickness $h_0=a-b_0$.

Current models of plasmodesmata stipulate that transport occurs in the gap between two idealized perfectly co-axial and straight cylinders. It is important to realize, however, that this picture is an approximation. Indeed, variations in the structure and alignment of the channel could occur. This provides impetus for reevaluating both basic assumptions. In particular, it is not unreasonable to assume that the desmotubule is sometimes positioned off-center, or, that the thickness of the cytoplasmic sleeve could vary along the length of the pore.

We begin by considering the effect of a radial displacement (Fig. 1e). In the ideal case, the co-axial alignment is perfect and the center of the pore and desmotubule overlap. If they do not line up perfectly, however, we denote the distance between their center coordinates $h_0\delta$, where the non-dimensional parameter $\delta$ varies from 0 to 1. It is clear that the displacement $h_0\delta <h_0=a-b_0$, since the desmotubule cannot penetrate the cell membrane. The desmotubule is also held in place by filamentous protein tethers that connect the membrane and desmotubule surfaces. There are about $n\approx 10$ tethers discernible when counting along the length of the pore (Fig. 1a, [3]). These, presumably, limit the transverse movement of the desmotubule. Assuming that the tethers act like a linear spring actuated by thermal motion, the energy required to displace the desmotubule center a distance $h_0\delta$ is $k (h_0\delta )^2/2$, where k is a spring constant that depends on the stiffness and number of tether proteins. To our knowledge, the spring constant has not been measured directly. However, it can be estimated from $k=3NEI_{\text {tether}}L_{\text {tether}}^{-3}$ if we assume the deformation of the tether proteins follow the deflection of a cantilever beam fixed at one end (e.g., at the plasma membrane) and experiencing a point load at the other (e.g., at the desmotubule) [8, 9]. Here, $N\sim 100$ is the total number of tethers, estimated as $n\sim 10$ along the length of the pore [3] multiplied by $\sim 10$ around the circumference of the pore [10]. $E\sim 10{-}1000$ MPa is Young’s modulus for soft and stiff tethers [11] and $I_{\text {tether}}=\pi d^4/64$ the area moment of inertia, with $d=0.5-1.5$ nm the diameter of the tethers. Finally, $L_{\text {tether}}=2h_0=6$ nm is the length of the tether proteins, taken as the largest possible gap between the desmotubule and plasma membrane. The ratio of the largest possible elastic potential energy to thermal energy varies from $\frac{1}{2}k(\delta h_0)^2/(k_BT)\sim 0.05-375$ (for $\delta =1$), where $k_B$ is the Boltzmann constant and T is temperature. If the tethers are relatively stiff ($\frac{1}{2}k(\delta h_0)^2/(k_BT)\gg 1$) the desmotubule remains fixed in place at the center and the mean radial displacement is $\langle h_0\delta \rangle =0$. In contrast, if the tethers are relatively soft and the desmotubule is free to move ($\frac{1}{2}k(\delta h_0)^2/(k_BT)\ll 1$), the mean displacement is $\langle h_0\delta \rangle =2h_0/3$ (see Appendix A). Notably, more angular positions are accessible when $h_0\delta >0$, hence the mean radial position is not the geometric center of the domain.

Having established the effects that influence the radial desmotubule displacement $h_0\delta$, we now turn to potential variations in transverse dimensions along the length of the pore (Fig. 1f). Our idea is that the radial positions of the inner cytoplasmic channel boundary b(x) could vary along the axial direction x. In some locations, the desmotubule might be wider than the mean $b_0$ and vice versa. We do not know the exact functional form of b(x), but for simplicity, we consider a harmonic function

$$\begin{aligned} b(x) = b_0-h_0\varepsilon \sin \frac{n\pi x}{L}, \end{aligned}$$

(1)

where n is the of number half waves along the length L of a plasmodesma. The amplitude $\varepsilon h_0$ cannot exceed $h_0$ (otherwise the desmotubule penetrates the cell membrane), so the perturbation parameter $\varepsilon <1$. We assume in the following that n is even, because this allows us to compare the relative performance of channels where the mean desmotubule radius $\langle b\rangle =b_0$ is constant. Note that the half wavelength L/n corresponds to the distance between adjacent tether proteins. Electron micrographs indicate $n\approx 10$ [3].

Given the aforementioned properties of the desmotubule shape function in Eq. (1), it is useful to consider how large are the energy fluctuations associated with the amplitude $\varepsilon h_0$ and wave number n. One difference between the uniform shape ($b(x)=b_0$) and perturbed system (Eq. (1)) is that the desmotubule surface area S increases with both $\varepsilon$ and n. The area gained by the harmonic variation is

$$\begin{aligned} \Delta S = 2\pi \int _0^Lb(x)\sqrt{1+b'(x)^2}\,\mathrm {d}x-S_0\approx S_0\left( \frac{\pi }{2}\frac{\varepsilon h_0 n}{L}\right) ^2, \end{aligned}$$

(2)

where $b'=\partial _xb$ and $S_0=2\pi b_0 L$ is the unperturbed desmotubule surface area. The last approximation holds for $n\varepsilon h_0/L\ll 1$. The energy needed to increase the surface area is $\gamma \Delta S$, where $\gamma$ is the energy per unit area of the desmotubule. The parameters $\varepsilon$, $h_0$, and L are constants, so the area $\Delta S$ can only grow by increasing the wave number n. If, however, the shape index n is constrained by the number of tether proteins $n\approx 10$, the relative area gain is at most $\Delta S/S_0\approx (\varepsilon h_0 n/L)^2 = 0.004$, as estimated for the maximum deformation ($\varepsilon =1$). The maximum change in surface energy is thus $0.4\%$, which is within the limits of small thermal fluctuations. In the following, we therefore assume that all states are equally likely.

2.2 Transport properties

Transport across plasmodesmata is facilitated by a combination of molecular diffusion and pressure-driven bulk flow [6]. Current models assume that trafficking occurs across a smooth and perfectly aligned cytoplasmic sleeve. In Sect. 2.1, however, we established two basic modes of plasmodesmata shape perturbations that deviate from the ideal conditions (Fig. 1). In the following sections, we consider the impact of pore shape perturbations on cell-to-cell transport processes.

2.2.1 Diffusion

Fig. 2

Impact of shape fluctuations on diffusive transport. a Current $I/I_0$ plotted as a function of the relative transverse offset $\delta$ (Eq. (4)). For small molecules, transport is not affected (for finite-sized particles, see Fig. 4). b Current $I/I_0$ plotted as a function of the radial fluctuation $\varepsilon$ (Eq. (7)). Transport is strongly reduced when the pore closes ($\varepsilon \rightarrow 1$)

We begin by considering molecular diffusion. In this process, a concentration difference $\Delta c=c_1-c_2$ between two adjacent cells leads to a net migration of molecules from high to low concentrations (Fig. 1). The molecular flux j is proportional to the concentration gradient

$$\begin{aligned} j= -D \partial _x c , \end{aligned}$$

(3)

where D is the diffusion constant. Equation (3) is known as Fick’s law, and typical values of D are $D\approx 10^{-9}{-}10^{-10}$ m$^2$/s for small ions and proteins, respectively, in unbounded space. The magnitude of D is also affected by the radius of the diffusing particle s, relative to the channel dimensions. We return to this phenomena in Sect. 2.3.

A basic problem, which is important for the interpretation of plasmodesmata experiments, is the diffusive current through the straight unperturbed pore. Here, the current is found by integrating Fick’s law across the pore area $A=\pi (a^2-b_0^2)$

$$\begin{aligned} I_0 = DA\frac{\Delta c}{L} = \pi D(a^2-b_0^2) \frac{\Delta c}{L}\approx 2\pi Db_0 h_0\frac{\Delta c}{L}, \end{aligned}$$

(4)

which is proportional to the concentration difference $\Delta c$ and scales linearly with the area A (Fig. 2a). In the last approximation, we have used that the gap height $h_0 = a-b_0$ is reasonably small when compared to a and $b_0$.

In the first mode of perturbation (radial displacement of the desmotubule), the open area A is not affected and the diffusive current $I = I_0$ is therefore not modified. There is an important exception to this rule, which occurs when the size of the diffusing molecule is comparable to the slit width $h_0=a-b_0$. We will deal with this special case in Sect. 2.3.

In the second case (axial variations in the desmotubule radius b(x)), the impact on transport is not negligible. Computing the diffusive current through an axially varying channel, however, is a complex problem, and exact solutions, based on, e.g., Fick–Jacobs theory, are only known in a few specific cases [12]. To get an idea of the impact on transport we will assume that the area A(x) varies slowly, i.e., $|\partial _xb(x)|\ll 1$, which should be representative of plasmodesmata in most configurations. In that case, we can model the pore as a serial connection of short straight segments. The diffusive current for a straight segment can be written as $I=\Delta c/R_D$, where $R_D=\Delta x/(DA)$ is the diffusive resistance a segment of length $\Delta x$ and area A (see Eq. (4)). For two straight segments placed after one another with resistances $R_{D,1}$ and $R_{D,2}$, the current is $I=\Delta c/(R_{D,1}+R_{D,2})$. The total resistance of M straight segments with lengths $\Delta x$ and cross-sectional areas A(x) in series is $R_D=\sum _{i=1}^M R_{D,i}=\sum _{i=1}^M \Delta x/(DA(i\Delta x))$. By letting the length of each segment be sufficiently small the sum can be approximated by an integral and if the total length of the M segments is $M\Delta x=L$, the total resistance $R_D\approx \frac{1}{D}\int _0^L A(x)^{-1}\,\mathrm {d}x$. Fick’s law (Eq. (3)) then leads to

$$\begin{aligned} I=D\Delta c\left( \int _0^L \dfrac{1}{A(x)}\,\mathrm {d}x\right) ^{-1}. \end{aligned}$$

(5)

The same result follows directly from Fick’s law by writing $I=-\int _A D\partial _x c\, \mathrm {d}A\approx -DA(x)\partial _x c$, because the concentration gradient does not vary substantially over the area A. The local cross-sectional area of the plasmodesma channel is $A(x)=\pi (a^2-b(x)^2)\approx 2\pi b_0h(x)$, assuming once again that we are in the small-gap limit. For a harmonically varying desmotubule with relative amplitude $\varepsilon$ and wave number n, the height h(x) follows from Eq. (1)

$$\begin{aligned} h(x)=a-b(x)=h_0\left[ 1+\varepsilon \sin \left( \frac{n\pi x}{L}\right) \right] . \end{aligned}$$

(6)

From Eq. (5), the diffusive current is

$$\begin{aligned} I&=2\pi bh_0D\frac{\Delta c}{L}\left( \frac{1}{n\pi }\int _0^{n\pi }\frac{1}{1+\varepsilon \sin q}\,\mathrm {d}q\right) ^{-1}=I_0 \sqrt{1-\varepsilon ^2} \end{aligned}$$

(7)

where we have introduced the short-hand notation $q=n\pi x/L$. The expression in Eq. (7) provides an estimate of the current I (Fig. 2b) for a specific magnitude of the desmotubule amplitude $\varepsilon h_0$. We note that it decreases as the occlusion increases ($\varepsilon \rightarrow 1$), consistent with experiments on single-particle diffusion in microchannels [13]. It is likely, however, that the level of occlusion is large ($\varepsilon =1$) in some pores while it is small ($\varepsilon =0$) in others. Recalling that the relative change in surface energy related to variations in gap size is small, we assume that all $\varepsilon$ states are equally likely. Averaging Eq. (7) over $0\le \varepsilon <1$ we find

$$\begin{aligned} \langle I \rangle = \frac{\pi }{4}I_0. \end{aligned}$$

(8)

In conclusion, perturbations in the cytoplasmic sleeve width along the length of the pore lead to an approximately 20% reduction in the diffusion current.

2.2.2 Advection

Having established the effects of pore shape on diffusive transport, we now continue our discussion by focusing on bulk fluid flow. We imagine a situation in which a pressure difference $\Delta p=p_1-p_2$ exists between two neighboring cells (Fig. 1). The intracellular pressure p exerted by fluid in a cell presses the membrane against the cell wall. This turgor pressure is what makes living plant tissue rigid. Loss of turgor, resulting from the loss of water from plant cells, causes flowers and leaves to wilt. The hydrostatic pressure p that develops in a cell depends on the chemical potential in the cell, and in the surrounding tissue. Close to equilibrium, and in the case of negligible external pressure and solute concentration, we can write the turgor pressure as $p=\varPi$, where $\varPi$ is the osmotic potential of the cellular fluid. For reasonably dilute solutions the osmotic pressure is given by the van’t Hoff relation $\varPi \approx RT{\tilde{c}}$, where R is the gas constant, T is the absolute temperature and $\tilde{c}$ is a molar concentration [14]. The concentration ${\tilde{c}}$ is the sum of all solute contributions. Plant cells contain a myriad of different molecules, from dilute hormones ($1\,\upmu$M) to concentrated electrolytes (100 mM) and sugars (100 mM) [15, 16]. This leads to a typical turgor pressure of $p\approx 1$ MPa. Note that the hormone concentration difference $\Delta c = c_1-c_2\sim 1\,\upmu \text {M}$ is too small to create a noticeable pressure imbalance and therefore the hormone synthesis and fluid flow processes are probably not directly coupled. However, a sugar or ion concentration imbalance created by active membrane pumps can generate a cell-to-cell pressure difference $\Delta p \approx RT({\tilde{c}}_1 - {\tilde{c}}_2)$ which would compel fluid to flow through the plasmodesmata pores.

The pressure imbalance between neighboring cells forces the cytoplasmic fluid to flow through the plasmodesmata pores, and we will now quantify how much material is transported by this process. If the concentration of the signal molecules differs between the two cells by an amount $\Delta c$, then the net current of particles through each channel is $I = Q\Delta c$, where Q is the volumetric flow rate, which depends on the pressure drop $\Delta p$, the viscosity of the cellular fluid $\eta$, and on the channel shape.

Pressure-driven fluid flow through plasmodesmata can be described by the Navier–Stokes and continuity equations, which in the steady-state and low-Reynolds-number limits are

$$\begin{aligned} \eta \nabla ^2\varvec{v}-\varvec{\nabla }p=\varvec{0}, \quad \text {and}\quad \varvec{\nabla }\cdot \varvec{v}=0. \end{aligned}$$

(9)

Here, $\varvec{v}$ is the velocity field, and the flow rate $Q=\int \varvec{v} \cdot \varvec{n} \,\mathrm {d}A$ is found by integration across the open pore surface area perpendicular to the flow, where $\varvec{n}$ is a unit normal vector. We note that the use of Eq. (9) to describe the flow through relatively small gaps, i.e., for $\varepsilon \rightarrow 1$, is an approximation based on the use of a continuum description, i.e., that length and time scales are much larger than those associated with molecular processes. The assumptions behind it are, however, the same used for Fick’s description of diffusion and for the diffusion constant D found through the Stokes–Einstein equation. Including slip in the model could reduce the drag [17], however, the viscous friction in the entrance region would then dominate [18]. For a straight and perfectly aligned pore, and with no-slip conditions ($\varvec{v}=\varvec{0}$) on the channel boundaries, the pressure-drop versus flow-rate relationship is [19]

$$\begin{aligned} Q=\dfrac{\Delta p\pi a^4}{8\eta L}\left[ 1-\left( \dfrac{b_0}{a}\right) ^2+\dfrac{((b_0/a)^2-1)^2}{\ln (b_0/a)}\right] . \end{aligned}$$

(10)

We notice two features of Eq. (10). First, when the desmotubule is narrow, the ratio $b_0/a\ll 1$, we recover the flow-rate relationship for a cylindrical pipe $Q = \pi a^4 \Delta p/(8\eta L)$. In contrast, when the gap $h_0=a-b_0$ is relatively small, i.e., $h_0\ll b_0$, the flow rate is

$$\begin{aligned} Q_0 = \frac{2\pi b_0 h_0^3\Delta p}{12\eta L}. \end{aligned}$$

(11)

This limit corresponds to pressure-driven flow in a shallow channel of width $2\pi b_0$ and height $h_0$, with negligible effects of channel curvature. This is equivalent to the lubrication limit, where the local axial velocity field $v_x$ is a parabolic function of the transverse coordinate y and it is proportional to the axial pressure gradient

$$\begin{aligned} v_x(y) = -\frac{1}{2\eta }(yh-y^2)\partial _x p. \end{aligned}$$

(12)

Note that $v_x$ fulfills the no-slip boundary conditions $v_x=0$ on the channel boundaries at $y=0$ and $y=h$.

Fig. 3

Impact of shape fluctuations on bulk flow. a Flow rate $Q/Q_0$ plotted as a function of the relative transverse offset $\delta$ (Eq. (15)). Transport is enhanced as the channel widens. b Flow rate $Q/Q_0$ plotted as a function of the radial fluctuation $\varepsilon$ (Eq. (16)). Transport is strongly reduced when the pore closes ($\varepsilon \rightarrow 1$)

It is straightforward to extend the ideal flow-rate equation (11) to other cases using the lubrication approximation in Eq. (12). Following the outline in Sect. 2.2.1, we begin by considering the effects of an off-center desmotubule. We first notice that the gap height can be expressed as function of the azimuthal angle $\theta$:

$$\begin{aligned} h(\theta )=h_0(1-\delta \cos \theta ), \end{aligned}$$

(13)

where we remind ourselves that $h_0\delta$ is the distance the inner cylinder is displaced from the center of the outer cylinder and that the gap $h_0$ is smaller than the desmotubule radius $b_0$. The angle $\theta$ varies as $0\le \theta \le 2\pi$. The flow rate is found by integrating the velocity distribution across the pore

$$\begin{aligned} Q&=\int _0^{2\pi }\int _0^h b_0v_x\mathrm {d}y \mathrm {d}\theta =-\dfrac{1}{12\eta }2\pi b_0h_0^3\left[ 1+\dfrac{3}{2}\delta ^2\right] \dfrac{\partial p}{\partial x}, \end{aligned}$$

(14)

corresponding to the pressure-drop versus flow-rate relationship

$$\begin{aligned} Q = Q_0(\Delta p)\left[ 1+\dfrac{3}{2}\delta ^2\right] , \end{aligned}$$

(15)

where $Q_0$ is the unperturbed current (Eq. (11)), see Fig. 3a. Recalling that the displacement $h_0\delta$ is limited by the initial gap height $h_0$ (i.e., $\delta <1$), we observe that the flow rate can at most increase by $150\%$ ($Q=5Q_0/2$), which occurs when $\delta = 1$ and the desmotubule is in contact with the cell membrane. If the desmotubule is equally likely to occupy all positions within the domain, the mean square displacement is $\langle \delta ^2 \rangle =1/2$ and the flow is enhanced by $75\%$ to $Q=7Q_0/4$. This is less than the theoretical maximum ($Q=5Q_0/2$), but still an appreciable increase when compared to the base flow rate in Eq. (11).

We continue our analysis of bulk flow by considering the effects of axial variations in the desmotubule shape. Using the sinusoidal channel height profile h(x) (see Eq. (6)) in the lubrication equation (12) leads to the flow-rate versus pressure-drop relation

$$\begin{aligned} Q=Q_0\left( \frac{1}{n\pi }\int _0^{n\pi }\frac{1}{(1+\varepsilon \sin q)^3}\,\mathrm {d}q\right) ^{-1} {=Q_0 \dfrac{2(1-\varepsilon ^2)^{5/2}}{2+\varepsilon ^2}}, \end{aligned}$$

(16)

see Fig. 3b. (We note that the last equality holds for n even.) The flow rate averaged over all accessible states ($0\le \varepsilon <1$) is ${\langle Q \rangle }/{Q_0}=3\pi (12\sqrt{6}-29)/8 \approx 0.5,$ so on average, fluctuations in the desmotubule radius thus leads to a $50\%$ reduction in pressure-driven flow capacity.

In summary, our analysis reveals that pressure-driven flow is enhanced by transverse displacement of the desmotubule, which creates larger channel paths for all x, but is reduced as a consequence of radial shape fluctuations, which have repeated axial regions of high resistance (small gap size).

2.2.3 Relative importance of advection and diffusion

We end this section by providing a brief discussion of the relative importance of advection and diffusion. To quantify their proportionate magnitude, we introduce the Peclet number Pe as the ratio of the molecular current facilitated by bulk flow $\Delta c Q_0$ (Eq. (11)) to the molecular diffusion current $I_0$ (Eq. (4))

$$\begin{aligned} \mathrm{Pe} = \frac{\text {advective transport rate}}{\text {diffusive transport rate}}=\frac{\Delta c Q_0}{I_0} = \frac{\Delta p h_0^2}{12\eta D }. \end{aligned}$$

(17)

Advection dominates when the Peclet number is large, while diffusion is most important when it is relatively small. It is, however, difficult to make broad statements about the precise magnitude of the Peclet number due to the large number of parameters that enter into Eq. (17). We therefore choose to consider two limiting cases. First, we can think about an isobaric tissue where cell-to-cell pressure differences are negligible, i.e., $\Delta p=0$. Here, Pe = 0 and diffusion dominates. To estimate the upper limit to the Peclet number Pe, we note again that the turgor pressure in a plant cell is around $p\approx 1$ MPa. However, even slender plant tissues rarely comprise fewer than ten cells along the transverse axis, hence an estimate of the greatest potential cell-to-cell pressure difference is of the order $\Delta p \approx 10^5$ Pa. This leads to Pe = 0.75, i.e., an approximately even distribution between diffusive and advective contributions to transport. These estimates nevertheless lead to the conclusion that in most cases, molecular diffusion provides the greatest contribution to transport. Consideration of the coupled diffusion–advection problem leads to a similar conclusion, see Appendix B. We note, however, that Eq. (17) is strongly dependent on geometry. In wider or tapering pores, such as the funnel plasmodesmata present in the phloem unloading zone, the contribution from advection is substantially larger [20].

2.3 The impact of shape fluctuations on selectivity

We end our analysis of transport across shape-perturbed nanochannels by considering the effects of molecular size. Plasmodesmata carry many different compounds; from small water molecules (diameter 0.3 nm) and ions (Stokes radius 0.2 nm), sugars (0.4–0.6 nm) [21], signaling molecules (e.g., auxin $\sim 0.5$ nm), to different fluorescent particles used in experiments, e.g., carboxyfluorescein diacetate (0.6 nm) and GFP (2.8 nm) [3]. Larger compounds, e.g., F-Dextran (3.2 nm) do not pass through plasmodesmata [22], but the exact pore size is still under debate [23]. It was recently reported that molecules with a radius s comparable to the cytoplasmic sleeve half-width $h_0/2$ are able to traverse some plasmodesmata pores [3]. This is surprising, since particle–wall interactions are known to hinder transport significantly [24]: both entropic [13] and hydrodynamic [24] effects hinder transport in axially varying channels when the radius of the diffusing particle is comparable to the smallest gap in the channel $h_0(1-\varepsilon )$. Interestingly, it was recently pointed out that temporal fluctuations in the axial shape can shuttle relatively large molecules across nanopores [25]. It remains unknown, however, how perturbations to the radial position of the desmotubule may impact transport. This question is addressed below.

We envision a situation in which a molecule of radius s is approaching the inlet of a perfectly aligned plasmodesma. If the width of the cytoplasmic sleeve $h_0 = a-b_0$ is larger than the particle diameter 2s, the particle can enter the pore. In contrast, if $2s>h_0$, the molecule is unable to pass. Because the diffusive current I is proportional to the open area A (Eq. (4)) we can, to a first approximation, quantify the probability of transport by considering the area available to a particle of radius s. We denote this area $A_s$. If the molecule is relatively small the entire pore is open and $A_s=A_0=\pi (a^2-b_0^2)$. In contrast, if the particle is larger than the slit width $(2s>h_0)$, the open area $A_s=0$. In the intermediate regime, the open area varies between these two extremes: $0<A_s<A_0$.

If we now allow the desmotubule to be displaced radially by the distance $h_0\delta$, the slit will shrink in some places, and expand in others. We write the total open area $A_s$ as a function of the relative displacement $\delta$ from the center as

$$\begin{aligned} A_s(\delta )&={\left\{ \begin{array}{ll} 0 &{} 1+\delta<2s/h_0 \\ \pi (\tilde{a}^2-\tilde{b}^2) &{} 0<\delta< 1-2s/h_0 \\ \pi \tilde{a}^2-A_{\text {lens}} &{} 1-2s/h_0<\delta <1 \end{array}\right. } \end{aligned}$$

(18)

where $\tilde{a}=a-s$ and $\tilde{b}=b_0+s$ are the reduced pore and desmotubule radii that take into account the inaccessible region of width s created by particle–wall interactions. The first region describes the case where there is no open area for the particle to pass through. This happens when the particle diameter, 2s, is larger than the widest possible gap for a pore displaced a distance $h_0\delta$, $h_0(1+\delta )$. The second region is where the open area remains constant as the desmotubule is displaced radially, i.e., when the gray areas in Fig. 4 do not overlap. The third region describes the open area when the gray areas do overlap and the open area depends on the radial displacement of the desmotubule $h_0\delta$. The area of the lens-shaped region (Fig. 4) is

$$\begin{aligned} A_{\text {lens}}&=\tilde{b}^2\arccos \left( \dfrac{-\tilde{a}^2+\tilde{b}^2+(h_0\delta )^2}{2h_0\delta \tilde{b}}\right) +\tilde{a}^2\arccos \left( \dfrac{\tilde{a}^2-\tilde{b}^2+(h_0\delta )^2}{2h_0\delta \tilde{a}}\right) \nonumber \\&\quad -\dfrac{1}{2}\sqrt{(\tilde{a}+\tilde{b}-h_0\delta )(h_0\delta -\tilde{a}+\tilde{b})(\tilde{a}-\tilde{b}+h_0\delta )(\tilde{a}+\tilde{b}+h_0\delta )}. \end{aligned}$$

(19)

Transverse displacement dramatically enhances the potential transport capacity for particle sizes comparable to the cytoplasmic sleeve width, as displayed in Fig. 4. For instance, the available area for molecules that take up $2s/h_0=0.9$ of the space is nearly quadrupled, while for $2s/h_0=0.5$ it increases by approximately 20%.

Fig. 4

Impact of shape fluctuations on selectivity. a Accessible area $A_s/A_0$ plotted as a function of relative offset $\delta$ for molecules of radius s (Eq. (18)). The open area $A_s$ increases with displacement $h_0\delta$. The effect is largest for particles with strongly restricted access to the unperturbed pore (i.e., $2s\approx h_0$). For instance, for $2s/h_0=0.9$, the relative available area increases almost fourfold (from 0.1 to 0.37) as $\delta$ varies from 0 to 1 and the desmotubule is shifted toward the channel periphery. The insets (b–d) visually illustrate the available area (white) to the center coordinate (black dot) of a particle of radius s (green circle). b For $\frac{2s}{h_0}=0$, the available area does not change as $\delta$ varies from 0 to 1. c For ${2s}/{h_0}=0.5$, the available area varies from $50\%$ to approximately $61\%$ of the full area $A_0$ as $\delta$ varies from 0 to 1. d For ${2s}/{h_0}=1$, the available area varies from 0 to approximately $32\%$ of the full area $A_0$ as $\delta$ varies from 0 to 1. Note that $A_s(\delta )=A_0$ when $\delta =0$ and $s=0$. The values from Table 1 were used in the plot, however, for small values of the unperturbed gap, $h_0\ll b_0$, the plot is almost independent of the values for a and $b_0$

3 Discussion and conclusion

Plasmodesmata nanopores, which are small channels linking neighboring cells in plants, enable exchange of nutrients and signaling molecules. Current models assume that the annular pore geometry is perfectly concentric and static [7, 26]. However, recent experiments hint at substantial variations in the conduit geometry [3]. In this study, we therefore considered the effects of shape perturbations on the diffusive and pressure-driven transport through plasmodesmata pores. We restricted our analysis to two classes of perturbations: (1) radial displacement of the central desmotubule rod and (2) harmonic variations in the cytoplasmic sleeve width along the length of the pore. These idealized cases do not necessarily represent the true pore shape, but they allow us to ascertain the approximate impact on the signal transduction capacity.

Our results indicate that an off-center desmotubule increases the rate of pressure-driven transport (Fig. 3a). Advection is increased by up to a factor of 2.5 compared to the flow rate through the unperturbed geometry, with the largest rate occurring when the desmotubule is in contact with the cell wall (Fig. 3a, Eq. (15)). The diffusive current is unchanged for particles much smaller than the cytoplasmic sleeve width (Fig. 2a). However, the diffusive current is dramatically enhanced if the size of the diffusing particles is comparable to the gap width. Surprisingly, our modeling suggests that particles larger than the mean cytoplasmic sleeve width are able to migrate for off-center desmotubules (Fig. 4a, Eq. (18)). In contrast, we find that harmonic variations in the cytoplasmic sleeve width along the length of the pore lead to a reduction in both diffusion (Fig. 2b, Eq. (7)) and advection (Fig. 3b, Eq. (16)). This effect becomes greater when the perturbation amplitude increases. On average, diffusion is reduced by 20% while advection is 50% lower.

The shape perturbations discussed in this paper are basic geometric effects which have surprising impact on both advection and diffusion. As such, they could help explain the observed transport of molecules nominally larger than the slit width by Nicolas et al. [3]. Even so, we note that there are several other ways in which the pore morphology could vary with potential impact on signal transport. For instance, it is possible that dynamic effects, such as wiggling [25] or peristaltic pumping [27], are involved in transport. Also, in large pores, it is possible that transport is enhanced by Taylor–Aris dispersion [28, 29]. However, more detailed knowledge of plasmodesmata geometry and temporal effects is needed to assess their significance. This points to the need for new experimental and theoretical methods being applied to intercellular transport in plants.

Appendices

Thermal model of desmotubule displacement

This appendix outlines the thermal theory of transverse desmotubule displacement. As described in Sect. 2.1, the desmotubule is anchored to the cell membrane by tether proteins that limit the transverse movement of the desmotubule. Assuming that the tethers act like a linear spring, the energy required to displace the desmotubule center a distance $h_0\delta$ is $k (h_0\delta )^2/2$. Here, k is a spring constant which depends on the stiffness and number of tether proteins. If the tethers are relatively stiff, the desmotubule remains fixed in place at the center and the mean radial displacement is $\langle h_0\delta \rangle =0$. In contrast, if the tethers are relatively soft and the desmotubule is free to move, the mean displacement is $\langle \delta \rangle =2/3$ because more angular positions are accessible when $\delta >0$, hence the mean radial position is not the geometric center of the domain.

In the intermediate energy regime, we can determine the probability $P(\delta )$ of observing the displacement $h_0\delta$ by considering the Boltzmann distribution:

$$\begin{aligned} P(\delta ) =\frac{2\pi h_0\delta \exp \left( -\frac{k(h_0\delta )^2}{2k_BT}\right) }{\int _0^{h_0}2\pi h_0\delta \exp \left( -\frac{k(h_0\delta )^2}{2k_BT}\right) \,\mathrm d(h_0\delta )}, \end{aligned}$$

(20)

where T is temperature and $k_B$ is the Boltzmann constant. The factor $2\pi h_0\delta$ accounts for the increasing number of angular positions available as the radial displacement $h_0\delta$ grows. The mean relative displacement is

$$\begin{aligned} \langle \delta \rangle&=h_0\int _0^{1} \delta P(\delta )\,\mathrm d\delta =\dfrac{1}{1-e^{-\alpha }}\left( \dfrac{\sqrt{\pi }}{2}\dfrac{1}{\sqrt{\alpha }}{{\,\mathrm{erf}\,}}(\sqrt{\alpha })-e^{-\alpha }\right) , \end{aligned}$$

(21)

where

$$\begin{aligned} \alpha = \frac{\frac{1}{2}kh_0^2}{k_BT}, \end{aligned}$$

(22)

is the ratio of potential elastic to thermal energy and ${{\,\mathrm{erf}\,}}()$ is the error function. When $\alpha$ is large, the desmotubule stays is place ($\langle \delta \rangle =0$) because the thermal energy is too small to deform the relatively stiff tether proteins. In contrast, when $\alpha$ is small, the comparatively soft tethers are unable to resist molecular perturbations. In this limit, the mean radial displacement is $\langle \delta \rangle =2/3$ and $\langle \delta ^2 \rangle =1/2$.

Coupled advection and diffusion

So far, we have considered the diffusive and advective currents separately. In this appendix, we look at how they may superimpose. Our goal is to compute the relative magnitude of the diffusive and advective currents. In doing so, we consider a simplified version of a plasmodesmata: a flat channel of length L in the x-direction and height h, with a velocity u in the x-direction and a concentration profile $c=c(x,t)$ with $c(0)=\Delta c$ and $c(L)=0$ at the upper and lower cell. (Here, t denotes the time.)

Before proceeding with a detailed calculation of the concentration profile in the channel, we will briefly justify why a flat channel can help us understand the impact of geometry in a complex PD. Our previous results have clearly demonstrated that introducing harmonic variations in the cytoplasmic sleeve width along the length of the pore decreases the current. This happens because the resistance to both flow and diffusion increases. The largest contribution to the resistance occurs near the point with the smallest gap. Instead of looking at the entire axially varying channel, we therefore consider a flat channel, where the height of the channel corresponds to the height of the smallest gap in the harmonically varying channel. On the other hand, having an off-center desmotubule increases the current through the pore (except for the case of diffusion of very small particles, where the current remains the same), and the resistance thus decreases. As the desmotubule is displaced off-center, most of the transport occurs at the side of the channel with the largest gap between the cell membrane and desmotubule. In this case, we therefore consider a flat channel with a height that corresponds to the largest gap between the cell membrane and desmotubule.

Fig. 5

The ratio of the diffusive to advective currents as a function of Peclet number, Pe (Eq. (29)). The biological range, shown in orange, extends from $\text {Pe}=0$ to $\text {Pe}=0.75$ (see Eq. (17))

To find the concentration profile in the channel, and thus the current across it, we consider the coupled diffusion–advection equation

$$\begin{aligned} \partial _t c+ u\partial _x c&=D\partial _x^2c \end{aligned}$$

(23)

Introducing the dimensionless variables $\tilde{T}=tD/L^2$, $C=c/\Delta c$ and $X=x/L$, it can be rewritten as

$$\begin{aligned} \partial _{\tilde{T}} C + \text {Pe}\,\partial _X C=\partial _X^2 C, \end{aligned}$$

(24)

where we have introduced the Peclet number as $\text {Pe}=uL/D$, with the boundary conditions $C(0)=1$ and $C(1)=0$. (We remind the reader that u is the mean velocity.) In the case of steady-state transport, the equation reduces to

$$\begin{aligned} \partial _X C=\dfrac{1}{\text {Pe}}\partial _X^2 C, \end{aligned}$$

(25)

which has the solution

$$\begin{aligned} C(X)=\dfrac{e^{\text {Pe}}-e^{\text {Pe}X}}{e^{\text {Pe}}-1}. \end{aligned}$$

(26)

The diffusive and advective fluxes leaving the upper cell are

$$\begin{aligned} j_{\text {diff}}&=-D\partial _x c(x)\mid _{x=0}=\dfrac{\Delta cD}{L}\dfrac{\text {Pe}}{e^{\text {Pe}}-1}, \quad \text {and} \end{aligned}$$

(27)

$$\begin{aligned} j_{\text {adv}}&=u\Delta c. \end{aligned}$$

(28)

Lastly, the ratio of the diffusive to advective current is found as

$$\begin{aligned} \dfrac{I_{\text {diff}}}{I_{\text {adv}}}=\dfrac{1}{e^{\text {Pe}}-1}, \end{aligned}$$

(29)

which only depends on the Peclet number. From Eq. (17), the Peclet numbers relevant for the biological system are between $\text {Pe}=0$ and $\text {Pe}=0.75$, shown in orange in Fig. 5. This corresponds to either the diffusive current being larger than the advective current ($\text {Pe}\rightarrow 0$) or the two being more or less equally important ($I_{\text {diff}}/I_{\text {adv}}=1$ for $\text {Pe}\approx 0.7$).