Appendix (Discretization)
There are two types of discretization in the VDQFEM method. According to Fig. 1, these discretizations can be described as follows: the domain under study is first discretized into a number of geometrical elements and then is mapped into the natural space with interpolation of position vector of each element using shape functions and corresponding nodal points (circular points). Afterwards, in order to perform the numerical differentiation and integration processes of VDQ method (which is specific to this technique), this space is discretized using the distribution of Chebyshev points. Two important control parameters for discretization and convergence can be thus considered in this approach: (1) finite element meshing and (2) distribution of nodal points of each element.
In this Appendix, vector–matrix relations are discretized on the domain of an arbitrary element. The discretization process is performed by means of the operator \(\left[\kern-0.15em\left[ {{\blacksquare }_{1} } \right]\kern-0.15em\right]_{{{\blacksquare }_{2} }}\) which discretizes the parameter ■1 on the space ■2. The concepts of discretization can be found in [26, 32, 33]. The following spaces and parameters are also considered for discretization of relations:
$$ \left\{ {\begin{array}{*{20}l} {{\mathfrak{A}}_{i} - {\text{space}}\left( {\text{thickness direction}} \right)} \hfill & {{\text{in }}X_{i} {\text{ direction}}} \hfill \\ {{\mathfrak{B}} - {\text{space }}\left( {\text{middle plane}} \right)} \hfill & {{\text{in }}X_{1} X_{2} {\text{ direction}}} \hfill \\ {{\mathfrak{C}} - {\text{space }}\left( {3{\text{D domain}}} \right)} \hfill & {{\text{in }}X_{1} X_{2} X_{3} {\text{ direction}}} \hfill \\ \end{array} } \right. $$
where
$$ \left\{ {\begin{array}{*{20}l} {n_{\xi } } \hfill & {\text{number of computational grid points along each natural direction in each element}} \hfill \\ {n = n_{\xi }^{2} } \hfill & {\text{number of total computational grid points in each element}} \hfill \\ {n_{e} } \hfill & {\text{number of elements}} \hfill \\ {n_{h} } \hfill & {\text{number of computational grid points along thickness direction}} \hfill \\ \end{array} } \right. $$
1.1 Material properties
According to the shifted Chebyshev–Gauss–Lobatto grid points on \(\left[ {a,b} \right]\), given by
$$ X = a + \frac{b - a}{2}\left( {1 - \cos \frac{i - 1}{{n - 1}}\pi } \right), i = 1,2, \ldots ,m $$
(67)
the discretized forms of \(X_{i}\) in \({\mathfrak{A}}_{i}\) and \({\mathfrak{B}}\) space become
$$ {\mathbf{X}}_{1}^{{{\mathfrak{A}}_{1} }} = \left[\kern-0.15em\left[ {X_{1} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{1} }} = \left[ {\frac{{L_{1} }}{2} + \frac{L}{2}\left( {1 - \cos \frac{i - 1}{{n_{\xi } - 1}}\pi } \right)} \right], i = 1,2, \ldots ,n_{\xi } $$
(68)
$$ {\mathbf{X}}_{2}^{{{\mathfrak{A}}_{2} }} = \left[\kern-0.15em\left[ {X_{2} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{2} }} = \left[ {\frac{{\theta_{0} }}{2}\left( {1 - \cos \frac{i - 1}{{n_{\xi } - 1}}\pi } \right)} \right], i = 1,2, \ldots ,n_{\xi } $$
(69)
$$ {\mathbf{X}}_{3}^{{{\mathfrak{A}}_{3} }} = \left[\kern-0.15em\left[ {X_{3} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ { - \frac{h}{2} - \frac{h}{2}\left( {1 - \cos \frac{i - 1}{{n_{h} - 1}}\pi } \right)} \right], i = 1,2, \ldots ,n_{h} $$
(70)
$$ {\mathbf{X}}_{\mathbf{1}}^{{\mathfrak{B}}} = \left[\kern-0.15em\left[ {X_{1} } \right]\kern-0.15em\right]_{{\mathfrak{B}}} = \mathbf{1}_{{n_{\xi } *1}} { \circledast }{\mathbf{X}}_{\mathbf{1}}^{{{\mathfrak{A}}_{1} }} , $$
(71)
$$ {\mathbf{X}}_{\mathbf{2}}^{{\mathfrak{B}}} = \left[\kern-0.15em\left[ {X_{2} } \right]\kern-0.15em\right]_{{\mathfrak{B}}} = \mathbf{1}_{{n_{\xi } *1}} { \circledast }{\mathbf{X}}_{\mathbf{2}}^{{{\mathfrak{A}}_{2} }} , $$
(72)
The discretized form of Eq. (78) can be thus written as
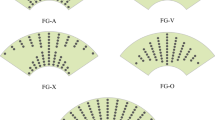
$$ {\mathbb{V}}_{GPL} = \left[\kern-0.15em\left[ {V_{GPL} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left\{ {\begin{array}{*{20}l} {V_{GPL}^{*} \mathbf{1}_{{n_{h} \times 1}} } \hfill & {{\text{UD}}} \hfill \\ {2\left( {1 - \left( {2\left| {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } \right|/h} \right)} \right)V_{GPL}^{*} } \hfill & {{\text{FGO}}} \hfill \\ {\left( {1 - \left( {2{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} /h} \right)} \right)V_{GPL}^{*} } \hfill & {{\text{FGO}}} \hfill \\ {4\left( {\left| {{\mathbf{X}}_{\mathbf{3}}^{{\mathfrak{A}}} } \right|/h} \right)V_{GPL}^{*} } \hfill & {{\text{FGX}}} \hfill \\ \end{array} } \right., $$
(73)
in which \(\left[\kern-0.15em\left[ {\blacksquare } \right]\kern-0.15em\right]\) and all the double-struck letters indicate the discretized form of corresponding parameters. Moreover, \(1_{{n_{h} \times 1}}\) denotes an all-ones \(n_{h} \times 1\) vector. The discretized form of Eqs. (70), (75) and (76) are written as
$$ {\mathbb{E}}_{C} = \left[\kern-0.15em\left[ {E_{C} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \frac{3}{8}\left( {1 + \xi_{L} \eta_{L} {\mathbb{V}}_{GPL} } \right) \circ \left( {1 - \eta_{L} {\mathbb{V}}_{GPL} } \right)^{ \circ - 1} E_{M} + \frac{5}{8}\left( {1 + \xi_{W} \eta_{W} {\mathbb{V}}_{GPL} } \right) \circ \left( {1 - \eta_{W} {\mathbb{V}}_{GPL} } \right)^{ \circ - 1} E_{M} , $$
(74)
$$ \overline{\overline{\rho }}_{c} = \left[\kern-0.15em\left[ {\rho_{c} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \rho_{M} + \left( {\rho_{GPL} - \rho_{M} } \right){\mathbb{V}}_{GPL} , $$
(75)
$$ \overline{\overline{\nu }}_{c} = \left[\kern-0.15em\left[ {\nu_{c} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \nu_{M} + \left( {\nu_{GPL} - \nu_{M} } \right){\mathbb{V}}_{GPL} , $$
(76)
Also, \({\mathbf{A}}^{{ \circ {\text{n}}}}\) shows that each element of matrix \({\mathbf{A}}\) is raised to the \(n\)-th power, i.e., \({\mathbf{A}}^{{ \circ {\text{n}}}} = \underbrace {{{\mathbf{A}} \circ {\mathbf{A}} \circ \ldots \circ {\mathbf{A}}}}_{n}\).
1.2 Displacement field
Additionally, the discretized form of Eq. (83) is presented as
$$ {\mathbb{P}}_{0} = \left[\kern-0.15em\left[ {{\mathbf{P}}_{0} } \right]\kern-0.15em\right]_{{\mathfrak{A}}} = \left[ {\begin{array}{*{20}c} {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0}
&\quad {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{\mathbf{3}} }} } &\quad \mathbf{0} &\quad
{c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } &\quad \mathbf{0} \\ \mathbf{0}
&\quad {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad
{{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } &\quad \mathbf{0} &\quad
{c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } \\ \mathbf{0} &\quad \mathbf{0}
&\quad {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\
\end{array} } \right],
$$
(77)
The each-block-diagonal form of Eq. (77) can be defined as follows:
$$ \mathop{{\mathbb{P}}_{0}}\limits^{\smile} = \left\langle {\left[\kern-0.15em\left[ {{\mathbf{P}}_{0} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} } \right\rangle_{{\mathbb{b}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \langle{{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} }\rangle &\quad \mathbf{0} &\quad \langle{c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}}}\rangle &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \langle{{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }}}\rangle &\quad \mathbf{0} &\quad \langle{c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}}}\rangle \\ \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\ \end{array} } \right],
$$
(78)
in which \(\left\langle {\blacksquare } \right\rangle_{{\mathbb{b}}}\) and \( \mathop{\blacksquare}\limits^{\smile} \) denote each-block-diagonal operator and \(\left\langle {\blacksquare } \right\rangle\) is the vector-diagonal operator which generates diagonal matrix from a given vector. Also, the discretized form of \({\mathbf{E}}_{0}\) is introduced as
$$ {\mathbb{E}}_{0} = \left[\kern-0.15em\left[ {{\mathbf{E}}_{0} } \right]\kern-0.15em\right]_{{\mathfrak{B}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\ 0 &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{1} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} \\ 0 &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad 1 &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} /s\user2{ }} \\ \end{array} } \right], $$
(79)
where
$$ {\mathbf{X}}_{\mathbf{1}}^{*} = \left\langle\left[\kern-0.15em\left[\frac{1}{{X_{1}}}\right]\kern-0.15em\right]_{{\mathfrak{B}}}\right\rangle = \left\langle{\mathbf{X}}_{\mathbf{1}}^{{\mathfrak{B} \circ - 1}}\right\rangle $$
(80)
Also, \({ \circledast }\) stands for the Kronecker product. It should be noted that \({\mathbf{I}}_{n}\) is an \(n \times n\) identity matrix. Furthermore, \(\left\langle {\mathbb{B}} \right\rangle_{{\mathbb{b}}}\) denotes each block diagonal of block matrix \({\mathbb{B}}\).
1.3 Unknown vectors
In addition, the discretized form of Eq. (84) is given by
$$ {\mathbb{d}} = \left[\kern-0.15em\left[{\mathbf{d}}\right]\kern-0.15em\right]_{{\mathfrak{B}}} = \left[ {\begin{array}{*{20}c} {{\mathbb{u}}^{{\text{T}}} } &\quad {{\mathbb{v}}^{{\text{T}}} } &\quad {{\mathbb{w}}^{{\text{T}}} } &\quad {\overline{\overline{\psi }}^{{\text{T}}} } &\quad {\overline{\overline{\phi }}^{{\text{T}}} } &\quad {\overline{\overline{\chi }}^{{\text{T}}} } &\quad {\overline{\overline{\gamma }}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} ,
$$
(81)
1.4 Strain tensor
The discretized form of matrices introduced in Eqs. (26) and (27) is given by
$$ \begin{aligned} {\mathbb{P}}_{1} & = \left[\kern-0.15em\left[ {{\mathbf{P}}_{1} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } \\ \end{array} } \right], \\ {\mathbb{P}}_{2} &\quad = \left[\kern-0.15em\left[ {{\mathbf{P}}_{2} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad {3c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 2}} } &\quad \mathbf{0} \\ \mathbf{0} &\quad {\mathbf{1}_{{n_{h} *1}} } &\quad \mathbf{0} &\quad {3c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 2}} } \\ \end{array} } \right], \\ {\mathbb{P}} &\quad = \left[\kern-0.15em\left[ {\mathbf{P}} \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {{\mathbb{P}}_{1} } &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\mathbb{P}}_{2} } \\ \end{array} } \right] \\ \end{aligned}
$$
(82)
Furthermore, the each-block-diagonal form of \({\mathbb{P}}_{1}\) and \({\mathbb{P}}_{2}\) can be presented as
$$ \begin{aligned} \mathop{{\mathbb{P}}_{1}}\limits^{\smile} & = \left\langle {\left[\kern-0.15em\left[ {{\mathbf{P}}_{1} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} } \right\rangle_{{\mathbb{b}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } \right\rangle } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } \right\rangle } &\quad \mathbf{0} &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } \right\rangle } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } \right\rangle } &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} }} } \right\rangle } &\quad \mathbf{0} &\quad \mathbf{0} &\quad {\left\langle {c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 3}} } \right\rangle } \\ \end{array} } \right] \\ \mathop{{\mathbb{P}}_{2}}\limits^{\smile} &\quad = \left\langle {\left[\kern-0.15em\left[ {{\mathbf{P}}_{2} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} } \right\rangle_{{\mathbb{b}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad {\left\langle {3c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 2}} } \right\rangle } &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\mathbf{I}}_{{n_{h} }} } &\quad \mathbf{0} &\quad {\left\langle {3c{\mathbf{X}}_{\mathbf{3}}^{{{\mathfrak{A}}_{3} \circ 2}} } \right\rangle } \\ \end{array} } \right], \mathop{\mathbb{P}}\limits^{\smile} = \left\langle {\left[\kern-0.15em\left[ {\mathbf{P}} \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} } \right\rangle_{{\mathbb{b}}} = \left[ {\begin{array}{*{20}c} \mathop{{{\mathbb{P}}}_{1}}\limits^{\smile} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathop{{\mathbb{P}}_{2}}\limits^{\smile} \\ \end{array} } \right] \\ \end{aligned}
$$
(83)
Also, the discretized form of \({\mathbf{E}}_{1}\), \({\mathbf{E}}_{2}\) is as follows:
$$ \begin{aligned} {\mathbb{E}}_{1} & = \left[\kern-0.15em\left[ {{\mathbf{E}}_{1} } \right]\kern-0.15em\right]_{{\mathfrak{B}}} = \left[ {\begin{array}{*{20}l} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ {{\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad {{\mathbf{X}}_{1}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} /t} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} - {\mathbf{X}}_{1}^{*} } \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} - {\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} \hfill &\quad \mathbf{0} \hfill &\quad {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} \hfill &\quad \mathbf{0} \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad {\left( {{\mathbf{X}}_{\mathbf{1}}^{*} } \right)^{ \circ 2} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s^{2} } \hfill \\ \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad \mathbf{0} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} - {\mathbf{X}}_{\mathbf{1}}^{*} } \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }} /s} \hfill &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} {\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }} /s - 2{\mathbf{X}}_{\mathbf{1}}^{*} /s} \hfill \\ \end{array} } \right] \\ {\mathbb{E}}_{2} &\quad = \left[\kern-0.15em\left[ {{\mathbf{E}}_{2} } \right]\kern-0.15em\right]_{{\mathfrak{B}}} = \left[ {\begin{array}{*{20}c} \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} \\ \mathbf{0} &\quad { - {\mathbf{X}}_{\mathbf{1}}^{*} /t} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad {{\mathbf{X}}_{\mathbf{1}}^{*} / s} \\ \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{I}}_{n} } &\quad \mathbf{0} &\quad {{\mathbf{X}}_{1}^{*} / s} \\ \end{array} } \right], \\ \end{aligned}
$$
(84)
in which \({\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{1} }}\) and \({\mathop {\varvec{\mathcal{D}}}\limits^{2d}}_{{X_{2} }}\) denote the 2-D differentiation operators in \(X_{1}\) and \(X_{2}\) directions, respectively [26, 32, 33].
1.5 Stress tensor
Discretizing Eqs. (34) and (55) leads to
$$ \begin{aligned} {\mathbf{Q}}_{\mathbf{11}} & = {\mathbf{Q}}_{\mathbf{22}} = \left[\kern-0.15em\left[{Q_{11} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = {\mathbb{E}}_{C} \circ \left( {1 - \overline{\overline{\nu }}_{C}^{ \circ 2} } \right)^{ \circ - 1} , \\ {\mathbf{Q}}_{\mathbf{12}} & = {\mathbf{Q}}_{\mathbf{21}} = \left[\kern-0.15em\left[{Q_{12} } \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \overline{\overline{\nu }}_{C} \circ {\mathbb{E}}_{C} \circ \left( {1 - \overline{\overline{\nu }}_{C}^{ \circ 2} } \right)^{ \circ - 1} , \\ {\mathbf{Q}}_{\mathbf{44}} & = {\mathbf{Q}}_{\mathbf{55}} = {\mathbf{Q}}_{\mathbf{66}} = \left[\kern-0.15em\left[{{\text{Q}}_{66}}\right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \frac{1}{2}{\mathbb{E}}_{C} \circ \left( {1 + \overline{\overline{\nu }}_{C} } \right)^{ \circ - 1} , \\ \end{aligned} $$
(85)
$$ \begin{aligned} {\hat{\mathbb{C}}}_{1} & = \left[\kern-0.15em\left[{{\hat{\mathbf{C}}}_{1}}\right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{Q}}_{\mathbf{11}} } &\quad {{\mathbf{Q}}_{\mathbf{12}} } &\quad \mathbf{0} \\ {{\mathbf{Q}}_{\mathbf{21}} } &\quad {{\mathbf{Q}}_{\mathbf{22}} } &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad {{\mathbf{Q}}_{\mathbf{66}} } \\ \end{array} } \right], \\ {\hat{\mathbb{C}}}_{2} &\quad = \left[\kern-0.15em\left[{{\hat{\mathbf{C}}}_{2}} \right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{Q}}_{\mathbf{55}} } &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\mathbf{Q}}_{\mathbf{44}} } \\ \end{array} } \right], \\ {\hat{\mathbb{C}}} &\quad = \left[\kern-0.15em\left[{{\hat{\mathbf{C}}}}\right]\kern-0.15em\right]_{{{\mathfrak{A}}_{3} }} = \left[ {\begin{array}{*{20}c} {{\hat{\mathbb{C}}}_{1} } &\quad \mathbf{0} \\ \mathbf{0} &\quad {{\hat{\mathbb{C}}}_{2} } \\ \end{array} } \right], \\ \end{aligned}
$$
(86)
The each-block-diagonal form of \({\hat{\mathbb{C}}}_{1}\), \({\hat{\mathbb{C}}}_{2}\) and \({\hat{\mathbb{C}}}\) can be defined as follows:
$$ \begin{aligned} \mathop{{\hat{\mathbb{C}}}_{1}}\limits^{\smile} & = \left\langle {\left[\kern-0.15em\left[ {{\hat{\mathbf{C}}}_{1}}\right]\kern-0.15em\right]}_{{\mathfrak{A}}_{3}}\right\rangle_ {\mathbb{b}} = \left[ {\begin{array}{*{20}c} \langle{{\mathbf{Q}}_{\mathbf{11}} }\rangle &\quad \langle{{\mathbf{Q}}_{\mathbf{12}}}\rangle &\quad \mathbf{0} \\ \langle{{\mathbf{Q}}_{\mathbf{21}}}\rangle &\quad {{\mathbf{Q}}_{\mathbf{22}} } &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathbf{0} &\quad \langle{{\mathbf{Q}}_{\mathbf{66}}}\rangle \\ \end{array} } \right], \\ \mathop{{\hat{\mathbb{C}}}_{2}}\limits^{\smile} &\quad = \left\langle {\left[\kern-0.15em\left[ {{\hat{\mathbf{C}}}_{2} } \right]\kern-0.15em\right]}_{{\mathfrak{A}}_{3}}\right\rangle_{\mathbb{b}} = \left[ {\begin{array}{*{20}c} \langle{{\mathbf{Q}}_{\mathbf{55}}}\rangle &\quad \mathbf{0} \\ \mathbf{0} &\quad \langle{{\mathbf{Q}}_{44}}\rangle \\ \end{array} } \right], \\ \mathop{\hat{\mathbb{C}}}\limits^{\smile} &\quad = \left\langle {\left[\kern-0.15em\left[ {{\hat{\mathbf{C}}}} \right]\kern-0.15em\right]}_{{\mathfrak{A}}_{3}}\right\rangle_{\mathbb{b}} = \left[ {\begin{array}{*{20}c} \mathop{{\hat{\mathbb{C}}}_{1}}\limits^{\smile} &\quad \mathbf{0} \\ \mathbf{0} &\quad \mathop{{\hat{\mathbb{C}}}_{2}}\limits^{\smile} \\ \end{array} } \right], \\ \end{aligned} $$
(87)