Supervised learning-based reconstruction of magnet errors in circular accelerators

Abstract

Magnetic field errors and misalignments cause optics perturbations, which can lead to machine safety issues and performance degradation. The correlation between magnetic errors and deviations of the measured optics functions from design can be used in order to build supervised learning models able to predict magnetic errors directly from a selection of measured optics observables. Extending the knowledge of errors in individual magnets offers potential improvements of beam control by including this information into optics models and corrections computation. Besides, we also present a technique for denoising and reconstruction of measurements data, based on autoencoder neural networks and linear regression. We investigate the usefulness of supervised machine learning algorithms for beam optics studies in a circular accelerator such as the LHC, for which the presented method has been applied in simulated environment, as well as on experimental data.

1 Introduction

Optics corrections are crucial for safe machine operation and reliably high performance in terms of luminosity balance between experiments. Currently, LHC optics corrections are performed in two steps, i.e., local corrections based on segment-by-segment technique [1, 2] or action phase jumps [3], and global corrections using response matrix approach [4]. Local corrections are applied in interaction regions (IRs) where the strongest error sources are usually observed, while global corrections are performed to mitigate the error sources globally, including the optics errors in the arcs. The corrections to be applied in the LHC are computed as a set of magnetic field strength changes—either in the so-called circuits (quadrupoles powered in series) or individual quadrupoles that can be trimmed independently.

These methods allow to achieve unprecedentedly low $\beta$-beating [5, 6]; however, the information about actual errors in individual magnets which caused the compensated perturbations remains unavailable. At the LHC, several steps of acquiring data for optics analysis, computing and applying local and global corrections for each beam separately are usually needed. Building a technique able to include the optics perturbations from both beams and to consider the whole set of individual error sources along the lattice promises to reduce the time needed for optics correction and allows to extend the knowledge about the present magnet errors. In this work, we demonstrate the ability of supervised regression models trained on a large number of LHC simulations to predict the individual quadrupole errors given the measured optics perturbations in one step for both beams simultaneously.

After a brief introduction to current optics corrections techniques and relevant ML concepts, we present the method of estimating the quadrupolar field errors using supervised learning and summarize the preliminary studies which demonstrated the promise of this approach. In Sect. 2, the details on data set generation and the setup of simulation environment are given, followed by the discussion on supervised training using the generated data and model selection with regards to generalization and accuracy presented in Sect. 3. Finally, in Sect. 4 we demonstrate the results of model prediction, obtained on realistic simulations considering individual magnet classes. The application of autoencoder to missing data reconstruction and denoising is presented in Sect. 5, followed by the validation of introduced ML methods on the experimental LHC data is presented in Sect. 6.

1.1 Traditional optics corrections techniques

The approach of the segment-by-segment technique used for the local corrections is to simulate the optics within the selected machine segment, which is then matched to the measured local phase errors by trimming the neighboring quadrupoles. Action phase jump analysis incorporates the idea of using the action and phase of the arcs outside the IR to estimate the distortion produced by a magnetic error in the IR. Global linear optics corrections at the LHC are usually computed by minimizing the deviation between the measured phase advance of adjacent BPMs and its values given by the corresponding ideal optics model. The changes in the phase advance and other optics variables introduced by available correcting magnets are described in a response matrix. The matrix is then computed from iterative simulations or using an analytical approach [7].

Selection of appropriate variables together with optimization of corresponding weighting factors are fundamental to produce efficient corrections. Although these optimizations can be achieved based on the existing optics model, in practice the variables and weights are defined empirically. Using supervised regression, this problem can be solved by learning the variable importance and weights automatically from the training data.

1.2 Supervised learning and regression

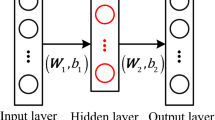
ML techniques aim to build computer programs and algorithms that automatically improve with experience by learning from examples with respect to some class of task and performance measure, without being explicitly programmed [8]. Depending on the problem and existence of learning examples, different approaches are preferred. If pairs of input and desired output are available, an algorithm can generalize the problem from the given examples and produce prediction for unknown input. ML algorithms that learn from input/output pairs are called supervised learning algorithms, i.e., supervision is provided to the algorithms in the form of determined outputs for each given example. During the training, predictions are made from the incoming input and are then compared to the true corresponding output. The target is to minimize the difference between predictions made during the training and the true output by updating adjustable parameters of a chosen model. The difference is defined as loss function (e.g., mean absolute error) which is minimized using one of optimization algorithms such as gradient descent or least-square minimization.

The complexity of the model depends strongly on the specific task and ranges from univariate linear regression to deep neural networks with customized architecture. Depending on the desired prediction target, i.e., category or a quantity, the problem can be defined either as classification or regression task. Here, we investigate regression models as the target is to quantify the size of magnet errors. The actual model training is followed by evaluation in order to measure the generalization ability and prediction accuracy of the designed estimator.

ML techniques have found their application in a wide range of accelerator control and optimization tasks [9,10,11,12], including early works on orbit corrections using artificial neural networks [13, 14] and Bayesian approach for linear optics corrections [15]. More recent advances on building surrogate models using supervised learning are presented in [16, 17]. In the following, we present the methodology of utilizing the supervised learning approach and linear regression for quadrupole field errors estimation based on measured optics perturbations.

1.3 General concept

Magnetic field and misalignment errors distort optics parameters of accelerators. The general idea of applying supervised learning to optics corrections is to create a regression model which will automatically learn the correlation between magnets error sources and the resulting optics perturbations, from the provided simulations data. Given a set of features $X = x_{1}, x_{2},..., x_{m}$ and targets $Y = y_{1}, y_{2},..., y_{n}$, an estimator can learn a regression model or a nonlinear approximation.

Such estimator should use the measured optics functions deviations from design as input and predict the error sources as output. Supervised training requires a large set of training data in order to be able to generalize and produce reliable results on unseen data. The correction results obtained in the past years are not suitable as training data source, since corrections are only performed few times per year in the LHC, and hence, not enough data is available. Moreover, the corrections applied in the LHC utilize the strength of “circuits,” sets of quadrupoles powered in series, and hence, the corrections do not reflect the errors of the individual elements.

Model training on a simplified case of introducing the errors in the circuits and model evaluation on the optics perturbed by individual quadrupole errors is presented in [18]. The regression models predict the strength changes in the circuits which can be applied to simulate the expected optics corrections. Different regression techniques have been compared demonstrating similar performance, producing corrections results on the level of the traditional response matrix approach [19] as shown in Table 1. However, the realistic errors of every single magnet have a different effect on the optics compared to the strength change in the circuits. In this work, we present the approach of simulating the optics perturbation in the training data using randomly generated individual magnet errors. The target is to predict the actual effective quadrupolar field errors, instead of obtaining the strength change to be applied to the circuits.

Table 1 $\beta$-beating after applying the predicted circuits errors as correction settings, the results are averaged over 100 simulations of perturbed collision optics with $\beta ^{*}=40$ cm

2 Data set generation

In order to build a data set for supervised training, we assign uniform distributed random field errors to all quadrupoles available in the LHC for both beams. Additionally, we apply quadrupolar errors also to the dipoles which are modeled as combined function magnets in order to obtain more realistic simulations. The generated errors are then added to the nominal model of collision optics with $\beta ^{*}$ = 40 cm, producing differences between the design and the optical functions produced in simulation. These deviations from ideal optics together with a set of associated magnet errors build a training sample for the supervised training. The summary of this concept is presented in Fig. 1.

Fig. 1

Conceptual representation of data generation and supervised model creation for the estimation of individual magnet errors from optics deviations

2.1 Simulating magnet errors as target variables

In this study, we consider quadrupolar integrated field errors, longitudinal misalignments of quadrupoles and sextupole transverse misalignments. The errors are simulated according to the magnet measurements [20] using MAD-X simulation framework. All quadrupoles in the lattice are assigned a random relative gradient error obtained from uniform distribution with the same rms error $\sigma$ per magnets family. In case of the triplet magnets, also the systematic error (the mean of the errors assigned to one magnet family) is defined as uniform distribution in a range [$-10^{-3}$,$10^{-3}$] for a single LHC simulation. The distribution of relative field errors is defined in Table  2 along with alignment errors of the sextupoles and triplet magnets.

Table 2 RMS values of integrated relative field errors $\sigma _{K}/K_{1}$ assigned to different quadrupole (MQ) families and misalignments of quadrupoles and sextupoles (MS), with $\sigma _{s}$ and $\sigma _{x}$ being the RMS of longitudinal and transverse misalignment, respectively, used for training data generation

Fig. 2

A fragmentary representation of LHC arc elements and $\beta$-function showing the adjacent placement of arc quadrupoles (MQ) and sextupoles (MS)

Transverse sextupole misalignments induce a quadrupolar field error. A dedicated study has been performed in order to explore replacing misalignment errors by modified field errors in quadrupoles while keeping the optics deviations produced by included error sources realistic. The target is to mitigate the degeneracy caused by the close proximity of the sextupoles to the quadrupoles in the LHC arc sections illustrated in Fig. 2. The approach is to match the $\beta$-beating produced by a single sextupole with 1 mm offset with the field change in the neighboring quadrupole. In case the residual $\beta$-beating is negligible, the offsets can be reflected by increasing quadrupolar field error with the approximation

$$\begin{aligned} \sigma _{K}/K_{1, \mathrm{new}}= \sqrt{\sigma _{K}/K_{1, \mathrm{original}}^{2} + \sigma _{x}^{2}(K_{2}L)^{2}/K_{1, \mathrm{original}}^{2}} \end{aligned}$$

(1)

where $K_{2}L$ is the integrated sextupolar strength and $\sigma _{K}/K_{1, \mathrm{original}}$ and $\sigma _{K}/K_{1, \mathrm{new}}$ being original rms of simulated arc quadrupole gradient field errors and the new rms which reflects the presence of sextupole transversal offset.

Fig. 3

The optics perturbation produced by the transversal misalignment of a sextupole can be matched by changing the adjacent quadrupole field strength, with an excellent agreement between the resulting rms $\beta$-beating values indicated in the legend

Figure 3 shows the reconstruction of the $\beta$-beating induced by the displacement of a sextupole in the arc on the right of IP2 (MS.13R2) changing the strength of the adjacent quadrupole. This result confirms that the optics deviation produced by the expected transversal offset of sextupoles is reproducible by increasing the rms of the quadrupolar field errors. Since the sextupoles are also used to correct chromaticity and the $\beta$-function in the arcs changes depending on the optics scheme, Eq. (1) is optics dependent.

This approach has been explored also to study the longitudinal offset of triplet magnets. According to matching results, a longitudinal error of one magnet cannot be fully replaced by a gradient field error.

Fig. 4

The comparison between $\beta$-beating produced by quadrupolar field errors in the triplet magnets ($\delta _{K}$) distributed according to Table 2, compared to $\beta$-beating caused by additionally adding longitudinal misalignments ($\delta _{S}$) of 6mm

It has been shown for the optics with $\beta ^{*}$ = 20 cm that $\beta$-beating introduced by longitudinal misalignments of the triplets can be reproduced with corresponding field errors [21]. Figure 4 shows an example for the optics with $\beta ^{*}$ = 40 cm, where the additional contribution of the misalignment to $\beta$-beating is small compared to the perturbations caused by gradient field errors. Hence, the longitudinal misalignments of the triplet magnets are neglected for the purpose of this study; however, the effect of the longitudinal offsets should be addressed in the future related work. In the following, we focus on the reconstruction of effective quadrupolar field errors.

2.2 Optics functions as input features

Feature engineering, i.e., the process of finding the most relevant properties in the input data for predicting the targets incorporates techniques to measure the feature importance and to build new input sets in order to simplify and improve the model training. Collecting appropriate data is a crucial milestone of the ML-pipeline since the model selection and achieved performance strongly depend on the amount and quality of the given data.

The correction of $\beta$-beating can be ensured with the phase beating correction [19]. Hence, the simulated phase advance deviation from the design between each pair of consecutive BPMs is considered as one input feature. The $\beta$-functions next to the interaction points (IPs) indicate the local optics errors which are dominated by the errors in the triplet magnets. Thus, the horizontal and vertical $\beta$ at the BPMs left and right of main interaction points (IP1, IP2, IP5, IP8) of both beams are included as input features into the regression model, in order to improve the prediction of the triplet errors. In practice, these $\beta$ functions are measured via K-modulation [22]. The deviations from the design optics in the measured dispersion function are related to quadrupolar errors. The measurement of normalized horizontal dispersion $D_{x} / \sqrt{\beta _{x}}$ is independent of BPM calibration errors [23], and hence, its deviation from the nominal values is also added to the set of important input parameters.

In total, 3346 features are extracted from the simulation data. Realistic noise estimated from the measurements data is added to phase advance and dispersion features. Phase advance noise is assumed to be $10^{-3} \times 2\pi$ in a BPM with $\beta$=171 m, and it is scaled with the $1/\sqrt{\beta }$ at the rest of locations. The normalized dispersion noise is estimated from the recent optics measurements with $\beta ^{*}$ = 25 cm [24] and is assumed to be a chi-square distribution with non-centrality parameter 4 and scaled with $10^{-3}\sqrt{\mathrm{m}}$ as demonstrated in Fig. 5. The random noise added to the original simulated deviations in normalized dispersion is generated accordingly.

Fig. 5

The noise distribution in the dispersion measurements of beam 1 and beam 2 [24] compared to the simulated noise generated as a chi-square distribution with non-centrality parameter 4

3 Model selection and training

As it was shown in [18], applying complex models such as convolution neural network does not result in significantly better corrections. Another reason for the choice of linear model is that the error sources to be predicted are known to introduce linear optics perturbations. We use a least-squares linear regression with weights regularization [25, 26], the so-called Ridge Regression as baseline model for the following studies. Ridge regression model minimizes the residual sum of squares between the true targets in the training data and the targets predicted by the linear approximation. The tuning parameter $\alpha$ is responsible for the weights regularization—special technique to control the weights update during the training. The regression problem is then formulated as

$$\begin{aligned} \min _{w} || \mathbf {X} w - \mathbf {y}||_2^2 + \alpha ||w||_2^2 \end{aligned}$$

(2)

where w is the matrix containing the weights of regression model, $\mathbf {X}$ is the input data vector, and $\mathbf {y}$ the vector of targets to be predicted by the model.

The trained model needs to be evaluated using adequate quality metrics considering the data representation, desired result and specific task to be solved. In order to conclude on the learning performance, the data set is separated into training (80%) and test (20%) sets. The typical figures of merit for regression tasks are the mean absolute error (MAE) to compare the difference between true target values and the output of the model and the coefficient of explained variance $R^{2}$ defined as

$$\begin{aligned} R^2(\mathbf {y}, \hat{\mathbf {y}})= & {} 1 - \frac{\mathrm{Var}\{\mathbf {y} - \hat{\mathbf {y}}\}}{\mathrm{Var}\{\mathbf {y}\}} \end{aligned}$$

(3)

$$\begin{aligned} \mathrm{MAE}(\mathbf {y}, \hat{\mathbf {y}})= & {} \frac{1}{n}\sum _{i=1}^{n}|y_i - \hat{y}_i| \end{aligned}$$

(4)

where $\hat{\mathbf {y}}$ is the predicted output with $\hat{y}_i$ being the predicted value of the ith sample, $\mathbf {y}$ the corresponding true values for N total samples, and Var is the variance, the square of the standard deviation.

While the basic linear regression model trained to predict the circuits settings produced slightly better results than Ridge, higher $R^{2}$ score is achieved by Ridge regression for both training and test data when trained models predict a larger number of targets variables as in the case of individual quadrupolar errors. Another technique to improve the prediction quality on unseen data is bagging. Bagging is based on the idea of generating multiple versions of an estimator and using the averages of targets over the versions for final predictions [27]. The multiple versions are formed by using subsets of the training data for a single estimator. After extensive validation, a model with 10 estimators, each using 80% of the training data, regularized by $\alpha =1 \times 10^{-3}$ has been found as the optimal setup, and hence, this model is used to obtain the results presented below.

Increasing the number of training samples does not necessarily result in a large increase of predictive power of the model. Considering the amount of time and storage needed to handle the training simulation data, especially for the future online application, we need to determine the optimal training set size. The change of the model scores with respect to the number of samples (learning curve) also indicates the ability of the model to learn from the given data and the data set size required to achieve the optimal model performance as shown in Fig. 6. In the next section, we present the results from the regression model with described parameters using 80,000 samples in total for training and test.

Fig. 6

Cross-validation of the optimal model based on the loss (MAE) and $R^{2}$ coefficient depending on the number of available samples. The loss is constantly decreasing with the growing number of samples, while $R^{2}$ is increasing. This trend indicates a reasonable learning behavior; however, using datasets larger than ca. 80,000 samples does not improve the scores significantly

4 Results on simulations

Identification of local error sources such as quadrupolar field errors is known to be a degenerate problem with multiple solutions. However, the estimates found by ML-model can be validated in two different ways—comparing the true simulated magnet errors to the ML-model prediction or by comparing the $\beta$-beating simulated by true errors to the $\beta$-beating produced by predicted errors. This allows to test how reliable prediction is on unseen data and to investigate the ability of the model to learn the physical correlations between the linear magnetic field errors and optics perturbations. The results presented below are obtained from LHC simulations using the collision optics settings with $\beta ^{*}=40$ cm and the magnet errors distribution listed in Table 1.

Fig. 7

Schematic of the magnets layout (triplet quadrupoles Q1, Q2, Q3 and sextupoles MS), with error bars indicating the lengths of elements and $\beta$-function around IP1 for the optics settings $\beta ^{*}$ = 40 cm as used in training data generation. Please note that the value of the beta is given at the end of each element

Fig. 8

Comparison between true and predicted relative magnet errors. The left column illustrates the prediction results obtained for the field errors in individual triplet quadrupoles, while the center and right columns correspond to the combination of Q1 and Q3 magnets and Q2A and Q2B magnets pieces, respectively. The slope in upper plots illustrates the systematic bias of regression model computed as correlation between residual error and corresponding true values

Fig. 9

The systematic and random components of the true simulated quadrupolar field errors, computed as mean $\mu$ and rms $\sigma$ of the errors distribution, compared to their values in the predicted results on validation data

4.1 Triplet errors

The field errors in the triplet magnets produce the largest contribution to the optics perturbations, and hence, their prediction is evaluated separately from the magnets in the arcs, to ensure the ability of the presented approach to reconstruct the most significant error source. Figure 7 demonstrates the large values of $\beta$-function in the triplet region and illustrates the layout of single magnets (Q1, Q2, Q3) in one triplet circuit.

Figure 8 summarizes the results of triplet errors prediction. In order to compare these results to the original simulated error distribution presented in Sect. 2, the model prediction is given as relative integrated field errors. To inspect the predictive power of the trained regression model, we compare the true simulated magnet error to corresponding residuals, computed as the difference between true and predicted values. The correlation between the individual simulated magnetic error and residuals demonstrates a systematic bias of prediction of 16%. The predicted errors are systematically smaller than in simulations. The systematic bias reduces by incorporating the knowledge about the relations between single magnets in the triplet circuits. Q1 and Q3 magnets are powered together, while Q2 magnets have two pieces (Q2A and Q2B), which strengths can be balanced. Averaging the values of Q1 and Q3 magnets, the systematic error is reduced by a factor of 2, while the combination of Q2A and Q2B pieces results in more significant reduction to 2%. The systematic prediction error for the arc magnets is 30%, being as expected larger compared to the triplet magnets, since the reconstruction of the error sources located in the arcs is affected by degeneracy stronger compared to the triplet magnets installed around the IPs. Inspecting the reconstruction of particular components of the simulated errors (systematic and random errors as described in Sect. 2), Fig. 9 demonstrates a very good agreement between the systematic components of the simulated and predicted triplet errors, whereas the random part appears to be the biggest contribution to the overall prediction error of the trained estimator. Combining individual triplet magnets also leads to a better agreement between rms values of simulated and predicted field errors. Table 3 provides a summary on the metrics used to evaluate the prediction of the quadrupolar field errors.

Table 3 Explained variance $R^{2}$, residual error of prediction relative to the corresponding simulated true values and comparison between predicted and simulated RMS ($\sigma _{pred}$, $\sigma _{sim}$) values of the relative integrated field errors

Fig. 10

The original $\beta$-beating generated in validation data, compared to the $\beta$-beating simulated using the predicted magnet errors and their differences. The histograms represent rms values of 100 simulations

We also evaluate the trained model in terms of reproducing the original $\beta$-beating simulated in validation data using the quadrupolar errors predicted from the corresponding simulations. For each validation sample, we compare the $\beta$-beating in the original optics simulation where the sample’s input has been extracted from, to the $\beta$-beating induced by the magnet errors predicted from the given input. Figure 10 summarizes the results for 100 validation simulations, per beam and per plane individually. The results demonstrate a very good agreement between the original and reconstructed optics errors, with the average rms difference of 1%.

4.2 Effect of noise

In order to investigate the effect of the noise on the predictive power of the regression model, we compare prediction errors between models trained on the input data given different noise levels. Two different feature groups included in the model input are treated separately—normalized dispersion noise and phase advance noise. Figure 11 shows the change in model performance depending on the noise added to the simulated normalized dispersion deviations, while keeping the phase advance noise unchanged. Figure 12 presents the results obtained from regression models trained using the phase advance features only, without adding the features containing normalized dispersion and $\beta$ information. This model is also applied later to the LHC measurements data obtained in 2016 LHC commissioning, where measurements of normalized dispersion and $\beta$ function around the IPs are not available. Alternative approaches for data reconstruction are presented in the next section.

In addition, we explored the accuracy of the triplet and arcs magnets error prediction as presented in Sect. 4, including the reconstruction of $\beta$-beating on simulations, on the noise-free data. The absence of noise in the training, as well as in validation input data, leads to the reduction of systematic prediction error for the arcs magnets from 30 to 1%, while for the triplet magnets the systematic error reduces to 12%. Considering the $\beta$-beating reconstruction using the predicted quadrupole errors, the rms difference between the original simulated and reconstructed $\beta$-beating reduces by a factor of 2.

Fig. 11

The effect of the noise added to normalized dispersion function ($\sigma \frac{D_{x}}{\sqrt{\beta _{x}}}$) used in training data simulation on the predictive power of a regression model. Mean absolute error (MAE) of prediction is given in the units of absolute quadrupole errors. $R^{2}$ defines the explained variance. The gray line marks the expected noise in the LHC measurements [24]

Fig. 12

The change of model scores trained on phase advance features only, depending on the noise added to simulated phase advance deviations as described in Sect. 2

The change of the phase advance noise has a bigger impact on the model performance, due to the stronger correlation between the magnetic errors and the deviations in the phase advances compared to the correlation with the dispersion perturbation, as the dispersion is suppressed in the quadrupoles located in the straight sections.

Reducing the noise in the measurements of optics observables used as input for magnetic errors reconstruction can potentially improve the prediction accuracy. Especially in terms of arc magnets errors, the noise becomes the biggest limitation for the presented approach. These results can be potentially used as future requirements on instrumentation and analysis techniques included into optics computation from turn-by-turn data.

5 Reconstruction and denoising of optics observables

Keeping the measurements noise as low as possible, as well as including all relevant variables into the training data, is crucial for the accuracy of the magnetic error reconstruction. The presence of the noise enforces acquisition of several turn-by-turn measurements for each beam in order to obtain statistically significant computation of the optics functions and uncertainties. Providing online measurements as input of regression models trained on simulations, missing data can be a possible issue. The signal of identified faulty BPMs is excluded from the optics analysis, and hence, the optics observables used as input features of regression model are missing at the locations of faulty BPMs. In the following, we focus specifically on these problems and its possible solution.

An ML-based approach to mitigate the effect of the noise and to reconstruct the missing data points is the application of autoencoder [28]. Autoencoder is a specific type of a neural network that is trained to reproduce its input in the output layer. The network consists of two parts: a learned encoder function $h = f(x)$ describing a set of hidden layers h and a decoder that produces a reconstruction $r = g(h)$. To perform denoising and data reconstruction, the encoder extracts relevant information from the input by lowering its dimension and filtering the noise. The original input is then reconstructed by the decoder. During the training, the encoder learns to recognize the noise patterns in the input and to keep only the signal relevant for the reconstruction performed by the decoder. In general, this learning process is described as minimization of a loss function $L(x,g(f(\tilde{x})))$ penalizing $g(f(\tilde{x}))$, where $\tilde{x}$ is the input corrupted by noise and x is original input. Since autoencoder is considered as a special case of a feedforward network, it can employ the same techniques for training, e.g., gradient descent and backpropagation.

Fig. 13

Example of reconstructing the phase advance deviations at the location of simulated missing BPMs in horizontal plane, beam 1 using autoencoder neural network

Fig. 14

Comparison between the noise added to original simulation of phase advance deviations in beam 1, horizontal plane to the reconstruction error from autoencoder prediction, performed on 1000 LHC simulations

In order to apply this approach to denoising and reconstruction of simulated phase advances, autoencoder network is trained using the noisy phase advances and the original simulated phase advances. The discussed results are obtained with an autoencoder consisting of 4 hidden layers, using MAE as loss function and Adam [29] as optimization algorithm. To simulate the missing data points in validation data, 10% of input values are omitted in each of the validation samples, according to statistical analysis of BPM discarded by cleaning tools [30]. Exemplary comparison between autoencoder prediction at the location of discarded data points and corresponding original simulated values is shown in Fig. 13 indicating a very good agreement. Processing the phase advance data with autoencoder also allows to reduce the noise by a factor of 2 as demonstrated in Fig. 14. The rms error of 100 validation samples, for both beams, horizontal and vertical planes, is $\mathrm {0.8 \times 10^{-3}\, [2\pi ]}$ which is below the used uncertainty estimate for the phase advance measurements in the LHC. The advantage of autoencoder is the possibility to combine two different objectives, namely the reconstruction of missing data and denoising.

Considering specifically the reconstruction of missing data, also linear regression appears as appropriate technique while enabling faster training and simpler model parameter tuning compared to autoencoder. We demonstrate the application of Ridge regression to reconstruct the $\beta$-function at the BPMs next to IPs and the full set of horizontal normalized dispersion deviations. These observables have been found to be important for the estimation of quadrupolar field errors; however, they are not always available in the measurements data. In order to obtain information about the dispersion function, several beam excitations on and off momentum are required. In the LHC, the $\beta$-function directly at the IP is typically computed using the k-modulation technique [22], which also produces accurate $\beta$ measurements at the BPMs around the four main experiments that are included in the input of regression models for magnetic errors estimation.

Fig. 15

Comparison between simulated and reconstructed $\beta$ in both planes and for both beams at the BPMs next to the main IPs for 1000 simulations, demonstrating the relative rms difference of 1%

The result of reconstructing the $\beta$ deviations is presented in Fig. 15. Ridge regression model is trained on 8000 training samples with simulated noisy phase advance deviations for both beams and planes being the input and $\beta$ deviations in horizontal and vertical planes simulated at the BPMs around the IPs 1, 2, 5 and 8 the output. The validation is then performed on a set of 1000 LHC simulations. The error of reconstruction defined as the difference between simulated and reconstructed values relative to simulated $\beta$ is 1% which is comparable to the uncertainty of k-modulation technique for the $\beta ^{*}$ measurements for the optics settings used in the presented study [31].

Fig. 16

Reconstruction of horizontal normalized dispersion deviations in beam 1 from noisy phase advance data. The left plot illustrates the agreement between simulated and reconstructed values in one simulation, while the histogram on the right shows statistics obtained from 1000 simulations with the rms reconstruction error of 7%

In order to assert the approach of reconstructing the normalized dispersion measurements from phase advance deviations, we train a Ridge regression model on 8000 samples generated with the setup described in Sect. 2. Here, individual regression models are built for each beam separately, and hence, the input consists of phase advance deviations in horizontal and vertical planes of one beam only. Figure 16 shows the comparison between normalized dispersion function predicted by regression model and corresponding actual simulated function. The relative rms prediction error of 1000 simulations is 7%.

6 Experimental data

The previously discussed results are obtained from LHC simulations. In this section, the trained regression model is verified against the application on historical LHC measurements data. The target is to estimate magnet errors from LHC commissioning data, measured with $\beta ^{*}=40$ cm, before applying any corrections to the machine. Since $\beta$-function at the BPMs next to IPs and normalized dispersion measurement are not present in the corresponding historical data, the model trained on the phase advance deviations only as input features is used. Due to the cleaning of faulty BPMs prior to the computation of phase advance, missing data points appear in the input features extracted from experimental LHC data. To obtain these data, we apply the autoencoder presented in the previous section. The output of the autoencoder, i.e., the full set of phase advance deviations is then provided to the regression model to predict the field errors in individual magnets.

The actual magnet errors that generate the measured optics perturbations in the uncorrected machine are unknown such that a comparison between model prediction and corresponding true values as in the case of simulations is not possible. Instead, we use the predicted errors to simulate optics perturbations and compare this simulation to the actual measurement. The residual difference indicates how well the estimated magnetic errors reflect the actual error sources present in the uncorrected machine. The optics is reconstructed using two different sets of magnet errors: (i) errors predicted from the phase advance deviations replacing the missing values with 0 and (ii) errors estimated from the output of autoencoder performing reconstruction of missing values along with denoising. Processing the original phase advance data with autoencoder results in reducing the rms of residual $\beta$-beating by 3% and the peak $\beta$-beating by 8% with respect to utilizing the original measured phase advances as predictor’s input.

The final results on comparing the optics simulated with predicted magnetic errors to the actual measurement in uncorrected machine are demonstrated in Fig. 17. The residual $\beta$-beating also indicates a potential optics correction that can be achieved by computing correction settings based on predicted errors. The agreement between the measured and reconstructed optics shows that rms $\beta$-beating in Beam 1 can be potentially reduced from 12 to 3% and from 54 to 9% in horizontal and vertical planes, respectively. For Beam 2, the rms $\beta$-beating decreases from 49 to 15% in the horizontal and from 12 to 2% in the vertical plane. Even though the $\beta$-beating for the uncorrected machine was above 100%, which is significantly larger than the $\beta$-beating introduced in the training simulations, the optics reconstruction using the predicted magnet errors results in 7% rms $\beta$-beating around the ring and below 3% at the two main experiments CMS and ATLAS.

Fig. 17

Comparison between original $\beta$-beating measured in the uncorrected machine and reconstructed optics simulated using the predicted quadrupole errors. The difference between measurement and simulation reflects the residual $\beta$-beating after potential correction in beam 1 (right) and beam 2 (left)

7 Conclusion and outlook

The traditional approaches used for optics corrections in circular accelerators aim to compute correction settings needed to compensate the measured optics deviations from design. Instead, the presented ML-based approach allows determining the actual individual quadrupole field errors currently present in the machine. The advantage of regression models is the ability of extracting an average linear response over the training population instead of only using the unperturbed model and the response of a single observable to a strength change in a single corrector, as it is done in the response matrix approach. Also, the weighting factors of specific observables are found automatically instead of defining them manually as needed for the application of currently available correction tools for the LHC.

The presented results based on simulations and historical data demonstrate successful verification of the proposed ML-based approach. We showed its potential to improve the optics corrections at the LHC by providing the knowledge about the local errors which is in particular of a great importance for the triplets. One of the limitations of the applied linear regression estimators is low prediction accuracy considering the quadrupoles located in the arcs, which can be explained with the fact that the error sources in the arcs exhibit a weaker effect on the optics compared to the triplet magnets located around the IPs. Therefore, it is more difficult to extract the relation patterns between provided model input and corresponding output during the training and produce accurate predictions. Potentially, additional input features which are relevant for arc magnets predictions have to be identified and included into the regression model.

Currently, individual regression models have to be generated for each specific optics design, since the response of the perturbations introduced in the input features by the magnet errors depends on particular optics. However, it is possible to allow more general application of created models by performing the training on the data simulated using different optics settings, reducing the effort for the model preparation in case of optics and machine settings modifications during operation.

The possibility to reconstruct normalized dispersion and $\beta$ around the IPs from phase advance measurements using supervised learning allows to include these observables into corrections computation even if dedicated measurements needed to obtain these optical functions have not been performed. This opens the perspective to extend offline optics analysis and to speed up optics measurements saving the costly operational time. Also the application of autoencoder has been found to be a promising solution for denoising and the reconstruction of phase advance measurements at the location of faulty BPMs, improving the quality of the input data provided to magnet error prediction models.

The most important future step towards applying the presented approach in LHC operation will be the computation of actual correction settings to be implemented in the LHC after predicting the individual magnet errors from measured optics. The significant decrease of prediction error after combining individual triplet magnets according to the correlations between these magnets promises improvements of local corrections around the IPs by using the predicted field errors. Future advances in instrumentation and optics analysis techniques, along with the application of denoising autoencoder, will allow significant gain in the accuracy of magnet errors reconstruction and consequently lead to better correction results and optics control.