Spin relaxation in six-pulse double-quantum coherence (DQC) signal: stretched exponential approach for a polycrystalline average

Abstract

Using the Redfield equation, the effect of electron-spin relaxation is taken into account on six-pulse double-quantum coherence (DQC) signal for coupled nitroxide radicals, each characterized by the electron spin $S = 1/2$ and nuclear spin $I = 1$. It is found that a two-dimensional time-domain ($t_{\rm dip}$, $t_{\rm echo} )$ signal for a single orientation of the external magnetic field with respect to the dipolar axis becomes multiplied by the decaying exponential factor: $\exp\left( { - \left( {2t_{\max} + t_{\rm echo} } \right)/T_{2}^{S} - 2t_{DQ} /T_{2}^{D} } \right) ,$ where T₂^S and T₂^D are the spin–spin relaxation times for that orientation of the magnetic field along the $p = \pm 1$ and $p = \pm 2$ coherence pathways, respectively; here $p$ is the coherence order, which represents the transverse magnetization, equal to $\pm 1$ for the single-quantum states and $\pm 2$ for the double-quantum states, $t_{DQ}$ is the time interval over which the two electrons are on a double-quantum $p = \pm 2$ coherence pathway, and $t_{\max}$ is the time between the first and the sixth pulse, which is kept constant in the six-pulse DQC sequence considered. To calculate the average effect of the orientation-dependent relaxation times on the signal for a polycrystalline sample, an overall stretched-exponential relaxation time is used. Several illustrative examples are included for chosen values of ($T_{2}^{S}$, $T_{2}^{D} ,{\beta }$), where ${\beta }$ is the exponent characterizing the stretched exponential, exhibiting the effect of relaxation on the intensity and width of the DQC signal along the echo-axis. However, there is absolutely no effect of relaxation on the shape of the Fourier transform of the signal along the dipolar axis, other than reducing its intensity, implying that six-pulse DQC experiment is a superior technique over other pulse arrangements, e.g. 2-pulse COSY/SECSY, 2-pulse DQ, 5-pulse double-quantum modulation (DQM), whose Pake doublets are broadened by relaxation, to use the splitting of the Pake doublet to determine the distance between the two nitroxide radicals. The Fourier transform of the polycrystalline six-pulse DQC signal shows very prominent Pake doublet at $\pm d$, with $d$ being 2D/3, where D is the dipolar interaction. This spacing can be used to estimate distances between the nitroxide radicals directly using the relationship $r\left[ {A^{ \circ } } \right] = 10\left( {51.9/D\left[ {{\text{MHz}}} \right]} \right)^{1/3}$.

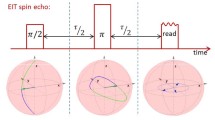
Graphic abstract

Appendix: Flowchart of calculation of the six-pulse DQC signal