1 Introduction

While geothermal heat has been exploited for centuries—if not for millennia—in the hot spots where the heat flux through Earth’s crust is anomalously high [1,2,3], utilization of this energy source in regions where no hot spots exist is still largely limited to small-scale installations. In recent years, the idea of providing district-wide heating with intermediate-to-deep geothermal wells in the Nordic countries has resurfaced and private companies [4,5,6] have duly taken the initiative towards commercializing the technology in the wake of renewed communal interest in low-carbon heat sources. For example Helsinki, the capital city of Finland, has announced a price of 1 million euros to whoever drafts to best plan to decarbonize the local annual 7 TWh district heating system [7].

As of yet, by and large, mainly the surface heat radiating from the Sun has been exploited in commercial applications, which target small houses by equipping their yards with networks of pipes installed in the ground surface layer. The resulting gain from such installations remains moderate, though, and consequently, the power per surface area remains too low to be utilized effectively in large apartment complexes that are densely packed in urban areas.

The temperature in the ground, however, increases the deeper one goes. At depths of roughly 20 m the temperature is no longer affected by the monthly variation and approaches a steady 2–6 \(^\circ \)C in Finland, while, at depths of 2 km, the temperature in the bedrock already reaches values close to 40 \(^\circ \)C. This prediction is based on the observation that the heat flux through Earth’s crust in the Nordic countries region is approximately 0.054 Wm\(^{-2}\) and the heat conductivity of bedrock granite is roughly 3.0 Wm\(^{-1}\)K\(^{-1}\), thus providing a temperature gradient of approximately 18 K/km. In contrast to settling for a modest 2–6 \(^\circ \)C at the surface, it is anticipated that drilling a deep enough hole in the ground, placing a hollow, vacuum-insulated coaxial pipe in the hole, and circulating water as a coolant fluid by pumping it down through the gap between the pipe and the wall (of the well), and sucking it back up through the pipe would improve the power-per-surface-area ratio and ultimately provide a sustainable, low-carbon heat source applicable to district heating purposes.

While the premise sounds appealing—drilling a city full of holes and getting heat from circulating water therein—one should also assess the sustainability and feasibility of such an endeavour. Because the equilibrium heat flux through Earth’s crust in the Nordic region is rather modest, one is immediately faced with two questions:

  1. 1.

    How much power extraction per surface area can the existing temperature gradient in the ground support?

  2. 2.

    What would be the longevity of such a heat source at the requested power level?

Both of these questions are crucial in addressing the scalability of intermediate–deep geothermal wells for district heating purposes in densely populated urban areas with strict requirements for the power density. It is, therefore, the purpose of this paper to provide approximate estimates to these questions that could prove useful for both policy makers and engineers.

We are interested in the temporal behaviour of the thermal power output without the use of additional heat pumps. Even if they were used in a large-scale system, we would anticipate them to be employed chiefly to lift the extracted heat to higher, better utilizable temperatures without actually aiming to increase the total produced power, for otherwise significant additional electricity demands could emerge. Limiting ourselves in this sense also mitigates the risk of incurring undersizing issues with respect to the coefficient of performance (CoP) of the heat pump. In addition, drilling deep enough is anticipated to provide sustainable heat at temperatures directly applicable to district heating without the intervention of heat pumps, especially for space heating.

Our assessment is based on analysing the problem of heat transfer from the bedrock to a coolant water flowing in the well, and setting the boundary conditions of the problem such that they correspond to a situation whereby several wells are drilled near each other, mimicking large-scale installations. The temporal behaviour of the system will yield information on the longevity question, while the boundary conditions furnish information on the achievable power per surface area.

Several analytical models have been developed and studies carried out for shallow geothermal wells [8,9,10,11,12,13,14], but their direct applicability to the intermediate-to-deep wells is questionable. The analytical solutions typically assume a Neumann type (fixed heat flux) boundary condition at the borehole and a flat initial temperature profile, while the boundary condition in reality is of nonlinear Robin type (heat transfer to a coolant) and the entire idea of intermediate-to-deep wells is based on a geothermal temperature gradient. Furthermore, in analysing the performance of well lattices, the principle of superposition is often applied, although it is incorrect—the single borehole solution does not satisfy the global boundary condition of the entire lattice installation. It is no surprise then that some recent studies mix analytical theory with numerical methods [15] or rely on numerical solutions alone in addressing intermediate-to-deep wells [16]. In our analysis, only in the case of a constant mass flow we do find a good agreement with a simplified analytical theory that we have developed in Appendix, and are thus able to accurately explain the characteristics of the more nuanced numerical solution. Notably, we find that in analysing the performance and longevity of intermediate-to-deep geothermal wells, the ratio of interest ought to be \(L^2/P\), with L being the well depth and P the requested power. This parameter differs significantly from the L/P-ratio typically used in analysing shallow wells.

We begin in Sect. 2 by describing the multi-physics model for the heat-transfer problem that couples the bedrock and the geothermal well. The simulation results are presented in Sect. 3, first illustrating the generic behaviour of the water outlet temperature under constant-mass-flow and constant-power-extraction scenarios, with good support from a simplified analytical model derived in Appendix. Then, we specify our definition for the longevity, which generally depends on the requested power, the size of the domain reserved for an individual well, and the depth of the well, before proceeding to performing scans with respect to these parameters to obtain accurate and easily accessible charts. Discussion and instructions for policy making, with regards to the use of intermediate-to-deep geothermal wells in district heating purposes, is provided in Sect. 4 using the parameter scans as a guiding principle and enabling quick assessments. We use the city of Helsinki and its district heating needs as an illustration. Finally, a summary of our results is provided in Sect. 5.

2 Model description

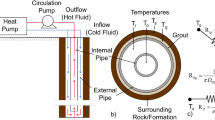
We consider a hexagonal lattice of intermediate-to-deep geothermal wells covering the surface area of a city or a fraction of it. We focus on the multi-physics problem of heat transfer from the bedrock to the circulating water in a single well by approximating the relevant domain to be in the shape of a hollow cylinder with an inner radius of \(r_1\sim 0.05-0.2\) [m], a large outer radius of \(r_2\sim 10-200\) [m], and an arbitrary depth of \(z_2\sim 1-10\) [km]. The distance between consecutive wells is effectively \(2r_2\). The city surface is taken at \(z_1=0\).

The circular shape of the top section of a cylinder is a reasonable approximation of a hexagon, and greatly simplifies the computation by allowing the temperature profile to be axially symmetric. The periodicity of the hexagonal well lattice has the effect that the heat flux approximately vanishes at the cylinder outer radius. Consequently, the temperature profile in the rock will be the three-variable function \(u_R(r,z,t)\) with \(r\in [r_1,r_2]\), \(z\in [0,z_2]\), and t referring to time. Heat transfer in the rock occurs only via conduction, and, as there are no volumetric heat sources, the rock temperature will obey the equation

$$\begin{aligned} \rho _R c_R\frac{\partial u_R}{\partial t}+\nabla \cdot \varvec{q}=0, \end{aligned}$$
(1)

where \(c_R\) [J kg\(^{-1}\) K\(^{-1}\)] is the specific heat coefficient of the rock and \(\rho _R\) [kg m\(^{-3}\)] the mass density. The heat flux inside the cylindrical chunk of rock is assumed to obey Fourier’s law

$$\begin{aligned} \varvec{q}=-k_R\nabla u_R, \end{aligned}$$
(2)

with \(k_R\) [Wm\(^{-1}\)K\(^{-1}\)] being the heat conductivity of the rock.

We assume the borehole to form an effectively open-concept coaxial pipe with two separate flow channels: the outer one down and the inner one up. The water will be assumed to enter the outer channel with \(r\in [r_0,r_1]\) at the some inlet temperature \(u_W(0,t)\) [\(^\circ \)C], and to be pumped down the cylinder (increasing z) to a predetermined depth of \(L\) [m] with a mass flow of G(t) [kg s\(^{-1}\)]. The downward-flowing water temperature is assumed to depend only on the depth so that it is given by the two-variable function \(u_W(z,t)\). Assuming slow timescale for the heat transfer in the rock, a large aspect ratio \(r_2/r_1\gg 1\), and advection-dominated heat transfer in the downward-flowing water, the corresponding energy equation can be greatly simplified. In terms of the mass flow G, the differential equation describing the bulk water temperature is given by

$$\begin{aligned} \frac{c_WG(t)}{2\pi r_1}\frac{\partial u_W(z,t)}{\partial z}=h_W(u_W,G)[u_R(r_1,z,t)-u_W(z,t)], \quad z\in [0,L] \end{aligned}$$
(3)

where \(h_W\) [WK\(^{-1}\)m\(^{-2}\)] is the rock–water heat-transfer coefficient and \(c_W\) is the specific heat of the water. The upward-flowing water is assumed to be at a constant temperature of \(u_W(L,t)\)—a hollow vacuum pipe is a good thermal insulator.

For computing the rock–water heat-transfer coefficient \(h_W=\text {Nu}\,k_W/d_h\), we use the Gnielinski correlation for the Nusselt number [17, 18]

$$\begin{aligned} \text {Nu}=\frac{(f/8)(\text {Re}-1000)\text {Pr}}{1+12.7(f/8)^{1/2}(\text {Pr}^{2/3}-1)} \end{aligned}$$
(4)

with the friction correlation developed by Pethukov [19]

$$\begin{aligned} f=(0.79 \ln \text {Re}-1.64)^{-2}. \end{aligned}$$
(5)

The dynamic viscosity \(\nu _W\) and the heat conductivity \(k_W\), which are needed for determining the Reynolds \(\text {Re}=Gd_h/(A\nu _W)\) and Prandtl number \(\text {Pr}=c_Wk_W/\nu _W\), are given by the Vogel–Fulcher–Tammann relation

$$\begin{aligned} \nu _W=0.02939\times 10^{-3} \exp \left( \frac{507.88}{u_W+123.85}\right) \end{aligned}$$
(6)

and by the correlation [20]

$$\begin{aligned} k_W=0.6065 (-1.48445+4.12292 x - 1.63866 x^2), \qquad x=\frac{273.15+u_W}{298.15}, \end{aligned}$$
(7)

where the water temperature \(u_W\) in both formulae is in the units of Celsius. Here \(A=\pi (r_1^2-r_0^2)\) is the cross sectional area of the downward flow channel and \(d_h=2(r_1-r_0)\) the corresponding hydraulic diameter. Note that \(h_W\) has a dependency on the water temperature and flow speed, requiring careful evaluation at different depths and mass flows.

The rock and water temperatures are coupled also via the boundary condition at the borehole wall surface \(r_1\). Mathematically this condition is of a Robin type and can be expressed as

$$\begin{aligned}&k_R\nabla u_R\cdot \varvec{\hat{r}}\Big |_{r=r_1}={\left\{ \begin{array}{ll} h_W(u_W,G)[u_R(r_1,z,t)-u_W(z,t)],\quad &{}z\in [0,L] \\ 0,\quad &{}z\in [L,z_2] \end{array}\right. } \end{aligned}$$
(8)

with \(\varvec{\hat{r}}\) denoting the radial unit vector of the cylindrical coordinate system. The boundary condition for the rock temperature at the outer radius, originating from the periodicity of the well lattice, is of the Neumann type

$$\begin{aligned} \nabla u_R\cdot \varvec{\hat{r}}\Big |_{r=r_2}=0, \quad z\in [0,z_2] \end{aligned}$$
(9)

The boundary condition at \(z=0\) for the rock is also of the Robin type

$$\begin{aligned} k_R \nabla u_R(r,0,t)\cdot \varvec{\hat{z}}\Big |_{z=0}&=h_A [u_R(r,0,t)-u_A], \quad r\in [r_1,r_2], \end{aligned}$$
(10)

where \(u_A\) is the average ambient air temperature at the surface and \(h_A\) the corresponding heat-transfer coefficient. The boundary condition at \(z=z_2\) is dictated by the Earth’s very low heat flux

$$\begin{aligned} k_R\nabla u_R\cdot \varvec{\hat{z}}\Big |_{z=z_2}=q_{\text {earth}}\end{aligned}$$
(11)

which is the reason for the pre-existing rock temperature gradient, and initial temperature profile given by

$$\begin{aligned} u_R(r,z,0) = u_{\text {sur}}+ \frac{q_{\text {earth}}}{k_R}z, \end{aligned}$$
(12)

where \(u_{\text {sur}}\) is the unperturbed surface temperature of the rock. The ambient heat-transfer coefficient can be determined from the equilibrium condition

$$\begin{aligned} h_A=\frac{q_{\text {earth}}}{u_{\text {sur}}-u_A}, \end{aligned}$$
(13)

by measuring the rock surface temperature and the ambient air temperature.

Finally, the thermal power output from the system is the rate of change in the heat content of the flowing water and given by

$$\begin{aligned} P_W(t)=c_WG(t)[u_W(L,t)-u_W(0,t)]. \end{aligned}$$
(14)

The coupled system of partial differential Eqs. (1–3) with the boundary conditions (8–11) and the initial condition (12) is then solved numerically.

3 Results

In order to address the question of longevity, we need to establish a definition for it to begin with. For this purpose, we investigate the overall performance of the geothermal wells over a prolonged period of time by solving the multi-physics problem described in Sect. 2 with a finite-element approach. The program has been implemented in Python, uses linear quadrilateral elements with the mesh packed polynomially near the borehole to resolve steep gradients, and is available upon request from the Authors. The programming paradigm has been to implement a Python class for the solver, which is flexible enough to be used in separate applications to investigate several different scenarios.

For all of the numerical studies in this section we shall assume initial surface and ambient temperatures of \(u_{\text {sur}}=6.0^\circ \)C and \(u_A=5.9^\circ \)C, respectively, a geothermal gradient of 15 \(^\circ \)C/km (\(k_R=3.0\) and \(q_{\text {earth}}=0.05\)), corresponding approximately to the conditions in the Helsinki region in Finland—a city that we shall later use as an example in assessing the potential of the geothermal wells for district heating purposes. We will also set the downward borehole channel dimensions to be \(r_1=0.1\, \text {m}\) and \(r_0=0.05\, \text {m}\), and the water inlet temperature to be \(u_W(0,t)=6.0^\circ \)C corresponding to the rock surface temperature. Once the longevity has been established, we perform several simulations varying the key parameters to obtain useful charts for assessment different instalments.

3.1 Evolution under constant flow and power

To gain a feeling for the behaviour of the water outlet temperature—and consequently that of the power—we first run a few simulations using a fixed mass flow adjusted to reach a desired initial power \(P_0\) and then repeat them by adjusting the mass flow to reach a constant power output. Figure 1 illustrates the temporal evolution of the water outlet temperature for both cases, with solid lines corresponding to the case of constant mass flow and the dashed lines to constant extracted power. In all cases considered, the water temperature at the bottom of the well initially undergoes a fairly rapid exponential drop over a period of 2–5 years. We refer to this as the initial transient phase. After this, the water temperature continues to decrease but at a slower rate, linearly in time. We refer to this as the linear phase.

The detailed parameters for the cases are listed in Table 1, including the inferred values for the depth, duration of the initial transient temperature drop and the rate of the subsequent, mostly linear decay of temperature for the constant mass flow case. From the listed values, we observe that, in the case of constant mass flow, (i) the transient drop depends linearly on the power and is inversely proportional to the well depth, (ii) the duration of the transient is not affected by the desired power or the well depth, and (iii) the rate of decay in the linear phase is directly proportional to the power density and inversely proportional to the well depth.

This behaviour is in line with the results from the simplified analytical model we have described in Appendix A and B, as summarized in the following approximate expressions

$$\begin{aligned} \varDelta t&=0.142\frac{\rho _Rc_R}{k_R}r_2^2, \end{aligned}$$
(15)
$$\begin{aligned} \varDelta u_W(L,\varDelta t)&=-\frac{P_0}{2\pi k_R L} \left[ \ln \left( \frac{r_2}{r_1}\right) -\frac{3}{4}\right] , \end{aligned}$$
(16)
$$\begin{aligned} \partial _tu_W(L, t\ge \varDelta t)&=-\frac{P_0}{ \rho _Rc_R \pi r_2^2L}. \end{aligned}$$
(17)

In fact, the agreement is quite good, with effectively all of the above analytical estimates falling within 10% of the values inferred from the numerical simulations. It is safe to claim that we have a good understanding of the temporal evolution of the wall outlet temperature under constant mass flow.

Fig. 1
figure 1

Temporal characteristics of water outlet temperature under constant mass flow (solid lines) and constant power extraction (dashed lines) for several well configurations (see Table 1)

Full size image
Table 1 Numerical results for the transient size, duration, and the subsequent linear rate of decay corresponding to the solid curves #1–#6 in Fig. 1 (the constant mass flow case). The corresponding analytical estimates are given in parentheses
Full size table

The scenarios with constant power have been implemented because, in real applications, operation of the geothermal well would more likely be based on constant power extraction rather than applying a constant mass flow. In such cases, the temporal behaviour of the outlet temperature deviates somewhat from the cases with constant flow as illustrated by the dashed lines in Fig. 1. It is also apparent that the deviations become more pronounced with increasing extracted power. This partly happens because the mass flow adjustments naturally have to be larger for higher requested power, thus leading to more visually evident relative changes.

Unfortunately, we have not been able to find reasonable analytical estimates for the characteristics of constant power extraction as we have for the constant mass flow case. Essentially, one has to resort to numerical simulations. The only exception to this rule occurs if the transient depth and the rate of linear decay in the constant mass flow case are small enough so that implementing constant power extraction does not lead to an immediate significant increase in the original mass flow. In such cases, the analytical estimates provide a reasonable description of the early temperature evolution as is evident from the cases #1, #3, and #5 in Fig. 1.

3.2 Definition of longevity

To gain a feeling for the longevity of an instalment, we simulate a modified, dynamically evolving scenario. We adjust the mass flow to extract constant power but, if the difference in water inlet and outlet temperatures drops below 3 \(^\circ \)C, the power extraction is halted for 5 years and resumed thereafter. The purpose of this simulation is to demonstrate that, even if the well temperature is allowed to recover for some time, the length of each subsequent period of power extraction drops and severely affects the overall performance of the well. A plausible reason behind this behaviour is the low conductivity of the rock, which drives fast transient-like temperature changes and steep temperature gradients in the rock near the borehole. Over a longer period, the transients of both decay and recovery average out and the overall performance drops.

Figure 2 illustrates such temporal behaviour of the rock and water outlet temperature and the evolution of the instant and cumulative average power together with the necessary mass flow to retain the power at the desired level. The example case is for a 2 km deep well with a target power extraction of 80 kW and the domain radius of \(r_2=30\) m. Although the temperature at the borehole wall and water recover quickly once the power extraction is halted, they drop even faster once the extraction is resumed, as anticipated. Since each subsequent cycle brings the average temperature lower, the average cumulative power extraction drops over time, as indicated by the black dashed line in the right panel of Fig. 2.

Fig. 2
figure 2

Temporal evolution of water and rock temperatures and of instant and average cumulative power for a 2 km deep well with \(r_2=30\,\text {m}\) together with the required mass flow

Full size image

Since a geothermal system providing district heating presumably should perform reliably with approximately constant power extraction on a year-to-year basis, we shall define our concept of the well longevity as the first time it takes for the system to reach the water inlet–outlet temperature difference of 3 \(^\circ \)C. This should guarantee an appropriate safety margin. The specific value for the trigger condition is of course a free parameter, and moreover, the inlet temperature could be lower than the 6.0 \(^\circ \)C we have used. It should nevertheless remain somewhat above zero to prevent the water from freezing when it comes back from the evaporator at the heat pump.

3.3 Parametric dependency of longevity under constant power extraction

With the definition for longevity as the time to reach a 3\(^\circ \)C inlet–outlet temperature difference, we are finally in the position to perform the parameter scans with respect to the domain size reserved for individual wells and to the power extracted from the well under a constant load. The results for 2 km and 3 km deep wells are recorded in Fig. 3. The black solid level sets represent the longevity in years and the dashed red level sets the power density any configuration would provide. Parameters are chosen to cover a wide range of plausible operation scenarios with longevities ranging from 10 to 450 years and beyond.

Fig. 3
figure 3

Level sets of longevity [years] (black solid curves) and power density [Wm\(^{-2}\)] (dashed red curves) for 2 km (left panel) and 3 km (right panel) deep geothermal wells from the numerical simulations. The domain in lower right corner would contain level sets with longevity values beyond 450 years and is thus omitted

Full size image

The behaviour in Fig. 3 is largely in line with our previous analysis and the analytical formulae. The longevity is improved by (i) increasing the domain reserved for a single well, (ii) lowering the extraction power, (iii) increasing the depth of the bore. The scaling with \(r_2\) arises because the approximate linear decay rate is linearly proportional to the power density. There is however a limit to this trend, especially at higher extraction powers where the longevity improves only little with increasing \(r_2\). In such case, the initial transient, with a weak logarithmic dependency on the domain size, dominates.

The parametric scans also make it apparent that, at a given power density level, longevity is increased by drilling more holes closer to each other and reducing the power extracted from an individual well. From an economic perspective one would, of course, opt for the minimum number of boreholes that is able to meet both the requisite longevity and power density.

A useful observation can be made after interpreting the formulae (16) and (17) slightly differently. If expressed in terms of the relative changes in power, the formulae transform into the dimensionless expressions

$$\begin{aligned} \frac{\varDelta P(\varDelta t)}{P_0}&=-\frac{P_0}{2\pi q_{\text {earth}}L^2} \left[ \ln \left( \frac{r_2}{r_1}\right) -\frac{3}{4}\right] , \end{aligned}$$
(18)
$$\begin{aligned} \varDelta t\frac{\partial _tP(t\ge \varDelta t)}{P_0}&=-0.284\frac{P_0}{2 \pi q_{\text {earth}}L^2}. \end{aligned}$$
(19)

One can further deduce the time \(t_F\) it would take for the power to drop to a fraction F of the initial power \(P_0\):

$$\begin{aligned} t_F=\varDelta t \left[ 1+3.52\left( \frac{2\pi q_{\text {earth}}L^2}{P_0}F+\ln \frac{r_1}{r_2}+\frac{3}{4}\right) \right] , \end{aligned}$$
(20)

This formula naturally requires the initial transient power drop to be less than 100% and assumes a constant mass flow.

The analytical expression for \(t_F\) predicts that, in the case of constant mass flow, the longevity would remain constant if the ratio \(L^2/P_0\) remains constant and other parameters are fixed. Moreover, setting \(F=1\) would provide the maximum expected lifetime. In the case of constant power extraction, though, we know from Fig. 1 that this relation is not exactly true but instead should provide an upper limit of sorts for the longevity. In particular, we could expect the formula to be reasonably accurate in predicting the longevity timescale if we set F just right. Additionally, if we have existing data available, for example the longevity level sets from Fig. 3, the analytical expression tells us that we can scale the data by keeping the ratio \(L^2/P_0\) constant to get an estimate of the lower limit of longevity for deeper wells.

We can demonstrate this behaviour by “lifting” the longevity level sets of the 2 km deep well from Fig. 3 to a depth of 3 km via using the scaling \(L ^2/P\) and by comparing the result with the analytical estimate. This is illustrated in Fig. 4 where, for every lifted level set of the 2 km deep well longevity, we observe that the 3 km deep well would last somewhat longer (left panel), as expected, whereas almost all of the analytically estimated longevity values are somewhat above the numerically calculated ones (right panel). In particular for power values for which the initial transient is not too severe, Fig. 4 demonstrates a reasonably good agreement between all the three options. Furthermore, since the red, dashed level sets in the left panel are consistently below the numerically computed level sets, the scaling \(L^2/P\) can be used for a quick and safe estimation of the lower limit performance of deeper wells based on available data.

Finally, in comparisons of the performance of shallow geothermal wells, we note that the parameter of interest is often the so-called line power P/L. In the case of intermediate-to-deep geothermal wells, the correct parameter of interest ought to be \(P/L^2\) instead. This observation is duly supported by both analytical theory and numerical simulations.

Fig. 4
figure 4

Comparison of the longevity level sets for the 3 km well (solid, black) with those of a “lifted” 2 km well with respect to keeping the ratio \(L^2/P\) constant (dashed, red, left panel) and those from the formula (20) with \(F=1/2\) (dashed, blue, right panel)

Full size image

4 Discussion and instructions for policy makers

The final aspect regarding the applicability of intermediate-to-deep geothermal wells for district heating purposes is, of course, the question of whether it can meet the demand from the standpoint of district heating. In Finland, the annual heat consumption per person is approximately 10 MWh [21] and in the city of Helsinki, with an average population density of 3060/km\(^2\) [22], the annual average heat requirement would correspond to 3.5 W/m\(^2\). Excluding the green areas, the population density in Helsinki, however, easily climbs to the range of 6000–9000/km\(^2\) and peaks at around 15000/km\(^2\) [22], corresponding to a typical annual power density demand of 7–10 W/m\(^2\) and with local peaks of up to 17 W/m\(^2\).

As can be seen from Fig. 3, both the 2 and 3 km wells could match the minimum power density requirement of 3.5 W/m\(^2\) as there are several configurations up and left of the red dashed curve of 4 W/m\(^2\). In Table 2 we list some combinations that all meet the power density requirement of 4 W/m\(^2\) and may hence theoretically provide the necessary level of district heating for Helsinki.

Rather than seeking to meet the minimum power requirement, the challenge lies in optimizing the number of necessary boreholes, the total area reserved for the wells and the surface infrastructure, and the longevity of the entire system. For example, settling for the power density of 4 W/m\(^2\) would mean covering the entire city area with the wells placed equidistantly from each other. In such a case, it might be challenging to organize the supportive piping and other infrastructure needed on the surface to deliver the heat to apartments that are located at denser clusters and potentially far away, especially if small unit sizes are used to improve the longevity.

Table 2 Examples of wells from Fig. 3 that meet a minimum power density requirement of 4 W/m\(^2\). The # of units and the percentage of land use are based on the requirements for covering the requirements of district heating in Helsinki
Full size table

One of the most important things to keep in mind is that, once the well has been depleted, its rather modest ability to recover leads effectively to a single-use solution unless additional charging is provided. This, however, would merely convert the well from a heat source into a heat storage, incurring additional, perhaps significant electricity costs. Hence, in sizing the well, one should consider choosing a configuration which guarantees a sustainable level of longevity and does not require re-drilling of the bore holes every few years.

Finally, if technology and financing permits, one should always consider drilling as deep as possible, all the way to depths of 4+ km. According to the parameter of interest, \(L^2/P\), the approximate lower limit for longevity decreases linearly with increasing power but increases quadratically with increasing well depth. For example, as is evident in Fig. 3, a 40 kW and 2 km deep well with a radius of \(r_2=40\, \text {m}\) has a longevity of 200 years, whereas a 3 km deep well with the same domain radius and longevity can extract approximately \((3/2)^2=2.25\) times more power, namely 90 kW. Thus using 3 km deep wells, the total length of boreholes drilled in this case could be reduced down to \(3/(2\times 2.25)=0.667\) times the total length required from 2 km deep wells. While it is conventional to think of the gain from shallow geothermal wells and surface heat applications as scaling with respect to the so-called linear power P/L, in the case of intermediate-to-deep wells, the approximate scaling is a far more favourable \(P/L^2\).

5 Summary

In this paper, we have analysed the longevity and power density of intermediate-to-deep geothermal wells for district heating purposes. We have provided numerical simulations for the parametric dependency of longevity on the well specifications and also derived useful analytical formulae to facilitate quick assessment of the associated temporal characteristics. The simulations and analytical formulae confirm that the key parameter of interest in analysing the longevity and performance of intermediate-to-deep geothermal wells is the ratio \(L^2/P\), with L being the well depth and P the requisite power. This scaling is far more favourable than the linear L/P rubric typically used in analysing shallow wells. This is because drilling twice as deep allows one to draw not twice but at least four times more power without reducing the longevity of the well. These results have been subsequently used to identify a variety of intermediate–deep geothermal well configurations, which would theoretically comply with the district heating needs of the city of Helsinki.

Since large urban areas cannot be easily moved from one location to another, a thorough understanding of the longevity of the planned heat sources is of paramount importance: inefficiently chosen parameters could result in quick decay of the heat source, after which it would take an unacceptably long timescale to recover. Aiming for an overly high power density via shallow wells may quickly drain and render them useless only in a few decades while moderating the power density and drilling deeper gives rise to installations that potentially last for several hundred years.