1 Introduction

A long-standing problem in theoretical physics is the issue of quantum gravity, how to merge general relativity with quantum field theory. Although substantial effort has been put forth for several decades, there is to date no clearly compelling candidate model. The main problem is that general relativity is not perturbatively renormalisable, which is a serious obstacle for standard quantisation techniques, leading to the breakdown of general relativity at small scales. Many models have been proposed to deal with this problem, such as string theory and loop quantum gravity, and while these theories do resolve some of the problems of general relativity, there are few avenues available to test them [1, 2]. Indeed, the fact that general relativity has passed every test so far indicates that it is an excellent model for the infrared (IR) behaviour or quantum gravity. This is natural since quantum gravitational effects are expected to emerge at energies close to the Planck energy. A natural course of action is then to study ultraviolet (UV) completions of general relativity, for example [3, 4]. Another interesting proposal for a UV-complete theory of gravity is Hořava–Lifshitz gravity, which contains general relativity as an IR fixed point [5]. The original formulation had problems such as ghost modes and instabilities, which were subsequently addressed in a series of papers, see for example [6,7,8]. Since then, much work has been done on the subject, ranging from cosmological studies [9,10,11,12,13,14,15,16], dark energy [17, 18], bouncing scenarios [19, 20], and strong coupling [21] among others. Hořava–Lifshitz gravity is a perturbatively renormalisable theory of gravity, which is accomplished by introducing a Lifshitz scaling between space and time in the UV [5] which explicitly breaks Lorentz invariance. It is important to mention that Lorentz invariance is a building block of modern physics, and breaking it may seem counterintuitive; however, since the Planck scale and quantum gravity likely will contain completely new physics on quantum scales it is useful to not a priori assume Lorentz invariance, which is a continuous symmetry, in this sector.

Recently, various measurements of the Hubble constant, \(H_0\), have revealed a discrepancy between the value at high and low redshift, respectively. In fact, this discrepancy has been confirmed by many independent observations (using \(\varLambda \)CDM as a background model) at low (quasars [22], gravitational waves [23,24,25], Cepheid stars [26,27,28]) and high (Cosmic Microwave Background [29], Baryon Acoustic Oscillations [30, 31], the inverse distance ladder [32, 33]) redshift. The difference in the value of the \(H_0\) from these different observations lies around 4–9%. Many scenarios have been put forth as explanations or alleviations of the \(H_0\) tension, for example dynamical dark energy [34], screened fifth forces [35], the late decay of dark matter [36] and more, but the \(H_0\) tension has proved difficult to resolve. In this paper, we investigate the presence of a preferred frame in the Universe and its effect of the \(H_0\) tension. Working in a Hořava–Lifshitz model, we constrain the discrepancy between our local frame and the preferred frame; moreover, we suggest that part of the Hubble constant discrepancy is due to Lorentz violation in the ultraviolet regime.

2 Hořava–Lifshitz gravity

Hořava–Lifshitz gravity is a proposal for a nonrelativistic theory of gravity, which breaks Lorentz invariance in the UV regime by introducing an anisotropic Lifshitz scaling between space and time of the form \(t\rightarrow b^{-z}t\), \(x^i\rightarrow b^{-1}x^i\) (breaking Lorentz invariance), where z is a critical exponent [5]. Lorentz invariance is restored for \(z=1\), but in order to obtain power-counting renormalisability it is necessary to have \(z\ge 3\) (for 3 spatial dimensions) [37], and we will set \(z=3\). The theory is power-counting renormalisable and is a candidate theory of quantum gravity. In the IR, the theory reduces to that of general relativity. Much work has been done on this theory, including some early contributions to cure some of the original inconsistencies [7,8,9, 11, 12, 14, 18, 19, 21, 38,39,40,41,42,43,44,45]. The presence of the anisotropic scaling in the theory leads to a natural description using the Arnowitt–Deser–Misner (ADM) formulation, in which the metric reads:

$$\begin{aligned} \hbox {d}s^2 = -N^2\hbox {d}t^2+g_{ij}\left( \hbox {d}x^i+N^i\hbox {d}t\right) \left( \hbox {d}x^j+N^j\hbox {d}t\right) , \end{aligned}$$
(1)

where N and \(N^j\) are the lapse function and the shift vector, which determine the foliation of spacetime by constant-time spacelike hypersurfaces. The breaking of Lorentz invariance in ultraviolet Hořava–Lifshitz gravity manifests as the appearance of a preferred foliation of spacetime, and the symmetry is most commonly assumed to be broken down to \(t\rightarrow \xi _0(t)\), \(x^i\rightarrow \xi ^i(t,x^k)\). Then, the theory is endowed with the foliation-preserving diffeomorphism group, denoted \(\text {Diff}[M,\mathcal {F}]\), where M is the manifold and \(\mathcal {F}\) is the preferred frame. Given this, we can write down the most general form of the theory as:

$$\begin{aligned} S=\int \hbox {d}^3x \hbox {d}t N \sqrt{g}\left[ K^{ij}K_{ij}-\lambda K^2-\mathcal {V}(g_{ij})\right] , \end{aligned}$$
(2)

where g is the determinant of the spatial metric, \(\lambda \) is a running coupling and \(\mathcal {V}\) is a potential. \(K_{ij}\) represents the extrinsic curvature of the foliation. The potential term contains only dimension 4 and 6 operators which can be constructed from the spatial metric \(g_{ij}\). Under the so-called detailed balance and projectability conditions, the action reads [43]:

$$\begin{aligned} S&= \int \hbox {d}t\hbox {d}^3x\sqrt{g}N\Bigg [\frac{2}{\kappa ^2}\left( K_{ij}K^{ij}-\lambda K^2\right) +\frac{\kappa ^2}{2w^4}C_{ij}C^{ij}-\frac{\kappa ^2\mu }{2w^2}\frac{\epsilon ^{ijk}}{\sqrt{g}}\mathcal {R}_{il}\nabla _j\mathcal {R}^i_k \nonumber \\&\quad +\frac{\kappa ^2\mu ^2}{8}\mathcal {R}_{ij}\mathcal {R}^{ij}+\frac{\kappa ^2\mu ^2}{8(1-3\lambda )}\Bigg (\frac{1-4\lambda }{4}\mathcal {R}^2+\varLambda \mathcal {R}-3\varLambda ^2\Big )\Big ] \end{aligned}$$
(3)

where \(\nabla _j\) is the spatial covariant derivative, \(\epsilon \) is the totally antisymmetric tensor, and \(\mu , w\), and \(\kappa \) are dimensionful constants (mass dimension 1, 0, \(-1\), respectively). Any higher-order terms are assumed to be Planck suppressed by \(M_\mathrm{Pl}^{-n}\) (at order n), where \(M_\mathrm{Pl}\) is the Planck mass. \(C^{ij}\) is the Cotton tensor, and \(\mathcal {R}_{ij}\) is the Ricci tensor related to the spatial metric. This action has been obtained from (2) by analytic continuation of the parameters \(\mu \) and \(\omega ^2\), which enables positive values of the bare cosmological constant \(\varLambda \), which does not occur in the original formulation of Hořava–Lifshitz gravity.

Although the detailed-balance condition leads to a succinct action, there is an ongoing debate in the literature whether this formulation is too restrictive. In fact, there are a number of problems with the detailed-balance scenario, such as instabilities, strong coupling at low energies, as well as problems with the value of the cosmological constant [9, 11, 37, 44]. As such, we choose to focus our efforts on the so-called beyond detailed balance scenario [21, 43, 46,47,48], where it is possible to include more terms in the potential \(\mathcal {V}\). Then, using the FLRW line element and populating the Universe with the canonical matter fields, the first Friedmann equation can be written:

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^2 = \frac{2\sigma _0}{3\lambda -1}(\rho _m+\rho _r)+\frac{2}{3\lambda -1}\left[ \frac{\varLambda }{2}+\frac{\sigma _3K^2}{6a^4}+\frac{\sigma _4K}{6a^6}\right] +\frac{\sigma _2K}{3a^2(3\lambda -1)}. \end{aligned}$$
(4)

Here, the objects \(\sigma _i\) are arbitrary constants.

3 Bounds on Hořava–Lifshitz gravity from the \(H_0\) tension

3.1 \(H_0\) tension as a preferred-frame effect

In [49], the authors suggest that the discrepancy [26, 50] between the value of the Hubble parameter \(H_0\) from CMB measurements and from local data is in fact a reference-frame artefact. Since Hořava–Lifshitz gravity is based on a preferred frame is it natural to also pose this question in this model. Following [49], we use a flat FLRW metric and define a geodesic observer in the CMB frame as \(v^\mu = (\sqrt{1+(\zeta /a)^2},0,0,\zeta /a^2)\), where \(\zeta \) is a parameter and a is the FLRW scale factor. For this observer, the metric takes the form:

$$\begin{aligned} \hbox {d}s^2 = -\hbox {d}T^2+a^2(T;Z)\left( \hbox {d}X^2+\hbox {d}Y^2+(1+(\zeta /a)^2)/(1+\zeta ^2)\hbox {d}Z^2\right) . \end{aligned}$$
(5)

Following [49], we use the transformation which relates the Hubble constant in the local geodesic frame to that in the CMB frame:

$$\begin{aligned} \frac{H_0^{\mathrm{CMB}}}{H_0^\mathrm{local}} = \frac{1}{\sqrt{1+\zeta ^2}}. \end{aligned}$$
(6)

Hence, the local measurement has to be larger than or equal to its CMB counterpart. The two values will coincide when \(\zeta \rightarrow 0\). We find the low and high-redshift values of the Hubble parameter using a Markov-Chain Monte Carlo analysis. Here, we adopt a methodology similar to [51] by using several different data sets from a wide, yet local, redshift range. For the local value of the Hubble constant, we use the PANTHEON dataset of supernovae type Ia [52], along with expansion rates of elliptical and lenticular galaxies [53], gamma-ray bursts [54] and quasars [55]. These sources are all within redshift range \(0.01<z<8.2\), a large redshift range with multiple sources which we define as our “local“ frame, as compared to the \(z\sim 1040\) for the CMB frame. For details of the method, see [9] and for a detailed discussion of how to obtain cosmological parameters in Hořava–Lifshitz gravity, see [56]. We find that \(H_0^\mathrm{local} = 70.18 \pm 0.02~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\) at 99.7%. Moreover, for the high-redshift (early Universe) value of the Hubble parameter we use Planck CMB data [29]. We find that, at 99.7%, the Hubble constant is \(67.21^{+5.1}_{-4.4}~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\), and using these two values of the Hubble constant in (6) we find that the parameter \(\zeta \), quantifying the discrepancy between the local frame and CMB frame, is (disregarding any negative values in order to keep \(\zeta \) real):

$$\begin{aligned} 0\le \zeta ^2 \le 0.25. \end{aligned}$$
(7)

As suggested in [49], we have found bounds on the parameter \(\zeta \) from observations of the Hubble parameter. Thus, \(\zeta \) defines a geodesic reference frame where the observed \(H_0\) tension would emerge naturally.

3.2 The \(H_0\) tension and the Hořava parameter \(\lambda \)

It is known that in Lorentz-violating field theories, the gravitational constant measured locally, \(G^\mathrm{local}\) does not coincide with the cosmological one [57]. In fact, we will show that also the gravitational constant can be thought of as frame dependent, and we will give it a superscript, \(G^{\mathrm{CMB}}\), to show that this is the value in the CMB frame. We may derive from Eq. (4) that the value of the gravitational constant at different energy scales is related by a single Hořava parameter [48]:

$$\begin{aligned} G^{\mathrm{CMB}} = \frac{2}{3\lambda ^{\mathrm{CMB}}-1}G^\mathrm{local}, \end{aligned}$$
(8)

where the superscript on \(\lambda \) is to highlight that it is the value of \(\lambda \) at the time of recombination. The infrared fixed point \(\lambda \rightarrow 1\) represents General Relativity, which is also when \(G^{\mathrm{CMB}} = G^\mathrm{local}\). Clearly, in this scenario, dynamics will be different on cosmological scales. This also has implications for the Hubble tension. We can write down a general form of the first Friedmann equation in the two frames as:

$$\begin{aligned} (H_0^{\mathrm{CMB}})^2&= \frac{8\pi }{3}G^{\mathrm{CMB}} \rho _0 \end{aligned}$$
(9)
$$\begin{aligned} (H_0^\mathrm{local})^2&= \frac{8\pi }{3}G^\mathrm{local} \rho _0 \end{aligned}$$
(10)

where \(\rho _0\) is the total energy density, which is the same in the two frames. On this basis we arrive to the same as (8) by dividing (9) by (10):

$$\begin{aligned} \left( \frac{H_0^{\mathrm{CMB}}}{H_0^\mathrm{local}}\right) ^2 = \frac{G^{\mathrm{CMB}}}{G^\mathrm{local}} = \frac{2}{3\lambda ^{\mathrm{CMB}}-1}. \end{aligned}$$
(11)

In the above relation, we have to assume that Lorentz violation only contributes to the Hubble tension rather than being the only cause of it. In light of this, it would be more accurate to write the right-hand side as \(2/(3\lambda ^{\mathrm{CMB}}-1) + f(\mathbf {\theta })\), where \(f(\theta )\) is an unknown function of one or more parameters. We can now use available Hubble constant data to put constraints on the parameter \(\lambda \), and also estimate the contribution of Lorentz violation to the Hubble tension.

3.2.1 Constraints on \(\lambda ^{\mathrm{CMB}}\)

Currently, the most accurate measurements of the Hubble constant come from the local distance ladder (\(74.03 \pm 1.42~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\) [26, 50, 58]) and Planck CMB (\(67.4 \pm 0.5~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\) [29]). Ignoring any model dependence of these bounds, we use Eq. (11) to find that \(\lambda ^{\mathrm{CMB}} = (0.86, 0.92)\) at 99.7%. Note that overlooking the model dependence of these constraints is a strong assumption (especially for the CMB value). Also note that all bounds on \(\lambda \) (with one exception) are derived constraints; in [56] we consider \(\lambda \) a free parameter and place constraints on it from cosmological data. This can be compared to the limits on \(H_0\) which we obtained in Hořava–Lifshitz using the beyond detailed balance formulation (\(H_0^\mathrm{local} = 70.18\pm 0.02~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\), \(H_0^{\mathrm{CMB}} = 67.21^{+5.1}_{-4.4}~\hbox {km s}^{-1}~\hbox {Mpc}^{-1}\)). Indeed, using those values of the Hubble parameters we arrive at \(0.95 \le \lambda ^{\mathrm{CMB}} \le 1.16\) at 99.7% confidence level. The bounds on \(\lambda ^{\mathrm{CMB}}\) from local distance ladder and Planck data are problematic, since \(1/3< \lambda < 1\) generally leads to ghost instabilities in the IR limit [47], whereas the limit from the Hubble parameters found from MCMC analysis of Hořava–Lifshitz still overlap with a non-pathological region.

From the same MCMC analysis which provided the bounds on the Hubble parameters, we also obtained direct constraints on \(\lambda ^{\mathrm{CMB}} = 1.06\pm 0.024\). This is encouraging, since the whole range lies in the non-pathological region for \(\lambda \); however, these constraints are less stringent than those in [56] and should be seen as indicative only. A summary of all derived limits can be seen in Table 1.

3.2.2 Constraints on the Hubble parameter

Using available constraints on \(\lambda \), we can get a value of the Hubble tension through Eq. (11). To our knowledge there is only one bound in the published literature, namely \(\lambda = (0.97, 1.01)\) [48]. Using this we find that \(H^{\mathrm{CMB}}/H^\mathrm{local} = (0.98, 1.01)\). This can be compared to the value from local distance ladder and Planck CMB measurements, where the same ratio works out to \(H^{\mathrm{CMB}}/H^\mathrm{local} = (0.89, 0.94)\). The central value of this interval is 0.915, leading to a Hubble tension of 8.5%. Taking a conservative approach, we use the upper bound of the calculated Hubble ratio from [48] and comparing to the observed 8.5% Hubble tension means that in this scenario, Lorentz violation can be the source of up to 12% of the Hubble tension. It is important to keep in mind that the constraints on \(\lambda \) in [48] were derived using a large set of cosmological data from both high and low redshift, and the resulting value must be considered an average\(\lambda \). However, since it is the only (to our knowledge) published constraint on \(\lambda \) so far, we have used it, keeping in mind the above discussion. Since \(\lambda \) runs with energy, we can assume that it was larger in the early Universe and therefore likely contributes more to the observed Hubble tension than our bound of \(\le 12\%\) indicates.

We may also use our derived constraints on \(\lambda ^{\mathrm{CMB}} = (0.95,1.16)\) and assuming Lorentz violation is the only source of the Hubble tension, the corresponding tension is 3.8%. By again comparing to the observed 8.5% this we can infer that, at 99.7% confidence level, Lorentz violation can be the source of up to 44.7% of the Hubble tension.

Finally, we may also use our direct constraint \(\lambda ^{\mathrm{CMB}} = 1.04\pm 0.024\). In order to find the most conservative estimate, we use the upper bound of \(\lambda ^{\mathrm{CMB}}\), which combined with the measured Hubble tension of 8.5% leads to a possible contribution of Lorentz violation of up to 38%. This is our main result.

Table 1 Summary table of constraints on preferred-frame effects on the Hubble tension, as well as constraints on \(\lambda \) and the Lorentz violation contribution to the Hubble tension
Full size table

4 Cosmographic analysis

Cosmography is a model-independent method for approximating the luminosity distance and scale factor as a series expansion. In doing this, one can obtain constraints on the expansion coefficients directly from data, without any of the underlying assumptions except for homogeneity, isotropy, and fixed spatial curvature [59] (for a discussion on cosmography in Hořava–Lifshitz gravity, see [60]). From the expansion of the scale factor, it is convenient to define the following quantities:

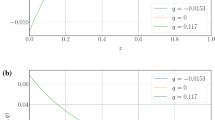
$$\begin{aligned} q = -\frac{1}{aH^2}\frac{\hbox {d}^2a}{\hbox {d}t^2}, \quad j = \frac{a}{H^3}\frac{\hbox {d}^3a}{\hbox {d}t^3}, \quad s = \frac{a}{H^4}\frac{\hbox {d}^4a}{\hbox {d}t^4}, \quad l = \frac{a}{H^5}\frac{\hbox {d}^5a}{\hbox {d}t^5}, \end{aligned}$$
(12)

called deceleration, jerk, snap, and lerk, respectively. These quantities can be directly bounded by observation, serving as a model-independent way of characterising the cosmological behaviour of the Universe. For example, the deceleration parameter measured today (denoted by index 0) is \(q_0<0\), indicating that the Universe is currently dominated by some kind of repulsive dark energy-type field, whereas \(s_0\) and \(l_0\) characterise the dynamics of the early Universe.

We can rewrite Eq. (4) (in the flat case) to

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^2 = \frac{2}{3\lambda -1}\left[ \varOmega _m a^{-3}+\varOmega _r a^{-4}+\varOmega _\varLambda \right] , \end{aligned}$$
(13)

where we have also neglected the dark-radiation term since it will be of order \(10^{-3}\) even in the very early Universe. As such, this simplified model represents flat \(\varLambda \)CDM scaled by the parameter \(\lambda \). Given Eqs. (12) and (13), and using that \(\varOmega _m = 0.324\), \(\varOmega _r = 9.24 \cdot 10^{-3}\) [56], we find the values of the cosmographic parameters for this model, which are presented in Table 2, for both \(\lambda ^{\mathrm{CMB}} = 1.06\) and \(\lambda ^{\mathrm{CMB}} = 1.04\) (we set \(\lambda ^{\mathrm{local}}\) to unity). Here, we have used the central values for \(\lambda \). The values for \(q_0\) and \(j_0\) are the same since those expressions are independent of \(\lambda \). All of these values lie within the \(1\sigma \) likelihoods presented in [59]; therefore, they deviate very little from the \(\varLambda \)CDM model. The cosmological behaviour of the cosmographic parameters can be seen in Fig. 1.

Table 2 Values of the cosmographic parameters using the central values for \(\lambda ^{\mathrm{CMB}}\)
Full size table
Fig. 1
figure 1

Cosmological behaviour of the cosmographic functions over time. Here, \(t=1\) represents the value today

Full size image

We now wish to examine the behaviour of luminosity distance, which can be written as:

$$\begin{aligned} d_L(z) = \frac{1+z}{H_0}\int _0^z \left[ \frac{2}{3\lambda -1}\left( \varOmega _m (1+z^\prime )^{3}+\varOmega _r (1+z^\prime )^{-4}+\varOmega _\varLambda \right) \right] ^{-1/2} \hbox {d}z^\prime . \end{aligned}$$
(14)

Here, we do not use a cosmographic expansion; instead, we wish to investigate how the behaviour of \(d_L(z)\) differs when using different values for \(H_0\) and \(\lambda \). This can be seen in Fig. 2 along with flat \(\varLambda \)CDM for comparison. At redshift \(z = 8.2\), which is the upper limit for our non-CMB data, the two Hořava models differ from \(\varLambda \)CDM by 3.6% and 9%, for the different values of \(\lambda ^{\mathrm{CMB}}\), where the CMB frame discrepancy is to be expected. The Hořava model approaches \(\varLambda \)CDM as \(\lambda \rightarrow 1\).

Fig. 2
figure 2

General behaviour of the luminosity distance \(d_L\) as a function of redshift

Full size image

In light of the above discussion we note the following: our Hořava–Lifshitz model for flat FLRW is merely a scaling of the \(\varLambda \)CDM model, but with a running scaling parameter; indeed, using the CMB value for \(\lambda \) to characterise all of cosmic evolution is something of a worst-case scenario which gives rise to the discrepancy in the luminosity distance as shown in Fig. 2. This difference in luminosity distance functions should actually make the Hubble tension even worse in Hořava–Lifshitz gravity, since the discrepancy between the two Hořava curves is larger than compared to the \(\varLambda \)CDM case.

Standard cosmography where one uses a Taylor expansion of \(d_L\) is only accurate for very low redshift; however, it is possible to use Padé or Chebyshev polynomials to get expansions valid out to redshift \(z\sim 2{-}3\) [59, 61, 62]. Since we have used analytic expressions for \(d_L\) in this analysis (integrated numerically), it is unlikely that using a series expansion will improve upon the situation, as our local data reaches well beyond the convergence radius of the cosmographic method. Since our expressions allow for the possibility of a tension in the Hubble parameter, and since the cosmographic parameters in Table 2 are in agreement with data, we expect similar behaviour as for \(\varLambda \)CDM, albeit with a larger Hubble tension. This may shrink to that of \(\varLambda \)CDM if one consider the case of a dynamical \(\lambda \).

5 Discussion and conclusions

In this article, we have provided new bounds on preferred-frame effects and Hořava–Lifshitz gravity through the \(H_0\) tension. Using a value for \(H_0\) in the CMB frame for Hořava–Lifshitz gravity along with a local value, we were able to place bounds on \(\zeta \), which determines the transformation from the CMB frame to the local geodesic frame. In [63], the authors point out an interesting consequence of a preferred frame. If the frame \(\mathcal {F}\) moves relativistically with respect to the CMB frame, there would be an observable effect in the form of a dipole anisotropy of high-energy cosmic rays in the sky. In fact, according to [64], there are indications of this at intermediate scales at \(3.4\sigma \) significance, with no known specific sources in the direction of the hotspot. These results are based on the observation of the northern hemisphere from May 2008 to May 2013, yielding 72 cosmic-ray events with energies higher than 57 EeV.

We have also founds tentative bounds on the Hořava–Lifshitz parameter \(\lambda \) using Hubble constant data; we find that some of these bounds overlap significantly with regions known to lead to ghost instabilities in the infrared limit of the theory, but that some bounds also cover a non-pathological parameter space of this model and discussed their implications. Furthermore, we have used available bounds on \(\lambda \) to estimate how much Lorentz-violating effects could contribute to the Hubble tension. Most significantly, we find that Lorentz violation can contribute to up to 38% of the Hubble tension when using our own bounds on \(\lambda \) from the beyond detailed balance scenario along with Planck CMB data. We also derived the cosmographic parameters for our model in a simple case. In light of this discussion it would make sense to also consider Lorentz-violating field theories in the search to find an explanation for the Hubble tension.