Advertisement

Network concepts for analyzing 3D genome structure from chromosomal contact maps

  • Jean-Baptiste Morlot
  • Julien MozziconacciEmail author
  • Annick LesneEmail author
Open Access
Research
First Online:

Abstract

Background

The recent experimental technique of chromosome conformational capture gives an in-vivo access to pairwise contact frequencies between genomic loci. We present how network analysis can be exploited to extract information from genome-wide contact maps.

Methods

We recently proposed to use graph distance for deriving a complete distance matrix from sparse contact maps. Completed with multidimensional scaling (MDS), this network-based method provided a fast algorithm, ShRec3D, for reconstructing 3D genome structures.

Results

We here develop an extension of this algorithm, by devising a tunable variant of the graph distance and introducing an alternative implementation of multidimensional scaling. This extended algorithm is shown to be more flexible so as to accommodate additional experimental constraints, focus on specific spatial scales, and produce tractable representations of human data.

Conclusions

Network representation of genomic contacts offers a path where physical and systemic approaches are joined to unravel the biological role of the 3D genome structure.

Keywords

3D genome structure Contact map Network analysis Graph distance 

Abbreviations

ChIA-PET

Chromatin interaction analysis using paired end tags

FISH

Fluorescence in situ hybridization

MDS

MultiDimensional scaling (with two variants, cMDS: classical MDS and mMDS: nonclassical metric MDS)

ShRec3D

Shortest-path 3D reconstruction algorithm

Background

A recent experimental technique, chromosome conformation capture, gives access to pairwise contacts between genomic sites in populations of living cell nuclei [1, 2, 3]. Completed with observations obtained by imaging techniques, it provides increasing evidence of the functional importance of the 3D genome structure, e.g. in the regulation of gene expression [4, 5]. Conformation capture data are usually processed into contact maps. We explore the benefits of considering a contact map as the adjacency matrix of an undirected graph, accordingly termed a contact network.

A first interest, reviewed in Section “Contact maps and contact networks”, is to use the concepts developed in statistical physics for complex network analysis [6, 7]. This path has already been explored to characterize the native structure of proteins [8]. In the genomic context, the challenge lies in the large size of the contact maps, their sparseness, and the fluctuating nature of the genome conformation, averaged over cells and time in the experiment.

A second interest, presented in Section “3D genome structure reconstruction”, is to use the contact network representation to compute the graph distance between any pair of genomic sites, including those displaying no (or very few) contact(s). It has been exploited in [9] to devise a fast reconstruction algorithm, named ShRec3D for Shortest-path 3D Reconstruction to underline the importance of taking graph distance as a starting point of multidimensional scaling methods for reconstructing the underlying 3D genome structure.

We propose in Section “Results and discussion: an extension of ShRec3D for human genome” an extension of this reconstruction algorithm, involving a tunable graph distance and two different MDS implementations. In the line of experiments using fluorescence in-situ hybridization (FISH) data, which evidenced a power-law correlation between contact frequencies and measured distances [2], we explore the relationships between the contact frequencies, the graph distances, and the distances within the reconstructed 3D structures. We dissect the transformations achieved by the different steps of the algorithm and benchmark its possible variants. As a result, we identify a trade-off between controlling the reconstruction at small scales or at large scales, and propose operational options for exploiting real data, typically human data in normal and pathological situations.

Contact maps and contact networks

Chromosome conformation capture

Chromosome conformation capture is an experimental protocol, implemented in a population of living cell nuclei, in which genomic sites are crosslinked pairwise when they are close enough in the nuclear space. These crosslinks are mediated by DNA-bound proteins, which are sensitive to the chemical (formaldehyde) used in the protocol. Then steps of restriction digestion, ligation, inverse crosslink and sequencing allow the identification of contacting genomic fragments, producing for each pair (i,j) a number of reads C ij . We focus on the analysis of genome-wide conformation capture data, known as Hi-C data [2]. This high-throughput technique has a limited resolution of several kilobases (kbs), down to fragments of 1kb in a recent implementation [3]. Data are often coarse-grained, by aggregating genomic fragments into larger bins, in order to reach good statistics. Numbers of reads are then processed to remove experimental biases and filter out noise. The resulting components are either thresholded to produce a binary contact matrix, as sketched in Fig. 1 a, or normalized into contact frequencies [10]. Both options preserve the symmetry of the matrix and produce a contact map F.
Fig. 1

Scheme of a contact map and associated contact network. a Each axis represents the linear position along the genome. A black pixel (i,j) and the symmetric pixel (j,i) correspond to a contact between the genomic sites i and j, each defined at a resolution of a few kbs, depending on the experimental protocol and possibly on a coarse-graining achieved in processing the raw data. b Considering the contact map as an adjacency matrix defines the contact network, whose nodes are the genomic sites. One contact and the corresponding undirected edge are underlined in red. The node labels are prescribed by the linear ordering along the genome

From contact maps to contact networks

The most standard approach is the direct analysis of contact maps using various statistical tools, e.g. contact density, Principal Component Analysis or motif finding [2, 3, 11]. An alternative approach is to consider a contact map F as the adjacency matrix of an undirected network. There are slightly different ways to implement this general idea, e.g. considering a network with multiple edges or with weighted edges. The simplest case of a binary contact map is presented on Fig. 1 b, using a network drawing minimizing the number of crossings between edges in the plane of the figure. Noticeably, labeling of the nodes in such networks is not purely conventional, like in most complex networks, but prescribed by their linear ordering along the genome.

Contact networks are spatially embodied networks with steric constraints on the node degrees: a node cannot establish a contact with an unlimited number of other nodes, exactly like a city cannot be connected by direct highways to an unlimited number of other cities. As such, they are not expected to satisfy the small-world property. These constraints are partly alleviated in Hi-C experiments done on cell populations, where the contact network originates from an average contact map, derived from a huge number of individual conformations.

Although such networks are sometimes called interaction networks [12], it should be noted that a contact only reflects a spatial proximity at the time of the experiment. It may result from random thermal motion of DNA, and does not necessarily imply a specific biochemical or physical interaction between the genomic sites. Only a special experimental protocol (chromatin interaction analysis using paired end tags, ChIA-PET, [13]), designed to extract the contacts mediated by a given protein, e.g. a polymerase, gives access to chromatin interaction networks [14].

Network representation can be exploited in different ways in the context of genomic studies. We present in the next section a short review of the alternative approaches and points of view. Our exploitation of contact networks for 3D genome reconstruction will appear to be quite novel and unrelated to previous works.

Contact network analysis of Hi-C maps: a short review

The network view of contact maps already gave systemic insights on the genome organization in the nuclear space.

In [15], the authors chose a network representation in which each observed contact is associated with an edge. Nodes are thus related by multiple edges, as many as the number of reads recorded in the experiment. By implementing a rewiring procedure at fixed degrees, they showed that the human contact network is different from a random graph, in particular as regards the histogram of the number of contacts.

In [12], the authors computed five graph-topological measures of the intra-chromosomal contact network: diameter, degree distribution, betweenness centrality, clustering coefficient and Jaccard index (relative number of neighbors shared by a pair of nodes). They actually used scale-dependent analogs of the standard notions, related to the diffusion kernel exp[ β(F−K)] (where K is the degree matrix) and presumed to capture network characteristics at different ranges of organization when the parameter β is varied [16]. Identifying each gene with the fragment containing its transcriptional start site, they showed a correlation between co-expression of genes and their 3D co-localization, that was proposed as a prediction tool.

In [17], a network approach of a human contact map at a resolution of 100kb has been developed to analyze the relationship between replication timing and genomic contacts. Replication origins located at the border of replication domains, termed master replication origins, are shown to correspond to nodes of maximal network centrality. This feature is observed for three network centralities (degree, betweenness and eigenvector centralities) in both the unweighted contact network and the network where edges are weighted by the number of reads.

Louvain algorithm devised to detect graph communities has been applied to the contact network of metagenomes, in order to identify the constituting genomes [18].

In [14], using a ChIA-PET protocol specifically targeting contacts involving a polymerase, the authors found that 40 % of the total genomic elements involved in chromatin interactions converged to a giant, scale-free-like, hierarchical network organized into chromatin communities, with a negative correlation between the degree and the clustering coefficient. In the context of genome-wide association studies, they observed that hubs of this transcription-associated interaction network lack disease-associated single-nucleotide polymorphisms.

3D genome structure reconstruction

The challenge

Beyond statistical analyses, another direction for exploiting contact maps is to reconstruct the underlying 3D genome structures and visualize the corresponding shapes in the 3D space. An issue is the large size of genomic contact maps, which requires fast reconstruction algorithms. Existing methods for reconstructing the native structure of a protein from its contact map, e.g. by targeted growth [19], are limited to a few hundreds of elements at the very most, hence do not apply to the large Hi-C contact maps. Standard reconstruction methods for genomic data are based on iterative structure optimization until experimental contacts are matched [20], and they are also limited to a small number of sites.

Another issue lies in the fact that not all the contacts are detected. The absence of reads for a pair of sites does not assess, and should not be handled as, an absence of contact.

In what follows, we consider binary contact maps only for explanation and illustration purposes, as in Fig. 1, and perform all the analyses with continuously-valued contact frequencies, so as to avoid the choice of a threshold and fully exploit the quantitative nature of Hi-C data.

From contact maps to distance matrices

The standard method to derive spatial distances from conformational capture data is to consider that distances are inversely proportional to numbers of contacts and to associate a distance L ij =1/F ij to the pair of sites (i,j) [21]. A difficulty arises at high resolution (typically less than 100 kb) due to the sparseness of the contact map F, in which a lot of components vanish. The corresponding distance matrix would thus contain a lot of infinite components. Nonvanishing but very small values of F ij are also problematic, in giving a very large value 1/F ij which does not correspond to the average distance between the sites i and j. Moreover, such a definition does not satisfy the triangular inequality, i.e. L is not a distance matrix.

Considering the contact map as the adjacency matrix of a network, we proposed to associate to a pair of sites (i,j) the distance D ij obtained by computing their graph distance, that is, the minimal number of edges in a path relating the nodes [9, 22]. This definition applies to any pair of sites, including those displaying no significant contact, hence provides a complete distance matrix D. This procedure in particular circumvents experimental limitations preventing to detect all the contacts.

However, the plain graph distance is too rough since it treats equally all the edges of the network, while a high contact frequency F ij reflects a close proximity of the sites i and j. Accordingly, we have endowed each contact-associated edge with a length L ij =1/F ij . The components of L are no longer used as distances, but as auxiliary weights involved in computing the path lengths, instead of simply counting a number of edges. This weighting does not change the fact that the shortest-path distance D ij is a true distance, satisfying the triangular inequality.

ShRec3D: implementing classical multidimensional scaling on graph distances

To achieve 3D genome reconstruction, we proposed a fast algorithm, termed ShRec3D for shortest-path 3D reconstruction [9], Fig. 2 a. It starts with the above-described derivation of the shortest-path distance matrix D from the contact map F, Fig. 2 b.
Fig. 2

Principle of ShRec3D reconstruction algorithm. a Sketch of the flowchart of the algorithm. The starting point is the contact map F, with either binary or normalized components. It defines a contact network, where each edge (i,j) is given a length L ij , equal to 1/F ij in the original version [9] and extended into a tunable relationship \(L_{ij}= F_{ij}^{-\alpha }\) with parameter α. The shortest-path distances between the nodes, illustrated in (b), produces a complete distance matrix D. Then a metric matrix M is derived using simple algebraic formulas. Classical multidimensional scaling (MDS, step singled out by green arrows) amounts to a truncation of M into a semidefinite positive matrix G of rank 3, supported by the spectrum of M, in (c). G is the Gram matrix of the desired 3D structure. The coordinate vectors V are deduced from the 3 nonvanishing eigenvalues and corresponding eigenvectors of G. The 3D structure obtained with α=1 is presented in (d). In what follows we investigate the relationships (sketched as blue arrows) between F and either the graph distances D or the reconstructed distances R for various values of α

The next step is the computation of the so-called metric matrix M, related to D by algebraic relationships (see Methods). In ideal situations, where the distance matrix components are the actual Euclidean distances between the points of 3D structure, M is semidefinite positive of rank equal to the underlying topological dimension, namely 3; a theorem from distance geometry then ensures that it coincides with the Gram matrix G (matrix of scalar products) of the structure [23], which is reversibly related to its 3D coordinates. When starting from experimental data, D is marred by errors, M is not semidefinite positive and the theorem no longer applies. Moreover, D is reconstructed from an average contact map, i.e. from a superposition of structures, which also reflects in the presence of more than 3 nonvanishing eigenvalues. Classical MDS cures both problems in a simple way, by considering the truncation G of rank 3 obtained by keeping the largest three eigenvalues of M. The associated eigenvectors yield the 3D coordinates V (see Methods).

The spectrum of M reflects up to what point the matrix D is close to the Euclidean distance matrix of a single 3D structure. MDS truncation of M enforces the existence of an underlying 3D structure, which is an optimal approximation in the sense that the quadratic error between the experimental distances D and the distances R in the reconstructed structure is minimal [24]. The quality of this approximation can be checked on the spectrum of M, displaying three isolated positive eigenvalues while the remaining part of the spectrum is concentrated around 0, Fig. 2 c. It is essential for the quality of the MDS approximation that D is a true distance matrix, satisfying the triangular inequality. In contrast, it has been checked in [9] that applying MDS to the matrix L (instead of D) gives very poor results, the reconstructed structure being then almost uncorrelated with the actual one.

Since the elements of D take dimensionless values, the 3D structure is obtained up to a scale transformation; only the ratio of the distances is meaningful. The reconstructed distances R could be calibrated with respect to the size of the nucleus. As we focus only on the topology of the 3D genome structure, we kept dimensionless values for the distances, Fig. 2 d.

Results and discussion: an extension of ShRec3D for human genome

A guideline based on fluorescence in-situ hybridization(FISH) experiments

FISH protocol associates fluorescent tags to a few specific genomic sites. It allows the accurate measurement in a population of fixed cells of the spatial distances between these sites and their distribution. However, the number of investigated sites is very limited, in contrast to the genome-wide coverage permitted by conformational capture techniques. FISH experiments have been used to check that conformational capture actually provides information on in-vivo distances. They provide the only independent constraint on the 3D reconstruction from Hi-C maps.

A negative correlation has been observed for the sites tagged by FISH between their distance d ij (average over numerous single cells) and the number C ij of Hi-C reads, or equivalently the contact frequency F ij [2]. This correlation was the argument for using L as a proxy for the 3D distances. In the experimental situation considered in [2], it could be satisfactorily summarized in a heuristic power-law \(d_{ij}\sim F_{ij}^{-\alpha _{FISH}}\), with a (non universal) exponent α FISH ≈0.227, Fig. 3.
Fig. 3

Contacts recorded in a FISH experiment. Fluorescence in-situ hybridization (FISH) protocol allows one to measure the 3D distance, inside living cells, between a few specific genomic sites tagged with fluorescent probes. The figure presents a log-log scatter plot of the number C of observed contacts (horizontal axis, Hi-C data) between the sites investigated using FISH and their 3D distance d (vertical axis, FISH data, in microns). These experimental data are consistent with a power-law relation \(d_{ij}\sim F_{ij}^{-0.227}\). From [2], Figure S3, with permission

In the analyses that follow, we used Hi-C data obtained in human cells (lymphoblastoids) as in [2], Fig. 3, but with a higher resolution [3], Fig. 4 a.
Fig. 4

Analysis of the weighted graph distance. a Hi-C contact map of a 10Mb-fragment of human chromosome 1 (1kb-resolution data from [3] binned at a resolution of 10kb, axes in Mb), in the form of a heat map where the color code represents the contact frequency (− log10 units). b Log-log scatter plot of the shortest-path distances D ij with respect to the contact frequencies F ij , for two values α=0.2 (top) and α=1 (bottom) of the exponent α involved in the prescription of the edge length. The upper boundary of the cloud of points is a line of slope −α, corresponding to the pairs of sites for which the direct edge (i,j) of length L ij is the shortest path. Minus the slope of the red line gives the exponent α Sh of the best power-law fit \(D_{ij}\sim F_{ij}^{-\alpha _{Sh}}\). c Increase of the percentage N Sh of pairs of sites for which the direct connection (i,j) is not the shortest path, when α increases. d Exponent α Sh as a function of α; the dashed blue line indicates the diagonal α Sh =α

Tunable graph distances

In the line of the power-law correlation observed in FISH data, we endow each contact-associated edge with a length \(L_{ij}\sim F_{ij}^{-\alpha }\), depending on a tunable parameter α. This extension, proposed for L used as an ansatz for the distances [25, 26], is here integrated in our network-based computation of the distances. We investigated the influence of the value of α on the properties of the shortest-path distance matrix D and its relationship with F (short blue arrow in Fig. 2 a), with two extreme cases α=0.2 (the rounded value of the exponent observed experimentally in the above-described situation) and α=1 (the value adopted in the original algorithm).

By definition, the shortest-path distance D ij is always smaller or equal to the edge length L ij , as can be seen on Fig. 4 b. It is expected —and intended— that D does not rely on low contact frequencies, associated with long edges in the contact network. Figure 4 b shows that the difference between D and L is indeed more marked for smaller contact frequencies, i.e. larger distances. We quantified this feature by the percentage N Sh of pairs (i,j) with nontrivial shortest-path distance D ij <L ij . The pairs of sites contributing to N Sh are those with low contact frequencies, for which the shortest-path travels through different and shorter connections than the edge (i,j). When α increases, the discrepancy between L and D is observed to increase, as illustrated by the two panels of Fig. 4 b. This trend is assessed by plotting the increase of the percentage N Sh when α increases, Fig. 4 c. The correlation between the contact frequency F ij observed for a pair of sites and their shortest-path distance D ij can be summarized in a scaling law, with an exponent α Sh (minus the slope of the red lines in Fig. 4 b). The dependence of α Sh as a function of α is shown on Fig. 4 d. A crossover is observed at a value α≈0.2.

Overall, the improvement brought by using shortest-path distances D as an input to MDS is more important for larger distances and larger values of α. However, choosing a large value of α is not necessarily the best choice: in this regime, the distances D are derived mainly from a few large contact frequencies measured in the Hi-C experiment while less frequent contacts do not contribute, which filters out noise and unreliable recordings but possibly also relevant information. Also, the scaling of the distances with respect to the contact frequencies is modified by the shortest-path computation, and Fig. 4 d provides a calibration curve for the considered data, allowing one to control α Sh by a proper choice of α. Further analysis is presented below, with a focus on the extreme values α=0.2 and α=1.

Effect of the multidimensional scaling

We further explored the relationship between the reconstructed distances R and the contact frequencies F (long blue arrow in Fig. 2 a) as a function of α. We moreover compared two versions of MDS, corresponding to different optimization criteria hence different approximations. Classical MDS corresponds to the minimization of \(\sum _{i,j}(D_{ij}-R_{ij})^{2}\). The strength of this method is to reduce to the determination of the three first eigenvectors of the metric matrix M, as explained above. Its weakness is the low constraint on small distances, since minimizing the error is achieved mainly by controlling the large distances. This dominance of large distances can be corrected by considering the relative error [25], leading to the so-called (nonclassical) metric MDS (see Methods). Importantly, both classical MDS and metric MDS are applied to the shortest-path distance matrix D. In contrast, MDS applied to L is highly unstable, due to the treatment of infinite or abnormal components of L and the fact that L is not a distance matrix [9]. As regards computational time, nonclassical MDS starts from the classical MDS solution hence takes more time. At larger sizes, their computational performances converge, due to the fact that the (common) limiting step is the computation of shortest paths, see Additional file 1: Figure S1.

As shown in Fig. 5, we observe a correlation between the reconstructed distances R and the contact frequencies F, which can be summarized by a power law with exponent α ∗ (minus the slope of the red lines in Fig. 5 a and b), depending on the value of α and MDS implementation. Note that we do not claim that these power-laws have a deep meaning, reflecting e.g. some self-similar or fractal structure of the chromosomes; the range of the fit is not large enough to make such a claim. These power-laws are used as the simplest way to quantitatively describe the correlation between F and distances matrices L, D and R. The comparison of the exponent α ∗ with α Sh (Fig. 4 c) and α (Fig. 5 d) provides a global quantification of the effect on the distances of the MDS step and the integrated algorithm, respectively. A local quantification will be implemented in the next section.
Fig. 5

Joint influence of the exponent α and MDS implementation. a, b Log-log scatter plot of the reconstructed distances R with respect to the contact frequencies F for two values α=0.2a and α=1b of the edge-length exponent α, and two MDS implementations: nonclassical metric MDS (mMDS, top) and classical MDS (cMDS, bottom). Minus the slope of the red line gives the exponent α ∗ of the best power-law fit \(R_{ij} \sim F_{ij}^{-\alpha ^{*}}\). As a guide for the eyes, the dashed black lines, with the same starting point as the red lines, represent the line with slope −0.227=−α FISH . c Exponent α ∗ as a function of α Sh (see Fig. 4) for cMDS (green line) and mMDS (red line); the dashed blue diagonal corresponds to α ∗=α Sh . d Exponent α ∗ as a function of α for cMDS (green line) and mMDS (red line); the dashed blue diagonal corresponds to α ∗=α. Same data as in Fig. 4 a

The value of α initially taken in the expression of edge lengths L is not recovered in the relationship between the reconstructed distance and the contact frequencies, with exponent α ∗. Part of the difference between the two exponents comes from the shortest-path computation, Fig. 4 d, and part from the MDS dimensional reduction, Fig. 5 c. This latter figure shows that metric MDS has a smaller impact on the exponent α ∗ than classical MDS. Using Fig. 4 d, it is possible to choose a value of α to get the desired correlation behavior in the reconstructed structure, with some limitations. Noticeably, the effect of MDS on α ∗ is weaker at larger α.

The value α FISH =0.227 is at the lower boundary of the accessible range for α ∗. However, this exponent has been obtained from experimental data corresponding to large distances. This experimental range is difficult to delineate precisely, so that a partial fit would not be reliable; it is nevertheless apparent on Figs. 5 a–d (dashed black line) that a smaller exponent α ∗ would be obtained in the large-distance range, supporting the experimental consistency of the reconstructed structure.

Flexibility of the extended ShRec3D algorithm

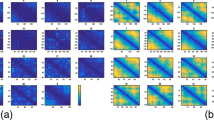
We computed the component-wise relative error |D ij −R ij | / D ij to analyze quantitatively the action of the MDS step according to the scale. The comparisons displayed in Fig. 6 a and b show that metric MDS better controls the error on small distances than classical MDS, which performs better at large distances, as expected mathematically. The trade-off offered by implementing either classical or metric MDS is more marked for α=1, see also Additional file 1: Figure S2.
Fig. 6

Comparison of classical and nonclassical metric MDS methods. a, b Action of the MDS step at various scales of the 3D structure, analyzed quantitatively by computing for each pair of sites (i,j) the relative difference |D ij −R ij | / D ij between the shortest-path distances D ij and the reconstructed distances R ij . This relative difference is represented component-wise as a scatter plot with respect to the distances D ij for two values α=0.2 and α=1 of the edge-length exponent α, for both nonclassical metric MDS (mMDS, top) and classical MDS (cMDS, bottom). The color scale is related to the density of points in the scatter plot (increasing density from blue to red). c, d 3D structures obtained for α=0.2 and α=1 with classical MDS (blue) and nonclassical MDS (red). A comparison between panels (c and d) would require a suitable 3D alignment, see Fig. 7 below. Same data as in Fig. 4 a

It also apparent on the respective 3D reconstructions, Fig. 6 c and Fig. 6 d, that metric MDS reproduces small-scale features (e.g. small loops), while the global shape is more clearly represented with classical MDS.

For small values of α (Fig. 6 c), the reconstructed structure is more compact, closer to the results of imaging experiments. For larger values of α (Fig. 6 d), the reconstructed 3D structure is more extended, which is specially suitable for 3D genome browsers. Tuning the exponent α thus allows one to focus either on short or large scales.

Note that a distortion arises in Fig. 6 c and d due to the 2D projection of the 3D structures on the printed sheet. The alignement of the structures obtained with different MDS implementations have been done without any rescaling, since they are based on the same distance matrix D.

Such a rescaling is necessary to compare the structures obtained for different values of α, as presented in Fig. 7. Small-scale features are reproduced with α=0.2, while the skeleton of the overall shape is better perceived with α=1. Intermediary values of α offer a continuous trade-off between these two extreme behaviors, as can be seen in Additional file 1: Figure S3. The reconstruction of the whole chromosome 1 is presented in Additional file 1: Figure S4, as an illustration of the performance of our algorithm at large sizes.
Fig. 7

3D reconstruction with two different values of the exponent α. The figure displays 3D structures obtained with metric MDS and either α=0.2 (blue) or α=1 (red). Data as in Fig. 4 a

Conclusion

Experimental advances permitted by the Hi-C protocol pointed to the need of bridging a physical viewpoint, enlightening the functional role of 3D genome structure, with a systemic viewpoint, based on genome-wide data and network analysis. A pillar of this bridge is the development of reconstruction algorithms, in which information limited to contacts is sufficient to get a 3D representation of the data. An auxiliary though important step is to transform the contact maps into complete distance matrices.

Our analysis shows that shortest-path distances, inspired by network concepts, is to date the best way to implement this step with human data, making it possible to deal with sparse chromosomal contact maps and match FISH data. The extension of ShRec3D presented here, with a tunable parameter α in the definition of the graph distances and two implementations of MDS, provides a flexible algorithm to accommodate various organisms, conditions and goals.

Methods

Experimental data: We used human Hi-C data obtained from lymphoblastoids (cell type GM12878) at a resolution of 1kb [3]. In the analyses presented here, we take as a benchmark a fragment of chromosome 1 of size 10 megabases (Mb).

These data have been coarse-grained into bins of 10 kb then unbiased and normalized according to the procedure explained in [10], yielding the contact map F presented in Fig. 4 a. It satisfies \(\sum _{j}F_{ij}=1\) for all sites i.

Contact network: In the binary representation considered for illustration purposes, Fig. 1, the diagonals (i,i±1) are included in the contact map in order to enforce the connectivity of the genome; accordingly the contact network is connected. It is thus possible to compute the shortest path between any pair of nodes. In the extension of our algorithm ShRec3D presented here, we use as an input continuous-valued contact maps F (contact frequencies), and the edge (i,j) is endowed with a length equal to \(F_{ij}^{-\alpha }\).

Classical MDS (cMDS): The metric matrix M is derived from the N×N distance matrix D according to:
$$ M_{ij}= {1\over 2}\;\left[D_{0i}^{2}+D_{0j}^{2}-D_{ij}^{2}\right] \hskip 3mm \text{where} \hskip 3mm D_{0i}^{2}={1\over N} \sum_{j=1}^{N}D_{ij}^{2} -{1\over N^{2}} \sum_{j=1}^{N}\sum_{k>j}^{N} D_{jk}^{2} $$
(1)
The metric matrix can be obtained in a more compact way as M=−(1/2)J D (2) J (double centering method) with \(D^{(2)}_{ij}=D_{ij}^{2}\) and J=Id N −N −1 1 N (where Id N is the the N×N identity matrix and 1 N the N×N matrix with all components equal to 1) [27]. Classical MDS relates the coordinates V of the reconstructed 3D structure (in the barycentric coordinate system) to the eigenvectors (E κ ) κ=1,2,3 (with norm equal to 1) associated with the largest three eigenvalues (λ κ ) κ=1,2,3 of M according to:
$$ V_{\kappa, i}= \sqrt{\lambda_{\kappa}} \,\times\, E_{\kappa}(i), \hskip 5mm (\kappa=1, 2, 3) $$
(2)

This structure is the best 3D approximation in the sense that it minimizes the quadratic error \(\sum _{i,j}(D_{ij}-R_{ij})^{2}\) between D and the distances R in the reconstructed structure. We here keep 3 eigenvectors in a supervised way, since we are looking for a 3D structure. The relevance of this choice can nevertheless be checked on the spectrum of M, which presents exactly 3 isolated eigenvalues, see Fig. 4 c. The same method could apply in any dimension, keeping m eigenvectors for a m-dimensional structure.

Nonclassical metric MDS (mMDS): this method is based on the minimization of the relative stress
$$\varepsilon ={\sum_{i,j}(D_{ij}-R_{ij})^{2} \over \sum_{ij}D_{ij}^{2}} $$
(3)

In contrast with classical MDS, there is no longer an analytical solution relating D with the optimal coordinates. The minimization of the stress is achieved by iterative optimization (MATLAB function mdscale with criterion metricstress). Noticeably, the procedure takes as a starting point the 3D structure provided by classical MDS, in order to reduce the nonconvex optimization problem to a local minimization problem and exploit the efficient dimensional reduction ensured by cMDS. In this way the computational performance remains satisfactory, especially at large sizes for which the duration of the MDS step is anyhow overwhelmed by the computation of the shortest-path distances (see Additional file 1: Figure S1). Other MDS options are possible [25, 26]. Beyond classical and metric MDS, we also investigated the specifications of ShRec3D when implemented with Sammon MDS [28] and nonmetric MDS [29, 30]. Basically these two latter options give results quite similar to metric MDS. Accordingly, we discuss in the main text the results obtained with classical and metric MDS, and present some additional tests comparing the four methods (classical MDS, metric MDS, Sammon MDS and nonmetric MDS) in the Supplementary Materials.

Numerical implementation: The original algorithm ShRec3D [9] has been extended to include the edge-length exponent α as a tunable parameter, and it now implements both classical and nonclassical metric MDS. The MATLAB code is available at: https://sites.google.com/site/julienmozziconacci/#TOC-Publicly-available-softwares

Notes

Acknowledgements

This work has been funded by the French Institut National du Cancer, grant INCa_5960 (AL), the French Agence Nationale de la Recherche, grant ANR-13-BSH3-0007 (AL) and grant ANR-15-CE11-0023-01 (JM), and University Pierre and Marie Curie, Emergence program, grant SU-15-R-EMR-08 (JM). The authors are grateful to Thierry Forné for his comments on the manuscript, and to Michel Quaggetto for his help with softwares. AL acknowledges the hospitality of Jacobs University, Bremen (Germany) during the WE Heraeus Physics School “The physics behind systems biology" (6–12 July 2015).

Supplementary material

40366_2016_29_MOESM1_ESM.pdf (484 kb)
Additional file 1 Supplementary material. (483 KB PDF)

References

  1. 1.
    Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002; 295:1306–11.CrossRefADSGoogle Scholar
  2. 2.
    Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009; 326(5950):289–93.CrossRefADSGoogle Scholar
  3. 3.
    Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2014; 159(7):1665–80.CrossRefGoogle Scholar
  4. 4.
    Dekker J, Misteli T. Long-range chromatin interactions. Cold Spring Harbor Perspect Biol. 2015; 7(10):019356.CrossRefGoogle Scholar
  5. 5.
    Ea V, Baudement MO, Lesne A, Forné T. Contribution of topological domains and loop formation to 3D chromatin organization. Genes. 2015; 6(3):734–50.CrossRefGoogle Scholar
  6. 6.
    Newman ME. The structure and function of complex networks. SIAM Rev. 2003; 45(2):167–256.MathSciNetCrossRefzbMATHADSGoogle Scholar
  7. 7.
    Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU. Complex networks: Structure and dynamics. Phys Reports. 2006; 424(4):175–308.MathSciNetCrossRefADSGoogle Scholar
  8. 8.
    Di Paola L, De Ruvo M, Paci P, Santoni D, Giuliani A. Protein contact networks: an emerging paradigm in chemistry. Chem Rev. 2012; 113(3):1598–613.CrossRefGoogle Scholar
  9. 9.
    Lesne A, Riposo J, Roger P, Cournac A, Mozziconacci J. 3D genome reconstruction from chromosomal contacts. Nat Methods. 2014; 11(11):1141–3.CrossRefGoogle Scholar
  10. 10.
    Cournac A, Marie-Nelly H, Marbouty M, Koszul R, Mozziconacci J. Normalization of a chromosomal contact map. BMC Genomics. 2012; 13:436.CrossRefGoogle Scholar
  11. 11.
    Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, Ren B. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature. 2012; 485(7398):376–80.CrossRefADSGoogle Scholar
  12. 12.
    Babaei S, Mahfouz A, Hulsman M, Lelieveldt BP, de Ridder J, Reinders M. Hi-C chromatin interaction networks predict co-expression in the mouse cortex. PLoS Comput Biol. 2015; 11(5):1004221.CrossRefGoogle Scholar
  13. 13.
    Singh Sandhu K, Li G, Sung WK, Ruan Y. Chromatin interaction networks and higher order architectures of eukaryotic genomes. J Cell Biochem. 2011; 112(9):2218–21.CrossRefGoogle Scholar
  14. 14.
    Sandhu KS, Li G, Poh HM, Quek YLK, Sia YY, Peh SQ, Mulawadi FH, Lim J, Sikic M, Menghi F, Thalamuthu A, Sung WK, Ruan X, Fulwood MJ, Liu E, Csermely P, Ruan Y. Large-scale functional organization of long-range chromatin interaction networks. Cell Reports. 2012; 2(5):1207–19.CrossRefGoogle Scholar
  15. 15.
    Botta M, Haider S, Leung IX, Lio P, Mozziconacci J. Intra-and inter-chromosomal interactions correlate with CTCF binding genome wide. Mol Syst Biol. 2010; 6(1):426.Google Scholar
  16. 16.
    Hulsman M, Dimitrakopoulos C, de Ridder J. Scale-space measures for graph topology link protein network architecture to function. Bioinformatics. 2014; 30(12):237–45.CrossRefGoogle Scholar
  17. 17.
    Boulos R, Arneodo A, Jensen P, Audit B. Revealing long-range interconnected hubs in human chromatin interaction data using graph theory. Phys Rev Lett. 2013; 111(11):118102.CrossRefADSGoogle Scholar
  18. 18.
    Marbouty M, Cournac A, Flot JF, Marie-Nelly H, Mozziconacci J, Koszul R. Metagenomic chromosome conformation capture (meta3c) unveils the diversity of chromosome organization in microorganisms. Elife. 2014; 3:03318.CrossRefGoogle Scholar
  19. 19.
    Vendruscolo M, Kussell E, Domany E. Recovery of protein structure from contact maps. Folding Design. 1997; 2(5):295–306.CrossRefGoogle Scholar
  20. 20.
    Serra F, Di Stefano M, Spill YG, Cuartero Y, Goodstadt M, Baù D, Marti-Renom MA. Restraint-based three-dimensional modeling of genomes and genomic domains. FEBS Lett. 2015; 589(20):2987–95.CrossRefGoogle Scholar
  21. 21.
    Fraser J, Rousseau M, Shenker S, Ferraiuolo MA, Hayashizaki Y, Blanchette M, Dostie J. Chromatin conformation signatures of cellular differentiation. Genome Biol. 2009; 10:37.CrossRefGoogle Scholar
  22. 22.
    Hirata Y, Horai S, Aihara K. Reproduction of distance matrices and original time series from recurrence plots and their applications. Eur Phys J Special Topics. 2008; 164(1):13–22.CrossRefADSGoogle Scholar
  23. 23.
    Havel TF, Kuntz I, Crippen GM. The theory and practice of distance geometry. Bull Math Biol. 1983; 45:665–720.MathSciNetCrossRefzbMATHGoogle Scholar
  24. 24.
    Torgerson WS. Multidimensional scaling: I. theory and method. Psychometrika. 1952; 17(4):401–19.MathSciNetCrossRefzbMATHGoogle Scholar
  25. 25.
    Zhang Z, Li G, Toh KC, Sung WK. 3D chromosome modeling with semi-definite programming and hi-c data. J Comput Biol. 2013; 20(11):831–46.MathSciNetCrossRefGoogle Scholar
  26. 26.
    Varoquaux N, Ay F, Noble W, Vert JP. A statistical approach for inferring the three-dimensional structure of the genome. Bioinformatics. 2014; 30:26–33.CrossRefGoogle Scholar
  27. 27.
    Wickelmaier F, Vol. 46. An introduction to MDS. Denmark: Sound Quality Research Unit, Aalborg University; 2003.Google Scholar
  28. 28.
    Sammon JW. A nonlinear mapping for data structure analysis. IEEE Trans Comput. 1969; 18(5):401–409.CrossRefADSGoogle Scholar
  29. 29.
    Kruskal JB. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika. 1964; 29(1):1–27.MathSciNetCrossRefzbMATHGoogle Scholar
  30. 30.
    Bécavin C, Tchitchek N, Mintsa-Eya C, Lesne A, Benecke A. Improving the efficiency of multidimensional scaling in the analysis of high-dimensional data using singular value decomposition. Bioinformatics. 2011; 27(10):1413–21.CrossRefGoogle Scholar

Copyright information

© Morlot et al. 2016

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.

Authors and Affiliations

  1. 1.Laboratoire de Physique Théorique de la Matière Condensée UMR 7600, CNRS, UPMCSorbonne UniversitésParis cedex 5France
  2. 2.Institut de Génétique Moléculaire de Montpellier UMR 5535, CNRSUniversité de MontpellierMontpellier cedex 5France

Personalised recommendations