Abstract
Over the last 70 years, Feynman diagrams have played an essential role in the development of many theoretical predictions derived from the standard model Lagrangian. In fact, today they have become an essential and seemingly irreplaceable tool in quantum field theory calculations. In this article, we propose to explore the development of computational methods for Feynman diagrams with a special focus on their automation, drawing insights from both theoretical physics and the history of science. From the latter perspective, the article particularly investigates the emergence of computer algebraic programs, such as the pioneering SCHOONSCHIP, REDUCE, and ASHMEDAI, designed to handle the intricate calculations associated with Feynman diagrams. This sheds light on the many challenges faced by physicists when working at higher orders in perturbation theory and reveal, as exemplified by the test of the validity of quantum electrodynamics at the turn of the 1960s and 1970s, the indispensable necessity of computer-assisted procedures. In the second part of the article, a comprehensive overview of the current state of the algorithmic evaluation of Feynman diagrams is presented from a theoretical point of view. It emphasizes the key algorithmic concepts employed in modern perturbative quantum field theory computations and discusses the achievements, ongoing challenges, and potential limitations encountered in the application of the Feynman diagrammatic method. Accordingly, we attribute the enduring significance of Feynman diagrams in contemporary physics to two main factors: the highly algorithmic framework developed by physicists to tackle these diagrams and the successful advancement of algebraic programs used to process the involved calculations associated with them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The standard model of elementary particle physics, which describes three of the four known fundamental forces in the universe—electromagnetic, weak and strong interactions; gravitation is excluded—provides us with an impressive comprehensive framework for understanding the behavior of the constituents of all visible matter, as well as all the unstable elementary particles that have been discovered, for example in cosmic rays or at particle accelerators. As such, it stands as one of the most rigorously tested theories in the realm of fundamental physics. Over the past decades, a myriad of different high-precision measurements have been performed and, remarkably, the nineteen free parameters of the Standard Model align perfectly—within statistical uncertainties—with these various experimental results. Nonetheless, the process of testing such a theory involves not only precise experiments but also accurate theoretical predictions. To achieve this, observables, i.e., measurable quantities like cross sections or the average lifetime of a particle, must be derived from the abstract Lagrangian of the Standard Model. This is done within the theoretical framework of quantum field theory (QFT).
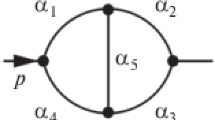
Aimed since the late 1920s at unifying quantum mechanics and special relativity, QFT builds nowadays on groundbreaking developments made in the late 1940s in the framework of quantum electrodynamics (QED), the relativistic theory that deals more specifically with the electromagnetic field. In particular, four leading physicists—Julian Schwinger, Sin-Itiro Tomonaga, Richard Feynman, and Freeman Dyson—developed techniques, known as renormalization, which enabled the infinities that had hitherto hindered the correct development of the theory to be discarded and replaced by finite measured values [1]. Generally, calculations within this framework are intricate and involved. However, driven by conceptual and mathematical issues, Richard Feynman devised an ingenious approach to address this complexity: the intuitive graphical notation known as Feynman diagrams (or graphs) [2]. These diagrams are employed to represent interaction processes, utilizing lines to depict particles and vertices to symbolize their interactions. The external lines in a graph symbolize the initial and final state particles, while the internal lines are associated with virtual particles (see Fig. 1). Thanks to the associated Feynman rules, mathematical terms are then assigned to each element of these diagrams.Footnote 1 This allows the translation of the visual representation of a particle processFootnote 2 into an algebraic expression providing its probability amplitude. Initially met with skepticism by established experts, Dyson succeeded in providing a rigorous derivation of Feynman diagrams and their related rules from the foundations of QED, thereby dispelling doubts [9, 10]. Since then, Feynman graphs have become an indispensable tool for calculations in QFT. In fact, they have played a crucial role in the development of the vast majority of theoretical predictions derived from the standard model Lagrangian.
Leading-order Feynman diagram for the process \(e^+e^-\rightarrow \mu ^+\mu ^-\). An electron–positron pair annihilates into a muon–antimuon pair via a virtual photon \(\gamma \). Throughout this paper, we define the external lines on the left (right) of the diagram to denote the initial (final) state of the process. All Feynman diagrams have been produced with FeynGame [11]
The success of Feynman diagrams has garnered significant attention from historians of physics, resulting in numerous works devoted to their study. Many of them focused on Feynman’s creative contributions to QED, analyzing their context in detail, the various influences received and unveiling their epistemic novelty [1, 12,13,14,15,16].Footnote 3 In a different vein, David Kaiser, who examined Feynman diagrams as calculation tools, delved into their dispersion in postwar physics as it provides “a rich map for charting larger transformations in the training of theoretical physicists during the decades after World War II” [3, p. xii]. This work remarkably expanded our understanding of the pivotal role Feynman graphs currently hold in high-energy physics. However, despite this existing literature, there are still notable gaps in historical investigations regarding an essential technical aspect related to the application of Feynman’s diagrammatic method in high-energy physics: the algebraic manipulation of the associated equations. Exploring this aspect in more depth would yield valuable insights, as it has long shaped the work of numerous theoretical physicists and remains particularly relevant in contemporary physics due to the many challenges it presents. Indeed, based on the so-called perturbation theory, which assumes the particle interactions to be small, calculations with Feynman diagrams are only approximate within QFT. A single graph represents only an individual term in the perturbative expansion, and to achieve higher accuracy, more and more Feynman diagrams of increasing complexity must be included, leading to more and more complex computations. In modern calculations, for phenomena such as those observed at the Large Hadron Collider (LHC), significant computational efforts on dedicated computer clusters are required, giving rise to a multitude of technical challenges in manipulating the expressions involved. The algorithmic evaluation of Feynman diagrams has consequently now almost evolved into a field of research in its own right.
The present paper therefore aims to address directly the topic of algebraic and algorithmic approaches to Feynman diagrams. Our goal is to provide some insights into related issues and current status of their solution. As we will see this naturally leads us to considerations on the question of automating the calculations associated with Feynman graphs. Indeed, the rather well-defined algebraic structure of amplitudes derived from Feynman diagrams has since long raised hope that the computation of physical observables like cross sections and decay rates can be automated to a very high degree. This became progressively more desirable as higher orders in perturbation theory were calculated to improve accuracy. As part of this process, the number of mathematical operations required increases dramatically, given that the number of Feynman diagrams can become very large, and that their individual computation involves very complicated mathematical expressions, in particular if some of the internal lines form closed loops (see Fig. 2). The question of automation, which remains particularly relevant today, then naturally throws light on the specific role played by computers in Feynman diagram calculations. This is why special attention will be paid to the development of dedicated algebraic programs. By enabling mathematical expressions to be manipulated at variable level, they have become absolutely crucial to the progress made over the last decades. And in fact, as computer algebra systems such as MATHEMATICA, MAXIMA or MAPLE [17,18,19] are now an integral part of the physicist’s daily toolbox, it is interesting to note—as our developments will illustrate—that questions initially posed by problems linked to the calculation of Feynman diagrams were instrumental in providing the initial impetus for the development of such programs and laid some of their foundations.Footnote 4
In line with the special issue it belongs to, this “tandem” article consists of two distinct parts. Section 2, authored by historian of science Jean-Philippe Martinez, delves into the emergence of algebraic programs designed for calculating Feynman diagrams. Specifically, it highlights three pivotal programs, namely SCHOONSCHIP, REDUCE, and ASHMEDAI, whose development began around 1963. These programs played an essential role in testing the validity of QED at higher orders of perturbation theory at the turn of the 1960s and 1970s. Moreover, they brought about significant changes in the practices associated with Feynman diagram computations. This last point is then examined through an analysis of the critical assessment made at this time of the introduction of algebraic programs in theoretical high-energy physics, revealing their success, future challenges and highlighting the theme of automation. Section 3, authored by physicist Robert V. Harlander, offers an overview of the developments toward the automated evaluation of Feynman diagrams since these pioneering days, up until today. Rather than aiming for a historically precise discussion though, the focus of this part is on an outline of the main algorithmic concepts developed for perturbative QFT calculations based on Feynman diagrams. Computer algebra systems play an even bigger role today, as the evaluation of the occurring momentum integrals has been largely mapped onto algebraic operations, as will be discussed in detail in Sect. 3.5. In order to give a realistic impression of the field to the interested non-expert, the presentation includes a number of technical details which should, however, still be accessible to the mathematically inclined layperson. An excellent review for specialists is given by Ref. [21] and pedagogical introductions to calculating Feynman diagrams can be found in Refs. [22, 23], for example. Note, however, that two appendices at the end of the paper (Appendices A and B) provide further resources on the structure of Feynman diagrams and the calculation of sample one-loop integrals, respectively. They are designed to provide further insights into the mathematics related to Feynman diagrams, but are not essential for the understanding of the issues explored in the main text of the article.
While each part can be read independently due to its self-contained nature, the article as a whole aims to achieve a sense of unity. However, as the above outline of the contents suggests, this is not attempted by a continuous historical treatment from the beginnings to today. Our main emphasis is on the origins of algebraic and algorithmic approaches to Feynman diagrams, and their current status. The rich and comprehensive developments at the intermediate stages, on the other hand, are beyond the scope of the current format, and shall be left for future investigations. Instead, the article strives to achieve unity not only through its introductory and concluding sections, but also by establishing a continuous link between the technical challenges faced in the early stages (Sect. 2) and those encountered in the present (Sect. 3). Thus, cross-references are used repeatedly to supply context for both the historical and physical developments. They provide a better understanding of the many questions that have arisen since the inception of theoretical evaluation of Feynman diagrams and highlight the transformations and prospects brought about by the advancement of computer algebraic programs.
2 The emergence of computer-aided Feynman diagram calculations
2.1 QED put to experimental test: toward the need of algebraic programs
2.1.1 1950s–1960s: higher-and-higher orders
Since its inception in the late 1920s, the development of QED faced numerous challenges that impeded its progress.Footnote 5 The most notable obstacle was the occurrence of divergent integrals when dealing with higher-order perturbative calculations. These integrals were leading to undefined results, in particular when considering the self-energy of the electron and the vacuum zero-point energy of electron and photon fields. As briefly mentioned in the introduction, the development of renormalization techniques in the late 1940s then sought to address the issue of divergent integrals in QED by absorbing infinities into “bare” parameters and replacing them with finite, measurable values (see Sect. 3.4). These techniques paved the way for the development of covariant and gauge invariant formulations of quantum field theories, enabling in principle the computation of observables at any order of perturbation theory. Consequently, in light of these remarkable results, the newly refined QED was promptly subjected to rigorous experimental testing.
The more accurate the experiments became, the more one had to calculate higher orders of the perturbative series to determine corrections to the theoretical values and check for potentially unknown physical effects. In most cases, higher-order irreducible elements appear, which require computation from scratch. Feynman’s diagrammatic approach provides physicists with powerful tools for such an undertaking. Thanks to the Feynman rules, each term of the perturbative expansion can be deduced from graphs whose number of vertices increases with the correction orders. The internal intricacy of the different diagrams, as expressed by the appearance of loops, then reflects the growing complexity of the calculations to be performed (more details in Sect. 3). Moreover, in all instances, it must be emphasized that the number of diagrams involved in each correction increases drastically. To give an overview, let us consider the magnetic moment \({\mathbf {\mu }}_e\) of the electron, defined as \({\mathbf {\mu }}_e=-g_e e{\textbf{S}}/2m_e\), where \(m_e\) is the electron mass and \(\textbf{S}\) is its spin. Taking into account only the tree-level Feynman diagram of Fig. 3a, the gyromagnetic ratio is \(g_e=2\). The QED corrections to this quantity are called the anomalous magnetic moment, also referred to as “\(g-2\).” At order \(e^2\), they are described by the single one-loop diagram of Fig. 3b; at order \(e^4\) by 7 two-loop diagrams (see Fig. 4); at order \(e^6\) by 72 three-loop diagrams; at order \(e^8\) by 891 four-loop diagrams; and so on\(\ldots \) (see, e.g, Ref. [24]).Footnote 6 As a result, the close relationship between experiment and theoretical calculations determined much of the dynamics of early postwar high-energy physics.Footnote 7
In fact, two essential calculations for the development and confirmation of QED at the lowest significant order were carried out before Feynman developed his diagrammatic method. They were related to the Lamb shift and the anomalous magnetic moment of the electron. The former refers to the energy difference between the \(^2S_{1/2}\) and \(^2P_{1/2}\) levels of the hydrogen atom, first observed in 1947 by Willis E. Lamb and Robert C. Retherford [28]. That same year, to explain this observation, Hans Bethe used non-relativistic quantum mechanics and the novel idea of mass renormalization to calculate the self-interaction of the electron with its own electromagnetic field [29]. His successful approach spurred several decisive developments in QED in the late 1940s [1, Chap. 5]. On the other hand, the successful theoretical approach to the contribution of quantum mechanical effects to the magnetic moment of an electron is due to Julian Schwinger, who in 1948 performed the first calculation of radiative corrections in QED [30]. His results were in good agreement with measurements realized at the same time by Polykarp Kusch and Henry M. Fowley at Columbia University [31, 32].
The implementation of Feynman diagrams in the theoretical scheme of QED allowed for improved computations and the study of higher-order corrections. Robert Karplus and Norman M. Kroll estimated for the first time in 1950 the anomalous magnetic moment of the electron at order \(e^4\) [33]. A few algebraic errors affecting results to the fifth decimal place were identified in the late 1950s by André PetermannFootnote 8 and Charles M. Sommerfield, whose new calculations anticipated the precision experiments performed in 1963 by David T. Wilkinson and Horace R. Crane [34,35,36]. Concerning the Lamb shift, the first calculations remained limited to relativistic corrections at the lowest order (see, e.g., Ref. [37]). It was only in 1960 that Herbert M. Fried and Donald R. Yennie, and, independently, Arthur J. Layzer, first calculated radiative corrections of order \(e^2\) [38, 39]. While various considerations to increase sophistication and accuracy were subsequently developed [40,41,42], it was not until 1966 that higher-order calculations were performed analytically by Maximilliano F. Soto Jr. [43]. In detail, he calculated the seven Feynman diagrams for the radiative corrections of order \(e^4\) to the elastic scattering of an electron in a Coulomb potential (Fig. 4).
Initially, Soto Jr.’s results were not independently verified by the community. This can be explained, in part, by the rather tedious nature of the calculations, as we will discuss further in Sect. 2.1.2. But it can also be seen as a form of disinterest. Indeed, despite small deviations, the agreement between theory and experiment was generally considered good in the mid-1960s, both for the Lamb shift and for the anomalous magnetic moment of the electron. In fact, the community was in no hurry to pursue research at higher orders of perturbation theory (see, e.g., Ref. [44]). And it was only after a rather long pause that advances in low-energy, high-precision QED experiments were made that turned the tide. In particular, a new experimental determination of the fine structure constant \(\alpha \)—the dimensionless coupling constant associated with electromagnetic interaction—was obtained in 1969 using the Josephson effect [45]. Predicted in 1962 by Brian D. Josephson, this tunnel effect manifests itself by the appearance of a current between two superconductors separated by a narrow discontinuity made of a non-superconducting insulating or metallic material [46]. The corresponding measurement of \(\alpha \) in 1969 differed from previous measurements by three standard deviations. The new value was subsequently used to reevaluate different theoretical expressions such as the Lamb shift, fine structure, and hyperfine splitting in different atoms, as well as the anomalous magnetic moments of the electron and the muon (see, e.g., Ref. [47]). From these results and further experimental refinements, theoretical and empirical values of the \(^2S_{1/2}\) and \(^2P_{1/2}\) splitting in hydrogen showed a severe disagreement [48, 49]. This untenable situation explicitly called for the reconsideration of Soto Jr.’s results, as will be discussed in detail in Sect. 2.2.4.
New considerations of the anomalous magnetic moment of leptons were also motivated by parallel experiments aimed directly at measuring it. For the electron, various observations in the late 1960s showed a discrepancy of three standard deviations to the value obtained by Wilkinson and Crane in 1963 (see, e.g., Ref. [50]). However, the situation turned out to be rather confusing, as these results were contradicted in the early 1970s by new experiments that, in addition, improved the accuracy [51, 52]. In the case of the muon, pioneering experiments had been carried out in the late 1950s in the Nevis cyclotron laboratories at Columbia University [53, 54].Footnote 9 They not only made possible the observation of parity violation in muon decay, but also provided a first estimate of its anomalous magnetic moment, in good agreement with the theoretical predictions of Vladimir B. Berestetskii, Oleg N. Krokhin, and Aleksandr K. Khlebnikov [56]. Nonetheless, while the \(g_\mu -2\) CERN experiment, launched in 1959, initially confirmed this result, new measurements performed in phase 2 with a precision 25 times higher indicated in 1968 a divergence from the theory [57, 58]. These different results, taken together, stimulated an increased interest in refining the theoretical value of the anomalous magnetic moment of leptons. To this end, higher-order terms in the perturbative series were progressively computed (to be also discussed in Sect. 2.2.4).
The verification of the agreement between experimental measurements and theoretical calculations of the anomalous magnetic moments of the electron and muon became the most critical test of QED in the late 1960s and early 1970s. For the first time, experiments were accurate enough to verify the validity of the renormalization procedure and confirm the perturbative expansion up to three-loop diagrams. As mentioned above, there are in this case 72 Feynman graphs that contribute to the anomalous magnetic moment of the electron (order \(e^6\) corrections). Due to mirror symmetry, only forty of these are distinct, and of these forty, twelve involve fermion loops (Fig. 5). Three of the latter have vacuum polarization insertions of order \(e^4\), seven have vacuum polarization insertions of order \(e^2\), and two have light-by-light scattering insertions. In the case of the muon, the difference with the electronic moment comes specifically from electron loop insertions in the muon vertices of these 12 diagrams. As the order and number of diagrams increase, so do the difficulty and length of the calculation work.
2.1.2 The providential computer
In addition to issues raised by the increasing complexity of the integrations to be performed in the computation of Feynman diagrams (which will be discussed in Sect. 2.3.4), the main concern of physicists in the 1960s stemmed from the presence of Dirac matrices—also called \(\gamma \)-matrices—in the expressions. Although straightforward in principle, the calculation of their traces results in a huge number of terms as the number of matrices grows. To give a rough idea, the trace of a product of twelve different \(\gamma \)-matrix expressions generates 10 395 different terms (more details in Sect. 3.3). The calculations resulting from the need to work at higher orders proved to be “hopelessly cumbersome,” “horrendous,” if not “inhuman” [40, p. 271] [25, p. 167] [59, p. 18]. In this respect, the help of digital computers revealed indispensable. The gradual democratization in the scientific field of this relatively new and rapidly evolving technology proved particularly providential in this context: it was the only one that could provide effective solutions for automating the tedious tasks to be performed.Footnote 10
The essential role played by computers in QED soon became recognized by different theoretical physicists. In their 1970 report on the state of the field, Stanley J. Brodsky and Sidney D. Drell explicitly mentioned the techniques underlying recent extensions of computational capabilities, along with new experimental measurements, as reasons for progress toward the successful confrontation of theory with experiment [25, p. 189]. Similarly, according to Ettore Remiddi, while the renewed interest at the turn of the 1960s and 1970s in evaluating higher-order radiative corrections found its “natural justification in the recent progress in high precision, low energy QED experiments,” it only “became possible on account of the increasing use of large digital computers” [44, p. 193]. Indeed, the growing complexity of calculations had been accompanied by a corresponding growth in computing facilities, and immediately the benefits proved to be enormous. Compared to the traditional pencil-and-paper approach, three main virtues of digital computers can be highlighted. Deeply interrelated, they proved decisive for the successful development of Feynman diagram computations, as will be described below. First of all, bookkeeping—i.e., the ability of computers to record, track, and manipulate vast data sets—emerged as a direct response to problems such as the massive generation of terms in the trace of Dirac matrices. It freed physicists from the endless collection of notebooks that kept track of intermediate expressions in operations. Moreover, computers considerably improved the accuracy of calculations. Not only do they eliminate human errors in arithmetic, they also handle complex mathematical operations with exceptional precision. Finally, the introduction of digital machines brought unprecedented speed and efficiency, ultimately enabling physicists to conduct more extensive and thorough investigations and to explore a much wider range of theoretical scenarios. As one of the pioneers in computer-assisted QFT, Anthony C. Hearn, stated as early as 1966: “At present, a known six months of human work can be done in less than fifteen minutes on an IBM 7090” [61, p. 574].
From a computer science point of view, calculations related to Feynman diagrams require symbolic manipulation, also called algebraic computation. This domain deals with algorithms operating on objects of a mathematical nature through finite and exact representations. For high-energy physics, according to Hearn:
It is really little more than a polynomial manipulation problem involving exotic data structures with well defined rules for simplification. In addition, one needs a mechanism for the substitution for variables and simple expressions. Rational algebra need not be used, because denominators, if they occur, have a very simple structure, and can therefore be replaced by variables or expressions in the numerator. Because one has to program these capabilities as efficiently as possible, successful systems designed for QED usually also make good general-purpose polynomial manipulation systems [59, p. 19].
In this framework, the procedure initially followed to compute Feynman diagrams can be briefly depicted as follows:
-
(i)
A one-to-one mapping between the diagram and the algebra is established following the Feynman rules. We call (a) the resulting expression.
-
(ii)
A procedure for the automatic recognition of divergences is included.
-
(iii)
Dirac traces of (a) are computed.
-
(iv)
Information collected on point (ii) is used to carry out the renormalization program.
-
(v)
Integration over the internal momenta of (a) is performed.
This procedure gives the diagram’s contributions to the scattering amplitude of the particular process under study in terms of multidimensional integrals. Their resolution then enables us to extract values such as contributions to the anomalous magnetic moment of the leptons, or to the Lamb shift. The product of the amplitude with its Hermitian conjugate also provides us with the contributions to the differential cross sections.Footnote 11
Historically, the initial steps toward setting up such a procedure on a computer were taken in the early 1960s through the pioneering development of algebraic programs whose initial purpose was none other than to perform Dirac matrix calculations. The first acknowledged reference to such a program was made by Feynman himself, at the Third International Conference on Relativistic Theories of Gravitation held in Poland in 1962. Relating his failure to compute a diagram as part of developments of a quantum theory of gravitation, he mentioned that “the algebra of the thing was [finally] done on a machine by John Matthews,” being probably for him “the first problem in algebra that [\(\ldots \)] was done on a machine that has not been done by hand” [62, p. 852]. Most likely, Matthews was then working on a Burroughs 220—a vacuum-tube computer with a small amount of magnetic-core memory produced since 1957 by ElectroData Corporation—for which he used the dedicated algebraic language, BALGOL, to write the program [59, p. 20] [63, p. 76]. Nevertheless, it seems that the latter remained confidential, and various independent projects with similar objectives soon appeared. In line with the remarkable character of Matthews’ work, which Feynman emphasized, the new dynamics they triggered proved so powerful that their success played a major role in placing algebraic programs and their development at the heart of scientific practice. Among the various technological innovations of the 1960s, SCHOONSCHIP, REDUCE, and ASHMEDAI proved to be the most impactful and played the most fundamental role in the critical evaluation of QED.
2.2 Technological innovations in the 1960s: SCHOONSCHIP, REDUCE, and ASHMEDAI
2.2.1 SCHOONSCHIP
The program SCHOONSCHIP was developed in the early 1960s by the Dutch theorist Martinus J. G. Veltman, co-recipient with Gerard ’t Hooft of the 1999 Nobel Prize in Physics for elucidating the quantum structure of electroweak interactions. In fact, it is precisely early work dealing with this specific research theme that was at the origin of Veltman’s interest in computer algebra. SCHOONSCHIP initially aimed at facilitating the resolution of a rather basic problem in this framework, that of radiative corrections to photons interacting with a charged vector boson. Various experimental successes in the late 1950s and early 1960s of the “vector-minus-axial vector” theory had indeed led many physicists to believe that vector bosons were mediators of weak interactions. This “V-A” theory, developed in 1957 by George Sudarshan and Robert Marshak, and independently by Feynman and Murray Gell-Mann, introduced in the Hamiltonian operator an axial vector current on which the parity operator has a different effect than on the polar vector currents [64,65,66]. It had been formulated to provide a theoretical explanation for the experimental observation in 1956 at Columbia University of parity violation for the weak interaction by Chien-Shiung Wu and her assistants [67]. They were following the working hypothesis on parity of Tsung-Dao Lee and Chen Ning Yang—a work for which they won the 1957 Nobel Prize—a duo who later began a systematic study of the interactions of vector bosons with photons and worked toward deriving their specific Feynman rules [68, 69]. In this context, Lee independently tackled in 1962 the calculations of the lowest order radiative corrections to the vector–boson–photon coupling [70]. This approach, which Veltman was eager to extend while working in the theory division at CERN, is specifically what inspired the development of SCHOONSCHIP [63, p. 77] [71, p. 342]. Indeed, the full calculations resulted in an expression with about 50,000 terms in the intermediate steps.
Designed during an extended stay at the Stanford Linear Accelerator Center, the first operational version of SCHOONSCHIP ran in December 1963 on an IBM 7094—a secondgeneration (transistorized) mainframe computer—and successfully contributed to solving a problem concerning the radiative corrections to photons interacting with a charged vector boson [63, 72]. According to Veltman’s recollections on receiving his Nobel Prize, its name, rather original and difficult for many to pronounce, was chosen “among others to annoy everybody not Dutch” [71, p. 342]. In Dutch, it literally means “clean ship,” and comes from a naval expression referring to clearing a messy situation. And SCHOONSCHIP was in principle prepared to clear up more messy situations than just electroweak interaction. After all, Veltman had not designed his code to be limited to one specific problem and it soon revealed itself to be a general-purpose symbolic manipulation program capable of supporting the study of a large variety of processes [59, 71] [73, p. 289]. SCHOONSCHIP was written in assembly language, considered a low-level programming language since it consists mainly of symbolic equivalents of the architecture’s machine code instructions. This choice was made partly because Veltman considered compilers—which allow machine-independent (high-level) programming languages to be efficiently converted on a specific computer—to be responsible for wasting memory and slowing down execution speed [20, 63] [74, p. 516]. In 1966, SCHOONSCHIP was ported to the CDC 6600, a machine manufactured by Control Data Corporation and considered as the first successful supercomputer [75]. With the development of hard disks and file storage, the program’s distribution to all existing CDC computers gradually became possible along the 1970s [76].
2.2.2 REDUCE
REDUCE was developed from 1963 by Hearn. As a postdoc in theoretical physics at Stanford working on Feynman diagrams, the Australian-born scientist was already interested in automating their calculations [61, 77]. In this perspective, John McCarthy, one of the founders of the field of artificial intelligence, encouraged him to use LISP, the computer language he had been developing at M.I.T since 1958 [78]. Primarily designed for symbolic data processing, this high-level language had already been used by 1962 for tasks as diverse as electrical circuit theory, mathematical logic, game playing, and—what concerned Hearn more specifically—symbolic calculations in differential and integral calculus [79]. It allowed for the development of a system that proved “easily capable of modification or extension [and also] relatively machine independent” [80, p. 80]. In 1963, McCarthy, who had just joined the Stanford Computer Science Department, also provided Hearn access to hardware facilities.
While Hearn’s work was initially oriented toward the calculation of the algebraic trace of a product of Dirac matrices and its application to various specific problems in high-energy physics, expectations were soon surpassed, as was the case with SCHOONSCHIP [61]. The program developed using batch processing on an IBM 7090 turned out to be a general-purpose algebraic simplification system and was released as such in 1967 [80]. It was capable of handling, among other things, expansion ordering and reduction of rational functions of polynomials, symbolic differentiation, substitutions for variables and expressions appearing in other expressions, simplification of symbolic determinants and matrix expansions, as well as tensor and non-commutative algebraic calculations. As Hearn later acknowledged, the name of the program, REDUCE, was also intended with a touch of playfulness: “algebra systems then as now tended to produce very large outputs for many problems, rather than reduce the results to a more manageable form. ‘REDUCE’ seemed to be the right name for such a system” [77, p. 20].
In addition to the main LISP package, specific facilities were provided to express outputs in the form of a FORTRAN source program [80, p. 88]. Originally developed for IBM in the 1950s by John Backus and his team, FORTRAN (FORmula TRANslating system) is a compiled imperative programming language that proved particularly accessible to engineers and physicists [81]. Indeed, long computational results were converted into a format suitable for numerical computation and graphical display. In 1970, REDUCE 2 was made available. This new version offered increased facilities for simplifying algebraic expressions [82]. It was written in an ALGOL-like syntax, called RLISP. ALGOL, short for “Algorithmic Language,” refers to a family of programming languages for scientific computations originally developed in 1958.Footnote 12 These additions and modifications later contributed to the wide distribution of REDUCE and the creation of a community of users. While in the early 1970s SCHOONSCHIP was available only for the CDC 6000/7000 series, REDUCE ran on the PDP-10, most IBM 360 and 370 series machines, the CDC 6400, 6500, 6600, and 6700, and began to be implemented on new systems such as the UNIVAC 1100 series [84, 85].
2.2.3 ASHMEDAI
The development of ASHMEDAI by Michael J. Levine, an American Ph.D. student at the California Institute of Technology, also began in the early 1960s. Its genesis seems to be closely linked to that of SCHOONSCHIP. Indeed, according to Veltman, the idea of developing such programs arose from a discussion, in which Levine took part, at CERN in the summer of 1963 [63, p. 77]. The two physicists were then working on phenomena related to the development of the V-A theory. More precisely, Levine’s dissertation was dealing with neutrino processes of significance in stars [86]. In particular, he was computing the transition probabilities and rates of dissipation of energy by neutrino–antineutrino pairs for several processes predicted by recent developments in the theory of weak interaction. ASHMEDAI, which supplied assistance for these tasks, was initially written in FAP (Fortran Assembly Program), a machine-oriented symbolic language designed “to provide a compromise between the convenience of a compiler and the flexibility of an assembler” [87, p. 1]. The initial package consisted of about 4000 commands, used 20,000 wordsFootnote 13 of storage, and ran for about 8 minutes per diagram on an IBM 7090 [86, pp. 80–81].
As a symbolic manipulation program, ASHMEDAI was promptly capable of performing operations such as substitution, collection of terms, permutation of Dirac matrices and taking traces of products of Dirac matrices [88, p. 69]. So, while it was developed to “do many of the tedious straightforward operations arising in Weak Interaction and Quantum Electrodynamics calculations,” Levine saw as early as 1963 that it could naturally become a more general algebraic language to be applied to various problems [86] [89, p. 359]. This prospect, however, was never realized to the extent of SCHOONSCHIP and REDUCE. ASHMEDAI remained seen as a special purpose program, with limited long-term success. But it should be noted that some of its features of specific interest to the development of high-energy physics were praised in the 1960s and 1970s (see, e.g., Refs. [26, 63]). In particular, Levine’s work to establish routines performing symbolic algebra manipulations for Dirac matrix and tensor algebra revealed particularly effective. Compared to REDUCE, ASHMEDAI had the advantage of being able to compute larger products of \(\gamma \)-matrices and was initially found to be more suitable for higher-order calculations [90].
In the late 1960s and early 1970s, ASHMEDAI experienced a complete makeover. FORTRAN became the high-level source language to “facilitate writing, debugging, modifying and disseminating the code,” and an improved user interface was developed [89, p. 359]. Moreover, some algorithms were degraded to facilitate coding and many features deemed unnecessary were removed. In addition to flexibility, the use of FORTRAN offered better portability as well. Already being implemented on a CDC 3600 in the late 1960s, ASHMEDAI was run by Levine on a Univac 1108 in the mid-1970s and was also available on many PDP-10 and IBM 360-370 machines [89, 90].
2.2.4 First applications
Naturally, the first results of calculations performed with the help of algebraic programs were supplied to the community by their creators and concerned electroweak interactions. For instance, motivated by the development of electron–electron and electron–positron colliding-beam projects—most notably at Stanford—Hearn collaborated in 1965 with Yung-su Tsai to compute the differential cross section for the as-of-then hypothetical process \(e^++e^-\rightarrow W^++W^-\rightarrow e^++\bar{\nu }_e+e^-+\nu _\mu \) [91]. Also, Levine, whose PhD results were at odds with some more recent estimations, published in 1967 the calculations to the lowest order in the coupling constants of the cross section contributions of four Feynman diagrams for a nonlocal weak interaction mediated by a charged vector meson [88]. These two cases are examples of a type of problem involving relatively little analytical work for which algebraic programs to compute traces of Dirac matrices gradually gained popularity at the turn of the 1960s and 1970s. The implementation of SCHOONSCHIP on a CDC 6600 computer at the Brookhaven National Laboratory near New York played an important role in this process. In several cases, it proved to be valuable for low order calculations related to projected processes in upcoming electron–positron colliders (see, e.g, Refs. [92, 93]).Footnote 14
Nevertheless, the real test of the usefulness and effectiveness of algebraic programs in high-energy physics would come directly from the situation presented in Sects. 2.1.1 and 2.1.2. The pioneering work of Veltman, Hearn, and Levine in the field of computational physics had actually anticipated the situation in which computer-assisted calculations would prove essential to ensure the validity of the new QED through a careful verification of the adequacy with experiment. Thus, as required by the increasing number and complexity of higher-order Feynman diagrams, these algebraic programs naturally began to be used around 1970 for the computation of the two-loop (order \(e^4\)) contributions to the Lamb shift, and the three-loop (order \(e^6\)) contributions to the anomalous magnetic moment of the electron and the muon. An interesting aspect of this process is that it quickly took on a strong collaborative dimension that allowed for testing not only the theory but also the new computational techniques that had just been developed. Indeed, while different teams were at work to calculate all the necessary Feynman diagrams, the results were systematically cross-checked using different algebraic programs.Footnote 15
As mentioned in Sect. 2.1, with respect to the Lamb shift, the determination of radiative corrections of order \(e^4\) requires the computation of the seven Feynman diagrams shown in Fig. 4.Footnote 16 First done analytically by hand in 1966 by Soto Jr., it was not until 1970 that computer-assisted calculations were performed at Stanford by Thomas Appelquist and Brodsky [43, 48, 49]. REDUCE automatically computed the traces of Dirac matrices, applied projections, and reduced the expressions to Feynman parametric integrals (see Appendix B.2). The new value obtained, in disagreement with Soto Jr.’s, was found to be in excellent conformity with the most recent experimental results. If John A. Fox also recalculated with REDUCE the specific contribution of the “crossed” graph, most of the verifications were made by physicists closely related to CERN, where SCHOONSCHIP was available [97].Footnote 17 Benny Lautrup, Petermann and Eduardo de Rafael computed the contributions at order \(e^4\) for the “corner” diagrams, and Lautrup independently checked the contribution of the vacuum polarization term [98]. Petermann also carried out calculations for the “crossed” graph [99]. Finally, on the CERN CDC 6600 and on that of the University of Bologna, Riccardo Barbieri, Juan Alberto Mignaco, and Remiddi recomputed the contributions from all seven Feynman diagrams [100, 101]. Overall, these SCHOONSCHIP results confirmed those obtained with REDUCE. But as a further verification of the methods, in the first and last cases at CERN, contributions at order \(e^4\) of the anomalous magnetic moment of the electron were also calculated and found in good agreement with the results initially obtained by Petermann in 1957 [34].
With regard to the evaluation of contributions of order \(e^6\) to the anomalous magnetic moment of the electron, as mentioned previously, 72 diagrams had to be calculated (the twelve graphs including fermion loops are reproduced in Fig. 5). Their first approach with algebraic programs then also took place at the turn of the 1960s and 1970s.Footnote 18 With the help of REDUCE, Janis Aldins, Brodsky, Andrew J. Dufner, and Toichiro Kinoshita, split between Stanford and Cornell, determined the corrections due to the two Feynman diagrams with light-by-light scattering insertions [102].Footnote 19 Following the same method, Brodsky and Kinoshita calculated the seven graphs with vacuum polarization insertions of order \(e^2\), while the three with vacuum polarization insertions of order \(e^4\) had been computed previously with SCHOONSCHIP at CERN by Mignaco and Remiddi [104, 105]. These ten diagrams were also investigated separately by Jacques Calmet and Michel Perrottet of the Centre de Physique Théorique of Marseille who found results in good agreement [106]. For this purpose, they used an independent program written in LISP by the former. Finally, in 1971, Levine and Jon Wright presented their results for the sum of the remaining diagrams [107, 108]. Specifically, they computed with ASHMEDAI all 28 distinct graphs that do not involve fermion loops.Footnote 20 This contribution alone justifies the special place occupied by Levine’s program in this historical account. Not only did it prove to be quite “elegant,” but it was also, by its magnitude and complexity, “one of the most spectacular calculations in quantum electrodynamics” performed in the early 1970s [26, p. 14] [63, p. 77]. Indeed, bosonic loop graphs, as opposed to those with closed fermion loops, are generally much more difficult to calculate. The results obtained were confirmed in 1972 by Kinoshita and Predrag Cvitanović who used the CDC 6600 version of SCHOONSCHIP at Brookhaven National Laboratory but also verified some of their calculations by hand and with a PDP-10 version of REDUCE 2 [110].
The overall result of this collective effort was found to be in good agreement with the recent precision experiments carried out in the late 1960s. This was also the case for the anomalous magnetic moment of the muon, for which contributions of order \(e^6\) had naturally been calculated together with those of the electron by the various actors mentioned above [96]. As a result, by the early 1970s, the situation was such that trust had not only been improved in the new QED and QFT but also been established in algebraic programs. The achievement of similar results, by separate teams using different machines, programs, and techniques, was the guarantee of their acceptance as indispensable computational tools in theoretical high-energy physics and beyond [59, p. 19] [73] [89, p. 364].
2.3 Early 1970s: initial assessment
The rise of algebraic programs to solve QFT problems, as described above, was in fact part of a much broader movement that saw, from the mid-1940s onward, the emergence of digital computers as fully fledged tools for scientists. As far as experimental high-energy physics is concerned, Peter Galison described in his seminal book Image and Logic: A Material Culture of Microphysics how computers invaded laboratories in the postwar period and profoundly altered practices [111]. This was particularly the case with the development of the Monte Carlo method—whose dissemination in the community, between experiment and theory, was recently reassessed by Arianna Borrelli [112]—a family of algorithmic techniques aimed at calculating approximate numerical values using random processes as inputs. Stemming from work linked to the early post-war developments of the American nuclear project—most notably by Nicholas Metropolis, Stanislaw Ulam, and John von Neumann—it played a major role, particularly from the early 1960s, in the gradual emergence of computer simulations of experiments, but also, for what concerns us more directly, in the numerical estimation of complicated integrals.
All things considered, it appears that the progressive democratization of the computer in the field of physics ultimately led to the creation of a veritable community of specialists. To this end, new scientific journals were created. The first issue of the Journal of Computational Physics appeared in 1966 and that of Computer Physics Communications in 1969. Also, international meetings were soon organized in response to the keen interest aroused. In the early 1970s, a Colloquium on Advanced Computing Methods in Theoretical Physics was held in Marseille [113]. From August 2 to 20, 1971, the International Centre for Theoretical Physics in Trieste organized extended research courses on the theme of “Computing as a Language of Physics” [114]. The European Physical Society also followed the lead and set up a long series of European conferences on computational physics, the first of which was held in Geneva in April 1972 [115]. This dynamic proved to lay new foundations. As Frederick James of CERN later stated:
The advent of these schools, conferences, and journals has been important, not only in advancing the techniques of computational physics, but also in helping to establish the identity of computational physics, and offering a forum for communication between physicists from different fields whose primary working tool is the computer [116, p. 412].
Computational physics, as a field, was born. And with it, the ability of computers to perform large amounts of elementary algebra began to be fully exploited.
Widely understood, computer-assisted algebraic manipulation was a rather fashionable theme in the early 1970s. But there was still a wide gap between aspirations and reality, as Veltman illustrated in his particular style: “Many programs doing this sort of work have been written. In fact, there are probably more programs than problems. And it is a sad thing that most of these programs cannot solve any of the problems” [63, p. 75]. QFT calculations—in addition to other successes in celestial mechanics and general relativity—had nevertheless proved that a promising future was possible. Programs such as SCHOONSCHIP and REDUCE had far exceeded the expectations of their initial goal and had become general-purpose algebraic manipulation systems. Hearn, among others, therefore envisioned a successful application of these techniques in other areas, particularly in quantum physics where they appeared relevant to many subfields, such as semiconductor theory, solid state physics, or plasma theory. However, this process was still in its infancy, and it was clear that it would rely heavily on experience developed up to that point within the specific framework of QFT [59, p. 18].
As a result of the general emulation created in the emerging field of computational physics and the prospect of widespread dissemination of new algebraic methods in physics, the early 1970s proved a propitious time for an initial assessment of the various achievements to date. Several publications and talks were explicitly aimed at establishing the state of the art in computer-assisted Feynman diagram calculations. In many respects, they also addressed the various challenges and prospects for their future development. In addition to the question of automation, which will be considered in Sect. 2.4, four recurring themes were discussed: hardware facilities, the calculation of Dirac matrix traces, the renormalization procedure, and the handling of integrations.
2.3.1 Hardware facilities
As the three examples of Sect. 2.2 show, the development of algebraic programs for QFT required the use of advanced programming techniques and resulted from the dedication of people with access to large computing facilities. The dependence of these programs on such installations led to the recognition of some hardware challenges in the early 1970s. The most obvious was that of dissemination and accessibility to a wider audience. In this regard, as has already been suggested several times, REDUCE was clearly the champion. The flexibility of the high-level language used and its machine independence greatly favored its portability and widespread use. In addition, the development of FORTRAN-like output generation was conducive to its use by non-specialists in digital computing. On the other hand, although ASHMEDAI shared similar characteristics to REDUCE, its dissemination seemed to suffer from its lack of generality. Its use apparently remained limited to Levine’s inner circle at the Carnegie Mellon University in Pittsburgh, which he had joined in 1968 [63, p. 77] [117] [118, p. 344]. Finally, as far as SCHOONSCHIP is concerned, although it has proved central to the results presented above, it turns out that the machine-dependence induced by the use of a low-level language has been a serious obstacle to its rapid expansion. In 1972, its availability was limited to a few strategic centers equipped with CDC 6000/7000 computers: CERN, Bologna, Brookhaven and the French Atomic Energy Commission, at Saclay near Paris [63, p. 77] [74, p. 517]. This problem was nevertheless recognized, and in recently published reminiscences in Veltman’s honor, Remiddi recalled that Hugo Strubbe, a student of the Nobel laureate, was hired by CERN in the early 1970s to work on implementing a version of SCHOONSCHIP for IBM mainframes [74, pp. 518–519] [76].Footnote 21
The distinction between machine-dependent and machine-independent programs (low-level and high-level languages) was also at the heart of one important hardware-related issue raised by developers in the early 1970s, that of memory shortage due to the “blow-up” problem [73, p. 237] [118]. It is well-known that algebraic problems, even the simplest ones beginning and ending with fairly short formulas, often lead to the appearance of long intermediate expressions. As mentioned in Sect. 2.1.2, at low orders this blow-up mainly originates in the calculation of traces of Dirac matrices.Footnote 22 Managing these intermediate expressions proves particularly costly in terms of memory, since they often have to be stored in core during the calculation. Sometimes, the memory capacities of hardware installations are even exceeded, condemning the process to failure. This situation represented a real challenge at the turn of the 1960s and 1970s and was well recognized by the various actors mentioned above. It led Hearn, for example, to explicitly recommend processing algebraic calculations on “a computer with a high speed memory of 40 000 words or more” [120, p. 580].Footnote 23
This time, in light of this challenge, the advantage clearly went to SCHOONSCHIP, which proved not only incredibly fast but also very economical in terms of storage [121]. Indeed, high-level languages such as LISP and FORTRAN required much more storage than their low-level counterparts, on the order of “about 20 times” more, according to Veltman [63, p. 76]. This led the Dutch physicist to seriously doubt the ability of high-level language programs to contribute extensively to problems considered beyond human capabilities. Nevertheless, before we even consider any hardware improvements that would fully refute this assertion, the developments of algebraic computations in QFT invite us to moderate it. Apart from the implementation of simplifying algorithms that will be discussed in the next section, the challenge posed by memory limitations was not perceived as a dead end by users of high-level languages. For them, it was above all a matter of manipulating data artfully, and for Hearn, a “clever programmer [could] make optimum use of whatever facilities he has at his disposal” [120, p. 580]. ASHMEDAI, which proved more efficient than REDUCE in this respect, was in fact the best example of this. In addition to using auxiliary memory, Levine provided for the possibility of treating the intermediate terms of calculations as “virtual” [89, p. 362]. Consider an initial polynomial \(P_1\), successively transformed into polynomials \(P_2\) and \(P_3\) by two different operations. By performing the operations on separate terms of \(P_1\), it is possible, once a corresponding term of \(P_3\) is obtained, to destroy the created but now useless part of \(P_2\). In this way, \(P_2\) turns out to be virtual, i.e., it never fully exists at any given time, allowing a more memory-efficient execution of ASHMEDAI.
2.3.2 Traces of Dirac matrices
As shown by the QFT computations described in Sect. 2.2.4, it is clear that the digital treatment of Dirac matrices was the great success of the 1960s. SCHOONSCHIP, REDUCE and ASHMEDAI had indeed fulfilled their initial function, enabling physicists to access in a very short time results that would have required years of work before the emergence of algebraic programs. This is why, while Hearn emphasized in the early 1970s that the greatest successes had arisen “from our ability to do polynomial manipulation, simple substitutions and differentiation” and Calmet asserted that “[p]resently, there is no real difficulty to handle the algebra for such calculations,” the revolution in computation times was naturally the subject of much praise [59, p. 19] [96, p. 1]. Hearn pointed out, for example, that the “algebraic reduction of a diagram might take fifteen minutes of computer times,” while Levine put forward a “[time] spent in Dirac Matrix manipulation [of] three minutes” for a single bosonic loop graph contributing at order \(e^6\) to the anomalous magnetic moment of the electron [59, p. 19] [89, p. 360]. Since SCHOONSCHIP proved to be faster than programs in high-level languages, this assessment period naturally proved propitious for Veltman to extol the merits of his program. In addition to the above-mentioned saving of memory by a factor of around twenty, he also suggested that calculations could be performed in an interval thirty times shorter than its competitors written in LISP [63, p. 76].
In fact, it is clear that memory and time were in many ways critical factors in the development of early algebraic programs. In this respect, in addition to hardware considerations and artful manipulation of data, implementing mathematical algorithms to simplify the expression of Dirac matrix traces, and consequently the weight of calculations, was highly valued. This was particularly the case within the REDUCE framework, for which the first algorithm to be put forward on several instances was proposed by John S. R. Chisholm [122]. It enables a product of traces sharing common indices to a sum of single traces. Nonetheless, in the course of its digital implementation, John A. Campbell and Hearn noted that its effectiveness was limited to cases of two shared indices, since for three or more “the same expression arises over and over again in the computation of seemingly different traces” [123, p. 324]. It was therefore superseded by another proposal by Joseph Kahane, which leads to the reduction of any partially contracted product of Dirac matrices to a simple canonical form involving only the uncontracted indices [124]. But despite their interest, in comparison with REDUCE’s competitors, such algorithms remained insufficient solutions to the abovementioned challenges. Hearn, therefore, set out to improve them. In the early 1970s, he was working with Chisholm on an extension of Kahane’s procedure, with a view to developing a new algorithm which, he claimed, would lead “to further efficiencies in trace calculation and also reduce the amount of computer code necessary” [125] [120, p. 579].
2.3.3 Renormalization
Among the various stages of the complete Feynman diagram calculation procedure described in Sect. 2.1.2, the question of renormalization has so far not been addressed. And with good reason: despite the hopes raised by the rise of algebraic programs, its consistent approach in a computer context had yielded very few concrete results by the early 1970s. This is illustrated by the various cases examined in Sect. 2.2.4, where the careful handling of divergences had to be carried out by renormalization or regularization methodsFootnote 24 in procedures that required a great deal of effort on the part of physicists, and for which the added value of computers was minimal. There were two main reasons for this. On the one hand, Hearn pointed out that the renormalization process was “the one in which heuristics play the greatest role in deciding how the expression should be manipulated” [120, p. 593]. On the other hand, as Brodsky and Kinoshita in particular recognized, the digital conversion of the standard renormalization procedure was far from being a straightforward process: “[\(\ldots \)] the usual prescription of renormalization found in every textbook of quantum electrodynamics is not necessarily the most convenient for practical calculation, in particular, for computer calculations” [105, p. 360]. In response to these difficulties, the two theorists put forward the development, around 1970, of various alternative renormalization schemes of a more algebraic nature (see also, e.g., Refs. [126, 127]). Nevertheless, their intuition proved somewhat unfortunate: the more algebraic the procedures, the more heuristic they turned out to be, ultimately preventing their easy implementation in computer programs [120, p. 593].
In the spirit of Feynman’s original method, an attempt to apply algebraic computational techniques to renormalization theory should nevertheless be highlighted. In the late 1960s, Calmet and Michel Perrottet developed a set of LISP and FORTRAN programs aimed at generating Feynman diagrams and their relative counterterms at a given order, as well as the integration over internal momenta and resulting suppression of divergences [128]. Nevertheless, their work remained limited to the renormalization of Feynman diagrams in the simplest case of scalar theory, where divergences appear only through vacuum polarization insertions of order \(e^2\). As a minor step toward potential generalization, Calmet also introduced in 1974 a procedure coded within the framework of REDUCE that offered a first advance toward automatic recognition of divergences in a Feynman diagram [129]. This procedure was not only able to recognize whether a graph was divergent or not but also to differentiate between vacuum polarizations, electron self-energies, and vertex divergences.Footnote 25
2.3.4 Integrations
The development of efficient routines for integration was another major issue addressed by physicists in their evaluation of computational methods for Feynman diagrams [44, 59, 73, 96, 118].Footnote 26 They had to deal with particularly messy and complex multidimensional integrals whose integrands present sharp spikes distributed over the integration region. In the early 1970s, numerical methods had to be widely used, but the integrals were so complicated that the usual Monte Carlo procedure failed in the majority of cases, leading to divergent results. The most successful approach was then an adaptive-iterative routine known as SPCINT, LSD, or RIWIAD, which combined the Monte Carlo and Riemann sum methods. It was based on an original idea by G. Clive Sheppey in 1964, subsequently improved and applied to elementary particle physics by Dufner and Lautrup [130] [96, p. 17] [131]. During its execution, the integration domain is divided into smaller subregions, and for each subregion, the value of the integrand and its variance are computed at randomly selected points. The variance obtained is utilized to enhance the selection of intervals along each axis, ensuring that more points are concentrated in regions where the function exhibits insufficient smoothness. This process is then iteratively repeated.Footnote 27
Among the various calculations mentioned in Sect. 2.2.4 as early successes in the development of algebraic programs, once the divergences had been eliminated by a renormalization or regularization procedure (see the discussion in Sect. 2.3.3), amplitudes were always integrated numerically, except in two cases. In calculating the crossed graph contributions of order \(e^4\) to the Lamb shift (see Fig. 4), Fox relied on the hand-operated analytical procedure developed by Soto Jr. in 1966 [43, 97]. Barbieri, Mignaco, and Remiddi also developed an analytical approach to the computation of the Lamb shift contributions from the seven two-loop Feynman diagrams, for which they were partially assisted in some specific algebraic manipulation tasks by SCHOONSCHIP [100, 101]. The singularity of these works does not, however, reflect a lack of interest in analytic integration and its possible computer implementation. It was recognized that the latter could prove faster, more accurate and more powerful than any numerical method [59, 134]. In the words of Antoine Visconti, “analytic integration method should [even] represent the final answer to the evaluation of Feynman integrals” [118, p. 336]. And in fact, according to one of its leading figures, Joel Moses, the field of symbolic integration had just gone through its “stormy decade” [134]. With the development of faster, more reliable computers, advances in integration theory in the 1960s had seen the emergence of procedures that completely solved the problem of integration for the usual elementary functions.
SIN (Symbolic INtegrator), developed by Moses, was probably the most successful program for this purpose at the beginning of the 1970s [134]. Originally written in LISP for the IBM 7094 during 1966–1967,Footnote 28 it was inspired by the pioneering work in artificial intelligence of James R. Slagle, who in 1961 developed a heuristic program, SAINT (Symbolic Automatic INTegrator), for solving basic symbolic integration problems [135, 136]. SIN developed a strategy of successive attempts—in three stages (cheap general method, methods specific to a certain class of integrals, general method)—to solve a problem using different integration methods. But while the results were promising, it could only calculate “simple” functions, proved inflexible for many multiple integrals, and was very demanding on memory [84, p. 35]. As such, it was insufficiently suited to the heavy calculations of QFT, which is why numerical solutions were preferred. The algebraic procedures required were too powerful, sometimes involving breaking the polynomial nature of the calculation to substitute certain known functions for simple variables in the result obtained. And in fact, as the orders of perturbation theory and the internal complexity of Feynman diagrams increased, the symbolic implementation of many integrations proved particularly difficult at the turn of the 1960s and 1970s.
The multiplicity of challenges in this field therefore meant that high-energy physicists had to invest heavily in finding solutions to their specific problems. This was notably the case for Petermann, who collaborated at CERN with Doris Maison on the development of the SINAC (Standard INtegrals Analytic Calculation) program, using the CDC 6600 version of SCHOONSCHIP [137, 138].Footnote 29 Their initial aim was to develop a procedure for calculating subtracted generalized polylogarithms, also known as subtracted Nielsen functions, a class of functions appearing in several physics problems—i.e., electrical network problems or Bose–Einstein and Fermi–Dirac statistics analyses. It was established that the analytical structure of many expressions relating to radiative corrections in QED could be enumerated in terms of Spence functions, a subclass of Nielsen functions [104, 140]. Nevertheless, the impact of Maison and Petermann’s work was rather limited in the early 1970s, as it only proved fully relevant for corrections of two-loop order. Indeed, at three-loop order, the integrals to be manipulated present a higher degree of complexity, and no similar regularity had yet been established for Nielsen functions. It was unclear whether previous methods could be extended, or whether new methods would have to be developed. In short, in Calmet’s words: “the analytical structure of solutions [was] still too poorly known to hope for a general solution” [141, p. 37].Footnote 30 To illustrate these difficulties, it is worth mentioning that in 1973 Levine and Ralph Roskies attempted to calculate analytically the integrals relating to Feynman diagrams without fermion loops contributing to the anomalous magnetic of the electron at order \(e^6\) [142]. Working within the algebraic framework of ASHMEDAI, they were only able to find a solution for six of the 28 independent graphs.
2.4 Toward complete automation?
2.4.1 Computers in physics: the specter of dehumanization
According to the previous assessment of the development of calculation techniques for Feynman diagrams, it appears that the various successes encountered were tempered by hardware limitations and a combination of heuristic and mathematical problems. However, on the whole, these difficulties were not seen as a dead end from a computer science point of view. On the one hand, physicists were working on “extremely elementary and for the most part rather crude” facilities, for which it was reasonable to foresee progress [73, p. 236]. On the other hand, as might be expected of any field in its formative years, the various algebraic programs used in high-energy physics in the early 1970s were highly evolutive. In 1971, Hearn simply regarded REDUCE as a “growing system” in its infancy [82, p. 132]. Its updated version, REDUCE 2, had just been released, only 3 years after the initial version. SCHOONSCHIP was also constantly modified to include new features. As a result, its manual had to be thoroughly revised in 1974 [85].
Optimism about possible improvements was certainly warranted, as it actually was for computational physics as a whole. Computers had only recently invaded laboratories, and their significance, importance, and great potential were already widely recognized (see, e.g., Refs. [143, 144]). In 1971, Lew Kowarski described an “intrusion,” a “sudden event” whose impact was “dramatic” and led to “spectacular applications” in the field of nuclear physics [145, p. 27]. For him, this was a great liberation in space and time for the scientist. Nevertheless, as he also suggested, this excitement was in fact dampened by voices expressing a growing fear of the dehumanization of scientific practices. In this respect, in his historical approach to the development of experimental high-energy physics, Galison described how automation and the prospect of its generalization became, in the 1960s, the object of concerns and tensions that have, in many ways, shaped the evolution of the field [111]. Part of the community feared that a form of dependence on the computer would lead physicists to lock themselves into a world of very fine measurements and no discoveries.
Hans Bethe, in his introduction to Computers and their Role in the Physical Sciences published in 1970 by Sidney Fernbach and Abraham Taub, remarkably echoed these debates from the point of view of a theoretical physicist [146]. As a member of the Manhattan Project, he had been a privileged witness to the introduction of digital computers into physics. As such, he deeply appreciated the progress they had made over more than two decades, in both pure and applied physics. But he also clearly saw their role as being “our servant, meant to make our life easier, and that [they] must never become our master” [146, p. 9]. He insisted that computers were not capable of understanding, that they were only there to carry out the orders they were given, in other words, that “[t]heir answers cannot be more intelligent than the questions they are asked” [146, p. 8]. Bethe was not only unoptimistic about the future usefulness of their learning abilities but also unwilling for them to lead to potential independence. In addressing the themes of understanding, intelligence and learning, Bethe was in fact projecting his own abilities as a theoretical physicist onto the computer. And, of course, he could not foresee any success for the latter regarding an activity as abstract as the conceptual development of theories.
For this last area, as a specialist in the development of algebraic programs, Hearn was also convinced that computers had made no contribution by the early 1970s:
In every generation there may arise an Einstein or Feynman who actually develops a new theory of nature completely different from any previously considered. Here is an area where computers so far have made zero impact, primarily, I suppose, because no one yet understands just how an Einstein first obtains that insight which suggests a new theory to him. Perhaps computers could help check some calculational point during the formulation of the work, but, by and large, the insight is produced by some rare quality we call ‘genius’ as yet impossible to classify in terms that a computer can simulate [59, p. 17].Footnote 31
But as the various italicized adverbs suggest, Hearn was not on the same wavelength as Bethe when it came to future expectations. It should be remembered that the former had developed REDUCE in circles close to McCarthy, a specialist in artificial intelligence. In this context, it appears that the dehumanization of physics did not really concern Hearn. On the contrary, the idea that computers could understand, be intelligent and learn was familiar to him, and he had clearly integrated it, at least in principle, into his framework of thought and research project. Thus, his general assessment of the development of algebraic programs in the early 1970s was marked by a certain enthusiasm for the future and the potential complete automation of Feynman diagram computation. At the Second Symposium on Symbolic and Algebraic Manipulation, held in Los Angeles in 1971, he declared: “At any rate, my dream of a completely automated theoretical physicist now looks a little closer to reality than two or three years ago” [59, p. 21].
2.4.2 The automated high-energy theoretical physicist
Hearn’s ideal of a fully automated theoretical physicist attracted attention at the turn of the 1960s and 1970s. For example, it was explicitly mentioned by David Barton and John Peter Fitch in their review of the applications of algebraic manipulation programs in physics [73, p. 297]. Calmet also readily shared this view. In 1972, at the First European Conference on Computational Physics in Geneva, the French physicist defended the idea that a completely automated treatment of QED seemed “quite reasonable because of the improvement in the algorithms and techniques for algebraic manipulationFootnote 32 and the availability of powerful computers.” In Hearn-inspired terminology, he even saw the “realization of an ‘automated QED physicists’ [as] a goal which [was] no longer out of reach” [84, pp. 202–203]. One good reason for believing in this possibility was provided by an article published by Campbell and Hearn in 1970 [123]. The former had worked a little earlier on extending the initial version of REDUCE in order to allow matrix elementsFootnote 33 to be derived from arbitrary Feynman diagrams [148].Footnote 34 At the end of the 1960s, his direct collaboration with Hearn became another ambitious extension. They developed a system of programs in LISP 1.5, working within the framework of REDUCE, which handled “all stages of calculation from the specification of an elementary-particle process in terms of a Hamiltonian of interaction or Feynman diagrams to the derivation of an absolute square of the matrix element for the process” [123, p. 280].
To this end, they first worked out the computer representation of a Feynman diagram and the automatic generation of all the graphs required for a given process at a given order. To do this, they relied in particular on Wick’s theorem, a method for reducing arbitrary products of creation and annihilation operators to sums of products of pairs of these operators. Several subroutines were used to examine potential pairs and generate appropriate diagrams. Thereafter, the set of programs developed by Campbell and Hearn was able to handle the specification of the Feynman rules and their application to a given diagram in order to determine physical matrix elements as a unique mapping of one data space onto another. It performed the algebra of Dirac matrices but was also trained to recognize integrals, proceed with their integration and finally calculate cross sections. This impressive result for its time, which demonstrated the theoretical possibility of automating a complete diagram calculation, nevertheless presented some serious limitations. Firstly, Campbell and Hearn’s identification of topologically equivalent diagrams proved to be rather laborious and was subsequently judged to be insufficiently efficient [149].Footnote 35 Also, as only the simplest cases were tackled, no renormalization procedure was carried out.
With regard to the latter shortcoming, the work of Calmet and Perrottet, as described in Sect. 2.3.3, was a clear and methodical manifestation of a genuine interest in developing a more complete, and therefore more automated, algebraic procedure for calculating Feynman diagrams. For a few years around 1970, their contributions made the Centre de Physique Théorique in Marseille—alongside the University of Utah where Hearn had been appointed in 1969—a leading institution in the progressive automation of theoretical high-energy physics.Footnote 36 There, Calmet and Perrottet benefited from the support of Visconti, an experienced figure in QFT. At the end of the 1960s, he had supervised their doctoral thesis on computer-assisted calculations of radiative corrections, and fully embraced the prospect of complete automation [118]. During this period, the number and variety of programs and subroutines used and developed by Calmet and Perrotet were considerable. In addition to the various renormalization packages already mentioned and Calmet’s program for calculating contributions of order \(e^6\) to the electron’s anomalous magnetic moment, mention should also be made of ACOFIS (Algebraic Computation of Feynman Integrals Scalar), written in LISP by Perrottet and designed to calculate diagrams that are at most logarithmically divergent. A FORTRAN program based on the Monte Carlo method was used for the numerical evaluation of numerous integrals on Feynman parameters, while much effort was also devoted to developing routines for generating Feynman diagrams [106, 128, 129]. FRENEY, developed by Perrottet in FORTRAN, was based on combinatorial analysis [151]. DIAG I and DIAG II, written in LISP by Calmet, were based on the generative functional formalism [128, p. 197]. In both cases, the elimination of unnecessary diagrams was achieved by the comparison method, which, however, required excessive memory usage [149].
This list, which is not entirely exhaustive, reveals one of the most striking aspects of attempts to automate QFT computation: the general situation was rather sketchy, lacking any coherence whatsoever, and in many respects resembling endless tinkering. This is all the more striking if we remember that this period was marked by a fundamental lack of compatibility between languages and limitations in access to computing facilities. For today’s scientists, the situation experienced by their elders may seem somewhat incongruous on many levels: in the late 1960s, physicists in Marseille were running LISP programs on an IBM 360-67 at the Institut de Mathématiques Appliquées in Grenoble, in the French Alps, and FORTRAN programs on a UNIVAC 1108 in Orsay, near Paris [128, p. 192]. Hearn clearly recognized this complex situation, as he himself attributed a system’s ability to perform a calculation fully automatically to the “combining” of several programs [120, p. 594]. Nevertheless, as his ideal of an automated theoretical high-energy physicist became more manifest, this concern seemed of minor importance. In fact, the emphasis was repeatedly placed on the human factor: “However, it is important to recognize that we are not really at the point yet where we can perform a non-trivial calculation in fourth-order QED by these means without human intervention” [120, p. 594].
The role of heuristics has already been mentioned a few times as a hindrance to progress in the development of algebraic programs for calculating Feynman diagrams. This was the case for renormalization, but also for integration, the two main obstacles encountered along the way. But actually, heuristics were part of the whole process and appeared during more elementary processes, such as selecting relevant diagrams or reducing traces. In short, heuristics always came into play when it was necessary to choose between alternatives in a situation where preferences were unclear, or when operations were not particularly well-defined. For Hearn, this omnipresence simply stemmed, in most cases, from a fairly common situation initially present in hand calculations: “many complicated heuristic decisions must be made during the calculation in order to keep the size of the intermediate expressions formed under control” [120, p. 594]. At the turn of the 1960s and 1970s, this question of control was at the heart of scientific practice. To keep expressions in a manipulable form, physicists had to accompany computational procedures, step by step, from start to finish. And with good reason, since the only “heuristic supervisor remain[ed] the physicist, who [sat] in front of a console, and direct[ed] the calculation” [123, p. 325]. As he expressed in his collaboration with Campbell, Hearn was nevertheless optimistic that future developments would free physicists from such a tedious task. Confronted with the specter of the dehumanization of physics, he went against the position of many of his colleagues. For him, automation simply meant liberation, and he welcomed the idea of the machine taking over: “Ultimately, we hope to include many of these ideas in a heuristic supervisory program which will automatically control the calculation from start to finish. The problems are fairly well-defined, even though no essential algorithms exist as such for their solution” [123, p. 325].
Irrespective of technological innovations, as shown by various considerations in Sect. 2.3, it was nevertheless clear by the early 1970s that further developments in algebraic programs for calculating Feynman diagrams would result first and foremost from the resolution of mathematical problems, the simplification of procedures and the development of algorithms better suited to computers. Many of these operations, whose developments to date are described in Sect. 3, would participate in the progressive reduction of the heuristic load of calculations and advances in QFT. As a matter of fact, despite the circumstance that some of the initial intuitions turned out to be rather misleading—as with Brodsky and Kinoshita’s initial consideration of renormalization schemes of a more algebraic nature (see Sect. 2.3.3) [105]—this has always been the path followed by most physicists. Including contributors like Calmet and Perrottet, whose systematic and rigorous approach to automation was deeply rooted in current QFT developments and proved, in many ways, rather problem-oriented. In particular, their work was directly integrated into Visconti’s program on renormalizable scalar theories within the framework of the functional formalism [128, 152,153,154]. And on the whole, Calmet simply argued that “the user who wants to solve a specific problem must not remain passive and wait for a language to provide him with all the techniques he needs. Instead, he should strive to create these techniques himself when they do not yet exist”[141, p. 37].Footnote 37 The development of SINAC by Petermann and Maison is a perfect illustration of this. The ultimate but insufficiently advanced project for a general symbolic integration program, most notably carried out by Moses, had to be set aside to concentrate on the specific class of integrals tackled in particle physics calculations. In the history of the development of algebraic programs, such a dynamic is symptomatic of an essential characteristic of the different systems considered: none can be considered the “best,” since different problems simply require different approaches.Footnote 38
The weight of problem-oriented approaches is not surprising in the development of a field whose very origin is none other than calculations related to specific processes in electroweak interaction theories. In fact, it is a dynamic that even founding fathers such as Veltman and Levine praised in later developments (see, e.g., Refs. [63, 89]). The former was particularly concerned about the deceptive illusion of simplicity resulting from programs developed without motivation from research not directly related to computer science. In his view, they would miss the real intricacies of the problem to be solved behind an apparently efficient formulation of the initial problem. On the other hand, it is also true that Hearn could not escape the general trend in the field. This is illustrated by his early collaboration with Tsai on electroweak interaction, or the recognition, in the course of his work with Campbell, that “the result of development of the diagram-generating program will probably depend on the most popular problems which require solution” [91] [123, p. 300]. Nevertheless, as a brief conclusion to this historical section, it is worth pointing out that, on the whole, Hearn clearly remained on the margins of the problem-oriented movement. Although trained as a theoretical physicist, he was in many ways a true computer scientist at heart. Early on, he made a virtue of the general character of REDUCE, and emphasized the capabilities of machines and their potential for development (see, e.g., Ref. [61]). He was convinced that progress in particle physics would result primarily from technical innovations in computing: “[i]f the more sophisticated capabilities, such as polynomial factorization and integration, become more readily available, and the straightforward calculations are all completed, we may see a new breed of calculations emerging” [59, p. 21]. As such, his direct contributions to the development of QFT may seem of minor importance, especially when compared with those of Veltman. But that is not what mattered to him. In fact, by explicitly and primarily addressing the question of the complete automation and computational treatment of heuristic problems, by placing the themes of the new field of artificial intelligence at the forefront of physics debates as early as the 1970s, Hearn was simply pursuing different goals from those of most of his colleagues. In this sense, he might appear today to have been ahead of his time.
3 The algorithmic evaluation of Feynman diagrams
As outlined in Sect. 2, the evaluation of Feynman diagrams has been one of the main driving forces for the development of computer algebra systems which today have become indispensable tools for research in many other fields. This is why this section, which provides an overview of the current situation and challenges in the field, seeks first and foremost to illustrate in more detail the primary reasons that motivated theoretical physicists to develop such systems.
But as suspected by Hearn and others (see Sect. 2.4.2), their initial efforts in the 1960s and 1970s were only the beginning of a journey toward full automation of perturbative calculations in quantum field theory. In fact, the developments in this direction have been enormous since these pioneering days. After all, Feynman diagrams carry the potential for a much higher degree of automation than just performing the required algebraic operations.
Therefore, we also want to provide some insight into the efforts that have been made and the methods that have been devised toward the full automation of perturbative calculations. Not surprisingly, this involves a number of rather involved mathematical tools. Since we want to go beyond a popular-science level presentation and give a realistic insight into the matter, the presentation may at times be difficult to digest for an outside reader. However, we made an effort to keep it self-contained and accessible for the non-expert, though mathematically inclined reader.
3.1 Feynman diagrams and algorithms
Most of the time when we speak of a Feynman diagram in this paper, we simultaneously refer to the visual image as well as the mathematical expression that it represents. The correspondence between the two is given by the Feynman rules. In this sense, physicists also speak of “calculating a Feynman diagram,” or “adding Feynman diagrams,” etc. The sum of all Feynman diagrams that contribute to a particular scattering reaction gives the scattering amplitude, or matrix element, for this process, typically denoted by \({\mathcal {M}}\). Taking its absolute square, \(|{\mathcal {M}}|^2\), and integrating it over the momenta of the final state particles (more precisely: the phase space) leads to the scattering cross section.
Each vertex in a diagram contributes one power of a coupling constant of the underlying theory. For simplicity, we will focus on QED in this paper.Footnote 39 QED only involves a single coupling constant e, the unit of electric charge. It is related to the dimensionless fine structure constant as \(e^2\sim \alpha \approx 1/137\). A Feynman diagram in QED with n vertices thus contributes a term of order \(\alpha ^{n/2}\) to the amplitude.
The theoretical basis of Feynman diagrams is the highly complicated formalism of QFT. Its basic objects are space–time dependent quantum operators (the quantum fields). Physical observables are related to matrix elements of products of these operators. The consistent definition of such products, in particular if they are taken at the same space–time point, remains a topic of research in mathematical physics until today.
Remarkably, Feynman diagrams reduce these calculations to a largely algorithmic procedure, albeit only in the limit of “small” interaction among the quantum fields. However, all of the known fundamental interactions (electromagnetic, weak, and strong)Footnote 40 become “small” in some energy range, which is one of the reasons why Feynman diagrams have become such a central tool in elementary particle physics.
In general, what we mean by “algorithmic procedure” in this paper is a method that solves a class of (mathematical) problems by following well-defined rules. The examples which are most relevant for our discussion are algebraic operations like matrix manipulations, or combinatorics, or the differentiation of a mathematical expression that is composed of elementary functions. A counter example is to find the integral of such an expression in analytic form: this task simply may not have a solution, and one cannot be sure if it does. Once an algorithmic procedure for a certain class of problems is known, the task of solving these problems can be automated, meaning that it can be implemented into a computer program.
Calculations based on Feynman diagrams involve combinatorial and algebraic aspects, but also integrations. The possibility of the automation of the first two is obvious, but required the development of suitable software: computer algebra systems, as elaborated on in Sect. 2, and Feynman diagram generators, whose origins were described in Sect. 2.4.2, while some current ones will be discussed in Sect. 3.2. The main efforts toward the automation of perturbative calculations in QFT, however, went into finding algorithms for evaluating the associated integrals. As indicated above, integration is a non-algorithmic task in general, and early attempts to approach it were discussed in Sect. 2.3.4. Integrals that occur in Feynman diagrammatic calculations (“Feynman integrals”) suffer from the additional complication that they are divergent. Before they can be assigned any meaningful result, they need to be regularized, which turns out to be an intricate task due to the restrictions from the underlying symmetries of the theory. The fact that algorithmic approaches for the evaluation of Feynman integrals can be found despite of these obstacles is due to the rather restricted structure of Feynman integralsFootnote 41—and the ingenuity of the respective protagonists. We will discuss some of the most important algorithms in the Sect. 3.5.
The algorithmic nature of calculations of Feynman diagrams is only one reason for the success of computer algebra systems in this field. As already alluded to in Sect. 2.1.2, the second one is the extent of these calculations due to the proliferation of mathematical terms arising in intermediate steps. As any particle physicist working in the field of perturbative calculations will have experienced, already the lowest order approximation for a simple physical observable, such as the cross section for \(e^+e^-\rightarrow e^+e^-\), can require pages and pages of manual calculations before the—often very short—final formula is found. Each calculational step may be almost trivial, but there can be just so many of them that the whole calculation becomes very cumbersome and error-prone. The amount of time it takes to finally arrive at the correct result multiplies with every small mistake one makes at one of the intermediate steps.
Computer algebra programs can perform all the simple intermediate steps very fast and flawlessly, and they keep track of virtually arbitrarily many terms. Nowadays, any serious student of QFT will appreciate this benefit rather sooner than later, and so it is not surprising that some of the brilliant pioneers of the field realized the need for such programs and engaged in their development, as discussed in Sect. 2. But Feynman diagrams allow for a much higher degree of automation than just performing algebraic steps. The following discussion will provide a comprehensive tour through the various aspects of the way toward a fully automated calculation.
3.2 Feynman diagram generators
The first step in evaluating a cross section in perturbation theory is to find all contributing diagrams. Consider, for example, the process of elasticFootnote 42 electron–positron scattering, \(e^-e^+\rightarrow e^-e^+\).Footnote 43 From the Feynman rules of QED it follows that the diagrams contributing to the corresponding scattering amplitude at order \(e^2\) are those of Fig. 6. In this case, this is the lowest order in perturbation theory, meaning that there are no diagrams with fewer vertices which would contribute to the amplitude.
The set of Feynman diagrams that contribute to a given process is obtained by connecting the external lines in all possible, topologically distinct waysFootnote 44 by using the available propagator lines and vertices of the underlying theory. The generation of the diagrams is thus mostly a combinatorial procedure and can therefore be automated.
A diagram which contributes at order \(e^4\) to this process must have the same external lines, but four instead of two vertices. This is only possible if the diagram contains closed loops, such as those shown in Fig. 7; the reader is encouraged to find all 26 diagrams that contribute at this order. At order \(e^6\), there are already 330 diagrams with two closed loops, increasing to 4546 and 69 154 at three- and four-level, respectively. In the Standard Model (SM), these numbers are still larger due to the increased particle content of that model. Eventually, any particle of the spectrum will appear in a loop; for example, Fig. 8a shows a diagram which contains a top quark and a Higgs boson. Merely drawing the diagrams by hand becomes very cumbersome and error-prone already at the one-loop level. Nevertheless, from the first attempts made as early as 1969 (see Sect. 2.4.2), it was not until the late 1980s that this clearly algorithmic task was generalized and effectively implemented in a computer program, named FeynArts [156, 157]. In fact, FeynArts is still one of the most popular “diagram generators,” in particular for one- and two-loop calculations. For higher orders, a number of other, more efficient or flexible diagram generators exist. For example, it takes qgraf [158, 159] only a few seconds to generate the 1 162 266 five-loop diagrams for the process \(e^{+}e^{-}\rightarrow e^{+}e^{-}\) in QED.
The main purpose of a Feynman diagram generator is to determine all topologically distinct graphs for a given particle process with a certain number of closed loops. Most of the time, a visual output for the diagrams (i.e., the actual image) is only of secondary importance (but can be useful for debugging purposes, for example, see [8]) and may not even be within the capabilities of the generator. What is important is that the output allows a unique translation into the mathematical expression of the amplitude by inserting the Feynman rules. FeynArts even directly performs this translation. In other cases, such as qgraf, the user has to supply additional code to perform this task.
The actual difficulties when working with Feynman diagrams are related to the evaluation of the resulting formula. Since each Feynman diagram corresponds to a unique mathematical expression, their sheer number makes it mandatory to use computers for the evaluation of the corresponding amplitudes at higher orders. But, as we will see, with every order of perturbation theory, the complexity also of each individual Feynman diagram increases enormously, so that the aid of computers becomes indispensable, both on the algebraic and the numerical side.
3.3 Tree level
Typically, the lowest order contribution to a scattering amplitude is represented by Feynman diagrams without any closed loops, referred to as tree-level diagrams (see Figs. 6 and 8b, for example). It turns out that tree-level diagrams correspond to purely algebraic expressions, i.e., the resulting amplitude obtained by replacing the lines and vertices according to the Feynman rules does not involve any integrals (see Appendix A.4). This means that only algebraic operations are required in order to evaluate the (complex) numerical value of the amplitude \({\mathcal {M}}\) for a given set of input parameters. Since algebraic operations are algorithmic, this task can be carried out fully automatically.
And indeed this is very helpful, because already at tree-level, the calculations can be quite extensive, in particular if the number of external particles is larger than two or three. The main reason for this is that the number of external legs also determines the number of vertices and the number of internal lines. In QED, every internal line and every vertex introduces a Dirac matrixFootnote 45 and the calculation of the amplitude requires to take the trace of their product. It has already been pointed out that this leads to a severe proliferation of terms. For example:
where \(g^{\mu \nu }\) is the metric tensor. Such traces appear for every diagram in QED. What adds to this is that, as mentioned above, one eventually needs to take the absolute square of the amplitude, \(|{\mathcal {M}}|^2\). Therefore, if there are 10 diagrams contributing to a process, each of which produces 10 terms after evaluating the fermion trace, this already results in \(10^4\) terms in the squared amplitude.Footnote 46
In order to arrive at the cross section, one needs to integrate the squared matrix element over a certain volume in the phase space of the final state (i.e., the momenta of the outgoing particles). This can be done in a very general way, for example by using Monte Carlo integration techniques (see Sect. 2.3.4), which can be included in an automated framework.
There is one caveat that needs to be pointed out here. Consider, for example, the process \(e^+e^-\rightarrow e^+e^-\gamma \), for which a diagram is shown in Fig. 8b. It turns out that the integral over the full phase space is divergent in this case—it does not exist. The divergences can be associated with regions of phase space where the photon in the final state becomes either soft (\(E\rightarrow 0\)) or collinear to one of the other two final state particles. At first glance, this may seem unphysical. However, these configurations correspond to the situation where the emitted photon cannot be observed in isolation. They are therefore experimentally equivalent to the process \(e^+e^-\rightarrow e^+ e^-\) and thus should be excluded if one is interested in the case where three separate particles are observed in the final state. As long as one stays away from soft and collinear regions, the structure of phase-space integrals is sufficiently well understood to evaluate them numerically in a fully automatic way. We will return to this issue in Sect. 3.8 though.
In effect, tree-level predictions for physical processes can be obtained fully automatically. Software tools to perform this task have existed for many years and have proven extremely useful in analyzing the data of particle colliders [160, 161].Footnote 47 Currently, the prime example for such a program—which actually works even at the one-loop level—is MadGraph5_aMC@NLO [163]. It is very easy to install and guides the user through the individual steps of defining the desired calculation. This amounts to specifying the final and initial state (e.g. “\(\texttt {e}{} \texttt {+} \texttt {e}{} \texttt {-} \texttt {>} \texttt {e}{} \texttt {+} \texttt {e}{} \texttt {-}\)”) and defining all the model and collider parameters (coupling strengths, masses, collider energy, etc.). The expert user can input all this information into a file which is read by MadGraph5_aMC@NLO and used to compute all the desired quantities without any human intervention.
3.4 Divergences, renormalization, and dimensional regularization
Let us now move on to higher orders. As pointed out above, this leads to Feynman diagrams with closed loops. In this case, momentum conservation at each vertex is no longer sufficient to uniquely express the momentum of the particles in the loop in terms of the external momenta. For example, the loop momentum k in Fig. 7a is completely arbitrary. Since quantum mechanics requires one to sum over all probability amplitudes for a certain process, a closed loop indicates that the amplitude involves an integration over a four-momentum (k in Fig. 7a), which is why one refers to this as a loop integral. At first sight, this seems to be a complication with respect to the tree-level case which can be overcome by including a numerical integration in the automated calculation of Feynman diagrams. After all, integration is already required for the phase space, as pointed out above, and several efficient and flexible algorithms for the numerical evaluation of multi-dimensional integrals have been developed over the last few decades (for a review, see Ref. [164]).
There is a major obstacle though. Like phase-space integrals, also loop integrals are divergent in general. But in contrast to the former, this issue cannot be avoided through physical restrictions of the phase space. In fact, it was these singularities that prevented the consistent development of QFT in the 1930s and 1940s. The problem was eventually resolved by the method of renormalization, for which Feynman, Tomonaga, and Schwinger were awarded the Nobel Prize in 1965 (see, e.g., Ref. [1]).
To understand the origin of these singularities, let us consider the following Feynman integral (cf. also Eq. A.26):
It arises in Feynman diagrams like the one shown in Fig. 7a, for example, where \(q=q_1+q_2\) is the momentum of the virtual photon, m is the mass of the particle in the loop, and k is the loop momentum. This integral is divergent, which can be seen by recalling that a D-dimensional integral of the form
is convergent only for \(a>D\). In the integration region of B(q, m) where \(k^2\) and all components of k are so large that m and q can be neglected, the integral takes the form of Eq. (3.3) with \(D=a=4\). The integral in Eq. (3.2) therefore does not exist; it does not have a finite numerical value.
Let us, for the moment, “regularize” the integral by introducing a cutoff \(\Lambda \), meaning that we restrict the integration region of k to values of \(|k|<\Lambda \), i.e., every component of k is restricted by \(\Lambda \). The resulting integral, denoted by \(B(q,m,\Lambda )\), is well-defined, but its value depends logarithmically on \(\Lambda \); say
where a and b are functions of q and m. Using this result, the theoretical prediction of an observable \({\mathcal {O}}\) which involves \(B(q,m,\Lambda )\) also depends logarithmically on \(\Lambda \) and thus does not exist as \(\Lambda \rightarrow \infty \). The idea of renormalization is now to replace the parameters \(g,m,\ldots \) of the Lagrangian by \(\Lambda \)-dependent quantities \(g(\Lambda ),m(\Lambda ),\ldots \), and to define their \(\Lambda \) dependence in such a way that it cancels the divergences that arise in the integrals. The theoretical prediction for an observable then becomes finite. \(g(\Lambda )\) and \(m(\Lambda )\) are called the bare parameters of the theory. Only observables \({\mathcal {O}}\) have a physical interpretation, the bare parameters are unphysical and should be seen as book-keeping devices only.Footnote 48 One may then define renormalized parameters by subtracting the divergent terms from the bare parameters in one or the other way, but this is irrelevant to our discussion.
As discussed in Sect. 2.3.3, renormalization was considered crucial in order to be able to evaluate the integrals, since only the proper combination of the integrals with the bare parameters gives a finite result. A way around this is to introduce the intermediate step of regularization, which allows one to separate the calculation of the integrals from the renormalization of the parameters. One way of regularizing the integral, by introducing a cutoff \(\Lambda \), was already discussed above, but it interferes severely with the symmetries of the theory (Lorentz invariance, gauge invariance) and leads to inconsistent results.
As of today, the method of dimensional regularization, introduced by ’t Hooft and Veltman [166], has proven most efficient to deal with divergences at higher orders in perturbation theory. The idea behind it is to replace the 4-dimensional integration measure in Eq. (3.2) by a D-dimensional one. Remarkably, it is possible to define Feynman integrals without specifying the value of D; we can leave it as a free parameter and assume that its value is such that the integral converges. The main reason why this works is that the formula for the surface of the D-dimensional unit sphere,
can be analytically continued to arbitrary complex values of D due to Euler’s generalization of the factorial to the complex plane in term of the \(\Gamma \) function. The physical limit \(D\rightarrow 4\) can thus be approached continuously. The divergences that occur in Feynman integrals at \(D=4\) will manifest themselves as inverse powers of \(\epsilon \equiv (4-D)/2\). The bare parameters of the Lagrangian then also contain such \(1/\epsilon \)-terms. The procedure of renormalization, which had been considered to be a major obstacle until the early 1970s, then reduces to the straightforward task of inserting these bare parameters into the final expression for the observable under consideration, which automatically subtracts all poles in \(1/\epsilon \) and allows one to take the limit \(\epsilon \rightarrow 0\).
Analytical continuation of the integration dimension D to the complex plane cannot be done for numerical integration though. Also, in order to cancel the divergences between the integrals and the bare parameters, one needs the explicit \(\epsilon \) dependence of the amplitude around the physical limit in the form
where n coincides with the number of loops (for UV divergences). This means that a straightforward numerical evaluation of higher-order contributions in perturbation theory as in the case of tree-level diagrams is no longer possible at higher orders. Rather, certain algebraic and analytic manipulations are necessary before numerical methods can be employed.
Since the problem of the proliferation of terms also exists at higher orders, and is actually much more severe, it was important that the methods to be applied to the calculation of loop integrals could be formulated algorithmically, so that the can be incorporated into an automatic setup. Not surprisingly, such algorithms were thus already developed very early on.
3.5 Integral reduction
The main strategy for evaluating Feynman integrals algorithmically is to express any given integral I algebraically in terms of a fixed, finite set of known integrals \(I_n\). Schematically,
where the \(I_n\) are tabulated (or available in the form of software), and the \(c_n\) are derived from algebraic operations via a so-called reduction algorithm.
3.5.1 One-loop
One of the most successful reduction algorithms for one-loop integrals was developed by Giampiero Passarino and Veltman in 1978 [167]. Consider, for example, an integral similar to Eq. (3.2), but with a non-unit numerator:
From Lorentz invariance, it follows that this integral must be proportional to \(p_\alpha \):
Contracting both sides by \(p^\alpha \), it is easy to show that
with B(p, m) from Eq. (3.2). In this way, the integral \(B_\alpha (p,m)\) has been reduced to B(p, m).
More complicated processes lead to many more of those integrals. For example, every additional external line in the diagram implies an additional factor \((k-q_i)^2-m^2\) in the denominator, where \(q_i\) is the external momentum associated with that line. In QED, m is either the electron or the photon mass (\(=0\)), but in other theories the factors in the denominator could involve different masses. There could also be several more factors \(k_\alpha \), \(k_\beta \), etc. in the numerator.
It turns out that any such one-loop integral (in a renormalizable theory) can be expressed in terms of only four basis integrals \(I_n\) (\(n=1,\ldots ,4\)). The Passarino–Veltman reduction algorithm allowed to derive the corresponding coefficients \(c_n\) in Eq. (3.7) in an algebraic way. It was essential for many next-to-leading order (NLO)-calculations in the context of precision physics at the Large Electron Positron Collider (LEP) at CERN. It remained the standard for about 30 years, when new insights into the structure of scattering amplitudes gave rise to the development of more efficient and numerically stable algorithms [168].
The four basis integrals depend on the numerical values of the external momenta and the masses of the particles in the loop. In simple cases, analytical results for these integrals are known and can be tabulated. For general values of the external parameters, efficient numerical integration routines have been developed which can be incorporated into an automatic setup (see, e.g., Refs. [169, 170]). A crucial method in the evaluation of these integrals goes back to the original paper by Feynman. For historical reasons, we briefly describe this method in Appendix B.2. It is also at the basis of a number of multi-loop techniques, such as sector decomposition (see Sect. 3.6.2).
3.6 Beyond one-loop
The complexity of Feynman integrals increases sharply with the number of loops. But the question of whether a process can be calculated with current methods or not depends not only on the number of loops, but also on the number of external parameters, meaning the masses of the internal particles and the independent momenta of the external (in- and outgoing) particles. At one-loop level, the problem can be considered solved for any number of external parameters, as we have described above. Also, certain specific quantities with no or only one external scale have been calculated up to five loops, most prominently the anomalous magnetic moment of the electron in QED [171], or certain renormalization group functions (see, e.g., Refs. [172,173,174]). But, in contrast, problems with, say, three external parameters, are still at the limit of current technology already at the two-loop level. Among the most relevant is double-Higgs production at the LHC, for example. It is induced by the collision of two gluons (which are part of the colliding protons). But gluons do not immediately couple to Higgs bosons. Rather, the process is mediated by a virtual top-quark loop (see Fig. 9a, b). This means that the leading-order prediction in perturbation theory already leads to one-loop integrals. The three kinematic variables are the Higgs mass, the top mass, and the center-of-mass energy. In order to obtain a reliable theoretical prediction, one therefore needs to include two-loop diagrams like the one shown in Fig. 9c.
Among the main challenges in the calculation of such multi-loop scattering processes are the number of integrals, their divergences, and their general complexity. A major complication with respect to one-loop integrals is the occurrence of overlapping divergences, which means that the divergences are no longer associated with the limit of a single loop momentum, but specific regions in the multi-dimensional integration volume.
3.6.1 Integration by parts
In order to minimize the complications in multi-loop calculations, one of the main goals is again the reduction of the vast number of integrals to a smaller set. The foundation for the most general way to achieve this goes back to a method developed in the early 1980s by Konstantin G. Chetyrkin and Fyodor V. Tkachov, named integration-by-parts (IbP) [175, 176].
The key to this method can be understood as follows. Let us defineFootnote 49
This integral becomes particularly simple if one of its indices \(n_1,\ldots ,n_5\) is equal to zero. For example, if \(n_5=0\), it is just the product of two one-loop integrals (see Fig. 10a). If any of the other indices is zero, it becomes a convolution of two one-loop integrals (see Fig. 10b). Both cases can be solved by a repeated application of the one-loop formula
where F(a, b, D) is a dimensionless function which is known for general values of its arguments. However, assume that we need the result for I(1, 1, 1, 1, 1), which is much more difficult to evaluate. The corresponding Feynman diagram is depicted in Fig. 10c. Using IbP, it is possible to express this integral by simpler ones by considering integrals of the form
For example, taking \(i=j=1\), the integrand becomes
Using relations like \(2p_1\cdot q = p_1^2+q^2-(p_1-q)^2\), one finds that
On the other hand, since integrals in dimensional regularization are finite, \(I^{(i,j)} = 0\) because it is the integral over a total derivative. Equation (3.15) is therefore an algebraic relation among integrals of the form in Eq. (3.11) with different values of indices. Each of the \(I^{(i,j)}\) thus establishes a relation. Interestingly, the combination \(I^{(1,1)} - I^{(2,1)}\) leads to
which expresses the original integral completely in terms of integrals where one of the indices is zero. By recursive application of the IbP identities, any integral of the form Eq. (3.11) with arbitrary indices can be expressed by a small set of relatively simple master integrals.
In principle, this method can be applied at any loop order and to any kind of Feynman integral. Establishing the IbP relations in analogy to Eq. (3.13) is trivial. For many years, however, the crucial step was to combine these relations to actual reductions that allow expressing complicated integrals by simpler ones. Originally, this required major intellectual efforts. Beyond the two-loop level, the application of IbP was therefore essentially restricted to integrals with a single external mass scale [175,176,177,178]. Nevertheless, once the recursion relations were established, they could be implemented in algebraic programs like FORM,Footnote 50 which then allowed expressing any integral of certain kinematics in terms of the associated master integrals (see, e.g., [179,180,181]). This becomes particularly helpful in combination with the method of asymptotic expansions to be discussed further below.
More systematic approaches to solving the problem of turning IbP identities into recursion relations started in the mid-1990s, but the breakthrough in the automation of IbP was achieved by Stefano Laporta in the year 2000 [182]. Starting from seed integrals of a certain class (defined by the external momenta and masses), his algorithm iteratively generates all integrals that follow from the IbP identities until one arrives at a system of equations which allows expressing the desired integrals in terms of master integrals.
In practical calculations, this can lead to systems involving millions of equations. This is why major efforts currently go into efficient implementations of the Laporta algorithm, or even just solving huge systems of linear equations (see, e.g., Refs. [183,184,185]). To a large extent, the evaluation of multiloop Feynman integrals is therefore reduced to an algebraic procedure which can generate huge intermediate expressions. In some sense, this mirrors the situation encountered in the 1960s with the computation of Dirac matrix traces (see Sect. 2.1.2), making the use of efficient computer algebra tools even more indispensable. Indeed, recent years saw significant investments into hard- and software developments tailored toward algebraic manipulations. For example, parallelized versions of FORM were developed [186], and theoretical research institutions acquired large computing clusters designated for integral reductions. In short, the development of the integration-by-parts method, which until this day is at the heart of virtually every perturbative calculation beyond the one-loop level, significantly extended the field of application of algebraic programs in high-energy physics.
3.6.2 Calculation of master integrals
What remains after the IbP reduction is the evaluation of the master integrals. While originally this usually required completely different methods and large intellectual efforts, in recent years a number of ingenious algorithms have been developed. For a pedagogical introduction to these methods, we refer the reader to Ref. [22].
One of them is by differential equations. The key idea is to take derivatives of the master integrals with respect to external parameters rather than loop momenta as in Eq. (3.13). Explicitly applying the derivatives to the integrand produces new integrals with modified indices (i.e., powers of the propagators, see Eq. (3.11)). However, they can again be reduced to master integrals using IbP reduction. This establishes a system of first order linear differential equations for the master integrals which can be solved, for example numerically, given that the integrals are known in some limit of the external parameters (the initial condition). The latter, however, is typically rather simple to obtain (see also the discussion in Sect. 3.7 below). In 2013, Johannes M. Henn found that, in many cases, the system can be brought to a canonical form which even allows for a fully algebraic solution, provided the initial condition is known [187]. Subsequently, this observation was also turned into an algorithmic procedure [188] (see Ref. [189] for an implementation).
There is also a fully numerical approach to evaluating multi-loop Feynman integrals. As indicated above, one of the problems in this respect is overlapping divergences. In 2000, Thomas Binoth and Gudrun Heinrich devised the sector decomposition algorithm that allows disentangling such overlapping divergences [190]. This makes it possible to write any Feynman integral before integration in the form of Eq. (3.6), where the \(a_i\) are then finite integrals which can be evaluated numerically. In complicated cases, this algorithm produces a large number of intermediate terms, and thus a large number of integrals to be evaluated, which again makes computer algebra indispensable. Implementations of this algorithm can be found in Refs. [191, 192], for example.
3.7 Approximation methods
In general, the more external parameters are involved in a certain calculation, the more complicated it becomes. For example, the result for a Feynman integral that depends only on a single parameter, say an external momentum \(q^2\), will be of the form \((q^2)^{aD-b}\,f(a,b,D)\), where a is the number of loops, b the sum of all propagator powers, and f(a, b, D) a function which is independent of q (for an illustration of this formula, see Eq. (3.12)). On the other hand, if an integral depends on more than one mass scale, say \(m^2\) and \(q^2\), their ratio can enter as argument for any complicated function, from \(\sqrt{1-m^2/q^2}\) to polylogarithms \(\textrm{Li}_n(m^2/q^2)\) and generalizations thereof. The integral may not even be expressible in terms of elementary functions in this case.Footnote 51
However, since Feynman diagrams represent approximations within QFT anyway, and since experimental measurements are always associated with an uncertainty, it may be sufficient to evaluate the integrals only approximately in certain limits of the external parameters. Obviously, it will simplify the result considerably if, say, only the first two terms in its Taylor expansion in \(m^2/q^2\) are required, rather than the full dependence in terms of polylogarithms, etc. But the actual question is, of course, whether one can obtain such an approximation in a relatively simple way directly from the integral, rather than by expanding the polylogarithms.
The answer to this question is positive, and there are algorithmic ways to obtain this approximate result. The most general one goes by the name of strategy of regions [194]. Consider again the integral of Eq. (3.2). Assume that we are only interested in the limit where m is much smaller than all components of q. As a first attempt, one could try to expand both factors in the denominator for small m:
One can now solve all occurring integrals (in D dimensions rather than four) by applying Eq. (3.12). However, this does not give the correct result. The reason is that the integral extends to values of k where \(m^2\) is not smaller than \(k^2\) or \((q-k)^2\), so that the expansion of the integrand becomes invalid. However, this can be cured by simply adding the expansions which are valid in these regions:
where, for example,
It can be shown that the doubly counted regions cancel among each other, so that one can indeed simply add all contributions. The first implementation of such an expansion algorithm was achieved in the late 1990s [195].
Note that, while the expansion reduces the number of mass parameters in the individual integrals, it raises the powers of the propagator. This method therefore develops its strength also due to the IbP algorithm which allows one to reduce integrals with higher powers of the propagators to master integrals (see Sect. 3.6.1).
3.8 IR subtraction
It is now time to discuss the problem already alluded to several times which goes by the name of infra-red (IR) divergences. So far, we were only concerned with UV divergences in loop integrals which arise from regions where the integration momentum becomes large. However, consider the integral
arising in the calculation of the Feynman diagram shown in Fig. 7c, for example. Here, m is the electron mass, and \(q_1\), \(q_2\) are the momenta of the outgoing electron and positron, respectively. For small k, using the on-shell condition \(q_1^2=q_2^2=m^2\), we can approximate
and similarly for the second electron propagator. Therefore, the integral in Eq. (3.20) behaves as
in the limit \(k\rightarrow 0\), and therefore develops an infra-red divergence at \(D=4\) when the integration momentum (which equals the momentum of the virtual photon) becomes soft. Even worse: if the electron mass were zero, one could write
where, without loss of generality, we assumed the electron momentum to be along the z axis. Given that
we see that Eq. (3.22) has additional divergences at \(k\rightarrow (k_0,0,0,\pm k_0)\). Note that this corresponds to the case where the virtual photon is on the mass shell (\(k^2=0\)) and collinear to either the electron or the positron.
The attentive reader may notice that these are exactly the kinematical regions mentioned at the end of Sect. 3.3 where the phase space integral for the process \(e^+e^-\rightarrow e^+e^-\gamma \) becomes divergent. And indeed, it turns out that in the expression
these infra-red singularities arising from real and virtual photons attached to the final state particles cancel. Note that the cancellation happens among terms of the same perturbative order. In our case this is \(\alpha ^3\), which corresponds to the leading-order contribution for the second term (the real emission), and the next-to-leading order contribution for the first term (the virtual correction).
It turns out that, like UV divergences, also these IR divergences can be regularized by going to \(D\ne 4\) space–time dimensions in both the loop and the phase-space integral. They again manifest themselves as poles in \(1/\epsilon \), this time even up to \(1/\epsilon ^2\) at one-loop level.
While this cancellation of divergences between phase-space and loop integrals can be proven to all orders in perturbation theory, its technical implementation is highly non-trivial. The main reason is that phase-space integrals typically need to be evaluated fully numerically, simply because the corresponding integration boundaries are dictated by the experimental setup, for example the energy and angular resolution or the fiducial volume of the detector. A theoretical algorithm thus needs to extract these soft and collinear divergences from phase-space integrals before integration. At NLO, general algorithms for this task were established in the 1990s [196,197,198].
At higher orders, the problem becomes considerably more complicated. For once, one now has to combine double-virtual two-loop corrections with mixed real-virtual and double-real emission contributions (see Fig. 11, for example). On the other hand, more combinations of particles can become collinear to one another, or both soft and collinear. Also, more than two particles can become simultaneously collinear. The need for high-precision calculations at the LHC produced a number of algorithms that work at next-to-next-to-leading order (NNLO) though [199,200,201]. Beyond that, only special cases can be treated up to now.
For completeness, let us remark that this cancellation of infra-red divergences between virtual corrections and real emission is complete only for photons attached to the final state particles. Note, however, that there are analogous corrections where the photon is attached to the initial state particles (see Fig. 12). In this case, after the combination of the real and virtual contributions, there are still collinear divergences left. Even though they require additional concepts like parton-distribution function in quantum chromodynamics (QCD)—the theory that describes strong interaction—they do not pose any genuinely new technical problems that would matter for the discussion in the current paper. We therefore disregard them here.
3.9 Ambiguities of perturbation theory
The cancellation of divergences through renormalization leaves a remnant ambiguity in the observables that we have kept quiet about so far, but which plays an important role in theoretical predictions. The origin can be understood by going back to the discussion of Sect. 3.4. We argued that both the Feynman integrals as well as the bare parameters depend on the regularization parameter \(\Lambda \), but the associated divergences at \(\Lambda \rightarrow \infty \) cancel in physical observables \({\mathcal {O}}\). However, consider the bare electro-magnetic coupling \(e_\text {B}(\Lambda )\), for example. It is a dimensionless quantity, so there must be another mass scale \(\mu _R\) which cancels the mass dimension of \(\Lambda \). This renormalization scale \(\mu _R\) is completely arbitrary a priori; in fact, it can be shown that physical observables are formally independent of \(\mu _R\), i.e.,
But as indicated in Eq. (3.26), this independence is broken by the uncalculated higher orders in perturbation theory. Working at fixed order, there is a residual numerical dependence on the arbitrary, and thus unphysical parameter \(\mu _R\) in the theory prediction of \({\mathcal {O}}\).
On the one hand, this ambiguity actually provides a means to estimate the impact of the higher orders. For this, one chooses \(\mu _R\) of the order of the “typical” mass scale of the observable \({\mathcal {O}}\), which could be the center-of-mass energy of the underlying scattering reaction, for example. Variations of \(\mu _R\) around this value will affect the numerical prediction of \({\mathcal {O}}\), which, according to Eq. (3.26), is related to the neglected higher orders. On the other hand, an observable may depend on many scales, which makes it difficult to choose a typical scale and may spoil the reliability of the perturbative result (for a discussion, see Ref. [202]). An analogous problem exists for the infra-red divergences which are related to initial state radiation. In this case, the unphysical scale is referred to as the factorization scale \(\mu _F\).
3.10 Final thoughts
As we have shown, today the calculation of the first two terms in the perturbative expansion can indeed be considered as fully automated. It is sufficient to specify the process to be considered, for example a specific collision reaction at a particle collider, as well as the associated input parameters (scattering energy, particle masses, etc.), and the computer will produce all the relevant results which can be directly compared to experimental measurements. The efforts gradually and successfully continue in this direction toward higher orders. This is made possible by a sort of “algebraization of integration,” where certain classes of integrals are reduced to a known set of basis integrals, as described in Sect. 3.5.
The automation procedure implies that no human actually needs to see, let alone draw, the relevant Feynman diagrams any more. But even though this means that their often-praised illustrative character has become irrelevant for the user, their actual structure is still crucial for the underlying computer algorithms. It is only the computer who “draws” (rather: generates) the diagrams, but it immediately processes them further into mathematical expressions made of numbers, matrices, and integrals. In this sense, one may wonder whether Feynman diagrams are really necessary at all, or whether there are representations of the scattering amplitudes that would be better suited for a fully automated treatment. This question becomes more and more relevant with the ever increasing efforts that are spent on calculating Feynman diagrams to higher-and-higher orders in perturbation theory. And indeed there have been promising ideas in this direction. A particularly successful one is related to an early observation of Stephen Parke and Tomasz Taylor of 1986, who discovered a remarkably simple formula for a particular setFootnote 52 of QCD amplitudes with an arbitrary number of external particles [203]. In 2004, Edward Witten found a new mathematical interpretation of this relation, which initiated a huge wave of activity, resulting in efficient algorithms to evaluate scattering amplitudes [204]. In turn, this research led to new insights and techniques also for traditional Feynman diagrammatic calculations, in particular generalized unitarity methods, which can be seen as generalizations of the well-known optical theorem [205]. Further steps in studying these structures beyond Feynman diagrams have led to the so-called amplituhedron, whose potential for applications to scattering reactions at particle colliders is still unclear though [206].
The issue of automated calculations of Feynman diagrams is thus not so much a fear of dehumanization, as expressed by some of the early witnesses to the introduction of computers in physics (see Sect. 2.4.1). After all, the current level of automation was achieved only through huge intellectual investments, and it is undeniable that Feynman diagrams have been and still are extremely successful in helping us understand nature. However, although it is certainly possible that there just is no more efficient way, it is unclear what could have been achieved by spending similar efforts on alternative approaches to calculations in QFT.Footnote 53 To put it more strikingly: what would Feynman say if he could see how much effort has been spent in taking his diagrams to the current level?
4 Conclusion
For over seven decades, Feynman diagrams have proven to be an invaluable tool for obtaining theoretical predictions from quantum field theories. Although their application is limited to perturbation theory at small coupling strengths—in the strong coupling regime non-perturbative methods like lattice gauge theory have to be applied—no other theoretical approach has resulted in such a vast amount and such a high precision of phenomenological results in particle physics. As illustrated by our developments, progress in this field had then required for every higher order in perturbation theory tremendous technological efforts and has generated ingenious mathematical ideas, methods, and tools. Modern calculations can now involve hundreds of thousands of Feynman diagrams, and it is clear in this situation that their initially much-praised visual benefit is minimal. Yet, in no way does this erode their importance to ongoing particle physics research.
This persistence of the importance of Feynman diagrams can be attributed to two key related factors: the highly algorithmic structure by which physicists have managed to tackle them and the successful development since the 1960s of algebraic programs aimed at processing the calculations. Today, leading-order and next-to-leading order calculations, involving tree-level and one-loop diagrams, can be considered fully automated. This includes not only the actual calculation of the amplitudes, but also renormalization, IR subtraction, phase space integrations, resummation of soft-collinear emissions (parton showers), and hadronization effects (the latter two have not been discussed in this paper; see Ref. [207], for example). Various tools exist for achieving these goals, with MadGraph5_aMC@NLO—which has been described briefly in Sect. 3.3—being the most prominent example currently. For other examples, see Refs. [163, 208, 209].
The results obtained thus far align with many hopes and expectations expressed in the early 1970s by pioneers of algebraic programs to compute Feynman diagrams. But unlike Hearn sometimes outlined, such progress was not achieved through a direct approach to heuristic questions with the help of artificial intelligence. While this field is now undergoing a major renewal that could potentially play a role in future developments, it is clear from our discussions that improvements in the computation of Feynman diagrams came from theoretical efforts in solving mathematical problems, simplifying procedures, and developing new algorithms. Most of the initial challenges faced by the field pioneers, particularly those related to computer implementation of renormalization and integration (as discussed in Sect. 2.3), have been successfully addressed by adopting problem-oriented approaches. Additionally, the initial tinkering and combination of relatively incompatible tools have been overcome by technological advances that enable the implementation of efficient and straightforward automated procedures. Nevertheless, despite the various accomplishments presented, we have also observed that the optimistic tone and high expectations generated at the start of the nascent field of computer algebra are partly at odds with various limitations still encountered today in the case of Feynman diagrams. The prospect of the “fully automated theoretical high-energy physicist” continues to face severe constraints starting at the two-loop level. While certain non-trivial steps in the calculation are already algorithmically accessible, the problems are still too diverse from process to process in order to allow for a fully automatic approach. At the three-loop level, many problems may have been solved, but a general solution will probably require many further technological breakthroughs.
Initial expectations were mostly built in the frame of the most elementary QED processes. However, as revealed by the developments in Sect. 3, the increase in the number of external parameters resulting from the complexity of processes within the Standard Model has become a crucial factor in explaining our current limitations in manipulating mathematical expressions related to Feynman diagrams. Moreover, higher orders in perturbation theory were found to lead to different, more conceptual issues. For example, any fixed-order result depends on unphysical parameters, whose numerical impact is formally of higher orders, in particular the renormalization and factorization scale introduced in Sect. 3.9. In order to make a numerical prediction, a particular choice for these quantities has to be made, and as of today, no convincing general solution for this problem has been devised. This can lead to ambiguities which are beyond the expected precision of a theoretical prediction.
From a more general point of view, it is expected that the perturbative expansion described by Feynman diagrams does not converge, but is at best asymptotic [210]. This means that one may expect that the approximation gets worse beyond a certain perturbative order, which may, however, be higher than any order that could ever be calculated in practice. Such considerations may indicate that the perturbative approach in general and Feynman diagrams in particular may reach their limits sooner or later. An alternative approach to QFT, however, may not be able to make predictions for the observables studied currently at particle collider. Since scattering experiments and thus the whole concept of particle colliders are so closely tied to Feynman diagrams, a conceptual shift in theory will most likely also imply new kinds of experiments or observables (see, e.g., the discussion in Ref. [211]). As we cannot look into the future, we want to refrain from further speculations at this point though.
In any case, looking back, the continuing success of Feynman diagrams and the enormous theoretical efforts spent on their evaluation are stunning. Recent discoveries and the progressive resolution of various higher-order challenges even suggest that this trend may actually persist for the foreseeable future. Nonetheless, to take the discussion begun in the concluding remarks of Sect. 3.10 a little further, considering the above-mentioned limitations, one may in fact question directly why no significant alternative approaches to phenomenological calculations in quantum field theories have so far been developed (aside from lattice gauge theory, and not counting re-organizations of the perturbative series, i.e., resummation methods and the like). Then, as our developments illustrate, it could well be that it was precisely the pivotal role played by the development of algebraic programs in the success of Feynman diagrammatic method and the perspective of complete automation that were standing in the way of making progress along different paths.
Notes
While it is widely accepted that Feynman diagrams do not provide a detailed realistic picture of particle processes, but only a simplified representation, long-standing debates concerning their physical reading must be acknowledged. They began right from the graphs’ inception in the late 1940s, around what David Kaiser has called the Feynman–Dyson split: “[the] tension between Feynman’s and Dyson’s positions, with their varying emphases on ‘intuition’ versus derivation, physical pictures versus topological indicators” [3, p. 263]. An interesting discussion of related interpretation issues can be found in Refs. [4,5,6,7,8]. As far as the present paper is concerned, by dealing with the algorithmic dimension of Feynman diagrams and computational methods, we distance ourselves from these debates. Thus, our use of the idea of “representation” remains in a rather instrumental vein.
It should be noted that this literature also contributes to a better understanding of the debates mentioned in Footnote 2.
The exact extent to which Feynman diagram calculations have had a direct impact on the design of modern computer algebra systems nevertheless requires further development beyond the scope of this article. It is worth noting, however, that Stephen Wolfram, the creator of MATHEMATICA recently elaborated on his own experience with SCHOONSCHIP—one of the programs initially dedicated to Feynman diagrams that will be featured in this paper—and acknowledged that it had had some influence during his career [20].
A detailed account of QED developments can be found in Ref. [1].
For consistency, we use the “order \(e^n\)” convention here. More details are given in Sect. 3.2 as well as other examples. Historically, corrections of order \(e^4\) and \(e^6\) were usually referred to as “fourth” and “sixth” order contributions, and by extension it was common to speak of “fourth and sixth order magnetic moment of leptons” or of “fourth-order Lamb shift.” We note in passing that the diagrams which determine \(g-2\) also contain information about the Lamb shift.
Note that his name is also often spelled “Peterman” in the primary and secondary literature.
On the history of the \(g_\mu -2\) experiments, see Ref. [55].
On the history of modern computing, see Ref. [60].
Some more technical details of the individual steps in (i–v) are discussed in Sect. 3. It will also become clear that the workflow and the focus points of a perturbative calculation are somewhat different today.
ALGOL 58, originally named IAL, resulted from the common efforts of the Association for Computing Machinery (ACM) and the German Gessellschaft für Angewandte Matematik und Mechanik (Society of Applied Mathematics and Mechanics) which held a joint meeting at ETH Zurich from May 27 to June 2, 1958, with the goal of elaborating a universal programming language [83].
In computing, a word is the natural unit of data that can be manipulated by a specific processor. The IBM 7090 used a word length of 36 bits.
For a more complete account of similar calculations performed with algebraic programs around 1970, see Ref. [73].
One of the first occurrences of cross-checked results using different algebraic programs is actually a bit out of this context and dates from 1967. Brodsky and Jeremiah D. Sullivan used REDUCE to confirm the results they had obtained with FTRACE for the low order W-boson contribution to the anomalous magnetic moment of the muon [94]. FTRACE was another, less influential, algebraic program written by Stanley M. Swanson in assembly language on an IBM 7090 at Stanford [95].
Most of the contributions presented here, as well as those concerning the anomalous magnetic moment of leptons, have been reviewed in Ref. [96].
Unlike Appelquist and Brodsky who performed the integration procedures numerically, Fox adopted Soto Jr.’s analytical approach on this point. His interest in this type of reasoning would later materialize in contributions to implementing integration methods in REDUCE. See the discussion in Sect. 2.3.4.
The following list highlights the main early contributions and do not pretend to be completely exhaustive.
Note that de Rújula, Lautrup and Petermann had previously calculated by hand the contributions of three of these diagrams and verified it with SCHOONSCHIP [109].
Although a first operational version was available in 1977, Remiddi pointed out that CERN decided not further support the dissemination of Veltman’s program and terminated Strubbe’s appointment. The question of SCHOONSCHIP’s portability then became, in the 1980s, one of the reasons for Jos Vermaseren’s development of FORM, one of the most widely used symbolic manipulation systems in high-energy physics to date [74, p. 519] [119]; see also Sect. 3.6.1.
In modern perturbative calculations, this has been superseded by integral reductions, see Sect. 3.5.
According to further developments in the quoted article, Hearn was certainly basing this comment on his experience with a PDP-10 using a 36-bit word length.
Infra-red divergences, which are particularly complex to implement (see Sect. 3.8), were not considered.
It still constitutes a major challenge today, the main technical details of which are presented in Sect. 3.
In the early 1970s it was also available for PDP-10, IBM 360, and CDC 6600 computers [134, p. 549].
“[\(\ldots \)] la structure analytique des solutions est encore trop mal connue pour espérer avoir une solution générale.” Our translation.
Emphasis is ours.
Calmet made explicit reference here to the Second Symposium on Symbolic and Algebraic Manipulation, held in Los Angeles in 1971 [147].
See Sect. 3.1.
In particular, Campbell’s set of programs was the first which was able to recognize combinations of denominators and replace them by results of four-dimensional integrals that arise from Feynman diagrams with loops.
More technical details on this point in Sect. 3.2.
It seems that the temporary nature of this situation can be explained by a certain lack of resources. As Werner M. Seiler recalled, although Calmet had initially been approached to extend the program he had developed during his doctoral thesis into a “French answer to REDUCE” he nevertheless felt that “he would not find the right conditions for this in France and decided to go to the USA instead to collaborate among others with Tony Hearn in Utah” [150, p. 14].
“[L]’utilisateur qui veut résoudre un problème spécifique ne doit pas rester passif et attendre qu’un langage lui apporte toutes les techniques dont il a besoin. Il doit s’efforcer de créer lui-même ces techniques lorsqu’elles n’existent pas encore.” Our translation.
An interesting discussion of this point at the turn of the 1970s and 1980s can be found in [155], which contrasts the “brute force” calculations of SCHOONSCHIP and the “intelligent” calculations of MACSYMA.
We do not consider gravity here, because a consistent quantum field theoretic description of this interaction is currently still missing.
An outline of the origin of this structure is given in Appendix A.
“Elastic” means that the particle content in the initial and final state is the same, but their momenta are different.
The reader is warned not to confuse the symbol for the electron \(e^-\) or the positron \(e^+\) with the unit of electric charge, e.
I.e., they cannot be transformed into one another without cutting and reconnecting lines.
This is a very naive way of counting, of course, because many terms will be identical and can thus be combined. But for illustration purposes, this example should be sufficient.
For a (somewhat outdated) overview of tools for the automated calculation of Feynman diagrams, see Ref. [162].
In a Wilsonian picture, they regain a physical meaning as effective parameters of a more fundamental theory which is valid at energies \(E>\Lambda \) [165].
It is understood that \(k^{2n} \equiv (k^2)^n\).
See Footnote 21.
In fact, a whole class of new analytic functions was inspired by their usefulness in calculating multi-loop Feynman integrals [193].
Those with maximal helicity violation.
We really refer to alternative approaches rather than complementary ones, such as lattice gauge theory.
A “fundamental” particle is one that is not composite, i.e., not a bound state of other particles. There are many composite scalar particles, for example the pions, which are bound states of two quarks.
As usual, we adopt the summation convention according to which a sum over indices which appear twice in a monomial is to be carried out. In this case, a sum is implied over \(\mu \in \{0,1,2,3\}\). Furthermore, unless stated otherwise, we use natural units where \(\hbar =c=1\), and the metric tensor \(g_{\mu \nu }=\textrm{diag}(1,-1,-1,-1)\).
Unless stated otherwise, we restrict ourselves to flat space–time with \(g^{\mu \nu }=\textrm{diag}(1,-1,-1,-1)\) in this article.
For massless vector bosons, it is sufficient that this holds only in Lorentz gauge where \(\partial _\mu A^\mu =0\).
For massless particles, it is \(m=0\), of course. For the vector particles, the derivation requires “gauge fixing,” meaning that the Feynman propagator depends on an arbitrary parameter which drops out when calculating a physical quantity. Furthermore, for non-Abelian gauge theories like quantum chromodynamics, gauge fixing requires the introduction of Faddeev–Popov ghosts which are auxiliary, unphysical “particles.”
Annihilation into a single photon is kinematically forbidden.
For \(b\in \{0,-1,-2,\ldots \}\), also the denominator is divergent, and the integral would require further investigation. In fact, it can be shown that for any \(b<0\), one can consistently set \(A^{(b)}(m)=0\).
References
S. S. Schweber, QED and the men who made it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton: Princeton University Press, 1994.
R. P. Feynman, Space-time approach to quantum electrodynamics, Physical Review 76 (1949) 769–789. https://doi.org/10.1103/PhysRev.76.769
D. Kaiser, Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics. Chicago: University of Chicago Press, (2005).
L. Meynell, Why Feynman Diagrams Represent, International Studies in the Philosophy of Science 22 no. 1, (2008) 39–59. https://doi.org/10.1080/02698590802280902
A. Wüthrich, Interpreting Feynman diagrams as visual models, Spontaneous Generations: A Journal for the History and Philosophy of Science 6 no. 1, (2012) 172–181.
L. Meynell, Picturing Feynman Diagrams and the Epistemology of Understanding, Perspectives on Science 26 no. 4, (2018) 459–481. https://doi.org/10.1162/posc_a_00283
M. Stöltzner, Feynman Diagrams: Modeling between Physics and Mathematics, Perspectives on Science 26 no. 4, (2018) 482–500.https://doi.org/10.1162/posc_a_00284
R. Harlander, Feynman diagrams: From complexity to simplicity and back, Synthese 199 no. 5-6, (2021) 15087–15111. https://doi.org/10.1007/s11229-021-03387-y
F. J. Dyson, The Radiation Theories of Tomonaga, Schwinger, and Feynman, Physical Review 75 (1949) 486–502. https://doi.org/10.1103/PhysRev.75.486
F. J. Dyson, The S Matrix in Quantum Electrodynamics, Physical Review 75 (1949) 1736–1755. https://doi.org/10.1103/PhysRev.75.1736
R. V. Harlander, S. Y. Klein, and M. Lipp, FeynGame, Computer Physics Communications 256 (2020) 107465. https://doi.org/10.1016/j.cpc.2020.107465
A. Wüthrich, The genesis of Feynman diagrams. Dordrecht: Springer, (2010).
A. S. Blum, The state is not abolished, it withers away: How quantum field theory became a theory of scattering, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 60 (2017) 46–80. https://doi.org/10.1016/j.shpsb.2017.01.004
A. Wüthrich, The exigencies of war and the stink of a theoretical problem: Understanding the genesis of Feynman’s quantum electrodynamics as mechanistic modelling at different levels, Perspectives on Science 26 no. 4, (2018) 501–520. https://doi.org/10.1162/posc_a_00285
O. Darrigol, The magic of Feynman’s QED: from field-less electrodynamics to the Feynman diagrams, The European Physical Journal H 44 no. 4-5, (2019) 349–369. https://doi.org/10.1140/epjh/e2019-100025-2
M. Forgione, Feynman’s space-time view in quantum electrodynamics, Studies in History and Philosophy of Science 93 (2022) 136–148. https://doi.org/10.1016/j.shpsa.2022.03.006
S. Wolfram, The Mathematica Book. Champaign: Wolfram Research Inc., 2000.
D. Joyner, OSCAS: Maxima, ACM Communications in Computer Algebra 40 no. 3-4, (2006) 108–111. https://doi.org/10.1145/1279721.1279726
M. B. Monagan, K. O. Geddes, K. M. Heal, G. Labahn, S. M. Vorkoetter, J. McCarron, and P. DeMarco, Maple 10 Programming Guide. Waterloo: Maplesoft, 2005.
S. Wolfram, Tini Veltman (1931-2021): From Assembly Language to a Nobel Prize, 2021. https://writings.stephenwolfram.com/2021/01/tini-veltman-1931-2021-from-assembly-language-to-a-nobel-prize/.
G. Heinrich, Collider Physics at the Precision Frontier, Physics Reports 922 (2021) 1–69. https://doi.org/10.1016/j.physrep.2021.03.006
V. A. Smirnov, Feynman integral calculus. Berlin, Heidelberg: Springer, 2006.
S. Weinzierl, Feynman Integrals: A Comprehensive Treatment for Students and Researchers. Cham: Springer, 2022. https://doi.org/10.1007/978-3-030-99558-4
T. Aoyama, T. Kinoshita, and M. Nio, Theory of the Anomalous Magnetic Moment of the Electron, Atoms 7 no. 1, (2019) 28. https://doi.org/10.3390/atoms7010028
S. J. Brodsky and S. D. Drell, The Present Status of Quantum Electrodynamics, Annual Review of Nuclear Science 20 no. 1, (1970) 147–194. https://doi.org/10.1146/annurev.ns.20.120170.001051
S. J. Brodsky, Radiative problems and quantum electrodynamics, in Proceedings of the 1971 International Symposium on Electron and Photon Interactions at High Energies: Cornell University, Ithaca, N.Y., August 23-27, 1971, N. B. Mistry, ed., pp. 13–35. Ithaca: Laboratory of Nuclear Studies, Cornell University, 1972.
B. E. Lautrup, A. Peterman, and E. de Rafael, Recent developments in the comparison between theory and experiments in quantum electrodynamics, Physics Reports 3 no. 4, (1972) 193–259. https://doi.org/10.1016/0370-1573(72)90011-7
W. E. Lamb and R. C. Retherford, Fine Structure of the Hydrogen Atom by a Microwave Method, Physical Review 72 (1947) 241–243. https://doi.org/10.1103/PhysRev.72.241
H. A. Bethe, The Electromagnetic Shift of Energy Levels, Physical Review 72 (1947) 339–341. https://doi.org/10.1103/PhysRev.72.339
J. Schwinger, On Quantum-Electrodynamics and the Magnetic Moment of the Electron, Physical Review 73 (1948) 416–417. https://doi.org/10.1103/PhysRev.73.416
P. Kusch and H. M. Foley, Precision Measurement of the Ratio of the Atomic ‘g Values’ in the \(^{2}P_{\frac{3}{2}}\) and \(^{2}P_{\frac{1}{2}}\) States of Gallium, Physical Review 72 (1947) 1256–1257. https://doi.org/10.1103/PhysRev.72.1256.2
H. M. Foley and P. Kusch, On the Intrinsic Moment of the Electron, Physical Review 73 (1948) 412–412. https://doi.org/10.1103/PhysRev.73.412
R. Karplus and N. M. Kroll, Fourth-Order Corrections in Quantum Electrodynamics and the Magnetic Moment of the Electron, Physical Review 77 (1950) 536–549. https://doi.org/10.1103/PhysRev.77.536
A. Petermann, Fourth order magnetic moment of the electron, Helvetica Physica Acta 30 (1957) 407–408. https://doi.org/10.5169/seals-112823
C. M. Sommerfield, The magnetic moment of the electron, Annals of Physics 5 no. 1, (1958) 26–57. https://doi.org/10.1016/0003-4916(58)90003-4
D. T. Wilkinson and H. R. Crane, Precision Measurement of the g Factor of the Free Electron, Physical Review 130 (1963) 852–863. https://doi.org/10.1103/PhysRev.130.852
M. Baranger, H. A. Bethe, and R. P. Feynman, Relativistic Correction to the Lamb Shift, Physical Review 92 (1953) 482–501. https://doi.org/10.1103/PhysRev.92.482
H. M. Fried and D. R. Yennie, Higher Order Terms in the Lamb Shift Calculation, Physical Review Letters 4 (1960) 583–584. https://doi.org/10.1103/PhysRevLett.4.583
A. J. Layzer, New Theoretical Value for the Lamb Shift, Physical Review Letters 4 (1960) 580–582. https://doi.org/10.1103/PhysRevLett.4.580
G. W. Erickson and D. R. Yennie, Radiative level shifts, I. Formulation and lowest order lamb shift, Annals of Physics 35 no. 2, (1965) 271–313. https://doi.org/10.1016/0003-4916(65)90081-3
G. W. Erickson and D. R. Yennie, Radiative level shifts II: Higher order contributions to the lamb shift, Annals of Physics 35 no. 3, (1965) 447–510. https://doi.org/10.1016/0003-4916(65)90250-2
S. J. Brodsky and G. W. Erickson, Radiative Level Shifts. III. Hyperfine Structure in Hydrogenic Atoms, Physical Review 148 (1966) 26–46.https://doi.org/10.1103/PhysRev.148.26
M. F. Soto Jr., New Theoretical Values for the Lamb Shift, Physical Review Letters 17 (1966) 1153–1155. https://doi.org/10.1103/PhysRevLett.17.1153
E. Remiddi, Radiative correction in quantum electrodynamics, Computer Physics Communications 4 no. 2, (1972) 193–198.https://doi.org/10.1016/0010-4655(72)90007-0
W. H. Parker, D. N. Langenberg, A. Denenstein, and B. N. Taylor, Determination of \(\frac{e}{h}\), Using Macroscopic Quantum Phase Coherence in Superconductors. I. Experiment, Physical Review 177 (1969) 639–664.https://doi.org/10.1103/PhysRev.177.639
B. D. Josephson, Possible new effects in superconductive tunnelling, Physics Letters 1 no. 7, (1962) 251–253.https://doi.org/10.1016/0031-9163(62)91369-0
B. N. Taylor, W. H. Parker, and D. N. Langenberg, Determination of \(\frac{e}{h}\),Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants, Reviews of Modern Physics 41 (1969) 375–496.https://doi.org/10.1103/RevModPhys.41.375
T. Appelquist and S. J. Brodsky, Order \({\alpha }^{2}\) Electrodynamic Corrections to the Lamb Shift, Physical Review Letters 24 (1970) 562–565.https://doi.org/10.1103/PhysRevLett.24.562
T. Appelquist and S. J. Brodsky, Fourth-Order Electrodynamic Corrections to the Lamb Shift, Physical Review A 2 (1970) 2293–2303.https://doi.org/10.1103/PhysRevA.2.2293
A. Rich, Corrections to the Experimental Value for the Electron \(g\)-Factor Anomaly, Physical Review Letters 20 (1968) 967–971. https://doi.org/10.1103/PhysRevLett.20.967
J. C. Wesley and A. Rich, Preliminary Results of a New Electron \(g-2\) Measurement, Physical Review Letters 24 (1970) 1320–1325. https://doi.org/10.1103/PhysRevLett.24.1320
J. C. Wesley and A. Rich, High-Field Electron \(g-2\) Measurement, Physical Review A 4 (1971) 1341–1363. https://doi.org/10.1103/PhysRevA.4.1341
R. L. Garwin, L. M. Lederman, and M. Weinrich, Observations of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays: the Magnetic Moment of the Free Muon, Physical Review 105 (1957) 1415–1417.https://doi.org/10.1103/PhysRev.105.1415
R. L. Garwin, D. P. Hutchinson, S. Penman, and G. Shapiro, Accurate Determination of the \(\mu ^{+}\) Magnetic Moment, Physical Review 118 (1960) 271–283. https://doi.org/10.1103/PhysRev.118.271
B. L. Roberts, The history of the muon \(g-2\) experiments, SciPost Physics Proceedings 1 (2019) 032.https://doi.org/10.21468/SciPostPhysProc.1.032
V. B. Berestetskii, O. N. Krokhin, and A. K. Khlebnikov, Concerning the radiative correction to the \(\mu \)-meson magnetic moment, Soviet Physics, JETP 3 no. 5, (1956) 761–762.
G. Charpak, F. J. M. Farley, R. L. Garwin, T. Muller, J. C. Sens, V. L. Telegdi, and A. Zichichi, Measurement of the Anomalous Magnetic Moment of the Muon, Physical Review Letters 6 (1961) 128–132.https://doi.org/10.1103/PhysRevLett.6.128
J. Bailey, W. Bartl, G. Von Bochmann, R. Brown, F. Farley, H. Jöstlein, E. Picasso, and R. Williams, Precision measurement of the anomalous magnetic moment of the muon, Physics Letters B 28 no. 4, (1968) 287–290.https://doi.org/10.1016/0370-2693(68)90261-X
A. C. Hearn, Applications of Symbol Manipulation in Theoretical Physics, in Proceedings of the Second ACM Symposium on Symbolic and Algebraic Manipulation, SYMSAC ’71, p. 17-21. New York: Association for Computing Machinery, 1971. https://doi.org/10.1145/800204.806262
P. E. Ceruzzi, A History of Modern Computing. Cambridge: The MIT Press, 2nd ed., 2012.
A. C. Hearn, Computation of Algebraic Properties of Elementary Particle Reactions Using a Digital Computer, Communications of the ACM 9 no. 8, (1966) 573-577. https://doi.org/10.1145/365758.365766
R. P. Feynman, Quantum Theory of Gravitation, Acta Physica Polonica 24 (1963) 841–866.
M. Veltman, Algebraic techniques, Computer Physics Communications 3 no. suppl. 1, (1972) 75–78. https://doi.org/10.1016/0010-4655(72)90115-4
E. C. G. Sudarshan and R. E. Marshak, The Nature of the Four-Fermion Interaction, in Proceedings of the Conference on Mesons and Newly Discovered Particles, Padua, Venice, Italy, 22-27 September 1957, pp. V–14. 1957.
E. C. G. Sudarshan and R. E. Marshak, Chirality Invariance and the Universal Fermi Interaction, Physical Review 109 (1958) 1860–1862. https://doi.org/10.1103/PhysRev.109.1860.2
R. P. Feynman and M. Gell-Mann, Theory of the Fermi Interaction, Physical Review 109 (1958) 193–198. https://doi.org/10.1103/PhysRev.109.193
C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, and R. P. Hudson, Experimental Test of Parity Conservation in Beta Decay, Physical Review 105 (1957) 1413–1415. https://doi.org/10.1103/PhysRev.105.1413
T. D. Lee and C. N. Yang, Question of Parity Conservation in Weak Interactions, Physical Review 104 (1956) 254–258. https://doi.org/10.1103/PhysRev.104.254
T. D. Lee and C. N. Yang, Theory of Charged Vector Mesons Interacting with the Electromagnetic Field, Physical Review 128 (1962) 885–898. https://doi.org/10.1103/PhysRev.128.885
T. D. Lee, Application of \(\xi \)-Limiting Process to Intermediate Bosons, Physical Review 128 (1962) 899–910. https://doi.org/10.1103/PhysRev.128.899
M. J. G. Veltman, Nobel Lecture: From weak interactions to gravitation, Reviews of Modern Physics 72 (2000) 341–349. https://doi.org/10.1103/RevModPhys.72.341
M. Veltman and D. N. Williams, Schoonschip ’91, arXiv:hep-ph/9306228 [hep-ph].
D. Barton and J. P. Fitch, Applications of algebraic manipulation programs in physics, Reports on Progress in Physics 35 no. 1, (1972) 235. https://doi.org/10.1088/0034-4885/35/1/305
E. Remiddi, SCHOONSCHIP, the Largest Time Equation and the Continuous Dimensional Regularisation, Acta Physica Polonica B 52 (2021) 513–532. https://doi.org/10.5506/APhysPolB.52.513
M. J. G. Veltman, SCHOONSCHIP, A CDC 6600 program for symbolic evaluation of algebraic expressions. CERN Technical Report, 1967.
H. Strubbe, Converting Schoonschip to IBM. CERN Report DD-77-1, 1977.
A. C. Hearn, REDUCE: The First Forty Years, in Algorithmic Algebra and Logic, in Proceedings of A3L 2005, April 3-6, Passau, Germany. Conference in Honor of the 60th Birthday of Volker Weispfenning, A. Dolzmann, A. Seidl, and T. Sturm, eds., pp. 19–24. 2005.
J. McCarthy, Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I, Communications of the ACM 3 no. 4, (1960) 184–195. https://doi.org/10.1145/367177.367199
J. McCarthy et al., LISP 1.5 Programmer’s Manual. Cambridge: The M.I.T Press, 1962.
A. C. Hearn, REDUCE: A user-oriented interactive system for algebraic simplification, in Interactive Systems for Experimental Applied Mathematics., M. Klerer and J. Reinfelds, eds., pp. 79–90. New York: Academic Press, 1968.
J. Backus, The History of Fortran I, II, and III, in History of Programming Languages, R. L. Wexelblat, ed., pp. 25–74. New York: Association for Computing Machinery, 1978.
A. C. Hearn, REDUCE 2: A System and Language for Algebraic Manipulation, in Proceedings of the Second ACM Symposium on Symbolic and Algebraic Manipulation, SYMSAC ’71, p. 128-133. New York: Association for Computing Machinery, 1971. https://doi.org/10.1145/800204.806277
A. J. Perlis and K. Samelson, Preliminary Report: International Algebraic Language, Communications of the ACM 1 no. 12, (1958) 8-22. https://doi.org/10.1145/377924.594925
J. Calmet, A REDUCE approach to the calculation of Feynman diagrams, Computer Physics Communications 4 no. 2, (1972) 199–204. https://doi.org/10.1016/0010-4655(72)90008-2
H. Strubbe, Manual for SCHOONSCHIP a CDC 6000/7000 program for symbolic evaluation of algebraic expressions, Computer Physics Communications 8 no. 1, (1974) 1–30. https://doi.org/10.1016/0010-4655(74)90081-2
M. J. Levine, Neutrino processes of significance in stars. Ph.D. dissertation defended at the California Institute of Technology, 1963.
IBM, FORTRAN Assembly Program (FAP) for the IBM 709/7090. International Business Machines Corporation, 1961.
M. J. Levine, The process \(\gamma +\gamma \rightarrow \nu +\bar{\nu }\), Il Nuovo Cimento A 48 (1967) 67–71. https://doi.org/10.1007/BF02721342
M. J. Levine and R. Roskies, ASHMEDAI and a Large Algebraic Problem, in Proceedings of the Third ACM Symposium on Symbolic and Algebraic Computation, SYMSAC ’76, p. 359-364. New York: Association for Computing Machinery, 1976. https://doi.org/10.1145/800205.806357
M. Levine, Dirac matrix and tensor algebra on a digital computer, Journal of Computational Physics 1 no. 3, (1967) 454–455. https://doi.org/10.1016/0021-9991(67)90051-4
Y. S. Tsai and A. C. Hearn, Differential Cross Section for \({e}^{+}+{e}^{-}\rightarrow {W}^{+}+{W}^{-}\rightarrow {e}^{-}+{\overline{\nu }}_{e}+{\mu }^{+}+{\nu }_{\mu }\), Physical Review 140 (1965) B721–B729. https://doi.org/10.1103/PhysRev.140.B721
K. O. Mikaelian and J. Smith, Production of Single \(W\) Bosons in Electron-Positron Colliding Beams, Physical Review D 4 (1971) 785–794. https://doi.org/10.1103/PhysRevD.4.785
R. W. Brown and I. J. Muzinich, Study of Photon-Photon Interactions via Electron-Electron and Electron-Positron Colliding Beams, Physical Review D 4 (1971) 1496–1506. https://doi.org/10.1103/PhysRevD.4.1496
S. J. Brodsky and J. D. Sullivan, \(W\)-Boson Contribution to the Anomalous Magnetic Moment of the Muon, Physical Review 156 (1967) 1644–1647. https://doi.org/10.1103/PhysRev.156.1644
S. M. Swanson, FTRACE: A FAP subroutine for Dirac gamma matrix algebra. Institute of Theoretical Physics, Stanford University, unpublished report ITP-120, 1964.
J. Calmet, A review of computational QED, in Third International Colloquium on Advanced Computing Methods in Theoretical Physics, 25-29 Jun 1973, Marseille, France, vol. C1, pp. 1–39. Marseille: Centre de Physique Théorique, CNRS, 1973.
J. A. Fox, Recalculation of the Crossed-Graph Contribution to the Fourth-Order Lamb Shift, Physical Review D 3 (1971) 3228–3231. https://doi.org/10.1103/PhysRevD.3.3228
B. Lautrup, A. Peterman, and E. De Rafael, Confirmation of a new theoretical value for the Lamb shift, Physics Letters B 31 no. 9, (1970) 577–579. https://doi.org/10.1016/0370-2693(70)90699-4
A. Peterman, Analytic 4th order crossed ladder contribution to the lamb shift, Physics Letters B 35 no. 4, (1971) 325–326. https://doi.org/10.1016/0370-2693(71)90270-X
R. Barbieri, J. A. Mignaco, and E. Remiddi, On the Fourth-Order Radiative Corrections to the Electron-Photon Vertex, Lettere al Nuovo Cimento 3 no. 18, (1970) 588–591. https://doi.org/10.1007/BF02755435
R. Barbieri, J. A. Mignaco, and E. Remiddi, Fourth-order radiative corrections to electron-photon vertex and the Lamb-shift value, Il Nuovo Cimento A 6 no. 1, (1971) 21–28. https://doi.org/10.1007/BF02721342
J. Aldins, S. J. Brodsky, A. J. Dufner, and T. Kinoshita, Photon-Photon Scattering Contribution to the Sixth-Order Magnetic Moments of the Muon and Electron, Physical Review D 1 (1970) 2378–2395. https://doi.org/10.1103/PhysRevD.1.2378
J. Calmet and A. Peterman, A new value of the anomalous magnetic moment of the electron, Physics Letters B 47 no. 4, (1973) 369–370. https://doi.org/10.1016/0370-2693(73)90626-6
J. A. Mignaco and E. Remiddi, Fourth-order vacuum polarization contribution to the sixth-order electron magnetic moment, Il Nuovo Cimento A 60 (1969) 519–529. https://doi.org/10.1007/BF02757285
S. J. Brodsky and T. Kinoshita, Vacuum-Polarization Contributions to the Sixth-Order Anomalous Magnetic Moment of the Muon and Electron, Physical Review D 3 (1971) 356–362. https://doi.org/10.1103/PhysRevD.3.356
J. Calmet and M. Perrottet, On the Fourth-Order Radiative Corrections to the Anomalous Magnetic Moment of the Electron, Physical Review D 3 (1971) 3101–3107. https://doi.org/10.1103/PhysRevD.3.3101
M. J. Levine and J. Wright, Sixth-Order Magnetic Moment of the Electron, Physical Review Letters 26 (1971) 1351–1353. https://doi.org/10.1103/PhysRevLett.26.1351
M. J. Levine and J. Wright, Anomalous Magnetic Moment of the Electron, Physical Review D 8 (1973) 3171–3179. https://doi.org/10.1103/PhysRevD.8.3171
A. De Rújula, B. Lautrup, and A. Peterman, On sixth-order corrections to the anomalous magnetic moment of the electron, Physics Letters B 33 no. 8, (1970) 605–606. https://doi.org/10.1016/0370-2693(70)90361-8
T. Kinoshita and P. Cvitanović, Sixth-Order Radiative Corrections to the Electron Magnetic Moment, Physical Review Letters 29 (1972) 1534–1537. https://doi.org/10.1103/PhysRevLett.29.1534
P. Galison, Image and Logic: A Material Cultural of Microphysics. Chicago: University of Chicago Press, 1997.
A. Borrelli, Program FAKE: Monte Carlo Event Generators as Tools of Theory in Early High Energy Physics, NTM Zeitschrift für Geschichte der Wissenschaften, Technik und Medizin 24 no. 4, (2019) 479–514. https://doi.org/10.1007/s00048-019-00223-w
A. Visconti, ed., Third International Colloquium on Advanced Computing Methods in Theoretical Physics, 25-29 Jun 1973, Marseille, France. Marseille: Centre de Physique Théorique, CNRS, 1974.
Abdus Salam International Centre for Theoretical Physics, Computing as a Language of Physics. Vienna: International Atomic Energy Agency, 1972.
G. R. McLeod, ed., The impact of computers on physics: proceedings of the first European Conference on Computational Physics organized by the Interdivisional Group for Computational Physics of the European Physical Society, CERN, Geneva, 10-14 April 1972. Amsterdam: New Holland, 1972.
F. James, Computational physics: establishing an identity, Physics Bulletin 29 no. 9, (1978) 412. https://doi.org/10.1088/0031-9112/29/9/028
R. Roskies, New Technique in the \(g\) – 2 Calculation, in Third International Colloquium on Advanced Computing Methods in Theoretical Physics, 25-29 Jun 1973, Marseille, France, vol. C1, pp. C–VII. Marseille: Centre de Physique Théorique, CNRS, 1973.
A. Visconti, The Present Status of the Computing Methods in Quantum Electrodynamics, in Renormalization and Invariance in Quantum Field Theory, E. R. Caianiello, ed., pp. 329–366. Boston: Springer US, 1974. https://doi.org/10.1007/978-1-4615-8909-9_15
B. Ruijl, T. Ueda, and J. Vermaseren, FORM version 4.2, arXiv:1707.06453 [hep-ph].
A. C. Hearn, Computer Solution of Symbolic Problems in Theoretical Physics, in Computing as a Language of Physics, pp. 567–596. Vienna: IAEA, 1972.
H. Strubbe, Presentation of the SCHOONSCHIP System, SIGSAM Bulletin 8 no. 3, (1974) 55-60. https://doi.org/10.1145/1086837.1086845
J. S. R. Chisholm, Relativistic scalar products of \(\gamma \) matrices, Il Nuovo Cimento 30 (1963) 426–428. https://doi.org/10.1007/BF02750778
J. Campbell and A. C. Hearn, Symbolic analysis of Feynman diagrams by computer, Journal of Computational Physics 5 no. 2, (1970) 280–327. https://doi.org/10.1016/0021-9991(70)90064-1
J. Kahane, Algorithm for Reducing Contracted Products of \(\gamma \) Matrices, Journal of Mathematical Physics 9 no. 10, (1968) 1732–1738. https://doi.org/10.1063/1.1664506
J. Chisholm, Generalisation of the Kahane algorithm for scalar products of \(\lambda \)-matrices, Computer Physics Communications 4 no. 2, (1972) 205–207. https://doi.org/10.1016/0010-4655(72)90009-4
T. Appelquist, Parametric integral representations of renormalized Feynman amplitudes, Annals of Physics 54 no. 1, (1969) 27–61. https://doi.org/10.1016/0003-4916(69)90333-9
P. Kuo and D. Yennie, Renormalization theory, Annals of Physics 51 no. 3, (1969) 496–560. https://doi.org/10.1016/0003-4916(69)90141-9
J. Calmet and M. Perrottet, An attempt to evaluate renormalized radiative corrections by computer, Journal of Computational Physics 7 no. 2, (1971) 191–200. https://doi.org/10.1016/0021-9991(71)90084-2
J. Calmet, Computer Recognition of Divergences in Feynman Diagrams, SIGSAM Bulletin 8 no. 3, (1974) 74-75. https://doi.org/10.1145/1086837.1086849
W. Czyż, G. C. Sheppey, and J. D. Walecka, Neutrino production of lepton pairs through the point four-fermion interaction, Il Nuovo Cimento 34 (1964) 404–435. https://doi.org/10.1007/BF02734586
B. E. Lautrup, RIWIAD. CERN Program Library D114, 1982.
G. P. Lepage, A new algorithm for adaptive multidimensional integration, Journal of Computational Physics 27 no. 2, (1978) 192-203. https://doi.org/10.1016/0021-9991(78)90004-9
G. P. Lepage, VEGAS – an adaptive multi-dimensional integration program, tech. rep., Ithaca: Cornell University, Laboratory of Nuclar Studies, 1980.
J. Moses, Symbolic Integration the Stormy Decade, in Proceedings of the Second ACM Symposium on Symbolic and Algebraic Manipulation, SYMSAC ’71, pp. 427–440. New York: Association for Computing Machinery, 1971. https://doi.org/10.1145/800204.806313
J. R. Slagle, A heuristic program that solves symbolic integration problems in freshman calculus, Symbolic Automatic INTegrator (SAINT). Ph.D. dissertation defended at the Massachusetts Institute of Technology, 1961.
J. Moses, Symbolic Integration. Ph.D. dissertation defended at the Massachusetts Institute of Technology, 1967.
A. Petermann, Subtracted generalized polylogarithms and the SINAC program. CERN Preprint Ref. TH. 1451-CERN, 1972.
D. Maison and A. Petermann, Subtracted generalized polylogarithms and the SINAC program, Computer Physics Communications 7 no. 3, (1974) 121–134. https://doi.org/10.1016/0010-4655(74)90002-2
J. A. Fox and A. C. Hearn, Analytic computation of some integrals in fourth order quantum electrodynamics, Journal of Computational Physics 14 no. 3, (1974) 301–317. https://doi.org/10.1016/0021-9991(74)90055-2
K. Kölbig, J. Mignaco, and E. Remiddi, On Nielsen’s generalized polylogarithms and their numerical calculation, BIT Numerical Mathematics 10 (1970) 38–73. https://doi.org/10.1007/BF01940890
J. Calmet, Utilisation des langages formels en théorie des champs, in Utilisation des calculateurs en mathématiques pures (Limoges, 1975), pp. 31–39. Mémoires de la Société Mathématique de France, no. 49-50, 1977. https://doi.org/10.24033/msmf.211
M. J. Levine and R. Roskies, New Technique for Vertex Graphs, Physical Review Letters 30 (1973) 772–774. https://doi.org/10.1103/PhysRevLett.30.772
S. Fernbach and A. Taub, eds., Computers and their Role in the Physical Sciences. London and New York: Gordon and Breach, 1970.
K. V. Roberts, Computers and Physics, in Computing as a Language of Physics, pp. 3–26. Vienna: IAEA, 1972.
L. Kowarski, The impact of computers on nuclear science, in Computing as a Language of Physics, pp. 27–37. Vienna: IAEA, 1972.
H. Bethe, Introduction, in Computers and their Role in the Physical Sciences, S. Fernbach and A. Taub, eds., pp. 1–9. London and New York: Gordon and Breach, 1970.
S. R. Petrick, ed., Proceedings of the Second Symposium on Symbolic and Algebraic Manipulation, March. 23-25, 1971, Los Angeles, California. New York: Association for Computing Machinery, 1971.
J. Campbell, Algebraic computation of radiative corrections for electron-proton scattering, Nuclear Physics B 1 no. 5, (1967) 283–300. https://doi.org/10.1016/0550-3213(67)90129-0
T. Sasaki, Automatic generation of Feynman graphs in QED, Journal of Computational Physics 22 no. 2, (1976) 189–214. https://doi.org/10.1016/0021-9991(76)90075-9
W. M. Seiler, Jacques Calmet Dies at 77, ACM Communications in Computer Algebra 54 no. 1, (2020) 14-15. https://doi.org/10.1145/3419048.3419050
M. Perrottet, Generation of Feynman Diagrams by the Use of FORTRAN, in Computing as a Language of Physics, pp. 555–565. Vienna: IAEA, 1972.
Y. Le Gaillard and A. Visconti, On the Structure of the Finite Parts of the Generating Functional of Propagators in Quantumelectrodynamics, Journal of Mathematical Physics 6 no. 11, (1965) 1774–1785. https://doi.org/10.1063/1.1704723
J. Soffer and A. Visconti, Method for the Computation of Higher-Order Radiative Corrections; Application to the g\(\phi ^3\) Model. I. Method, Physical Review 162 no. 5, (1967) 1386. https://doi.org/10.1103/PhysRev.162.1386
J. Calmet, J. Soffer, R. Seneor, and A. Visconti, Method for the Computation of Higher-Order Radiative Corrections; Application to the g\(\phi ^3\) Model. II. Computational Techniques, Physical Review 162 no. 5, (1967) 1390. https://doi.org/10.1103/PhysRev.162.1390
A. D. Kennedy, Comments on the use of computer symbolic algebra for theoretical physics, Surveys in High Energy Physics 2 no. 1-2, (1980) 127–155. https://doi.org/10.1080/01422418008229985
J. Küblbeck, H. Eck, and R. Mertig, Computer algebraic generation and calculation of Feynman graphs using FeynArts and FeynCalc, Nuclear Physics B Proc. Suppl. 29 (1992) 204–208.
T. Hahn, Generating Feynman diagrams and amplitudes with FeynArts 3, Computer Physics Communications 140 (2001) 418–431. https://doi.org/10.1016/S0010-4655(01)00290-9
P. Nogueira, Automatic Feynman graph generation, Journal of Computational Physics 105 (1993) 279–289. https://doi.org/10.1006/jcph.1993.1074
P. Nogueira, Abusing qgraf, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 559 (2006) 220–223. https://doi.org/10.1016/j.nima.2005.11.151
T. Stelzer and W. F. Long, Automatic generation of tree level helicity amplitudes, Computer Physics Communications 81 (1994) 357–371. https://doi.org/10.1016/0010-4655(94)90084-1
A. Pukhov, E. Boos, M. Dubinin, V. Edneral, V. Ilyin, D. Kovalenko, A. Kryukov, V. Savrin, S. Shichanin, and A. Semenov, CompHEP: A Package for evaluation of Feynman diagrams and integration over multiparticle phase space, arxiv: org/abs/hep-ph/9908288
R. Harlander and M. Steinhauser, Automatic computation of Feynman diagrams, Progress in Particle and Nuclear Physics 43 (1999) 167–228. https://doi.org/10.1016/S0146-6410(99)00095-2
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H. S. Shao, T. Stelzer, P. Torrielli, and M. Zaro, The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations, Journal of High Energy Physics 07 (2014) 079. https://doi.org/10.1007/JHEP07(2014)079
A. Freitas, Numerical multi-loop integrals and applications, Progress in Particle and Nuclear Physics 90 (2016) 201–240. https://doi.org/10.1016/j.ppnp.2016.06.004
K. G. Wilson, The Renormalization Group: Critical Phenomena and the Kondo Problem, Reviews of Modern Physics 47 (1975) 773. https://doi.org/10.1103/RevModPhysics47.773
G. ’t Hooft and M. J. G. Veltman, Regularization and Renormalization of Gauge Fields, Nuclear Physics B 44(1972) 189–213. http://doi.org/10.1016/0550-3213(72)90279-9.
G. Passarino and M. J. G. Veltman, One loop corrections for \(e^+ e^-\) annihilation into \(\mu ^+ \mu ^-\)in the Weinberg model, Nuclear Physics B 160 (1979) 151–207. https://doi.org/10.1016/0550-3213(79)90234-7
G. Ossola, C. G. Papadopoulos, and R. Pittau, Reducing full one-loop amplitudes to scalar integrals at the integrand level, Nuclear Physics B 763 (2007) 147–169. https://doi.org/10.1016/j.nuclphysb.2006.11.012
G. J. van Oldenborgh, FF: A Package to evaluate one loop Feynman diagrams, Computer Physics Communications 66 (1991) 1–15. https://doi.org/10.1016/0010-4655(91)90002-3
S. Carrazza, R. K. Ellis, and G. Zanderighi, QCDLoop: a comprehensive framework for one-loop scalar integrals, Computer Physics Communications 209 (2016) 134–143. https://doi.org/10.1016/j.cpc.2016.07.033
T. Aoyama, M. Hayakawa, T. Kinoshita, and M. Nio, Tenth-Order QED Contribution to the Electron \(g\)–2 and an Improved Value of the Fine Structure Constant, Physical Review Letters 109 (2012) 111807. https://doi.org/10.1103/PhysRevLett.109.111807
P. A. Baikov, K. G. Chetyrkin, and J. H. Kühn, Five-Loop Running of the QCD coupling constant, Physical Review Letters 118 no. 8, (2017) 082002. https://doi.org/10.1103/PhysRevLett.118.082002
T. Luthe, A. Maier, P. Marquard, and Y. Schröder, The five-loop Beta function for a general gauge group and anomalous dimensions beyond Feynman gauge, Journal of High Energy Physics 10 (2017) 166. https://doi.org/10.1007/JHEP10(2017)166
F. Herzog, B. Ruijl, T. Ueda, J. A. M. Vermaseren, and A. Vogt, The five-loop beta function of Yang-Mills theory with fermions, Journal of High Energy Physics 02 (2017) 090. https://doi.org/10.1007/JHEP02(2017)090
F. V. Tkachov, A Theorem on Analytical Calculability of Four Loop Renormalization Group Functions, Physics Letters B 100 (1981) 65–68. https://doi.org/10.1016/0370-2693(81)90288-4
K. G. Chetyrkin and F. V. Tkachov, Integration by Parts: The Algorithm to Calculate beta Functions in 4 Loops, Nuclear Physics B 192 (1981) 159–204. https://doi.org/10.1016/0550-3213(81)90199-1
D. J. Broadhurst, Three-loop on-shell charge renormalization without integration: \(\Lambda ^{\overline{\rm MS\rm }_{\rm QED}}\) to four loops, Zeitschrift für Physik C Particles and Fields 54 (1992) 599–606. https://doi.org/10.1007/BF01559486
K. Melnikov and T. v. Ritbergen, The three-loop relation between the \(\overline{\rm MS}\) and the pole quark masses, Physics Letters B 482 (2000) 99–108. https://doi.org/10.1016/S0370-2693(00)00507-4
S. G. Gorishnii, S. A. Larin, L. R. Surguladze, and F. V. Tkachov, Mincer: Program for Multiloop Calculations in Quantum Field Theory for the Schoonschip System, Computer Physics Communications 55 (1989) 381–408. https://doi.org/10.1016/0010-4655(89)90134-3
S. A. Larin, F. V. Tkachov, and J. A. M. Vermaseren, The FORM version of MINCER. NIKHEF-H-91-18, 1991.
M. Steinhauser, MATAD: A Program package for the computation of MAssive TADpoles, Computer Physics Communications 134 (2001) 335–364. https://doi.org/10.1016/S0010-4655(00)00204-6
S. Laporta, High precision calculation of multiloop Feynman integrals by difference equations, International Journal of Modern Physics A 15 (2000) 5087–5159. https://doi.org/10.1142/S0217751X00002159
P. Maierhöfer, J. Usovitsch, and P. Uwer, Kira–A Feynman integral reduction program, Computer Physics Communications 230 (2018) 99–112. https://doi.org/10.1016/j.cpc.2018.04.012
J. Klappert and F. Lange, Reconstructing rational functions with FireFly, Computer Physics Communications 247 (2020) 106951. https://doi.org/10.1016/j.cpc.2019.106951
J. Klappert, F. Lange, P. Maierhöfer, and J. Usovitsch, Integral reduction with Kira 2.0 and finite field methods, Computer Physics Communications 266 (2021) 108024. https://doi.org/10.1016/j.cpc.2021.108024
M. Tentyukov and J. A. M. Vermaseren, The Multithreaded version of FORM, Computer Physics Communications 181 (2010) 1419–1427. https://doi.org/10.1016/j.cpc.2010.04.009
J. M. Henn, Multiloop integrals in dimensional regularization made simple, Physical Review Letters 110 (2013) 251601. https://doi.org/10.1103/PhysRevLett.110.251601
R. N. Lee, Reducing differential equations for multiloop master integrals, Journal of High Energy Physics 04 (2015) 108. https://doi.org/10.1007/JHEP04(2015)108
M. Prausa, epsilon: A tool to find a canonical basis of master integrals, Computer Physics Communications 219 (2017) 361–376. https://doi.org/10.1016/j.cpc.2017.05.026
T. Binoth and G. Heinrich, An automatized algorithm to compute infrared divergent multiloop integrals, Nuclear Physics B 585 (2000) 741–759. https://doi.org/10.1016/S0550-3213(00)00429-6
S. Borowka, G. Heinrich, S. Jahn, S. P. Jones, M. Kerner, J. Schlenk, and T. Zirke, pySecDec: a toolbox for the numerical evaluation of multi-scale integrals, Computer Physics Communications 222 (2018) 313–326. https://doi.org/10.1016/j.cpc.2017.09.015
A. V. Smirnov, Algorithm FIRE – Feynman Integral REduction, Journal of High Energy Physics 10 (2008) 107. https://doi.org/10.1088/1126-6708/2008/10/107
E. Remiddi and J. A. M. Vermaseren, Harmonic polylogarithms, International Journal of Modern Physics A 15 (2000) 725–754. https://doi.org/10.1142/S0217751X00000367
M. Beneke and V. A. Smirnov, Asymptotic expansion of Feynman integrals near threshold, Nuclear Physics B 522 (1998) 321–344. https://doi.org/10.1016/S0550-3213(98)00138-2
R. Harlander, T. Seidensticker, and M. Steinhauser, Corrections of \(\cal{O}(\alpha \alpha _s)\) to the decay of the \(Z\) Boson into bottom quarks, Physics Letters B 426 (1998) 125–132. https://doi.org/10.1016/S0370-2693(98)00220-2
H. Baer, J. Ohnemus, and J. F. Owens, A Next-to-leading Logarithm Calculation of Direct Photon Production, Physical Review D 42 (1990) 61–71. https://doi.org/10.1103/PhysRevD.42.61
S. Catani and M. H. Seymour, A General algorithm for calculating jet cross-sections in NLO QCD, Nuclear Physics B 485 (1997) 291–419. [Erratum: Nuclear Physics B 510, 503–504 (1998)]. https://doi.org/10.1016/S0550-3213(96)00589-5
S. Frixione, Z. Kunszt, and A. Signer, Three jet cross-sections to next-to-leading order, Nuclear Physics B 467 (1996) 399–442. https://doi.org/10.1016/0550-3213(96)00110-1
S. Catani and M. Grazzini, An NNLO subtraction formalism in hadron collisions and its application to Higgs boson production at the LHC, Physical Review Letters 98 (2007) 222002. https://doi.org/10.1103/PhysRevLett.98.222002
M. Czakon, A novel subtraction scheme for double-real radiation at NNLO, Physics Letters B 693 (2010) 259–268. https://doi.org/10.1016/j.physletb.2010.08.036
I. W. Stewart, F. J. Tackmann, and W. J. Waalewijn, N-Jettiness: An Inclusive Event Shape to Veto Jets, Physical Review Letters 105 (2010) 092002. https://doi.org/10.1103/PhysRevLett.105.092002
M. Czakon, D. Heymes, and A. Mitov, Dynamical scales for multi-TeV top-pair production at the LHC, Journal of High Energy Physics 04 (2017) 071. https://doi.org/10.1007/JHEP04(2017)071
S. J. Parke and T. R. Taylor, An Amplitude for \(n\) Gluon Scattering, Physical Review Letters 56 (1986) 2459. https://doi.org/10.1103/PhysRevLett.56.2459
E. Witten, Perturbative Gauge Theory as a String Theory in Twistor Space, Communications in Mathematical Physics 252 (2004) 189-258. https://doi.org/10.1007/s00220-004-1187-3
R. Britto, F. Cachazo, and B. Feng, Generalized unitarity and one-loop amplitudes in N=4 super-Yang-Mills, Nuclear Physics B 725 (2005) 275–305. https://doi.org/10.1016/j.nuclphysb.2005.07.014
N. Arkani-Hamed and J. Trnka, The Amplituhedron, Journal of High Energy Physics 10 (2014) 030. https://doi.org/10.1007/JHEP10(2014)030
J. M. Campbell, J. W. Huston, and W. J. Stirling, Hard Interactions of Quarks and Gluons: A Primer for LHC Physics, Reports on Progress in Physics 70 (2007) 89. https://doi.org/10.1088/0034-4885/70/1/R02
OpenLoops 2, F. Buccioni, J.-N. Lang, J. M. Lindert, P. Maierhöfer, S. Pozzorini, H. Zhang, and M. F. Zoller, OpenLoops 2, European Physical Journal C 79 no. 10, (2019) 866. https://doi.org/10.1140/epjc/s10052-019-7306-2
G. Bevilacqua, M. Czakon, M. V. Garzelli, A. van Hameren, A. Kardos, C. G. Papadopoulos, R. Pittau, and M. Worek, HELAC-NLO, Computer Physics Communications 184 (2013) 986–997. https://doi.org/10.1016/j.cpc.2012.10.033
F. J. Dyson, Divergence of perturbation theory in quantum electrodynamics, Physical Review 85 (1952) 631–632. https://doi.org/10.1103/PhysRev.85.631
R. Harlander, J.-P. Martinez, and G. Schiemann, The end of the particle era?, European Physical Journal H 48 no. 1, (2023) 6. https://doi.org/10.1140/epjh/s13129-023-00053-4
G. ’t Hooft and M. J. G. Veltman, Scalar One Loop Integrals, Nuclear Physics B 153 (1979) 365–401. https://doi.org/10.1016/0550-3213(79)90605-9
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) Research Unit “The Epistemology of the Large Hadron Collider” (Grant FOR 2063).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the development of this article in roughly equal amounts. Most of Sect. 2 was written by Jean-Philippe Martinez, while the largest part of Sect. 3 and “Appendices A and B” was composed by Robert Harlander. The introduction and conclusion were prepared collectively. Both authors approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Appendices
The structure of Feynman diagrams
In Sect. 3.1, we argue that it is the restricted structure of Feynman integrals that allows for their extensive algorithmic solution. In this appendix, we explain the origin of this structure by giving a brief tour from the fields and the corresponding field equations to their representation in Feynman diagrams. Of course, this exposition cannot replace a proper course on QFT where these issues are discussed in detail. However, we hope that it helps the interested reader who is not familiar with these concepts to contextualize the issues discussed in this paper.
1.1 Field equations
Within the realm of relativistic QFT, the structure of Feynman diagrams is remarkably uniform. To a large extent, this is due to the fact that Poincaré invariance strongly restricts the form of relativistic fields and their quanta, which we call particles. In particular, only particles of spin 0 (scalars), spin 1/2 (fermions), and spin 1 (vector bosons) are known to lead to consistent quantum field theories in four space–time dimensions.
The only known fundamental scalar particle is the Higgs boson, discovered in 2012.Footnote 54 The known fundamental fermions are the charged leptons (electron, muon, tau) and their associated neutrinos (\(\nu _e\), \(\nu _\mu \), \(\nu _\tau \)), as well as the quarks. The known vector particles are the gluons, the W bosons, the Z boson, and the photon. All of the latter are gauge bosons, meaning that they arise in the theoretical description of the fundamental set of particles as manifestations of an underlying gauge symmetry. Theories beyond the Standard Model typically introduce new particles, but their spin is also either 0, 1/2, or 1. For example, supersymmetry introduces a new spin-1/2 particle for every spin-1 and spin-0 particle of the Standard Model, and a spin-0 particle for every Standard Model fermion.
The gravitational field according to general relativity, on the other hand, has spin-2 and leads to a non-renormalizable field theory in four space–time dimensions. Its superpartner, the gravitino, would carry spin-3/2. We will not consider them any further here, even though they would not significantly change the main messages of the paper.
The space–time dependence of each of these fields is governed by a specific field equation. For a spin-0 particle \(\phi (x)\) this is the Klein–Fock–Gordon equationFootnote 55:
where m is the mass of the particle and
denotes the derivative w.r.t. the space–time variable \(x=(t,{\textbf{x}})\). It is easy to verify that one solution to Eq. (A.1) is given by plane waves:
where \(N_\pm (p)\) is a normalization factor, and \(p=(E,{\textbf{p}})\) is the 4-momentum satisfying the relativistic relation between energy, momentum, and mass:
Vector bosons \(A_\mu (x)\), on the other hand, obey the field equation
For a photon, it is \(m=0\), and Eq. (A.5) reduces to the well-known Maxwell equations (in the absence of charges and currents, see below). The Lorentz index in \(A_\mu (x)\) indicates that it has four components, not all of which are independent, though. They correspond to the polarization degrees of freedom well-known from classical optics. In the quantized language, they reflect the spin-orientation relative to the particle’s momentum direction, also known as helicity. A solution to Eq. (A.5) is again given by plane waves:
where the polarization vector \(\epsilon ^\pm _\mu (p)\) satisfies
and again \(p^2=m^2\).
Fermions obey the Dirac equation:
where the \(\gamma ^\mu \) are the 4\(\times \)4 Dirac matrices. Their defining properties are
with \(g^{\mu \nu }\) the metric tensor.Footnote 56 Thus, Eq. (A.8) is really a matrix equation, and \(\psi (x)\) is again a field with four components. Two of them are needed to describe the particle’s helicity (parallel or anti-parallel to its momentum direction), the other two encode the degrees of freedom for the anti-particle. Also the Dirac equation has plane-wave solutions,
with \(p^2=m^2\) and the 4-component spinors \(u_\pm (p)\) obeying the algebraic matrix equation
For the following section, it is important to realize that each component of vector and Dirac fields also obeys the Klein–Fock–Gordon equation (Eq. (A.1)), as can be shown by simple manipulations of Eqs. (A.5) and (A.8).Footnote 57 The latter just impose additional constraints on the components of the corresponding fields.
1.2 Feynman propagators
All of the field equations discussed in the previous section correspond to free fields, i.e., they do not take into account interactions. The latter introduce non-linear terms on the right-hand side of these equations, which may involve products of all possible fields. A common way to tackle the solution of such equations is via Green’s functions, which corresponds to solving them in the case where the right-hand side is proportional to a four-dimensional delta function \(\delta ^{(4)}(x)\) (possibly times x-independent factors that ensure Poincaré invariance of the equation). Consider, for example, the Klein–Fock–Gordon equation (Eq. (A.1)) with such a term:
Replacing D(x) by its Fourier transform \({\tilde{D}}(p)\)
turns this into an algebraic equation
which can be solved trivially as long as \(p^2\ne m^2\). However, the inverse Fourier transform back to D(x) involves an integration over all p, including the singularity at \(p^2=m^2\). This leads to an ambiguity in the solution for Eq. (A.12) which Feynman suggested resolving by introducing the so-called “\(i\epsilon \)” prescription, leading to the unique solution
where the limit \(\epsilon \rightarrow 0_+\) is implied. It can be shown that, for \(x_0>y_0\), the Feynman propagator \(D(x-y)\) encodes the probability that a particle which is created at the space–time point y will be annihilated at x. On the other hand, if \(x_0<y_0\), it encodes the probability that an anti-particle which is created at x will be annihilated at y.
The Feynman propagators for fermions and vector particles only differ from this by the numeratorsFootnote 58:
In Feynman’s original interpretation of his diagrams, propagators are depicted as lines that connect space–time points. Conventionally, one uses solid lines for fermions, wavy lines for vector bosons, and dashed lines for scalars (see Fig. 13). Note that the direction of the arrow differentiates fermions from anti-fermions.
1.3 Vertices
The Green’s function can be viewed as the response of the field to a disturbance which is 100% localized in space and time, described by the \(\delta \)-function in Eq. (A.12). A general interaction is then taken into account by the superposition of such infinitesimal disturbances.
Let us consider QED, the theory of electrons (and their anti-particles, the positrons) and photons. Including interactions, instead of the free equations Eqs. (A.5) and (A.8), the field equations read
where e is the unit of electric charge, which in natural units (\(\hbar =c=1\)) is a dimensionless number, \(e=\sqrt{4\pi \alpha } \approx 0.3\), where \(\alpha \approx 1/137\) is the fine structure constant.
For many reasons, it is more convenient to work with Lagrangians rather than field equations. For example, both equations above follow from the QED Lagrangian
where
by applying the Euler–Lagrange equations
for \(\phi =A_\mu \) and \(\phi =\bar{\psi }\), respectively. The first two terms in Eq. (A.18) lead to the free field equations, while the third term incorporates both interaction terms in Eq. (A.17). In fact, it is this term that defines the interaction vertex, and the graphical representation is as simple as translating each field factor into a line (see Fig. 14). Notice that \(\psi \) and \(\bar{\psi }\) are distinguished by the “fermion direction,” indicated by the arrow on the line.
1.4 Feynman diagrams
It is now remarkably simple to draw the Feynman diagrams that need to be calculated in order to obtain the probability amplitude for a certain process in QED. Assume, for example, that we want to calculate the probability that electrons and positrons annihilate into photons when they collide with a certain relative velocity. Theoretically, this is described as the transition from an initial state consisting of an \(e^+e^-\) pair at \(t=-\infty \) to a final state of two photons at \(t=+\infty \).Footnote 59 Only these two asymptotic states are considered to be observable. Ontological interpretations of any other part of a Feynman diagram are difficult, to say the least, but this shall not be the issue of the current paper (see, e.g., [4,5,6,7,8]).
The corresponding Feynman diagrams at the lowest order in perturbation theory are shown in Fig. 15. The external lines on the left and right of the diagram describe the initial and final state. Mathematically, they correspond to the solutions of the free wave equations. For fixed external momenta, they are thus replaced by plane waves. The interaction is encoded in the two vertices at \(x_1\) and \(x_2\) which are connected by an electron propagator (see Fig. 13). According to the Feynman rules, the diagrams in Fig. 15 are proportional to \(e^2\approx 0.09\). Higher orders in perturbation theory correspond to Feynman diagrams with higher powers of e, and thus a larger number of vertices. But since the initial and final states should be the same as in Fig. 15, higher orders correspond to Feynman diagrams with closed loops, such as those shown in Fig. 16.
The diagrams of Figs. 15 and 16 are immediately converted into mathematical expressions if we translate the graphical notation of the propagators and vertices according to Figs. 13 and 14. In order to obtain the full leading-order amplitude for the process, we need to sum over all possible diagrams, however. Since the intermediate particles are unobservable, this means that we need to integrate over all space–time points. In this sense, the specific diagram in Fig. 15a is just a representative of an infinite number of Feynman diagrams.
Specifically, up to numerical factors, the amplitude for the diagram in Fig. 15 reads
Note that the only space–time dependence is through the exponentials of the external plain wave functions and the propagators. Thus, integration over the two space–time variables \(x_1\), \(x_2\) is easily performed using the relation
resulting in two \(\delta \)-functions
One of them can be used to solve the p-integral, so that the remaining expression is purely algebraic:
where p is no longer an integration variable, but a short-hand notation for \(p\equiv p_1-k_1=k_2-p_2\). All integrations have been carried out, and momentum conservation is manifest, both overall via the \(\delta \)-function, as well as at each vertex via the momentum assignments. This is a general feature of tree diagrams, i.e., diagrams without any closed loops. What remains in this case is a purely algebraic expression which, aside from the fundamental parameters of the theory like masses and couplings, depends only on the momenta of the external particles.
As already indicated in Appendix A.4, in Feynman’s original paper, he suggested a space–time reading of his diagrams, in the sense that the lines represent world lines connecting vertices at specific space–time points. However, due to the discussion above, it has become more common to adopt a momentum-space reading of Feynman diagrams. The actual position (relative and absolute) of the vertices is irrelevant, only the flow of momenta (the “topology”) is important. In order to obtain the probability amplitude for a certain process, one needs to add up all topologically distinct Feynman diagrams. In the case under consideration, these are indeed given by Fig. 15, because the momentum flowing through the propagator is different (\(p=p_1+k_2=k_1-p_2\) in Fig. 15b).
Consider now the case of a Feynman diagram with a closed loop, for example the one in Fig. 16a. The momenta of the propagators in the loop are no longer fully determined by the external momenta; we can add an arbitrary momentum l to each of them without violating momentum conservation at the vertices. Following the same operations that led to Eq. (A.24), one will find that there are indeed not enough \(\delta \)-functions to eliminate all momentum integrations. Instead, the integration over the four-dimensional loop momentum l remains (the \(\delta \)-function that ensures overall momentum conservation will still be present though). In general, a Feynman diagram with n closed loops involves n four-dimensional momentum integrations.
We thus see that the general structure of a Feynman diagram with external momenta \(q_1,q_2,\ldots \) (the dependence on the particle masses will be suppressed) is necessarily of the following form:
where \(T^{\mu \nu \cdots }\) is an algebraic component which, aside from trivial factors like coupling constants, involves the external momenta, Dirac matrices, spinors, and polarization vectors. The Feynman integral takes the form
Despite the uniform structure of Feynman diagrams, their evaluation can be highly involved, with the complexity increasing enormously with the number of loops.
Calculation of sample one-loop integrals
1.1 Tadpole
Let us consider the following one-loop Feynman integral in dimensional regularization (see Sect. 3.4):
For \(b=1\), it corresponds to a Feynman diagram as shown in Fig. 17. According to its form, it is usually referred to as a tadpole diagram. Note that momentum conservation implies that the external momentum \(q=0\). For reasons that will become clear below, we evaluate the integral for general values of \(b>0\).
One complication when evaluating this integral is that the four-momentum k is defined in Minkowski space, which means that its square \(k^2=k_0^2-{\textbf{k}}^2\) is not positive definite. Further manipulations of the integral are much more transparent when applying a so-called Wick rotation, which means to substitute \(k_0= ik_{0,E}\), leading to \(k^2\rightarrow -k_E^2\), where \(k_E^2=k_{0,E}^2+{\textbf{k}}^2\) is positive definite. It can be shown that the only effect of this rotation on the integration measure is an additional factor i. Therefore,
Since the integrand in \(A^{(b)}(m)\) depends only on the modulus of \(k_E\), one can perform the \((D-1)\)-dimensional angular integration to obtain
where the surface of the unit sphere in D-dimensional space is given by Eq. (3.5). Euler’s \(\Gamma \)-function is defined through
It is well-defined in the whole complex plane, except for \(z=0,-1,-2,\cdots \), where it develops poles. The remaining one-dimensional integral can be brought to the form of Riemann’s beta function:
leading to
Since D is arbitrary, it can always be chosen such that this expression is finite. In the limit \(D\rightarrow 4\), however, it diverges for \(b\in \{1,2\}\) because the \(\Gamma \) function in the numerator diverges in these cases.Footnote 60 In fact, we could have anticipated this problem already from Eq. (B.2). Similar to the discussion related to Eqs. (3.2) and (3.3), one concludes that, for these values of b, the integral diverges at \(D=4\) in the region where all components of the integration momentum get large.
1.2 Feynman parameters
Let us now consider the integral Eq. (3.2). Already Feynman in his original paper of 1949 suggested a way to compute it by introducing what today is called Feynman parameters:
Applying this to Eq. (3.2), one obtains
Completing the square in the denominator and shifting the integration momentum leads to
The k-dependence of the integrand is now the same as in Eq. (B.1), so we can use Eq. (B.6) to obtain
What remains is a one-dimensional integral over the polynomial \(M^2(x)\), raised to an \(\epsilon \)-dependent power \(D/2-2=-\epsilon \), for which there are standard methods to evaluate.
1.3 Tensor decomposition
So far, the integrands did not have any k-dependence in the numerator in this section. However, as we saw in Eq. (3.8), in general an amplitude may involve tensor integrals. But using Lorentz covariance, any tensor integral can be expressed by a scalar integral. For example, an integral of the form
must transform like a 1\(^\text {st}\)-rank Lorentz tensor (i.e., a vector). Lorentz covariance then implies that it must be proportional to \(q^\mu \), and therefore
where
is a scalar integral. One can even go further and use
which results in three integrals without any loop momentum in the numerator.
In the general case of higher-rank tensor integrals, or integrals which depend on more than one external momentum, more than one tensor structure can emerge. Consider, for example,
We make an ansatz with all possible tensor structures:
where the coefficients \(A_i\) depend on the invariants \(q_1^2\), \(q_2^2\), and \(q_1\cdot q_2\), and we have already taken into account the symmetry in \(\mu \leftrightarrow \nu \) and \(q_1\leftrightarrow q_2\). Contracting this ansatz successively by the three tensor structures leads to a system of equations which can be solved for the \(A_i\), and which involves only scalar integrals.
It has been realized by Passarino and Veltman that this can be turned into a recursive algorithm [167]. In principle, it reduces any one-loop tensor Feynman integral to a unique set of a few basis integrals which had been previously studied by ’t Hooft and Veltman [212] (see also Sect. 3.5).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Harlander, R.V., Martinez, JP. The development of computational methods for Feynman diagrams. EPJ H 49, 4 (2024). https://doi.org/10.1140/epjh/s13129-024-00067-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjh/s13129-024-00067-6