Motility and swimming: universal description and generic trajectories

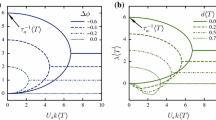
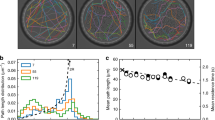
Abstract

Autonomous locomotion is a ubiquitous phenomenon in biology and in physics of active systems at microscopic scale. This includes prokaryotic, eukaryotic cells (crawling and swimming) and artificial swimmers. An outstanding feature is the ability of these entities to follow complex trajectories, ranging from straight, curved (circular, helical...), to random-like ones. The non-straight nature of these trajectories is often explained as a consequence of the asymmetry of the particle or the medium in which it moves, or due to the presence of bounding walls, etc... Here, we show that for a particle driven by a concentration field of an active species, straight, circular and helical trajectories emerge naturally in the absence of asymmetry of the particle or that of suspending medium. Our proof is based on general considerations, without referring to an explicit form of a model. We show that these three trajectories correspond to self-congruent solutions. Self-congruency means that the states of the system at different moments of time can be made identical by an appropriate combination of rotation and translation of the coordinate space. We show that these solutions are exhibited by spherically symmetric particles as a result of a series of pitchfork bifurcations, leading to spontaneous symmetry breaking in the concentration field driving the particle motility. Self-congruent dynamics in one and two dimensions are analyzed as well. Finally, we present a simple explicit nonlinear exactly solvable model of fully isotropic phoretic particle that shows the transitions from a non-motile state to straight motion to circular motion to helical motion as a series of spontaneous symmetry-breaking bifurcations. Whether a system exhibits or not a given trajectory only depends on the numerical values of parameters entering the model, while asymmetry of swimmer shape, or anisotropy of the suspending medium, or influence of bounding walls are not necessary.

Graphical Abstract

Appendices

Appendix A: Explicit model: autophoretic particle in 2D

Let us consider an explicit model studied in [16, 17, 19, 21]. This is an autophoretic particle which can emit (or absorb) a chemical substance at its surface. In that case the tangential velocity field along the particle is related to the surface gradient of the chemical concentration. The flow equations can be solved for to express the fluid velocity in terms of the concentration field at the particle surface. The concentration dynamics in the bulk, which obeys an advection–diffusion equation, defines a nonlinear evolution equation for the concentration in the bulk and at the surface [16, 17, 19, 21]. For example, the evolution equation reads

$$\begin{aligned} \begin{aligned}&\dot{c}(\varvec{r},t)= \sum _k { c_k(1,t) M e^{ik\phi } \over 2 r^{\vert k\vert +1} } \\&\quad \left[ (r^2-1)k^2 \frac{\partial c (\varvec{r},t) }{\partial r} +ik(2r^2 +(1-r^2) \vert k\vert ) \frac{\partial c (\varvec{r},t)}{\partial \phi } \right] \\&\quad +\frac{1}{Pe}\Delta c (\varvec{r},t) \\ {}&\equiv {\mathcal {G}}\{c(\varvec{r}',t)\}(\varvec{r}) \end{aligned} \end{aligned}$$

(A1)

in 2D for a circular particle. This is a nonlocal equation since the evolution of the field c at the considered point $\varvec{r}$ in the bulk depends on concentration elsewhere: the knowledge of the field along the bead surface at $r=1$ and at infinitesimally close points. The latter information is needed to calculate the derivatives of the concentration field. Here $c_k$ refers to k-th Fourier component, $\phi$ is the polar angle, and M is a real constant relating the tangential velocity of the fluid and the gradient of c along the bead [16, 17, 19, 21]. The particle velocity is calculated as $(-M\Re c_1(1,t),M\Im c_1(1,t))$. This defines the full evolution of the concentration in the laboratory frame.

Appendix B: Absence of swimming for a variational problem

Here we show the absence of swimming for a variational problem. Suppose we have

$$\begin{aligned} \dot{c}(x)={\mathcal {G}}\{c(x')\}(x), \end{aligned}$$

(B2)

where

$$\begin{aligned} {\mathcal {G}}\{c(x')\}(x)=-\frac{\delta F\{c(x')\}}{\delta c(x)} \end{aligned}$$

(B3)

for some non-linear functional F, and where $\delta F/\delta c$ refers to functional derivative. Equation (B3) can be rewritten, in view of the very definition of functional derivative, as

$$\begin{aligned}{} & {} \lim _{h\rightarrow 0}\frac{F\{c(x)+h\delta c(x)\}-F\{c(x)\}}{h}\nonumber \\{} & {} \quad =-\int {\mathcal {G}}\{c(x')\}(x)\delta c(x) dx. \end{aligned}$$

(B4)

1.1 B.1 Proof 1

We can write that

$$\begin{aligned} F\{c(x)\}=F\{c(x+h)\}=F\{c(x)+h\partial _{x}c(x)\}+O(h^2) \end{aligned}$$

(B5)

because of the translational invariance of F. Setting $\delta c$ to $\partial _x c$ in Eq. (B4) and comparing with Eq. (B5) shows that

$$\begin{aligned} \int {\mathcal {G}}\{c(x')\}(x)\partial _x c(x) dx=0. \end{aligned}$$

(B6)

Multiplying Eq. (B2) by $\partial _x c$ and integrating with respect to x yields

$$\begin{aligned} \int \dot{c}(x)\partial _xc(x)dx=\int \mathcal G\{c(x')\}(x)\partial _xc(x)dx=0. \end{aligned}$$

(B7)

Substituting the self-congruent solution $\dot{c}(x)=v\partial _x c(x)$ in Eq. (B7) shows that $v=0$ unless $\partial _x c(x)$ is zero everywhere.

1.2 B.2 Proof 2

The function $F\{c(x,t)\}$ is constant in time for a self-congruent solution due to the invariance of F under rotations and translations of the concentration field c. This expands to

$$\begin{aligned} \begin{aligned}&0=\frac{dF\{c(x,t)\}}{dt}\\&\quad \equiv \lim _{h\rightarrow 0}\frac{ F\{c(x,t+h)\}-F\{c(x,t)\}}{h}\\&\quad =\lim _{h\rightarrow 0}\frac{F\{c(x,t)+h\dot{c}(x,t)\}-F\{c(x,t)\}}{h}\\&\quad =-\int {\mathcal {G}}\{c(x')\}(x) \dot{c}(x)dx=-\int \dot{c}(x)^2 dx, \end{aligned} \end{aligned}$$

(B8)

where the last equality uses (B2). The right hand side of Eq. (B8) can be equal to zero only if $\dot{c}(x,t)=0$ for all x. This shows that there are no motile self-congruent solutions of Eq. (B2) with variational right hand side.

Appendix C: Extended analysis of the motility of a segment particle in 1D

We analyze the non-linear dynamics of the 1D model by taking higher-order terms in the expansion (22):

$$\begin{aligned}{} & {} {\mathcal {G}}\{c_0(x')+\varepsilon \delta c(x')\}(x)=\varepsilon {\mathcal {G}}_1\{\delta c(x')\}(x)\nonumber \\{} & {} \qquad +\varepsilon ^2 {\mathcal {G}}_2\{\delta c(x'),\delta c(x'')\}(x)\nonumber \\{} & {} \qquad +\varepsilon ^3{\mathcal {G}}_3\{\delta c(x'),\delta c(x''),\delta c(x''')\}(x)+O(\varepsilon ^4).\nonumber \\ \end{aligned}$$

(C9)

Here ${\mathcal {G}}_2$ and ${\mathcal {G}}_3$ are bilinear and trilinear operators, respectively. That is, ${\mathcal {G}}_2$ and ${\mathcal {G}}_3$ are operators that take, respectively, 2 and 3 functions (here listed inside the curly brackets) of x and return another function of x. They are linear with respect to each variable inside the curly brackets.

We write the time-dependent solution of Eq. (5) as

$$\begin{aligned} \begin{aligned} c(x,t)&=c_0(x-x_c(t))+\varepsilon \delta c(x-x_c(t),t),\\ \varepsilon \delta c(x-x_c(t),t)&=\varepsilon \delta c_1(t) f_1(x-x_c(t))\\&\quad +\varepsilon ^2\sum \limits _{i=2}^\infty \delta c_i(t) f_i(x-x_c(t)), \end{aligned} \end{aligned}$$

(C10)

where $\varepsilon$ is a small parameter of the expansions and $\delta c_i(t)$ are the amplitudes of the different modes in perturbation. The assumption that the amplitudes of $f_i(x-x_c(t))$ are of order $O(\varepsilon ^2)$ for $i>1$ is validated below by the consistency of equations. The velocity of the comoving frame $\dot{x}_c(t)$ is also small for Pe close to $Pe_1$. We further take $Pe-Pe_1=O(\varepsilon ^2)$ for consistency of Eq. (28).

We express the amplitudes $\delta c_i(t)$ for $i>2$ as a function of $\delta c_1(t)$ by substituting (C9) into the right hand side of Eq. (5) and expanding the result in the basis $f_i(x-x_c(t))$.

$$\begin{aligned} \varepsilon ^2\dot{\delta c}_i+O(\varepsilon ^3)= & {} \varepsilon G_1^{(i)}\{\delta c(x')\}+\varepsilon ^2 G_2^{(i)}\{\delta c(x'),\delta c(x'')\}\nonumber \\ {}{} & {} +O(\varepsilon ^3)\nonumber \\= & {} \varepsilon ^2\lambda _i \delta c_i(t)+\varepsilon ^2 G_2^{(i)}\{f_1(x'),f_1(x'')\}\delta c_1^2\nonumber \\ {}{} & {} +O(\varepsilon ^3), \end{aligned}$$

(C11)

where the k-linear functionals $G_k^{(i)}$ are defined by

$$\begin{aligned} {\mathcal {G}}_k\{\delta c(x'),...\}(x)=\sum _{i=0}^\infty G_k^{(i)}\{\delta c(x'),...\}f_i(x). \end{aligned}$$

(C12)

The leading term of the right hand side of Eq. (C11) is $\lambda _i \delta c_i(t)$. Since $\lambda _i$ is negative and has a large absolute value, the solution of (C11) relaxes to a steady-state solution $\delta c_i^0$ on a time scale that is small compared to the dynamics of the $\delta c_1$ mode. This is where the discrete nature of the set of eigenvalues becomes important: For a finite set, it is always possible to find the eigenvalue with the smallest absolute value and set Pe sufficiently close to $Pe_1$ to ensure that $|\lambda _1|<|\lambda _i|$ for all i. Since the set of $\lambda _i$ is infinite, it is not possible to exclude a priori a situation where for any value of $\lambda _1>0$ there is another i such that $|\lambda _i|<\lambda _1$. The adiabatic elimination may not work in this case.

We find from Eq. (C11) the steady-state value of $\delta c_i$ as

$$\begin{aligned} \delta c_i^0=-\delta c_1^2\frac{G_2^{(i)}\{f_1(x'),f_1(x'')\}}{\lambda _i}+O(\varepsilon ), \end{aligned}$$

(C13)

which confirms that the amplitudes of $f_i(x-x_c(t))$ in ansatz (C10) are of order $O(\varepsilon ^2)$ for $i>1$. Note also that ${\mathcal {G}}_2\{f_1(x')f_1(x'')\}(x)$ is an even function of x,  so that $G_2^{(i)}\{f_1(x')f_1(x'')\}=0$ if $f_i(x)$ is an odd function. This means that $\delta c_i^0=O(\varepsilon ^3)$ for such values of i.

Equation (C13) is obtained for a fixed value of $\delta c_1(t)$ but it remains approximately valid if $\delta c_1(t)$ is a slowly varying function of time. In particular, it is valid if $\delta c_1(t)$ saturates to a constant.

With $\delta c_i(t)$ for $i>1$ expressed as functions of $\delta c_1(t)$, the evolution equation (5) for the concentration field (C10) reduces to a closed equation for $\delta c_1(t)$ and $x_c(t)$. The linear analysis of this equation is shown in Sect. 4. The quadratic terms are absent for symmetry reasons. Indeed, substituting (C10) in (5) yields two potential contributions of order $O(\varepsilon ^2)$: First, the advection of the solution produces the term $\dot{x}_c(t)\varepsilon \delta c_1(t)\partial _xf_1(x-x_c(t))$ in the left hand side of Eq. (5). This term, as a derivative of an anti-symmetric function, is a symmetric function and thus does not have a $f_1(x-x_c(t))$ component. The second potential contribution comes from the right hand side of Eq. (5), where the term $\varepsilon ^2 {\mathcal {G}}_2\{f_1(x'),f_1(x'')\}(x-x_c(t))\delta c_1(t)^2$ is also symmetric. Consequently, the terms of order $O(\varepsilon ^3)$ are the next order after the linear terms. There are so many different terms at this order that listing them in general case would not be practical but it is easy to show that each of them can be reduced to terms proportional to $\varepsilon ^3\delta c_1(t)^3$. This yields the Eq. (28).