Abstract
The structure of scientific collaborations has been the object of intense study both for its importance for innovation and scientific advancement, and as a model system for social group coordination and formation thanks to the availability of authorship data. Over the last years, complex networks approach to this problem have yielded important insights and shaped our understanding of scientific communities. In this paper we propose to complement the picture provided by network tools with that coming from using simplicial descriptions of publications and the corresponding topological methods. We show that it is natural to extend the concept of triadic closure to simplicial complexes and show the presence of strong simplicial closure. Focusing on the differences between scientific fields, we find that, while categories are characterized by different collaboration size distributions, the distributions of how many collaborations to which an author is able to participate is conserved across fields pointing to underlying attentional and temporal constraints. We then show that homological cycles, that can intuitively be thought as hole in the network fabric, are an important part of the underlying community linking structure.
Similar content being viewed by others
1 Introduction
Since early on in the study of complex networks, the structure of scientific collaborations has been the object of intense interest [1–5], because of the potential societal and scientific impacts that understanding progress and innovation could have [6–8], the theoretical interest in the detection of overlapping groups or communities [9–13] and the accessibility and richness of publication data [14, 15]. Existing approaches have however predominantly put their focus on network-based descriptions that translate the original publication data in structures that are fully characterized by links between pairs of authors [16–18]. Others have instead proposed models for the growth of team size [19] or for prediction of their success [20] which rely on group dynamics that were essentially mean-field models.
However, the units of collaboration are usually shared scientific publications, which describe group micro-interactions and often involve small groups of authors rather than just two [19]. Hence, it would be beneficial to develop a language that encodes explicitly higher-order connectivity patterns and can distinguish them from sums of low order interactions. When adopting a network perspective, this information is not completely lost naturally, because it is in some measure hidden in the clique structure of the resulting network and can therefore be accessed to some degree via clique percolation techniques [21, 22], as for example in the case of social groups and proteins [9]. Looking at the k-clique structure is however not sufficient to characterize the mesoscopic shape of academic collaborations, as described by how the clique- and community-structure of the networks link and wrap on themselves. To avoid this, we need to take a topological perspective, which allows to extract, in a principled way, a notion of shape for a dataset. That is, we adopt a new description framed in the language of topological data analysis [23, 24], which has at its core the notion of multi-agent interactions: simplicial complexes [25]. It is mesoscopic because it relies on the coordination of a large number of collaborations and does not rely on local properties or global distributions. It goes beyond k-clique descriptions because it allows to distinguish between sums of pairwise interactions, and genuine higher-order ones. It also grants access to the homology of a dataset, that encodes a notion of multi-dimensional shape of a system [23, 26].
The aim of this paper is to introduce a higher-order language for the study of co-authorship data and illustrate the type of novel information it provides. In the following, after introducing the dataset, we describe in simple terms the notions required for the topological description of the collaboration data. We then look at the properties of arXiv data in terms of their higher-order elements, maximal simplices called facets. We show that different patterns of collaboration exist across the various scientific communities within arXiv at the individual and group level, in terms of distribution of collaboration sizes and in terms of how sparse locally collaborations grow into denser, larger co-authorship groups. We then focus on the linking patterns among network communities, finding them to be well correlated with the hole structure of an associated topological object, highlighting an unexpected separation between the local and long range collaboration scales. Our results suggest thus that different mechanisms might be at play that structure the high-order connectivity features of scientific collaborations.
2 Dataset description
The dataset we analyze here has been scraped in raw xml format (see the IOA help of arXiv.org for details). The data span 9 years, from 2007 to 2016, and are split according to the 18 major categories of arXiv. This major categories correspond to different thematic areas and thus can be used as rough representative of different scientific fields. Due to arXiv’s history, there is a bias toward mathematical and physical topics, although the categories also cover computer science and quantitative finance. The full list of categories is reported in Table 1, where we also report the size in terms of number of papers and authors per category. For each published paper, we know the complete list of authors and in which category and sub-category it is classified.
Note that the number of authors and papers can change by various orders of magnitude across categories, e.g. the smallest category by far is quantitative finance (q-fin), while the category with the largest number of authors is astrophysics (astro-ph) and the one with most papers is condensed matter (cond-mat). Because of structural properties of simplicial complexes, we only retain papers that have author sets that are not fully contained in the author sets of other papers. These are akin to maximal cliques and are called facets of a simplicial complex. We explain these concepts in detail in the next section (Section 3.1).
In Table 1 we report the percentage of retained papers (facets), showing how the use of this approach impacts the study of the different categories. For hep-ex and nucl-ex the percentage of papers in each category that are also facets of the relative simplicial complex is higher than for other categories. For the former the percentage is above 94% (95.19%, 94.30% respectively) while for the latter, i.e. the more theoretical aspects of these disciplines (high energy physics lattice, phenomenology and theory - hep-lat, hep-ph, hep-th-, and nuclear physics theory - nucl-th -), the values drop to a range between 81% and 78%, suggesting that in these categories the same group of authors tends to publish more than one paper together.
For this work, we consider as the same individual authors with same surname and same first initial [3]. As previously stated, we consider the papers whose author set is not contained in any other. Therefore, in order to assess the impact of the author name ambiguity on our results, we performed large random sub-samplings of the author set in each category, and found there were no relevant statistical changes in the paper size distribution and mesoscopic features of the resulting simplicial complex. We then also checked for changes under removal of the most connected authors and found non-significant changes to the dataset properties. Moreover, for computational reasons (see Section 3.2.1 for details) we removed up to 0.0001% of the authors with most publications in hep-ex, physics, cs, nucl-ex, hep-ph.
3 Methods
3.1 A simplicial language: complexes and networks
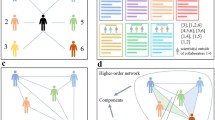
Networks have proven themselves an extremely powerful language to describe the patterns of interactions that characterize complex systems [3]. They allow to make predictions about the structure and evolution of such systems [27], and to even control them in some cases [28]. There is however an implicit assumption made when using network descriptions: that the system’s structure can be fully described by combinations of pairwise interactions. This assumption is justified when studying certain types of processes, as for example in the case of epidemic models where the probability of a node becoming infected is determined by which of its neighbors are themselves infected. Other types of complex contagions too can be faithfully represented on networks [27]. There are however certain systems (and datasets) that come naturally in a richer format and that could benefit from a higher-order description than the network one. Data about co-authorship of scientific papers is one of these: each paper is a multi-node interaction and the number of authors per paper naturally varies greatly. Formally, we say that each paper is a simplex and is defined by its set of authors (or vertices in general settings). A paper with k authors is then a \((k-1)\)-simplex, where the \(k-1\) comes from the fact that we also allow single author papers which are then mapped to a single point, a zero-dimensional simplex. A set of simplices constitutes a simplicial complex in a similar way to how a set of edges constitutes a network. There is a caveat: a simplicial complex K is valid only if, for each k-simplex \(\sigma= [p_{0}, \ldots, p_{k-1}] \in K\), all sub-simplices \(\sigma' \subset\sigma\) are in K too. This is a formal requirement in our case and we fulfill it by considering the maximal simplices, usually called facets, of the simplicial complex, these correspond to the set of papers whose author set is not contained in any other paper’s author set. Considering facets (and implicitly all their subsets) is sufficient to have a complete description of a simplicial complex.
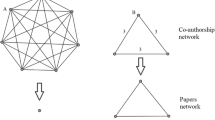
To gain an intuitive understanding of the differences between a network and a simplicial representation of the same data, consider the following toy example. Let us imagine that we are given seven papers with the following list of author sets:
as shown in Figure 1. Consider first the papers \([a,b]\), \([b,h]\), \([a,h]\). These three papers from a network point of view create a triangle. However, also the paper \([a,b,h]\) would be described as the corresponding triangle in a co-authorship network. Adopting a simplicial language instead, we have immediately access to a richer interactions codebook from which to choose: the three papers \([a,b]\), \([b,h]\), \([a,h]\) are mapped in a set of three 1-simplices (as defined by their author set), while the paper \([e,f,g]\) is a 2-simplex is defined by its three authors and represented as a filled triangle. Already in such a simple example, we see that simplices and simplicial complexes are able to capture richer and more varied layouts as compared with networks.
Simplicial complexes vs networks. The figure shows the advantages of the simplicial compared to a network approach. A co-authorship dataset can be encoded both as a network, and as a simplicial complex (a). It easy to see how the simplicial complex approach are able to capture a richer layouts compared with networks. In fact the three papers [a,b], [a,h], [b,h] are mapped in an empty triangle in the simplicial complex, while the single paper [e,f,g] is represented as a filled triangle. This difference is crucial in the detection of holes in the simplicial complex. In both cases depicted in (b) the cycle [1, 2, 3, 4, 5, 6] is cordless in the network representation, but only in the bottom case it corresponds to meaningful information, and can be considered a homological cycle.
Note that, while cliques are closely related to the concept of simplices, the latter retain a deeper descriptive power. Indeed, it is easy to see that, when comparing a simplicial and a network description of the same data, each \((k-1)\)-simplex in the simplicial complex will be associated with a k-clique on the same vertices in the network. However, the converse is not true: not every k-clique in the network corresponds to a \((k-1)\)-simplex in the complex, just like the three edges in Figure 1 do not correspond to the filled triangle. This is a direct example of how high-order information cannot always be reconstructed from lower-order interactions.
3.2 Simplicial measures
Simplicial complexes provide access to a larger set of local and mesoscopic observables. At the local level, we focus on two main features of the simplicial complexes: the distribution \(P(s)\) of sizes s of facets (maximal simplices); and the distribution \(P(d)\) of simplicial degree d of authors, defined as the number of facets that an author belongs to.
We can also ask new questions: for example, we can study a simplicial version of structural holes [29]. Where at the network level one looks for how many of the existing wedges are closed by a third edge, hence probing the local clustering structure, at the simplicial level we can ask how many of the set of three edges (1-simplices) that are arranged in a triangle are covered by a full triangle (2-simplex). The two possibilities are shown in Figure 1(a), where we see that the authors e, f, g collaborated together on one paper, while the authors a, b, h published in pairs, but never all of them together. Therefore measuring the number of filled triangles over the total number of possible triangles measures how much collaborations are integrated in a given field. Note also that this distinction could not have been made using the network projection (shown too in Figure 1).
Configurations like the empty triangle just described, and more general pattern of disconnectivity, are captured by the homology of a simplicial complex. Homology can be thought intuitively as the study of the holes in all dimensions of a certain dataset, and then implicitly of its shape. It provides a representation of the dataset complementary to that obtained by looking only at the dense regions (communities), and which is impossible to obtain from k-clique decompositions or other standard network methods [30, 31]. To compute homology means to detect and identify the empty spaces that are bounded by k-simplices. At low dimensions the results can be easily interpreted as connected components and holes in the simplicial complex, but higher-order cavities can be of more difficult interpretation.
We are going to focus on the study of 1-dimensional homological cycles, i.e. two-dimensional holes bounded by edges, of the co-authorship simplicial complex. Homology is not only limited to small cycles (like triangles), but can probe larger holes which span significant parts of a simplicial complex. These features give a unique prospective, since they represent the cycles in the network (cordless closed paths) which cannot be reduced to a point when collapsing all the 2-simplices (triangles) in the simplex. This fundamental property is depicted in Figure 1. The two complexes in Figure 1(b) are composed by the same facets (the six full triangles). They have however a different shape (or technically, one-dimensional homology): the top one is essentially a large disk and can be contracted to a point, while the bottom one is akin to a ring, since the simplices bound an empty cycle. Note also that the cycle [0,1,2,3,4,5] is cordless in both cases, but only in the bottom case it cannot be contracted and hence it corresponds to meaningful information. In this sense, it provides mesoscopic information and we will use it to study the shape of the co-authorship simplicial complexes at different scales.
In particular, we will calculate explicitly all the cycles that bound one-dimensional holes. Using this information, we then calculate first the fraction of empty triangles over all the possible closed paths of length three. This gives us a higher-order notion of structural cohesiveness, inspired by that of structural holes, but informed by homological information. We dub this measure simplicial closure for short. We then consider all the 1-dimensional homological cycles and analyze their trajectories through the simplicial complex. As by definition homological cycles bound holes, we study how they link dense parts of the complex together. In order to do this, we detect communities (using InfoMap [32]) on the simplicial complex and study how cycles link different communities with each other.
Note also that we ignore the quantity of papers published by the same group of authors, acknowledging only their collaboration as a simplex in the simplicial complex. Naturally, repeated collaborations - similarly to collaboration networks - can be encoded by assigning weights to simplices. In this case one would need to employ a parameterized version of homology, called persistent homology, which allows to deal with weighted simplices, as for example was done in [31]. However, we found that in our dataset adding weights did not yield significant additional information and thus restricted ourselves to an unweighted representation.
3.2.1 Simplicial contraction and complexity reduction
The rich information encoded in simplicial complexes comes at the expense of an increased computational cost. Although storing a simplicial complex as a list of facets is extremely parsimonious, the calculation of homology requires to list all the possible subsets. Therefore, even though the algorithm is polynomial, it can be very impractical when working with large simplices. This is due to the fact that each \((s-1)\)-facet gives rise to \(2^{s}\) simplices and thus the complexity of the computation of homology scales exponentially with the dimension of the simplicial complex \(O(m^{3})>O([2^{\delta}]^{3})\), where m is the number of simplices in the simplicial complex, and δ is its dimension. This prevents us from directly computing the homology of systems where large simplices are present - as is the case of the whole arXiv dataset. It is however possible to solve this exponential escalation in complexity and memory usage by studying an appropriately reduced but similar simplicial complex: we take inspiration here from the tidy set [33] and the simplicial strong collapse [34] to build a new simplicial complex, which contains fewer simplices but has the same homology groups. Each facet of the original simplicial complex K is represented by a node in a new one \(\chi(K)\), and \(k+1\) nodes in \(\chi(K)\) span a k-simplex if the corresponding facets have at least one node (author) in common. The simplicial complex created this way is homologically equivalent to the original one due to the nerve theorem [25]. In fact, the complex \(\chi(K)\) is what in mathematics is defined as the nerve of an open covering - in this case, the simplicial complex K bestowed with the Alexandrov topology [25]. We illustrate the transformation with a toy example in Figure 2.
Reduction of simplicial complex size. The figure shows an example of simplicial complex (a) and its correspondent dual complex (b). Each facet of the original simplicial complex is represented by a node in the dual complex, and \(k+1\) nodes span a k-simplex if the corresponding \(k+1\) facets have at least a node in common. In both simplicial complexes, the facets are colored according to their dimension. It is easy to see that applying the complexity reduction to the simplicial complex (a) reduces the total number of simplices from 91 to 28, while fixing the homology (both complexes have one connected component, and one hole (1-dimensional cycle).
The correspondence \(\chi: K\to\chi(K)\) described above however does not guarantee automatically that \(\chi(K)\) will have fewer simplices as compared with the original one. Indeed, it is possible to build simple examples showing a decided increase of the number of simplices after the transformation, e.g. consider a simplicial complex composed by many simplices all attached by a single node, which when transformed will yield a new simplicial complex with a simplex of dimension the original node’s simplicial degree. More generally, if \(\max d \gg\delta= \max s\), that is the maximum simplicial degree is much larger than the dimension of K, which is the maximum facet size in the original complex, then \(\chi(K)\) will very likely have a larger number of simplices with respect to K and it is therefore not computationally advantageous to analyse the former. This is because each \((s-1)\)-facet gives rise to \(2^{s}\) simplices and thus the number of simplices \(n(K)\) of a simplicial complex K with facet size sequence \(\{k\}\) is bounded by \(\sum_{\{s\}} 2^{s}\), which for large s is dominated by \(2^{\max s}\). Under the transformation χ each node in K becomes a \((d-1)\)-simplex in \(\chi(K)\), hence a first heuristic to perform χ is that \(\max s \gg\max d\).
This criterion relies on the fact that the presence of large tails in the facet size distribution will create a very large number of simplices if one does not transform to \(\chi(K)\). In Figure 3 we give evidence for this by generating random simplicial complexes with facet size taken from a three different distributions: exponential (\(p(x) \sim e^{-x/\nu}\)), Zipf’s (\(p(x) \sim x^{-\gamma}\)) and Poisson (\(p(x) \sim\lambda^{x} e^{-x}/x!\)). In all cases, we find a reduction of a few orders of magnitude of n going from K to \(\chi(K)\). As expected, we also find the largest reduction \(n(K)/n(\chi(K))\) happening when the facet size distribution \(f(K)\) is characterized by longer tails (respectively lower γ for Zipf, larger λ for Poisson and smaller ν for exponential), as the tails represent large facets in K that are mapped to a single point in \(\chi(K)\).
Performance of reduction of simplicial complex size. The panels show the total simplex number (solid lines) and the upper bound (dashed lines) for simplicial complexes built with facet size sequence sampled from the exponential (left), Zipf distribution (middle) and Poisson (right). On the x-axis we plot (from left to right) the power law exponent γ, the average value λ and the exponent ν. It is easy to see that in all cases and for a range of parameters there is a large reduction in simplex number going from K to \(\chi(K)\). Moreover, the bounds on \(n(K)\) and \(n(\chi(K))\), although not tight, reflects closely that between \(n(K)\) and \(n(\chi (K))\) and can therefore be used as a good proxy to decide whether applying the simplicial reduction χ is appropriate or not.
3.3 Information-theoretic comparison of size distributions
In order to assess whether two categories share common statistical properties - for example of their facets or degrees - we need a robust measure of the distance between distributions. Here we adopt the Jensen-Shannon Divergence [35] (JSD) that for two distributions P and Q is defined as: \(\operatorname{JSD}(P,Q) = \frac{1}{2} D_{\mathrm{KL}}(P|M) + \frac{1}{2} D_{\mathrm{KL}}(Q|M)\), where \(M = P + Q\) and \(D_{\mathrm{KL}}(P|Q) = - \sum_{x} P(x) \log\frac{P(x)}{Q(x)} \) is the Kullback-Leibler divergence. It is easy to see how this measure is symmetric and alway positive. Moreover, it is bound in \((0, \ln 2)\).
In our case, we will need to compare distributions defined on very different supports, e.g. the facet size distributions of math and hep-ex. Moreover, we want to compare the different functional dependencies of the distributions we are testing, rather than how different their supports are. So for all the JSD results, we first map both distributions from their original supports to the support \((0,1)\) in the natural way and then calculate the JSD between the two distributions.
4 Results
4.1 Summary statistics
Table 2 gives a summary of some of the characteristics of the categories of the arXiv data set and in Figures 4 and 5 we show respectively the facet size and simplicial degree distributions for all categories. Excluding the two experimental physics categories hep-ex, nucl-ex, we find that the average number of authors on a paper for the entire arXiv dataset is \(\langle s\rangle = 4.5\) with a standard deviation of \(\sigma _{s} = 11.8\), which is consistent with the values of \(\langle s\rangle\) obtained by restricting to individual categories. We also remark that the standard deviations and medians of s are smaller for the mathematical disciplines, highlighting the known patterns of small collaborations in mathematics [36].
Comparison of simplicial degree distributions. We show the simplicial degree distributions (top) and their Jensen-Shannon divergence (bottom right) for all categories, ordered by maxd value. As opposed to the facet distributions, we find two main groups of categories, which we highlight with different colors (bottom left).
Unsurprisingly, the two outliers, hep-ex and nucl-ex, have very large \(\langle s\rangle\) and \(\sigma_{s}\), likely due to large-scale experiments (e.g. the The STAR Experiment in Brookhaven National Laboratory, or the ATLAS experiment in CERN). They however display different median s values, 4 for hep-ex and 9 for nucl-ex suggesting that most of the collaborations are smaller in experimental high energy physics than in nuclear physics.
The average number of disjoint collaborations an author belongs to, described by the author’s simplicial degree, is \(\langle d\rangle = 2.52 \), with standard deviation \(\sigma_{d} = 6.46\), and is consistent across all categories, with the exception of hep-ex. Moreover, we also find coefficient of variation across categories for \(c_{v}(\langle d\rangle) = 0.54\) is much smaller than for \(\langle s\rangle\) and the number of papers and authors (\(c_{v}(\langle s\rangle) = 1.59\), \(c_{v}(\text{\# papers}) = 1.05\), \(c_{v}(\text{\# authors}) = 1.03\)). We also find that, while most papers are written by small groups of authors (median s around 3-4 for most categories), a large number of authors belongs to a single collaboration (median \(d = 1\) for all categories).
4.2 Facet and simplicial degree distributions
Going one step further, we focus on the facet size distribution \(P(s)\) (Figure 4) and the simplicial degree distribution \(P(d)\) of the nodes (Figure 5). Similar to many other social systems [9], the two distributions for s and d for all categories span a few order of magnitudes and all display broad tails, signaling the presence of both large collaborations and of authors with a large number of different collaborations. In order to quantify the similarities among categories in terms of their facet and degree profiles we calculated the Jensen-Shannon divergence (JSD) [35] between all pairs of distributions as described in the Methods section. If we order the categories by increasing maxs, three groups can be clearly identified (Figure 4(bottom right)), highlighting that the three different \(P(s)\) profiles correspond to categories characterized by progressively larger s support. In particular, the group characterized by small maxs contains the more mathematical categories (hep-th, q-fin, math-ph, stat), while the one characterized by large maxs contains the experimental and high-energy physics categories (hep-ph, physics, gr-qc, nucl-ex, astro-ph, hep-ex). In Figure 4(bottom left) we plot for each group the envelop of the distributions of the corresponding categories. In Figure 5 we report the results of the same analysis for the simplicial degree distributions. In this case in Figure 5(bottom right) we ordered the categories by increasing maxd, highlighting the presence of two category subgroups, a small one containing q-fin, stat, math-ph, q-bio, the second one containing the others. We also observe that the JSD values between the facet size distributions (Figure 4(bottom right)) are consistently larger (of about an order of magnitude) than those between the simplicial degree distributions (Figure 5(bottom right)), implying that the simplicial degree distributions are much closer to each other than the facet size ones.
4.3 Simplicial closure, large-scale structure and homological cycles
We are interested in probing both the local and the large scale structure - or shape, in short - of co-authorship data. In general, this has been done by finding communities or dense subgraphs which are generally thought to represent specific disciplines or subfields. However, this approach does not provide information about how such communities relate to each other. To investigate these relationships, for all categories we computed the homology of the associated simplicial complexes, that is we found all the (homological) cycles, as described in Figure 1. In Table 3 we report the results for the number of one-dimensional cycles in each complex.
We focus first on the shortest possible cycles, triangles. We find that the fraction of cycles of length 3 that are not covered by a full triangle (2-simplex) is very small for all categories, ranging between 10−7 for nucl-ex and ∼10−2 for math. In other words, adapting the term from the network literature [29], we can say that we find evidence of a very strong simplicial closure: in the great majority of cases whenever three authors have collaborated in pairs, they also have collaborated on a paper together.
One might expect this to be related to the number of cycles, \(\beta_{1}\), present in the simplicial complex, with a larger abundance of cycles implying a smaller triadic closure. However, we find no significant correlation between the ratio of open triangles to closed triangles and the total number of cycles (\(p>0.05\) for Spearman correlation). Interestingly, we find instead a negative (Spearman) significant correlation (\(p=0.02\)) between the number of open triangles and the ratio \(\beta_{1}/n\) of overall number of cycles \(\beta_{1}\) and the number of facets n of the category’s simplicial complex.
We move our attention now to all homological cycles, not only the short ones. In Figure 6 we report the distribution of cycle lengths for all categories, shown in order of growing values of \(\beta _{1}/n\). The JSD matrix shows again a clean 2-block structure once it is ordered by growing order of \(\beta_{1}/n\), with a group formed by the large categories (hep-ex, hep-ph, gr-qc, nucl-ex), with a narrower distribution of cycle lengths, and a second with all the other categories displaying cycle length distributions with broader tails. We observe that the categories in the first group also display generally strong simplicial closure.
Cumulative distributions of cycle length. We show the cycle length distributions (top) and their Jensen-Shannon divergence (bottom right) for all categories, ordered by \(\beta_{1}/n\) value. We find two main groups of categories, which we highlight with different colors (bottom left). We groups categories in the subplots by growing values of \(\beta_{1}/n\) (top, from left to right) and note that as the cycle sparsity increases, the maximum cycle length decreases.
Finally, we study how homological cycles explore the complex’s structure. We do this by first detecting communities on the simplicial complex and then quantifying how many communities a cycle traverses as a function of its length. However, for gr-qc, hep-ex, hep-ph, nucl-ex, nucl-th, physics, q-bio we need to perform the simplicial reduction (described in Section 3.2.1) to calculate the homology. Therefore, we detected the communities also on the transformed simplicial complexes. In Figure 7 we show the community size distributions for all categories in the green box, and for the transformed categories in the red box. We found that overall the community size distributions are very similar across all categories (average JSD across all pairs 0.05). Also, for the categories that underwent the simplicial reduction, we find a very small distance between the distributions before and after the reduction (blue diagonal of matrix in Figure 7). Additionally, we find a small accentuation of the distances between community size distributions for categories. This can be seen by comparing the symmetric elements in the green and red shaded regions of the matrix of Figure 7. Despite this the most distributions are still very close after the transformation.
Distribution of community sizes. In the green box, we plot the community size distributions obtained from the underlying graph of the original simplicial complex. In the red box, we plot the community size distributions for the categories for which we performed the simplicial reduction. The central matrix shows: the JSD between the community size distributions of the original categories (green cells, upper triangular matrix), the JSD between the community size distributions for the transformed complexes (red cells, lower triangular matrix), and the JSD between the size community size distributions of the categories before and after the reduction. In all cases we find that the differences between the various distributions are small (JSD is defined in \((0, \log2)\)).
Since cycle bound regions of disconnectivity, we expect them to behave as bridges between communities and to go through a large number of them. If cycles were not associated with the bridging of communities, we would expect them to run through and around communities randomly and hence the number of communities a cycle goes through should be proportional to the fraction of total edges between communities multiplied by the cycle length. We can therefore use this as a lower bound to assess whether cycles are actually bridging between communities or not. In Figure 8 we plot the diagonal as the upper bound on the number of communities a cycle can cross (a cycle cannot traverse more communities that the number of its nodes) and the expected number of communities a cycle of given length should traverse (black dashed line) as a proxy for whether cycles tend to bridge between communities or not. We find indeed that in all case the number of communities traversed by each cycle is much larger than random expectation, confirming their role as important features linking together different regions of the collaboration simplex.
Cycles and community counts. Color intensity represents the number of cycles of length ℓ linking n communities. Red dashed lines represent the upper bound on the number of traversed communities, while black dashed lines the random expectation. We provide also a linear fit to the data (black solid lines, with confidence intervals) showing that cycles are strongly associated with community bridging.
5 Discussion
In this paper we studied the topological structure of the collaboration data in different scientific communities, constructed from data from arXiv. In particular, we looked at the properties of arXiv categories in terms of their higher-order elements through topological data analysis methods. This approach allows us to identify the set of different collaborations that authors belonged to over the timespan covered by our dataset (2007-2016). We found that, while categories, thought as a proxy for the corresponding scientific community, are characterized by different collaboration size distributions, the distributions of how many collaborations an author belongs to appears to be much more similar (as displayed by smaller JSD distances between \(P(d)\) than between \(P(s)\)). Moreover, we also found that, despite different organizational and cultural differences across categories, the individual capacity to participate in collaborations is similar - as displayed by the low values of average and median d for all categories -, while collaboration sizes themselves tend to be more varied.
We also identified three groups of categories on the basis of their different functional forms for \(P(s)\). Although the JSD differences are obtained in a way as to make them independent from the size of the category or of its maxs, we find that indeed the maximum s of a category predicts well the blocks observed in Figure 4. This is also reminding of the observations made in [20, 37] about the performance of teams of small, medium and large size. In our dataset, we do not have measures of performance, hence we cannot make a direct link between a category’s structural properties and its success. However, we do see the group’s \(P(s)\) change functional form, becoming broader and broader, as we move from group s1 to group s3 (Figure 4), highlighting different organizational structures likely due to the different topics (e.g. group s1 is mainly theoretical work, s3 is mainly experimental work).
In fact, these results suggest that authors in experimental categories tend to collaborate in more large and not fully overlapping groups. Again, thinking about the dynamics of large experiments, this is reasonable since they acquire new authors and lose others over time leading to different facets, whereas the lower number of papers that are also facets in the most theoretical aspects of the same disciplines implies a slower turnover of members in time, and smaller repeated collaborations within larger groups.
We also introduced a simplicial analog of the triadic closure, simplicial closure, which could not be defined using networks or cliques alone. We found a very strong closure in all categories, which implies that - with high probability - a triple of authors that collaborated in pairs will also collaborate as a group. This cohesiveness indicates the presence of a higher-order clustering: instead of creating a link to the friend of my friend, what we are seeing here is that the three of us become a group of three. Note also that this observation is possible because we are adopting a simplicial description. Interestingly, this type of structural cohesiveness is consistent with what one would expect in models of local growth by copying previously reported for co-authorship and social networks [38, 39]. However, the patterns of local cohesiveness did not correlate with the number of authors or the size of collaborations. Interestingly, we also found that the local cycle structure does not correlate with the large-scale (homological) cycle structure, encoded in the cycle length distributions and in \(\beta_{1}/n\). For example, the group of categories characterized by narrower cycle length distribution (blue distribution in Figure 6) have very different simplicial closure values. These observations are consistent with local growth mechanisms that are responsible for the local dense patterns but cannot justify the large scale cycles that, instead, we find link together communities across the whole complex, acting as a scaffold [40] supporting the dense communities, again highlighting a difference between the (quasi)-local structure and the large-scale structure, possibly organized along funding and academic leadership lines [7, 41].
An interesting direction for future work is to build minimal models reproducing these multiscale properties, both the order of interactions and the range of scales form local to mesoscales. Indeed, collaboration models built on networks cannot reproduce this by construction, because they lack higher order interactions and because homology has been shown to be poorly captured by network models [42]. A possibility would be to adapt to this case recent simplicial growth models [43–46] which have been shown to create rich local and non-local homological structure. Indeed, the difference we observed between the individual (d) and the collaboration (s) levels suggests the presence of attentional and temporal limit on the individual collaboration capacity (e.g. in- and out-groups [19]) and of infrastructural or organizational constraints [47], which would likely benefit from a simplicial modeling. This would also open the door to generalizations of our observations to the case of weighted simplices, which could be achieved with a persistent homology approach [23], and to the inclusion of temporal features of the network, which again could find a likely phrased within the framework of zigzag homology [48].
References
Clarke BL (1964) Multiple authorship trends in scientific papers. Science 143(3608):822-824
Clarke BL (1967) Communication patterns of biomedical scientists. I. Multiple authorship and sponsorship of federal program volunteer papers. Fed Proc 26:1288-1292
Newman ME (2001) The structure of scientific collaboration networks. Proc Natl Acad Sci USA 98(2):404-409
Girvan M, Newman ME (2002) Community structure in social and biological networks. Proc Natl Acad Sci USA 99(12):7821-7826
Palla G, Barabási A-L, Vicsek T (2007) Quantifying social group evolution. Nature 446(7136):664-667
Börner K, Contractor N, Falk-Krzesinski HJ, Fiore SM, Hall KL, Keyton J, Spring B, Stokols D, Trochim W, Uzzi B (2010) A multi-level systems perspective for the science of team science. Sci Transl Med 2(49):49cm24
Glänzel W, Schubert A (2004) Analysing scientific networks through co-authorship. In: Handbook of quantitative science and technology research. Springer, Berlin, pp 257-276
Bettencourt LM, Kaur J (2011) Evolution and structure of sustainability science. Proc Natl Acad Sci USA 108(49):19540-19545
Palla G, Derényi I, Farkas I, Vicsek T (2005) Uncovering the overlapping community structure of complex networks in nature and society. Nature 435(7043):814-818
Ruan J, Zhang W (2008) Identifying network communities with a high resolution. Phys Rev E 77(1):016104
Sales-Pardo M, Guimera R, Moreira AA, Amaral LAN (2007) Extracting the hierarchical organization of complex systems. Proc Natl Acad Sci USA 104(39):15224-15229
Coccia M, Wang L (2016) Evolution and convergence of the patterns of international scientific collaboration. Proc Natl Acad Sci USA 113(8):2057-2061
Lancichinetti A, Fortunato S, Kertész J (2009) Detecting the overlapping and hierarchical community structure in complex networks. New J Phys 11(3):033015
Guimera R, Uzzi B, Spiro J, Amaral LAN (2005) Team assembly mechanisms determine collaboration network structure and team performance. Science 308(5722):697-702
Castellano C, Fortunato S, Loreto V (2009) Statistical physics of social dynamics. Rev Mod Phys 81(2):591
Börner K, Dall’Asta L, Ke W, Vespignani A (2005) Studying the emerging global brain: analyzing and visualizing the impact of co-authorship teams. Complexity 10(4):57-67
Wagner CS, Leydesdorff L (2005) Network structure, self-organization, and the growth of international collaboration in science. Res Policy 34(10):1608-1618
Pan RK, Saramäki J (2012) The strength of strong ties in scientific collaboration networks. Europhys Lett 97(1):18007
Milojević S (2014) Principles of scientific research team formation and evolution. Proc Natl Acad Sci USA 111(11):3984-3989
Kenna R, Berche B (2012) Managing research quality: critical mass and optimal academic research group size. IMA J Manag Math 23(2):195-207
Derényi I, Palla G, Vicsek T (2005) Clique percolation in random networks. Phys Rev Lett 94(16):160202
Ding Z, Zhang X, Sun D, Luo B (2016) Overlapping community detection based on network decomposition. Sci Rep 6:24115
Weinberger S (2011) What is…persistent homology? Not Am Math Soc 58(1):36-39
Patania A, Vaccarino F, Petri G (2017) Topological analysis of data. EPJ Data Sci 6(1):7
Hatcher A (2002) Algebraic topology. Cambridge University Press, Cambridge
Vejdemo-Johansson M, Skraba P (2016) Topology, big data and optimization. In: Big data optimization: recent developments and challenges. Springer, Berlin, pp 147-176
Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A (2015) Epidemic processes in complex networks. Rev Mod Phys 87(3):925
Liu Y-Y, Barabási A-L (2016) Control principles of complex systems. Rev Mod Phys 88(3):035006
Burt RS (2009) Structural holes: the social structure of competition. Harvard University Press, Cambridge
Ghrist R (2008) Barcodes: the persistent topology of data. Bull Am Math Soc 45(1):61-75. doi:10.1090/S0273-0979-07-01191-3
Carstens C, Horadam K (2013) Persistent homology of collaboration networks. Math Probl Eng 2013:815035
Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc Natl Acad Sci USA 105(4):1118-1123
Zomorodian A (2010) The tidy set: a minimal simplicial set for computing homology of clique complexes. In: Proceedings of the twenty-sixth annual symposium on computational geometry. ACM, New York, pp 257-266
Wilkerson AC, Moore TJ, Swami A, Krim H (2013) Simplifying the homology of networks via strong collapses. In: 2013 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, pp 5258-5262
Lin J (1991) Divergence measures based on the Shannon entropy. IEEE Trans Inf Theory 37(1):145-151
Newman ME (2004) Coauthorship networks and patterns of scientific collaboration. Proc Natl Acad Sci USA 101(Suppl 1):5200-5205
Kenna R, Berche B (2011) Critical mass and the dependency of research quality on group size. Scientometrics 86(2):527-540
Krapivsky PL, Redner S (2005) Network growth by copying. Phys Rev E 71(3):036118
Szulanski G, Jensen RJ (2008) Growing through copying: the negative consequences of innovation on franchise network growth. Res Policy 37(10):1732-1741
Petri G, Expert P, Turkheimer F, Carhart-Harris R, Nutt D, Hellyer PJ, Vaccarino F (2014) Homological scaffolds of brain functional networks. J R Soc Interface 11(101):20140873. doi:10.1098/rsif.2014.0873
Carayol N, Matt M (2006) Individual and collective determinants of academic scientists’ productivity. Inf Econ Policy 18(1):55-72
Petri G, Scolamiero M, Donato I, Vaccarino F (2013) Topological strata of weighted complex networks. PLoS ONE 8(6):66506. doi:10.1371/journal.pone.0066506
Bianconi G, Rahmede C, Wu Z (2015) Complex quantum network geometries: evolution and phase transitions. Phys Rev E 92(2):022815
Courtney OT, Bianconi G (2017) Weighted growing simplicial complexes. arXiv:1703.01187
Young J-G, Petri G, Vaccarino F, Patania A (2017) Construction of and efficient sampling from the simplicial configuration model. arXiv:1705.10298
Wu Z, Menichetti G, Rahmede C, Bianconi G (2015) Emergent complex network geometry. Sci Rep 5:10073
Ponds R (2009) The limits to internationalization of scientific research collaboration. J Technol Transf 34(1):76-94
Carlsson G, De Silva V, Morozov D (2009) Zigzag persistent homology and real-valued functions. In: Proceedings of the twenty-fifth annual symposium on computational geometry. ACM, New York, pp 247-256
Acknowledgements
We thank the anonymous reviewers for their constructive comments and J.-G. Young for collecting and sharing the arXiv dataset for this study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Funding
GP and AP acknowledge the support of the ADnD project by Compagnia San Paolo. FV acknowledge the support of the Laboratorio Lagrange project by Fondazione CRT.
Availability of data and materials
Due to the size, the raw dataset used is freely available upon request from the corresponding author.
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AP, FV and GP conceived and designed the study, performed the analysis and wrote the manuscript. All authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Patania, A., Petri, G. & Vaccarino, F. The shape of collaborations. EPJ Data Sci. 6, 18 (2017). https://doi.org/10.1140/epjds/s13688-017-0114-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjds/s13688-017-0114-8