1 Introduction

Collisions between ions and atoms have been studied quite extensively due to their importance in fusion and astrophysical research [1, 2]. Theoretical studies on ion-molecule collisions, however, have been quite scarce because of complications it presents in comparison to modelling ion-atom collisions. For example, despite being the simplest diatomic molecule, collision processes involving H\(_2\) prove to be very challenging to model due to the two-center structure of the target. Furthermore, using an accurate structure of the molecule when solving the scattering equations would require a considerably greater amount of computational resources compared to atomic targets. However, recent developments in the field of hadron therapy [3] have created a demand for cross sections of processes occurring in collisions of a variety of ions with numerous molecules. Modelling collisions between ions and H\(_2\) is the first step towards building a database of cross section data for collisions of ions with more complex biologically-relevant molecules.

Current hadron therapy centres generally use beams of protons or carbon ions, however, it has been shown that helium ions can be more effective against certain types tumors [4]. To aid such research, we calculate the non-dissociative electron capture and ionisation cross sections in collisions between He\(^{2+}\) ions and H\(_2\) molecules over the intermediate energy range where they are the dominant electronic energy-loss mechanisms.

Experimental measurements of the cross section for electron capture in He\(^{2+}+\)H\(_2\) collisions were first made by Allison [5] at energies from 40–100 keV/u. They measured the total cross sections for both single- and double-electron capture and found that the cross section for single-electron capture was at least an order of magnitude greater than that for double-electron capture at all the energies they considered. Later, Pivovar et al. [6] measured the total electron-capture cross section (TECS) over the 50–225 keV/u energy range. Baragiola and Nemirovsky [7], Shah and Gilbody [8], and Bayfield and Khayrallah [9] measured the single- and double-electron capture cross section at low projectile energies. Furthermore, Shah and Gilbody [8] also measured the cross sections for single-electron capture into the 2s state of the outgoing He\(^+\) projectile. More measurements were made by Hvelplund et al. [10] and Olson et al. [11], with Hvelplund et al. [10] at high and intermediate energies, respectively. Shah and Gilbody [12] extended the energy range of their earlier data for the total and state-selective 2s electron-capture cross sections to 2–115 keV/u. Nutt et al. [13], Itoh et al. [14] and Hvelplund and Andersen [15] made more measurements for the total cross section with the measurements by Nutt et al. [13] being made at very low energies whilst Itoh et al. [14] and Andersen [15] extended the available experimental data to higher energies. Ciric et al. [16] measured the cross sections for Lyman and Balmer emission from the He\(^+\) ion produced in He\(^{2+}+\)H\(_2\) collisions. In this work, they also presented measurements of the partial cross sections for electron capture into the 2p, 3p and 4p states of the outgoing He\(^+\) projectile. Rudd et al. [17] measured the total electron-capture cross section over the 10–300 keV/u energy range. This was followed by measurements of the partial 4l cross sections for electron capture by Frieling et al. [18]. Hoekstra et al. [19] also measured the partial 2p, 3p and 4p cross sections for electron capture over the 2–25 keV/u energy range. The latest set of results available are the high-energy measurements by Sant’Anna et al. [20] of the total single-electron-capture cross section.

Fewer measurements are available for the total ionisation cross section (TICS). Puckett et al. [21] made measurements at intermediate and high energies, followed by measurements by Rudd et al. [17] over the 10–300 keV/u energy range. Shah and Gilbody [22] and Shah et al. [23] measured the dissociative and non-dissociative total ionisation cross sections separately, demonstrating that non-dissociative ionisation was significantly more likely over most of the energy range. They collectively made measurements over the wide 10–600 keV/u energy range.

Various theoretical methods have also been applied to model He\(^{2+}+\)H\(_2\) collisions, although, majority of them only make calculations for the total electron capture cross section. The earliest of these are the atomic-orbital close-coupling (AOCC) calculations by Shingal and Lin [24] and Fritsch [25]. Both approaches operate within a one-electron model, but attempt to account for the two-centre nature of the H\(_2\) molecule. Shingal and Lin [24] have made calculations for the TECS over the 10–500 keV/u impact energy range. On the other hand, Fritsch [25] have calculated the TECS and the state-resolved cross section for electron capture into the 2s state of the He\(^+\) ions over the 1–100 keV/u impact energy range. Molecular-orbital close-coupling (MOCC) calculations were made by Saha et al. [26] and Errea et al. [27]. Khoma et al. [28] used an asymptotic semiclassical coupled-channel (ASCC) approach within the framework of the nonperturbative Landau-Herring method. Errea et al. [27] and Khoma et al. [28] calculated the total dissociative and non-dissociative single-electron capture cross sections. Errea et al. [27] also presented results for the partial cross sections for capture into the 2s and 2p states of the outgoing He\(^+\) projectile. It should be noted that, at projectile energies above 3 keV/u, Errea et al. [27] used a basis of one-electron diatomic molecule (OEDM) orbitals and applied the independent particle model (IPM) to calculate their cross sections. They label these the IPM-OEDM calculations. Saha et al. [26] calculated the partial cross section for electron capture into the 2p state of the outgoing He\(^+\) projectile over the 0.3–3 keV/u energy range.

The classical-trajectory Monte Carlo (CTMC) method has also been applied to He\(^{2+}+\)H\(_2\) collisions by Meng et al. [29, 30], Illescas and Riera [31] and Ghavaminia et al. [32]. Meng et al. [29] used a two-electron three-centre approach to calculate the TICS over the 20–1000 keV/u projectile energy range. They also extended the method to calculate state-selective cross sections for electron capture into states \(n\le 6\) and \(l\le 2\) over the 30–200 keV/u energy range, where n and l are the final-state principal and orbital angular momentum quantum numbers, respectively. They found reasonable agreement with the experiments for the ionisation and electron-capture cross sections. Illescas and Riera [31] calculated the electron capture and non-dissociative ionisation cross sections in He\(^{2+}+\)H\(_2\) collisions. They find good agreement with the experiments for the TICS, however, their results appear to overestimate the TECS at low energies. Ghavaminia et al. [32] also calculated the electron capture cross section. Above 10 keV/u, their results are in good agreement with the CTMC calculations by Meng et al. [30]. However, their cross section continues to increase as the projectile energy decreases, and hence, significantly overestimates the experiments at projectile energies below 10 keV/u.

A number of perturbative approaches have also been applied to calculate the TECS in He\(^{2+}+\)H\(_2\) collisions. Busnengo et al. [33] applied the continuum distorted wave (CDW), continuum distorted wave-eikonal initial state (CDW-EIS) and continuum distorted wave-eikonal final state (CDW-EFS) approaches to calculate the total electron capture cross section from 20 to 1000 keV/u. At energies below 100 keV/u, their CDW-EIS calculations are in good agreement with the theory, whilst the CDW and CDW-EFS calculations are significantly larger. At higher energies, all of the CDW calculations converge together, but underestimate the experimental data. Halder et al. [34] also applied a variation of the CDW approximation, the first-order molecular target continuum distorted wave (MTCDW) approximation, to calculate the total electron capture cross section for this collision system. They find reasonable agreement with the experimental data at energies below 60 keV/u, but their results underestimate the experiments at higher energies. A different perturbative approach applied to the He\(^{2+}+\)H\(_2\) collision system is the boundary-corrected first-order Born (B1B) approximation by Ghanbari-Adivi [35]. They calculated the total electron capture cross section over the 0.1–1 MeV/u energy range. However, their results significantly overestimate the experimental data.

The two-centre wave-packet convergent close-coupling (WP-CCC) method has previously been applied to model electron capture and ionisation processes occurring in collisions between multiply charged ions and various atomic targets. Earlier works include, but are not limited to, collisions of ions with ground-state hydrogen atoms [36,37,38,39], collisions between ions and hydrogen atoms in an excited state [40, 41] and ions incident on helium atoms [42,43,44,45]. The WP-CCC method has also been extended to model collisions with molecular targets and has been applied to calculate integrated and differential cross sections for all one-electron non-dissociative processes occurring in p\(+\)H\(_2\) collisions [46, 47]. In this work, we apply the WP-CCC method to calculate integrated cross sections for non-dissociative electron capture and ionisation in He\(^{2+}+\)H\(_2\) collisions, including state-resolved electron capture cross sections. Atomic units are used throughout unless stated otherwise.

2 Formalism

The details of the WP-CCC method have been given in [36, 38, 48] and extended to molecular targets in [46]. Here we provide a brief overview of the theory.

Using a model-potential method, we reduce the collisions of bare ions with molecular hydrogen to a three-body Coulomb scattering problem. In the energy range considered in this work, single-electron processes dominate and experimental data are averaged over all molecular orientations. Therefore, the effective one-electron spherically symmetric model provides a suitable description of the target. The scattering system then is governed by the three-body Schrödinger equation, \(H\varPsi _i^+=E\varPsi _i^+\), where H is the full Hamiltonian of the three-body system and E is the total energy. The total scattering wave function, subject to the outgoing wave boundary conditions, is denoted as \(\varPsi _i^+\), where the subscript i refers to the initial channel which the wave developed from.

The two-centre expansion of the total scattering wave function assumes a solution of the following form

$$\begin{aligned} \varPsi _i^+\approx&\sum _{\alpha =1}^N F_\alpha (t,\varvec{b})\psi _\alpha (\varvec{r}_\text {T})e^{i\varvec{q}_\alpha \cdot \varvec{\rho }} \nonumber \\&\quad +\sum _{\beta =1}^M G_\beta (t,\varvec{b})\psi _\beta (\varvec{r}_\text {P})e^{i\varvec{q}_\beta \cdot \varvec{\sigma }}, \end{aligned}$$
(1)

where \(\psi _\alpha \) and \(\psi _\beta \) are the target and projectile pseudostates, N and M are the sizes of the target and projectile bases, \(F_\alpha \) and \(G_\beta \) are the time-dependent expansion coefficients, \(\varvec{r}_\text {T}\) and \(\varvec{r}_\text {P}\) are the positions of the electron relative to the target and projectile nuclei, respectively, and \(\varvec{b}\) is the impact parameter. Vector \(\varvec{q}_\alpha \) is the momentum of the projectile relative to the target, where the active electron is in quantum state \(\alpha \) of the target. Similarly, \(\varvec{q}_\beta \) is the momentum of the outgoing He\(^{+}\) ion (formed through electron capture) relative to the residual target ion, where \(\beta \) denotes a certain quantum state in the rearrangement channel. Jacobi variable \(\varvec{\rho }\) is the position of the projectile relative to the target’s centre of mass and \(\varvec{\sigma }\) is the position of the outgoing atom’s centre of mass relative to the target nucleus.

The full three-body Hamiltonian can be expressed as

$$\begin{aligned} H=H_0+V. \end{aligned}$$
(2)

The free Hamiltonian can be written as

$$\begin{aligned} H_0 = -\frac{1}{2\mu _\text {T}} \nabla ^2_{\varvec{\rho }}- \frac{1}{2}\nabla ^2_{\varvec{r}_\text {T}} = -\frac{1}{2\mu _\text {P}} \nabla ^2_{\varvec{\sigma }} - \frac{1}{2}\nabla ^2_{\varvec{r}_\text {P}}, \end{aligned}$$
(3)

where \(\mu _\text {T}\) is the reduced mass of the projectile-target system and \(\mu _\text {P}\) is the reduced mass of the He\(^+\) + H\(_2^+\) system. The total interaction potential is written as

$$\begin{aligned} V = Z_{\text {P}} V_{\text {mod}}(R) - V_{\text {mod}}(r_\text {T}) - \frac{Z_{\text {P}}}{r_\text {P}}, \end{aligned}$$
(4)

where \(Z_{\text {P}}\) is the charge of the projectile and R is the distance between the projectile and the target. For \(V_{\text {mod}}\) we use the effective one-electron model proposed by Vanne and Saenz [49]. In the effective one-electron treatment of H\(_2\), the field of the residual target ion is collectively represented using the model effective potential. Parameters of the potential are chosen to ensure the ionisation energy of the target corresponds to the ionisation energy of H\(_2\) at the equilibrium internuclear distance. For a more detailed discussion of the target description see [50].

We use a semiclassical approximation where the incoming projectile is assumed to follow a straight line trajectory. Accordingly, we set \(\varvec{R}=\varvec{b}+\varvec{v}t\), where \(\varvec{R}\) is the position of the projectile relative to the target nucleus and \(\varvec{v}\) is the velocity of the projectile, with \(\varvec{v}\cdot \varvec{b}=0\). Using the two-centre expansion and the semiclassical approximation, the Schrödinger equation yields the following set of coupled first-order differential equations

$$\begin{aligned} {\left\{ \begin{array}{ll} i{\dot{F}}_{\alpha '} + i\mathop \sum \limits _{\beta =1}^M {\dot{G}}_\beta {\widetilde{K}}_{\alpha '\beta } = \mathop \sum \limits _{\alpha =1}^N F_\alpha D_{\alpha '\alpha } + \mathop \sum \limits _{\beta =1}^M G_\beta {\widetilde{Q}}_{\alpha '\beta }, \\ i\mathop \sum \limits _{\alpha =1}^N {\dot{F}}_\alpha K_{\beta '\alpha } + i{\dot{G}}_{\beta '} = \mathop \sum \limits _{\alpha =1}^N F_\alpha Q_{\beta '\alpha } + \mathop \sum \limits _{\beta =1}^M G_\beta {\widetilde{D}}_{\beta '\beta }, \\ \alpha '=1,2,...,N, \ \ \beta '=1,2,...,M, \end{array}\right. } \end{aligned}$$
(5)

where \({\dot{F}}_\alpha \) and \({\dot{G}}_\beta \) are time derivatives of \(F_\alpha \) and \(G_\beta \), respectively. Moreover, \({\widetilde{K}}_{\alpha '\beta }\) and \(K_{\beta '\alpha }\) are the overlap integrals, \(D_{\alpha '\alpha }\) and \({\widetilde{D}}_{\beta '\beta }\) are the direct-scattering matrix elements and the electron-transfer matrix elements are given by \({\widetilde{Q}}_{\alpha '\beta }\) and \(Q_{\beta '\alpha }\). Further details are given in [38].

The expansion coefficients are subject to the following initial boundary condition

$$\begin{aligned}{} & {} F_\alpha (-\infty ,\varvec{b})=\delta _{\alpha i}, \ \ \alpha =1,2,...,N, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} G_\beta (-\infty ,\varvec{b})=0, \ \ \beta =1,2,...,M. \end{aligned}$$
(7)

The probability of a specific transition is given by the magnitude squared of the expansion coefficient in the limit as time goes to infinity. The cross section for the transition is then obtained by integrating the weighted probability over all the impact parameters. From this, the TECS can be calculated by summing the individual partial cross sections for capture into bound states of the projectile (i.e. if the energy of the projectile state is negative). Similarly, the TICS is given by the sum of the partial cross sections for excitation into positive-energy pseudostates of both the target and projectile.

3 Results

3.1 Details of calculations

To ensure the accuracy of the results presented, we established convergence in the cross sections with respect to the size of target and projectile bases. The basis depends on the parameters \(n_\text {max}\) and \(l_\text {max}\), which are the maximum principle quantum number and the maximum angular momentum quantum number, respectively, of the bound states. The basis also contains positive-energy pseudostates that represent the continuua of the target and the ion formed by the projectile. Details of the wave-packet approach to discretising the continuum are given in our earlier works (e.g. see Ref. [46]). In this work, we used a symmetric basis, in which the same number of states are included on the projectile and target centres.

For projectile energies below 25 keV/u, \(n_\text {max}=10\) and \(l_\text {max}=4\) was found to be sufficient for the results to converge. At these energies, the continuum was discretised by using 15 bins and the ejected-electron energy was cut off at a large enough value, \(\varepsilon _\text {max}\), where its contribution towards the total ionisation cross sections is negligible. At the 1 keV/u projectile energy, we set \(\varepsilon _\text {max}=30\) eV and increased it to \(\varepsilon _\text {max}=600\) eV at 25 keV/u. At the projectile energies between 25 keV/u and 1 MeV/u, the values of \(n_\text {max}\) and \(l_\text {max}\) required for convergence remained unchanged, but the number of bins was increased to 20. Additionally, \(\varepsilon _\text {max}\) also had to be increased with the projectile energy, up to 1700 eV at 1 MeV/u. At energies above 1 MeV/u, we found that \(n_\text {max}\) and \(l_\text {max}\) could be reduced to 9 and 3, respectively, whilst the number of bins had to be increased to 35 to ensure that the ionisation cross section had converged sufficiently. At 2 MeV/u, which is the highest projectile energy considered in this work, \(\varepsilon _\text {max}\) had to be increased to 2300 eV. In the calculations, the z component of the projectile’s position is varied discretely, with \(n_z\) points adaptively distributed between \(-z_\text {max}\) and \(+z_\text {max}\). In this work, \(z_\text {max}=300\) a.u. and \(n_z=1000\) was found to be sufficient to get converged results at all the projectile energies considered. The probabilities were calculated on an impact-parameter grid ranging from 0 to 22 a.u. containing 32 points. Using these parameters, the integrated cross sections presented here have converged to within \(1\%\) over the entire 1–2000 keV/u energy range.

3.2 Total cross sections

Fig. 1
figure 1

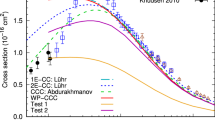
The total cross section for non-dissociative electron capture in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. Included are the present WP-CCC calculations, AOCC calculations by Shingal and Lin[24] and Fritsch [25], CTMC calculations by Meng et al. [30], Illescas and Riera [31] and Ghavaminia et al. [32], CDW-EIS calculations by Busnengo et al. [33], MOCC calculations by Errea et al. [27], ASCC calculations by Khoma et al. [28], B1B calculations by Ghanbari-Adivi [35] and MTCDW calculations by Halder et al. [34]. Experimental measurements are by Allison [5], Pivovar et al. [6], Baragiola and Nemirovsky [7], Shah and Gilbody [8, 12], Bayfield and Khayrallah [9], Hvelplund et al. [10], Hvelplund and Andersen [15], Olson et al. [11], Nutt et al. [13], Itoh et al. [14], Rudd et al. [17], and Sant’Anna et al. [20]

Full size image

Fig. 1 presents the total non-dissociative electron-capture cross section in He\(^{2+}+\)H\(_2\) collisions. The results are shown by points connected by straight lines to guide the eye. In general, our results agree with the experimental data quite well in the entire energy range, although, they seem to lie above the experimental measurements at energies greater than 5 keV/u. The difference between our results and the experiments is largest at the 20 keV/u projectile energy, which is where the cross section peaks. At projectile energies greater than 100 keV/u, our results are in good agreement with the measurements by Hvelplund et al. [10], Hvelplund and Andersen [15] and Sant’Anna et al. [20]. However, at these energies we still appear to overestimate the measurements by Pivovar et al. [6]. Despite the disagreement at the intermediate energies, the shape of the WP-CCC results is still similar to that of the experimental measurements. At projectile energies below 3 keV/u, our cross section is smaller than the measurements by Shah et al. [51] and Nutt et al. [13]. The AOCC calculations by Fritsch [25] overestimate the experimental measurements at projectile energies between 5 and 200 keV/u. At energies above 200 keV/u, their calculations are in reasonable agreement with the experiments. The same is true for the CTMC calculations by Meng et al. [30], although they are only available at energies above 300 keV/u. The MOCC calculations by Errea et al. [27] underestimate the experimental measurements at low energies. Their IPM-OEDM calculations appear to be in better agreement with the experiments over the 5–10 keV/u energy range. However, their cross section peaks at a lower energy than the experiemental measurements suggest. The CDW-EIS calculations by Busnengo et al. [33] appear to be much smaller than the experimental measurements over the entire energy range where they are present. The ASCC calculations by Khoma et al. [28] also underestimate all the experimental measurements at low energies. The B1B calculations by Ghanbari-Adivi [35], on the other hand, significantly overestimate both the WP-CCC results and the experimental data from 0.1–1 MeV/u. However, the B1B appear to be converging towards our results at high energies. As a first-order perturbative approach, the B1B calculations are expected to be sufficiently accurate at high energies. The MTCDW calculations are in good agreement with the experimental measurements by Pivovar et al. [6]. However, as stated earlier, the measurements by Pivovar et al. [6] are in disagreement with the other experimental measurements present at high energies.

In Fig. 2 we present the total non-dissociative ionisation cross section for He\(^{2+}+\)H\(_2\) collisions. At energies above 100 keV/u, the WP-CCC results are in good agreement with the measurements by Puckett et al. [21] and Rudd et al. [17]. On the other hand, below 100 keV/u, our results appear to underestimate both experiments. However, the measurements by Puckett et al. [21] and Rudd et al. [17] are for the total single-ionisation cross section, which is the sum of the dissociative and non-dissociative single-ionisation cross sections. Hence our results are expected to be smaller than their measurements. In fact, Shah and Gilbody [22] and Shah et al. [23] made measurements for the dissociative and non-dissociative single-ionisation cross sections separately and these measurements have also been plotted in Fig. 2. Their data suggest that dissociative ionisation dominates over non-dissociative ionisation at projectile energies below 30 keV/u, whereas at energies above 30 keV/u, non-dissociative ionisation dominates with dissociative ionisation eventually becoming negligible in comparison. Thus, the WP-CCC results should underestimate the measurements by Puckett et al. [21] and Rudd et al. [17] at low energies, but then overlap at the higher energies. This is indeed what we observe in Fig. 2. Despite this, it is also evident that the WP-CCC results appear to overestimate the measurements by Shah and Gilbody [22] and Shah et al. [23] at projectile energies between 50 and 200 keV/u. The reason for this is unclear thus far, but we do note that similar behaviour was also observed in other collision systems studied with the WP-CCC method [39, 52]. Thus, it is possible that this discrepancy is unrelated to our model-potential treatment of the molecular hydrogen target.

The only other calculations of the TICS available are the CTMC results by Meng et al. [29] and Illescas and Riera [31]. The former include both dissociative and non-dissociative ionisation, while the latter only consider non-dissociative ionisation. The results by Meng et al. [29] show a similar level of agreement with experiment as the present WP-CCC calculations. However, above 200 keV/u the CTMC calculations underestimate the experimental data and WP-CCC results. The CTMC calculations by Illescas and Riera [31] are only available for a few incident energies. Near the peak of the TICS they agree more closely with the experimental data of Shah and Gilbody [22] than the other experiments and theoretical results. However, at high energies the calculations by Illescas and Riera [31] underestimate experiment, instead agreeing with the CTMC results by Meng et al. [29].

Fig. 2
figure 2

The total cross section for non-dissociative ionisation in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. The present WP-CCC calculations are compared with the CTMC calculations by Meng et al. [29] for the total ionisation cross section and the CTMC results by Illescas and Riera [31] for the total non-dissociative ionisation cross section. The experimental data are the measurements by Puckett et al. [21] and Rudd et al. [17] for the total ionisation cross section and the measurements by Shah and Gilbody [22] and Shah et al. [23] for the non-dissociative and total ionisation cross sections

Full size image

3.3 State-selective electron capture

We have also calculated the nl-resolved cross sections for non-dissociative electron capture into states with \(n\le 4\) in He\(^{2+}+\)H\(_2\) collisions which are plotted in Figs. 3, 4, 5 and 6 for each n considered. In general, fewer calculations and experimental data are available for these cross sections in comparison to the total electron-capture cross section. The only theoretical results available are the CTMC calculations by Meng et al. [30], the MOCC calculations by Saha et al. [26] and Errea et al. [27] and the AOCC calculations by Fritsch [25]. However, Fritsch [25], Saha et al. [26] and Errea et al. [27] have only made calculations for the 2l electron-capture cross sections. Additionally, the CTMC calculations by Meng et al. [30] are only available over a narrow energy range of 30–200 keV/u. The experimental data available for these cross sections are the low-energy measurements by Ciric et al. [16] for electron capture into states with \(l=1\), the intermediate-energy measurements by Frieling et al. [18] for the 4l partial electron-capture cross sections, and the measurements by Shah and Gilbody [12] for electron capture into the 2s state.

Fig. 3
figure 3

The partial cross section for non-dissociative electron capture into the 1s state in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. The present WP-CCC calculations are compared with the CTMC calculations by Meng et al. [30]

Full size image
Fig. 4
figure 4

The partial cross sections for non-dissociative electron capture into 2l states in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. Included are the present WP-CCC calculations, AOCC calculations by Fritsch [25], CTMC calculations by Meng et al. [30] and MOCC calculations by Errea et al. [27] and Saha et al. [26]. Experimental measurements are by Shah and Gilbody [12], Ciric et al. [16] and Hoekstra et al. [19]

Full size image
Fig. 5
figure 5

The partial cross sections for non-dissociative electron capture into 3l states in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. Included are the present WP-CCC calculations and CTMC calculations by Meng et al. [30]. Experimental measurements are by Ciric et al. [16] and Hoekstra et al. [19]

Full size image

Fig. 3 presents the cross section for electron capture into the ground-state of the He\(^{+}\) ion in He\(^{2+}+\)H\(_2\) collisions. The WP-CCC results lie slightly above the CTMC calculations Meng et al. [30] over the entire energy range where their results are present, however, the difference between the two sets of results decreases at the higher energies. Fig. 4 presents the 2l partial electron-capture cross sections alongside the available theoretical calculations and experimental data. As was the case for electron capture into the ground-state, our cross section for capture into the 2s state is larger than the CTMC calculations by Meng et al. [30]. However, for this transition, the AOCC calculations by Fritsch [25] are also available and we find good agreement with their results over the wide energy range of 1–100 keV/u. We find reasonable agreement with the MOCC calculations by Errea et al. [27] at projectile energies below 10 keV/u. However, above 10 keV/u, their results become significantly smaller than ours and they even begin underestimating the CTMC calculations. Experimental data is also available for capture into this state and although the present results reproduce the shape of the experimental measurements by Shah and Gilbody [12], they consistently overestimate the magnitude of the experimental data. This difference is greatest near the peak of the cross section, much like what was observed in total electron capture cross section. This makes sense as we find capture into the \(n=2\) state to be the dominant state for capture by the projectile near the peak of the TECS. But it is also evident from Fig. 4 that capture into the 2p state is more likely than capture into the 2s state at these energies. Subsequently, we would expect the 2p cross section to also overestimate the experimental data in order to account for the discrepancy observed in the TECS. However, in the bottom panel of Fig. 4, we find good agreement with the experimental measurements by Ciric et al. [16] and Hoekstra et al. [19] near the peak of the cross section. More intermediate-energy measurements for electron capture into the 2p state are needed to be able to draw any definite conclusions. As it stands, it appears the discrepancy we observe between the WP-CCC results and the experimental measurements for the TECS is not due to the overestimation of the partial cross section for electron capture into the dominant channel. Instead, it appears to be due to a systematic overestimation of the other partial electron-capture cross sections. For the 2p cross section, our results are larger than the MOCC calculations by Saha et al. [26] and Errea et al. [27] at energies below 3 keV/u. We also do not observe any pronounced oscillations, unlike the MOCC calculations by Saha et al. [26]. Between 3 and 15 keV/u, our results are in good agreement with the MOCC calculations by Errea et al. [27]. However, within 15–25 keV/u, the WP-CCC calculations slightly overestimate the MOCC calculations and the measurements by Hoekstra et al. [19].

Fig. 6
figure 6

The partial cross sections for non-dissociative electron capture into 4l states in He\(^{2+}+\)H\(_2\) collisions as a function of the projectile energy. Included are the present WP-CCC calculations and CTMC calculations by Meng et al. [30]. Experimental measurements are by Frieling et al. [18], Ciric et al. [16] and Hoekstra et al. [19]

Full size image

Fig. 5 presents the 3l partial electron-capture cross sections alongside the CTMC calculations by Meng et al. [30] and the experimental measurements by Ciric et al. [16] and Hoekstra et al. [19]. For the 3s cross section, we observe the same behaviour as the 1s and 2s case, where near the peak of the cross section, our results are larger compared to the CTMC calculations by Meng et al. [30] but the two converge to each other at higher energies. We also observe oscillations in the cross section at the low energies, however, more theoretical calculations or experimental measurements at these energies would be required to check the accuracy of these structures. For the 3p and 3d cross sections, there are significant differences between the present results and the CTMC calculations [30]. This could be occurring because the magnitude of these cross sections are smaller than the cross sections for electron capture into the dominant channels. Thus, numerical inaccuracies present in the calculations can have a greater effect on these cross sections compared to the cross sections with a comparable magnitude to the cross sections for electron capture into the dominant states. Measurements by Ciric et al. [16] and Hoekstra et al. [19] are also available for the 3p cross section and the present calculations are in reasonable agreement with these data. There are no CTMC results available at these energies.

Fig. 6 presents the 4l partial electron-capture cross sections alongside the CTMC calculations by Meng et al. [30] and the experimental measurements by Frieling et al. [18], Ciric et al. [16] and Hoekstra et al. [19]. At energies below 4 keV/u, numerical inaccuracies led to unphysical behaviour. So, the 4l partial cross sections are presented over the 4–1000 keV/u energy range. Comparison with the CTMC calculations by Meng et al. [30] is largely the same as what was observed in the other partial electron-capture cross sections. For capture into the 4s state, the WP-CCC results are larger in magnitude but the results converge to each other at higher energies. For the 4p and 4d cross sections, the shape of the CTMC results differs from the present results and for the 4d cross section, the agreement appears to worsen at higher energies. For the 4s cross section, the experimental measurements of Frieling et al. [18] are in good agreement with the CTMC calculations of Meng et al. [30]. Although Frieling et al. [18] have measured the cross section for electron capture into the 4p state, the dispersion in their data makes it hard to define where their cross section peaks. Thus, it is difficult to determine which theoretical calculation is in better agreement with the experimental measurements at intermediate energies. However, we do get reasonable agreement with the measurements by Ciric et al. [16] and Hoekstra et al. [19] at the lower energies. For the 4d cross section, the present results demonstrate good agreement with the experimental measurements by Frieling et al. [18], whilst the CTMC results by Meng et al. [30] are much larger. This agreement suggests that our result for the 3d cross section is more accurate at these energies compared to the CTMC calculations as a similar behaviour is observed for that cross section. We also get reasonable agreement with the measurements reported in Ref. [18] for capture into the 4f state of the projectile, although, our result appears to be slightly smaller than the experimental data.

4 Conclusion

Collisions of bare helium ions with molecular hydrogen has been modelled over the projectile energy range from 1 keV/u to 2 MeV/u using the WP-CCC approach. Cross sections for non-dissociative electron capture and ionisation have been calculated by using a model potential, which represents the H\(_2\) molecule as an effective one-electron target. The nl-resolved non-dissociative electron capture cross sections have also been calculated for final states with principal quantum numbers up to \(n=4\). A sufficiently large basis has been used to ensure that all of the calculated integrated cross sections have converged to within 1%.

The present results for the total non-dissociative electron-capture cross section are larger than the experimental data at projectile energies near 20 keV/u, where the cross section peaks. However, at higher energies, the WP-CCC results are in good agreement with experiment. For the nl-resolved non-dissociative electron-capture cross sections, the WP-CCC results are overall in reasonable agreement with experiment and other theoretical calculations. The main discrepancy is present in the cross sections for capture into the 1s, 2s, 3s and 4s states of the outgoing He\(^+\) projectile. For these cross sections, our results consistently lie above the experimental measurements and the CTMC calculations by Meng et al. [30]. However, for capture into 4d, our calculations appear to be in better agreement with the measurements by Frieling et al. [18]. More experimental measurements and theoretical calculations are required in order to resolve this discrepancy. The present calculations of the total cross section for non-dissociative ionisation are in good agreement with the experimental data. Our results overestimate the experimental measurements by Shah and Gilbody [22] and Shah et al. [23] near the peak of the cross section, however, they are in agreement with the other sets of experiments at these energies. At high energies, the WP-CCC results are in better agreement with experiment than previous theories for the total electron-capture and ionisation cross sections. Thus, we conclude that, overall, the presented method gives a good description of the interconnected processes taking place in He\(^{2+}+\)H\(_2\) collisions. Additionally, this study also significantly extends the energy range of available calculations all within a single unified theory. Previous results are either available over narrow energy ranges or for select processes. In the future, we intend on calculating differential cross sections for all one-electron non-dissociative processes occurring in He\(^{2+}+\)H\(_2\) collisions.