1 Introduction

The simplest homonuclear diatomic molecule is two-electron molecular hydrogen. The multicentre nature of \({\hbox {H}_2}\) makes it difficult to accurately represent its structure, requiring complex theoretical descriptions and computationally demanding codes. However, as the most abundant molecule in nature and the simplest molecular target it represents a useful first step towards scattering on more complex targets. Molecular hydrogen has attracted significant attention with a number of recent works published analysing collisions with ions, see e.g. Ref. [1] and references therein. This is partly due to the emergence of hadron therapy for treatment of cancer and the consequential requirements [2, 3] for accurate scattering calculations of ion collisions with complex molecules.

Proton scattering on molecular hydrogen has been extensively investigated experimentally. Stier and Barnett [4] performed a comprehensive experiment to determine both total electron-loss and electron-capture cross sections in \(\mathrm {p}+{\hbox {H}_2}\) collisions at low incident energies. The measurements of the total electron-loss cross section by Hooper et al. [5] provided data for ionisation at high energies where the electron-capture contribution to total electron loss is negligible in comparison with ionisation. Electron capture was measured across a wide energy range by Barnett and Reynolds [6], McClure [7] and Toburen et al. [8]. No distinction was made between capture that left the residual molecular ion intact or in a dissociative state. However, measurements by Shah et al. [9] and Shah and Gilbody [10] of the separate dissociative and non-dissociative capture channels showed that the contribution from capture events leading to dissociation are approximately an order of magnitude smaller than non-dissociative capture processes. Additionally, Rudd et al. [11] made empirical calculations and estimated uncertainties by fitting an analytical formula to the range of available experimental data.

Total ionisation cross sections were measured by Toburen and Wilson [12] at high impact energies where dissociative ionisation is negligible. Edwards et al. [13] and Shah et al. [9] explicitly measured non-dissociative ionisation and showed that dissociative ionisation becomes negligible in comparison with non-dissociative ionisation at impact energies higher than 20 keV. Electron-capture cross sections into the 2s state were measured by Andreev et al. [14], Bayfield [15], Birely and McNeal [16], Hughes et al. [17], and Shah et al. [18], although only the apparatus of Andreev et al. [14], Shah et al. [18] were calibrated to give absolute cross sections. Capture into the 2p state was experimentally measured by Birely and McNeal [16] and Hughes et al. [19]. Hughes et al. [20] measured cross sections for 3s, 3p, and 3d capture, while Williams et al. [21] obtained data only for 3s and Dawson and Loyd [22] for 3p and 3d. Furthermore, the total ionisation cross section for antiproton collisions with molecular hydrogen was measured by Knudsen et al. [23], Hvelplund et al. [24], and Andersen et al. [25].

Thus far, the majority of theoretical works on ion collisions with molecular hydrogen is limited to negatively charged projectiles such as antiprotons [1, 26,27,28,29,30]. This removes the possibility of charge-exchange processes, significantly simplifying the collisional problem. Modelling scattering of positively charged projectiles brings additional challenges due to electron capture into bound and continuum states of the projectile having significant contributions to the total electron-loss cross section. Separating these processes from direct ionisation requires more elaborate theories such as two-centre expansion approaches. However, this greatly increases computational complexity [31]. An alternative approach that projects a bound state of the projectile atom onto the total scattering wave function has been recently developed to calculate electron capture using only a one-centre expansion [32]. This significantly simplifies the theory compared to a two-centre approach and provided very good agreement with both experiment and two-centre calculations for p+H collisions. This approach was used for multielectron atom targets and is currently being extended to molecular hydrogen.

The boundary-corrected first Born (B1B) approximation developed by Belkić et al. [33] was extended by Corchs et al. [34] to calculate capture cross sections into the ground state of the projectile in \(\hbox {p}+{\hbox {H}_2}\) collisions for collision energies from 100 to 1000 keV. This perturbative approach works well in the high-energy region, but its assumptions break down at lower incident energies.

Another type of perturbative methods is based on the continuum-distorted-wave (CDW) approach. The CDW approach was used to calculate single-electron capture cross sections to all bound projectile states in \(\hbox {p}+{\hbox {H}_2}\) collisions over a wide energy range from 20 keV to 10 MeV [35] and state-selective cross sections for capture into the 2s, 3s, 2p, 3p, and 3d orbitals of the projectile. While they generally show good agreement with experiment [15, 17, 19,20,21] at intermediate impact energies, the CDW approaches deviate from one another and some significantly overestimate the low-energy experimental data [36]. Single ionisation cross sections for proton collisions with molecular hydrogen were calculated using the continuum-distorted-wave eikonal-initial-state (CDW-EIS) model by Galassi et al. [37]. They used an eikonal representation of the initial channel to simplify the formalism. Although good agreement with the recommended data from Rudd et al. [11] and Rudd et al. [38] was obtained at high energies, they found it was necessary to modify the distortion potential to better reflect the multicentre nature of the target in order to obtain good agreement with experiment in the intermediate-energy region. As with the B1B approach, the approximations used in formulating the CDW theory are not valid at low projectile energies. In addition, the distorting potentials can be chosen in many ways somewhat arbitrarily, such that there is no way of knowing which CDW formalism provides the correct description of the scattering system.

Meng et al. [39] used the classical-trajectory Monte Carlo (CTMC) method to calculate single-ionisation and electron-capture cross sections. This method solves the classical Hamilton equations arising at each time-step of the projectile motion. In a later work, they used the same approach to calculate state-resolved cross sections for transfer into the 2s, 2p, 3s, and 3p states of the projectile [40]. Results from Illescas and Riera [41] using the CTMC method show good agreement with experimental ionisation and electron capture cross sections from Refs. [5, 9, 12] over an energy range from 9 to 225 keV. The CTMC approach of Meng et al. [39] was also applied by Schultz et al. [1] to calculate total electron-capture and ionisation cross sections from 1 keV to 25 MeV. After applying a Born correction and normalising to recommended data from Ref. [42], their results agree well with the experimental results reported in Refs. [6,7,8,9,10,11, 13]. However, this classical method fails to model quantum mechanical effects which could be a possible reason for discrepancies with experiment at low energies.

Accurate ionisation cross sections for antiproton scattering on molecular hydrogen were calculated by Abdurakhmanov et al. [28, 29] over a projectile energy range from 1 to 2000 keV. The method was used to calculate antiproton stopping power in \({\hbox {H}_2}\) [43, 44]. They used a full two-electron two-centre treatment of the target, constructing the electronic wavefunctions using a configuration-interaction expansion in terms of the product of two one-electron orbitals. While they obtained very good agreement with experiment, even at low energies where other theories deviate significantly, the treatment of the target structure significantly increased the complexity of the theory and computational implementation when compared to methods that use a spherically symmetric effective one-electron target description [27]. Lühr and Saenz [26] also used a close-coupling method to calculate ionisation cross sections for \(\bar{\hbox {p}}+{\hbox {H}_2}\) scattering. However, the same caveats apply whereby the two-electron non-spherical treatment of the hydrogen molecule complicates the theory. Furthermore, this complicates the generalisation of these sophisticated single-centre approaches to include the second centre required for allowing capture of one or both electrons from the target.

To study proton collisions with \({\hbox {H}_2}\), Kimura [45] used a close-coupling method with a two-state basis containing only the ground states of the target and projectile. They calculated the electron capture cross section within a modified molecular-orbital (MMO) semiclassical close-coupling formalism and provided results for proton scattering on molecular hydrogen from 1 to 20 keV. Shingal and Lin [46] calculated ground-state electron-capture cross sections for proton scattering on molecular hydrogen using a different implementation of the semiclassical close-coupling formalism. They first calculated the scattering amplitudes for protons colliding on atomic hydrogen using the so-called travelling atomic orbital-expansion (AO) method. Then, by constructing the molecular states as a linear combination of atomic orbitals (LCAO), they used a first-order perturbative method to obtain scattering amplitudes for the molecular hydrogen target in terms of the amplitudes for the atomic target. Their results overestimate the calculations by Kimura [45] for energies below 20 keV.

An alternative approach is to represent the target using a simple model potential that can be used to generate a ground-state with an ionisation energy matching that of the hydrogen molecule. Vanne and Saenz [47] proposed such a treatment for a theoretical analysis of the behaviour of molecular hydrogen when exposed to ultra-short laser pulses. The potential they used represents the target as a spherically symmetric effective one-electron system, simplifying the theoretical requirements to a level of complexity similar to that required for hydrogen-like atomic targets. One-centre close-coupling calculations using this approach to the target structure showed good agreement with experiment for ionisation in collisions with antiprotons [27]. This technique was applied to positive projectiles to calculate total electron loss from 10 to 4000 keV and 2p excitation [48] (above 100 keV) cross sections for proton scattering on molecular hydrogen. Elizaga et al. [49] calculated electron-loss cross sections for proton scattering on \({\hbox {H}_2}\) using a model potential representation in a molecular orbital (MO) treatment based on the optimised dynamical pseudostates (ODP) method and eikonal classical trajectory Monte Carlo (CTMC) approach. Their results agree closely with those of Lühr et al. [48], except below 30 keV where the CTMC results underestimate both the experimental data [11] and the other calculations. However, the aforementioned methods cannot give any information on electron capture.

In this work, we use the semiclassical two-centre wave-packet convergent close-coupling (WP-CCC) approach [31, 50,51,52,53] together with the effective one-electron model potential description of molecular hydrogen originally proposed by Vanne and Saenz [47]. The WP-CCC formalism represents the motion of the projectile ion with a classical straight-line trajectory, while the electron dynamics is described fully quantum-mechanically. An advantage of this approach over other theories is the simultaneous inclusion of pseudostates (and hence inclusion of strong coupling effects between all channels) in both target and projectile-centred bases. It has previously been applied to calculate total and differential state-resolved cross sections for all processes taking place in proton and multicharged-ion scattering on atomic hydrogen [31, 54, 55] and multielectron targets [56,57,58]. Incorporating a spherically symmetric potential to represent the hydrogen molecule with a single active electron allows us to use the two-centre WP-CCC formalism to calculate cross sections for all one-electron processes in proton collisions with molecular hydrogen using already available computer code proven to be reliable.

To a certain degree, this work can be considered as an extension of the method developed by Lühr and Saenz [27] to explicitly include electron-capture channels. The treatment of the target resembles the recently developed effective one-electron method [58]. The method is based on generating a numerical pseudopotential to reduce a multielectron target to a single-electron one. It has been applied to proton-alkali [58] and proton-helium [57, 59] collisions and produced very good results for electron capture and ionisation. However, here we use the effective potential given in [47] in an analytic form.

Unless specified otherwise, atomic units are used throughout this manuscript.

2 Two-centre wave-packet convergent close-coupling method

The WP-CCC approach to proton-hydrogen collisions was developed in [50] and extended to include rearrangement processes in [31]. It has been applied to proton scattering on the two-electron helium target in [56]. In this section, we consider the molecular hydrogen target in a single-electron, spherically symmetric representation. The formalism is the same as for atomic targets; however, the form of the potential for the interaction of the active electron and projectile with the target core ion (i.e. H\(_2^+\)) is different. We refer the reader to Refs. [31, 54] for details of the WP-CCC approach to single-electron targets. Here, we give a summary of the method, focusing on the aspects that change when we consider the different functional form of the scattering potential.

2.1 Close-coupling formalism

Let us consider the WP-CCC approach to ion collisions with one-electron targets. We denote the total scattering wave function developing from initial state i by \(\mathrm {\Psi }^{+}_i\), the full three-body Hamiltonian of the collision system by H, and the total energy by E. The total scattering wave function satisfies the Schrödinger equation

$$\begin{aligned} (H-E) \mathrm{\Psi }^{+}_i = 0, \end{aligned}$$
(1)

subject to the outgoing-wave boundary conditions. In Jacobi coordinates, the projectile position relative to the centre of mass of the target system is given by \({{\varvec{\rho }}}\), and the position of the projectile–electron pair relative to the target nucleus is \({{\varvec{\sigma }}}\). The target nucleus is fixed at the origin, and the projectile moves along a classical straight-line trajectory parallel to the z-axis according to \({\varvec{R}} = {\varvec{b}} + {\varvec{v}}t\). The impact parameter, \({\varvec{b}}\), is defined such that \({\varvec{b}} \cdot {\varvec{v}}=0\). The position vector of the active electron with respect to the target nucleus is \({{\varvec{r}}}_{\mathrm{t}}\), and the position of the active electron relative to the projectile is \({{\varvec{r}}}_{\mathrm{p}}\). The total Hamiltonian is given by the sum of the free three-particle Hamiltonian for the projectile, active electron, and target nucleus, and the interaction between each of them,

$$\begin{aligned} H&=H_0+V. \end{aligned}$$
(2)

The free Hamiltonian can be expressed as

$$\begin{aligned} H_0=-\frac{1}{2\mu }\nabla _{{\varvec{\rho }}}^2-\frac{1}{2}\nabla _{{\varvec{r}}_{\mathrm{{t}}}}^2 \end{aligned}$$
(3)

and

$$\begin{aligned} H_0=-\frac{1}{2\mu }\nabla _{{\varvec{\sigma }}}^2-\frac{1}{2}\nabla _{{\varvec{r}}_{\mathrm{{p}}}}^2. \end{aligned}$$
(4)

Here, \(\mu \) is the reduced mass of the projectile–target system. The potential is given by the sum of interaction between the target ion and projectile nucleus, as well as the interaction between the active electron and both the target ion and projectile nucleus,

$$\begin{aligned} V=Z_{\mathrm{{p}}}V_{\mathrm{{mod}}}(R)-V_{\mathrm{{mod}}}(r_{\mathrm{{t}}})-\frac{Z_{\mathrm{{p}}}}{r_{\mathrm{{p}}}}. \end{aligned}$$
(5)

where the projectile charge is \(Z_{\mathrm{{p}}}=+1\) for a proton and \(-1\) for an antiproton. We define \(V_{\mathrm{{mod}}}\) using the following model potential [48]

$$\begin{aligned} V_{\mathrm{{mod}}}(r)=\frac{Z_{\mathrm{{t}}}}{r}(1+\exp [-\zeta r]). \end{aligned}$$
(6)

Here, \(Z_{\mathrm{{t}}}=+1\) for the hydrogen molecule target. This gives an effective single-electron representation of the hydrogen molecule, where the active electron is exposed to this spherically symmetric model potential that represents the combined effect of the other electron and the two protons. The parameter \(\zeta \) is set at 5.4824 to obtain a ground-state energy of \(-0.5976\) au. This corresponds to the difference in energy between the rovibronic ground states of \({\hbox {H}_2}\) and \({\hbox {H}^+_{2}}\) at the equilibrium internuclear distance for the \({\hbox {H}_2}\) molecule of 1.45 au. This effectively represents the hydrogen cation as a spherically symmetric system. In this model, there is no possibility of the residual ion existing in a rovibrationally excited state after the collision. Hence, this ground-state energy is analogous to the adiabatic ionisation energy of \({\hbox {H}_2}\), rather than the vertical ionisation energy.

We then use a two-centre expansion of the total scattering wave function in terms of target-centred (\(\psi _\alpha \)) and projectile-centred (\(\psi _\beta \)) pseudostates and a plane wave representing the relative motion of the other particle, to allow us to differentiate between direct ionisation, electron capture, and electron capture into the continuum of the projectile,

$$\begin{aligned} \Psi ^{+}_i&\approx \sum _{\alpha =1}^{N} F_{\alpha }(t,{{\varvec{b}}}) \psi _{\alpha }({{\varvec{r}}}_{\mathrm{t}}) e^{{i}{{\varvec{q}}}_{\alpha } \cdot {{\varvec{\rho }}}} \nonumber \\&\quad +\,\sum _{\beta =1}^{N} G_{\beta }(t,{{\varvec{b}}}) \psi _{\beta }({{\varvec{r}}}_{\mathrm{p}}) e^{{i}{{\varvec{q}}}_{\beta } \cdot {{\varvec{\sigma }}}} , \end{aligned}$$
(7)

where \(F_{\alpha }\) and \(G_{\beta }\) are unknown time-dependent expansion coefficients. The projectile has momentum relative to the target given by \({{\varvec{q}}}_\alpha \), and the relative motion between the projectile–atom and residual ion in the rearrangement channel has momentum \({{\varvec{q}}}_\beta \). The number of basis functions on each centre N is the combination of \(N_b\) negative-energy eigenstates and \(N_c\) positive-energy pseudostates so that in total there are \(2N=2N_b+2N_c\) target and projectile pseudostates. The size of the target and projectile bases is chosen to be sufficiently large that the cross sections of interest converge.

Writing the target pseudostates in terms of radial and angular parts as

$$\begin{aligned} \psi _{\alpha }\equiv \psi _{n\ell m}({\varvec{r}})=\phi _{n\ell }(r)Y_{\ell m}(\hat{{\varvec{r}}}), \end{aligned}$$
(8)

we can construct them by solving the radial Schrödinger equation with the model potential using an iterative Numerov approach. The positive-energy pseudostates are described by wave-packets formed from continuum waves. The continuum is divided into \(N_c\) non-overlapping subintervals from a minimum momentum \(\kappa _{\mathrm{{min}}}\) up to a maximum momentum, denoted \(\kappa _{\mathrm{{max}}}\). Integrating over the continuum wave from \(\kappa _{n-1}\) to \(\kappa _{n}\) in momentum space gives the radial wave function for the \(n^{\mathrm{th}}\) positive-energy pseudostate. Combined, the negative and positive-energy states are orthonormal to each other and diagonalise the target Hamiltonian, i.e.

$$\begin{aligned} \left\langle \psi _{\alpha '}\vert \psi _\alpha \right\rangle =\delta _{\alpha '\alpha }, \quad \langle \psi _{\alpha '}\vert H_\alpha \vert \psi _\alpha \rangle =\delta _{\alpha '\alpha }\varepsilon _\alpha , \end{aligned}$$
(9)

where \(\varepsilon _\alpha \) denotes the energy of the target state described by \(\psi _\alpha \). The bound-state energies are given by the eigenvalues of the Schrödinger equation describing the target.

The continuum functions used in constructing the positive-energy pseudostates converge to a plane wave with increasing distance from the nucleus. To prevent ill conditioning of the scattering equations, the pseudostates need to be known to a high level of precision. This in turn ensures that the matrix elements are sufficiently accurate. To ensure the radial grid extends far enough, we use a very large r-grid (up to 15,000 au) to generate the continuum waves used for construction of the target positive-energy pseudostates. Then, a smaller value of 300 au is selected when solving the scattering equations which is checked to ensure it is sufficiently large for the results to converge. Additionally, we set the minimum momentum of the lowest-energy wave-packet to 0.01 au to assist in accurately calculating the first pseudostate. Excluding the small section of the continuum below 0.01 au has a negligible impact on the calculated total cross sections.

The projectile basis is constructed using the eigenstates of the hydrogen atom and wave-packets representing negative and positive-energy states, respectively (see Ref. [31] for details). The wave packets are defined in terms of the Coulomb wave. Similarly to the target-centred basis, the projectile pseudostates are orthonormal and diagonalise the projectile–atom Hamiltonian, see Eq. (9). It should be noted that the target-centred basis and projectile-centred basis are not orthogonal to one another.

For both the target and projectile continuum pseudostates, the wave-packet energy is given by the midpoint of the momentum bin,

$$\begin{aligned} \varepsilon _n=\frac{\kappa _n^2+\kappa _n\kappa _{n-1}+\kappa _{n-1}^2}{6}, \end{aligned}$$
(10)

in energy space.

Substituting the expansion given in Eq. (7) into Eq. (1), we then formulate the scattering equations in the usual manner used in the WP-CCC approach to ion–atom collisions with single-electron targets as given in Ref. [31],

$$\begin{aligned} \left\{ \begin{aligned}&i {\dot{F}}_{\alpha ^\prime } + i\sum _{\beta =1}^{N} {\dot{G}}_\beta {\tilde{K}}_{\alpha ^\prime \beta } = \sum _{\alpha =1}^{N} F_\alpha D_{\alpha ^\prime \alpha } +\sum _{\beta =1}^{N} G_\beta \tilde{Q}_{\alpha ^\prime \beta },\\&i\sum _{\alpha =1}^{N} {\dot{F}}_\alpha K_{\beta ^\prime \alpha } +i {\dot{G}}_{\beta ^\prime } = \sum _{\alpha =1}^{N} F_\alpha Q_{\beta ^\prime \alpha } +\sum _{\beta =1}^{N} G_\beta \tilde{D}_{\beta ^\prime \beta },\\&\alpha ^\prime =1,2, \dots , N, \quad \beta ^\prime =1,2, \dots , N, \end{aligned}\right. \nonumber \\ \end{aligned}$$
(11)

and solve them for the time-dependent coefficients. Here the dots over \(F_\alpha \) and \(G_\beta \) denote time derivatives, \(D_{\alpha ' \alpha }\), \(K_{\beta ' \alpha }\), and \(Q_{\beta ' \alpha }\) are the direct-scattering matrix elements, overlap integrals, and exchange matrix elements, respectively. Tildes denote the corresponding quantities in the projectile centre. The difference here compared to the WP-CCC approach to p+H scattering is that the interaction potential with the target nucleus has a different form to the Coulomb potential for atomic hydrogen and the target pseudostates are constructed by solving the Schrödinger equation of the target with the model potential.

2.2 Solving the scattering equations

The direct-scattering matrix elements are given by the same expressions as in the WP-CCC approach to one-electron atomic targets,

$$\begin{aligned} D_{\alpha ' \alpha } ({{\varvec{R}}})=&\langle \psi _{\alpha '}| {\overline{V}}_{\alpha } |\psi _{\alpha }\rangle \exp [i (\varepsilon _{\alpha '}-\varepsilon _{\alpha })t] , \end{aligned}$$
(12)
$$\begin{aligned} {\tilde{D}}_{\beta ' \beta } ({{\varvec{R}}})=&\langle \psi _{\beta '}| {\overline{V}}_{\beta } |\psi _{\beta }\rangle \exp [i (\varepsilon _{\beta '}-\varepsilon _{\beta })t], \end{aligned}$$
(13)

but the interaction potentials, \({\overline{V}}_\alpha \) and \({\overline{V}}_\beta \), have the following modified forms:

$$\begin{aligned} {\overline{V}}_{\alpha }=Z_{\mathrm{{p}}}V_{\mathrm{{mod}}}(R)-\frac{Z_\mathrm{p}}{\left| {\varvec{r}}_{\mathrm{p}}\right| } \end{aligned}$$
(14)

and

$$\begin{aligned} {\overline{V}}_{\beta }=Z_{\mathrm{{p}}}V_{\mathrm{{mod}}}(R)-V_{\mathrm{{mod}}}(\left| {\varvec{r}}_{\mathrm{t}}\right| ). \end{aligned}$$
(15)

In \({\overline{V}}_{\alpha }\), the distance between the electron and the projectile is given by \({\varvec{r}}_{\mathrm{{p}}}={\varvec{r}}_{\mathrm{{t}}}-{\varvec{R}}\), and in \({\overline{V}}_{\beta }\) the distance between the electron and target nucleus expressed in the projectile coordinates is \({\varvec{r}}_{\mathrm{{t}}}={\varvec{R}}+{\varvec{r}}_{\mathrm{{p}}}\). Evaluation of the integrals in the matrix elements, \(V_{\alpha '\alpha }({\varvec{R}})\equiv \langle \psi _{\alpha '}\vert {\overline{V}}_\alpha \vert \psi _\alpha \rangle \) and \(V_{\beta '\beta }({\varvec{R}})\equiv \langle \psi _{\beta '}\vert {\overline{V}}_\beta \vert \psi _\beta \rangle \) is performed in spherical coordinates by separating the radial and angular momentum parts, allowing the latter to be analytically calculated, increasing their accuracy and decreasing the computational intensity.

First, consider the direct-scattering matrix elements in the \(\alpha \rightarrow \alpha '\) channel,

$$\begin{aligned} V_{\alpha '\alpha }({\varvec{R}})=\int d{\varvec{r}}_{\mathrm{{t}}}\psi _{\alpha '}^{*}({\varvec{r}}_{\mathrm{{t}}}){\overline{V}}_\alpha \psi _\alpha ({\varvec{r}}_{\mathrm{{t}}}). \end{aligned}$$
(16)

Equation (6) is substituted into the expression for the potential in Eq. (14) and the interaction between the projectile nucleus and active electron is expanded in partial waves. Thus, the potential operator, \({\overline{V}}_{\alpha }\), can be expressed in the following form,

$$\begin{aligned} {\overline{V}}_\alpha&=\frac{Z_{\mathrm{{p}}}}{R}+\frac{Z_{\mathrm{{p}}}}{R}\exp [-\zeta R]-\frac{Z_{\mathrm{{p}}}}{\left| {\varvec{R}}-{\varvec{r}}_{\mathrm{{t}}}\right| } \end{aligned}$$
(17)
$$\begin{aligned}&=4\pi \sum _{\lambda \mu }\frac{1}{2\lambda +1} \mathcal {U}_{\lambda }(R,r_{\mathrm{{t}}})Y_{\lambda \mu }^*(\hat{{\varvec{R}}})Y_{\lambda \mu }(\hat{{\varvec{r}}}_{\mathrm{{t}}}), \end{aligned}$$
(18)

where

$$\begin{aligned} \mathcal {U}_{\lambda }(R,r)= \left\{ \begin{aligned} \delta _{\lambda 0}Z_{\mathrm{{p}}}V_{\mathrm{{mod}}}(R) -\frac{Z_{\mathrm{{p}}}R^\lambda }{r^{\lambda +1}},&\quad R \le r, \\ \delta _{\lambda 0}Z_{\mathrm{{p}}}V_{\mathrm{{mod}}}(R) -\frac{Z_{\mathrm{{p}}}r^\lambda }{R^{\lambda +1}},&\quad R > r. \end{aligned} \right. \end{aligned}$$
(19)

After substituting Eq. (18) into Eq. (16), we explicitly separate the radial and angular components of the integral taking into account Eq. (8). This leads to

$$\begin{aligned} V_{\alpha '\alpha }({\varvec{R}})&=4\pi \sum _{\lambda \mu }\frac{Y_{\lambda \mu }^{*}(\hat{{\varvec{R}}})}{2\lambda +1}\nonumber \\&\quad \times \, \int d r_{\mathrm{{t}}}r_\mathrm{t}^2\phi _{n_{\alpha '}\ell _{\alpha '}}(r_{\mathrm{{t}}})\phi _{n_{\alpha }\ell _{\alpha }}(r_{\mathrm{{t}}}) \mathcal {U}_{\lambda }(R,r_{\mathrm{{t}}}) \nonumber \\&\quad \times \, \int d\hat{{\varvec{r}}_{\mathrm{{t}}}}Y_{\alpha '}^{*}(\hat{{\varvec{r}}}_{\mathrm{{t}}})Y_{\alpha }(\hat{{\varvec{r}}}_{\mathrm{{t}}})Y_{\lambda \mu }(\hat{{\varvec{r}}}_{\mathrm{{t}}}). \end{aligned}$$
(20)

The angular integral is taken analytically according to

$$\begin{aligned}&\int d\hat{{\varvec{r}}}Y_{\alpha '}^{*}(\hat{{\varvec{r}}})Y_{\alpha }(\hat{{\varvec{r}}})Y_{\lambda \mu }(\hat{{\varvec{r}}}) \nonumber \\&=\sqrt{\frac{(2\ell _\alpha +1)(2\lambda +1)}{4\pi (2\ell _{\alpha '}+1)}} C_{\ell _{\alpha }0\lambda 0}^{\ell _{\alpha '}0} C_{\ell _{\alpha }m_{\alpha }\lambda \mu }^{\ell _{\alpha '}m_{\alpha '}}. \end{aligned}$$
(21)

With that, the expression for the direct matrix elements in the target-centre simplifies to

$$\begin{aligned} V_{\alpha '\alpha }({\varvec{R}})&=\sum _{\lambda \mu }\sqrt{\frac{4\pi (2\ell _\alpha +1)}{(2\ell _{\alpha '}+1)(2\lambda +1)}} \nonumber \\&\quad \times C_{\ell _{\alpha }0\lambda 0}^{\ell _{\alpha '}0} C_{\ell _{\alpha }m_{\alpha }\lambda \mu }^{\ell _{\alpha '}m_{\alpha '}} Y_{\lambda \mu }^{*}(\hat{{\varvec{R}}}) \nonumber \\&\quad \times \int d r_{\mathrm{{t}}}r_\mathrm{t}^2\phi _{n_{\alpha '}\ell _{\alpha '}}(r_{\mathrm{{t}}})\phi _{n_{\alpha }\ell _{\alpha }}(r_{\mathrm{{t}}}) \mathcal {U}_{\lambda }(R,r_{\mathrm{{t}}}) . \end{aligned}$$
(22)

In Eq. (22), only the radial part of the integral need be numerically evaluated.

Similarly, for the direct-scattering matrix elements in the \(\beta \rightarrow \beta '\) channel we have

$$\begin{aligned} V_{\beta '\beta }({\varvec{R}})=\int d{\varvec{r}}_{\mathrm{{p}}}\psi _{\beta '}^{*}({\varvec{r}}_{\mathrm{{p}}}){\overline{V}}_\beta \psi _\beta ({\varvec{r}}_{\mathrm{{p}}}). \end{aligned}$$
(23)

However, the form of the interaction of the captured electron with the residual target ion differs from the \(\alpha \rightarrow \alpha '\) channel. There is an additional term with an exponential factor due to the model potential acting between the residual target ion and electron (but not between the projectile and electron). This additional term can be partial-wave expanded in terms of the product of spherical Bessel and spherical Hankel functions [60], leading to

$$\begin{aligned} {\overline{V}}_\beta&= \frac{Z_{\mathrm{{p}}}}{R}+\frac{Z_{\mathrm{{p}}}}{R} \exp [-\zeta R]\nonumber \\&\quad -\,\frac{1}{\left| {\varvec{R}}+{\varvec{r}}_{\mathrm{{p}}}\right| } -\frac{1}{\left| {\varvec{R}}+{\varvec{r}}_{\mathrm{{p}}}\right| }\exp [-\zeta \left| {\varvec{R}}+{\varvec{r}}_{\mathrm{{p}}}\right| ] \nonumber \\&=4\pi \sum _{\lambda \mu }\frac{(-1)^{\lambda }}{2\lambda +1} \tilde{\mathcal {U}}_{\lambda }(R,r_{\mathrm{{p}}})Y_{\lambda \mu }^*(\hat{{\varvec{R}}})Y_{\lambda \mu }(\hat{{\varvec{r}}}_{\mathrm{{p}}}). \end{aligned}$$
(24)

The expansion coefficients are defined as

$$\begin{aligned} \tilde{\mathcal {U}}_{\lambda }=\mathcal {U}_{\lambda }+ \left\{ \begin{aligned} \zeta (2\lambda +1) j_\lambda (i\zeta R) h_\lambda ^{(1)}(i\zeta r),&\quad R \le r, \\ \zeta (2\lambda +1) j_\lambda (i\zeta r) h_\lambda ^{(1)}(i\zeta R),&\quad R > r, \end{aligned} \right. \end{aligned}$$
(25)

where \(j_\lambda \) and \(h_\lambda ^{(1)}\) denote the spherical Bessel and spherical Hankel functions of the first kind, respectively. Evaluating these special functions with complex arguments accurately is challenging. We used the coulcc subroutine from Thompson and Barnett [61].

Following the same steps as before we separate the radial and angular components and evaluate the angular integral analytically in terms of the appropriate Clebsch–Gordan coefficients. Finally, we arrive at the following expression,

$$\begin{aligned} V_{\beta '\beta }({\varvec{R}})&=(-1)^{\ell _{\beta '}+ \ell _{\beta }}\sum _{\lambda \mu }\sqrt{\frac{4\pi (2\ell _\beta +1)}{(2\ell _{\beta '}+1)(2\lambda +1)}} \nonumber \\&\quad \times \, C_{\ell _{\beta }0\lambda 0}^{\ell _{\beta '}0} C_{\ell _{\beta }m_{\beta }\lambda \mu }^{\ell _{\beta '}m_{\beta '}} Y_{\lambda \mu }^{*}(\hat{{\varvec{R}}}) \nonumber \\&\quad \times \, \int d r_{\mathrm{{p}}}r_\mathrm{p}^2\phi _{n_{\beta '}\ell _{\beta '}}(r_{\mathrm{{p}}})\phi _{n_{\beta }\ell _{\beta }}(r_{\mathrm{{p}}}) \tilde{\mathcal {U}}_{\lambda }(R,r_{\mathrm{{p}}}). \end{aligned}$$
(26)

Evaluating the direct matrix elements this way is more accurate compared to a purely numerical approach. This has a significant effect for low-energy projectile scattering where small inaccuracies can exaggerate the ill-conditioning caused by the lack of orthogonality between the two basis sets. All results presented herein conserve unitarity, meaning that the norm of the total scattering wave function is conserved.

The overlap matrix elements in Eq. (11) are written as

$$\begin{aligned} K_{\beta ' \alpha } ({{\varvec{R}}})&= \langle \psi _{\beta '}|\exp [-i {{\varvec{v}}} \cdot {{\varvec{r}}}_\mathrm{p}]|\psi _{\alpha }\rangle \nonumber \\&\quad \times \, \exp [i v^2 t/2 + i (\varepsilon _{\beta '}-\varepsilon _{\alpha })t], \end{aligned}$$
(27)
$$\begin{aligned} {\tilde{K}}_{\alpha ' \beta } ({{\varvec{R}}})=&\langle \psi _{\alpha ' }| \exp [i {{\varvec{v}}} \cdot {{\varvec{r}}}_{\mathrm{t}}] |\psi _{\beta }\rangle \nonumber \\&\quad \times \,\exp [-i v^2 t/2 + i (\varepsilon _{\alpha '}-\varepsilon _{\beta })t] , \end{aligned}$$
(28)

and the exchange matrix elements are given by

$$\begin{aligned} Q_{\beta ' \alpha } ({{\varvec{R}}})&= \langle \psi _{\beta '}| \exp [-i {{\varvec{v}}} \cdot {{\varvec{r}}}_{\mathrm{p}}] (H_{\alpha } + {\overline{V}}_{\alpha } - \varepsilon _{\alpha }) |\psi _{\alpha }\rangle \nonumber \\&\quad \times \, \exp [i v^2 t/2 + i (\varepsilon _{\beta '}-\varepsilon _{\alpha })t], \end{aligned}$$
(29)
$$\begin{aligned} {\tilde{Q}}_{\alpha ' \beta } ({{\varvec{R}}})=&\langle \psi _{\alpha '}| \exp [i {{\varvec{v}}} \cdot {{\varvec{r}}}_{\mathrm{t}}] (H_{\beta } + {\overline{V}}_{\beta } - \varepsilon _{\beta }) |\psi _{\beta }\rangle \nonumber \\&\quad \times \,\exp [-i v^2 t/2 + i (\varepsilon _{\alpha '}-\varepsilon _{\beta })t], \end{aligned}$$
(30)

where \(H_{\alpha }\) and \(H_{\beta }\) are the target and projectile–atom Hamiltonians, respectively. The overlap and exchange matrix elements are evaluated numerically in spheroidal coordinates (see Ref. [51] for details). We used a Gauss–Legendre quadrature with 96 points for low projectiles energies, increasing to 1000 at the highest energies where the highly oscillatory nature of the exponential term renders numerical integration more difficult.

In the impact-parameter representation, expansion coefficients in Eq. (7), \(F_\alpha (t,{{\varvec{b}}})\) and \(G_\beta (t,{{\varvec{b}}})\), yield the scattering amplitudes for the associated final channel, \(\alpha \) and \(\beta \), in the limit as \(t \rightarrow +\infty \). In the limit as \(t\rightarrow -\infty \) they satisfy the initial boundary condition

$$\begin{aligned} \left. \begin{aligned} F_{\alpha }(-\infty ,{{\varvec{b}}}) =&\delta _{\alpha 1},&\alpha =1, 2, \dots , N, \\ G_{\beta }(-\infty ,{{\varvec{b}}})=&0,&\beta =1, 2, \dots , N. \end{aligned} \right. \end{aligned}$$
(31)

This condition means that the active electron is in the ground state of the target in the initial channel.

2.3 Cross sections

Once again, we emphasise the utility of this approach is that the formalism for one-electron atomic targets does not need modification. Not only solving the differential equations is performed the same way, but determining the cross sections from the expansion coefficients is also unchanged. Thus, we only give a brief overview here and refer the reader to Refs. [31, 54] for additional details.

After calculating the expansion coefficients, by solving Eq. (11), the integrated cross section for transition into a given final channel is determined as

$$\begin{aligned} \sigma _{f}=2\pi \int _{0}^{\infty }db b P^{\mathrm{}}_{f}(b), \end{aligned}$$
(32)

where \(\sigma _f\) denotes the total cross section for transition into the final target (projectile) channel \(f=\alpha (\beta )\). The single-electron probability of direct scattering and electron capture is given by

$$\begin{aligned} P^\mathrm{SE}_{\alpha }(b)=\left| F_{\alpha }(+\infty ,{\varvec{b}})-\delta _{\alpha i}\right| ^2 \end{aligned}$$
(33)

and

$$\begin{aligned} P^{\mathrm{SE}}_{\beta }(b)=\left| G_{\beta }(+\infty ,{\varvec{b}})\right| ^2. \end{aligned}$$
(34)

To calculate cross sections for scattering from the two-electron \({\hbox {H}_2}\) target, we can write the probability entering Eq. (32) as

$$\begin{aligned} P_{f}(b)=2P_{f}^{\mathrm{SE}}(b), \end{aligned}$$
(35)

to account for the equivalent chance of either electron transitioning to the final state f in the physical two-electron collision system [48]. The reason for the factor of 2 is the fact that there are 2 electrons and both of them can be modelled in exactly the same way. In other words, the two-electron problem is cut into two equal effective single-electron halves. When the single-electron problem is solved, the two halves must be brought together, hence, the factor of 2.

The total cross section for direct scattering or rearrangement is simply given by the sum of the corresponding partial cross sections. Here, we show results for elastic scattering, excitation, single ionisation, and single-electron capture.

The total ionisation cross section (TICS) is the sum of direct ionisation and electron capture into the continuum. Since total cross sections are invariant under coordinate-frame transformations, they can be straightforwardly added without the need to transform the amplitudes into a common frame of reference, i.e.

$$\begin{aligned} \sigma ^{\mathrm{{TICS}}}=\sum _{\alpha =N_b+1}^{N}\sigma _\alpha + \sum _{\beta =N_b+1}^{N}\sigma _\beta . \end{aligned}$$
(36)

3 Results of calculations

In this section, we present the total cross sections for elastic scattering, excitation, electron loss, single ionisation, and single electron capture in proton collisions with \({\hbox {H}_2}\). Additionally, we present state-resolved capture cross sections for exchange into the 1s, 2s, 2p, 3s, 3p, and 3d states of the projectile. To test the approach, we first calculate the total ionisation cross section for antiproton scattering on molecular hydrogen. With no electron capture to consider and the probability of protonium formation being negligible, a one-centre expansion is sufficient. In this case, the only surviving matrix elements in Eq. (11) are \(D_{\alpha ' \alpha }\).

Setting \(Z_{\mathrm{{p}}}=-1\) in the one-centre expansion, we consider antiproton scattering on effective one-electron \({\hbox {H}_2}\). For these calculations, the radial grid extended to 300 au. We solve the system of differential equations in Eq. (11) using the Runge–Kutta method. The projectile trajectory was discretised along the \(z=vt\) axis, from \(-100\) to +100 au relative to the target nucleus located at the origin. We found that 400 z-points were sufficient to obtain converged results. A total of 32 impact parameter points which ranged from 0 to 22 au were used for antiproton scattering. The probabilities for the investigated processes fell off several orders of magnitude with these parameters and additional range and discretisation made no significant contribution to the final results. The maximum momentum value \(\kappa _{\mathrm{{max}}}\) for the continuum pseudostates varied from 5 to 8 au across the energy range from 10 to 1000 keV. Increasing \(\kappa _{\mathrm{{max}}}\) further made no appreciable difference to the results.

Figure 1 shows the total cross section for ionisation in \(\bar{\hbox {p}}+{\hbox {H}_2}\) collisions as a function of projectile energy. At high impact energies, there is good agreement between our results and experiments by Andersen et al. [25] and Hvelplund et al. [24]. Between 30 and 80 keV, the WP-CCC results underestimate the experimental data which includes the region near the peak of the electron-loss cross section. However, the same is true of the other theoretical results shown in Fig. 1. At low energies, our results do not fall sufficiently to match the experimental data, as is also seen in the results of Ref. [27] which use the same model potential representation in a close-coupling formalism. We see small deviations from the results of [27]. These are due to different types of the pseudostates used. The theoretical works that use a full two-electron treatment of the target [26, 28] both fall in a similar fashion to the experiment at low energies. The calculations by Abdurakhmanov et al. [28] showed that the reduction of the ionisation cross section at low energies observed in experiment is due to the two-centre nature of the molecular target. It follows that theories which use spherically symmetric target structures would not replicate this so-called target structure-induced suppression of the ionisation cross section. This suggests that the simple effective potential cannot accurately model the properties of the hydrogen molecule in low-energy antiproton collisions. Proton collisions are fundamentally different, however, due to low-energy collisions being dominated by electron-capture processes.

Fig. 1
figure 1

Total cross section for ionisation in \(\bar{\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy. Experimental data are by Andersen et al. [25], Hvelplund et al. [24], and Knudsen et al. [23]. The theoretical results are: present WP-CCC approach, WP-CCC without the additional factor of 2 in Eq. (35) (Test 1), WP-CCC using the independent particle model in Eq. (37) (Test 2); effective one-electron close-coupling method by Lühr and Saenz [27]; two-electron close-coupling method of Lühr and Saenz [26]; two-electron CCC approach by Abdurakhmanov et al. [28]

Full size image

In Fig. 1, we also compare our results with those obtained in two test calculations. In Test 1, the factor of 2 in Eq. (35) is dropped, while Test 2 is based on the independent particle model (IPM) [62]. The IPM writes the probability of a single-electron process as

$$\begin{aligned} P_{f}^{\mathrm{IPM}}(b)=2P_f^{\mathrm{SE}}(b)[1-P_f^{\mathrm{SE}}(b)]. \end{aligned}$$
(37)

This corresponds to one electron occupying the state f while preventing the other electron from occupying the same state. Agreement with experiment is significantly worse in Test 1 at intermediate and high energies. The Test 2 results are not too bad, but clearly this approach does not change the low-energy behaviour of the cross section. That is because this disagreement with experiment is purely due to the single-electron spherical treatment of the target structure. Such an approximation cannot account for the target-structure-induced suppression responsible for the shape of the low-energy \({{\bar{\mathrm{p}}}}+{\hbox {H}_2}\) ionisation cross section [28, 29]. We conclude that multiplying the single-electron probability by 2 confirms the widely used approach. In addition, we should note that in our approach there is no need to explicitly prevent the second electron from occupying the same final state as there is no second electron. We use Eq. (35) for all following results. Since our model cannot differentiate between one- and two-electron processes, to avoid confusion, we label our result as a single-electron one. We note, however, that the probability of double electron capture, double ionisation, and transfer ionisation is very small compared to the probability of the single-electron processes.

Switching the charge of the projectile to \(+1\), we calculate the electron-loss cross section for proton scattering on \({\hbox {H}_2}\). Now, we use a two-centre expansion and solve the full set of coupled equations given in Eq. (11). The total electron-loss cross section is given by the sum of the total ionisation and total electron-capture cross sections. The required basis for converged results contained bound states with principal quantum numbers up to \(n_{\mathrm{max}}=10-\ell \) and angular momentum up to \(\ell _\mathrm{max}=4\), except at the very high impact energies where \(n_\mathrm{max}=8-\ell \) and \(\ell _{\mathrm{max}}=3\) was found to be sufficient. For incident energies below 25 keV the continuum was discretised with 15 bins up to a maximum electron momentum of \(\kappa _\mathrm{max}=4\ \mathrm{au}\). Then, from 25 keV we used 20 bins and \(\kappa _\mathrm{max}\) was increased up to 7 au at a projectile energy of 500 keV. At the highest impact energies considered 35 continuum bins were required to obtain sufficient continuum discretisation up to \(\kappa _{\mathrm{max}}=11\ \mathrm{au}\). Thus, the largest basis required in this work contained 2010 states. The z-grid extended from \(-300\) to \(+300\) au with 600–1000 points depending on the incident energy. These parameters were sufficient for the elastic, total capture, and ionisation cross sections (and state-resolved capture cross sections), presented below, to reach 99% convergence. The net excitation cross section has converged to within 95%, with \(n_{\mathrm{max}}=10\), however, adding additional states caused unitarity violations at low incident energies. A total of 32 impact parameters ranging from 0 to 22 au were used at low impact energies, while 64 points from 0 up to 40 au were required to obtain convergence in the results at high impact energies.

Fig. 2
figure 2

Total cross section for electron loss in non-dissociative \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy (top and bottom panels linear and log scales, respectively). Experimental data are by Stier and Barnett [4], Hooper et al. [5], Rudd et al. [11], and by Shah et al. [9]. The theoretical results are: present 2-centre WP-CCC approach; eikonal classical trajectory Monte Carlo approach, molecular orbital approach, and optimised dynamical pseudostates method by Elizaga et al. [49]; classical trajectory Monte Carlo method by Schultz et al. [1]; effective one-electron single-centre close-coupling method by Lühr et al. [48]

Full size image

The total electron-loss cross section for \({\hbox {p}}+{\hbox {H}_2}\) collisions is shown in Fig. 2. Here and in all following figures, we show our calculated points connected with straight lines to guide the eye. The distribution of the calculated energy points was chosen to ensure an accurate representation of the structure in all processes we investigated. The present results agree well with available experimental data and single-centre close-coupling calculations by Lühr et al. [48] as well as MO and ODP results by Elizaga et al. [49] from 20 to 1000 keV. The CTMC results by Schultz et al. [1] are shown with points connected with straight lines. They underestimate the experimental results by Rudd et al. [11] and Shah et al. [9] as well as the present ones below 70 keV, but are slightly larger than the experimental data by Stier and Barnett [4]. However, above 100 keV the CTMC calculations underestimate both the experiment by Hooper et al. [5] and our calculations. At lower incident energies, our results overestimate the cross section. As discussed below, this is due to an increasing contribution from capture into the 1s state of the projectile.

Fig. 3
figure 3

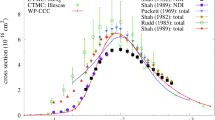
Cross section for single-electron capture in non-dissociative \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy (top and bottom panels linear and log scales, respectively). Experimental data are by Stier and Barnett [4], Barnett and Reynolds [6], McClure [7], Toburen et al. [8], Rudd et al. [11], and Shah et al. [9]. The theoretical results are: present 2-centre WP-CCC approach; classical trajectory Monte Carlo methods by Meng et al. [39], Illescas and Riera [41], and Schultz et al. [1]; continuum-distorted-wave eikonal-initial-state, method by Busnengo et al. [35]

Full size image

Using our two-centre method, we are able to decompose the electron-loss cross section into electron-capture and single-ionisation contributions. The total electron-capture cross section is shown in Fig. 3. Our results overestimate the experiments of Shah et al. [9] and McClure [7] below 30 keV, but converge to their data above 60 keV. The empirical data from Rudd et al. [11] are higher than the other experimental results, and our calculation agrees more with these data. In the high-energy regime, our results are slightly larger than the experimental data by Toburen et al. [8] and Barnett and Reynolds [6]. Across the entire energy range shown, the WP-CCC cross sections are larger than the CTMC results of Schultz et al. [1]. We also show the CDW-EIS calculations of Busnengo et al. [35]. Our calculations are consistently larger than the CDW-EIS results across the entire energy range considered.

Fig. 4
figure 4

Cross section for single ionisation in \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy. Experimental data are by Hooper et al. [5], Toburen and Wilson [12], Edwards et al. [13], Shah and Gilbody [10], and Shah et al. [9]. The theoretical results are: present 2-centre WP-CCC approach; classical trajectory Monte Carlo methods by Meng et al. [39], Illescas and Riera [41], and Schultz et al. [1]; continuum-distorted-wave eikonal-initial-state molecular-orbital method by Galassi et al. [37]

Full size image

We show the results for the non-dissociative single-ionisation cross section in Fig. 4; however, this provides a good representation of the total cross section for single ionisation since the dissociative channel contributes significantly less (see Ref. [9]). The WP-CCC results shown agree very well with available experimental data from 30 to 1000 keV. This indicates that the total ionisation cross section is less sensitive (than the electron-capture one) to the accuracy of the target wave function. At higher energies, our calculations fall between the experimental results of Toburen and Wilson [12] and Shah and Gilbody [10], very close to the data from Hooper et al.[5]. The results by Edwards et al. [13] overestimate the other experiments and theories around the peak in the ionisation spectrum but converge to those of Shah and Gilbody [10] at higher energies. Our results agree well with the CTMC calculations in the energy region below 100 keV. However, above 100 keV the calculations of Schultz et al. [1] are somewhat higher and those from Illescas and Riera [41] are lower than ours, with all three sets of results being within the experimental uncertainty. The CDW-EIS-MO calculations by Galassi et al. [37] produce larger cross sections than the WP-CCC method, especially at lower energies where the CDW approaches are less reliable. In particular, they overestimate the ionisation cross section in the region of its maximum around 100 keV, whereas our calculations agree well with the experimental results.

Fig. 5
figure 5

Cross section for elastic scattering in \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy. The theoretical results are: present 2-centre WP-CCC approach and classical trajectory Monte Carlo approach by Schultz et al. [1]

Full size image

The total cross section for elastic scattering of protons on molecular hydrogen is shown in Fig. 5. The only other calculation available in the literature that we are aware of is the CTMC one by Schultz et al. [1]. The authors state a lack of available elastic scattering cross sections for this system and produced this estimate based on their previous works. Our results appear to significantly differ from the CTMC ones in the entire energy range. More theoretical calculations are required.

Fig. 6
figure 6

Net cross section for excitation in \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy. The theoretical results are: present 2-centre WP-CCC approach and classical trajectory Monte Carlo approach by Schultz et al. [1]

Full size image

Figure 6 presents the net cross section for excitation into all states included in the target-centred basis (\(n_{\mathrm{{max}}}=10\) and \(\ell _{\mathrm{{max}}}=4\)). The results of Schultz et al. [1] are also shown. Note that unlike their other results the excitation cross section is not normalised to the recommended experimental data from Hunter et al. [42]. The CTMC results from [1] are larger than ours above 50 keV generally agreeing in shape. Below 20 keV the shape of our results is different. However, we should note that this is the energy region where our model potential is expected to become less reliable.

Fig. 7
figure 7

State-selective electron-capture cross sections in \({\hbox {p}}+{\hbox {H}_2}\) collisions as a function of impact energy. Experimental data by Andreev et al. [14], Bayfield [15], Hughes et al. [20], Hughes et al. [17], Hughes et al. [19], Birely and McNeal [16], Dawson and Loyd [22], Shah et al. [18], Williams et al. [21]. The theoretical results are: present 2-centre WP-CCC approach; boundary-corrected first Born approximation by Corchs et al. [34]; modified molecular-orbital close coupling calculations by Kimura [45]; atomic orbital close-coupling method by Shingal and Lin [46]; classical trajectory Monte Carlo method by Meng et al. [40]; continuum-distorted-wave eikonal-initial-state method by Busnengo et al. [36]

Full size image

The state-selective electron-capture cross sections are presented in Fig. 7 for those channels for which experimental or theoretical data is available. Note that the experimental results of Shah et al. [18] are normalised absolutely, as are those from Andreev et al. [14]. However, the other experimental data are normalised to cross sections from other scattering systems (see Ref. [18] for a detailed discussion). In general, our results reproduce the shape of experimental data but differ in magnitude for some channels. The CDW-EIS results by Busnengo et al. [36] agree well with experiment at high energies but fail to reproduce the shape of the experimental data around and below the region of the peak. The CTMC calculations by Meng et al. [40] generally exhibit better agreement with our results and the experimental data than the distorted-wave models but are only available over a limited energy range. Interestingly, our results significantly overestimate other theoretical calculations for charge transfer into the ground state yet generally agree well with experimental data for low energy capture into 2\(\ell \) and 3\(\ell \) states. Below, we discuss each considered channel in more detail.

The top left panel in Fig. 7 shows that capture into the ground state of the projectile gives the dominant contribution to the total electron-capture cross section. Our results are in good agreement with the B1B calculations by Corchs et al. [34] at 100 keV and above. Below 30 keV, the WP-CCC results overestimate the close-coupling calculations of Kimura [45] and Shingal and Lin [46]. Although above 40 keV the AO calculations are larger than both the boundary-corrected first Born calculations and our results.

For capture into the 2s state of the projectile (middle left panel), our results agree well with the absolute measurements of Shah et al. [18] and Andreev et al. [14]. The experimental results of Hughes et al. [20] are slightly smaller than the WP-CCC calculation, particularly around the peak region, although our calculation converges to their data above 70 keV. Data from Bayfield [15] agree with our calculations below 10 keV but are similarly smaller in the peak region. However, the authors of that work estimate a 55% normalisation error in addition to the displayed error bars. CTMC calculations by Meng et al. [40] agree well with our result. Our result reproduces the shape and magnitude of the experimental works at all energies, except for overestimating the data from Hughes et al. [20].

Capture into the 2p projectile state is shown in the bottom left panel. We see very good agreement with the experimental results of both Birely and McNeal [16] and Hughes et al. [19] at low and intermediate energies. The CDW-EIS results from Busnengo et al. [36] agree well with the WP-CCC method above 30 keV. The CTMC calculations by Meng et al. [40] generally agree with the shape of experiment and our results. As with capture into the 2s state, here we find that the WP-CCC results reproduce the magnitude and shape of the available experimental data very well.

Agreement between other theories and our results for electron capture into the 3s state (top right panel) is very similar to capture into the 2s state. Our calculations are consistently larger than the CDW-EIS calculations. The CTMC calculations agree fairly well with the WP-CCC results, but deviate below 40 keV. Our results agree well with the experiment of Williams et al. [21] above 20 keV, but underestimate it below this energy. Experimental data from Hughes et al. [20] are smaller than the WP-CCC results like for 2s capture.

In the middle right panel, we see that the WP-CCC results overestimate the experimental data from Hughes et al. [20] for capture into the 3p projectile state. However, at low energies our calculations agree with the data from Dawson and Loyd [22], although not in the same shape as their points suggest. The CDW-EIS agrees well with our results above 50 keV. The CTMC calculations by Meng et al. [40] again agree with the WP-CCC results.

We finally consider subshell capture into the 3d state of atomic hydrogen. Here, our result is slightly larger than the experimental data by Dawson and Loyd [22] below 10 keV. Above 40 keV, we underestimate the experimental points of Hughes et al. [20]. The CDW-EIS calculation of Busnengo et al. [36] is the same as ours above 50 keV but suggests a different shape to the experimental data at lower energies.

4 Conclusion

Using an effective one-electron model potential to describe the \({\hbox {H}_2}\) target within the two-centre WP-CCC approach, we have calculated total cross sections for all one-electron processes taking place in \(\hbox {p}+{\hbox {H}_2}\) collisions. This approach allows us to utilise the efficient computational techniques developed in our one-electron code and avoid significant complexities associated with a two-electron target description. Despite the simplicity of the approach, the converged total cross sections for single-electron capture and ionisation show good agreement with experiment in a wide energy range. While previous close-coupling methods applied to this system used only a single-centre expansion, our two-centre method allows differentiation between ionisation and electron capture, providing a more detailed picture of the collision process. We also calculate state-resolved capture cross sections and find reasonably good agreement with experiment. Overall, our results improve over previous theoretical studies. Next, we plan to apply our approach to calculate angular differential electron capture and excitation and differential ionisation cross sections.