Abstract
The splitting of carbon dioxide was investigated for a coaxial dielectric barrier discharge, which was operated with nanosecond high-voltage pulses of 500 ns and amplitudes up to 20 kV at ambient temperature and atmospheric pressure. A non-thermal plasma could be established across a gap distance of 4 mm and a length of 90 mm for gas flows of 30–210 sccm of pure CO2 and with admixtures of Argon. The application of high-voltage pulses of either positive or negative polarity resulted in distinct differences in effective conversion and CO production. The highest observed conversion of 6.6%, corresponding to a CO production of 7%, was achieved for positive high-voltage pulses of 20 kV that were applied with a repetition rate of 3 kHz for a ratio of CO2:Ar of 1:2 at a flow rate of 30 sccm. Conversely, an operation with negative high-voltage pulses, for otherwise the same operating parameters, resulted in an effective conversion of only 5.3% and CO production of 5.4%. The corresponding conversion rates for specific energy input (SEI), concerning different operating parameters, could be related to reaction enthalpies that were calculated from thermodynamic functions. The differences in polarity were associated with discharge characteristics, i.e., plasmas appeared more filamentary for positive high-voltage pulses. In this case, a visible plasma could also be established for much lower pulse amplitudes.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The rising concentration of carbon dioxide (CO2) in the atmosphere is of substantial concern with respect to global warming [1,2,3,4]. Conversely, CO2 is a carbon resource, which can be the basis of value-added chemicals and fuels, e.g., methanol (CH3OH). For example, the conversion of CO2 with CH4 is regarded a promising method to produce syngas as chemical feedstock for the generation of oxygenates and liquid hydrocarbons [1, 4]. Traditionally, CO2 is reduced with hydrogen through chemical catalysis, electro- or photochemically [1, 4]. However, the high stability of the CO2 molecule is a major challenge. As indicated by Eq. 1, a large amount of energy is required to break the double bonds (C=O=O) [1].
Non-thermal plasma (NTP) presents an innovative alternative to address this challenge. Thermodynamically unfavorable reactions, such as CO2 splitting, can be induced by electron impact already at or close to room temperature, i.e., without significant elevation of the overall process temperature [1,2,3,4,5,6,7,8]. Depending on the operating gas, and the method for generating the plasma, electrons can attain kinetic energies corresponding to temperatures of 1–10 eV. In comparison, kinetic energies for heavier particles (ions, atoms, molecules), which determine the actual gas temperature, remain rather low [9].
The energetic electrons in NTPs determine their unusual chemistry, which is able to activate and dissociate stable molecules and atoms and initiate subsequent reactions with and between them [1, 4, 10]. Other merits of the technology for gas conversion are flexibility, versatility, and cost-effective operation [10]. The latter benefits in particular from the possibility of an operation at atmospheric pressure and ambient temperature. Accordingly, several types of plasma have been studied for CO2 splitting already, e.g., dielectric barrier discharge (DBD) [1,2,3,4, 8, 11,12,13,14], microwave (MW) discharge [1, 4], gliding arc (GA) discharge [1, 4], and nanosecond pulsed (NSP) discharge [1, 4, 7, 14,15,16,17,18]. Specific differences in plasma generation and operation provide different chemical conversions and energy efficiencies [4]. MW discharges already exceeded the targets for energy efficiency (60%) and CO2 conversion (40%) [1, 4]. A caveat of the approach is the necessary operation at lowered pressures. GA discharges were also found promising with energy efficiencies close to 60% although for a conversion of only 20% [1, 4]. The energy efficiency of DBDs was found quite low and did not reach above 18% together with conversions, which did not exceed 40% [1]. The specific appeal of this type of plasma is the rather simple configuration and operating principle. In addition, the approach is intrinsically scalable and already laboratory systems can generate sizeable plasma volumes. Moreover, especially coaxial arrangements can be easily implemented as flow-through systems, modified, e.g., as packed-bed reactors, or combined with catalysts [1, 4]. Commonly, AC high-voltages were applied to establish a DBD-plasma [1, 3, 4, 11, 19], but an operation with high-voltage pulses of microsecond or nanosecond duration was also demonstrated [4, 14]. In combination with different procedural, configurational, and operational parameters, the approach has been reported to improve the energy efficiency of DBDs for CO2 conversion. Niu et al. investigated the effect of applied voltage, discharge length, and flow rate on CO2 splitting using a multi-electrode cylindrical DBD. For the tested conditions, they reported a maximum of 18.5% and 12.83% for CO2 conversion and energy efficiency, respectively [3]. Paulussen et al. studied the influence of applied power, frequency, gas flow rate, and gas temperature and found a conversion of 30% for a flow rate of 0.05 L/min, a power density of 15 Wcm−3, and a frequency of 60 kHz [20]. While these studies were conducted for pure CO2 flows, have others confirmed that admixtures of inert gasses, i.e., nitrogen or argon, facilitate plasma ignition and provide more stable discharges but can also increase CO2 conversion [1, 2, 4, 7, 19]. The application of the DBD with nanosecond high-voltage pulses, i.e., NSP-DBD, offers the potential to increase especially the kinetic energy of free electrons. This is possible by a high electric field, which is provided during the short pulse duration. In comparison with the regular operation of a DBD with oscillating voltages will the increase in the kinetic energy of the much heavier ions be conceivably much lower. A corresponding advantage is an expected improved CO2 conversion [4]. NSP-DBDs have, hence, found growing attention for the conversion of CO2 and CH4 [4, 7, 16,17,18, 21]. For very short, repetitively applied, high-voltage pulses of 10 ns have Bak et al. studied the splitting of CO2 to CO and found a maximum conversion and energy efficiency of 7.3% and 11.5% [7]. Apparently better homogeneity of the plasma was associated with a higher number of microdischarges that are characteristic of a DBD [22]. Accordingly, the probability of an interaction with gas molecules passing through is increasing [14, 23]. Furthermore, more non-equilibrium states of molecular vibrations could be demonstrated for excitation with short high-voltage pulses [24]. Correspondingly, Khalife et al. achieved a maximum energy efficiency of 7.2% for CH4 reforming, due to the associated heating, for the decomposition by an NSP-DBD [25]. The influence of pulse parameters for the pulsed operation of a DBD reactor was also investigated by Wang et al. for CH4 reforming with CO2, who achieved a higher conversion of CO2 (22.9%) and CH4 (39.6%) [21].
Regardless, the studies on NSP-DBDs have so far not exploited the full potential of the approach. Based on different underlying mechanisms, especially polarity effects could be expected. With the here presented investigation, respective differences for the application of either positive or negative high-voltage pulses were revealed for CO2 splitting. The actual energy efficiency and conversion depended both on the pulse repetition rate and the gas flow rate in a similar fashion. An admixture of argon improves plasma formation. For completeness, the conversion of CO2-Ar mixtures into CO and other products was compared by thermodynamic calculations with respect to enthalpy, Δh, reversible work (Gibb’s free energy), Δg, and heat exchange, TΔs, and related to the specific energy input, SEI. The study, in general, shows opportunities to further improve the CO2 conversion with DBDs by an operation with nanosecond high-voltage pulses.
2 Material and methods
2.1 Plasma reactor
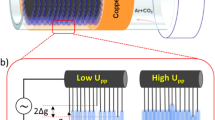
A coaxial dielectric barrier discharge plasma reactor was designed and constructed, which is shown at the center of Fig. 1. A borosilicate glass tube with a wall thickness of 2.5 mm and a length of 130 mm constituted the dielectric barrier. The inner and outer diameters of the glass tube were 17 and 22 mm, respectively. The inner electrode was a threaded rod (M8) of stainless steel along the central axis, corresponding to a discharge gap of 4 mm. Nine separate but connected aluminum rings were tightly fitted to the outside of the glass tube as the counter electrode. Each ring had a height of 10 mm and an outer diameter of 32 mm. This resulted in a discharge length of 90 mm and a plasma volume of about 16 ml. Operating gases were flown from top to bottom through the reactor by in- and outlets with an inner diameter of 6 mm. The reactor itself and the fittings (as well as any other component of the feed gas system) were airtight.
2.2 Experimental setup
The entire experimental setup is shown in Fig. 1. A gas mixture of CO2 and Ar in the mass ratio of 1:2 was run through the DBD reactor with a flow rate that was varied from 30 to 210 ml/min by individual mass flow controllers (MKS Instruments, 647C). The initial experiments showed that this ratio provided the most reliable conditions for the operation of the DBD over a wide range of operating conditions, i.e., pulse amplitudes, pulse repetition rates, and gas flow rates, that were of interest for the study. Negative high-voltage pulses were applied to either the central electrode or the ring electrodes, while the other electrode configuration was grounded. Accordingly, a plasma was always initiated from the threaded rod either by the negative or positive potential difference across the reactor gap. The high-voltage pulses of 500 ns in duration and an amplitude of at most 20 kV were applied with frequencies of 1, 2, and 3 kHz with a pulse generator (NSP-120-20-N-250, Eagle Harbor Technologies).
2.3 Electrical measurements
Electrical signals, i.e., voltage and current, were recorded on a digital oscilloscope (Wavesurfer 4104 HD, Teledyne LeCroy). The high-voltage pulses that were applied to the plasma reactor were monitored with a high-voltage probe (P6015A, Tektronix) and pulsed currents with a Rogowski current monitor (CT-F2-5-BNC, Magnelab). The energy, Ep, which was dissipated in the reactor per applied pulse, was obtained by integration of these measurements and together with the pulse repetition rate, f, while the electrical power was derived according to Eq. 2. (Time delays due to different cable lengths were explicitly considered.)
2.4 Discharge imaging
Images were recorded with a digital camera (D5100, Nikon) to determine the discharge appearance for positive and negative high-voltage polarity. The photographs were taken with a resolution of 3265 × 4928 pixels through a viewport in the ring electrodes of 7 mm in diameter. With an exposure time of 1/3 of a second, each image included more than 300 individual discharges for a pulse repetition rate of 1 kHz.
2.5 Derivation of CO2 conversion parameters
The gaseous effluents from the reactor were analyzed by Fourier transform infrared spectroscopy (FTIR). The spectrometer (Matrix MG5, Bruker) was operated at ambient temperature and atmospheric pressure. The multi-pass cell with a volume of 250 ml provided an overall absorption length of 5 m. The quantification of gaseous constituents, contributing to the spectra, was based on a resolution of 1 cm−1 and conducted with the software provided with the spectrometer (OPUS GA, Bruker).
Pertinent parameters for the conversion of CO2 were derived according to formulations previously summarized by Snoeckx et al. [1]. The absolute conversion of CO2, \(X_{{{\text{CO}}_{{2}} ,{\text{abs}}}}\), was calculated according to Eq. 3.
The effective conversion, \(X_{{{\text{CO}}_{{2}} ,{\text{eff}}}}\), describes for gas mixtures the respective value only for CO2 according to Eq. 4.
The carbon balance, B, was calculated from Eq. 5 [26].
The specific energy input (SEI) in the plasma was determined from the electrical power, dissipated in the discharge according to Eq. 2, and the gas flow rate, F, by Eq. 6.
Eventually, the energy efficiency of CO2 conversion, η, was defined according to Eq. 7.
The reaction enthalpy, ΔRH0, for the splitting of a CO2 molecule, i.e., \({\text{CO}}_{{2}} \to {\text{CO}} + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{O}}_{{2}}\), amounts to 279.8 kJ mol−1 (2.9 eV). Note that the conversion factor of 24.5 l mol−1 is strictly only valid for an operating temperature of 298 K and atmospheric pressure. However, the operating conditions were close enough to provide a reasonable estimation with actual values that were verified not to differ significantly, especially for only slightly higher temperatures. Furthermore, the temperature did not have a significant impact on the conversion as described in the results and discussion.
Correspondingly, the energy cost, i.e., the energy that was consumed for CO2 splitting can be obtained by Eqs. 8 and 9.
3 Results
3.1 Electrical and visual discharge characteristics
High-voltage pulses of either positive or negative polarity were applied to the reactor by switching high-voltage and ground connections (c.f. Fig. 1). In both cases, pulse amplitudes were increased from 8 to 20 kV in increments of 1 kV for a gas flow of 30 ml/min of the carbon dioxide–argon mixture (provided in a ratio of 1:2). The inception voltages were determined for both pulse polarities. The corresponding discharge probabilities, i.e., the actual number of discharges that were investigated for the repetitively applied high-voltage pulses, could be unambiguously determined from the current–voltage characteristic. Therefore, voltage and current were recorded for 100 consecutive pulses. Pulses that were not resulting in the formation of plasma drew capacitively dominated currents and were characterized by significantly lower resistive currents (data not shown). The threshold for pulse amplitudes to initiate a discharge was for positive polarity around 10 kV but with 15 kV much higher for negative polarity as shown in Fig. 2. The probability for discharge inception was increasing with pulse amplitude for both polarities. Eventually, a plasma was formed with every applied pulse, for a nominal amplitude of 20 kV, i.e., as set at the pulse generator.
Differences in discharge development with increasing pulse amplitude could be confirmed by respective time-integrated images of superimposed discharge events as shown in Fig. 3. The DBD was operated with a gas flow of 30 ml/min for a 1:2 CO2-Ar mixture. For positive polarity, a faint plasma was observed for voltages as low as 10 kV, but no discharge was apparent for this amplitude for negative high-voltage pulses. Comprehensive coverage of the high-voltage electrode was observed starting with a voltage of 15 kV. When not every applied pulse resulted in the formation of plasma, i.e., for the lower pulse amplitudes, the overall intensities were still rather weak. Discharges were generally confined to the vicinity of the sharp edges of the threaded rod. This filamentary appearance seemed more pronounced for the positive polarity, which became more obvious at 20 kV. More distinct filaments, which were also expanding further away from the edges of the threaded rod, were observed for positive high-voltage polarity. For negative high-voltage polarity, the plasma was found more homogeneous and remaining closer to the edges of the threaded rod.
Corresponding typical voltage and current signals for high-voltage pulses that were applied with positive polarity or negative polarity are shown in Fig. 4. The DBD was otherwise operated in a 1:2 CO2-Ar mixture with a gas flow rate of 30 ml/min. Notable are capacitive current spikes for the rising and falling edge of the applied high-voltage pulses, indicating charging and discharging of the dielectric. Once the voltage pulse amplitude was established, a short but distinct resistive current plateau was observed. For an increase in pulse frequency from 2 to 3 kHz, the applied voltages were noticeably smaller than the nominal setting of 20 kV at the pulse generator. This suggested that the output power was no longer sufficient to continuously sustain the amplitude at this pulse repetition rate. Concurrently, peak currents were becoming smaller and the resistive plateau became longer as a consequence of a decreasing pulse steepness and due to the associated limitation of the pulse generator.
Typical voltage and current signals for high-voltage pulses that were applied with positive polarity (a, c, e) or negative polarity (b, d, f) with a nominal amplitude of 20 kV and pulse repetition rates of 1 kHz (a, b), 2 kHz (c, d) or 3 kHz (e, f). A constant value between the capacitive spikes indicates the resistive current through the plasma
3.2 Effect of pulse polarity on CO2 conversion
CO2 conversion was compared for both polarities by keeping other operating parameters the same. Flow rates of 30 and 60 ml/min were investigated for a fixed mixture ratio of CO2:Ar of 1:2. The frequency of the applied pulses was varied from 1 to 3 kHz for a nominal pulse amplitude of 20 kV. An unstable plasma formation was observed for the lower voltages (c.f. Fig. 3). Figure 5a summarizes the corresponding effective CO2 conversion as a function of pulse repetition rate. The effective CO2 conversion was always higher for positive polarity for otherwise the same parameters, e.g., flow rate and pulse repetition rate. Effective conversion decreased with increasing flow rate and increased with pulse repetition rate for both polarities. The highest effective CO2 conversion of 6.6% was observed for high-voltage pulses with positive polarity, which were applied with 3 kHz and a gas flow rate of 30 ml/min. For completeness, it should be mentioned that generally a low amount of ozone (ppm range) was observed.
The corresponding CO production, shown in Fig. 5b, followed the same almost linear trend for an increase in pulse repetition rate. Again, production was always higher for positive than for negative polarity for the same flow rate and pulse repetition rate. The highest conversion, with a concentration of 7% of CO in the effluent, was observed for the lowest investigated flow rate of 30 ml/min and the highest applied pulse frequency of 3 kHz. Corresponding to CO2 conversion and CO production, the carbon balance, B, was calculated according to Eq. 5. The results amount to 100% for all investigated conditions with only slight deviations based on the accuracy of the underlying measurements (data not shown).
Figure 6 shows the specific energy input, SEI, as a function of the pulse repetition rate for the observed CO2 conversion (c.f. Fig. 5a). The specific energy was generally increasing with pulse repetition rate in a similar fashion (indicated by trend lines) regardless of flow rate and polarity of the applied high-voltage pulses. Longer residence times, as a result of cutting flow rates from 60 ml/min in half to 30 ml/min, were proportionally reflected. However, for the same flow rate and pulse repetition rate, pulses that were applied with positive polarity consistently dissipated more energy. This difference was only obvious for 30 ml/min. SEI did not change significantly for an increase in pulse frequency from 2 to 3 kHz. This was most likely due to the limitations of the pulse generator, which could not match the power that could have been dissipated in discharges at the highest frequency (c.f. Fig. 4). When a pulse generator with a nominal output power of 1.5 kW (NSP-1500-20-F-500-T-L, Eagle Harbor Technologies) instead of 120 W was used, the linear increase in power that was observed for an increase in pulse repetition rate from 1 to 2 kHz could be extended to 3 kHz. However, in this case, the operating gas and discharge configuration were heating up considerably and an unambiguous comparison with results obtained for the 120-W pulse generator was not possible. Interestingly, the linear trends that were observed for effective CO2 conversion (Fig. 5a) and CO production (Fig. 5b) for an increase in pulse frequency from 2 to 3 kHz were not affected by the almost constant SEI for this change in frequency for the less powerful generator. Altogether, results that were determined for 1 and 2 kHz were more indicative of underlying discharge characteristics and their dependency on operating parameters. Regardless, results for the higher pulse repetition rate of 3 kHz are still presented for completeness.
The dependencies that were observed between CO2 conversion and SEI for different discharge frequencies and flow rates were conveyed into the energy efficiencies and energy costs as shown in Fig. 7a and b, respectively. For the same pulse repetition rate and flow rate, the energy efficiency was higher for the positive polarity, especially for the higher flow rate. Accordingly, the energy cost was lower. The highest energy efficiency of about 3% was achieved for positive polarity for an operation at 1 kHz and a flow rate of 60 ml/min. This corresponded to the lowest energy cost of about 94.4 eV/molecule.
An increase in pulse frequency from 1 to 2 kHz caused a substantial drop in energy efficiency. Changes for a further increase from 2 to 3 kHz were marginal. The opposite trend was observed for the flow rate. The energy efficiency doubled (for the same frequency) in this case with respect to results that were obtained for the lower flow rate. However, the energy efficiency was significantly higher for 60 ml/min. Conversely, the results for different polarities were indistinguishable from each other for 30 ml/min. The highest energy efficiency was associated with the lowest investigated frequency and the highest flow rate. A better conversion could be achieved by increasing pulse frequency although at a higher energetic expense.
The results suggest a linear increase in conversion with the pulse frequency that is associated with a corresponding decrease in energy efficiency. Consequently, the dependency on flow rate was less obvious and was, therefore, investigated in more detail for negative high-voltage pulses for a frequency of 1 kHz and nominal pulse amplitude of 20 kV.
Accordingly, gas flow rates of interest were set at 30, 60, 90, 120, 150, 180, and 210 ml/min for the application of high-voltage pulses of nominal 20 kV that were applied with negative polarity with a pulse repetition rate of 1 kHz. The respective effective CO2 conversion is shown in Fig. 8a. The results illustrate that by increasing the gas flow rate the effective conversion decreased significantly from 4.33% to 1.7%. Figure 8b describes the production of CO. The maximum concentration of CO of 4.4% was attributed to a flow rate of 30 ml/min. The values then sharply decreased to 1.5% for 210 ml/min. According to Fig. 5a and b, the same trend is anticipated for pulses of positive polarity.
3.3 Comparison between specific energy input, SEI, and specific energy requirement, SER
Thermodynamic calculations have been conducted to compare the SEI with the specific energy requirement (SER) for the measured CO2 conversion. These calculations also show how much electrical work and reversible heat were necessary for the relevant reactions.
The conversion of CO2 can be described from the reactants to the products, e.g., for the splitting as shown by Eq. 1, or vice versa for the inverse reaction. For the latter, reaction enthalpy, Δh, Gibbs free energy, Δg, and changes in entropy at a fixed temperature, TΔs, were derived from known thermodynamic functions by the solver FactSage 6.1 (GTT Gesellschaft für Technische Thermochemie und -physik mbH). Respective absolute values for forward and backward reactions are the same with only reversed algebraic prefixes. The calculations were based on the behavior of ideal gases. Only the composition of the mixture of the initial reactants and the products after the reaction has to be known for the derivation of the energetic changes. The individual process on the molecular level, which was taking place in the plasma, does not play a role. The splitting of CO2 can only be achieved when energy is provided. The product, i.e., effluent, which contains CO and O2, differs energetically from the reactant by the amount of the reaction enthalpy, which is the sum of Gibbs free energy and changes in entropy, i.e., Δh = Δg + TΔs. The enthalpy of the relevant reaction CO + ½O2 → CO2 is positive, hence describing an endothermic reaction. The Gibbs free energy, Δg, represents the reversible useful work, and TΔs the reversible heat exchange. Thus, Δg contributes to the enthalpy of the reaction that must be expended as work, which is for the operation of the DBD actual electrical work, while the contribution of TΔs must be expended as heat to split CO2. Both quantities enter the balance with positive values. Since Δg > 0, the reaction is called ‘endergon.’ Reversible work and heat are stored in the gaseous product of the reaction. The sum of Δg and TΔs can be completely recovered by combustion as reaction heat, Δh. In contrast, only Δg can be recovered in the form of electrical work in a reconversion, e.g., in a fuel cell, while TΔs is released as heat.
The reaction enthalpy, related to the reactant volume, was equal to the specific energy requirement (SER) to achieve the corresponding CO production. The SER or the enthalpy of the reaction, as well as its partial amounts Δg/vreactant and TΔs/vreactant with respect to the volume of the reactant, vreactant, depend on the change of the chemical composition of the gas. The SER is the minimum energy required to change the chemical gas composition of the feed gas to that of the effluent. Thus, it is a benchmark for any process in which energetic considerations play a role. As CO2 conversion and CO production increased with pulse repetition rate (c.f. Fig. 5), SER, Δg, and TΔs also increased as demonstrated in Fig. 9.
Since an increase in temperature is to be expected when heat is released by chemical reactions, the influence of temperature on CO2 conversion was calculated as well. For the calculation, the input of the electric work, Δg, was kept constant at 12.3 kJ/mol. This value corresponds to the work required for an observed effective CO2 conversion of about 4% for one mole of a CO2-Ar gas mixture in a mass ratio of 1:2. Notable is an apparent steeper increase of Δg/v for a flow rate of 60 ml/min for an increase in pulse frequency from 2 to 3 kHz, which, however, needs clarification by further studies. In the calculated temperature range of 16.8 °C to 226.8 °C (290–500 K), an increase in effective CO2 conversion of about 0.53% can be expected as a result of the increase in temperature. This demonstrates the only negligible impact of temperature (in this range).
4 Discussion
The conversion of CO2 and the energy efficiency in the splitting of CO2 with a dielectric barrier discharge (DBD) are affected by a wide range of operating parameters, including electrical supply (AC or pulsed), input power, gas admixtures, gas flow rate, dielectric materials, the volume of the discharge and discharge repetition rate [4]. The conversion of CO2 can usually be improved when a comprehensive and intense plasma can be established in the reaction volume. For DBDs, this is commonly associated with a large number of microfilaments as processing centers. This has, for example, been confirmed by Mei and Tu, who found a higher CO2 conversion related to a higher number of microdischarges, which both increased when the power to the dielectric barrier discharge increased [4]. Likewise reported Jiang et al. that the operation of a DBD by high-voltage pulses improved the stability and uniformity of the plasma to the point where individual microdischarges could no longer be resolved [23]. Accordingly, the possibility of plasma-chemical reactions, e.g., for CO2 molecules, should increase [14]. For NSP-DBDs, it has been claimed that predominantly energetic electrons can be held responsible [4]. Concurrently, Moss et al. investigated CO2 splitting using nanosecond pulsed corona discharges and reported a maximum effective CO2 conversion and energy efficiency of 3.2% and 26%, respectively, for a CO2-Ar mixture (mass ratio 1:1) [7]. Bak et al. achieved a maximum conversion of 7.3% and the highest energy efficiency of 11.5% [4] for the application of 10-ns high-voltage pulses. Recently, Mai et al. also studied a NSP-DBD for reforming CH4 with CO2 [18]. They demonstrated that conduction current and transferred charge increased significantly by increasing the applied voltage and length of the discharge, which was considered beneficial for promoting reaction chemistries. For the applied high-voltage pulse of 26 kV and a flow rate of 25 ml/min with a CH4:CO2 molar ratio of 1:1, the total highest gas conversion of 30.3% was obtained in a discharge length of 10 cm. Conversely, for a higher flow rate of 50 ml/min but a lower applied voltage of 20 kV, the highest energy efficiency was 12.4%.
The different reports support the possibility to control the operation of a DBD by pulse parameters with the goal to benefit electron generation mechanisms and consequently foster chemical reactions. These are obviously pulse duration, pulse rise time, pulse fall time, duty cycle, pulse amplitude, and pulse repetition rate, which primarily determine the energy that is dissipated in the plasma. In general, pulse voltage has a more pronounced effect on chemistries than pulse repetition rate. A respective increase in SEI was associated with higher conversion [1].
However, a so far mostly overlooked but arguable interesting and relevant feature are pulse polarities, which are associated with distinct differences in the underlying physical mechanisms. Briels et al. reported that in ambient air, inception characteristics and propagation processes are different for negative and positive streamers, which should also apply to the development of microdischarges in a DBD. Negative streamers appeared only when a voltage above 40 kV was applied, whereas positive streamers were already initiated for voltages of 5 kV [27]. The findings confirm the results that are shown in Fig. 2 with lower amplitudes of 10 kV already sufficient for the formation of a plasma by high-voltage pulses of positive polarity, while a voltage of 15 kV is needed for the generation of a plasma with negative polarity. The branching of positive and negative streamers was also found to be explicitly different, directly affecting the number, but also length, of plasma filaments. Zhang et al. demonstrated for pulsed DBDs that a greater number of branches appeared along the dielectric for positive streamers, while negative streamers spread uniformly on the surface of the dielectric and no branches were observed [28]. This characteristic was also indicated by the images shown in Fig. 3. The implied more numerous, more intense and longer filaments for the positive polarity, hence, explain the higher conversion and chemical production. According to Zhang et al., a positive space charge region in front of the streamer heads enables an efficient acceleration of electrons toward the anode. The corresponding strong electric field at the head is a more effective electron production and streamer propagation mechanism than supplied by the electron drift for negative streamers, i.e., for the application of negative high-voltage pulses [28].
These differences and their potential also motivated the presented study. A coaxial dielectric barrier discharge was operated with nanosecond high-voltage pulses at atmospheric pressure and room temperature in a mixture of argon and carbon dioxide. The conversion of the molecular constituents should be affected by the same processes in a similar fashion as previously observed in related settings. Accordingly, the influence of positive and negative polarity for the discharge development on CO2 splitting and CO production was investigated. Indeed, the application of high-voltage pulses of positive polarity was found more effective, resulting in a higher CO2 conversion and higher CO production as demonstrated in Fig. 5. Although, how plasma chemistries are affected in detail requires further studies.
Other relevant process parameters, besides polarity and pulse repetition rate, are residence times or gas flow rates [8]. The influence of pulse frequency is shown in Fig. 5. Both effective CO2 conversion and CO production similarly increased with higher frequency for both positive and negative polarity and the same gas flow rate. This implies that rather more reactants were exposed to the respective plasma chemistries. However, these processes were not affected by the pulse repetition rate itself. Notable, doubling the frequency from 1 to 2 kHz did neither double CO2 conversion nor CO production, which suggests that still a major amount of CO2 was not interacting with the plasma. The further increase, associated with a change in pulse repetition rate from 2 to 3 kHz, was less steep, conceivably due to limitations of the pulse generator to supply amplitudes of the nominal voltage of 20 kV and the same currents as for an operation at 1 or 2 kHz [23]. However, the applied frequencies might, overall, still be much too low to affect a larger share of CO2. This was further confirmed by the carbon balance, i.e., the carbon could be completely accounted for.
Paulussen et al. have demonstrated that an optimum operating frequency (AC) for CO2 conversion in an atmospheric pressure DBD depends on the provided power. An optimum frequency for the highest investigated power of 200 W was found to lie between 30 and 60 kHz. A further increase in frequency up to 90 kHz was not beneficial for conversion. A different behavior was observed for pulsed glow discharges with an increase in CO2 conversion from 6 to 14% as a result of an increase in discharge frequency from 1 to 5 kHz for the same voltage. The comparison hints at the need to investigate possible mechanisms, e.g., residual ionization or differences in energy dissipation channels that could be affected by discharge frequency for different plasma settings still in more detail.
Of course, instead of higher frequencies, residence times could also be extended by reducing flow rates, which has been repeatedly reported. For example, Niu et al. presented for a cylindrical DBD with a multi-electrode system the highest conversion of 18.5% for the lowest flow rate of 30 ml/min for pure CO2 [3]. However, with a future application of large volume treatments in mind, the approach to reduce flow rate appears counterproductive. Nevertheless, the flow rate was confirmed as another crucial parameter in the observed process of CO2 splitting. Not surprisingly, effective CO2 conversion and CO production decreased by increasing the flow rate, while energy efficiency and energy consumption increased. Accordingly, the highest value for effective CO2 conversion was observed for 30 ml/min (Fig. 5a), while the best energy efficiency was achieved at 210 ml/min (Fig. 8a). The reason for the inverse behavior of the CO2 conversion and energy efficiency can be explained by the back reaction (CO + O → CO2). The higher the conversion, the more CO and O2 are formed. Presumably, the back reaction then accelerates and becomes more important with more O2 [29, 30] However, a recent detailed study on the back reaction by Navascués et al. did actually suggest the opposite development [31].
Regardless, the electrical power, which was provided for the operation of the discharge (Eq. 2), was primarily determined by the pulse repetition rate. The electrical operating parameters describe, together with the gas flow rate, the energy, i.e., specific energy input, SEI (Eq. 6), which was in principle available for chemical reactions. A higher pulse voltage or repetition rate provided a higher power, which, hence, increased the SEI as shown in Fig. 6. However, the values did not increase linearly as could be expected from Eq. 6. Although this might still be valid for an increase in pulse repetition rate from 1 to 2 kHz, the further increase to 3 kHz might suffer from the limitations of the pulse generator as already discussed.
Concurrently, the SEI was decreasing with gas flow rate as shown in Fig. 6 for 30 and 60 ml/min and the wider range presented in Fig. 8. These results at least indicated that the dependency on flow rate is not strictly proportional to the inverse flow rate as suggested by Eq. 6. Accordingly, the relation between pulse repetition rate and flow rate could be more intricate than described by this formulation. A correlation between discharge power and the flow rate has also been reported in other studies, which confirm these general findings [1, 3, 4].
In general, a higher CO2 conversion was achieved for higher SEI, which is explicitly shown in Fig. 8 and in agreement with other reports [1, 3, 4]. However, the supplied energy is neither completely directed into the conversion of the CO2 nor was the entire volume of CO2 comprehensively treated. The relation between SEI and conversion was, again, not linear because of the already described interrelated contributions of electrical power, i.e., pulse frequency, and flow rate but also other aspects concerning discharge configurations and their operation. Overall, the performance of any system suffers when ‘overwhelmed’ by the volume that has to be treated.
Consequently, energy efficiencies were rapidly decreasing with pulse repetition rate although increasing with flow rate simply because the same energy was dissipated in a larger volume without necessarily corresponding to higher conversion. Accordingly, an increase in the SEI actually reduced energy efficiency, with the lowest value of 1.65% for the highest observed SEI of 30 kJ/L for a flow rate of 30 ml/min (Fig. 8). Conversely, effective CO2 conversion was decreasing with increasing flow rate (c.f. Figs. 5a, 8a). Equation 7 describes this characteristic, where pulse frequency and flow rate are implicitly considered in the SEI. More importantly, the equation addresses the actual need, i.e., reaction enthalpy, ΔRH0, for the splitting of CO2. Correspondingly, this was addressed by the energy cost for CO2 splitting as described by Eqs. 8 and 9, respectively. A similar argument for the influence of pulse repetition rate with respect to flow rate can explain the lowest obtained energy cost of about 94.4 eV/molecule for an operation at a lower frequency and higher flow rate (c.f. Fig. 7b). The correlated variation of these parameters was most effective to achieve high CO2 conversion and CO production for high-voltage pulses that were applied with positive polarity (c.f. Fig. 5). Although the results are in the same range as for previously reported experiments [7], a more detailed investigation in conjunction with modifications of setup and approach still leaves room for improvement. This is also expressed by the comparison of the results, specifically as shown in Fig. 5, and the thermodynamic calculations presented in Fig. 9. The actual energy (SEI) expended for the conversion was about 20 to 100 times higher than the thermodynamically required energy (SER). The difference between both was primarily released as heat. Interestingly, the difference is significantly smaller for the processes carried out with negative polarity than for those with positive polarity, although the effective conversion was higher for the latter. However, the increase in effective CO2 conversion, which was caused by an increase in pulse frequency, was in the range of 1.5–2%. These values are significantly higher than those calculated from a possible temperature increase. Thus, a thermal effect can be excluded for the increase in the effective CO2 conversion. Corollary, this further supports the assumption that distinct differences in the underlying mechanisms in the discharge development for positive and negative high-voltage pulses are responsible for the results.
5 Conclusion
The effect of high-voltage pulse polarity on CO2 splitting was investigated for a nanosecond pulsed DBD, which has not been reported so far. The operation with high-voltage pulses of positive polarity demonstrated a higher CO2 conversion. Although the identified energy efficiency was still low (for both polarities), the approach warrants further investigation. Especially shorter pulse durations could offer a way to optimize conversion efficiencies further. So far, the studies were limited to pulses of 500 ns in duration. In addition, changes in the configuration, e.g., multi-electrode systems, different geometries, and packed bed fillings, as well as the control of operating parameters, e.g., temperatures, admixtures of hydrogen to the operating gas or the use of catalysts in the reactor, could lead to further improvements. Regardless, a better understanding of underlying mechanisms for the discharge development for positive and negative high-voltage pulses seems necessary.
Data Availability Statement
This manuscript has no associated data, or the data will not be deposited. [Authors’ comment: The data that support the findings of this study are available within the article.]
References
R. Snoeckx, A. Bogaerts, Plasma technology—a novel solution for CO2 Conversion? Chem. Soc. Rev. 46(19), 5805–5863 (2017). https://doi.org/10.1039/c6cs00066e
R. Snoeckx, S. Heijkers, K. Van Wesenbeeck, S. Lenaerts, A. Bogaerts, CO2 conversion in a dielectric barrier discharge plasma: N2 in the mix as a helping hand or problematic impurity? Energy Environ. Sci. 9(3), 999–1011 (2016). https://doi.org/10.1039/c5ee03304g
G. Niu, Y. Qin, W. Li, Y. Duan, Investigation of CO2 splitting process under atmospheric pressure using multi-electrode cylindrical DBD plasma reactor. Plasma Chem. Plasma Process. 39(4), 809–824 (2019). https://doi.org/10.1007/s11090-019-09955-y
A. George, B. Shen, M. Craven, Y. Wang, D. Kang, C. Wu, X. Tu, A review of non-thermal plasma technology: a novel solution for CO2 conversion and utilization. Renew. Sustain. Energy Rev. 135, 109702 (2021). https://doi.org/10.1016/j.rser.2020.109702
B. Eliasson, U. Kogelschatz, Nonequilibrium volume plasma chemical processing. IEEE Trans. Plasma Sci. 19(6), 1063–1077 (1991). https://doi.org/10.1109/27.125031
C.-J. Liu, G.-H. Xu, T. Wang, Non-thermal plasma approaches in CO2 Utilization. Fuel Process. Technol. 58(2–3), 119–134 (1999). https://doi.org/10.1016/s0378-3820(98)00091-5
M.S. Moss, K. Yanallah, R.W. Allen, F. Pontiga, An investigation of CO2 splitting using nanosecond pulsed corona discharge: Effect of argon addition on CO2 Conversion and energy efficiency. Plasma Sources Sci. Technol. 26(3), 035009 (2017). https://doi.org/10.1088/1361-6595/aa5b1d
A. Ozkan, T. Dufour, T. Silva, N. Britun, R. Snyders, A. Bogaerts, F. Reniers, The influence of power and frequency on the filamentary behavior of a flowing DBD—application to the splitting of CO2. Plasma Sources Sci. Technol. 25(2), 025013 (2016). https://doi.org/10.1088/0963-0252/25/2/025013
B. Eliasson, U. Kogelschatz, Modeling and applications of Silent Discharge Plasmas. IEEE Trans. Plasma Sci. 19(2), 309–323 (1991). https://doi.org/10.1109/27.106829
G. Chen, R. Snyders, N. Britun, CO2 conversion using Catalyst-free and catalyst-assisted plasma-processes: Recent progress and understanding. J. CO2 Util. 49, 101557 (2021). https://doi.org/10.1016/j.jcou.2021.101557
R. Aerts, W. Somers, A. Bogaerts, Carbon dioxide splitting in a dielectric barrier discharge plasma: a combined experimental and computational study. Chemsuschem 8(4), 702–716 (2015). https://doi.org/10.1002/cssc.201402818
T. Wang, H. Liu, X. Xiong, X. Feng, Conversion of carbon dioxide to carbon monoxide by pulse dielectric barrier discharge plasma, in IOP Conference Series: Earth and Environmental Science, vol 52, p. 012100 (2017). https://doi.org/10.1088/1742-6596/52/1/012100
D. Ray, C. Subrahmanyam, CO2 decomposition in a packed DBD plasma reactor: Influence of Packing Materials. RSC Adv 6(45), 39492–39499 (2016). https://doi.org/10.1039/c5ra27085e
A. Ozkan, T. Dufour, T. Silva, N. Britun, R. Snyders, F. Reniers, A. Bogaerts, DBD in burst mode: Solution for more efficient CO2 conversion? Plasma Sources Sci Technol 25(5), 055005 (2016). https://doi.org/10.1088/0963-0252/25/5/055005
M.S. Bak, S.-K. Im, M. Cappelli, Nanosecond-pulsed discharge plasma splitting of carbon dioxide. IEEE Trans. Plasma Sci. 43(4), 1002–1007 (2015). https://doi.org/10.1109/tps.2015.2408344
S. Heijkers, L.M. Martini, G. Dilecce, P. Tosi, A. Bogaerts, Nanosecond pulsed discharge for CO2 Conversion: kinetic modeling to elucidate the chemistry and improve the performance. J. Phys. Chem. C 123(19), 12104–12116 (2019). https://doi.org/10.1021/acs.jpcc.9b01543
Y. Gao, S. Zhang, H. Sun, R. Wang, X. Tu, T. Shao, Highly efficient conversion of methane using microsecond and nanosecond pulsed spark discharges. Appl. Energy 226, 534–545 (2018). https://doi.org/10.1016/j.apenergy.2018.06.006
D. Mei, P. Zhang, G. Duan, S. Liu, Y. Zhou, Z. Fang, X. Tu, CH4 reforming with CO2 using a nanosecond pulsed dielectric barrier discharge plasma. J. CO2 Util. 62, 102073 (2022). https://doi.org/10.1016/j.jcou.2022.102073
D. Ray, R. Saha, S. Ch, DBD plasma assisted CO2 decomposition: Influence of diluent gases. J. Catal. 7(9), 244 (2017). https://doi.org/10.3390/catal7090244
S. Paulussen, B. Verheyde, X. Tu, C. De Bie, T. Martens, D. Petrovic, A. Bogaerts, B. Sels, Conversion of carbon dioxide to value-added chemicals in atmospheric pressure dielectric barrier discharges. Plasma Sources Sci. Technol. 19(3), 034015 (2010). https://doi.org/10.1088/0963-0252/19/3/034015
X. Wang, Y. Gao, S. Zhang, H. Sun, J. Li, T. Shao, Nanosecond pulsed plasma assisted dry reforming of CH4: The effect of plasma operating parameters. Appl. Energy 243, 132–144 (2019). https://doi.org/10.1016/j.apenergy.2019.03.193
T. Hoder, H. Höft, M. Kettlitz, K.-D. Weltmann, R. Brandenburg, Barrier discharges driven by sub-microsecond pulses at atmospheric pressure: Breakdown manipulation by pulse width. J. Plasma Phys. 19(7), 070701 (2012). https://doi.org/10.1063/1.4736716
H. Jiang, T. Shao, C. Zhang, Z. Niu, Y. Yu, P. Yan, Y. Zhou, Comparison of AC and nanosecond-pulsed DBDs in Atmospheric Air. IEEE Trans. Plasma Sci. 39(11), 2076–2077 (2011). https://doi.org/10.1109/tps.2011.2146280
A. Ghorbanzadeh, R. Lotfalipour, S. Rezaei, Carbon dioxide reforming of methane at near room temperature in low energy pulsed plasma. Int. J. Hydrog. Energy 34(1), 293–298 (2009). https://doi.org/10.1016/j.ijhydene.2008.10.056
O. Khalifeh, A. Mosallanejad, H. Taghvaei, M.R. Rahimpour, A. Shariati, Decomposition of methane to hydrogen using nanosecond pulsed plasma reactor with different active volumes, voltages and frequencies. Appl. Energy 169, 585–596 (2016). https://doi.org/10.1016/j.apenergy.2016.02.017
Y. Zeng, X. Tu, Plasma-catalytic hydrogenation of CO2 for the cogeneration of CO and CH4 in a dielectric barrier discharge reactor: Effect of argon addition. J. Phys. D 50(18), 184004 (2017). https://doi.org/10.1088/1361-6463/aa64bb
T.M. Briels, J. Kos, G.J. Winands, E.M. van Veldhuizen, U. Ebert, Positive and negative streamers in ambient air: Measuring diameter, velocity and dissipated energy. Appl. Phys. D 41(23), 234004 (2008). https://doi.org/10.1088/0022-3727/41/23/234004
Q.Z. Zhang, L. Zhang, D.Z. Yang, J. Schulze, Y.N. Wang, A. Bogaerts, Positive and negative streamer propagation in volume dielectric barrier discharges with planar and porous electrodes. Plasma Process Polym 18(4), 2000234 (2021). https://doi.org/10.1002/ppap.202000234
Y. Uytdenhouwen, S. Van Alphen, I. Michielsen, V. Meynen, P. Cool, A. Bogaerts, A packed-bed DBD micro plasma reactor for CO2 dissociation: does size matter? Chem. Eng. J. 348, 557–568 (2018). https://doi.org/10.1016/j.cej.2018.04.210
Y. Uytdenhouwen, K.M. Bal, I. Michielsen, E.C. Neyts, V. Meynen, P. Cool, A. Bogaerts, How process parameters and packing materials tune chemical equilibrium and kinetics in plasma-based CO2 Conversion. Chem. Eng. J. 372, 1253–1264 (2019). https://doi.org/10.1016/j.cej.2019.05.008
P. Navascués, J. Cotrino, A.R. González-Elipe, A. Gómez-Ramírez, Plasma assisted CO2 dissociation in pure and gas mixture streams with a ferroelectric packed-bed reactor in ambient conditions. Chem. Eng. J. 430, 133066 (2022). https://doi.org/10.1016/j.cej.2021.133066
Acknowledgements
This project is supported by the ‘Leibniz ScienceCampus ComBioCat.’
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
SMB performed all the experiments, collected all of the data, analyzed the measurements, and wrote all drafts of the paper under the guidance of JFK, who then revised it before submission. VB contributed to the scientific discussions and was involved in drafting the final paper. Funding acquisition was performed by VB.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interests to declare that are relevant to the content of this article.
Additional information
Electron-Driven Processes from Single Collisions to High-Pressure Plasmas. Guest editors: Jose L Lopez, Michael Brunger, Holger Kersten.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mousazadeh Borghei, S., Brüser, V. & Kolb, J.F. Polarity dependence of CO2 conversion in nanosecond pulsed large gap dielectric barrier discharges. Eur. Phys. J. D 77, 36 (2023). https://doi.org/10.1140/epjd/s10053-023-00611-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-023-00611-x