1 Introduction

Magnetic fields are integral to astrophysics since they are detectable and measurable for nearly all celestial bodies and substantially affect charged entities. Hence, one must know how magnetized objects’ dipole moment interacts with the BH’s external magnetic field to analyze the test particle dynamics. The existence of magnetic fields around BHs is a factor in testing gravity theories. Wald [1] investigated the electromagnetic fields around a Kerr BH in an asymptotically uniform external magnetic field. Later, in the presence of external magnetic fields such as uniform, dipolar, and split monopole magnetic fields, several researchers have investigated electromagnetic fields near various spacetime models [2,3,4,5,6,7,8,9,10,11,12].

In astrophysics, the motion of electrically charged and neutral test particles near BHs is important. Charged-particle motions are particularly intriguing, as they are essential for comprehending the impact of magnetic fields on the accretion process. By studying the motion of particles near magnetized BHs, Konoplya [13] found that the tidal charge significantly affects the motion of massive and massless particles. Particle collision in the ergosphere and the dynamics of particles are examined in Kerr, Kerr–Newman–Kasuya BHs and various charged BHs [14,15,16,17,18,19,20,21,22]. The electric Penrose mechanism and charged particle collisions near charged BHs in KR gravity were recently examined in Ref. [23]. A comprehensive and detailed analysis of charged particle dynamics in magnetized BHs can be found in Refs. [24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Khan and Chen examined charged-particle dynamics near Kerr BHs in a split monopole magnetic field. They focused on determining the location of stable circular orbits and found that a positive magnetic field enhances the stability of the effective potential [10].

The Rossi X-ray Timing Explorer (RXTE) project made several observations of BH transients, making it a valuable resource for studying X-ray binaries [38, 39]. This field of research is of significant interest because of the potential it provides for probing basic physics. QPO in X-ray flux curves remains well documented in binary systems with stellar-mass BHs. These oscillations are regarded as a very effective means of testing the accuracy of strong gravity theories [40,41,42,43,44,45]. These changes closely resemble the behavior of the BH and exhibit frequencies that are inversely proportional to the BH’s mass. Based on the recorded frequency of QPOs, which span from a few mHz to 0.5 kHz, many categories of QPOs were identified. Primarily, they refer to high-frequency (HF) and low-frequency (LF) QPOs with maximum frequencies of 500 Hz and 30 Hz, respectively. The RXTE project identified complicated irregularity structures, encompassing the finding of QPO at frequencies above 40Hz [39]. HF QPOs provide insights into neutron stars’ radii and masses [46, 47], as well as the spin and masses of core entities [48].

Microquasars consist of a BH and a companion star in a binary system. The matter from the companion star creates an accretion disc around the BH, which gives rise to relativistic jets, which are bipolar outflows of matter along the rotation axis of the accretion disc. Friction inside the accretion disc causes the matter to heat up and release electromagnetic radiation, which may be detected through X-rays and near the BH’s horizon [49].

Following the first discovery of QPOs, several efforts were made to analyze the observed QPOs accurately. Several hypotheses were put forward, including the Disko-seismic models, hot spot models, warped disk models, and numerous iterations of resonance models. Among other models, the geodesic oscillatory model is the most commonly used, in which the frequencies are connected to the frequencies of the geodesic orbital and epicyclic motion. Refer to [32] for a comprehensive discussion. This article examines the effects of various factors on the motion of charged test particles in BHs of KR gravity under the influence of an external magnetic field. The QPOs for neutral test particles were previously studied in [50]. In recent years, the investigation of QPOs around BHs, microquasars, and wormholes has attracted many researchers [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. The manuscript is organized as follows: in the coming section, we will analyze test particle emotion around static and spherically symmetric BHs in the KR gravity. In Sect. 3, we aim to examine quasi-periodic and harmonic oscillations using the concept of fundamental frequencies. Section 4 of our article explores the QPO models in KR gravity. Finally, in Sect. 6, we will conclude our findings with concluding remarks.

2 Circular motion of test particle around KR BHs

In heterotic string theory [66], we attribute the KR field [67], a second-rank self-interacting antisymmetric tensor field, to closed string excitation. The non-minimal connection between the tensor field’s non-zero vacuum expectation value and the gravity sector results in spontaneous Lorentz symmetry violation; the ground state of a physical quantum system is defined by non-trivial vacuum expectation values [68,69,70,71,72]. The KR field has numerous implications, such as the ability to twist spacetime [73], affecting the discovered anisotropy in the cosmic microwave background field [74], topological defects causing galaxies to have intrinsic angular momentum [75], and providing insights into the leptogenesis [76,77,78,79,80,81,82,83,84,85,86].

In this section, we will precisely review the dynamics of test particles around static and spherically symmetric BHs in gravity with a background KR field described by the following metric [87],

$$\begin{aligned} ds^2=-F(\text {r})dt^2+\dfrac{1}{F(\text {r})}dr^2+r^2( d\theta ^2+\sin ^2\theta d\phi ^2) \end{aligned}$$
(1)

with the lapse function,

$$\begin{aligned} F(\text {r}) = \frac{1}{1-l}-\frac{2 M}{r}, \end{aligned}$$
(2)

where the dimensionless parameter l defines the effect of Lorentz violation caused by the nonzero vacuum expectation value (VEV) of the KR field on spacetime [69, 87, 88]. This section inspects the test particle dynamics in the spacetime (1) around static and spherically symmetric BHs in KR gravity.

2.1 Equation of motion

First, we consider the motion of a test particle in the geometry of static and spherically symmetric BH in KR gravity. The equation of motion of a neutral particle of mass m can be obtained by using the Lagrangian density [89]

$$\begin{aligned} \mathcal {L}_p=\frac{1}{2}m g_{\mu \nu } {u}^{\mu } {u}^\nu , \end{aligned}$$
(3)

time translation and rotational symmetry of the geometry corresponds to the conserved quantities that can be calculated using the Killing vectors

$$\begin{aligned} \xi _{(t)}^{\mu }\partial _{\mu }=\partial _{t} , \qquad \xi _{(\phi )}^{\mu }\partial _{\mu }=\partial _{\phi }, \end{aligned}$$
(4)

here \(\xi _{(t)}^{\mu }=(1,~0,~0,~0)\) and \(\xi _{(\phi )}^{\mu }=(0,~0,~0,~1) \), and the corresponding conserved quantities are the specific energy \(\mathcal {E}=E/m\) of the moving particle and its angular momentum \(\mathcal {L}=L/m\)

$$\begin{aligned} \dot{t}=-\frac{\mathcal {E}}{g_{tt}},~~~~ \dot{\phi }=\frac{\mathcal {L}}{g_{\phi \phi }}. \end{aligned}$$
(5)

The particle’s motion is restricted to the equatorial plane, that is, for a constant angle \(\theta =\pi /2\), so \(\dot{\theta }=0\) [9]. The normalization condition governs equations of motion for a test particle,

$$\begin{aligned} g_{\mu \nu }u^{\mu }u^{\nu }=\epsilon \ , \end{aligned}$$
(6)

where \(\epsilon \) takes the values 0 and \(-1\) for massless and massive particles, respectively. For the particles with non-zero rest mass, the equation of motion can be governed by time-like geodesics of spacetime. Using the condition (6), one can easily obtain the equations of motion as

$$\begin{aligned} \dot{r}^2= & {\mathcal {E}}^2+g_{tt}\left( 1+\frac{\mathcal {K}}{r^2}\right) \, \end{aligned}$$
(7)
$$\begin{aligned} \dot{\theta }= & \frac{1}{g_{\theta \theta }^2}\Big (\mathcal{K}-\frac{\mathcal{L}^2}{\sin ^2\theta }\Big )\, \end{aligned}$$
(8)
$$\begin{aligned} \dot{\phi }= & \frac{\mathcal{L}}{g_{\phi \phi }}\, \end{aligned}$$
(9)
$$\begin{aligned} \dot{t}= & -\frac{\mathcal{E}}{g_{tt}}\, \end{aligned}$$
(10)

where \(\mathcal{K}\) is the constant for the angular motion, also known as the Carter constant, and corresponds to the total angular momentum of the test particle.

In our further studies, we consider the motion of the particles to be restricted to occur in the equatorial plane where \(\theta =\pi /2\), \(\dot{\theta }=0\), and the Carter constant is \(\mathcal{K}=\mathcal{L}^2\), the equation for the radial motion of the particles becomes

$$\begin{aligned} \dot{r}^2=\mathcal{E}^2-V_\textrm{eff}\, \end{aligned}$$
(11)

where the effective potential is

$$\begin{aligned} V_\textrm{eff} = F(r)\left( 1+\frac{\mathcal{L}^2}{r^2}\right) . \end{aligned}$$
(12)
Fig. 1
figure 1

The radial dependence of a test particle’s effective potential for different parameter values l

Full size image

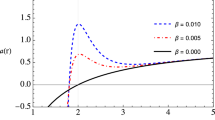
Figure 1 represents the radial dependence of the effective potential for the radial motion of test particles for the critical value of dimensionless parameter l compared to the Schwarzschild BH case \((l=0)\). We can see that the presence of the parameter l causes an increase in the effective potential, while its negative value reduces it. Thus, we can say that the dimensionless parameter l contributes to the instability of effective potential.

2.2 Circular orbits

Next, we study circular orbits of test particles around BHs in KR gravity using the below conditions [90],

$$\begin{aligned} \dot{r}=0,\quad V_\textrm{eff}=\mathcal {E}, \quad \partial _r V_\textrm{eff}=0, \end{aligned}$$
(13)

here, \(\partial _{r}\) refers to the first-order (partial) derivative w.r.t. the radius of orbits r. The first-order derivative represents the stationary points in the effective potential curve, and the last condition corresponds to the minimum values of the effective potential.

Using the above conditions, the following expressions for the energy and angular momentum of the particles corresponding to circular orbits can be obtained:

$$\begin{aligned} \mathcal{L}^2= & \frac{(1-l) M r^2}{r-3 (1-l) M}\, \end{aligned}$$
(14)
$$\begin{aligned} \mathcal{E}^2= & \frac{1}{(1-l) r }\frac{(r-2 (1-l) M)^2}{r-3 (1-l) M}. \end{aligned}$$
(15)
Fig. 2
figure 2

The radial dependence of specific angular momentum (left panel) and energy (middle and right panels) for circular orbits for different values of parameter l

Full size image

Figure 2 shows the radial profiles of the specific energy and angular momentum. We observed that the parameter l diminishes the specific angular momentum while increasing energy along the radial profile r. However, the negative values of l influence them in reverse order. Thus, compared with Schwarzschild BHs, KR BHs have a lower specific angular momentum and a greater specific energy for \(l>0\), and vice versa for \(l<0\). Furthermore, the graphical illustration of specific energy along \(\mathcal{L}\) shows that the specific angular momentum contributes to the energy, whereas l influences it in the same way as in the previous case.

2.3 Innermost stable circular orbits

Stable circular orbits occur at radius \(r = r_{min}\), where the particles’ minimum energy and angular momentum correspond to circular orbits. For the innermost stable circular orbits (ISCOs), the conditions \(\partial _r V_\textrm{eff}=0,\) and \(\partial _{rr}V_\textrm{eff}=0\) must be satisfied, leading to the same results. After some algebraic simplifications, the expression of the ISCO radius took the form \(r_{ISCO}=6M (1-l)\), and the minimum radius of circular orbits can be found using Eq. (14) as \(r_{ph}=3M (1-l)\). One can get that

$$\begin{aligned} \frac{r_{ISCO}}{6M}=\frac{r_{ph}}{3M}=1-l. \end{aligned}$$
(16)
Fig. 3
figure 3

Radius of the ISCO and photosphere as a function of the dimensionless parameter l in KR gravity

Full size image

In Fig. 3, we show dependencies of normalized values of ISCO/photonsphere radius to 6M/3M from the KR field parameter. In the GR limit \(l=0\), the ISCO radius takes 6M, and the photonsphere is located at 3M, while in the limit \(l=1\), both become zero.

In the following, we also analyze the dependencies of energy (\(\mathcal{E}\, |_\textrm{ISCO}\)) and angular momentum of the particles at ISCO, as well as the energy efficiency \(\eta =1-\mathcal{E}\, \Big |_{\,r=r_\textrm{ISCO}}\) on the KR parameter graphically.

Fig. 4
figure 4

Graphical illustration of the ISCO radius, specific angular momentum, specific energy, and energy efficiency at the ISCO radius of neutral particles for different values of the parameter l

Full size image

In Fig. 4, we show the dependence of the specific energy and angular momentum at the ISCO and energy efficiency along l (top row) and \(r_{ISCO}\) (bottom row). From the graphical description, we note that the angular momentum and energy at the ISCO decrease and increase, respectively, along l. In other words, l contributes to the energy at ISCO, whereas it diminishes the angular momentum at ISCO. Moreover, l has a considerable influence on energy efficiency as \(l<0\) cases increase while \(l<0\) decreases it.

The bottom row of Fig. 4 shows a connection between the specific energy, angular momentum, and particle’s radius at the ISCO. Unlike the upper row in the lower row, we observe that energy at the ISCO decreases while angular momentum at the ISCO increases along the radial profile of the ISCO. In addition, in the bottom right panel, we noticed a similar behavior of the energy at the ISCO vs. the angular momentum at the ISCO, i.e., energy and angular momentum are inversely proportional to each other at the ISCO.

3 Fundamental frequencies

This section details the derivation of the expression for the fundamental frequencies governed by test particles orbiting around BHs in KR gravity. This is one of the simple models to explain the QPO observable around compact astrophysical objects.

3.1 Keplerian frequency

The angular velocity (\(\Omega _K=\frac{d\phi }{dt}\)) measured by a distant observer is the same as the pure Schwarzschild case [63],

$$\begin{aligned} \Omega _K^2=\frac{M}{r^3} . \end{aligned}$$
(17)

To compare the fundamental frequencies with the corresponding astrophysical quantities, we will express them in units of Hz using the relation,

$$\begin{aligned} \nu _{K,r,\theta } = \frac{1}{2\pi }\frac{c^3}{GM} \Omega _{K,r,\theta }\ , [\textrm{Hz}]\ . \end{aligned}$$
(18)

By converting the frequencies from geometrical units to the unit of Hz in the international unit of systems, we use the speed of light in vacuum and gravitational constant as \(c=3\cdot 10^8 \,\textrm{m}/\textrm{s}\) and \(G=6.67\cdot 10^{-11}\,\textrm{m}^3/(\textrm{kg}^2\cdot \textrm{s})\), respectively.

Fig. 5
figure 5

Relations between the frequencies of upper and lower picks of twin peak QPOs in the RP, WD, and ER2-4 models around Schwarzschild BH and BHs in the KR gravity for different values of the parameter l

Full size image

3.2 Harmonic oscillations

In this subsection, we present the analysis of the fundamental frequencies operated by the oscillation of the motion of the test particles around BH in KR gravity. The fundamental radial and vertical frequencies can be calculated by considering small perturbations along the radial \(r\rightarrow r_0+\delta r\) and vertical \(\theta \rightarrow \theta _0+\delta \theta \) directions around the circular orbit, respectively. The effective potential can be extended in terms of r and \(\theta \) in the form,

$$\begin{aligned} & V_\textrm{eff}(r,\theta )=V_\textrm{eff}(r_0,\theta _0) \nonumber \\ & \quad + \, \delta r\,\partial _r V_\textrm{eff}(r,\theta )\Big |_{r_0,\theta _0} +\delta \theta \, \partial _\theta V_\textrm{eff}(r,\theta )\Big |_{r_0,\theta _0} \nonumber \\ & \quad + \, \frac{1}{2}\delta r^2\,\partial _r^2 V_\textrm{eff}(r,\theta )\Big |_{r_0,\theta _0}+\frac{1}{2}\delta \theta ^2\,\partial _\theta ^2 V_\textrm{eff}(r,\theta )\Big |_{r_0,\theta _0} \nonumber \\ & \quad + \, \delta r\,\delta \theta \,\partial _r\partial _\theta V_\textrm{eff}(r,\theta )\Big |_{r_0,\theta _0}+\mathcal{O}\left( \delta r^3,\delta \theta ^3\right) . \end{aligned}$$
(19)

Careful analysis of the extension (19) shows that its first term disappears due to the condition \(\partial _rV_\textrm{eff}=0\). On the other hand, the second, third, and last terms can be removed using the stability conditions of the effective potential in Eq. (12). Finally, only two terms proportional to the second-order derivatives from the effective potential relating r and \(\theta \) remain. To obtain physical quantities measured by a distant observer in the equation of motion, we replace a derivation relating the affine parameter with the time derivation (\(dt/d\lambda =u^t\)). By substituting Eq. (19) into Eq. (12) and taking into account argument imaginations, one may easily take harmonic oscillator equations for displacements \(\delta r\) and \(\delta \theta \) in the form,

$$\begin{aligned} \frac{d^2\delta r}{dt^2}+\Omega _r^2 \delta r=0\,, \qquad \frac{d^2\delta \theta }{dt^2}+\Omega _\theta ^2 \delta \theta =0\ . \end{aligned}$$
(20)

The quantities \(\Omega _r\) and \(\Omega _\theta \) in Eq. (20) are the radial and vertical angular frequencies identified by a distant observer, respectively, and can be described as

$$\begin{aligned} & \Omega _r^2=-\frac{1}{2g_{rr}\dot{t}^2}\partial _r^2V_\textrm{eff}(r,\theta )\Big |_{\theta =\pi /2}, \end{aligned}$$
(21)
$$\begin{aligned} & \Omega _\theta ^2=-\frac{1}{2g_{\theta \theta }\dot{t}^2}\partial _\theta ^2V_\textrm{eff}(r,\theta )\Big |_{\theta =\pi /2}, \end{aligned}$$
(22)
$$\begin{aligned} & \Omega _{\phi }=\frac{d\phi }{dt}. \end{aligned}$$
(23)

Finally, the radial and vertical frequencies in the spacetime of BHs in KR gravity will take the following form:

$$\begin{aligned} \Omega _r= & \Omega _K \sqrt{\frac{1}{1-l}-\frac{6 M}{r}}, \nonumber \\ \Omega _\theta= & \Omega _\phi = \Omega _K . \end{aligned}$$
(24)

For the theoretical understanding of the fundamental frequencies, one can express them in the unit of Hz:

$$\begin{aligned} \nu = \frac{1}{2\pi }\frac{c^3}{GM} \Omega \ , [\textrm{Hz}]\ . \end{aligned}$$
(25)

4 QPO models in KR gravity

This section will explore the possible frequencies of twin peak QPOs around BHs in KR gravity compared to the standard Schwarschild BHs in various models of twin peak QPOs. We write equations for the upper and lower frequencies as functions of the radial coordinate and BH parameters, according to the QPOs model. After this, we supply values of the frequencies to keep the BH parameters constant and plot all possible values of the lower and upper frequencies at the distances from the ISCO radius up to infinity. For example, we use the following standard models [49]:

(I) RP model, which describes the upper and lower frequencies of the twin peak QPOs by radial and orbital frequencies as \(\nu _U=\nu _\phi \) and \(\nu _L=\nu _\phi -\nu _r\), respectively.

(II) ER2, ER3, and ER4 models. In the ER models, the accretion disk is assumed to be thick enough, and QPOs appear due to the resonance oscillations of uniformly radiating particles along geodesic orbits. The frequencies for the ER2, ER3, and ER4 models are defined through the orbital and epicyclic oscillation frequencies as \(\nu _U=2\nu _\theta -\nu _r\), \(\nu _L=\nu _r\), \(\nu _U=\nu _\theta +\nu _r\), \(\nu _L=\nu _\theta \), and \(\nu _U=\nu _\theta +\nu _r\), \(\nu _L=\nu _\theta -\nu _r\), respectively.

(III) The WD model implies that QPOs can be created in the thin accretion disk by oscillating test particles. The upper and lower frequencies are \(\nu _U=2\nu _\phi -\nu _r\), \(\nu _L=2(\nu _\phi -\nu _r)\).

Figure 5 demonstrates possible values for the relations between upper and lower frequencies of twin-peaked QPOs around BHs in KR gravity and Schwarzschild BHs at the distance from ISCO radius to infinity in the frame of RP, WD, and ER2-4 models for different values of the dimensionless parameter l. We have used mass \(5M_{\odot }\) by converting the frequencies to Hz in the numerical calculations. One can see from inclined lines giving possible values of the upper and lower frequencies with the ratio 3:2, 4:3, 5:4, and the line with the ratio 1:1 (called graveyard for twin peak QPOs) implying that if a QPO object lies on this line, the two peaks coincide with each other, resulting in a single peak.

4.1 QPO orbits

In this subsection, we explore the effects of spacetime deviation parameters on the radius of orbits where QPOs with the ratios 3:2, 4:3, and 5:4 can be generated in the entire model using the following equations:

$$\begin{aligned} & p\nu _L(M,r,l)=q\nu _U(M,r,l), \end{aligned}$$
(26)

where p and q are resonant numbers which can take integers. One can easily solve Eq. (26) concerning r analytically for RP, WD, and ER2-4 models (Table 1).

In the following, we analyze the effects of the KR parameter on the distance between QPO orbits (\(\delta r=r_{QPO}-r_{ISCO}\)) and ISCOs. This implies how the QPO orbit is located close to ISCO.

Fig. 6
figure 6

Distance between QPO orbits and ISCO as a function of the dimensionless parameter l, in RP, WD, and ER2-4 models

Full size image
Table 1 Expression of QPO orbits for the frequency ratio p : q in RP, WD and ER2-4 models
Full size table

In Fig. 6, we graphically illustrate the behavior of \(\delta r/r_{ISCO}\) of the QPOs with the upper and lower frequency ratios around the Schwarzschild and KR BHs as a function of the dimensionless parameter l. From its graphical description, we note that the ER2 model has the highest magnitude of QPOs, followed by the WD model, while the ER4 model has the least QPOs. Like in the previous case, the QPO orbits decrease quasi-linearly along l.

Table 2 The Gaussian priors (\(\mu \) is the mean value and \({{\sigma }}\) the variance) of the KR from QPOs of the sources with positive values of l
Full size table
Table 3 The same table with Table 2, but for negative values of l
Full size table
Table 4 Best fit values of M, positive values of l, and r parameters for XTE J1550-564, GRO J1655-40 Sgr A* and M82 X-1
Full size table
Fig. 7
figure 7

Constraints on the KR parameter, the BH mass, and the radius of the QPO orbit from a three-dimensional MCMC analysis using the QPO data for the stellar-mass BHs GRO J1655-40 (top row) and XTE J1550-564 (bottom row) in the RP model in cases positive (left column) and negative (right column) values of l

Full size image
Fig. 8
figure 8

The same figure with Fig. 7, but for intermediate-mass M82 X-1 with positive and negative l

Full size image
Fig. 9
figure 9

The same figure with Fig. 7, but for Sgr A\(^*\) with positive and negative l

Full size image

5 Monte Carlo Markov chain (MCMC) priors for EMPG parameters

This section is devoted to obtaining constraints on the mass and metric parameters (1). Here, we select 3 different BH candidates: stellar-mass, intermediate-mass, and supermassive BHs. For example, we use Well-known stellar-mass BHs located at the center of the microquasars GRO J1655-40 and XTE 1550-564. We also used QPO data from (ii) M82 X-1 [91]. The intermediate-mass BH is at an ultraluminous X-ray source in galaxy M82. Its mass is estimated to be around 100 to 1000 solar masses in literature [92, 93]. The supermassive BH Sgr A* is also in our focus with microsecond QPOs. To obtain the constraints, we use the Python library emcee [94,95,96] and perform MCMC analysis in the RP model. The posterior distribution is [97, 98],

$$\begin{aligned} \mathcal {P}(\theta |\mathcal {D},\mathcal {M})=\frac{P(\mathcal {D}|\theta ,\mathcal {M})\ \pi (\theta |\mathcal {M})}{P(\mathcal {D}|\mathcal {M})}, \end{aligned}$$
(27)

where the functions: \(\pi (\theta )\) is the prior function and \(P(\mathcal{D}|\theta ,M)\) is the likelihood one. We consider priors to have normal distribution known as Gaussian distribution within suitable boundaries (see Tables 2 and 3), i.e., \(\pi (\theta _i) \sim \exp \left[ {\frac{1}{2}\left( \frac{\theta _i - \theta _{0,i}}{\sigma _i}\right) ^2}\right] \), \(\theta _{\text {low},i}<\theta _i<\theta _{\text {high},i}\). Here, the parameters are \(\theta _i=\{M,l,r/M\}\) and \(\sigma _i\) are their deviations. We provide MCMC analysis using the orbital, vertical, and radial frequencies calculated in the previous section. The likelihood function \(\lambda \) has form,

$$\begin{aligned} \log \lambda = \log \lambda _\textrm{U} + \log \lambda _\textrm{L}, \end{aligned}$$
(28)

where \(\log \lambda _\textrm{U}\) denotes the likelihood of the upper and lower frequencies,

$$\begin{aligned} \log \lambda _\textrm{U} = - \frac{1}{2} \sum _{i} \frac{(\nu _{\phi \mathrm , obs}^i -\nu _{\phi \mathrm , th}^i)^2}{(\sigma ^i_{\phi ,\textrm{obs}})^2} \ , \end{aligned}$$
(29)

where \(\log \lambda _\textrm{L}\) is the probability (likelihood) of the lower frequency data.

$$\begin{aligned} \log \lambda _\textrm{L} =-\frac{1}{2} \sum _{i} \frac{(\nu _\textrm{L, obs}^i -\nu _\textrm{L, th}^i)^2}{(\sigma ^i_\mathrm{L,\textrm{obs}})^2}\ , \end{aligned}$$
(30)

Here \(\nu ^i_{\phi ,\mathrm obs}\), \(\nu ^i_\mathrm{L,\mathrm obs}\) are direct observational results of the orbital/Keplerian frequencies (\(\nu _\textrm{K}\)), periastron precession frequencies \(\nu _{\text {L}}=\nu _\textrm{K}-\nu _\textrm{r}\) for the source of our interest. On the other side, \(\nu ^i_{\phi ,\mathrm th}\), \(\nu ^i_\mathrm{L,\mathrm th}\) are the respective theoretical estimations.

Next, we perform the MCMC simulation to constrain the parameters (M, l, r/M) for BHs in KR gravity. We use Gaussian priors based on parameter values from existing literature on QPO data processing. We sampled approximately \(10^5\) points from a prior Gaussian distribution for each parameter. This allowed us to explore the physically possible parameter space within set boundaries and identify the best-fitting parameter values (Table 4).

Having established the priors, we use the available data to perform an MCMC simulation to determine the plausible range of the parameters {M, \(l,\sigma \), r/M} for KR BH spacetime. Considering the Gaussian prior distribution, we sample \(10^5\) points for every parameter. This approach allows us to investigate the physically allowed multidimensional parameter space within defined limits and obtain the parameter values that best match the data.

In Figs. 7, 8 and 9, we show the results of the MCMC analysis of the KR gravity parameter by using the QPO data from 4 different BHs (two stellar-mass BH candidates, one intermediate-mass and supermassive BHs). We use the emcee package to obtain the posterior distribution with the possible choice of the prior given in Tables 2 and 3. In the analysis, the contour plots highlight the confidence levels (1\(\sigma \) for 68%, 2\(\sigma \) for 95%, and 3\(\sigma \) for 99%) of the posterior probability distributions for the entire set of parameters. The shaded regions on the contour plots reflect these confidence levels.

6 Conclusion

Astrophysical observation data helps test gravity theories in various areas of astrophysics and cosmology. One way to test a gravity theory is through the theoretical connection between epicyclic frequencies of particle oscillations and QPOs observed in microquasars and galactic centers. The present work is devoted to studying the circular motion of test particles and their oscillations with the QPO applications. First, we have derived equations of motion and analyzed how effective potential for circular orbits behave in KR gravity. It is shown that the positive value of the KR coupling parameter causes an increase in the maximum effective potential, showing an additional gravity effect. However, when negative, the KR field behaves as an antigravitating. Also, we have studied the energy and angular momentum of particles corresponding to circular orbits. We obtained that the minimum of the angular momentum increases (decreases) at the negative (positive) KR coupling parameter while the minimum of the energy decreases (increases). Moreover, we have analyzed the stability of circular orbits. It is shown that the radius of the innermost stable circular orbits is inversely linearly proportional to the KR parameter. We also want to test particles’ energy and angular momentum at ISCO around the KR BHs. Additionally, we have studied the efficiency of energy release from thin accretion discs around BHs in KR gravity in the Novikov-Thorn model. The efficiency can reach up to 40% at \(l=-0.5\) and increase for higher negative KR field parameters.

Table 5 The same table with Table 5, but for negative values of l
Full size table

We have calculated and found that the Keplerian frequency for the test particles in KR gravity is the same as that in GR, but the frequency of radial oscillation differs. Further, we have studied the QPOs by applying epicyclic oscillations in the RP, WD, and ER models. We have also analyzed QPO orbits in the resonance cases of upper and lower frequencies 3:2, 4:3, and 5:4 in the abovementioned QPO models. The QPO orbits in the ER2 and RP models are shown to be close to ISCO.

Finally, we have performed a detailed MCMC analysis of BH mass and KR parameters using the observational data from the twin-peak QPOs observed in the stellar-mass BH candidates in microquasars GRO J1655-40, XTE-J 1550-564 & GRS 1915-105, the intermediate-mass BH in M82-X1, and the supermassive BH SgA* in the Milky Way galaxy in Figs. 7, 8 and 9. More information on the best-fit values of these three parameters is given in Table 5.