Probing the regular black hole with an asymptotically Minkowski core by precessing motion of S2 star and OJ 287

Abstract

We investigate the precessing motion around the the regular black hole with an asymptotically Minkowski core which has a suppression parameter $\ell$. We obtain the third-order post-Newtonian quasi-Keplerian motion of a test particle in this spacetime and find its relativistic periastron advance. Then, we test this model with the precessing motion of the star S2 and of OJ 287 and determine the upper limits of the dimensionless suppression parameter as $\ell /m \sim 10^{-3}$, where m is the mass of the black hole. Compared with the bound given by the shadow of Sgr A*, our bound on $\ell /m$ is reduced by 2 orders of magnitude, although our upper limit of $\ell$ still needs further improvement.

1 Introduction

The detection of gravitational waves [1,2,3,4,5,6,7,8,9] and the direct images of supermassive black holes in the center of both galaxy M87 [10,11,12,13,14,15] and the galaxy Sgr A* [16,17,18,19,20,21] indicates the widespread existence of black holes [22, 23] in the Universe, serving as a compelling testament to the correctness of General Relativity (GR), which has been thought to be the best gravitation theory at present, though there exist some unsolved questions [24, 25]. As the simplest object predicted by GR [26], black holes possess distinctive features, such as the event horizon and the central singularity [27, 28], both of which give rise to specific challenges, including information loss and the breakdown of GR. To circumvent the spacetime singularities, various approaches have been proposed, such as bouncing by quantum pressure [29,30,31], considering a regular core [32,33,34,35,36,37,38,39,40], and building a quasi-black hole [41,42,43,44].

In recent years, considerable attention has been devoted to the family of regular black holes, which typically have a de Sitter core with finite central energy density and an equal-but-opposite central pressure [32,33,34,35,36,37,38,39,40]. The properties of these regular black holes have been widely investigated [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. A de Sitter core implies the far region which has positive curvature and accelerated expansion due to dark energy including cosmological constant, whereas a Minkowski core implies the far region which has a flat spacetime. In this work, we focus on a new kind of regular black hole which has an asymptotically Minkowski core instead of a de Sitter one [65]. It is realized through an exponential reduction of the Misner–Sharp quasi-local mass with a suppression parameter $\ell$ and exhibits finite curvature everywhere. This model offers the potential for greatly simplifying the physics in the deep core by replacing high-order polynomial modifications of the metric coefficients with more elegant special functions, such as an exponential function [65]. Its geometric properties were thoroughly examined [66,67,68], and a discussion on the thin-shell traversable wormholes derived from it was also conducted [69]. Extensive investigations have been carried out on the circular time-like and null orbits around it [70, 71], while comprehensive tests of such a black hole at the horizon scale were also undertaken [72,73,74,75]. In particular, an upper bound of the suppression parameter $\ell$ was determined to be $10^{8}\ \textrm{m}$ based on observations of the shadow of Sgr A* [75].

However, little attention has been paid in testing this model by the motion of a celestial body. Therefore, in the present work, we will consider the bound orbits around the regular black hole with an asymptotically Minkowski core and test such a spacetime with the precessing motion. Since the advance of the perihelion of Mercury becomes one of the strongest evidences of the GR [76], precessing orbits have been a useful tool for understanding properties of spacetimes. In principle, the advance of the mean anomaly at epoch may be fruitfully adopted together with relativistic periastron advance in tests of GR and several modified models of gravity [77]. Especially, the potential of a possible use of the mean anomaly at epoch in the ongoing tests with the satellites LAGEOS and LAGEOS II is discussed in Ref. [78]. In GR, ones usually employ the post-Newtonian (PN) approximation method to study the precessing motion of bodies. Several analytical formulas have been derived that account for first and higher-order corrections, which are proportional to the mass of a central body [79,80,81,82,83,84,85,86,87,88,89,90,91,92] and its spin [93,94,95,96,97,98,99,100,101,102,103]. The research on the precessing motion of test particles has been extended to include the effects of the charge in Reissner–Nordström spacetime [104,105,106], as well as the second-order post-Newtonian (2PN) corrections due to the spin-induced quadrupole on the equatorial motion in Kerr spacetime [107, 108]. Additionally, the next-to-leading spin-orbit coupling effects on the generally inclined motions in Kerr spacetime have been investigated [109]. The 2PN precessing motion [110] around the regular Bardeen black hole has also been studied [111]. On the other hand, the precessing motion have been proved to a powerful way for testing alternative theories of gravity by the planets around the Sun [112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127], by the exoplanets around other stars [128,129,130,131,132,133,134,135,136,137], by the binary pulsars [138,139,140,141,142,143,144,145,146,147,148,149], and by the stars around Sgr A* [150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165].

Inspired by the regular black hole with an asymptotically Minkowski core [65], we take this model as the description of a black hole, whose deviation from the Schwarzschild spacetime is characterized by the suppression parameter $\ell$. We will derive the 3PN solution for the quasi-Keplerian motion of a test particle in this spacetime, as well as its relativistic periastron advance. Then we will test this model with the star S2 around Sgr A* [166] and with OJ 287 [167], and determine the upper limit of $\ell$. Our analysis will show that, compared with the bound on $\ell /m \sim 10^{-1}$ based on the shadow of Sgr A* [75] where m is the mass of the black hole, our upper limit would be improved by 2 orders of magnitude.

The rest of this paper is organized as follows. In Sect. 2, we briefly review the metric of the regular black hole with an asymptotically Minkowski core and give the 3PN Lagrangian for a test particle on this black hole background, including the particle’s orbital energy and angular momentum. In Sect. 3, we provides the 3PN solution for the quasi-Keplerian motion of the particle and derives its advance of periastron with the effects of the suppression parameter $\ell$. In Sect. 4, we estimate the upper bounds for $\ell$ based on the detection of the precession of the star S2 around Sgr A* and of OJ 287. Finally, Sect. 5 is devoted to the summary and discussion on our work. In Appendix A, we gives the standard perturbative calculation of the relativistic periastron advance and the mean anomaly at epoch.

2 3PN Lagrangian of a test particle in the spacetime

The spacetime of the regular black hole with an asymptotically Minkowski core reads ($c=G=1$) [65]

$$\begin{aligned} ds^{2}= & -\Big (1-\frac{2m\,e^{-\ell /r}}{r}\Big )dt^{2}+\frac{dr^2}{1-\frac{2m\, e^{-\ell /r}}{r}}\nonumber \\ & + r^2d\theta ^2+r^2\sin \theta ^2 d\phi ^2, \end{aligned}$$

(1)

where m denotes the standard gravitational mass. As the suppression parameter $\ell \rightarrow 0$, the spacetime asymptotically approaches the Schwarzschild spacetime in standard coordinates. Thus, $\ell$ can be seen as a measure of the deviation from Schwarzschild spacetime.

Using the Cartesian coordinates

$$\begin{aligned} x^{0}= & t,~x^{1}=r\sin \theta \cos \phi ,\nonumber \\ x^{2}= & r \sin \theta \sin \phi ,\quad x^{3}=r\cos \theta , \end{aligned}$$

(2)

we can transform the metric (1) into

$$\begin{aligned} ds^{2}= & -\Bigg (1-\frac{2m\,e^{-\ell /r}}{r}\Bigg )dt^{2}+\Bigg [\Bigg (1-\frac{2m\,e^{-\ell /r}}{r}\Bigg )^{-1}-1\Bigg ]\nonumber \\ & \times \Bigg (\frac{{\varvec{x}} \cdot d{\varvec{x}}}{r}\Bigg )^2+d{\varvec{x}}^2, \end{aligned}$$

(3)

where $\varvec{x}=(x^0,x^1,x^2,x^3)$. In accordance with the PN approximation method, the metric (3) can be expanded in powers of m/r where $r=|\varvec{x}|$.

In the harmonic coordinates, the metric of the regular black hole with an asymptotically Minkowski core in the 3PN approximation can be written as

$$\begin{aligned} g_{00}= & -1 +\frac{2m}{r}-\frac{2m^2}{r^2}\Big (1+\frac{\ell }{m}\Big )+\frac{2m^3 }{r^3}-\frac{2m^4 }{r^4},\end{aligned}$$

(4)

$$\begin{aligned} g_{0i}= & 0,\end{aligned}$$

(5)

$$\begin{aligned} g_{ij}= & \delta _{ij}\Big (1+\frac{2m}{r}+\frac{m^2}{r^2}\Big )+\Big (1+\frac{2m}{r}\Big )\frac{m^2}{r^2}\frac{x^ix^j}{r^2}, \end{aligned}$$

(6)

where i and j range from 1 to 3 and $\epsilon _{ijk}$ represents the Levi-Civita symbol. In the above metric, we only retain the leading contribution of $\ell$, since we expect its effects on the orbital motion would be significantly smaller than those from GR and very hard to detect with the current observational capabilities.

Therefore, we can find the Lagrangian for the test particle as

$$\begin{aligned} \textrm{L}= & \frac{1}{2}\varvec{v}^{2}+\frac{m}{r}+\frac{1}{8}\varvec{v}^{4} +\frac{3}{2}\frac{m}{r}\varvec{v}^{2}-\frac{m^2}{2r^2}\Bigg (1+\frac{2\ell }{m}\Bigg )\nonumber \\ & +\frac{1}{16}\varvec{v}^{6}+\frac{7}{8}\frac{m}{r}\varvec{v}^{4}+\frac{7}{4}\frac{m^2}{r^2}\varvec{v}^{2}+\frac{m^2(\varvec{v} \cdot \varvec{x})^2}{2r^4}+\frac{m^3}{2r^3}\nonumber \\ & +\frac{5}{128}\varvec{v}^{8}+\frac{11}{16}\frac{m}{r}\varvec{v}^{6}+\frac{45}{16}\frac{m^2}{r^2}\varvec{v}^{4}+\frac{5}{4}\frac{m^3}{r^3}\varvec{v}^{2}\nonumber \\ & +\frac{3m^3(\varvec{v} \cdot \varvec{x})^2}{2r^5}+\frac{m^2(\varvec{v} \cdot \varvec{x})^2}{4r^4}\varvec{v}^{2}-\frac{3}{8}\frac{m^4}{r^4}, \end{aligned}$$

(7)

where $\varvec{v}$ is the velocity of the test particle, and the energy $\mathcal {E}$ and the angular momentum $\mathcal {J}$ for this particle in the equatorial plane as

$$\begin{aligned} \mathcal {E}= & \frac{1}{2}\varvec{v}^{2}-\frac{m}{r}+\frac{3}{8}\varvec{v}^{4}+\frac{3}{2}\frac{m}{r}\varvec{v}^{2}+\frac{1}{2}\frac{m^2}{r^2}\Big (1+\frac{2\ell }{m}\Big )\nonumber \\ & +\frac{5}{16}\varvec{v}^{6}+\frac{21}{8}\frac{m}{r}\varvec{v}^{4}+\frac{7}{4}\frac{m^2}{r^2}\varvec{v}^{2}+\frac{m^2(\varvec{v} \cdot \varvec{x})^2}{2r^4}-\frac{m^3}{2r^3}\nonumber \\ & +\frac{35}{128}\varvec{v}^{8}+\frac{55}{16}\frac{m}{r}\varvec{v}^{6}+\frac{135}{16}\frac{m^2}{r^2}\varvec{v}^{4}+\frac{5}{4}\frac{m^3}{r^3}\varvec{v}^{2}\nonumber \\ & +\frac{3m^3(\varvec{v} \cdot \varvec{x})^2}{2r^5}+\frac{3m^2(\varvec{v} \cdot \varvec{x})^2}{4r^4}\varvec{v}^{2}+\frac{3}{8}\frac{m^4}{r^4}, \end{aligned}$$

(8)

$$\begin{aligned} \mathcal {J}= & |\varvec{x}\times \varvec{v}|\Big [1+\frac{1}{2}\varvec{v}^{2} +\frac{3m}{r}+\frac{3}{8}\varvec{v}^{4}+\frac{7}{2}\frac{m}{r}\varvec{v}^{2}+\frac{7}{2}\frac{m^2}{r^2}\nonumber \\ & +\frac{5}{16}\varvec{v}^{6}+\frac{33}{8}\frac{m}{r}\varvec{v}^{4}+\frac{45}{4}\frac{m^2}{r^2}\varvec{v}^{2}+\frac{5}{2}\frac{m^3}{r^3}+\frac{m^2(\varvec{v} \cdot \varvec{x})^2}{2r^4}\Big ].\nonumber \\ \end{aligned}$$

(9)

It is evident that when $\ell =0$, the the Lagrangian, the energy and the angular momentum of the particle revert to those for the Schwarzschild spacetime. In the following section, we will use them to derive the analytical solution for the quasi-Keplerian motion of the particle, including its advance of periastron affected by the suppression parameter.

3 3PN solution for quasi-Keplerian motion

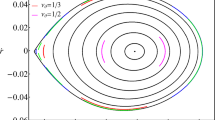
The trajectory of the test particle in the equatorial plane of the regular black hole with an asymptotically Minkowski core can be written as

$$\begin{aligned} \varvec{x} = r(\cos \phi \,\varvec{e}_{x}+\sin \phi \,\varvec{e}_{y}), \end{aligned}$$

(10)

where $\phi$ represents the azimuthal angle, and $\varvec{e}_{x}$ and $\varvec{e}_{y}$ denote the unit vectors along the x-axis and y-axis, respectively.

By using the procedure given by Ref. [79], we can obtain the 3PN solution for the quasi-Keplerian motion of this particle as

$$\begin{aligned} \varvec{x}= & r(\cos \phi \,\varvec{e}_{x}+\sin \phi \,\varvec{e}_{y}),\end{aligned}$$

(11)

$$\begin{aligned} r= & a_{r}(1-e_{r} \cos u),\end{aligned}$$

(12)

$$\begin{aligned} \phi \Big (\frac{2\pi }{\Phi }\Big )= & \upsilon + N_1 \sin 2\upsilon ,\end{aligned}$$

(13)

$$\begin{aligned} \upsilon= & 2 \arctan \Big (\sqrt{\frac{1+e_{\phi }}{1-e_{\phi }}}\tan \frac{u}{2}\Big ),\end{aligned}$$

(14)

$$\begin{aligned} n\, t= & u-e_t \sin {u}+ N_2 (\upsilon -u)+ N_3 \sin \upsilon , \end{aligned}$$

(15)

with

$$\begin{aligned} a_{r}= & \frac{m}{-2\mathcal {E}}\Big [1+\frac{7}{2}\mathcal {E}+\frac{1}{4}\mathcal {E}^2+8\frac{m^2}{\mathcal {J}^2}\mathcal {E} \nonumber \\ & -\frac{1}{8}\mathcal {E}^3+16\frac{m^2}{\mathcal {J}^2}\mathcal {E}^2+ 64\frac{m^4}{\mathcal {J}^4}\mathcal {E}\Big ],\end{aligned}$$

(16)

$$\begin{aligned} e_r^2= & 1+\frac{2\mathcal {E}\mathcal {J}^2}{m^2}-\mathcal {E}\Big [12\Big (1-\frac{\ell }{3m}\Big )+15\frac{\mathcal {E}\mathcal {J}^2}{m^2}\Big ]\nonumber \\ & +\,\mathcal {E}^2\Big [30+80\frac{\mathcal {E}\mathcal {J}^2}{m^2}-32\frac{m^2}{\mathcal {E}\mathcal {J}^2}\Big ]\nonumber \\ & +\,\mathcal {E}^3\Big [4-372\frac{\mathcal {E}\mathcal {J}^2}{m^2}-48\frac{m^2}{\mathcal {E}\mathcal {J}^2}-256\frac{m^4}{\mathcal {E}^2\mathcal {J}^4}\Big ],\end{aligned}$$

(17)

$$\begin{aligned} e_t= & e_r\Big [1+8\,\mathcal {E}+\mathcal {E}^2\Big (36+8\frac{m^2}{\mathcal {E}\mathcal {J}^2}-\frac{30m}{\sqrt{-2\mathcal {E}\mathcal {J}^2}}\Big )\nonumber \\ & + \mathcal {E}^3\Big (160+52\frac{m^2}{\mathcal {E}\mathcal {J}^2}+64\frac{m^4}{\mathcal {E}^2\mathcal {J}^4}\nonumber \\ & -\frac{765m}{2\sqrt{-2\mathcal {E}\mathcal {J}^2}}+\frac{420m^3}{\sqrt{(-2\mathcal {E}\mathcal {J}^2)^3}}\Big )\Big ],\end{aligned}$$

(18)

$$\begin{aligned} e_{\phi }= & e_r \Big [1-\frac{m^2}{\mathcal {J}^2}\mathcal {E}\Big (10-11\mathcal {E}+92\frac{m^2}{\mathcal {J}^2}\Big )\Big ],\end{aligned}$$

(19)

$$\begin{aligned} \Phi= & 2\pi \Big [1+3\frac{m^2}{\mathcal {J}^2}\Big (1-\frac{\ell }{3m}\Big )+\frac{15}{2}\frac{m^2}{\mathcal {J}^2}\mathcal {E}+\frac{105}{4}\frac{m^4}{\mathcal {J}^4}\nonumber \\ & +\frac{15}{4}\frac{m^2}{\mathcal {J}^2}\mathcal {E}^2+\frac{315}{2}\frac{m^4}{\mathcal {J}^4}\mathcal {E}+\frac{1155}{4}\frac{m^6}{\mathcal {J}^6}\Big ],\end{aligned}$$

(20)

$$\begin{aligned} N_1= & \frac{1}{8}\frac{m^4}{\mathcal {J}^4}\Big [1+\frac{2\mathcal {E}\mathcal {J}^2}{m^2}+\mathcal {E}\Big (36+\frac{\mathcal {E}\mathcal {J}^2}{m^2}\Big )+20\frac{m^2}{\mathcal {J}^2}\Big ],\end{aligned}$$

(21)

$$\begin{aligned} N_2= & \frac{30m \,\mathcal {E}^2 }{\sqrt{-2\,\mathcal {E}\mathcal {J}^2}}\Big [1+\mathcal {E}\Big (\frac{19}{4}+7\frac{m^2}{\mathcal {E}\mathcal {J}^2}\Big )\Big ],\end{aligned}$$

(22)

$$\begin{aligned} N_3= & 40\,\mathcal {E}^2\frac{m^2}{\mathcal {J}^2}\frac{m}{\sqrt{-2\,\mathcal {E}\mathcal {J}^2}}\Big (1+\frac{2\,\mathcal {E}\mathcal {J}^2}{m}\Big )^{\frac{1}{2}},\end{aligned}$$

(23)

$$\begin{aligned} n= & \frac{(-2\mathcal {E})^{\frac{3}{2}}}{m}\Big [1+\frac{15}{4}\mathcal {E}+\frac{555}{32}\mathcal {E}^2+\frac{9795}{128}\mathcal {E}^3\nonumber \\ & -\frac{30m\mathcal {E}^2}{\sqrt{-2\mathcal {E}\mathcal {J}^2}}\Big (1+\frac{17}{2}\mathcal {E}+7\frac{m^2}{\mathcal {J}^2}\Big )\Big ], \end{aligned}$$

(24)

where $a_{r}$, $e_{r}$, $e_{t}$, $e_{\phi }$, u and $\upsilon$ denote the semi-major axis, the radial eccentricity, the time eccentricity, the angular eccentricity, the eccentric anomaly and the true anomaly of the quasi-Keplerian motion in the 3PN approximation, respectively. n denotes the unperturbed mean motion, given by $n=2\pi /P$, P being the radial period.

Then, we find its 3PN periastron advance as

$$\begin{aligned} \Delta \phi\equiv & \Phi -2\pi \nonumber \\= & 2\pi \Bigg [3\frac{m^2}{\mathcal {J}^2}\Bigg (1-\frac{\ell }{3m}\Bigg )+\frac{15}{2}\frac{m^2}{\mathcal {J}^2}\mathcal {E}+\frac{105}{4}\frac{m^4}{\mathcal {J}^4}\nonumber \\ & +\frac{15}{4}\frac{m^2}{\mathcal {J}^2}\mathcal {E}^2+\frac{315}{2}\frac{m^4}{\mathcal {J}^4}\mathcal {E}+\frac{1155}{4}\frac{m^6}{\mathcal {J}^6}\Bigg ]. \end{aligned}$$

(25)

As the suppression parameter $\ell$ approaches zero, Eq. (25) reduces to the 3PN periastron advance of the binary system in the extreme-mass-ratio limit given by Refs. [87, 88]. For practical purposes, it would be useful to express the above equation in terms of the the orbital elements, we can obtain the periastron advance as follows:

$$\begin{aligned} & \Delta \phi = \Delta \phi _\mathrm{{GR}}+ \Delta \phi _{\ell }, \end{aligned}$$

(26)

where the advance due to GR has three components $\Delta \phi _\mathrm{{GR}}=\Delta \phi _\mathrm{{1PN}}+\Delta \phi _\mathrm{{2PN}}+\Delta \phi _\mathrm{{3PN}}$ [87, 88], and we have

$$\begin{aligned} \Delta \phi _\mathrm{{1PN}}= & 3\,\xi (1-e_t^2)^{-1},\end{aligned}$$

(27)

$$\begin{aligned} \Delta \phi _\mathrm{{2PN}}= & \xi ^2(1-e_t^2)^{-2}(78+51e_t^2)/4,\end{aligned}$$

(28)

$$\begin{aligned} \Delta \phi _\mathrm{{3PN}}= & \xi ^3(1-e_t^2)^{-3}[18240+28128e_t^2+2496e_t^4\nonumber \\ & +(1920+3840e_t^2)\sqrt{1-e_t^2}]/128,\end{aligned}$$

(29)

$$\begin{aligned} \Delta \phi _{\ell }= & -\ell \,\xi \, (G\, m)^{-1}c^2 (1-e_t^2)^{-1}, \end{aligned}$$

(30)

where $\xi =(G\, m\, n/c^3)^{2/3}$ and $m=m_1+m_2$. We restore the speed of light c and the gravitational constant G in the above equations for later convenience.

4 Confrontation of the suppression parameter with observational data sets

In this section, we will estimate the upper bounds for the suppression parameter $\ell$, based on the detected precession of the star S2 [166] and of OJ 287 [167].

4.1 Star S2

The detection of the Schwarzschild precession in the orbit of S2 around the supermassive black hole at the Galactic Center, Sgr A*, was reported in [166]. This detection was achieved through a combination of astrometric and spectroscopic measurements, with a particular focus on the astrometry conducted by the four-VLT-telescope interferometric beam combiner instrument GRAVITY. The inferred precession was found to be in agreement with the predicted precession, as indicated by [166]

$$\begin{aligned} & f_\mathrm{{SP}}=\frac{\Delta \phi _\mathrm{{S2}}}{\Delta \phi _\mathrm{{GR}}}=1.10\pm 0.19. \end{aligned}$$

(31)

Assuming Sgr A* is a regular black hole with an asymptotically Minkowski core, the precession of S2 can be modeled as

$$\begin{aligned} & \Delta \phi _\mathrm{{S2}}=\Delta \phi _\mathrm{{1PN}} + \Delta \phi _{\ell }, \end{aligned}$$

(32)

where the 1PN term and the suppression parameter one are, respectively, Eqs. (27) and (30). Here, we only retain the 1PN term of periastron advance in GR, neglect the 2PN and 3PN terms in Eq. (26), since these higher-order effects on the orbit of S2 are beyond the ability of the current technology.

Utilizing the best-fit orbit parameters of S2 as detailed in Appendix E of Ref. [166], we obtain

$$\begin{aligned} & \ell =(-1.89\pm 3.58)\times 10^{11}\, \textrm{m}, \end{aligned}$$

(33)

or

$$\begin{aligned} & \ell _{\bullet }=\frac{\ell }{m_{\mathrm {SgrA*}}}=-0.30\pm 0.57. \end{aligned}$$

(34)

4.2 OJ 287

Blazar OJ 287 is one of the first candidates with the assumed compact system of two supermassive black holes in the center, which is discussed as a new precision testing ground for GR and alternate gravity theories. By analyzing the accurately extracted (observed) starting epochs of ten optical outbursts of OJ 287 to track the binary orbit, the independent and dependent parameters of the binary black hole system in OJ 287 have been determined [167].

By including the leading terms associated with the suppression parameter, the precession of OJ 287 can be expressed as follows:

$$\begin{aligned} & \Delta \phi _\mathrm{{OJ 287}}=\Delta \phi _\mathrm{{1PN}} +\Delta \phi _\mathrm{{2PN}}+\Delta \phi _\mathrm{{3PN}}+ \Delta \phi _{\ell }, \end{aligned}$$

(35)

where the 1PN, 2PN, 3PN and suppression parameter terms of periastron advance are, respectively, Eqs. (27)-(30). Using the independent and dependent parameters of the binary black hole system in OJ 287 of Table 2 in Ref. [167], including the precession rate of the major axis per period $\Delta \phi =38.62 \pm 0.01$ deg, the eccentricity $e=0.657$, the present (redshifted) orbital period $P_\textrm{orb}^{2017}=12.062$ year etc, we obtain

$$\begin{aligned} & \ell =(-4.87\pm 2.75)\times 10^{10}\, \textrm{m}, \end{aligned}$$

(36)

or

$$\begin{aligned} & \ell _{\bullet }=\frac{\ell }{m_{\textrm{OJ287}}}=-0.0018\pm 0.0010. \end{aligned}$$

(37)

A summary of our results is presented in Table 1. It is anticipated that, as observational accuracy and precision continue to improve in the future, tests in the star S2 and in OJ 287 will yield more stringent upper bounds on the the suppression parameter $\ell$.

Table 1 Upper bounds on $\ell$

4.3 Discussion

The Ghosh–Culetu black hole [168, 169] is a rotating non-singular black hole characterized by a charge g. When its spin vanishes, its metric might reduce to the one of the regular black hole with an asymptotically Minkowski core so that we can find the relation $\ell =g^2/(2m_\mathrm )$. With the Event Horizon Telescope observations of the black hole shadow in Sgr A*, the authors of Ref. [75] obtained the constraint on the charge as $0.18345\ m_\mathrm{Sgr A*} \leqslant g \leqslant 0.62058\ m_\mathrm{Sgr A*}$. Since the combined effects of the spin of Sgr A* and its inclination on the size of the shadow and the circularity of its shape are no more than 4 and 7% [170], we might ignore its spin at least for the leading order and roughly estimate its resulting bounds on $\ell$ as $1.08\times 10^{8}\, \textrm{m}\leqslant \ell \leqslant 1.23\times 10^{9}\,\textrm{m}$ from the constraints on g, i.e., $0.0168 \leqslant \ell _{\bullet } \equiv \ell /m_\mathrm{Sgr A*} \leqslant 0.1926$. Although our bounds on $\ell$ are less competitive with the one of Ref. [75], the bound on $\ell _{\bullet }$ from OJ 287 is reduced by 2 orders of magnitude than it, see Table 1 for a comparison.

5 Conclusion and discussion

Inspired by the regular black hole with an asymptotically Minkowski core, we take this model as a description of Sgr A* and OJ 287, whose deviation from the Schwarzschild spacetime is characterized by the suppression parameter $\ell$. We obtain the 3PN quasi-Keplerian motion of a test particle in this spacetime and find its relativistic periastron advance affected by $\ell$. Using the data sets of the star S2 and of OJ 287, we find the bounds on $\ell /m \sim 10^{-3}$, which is improved by 2 orders of magnitude than the one from the shadow of Sgr A*, although our upper limit of $\ell$ still needs further improvement. With the continuous progress in techniques of interferometry, such as GRAVITY+, we could expect that the orbit of S2 would be considerably improved and its bound on the suppression parameter would be tightened further. The precessing motion we focus on in this work is more or less in the regime of the weak gravitational field, which may reduce the manifestation of the suppression parameter. Therefore, we believe periodic orbits [171,172,173,174,175,176,177] in the strong field of the regular black hole with an asymptotically Minkowski core would also provide new insights.

And the other thing to point out, the constraints we obtained are only preliminary constraints strictly speaking. It is so because we compared theoretical prediction for extra precession with the measured S2 precession obtained without modeling the exotic effects. A genuine constraint could be obtained only by explicitly modeling the exotic effect one is interested in and estimating some dedicated solve-for parameter(s). Thus, our results is just a-nonethless important-guess about what could be possible obtain in real, dedicated data analysis. Such kind of issue was tackled, in the context of Solar System, in [178].

Appendix A: Applying the Gauss equations to calculate the periastron advance and the mean anomaly at epoch

Several approaches have been used to derive the relativistic precession per orbit beyond the 1PN approximation [84, 85, 179,180,181,182]. Damour and Schäfer [84] applied the Hamilton-Jacobi method to derived a secular advance of the orbital pericenter in the 2PN approximation of the two-body problem. Kopeikin and Potapov [85] used the Gauss method, i.e., ‘osculating orbit elements’ [78,79,80,81,82,83,84,85, 179,180,181,182,183,184,185,186], for analyzing the 2PN secular shift of the periastron of a binary system in GR. Their results were found to be in exact agreement with those of Damour and Schäfer [84]. However, various complexities in the calculations have led to discrepancies among results reported by different authors. Initial controversies between the 2PN results presented in [85, 181] were resolved in a subsequent correction [182]. More recently, direct calculation have demonstrated that the 2PN secular periastron shift from the osculating elements technique yields exactly the same result as the one obtained by the Hamilton-Jacobi method [180].

The derivation of the 3PN periastron advance in GR has been previously studied [87, 88] using the Hamilton-Jacobi method, with consistent results reported in both references. We have chosen to utilize these results due to their established use in the literature for modeling OJ287’s precession formula [167]. In contrast, Tucker and Will [179] described the orbit using osculating orbit elements, and analyzed the ‘Lagrange planetary equations’ to obtain the 3PN pericenter advance in GR. Through the transformation connecting these two kinds of orbital elements [179, 187], we have confirmed that the 3PN precession obtained using the Gauss method [179] is consistent with the result derived from the Hamilton-Jacobi method [87, 88] presented in our main text.

Therefore, with the help of the previous works on the consistency among various methods of deriving the 3PN secular pericenter advance in GR, we assume that the leading contribution of $\ell$ to periastron advance is linearly combined with the 3PN contribution from GR which are taken from Refs. [87, 88], and we will focus on re-deriving the term involving $\ell$ using the standard perturbative calculation with the Gauss equations here. Additionally, we will incorporate the effect of $\ell$ on the rate of the mean anomaly at epoch, while the GR contribution has been discussed by Iorio [77, 78].

From the Lagrangian (7) and the Euler–Lagrange equation

$$\begin{aligned} & \frac{d}{dt}\frac{\partial \textrm{L}}{\partial \varvec{v}}= \frac{\partial \textrm{L}}{\partial \varvec{x}}, \end{aligned}$$

(A.1)

we can obtain the 3PN geodesic equations for test particle as follows

$$\begin{aligned} \frac{d\varvec{v}}{dt}= & -\frac{m \varvec{x}}{r^3}\Bigg [1+\varvec{v}^2-4\frac{m}{r}\Big (1+\frac{\ell }{2m}\Big )+9\frac{m^2}{r^2}-16\frac{m^3}{r^3}\Bigg ]\nonumber \\ & +\,2\frac{m^2(\varvec{v}\cdot \varvec{x})^2\,\varvec{x}}{r^6}\Bigg (1-\frac{m}{2r}\Bigg )\nonumber \\ & +\,4\frac{m(\varvec{v}\cdot \varvec{x})\, \varvec{v}}{r^3}\Bigg (1-\frac{m}{2r}+\frac{m^2}{r^2}\Bigg ) . \end{aligned}$$

(A.2)

Starting from here, we will only retain the term containing $\ell$ for convenience. We write (A.2) in the form

$$\begin{aligned} & \varvec{a}=-\frac{m \varvec{x}}{r^3}+\varvec{a}_{\ell }, \end{aligned}$$

(A.3)

i.e., we interpret (A.2) as the standard equation of motion of a perturbed Keplerian problem that we can treat with the means of classical perturbation theory. We decompose it as

$$\begin{aligned} & \varvec{a}_{\ell }=A_\textrm{R}\, \textbf{N}+A_\textrm{T}\,\textbf{T}, \end{aligned}$$

(A.4)

where

$$\begin{aligned} A_\textrm{R}= & 2\frac{m\, \ell }{r^3},\end{aligned}$$

(A.5)

$$\begin{aligned} A_\textrm{T}= & 0, \end{aligned}$$

(A.6)

here $A_\textrm{R}$ is the component of perturbing acceleration along the unit vector $\textbf{N}$ in the direction of the instantaneous radius vector $\varvec{x}$, and where $A_\textrm{T}$ is the component of perturbing acceleration along the unit vector $\textbf{T}$ in the instantaneous orbital plane, perpendicular to the radius vector in the sense of motion.

The Gauss equation for the rate of change of the longitude of periastron is

$$\begin{aligned} & \frac{d\omega }{dt}=\frac{\sqrt{1-e^2}}{n ae}\Big [-A_\textrm{R} \cos \phi +\frac{\sin \phi (2+e \cos \phi )}{1+e\cos \phi }A_\textrm{T}\Big ].\nonumber \\ \end{aligned}$$

(A.7)

Substituting (A.5) and (A.6) into the above equation, we can average the fast changing variable over one orbital revolution, and obtain

$$\begin{aligned} & \dot{\omega } \equiv \Big \langle \frac{d\omega }{dt} \Big \rangle =-\frac{n\, \ell }{p} , \end{aligned}$$

(A.8)

where the operator $\langle \cdot \rangle$ means calculating the average value during one Keplerian period and $p=a(1-e^2)$ being the semi-latus rectum. Making use of the relations $\Delta \omega \equiv 2\pi \,\dot{\omega }/ n$ and $n^2a^3=G m$, we obtain that the contribution of $\ell$ to the periastron advance is consistent with Eq. (30).

The mean anomaly at epoch $\eta$ is one of the standard six Keplerian orbital elements. The Gauss equation for its rate of change is

$$\begin{aligned} \frac{d\eta }{dt}= & -\frac{2}{n a}A_\textrm{R}\Big (\frac{r}{a}\Big )\nonumber \\ & -\frac{(1-e^2)}{n a e}\Bigg [-A_\textrm{R} \cos \phi +A_\textrm{T}\Big (1+\frac{r}{p}\Big )\sin \phi \Bigg ].\nonumber \\ \end{aligned}$$

(A.9)

Substituting (A.5) and (A.6) into the above equation, we can straightforwardly work out its secular rates of change which turn out to be

$$\begin{aligned} & \dot{\eta } \equiv \Big \langle \frac{d\eta }{dt} \Big \rangle =-3 \frac{G \,\ell \,n}{c^2\, a\, \sqrt{1-e^2}}, \end{aligned}$$

(A.10)

here, we restore the speed of light c and the gravitational constant G in the above equation. The effect of this model on the mean anomaly at epoch is characterized by the term containing $\ell$. The 1PN rate of change of the mean anomaly at epoch $\eta$ over one orbital revolution in GR is given by Refs. [77, 78].