Counting $U(N)^{\otimes r}\otimes O(N)^{\otimes q}$ invariants and tensor model observables

Abstract

$U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants are constructed by contractions of complex tensors of order $r+q$, also denoted (r, q). These tensors transform under r fundamental representations of the unitary group U(N) and q fundamental representations of the orthogonal group O(N). Therefore, $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants are tensor model observables endowed with a tensor field of order (r, q). We enumerate these observables using group theoretic formulae, for tensor fields of arbitrary order (r, q). Inspecting lower-order cases reveals that, at order (1, 1), the number of invariants corresponds to a number of 2- or 4-ary necklaces that exhibit pattern avoidance, offering insights into enumerative combinatorics. For a general order (r, q), the counting can be interpreted as the partition function of a topological quantum field theory (TQFT) with the symmetric group serving as gauge group. We identify the 2-complex pertaining to the enumeration of the invariants, which in turn defines the TQFT, and establish a correspondence with countings associated with covers of diverse topologies. For $r>1$, the number of invariants matches the number of (q-dependent) weighted equivalence classes of branched covers of the 2-sphere with r branched points. At $r=1$, the counting maps to the enumeration of branched covers of the 2-sphere with $q+3$ branched points. The formalism unveils a wide array of novel integer sequences that have not been previously documented. We also provide various codes for running computational experiments.

1 Introduction

Table 1 Some correspondences: bijections between sets or equality with a correlator (FG stands for Feynman graphs, Obs for observables)

Lattice gauge theory provides a framework for the enumeration of observables and Feynman diagrams and the computation of correlators across a variety of quantum field theories (QFTs) [1, 2]. These gauge theories, known as topological quantum field theories (TQFTs), employ finite groups, in particular permutation groups, as gauge groups. Their foundation lies in the Dijkgraaf-Witten two-dimensional TQFTs [3,4,5,6,7,8] and since their establishment, they have been developed in several contexts, for instance in gauge theories, including supersymmetric Yang Mills and matrix models, [1, 9,10,11,12,13,14,15,16], and also tensor models [17,18,19,20,21,22]. TQFTs have also illuminated and bridged multiple domains: in the realm of mathematical physics, obviously, as they shed light on QFTs and quantum gravity conundrums, in combinatorics through unveiling novel enumerative constructions and correspondences, which in turn have enriched Algebra, especially Representation Theory, and, more recently, Quantum Computing [23, 24].

Permutation-TQFTs, which are TQFTs with permutation groups as their gauge groups, have been instrumental in addressing various enumerations associated with Feynman diagrams in QFTs and matrix models [1, 2]. The enumeration of such graphs is framed in a double coset formulation: $H_1 \! \! \setminus \! G / H_2$, where G is a permutation group governing the incidence relations between vertices representing the fields, and $H_1$ and $H_2$ are two subgroups of G managing the symmetry of the vertices. Each equivalence class in the double coset represents a graph. The graph enumeration is delivered by Burnside’s lemma for the left and right action of the subgroups $H_1$ and $H_2$ on G. This formalism, at first glance, can be traced back to Read, who introduced a counting for unlabeled edge-colored graphs [25]. In fact, Read applied the Burnside lemma to obtain his counting formula, but this line of ideas, namely finding equivalence classes of graphs under some symmetry groups, dates back even further. One notable result of the 19th century was Cayley’s enumeration of trees, which pioneered enumerative combinatorics. The next century saw the subject culminate in Pólya’s famous enumeration theorem for decorated necklaces [26]. Pólya’s results also relies on Burnside’s lemma applied to arrangements and permutation groups.

The enumeration via the double coset framework has demonstrated robustness when applied to the enumeration of observables in a large set of theories, from gauge theory, to matrix and tensor models as mentioned above. Owing to the richness of the formalism, this approach has led to the discovery of unexpected bijections between sets of graphs and quantities that, apparently, look very different. A glimpse and brief account of one of the most surprising correspondences is provided in Table 1. It is noteworthy that the last correspondence was initially identified for tensors of order-3 within the double coset formulation [17] but was subsequently extended to any order, employing a different algebraic setting based on cut and join operations [27].

Though a relatively recent development in quantum gravity, tensor models (TM) have already ramified into multiple directions, making its review a complex and labyrinthine quest. The series of contributions [28,29,30,31,32,33,34,35,36], along with [37,38,39,40,41] attest to the broad spectrum of applications of TM today. We give in the following a short review of the results obtained in this topic in connection with our present work.

From their inception, TM have been introduced as an approach for addressing quantum gravity [42,43,44] and as an extension of matrix models (MM) [45]. Indeed, in the same way that MM generate ribbon graphs, maps or 2D discretizations of surfaces, TM produce discretizations of higher dimensional (pseudo) manifolds. After, they were formulated as lattice gauge field theories with gauge groups labeling the holonomies of the corresponding complex [46, 47]. Recent progress in the field has been documented in [48, 49].

In MM, the continuum limit rests upon the large N limit and genus expansion in the sense of ’t Hooft [50] and leads to the Brownian sphere [51]. In TM, the notion of large N limit for tensors was established in [52] and unlocked the computation of their continuum limit: TM give rise to branched polymers, a tree-like geometry. Adjusting the scaling of couplings leads to the emergence of new universality classes for TM, notably maps and the Brownian sphere [53]. Although the universality class of TM is subject to change, no higher-dimensional geometry, starting at dimension three, has transpired from this approach so far. Nevertheless, there are indications that such a higher-dimensional phase might be attainable [54,55,56]. The pursuit of new continuum limits and universality classes in TM remains an active area of research.

We return to our main theme which is the enumerations of TM observables. Since the present paper goes beyond this enumeration, reviewing recent progress in the matter is pertinent. Starting with $U(N)^{\otimes d}$ invariants, namely unitary invariants obtained from contractions of d-index tensors, their enumeration was achieved in [17]. These invariants constitute the orbits of the diagonal actions of two subgroups of the permutation group $S_n$ (the permutation group of n objects), acting on d-tuples of permutations. Through the TQFT picture, the counting of unitary invariants of order-d matches with the counting of branched covers of the sphere with d branched points. As branched covers in 2 dimensions relate to Belyi maps [57], or holomorphic maps, this opens new avenues of investigations presenting a geometrical perspective to tensor models that requires further clarification. At the algebraic level, the orbits form the basis elements of a permutation centralizer algebra which is, moreover, semi-simple [18]. This development was central to the combinatorial construction of the Kronecker coefficients [23]. These are positive integers that appear in the representation theory of the symmetric group [58] and have intrigued combinatorialists for eight decades [59, 60], as well as computer scientists more recently [61,62,63].

The enumeration of $O(N)^{\otimes d}$ orthogonal invariants can also be performed using similar techniques, based on the enumeration of orbits in a double coset space [20]. However, they differ from unitary invariants, firstly, by their greater number (certain contractions are precluded in the unitary case), and secondly, by their TQFT interpretation. They correspond to the covers of cylinders with defects. (Note that our present work will shed another light on this counting.) Ultimately, $O(N)^{\otimes d}$ invariants span an associative semi-simple algebra that could serve the simplification of the combinatorial construction of specific Kronecker coefficients.

One might question whether the varied results listed above, concerning the enumeration of tensor invariants and their implications, extend to other types of group symmetries and whether they yield new physical insights. The real symplectic group $Sp(2N)^{\otimes d}$ has been discussed preliminary in [20], and refined/optimized algorithms demonstrate that the tetrahedron-like interaction does not vanish [64]. Although not yet systematically explored, the enumeration of $Sp(2N)^{\otimes d}$ invariants is widely conjectured to align with the enumeration of $O(2N)^{\otimes d}$ invariants. The watermark answer to this question might be found in [65, 66] which reveals a correspondence between the correlators in orthogonal and symplectic models.

Another type of Lie group invariants have been investigated where the tensor transforms under both unitary and orthogonal symmetries. To our knowledge, the $U(N)^{\otimes 2} \otimes O(N)$ model first appeared in the quantum gravity context as the multi-orientable TM [67, 68]. This model shares a similar large N limit with the colored TM [52], albeit without reflecting field coloration. The decomposition in identifiable cells of different dimensions within this model inherently contributes to its importance. Note that the continuum limit of the multi-orientable model does not deviate from that of ordinary TM.

In a slightly different context, the $U(N)^{\otimes 2} \otimes O(D)$ model was examined in [69, 70]. By fixing an index $\mu$ in the O(D) sector of the tensor, one acquires a vector of matrices $(X_\mu )_{ab}$. The model under consideration consists of D matrices, each of size $N \times N$, thus falling within the domain of multi-matrix models. Such a tensor $(X_\mu )_{ab}$ relates to transverse string excitations. String theory interprets the large D limit of this model as analogous to the limit of large spacetime dimension d in general relativity [71].

From yet another perspective, a complex TM with $U(N)^{\otimes 2} \otimes O(N)$ symmetry shares similar properties with the SYK model with complex fermions at large N [72, 73]. This particular symmetry triggers the tetrahedron interaction within the theory, a key observable for generating ladder operators susceptible to influence the infrared limit of these models. We recall that this study emanates from significant developments undergone by TM since Witten uncovered that the large N limit of colored TM [52] coincides with that of the SYK model, and therefore mimics its features at large N but without disorder coupling [74]. The SYK model, a condensed matter model [75, 76], is a unique laboratory for testing holography, via AdS/CFT correspondence in $1 + \epsilon$ dimensions. In [73], the enumeration of singlets in the $U(N)^{\otimes 2} \otimes O(N)$ model was performed, demonstrating behavior akin to the corresponding $O(N)^{\otimes 3}$ singlets as the number of fields increases. Analytic methods were used for counting [77]. The introduction of other types of symmetry for both bosonic and fermionic statistics, including constraints on the tensors (symmetric or traceless conditions), suggests the potential benefit of a universal group-theoretic formalism to encapsulate these symmetries.

In the exploration of new TM, the enduring question of discovering phases distinct from branched polymers in higher dimensions must be addressed. Recently, the $U(N)^{\otimes 2} \otimes O(N)$ model was scrutinized in [78] to reveal its critical behavior. The presence of two large parameters, N and D, allows for a refined classification of Feynman graphs within this model in terms of a new parameter called grade $\ell$ that governs the expansion of the partition function. After a thorough recursive characterization of the Feynman graphs of arbitrary genus g which survive in the double-scaling limit, i.e. at $\ell =0$, a triple-scaling limit focusing on two-particle irreducible graphs reveals that the critical behavior of such a model falls in the universality class of the Brownian sphere. In [79], the analysis was led further and aimed to classify Feynman graphs of any genus g and at higher grade $\ell =1, 2,3$.

Stemming from these motivations, this paper systematically addresses the enumeration of $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants, constructed from contractions of complex tensors with $r+q$ indices, for any positive integers r and q. These are referred to as UO invariants. While not explicitly stated, all results are extendable to multiple dimensions: $\big (\bigotimes _{i=1}^r U(N_i) \big )\otimes \big (\bigotimes _{j=1}^q O(N_j)\big )$. The goal is not only to extend the previous countings in the present setting, which is in any case a non-trivial endeavor, but also to showcase the richness of this class of models. UO invariants offer a new theory space for probing new continuum limits in random geometry, deepening the connection with TQFT, encompassing more general algebras for potential applications, but also forging links with renowned challenges, especially in combinatorics. The method is group theoretic-based as it has demonstrated its robustness and adaptability. A standard procedure sorts the number of connected UO invariants. At $q=0$, we recover the $U(N)^{\otimes r}$ counting [17], but a subtlety prevents to align $r=0$ with the $O(N)^{\otimes q}$ counting [20]. Several illustrations are provided for diverse sets of r and q. The lower-order cases $r,q\in \{1,2\}$ are also discussed, as they graphically coincide with a mixture of cyclic graphs with matching/pairing decorations. The UO model at order $(r=2,q=1)$ precisely delivers the sequence from [73] for the total and for the connected instances. Remarkably, aside from the sequences at $(r=2,q=1)$, and to the best of our knowledge, no sequences presented in this paper appear elsewhere, including on the OEIS website. Focusing on the order $(r=1,q=1)$, the UO invariants can be described with precision: they are in one-to-one correspondence with a set of cyclic words composed with an alphabet of 2 or 4 letters and are bounded by constraints (those pertain to vertex coloration and a bipartite sector in each graph). Cyclic words over a finite alphabet resonate profoundly: they qualify as Pólya necklaces. Thus, UO invariants at order-(1, 1) are essentially constrained Pólya necklaces. The constraints we encounter are stringent, and counting order-(1, 1) UO invariants is a less detailed process than enumerating Pólya necklaces of a specified length: we count all Pólya necklaces of varying lengths subject to identified constraints (pattern or string avoidance).

In a different vein, the group theoretic formalism enables us to have a correspondence with other countings through its translation into TQFT terms. We explore the topological covers that are encountered in our scenario: we learn that the $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants are in one-to-one correspondence with the covers of a 2-cellular complex made of $r+q$ glued cylinders along boundary circles. After some integrations, the same counting of UO invariants bijectively equates to the number of weighted branched covers of the 2-sphere with r branched points and degree n (or weighted covers of the 2-torus with $r-2$ branched points). The weight is expressed in terms of holonomies in the complex, constrained to a subgroup of the gauge group. In [2], these were attached to defects (marked cycle generators). The case $(r=1,q)$ deserves a particular attention: it counts certain branched covers of the 2-sphere with $q+3$ branched points. The method pushes the integration of group variables until no delta functions are left: each generator becomes either free or one of a torus. Depending on the convolution of group elements in the residual sums of the partition function, the enumeration can be interpreted as covers of 2-spheres or tori with specified weights, or merely a subset thereof.

The paper is organized as follows. In Sect. 2, we introduce our notation and set up the group action that corresponds to the desired counting. For simplicity, we specialize to $U(N)^{\otimes 3} \otimes O(N)^{\otimes 3}$ and provide concrete illustrations. Specific examples and listing all the graphs for 4 tensors confirm the counting (108 configurations computed with 4 tensor contractions up to color symmetry). We derive the general counting of $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants by generalizing the previous ideas. We then address the counting of connected invariants according to a standard procedure involving the so-called plethystic logarithm. Section 3 narrows the counting to lower order cases. In particular, we name them for obvious reasons vector-vector ($U(N) \otimes O(N)$) vector-matrix ($U(N) \otimes O(N)^{ \otimes 2}$), matrix-vector ($U(N)^{ \otimes 2} \otimes O(N)$), and matrix-matrix ($U(N)^{ \otimes 2} \otimes O(N)^{ \otimes 2}$) models. Especially, we delve into the vector-vector model ($U(N) \otimes O(N)$), extending our analysis by reinterpreting the counting in terms of counting words and necklaces. Section 4 presents two specific refined countings of UO invariants. Both cases factorize the unitary and orthogonal sectors in a different way. In Sect. 5, we discuss the TQFT picture associated with the counting UO invariants and map it to countings of (branched) covers of some topological manifolds. Section 6 gives concluding remarks and outlook of the present work. An appendix compiles the codes used to derive our sequences and extends the lists of sequences for various couples (r, q).

2 Counting $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants

This section exposes our main results on the counting of $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants made by the contraction of n covariant tensors T and n contravariant tensors ${\bar{T}}$. These invariants therefore provide the set of observables of tensor models with a tensor field that transforms under the fundamental representation of the Lie group $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$. At the beginning, for the sake of generality we consider generic tensors of multiple sizes.

2.1 UO invariants

Let r, q be two positive integers. Let $V_i$, $i=1,2,\dots , r$, be some complex vector spaces of respective dimension $N_i$, and $V^o_j$, $j=1,2,\dots , q,$ be some real vector spaces of respective dimension $N_j^o$. Let T be a covariant tensor of order-$(r+q)$ with components denoted $T_{a_1,a_2,\dots , a_r, b_1,b_2, \dots , b_{q}}$, with $a_i\in \{1,\dots , N_i\}$, and $b_j\in \{1,\dots , N_j^o\}$. We may also refer to the couple (r, q) as the order of the tensor T (rather than $r+q$) since cases such as (0, q) or (r, 0) may be discussed as special.

We require that T transforms under the action of the fundamental representation of the Lie group $(\bigotimes _{i=1}^{r} U(N_i) )\otimes (\bigotimes _{j=1}^{q} O(N_j^o))$. In symbols, we write:

$$\begin{aligned}{} & {} T_{a_1,a_2, \dots , a_r, b_1,b_2, \dots , b_q} \rightarrow U^{(1)}_{a_1c_1} U^{(2)}_{a_2c_2} \dots U^{(r)}_{a_rc_r} O^{(1)}_{b_1d_1} O^{(2)}_{b_2d_2}\nonumber \\{} & {} \quad \dots O^{(q)}_{b_qd_q} T_{c_1,c_2, \dots , c_r, d_1,d_2, \dots , d_q} , \end{aligned}$$

(2.1)

where the indices $a_i,b_i,c_i$, and $d_i$ should be taken in the correct range and repeated indices are summed over. Note that each unitary and orthogonal group acts on a specific index independently. Dealing with the contravariant complex conjugate tensor ${\bar{T}}$, we demand that it transforms as:

$$\begin{aligned}{} & {} {\bar{T}}_{a_1,a_2, \dots , a_r, b_1,b_2, \dots , b_q} \rightarrow {\bar{U}}^{(1)}_{a_1c_1} {\bar{U}}^{(2)}_{a_2c_2} \dots {\bar{U}}^{(r)}_{a_rc_r} O^{(1)}_{b_1d_1} O^{(2)}_{b_2d_2}\nonumber \\{} & {} \quad \dots O^{(q)}_{b_qd_q} {\bar{T}}_{c_1,c_2, \dots , c_r, d_1,d_2, \dots , d_q} . \end{aligned}$$

(2.2)

In this context, a $(\bigotimes _{i=1}^{r} U(N_i) )\otimes (\bigotimes _{j=1}^{q} O(N_j^o))$ invariant, shortly called hereafter UO-invariant, is built by contracting a given number of tensors T, say n of them, and the same number of complex conjugate tensors ${\bar{T}}$. A UO-invariant in this theory is algebraically denoted

$$\begin{aligned} \textrm{Tr}_{K_n}(T, {\bar{T}})= & {} \sum _{a^{i}_k, b^{i}_k, a'^{i}_k, b'^{i}_k} K_n(\{a^{i}_k,b^{i}_k\}; \{a'^{i}_k, b'^{i}_k\}) \nonumber \\{} & {} \times \prod _{i=1}^n T_{a^{i}_1,a^{i}_2,\dots , a^{i}_r, b^{i}_1, b^{i}_2, \dots ,b^{i}_q} {\bar{T}}_{a'^{i}_1,a'^{i}_2,\dots , a'^{i}_r, b'^{i}_1, b'^{i}_2,\dots , b'^{i}_q } .\nonumber \\ \end{aligned}$$

(2.3)

Here, $K_n$ is a kernel composed of a product of Kronecker delta functions that match the indices of n copies of T’s and those of n copies of $\bar{T}$’s. It is a well-known fact that a given tensor contraction dictates the pattern of an edge-colored graph, which can, in turn, be used to label the invariant. In the case of a unitary invariant, the resulting graph is an edge-colored bipartite graph with 2n vertices (with n black and n white vertices), each vertex having a valence equal to the tensor order [17]. For an orthogonal invariant, one obtains an edge-colored graph with 2n vertices, where each vertex’s valence is again determined by the tensor order [20]. The underlying graph of a contraction pattern leads to a group-theoretic counting procedure that determines the number of inequivalent tensor contractions. This principle is utilized in the subsequent discussion.

In the following, we will restrict to the case where $r+q \ge 2$ and $N_i \gg n$ and $N^o_j \gg n$, as the boundary cases where $N_i \sim n$ and $N_j^o \sim n$ should require a much more care [19, 21, 80, 81]. At time we will even collapse all indices to $N_i = N$ and $N^o_j = N^o$, yielding a uniform $U(N)^{\otimes r} \otimes O(N^o)^{\otimes q}$. For the limit cases

• when $q=0$, it reduces to the theory unitary invariants and their counting and therefore, at $r\ge 3$, we recover the results of [17];

• when $r=0$, it does not reduce to the theory of orthogonal invariants [20] but only a subset of them.

2.2 Counting UO-invariants

We address now the enumeration of $(\bigotimes _{i=1}^{r} U(N_i) )\otimes (\bigotimes _{j=1}^{q} O(N_j^o))$ invariants using a group theoretic procedure. For clarity, we will focus on $r=3$ and $q=3$ already quite involved and general. Indeed, although one may think that $r=q$ is a special case, all terms can be kept in track without ambiguity. The study will be then extended to arbitrary (r, q).

2.2.1 UO invariants of order (3, 3)

Consider a covariant tensor T of order (3, 3), uniquely represented by a white vertex with $3+3$ half-lines, distinguishing its indices. In contrast, the complex conjugate tensor $\bar{T}$ corresponds to a black vertex with an identical configuration, as detailed in [38, 52]. This procedure is explained in the following.

The contraction of n tensors T with n tensors $\bar{T}$ follows the schematic in Fig. 1, featuring n white and n black vertices, respectively. Therein, there are n white vertices identified with T, and n black vertices identified with ${\bar{T}}$. Note that the vertices are labeled for the moment. An edge is colored by an index i that we call color, and it means that the corresponding index $a_i$ of the tensor T at position i is contracted with another $a_i$ of some ${\bar{T}}$. If this happens, we have $\sum _{a_i}T_{\dots , a_i, \dots , }{\bar{T}}_{\dots , a_i, \dots , }$. The contraction of all indices at position i is orchestrated by an element $\sigma _i\in S_n$, where $S_n$ is the permutation group of n objects. As we have r colors, $i=1,2,\dots , r$, r permutations $\sigma _i$ perform this task. These connections implement the unitary sector of the invariants. The logic remains the same in the orthogonal sector without the restriction of connecting a white vertex and a black vertex. Each edge has a color $j=1,2,\dots , q,$ and represents a contraction of indices lying in the orthogonal sector of the tensors. This is governed by a permutation $\tau _j$, an element of $S_{2n}$, the permutation group of 2n objects. To implement all edge connections representing the orthogonal sector, we must have q permutations $\tau _j$, $j=1,2,\dots , q$.

Fig. 1

Diagram of contraction of n tensors T and n tensors ${\bar{T}}$: for a given color $i=1,2,\dots , r$, $\sigma _i$ represents the contraction in the unitary sector and, for any color $j=1,2,\dots , q$, $\tau _j$ represents the contraction in the orthogonal sector

Focusing on the case $(r=3,q=3)$, a UO-invariant is defined by a $3+3$-tuple of permutations $(\sigma _1, \sigma _2, \sigma _3, \tau _1, \tau _2, \tau _3)$ from the product space $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$. Vertex label removal introduces a permutation of these labels, rendering two configurations equivalent if their resulting unlabeled graphs coincide. We write this equivalence as:

$$\begin{aligned} ( \sigma _1, \sigma _2 , \sigma _3 , \tau _1, \tau _2 , \tau _3 )\sim & {} ( \gamma _1 \sigma _1 \gamma _2, \; \gamma _1 \sigma _2 \gamma _2, \; \gamma _1 \sigma _3 \gamma _2, \; \nonumber \\ {}{} & {} \gamma _1 \gamma _2 \tau _1 \varrho _1 , \; \gamma _1 \gamma _2 \tau _2 \varrho _2 , \; \gamma _1 \gamma _2 \tau _3 \varrho _3 ), \nonumber \\ \end{aligned}$$

(2.4)

where $\gamma _1, \gamma _2 \in S_n$, and $\varrho _1,\varrho _2, \varrho _3 \in S_{n}[S_2]$ the so-called wreath product subgroup of $S_{2n}$.

As $\gamma _1$ and $\gamma _2$ are elements of $S_n$, it is necessary to interpret $\gamma _1\gamma _2$ as an element of $S_{2n}$ in order to make sense of a composition $\gamma _1\gamma _2 \tau _i$, for $i=1,2, 3$. This can be easily achieved by stipulating that $\gamma _1$ acts on the first set of indices ${1,\dots , n}$ and $\gamma _2$ acts on the second set of indices ${n+1,\dots , 2n}$ and therefore we can write $\gamma _1 \gamma _2= \gamma _2 \gamma _1$. To avoid cumbersome notation, we retain the same symbols for these permutations when extended to ${1,2,\dots , 2n}$.

Fig. 2

UO-invariant graphs at order $(r,q)=(3,3)$ at $n = 2$

Inspecting (2.4), we observe that this equivalence relation cannot be uniquely described by a double coset action. Indeed, $\gamma _2$ is acting both on the left and on the right and on different slots. This shows that this computation extends nontrivially the previous ones, in particular, those in [2, 17, 20] that always dealt with double coset action. However, there is a group action on $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$ that we make now explicit. Consider the subgroups of $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$ defined as $H_1= H_2 = \textrm{Diag} _{3+3}(S_n)$ that are the diagonal of $(S_n)^{\times (3+3)}$. While the action of $H_1$ on $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$ is simply a multiplication on the left, we define the action of $H_2$ as follows

$$\begin{aligned}{} & {} ( \gamma , \gamma , \gamma , \gamma , \gamma , \gamma ) \cdot _{L,R} ( \gamma _1, \gamma _2, \gamma _3, \tau _1, \tau _2, \tau _3 )\nonumber \\{} & {} \quad = ( \gamma _1 \gamma , \gamma _2 \gamma , \gamma _3 \gamma , \gamma \tau _1, \gamma \tau _2, \gamma \tau _3 ) . \end{aligned}$$

(2.5)

Then, the subgroup $H_3 = (S_{n}[S_2])^{\times 3}$ acts on $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$ on the right and on the left of the last 3 slots.

$$\begin{aligned}{} & {} ( \varrho _1, \varrho _2, \varrho _3 ) \cdot ( \gamma _1, \gamma _2, \gamma _3, \tau _1, \tau _2, \tau _3 ) \nonumber \\{} & {} \quad = ( \gamma _1, \gamma _2, \gamma _3, \tau _1 \varrho _1, \tau _2\varrho _2, \tau _3\varrho _3 ) \;. \nonumber \\ \end{aligned}$$

(2.6)

The enumeration of graphs has quite a long history [25]. Read set up a double coset formulation for the extraction of the orbit number of the left and right action of two subgroups $H_1$ and $H_2$ of a group G. Based on Burnside’s lemma, the cardinality of the double coset $|H_1 {\setminus } G / H_2|$ is given by

$$\begin{aligned} |H_1 {\setminus } G / H_2| = \frac{1}{ |H_1| | H_2 | } \sum _{ C } Z_C^{ H_1 \rightarrow G } Z^{ H_2 \rightarrow G }_C \, \hbox {Sym} ( C ) ,\nonumber \\ \end{aligned}$$

(2.7)

where the sum is performed over conjugacy classes of G; $Z_C^{ H \rightarrow G }$ is the number of elements of H in the conjugacy class C of G. In full generality, Burnside’s lemma extends to the action of any family of subgroups $\{H_i\}_{i\in I}$, I finite, on a group G. The cardinality of the number of orbits of the collective action of $\{H_i\}_{i\in I}$ is given by

$$\begin{aligned} | G / \prod _{i\in I} H_i | = {1 \over \prod _{i\in I} |H_i| } \sum _{C} \left( \prod _{i\in I} Z_C^{ H_i \rightarrow G }\right) \; \hbox {Sym} (C). \nonumber \\ \end{aligned}$$

(2.8)

We start by writing the number of orbits of the action of $H_1H_2H_3$ on $(S_n)^{\times 3} \times (S_{2n})^{\times 3}$ which, using Burnside’s Lemma, reduces to the mean value of the number of fixed points of the action:

$$\begin{aligned} Z_{(3,3)}(n)= & {} { 1 \over {(n!)^2 [n! (2!)^{n}]^3}} \sum _{ \gamma _1, \gamma _2 \in S_{n}} \sum _{\varrho _1,\varrho _2, \varrho _3 \in S_n[S_2]}\nonumber \\{} & {} \times \sum _{\begin{array}{c} \sigma _1, \sigma _2, \sigma _3 \in S_{n} \\ \tau _1,\tau _2,\tau _3 \in S_{2n} \end{array}} \left[ \prod _{i=1}^{3} \delta (\gamma _1 \sigma _i \gamma _2 \sigma _i^{-1} ) \right] \nonumber \\{} & {} \times \left[ \prod _{i=1}^{3} \delta (\gamma _1 \gamma _2\tau _i \varrho _i \tau _i ^{-1} ) \right] , \end{aligned}$$

(2.9)

where the $\delta$ function on $S_n$ is defined by $\delta (\sigma ) =1$, if $\sigma =id$, and equals 0 otherwise. We recast the above sum in terms of conjugacy classes ${{{\mathcal {C}}}}_p$ of $S_n$ which are labeled by partitions p of n:

$$\begin{aligned} Z_{(3,3)}(n)= & {} \frac{1}{[(n!)^2(n!2^n)^3]} \sum _{p \vdash n} \big (Z_{p}^{ S_n \rightarrow S_n }\big )^2\big (Z_{p}^{ S_n[S_2]\rightarrow S_{2n}}\big )^3 \nonumber \\{} & {} \times \big ( \hbox {Sym} (p)\big )^3 \big ( \hbox {Sym} (2 p )\big )^3 , \end{aligned}$$

(2.10)

where $p \vdash n$ denotes a partition of n and $2p\vdash 2n$ is the partition of 2n obtained from p by doubling its parts. For instance, if $p=[1^{p_1},2^{p_2}, \dots , k^{p_k}] \vdash n$, then $2p=[1^{2p_1},2^{2p_2}, \dots , k^{2p_k}]\vdash 2n$. Given $p=(p_\ell )_{\ell =1}^n$, $\hbox {Sym} (p) = \prod _{\ell } \ell ^{p_\ell } p_\ell !$ is the so-called symmetry factor of the class p or the order of the centralizer of a permutation of the class ${{{\mathcal {C}}}}_p$.

Some factors in $Z_{(3,3)}$ must be explained: inspecting (2.9), we have $\delta (\gamma _1 \sigma _i \gamma _2 \sigma _i^{-1})$ which demands that $\gamma _1$ and $\gamma _2$ belong to the same conjugacy class. Moreover, in the last product of (2.9), the delta function $\delta (\gamma _1 \gamma _2\tau _i \varrho _i \tau _i^{-1})$ enforces the condition that $\gamma _1 \gamma _2$ and $\varrho _i$ belong to the same conjugacy class. Given that $\gamma _1$ and $\gamma _2$ share the same class, the conjugacy class of $\varrho _i$ is a concatenation of 2 partitions p and becomes 2p.

Since $Z_{p}^{ S_n \rightarrow S_n } = |{{{\mathcal {C}}}}_p| = n!/ \hbox {Sym} (p)$ is the size of the conjugacy class ${{{\mathcal {C}}}}_p$ (via orbit stabilizer theorem), we can simplify $Z_{(3,3)}(n)$:

$$\begin{aligned} Z_{(3,3)}(n)= & {} \frac{1}{(n!)^2(n!2^n)^3} \sum _{p \vdash n} \left( {n! \over \hbox {Sym} (p)}\right) ^2 \nonumber \\{} & {} \times \big (Z_{p}^{ S_n[S_2]\rightarrow S_{2n}}\big )^3 \big ( \hbox {Sym} (p)\big )^3\big ( \hbox {Sym} (2 p )\big )^3 \\\\= & {} \frac{1}{(n!2^n)^3} \sum _{p \vdash n} \big ( Z_{2p}^{S_n[S_2]\rightarrow S_{2n}} \hbox {Sym} (2p)\big )^3 \; \hbox {Sym} (p). \nonumber \\ \end{aligned}$$

(2.11)

To be able to reach the number $Z_{2p}^{S_n[S_2]\rightarrow S_{2n}}$, we use known facts about generating series. Given a partition $\alpha = (\alpha _l)_l \vdash 2n$, we can get a single factor in this product as

$$\begin{aligned}{} & {} { 1 \over {n! (2!)^{n} }} Z_{\alpha }^{ S_{n}[S_2] \rightarrow S_{2n} } \nonumber \\{} & {} \quad = \hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{\alpha _1} x_2^{\alpha _2}\dots x_{n} ^{\alpha _{n} } ] , \end{aligned}$$

(2.12)

where, given d a positive integer, ${{{\mathcal {Z}}}}_{d}^{S_\infty [S_d]}(t, \vec x)$ is the generating function of the number of wreath product elements in a certain conjugacy class $\alpha$, namely

$$\begin{aligned} {{{\mathcal {Z}}}}_{d}^{S_\infty [S_d]}(t, \vec x){} & {} = \sum _{n} t^n Z^{ S_n[S_d]}(\vec x) \nonumber \\{} & {} = e^{ \sum _{i=1}^{\infty } \, \frac{t^i}{i}\, \left[ \sum _{q \vdash d} \prod _{\ell =1}^{d} \left( \frac{ x_{i\ell } }{ \ell } \right) ^{\nu _\ell } \frac{1}{ \nu _\ell ! } \right] } , \end{aligned}$$

(2.13)

with $\vec x = (x_1, x_2, \dots )$, $q= (\nu _\ell )_\ell$ a partition of d, such that $\sum _{\ell } \ell \nu _\ell = d$.

Now we apply (2.12) when $\alpha = 2p$ and get a new expression for (2.11) as:

$$\begin{aligned} Z_{(3,3)}(2n)= & {} \sum _{ p \,\vdash n } \big (\hbox {Coefficient }[ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x),\nonumber \\{} & {} t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n} } ] \; \hbox {Sym} (2p) \big )^3 \hbox {Sym} ( p ) \, .\nonumber \\ \end{aligned}$$

(2.14)

We can generate the sequence $Z_{(3,3)}(n)$, for $n=(1, \ldots , 7$) using a code given in Appendix A.1. We obtain the sequence:

$$\begin{aligned}{} & {} 1, 108, 20385, 27911497, 101270263373,\nonumber \\{} & {} \quad 808737763302769, 12437533558341538117. \end{aligned}$$

(2.15)

Figure 2 showcases a complete set of UO-invariant graphs for $(r,q)=(3,3)$ and $n=2$. The graphs employ a color-coding scheme for clarity. White and black nodes represent the tensors T and ${\bar{T}}$, with each node connecting to six edges, mirroring the tensors’ $3+3$ structure. Edges colored in black and red indicate contractions within O(N) and U(N) tensors, marked by integers i that determine the graph’s configuration based on the index colors $i=1,2,3$.

For graphs with labels like i, j, the invariants depend on these indices, with each taking values from 1 to 3. Red lines denote orthogonal invariants, while black lines represent unitary ones. Notably, graphs remain bipartite after excluding the red edges.

The integer below each graph enumerates the various possibilities based on index colors, summing to 108 for all configurations, as sequence (2.15) specifies for $n=2$ (this 2 black and 2 white vertices). It is crucial to notice that this counting depends on the bipartiteness condition only within the U(N) sector (black edges). However, as they should, the graphs associated with UO invariants are not bipartite.

We can compare the enumeration of the UO invariants of order (r, q) with the enumeration of the other classical invariants of same order. The $O(N)^{\otimes 6}$ invariants [20] yield the sequence for 2n tensors, for $n=1,2,\dots , 7$:

$$\begin{aligned}{} & {} 1, 122, 18373, 33884745, 196350215004,\nonumber \\{} & {} \quad 2634094790963313, 69856539937093983210. \end{aligned}$$

(2.16)

Meanwhile, the number of $U(N)^{\otimes 6}$ invariants within the same range of n gives:

$$\begin{aligned}{} & {} 1, 32, 1393, 336465, 207388305, \nonumber \\{} & {} \quad 268749463729, 645244638648481. \end{aligned}$$

(2.17)

For each order n, with the exception of $n=3$, the number of $O(N)^{\otimes 6}$ invariants surpasses that of the UO invariants of order $(r=3,q=3)$. The latter, in turn, exceeds the counting of $U(N)^{\otimes 6}$ invariants. We will observe that for lower order cases, specifically for $(r,q)=(1,2)$, this pattern does not hold for small values of $n\ge 15$. Nevertheless, it cannot be ruled out that at higher values of n, the predominance of the number of orthogonal invariants may re-emerge. An asymptotic analysis, for instance like the one performed in [82], could be useful to understand the large n behavior of these countings.

2.2.2 General case: UO invariants of order (r, q)

In general, for any arbitrary order (r, q), where $r \ge 1$ and $q \ge 1$, the preceding analysis can be methodically replicated without difficulties. We concisely present the key aspects that contribute to the enumeration formula for UO invariants.

Any UO invariant made with (r, q) tensors is defined by the equivalence relation generalizing (2.4):

$$\begin{aligned}{} & {} ( \sigma _1, \sigma _2 , \dots , \sigma _p , \tau _1, \tau _2 , \dots , \tau _q ) \nonumber \\{} & {} \quad \sim ( \gamma _1 \sigma _1 \gamma _2, \; \gamma _1 \sigma _2 \gamma _2, \; \dots , \gamma _1 \sigma _r \gamma _2, \nonumber \\ {}{} & {} \quad \gamma _2 \gamma _1 \tau _1 \varrho _1 , \; \gamma _2 \gamma _1 \tau _2 \varrho _2 , \; \dots , \; \gamma _2 \gamma _1 \tau _q \varrho _q ). \end{aligned}$$

(2.18)

We therefore consider the action of the subgroups of $(S_n)^{\times r} \times (S_{2n})^{\times q}$ defined as $H_1= H_2 = \textrm{Diag} _{r+q}(S_n)$ and $H_3 = (S_n[S^2])^{\times q}$. The action of $H_1$, $H_2$ and $H_3$ can be derived from (2.18) without ambiguity.

Burnside’s lemma allows us to enumerate the orbits of the action of $H_1H_2H_3$ on $(S_n)^{\times r} \times (S_{2n})^{\times q}$:

$$\begin{aligned} Z_{(r,q)}(n)= & {} { 1 \over {(n!)^2 [n! (2!)^{n}]^q}} \sum _{ \gamma _1, \gamma _2 \in S_{n}} \sum _{\varrho _1,\dots ,\varrho _q \in S_n[S_2]}\nonumber \\{} & {} \times \sum _{\begin{array}{c} \sigma _1,\dots , \sigma _r \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \end{array}}\left[ \prod _{i=1}^{r} \delta (\gamma _1 \sigma _i \gamma _2 \sigma _i^{-1} ) \right] \nonumber \\{} & {} \times \left[ \prod _{i=1}^{q} \delta (\gamma _1 \gamma _2\tau _i \varrho _i \tau _i ^{-1} ) \right] , \end{aligned}$$

(2.19)

which must be compared to (2.9). In terms of partitions $p \vdash n$, the same sum expresses :

$$\begin{aligned} Z_{(r,q)}(n)= & {} \frac{1}{[(n!)^2 (n!2^n)^q]} \sum _{p \vdash n} \big (Z_{p}^{ S_n \rightarrow S_n }\big )^2\nonumber \\{} & {} \times \Big (Z_{p}^{ S_n[S_2]\rightarrow S_{2n}}\Big )^q \; \big ( \hbox {Sym} (p)\big )^r \big ( \hbox {Sym} (2 p )\big )^q , \nonumber \\ \end{aligned}$$

(2.20)

which simplifies as

$$\begin{aligned} Z_{(r,q)}(n )= & {} \sum _{ p \,\vdash n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{2p_1} x_2^{2p_2}\nonumber \\{} & {} \times \dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p )\Big )^q \big ( \hbox {Sym} ( p )\big )^{r-2}. \end{aligned}$$

(2.21)

Remarkably, at $q=0$, $Z_{r,0}(n)$ recovers as promised the counting of unitary invariants $Z_q^{U}(n)$ [17]. However, at $r=0$, there is a notable difference with the counting of orthogonal invariants. We have

$$\begin{aligned} Z_{(0,q)}(n )= & {} \sum _{ p \,\vdash n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{2p_1}\nonumber \\{} & {} \times x_2^{2p_2}\dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p )\Big )^q , \end{aligned}$$

(2.22)

which does not correspond to the counting of $O(N)^{\otimes q}$ given by [20]:

$$\begin{aligned} Z^{O}_q (2n)= & {} \sum _{ p \,\vdash 2n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{p_1}\nonumber \\{} & {} \times x_2^{p_2}\dots x_{n} ^{p_{n} } ]\;\Big )^q ( \hbox {Sym} ( p ))^{q-1}. \end{aligned}$$

(2.23)

This is due to the presence of $\gamma _1 \gamma _2$, instead of a single $\gamma$ acting on the tuple in the gauge invariance of the orthogonal sector.

Table 2 The number of UO invariants of order (r, q) for $n\in \{1,2,3,4 ,5\}$

Table 3 The number of connected UO invariants for various order (r, q) for $n\in \{1,2,3,4 \}$

Using the code in Appendix A.1, we compute various sequences $(r,q)\in \{(2,3),(2,4),$ $(3,2), (3,3), (3,4)\}$ for $n\in \{1,2,\dots ,5\}$, see Table 2. The interested reader will find in Appendix B, extended sequences for wider range of r, q and n.

2.3 On the enumeration of $\otimes _{i} (U(N)^{\otimes r_i} \otimes O(N)^{\otimes q_i})$ invariants

This is a further generalization of the previous enumeration formulas. We will conduct the counting through a streamlined analysis, as the previous enumeration of UO invariants primarily contains all the information required to obtain the result.

Consider a partition $(r_i)_i$ of r, satisfying $\sum _{i=1}^{k} r_i = r$, and a second partition $(q_j)_j$ of q, satisfying $\sum _{j=1}^{k} q_j = q$. It is not necessary to have the information on the multiplicity of any given part but important to note that we select partitions of the same length k. If the partitions were of different lengths, the forthcoming formulas could be simplified by combining several parts to make them larger.

Let us assume that the indices of tensor T can be packaged in the form

$$\begin{aligned}{} & {} T_{a^{1}_1,a^{1}_2,\dots , a^{1}_{r_1}, b^{1}_1,b^{1}_2, \dots , b^{1}_{q_1}, a^{2}_{1},a^{2}_2,\dots , a^{2}_{r_2}, b^{2}_1,b^{2}_2, \dots ,}\nonumber \\{} & {} \qquad {}_{b^{2}_{q_2}, \dots a^{k}_{1},a^{k}_2,\dots , a^{k}_{r_k}, b^{k}_1,b^{k}_2, \dots , b^{k}_{q_k} }. \end{aligned}$$

(2.24)

All the $a^{i}_{j}$ indices transform under the fundamental representation of U(N), and all the $b^{i}_{j}$ indices under the fundamental representation of O(N). Likewise, we introduce the complex conjugate tensor $\bar{T}$, and we are interested in enumerating the number of $\bigotimes _{i=1}^k ( U(N)^{\otimes r_i} O(N)^{\otimes q_i})$ invariants made by contracting n tensors T and n tensors $\bar{T}$.

The previous formalism of section 2.2.2 extends with no obstruction, and we refrain from inserting it here. We compute the number of equivalence classes lying in

$$\begin{aligned}{} & {} \prod _{i=1}^k (S_{n}^{\times r_i} \times S_{2n}^{\times q_i}) / H_1 H_2 \prod _{i=1}^k H_3^i , \nonumber \\{} & {} \qquad H_1 = H_2 = \textrm{Diag}_{ r+q }(S_n)\; , H_3^{i} = (S_n[S_2])^{\times q_i}. \end{aligned}$$

(2.25)

$H_1$ has a left action, $H_2$ is a right action on the $r_i$ slots and a left action on the $q_i$ slots, $H_3$ right action on the $q_i$ slots.

Applying step by step the above procedure leads us to the number $Z_{\{r_i\}, \{q_i\}} (n)$ of invariants in the present setting as

$$\begin{aligned} Z_{\{r_i\}, \{q_i\}} (n) = Z_{(r,q)}(n). \end{aligned}$$

(2.26)

Hence, considering different slots alternating the orthogonal and the unitary sector does not change the counting.

2.4 Connected UO invariants

In this framework, the number of connected UO invariants can be obtained by the so-called plethystic logarithm. Such generating series and its inverse the plethystic exponential have sundry remarkable applications in theoretical physics in [83].

We recall that the generating function of the previous counting of UO invariant at order (r, q) is given by

$$\begin{aligned} Z_{(r,q)}(x) = \sum _{n=0}^{\infty } Z_{(r,q)}(n) x^n. \end{aligned}$$

(2.27)

This function enters in the definition of the plethystic logarithm function defined by

$$\begin{aligned} \textrm{PLog}_{(r,q)}(x) = \sum _{i=1}^{\infty } \frac{\mu (i)}{i} \log [Z_{(r,q)}(x^i)] , \end{aligned}$$

(2.28)

where $\mu$ the Mobius function defined such that $\mu (1)= 1$, $\mu (i)= 0$, if i has repeated prime numbers; $\mu (i)= (-1)^{k_0}$ if i is a product of $k_0$ distinct prime numbers.

We can implement the PLog function using a program, see Appendix A.3. We obtain the following sequence for diverse (r, q) pairs as recorded in Table 3.

Table 4 Comparing the enumerations of UO invariants of order (1, 1), of $O(N)^{\otimes 2}$ and of $U(N)^{\otimes 2}$ invariants for $n\in \{1,2,\dots ,10 \}$

Fig. 3

The UO invariants at order (1, 1) for $n=1$ (A), $n=2$ (B1–B3) and $n=3$ (C1–C5). Remark here that for example, each set (B2 and B3), (C2 and C3), and (C4 and C5) are indistinguishable in the pure orthogonal case

3 Reductions to lower order cases

Lower order cases are defined by $r,q \in \{1,2\}$ and they make the unitary or orthogonal sector either as a matrix or vector invariant. The resulting UO invariant becomes a gluing of those 2 types of invariants, making a new UO invariant of order (r, q). It is essential to observe that the resulting tensor may be very well of an order larger than 2. Thus, we will compare the number of the UO invariants of order (r, q) with the classical countings of orthogonal and unitary invariants at order $r+q$.

3.1 Vector-vector-like model: words and necklaces

We call vector-vector model the UO model defined by $(r=1,q=1)$. We run the same principle as discussed in section 2.2.

The counting Any UO invariant made with (1, 1)-order tensors is defined by the equivalence relation,

$$\begin{aligned} ( \sigma , \tau )\sim & {} ( \gamma _1 \sigma \gamma _2, \gamma _1 \gamma _2 \tau \varrho _1 ) , \end{aligned}$$

(3.1)

written in the same previous notation. This leads us to the counting:

$$\begin{aligned} Z_{(1,1)} (n)= & {} \frac{1}{(n! 2^n)} \sum _{p \vdash n} {{\mathcal {Z}}}^{S_n [S_2] \rightarrow S_{2n}}_{2 p} \, \frac{{ \hbox {Sym} } (2 p) }{{ \hbox {Sym} } (p)} \nonumber \\= & {} \sum _{p \vdash n} \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{2p_1}\nonumber \\{} & {} \times x_2^{2p_2}\dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p )\Big ) \; \hbox {Sym} (p)^{-1}. \end{aligned}$$

(3.2)

We notice that the formula $Z_{(r,q)}$ (2.19) extends at $r=1$. A code in Appendix A.2 evaluates $Z_{(1,1)} (n)$ for n running from 1 to 10 and compare it with the enumeration of $O(N)^{\otimes 2}$ and $U(N)^{\otimes 2}$ invariants. Table 4 records these sequences.

In Fig. 3, we illustrate the invariants at $n=1,2$ and 3. Note that the red edge identifies with the contraction of an orthogonal index of the tensor, while the black edge determines the contraction of the unitary index.

It is well known that $O(N)^{\otimes 2}$ and $U(N)^{\otimes 2}$ invariants of the form of matrix traces with 2n matrices are enumerated by p(n), the number of partitions of n (the cycle length that decomposes n). Up to $n\le 15$, the number of UO invariants dominates the number of classical Lie group invariants. In Fig. 3, this is manifest since some cycles are repeated.

Table 5 presents the counting of connected (1, 1)-order UO invariants computed using the plethystic logarithm.

Table 5 Number of connected UO invariants at order (1, 1) for $n\in \{1,2,\dots , 15\}$ and the OEIS sequence A053656

The first ten terms of the sequence of connected invariants correspond to the first ten terms of the OEIS sequence A053656 [84], which enumerates the number of cyclic graphs with oriented edges on n nodes, considering the symmetry of the dihedral group. The correspondence fails beyond the 11th up to the 15th term by one. Nothing excludes that the discrepancy increases as n becomes larger. The cyclic symmetry of the (1, 1)-order UO invariants has additional implications, which will be highlighted in the subsequent section.

Invariants, words and necklaces Another interpretation of the counting of connected UO invariants of order-(1, 1) can be understood through specific words, which we will now explain.

Fig. 4

The connected UO invariants at order (1, 1) for $n=5$

Graphically, the construction of these invariants is governed by a few rules:

• R1 – There are n black and n white vertices on a cycle, exhibiting cyclic symmetry.

• R2 – No more than two vertices of the same color may be adjacent; this ensures that a vertex does not have two edges of the same color, adhering to unitary and orthogonal contractions.

• R3 – There are n black edges connecting white and black vertices, representing a bipartite sector corresponding to unitary contractions.

While R1 is straightforward, one might question whether R2 and R3 are redundant. To demonstrate the necessity of both rules, we can examine the distinct connected invariants at $n=5$, as shown in Fig. 4.

Consider the configuration in Fig. 5. It satisfies R1 and R2 but does not meet the requirement of having $n=5$ edges incident to both white and black vertices. Therefore, all conditions must be simultaneously fulfilled.

Let $\mu _b$ and $\mu _w$ be two partitions of an integer n into parts of size at most 2. Without loss of generality, we initiate a selection procedure with $\mu _b$ but must conclude it with $\mu _w$ (or vice versa), as cyclic symmetry in the following dictates this requirement. By selecting a part from $\mu _b$, followed by a part from $\mu _w$, and repeating this process, we generate a sequence composed of 1s and 2s. If $\mu _b$ possesses a number of parts different from that of $\mu _w$, it implies that the process will terminate prematurely, leaving some parts of one partition unincorporated. This imposes a constraint on the number of parts within the chosen partition to ensure the alternating sequence begins with one partition and ends with the other. On the other hand, two partitions with the same number of parts, composed uniquely of parts of size 2 and 1 having the same number of parts, must be identical: $\mu _b = \mu _w$. This can be easily checked as a linear system obeyed by the multiplicities of 2 and 1.

The next concept involves using a partition $\mu$ to encode a (1, 1)-order UO invariant. Consider an alphabet consisting of four letters divided into $V = \{1,2\}$ and ${\bar{V}} = \{{\bar{1}}, {\bar{2}}\}$. Select a partition $\mu$ of n, and construct the list $\bar{\mu }$ by substituting each 1 with a ${\bar{1}}$, and each 2 with a ${\bar{2}}$. We denote the number of parts of $\mu$ by $|\mu |$. Our objective is to enumerate all words that obey certain constraints. We construct a word ${\textbf {w}}$ such that:

Fig. 5

A failing configuration

• r1 – ${\textbf {w}}$ is cyclically symmetric of length $\ell = 2|\mu |$;

• r2 – ${\textbf {w}}$ is constructed by alternately choosing parts from $\mu$ and $\bar{\mu }$;

• r3 – ${\textbf {w}}$ is free of the substrings (patterns) $2 {\bar{1}} 2$ and ${\bar{2}} 1 {\bar{2}}$.

We denote $Z_{\mu }(n)$ the number of words obeying the rules r1 to r3. The following statement holds.

Theorem 1

Given a positive integer, n,

$$\begin{aligned} Z_{(r,q)}(n) = \sum _{ \begin{array}{c} \mu \vdash n \\ \mu _i \le 2 \end{array} } Z_{\mu }(n) , \end{aligned}$$

(3.3)

where the sum is performed over partitions $\mu$ of n with parts $\mu _i$ of size at most 2.

Proof

We demonstrate that each word bijectively maps to a specific (1, 1) invariant. To achieve this, one must prove that the rules r1, r2, and r3 uniquely implement R1, R2, and R3, respectively, and vice versa. In fact, the converse will be evident by construction. The goal is to construct a cyclic graph associated with an invariant simply by the code given by the selected word.

Let ${\textbf{w}}$ be a word of length $\ell _\mu$ corresponding to a partition $\mu$ of a given n, and adhering to the rules r1–r3.

Each 2 in $\mu$ (respectively, $\bar{2}$ in $\bar{\mu }$) corresponds to two adjacent white vertices (respectively, two adjacent black vertices). Each 1 (respectively, $\bar{1}$) corresponds to a single white vertex (respectively, a single black vertex). Thus, the parts of $\mu$ and $\bar{\mu }$ map either to a pair of vertices of the same color or to a single vertex of a specific color, yielding n white and n black vertices. To implement the cyclic symmetry r1, we arrange the vertices in a circle, thereby satisfying R1.

Rule r2 instructs us to alternately select parts from $\mu$ and $\bar{\mu }$. This enforces the condition that no sequence of vertices of the same color exceeds 2 in length (as we do not have part of size larger than 2 in $\mu$ or $\bar{\mu }$). Naturally, such an arrangement of pairs and single vertices satisfies R2.

Rule r3 mandates the avoidance of the substrings $\bar{2}1\bar{2}$ and $2\bar{1}2$. Observing the substring $\bar{2}1\bar{2}$, we see that a sequence of 2 black vertices is followed by 1 white vertex, which in turn is followed by another pair of black vertices. Adjacency of two black vertices is assigned to an orthogonal contraction. Therefore, the edge connecting one of these black vertices to the white vertex must signify a unitary contraction. On the opposite side of the white vertex, a similar situation occurs, indicating that this white vertex cannot possess two unitary connections, which is prohibited. The same reasoning applies to the substring $2\bar{1}2$, with the roles of black and white vertices interchanged, thereby satisfying R3.

The final aspect to consider for deriving (3.3) is that the sets of words of a given length are mutually exclusive. Each partition $\mu$ of parts $\mu _i\le 2$ is of specific length and yields a unique word. Summing over all possible partitions yields the complete set of possible words. $\square$

Examples. Let us give some examples.

(1) If $n=1$, $\mu = \bar{\mu }= [1]$, the length of the word must be $\ell = 2$. Under such conditions, we can only construct a single word ${\textbf{w}} = 1 {\bar{1}}$. This corresponds to Fig. 3A.

(2) If $n=2$, two cases can occur:

(21) $\mu = \bar{\mu }= [1^2]$, the word length must be $\ell = 4$. The sole possible word is: ${\textbf{w}}_1 = 1 {\bar{1}} 1 {\bar{1}}$ which corresponds to Fig. 3B1.

(22) $\mu = \bar{\mu }= [2]$, then $\ell = 2$. We have simply ${\textbf{w}}_2 = 2 {\bar{2}}$ and this corresponds to Fig. 3B2.

(3) If $n=3$, there are 2 partitions made of 1 and 2 cycles:

(31) $\mu = \bar{\mu }= [1^3]$, the length of the word must be $\ell = 6$. We obtain the word : ${\textbf{w}}_1 = 1 {\bar{1}} 1 {\bar{1}} 1 {\bar{1}}$. This correspond to Fig. 3C4.

(32) $\mu = \bar{\mu }= [2,1]$, the length of the word must be $\ell = 4$. The ${\textbf{w}}_2 = 2 {\bar{2}} 1 {\bar{1}}$. This correspond to Fig. 3C5.

The cyclic words or graphs that bijectively correspond to (1, 1) UO invariants refine the concept of k-ary necklaces as described by [85]. For two positive integers k and n, a k-ary necklace of length n is defined as an equivalence class of words of length n from an alphabet of size k, under cyclic permutations. The terminology alludes to a necklace composed of n beads in k distinct colors. The enumeration of inequivalent necklaces was addressed by the renowned Pólya theorem [26], becoming a cornerstone in combinatorial studies.

Intriguingly, Theorem 1 suggests that the enumeration of UO invariants of order (1, 1) facilitates the counting of special 4-ary necklaces, not confined to a specific length but encompassing all lengths up to 2n. This approach results in a broader, albeit less granular, enumeration. It is crucial to note the presence of a substring exclusion prior to counting, which means that the enumeration (3.3) does not align with the sum over $\ell$ of $N_{4}(\ell )$, the number of 4-ary necklaces of length $\ell$:

$$\begin{aligned} N_{4}(\ell ) = \frac{1}{\ell } \sum _{d | \ell } \varphi (d) 4^{\ell /d} = \frac{1}{\ell } \sum _{i=1}^{\ell } 4^{\text {gcd}(i,\ell )}, \end{aligned}$$

(3.4)

where $\varphi$ denotes Euler’s totient function. Moreover, it is also instructive to unfold the parts encoded by the 2 and ${{\bar{2}}}$, creating a binary code represented in terms of 1 and ${{\bar{1}}}$. Under this representation, the substring exclusions can be translated into $11{{\bar{1}}}11$ and ${{\bar{1}}}{{\bar{1}}}1{{\bar{1}}}{{\bar{1}}}$. Consequently, the counting of UO-invariants of order (1, 1) consists of binary necklaces of length 2n with certain substring excluded. We therefore have:

$$\begin{aligned} Z_{(1,1)}(n) \le N_2(2n). \end{aligned}$$

(3.5)

Understanding the enumeration of UO invariants may shed light on the counting of k-ary necklaces with substring exclusions. Pólya’s method, which closely mirrors our approach, is grounded in Burnside’s lemma. Integrating both methodologies and applying substring exclusions at the level of cyclic symmetry is necessary. In our current framework, the exclusion, represented by $\tau \in S_n[S_2]$ (3.1), prohibits specific configurations that are identifiable. Addressing this issue of reconciling both enumeration methods requires novel tools and is left for future investigation.

3.2 On other lower order cases

In this section, we briefly review some features of lower order cases.

Matrix-vector and vector-matrix like models We inspect now the case of $(r=2,q=1)$-order and $(r=1, q=2)$-order UO invariants that we compare with $O(N)^{\otimes 3}$ and $U(N)^{\otimes 3}$ invariants.

Considering its equivalence relation $( \sigma _1, \sigma _2, \tau ) \sim ( \gamma _1 \sigma _1 \gamma _2, \gamma _1 \sigma _2 \gamma _2, \gamma _2 \gamma _1 \tau \varrho _1 )$, one obtains, for the matrix-vector model, the counting formula:

$$\begin{aligned} Z_{(2,1)}(n )= & {} \frac{1}{(n! 2^n)} \sum _{p \vdash n} {{\mathcal {Z}}}^{S_n [S_2] \rightarrow S_{2n}}_{2 p} \, { \hbox {Sym} } (2 p) \\\\= & {} \sum _{ p \,\vdash n } \hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{2p_1}\nonumber \\{} & {} \times x_2^{2p_2}\dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p ) \end{aligned}$$

(3.6)

which can be also obtained from (2.19) specializing to $(r=2, q=1)$.

Similarly, for the vector-matrix model, i.e., $(r, q) = (1, 2)$, after identifying the equivalence relation, $( \sigma , \tau _1, \tau _2) \sim ( \gamma _1 \sigma \gamma _2 , \gamma _1 \gamma _2 \tau _1 \varrho _1, \gamma _1 \gamma _2 \tau _2\varrho _2)$, we count the number of its invariants as

$$\begin{aligned} Z_{(1,2)} (n)= & {} \frac{1}{(n! 2^n)^2} \sum _{p \vdash n} \Big ( {{\mathcal {Z}}}^{S_n [S_2] \rightarrow S_{2n}}_{2 p} \, { \hbox {Sym} } (2 p) \Big )^2 ( \hbox {Sym} (p)) ^{-1}.\\\\= & {} \sum _{ p \,\vdash n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) ,\nonumber \\{} & {} t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p )\Big )^2 \big ( \hbox {Sym} ( p )\big )^{-1} , \end{aligned}$$

(3.7)

obtained from (2.19) by applying $(r=1,q=2)$. This shows once more, that $Z_{(r,q)}$ extends to $r=1$ without obstructions.

Table 6 shows the enumeration at the first few orders and Table 7 gives the enumeration of the connected invariants.

Table 6 The numbers of UO invariants of order (2, 1) and (1, 2) compared to $O(N)^{\otimes 3}$ and $U(N)^{\otimes 3}$ invariants for $n\in \{1,2,\dots ,10 \}$

Table 7 The numbers of connected UO invariants of order (2, 1) and (1, 2) compared to connected $O(N)^{\otimes 3}$ and $U(N)^{\otimes 3}$ invariants for $n\in \{1,2,\dots ,10 \}$

Table 8 The numbers of UO invariants of order (2, 2), compared to $O(N)^{\otimes 4}$ and $U(N)^{\otimes 4}$ invariants for $n\in \{1,2,\dots ,8 \}$

At this order, up to a total number of vertices $2n=20$, in a manner akin to what was observed in the (1, 1) model, the number of UO invariants dominates the other invariants. The sequence for the (1, 2)-order case, encompassing both general and connected invariants, was calculated in [73] employing analytic methods.

We discuss here how the prior bijection between (1, 1) order invariants and necklaces extends to the current models.

A UO invariant of order (2, 1) or (1, 2) inherently includes a (1, 1)-sector. Indeed, in symbol, we have $U^2 O = U (UO)$ and similarly $UO^2 = (UO) O$. Consequently, within such invariants, a 4-ary necklace can be isolated, incorporating the same pattern avoidance. Moreover, in the necklace, each vertex is further connected by an additional incident edge. The characterization becomes more complex in this scenario: we are enumerating 4-ary necklaces coupled with an additional vertex pairing. Nonetheless, a UO-invariant of order (2, 1) possesses an even more strict description due to the inclusion of a bipartite cycle associated with the $U(N)^{\otimes 2}$ sector. Each vertex of this bipartite cycle is linked by another incident edge corresponding to an orthogonal tensor index. The enumeration of inequivalent configurations in this instance ought to be constrained by the dihedral group action on the graph. This deserves further investigation.

Matrix-matrix-like model Finally, we want to explicitly illustrate the counting of UO invariants of order $(r=2,q=2)$

$$\begin{aligned} Z_{(2,2)} (n)= & {} \frac{1}{(n! 2^n)^2} \sum _{p \vdash n} \Big ( {{\mathcal {Z}}}^{S_n [S_2] \rightarrow S_{2n}}_{2 p} \, { \hbox {Sym} } (2 p) \Big )^2 \, \\\\= & {} \sum _{ p \,\vdash n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) ,\nonumber \\{} & {} t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n} } ]\; \hbox {Sym} ( 2p )\Big )^2 , \end{aligned}$$

(3.8)

which is derived by the equivalence relation:

$$\begin{aligned} ( \sigma _1, \sigma _2, \tau _1,\tau _2 )\sim & {} ( \gamma _1 \sigma _1 \gamma _2, \gamma _1 \sigma _2 \gamma _2, \gamma _2 \gamma _1 \tau _1 \varrho _1, \gamma _2 \gamma _1 \tau _2 \varrho _2 ).\nonumber \\ \end{aligned}$$

(3.9)

The enumeration corresponds to (2.19) with the correct parameters $(r,q) = (2, 2)$. The sequence produced in this expression for $n = 1, \ldots , 8$ is recorded in Table 8.

The number of UO invariants at this order $(r, q) = (2,2)$ and up to $2 n = 16$ still dominates the numbers of orthogonal and unitary invariants (Table 9).

Table 9 The numbers of connected UO invariants of order (2, 2), compared to connected $O(N)^{\otimes 4}$ and $U(N)^{\otimes 4}$ invariants for $n\in \{1,2,\dots ,8 \}$

Another graphical description of the UO invariant of order (2, 2) is the following: the unitary contractions form a bipartite cycle, whereas the orthogonal contractions produce another and distinct cycle. The UO invariant results in the gluing of these two cycles at their vertices. The orthogonal cycle becomes a Hamiltonian cycle within the graph (obviously, also the bipartite cycle). We postulate that the enumeration of UO invariants at this order may once again be associated with the orbits of the dihedral group action on such particular graphs.

4 Refined countings

Our focus now shifts to two other subclasses of UO invariants and their respective enumeration strategies. These subclasses of invariants are characterized either by specific subgroup selections that act on $G = (S_n)^{\times r} \times (S_{2n})^{\times q}$, or by changing the main group G itself. From any subgroup H acting on G, a different counting emerges. And changing G itself will obviously modify the enumeration. The essential point remains to attach a combinatorial meaning to the counting in terms of invariants, a task not entirely obvious in such a general context.

Labeled-Unlabeled UO invariants A UO invariant of order (r, q), seen as a graph, is composed by gluing of two graphs: an edge-colored bipartite graph representing a unitary invariant of order r, and an edge-colored graph representing an orthogonal invariant of order q.

Without loss of generality, let us choose a unitary invariant. Hence, select a unitary invariant as an edge colored graph ${{{\mathcal {G}}}}_u$ made of n white and n black vertices. Then, label the vertices on ${\mathcal {G}}_u$ from 1 to 2n. We insert q other half-lines exiting from each vertex (in such a way that all graph vertices now have fixed valence of $r+q$). We inquire how many inequivalent orthogonal invariants we can make with the new half-edges.

Our task is to enumerate those UO invariants made of the gluing of a unitary and an orthogonal in the way we combinatorially describe above. These are termed LULU UO-invariant (Labeled-Unlabeled twice, recalling that the construction of the unitary invariant already required a labeling and unlabeling). This classification sets them apart from the standard UO invariants which are derived from a unique labeling followed by comprehensive unlabeling.

Using the same notation as in (2.18), the equivalence relation of the (r, q) permutation tuple is given by:

$$\begin{aligned} ( \sigma _1,{} & {} \sigma _2 , \dots , \sigma _p , \tau _1, \tau _2 , \dots , \tau _q ) \sim ( \gamma _1 \sigma _1 \gamma _2, \; \gamma _1 \sigma _2 \gamma _2, \; \dots ,\nonumber \\{} & {} \quad \gamma _1 \sigma _p \gamma _2, \; \gamma \tau _1 \varrho _1 , \; \gamma \tau _2 \varrho _2 , \; \dots , \; \gamma \tau _q \varrho _q ) \end{aligned}$$

(4.1)

which introduces a new permutation $\gamma \in S_{2n}$, and therefore a new independent diagonal action on the left of the orthogonal sector.

We therefore recover, in this case, a double coset formulation for enumerating the orbits of the previous subgroups actions:

$$\begin{aligned}{} & {} \textrm{Diag} _r(S_n) \times \textrm{Diag} _q(S_{2n}) \setminus (S_n)^{\times r} \times (S_{2n})^{\times q} / \textrm{Diag} _r(S_n)\nonumber \\{} & {} \quad \times S_n[S_2]^{\times q}. \end{aligned}$$

(4.2)

The double coset space factorizes and gives

$$\begin{aligned}{} & {} \Big ( \textrm{Diag} _r(S_n) \setminus (S_n)^{\times r} / \textrm{Diag} _r(S_n) \Big )\nonumber \\{} & {} \quad \times \Big ( \textrm{Diag} _q(S_{2n}) \setminus (S_{2n})^{\times q} / S_n[S_2]^{\times q} \Big ). \end{aligned}$$

(4.3)

This implies that the number of LULU UO-invariants, that we denote $Z^{LU}_{(r,q)}(n)$, factorizes as

$$\begin{aligned} Z^{LU}_{(r,q)}(n) = Z^{U}_{r}(n) \cdot Z^{O}_{q}(2n) , \end{aligned}$$

(4.4)

where $Z^{U}_{r}(n)$ enumerates the number unitary invariants made of n tensors of order r and their n complex conjugate tensors, see [17], and $Z^{O}_{q}(2n)$ enumerates the number of orthogonal invariants made of 2n tensors of order q, see [20]. We get:

$$\begin{aligned} Z^{LU}_{(r,q)}(n)= & {} \left[ \sum _{p\vdash n} ( \hbox {Sym} (p))^{r-2} \right] \nonumber \\{} & {} \times \left[ \sum _{p\vdash 2n} \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , \right. \nonumber \\{} & {} \left. t^{n} x_1^{p_1} x_2^{p_2}\dots x_{2n} ^{p_{2n} } ]\; \Big ) ^{q-2} ( \hbox {Sym} ( p ))^{q-1} \right] . \end{aligned}$$

(4.5)

This enumeration can be easily recovered by simply multiplying tables obtained in [17] and [20]. Finally, note that the counting corresponds to the counting of disconnected sum of a unitary and an orthogonal invariants.

O-Factorized UO invariants There exists another family of UO invariants whose enumeration can be delivered because of their combinatorial structure. They are defined in such a way that orthogonal sector may become factorized: no orthogonal contractions occur between the T’s and the $\bar{T}$’s. Graphically, this reflects as the absence of edges connecting the black and white vertices within the orthogonal sector. In fact, this set of invariants was shortly introduced in [86] (in the conclusion) as the set of all $U(N)^{\otimes r}\otimes O(N)^{\otimes q}$ invariants. This shortcoming is now corrected as they only generate a subset of them.

The group theory that structures this property requires that for every j, the former $\tau _j$ decomposes into $\tau _j \tilde{\tau }_j$, where each $\tau _j$ and $\tilde{\tau }_j$ belongs to $S_{n}$, and for all $j=1,2,\ldots , q$. It is important to note that for such a factorization to occur, n must be an even number. We assume this fact from now on.

Each invariant of the desired type, called O-factorized UO invariant, is determined by a tuple

$$\begin{aligned}{} & {} ( \sigma _1, \sigma _2 , \dots , \sigma _r , \tau _1, \tau _2, \dots , \tau _q, \tilde{\tau }_1 , \tilde{\tau }_2, \dots , \tilde{\tau }_q ) \in (S_n)^{\times r}\nonumber \\{} & {} \quad \times (S_{n})^{\times q} \times (S_{n})^{\times q}. \end{aligned}$$

(4.6)

See Fig. 6 for an illustration. Two invariants are claimed equivalent if they are related as follows:

$$\begin{aligned}{} & {} ( \sigma _1, \sigma _2 , \dots , \sigma _p , \tau _1, \tau _2, \dots , \tau _q, \tilde{\tau }_1 , \tilde{\tau }_2, \dots , \tilde{\tau }_q ) \nonumber \\{} & {} \quad \sim ( \gamma _1 \sigma _1 \gamma _2, \; \gamma _1 \sigma _2 \gamma _2, \; \dots , \gamma _1 \sigma _p \gamma _2, \; \gamma _1 \tau _1 \varrho _1, \gamma _1 \tau _2 \varrho _2, \dots , \nonumber \\ {}{} & {} \qquad \times \gamma _1 \tau _q \varrho _q, \tilde{\varrho }_1 \tilde{\tau }_1 \gamma _2 , \tilde{\varrho }_2 \tilde{\tau }_2 \gamma _2, \dots , \tilde{\varrho }_q \tilde{\tau }_q \gamma _2 ) \end{aligned}$$

(4.7)

Fig. 6

O-factorized diagram of contraction of n tensors T and n tensors ${\bar{T}}$

where $\varrho _{j}, \tilde{\varrho }_{j} \in S_{n/2}[S_2]$, for all $j=1,2,\dots , q$. This leads us to a double coset action of the form:

$$\begin{aligned}{} & {} \textrm{Diag} _r(S_n) \times \textrm{Diag} _q(S_{n})\times S_n[S_2]^{\times q} \setminus (S_n)^{\times r} \times (S_{n})^{\times q}\nonumber \\{} & {} \quad \times (S_{n})^{\times q} / \textrm{Diag} _r(S_n) \times \textrm{Diag} _q(S_{n})\times (S_{n/2}[S_2])^{\times q}. \nonumber \\ \end{aligned}$$

(4.8)

Using the Burnside’s lemma we can enumerate the orbits of this action as:

$$\begin{aligned} Z^{OF}_{(r,q)}(n)= & {} { 1 \over {(n!)^2 [n! (2!)^{n}]^q}} \sum _{ \gamma _1, \gamma _2 \in S_{n}} \sum _{\begin{array}{c} \varrho _1,\dots , \varrho _q \in S_{n/2}[S_2]\\ \tilde{\varrho }_1,\dots , \tilde{\varrho }_q \in S_{n/2}[S_2] \end{array}}\sum _{\begin{array}{c} \sigma _1,\dots , \sigma _r \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{n}\\ \tilde{\tau }_1,\dots ,\tilde{\tau }_q \in S_{n} \end{array}}\nonumber \\{} & {} \quad \times \left[ \prod _{i=1}^{r} \delta (\gamma _1 \sigma _i \gamma _2 \sigma _i^{-1} ) \right] \left[ \prod _{i=1}^{q} \delta (\gamma _1 \tau _i \varrho _i \tau _i ^{-1} ) \right] \nonumber \\{} & {} \quad \times \left[ \prod _{i=1}^{q} \delta (\tilde{\varrho }_i \tilde{\tau }_i \gamma _2\tilde{\tau }_i ^{-1} ) \right] . \end{aligned}$$

(4.9)

In terms of partitions $p \vdash n$, the same sum can be expressed as

$$\begin{aligned} Z^{OF}_{(r,q)}(n)= & {} \frac{1}{[(n!)^2 (n!2^n)^q]} \sum _{p \vdash n} \big (Z_{p}^{ S_n \rightarrow S_n }\big )^2 \left( Z_{p}^{ S_{n/2}[S_2]\rightarrow S_{n}}\right) ^{2q} \;\nonumber \\{} & {} \big ( \hbox {Sym} (p)\big )^r \big ( \hbox {Sym} (p )\big )^{2q} \end{aligned}$$

(4.10)

which simplifies as

$$\begin{aligned} Z^{OF}_{(r,q)}(n )= & {} \sum _{ p \,\vdash n } \Big (\hbox {Coefficient } [ {{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{p_1}\nonumber \\{} & {} x_2^{p_2}\dots x_{n} ^{p_{n} } ]\; \hbox {Sym} ( p )\Big )^{2q} \big ( \hbox {Sym} ( p )\big )^{r-2}. \end{aligned}$$

(4.11)

The $U(N)^{\otimes 3}\otimes O(N)^{\otimes 3}$ invariants yields the sequence, for $n=2,4,6, 8, 12$:

$$\begin{aligned} 4, 32, 46772, 280244, 114897770796. \end{aligned}$$

(4.12)

Appendix A.4 provides a code that computes this sequence. The number 4 is associated with $n=2$: this represents a single instance of the second graph shown on the top row of Fig. 2, in addition to three configurations from the third graph in the same row of Fig. 2. These are depicted in Fig. 7. The aforementioned sequence, computed up to $n\le 12$, also suggests that all integers contained within it are even (perhaps multiples of 4).

Fig. 7

O-Factorized UO-invariant graphs at order $(r,q)=(3,3)$ at $n = 2$

5 Topological quantum field theory

This section presents an alternative perspective on the enumeration of UO invariants, specifically through permutation-TQFT. We will first address the general case for $(r>1, q\ge 1)$ order tensors, and subsequently examine the special case $(r=1,q\ge 1)$, as it turns out that $r=1$ introduces a nuance in the interpretation.

5.1 Permutation-TQFT

In this section, we discuss the TQFT that reformulates our enumeration.

The counting of UO invariants of order (r, q) is recalled to be as follows:

$$\begin{aligned}{} & {} Z_{(r,q)}(n) \nonumber \\{} & {} \quad = { 1 \over {(n!)^2 [n! (2!)^{n}]^q}} \sum _{ \gamma _1, \gamma _2 \in S_{n}} \sum _{\varrho _1,\dots , \varrho _q \in S_n[S_2]}\sum _{\begin{array}{c} \sigma _1,\dots , \sigma _r \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \end{array}} \nonumber \\{} & {} \qquad \times \left[ \prod _{i=1}^{r} \delta (\gamma _1 \sigma _i \gamma _2 \sigma _i^{-1} ) \right] \left[ \prod _{i=1}^{q} \delta (\gamma _1 \gamma _2\tau _i \varrho _i \tau _i ^{-1} ) \right] \, . \end{aligned}$$

(5.1)

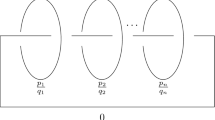
As expected, $Z_{(r,q)}(n)$ has an interpretation as a partition function of a TQFT$_2$ on a 2-cellular complex that is determined in the following way: each permutation $\sigma _i,\tau _j, \gamma _i$ or $\varrho _j$, is a group data associated with a given 1-cell; each delta function that enforces a flatness condition, introduces a plaquette weight. An illustration of such a complex for the case $(r=3, q=4)$ is given in Fig. 8. The topology associated with this complex is that of $r+q$ cylinders, r cylinders labeled by $\sigma _1,\dots , \sigma _q$ that we refer to $\sigma$-cylinders, and q labeled by $\tau _1,\dots ,\tau _q$, named $\tau$-cylinders. The $\sigma$-cylinders share two boundary circles labeled by $\gamma _1$ and $\gamma _2$ joining at a point p, making a larger new boundary component $b_{ \gamma _1 \gamma _2}$ with group data $\gamma _1 \gamma _2$. The $\tau$-cylinders share $b_{ \gamma _1 \gamma _2}$. Each $\tau$-cylinder, on its opposite boundary has a distinct boundary circle labeled by a given $\varrho _j$ which belongs to $S_n[S_2]$. The fact that $\varrho _j$ belongs to a subgroup of $S_n$, unlike other generators, has implications that we will discuss. Thus, $Z_{(r,q)}(n)$ counts the number of coverings of that 2-cellular complex with boundaries labeled by group data different from the rest of complex.

Fig. 8

2-cellular complex associated with the TQFT$_2$ of $Z_{(3,4)}$ made of 3+4 cylinders sharing some boundaries

Another remark is that, in Fig. 8, the 2-cellular complex is composed by the gluing of the two complexes: one coming from the $U(N)^{\otimes r}$ counting (associated with the $\sigma$-cylinders) [17] and one from the $O(N)^{\otimes q}$ (associated with the $\tau$-cylinders, with $\gamma _1 \gamma _2$ viewed as a single boundary component) [20]. These two complexes are identified along $b_{ \gamma _1 \gamma _2}$.

There are alternative countings provided by this picture if we integrate a few $\delta$ functions. So we solve for $\gamma _1$ using $\delta ( \gamma _1 \sigma _1 \gamma _2 \sigma _1^{-1})$, then change variables $\sigma _i \rightarrow \sigma _1^{-1} \sigma _i$ for all i. This integration makes all the generators $\sigma _i$’s, $\tau _i$’s and $\gamma _2$ meet at the same point p.

This enables us to re-express the above as, renaming $\gamma _2= \gamma$,

$$\begin{aligned} Z_{(r,q)}(n)= & {} { 1 \over {(n!)^2 [n! (2!)^{n}]^q}} \sum _{ \gamma \in S_{n}} \sum _{\varrho _1,\dots , \varrho _q \in S_n[S_2]}\sum _{\begin{array}{c} \sigma _1,\dots , \sigma _r \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \end{array}}\nonumber \\{} & {} \times \left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \nonumber \\{} & {} \times \left[ \prod _{i=1}^{q} \delta ( \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \varrho _i \tau _i ^{-1} ) \right] . \end{aligned}$$

(5.2)

Note this expression makes only sense if $r\ge 2$. The special case $r=1$ will be further detailed later on.

To illustrate (5.2), the previous 2-complex of Fig. 8 is now simplified as the complex depicted in Fig. 9 for $(r=3,q=4)$. In general, the topology that is drawn is of the form

$$\begin{aligned} {{{\mathcal {G}}}}_{r,q} = F_1 \vee _p \left[ (F_{r-1} \times S_1) \cup _{S_1} [( F_{q} \times S_1 ) ; D_{S_n[S_2]}^{q}] \right] , \nonumber \\ \end{aligned}$$

(5.3)

where $F_k$ is the bouquet of k loops, the vertex union, denoted $\vee _v$, joins two graphs along a vertex v, $\cup _{S_1}$ is a gluing along $S_1$; $D_{S_n[S_2]}^{q}$ stands for the presence of q defects on $F_{q} \times S_1$. Here, the defects are associated with generators $\varrho _1, \dots , \varrho _q$ which should all pass through p. Note that $F_1$ is associated with the generator corresponding to $\sigma _1$. The bouquet $F_{r-1}$ is associated with the generators $\sigma _2, \sigma _3, \dots , \sigma _r$ (the unitary sector), and the bouquet $F_q$ associated with generators $\tau _1, \dots , \tau _q$, (the orthogonal sector). $S_1$ is associated with the generator $\gamma _2= \gamma$.

$Z_{(r,q)}(n)$ therefore computes the number of 2n degree covering of the space ${{{\mathcal {G}}}}_{r,q}$

$$\begin{aligned} Z_{(r,q)}(n) = Z[{{{\mathcal {G}}}}_{r,q}; S_{2n}]. \end{aligned}$$

(5.4)

The degree is 2n as we can always embed $S_n$, associated with the generators $\sigma _i$, into $S_{2n}$.

The cellular complex ${{{\mathcal {G}}}}_{(r,q)}$ defines a topology of a circle, i.e. $\sigma _1$, glued along $r+q-1$ tori themselves glued along one generator, say $\gamma$. The topology also contains defects each of which related to one $\varrho _i$ and is located on each of the q tori. A defect corresponds to a marked circle (generator) which constrains the holonomy to the subgroup $S_n[S_2]$. $Z_{(r,q)}(n)$ counts the covers of this topology.

Fig. 9

Lattice after integration of $\gamma _1$ and a change of variable

At fixed, $\sigma _i$, $i=2,3,\dots , r$, and $\tau _j$, $j=1,2,\dots , q$, we are interested in the order of the automorphism of the graph defining the invariant. This is given by:

$$\begin{aligned}{} & {} \textrm{Aut} (G_{\{ \sigma _i\}_{i=2,\dots ,r};\{\tau _i\}_{i=1,\dots ,q}} ) \nonumber \\{} & {} \quad = \sum _{ \gamma \in S_{n}} \sum _{ \varrho _1,\dots , \varrho _q \in S_n[S_2]} \left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \sum _{ \sigma _1 \in S_n}\nonumber \\{} & {} \qquad \times \left[ \prod _{i=1}^{q} \delta ( \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \varrho _i \tau _i ^{-1} ) \right] , \end{aligned}$$

(5.5)

which is also the order of the stabilizer of the subgroup $\textrm{Diag}_{r+q-1}(S_n) \times \textrm{Diag}_{q}(S_n) \times S_n[S_2]^{\times q}$, acting on the tuple $( \sigma _2, \sigma _3,\dots , \sigma _r, \tau _1,\tau _2,\dots , \tau _q)$. Note that, in this description, $\sigma _1$ becomes gauge, just like $\gamma$ and $\varrho _i$.

5.2 Integration of boundary variables: A branched cover picture

One might wonder there exists another characterization of the topology underpinning (5.1) in terms of a (punctured) torus or a (punctured) sphere, and consequently, whether the partition function enumerates (branched) covers of said topology. Addressing this is the purpose of this section.

Using the description of [2], Fig. 8 represents the cellulation of cylinders glued along two generators and among them q cylinders have defects, labeled by a subgroup of $S_n$, on one of their boundaries. In this sense, the partition function (5.5) counts covers of topology with defects.

In fact, we could perform more integrations focusing on $\varrho _i$. Observing (5.2), each sum over one $\varrho _i$ eliminates one $\delta ( \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \varrho _i \tau _i ^{-1} )$ resulting in loss of relation between generators. Thus, all $\tau _i$ and $\sigma _1$ become free generators glued at the point p. However, the integration demands that $\tau _i ^{-1} \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \in S_n[S_2]$. After integrating over $\varrho _i$, the partition function $Z_{(r,q)}(n)$ assumes the form:

$$\begin{aligned} Z_{(r,q)}(n)= & {} { 1 \over {(n!)^2 [n! (2!)^{n}]^q}} \sum _{ \gamma \in S_{n}}\sum _{ \sigma _2, \sigma _3\dots , \sigma _r \in S_{n}} \left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \nonumber \\{} & {} \times \sum _{\begin{array}{c} \sigma _1 \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \\ \tau _i ^{-1} \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \in S_n[S_2] \end{array}} 1 \, . \end{aligned}$$

(5.6)

We derive the following topology: $[( S_1 \times S_1) \cup _{ \gamma _p } (S_1 \times S_1) \cup _{ \gamma _p } \dots \cup _{ \gamma _p } (S_1 \times S_1 )] \vee _{p} (S_1)^{q+1}$. In other words, this is $r-1$ tori glued along one generator, $\gamma _p$, all marked with a point p where we glue $q+1$ circles, specifically $\tau _i$ and $\sigma _1$. We are enumerating certain covers (due to the constraints on the holonomies to be in a subgroup) of this topology.

This picture can be further simplified by employing the following scheme. Introducing the weight

$$\begin{aligned} Z^q_{n;\, \gamma } = { 1 \over (n!)[n! (2!)^{n}]^q } \sum _{\begin{array}{c} \sigma _1 \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \\ \tau _i ^{-1} \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \in S_n[S_2] \end{array}} 1 \end{aligned}$$

(5.7)

that we will provide an interpretation in a moment, we re-express $Z_{(r,q)}(n)$ in the form:

$$\begin{aligned} Z_{(r,q)}(n)= & {} { 1 \over n! } \sum _{ \gamma \in S_{n}} Z^q_{n;\, \gamma } \sum _{ \sigma _2, \sigma _3\dots , \sigma _r \in S_{n}} \left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \; \\\\= & {} { 1 \over {n!}} \sum _{ \gamma \in S_{n}} Z^q_{n;\, \gamma } \; \sum _{ \sigma _0, \sigma _2, \sigma _3\dots , \sigma _r \in S_{n}}\left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \nonumber \\{} & {} \times \delta ( \gamma ^{-1} \sigma _0 \gamma \sigma _0^{-1} ) \delta ( \sigma _0\prod _{i=2}^r \sigma _i ) \; . \end{aligned}$$

(5.8)

We have introduced another generator $\sigma _0$ which is trivial from the last constraint $\sigma _0\prod _{i=2}^r \sigma _i= \mathrm id$, and remains invariant under conjugation.

The first line of (5.8) instructs us that we are counting $Z^q_{n;\, \gamma }$-weighted covers of degree n of $r-1$ tori $(S_1 \times S_1) \cup _{ \gamma } (S_1 \times S_1) \cup _{ \gamma } \dots \cup _{ \gamma } (S_1 \times S_1)$ glued along the generator $\gamma$.

An alternative interpretation arises from the second line: $Z_{(r,q)}(n)$ enumerates $Z^q_{n;\, \gamma }$-weighted equivalence classes of branched covers of degree n of the sphere $S_2$ with r branched points. This counts covers of the r-punctured sphere, with each cover assigned a weight by $Z^q_{n;\, \gamma }$.

For $r\ge 3$, we have an isomorphism between the fundamental groups:

$$\begin{aligned} \pi _1(S_{2; r*}) \equiv \pi _1((S_1\times S_{1})_{(r-2)*}) , \end{aligned}$$

(5.9)

where $S_{2; r*}$ is the sphere $S_2$ with r punctures and $(S_1\times S_{1})_{(r-2)*}$ is the torus $S_1\times S_1$ with $r-2$ punctures. Therefore their number of branched covers must coincide.

This also means that the number of equivalence classes of branched covers of the torus with $r-2$ branched points, up to $Z^q_{n;\, \gamma }$, is equal to the number of covers of the space $(S_1\times S_1) \cup _{ \gamma }(S_1\times S_1) \cup _{ \gamma } \dots \cup _{ \gamma } (S_1\times S_1)$.

The number of branched covers of the sphere has appeared in several countings of graphs in the recent years [1, 2, 17]. In general, this counting is made with a particular weight. For instance, in [2], each branched cover has the weight the inverse of the automorphism group of the cover, meanwhile in [17], each equivalence class of branched covers is counted only once. In the present work, the ponderation is different and stems from the integration of the whole $O(N)^{\otimes q}$ sector. This was possible because of the presence of defects on the tori that could be fully integrated.

Interpreting the weight $Z^q_{n;\, \gamma }$ We give an interpretation of the weight $Z^q_{n;\, \gamma }$ which appears in the counting (5.8). We recall that $Z^q_{n;\, \gamma }$ is given by (5.7) which also expresses, before integration of the $\varrho _i$’s, as

$$\begin{aligned} Z^q_{n;\, \gamma }= & {} { 1 \over (n!)[n! (2!)^{n}]^q } \sum _{\begin{array}{c} \sigma _1 \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \end{array}}\nonumber \\{} & {} \times \sum _{ \varrho _1,\dots , \varrho _q \in S_n[S_2]} \left[ \prod _{i=1}^{q} \delta ( \sigma _1 \gamma ^{-1} \sigma _1^{-1} \gamma \tau _i \varrho _i \tau _i ^{-1} ) \right] .\nonumber \\ \end{aligned}$$

(5.10)

First, we undo the gauge fixing, coming back to an earlier expression as:

$$\begin{aligned} Z^q_{n;\, \gamma }= & {} { 1 \over (n!)[n! (2!)^{n}]^q } \sum _{\begin{array}{c} \sigma _1 , \gamma ' \in S_{n} \\ \tau _1,\dots ,\tau _q \in S_{2n} \end{array}} \nonumber \\{} & {} \times \sum _{ \varrho _1,\dots , \varrho _q \in S_n[S_2]} \left[ \delta ( \gamma ' \sigma _1 \gamma \sigma _1^{-1}) \prod _{i=1}^{q} \delta (\gamma ' \gamma \tau _i \varrho _i \tau _i ^{-1} ) \right] . \end{aligned}$$

(5.11)

We recognize the counting of (1, q)- UO invariants formed by the contraction of n unlabeled tensors T and n tensors ${\bar{T}}$ labeled by $\gamma$. The weight $Z^q_{n;\, \gamma }$ counts UO invariants which, seen as graphs, have vertices ${\bar{T}}$ labeled by $\gamma$ (i.e. fix arbitrary labels and let $\gamma$ acting once on them). Thus, in the branched cover picture, $Z_{(r,q)}(n)$ in (5.8) counts equivalence classes of branched covers of the sphere each with such a combinatorial weight $Z^q_{n;\, \gamma }$ associated with the counting of labeled-UO-invariants.

We can evaluate (5.11) further as follows. Again, noting that $\gamma$ and $\gamma '$ belong to the same conjugacy class, we recast (5.11) using conjugacy classes of n via the same arguments leading to (2.10) (or to (2.21)):

$$\begin{aligned} Z^q_{n;\, \gamma }= & {} \sum _{p\vdash n} \delta _{[ \gamma ], p} \Big [ \hbox {Coefficient } [{{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) ,\nonumber \\{} & {} \times t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n}}] \hbox {Sym} (2p)\Big ]^q. \end{aligned}$$

(5.12)

The delta $\delta _{[ \gamma ], p}$ requires that $\gamma$ belongs to the conjugacy class p which is that of $\gamma '$. Compared to (2.21), we notice that the unitary sector is not contributing to this partition function.

To check the validity of this weight, we complete the calculation of (5.8) using the expression (5.12):

$$\begin{aligned} Z_{(r,q)}(n)= & {} { 1 \over n! } \sum _{ \gamma \in S_{n}} \left[ \sum _{p\vdash n} \delta _{[ \gamma ], p} \Big [ \hbox {Coefficient } [{{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) ,\right. \nonumber \\{} & {} \times \left. t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n}}] \hbox {Sym} (2p)\Big ]^q \right] \\\\{} & {} \times \sum _{ \sigma _2, \sigma _3\dots , \sigma _r \in S_{n}} \left[ \prod _{i=2}^{r} \delta ( \gamma ^{-1} \sigma _i \gamma \sigma _i^{-1} ) \right] \; \\\\= & {} { 1 \over n! } \sum _{p' \vdash n} \sum _{p\vdash n} \delta _{p', p} \Big [ \hbox {Coefficient } [{{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) ,\nonumber \\{} & {} \times t^{n} x_1^{2p_1} x_2^{2p_2}\dots x_{n} ^{2p_{n}}] \hbox {Sym} (2p)\Big ]^q \\\\{} & {} \times \frac{n!}{ \hbox {Sym} (p')} ( \hbox {Sym} (p'))^{r-1} \\\\= & {} \sum _{p\vdash n} \Big [ \hbox {Coefficient } [{{{\mathcal {Z}}}}_{2}^{S_\infty [S_2]}(t, \vec x) , t^{n} x_1^{2p_1} \nonumber \\{} & {} \times x_2^{2p_2}\dots x_{n} ^{2p_{n}}] \hbox {Sym} (2p)\Big ]^q ( \hbox {Sym} (p))^{r-2}\nonumber \\ \end{aligned}$$

(5.13)

which coincides with (2.21).

5.3 Lower order cases

Vector-vector case $(r=1,q=1)$ At lower order, in particular at $(r=1, q=1)$ several steps that were performed above are not well defined. We will therefore do the analysis in this specific situation.

We start by the partition function:

$$\begin{aligned} Z_{(1,1)} (n)= & {} \frac{1}{(n!)^2 \; n! (2!)^n } \sum _{\gamma _1 \in S_{n}} \sum _{\gamma _2 \in S_{n}} \nonumber \\{} & {} \times \sum _{\sigma _1 \in S_n} \sum _{\tau _1 \in S_{2n}} \sum _{\varrho _1 \in S_n[S_2]} \delta (\gamma _1 \sigma _1 \gamma _2 \sigma _1^{-1})\nonumber \\{} & {} \delta (\gamma _1 \gamma _2 \tau _1 \varrho _1 \tau _1^{-1}). \end{aligned}$$

(5.14)

The 2-complex associated with this $S_n$-TQFT can be still drawn in the way of Fig. 8, with a single plaquette both for the U(N) and for the O(N) sector. We have two possibilities integrating $\varrho _1$ or $\gamma _i$. We start by the first.

On the 2-complex, one first notices that $\varrho _1$ can be retracted such that the plaquette is reduced to its 1-cells, $\tau _1$, $\gamma _2$ and $\gamma _1$. Therefore, $\gamma _1$ and $\gamma _2$ are actually still boundaries of the 2-complex.

Without a loss of generality, we select $\gamma _1$ and sum over it. As $\gamma _1$ is a boundary, another retraction can be performed on it. The remaining plaquette is reduced to its 1-cells which are labelled by $\sigma _1$ and $\gamma _2$. At this point, all generators $\tau _1$, $\sigma _1$ and $\gamma _2$, become free. We readily identify that the fundamental group of the cellular complex to be that of the sphere with 4 punctures, or of the torus with 2 punctures.

In formulas, we successively integrate out $\varrho _1$ and then $\gamma _1$ and obtain:

$$\begin{aligned} Z_{(1,1)} (n)= & {} \frac{1}{(n!)^2 \; n! (2!)^n } \sum _{\begin{array}{c} \gamma _1, \gamma _2, \sigma _1 \in S_{n} \\ \tau _1 \in S_{2n} \\ \tau _1^{-1}\gamma _1 \gamma _2 \tau _1 \in S_n[S_2] \end{array}} \delta (\gamma _1 \sigma _1 \gamma _2 \sigma _1^{-1}) \\\\= & {} \frac{1}{(n!)^2 \; n! (2!)^n } \sum _{\begin{array}{c} \sigma _1 ,\gamma _2 \in S_{n}, \tau _1 \in S_{2n} \\ \tau _1^{-1} \sigma _1 \gamma _2^{-1} \sigma _1^{-1} \gamma _2 \tau _1 \in S_n[S_2] \end{array}} 1.\nonumber \\ \end{aligned}$$

(5.15)

The three generators $\sigma _1 ,\gamma _2$, and $\tau _1$ are free of relation, but subject to a constraint on their domain. We introduce another permutation $\sigma _0$ that fulfils $\sigma _0 \sigma _1 \gamma _2 \tau _1 = \mathrm id$ and write:

$$\begin{aligned} Z_{(1,1)} (n)= \frac{1}{(n!)^2 \; n! (2!)^n } \sum _{\begin{array}{c} \sigma _1 ,\gamma _2 \in S_{n}, \sigma _0, \tau _1 \in S_{2n} \\ \tau _1^{-1} \sigma _1 \gamma _2^{-1} \sigma _1^{-1} \gamma _2 \tau _1 \in S_n[S_2] \end{array}} \delta ( \sigma _0 \sigma _1 \gamma _2 \tau _1 ).\nonumber \\ \end{aligned}$$

(5.16)

We conclude that this partition function is counting certain branched covers of the sphere $S_2$ of degree 2n with 4 branched points. This restriction comes from the domain of the holonomies.

Vector-tensor case $(r=1,q)$ This case extends the previous one. Doing step by step the above analysis, namely integrating all $\varrho _i$ and then $\gamma _1$, one obtains:

$$\begin{aligned} Z_{(1,q)} (n)= & {} \frac{1}{(n!)^2 \; ( n! (2!)^n)^q } \sum _{\begin{array}{c} \gamma _1, \gamma _2, \sigma _1 \in S_{n} \\ \tau _1,\dots \tau _q \in S_{2n} \\ \tau _i^{-1}\gamma _1 \gamma _2 \tau _i \in S_n[S_2] \end{array}} \delta (\gamma _1 \sigma _1 \gamma _2 \sigma _1^{-1}) \\\\= & {} \frac{1}{(n!)^2 \; n! (2!)^n } \sum _{\begin{array}{c} \sigma _1 ,\gamma _2 \in S_{n}, \\ \tau _1,\dots , \tau _q \in S_{2n} \\ \tau _i^{-1} \sigma _1 \gamma _2^{-1} \sigma _1^{-1} \gamma _2 \tau _i \in S_n[S_2] \end{array}} 1 \\\\= & {} \frac{1}{(n!)^2 \; (n! (2!)^n)^q } \sum _{\begin{array}{c} \sigma _1 ,\gamma _2 \in S_{n}, \\ \sigma _0, \tau _1,\dots , \tau _q \in S_{2n} \\ \tau _1^{-1} \sigma _1 \gamma _2^{-1} \sigma _1^{-1} \gamma _2 \tau _1 \in S_n[S_2] \end{array}} \delta ( \sigma _0 \sigma _1 \gamma _2 \prod _{i=1}^q\tau _i ).\nonumber \\ \end{aligned}$$

(5.17)

We recognize the fundamental group of $q+3$ generators submitted to one relation

$$\begin{aligned} \sigma _0 \sigma _1 \gamma _2 \prod _{i=1}^q\tau _i = \mathrm id, \end{aligned}$$

(5.18)

which is that of the sphere $S_2$ with $q+3$ punctures. We infer that $Z_{(1,q)}(n)$ is counting the number of certain branched covers of the sphere $S_2$ of degree 2n with $q+3$ branched points.

6 Conclusion and outlook

Summary Building upon previous studies on the enumeration of tensor invariants, this work has undertaken the enumeration of $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ invariants, for r and q positive integers. We have established the appropriate symmetric group formalism to construct the invariants as edge-colored graphs, subject to specific equivalence relations. Burnside’s lemma was used to derive the number of orbits, which corresponds to the desired enumeration. Initially, the process yields all invariants, including disconnected ones (which, in matrix models, equate to multi-traces). Then, we have used the plethystic logarithm to extract the number of connected invariants (in matrix models, these are single-traces). At $q=0$, we recover the previous counting of unitary invariants. However, setting $r=0$ does not ensure to obtain the counting of orthogonal invariants. This is attributed to the fact that the UO counting formula (2.19) first builds the unitary part and then the action reverberates on the orthogonal part: $\gamma _1 \gamma _2 \in S_{2n}$, and the summations over $\gamma _1 \in S_{n}$ and $\gamma _2 \in S_{n}$ cannot be straightforwardly substituted by a summation over $\gamma _1 \gamma _2 \in S_{2n}$.

Aside from the case $(r=2,q=1)$ that can be found in [73], the integer sequences corresponding to our countings of invariants with $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$ symmetry, for different r and q, find no matching of series online, or on the OEIS database. To the best of our knowledge, these are novel sequences.

The vector-vector case $(r, q) = (1,1)$, representative of a matrix model, is particularly noteworthy. We identified our counting with that of a set of cyclic words with particular forbidden substrings/patterns, or equivalently, to Pólya’s 4-ary necklaces with constraints. We have formulated an expression that accounts for the number of 4-ary necklaces of varying lengths with pattern avoidance. This analogy may provide insights into the enumeration of necklaces and bracelets (the latter being necklaces invariant under reflection symmetry) with pattern exclusions across different lengths. The complexity of counting cyclically symmetric words with pattern avoidance lies in the intricate nature of cyclic symmetry which, combined with the need to exclude certain patterns, makes the problem even more challenging [87]. It is remarkable that $Z_{(1,1)}$ gives a rapid derivation of a formula for specific pattern exclusions.

Moreover, we have explored topological interpretations of these enumerations through the $S_n$-TQFT framework. The counting of UO invariants corresponds to the enumerations of covering spaces of various topologies. In the general case of $U(N)^{\otimes r} \otimes O(N)^{\otimes q}$, with $r>1$, its enumeration corresponds to the number of certain weighted covers of $(r-1)$-number of tori $(S_1\times S_1) \cup _{ \gamma }(S_1\times S_1) \cup _{ \gamma } \dots \cup _{ \gamma } (S_1\times S_1)$ glued along the generator, $\gamma$. An alternative enumeration pertains to the number of weighted equivalence classes of branched covers of the sphere $S_2$ with r branched points (or, equivalently, covers of the r-punctured sphere). For the case $r=1$ for any q, we have deduced that the number of tensor invariants corresponds to the number of specific covers of the sphere $S_2$ with $q+3$ punctures (equivalently certain branched covers with $q+3$ branched points of the sphere). The restriction comes from the fact that some holonomies of the complex are constrained to a subgroup of the gauge group.

Asymptotics  Considering the likely super-exponential growth of several sequences presented in this work, a primary task that emerges is to elucidate their asymptotic behaviors. We can adapt the techniques developed in [82] to probe the behavior of $Z_{(r,q)}(n)$ at large n. For a partition p of n, the symmetry factors $\hbox {Sym} (p)$ and $\hbox {Sym} (2p)$, as introduced in (2.19), are anticipated to be easy to address: they will be dominated by partitions consisting mostly of 1 and 2. In particular, we conjecture that the dominant term should include either or both factors $(n!)^{r-2}$ or $((2n)!)^{q}$. This warrants a full-fledged analysis.

Correlators and orthogonal bases Gaussian correlators of observables can be addressed in the current framework. They correspond to the moments of the measure

$$\begin{aligned} d\nu (T,{\bar{T}})= & {} \prod _{a_i, b_j} dT_{a_1,\dots ,a_r,b_1,\dots b_q } d{\bar{T}}_{a_1,\dots ,a_r,b_1,\dots b_q }\nonumber \\{} & {} \times e^{ - (\sum _{a_i,b_j}T_{a_1,\dots ,a_r,b_1,\dots b_q } {\bar{T}}_{a_1,\dots ,a_r,b_1,\dots b_q })} \end{aligned}$$

(6.1)

calculated for observables that are UO invariants characterized by permutation tuples and obeying

$$\begin{aligned} O_{\{ \sigma _i\}; \{\tau _j\}} = O_{\{ \gamma _1 \sigma _i \gamma _2\}; \{ \gamma _1 \gamma _2\tau _j \varrho _j\}}. \end{aligned}$$

(6.2)

The computation of the correlator $\langle O_{\{ \sigma _i\}; \{\tau _j\}}\rangle$ formulates in terms of cycles of the permutations labeling the observable, namely $\{ \sigma _i\}$ and $\{\tau _j\}$, and another permutation implementing the Wick theorem. Moreover, it is known that the representation theoretic basis corresponding to normal ordered correlators forms an orthogonal basis for two-point functions [18, 20]. Investigating whether this property extends to UO-invariants presents another significant question for discussion.

Finding TM observables for a given TQFT The correspondence between the enumeration of tensor invariants and 2-dimensional lattice gauge theory of permutation groups may give a wealth of new insights in topology and geometry. We will delve into a particular curiosity that promises to enhance our understanding of this correspondence by exploring the inverse relationship. So far, regardless of whether the invariants are unitary, orthogonal, or UO symmetric, we consistently find a correspondence with (branched) covers of either the sphere or the torus, which may include punctures. Looking ahead, it would be enlightening to determine which types of tensors, transformations, and tensor contractions can lead to the enumeration of covers of non-orientable manifolds. Specifically, the Klein bottle, as a closed manifold, might represent one of the simplest cases for exploration. Broadly speaking, the question is: starting from a TQFT over a 2-cellular complex, what are the minimal requirements to achieve an enumeration of certain tensor invariants?

Representation theory and combinatorial construction of Kronecker coefficients Using Representation Theory of the symmetric group, the counting of unitary and orthogonal invariants can be expressed in terms of the Kronecker coefficients. For a triple of Young diagrams, $R_1,R_2,R_3$, each with n boxes, the Kronecker coefficient $C(R_1,R_2,R_3)$ counts the multiplicity of the irreducible representation (irrep) $R_3$ in the tensor product of irreps $R_1$ by $R_2$ [58]. A combinatorial method for constructing the Kronecker coefficient for such a triple $(R_1,R_2,R_3)$ was introduced in [23]. The proof is based on the fact that the number of unitary invariants of order 3 reduces to the sum of all squares $C(R_1,R_2,R_3)^2$. According to [20], the enumeration of all orthogonal invariants is reduced to a sum of Kronecker coefficients $C(R_1,R_2,R_3)$, provided that each $R_i$ consists of parts with even lengths. We conjecture that, under these circumstances, the construction of the Kronecker coefficient can be simplified; however, this simplification may not hold for every triple $(R_1,R_2,R_3)$. In the realm of representation theory, exploring whether the enumeration of UO invariants of orders (2, 1) and (1, 2) – both still of order 3 – could unveil new dimensions to this puzzle.

Appendices

Appendix

Codes

We provide a detailed outline of the algorithms used to compute the number of UO invariants and various integer sequences reported in the text. The algorithms are implemented in Mathematica.

1.1 Code for $Z_{(r,q)}(n)$

Our goal is to determine the number $Z_{r, q}(n)$ of order (r, q) UO invariants composed of 2n tensors. To achieve this, we initially program the generating function, Z[X, t], whose coefficients give the numbers of elements of the wreath product $S_n[S_2]$ in a given conjugacy class of $S_{2n}$. We use Mathematica’s Count[list, pattern] function to count occurrences in a list that match a given pattern. Subsequently, we identify the coefficients of $t^n \prod _{i=1}^{n} x_i^{p_i}$ from Z[X, t] for a given partition $p = (p_i) \vdash n$, which are used in Zdrq[X, n, r, q] representing $Z_{r,q}(n)$. Finally, we provide the explicit countings for orders $(r, q)=(3,3)$ and (3, 4) for n ranging from 1 to 10.

The code below generates the number of $O(N)^{\otimes d}$ invariants.

1.2 Lower order cases

The following 1-line code delivers the enumeration of the lower order cases, i.e. for all pairs (r, q), with $r,q=1,2$, and for $n=1,2,\dots , n$.

1.3 Code for connected invariants

The present appendix outlines a code for enumerating the connected UO invariants. It uses the plethystic logarithm applied on the generating series of $Z_{(r,q)}(n)$ to extract specific numbers. The plethystic logarithm is denoted |PLog[F, M, r, q, t]|, and the generating series for the number of UO invariants is denoted by |Zseriesrq|.

1.4 Code for O-factorized invariants

The present appendix provides a code dedicated to the enumeration of O-factorized UO invariants. Within this code, the functions |CC|, |Sym| and |PP| follow the definitions presented in section A.1. To compute the number of factorized $U(N)^{\otimes r}\otimes O(N)^{\otimes q}$ invariants, execute the following code:

Enumeration of UO invariants

In this appendix, we compute a catalogue for $Z_{(r,q)}(n)$, for all $r\in \{1,2,3,4\}$, $q\in \{1,2,3\}$, for $n\in \{1,\dots , 10\}$. All these integer sequences, at fixed (r, q) are not yet reported in the OEIS.

$$\begin{aligned} \begin{array}{l|l | l } Z_{(1 ,1)}(1) = 1 &{} Z_{(2 ,1)}(1) = 1 &{} Z_{(3 ,1)}(1) = 1 \\ Z_{(1 ,1)}(2) = 3 &{} Z_{(2 ,1)}(2) = 6 &{} Z_{(3 ,1)}(2) = 12 \\ Z_{(1 ,1)}(3) = 5 &{} Z_{(2 ,1)}(3) = 21 &{} Z_{(3 ,1)}(3) = 105 \\ Z_{(1 ,1)}(4) = 12 &{} Z_{(2 ,1)}(4) = 147 &{} Z_{(3 ,1)}(4) = 2785 \\ Z_{(1 ,1)}(5) = 20 &{} Z_{(2 ,1)}(5) = 1043 &{} Z_{(3 ,1)}(5) = 114293 \\ Z_{(1 ,1)}(6) = 44 &{} Z_{(2 ,1)}(6) = 11239 &{} Z_{(3 ,1)}(6) = 7518265 \\ Z_{(1 ,1)}(7) = 76 &{} Z_{(2 ,1)}(7) = 139269 &{} Z_{(3 ,1)}(7) = 681822469 \\ Z_{(1 ,1)}(8) = 157 &{} Z_{(2 ,1)}(8) = 2071918 &{} Z_{(3 ,1)}(8) = 81778527514 \\ Z_{(1 ,1)}(9) = 281 &{} Z_{(2 ,1)}(9) = 34939776 &{} Z_{(3 ,1)}(9) = 12508819139938 \\ Z_{(1 ,1)}(10) = 559 &{} Z_{(2 ,1)}(10) = 661739366 &{} Z_{(3 ,1)}(10) = 2376379599992478 \\ \end{array} \\ \begin{array}{l | l } Z_{(4 ,1)}(1) = 1 &{} Z_{(1 ,2)}(1) = 1 \\ Z_{(4 ,1)}(2) = 24 &{} Z_{(1 ,2)}(2) = 9 \\ Z_{(4 ,1)}(3) = 579 &{} Z_{(1 ,2)}(3) = 45 \\ Z_{(4 ,1)}(4) = 62331 &{} Z_{(1 ,2)}(4) = 567 \\ Z_{(4 ,1)}(5) = 13616933 &{} Z_{(1 ,2)}(5) = 7727 \\ Z_{(4 ,1)}(6) = 5390301533 &{} Z_{(1 ,2)}(6) = 155015 \\ Z_{(4 ,1)}(7) = 3432811877335 &{} Z_{(1 ,2)}(7) = 3664063 \\ Z_{(4 ,1)}(8) = 3295405426920046 &{} Z_{(1 ,2)}(8) = 102746234 \\ Z_{(4 ,1)}(9) = 4537723725387633528 &{} Z_{(1 ,2)}(9) = 3289881694 \\ Z_{(4 ,1)}(10) = 8621636139317650810694 &{} Z_{(1 ,2)}(10) = 118618441134 \\ \end{array}\\ \begin{array}{l| l} Z_{(2 ,2)}(1) = 1 &{} Z_{(3 ,2)}(1) = 1 \\ Z_{(2 ,2)}(2) = 18 &{} Z_{(3 ,2)}(2) = 36 \\ Z_{(2 ,2)}(3) = 243 &{} Z_{(3 ,2)}(3) = 1395 \\ Z_{(2 ,2)}(4) = 11765 &{} Z_{(3 ,2)}(4) = 270051 \\ Z_{(2 ,2)}(5) = 895887 &{} Z_{(3 ,2)}(5) = 107193497 \\ Z_{(2 ,2)}(6) = 108273795 &{} Z_{(3 ,2)}(6) = 77810503805 \\ Z_{(2 ,2)}(7) = 18269868567 &{} Z_{(3 ,2)}(7) = 92039748242635 \\ Z_{(2 ,2)}(8) = 4109854359606 &{} Z_{(3 ,2)}(8) = 165669458018180870 \\ Z_{(2 ,2)}(9) = 1187617940061334 &{} Z_{(3 ,2)}(9) = 430904230704984688456 \\ Z_{(2 ,2)}(10) = 428707395212694994 &{} Z_{(3 ,2)}(10) = 1555561267573626048247306 \\ \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{l| l} Z_{(4 ,2)}(1) = 1 &{} Z_{(1 ,3)}(1) = 1 \\ Z_{(4 ,2)}(2) = 72 &{} Z_{(1 ,3)}(2) = 27 \\ Z_{(4 ,2)}(3) = 8217 &{} Z_{(1 ,3)}(3) = 585 \\ Z_{(4 ,2)}(4) = 6392177 &{} Z_{(1 ,3)}(4) = 50410 \\ Z_{(4 ,2)}(5) = 12859898457 &{} Z_{(1 ,3)}(5) = 7042418 \\ Z_{(4 ,2)}(6) = 56016726769345 &{} Z_{(1 ,3)}(6) = 1561499110 \\ Z_{(4 ,2)}(7) = 463870975306048081 &{} Z_{(1 ,3)}(7) = 489732884134 \\ Z_{(4 ,2)}(8) = 6679737385293528568074 &{} Z_{(1 ,3)}(8) = 206586801010120 \\ Z_{(4 ,2)}(9) = 156365941798233727835344210 &{} Z_{(1 ,3)}(9) = 112768191495889504 \\ Z_{(4 ,2)}(10) = 5644810136397880752393218670450 &{} Z_{(1 ,3)}(10) = 77345945611296509292 \\ \end{array} \end{aligned}$$

$$\begin{aligned} Z_{(2 ,3)}(1)= & {} 1\\ Z_{(2 ,3)}(2)= & {} 54\\ Z_{(2 ,3)}(3)= & {} 3429\\ Z_{(2 ,3)}(4)= & {} 1174131\\ Z_{(2 ,3)}(5)= & {} 844017083\\ Z_{(2 ,3)}(6)= & {} 1123310441071\\ Z_{(2 ,3)}(7)= & {} 2467786415270493\\ Z_{(2 ,3)}(8)= & {} 8328732420291192478\\ Z_{(2 ,3)}(9)= & {} 40918978820737449535320\\ Z_{(2 ,3)}(10)= & {} 280663043379143953171486670\\ Z_{(3 ,3)}(1)= & {} 1\\ Z_{(3 ,3)}(2)= & {} 108\\ Z_{(3 ,3)}(3)= & {} 20385\\ Z_{(3 ,3)}(4)= & {} 27911497\\ Z_{(3 ,3)}(5)= & {} 101270263373\\ Z_{(3 ,3)}(6)= & {} 808737763302769\\ Z_{(3 ,3)}(7)= & {} 12437533558341538117\\ Z_{(3 ,3)}(8)= & {} 335813302012103944044442\\ Z_{(3 ,3)}(9)= & {} 14848655511669834312208790386\\ Z_{(3 ,3)}(10)= & {} 1018469253608232433396757806687350\\ Z_{(4 ,3)}(1)= & {} 1\\ Z_{(4 ,3)}(2)= & {} 216\\ Z_{(4 ,3)}(3)= & {} 121851\\ Z_{(4 ,3)}(4)= & {} 667805907\\ Z_{(4 ,3)}(5)= & {} 12152298379613\\ Z_{(4 ,3)}(6)= & {} 582289005438959573\\ Z_{(4 ,3)}(7)= & {} 62685142852496536121863\\ Z_{(4 ,3)}(8)= & {} 13539990635493052141269235966\\ Z_{(4 ,3)}(9)= & {} 5388279875096642811025933948192104\\ Z_{(4 ,3)}(10)= & {} 3695821163147476937945397151019067068750 \end{aligned}$$