1 Introduction

As a thermodynamic system, the black hole is closely related to classical thermodynamics, gravitation, and quantum systems. The study of the thermodynamic properties and phase transitions of anti-de Sitter (AdS) black holes or dS spacetimes with black holes has received considerable attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Treating the cosmological constant \(\Lambda \) as a thermodynamic pressure and its conjugate quantity as a thermodynamic volume established the first law of black hole thermodynamics in the extended phase space. This approach allowed for the investigation of the thermodynamic properties of AdS black holes. Notably, the thermodynamic properties of black holes in AdS space differ significantly from those of black holes in asymptotically flat spacetime or in de Sitter space. In AdS space, the phase transition can be explained through the AdS/conformal field theory (CFT) correspondence [28,29,30]. The phase transition of charged AdS black holes is quite similar to that of a van der Waals (vdW) system. Furthermore, black hole chemistry has revealed a broad range of new phenomena associated with black holes, such as triple points [31], reentrant phase transitions [32], and heat engines [33].

Astronomical observations indicate that the expansion of our universe is accelerating [34,35,36], suggesting that it will eventually become an asymptotic de Sitter universe. The study of the thermodynamics of asymptotic de Sitter black holes has been motivated by the formulation of the dS/CFT correspondence [30] and the physical relevance of de Sitter black holes in cosmology [37]. If we consider the cosmological constant as dark energy, our universe will eventually enter a new dS phase. Therefore, a clear understanding of dS spacetime is essential [38,39,40]. However, this subject is not well understood. In dS space, the absence of a Killing vector, which is time-like everywhere outside the black hole horizon, raises questions about the notion of asymptotic mass [38]. Additionally, the presence of both the black hole horizon and cosmological horizon, which have different temperatures, suggests that the system does not meet the requirements of thermodynamic equilibrium. The thermodynamic properties of dS spacetime are of direct interest to cosmology, but these features present unfortunate difficulties. There have been a few attempts to investigate the thermodynamics of black holes in dS spacetime and overcome this problem. One way to deal with the thermodynamics of asymptotically dS black hole spacetimes is to first formulate several separate thermodynamic laws, one for each “physical” horizon present in the spacetime [41,42,43]. One way to approach this task is by using the concept of effective temperature [44,45,46]. This involves focusing on an observer situated in an “observable part of the universe,” located between the black hole horizon and the cosmological horizon. Another approach is to examine de Sitter black holes that are enclosed in an isothermal cavity at a fixed temperature. This fragment describes the definition of a grand canonical ensemble in which the cavity acts as a reservoir, allowing for the existence of thermodynamically stable black holes. Brown [47] first explored this approach, demonstrating the stability of the ensemble. Later, Carlip and Vaidya [48] found a Hawking–Page-like phase transition in both the asymptotically flat and de Sitter cases.

Nonlinear field theories are of interest to various branches of mathematical physics because most physical systems are inherently nonlinear. The main reason for considering nonlinear electrodynamics (NLED) is that these theories have considerably richer content than the Maxwell field, and in special cases, they reduce to the linear Maxwell theory. The authors in [49] presented (\(n+1\))-dimensional topological static black hole solutions of Einstein gravity in the presence of NLED. They checked the first law of thermodynamics and studied the stability of the solutions in both canonical and grand canonical ensembles [50, 51]. Additionally, they analyzed the effect of the nonlinear charge correction on the thermodynamic properties of the black hole [52,53,54,55,56]. A natural question that arises is whether a dS spacetime with a nonlinear charge source has thermodynamic properties similar to an AdS black hole. In this work, the higher-dimensional dS spacetime with the nonlinear charge correction is considered an ordinary thermodynamic system by examining the correlation between two horizons. The focus is on investigating the thermodynamics and phase transitions of the (\(n+1\))-dimensional dS spacetime. The analysis also considers the effect of nonlinear charge correction on the phase transition. The results show that the latent heat of phase transition and the two-phase coexistence region are similar to those of an ordinary thermodynamic system.

The remainder of this paper is organized as follows: In Sect. 2, we briefly present the thermodynamic quantities in HDTNS and establish the state equation of HDTNS which corresponds to the ordinary thermodynamic system [57,58,59,60]. Then the \(P_{\textrm{eff}}^{0}-T_{\textrm{eff}}^{0}\) curves, the phase diagrams in \(P_{\textrm{eff}}^{0}-V\), and the \(\frac{q^2}{r_{2}^{2n-4}}-x\)(y) curves in HDTNS are presented. The effects of the ratio x between two horizons and the spacetime dimensions n on them are discussed in Sect. 3. The slope of the \(P_{\textrm{eff}}^{0}-T_{\textrm{eff}}^{0}\) curve for different spacetime dimensions n is given, which corresponds to the Clapeyron equation. The latent heat of the phase transition for the first-order phase transition in HDTNS and the effect of the ratio x between two horizons and the spacetime dimensions n on it are given in Sect. 4. Finally, a brief summary is given in Sect. 5.

2 Topological black hole with nonlinear source

The (\(n+1\))-dimensional action of Einstein gravity with nonlinear electrodynamics is [49,50,51, 61]:

$$\begin{aligned} I_{G}&=-\frac{1}{16\pi }\int _{\mathcal {M}}\textrm{d}^{n+1}x\root \of {-g}[R-2\Lambda +L(\mathcal {F})]\nonumber \\&\quad -\frac{1}{8\pi }\int _{\partial {\mathcal {M}}}\textrm{d}^{n}x\root \of {-\gamma }\Theta (\gamma ), \end{aligned}$$
(2.1)

where R is the scalar curvature and \(\Lambda \) is the cosmological constant. In this action,

$$\begin{aligned} L(\mathcal {F})&=-\mathcal {F}+{\alpha }\mathcal {F}^2+\mathcal {O}({\alpha }^2), \end{aligned}$$
(2.2)

is the Lagrangian of nonlinear electrodynamics. \(\mathcal {F}\)=\(F_{{ \mu \nu }}F^{{ \mu \nu }}\) is the Maxwell invariant, in which \(F_{{ \mu \nu }}\)=\(\partial _{{ \mu }}A_{{ {\nu }}}-\partial _{{ \nu }}A_{{ {\mu }}}\) is the electromagnetic field tensor and \(A_{{ {\mu }}}\) is the gauge potential. In addition, \(\alpha \) denotes the nonlinearity parameter, which is small, so the effects of nonlinearity should be considered as a perturbation. In the second integral, \(\gamma \) and \(\Theta \) are, respectively, the trace of induced metric, \({\gamma }_{i,j}\), and the extrinsic curvature \({\Theta }_{i,j}\) on the boundary \(\partial {M}\). The variation of the action (2.1) with respect to the metric tensor \(g_{{\mu }{\nu }}\) and the Faraday tensor \(F_{{\mu }{\nu }}\) leads to

$$\begin{aligned}&G_{{\mu }{\nu }}+{\Lambda }g_{{\mu }{\nu }} =\frac{1}{2}g_{{\mu }{\nu }}L(\mathcal {F})-2L_\mathcal {F}F_{{\mu }{\lambda }}F_{\mu }^{\lambda }, \end{aligned}$$
(2.3)
$$\begin{aligned}&{\partial }_{\mu }(\root \of {-g}L_\mathcal {F}F^{{\mu }{\nu }})=0, \end{aligned}$$
(2.4)

where \(G_{{\mu }{\nu }}\) is the Einstein tensor and \(L_\mathcal {F}=dL(\mathcal {F})/d\mathcal {F}\).

The (\(n+1\))-dimensional topological black hole solutions can take the form of

$$\begin{aligned} \textrm{d}s^2&=-f(r)\textrm{d}t^2+\frac{\textrm{d}r^2}{f(r)}+r^2\textrm{d}\Omega _{n-1}^2, \end{aligned}$$
(2.5)

where

$$\begin{aligned} f(r)&=k-\frac{m}{r^{n-2}}-\frac{2\Lambda r^2}{n(n-1)}+\frac{2q^2}{(n-1)(n-2)r^{2n-4}}\nonumber \\&\quad -\frac{4q^4\alpha }{(3n^7-7n+4)r^{2n-6}}, \end{aligned}$$
(2.6)

m is an integration constant which is related to the mass of the black hole, and the last term in Eq. (2.6) indicates the effect of nonlinearity. The asymptotic behavior of the solution is AdS or dS provided \(\Lambda <0\) or \(\Lambda >0\), and the case of the asymptotically flat solution is permitted for \(\Lambda =0\) and \(k=1\).

When \(\Lambda >0\), the black hole horizon \(r_+\) and the cosmological horizon \(r_c\) exist in spacetime, and the position of two horizons satisfies the equation \(f(r_{+,c})=0\). The radiation temperature of the two horizons is given by

$$\begin{aligned} T_+&= \frac{f'(r_+)}{4\pi } =\frac{1}{2\pi (n-1)}\nonumber \\&\quad \times \left( \frac{(n-1)(n-2)k}{2r_+}-\Lambda r_+ -\frac{q^2}{r_{+}^{2n-3}}+\frac{2q^4\alpha }{r_{+}^{4n-5}}\right) . \end{aligned}$$
(2.7)
$$\begin{aligned} T_c&= -\frac{f'(r_c)}{4\pi }=-\frac{1}{2\pi (n-1)}\nonumber \\&\quad \times \left( \frac{(n-1)(n-2)k}{2r_c}-\Lambda r_c -\frac{q^2}{r_{c}^{2n-3}}+\frac{2q^4\alpha }{r_{c}^{4n-5}}\right) . \end{aligned}$$
(2.8)

The mass of the black hole

$$\begin{aligned} M&= \frac{V_{n-1}(n-1)}{16\pi }\nonumber \\&\quad \times \left( kr_+^{n-2}-\frac{2\Lambda r_+^n}{n(n-1)}+\frac{2q^2}{(n-1)(n-2)r_+^{n-2}}\right. \\&\quad \left. -\frac{4q^4\alpha }{\left[ 2(n-2)(n+2)+(n-3)(n-4)\right] r_+^{3n-4}}\right) \end{aligned}$$

or

$$\begin{aligned} M&= \frac{V_{n-1}(n-1)}{16\pi }\nonumber \\&\quad \times \left( kr_c^{n-2}-\frac{2\Lambda r_c^n}{n(n-1)}+\frac{2q^2}{(n-1)(n-2)r_c^{n-2}}\right. \nonumber \\&\quad \left. -\frac{4q^4\alpha }{\left[ 2(n-2)(n+2)+(n-3)(n-4)\right] r_c^{3n-4}}\right) . \end{aligned}$$
(2.9)
$$\begin{aligned} V_{n-1}&=\frac{2\pi ^{n/2}}{\Gamma (n/2)},~~S_{+,c}=\frac{V_{n-1}r_{+,c}^{n-1}}{4},\nonumber \\ V_{+,c}&=\frac{V_{n-1}r_{+,c}^n}{n},~~Q=\frac{q}{4\pi }V_{n-1}, \nonumber \\ \Phi _{+,c}&=\frac{q}{(n-2)r_{+,c}^{n-2}}-\frac{4q^3\alpha }{(3n-4)r_{+,c}^{3n-4}},\nonumber \\ P&=-\frac{\Lambda }{8\pi },~~M=\frac{V_{n-1}(n-1)m}{16\pi }. \end{aligned}$$
(2.10)

Thermodynamic quantities corresponding to two horizons satisfy the first law of thermodynamics

$$\begin{aligned} {} \textrm{d}M&= T_{{ +,c}}\textrm{d}S_{{ +,c}}+\Phi _{{ +,c}}\textrm{d}Q+V_{{ +,c}}\textrm{d}P. \end{aligned}$$
(2.11)

Treating the spacetime of HDTNS, which includes the horizons of both black holes and cosmology, as a thermodynamic system, it must adhere to the universal first law of thermodynamics according to Eq. (2.11). [27]

$$\begin{aligned} {} \textrm{d}M&= T_{\textrm{eff}}\textrm{d}S+P_{\textrm{eff}}\textrm{d}V+\Phi _{\textrm{eff}}\textrm{d}Q, \end{aligned}$$
(2.12)

Here, the thermodynamic volume is that between the black hole horizon and the cosmological horizon, namely [38]

$$\begin{aligned} {} V&= V_{{ c}}-V_{{ +}}=\frac{V_{n-1}r_c^n}{n}(1-x^n). \end{aligned}$$
(2.13)

Taking the dimension into account, we set the entropy of the spacetime as follows

$$\begin{aligned} {} S&= \frac{V_{n-1}r_c^{n-1}}{4}F_n(x). \end{aligned}$$
(2.14)

with \(F_n(x)\) as a function of x, where \(x=r_+/r_c\) denotes the position ratio between the black hole horizon \(r_+\) and the cosmological horizon \(r_c\), and the effective temperature \(T_{\textrm{eff}}\), the effective pressure \(P_{\textrm{eff}}\), and the effective potential \(Q_{\textrm{eff}}\) of the system are determined from Eq. (2.12), respectively

$$\begin{aligned} {} T_{\textrm{eff}}&= \frac{f_1(x)}{r_c}+\frac{q^2f_2(x)}{r_c^{2n-3}}-\frac{4q^4\alpha f_3(x)}{r_c^{4n-5}}, \end{aligned}$$
(2.15)

with

$$\begin{aligned} f_1(x)&= \frac{k\left( (n-2-nx^2)(1-x^n)+2(n-1)x^n(1-x^2)\right) }{4\pi x(1+x^{n+1})},\nonumber \\ f_2(x)&= \frac{nx^n(1-x^{n-2})-(n-2)(1-x^{3n-2})}{2\pi x^{2n-3}(1+x^{n+1})(n-1)(n-2)},\nonumber \\ f_3(x)&= \frac{-(3n-4)+(3n-4)x^{5n-4}+nx^n(1-x^{3n-4})}{\pi (1+x^{n+1})(3n-4)(n-1)x^{4n-5}},\nonumber \\ F_n(x)&= \frac{3n-1}{2n-1}(1-x^n)^{(n-1)/n}\nonumber \\&\quad -\frac{n(1+x^{2n-1})-(2n-1)x^{n-1}(1+x)}{(2n-1)(1-x^n)}. \end{aligned}$$
(2.16)
$$\begin{aligned} \Phi _{\textrm{eff}}&= \left( \frac{\partial M}{\partial Q}\right) _{S,V}\nonumber \\&=\frac{(n-1)(1-x^{2n-2})q}{(1-x^n)r_c^{n-2}x^{n-2}}\left[ \frac{1}{(n-1)(n-2)}\right. \nonumber \\&\quad \left. -\frac{4q^2\alpha }{(3n^2-7n+4)r_c^{2n-2}}\frac{(1+x^{2n-2})}{x^{2n-2}}\right] . \end{aligned}$$
(2.17)
$$\begin{aligned} P_{\textrm{eff}}&= \frac{f_4(x)}{r_c^2}+\frac{q^2f_5(x)}{r_c^{2n-2}}-\frac{q^4\alpha f_6(x)}{r_c^{4n-4}} \end{aligned}$$
(2.18)

with

$$\begin{aligned} {} f_4(x)&= \frac{-k}{16\pi (1+x^{n+1})} \left( \frac{F_n(x)(n-1)(n-2-nx^2+2x^n)}{x(1-x^n)}-F'_n(x)(1-x^2)(n-2)\right) \nonumber \\ f_5(x)&= \frac{-1}{8\pi x^{2n-3}(n-1)(1+x^{n+1})} \left( \frac{F_n(x)(n-1)[2(n-1)x^n-(n-2)-nx^{2n-2}]}{(n-2)(1-x^n)}+xF'_n(x)(1-x^{2n-2})\right) \nonumber \\ f_6(x)&= -\frac{F_n(x)(n-1)[(3n-4)+4(n-1)x^n-nx^{4n-4}]+xF'_n(x)(3n-4)(1-x^n)(1-x^{4n-4})}{4\pi x^{4n-5}(1+x^{n+1})(1-x^n)(3n-4)(n-1)}. \end{aligned}$$
(2.19)

substituting Eq. (2.15) into Eq. (2.18), one obtain

$$\begin{aligned} P_{\textrm{eff}}&= \frac{f_6(x)T_{\textrm{eff}}}{r_cf_3(x)}-\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_c^2f_3(x)}\nonumber \\&\quad +\frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))}{r_c^{2n-2}f_3(x)}. \end{aligned}$$
(2.20)

The thermodynamic quantities presented above are obtained by treating the whole HDTNS spacetime as a thermodynamic system. Therefore, this approach enables us to obtain thermodynamic quantities that reflect the thermodynamic properties of the HDTNS spacetime. Based on this analysis, the thermodynamic properties of the HDTNS spacetime can be evaluated.

3 The construction of the equal-area law in the \(P-V\) diagram

When the ratio x of the two horizons in the HDTNS spacetime is constant, the effective temperature is \(T_{\textrm{eff}}^{0}\) (\(T_{\textrm{eff}}^{0}\le T_{\textrm{eff}}^{c}\)), and \(T_{\textrm{eff}}^{c}\) is the critical temperature. For the system to satisfy the thermodynamic equilibrium condition, the horizontal coordinates of the boundaries of the two-phase coexistence region in the HDTNS spacetime must be \(V_2\) and \(V_1\), respectively, and the vertical coordinate of the pressure is \(P_{\textrm{eff}}^{0}\). The value of \(P_{\textrm{eff}}^{0}\) is determined by the cosmological horizon radius \(r_c\). By Maxwell’s equal-area law [27, 57, 58, 60]

$$\begin{aligned} {} P_{\textrm{eff}}^{0}(V_{2}-V_{1})&=\int _{V_1}^{V_2}P_{\textrm{eff}}\textrm{d}V, \end{aligned}$$
(3.1)

through Eq. (3.1), we obtain

$$\begin{aligned} P_{\textrm{eff}}^{0}&= \frac{f_6(x)T_{\textrm{eff}}^0}{r_1f_3(x)}-\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_1f_3(x)}\nonumber \\&\quad +\frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))}{r_{1}^{2n-2}f_3(x)} \end{aligned}$$
$$\begin{aligned} P_{\textrm{eff}}^{0}&= \frac{f_6(x)T_{\textrm{eff}}^{0}}{r_2f_3(x)}-\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_2f_3(x)}\nonumber \\&\quad +\frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))}{r_{2}^{2n-2}f_3(x)}, \end{aligned}$$
(3.2)

where \(r_2\) and \(r_1\) stand for the positions of the cosmological horizons of two regions of phase coexistence, respectively.

$$\begin{aligned} P_{\textrm{eff}}^{0}\frac{r_{2}^{n}}{n}(1-y^n)&= \frac{T_{\textrm{eff}}^{0}f_6(x)r_2^{n-1}(1-y^{n-1})}{(n-1)f_3(x)}\nonumber \\&\quad -\frac{[f_1(x)f_6(x)-f_4(x)f_3(x)]r_2^{n-2}(1-y^{n-2})}{(n-2)f_3(x)}\nonumber \\&\quad +\frac{q^2(f_2(x)f_6(x)-f_5(x)f_3(x))(1-y^{n-2})}{(n-2)r_2^{n-2}y^{n-2}f_3(x)}. \end{aligned}$$
(3.3)

Through Eq. (3.2), we obtain

$$\begin{aligned} 0&= -f_6(x)T_{\textrm{eff}}^{0}(1-y)\nonumber \\&\quad +\frac{(f_1(x)f_6(x)-f_4(x)f_3(x))(1-y^2)}{r_2y}\nonumber \\&\quad -\frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))(1-y^{2n-2})}{r_2^{2n-3}y^{2n-3}},\nonumber \\ \end{aligned}$$
(3.4)
$$\begin{aligned} P_{\textrm{eff}}^{0}&= \frac{f_6(x)T_{\textrm{eff}}^{0}(1+y)}{2r_2yf_3(x)}\nonumber \\&\quad -\frac{(f_1(x)f_6(x)-f_4(x)f_3(x))(1+y^2)}{2r_2^2y^2f_3(x)}\nonumber \\&\quad +\frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))(1+y^{2n-2})}{2r_2^{2n-2}y^{2n-2}f_3(x)}.\nonumber \\ \end{aligned}$$
(3.5)

where \(y=r_1/r_2\) is the cosmological (black hole) horizon position ratio of the two-phase coexistence region. Through Eqs. (3.3) and (3.5), we obtain

$$\begin{aligned}&\frac{f_6(x)T_{\textrm{eff}}^{0}[(1+y)(1-y^n)-n(1-y)(1+y^n)]}{2(n-1)} \nonumber \\&\qquad +\frac{(f_1(x)f_6(x)-f_4(x)f_3(x))[(n-2)(1-y^{n+2})-(n+2)y^2(1-y^{n-2})]}{2r_2y(n-2)}\nonumber \\&\quad = \frac{q^2(f_5(x)f_3(x)-f_2(x)f_6(x))[(n-2)(1+y^{2n-2})(1-y^n)-2ny^n(1-y^{n-2})]}{2r_2^{2n-3}y^{2n-3}(n-2)}. \end{aligned}$$
(3.6)

Through Eqs. (3.4) and (3.6), we obtain

$$\begin{aligned} {} \frac{q^2}{r_2^{2n-4}y^{2n-4}}&= \frac{f_1(n,y)}{f_2(n,y)}\frac{[f_1(x)f_6(x)-f_4(x)f_3(x)]}{[f_5(x)f_3(x)-f_2(x)f_6(x)]},\nonumber \\ \end{aligned}$$
(3.7)

with

$$\begin{aligned} f_1(n,y)&=\left[ \frac{(1+y)\left[ (1+y)(1-y^n)-n(1-y)(1+y^n)\right] }{(n-1)}+\frac{\left[ (n-2)(1-y^{n+2})-(n+2)y^2(1-y^{n-2})\right] }{(n-2)}\right] \\ f_2(n,y)&=\left[ \frac{\left[ (n-2)(1+y^{2n-2})(1-y^n)-2ny^n(1-y^{n-2})\right] }{(n-2)}+\frac{(1-y^{2n-2})\left[ (1+y)(1-y^n)-n(1-y)(1+y^n)\right] }{(n-1)(1-y)}\right] \end{aligned}$$

From Eq. (3.2), we obtain

$$\begin{aligned} P_{\textrm{eff}}^0&=\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_{2}^{2}yf_3(x)}\nonumber \\&\quad \times \left( 1-\frac{(1-y^{2n-3})}{(1-y)}\frac{f_1(n,y)}{f_2(n,y)}\right) \end{aligned}$$
(3.8)
$$\begin{aligned} T_{\textrm{eff}}^0&=\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_{2}yf_6(x)}\nonumber \\&\quad \times \left( (1+y)-\frac{(1-y^{2n-2})}{(1-y)}\frac{f_1(n,y)}{f_2(n,y)}\right) \end{aligned}$$
(3.9)

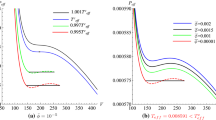
Combining Eqs. (3.8) and (3.9), the \(P_{\textrm{eff}}^0-T_{\textrm{eff}}^0\) curve for the two-phase equilibrium coexistence is shown in Fig. 1.

Fig. 1
figure 1

The \(P_{\textrm{eff}}^0-T_{\textrm{eff}}^0\) curve in two-phase equilibrium coexistence (setting \(q=1\))

Full size image

From Fig. 1, the effective transition temperature \(T_{\textrm{eff}}^0\) and pressure \(P_{\textrm{eff}}^0\) of the two-phase coexistence are affected by the spacetime dimension n and the ratio x when the phase transition occurs in the HDTNS spacetime. As shown in Fig. 1a, the position of the critical point in HDTNS spacetime increases with increasing x, the critical temperature \(T_{\textrm{eff}}^c\) and the pressure \(p_{\textrm{eff}}^c\) (the endpoint of the curve) increase with n, and the behavior of the effective transition pressure \(P_{\textrm{eff}}^0\) decreases with increasing n for a given effective transition temperature \(T_{\textrm{eff}}^0\). Figure 1b shows that the behavior of the critical temperature \(T_{\textrm{eff}}^c\) in HDTNS spacetime decreases with the increase in the value of x. However, the behavior of the critical pressure \(P_{\textrm{eff}}^c\) in HDTNS spacetime increases with the increasing value of x. The behavior of the effective transition pressure \(P_{\textrm{eff}}^0\) increases with the increasing value of x for a given effective transition temperature \(T_{\textrm{eff}}^0\).

When \(y\rightarrow 1\), by Eq. (3.7), the position of the critical point of the cosmological horizon, \( {r_{cc}}\), for different dimensions n in HDTNS spacetime satisfies

$$\begin{aligned} {} r_{cc}^{2n-4}&= \frac{q^2(n-1)(2n-3)(f_5(x)f_3(x)-f_2(x)f_6(x))}{f_1(x)f_6(x)-f_4(x)f_3(x)}. \end{aligned}$$
(3.10)

The critical temperature \(T_{\textrm{eff}}^{c}\) and the critical pressure \(P_{\textrm{eff}}^{c}\) satisfy the following equation

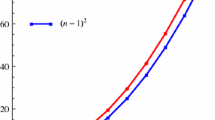
$$\begin{aligned} {} T_{\textrm{eff}}^c&= \frac{4(n-2)[f_1(x)f_6(x)-f_4(x)f_3(x)]}{(2n-3)f_6(x)r_{{ cc}}}\nonumber \\&=\frac{4(n-2)[f_1(x)f_6(x)-f_4(x)f_3(x)]}{(2n-3)f_6(x)}\nonumber \\&\quad \times \left( \frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{q^2(n-1)(2n-3)(f_5(x)f_3(x)-f_2(x)f_6(x))}\right) ^{1/(2n-4)}, \nonumber \\ P_{\textrm{eff}}^c&= \frac{(n-2)(f_1(x)f_6(x)-f_4(x)f_3(x))}{(n-1)f_3(x)r_{{ cc}}^2}. \end{aligned}$$
(3.11)

The values of x in Eqs. (3.10) and (3.11) can take on any value of \(0<x<1\). However, for a thermodynamic system, these values must satisfy \(r_{cc}>0\), \(P_{\textrm{eff}}^c>0\), \(T_{\textrm{eff}}^c>0\). The critical values for the reaction in Fig. 2 vary depending on the value of x.

Fig. 2
figure 2

The behavior of \(r_{cc}^{2n-4}\), \(T_{\textrm{eff}}^c\), and \(P_{\textrm{eff}}^c\) as a function of x (setting \(q=1\))

Full size image

Figure 2 shows the critical horizon position \(r_{cc}\), the critical temperature \(T_{\textrm{eff}}^c\), and the critical pressure \(P_{\textrm{eff}}^c\) of spacetime for a fixed x increase with increasing spacetime dimension n.

Taking \(T_{\textrm{eff}}^0=\chi {T_{\textrm{eff}}^c}\), from Eqs. (3.9) and (3.11) we obtain

$$\begin{aligned} {} \chi&= \frac{(2n-3)}{4(n-2)(1-y)}\left( \frac{(n-1)(2n-3)f_1(n,y)}{f_2(n,y)}\right) ^{1/(2n-4)}\nonumber \\&\quad \times \left[ (1-y^2)-\frac{(1-y^{2n-2})f_1(n,y)}{f_2(n,y)}\right] . \end{aligned}$$
(3.12)
Fig. 3
figure 3

The behavior of \(\chi \) as a function of y

Full size image

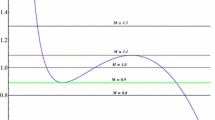
Figure 3 shows the change in the effective temperature \(T_{\textrm{eff}}\) of spacetime as a function of the cosmological (or the black hole) horizon position ratio y of the two-phase coexistence region during a first-order phase transition. Figure 3 shows that the effective temperature \(T_{\textrm{eff}}^{0}\) of the coexistence region for a fixed y decreases with increasing spacetime dimension n.

Fig. 4
figure 4

The behavior of the effective pressure \(P_{\textrm{eff}}\) as a function of V, a for different \(\chi \), b for different x, c for different n (setting \(q=1\))

Full size image

Because of the existence of gravity in the system, the interplay between the black hole and cosmology horizons should be considered, and we say that the thermodynamic volume is that between the black hole horizon and the cosmological horizon, \(V=V_{c}-V_{+}\), i.e., Eq. (2.13) in this work. On the other hand, for the space between the black hole outer horizon (generally called the black hole horizon) and cosmology horizon, the different Hawking temperatures on the two horizons prevent a dS spacetime with a black hole in equilibrium as similar to an ordinary thermodynamic system, while there are common parameters M, Q on the black hole and cosmological horizons. Thus, the thermodynamic quantities on the two horizons are not independent. The interplay between the two horizons must be taken into account when constructing the effective quantities of a dS spacetime with a black hole in thermodynamic equilibrium. From \(V_{+,c}\) in Eq. (2.10) and the definition \(x=r_{+}/r_{c}\), the relationship of the effective pressure \(P_{\textrm{eff}}\) and the ratio x is established. Based on these and Ehrenfest’s classification of phase transitions, the system undergoes a phase transition that satisfies the conditions for a first-order phase transition when \(0<x<1\). By substituting Eq. (3.12) into Eq. (2.20), we obtain

$$\begin{aligned} {} P_{\textrm{eff}}&= \chi \frac{4(n-2)\left[ f_1(x)f_6(x)-f_4(x)f_3(x)\right] }{(2n-3)r_cf_3(x)r_{cc}}\nonumber \\&\quad -\frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{r_c^2f_3(x)}\nonumber \\&\quad +\frac{q^2\left( f_5(x)f_3(x)-f_2(x)f_6(x)\right) }{r_c^{2n-2}f_3(x)}, \end{aligned}$$
(3.13)

The \(P_{\textrm{eff}}-V\) curve for different \(\chi \), x, and n can be plotted from Eqs. (2.13) and (3.13) in Fig. 4.

The values of \(V_2\) and \(V_1\) for different effective temperatures \(T_{\textrm{eff}}\) (i.e., different values of \(\chi \)) can be found using Eqs. (2.13) and (3.7). The red dots in the Fig. 4a indicate the boundary point of the coexistence region, and the intervals between the parallel horizontal coordinates of the two red dots represent the two-phase coexistence region. Figure 4b shows the behavior of effective pressure \(P_{\textrm{eff}}\) as a function of thermodynamic volume V under fixed spacetime dimension n and effective critical temperatures \(T_{\textrm{eff}}^{c}\) for the occurrence of the phase transition in HDTNS. By examining Fig. 4b, from the position ratio x of the two horizons, it is observed that the behavior of the effective pressure \(P_{\textrm{eff}}\) is different in different thermodynamic volume ranges, keeping the thermodynamic volume V constant. In the small (large) thermodynamic volume range, the effective pressure \(P_{\textrm{eff}}\) during the phase transition increases (decreases) with an increase in the position ratio x of the two horizons in the case of fixed V. Figure 4c shows that for the same thermodynamic volume V and position ratio x of the two horizons, the effective pressure \(P_{\textrm{eff}}\) increases with increasing spacetime dimension n.

The Gibbs free energy in HDTNS spacetime can be expressed as follows:

$$\begin{aligned} G({{r}_{c}},x)&=M-{{T}_{\textrm{eff}}}S+{{P}_{\textrm{eff}}}V. \end{aligned}$$
(3.14)

The \(G_{T_{\textrm{eff}}}-P_{\textrm{eff}}\) curves for different \(\chi \) are plotted in Fig. 5.

Fig. 5
figure 5

The behavior of Gibbs free energy \(G_{T_{\textrm{eff}}}\) as a function of the effective pressure \(P_{\textrm{eff}}\) given fixed \(x=0.4,~n=3\) for different \(\chi \) (setting \(q=1\))

Full size image

Comparing Fig. 4a with Fig. 5, when \({\chi }=0.9\), that is, the effective temperature \({T_{\textrm{eff}}}<{T_{\textrm{eff}}^{c}}\), it is found that the \(G_{T_{\textrm{eff}}}-P_{\textrm{eff}}\) curve contains an intersection, which is similar to that of the van der Waals system and the Ads black hole. The first-order phase transition occurs at the intersection of the isothermal \(G_{T_{\textrm{eff}}}-P_{\textrm{eff}}\) curve in HDTNS spacetime according to the Gibbs free energy criterion at isothermal and isobaric conditions. When \({\chi }=1\), the isothermal \(G_{T_{\textrm{eff}}}-P_{\textrm{eff}}\) curve varies continuously with a single value, indicating that the HDTNS spacetime is in a single state. This state corresponds to the vapor phase of the VdW system.

To ensure that the thermodynamic system meets the requirements of equilibrium stability, the isothermal \(P_{\textrm{eff}}-V\) curve cannot have negative pressure, and therefore the lowest temperature meets the requirements of

$$\begin{aligned} {} {\left( \frac{\partial {P_{\textrm{eff}}}}{\partial {V}}\right) }_{T_{\textrm{eff}}}&= {\left( \frac{\partial {P_{{ eff}}}}{\partial {r_{c}}}\right) }_{T_{{ eff}}}{\left( \frac{\partial {r_{c}}}{\partial {V}}\right) }_{T_{{ eff}}}=0,~~P_{\textrm{eff}}(V,T_{\textrm{eff}})\nonumber \\&=0. \end{aligned}$$
(3.15)
Fig. 6
figure 6

The behavior of the lowest effective temperature \(T_{{ eff}}^{{ min}}\) as a function of x for different n

Full size image
Fig. 7
figure 7

The behavior of \(\frac{q^2}{r_{2}^{2n-4}}\) as a function of x and y for different n, respectively

Full size image

From Eq. (3.12), we obtain

$$\begin{aligned} {} \frac{q^2}{r_{cmin}^{2n-4}}&= \frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{(2n-3)\left( f_5(x)f_3(x)-f_2(x)f_6(x)\right) }. \end{aligned}$$
(3.16)

The minimum temperature \(T_{\textrm{eff}}^\textrm{min}\) of the spacetime satisfies

$$\begin{aligned} {} T_{\textrm{eff}}^\textrm{min}&= \frac{2(n-2)\left( f_1(x)f_6(x)-f_4(x)f_3(x)\right) }{(2n-3)f_6(x)}\nonumber \\&\quad \times \left( \frac{f_1(x)f_6(x)-f_4(x)f_3(x)}{(2n-3)q^2\left( f_5(x)f_3(x)-f_2(x)f_6(x)\right) }\right) ^{1/(2n-4)}. \end{aligned}$$
(3.17)

The ratio of the minimum effective temperature \(T_{\textrm{eff}}^\textrm{min}\) to the critical temperature \(T_{\textrm{eff}}^{c}\) of the spacetime

$$\begin{aligned} {} \frac{T_{\textrm{eff}}^\textrm{min}}{T_{\textrm{eff}}^{c}}&= \frac{(n-1)^{1/(2n-4)}}{2}, \end{aligned}$$
(3.18)

is independent of the ratio x of the positions of the two horizons, and is only related to the dimension n of the spacetime. The \(T_{\textrm{eff}}^\textrm{min}-x\) curve is plotted in Fig. 4 for different spacetime dimensions n. The behavior of \(T_{\textrm{eff}}^\textrm{min}\) for a fixed x also increases with increasing n, which is consistent with Fig. 2b (Fig. 6).

The \(\frac{q^2}{r_{2}^{2n-4}}-x\) and \(\frac{q^2}{r_{2}^{2n-4}}-y\) curves for different n are plotted in Fig. 7 from Eq. (3.7). Figure 7 displays the correlation between the potential at the horizon and the spacetime dimension n during a phase transition. Additionally, Fig. 7a depicts the behavior of the potential at the transition point as a function of the ratio x, which represents the black hole horizon position to the cosmological horizon position, for a given ratio y of the cosmological (or the black hole) horizon position of the two-phase coexistence regions. Furthermore, the potential at the boundary of the coexistence region decreases as the spacetime dimension n increases. Figure 7b illustrates the behavior of the potential at the phase transition point as a function of the ratio y, which represents the cosmological (or black hole) horizon position of the two-phase coexistence regions in spacetime, for a given ratio x of the black hole horizon position to the cosmological horizon position. It is evident from Eqs. (3.7) and (3.10) that the phase transition of the HDNTS spacetime depends on the cosmological (or black hole) horizon potential for a given effective temperature \(T_{\textrm{eff}}\) (i.e., \(\chi \) is fixed), rather than that between a large black hole and a small black hole. The potential \(\varphi _1=\frac{q}{r_{1}^{2n-2}}\) at phase 1 with a small cosmological horizon radius is larger than the potential \(\varphi _2=\frac{q}{r_{2}^{2n-2}}\) at phase 2 with a large cosmological horizon radius, i.e. \(\varphi _1>\varphi _2\). In fact, for the given effective temperature \(T_{\textrm{eff}}\), the HDTNS spacetime will be in a two-phase coexistence state if the corresponding potential satisfies \(\varphi _1\ge \varphi \ge \varphi _2\), while it will be in a single-phase state if the potential satisfies \(\varphi >\varphi _1\) or \(\varphi <\varphi _2\). Therefore, the HDTNS spacetime with the potential satisfied by \(\varphi >\varphi _1\) or \(\varphi <\varphi _2\) corresponds to the liquid or gas phase of the vdW system, respectively, and the HDTNS spacetime with the potential in the interval of \(\varphi _1\ge \varphi \ge \varphi _2\) corresponds to the gas–liquid coexistence region.

4 Two-phase equilibrium coexistence curve

In the two-phase coexistence region of a thermodynamic system, the Gibbs free energies must be equal. If pressure and temperature are altered during two-phase coexistence, the Gibbs free energy of both phases must change by the same amount, i.e. \(\textrm{d}G^1=\textrm{d}G^2\). However, the Gibbs free energy of the two phases is not yet fully known for ordinary thermodynamic systems. To gain a better understanding of the two-phase coexistence region, the slope of the \(P-T\) curve at the boundary of the two-phase coexistence, i.e. the Clapeyron equation, is provided.

$$\begin{aligned} {} \frac{\textrm{d}P}{\textrm{d}T}&= \frac{L}{T(V_{2}-V_{1})}, \end{aligned}$$
(4.1)

Here, \(L=T(S_{2}-S_{1})\) represents the latent heat of the phase transition, and \(V_1\) and \(V_2\) stand for the volume of the system in phase 1 and phase 2, respectively. The Clapeyron equation agrees well with the experimental results for ordinary thermodynamic systems, providing direct verification of thermodynamic correctness. For the HDTNS spacetime thermodynamic system, by substituting Eq. (3.7) into Eqs. (3.6) and (3.5), we obtain the following.

When \(n=3\),

When \(n=4\),

When \(n=5\),

with

$$\begin{aligned} F_1(y) =\frac{(3+4y+3y^2)}{(3+12y+30y^2+60y^3+70y^4+60y^5+30y^6+12y^7+3y^8)}. \end{aligned}$$

The slope of the two-phase equilibrium \(P_{\textrm{eff}}^0-T_{\textrm{eff}}^0\) curve from Eqs. (4.2A) and (4.2B) for HDTNS satisfies the following.

When \(n=3\),

with

When \(n=4\),

with

When \(n=5\),

with

Equations (4.4A-C) represent the slope of the \(P_{\textrm{eff}}^0-T_{\textrm{eff}}^0\) curve when the two phases coexist in equilibrium.

The latent heat L of the phase transition of the HDTNS spacetime thermodynamic system can be obtained from Eqs. (4.1) and (4.4).

The latent heat of the phase transition can be expressed as a function of x and y by using Eq. (4.6) with q set to 1. The plotted \(L-y\) curve is shown in Fig. 8.

Fig. 8
figure 8

The behavior of L as a function of y for different x and n, respectively (setting \(q=1\))

Full size image

Figure 8a shows that the latent heat L of a first-order phase transition in spacetime decreases as the ratio x of the positions of the two horizons increases for a fixed y, while keeping the spacetime dimensions n fixed. The data presented in Fig. 8b show that the latent heat L of the phase transition increases as the spacetime dimensions n increase, while keeping the ratio x of the positions of the two horizons fixed. Additionally, based on Fig. 8, the effect of the ratio x of the positions of the two horizons on the latent heat L of the phase transition for first-order phase transition in spacetime is less significant than that of spacetime dimensions n, provided that all other factors remain constant.

5 Conclusion

Black hole thermodynamics serve as a connection between general relativity, classical thermodynamics, and quantum mechanics. The topic is of significant interest due to its direct relation to various fields of physics, including gravity, statistics, and particle and field theory, in which black hole thermodynamics play a crucial role. Although the statistical description of the corresponding thermodynamic states of black holes remains unclear, the study of the thermodynamic properties of black holes and the critical phenomena remain of interest. This paper extends the study of black hole thermodynamic properties to the HDTNS spacetime and discusses the extended phase transition based on the effective thermodynamic quantities in HDTNS spacetime. The phase transition of HDTNS spacetime is analyzed by applying Maxwell’s equal-area law, revealing similarities to the van der Waals system. The potential at the horizon depends on the horizon position, the potential charge, and the position ratio x between the two horizons, as given by Eq. (3.7), when the effective temperature \(T_\textrm{eff}^{0}\) of spacetime is provided. It is important to note that this differs from the phase transition observed in AdS black holes [57, 58]. Figure 7 illustrates the relationship between the potential at the horizon and the position ratio x between two horizons, as well as the spacetime dimension n, when a phase transition occurs in spacetime. In the vdW system, the phase transition at a fixed temperature is primarily due to the interaction between molecules within the system. In HDTNS spacetime, however, the phase transition is mainly caused by the magnitude of the electric field experienced by the “molecules” of this system. For the system in the high potential state, where the “molecules” are arranged in an orderly manner under the influence of a strong electric field, the system is in an ordered phase. Conversely, in the low potential phase, where the “molecules” are arranged in a disorderly manner under the influence of a weak electric field, the system is in a disordered phase. The molecules affected by thermal fluctuations and electric fields are in the phase transition region between disorder and order, or order and disorder, when the system is in the two-phase coexistence state.

According to the discussion in Sect. 3, when the HDTNS spacetime has a temperature greater than its minimum effective temperature, \(T_\textrm{eff}^\textrm{min}\), its effective pressure, \(P_\textrm{eff}\), is also greater than zero. This meets the requirement for the thermodynamic system to be in a stable equilibrium state. Therefore, we consider the sign in front of the \(P_\textrm{eff}dV\) term in Eq. (2.12) to be a positive sign, which satisfies the first law of thermodynamics relative to HDTNS spacetime. This is different from the literature [62], where the \(P_\textrm{eff}dV\) term in Eq. (5) is taken as a negative sign. Equation (3.18) demonstrates that the ratio between the minimum effective temperature \(T_\textrm{eff}^\textrm{min}\) and the critical effective temperature \(T_\textrm{eff}^{c}\) of the HDTNS spacetime is independent of the ratio x between the two horizons. This conclusion is consistent with the findings for AdS black holes [63, 64].

This work examines the thermodynamic properties of HDTNS spacetime and investigates the effect of spacetime dimensions n and the ratio x between two horizons on these properties. The microstates of the internal “molecules” during the phase transition of spacetime are useful for exploring the microstructure of dS spacetime in depth. The study of the microstructure of black holes is particularly important for understanding their fundamental properties in gravity and for the establishment of quantum gravity.