Searching for the open flavor tetraquark $T_{c\bar{s}0}(2900)^{++}$ in the process $B^+\rightarrow K^+ D^+ D^-$

Abstract

Inspired by recent observations of $T_{c\bar{s}0}(2900)^0$ in the $D_s^+ \pi ^-$ invariant mass distribution of $B^0 \rightarrow \bar{D}^0 D_s^+ \pi ^-$ decay and $T_{c\bar{s}0}(2900)^{++}$ in the $D_s^+ \pi ^+$ invariant mass distribution of $B^+ \rightarrow D^- D_s^+ \pi ^+$ decay, we investigate the $T_{c\bar{s}0}(2900)^{++}$ contribution to the $B^+ \rightarrow K^+ D^+ D^-$ decay in a molecular scenario, where we consider $T_{c\bar{s}0}(2900)^{++}$ as a $D^{*+} K^{*+}$ molecular state. Our estimations indicate that the fit fraction of $T_{c\bar{s}0}(2900)^{++}$ in the $B^+ \rightarrow K^+ D^+ D^-$ is about $13\%$, and its signal is visible in the $D^+ K^+$ invariant mass distribution. With the involvement of $T_{c\bar{s}0}(2900)^{++}$, the fit fractions of $\chi _{c0}(3915)$ and $\chi _{c2}(3930)$ may be much different with the ones obtained by the amplitude analysis in Ref. [Aaij et al. Phys. Rev. D 102:112003, 2020], which may shed light on the long standing puzzle of $\chi _{c0}(3915)$ as the conventional charmonium.

1 Introduction

The B meson decay process is the most productive and important platform of searching for the quantum chromodynamics (QCD) exotic states. Two typical types of exotic candidates could be observed in this process. One is the charmonium-like states observed in the invariant mass distributions of a charmonium plus one or more light meson, such as the first observed charmonium-like state, X(3872), which was first observed in the $\pi ^+ \pi ^- J/\psi$ invariant mass distribution of the process $B^\pm \rightarrow K^\pm \pi ^+ \pi ^- J/\psi$ by the Belle Collaboration in the year of 2003 [1], and then confirmed by the BaBar [2,3,4,5,6,7,8,9,10,11], CDF [12,13,14,15], D0 [16], CMS [17,18,19,20,21,22], and LHCb [23,24,25,26,27,28,29,30,31,32,33,34,35,36] Collaborations in the B decay process, as well as the BESIII [37,38,39,40] Collaboration in the electron-positron annihilation process. Besides the charmonium-like states, another type of exotic candidates observed in the B decay processes is the open-charm states with strangeness observed in the invariant mass spectra of a charmed meson and a (anti-)kaon meson or $D_s \pi$, such as $D_{s0}^*(2317)$ and $D_{s1}(2460)$, which were first observed by BaBar [41] and CLEO [42] Collaborations, respectively.

In the year of 2020, the LHCb Collaboration performed the amplitude analysis of the process $B^+ \rightarrow D^- D^+ K^+$ [43, 44], and two new structures with spin-0 (named $X_0(2900)$) and spin-1 (named $X_1(2900)$), were reported in the $D^- K^+$ invariant mass distribution. It should be pointed that those two states were predicted more than ten years ago in Ref. [45]. The masses and widths of these two states are measured to be [43, 44],

$$\begin{aligned} m_{X_0(2900)}= & {} (2866\pm 7\pm 2)~\textrm{MeV}\,\nonumber \\ \Gamma _{X_0(2900)}= & {} (57\pm 12\pm 4)~\textrm{MeV}\,\nonumber \\ m_{X_1(2900)}= & {} (2904\pm 5\pm 1)~\textrm{MeV}\,\nonumber \\ \Gamma _{X_1(2900)}= & {} (110\pm 11\pm 4)~\textrm{MeV}\, \end{aligned}$$

(1)

respectively.

It is interesting to notice that both $X_0(2900)$ and $X_1(2900)$ are fully open-flavor states and their minimal quark components are $\bar{c}\bar{s} u d$, which indicates that $X_0(2900)$ and $X_1(2900)$ could be good candidates of tetraquark states [46,47,48,49,50,51,52,53]. In addition, the observed masses of $X_0(2900)$ and $X_1(2900)$ are close to the threshold of $D^*\bar{K}^*$, then the $D^*\bar{K}^*$ molecular interpretations have been proposed [54,55,56,57,58,59,60,61,62,63].

Recently, the LHCb Collaboration reported two new tetraquark states $T_{c\bar{s}0}(2900)^0$ and $T_{c\bar{s}0}(2900)^{++}$ in the $D_s^+ \pi ^-$ and $D_s^+ \pi ^+$ mass distributions of the $B^0 \rightarrow \bar{D}^0 D_s^+ \pi ^-$ and $B^+ \rightarrow D^- D_s^+ \pi ^+$, respectively [64, 65]. The masses and widths of the $T_{c\bar{s}0}(2900)^0$ and $T_{c\bar{s}0}(2900)^{++}$ are measured to be [64, 65],

$$\begin{aligned} m_{T_{c\bar{s}0}(2900)^{0}}= & {} (2892\pm 14\pm 15)~\textrm{MeV}\,\nonumber \\ \Gamma _{T_{c\bar{s}0}(2900)^{0}}= & {} (119\pm 26\pm 13)~\textrm{MeV}\,\nonumber \\ m_{T_{c\bar{s}0}(2900)^{++}}= & {} (2921\pm 17\pm 20)~\textrm{MeV}\,\nonumber \\ \Gamma _{T_{c\bar{s}0}(2900)^{++}}= & {} (137\pm 32\pm 17)~\textrm{MeV}. \end{aligned}$$

(2)

The resonance parameters of these two states are consistent with each other, which indicates that they are two of isospin triplet. When taking the isospin relationship into consideration, the mass and width of $T_{c\bar{s}0}(2900)$ are fitted to be [64, 65],

$$\begin{aligned} m_{T_{c\bar{s}0}(2900)}= & {} (2908\pm 11\pm 20)~\textrm{MeV}\,\nonumber \\ \Gamma _{T_{c\bar{s}0}(2900)}= & {} (136\pm 23\pm 13)~\textrm{MeV}. \end{aligned}$$

(3)

In addition, the amplitude analysis indicates the quantum numbers of $T_{c\bar{s}0}(2900)$ are $J^P=0^+$.

From the observed processes, one can find the minimal quark components of $T_{c\bar{s}0}(2900)^0$ and $T_{c\bar{s}0}(2900)^{++}$ are $c\bar{s} \bar{u} d$ and $c\bar{s} \bar{d} u$, respectively, which indicates that both $T_{c\bar{s}0}(2900)^0$ and $T_{c\bar{s}0}(2900)^{++}$ are also fully open flavor tetraquark states, and in addition, $T_{c\bar{s}0}(2900)^{++}$ is the first observed doubly charged tetraquark state. These particular properties have stimulated theorists’ great interests. By using the QCD sum rule method, the authors in Refs. [66, 67] investigated the spectrum and strong decay properties of $T_{c\bar{s}0}(2900)$ in the $c\bar{s}q\bar{q}$ tetraquark frame. The estimations in the nonrelativistic quark model indicated that $T_{c\bar{s}0}(2900)$ could be assigned to be the lowest 1S-wave tetraquark states [68]. Considering the flavor symmetry of the light quarks, the authors in Ref. [69] argued that $T_{c\bar{s}0}(2900)^{++}$, $T_{c\bar{s}0}(2900)^{0}$ and $\bar{X}_0(2900)$ should be the members of an $\textrm{SU}_F(3)$ sextet. The production of $T_{c\bar{s}0}(2900)$ in the high energy multi-production processes has been also investigated in Ref. [70] in the tetraquark frame.

In addition, the observed mass of $T_{c\bar{s}0}(2900)$ is close to the threshold of $D^*K^*$. Together with $D_{s0}^*(2317)$ closing to the DK threshold and $D_{s1}(2460)$ closing to the $D^*K$ threshold, the observation of $T_{c\bar{s}0}(2900)$ enriches the exotic candidates near the threshold of a charmed meson and a strange meson. Similar to the cases of $D_{s0}^*(2317)$ and $D_{s1}(2460)$¹, $T_{c\bar{s}0}(2900)$ has also been proposed to be the $D^*K^*$ molecular state with isospin $I=1$. By means of the QCD two-point sum rule, the mass and decay width could be reproduced in the $D^*K^*$ molecular scenario [71]. In the one-boson-exchange model, the authors in Ref. [72] found that the masses of $D_{s0}^{*}(2317)$, $D_{s1}(2460)$ and $T_{c\bar{s}0}(2900)$ could be reproduced. In an effective Lagrangian approach, the decay properties of $T_{c\bar{s}0}(2900)$ were also investigated in Ref. [73]. Besides the resonant interpretations, the $T_{c\bar{s}0}(2900)$ was interpreted as the threshold effect. In addition, in Ref. [74], the authors found that within the $D^*K^*$ and $D_s^* \rho$ coupled-channel interactions, the diagonal terms of the system’s interaction matrix are zero. However, the transition potential between these channels generates an attractive force. Although this attraction is insufficient for binding, it leads to a pronounced cusp. Incorporating the widths of the $\rho$ and $K^*$, this cusp transforms into a peak structure, which can be interpreted as a virtual state, emerging from the interaction of the $D^*K^*$ and $D_s^* \rho$ channels. Moreover, the investigations in Ref. [75] found that $T_{c\bar{s}0}(2900)$ could be simulated by the triangle singularity peak generated from $\chi _{c1} K^*D^*$ loop.

On the experimental side, searching for more decay modes of $T_{c\bar{s}0}(2900)$ can help us to reveal its internal structure [76, 77]. In the $B^+ \rightarrow D^- D^+ K^+$ process where the tetraquark states $X_0(2900)$ and $X_1(2900)$ were observed, the LHCb Collaboration also present the $D^+ K^+$ invariant mass distribution [43, 44]. From the measured data, one can find that the $D^+ K^+$ invariant mass distribution can not be well described in the vicinity of 2.9 GeV and more details can be found in Fig. 10-(c) of Ref. [44], which indicates that some other effects, such as additional resonances, should be taken into account. To further analyse the resonance contributions to $B^+ \rightarrow D^- D^+ K^+$ process, we find,

• Besides the resonance parameters of $T_{c\bar{s}0}(2900)$, the LHCb Collaboration also reported the fit fraction of $T_{c\bar{s}0}(2900)^{++}$ component in the $B^+ \rightarrow D^- D_s^+ \pi ^+$, which is $(1.96\pm 0.87 \pm 0.88)\%$ [64, 65]. In other words, in the $B^+ \rightarrow D^- D_s^+ \pi ^+$ process, the contribution of $T_{c\bar{s}0}(2900)^{++}$ could be non-negligible.

• In the $D^*K^*$ molecular scenario, the decay properties of the $T_{c\bar{s}0}(2900)^0$ were investigated in Ref. [73]. Their estimations indicate that the $T_{c\bar{s}0}(2900)^0$ dominantly decays into $D^0 K^0$, and accordingly $T_{c\bar{s}0}(2900)^{++}$ should dominantly decay into $D^+ K^+$ on account of the isospin symmetry.

Based on the above experimental measurements and theoretical estimations, we can anticipate that the tetraquark state $T_{c\bar{s}0}(2900)^{++}$ should have non-negligible contribution to the process $B^+ \rightarrow K^+ D^+ D^-$.

In addition, the involvement of $T_{c\bar{s}0}(2900)^{++}$ in the process $B^+\rightarrow K^+ D^+ D^-$ may also shed light on another long standing puzzle for $\chi _{c0}(3930)$ as conventional charmonium [78,79,80,81,82,83]. The measurements from the BaBar Collaboration indicated that the branching fraction of $B^+\rightarrow K^+ \chi _{c0}(3930) \rightarrow K^+ J/\psi \omega$ is $(3.0^{+0.7+0.5}_{-0.6-0.3})\times 10^{-5}$ [84], while the branching fraction of $B^+ \rightarrow K^+ \chi _{c0}(3930) \rightarrow K^+ D^+ D^-$ is reported to be $(8.1\pm 3.3)\times 10^{-6}$ [44]. Thus, one can conclude that the branching fraction for $\chi _{c0}(3930)\rightarrow J/\psi \omega$ is about 3.7 times larger than the one of $\chi _{c0}(3930) \rightarrow D^+ D^-$, which is inconsistent with the expectations of the conventional charmonium assignment of $\chi _{c0}(3930)$. If carefully checking the invariant mass distributions of $B^+ \rightarrow K^+ D^+ D^-$ in Ref. [44], one can find that the $\chi _{c0}(3930)$ and $\chi _{c2}(3930)$ states make roughly equal contributions to the peak in the $D^+ D^-$ spectrum. But only one of them, namely $\chi _{c2}(3930)$, plays a role (obviously through reflection) in the $D^+ K^+$ and $D^+ K^-$ spectrums, mainly in the 2.9 GeV region. Then, varying the fit fractions of these states while simultaneously including the $T_{c\bar{s}0}(2900)^{++}$ could lead to similar quality fits, but with rather different physical consequences. Thus, in the present work, we investigate the possible contribution of $T_{c\bar{s}0}(2900)^{++}$ in the process $B^+ \rightarrow D^- D^+ K^+$ in the framework of the molecular scenario, where $T_{c\bar{s}0}(2900)^{++}$ is considered as a $D^{*+} K^{*+}$ molecular state.

This paper is organized as follows. After the introduction, we will show the relevant formalism employed in the present estimations in Sect. 2. Our calculated results and related discussions will be presented in Sects. 3, and 4 will be devoted to a short summary.

Fig. 1

Diagrammatic decay at the quark level for the $B^+ \rightarrow D^- D^{*+} K^{*+}$ reaction

Fig. 2

A sketch diagram of the rescatting of $D^{*+} K^{*+}$ to give the resonance $T_{c\bar{s}0}(2900)^{++}$ (diagram a), and further decay of $T_{c\bar{s}0}(2900)^{++}$ to $D^+ K^+$ (diagram b)

2 Formalism

In the molecular scenario, the $T_{c\bar{s}0}(2900)^{++}$ is considered as a molecular state composed of $D^{*+} K^{*+}$, which is,

$$\begin{aligned} \left| T_{c\bar{s}0}(2900)^{++}\rangle \right. = \left| D^{*+} K^{*+}\rangle \right. . \end{aligned}$$

(4)

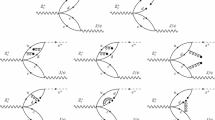
Considering the strong coupling between the molecular state and its components, we only include the $D^*K^*$ loop contributions in the present estimation. Thus the primary reaction that could produce $T_{c\bar{s}0}(2900)^{++}$ should be $B^+ \rightarrow D^- D^{*+} K^{*+}$. As shown in Fig. 1, this reaction proceeds via the $W^+$ internal emission, where the $\bar{b}$ quark transits into $\bar{c}$ quark by emitting a $W^+$ boson, while the $W^+$ boson couples to the $c\bar{s}$ quarks pair. The $\bar{s}$ quark and the u quark from the initial $B^+$ meson form a $K^{*+}$ meson, while the rest $c\bar{c}$ and $d\bar{d}$ created from vacuum hadronize into $D^{-}$ and $D^{*+}$ mesons. In the hadron level, one can construct the S wave component of the transition amplitude by matching the angular momentum of $B^+$ meson [85, 86], which is,

$$\begin{aligned} -i t_1 = -i C_1 {{\varvec{\epsilon }}(D^{*+} ) } \cdot {{\varvec{\epsilon }}(K^{*+} ) }, \end{aligned}$$

(5)

where the $\epsilon (D^{*+} )$ and $\epsilon (K^{*+})$ are the polarization vectors of the $D^{*+}$ and $K^{*+}$, respectively. $C_1$ is an unknown coupling constant, which will be discussed later. Then the $D^{*+}$ and $K^{*+}$ couple to the molecular state $T_{c\bar{s}0}(2900)^{++}$ with $I(J^P)=1(0^+)$ as presented in Fig. 2a. As indicated in Ref. [87], the $D^{*+} K^{*+}$ system could project into different angular momentum, for example, the vertex for $R_{J}\rightarrow D^{*+} K^{*+}$ with $J=0,1,2$ could be constructed as,

$$\begin{aligned} \mathcal {V}^{(0)}= & {} \frac{1}{3} \epsilon _l(D^{*+}) \epsilon _l(K^{*+}) \delta _{ij}, \nonumber \\ \mathcal {V}^{(1)}= & {} \frac{1}{2} \left[ \epsilon _i(D^{*+}) \epsilon _j(K^{*+}) -\epsilon _j(D^{*+}) \epsilon _i(K^{*+}) \right] , \nonumber \\ \mathcal {V}^{(2)}= & {} \frac{1}{2} \left[ \epsilon _i(D^{*+}) \epsilon _j(K^{*+}) +\epsilon _j(D^{*+}) \epsilon _i(K^{*+}) \right] \nonumber \\{} & {} - \frac{1}{3} \epsilon _l(D^{*+}) \epsilon _l(K^{*+}) \delta _{ij}. \end{aligned}$$

(6)

The experimental analysis indicated that the angular momentum of $T_{c\bar{s}0}(2900)$ is zero. Thus, one can obtain the transition amplitude of $B^+ \rightarrow D^- T_{c\bar{s}0}(2900)^{++}$ corresponding to Fig. 2a, which is,

$$\begin{aligned} -i t_{2a}= & {} -i C_1 \epsilon _{\alpha } (D^{*+} ) \epsilon _{\beta } (K^{*+} ) \delta ^{\alpha \beta } \nonumber \\{} & {} G'(M_\textrm{inv}(D^+K^+),m_{D^*},m_{K^*}) \nonumber \\{} & {} \times \frac{1}{3} \epsilon _l^* (D^{*+} ) \epsilon _l^* (K^{*+} ) \delta _{ij} g_{T^{++}_{c\bar{s}0}D^* K^*} \nonumber \\= & {} -i C_1 \delta _{ij} G'(M_\textrm{inv}(D^+K^+),m_{D^*},m_{K^*}) g_{T^{++}_{c\bar{s}0}D^* K^*},\nonumber \\ \end{aligned}$$

(7)

where $\sum \limits _{pol} \epsilon _i (R) \epsilon _j^* (R) = \delta _{ij}$, $R = D^{*+}$ or $K^{*+}$, and the sum over the same indices of the Kronecker delta function is equal to 3, i.e., $\sum \limits _{ij} |\delta _{ij}|^2 = 3$. $G'(M_\textrm{inv}(D^+K^+),m_{D^*},m_{K^*})$ is the loop function of the two-meson $D^*$ and $K^*$, which will be discussed later.

Similarly, one can obtain the transition amplitude of $B^+ \rightarrow D^- T_{c\bar{s}0}(2900)^{++} \rightarrow D^- D^+ K^+$ corresponding to Fig. 2b, which is,

$$\begin{aligned} -it_{2b}= & {} -i C_1 \delta _{ij} G'(M_\textrm{inv}(D^+K^+),m_{D^*},m_{K^*}) \nonumber \\{} & {} \times \frac{g_{T^{++}_{c\bar{s}0}D^* K^*} g_{T^{++}_{c\bar{s}0}D K}}{M^2_\textrm{inv}(D^+K^+) -m^2_{T^{++}_{c\bar{s}0}}+i m_{T^{++}_{c\bar{s}0}}\Gamma _{T^{++}_{c\bar{s}0}}}, \end{aligned}$$

(8)

and then the square of the transition amplitude is,

$$\begin{aligned} \sum |t_{2b}|^2= & {} 3 C_1^2 \ \Big |G'(M_\textrm{inv}(D^+K^+),m_{D^*},m_{K^*}) \Big |^2\ \nonumber \\{} & {} \times \frac{\Big |g_{T^{++}_{c\bar{s}0} D^* K^*}\Big |^2 \Big |g_{T^{++}_{c\bar{s}0} D K}\Big |^2}{\left[ M^2_\textrm{inv}(D^+K^+)-m^2_{T^{++}_{c\bar{s}0}}\right] ^2+ m_{T^{++}_{c\bar{s}0}}^2 \Gamma ^2_{T^{++}_{c\bar{s}0}}},\nonumber \\ \end{aligned}$$

(9)

with $M^2_\textrm{inv}(D^+K^+)=(P_{D^+}+P_{K^+})^2$, and the general two-meson loop function is given by,

$$\begin{aligned}{} & {} G(\sqrt{s},m_1,m_2)\nonumber \\{} & {} \quad =i\int \frac{d^4q}{(2\pi )^4}\frac{1}{q^2-m_1^2+i\epsilon }\frac{1}{(q-P)^2-m_2^2+i\epsilon }, \end{aligned}$$

(10)

with $m_1$ and $m_2$ the masses of the two mesons involved in the loop. q is the four-momentum of the meson in the centre of mass frame, and P is the total four-momentum of the meson-meson system. In the present work, we use the dimensional regularization method as indicated in Ref. [88], and in this scheme, G can be expressed as,

$$\begin{aligned} G(\sqrt{s},m_1,m_2)= & {} \frac{1}{16\pi ^2}\left[ \alpha +\log \frac{m_1^2}{\mu ^2}+\frac{m_2^2-m_1^2+s}{2s}\log \frac{m_2^2}{m_1^2}\right. \nonumber \\{} & {} +\frac{|\vec {q}\,|}{\sqrt{s}}\left( \log \frac{s-m_2^2+m_1^2+2|\vec {q}\,|\sqrt{s}}{-s+m_2^2-m_1^2+2|\vec {q}\,|\sqrt{s}}\right. \nonumber \\{} & {} +\left. \left. \log \frac{s+m_2^2-m_1^2+2|\vec {q}\,|\sqrt{s}}{-s-m_2^2+m_1^2+2|\vec {q}\,|\sqrt{s}}\right) \right] , \end{aligned}$$

(11)

where $s=P^2=M^2_\textrm{inv}(D^+K^+)$, and $\vec {q}\,$ is the three-momentum of the meson in the centre of mass frame, which reads,

$$\begin{aligned} |\vec {q}\,|=\frac{\sqrt{\left[ s-(m_1+m_2)^2\right] \left[ s-(m_1-m_2)^2\right] }}{2\sqrt{s}} , \end{aligned}$$

(12)

here we take $\mu =1500$ MeV and $\alpha =-1.474$, which are the same as those in the study of the $D^*\bar{K}^*$ interaction [85, 86]. Moreover, the width of $K^*$ is about 50 MeV, which could make a contribution to amplitude through the loop function as shown in Fig. 2. So we should take the effect of the finite width of the $K^*$ into consideration by folding the loop function with the $K^*$ spectral function [89, 90],

$$\begin{aligned} F(s_{K^*})=-\frac{1}{\pi }\textrm{Im}\left\{ \frac{1}{s_{K^*}-m^2_{K^*}+im_{K^*}\Gamma _{K^*}}\right\} \end{aligned}$$

(13)

such that

$$\begin{aligned}{} & {} G'(\sqrt{s},m_{D^*},m_{K^*})\nonumber \\{} & {} \quad =\frac{\displaystyle \int ^{(m_{K^*}+2\Gamma _{K^*})^2}_{(m_{K^*}-2\Gamma _{K^*})^2}ds_{K^*}G(\sqrt{s},\sqrt{s}_{K^*},m_{D^*}) F(s_{K^*})}{\displaystyle \int ^{(m_{K^*}+2\Gamma _{K^*})^2}_{(m_{K^*}-2\Gamma _{K^*})^2}ds_{K^*}F(s_{K^*})},\nonumber \\ \end{aligned}$$

(14)

where we take a reasonable interval, $(m_{K^*}\pm 2\Gamma _{K^*})^2$, in the $s_{K^*}$ integration. The effect of the finite width of $K^*$ could be taken into account by replacing the propagator in Eq. (11) with the one in Eq.  (14) in the present work.

Besides the two-meson loop function, two coupling constants $g_{T^{++}_{c\bar{s}0} D^* K^*}$ and $g_{T^{++}_{c\bar{s}0} D K}$ are unknown. In the molecular scenario, the coupling constant $g_{T^{++}_{c\bar{s}0} D^* K^*}$ refers to the coupling between $T_{c\bar{s}0}(2900)^{++}$ and $D^{*+} K^{*+}$, which could be related to the binding energy by [91,92,93],

$$\begin{aligned} g_{T^{++}_{c\bar{s}0} D^{*+} K^{*+}}^2=16 \pi (m_{D^{*+}}+m_{K^{*+}})^2 \tilde{\lambda }^2 \sqrt{\frac{2 \Delta E}{\mu }} , \end{aligned}$$

(15)

where $\tilde{\lambda } =1$ gives the probability to find the molecular component in the physical states, $\Delta E = m_{D^*}+m_{K^*} - m_{T^{++}_{c\bar{s}0}}$ denotes the binding energy, and $\mu = m_{D^*} m_{K^*} / (m_{D^*}+m_{K^*})$ is the reduced mass.

As for $g_{T^{++}_{c\bar{s}0} D K}$, we determine its value by the corresponding partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$, with an effective Lagrangian approach, the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$ could be obtained as,

$$\begin{aligned} \Gamma _{T^{++}_{c\bar{s}0} \rightarrow D^+K^+}= & {} \frac{1}{8\pi } \frac{1}{m^2_{T^{++}_{c\bar{s}0}}} |g_{T^{++}_{c\bar{s}0} D^+ K^+}|^2 |\vec {q}_{K^+}|, \end{aligned}$$

(16)

with

$$\begin{aligned} |\vec {q}_{K^+}|= & {} \frac{\lambda ^{1/2}(m^2_{T^{++}_{c\bar{s}0}},m^2_{D^+},m^2_{K^+})}{2 m_{T^{++}_{c\bar{s}0}}}, \end{aligned}$$

(17)

to be the momentum of $K^+$ in the $T_{c\bar{s}0}(2900)^{++}$ rest frame, and $\lambda (x,y,z)=x^2+y^2+z^2-2xy-2yz-2xz$ is the K$\ddot{\text {a}}$llen function. In the $D^*K^*$ molecular frame, $T_{c\bar{s}0}(2900)$ could transit into DK by exchanging a light unflavored meson, such as $\pi ^0,\ \eta ,\ \eta ^\prime ,\ \rho ^0$, and $\omega$. The estimations in Ref. [73] indicated that the $T_{c\bar{s}0}(2900)^{++}$ dominantly decay into DK, and the partial width of DK channel was estimated to be $(52.6\sim 101.7)$ MeV in the considered parameter range. In the present work, we take the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$ to be 85 MeV to estimate the coupling constant $g_{T_{c\bar{s}0}^{++} D^+K^+}$.

In addition, we would like to compare the above mass distribution with the one of the background for the reaction $B^+ \rightarrow D^- D^+ K^+$. By analogy to Eq. (5), we can obtain the transition matrix for $B^+ \rightarrow D^- D^+ K^+$, which is,

$$\begin{aligned} -i t_3 = -i C_3. \end{aligned}$$

(18)

where $C_3$ is the coupling constant, which will be discussed in the following section.

It should be noted that the interference between different contributions, such as the contributions from non-resonance, and the resonances including the charmonia, $X_{0,1}(2900)$ and $T_{c\bar{s}0}(2900)^{++}$, are important in reproducing the experimental data. Here we take the interference between the $T_{c\bar{s}0}(2900)$ and the background as an example to show how the interference changes the lineshape. After taking the interference into consideration, the $D^+K^+$ invariant mass distribution can be expressed as,

$$\begin{aligned} \frac{d\Gamma }{dM_\textrm{inv} (D^+ K^+)}{} & {} =\frac{1}{(2\pi )^3} \frac{1}{4m^2_{B^+}} p_{D^-} \tilde{p}_{K^+} \nonumber \\{} & {} \quad \sum \left| t_{2b} + C_3 e^{i\phi }\right| ^2, \end{aligned}$$

(19)

where

$$\begin{aligned} p_{{D}^-}= & {} \frac{\lambda ^{1/2}\left( m^2_{B^+},m^2_{D^-},M^2_\textrm{inv}(D^+ K^+)\right) }{2 m_{B^+}}, \nonumber \\ \tilde{p}_{K^+}= & {} \frac{\lambda ^{1/2}\left( M^2_\textrm{inv}(D^+ K^+),m^2_{D^+},m^2_{K^+}\right) }{2 M_\textrm{inv}(D^+ K^+)}, \end{aligned}$$

(20)

and $\phi$ is the phase angle between the resonance and the background. With $C_3=0$, we can obtain the contribution from $T_{c\bar{s}0}(2900)^{++}$, while with $C_1=0$, i.e., $t_{2b}=0$, we can obtain the background contribution.

3 Numerical results and discussions

To calculate the $D^{+} K^{+}$ invariant mass distribution of $B^+\rightarrow K^+ D^+ D^-$ as presented in Eq. (19), the coupling constant $C_1$ is needed. However, the experimental measurement of $B^+ \rightarrow K^{*+} D^{*+} D^{-}$ is not available to date. Similar to $B^{+}\rightarrow K^+ D^+ D^-$, the process $B^+ \rightarrow K^{*+} D^{*+} D^{-}$ should also occur via $W^+$ internal emission process. One can obtain the diagrammatic decay at the quark level for the $B^+ \rightarrow K^+ D^+ D^-$ by replacing $K^{*+}$ and $D^{*+}$ in Fig. 1 with $K^+$ and $D^+$, which indicates some similarities between the processes $B^+ \rightarrow K^+ D^+ D^-$ and $B^+ \rightarrow K^{*+} D^{*+} D^{-}$. However, there are also some differences between these two processes. As indicated in the amplitude analysis of $B^+ \rightarrow K^+ D^+ D^-$ in Ref. [44], the typical resonance contributions to this process are $B^+ \rightarrow K^+ (c\bar{c})\rightarrow K^+ D^+ D^-$, where the charmonia include $\psi (3770)$, $\chi _{c0}(3930)$, $\chi _{c2}(3930)$, $\psi (4040)$, $\psi (4160)$, and $\psi (4415)$. These charmonia contributions should be suppressed due to phase space of the process $B^+ \rightarrow K^{*+} D^{*+} D^-$. In addition to the charmonia contributions, the LHCb Collaboration also observed the signals of $X_{0}(2900)$ and $X_1(2900)$ in the $D^- K^+$ invariant mass spectra, these contributions also vanish in the $B^+ \rightarrow K^{*+} D^{*+} D^{-}$ process. Besides the resonance contributions, the amplitude analysis also indicates sizable nonresonant contribution, which should be the same for both $B^+ \rightarrow K^+ D^+ D^-$ and $B^+ \rightarrow K^{*+} D^{*+} D^{-}$, thus, in the present work, we first estimate the background distribution of $B^+\rightarrow K^+ D^+ D^-$ with the branching fraction of the nonresonant contribution from LHCb analysis, which is $(5.3 \pm 1.8)\times 10^{-5}$ [94]. From Eqs. (18) and (19), one can determine the coupling constant $C_3$. Considering the similarity between $B^+ \rightarrow K^+ D^+ D^-$ and $B^+ \rightarrow K^{*+} D^{*+} D^{-}$, we consider $C_1$ and $C_3$ are similar, and then roughly estimate the $D^+ K^+$ invariant mass distribution resulted from $T_{c\bar{s}0}(2900)^{++}$.

Fig. 3

The $D^+ K^+$ invariant mass distribution for the $B^+ \rightarrow D^- D^+ K^+$ reaction with the assumption $C_1=C_3$. The black data points with error bar are the LHCb measurements from Fig.10-(c) of Ref. [44]. The magenta-dotted and black-dashed curves are the nonresonant contribution determined by the LHCb amplitude analysis and our estimated background, respectively. The red-solid curve is the resonant contribution from $T_{c\bar{s}0}(2900)^{++}$, the orange band corresponds to the uncertainties resulted from the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$, and the blue band corresponds to the total uncertainties resulted from both the $T_{c\bar{s}0}(2900)^{++}$ width and the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$. The black-dashed and red-solid curves are obtained by calculating Eq. (19) with $C_1=0$ and $C_3=0$, respectively

With the above formalism, we can evaluate the $D^+ K^+$ invariant mass distribution by assuming the values of $C_1$ and $C_3$ are the same for the first step. In Fig. 3, we present the individual contributions from the background and $T_{c\bar{s}0}(2900)^{++}$. To further compare with the experimental measurements, we normalize the background contribution to the LHCb experimental nonresonant contribution in Fig. 3, where the magenta-dash-dotted and black-dashed curves are the nonresonant contribution determined by the LHCb amplitude analysis and our estimated background, respectively. The red-solid curve is the resonant contribution from $T_{c\bar{s}0}(2900)^{++}$, which is obtained with the resonance parameters of $m_{T_{c\bar{s}0}^{++}}=2885 \ \textrm{MeV}$ and $\Gamma _{T_{c\bar{s}0}^{++}}=136 \ \textrm{MeV}$. While the orange band corresponds to the uncertainties of the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$ and the blue band corresponds to the total uncertainties of the $T_{c\bar{s}0}(2900)^{++}$ width and the partial width of $T_{c\bar{s}0}(2900)^{++} \rightarrow D^+ K^+$. From Fig. 3, one can find that the $D^+K^+$ invariant mass distribution around 2.9 GeV can not be well described by LHCb fit [44], which indicates that there should be an additional sources in the $B^+ \rightarrow D^+ D^- K^+$. Our results show that the $T_{c\bar{s}0}(2900)^{++}$ plays an important role in this region, thus we suggest that contribution from the $T_{c\bar{s}0}(2900)^{++}$ should be considered in the future amplitudes analysis.

Furthermore, we can integrate the invariant mass $M_\textrm{inv} (D^+ K^+)$ over the whole invariant mass range for the signal and background, and their ratio is given by,

$$\begin{aligned} R=\frac{\int \frac{d\Gamma }{dM_\textrm{inv} (D^+ K^+)}}{\int \frac{d\Gamma _{bac}}{dM_\textrm{inv} (D^+ K^+)}} \simeq 0.55^{+0.05}_{-0.06}, \end{aligned}$$

(21)

where the uncertainties are resulted from the $T_{c\bar{s}0}(2900)^{++}$ width and the partial width of $T_{c\bar{s}0}(2900)^{++}\rightarrow D^+ K^+$ as well. With the nonresonant fit fraction obtained by the amplitude analysis, we can roughly estimate the fit fraction of $B^+\rightarrow T_{c\bar{s}0}(2900)^{++}D^-\rightarrow D^+D^-K^+$ to be about $13\%$, which is greater than that of $\chi _{c0}(3930)$ and $\chi _{c2}(3930)$. Thus, the involvement of $T_{c\bar{s}0}(2900)^{++}$ will certainly influence the fit fractions of $\chi _{c0}(3930)$ and $\chi _{c2}(3930)$.

Fig. 4

The $D^+ K^+$ invariant mass distribution for the $B^+ \rightarrow D^- D^+ K^+$ reaction calculated by Eq. (19) with the assumption $C_1=C_3$ and the phase angle $\phi =0, \pi /3, 2\pi /3$, and $\pi$ respectively

As shown in Eq. (19), the interference between the contributions from $T_{c\bar{s}0}(2900)$ and the background should be important in reproducing the experimental data. Here, we take several typical values of $\phi$, which are 0, $\pi /3$, $2\pi /3$, and $\pi$, respectively, to show the interference effect to the lineshape of $D^+ K^+$ invariant mass distribution. The corresponding results are shown in Fig. 4, where one can find that the peak shifts from 2866 to 2928 MeV with $\phi$ increasing from 0 to $\pi$.

Fig. 5

The same as Fig. 4 but with the phase angle $\phi = 0$ and $C_1/C_3=2.0$, 1.5, 1.0, and 0.5, respectively

Moreover, in the above estimations, the assumption $C_1/C_3 = 1$ is adopted. In the following, we further discuss the uncertainty resulted from the deviation of $C_1$ from $C_3$. In Ref. [85], $X_0(2900)$ has been investigated as a $D^{*}\bar{K}^{*}$ molecular state, the couplings ratio of $\bar{B}^0 \rightarrow K^- D^{*+} K^{*0}$ and $\bar{B}^0 \rightarrow K^0 D^+ K^-$ is $C'/C'' \simeq 2$. Here, we take several typical values of $C_1/C_3$, which are 0.5, 1.0, 1.5, and 2.0, to check the lineshape of $D^+K^+$ invariant mass distributions depending on the value of $C_1/C_3$ as shown in Fig. 5, where the interference between $T_{c\bar{s}0}(2900)^{++}$ and the background is also included. The lineshapes show that the peak of $T_{c\bar{s}0}(2900)^{++}$ is very clear in a large range of $C_1/C_3$.

Fig. 6

The $D^+K^+$ invariant mass distribution for the $B^+ \rightarrow D^- D^+ K^+$ reaction calculated by Eq. (19) with the fitted $C_1/C_3$ and $\phi$. The other explanations are same as Fig. 3

When considering the interference, we find that the peak position could be shifted with different phase angle. Here, we perform a fit to the LHCb data in the range of $2.7\sim 3.0$ GeV, and one can obtain the values of parameters are $C_1/C_3=1.28\pm 0.51$, $\phi =(6.21\pm 0.33)\times 10^{-5}$. With the center values of the fitted parameters, we present the $D^+K^+$ invariant mass distributions in Fig. 6, and find the interference lineshape is comparable with the experimental data around 2.9 GeV.

4 Summary

Recently, the LHCb Collaboration reported their amplitude analysis of the decays $B^0 \rightarrow \bar{D}^0 D_s^+ \pi ^-$ and $B^+ \rightarrow D^- D_s^+ \pi ^+$, where two tetraquark states $T_{c\bar{s}0}(2900)^{0}$ and $T_{c\bar{s}0}(2900)^{++}$ were reported in the $D_s \pi$ invariant mass distributions. The resonance parameters of these two resonances indicate that they are two of the isospin triplet. Similar to $T_{c\bar{s}0}(2900)$, the LHCb Collaboration reported another two tetraquark candidates $X_{0,1}(2900)$ in the $D^- K^+$ invariant mass distribution in the $B^+ \rightarrow D^- D^+ K^+$ reaction in the year of 2020  [43, 44]. In the $D^+ K^+$ invariant mass distribution of the $B^+ \rightarrow D^- D^+ K^+$ reaction, we find that the experimental data of the $D^+K^+$ invariant mass distribution around 2.9 GeV can not be well described, which indicates that there should be an additional resonance contributing to this process. Inspired by the recent observation of the $T_{c\bar{s}0}(2900)$ [64, 65] and the decay properties of $T_{c\bar{s}0}(2900)$, we find that $T_{c\bar{s}0}(2900)^{++}$ is likely to contribute to the $D^+ K^+$ invariant mass distribution. Thus, in the present work we study the role of $T_{c\bar{s}0}(2900)^{++}$ in the $D^+ K^+$ invariant mass distribution of the process $B^+ \rightarrow D^- D^+ K^+$.

In the present work, we estimate $T_{c\bar{s}0}(2900)^{++}$ contribution to the process $B^+ \rightarrow D^- D^+ K^+$ in a molecular scenario, where we have considered $T_{c\bar{s}0}(2900)^{++}$ as a $D^{*+} K^{*+}$ molecular state. However, due to the lack of the experimental information of $B^+ \rightarrow D^- D^{*+} K^{*+}$, we have made an assumption that the coupling constant for $B^+ \rightarrow D^- D^{*+} K^{*+}$ is similar to the one for nonresonant contribution in $B^+ \rightarrow D^- D^{ +} K^{+}$. Based on this assumption, our estimations indicate that the contribution from $T_{c\bar{s}0}(2900)^{++}$ is significant in the process $B^+ \rightarrow D^- D^+ K^+$, and the $T_{c\bar{s}0}(2900)^{++}$ signal in the $D^+ K^+$ invariant mass distribution is visible. In addition, the fit fraction of $B^+ \rightarrow D^- T_{c\bar{s}0}(2900)^{++}\rightarrow K^+ D^+ D^-$ is roughly estimated to be $13\%$, which could be tested by further experimental analysis by the LHCb Collaboration.

Before the end of this work, it is worth mentioning that the branching fractions of $B^0 \rightarrow D^- D^0 K^+$ and $B^0 \rightarrow D^- D^+ K^0$ decays are $( 1.07 \pm 0.07 \pm 0.09 ) \times 10^{-3}$ and $( 0.75 \pm 0.12 \pm 0.12 ) \times 10^{-3}$, respectively [94]. In the $D^0 K^+$ invariant mass distributions of these process, there should be the signal of $T_{c\bar{s}0}(2900)^+$, which can be accessible for the LHCb Collaboration.