$Z_c(4200)^+$ decay width as a charmonium-like tetraquark state

Abstract

To identify the nature of the newly observed charged resonance $Z_c(4200)^+$, we study its hadronic decays $Z_c(4200)^+\rightarrow J/\psi \pi ^+, Z_c(4200)^+\rightarrow \eta _c\rho ^+$ and $Z_c(4200)^+\rightarrow D^+\bar{D}^{*0}$ as a charmonium-like tetraquark state. In the framework of the QCD sum rules, we calculate the three-point functions and extract the coupling constants and decay widths for these interaction vertices. Including all these channels, the full decay width of the $Z_c(4200)^+$ state is consistent with the experimental value reported by the Belle Collaboration, supporting the tetraquark interpretation of this state.

1 Introduction

Recently, a new charged charmonium-like resonance $Z_c(4200)^+$ was observed by the Belle Collaboration [1]. It was observed in the $Z_c(4200)^+\rightarrow J/\psi \pi ^+$ process with the mass and decay width $M=4196^{+31+17}_{-29-13}$ MeV and $\varGamma =370^{+70+70}_{-70-132}$ MeV, with a significance of $6.2\sigma$. Its preferred assignment of the quantum numbers is $J^P=1^+$. The G-parity of $Z_c(4200)^+$ is positive. Thus, the quantum numbers of its neutral partner is $I^GJ^{PC}=1^+1^{+-}$.

The family of the charged charmonium-like states have become more abundant after the discovery of $Z_c(4200)^+$ [1] and $Z_c(4050)$ [2]. Before this, the first member $Z(4430)^+$ was observed in the $\psi (2S)\pi ^+$ invariant mass spectrum in the process $\bar{B}^0\rightarrow \psi (2S)\pi ^+K^-$ by the Belle Collaboration [3] and confirmed recently by the LHCb Collaboration [4]. Later, Belle also reported a broad doubly peaked structure in the $\pi ^+\chi _{c1}$ invariant mass distribution, of which the peaks are called $Z(4050)^+$ and $Z(4250)^+$ [5]. Several other similar charged states were observed in last two years. In 2013, the BESIII Collaboration reported $Z_c(3900)^+$ in $J/\psi \pi ^+$ final states in the process $Y(4260)\rightarrow J/\psi \pi ^+\pi ^-$ [6]. $Z_c(3900)^+$ was also observed by Belle [7] and confirmed in CLEO data [8]. The BESIII Collaboration also observed $Z_c(4025)^{\pm }$ in the $\pi ^{\mp }$ recoil mass spectrum in the $e^+e^-\rightarrow (D^{*}\bar{D}^{*})^{\pm }\pi ^{\mp }$ process [9] and $Z_c(4020)^{\pm }$ in the $h_c\pi ^{\pm }$ mass spectrum in the process $e^+e^-\rightarrow h_c\pi ^+\pi ^-$ [10]. Moreover, the Belle Collaboration also observed two charged bottomonium-like states $Z_b(10610)$ and $Z_b(10650)$ in the $\pi ^{\pm }\varUpsilon (nS)$ and $h_b\pi ^{\pm }$ mass spectra in the $\varUpsilon (5S)$ decay [11].

These newly observed charged states have the exotic flavor contents $c\bar{c}u\bar{d}$ for $Z_c$ states and $b\bar{b}u\bar{d}$ for $Z_b$ states. It is natural to understand them as different manifestations of four-quark states: hadron molecules [12–18], tetraquark states [19–21], or many other configurations [22–24]. For example, $Z(4430)^+$ was described as a $D^{*}\bar{D}_1$ molecular state in Refs. [25–28] and a tetraquark state in Refs. [29–31]; the $Z_c(3900)^+$ was speculated to be a molecular state in Refs. [32–34]; the $Z_c(4025)^+$ was interpreted as a $D^*\bar{D}^*$ molecular state in Ref. [35]; the $Z_b(10610)$ and $Z_b(10650)$ were studied as $\bar{B}B^{*}$ and $\bar{B}^{*}B^{*}$ molecular states in Ref. [36]. One can consult Refs. [37–42] and references therein for recent reviews of these charged resonances.

Being composed of a diquark and antidiquark pair, a hidden-charm tetraquark state can decay very easily into a pair of open-charm D mesons or one charmonium state plus a light meson through quark rearrangement, implying that tetraquark states should be very broad resonances, while the experimental XYZ states are usually quite narrow, such as $Z_c(3900)^+$ [6–8] and $Z_c(4025)^+$ [9, 10]. However, the experimental width value of the $Z_c(4200)^+$ [1] is broad enough to be a good tetraquark candidate. In Ref. [43], $Z_c(4200)^+$ was studied as a tetraquark state by considering the color-magnetic interaction. In Ref. [44], the authors tried to search for $Z_c^+$ exotic states in lattice QCD. However, they found no convincing signal for $Z_c^+$ state below 4.2 GeV.

The hidden-charm tetraquark states with $J^{PC}=1^{+-}$ has been studied using the method of QCD sum rule in Refs. [24, 45–50]. We have also done similar QCD sum-rule studies in Refs. [51, 52], in which the extracted mass was found to be consistent with the experimental value of the $Z_c(4200)^+$ mass. In this work, we will study the hadronic decays of the $Z_c(4200)^+$ as a tetraquark state in QCD sum rules. The three-point functions for the $Z_cJ/\psi \pi , Z_c\eta _c\rho$, and $Z_cDD^{*}$ vertices will be studied to calculate the corresponding coupling constants needed to extract the decay widths.

This paper is organized as follows. In Sect. 2, we study the three-point functions for the $Z_cJ/\psi \pi$, $Z_c\eta _c\rho$ and $Z_cDD^{*}$ vertices. We will calculate the operator product expansion (OPE) series up to dimension five condensates. Then we compute the coupling constants and the decay widths for these channels. Finally, we give a short summary and discuss the possibility of searching for such exotic resonances decaying into $\eta _c$ charmonium.

2 QCD sum rules and three-point correlation function

In the past several decades, QCD sum rule has proven to be a very powerful non-perturbative approach to study hadron properties such as masses, magnetic moments and coupling constants, associated with the low-lying baryons and mesons [53–57]. Recently, this method was used to yield predictions on the spectroscopy of the new hadron XYZ states [24, 39, 45–52, 58].

To calculate the decay width of the $Z_c(4200)$ meson into two hadrons, one needs first to study the three-body coupling vertices $Z_c(4200)AB$, where A, B denote the decay products. In QCD sum rules, we consider the three-point correlation function

$$\begin{aligned}&\varPi _{\mu \nu }(p, p^{\prime }, q)\nonumber \\&\quad = \int \mathrm{d}^4x\mathrm{d}^4y \,e^{ip^{\prime } \cdot x}e^{iq \cdot y}\,\langle 0|T[J^A(x)J^B(y)J_{\nu }^{Z_c\dag }(0)]|0\rangle , \end{aligned}$$

(1)

where $J_{\nu }^{Z_c}$ is the interpolating current for the $Z_c(4200)^+$ meson while $J^A$ and $J^B$ are the currents for the final states A and B, respectively. In this paper, we consider the $Z_c(4200)^+$ meson as a charmonium-like tetraquark state. The corresponding tetraquark current is given by

$$\begin{aligned} J_{\nu }^{Z_c}&=u^T_{a}C\gamma _5c_{b}(\bar{d}_{a}\gamma _{\nu }C\bar{c}^T_{b}+\bar{d}_{b}\gamma _{\nu }C\bar{c}^T_{a})\nonumber \\&\quad - u^T_{a}C\gamma _{\nu }c_{b}(\bar{d}_{a}\gamma _{5}C\bar{c}^T_{b}+\bar{d}_{b}\gamma _{5}C\bar{c}^T_{a}), \end{aligned}$$

(2)

in which the subscripts a, b are color indices, and u, d, and c represent up, down, and charm quarks, respectively. C is the charge-conjugation matrix. We have studied this charmoniun-like tetraquark scenario and the extracted mass is around 4.16 GeV [51] consistent with the observed mass of the $Z_c(4200)^+$ meson [1]. This current can couple to the $Z_c(4200)^+$ meson via

$$\begin{aligned} \langle 0|J_{\nu }^{Z}|Z_c(p)\rangle =f_{Z}\epsilon _{\nu }(p), \end{aligned}$$

(3)

in which $\epsilon _{\nu }(p)$ is a polarization vector and $f_Z$ is the coupling constant of the current to the physical state.

The $Z_c(4200)$ meson can decay into several different channels such as hidden-charm decay modes $J/\psi \pi ^+, \eta _c\rho ^+$, and open-charm decay modes $D^+\bar{D}^{*0}, \bar{D}^0D^{*+}$. Such decay properties are similar to those for the charmonium-like state $Z_c(3900)$. Assuming $Z_c(3900)$ to be a tetraquark state with the same quantum numbers as the $Z_c(4200)$, the hadronic decay modes of $Z_c(3900)$ to $J/\psi \pi ^+, \eta _c\rho ^+, D^+\bar{D}^{*0}$, and $\bar{D}^0D^{*+}$ were studied in Ref. [47]. Building upon these methods, we will study the same decay channels for the $Z_c(4200)$ tetraquark state to estimate its decay width.

2.1 Decay mode $Z_c^+(4200)\rightarrow J/\psi \pi ^+$

In this subsection, we study the hidden-charm decay $Z_c^+(4200)\rightarrow J/\psi \pi ^+$, in which mode the $Z_c^+(4200)$ meson was observed. To calculate the three-point function in Eq. (1) for the vertex $Z_c^+(4200)J/\psi \pi ^+$, we need the interpolating currents for $J/\psi$ and $\pi$ mesons

$$\begin{aligned} J_{\mu }^{\psi }= & {} \bar{c}_a\gamma _{\mu }c_a, \end{aligned}$$

(4)

$$\begin{aligned} J^{\pi }= & {} \bar{d}_a\gamma _5 u_a, \end{aligned}$$

(5)

which can couple to the $J/\psi$ and $\pi$ mesons, respectively, via the following relations:

$$\begin{aligned} \langle 0|J_{\mu }^{\psi }|J/\psi (p^{\prime })\rangle= & {} f_{\psi }\epsilon _{\mu }(p^{\prime }),\end{aligned}$$

(6)

$$\begin{aligned} \langle 0|J^{\pi }|\pi (q)\rangle= & {} f_{\pi }^{\prime }=\frac{2i\langle \bar{q}q\rangle }{f_{\pi }}, \end{aligned}$$

(7)

where $f_{\psi }$ and $f_{\pi }^{\prime }$ are coupling constants. Using these relations and Eq. (3), we can write down the three-point function in the phenomenological side

$$\begin{aligned}&\varPi _{\mu \nu }^{\psi \pi }(p, p^{\prime }, q)\nonumber \\&\quad =\int \mathrm{d}^4x\mathrm{d}^4y \,e^{ip^{\prime } \cdot x}e^{iq \cdot y}\,\langle 0|T[J_{\mu }^{\psi }(x)J^{\pi }(y)J_{\nu }^{Z\dag }(0)]|0\rangle \nonumber \\&\quad = g_{Z\psi \pi }g_{\mu ^{\prime }\nu ^{\prime }}\left( g_{\mu \mu ^{\prime }}{-}\frac{p^{\prime }_{\mu }p^{\prime }_{\mu ^{\prime }}}{m_{\psi }^2}\right) \left( g_{\nu \nu ^{\prime }}-\frac{p_{\nu }p_{\nu ^{\prime }}}{m_{Z}^2}\right) \nonumber \\&\qquad \times \frac{f_{\psi }({-}if_{\pi }^{\prime })f_{Z}}{(p^2-m^2_{Z}{+}i\epsilon )(p^{\prime 2}{-}m^2_{\psi }{+}i\epsilon )(q^2-m^2_{\pi }+i\epsilon )}+\cdots \nonumber \\&\quad =\frac{g_{Z\psi \pi }(q^2)f_{\psi }(-if_{\pi }^{\prime })f_{Z}}{(p^2-m^2_{Z}+i\epsilon )(p^{\prime 2}-m^2_{\psi }+i\epsilon )(q^2-m^2_{\pi }+i\epsilon )}\nonumber \\&\qquad \times \left( g_{\mu \nu }-\frac{q_{\mu }p^{\prime }_{\nu }+q_{\mu }q_{\nu }}{m_Z^2}-\frac{p^{\prime }_{\mu }p^{\prime }_{\nu }}{m_{\psi }^2}\right. \nonumber \\ {}&\qquad \left. + \frac{p^{\prime }\cdot q(p^{\prime }_{\mu }p^{\prime }_{\nu }+q_{\nu }p^{\prime }_{\mu })}{m_Z^2m_{\psi }^2}\frac{}{}\right) +\cdots , \end{aligned}$$

(8)

in which “...” represents the contributions of all higher excited states. We have used the relation $p=p^{\prime }+q$ in the last step. The coupling constant (form factor) $g_{Z\psi \pi }(q^2)$ is defined via

$$\begin{aligned} \mathcal {L}=g_{Z\psi \pi }g^{\mu \nu }Z_{c\nu }^{+}\pi ^-\psi _{\mu }+h.c.. \end{aligned}$$

(9)

In Eq. (8), the three-point function $\varPi _{\mu \nu }^{\psi \pi }(p, p^{\prime }, q)$ is divergent at $q^2=0$ when we take the limit $m_{\pi }=0$. To simplify the calculation in OPE side, we establish a sum rule at the massless pion-pole, which was first suggested in Ref. [54] for the pion nucleon coupling constant.

At the quark–gluon level, the three-point function in Eq. (1) can be evaluated via the OPE method. We insert the three currents, Eqs. (2), (4) and (5), into the three-point function, Eq. (8), and do the Wick contraction:

$$\begin{aligned}&\langle 0|T[J_{\mu }^{\psi }(x)J^{\pi }(y)J_{\nu }^{Z\dag }(0)]|0\rangle \nonumber \\&\quad = -\mathbf{Tr} [ S^c_{ab'}(x)\gamma _{5} S^{'u}_{ba'}(y)\gamma _5 S^{'d}_{a'b}(-y)\gamma _{\nu }S^c_{b'a}(-x)\gamma _{\mu }]\nonumber \\&\qquad -\mathbf{Tr} [ S^c_{ab'}(x)\gamma _{5} S^{'u}_{ba'}(y)\gamma _5 S^{'d}_{b'b}(-y)\gamma _{\nu }S^c_{a'a}(-x)\gamma _{\mu }]\nonumber \\&\qquad -\mathbf{Tr} [ S^c_{ab'}(x)\gamma _{\nu } S^{'u}_{ba'}(y)\gamma _5 S^{'d}_{a'b}(-y)\gamma _{5}S^c_{b'a}(-x)\gamma _{\mu }]\nonumber \\&\qquad -\mathbf{Tr} [ S^c_{ab'}(x)\gamma _{\nu } S^{'u}_{ba'}(y)\gamma _5 S^{'d}_{b'b}(-y)\gamma _{5}S^c_{a'a}(-x)\gamma _{\mu }], \end{aligned}$$

(10)

where the subscripts $a, b, a^{\prime }$, and $b^{\prime }$ are color indices, and the superscripts u, d, and c denote the quark propagators for up, down, and charm quark, respectively. Throughout our evaluation, we use the coordinate-space expression for the light quark propagator and momentum-space expression for the heavy quark propagator [54, 59]:

(11)

(12)

where $m_c$ is the mass of the charm quark. We neglect the chirally suppressed contributions from the current quark masses ($m_q=0$ in the chiral limit) because they are numerically insignificant. In Eq. (10), the light quark propagator is defined as $iS_{ab}^{'q}(x)=C(iS_{ab}^q)^TC$ in which T represents only the transpose operation to the Dirac indices. As indicated above, we will pick out the $1/q^2$ terms in the OPE series and work at the limit $q^2\rightarrow 0$. We note that this is the assumption used in Ref. [54], and then we can establish a sum rule by comparing with the three-point function expression of Eq. (8) at the hadron level.

Fig. 1

Feynman diagrams for the leading order contributions of the three-point function. Wave lines depict vector and axial-vector mesons, dashed lines pion, solid lines quarks and curly lines gluons. Graphs related by symmetry are not shown

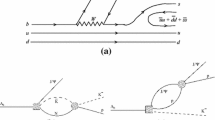
On the phenomenological side in Eq. (8), there are five different tensor structures $g_{\mu \nu }, q_{\mu }q_{\nu }, q_{\mu }p^{\prime }_{\nu }, q_{\nu }p^{\prime }_{\mu }$, and $p^{\prime }_{\mu }p^{\prime }_{\nu }$. On the QCD side, we evaluate the three-point function and spectral density up to the dimension five terms. In addition to the perturbative term, we calculate the quark condensate, the gluon condensate and the quark–gluon mixed condensate for the power corrections. The Feynman diagrams for these terms are shown in Fig. 1. In our result for the OPE series, the $g_{\mu \nu }$ structure contributes to all expansion terms including the perturbative part, quark condensate, gluon condensate and quark–gluon mixed condensate. Other tensor structures contribute just some of these terms in the OPE at leading order. For example, the $q_{\mu }q_{\nu }$ and $q_{\nu }p^{\prime }_{\mu }$ structures appear only in the gluon condensate while $p^{\prime }_{\mu }p^{\prime }_{\nu }$ appears in the perturbative term and the gluon condensate. The structure $q_{\mu }p^{\prime }_{\nu }$ gives no contributions to the perturbative term.

To obtain the greatest number of terms in the OPE series, we therefore study the $g_{\mu \nu }$ structure in the following analysis. Finally, we obtain the spectral density proportional to $1/q^2$ in the $g_{\mu \nu }$ structure

$$\begin{aligned} \rho (s)=-\frac{\langle g_s^2GG\rangle (s+2m_c^2)}{192\pi ^4}\sqrt{1-\frac{4m_c^2}{s}}, \end{aligned}$$

(13)

where we find that only the gluon condensate gives contributions to the spectral density at order $1/q^2$. There are three kinds Feynman diagrams for the gluon condensate in Fig. 1, in which the third one is color connected and the former two are color disconnected [47]. In our caculation, the spectral density in Eq. (13) comes from only the first color-disconnected diagram in Fig. 1. The second color-disconnected diagram and the color-connected diagrams give no contribution to $\rho (s)$.

To establish a sum rule for the coupling constant $g_{Z\psi \pi }$, we assume $p^2=p^{\prime 2}=P^2$ in Eq. (8) and then perform the Borel transform ($P^2\rightarrow M_B^2$) to suppress the higher state contributions. For the $g_{\mu \nu }$ structure, we arrive at the sum rule

$$\begin{aligned}&g_{Z\psi \pi }(s_0, M_B^2)|_{Q^2\rightarrow 0}\nonumber \\&\quad =\frac{1}{f_{\psi }(-if^{\prime }_{\pi })f_{Z}}\frac{m^2_{Z}-m^2_{\psi }}{e^{-m^2_{\psi }/M_B^2}-e^{-m^2_{Z}/M_B^2}}\nonumber \\&\qquad \times \,\int _{4m_c^2}^{s_0}\rho (s)e^{-s/M_B^2}\mathrm{d}s, \end{aligned}$$

(14)

in which $Q^2=-q^2$ and $s_0$ is the continuum threshold parameter for the $Z_c(4200)$ meson.

To perform the QCD sum-rule numerical analysis, we use the following values of quark masses and various condensates [37, 54, 60, 61]:

$$\begin{aligned} \begin{aligned}&m_c(\mu =m_c)=\overline{m}_c=(1.275\pm 0.025)\,\text{ GeV },\\&\langle \bar{q}q\rangle =-(0.23\pm 0.03)^3\text { GeV}^3,\\&\langle \bar{q}g_s\sigma \cdot Gq\rangle =-M_0^2\langle \bar{q}q\rangle ,\\&M_0^2=(0.8\pm 0.2)\text { GeV}^2,\\&\langle g_s^2GG\rangle =(0.48\pm 0.14)\text { GeV}^4, \end{aligned} \end{aligned}$$

(15)

in which the charm quark mass is the running mass in the $\overline{\mathrm{MS}}$ scheme. Note that there is a minus sign implicitly included in the definition of the coupling constant $g_s$ in this work. We use the following values of the hadron parameters [1, 37, 51, 54]:

$$\begin{aligned} \begin{aligned}&m_{\psi }=(3.097\pm 0.011)~\text{ GeV },\\&f_{\psi }=(1.288\pm 0.037)~\text{ GeV }^2,\\&m_{\pi }=139.6~\text{ MeV },\quad f_{\pi }=133~\text{ MeV },\\&m_{Z_c}=(4.196^{+0.048}_{-0.042})~\text{ GeV },\\&f_{Z_c}=(6.9\pm 0.4)\times 10^{-3}~\text{ GeV }^5, \end{aligned} \end{aligned}$$

(16)

in which the coupling parameter $f_{Z_c}$ is determined by the mass sum rules in Ref. [51].

In Eq. (14), the coupling constant $g_{Z\psi \pi }(q^2)$ depends on the continuum threshold value $s_0$ and the Borel mass $M_B$ in the limit $q^2\rightarrow 0$. We use the continuum threshold value $s_0=21$ GeV$^2$, which is the same value as used in the mass sum rule in Ref. [51]. Using this value of $s_0$ and the parameters given in Eqs. (15) and (16), we show the variation of the coupling constant $g_{Z\psi \pi }$ with the Borel parameter $M_B^2$ in Fig. 2. We find that the sum rule gives a minimum (stable) value of the coupling constant $g_{Z\psi \pi }=(6.27\pm 1.93)$ GeV with $M_B^2\sim 1.9$ GeV$^2$. The errors come from the uncertainties of the charm quark mass, the gluon condensate, hadron masses and hadron couplings.

Fig. 2

Coupling constant $g_{Z\psi \pi }$ dependence on the Borel parameter $M_B^2$

To calculate the decay width of a process $A\rightarrow BC$, we use the following relation, given by Refs. [47, 62]:

$$\begin{aligned}&\varGamma (A\rightarrow BC)=\frac{p^*(m_A, m_B, m_C)}{8\pi m_A^2} \nonumber \\&\quad \times \frac{g^2_{ABC}}{3} \left( 3+\frac{p^*(m_A, m_B, m_C)^2}{m_B^2}\right) , \end{aligned}$$

(17)

where $g_{ABC}$ is the coupling of the three-point vertex ABC and $p^*(m_A, m_B, m_C)$ is defined as

$$\begin{aligned} p^*(a, b, c)=\frac{\sqrt{a^4+b^4+c^4-2a^2b^2-2b^2c^2-2c^2a^2}}{2a}. \end{aligned}$$

(18)

For the decay mode $Z_c^+(4200)\rightarrow J/\psi \pi ^+$, we then can calculate its decay width using Eq. (17)

$$\begin{aligned} \varGamma (Z_c^+(4200)\rightarrow J/\psi \pi ^+)=(87.3\pm 47.1)\,\text{ MeV }, \end{aligned}$$

(19)

in which the dominate error source is the uncertainty of the gluon condensate.

2.2 Decay mode $Z_c^+(4200)\rightarrow \eta _c\rho ^+$

We study the decay mode $Z_c^+(4200)\rightarrow \eta _c\rho ^+$ in this subsection. To calculate the corresponding three-point function, we consider the following interpolating currents for $\eta _c$ and $\rho$ mesons:

$$\begin{aligned} J^{\eta _c}&=\bar{c}_a\gamma _{5}c_a, \end{aligned}$$

(20)

$$\begin{aligned} J_{\mu }^{\rho }&=\bar{d}_a\gamma _{\mu } u_a, \end{aligned}$$

(21)

with the current-meson coupling relation

$$\begin{aligned} \langle 0|J^{\eta _c}|\eta _c(p^{\prime })\rangle&=f^{\prime }_{\eta _c}=-i\frac{f_{\eta _c}m_{\eta _c}^2}{2m_c},\end{aligned}$$

(22)

$$\begin{aligned} \langle 0|J_{\mu }^{\rho }|\rho (q)\rangle&=f_{\rho }\epsilon _{\mu }(q), \end{aligned}$$

(23)

where $f_{\eta _c}$ and $f_{\rho }$ are coupling constants for $\eta _c$ and $\rho$, respectively. Then we can obtain the three-point function at the hadron level

$$\begin{aligned}&\varPi _{\mu \nu }^{\eta _c\rho }(p, p^{\prime }, q) \nonumber \\&\quad =\int \mathrm{d}^4x\mathrm{d}^4y \,e^{ip^{\prime } \cdot x}e^{iq \cdot y}\,\langle 0|T[J^{\eta _c}(x)J^{\rho }_{\mu }(y)J_{\nu }^{Z\dag }(0)]|0\rangle \nonumber \\&\quad =\frac{g_{Z\eta _c\rho }(q^2)f_{\rho }(-if^{\prime }_{\eta _c})f_{Z}}{(p^2-m^2_{Z}+i\epsilon )(p^{\prime 2}-m^2_{\eta _c}+i\epsilon )(q^2-m^2_{\rho }+i\epsilon )}\nonumber \\&\qquad \times \left( g_{\mu \nu }-\frac{q_{\nu }p^{\prime }_{\mu }+p^{\prime }_{\mu }p^{\prime }_{\nu }}{m_Z^2}-\frac{q_{\mu }q_{\nu }}{m_{\rho }^2}\right. \nonumber \\&\qquad \left. + \frac{p^{\prime }\cdot q(q_{\mu }q_{\nu }+q_{\mu }p^{\prime }_{\nu })}{m_Z^2m_{\rho }^2}\right) +\cdots , \end{aligned}$$

(24)

where the coupling constant $g_{Z\eta _c\rho }(q^2)$ is defined via

$$\begin{aligned} \mathcal {L}=g_{Z\eta _c\rho }g^{\mu \nu }Z_{c\nu }^{+}\eta _c\rho _{\mu }^-+\mathrm{h.c.}. \end{aligned}$$

(25)

At the quark–gluon level, we calculate the three-point correlation function $\varPi _{\mu \nu }^{\eta _c\rho }(p, p^{\prime }, q)$ by considering diagrams similar to Fig. 1. As outlined in Ref. [47], the coupling constant varies slowly with the Euclidean momentum $Q^2=-q^2$, and hence for sufficiently large $Q^2$ it is only necessary to extract the $1/Q^2$ term in Eq. (24) for the three-point correlation function $\varPi _{\mu \nu }^{\eta _c\rho }(p, p^{\prime }, q)$.

Thus, for an appropriate range of $Q^2$ we keep the invariant function proportional to $1/Q^2$ in the $g_{\mu \nu }$ structure. In this assumption [47], we obtain the spectral density on the OPE side

$$\begin{aligned} \rho (s)=-\left( \frac{m_c\langle \bar{q}g_s\sigma \cdot Gq\rangle }{6\pi ^2}+\frac{\langle g_s^2GG\rangle s}{192\pi ^4}\right) \sqrt{1-\frac{4m_c^2}{s}}, \end{aligned}$$

(26)

in which only the gluon condensate and quark–gluon mixed condensate give contributions to the spectral density in this order. Similarly to the spectral density in Eq. (13), the color-connected diagrams in Fig. 1 give no contributions to this spectral density in Eq. (26). Then the sum rule for the coupling constant $g_{Z\eta _c\rho }$ can be established by assuming $p^2=p^{\prime 2}=P^2$ and performing the Borel transform ($P^2\rightarrow M_B^2$)

$$\begin{aligned} g_{Z\eta _c\rho }(s_0, M_B^2, Q^2)&= \frac{1}{f_{\rho }(-if^{\prime }_{\eta _c})f_{Z}}\frac{m^2_{Z}-m^2_{\eta _c}}{e^{-m^2_{\eta _c}/M_B^2}-e^{-m^2_{Z}/M_B^2}}\nonumber \\&\quad \times \left( \frac{Q^2+m_\rho ^2}{Q^2}\right) \int _{4m_c^2}^{s_0}\rho (s)e^{-s/M_B^2}\mathrm{d}s, \end{aligned}$$

(27)

in which $Q^2=-q^2$.

To perform the numerical analysis, we use the following parameters for the $\eta _c$ and $\rho$ mesons [37, 47]:

$$\begin{aligned} m_{\eta _c}&=(2.980\pm 0.001)~\text{ GeV },\quad f_{\eta _c}=0.35~\text{ GeV },\nonumber \\ m_{\rho }&=(775.26\pm 0.25)~\text{ MeV },\quad f_{\rho }=157~\text{ MeV }. \end{aligned}$$

(28)

Fig. 3

Variation of the coupling constant $g_{Z\eta _c\rho }(Q^2)$ with the Borel parameter $M_B^2$ for $Q^2=8$ GeV$^2$

In Fig. 3, we show the variation of $g_{Z\eta _c\rho }(Q^2)$ with the Borel parameter for $Q^2=8$ GeV$^2$. We choose $m_{\rho }^2\ll Q^2\sim m_{\eta _c}^2$ so that the $m_{\rho }$ can be ignored and the OPE is valid. It shows that the minimum value of $g_{Z\eta _c\rho }$ appears around $M_B^2=1.6$ GeV$^2$. However, the coupling constant is required at the pole $Q^2=-m_\rho ^2$, where the QCD sum rule is not valid. To obtain the coupling constant $g_{Z\eta _c\rho }(Q^2=-m_\rho ^2)$, we need to extrapolate the coupling constant $g_{Z\eta _c\rho }(Q^2)$ from the QCD sum-rule region to the physical pole $Q^2=-m_\rho ^2$. Following Ref. [47], we use the exponential model to achieve this extrapolation

$$\begin{aligned} g_{Z\eta _c\rho }(Q^2)=g_1e^{-g_2Q^2}, \end{aligned}$$

(29)

where $g_1$ and $g_2$ can be determined by fitting the QCD sum-rule result of $g_{Z\eta _c\rho }(Q^2)$, using Eq. (29). In Fig. 4, we show the QCD sum-rule result of the coupling constant $g_{Z\eta _c\rho }(Q^2)$ with $s_0=21$ GeV$^2$ and $M_B^2=1.6$ GeV$^2$ (dotted line). We fit this result by using the model Eq. (29) with the parameters $g_1=11.65$ GeV and $g_2=9.93\times 10^{-3}$ GeV$^2$. Then we extrapolate the coupling constant $g_{Z\eta _c\rho }(Q^2)$ to the physical pole $Q^2=-m_\rho ^2$ to obtain the coupling constant

$$\begin{aligned} g_{Z\eta _c\rho }(Q^2=-m_\rho ^2)=(11.72\pm 2.10)~\text{ GeV }, \end{aligned}$$

(30)

in which the uncertainties of the charm quark mass, the QCD condensates, the hadron masses and the hadron couplings are considered to give the error of this prediction. Inserting this value into Eq. (17), we can calculate the decay width of the process $Z_c^+(4200)\rightarrow \eta _c\rho ^+$

$$\begin{aligned} \varGamma (Z_c^+(4200)\rightarrow \eta _c\rho ^+)=(334.4\pm 119.8)\text { MeV}. \end{aligned}$$

(31)

Fig. 4

Variation of the coupling constant $g_{Z\eta _c\rho }(Q^2)$ with $Q^2$. Data points shows the QCD sum-rule result with $s_0=21$ GeV$^2$ and $M_B^2=1.6$ GeV$^2$. Solid line gives the fit of the QCD sum-rule result through Eq. (29) and the extrapolation of the coupling constant $g_{Z\eta _c\rho }(Q^2)$ to the physical pole $Q^2=-m_\rho ^2$

2.3 Decay mode $Z_c^+(4200)\rightarrow D^+\bar{D}^{*0}$

In this subsection, we study the open-charm decay mode $Z_c^+(4200)\rightarrow D^+\bar{D}^{*0}$ with the interpolating currents for the $D^+$ and $\bar{D}^{*0}$ mesons

$$\begin{aligned} J^{D^+}= & {} \bar{d}_a\gamma _{5}c_a, \end{aligned}$$

(32)

$$\begin{aligned} J_{\mu }^{\bar{D}^{*0}}= & {} \bar{c}_a\gamma _{\mu } u_a, \end{aligned}$$

(33)

with the current-meson coupling relations

$$\begin{aligned} \langle 0|J^{D^+}|D^+(p^{\prime })\rangle= & {} f_{D}, \end{aligned}$$

(34)

$$\begin{aligned} \langle 0|J_{\mu }^{\bar{D}^{*0}}|D^{*0}(q)\rangle= & {} f_{D^{*}}\epsilon _{\mu }(q), \end{aligned}$$

(35)

where $f_{D}$ and $f_{D^{*}}$ are the current-meson coupling constants for D and $D^{*}$, respectively. The three-point function can be written at the hadron level

$$\begin{aligned}&\varPi _{\mu \nu }^{DD^{*}}(p, p^{\prime }, q)\nonumber \\&\quad =\int \mathrm{d}^4x\mathrm{d}^4y \,e^{ip^{\prime } \cdot x}e^{iq \cdot y}\,\langle 0|T[J^{D}(x)J^{\bar{D}^{*}}_{\mu }(y)J_{\nu }^{Z\dag }(0)]|0\rangle \nonumber \\&\quad =\frac{g_{ZDD^{*}}(q^2)f_{D^{*}}(-if_{D})f_{Z}}{(p^2-m^2_{Z}+i\epsilon )(p^{\prime 2}-m^2_{D}+i\epsilon )(q^2-m^2_{D^{*}}+i\epsilon )} \nonumber \\&\qquad \times \left( g_{\mu \nu }-\frac{q_{\nu }p^{\prime }_{\mu }+p^{\prime }_{\mu }p^{\prime }_{\nu }}{m_Z^2}-\frac{q_{\mu }q_{\nu }}{m_{D^{*}}^2}\right. \nonumber \\&\qquad \left. + \frac{p^{\prime }\cdot q(q_{\mu }q_{\nu }+q_{\mu }p^{\prime }_{\nu })}{m_Z^2m_{D^{*}}^2}\right) +\cdots , \end{aligned}$$

(36)

where the coupling constant $g_{ZDD^{*}}(q^2)$ is defined via

$$\begin{aligned} \mathcal {L}=g_{ZDD^{*}}g^{\mu \nu }Z_{c\nu }^{+}D^-\bar{D}^{*0}_{\mu }+h.c.. \end{aligned}$$

(37)

However, the evaluation of the three-point correlation function $\varPi _{\mu \nu }^{DD^{*}}(p, p^{\prime }, q)$ is a bit different from the other two decay modes discussed previously. Considering diagrams similar to Fig. 1, we calculate the OPE series in the momentum spaces. As discussed above, we keep the invariant function proportional to $1/Q^2$ in the $g_{\mu \nu }$ structure at the OPE side

$$\begin{aligned} \rho ^{\langle \bar{q}Gq\rangle }(s)&=\frac{m_c\langle \bar{q}g_s\sigma \cdot Gq\rangle }{192\pi ^2}\left( 6-\frac{5m_c^2}{s}+\frac{m_c^4}{s^2}-\frac{19m_c^2}{s-m_c^2}\right) \nonumber \\&\quad +\frac{\langle g_s^2GG\rangle }{6144\pi ^4s^2} \bigg [(4s^3+19m_c^2s^2-34m_c^4s-5m_c^6)\nonumber \\&\quad -(15m_c^2s^2-34m_c^4s-m_c^6)\log \left( 1+\frac{m_c^2}{Q^2}\right) \bigg ], \end{aligned}$$

(38)

in which $Q^2=-q^2$. Here the quark–gluon mixed condensated $\langle \bar{q}g_s\sigma \cdot Gq\rangle$ gives dominant contribution to the spectral density shown above. We find that for $\langle \bar{q}g_s\sigma \cdot Gq\rangle$, only the color-connected diagrams contribute to the spectral density shown above, which is different from the situations in $J/\psi \pi$ and $\eta _c\rho$ channels. For the gluon condensate $\langle g_s^2GG\rangle$, both the color-connected and the color-disconnected diagrams give contributions. Assuming $p^2=p^{\prime 2}=P^2$ and performing the Borel transform ($P^2\rightarrow M_B^2$) of the three-point function, the sum rule for the coupling constant $g_{ZDD^{*}}$ can be obtained as

$$\begin{aligned}&g_{ZDD^{*}}(s_0, M_B^2, Q^2)\nonumber \\&=\frac{1}{f_{D^{*}}(-if_{D})f_{Z}}\frac{m^2_{Z}-m^2_{D}}{e^{-m^2_{D}/M_B^2}-e^{-m^2_{Z}/M_B^2}}\nonumber \\&\quad \times \left( \frac{Q^2+m_{D^{*}}^2}{Q^2}\right) \int _{4m_c^2}^{s_0}\rho (s)e^{-s/M_B^2}\mathrm{d}s. \end{aligned}$$

(39)

We adopt the hadron parameters of $D^+$ and $D^{*0}$ from Refs. [37, 47]

$$\begin{aligned} m_{D^+}&=(1869.61\pm 0.10)~\text{ MeV }, f_{D}=(0.18{\pm }0.02)~\text{ GeV },\nonumber \\ m_{D^{*0}}&=(2006.96\pm 0.10)~\text{ MeV }, f_{D^{*}}=(0.24{\pm }0.02)~\text{ GeV }. \end{aligned}$$

(40)

Fig. 5

Variation of the coupling constant $g_{ZDD^{*}}(Q^2)$ with the Borel parameter $M_B^2$ for $Q^2=20$ GeV$^2$

In Fig. 5, we show the variation of $g_{ZDD^{*}}(Q^2)$ with the Borel parameter while $Q^2=20$ GeV$^2$. In this situation, the coupling constant increases monotonically with the momentum $Q^2$, and hence the result obtained below should be considered as an upper bound on the comparatively small decay width in this channel. To perform the QCD sum-rule analysis, we adopt the Borel window $3.0\le M_B^2\le 3.4$ GeV$^2$ used in Ref. [51] for the mass sum rules of the same current. We do the fitting at $M_B^2=3.4$ GeV$^2$ and $s_0=21$ GeV$^2$ in Fig. 6 using Eq. (29) with $g_1=-1.73$ GeV and $g_2=1.77\times 10^{-2}$ GeV$^2$. With these parameters, the model Eq. (29) can fit the QCD sum-rule result very well. To obtain the coupling constant, we extrapolate the coupling constant $g_{ZDD^{*}}(Q^2)$ to the physical pole $Q^2=-m_{D^{*}}^2$. Considering the uncertainties of the input parameters, the coupling constant $g_{ZDD^{*}}(Q^2=-m_{D^{*}}^2)$ is

$$\begin{aligned} g_{ZDD^{*}}(Q^2=-m_{D^{*}}^2)=-(1.86\pm 1.09)~\text{ GeV }. \end{aligned}$$

(41)

Finally, the decay width of this decay mode can be evaluated via Eq. (17)

$$\begin{aligned} \varGamma (Z_c^+(4200)\rightarrow D^+\bar{D}^{*0})=(6.6\pm 6.4) ~\text{ MeV }. \end{aligned}$$

(42)

In addition, the open-charm decay mode $Z_c^+(4200)\rightarrow \bar{D}^0D^{*+}$ should also be studied. Considering the SU(2) symmetry, the three-point function for the vertex $Z_c^+(4200)\bar{D}^0D^{*+}$ is exactly the same as that for the vertex $Z_c^+(4200)D^+\bar{D}^{*0}$. Using the hadron parameters of $D^0$ and $D^{*+}$ [37],

$$\begin{aligned} m_{D^0}= & {} (1864.84 \pm 0.07)~\text{ MeV },\\ ~m_{D^{*+}}= & {} (2010.26 \pm 0.07)~\text{ MeV }, \end{aligned}$$

we obtain the same values of the coupling constant and the decay width for $Z_c^+(4200)\rightarrow \bar{D}^0D^{*+}$ as those for $Z_c^+(4200)\rightarrow \bar{D}^+D^{*0}$.

Fig. 6

Variation of the coupling constant $g_{ZDD^{*}}(Q^2)$ with $Q^2$. Data points shows the QCD sum-rule result with $s_0=21$ GeV$^2$ and $M_B^2=3.4$ GeV$^2$. Solid line gives the fit of the QCD sum-rule result through Eq. (29) and the extrapolation of the coupling constant $g_{ZDD^{*}}(Q^2)$ to the physical pole $Q^2=-m_{D^{*}}^2$

3 Summary

In summary, we have studied the three-point functions of the processes $Z_c(4200)^+\rightarrow J/\psi \pi ^+, Z_c(4200)^+\rightarrow \eta _c\rho ^+$ and $Z_c(4200)^+\rightarrow D^+\bar{D}^{*0}$, considering $Z_c(4200)^+$ as a hidden-charm tetraquark state. We calculate the three-point functions by including the perturbative term, quark condensate, gluon condensate and quark–gluon mixed condensate.

To perform the QCD sum-rule analysis, we expand the three-point functions in QCD side with respect to $Q^2$ and isolate the terms proportional to 1/$Q^2$ from the $g^{\mu \nu }$ tensor structure. Only the gluon condensate and the mixed condensate give contributions to the three-point functions after this procedure. This approach is a modification of the QCD sum-rule analysis of the $Z_c(3900)^+$ decay width in Ref. [47], where the three-point functions were evaluated by considering the color-connected diagrams associated with a different tensor structure resulting in only mixed condensate contributions. Our predictions of the decay widths are

$$\begin{aligned} \varGamma ({Z_c(4200)^+\rightarrow J/\psi \pi ^+})&= (87.3\pm 47.1)\,\mathrm{MeV},\\ \varGamma ({Z_c(4200)^+\rightarrow \eta _c\rho ^+})&= (334.4\pm 119.8)\,\mathrm{MeV},\\ \varGamma ({Z_c(4200)^+\rightarrow D^+\bar{D}^{*0}})&= (6.6\pm 6.4)\,\mathrm{MeV},\\ \varGamma ({Z_c(4200)^+\rightarrow \bar{D}^0 D^{*+}})&= (6.6\pm 6.4)\,\mathrm{MeV}. \end{aligned}$$

Thus, the full decay width for $Z_c(4200)^+$ is predicted as

$$\begin{aligned} \varGamma _{Z_c(4200)^+}=(435\pm 180)~\mathrm{MeV}, \end{aligned}$$

(43)

which is in agreement with the experimental value of $Z_c(4200)^+$ width from the Belle Collaboration [1]. It is found that the branching fraction into $J/\psi \pi$ channel is about 24.7 %, which is slightly suppressed compared to 71.6 % for the $\eta _c\rho$ channel. The study of $Z_c\rightarrow \eta _c\rho$ decay may provide useful insights on the nature of the newly observed charged $Z_c$ states, helping us to discriminate the molecule and tetraquark interpretations of the charged state family [63].

The study of the three-point function sum rules gives support to the tetraquark interpretation of the newly observed $Z_c(4200)^+$ state. This conclusion is consistent with the result obtained from the mass sum rules in Ref. [51]. The branching ratio predictions of $J/\psi \pi , \eta _c\rho , D^+\bar{D}^{*0}$, and $\bar{D}^0 D^{*+}$ channels will be helpful for future experimental studies.