1 Introduction

Testing gravity theories using observational data is an important task of relativistic astrophysics because gravity theories are a key concept in understanding the formation and evolution of the universe and features of astronomical objects such as stars and galaxies, as well as the physics of compact gravitational relativistic objects: black holes and neutron stars [1]. One of the most essential and well-tested gravity theories is general relativity (GR), which describes gravity as a curvature of spacetime, which Albert Einstein developed in the early twentieth century. GR has been incredibly successful in explaining a wide range of astronomical phenomena, such as the bending of light around massive objects, the precession of Mercury’s orbit, and the existence of black holes [2, 3]. However, some open questions about gravity remain, such as dark matter’s nature and energy.

Also, in astrophysics, gravity effects and astrophysical magnetic fields are important for understanding the universe. Well-accepted astrophysically powerful sources of magnetic field are magnetars, pulsars, white dwarfs, stars, and black hole accretion disks [4,5,6]. From this point of view, gravity has a vital role in the structure of powerful magnetic fields.

Magnetic fields also play a vital role in explaining many astrophysical processes, such as the formation of stars, the acceleration of cosmic rays, and the formation and collisions of powerful relativistic outflows or jets from black holes [7, 8].

Astrophysical magnetic fields are difficult to observe directly. However, their effects can still be seen in various ways, such as the emission of polarized light and the acceleration of charged and magnetized particles. In this sense, gravity theories and astrophysical magnetic fields are important for understanding the universe. Studying the interaction between polarized particles (electromagnetic dipoles) and external electromagnetic fields near highly gravitating sources is a promising area of research in astrophysics [9]. The findings of Felice et al. [10, 11] revealed some intriguing information about how particles are confined and how energy is stored in black-hole fields. The numerical simulations of general relativistic magnetohydrodynamics (GRMHD) are an extremely reliable technique for studying the motion of relativistic magnetized accretion discs [12]. GRMHD and/or general-relativistic particle-in-cell (GRPIC) numerical techniques can also be used to evaluate the electromagnetic field configurations and develop a suitable black hole magnetosphere model [13,14,15,16].

Magnetic field solutions of Maxwell equations in the spacetimes of both Schwarzschild and Kerr black holes were first obtained by Wald [17]. In the past few years, using the Walds approach, several studies have been performed through the dynamics and radiation of charged and magnetized particles [18,19,20,21,22,23,24]. Petterson [25] proposed the dipole magnetic field, which may be formed using the circular current loops surrounding the black hole. Exploring charged particle dynamics near the Kerr black hole in split-monopole magnetic fields revealed that positive magnetic fields stabilize the effective potential [26]. Moreover, magnetized particle dynamics near the vicinity of black holes in the presence of external magnetic fields have been examined in [27,28,29,30,31,32,33,34,35].

The gravitational and electromagnetic interactions are vital in understanding the high-energy phenomena near black holes. Solid observational proofs suggest that magnetic fields are necessary near black holes [36, 37]. Based on their primary source, the magnitudes of magnetic fields near black holes may range from a few Gauses (Gs) to \(10^8\) Gs or even more. The magnetic field strength of supermassive black holes (SMBHs) is observed to be of the order of \(10^1-10^4\) Gs, whereas it is typically about \(10^8\) Gs for the stellar-mass black hole detected in the X-ray binaries [38, 39]. Given the insufficient magnetic field energy densities of such magnitudes, they do not significantly impact the background spacetime geometry.

Therefore, the lack of influence of the magnetic field on the geometry of spacetime in the vicinity of black holes can be counterbalanced by a high charge-to-mass ratio of fundamental particles. As a result, the magnetic fields of a few Gs may significantly impact the dynamics of these particles. To represent the ratio of gravitational and Lorentz forces, a dimensionless magnetic parameter \(\mathcal{B}\) can be introduced for a test particle charged with mass m and charge q near black holes of mass M submerged in the magnetic field of strength B. Assuming a relativistic electron encircling a black hole at the scale of the event horizon, the following ratio is estimated in Ref. [40] \(\mathcal{B} \approx \frac{q}{m}\frac{G M}{ c^4} B\), which is high enough owing to the substantial amounts of the specific charge q/m of fundamental particles.

In the present work, we aimed to study the motion of charged particles with magnetic dipole moments and electric charge around Schwarzschild black holes in the dipolar magnetic field. The paper is organized as follows: Sect. 2 briefly introduces a dipolar magnetic field around a spherically symmetric (static) black hole solution. Moreover, we also explore the circular orbits and ISCOs. Section 4 investigates particle collisions near black holes, critical angular momentum, and the center of mass energy of charged, neutral, and magnetized particles. We summarize the results obtained in Sect. 6. Throughout the paper, we use geometrized units \(c=G=1\) and run Latin indexes from 0 to 3, while Greek indexes from 1 to 3.

2 Magnetized-charged particles around magnetized Schwarzschild black holes

2.1 Magnetic fields around Schwarzschild black holes surrounded by a current loop

The following line element describes the geometry around a Schwarzschild black hole with mass M,

$$\begin{aligned} ds^2=-f(r)dt^2+f(r)^{-1}dr^2+r^2\left( d\theta ^2+\sin ^2\theta d\phi ^2\right) , \end{aligned}$$
(1)

where \(f(r)=1-2M/r\). We assume that a current loop surrounds the black hole and magnetic fields on the outside and inside the current loop have different forms, as defined by the following four potentials [25]:

$$\begin{aligned} A^\phi _i(r)=\frac{1}{2}BF_i(r)\sin ^2\theta , \end{aligned}$$
(2)

in which \(i=1,2\) stands for outside and inside the current loop, B is magnetic field strength near the loop \(B=\pi r_0^2\sqrt{1-2\,M/r_0}I\), where I is the current along the loop with the radius \(r_0\). The magnetic field in the inner region is uniform, and the field has a dipole-like structure in the outer region:

$$\begin{aligned} F_1(r)= & {} \ln f(r)+\frac{2M}{r}\left( 1+\frac{M}{r} \right) , r>r_0. \end{aligned}$$
(3)
$$\begin{aligned} F_2(r_0)= & {} \ln f(r_0)+\frac{2M}{r_0}\left( 1+\frac{M}{r_0} \right) , 2M<r\le r_0. \end{aligned}$$
(4)

To find non-zero components of the external magnetic field, we multiply \(u_\mu \) from both sides of the expression of the electromagnetic field \( F_{\alpha \beta }=u_{[\alpha }E_{\beta ]}-\eta _{\alpha \beta \sigma \gamma }u^{\sigma }B^{\gamma }\), and get,

$$\begin{aligned} B^\alpha =\frac{1}{2}\eta ^{\alpha \beta \sigma \mu }F_{\beta \sigma }u_\mu , \end{aligned}$$
(5)

where \( \eta ^{\alpha \beta \sigma \mu }=\frac{1}{\sqrt{-g}}\epsilon ^{\alpha \beta \sigma \mu }\) and \(g=det(g_{\mu \nu })\) with \(g=\mathrm{det|g_{\mu \nu }|}=-r^4\sin ^2\theta \) for spacetime metric (1) \(\epsilon _{0123}=1\) with even permutations, \(-1\) for odd ones, and zero for other combinations. The orthonormal components of the magnetic fields can be represented using the following expression:

$$\begin{aligned} B^{\hat{i}}= & {} \frac{1}{2}\epsilon _{ijk}\sqrt{g_{jj}g_{kk}}F^{jk}\nonumber \\= & {} \frac{1}{2}\epsilon _{ijk}\sqrt{g^{jj}g^{kk}}F_{jk}. \end{aligned}$$
(6)

As a result, the radial and vertical components of the magnetic field observed by the Zero Angular Momentum Observer (ZAMO) with velocities \(u^{\mu }_{\text {ZAMO}}=(u^t,0,0,0)\) where \(u^t=-1/g_{tt}\) take the following expressions for inner and outer regions:

$$\begin{aligned}{} & {} B^{\hat{r}}_{in}=B_0 \cos \theta F_2(r_0), \end{aligned}$$
(7)
$$\begin{aligned}{} & {} B^{\hat{\theta }}_{in}=\sqrt{f(r)}B_0 \sin \theta F_2(r_0). \end{aligned}$$
(8)

and

$$\begin{aligned}{} & {} B^{\hat{r}}_{out} =B_0 \cos \theta F_1(r), \end{aligned}$$
(9)
$$\begin{aligned}{} & {} B^{\hat{\theta }}_{out} = B_0 \sin \theta \left( F_1(r)+\frac{r}{2} \partial _rF_1(r) \right) . \end{aligned}$$
(10)

3 Circular motion of charged-magnetized particles

In this section, we will study the circular motion of particles with electric charge e, mass m, and magnetic dipole moment \(\mu ^{\nu }\) near Schwarzchild black holes in the presence of a dipole-like magnetosphere generated by a current loop around the black hole. First, we derive the effective potential for the particles in both the outer and inner regions with respect to the current loop and analyze the magnetic field’s effect on the effective potential’s radial profiles. Then, we study the energy and angular momentum of the particles along their circular orbits. Also, we study the particles’ ISCO behavior by varying the magnetic field and interaction parameters.

3.1 Effective potential

To obtain equations of motion of test magnetized-charged particles in the magnetized Schwarzschild spacetime, we use a hybrid form of the Hamilton–Jacobi method that is a valuable approach for elucidating the equations, which have the form:

$$\begin{aligned} g^{\mu \nu }\left( \frac{\partial \mathcal{S}}{\partial x^{\mu }}+ qA_\mu \right) \left( \frac{\partial \mathcal{S}}{\partial x^{\nu }}+qA_{\nu }\right) = -\Big (m+\mathcal{U} \Big )^2, \end{aligned}$$
(11)

where the term \(2\mathcal{U}=D^{\mu \nu }F_{\mu \nu }\) represents an interaction between the particle’s magnetic dipole and external magnetic fields; the polarization and the electromagnetic field tensors are \(D^{\mu \nu }\) and \(F_{\mu \nu }\), respectively. The expression for \(D^{\mu \nu }=\eta ^{\alpha \beta \sigma \nu }u_{\sigma }\mu _{\nu }\), where \(u^{\nu }\) is the four-velocity of the particle, satisfies \(D^{\alpha \beta }u_{\beta }=0\).

In our further analysis, we assume the direction of the dipole moment is perpendicular to the equatorial plane and has the following components: \(\mu ^{\hat{i}}=(0,\mu ^{\hat{ \theta }},0)\), which is always parallel to the magnetic field lines and perpendicular to the equatorial plane. Thus, the interaction term \(\mathcal{U}\) for the zero angular momentum observer (ZAMO) has the form \(\mathcal{U}=2\mu ^{\hat{\theta }}B_{\hat{\theta }}\), and at the equatorial plane, the interaction term takes the form, \(\mathcal{U}=2\mu B_0 G(r)\).

The following form Lagrangian is used for the integrals of motion of the particles with the electric charge and the magnetic dipole moment [41, see Eq.(7)]

$$\begin{aligned} \mathscr {L}=\frac{1}{2}\Big [(m+\mathcal{U})g_{\mu \nu }u^\mu u^\nu -k\mathcal{U}\Big ]+eA_\mu u^\mu , \end{aligned}$$
(12)

and correspondingly, we get the following expressions for the conserved quantities: the specific energy \(\mathcal{E}=E/m\) of the particles’ motion and their angular momentum \(\mathcal{L}=L/m\), as

$$\begin{aligned} {}-\mathcal{E}= & {} (1+\beta G(r))g_{tt}\dot{t}, \end{aligned}$$
(13)
$$\begin{aligned} \mathcal{L}= & {} (1+\beta G(r))g_{\phi \phi }\dot{\phi }+qA_\phi , \end{aligned}$$
(14)

where \(\beta = \mu B/(2m)\) stands for the magnetic coupling parameter corresponding to the magnetic interaction term in Eq. (11), and \(q=e/m\).

Fig. 1
figure 1

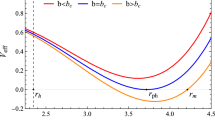
The radial dependence of the effective potential (16) for different values of \(\alpha , \beta \), and \(\omega \) parameters. The left panel is for the inner region, and the right is for the outer region

Full size image

The motion of electrically charged particles possessing a magnetic dipole moment as they orbit the dipole-like magnetized Schwarzschild black hole within the equatorial plane (\(\theta =\pi /2\) and \(u^{\theta }=\dot{\theta }=0\)) can be characterized by the ensuing action:

$$\begin{aligned} \mathcal{S}=-Et+L\phi +\mathcal{S}_r \ . \end{aligned}$$
(15)

Subsequently, by employing the Hamilton–Jacobi equation (11) alongside Eqs. (13) and (14), we can derive the equation governing the radial coordinate.

This approach allows us to express the variables individually within the Hamilton–Jacobi equation. Consequently, the radial trajectory of the particle can be outlined by

$$\begin{aligned} g_{rr}\dot{r}^2= & {} \mathcal{E}+V_\textrm{eff}(r) \,. \end{aligned}$$

In the context of circular motion, the effective potential \(V_{\text {eff}}\) corresponds to \(V_i\) for charged particles possessing a magnetic dipole moment, both in the outer and inner regions,

$$\begin{aligned} V_i(r)=f(r)\left\{ \left[ 1+\beta G(r) \right] ^2+\left[ \frac{\mathcal{L}}{r}+\omega r F_i(r) \right] ^2\right\} \, . \end{aligned}$$
(16)

In the above expression, \(\omega =eB/(2m)\) is responsible for the magnetic interaction between the particle’s electric charge and external magnetic fields. In our further analysis, we assume the current loop’s position at \(r_0=6M\).

In Fig. 1, we analyze the effects of magnetic interactions and magnetic field parameters on the effective potential for the circular motion of test-charged particles with a magnetic dipole in both inner (left panel) and outer (right panel) regions. It is observed from the left panel that in the inner region, the maximum in the effective potential of the particles is increased for \(\omega >0\). In contrast, it decreases for \(\beta >0\) and \(\omega <0\) cases. On the other hand, in the outer region case, \(\omega >0\) decreases, whereas \(\beta >0\) and \(\omega <0\) contribute to the minima of the effective potential (see right panel of Fig. 1). However, the behavior of the effective potential reaches its minimum at the ISCO.

3.2 Circular orbits

During the motion in circular orbits, radial forces are absent, or any existing forces offset each other at specific angular momentum values for the particles. The circularity of orbits followed by test-charged magnetized particles orbiting the magnetized black hole can be examined through conditions \(V_{\text {eff}}=\mathcal{E}\) and \(V_{\text {eff}}'=0\), where the prime denotes the partial derivative with respect to the radial coordinate. Consequently, by resolving the above mentioned equations, one can deduce the angular momentum and energy of particles associated with circular orbits.

Fig. 2
figure 2

Radial profiles of the angular momentum of a test-charged magnetized particle encircling the Schwarzschild black hole in the inner (left) and outer (right) regions, with varying values of the parameters \(\omega \) and \(\beta \)

Full size image
Fig. 3
figure 3

Radial profiles of the energy of a test-charged magnetized particle encircling the Schwarzschild black hole in the inner (left) and outer (right) regions, with varying values of the parameters \(\omega \) and \(\beta \)

Full size image
Fig. 4
figure 4

The dependence of the ISCO radius along \(\omega \) (top row) and \(\beta \) (bottom row) at various values of the magnetic field parameters \(\beta \) and \(\omega \). The left and right panels show the inner and outer regions, respectively

Full size image
Fig. 5
figure 5

Graphical illustration of the particle’s angular momentum and energy at the ISCO along \(\beta \) (top and third rows), whereas along \(\omega \) (second and last rows) for various discrete values of the magnetic intersections and field parameters

Full size image

Figure 2 demonstrates the graphical behavior of the angular momentum along the radial profile at various discrete values of \(\omega \) and \(\beta \). From the graphical illustration in the inner region, we observed that the positive values of \(\omega \) contribute to the angular momentum, whereas the magnetic fields \(\beta \) and \(\omega <0\) diminish it. On the other hand, unlike the inner region case, the magnetic field \(\beta \) in the outer region increases the angular momentum. Interestingly, the higher values of \(|\omega |\) and the effects of the magnetic field considerably influence the angular momentum at a larger radial distance. Similarly, \(\omega >0\) increases the energy along the radial distance r in the inner region case, while \(\beta \) and \(\omega <0\) decrease it. On the other hand, in the outer region case, \(\beta \) influences the energy conversely (for details, see Fig. 3).

3.3 Innermost stable circular orbits

Solving the condition \(V_\textrm{eff}'=0\) with respect to r helps to find the orbits where the effective potential has extreme values. The circular orbits become stable where the effective potential is minimal. Thus, as \(V_\textrm{eff}''(r)<0\), the orbits are unstable, and all stable circular orbits satisfy the condition \(\partial _{rr}V_\textrm{eff}(r_\textrm{SCO})>0\), while the ISCO satisfies \(\partial _{rr}V_\textrm{eff}(r_\textrm{ISCO})=0\). The ISCO around black holes is important because it is connected to the inner edge of the accretion disc.

In Figs. 4 and 5, we have presented the behavior of the radius of ISCO, the angular momentum at ISCO, and the energy at ISCO of neutral and charged particles, respectively, along \(\omega \) and \(\beta \) for different values of the magnetic field and magnetic interaction parameters between the electric charge and magnetic field of particles. From the graphical illustration, we note that the magnetic field contributes to the ISCO radius in the inner region. In contrast, it decreases it along \(\omega \) in the outer region case (for details, see the top row of Fig. 4). Moreover, we observed that \(|\omega |>0\) decreases the ISCO radius in the inner region case (for details, see the bottom left panel of Fig. 4). On the other hand, we surprisingly found that \(\omega >0\) and \(\omega <0\), respectively, decrease and increase the ISCO radius in the outer region (see the bottom right panel of Fig. 4). In other words, the ISCO radius has its minimum and maximum in the inner and outer regions, respectively, without a magnetic field \(\beta \).

From the graphical behavior of the angular momentum at ISCO, we observed that \(\beta \) diminishes \(\mathcal{L}\) in the inner region case. However, interestingly, \(\omega >0\) increases the angular momentum of the particles at ISCO, and \(\omega <0\) decreases it (see second-row left column of Fig. 5). On the other hand, in the outer region case (see the second-row right column of Fig. 5), these parameters influence the angular momentum of particles at ISCO inversely near the black hole horizon.

Similarly, we have shown that \(\omega >0\) increases the charged particle energy at ISCO, while \(\omega <0\) decreases it. Interestingly, the magnetic field diminishes the energy of charged particles at the ISCO in the cases of both inner and outer regions (refer to the last row of Fig. 5).

Interestingly, when test particles are in their Keplerian accretion disk, they fall into the central black hole and extract some energy, which may be converted to electromagnetic and gravitational radiation under certain conditions. The energy released through the radiation can be determined by the difference between the rest of the particle energy (measured by a suitable observer) and the ISCO energy of the particles (\(\mathcal{E}_\textrm{ISCO}\)). Consequently, the efficiency of the energy release from the accretion disk has the following form [42]

(17)

Below, we examine the energy efficiency at various discrete values of the magnetic field and magnetic interaction parameters between the particles’ electric charge and magnetic field, respectively.

Fig. 6
figure 6

The dependency of energy efficiency \(\eta \), along \(\beta \) (upper row), whereas along \(\omega \) (bottom row)

Full size image

In Fig. 6, we have graphically demonstrated the behavior of energy efficiency at various discrete values of \(\beta \) and \(\omega \) in the inner and outer regions, in the left and right columns, respectively. From our investigations, we found that magnetic field and \(\omega <0\) contribute to the efficiency of energy extraction, while \(\omega >0\) results in its decrease in the inner region (for details, see Fig. 6 left column). In other words, the positive magnetic interaction parameters between the electric charge and magnetic field of charged particles populate the ergosphere. As a result, the efficiency of energy extraction decreases. Interestingly, energy extraction efficiency in the outer region case behaves differently in response to the magnetic interaction parameters \(\omega \).

4 Particle collisions near magnetized Kerr black holes

Estimating the total amount of energy released by different processes occurring near black holes can explain why the luminosity of AGN is of the order \( 10^{45}\mathrm{erg/s}\), sourced by supermassive black holes.

Several physical models have been proposed as energy extraction mechanisms from black holes. For the first time, Penrose has proposed a simple mechanism  [43] by which a particle coming into the ergosphere around a rotating Kerr black hole decays into two particles, one falling into the black hole. At the same time, the other one goes to infinity and possesses more energy than the initial one. This mechanism has been developed over the years in the literature (for example, [44,45,46,47]).

Banados–Silk–West (BSW) [48, 49] have considered collisions of particles near the black hole horizon as an energy extraction model. The model has also been developed in  [49,50,51,52,53,54,55,56,57,58,59,60,61,62]. It is shown that the energy efficiency extracted from the central black hole is more effective in cases of head-on collisions.

Here, we study collisions of electrically charged, neutral, and magnetized particles in the spacetime of a magnetized Schwarzschild black hole. We follow the general expression for the center of mass energy \(E_\textrm{cm}\) of colliding particles given in Ref. [48]

$$\begin{aligned} \left( \frac{1}{\sqrt{-g_{00}}} \ E_\textrm{cm}, 0, 0, 0\right) = m_{1}u_{(1)}^{\mu }+m_{2}u_{(2)}^{\nu }, \end{aligned}$$
(18)

where \(u_{(i)}^{\mu }\) and \(m_{i}\) are respectively the four-velocity and mass of the ith particle. One can obtain the expression for \(E_\textrm{cm}\) using the normalization condition \(g_{\mu \nu }u^{\mu }u^{\nu }=-1\) in the following form,

$$\begin{aligned} \frac{E^2_{cm}}{m_1m_2}=\frac{m_1^2+m_2^2}{m_1m_2}-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2\, . \end{aligned}$$
(19)

In our subsequent studies, we investigate the simple situations of particle masses, i.e., \(m_1=m_2=m\).

4.1 Critical angular momentum of colliding particles

The center of mass energy in particle collisions takes maximum value in close orbits near the black hole horizon. The radial velocity of the colliding particles satisfies the condition \(\dot{r}^2\ge 0\) as a function of the angular momentum \(\dot{r}^2(\mathcal {L})\) and other parameters. As the angular momentum increases, the radial velocity decreases. On the other hand, when the angular momentum takes a critical value, the radial velocity and its first derivative along r become zero: \(\dot{r}=0\), and \(\partial _r (\dot{r}^2)=0\). We solve the system of equations numerically, which have a complicated form.

Figure 7 illustrates the graphical behavior of the critical angular momentum of charged and magnetized particles as a function of \(\beta \) in the inner (top row) and outer (bottom row) regions at various values of \(\omega \) and \(\beta \). In the inner region case, the magnetic interaction parameter \(\omega \) contributes to the critical angular momentum. A similar effect of \(\omega \) is observed for the outer region but with less dominance than the inner region. Moreover, the critical angular momentum decreases along \(\beta \) in the outer and inner areas.

4.2 Center of mass energy of particles in different scenarios

In this subsection, we study the collisions of several particles, including electrically neutral, charged, magnetized, and electrically charged, with a magnetic dipole moment.

The center of mass energy is given in Eq. (19) for the same mass particles and takes the following form:

$$\begin{aligned} \frac{E^2_{cm}}{m^2}=2\left( 1-g_{\mu \nu } u^{\mu }_1u^{\nu }_2\right) \, . \end{aligned}$$
(20)

The energy in dimensionless form reduces to

$$\begin{aligned} \mathcal{E}^2_{cm}=E^2_{cm}/(2m^2)=1-g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(21)
Fig. 7
figure 7

Graphical demonstration of the critical value of angular momentum as a function of \(\beta \) for the inner and outer regions in the top and bottom rows, respectively

Full size image

4.2.1 The collision of neutral and electrically charged particles

First, we consider the collisions of electrically neutral particles with electrically charged particles. The equations of motion, i.e., Eqs. (13)–(16), turn out to be the case of neutral particles if \(\beta =\omega =0\).

Fig. 8
figure 8

Radial dependence of the center of mass energy of the collisions of electrically neutral with electrically charged particles in the inner and outer regions, respectively, in the left and right panels

Full size image

In Fig. 8, we have plotted the graphical behavior of the center of mass energy for the cases of electrically neutral and electrically charged particle collisions. Our analysis observed that the energy decreases in the repulsive case of magnetic intersections (\(\omega _1>0\)). In contrast, the attractive case (\(\omega _1<0\)) contributes to the energy of the center of mass in both inner and outer region cases. Also, the center of mass energy decreases along the radial profile, which shows that the energy release rate is much higher near the black hole horizon. Moreover, in the inner region, it is worth noting that at far distances from the black hole, the center of mass energy vanishes due to the repulsive and attractive behaviors of the interaction of charged particles. That means, in the case of \(\omega >0\), the Lorentz force is attractive, causes falling into the central black hole, and cannot collide in orbits close to the black hole horizon. While, when \(\omega <0\) cases, the Lorentz force takes a direction with the centrifugal forces, and at far orbits, the force dominates and pulls out the particles. Consequently, particles cannot see each other again. However, in the outer region, there are no similar scenarios.

4.2.2 The collision of electrically neutral and magnetized particles

Here, we consider the collisions of electrically neutral particles with magnetized particles.

Fig. 9
figure 9

The same figure is shown in Fig. 8, but for the collisions of electrically neutral particles with magnetized particles

Full size image

In Fig. 9, we have illustrated the graphical interpretation of the center of mass energy for the collisions of electrically neutral with magnetized particles. In this case, our examination shows that the magnetic field (\(\beta _2\)) decreases the center of mass energy along the radial distance r in both the inner and outer regions.

Fig. 10
figure 10

The same figure is shown in Fig. 8, but for the collisions of neutral particles with electrically charged and magnetized particles

Full size image

4.2.3 The collisions of neutral and electrically charged magnetized particles

Figure 10 represents the graphical behavior of the center of mass energy in the case of neutral particles with electrically charged and magnetized particle collisions. From our graphical illustration, we noticed that the magnetic field and repulsive magnetic interaction (\(\omega _2>0\)) diminish the center of mass energy in the inner region. On the other hand, its negative value (\(\omega _2<0\)) increases the center of mass energy.

Fig. 11
figure 11

The same figure is shown in Fig. 8, but for the collisions of electrically charged particles with magnetized and electrically charged particles

Full size image

4.2.4 The collisions of electrically charged with magnetized and electrically charged particles

In Fig. 11, we have illustrated the graphical description of the center of mass energy for the collision of electrically charged with magnetized and electrically charged particles. Our result summarizes that at the small radial distance, the collisions of attractive magnetic interaction cases (\(\omega _1 = - \omega _1\)) release a much higher center of mass energy as compared to the collisions between positive magnetic interaction scenarios (\(\omega _1 = \omega _1\)) in the inner region (for details, see the left panel of Fig. 11). Interestingly, in the outer region case, the collisions between positive and negative magnetic interaction cases influence the center of mass energy inversely as they decrease it. Moreover, the presence of a magnetic field diminishes the center of mass energy in both the inner and outer regions.

Fig. 12
figure 12

The same figure is shown in Fig. 8 but for the collisions of electrically charged particles with magnetized particles

Full size image

4.2.5 The collisions of electrically charged with magnetized particles

We have plotted the graphical behavior of the center of mass energy for the collision of electrically charged particles with magnetized particles in Fig. 12. From its graphical behavior, we note that the positive magnetic interaction (\(\omega _1>0\)) increases the center of mass energy in the inner region while decreasing it in the outer region. Conversely, the negative magnetic interaction acts in reverse order. Furthermore, like in the previous case, the magnetic field reduces the center of mass energy in the inner and outer regions.

Fig. 13
figure 13

The same figure is shown in Fig. 8, but for the collisions of magnetized particles with electrically charged magnetized particles

Full size image

4.2.6 The collisions of magnetized with electrically charged magnetized particles

The graphs in Fig. 13 show how the center of mass energy changes when magnetized and electrically charged magnetized particles collide. Our obtained result shows interesting behavior, that is, \(\omega _1<0\) significantly contributes to the center of mass energy in the inner region case, while its positive value reduces it. On the contrary, in the outer region, both \(\beta \) and \(\omega _1>0\) rise, whereas, unlike the inner region, \(\omega _1<0\) reduces the center of mass energy. Our result shows engaging reactions; due to the interaction of magnetized–magnetized particles, the behavior of the center of mass energy is completely different from its behavior in the previous case, i.e., the collisions between non-magnetized and magnetized particles.

Fig. 14
figure 14

The same figure is shown in Fig. 8 but for the collisions of two magnetized and electrically charged particles

Full size image
Fig. 15
figure 15

The same figure is shown in Fig. 8 but for the collisions of electrically neural and magnetized particles in the inner and outer regions

Full size image

4.2.7 The collisions between magnetized and electrically charged particles

The graphical illustration of the center of mass energy for the collisions between two magnetized and electrically charged particles is plotted in Fig. 14. The detailed analysis in the inner and outer regions at different choices of the interaction parameter \(\omega _1=\omega _2\) is plotted in the left and right panels, respectively. Our investigation revealed fascinating behavior, as, unlike previous cases, the magnetic interaction increased the center of mass energy in both inner and outer regions.

4.2.8 The collisions between electrically charged and magnetized particles

Figure 15 demonstrates the graphical behavior of the center of mass energy for the collisions between electrically charged and magnetized particles. Interestingly, from the graphical illustration, we observed that, like some previous cases, the magnetic field (\(\beta \)) considerably influences the center of mass energy and decreases along the radial profile r in both inner and outer regions.

5 Astrophysical objects with magnetic dipole moments and electric charge

Current astronomical observations using Very Long Baseline Interferometry (VLBI), the Black Hole Cam, and the Event Horizon Telescope (EHT) are essential for precisely measuring parameters related to astrophysical black holes. Sagittarius A* (Sgr A*) at the center of the Milky Way is a key laboratory for studying black hole accretion disks, jet formation, and magnetic fields. In this context, it is crucial to consider the motion of neutron stars orbiting supermassive black holes like Sgr A* and the behavior of elementary particles (e.g., protons) in accretion disks around stellar-mass black holes. We aim to perform estimations for the values of the parameters \(\omega \) and \(\beta \) for magnetized neutron stars, white dwarfs, rotating stellar-mass black holes, and elementary particles.

5.1 Magnetized neutron stars and white dwarfs

Neutron stars and white dwarfs are magnetized objects with magnetic dipole moments. Their rotation and significant surface magnetic fields generate an induced electric field, \(E_\textrm{ind} = (1/c)\Omega R B_s\), where R is the object’s radius and \(B_s\) is the surface magnetic field.

We estimate the parameters \(\beta \) and \(\omega \) for neutron stars and white dwarfs orbiting a supermassive black hole in an externally uniform magnetic field. Assuming the neutron star has a magnetic moment \(\mu = (1/2)B_{s}R^3\), the magnetic coupling parameter \(\beta \) is

$$\begin{aligned} \beta _\textrm{NS}=0.032\frac{B_{12}R^3_6B_2}{M_{14}}\, , \quad {\beta _\textrm{WD}=0.451\frac{B_{4}R^3_9B_2}{M_{1}}\, ,} \end{aligned}$$
(22)

where the external magnetic field \(B_2\) is normalized to 100 G, and the surface magnetic field of neutron stars and white dwarfs are normalized to \(10^{12}\) and \(10^4\) Gs, respectively. Similarly, their radii were also normalized to \(10^{6} \mathrm cm\) and \(10^{9} \mathrm cm\), respectively.

A neutron star and white dwarf, due to their rotation, generate an induced electric field proportional to the surface magnetic field, and the induced electric charge (\(q_\textrm{ind}\sim E_\textrm{ind}{R^2}\)) is

$$\begin{aligned} q_\textrm{ind}\sim \Omega BR^3\, . \end{aligned}$$
(23)

Now, we evaluate the value of the total induced charge for typical neutron stars and white dwarfs,

$$\begin{aligned} q_\mathrm{ind(NS)}= & {} 2.1\times 10^6R_6^3B_{12}P_s^{-1} \ \textrm{cm }\nonumber \\= & {} 2.525\times 10^{21} R_6^3B_{12}P_s^{-1} \ \textrm{Coulomb}, \nonumber \\ q_\mathrm{ind(WD)}= & {} 1.7\times 10^4R_9^3B_{4}P_3^{-1} \ \textrm{cm }\nonumber \\= & {} 1.972\times 10^{19} R_9^3B_{4}P_3^{-1} \ \textrm{Coulomb}, \end{aligned}$$
(24)

where \(P_s\) and \(P_3\) are periods of the neutron star and white dwarf normalized to 1 s and \(10^3\) s, respectively. In charge to mass relations, we have,

$$\begin{aligned} \frac{q_\textrm{ind}}{M_\textrm{NS}} \simeq 10.35 \frac{R_6^3B_{12}}{P_{s}M_{14}}, \quad \frac{q_\textrm{ind}}{M_\textrm{WD}} \simeq 0.0185\frac{R_9^3B_{4}}{P_{3}M_{1}}, \end{aligned}$$
(25)

where the masses of neutron stars and white dwarfs are normalized to 1.4\(M_\odot \) and 1\(M_\odot \), respectively. The estimation of \(\omega \) for neutron stars and white dwarfs using the above assumptions takes the value,

$$\begin{aligned}{} & {} \omega _\textrm{NS}\simeq 0.221\frac{R_6^3B_{12}B_2M_6}{M_{14}P_s}, \nonumber \\{} & {} {\omega _\textrm{WD}\simeq 0.00227\frac{R_9^3B_{4}B_2M_6}{M_{1}P_3},} \end{aligned}$$
(26)

Applying these calculations to the magnetar SGR (PSR) J1745-2900 orbiting Sagittarius A* (Sgr A*), with a magnetic field around Sgr A* of about 10 G, a magnetic dipole moment of \(\mu \approx 1.6 \times 10^{32} \mathrm G \, cm^{3}\), and a mass of \(1.4 M_{\odot }\) [63] results in \(\beta \simeq 0.67\) and \(\omega \simeq 5\). The high \(\beta \) and \(\omega \) values suggest strong magnetic interactions, possibly explaining the magnetar’s distance from Sgr A* and the absence of observed neutron stars in this region.

5.2 Rotating stellar-mass black hole

Stellar-mass black holes with ionized accretion discs can generate a dipolar magnetic field, acting as charged-magnetized particles orbiting supermassive black holes. According to Ref. [64], the magnetic field can be around \(10^8\) Gauss for stellar-mass black holes and \(10^4\) Gauss for supermassive black holes. The magnetic dipole moment of the current loop around a stellar-mass black hole is \(\mu _{cl}=(1/2)B_{cl}r_{cl}^3\), where \(B_{cl}\) is the magnetic field from the current loop, assumed to be near the ISCO. To estimate the magnetic parameter for a magnetized stellar-mass black hole with Kerr parameter \(a_*\), we first calculate the radius of the current loop using the ISCO radius expression,

$$\begin{aligned} r_\textrm{ISCO}= 3 + Z_2 \pm \sqrt{(3- Z_1)(3+ Z_1 +2 Z_2 )}, \end{aligned}$$

where \(+\) and − signs stand for retrograde and prograde orbits/loops, respectively, and

$$\begin{aligned} Z_1= & {} 1+\left( \root 3 \of {1+a_*}+ \root 3 \of {1-a_*} \right) \root 3 \of {1-a^2_*},\\ Z_2= & {} \sqrt{3 a^2_*+ Z_1^2}. \end{aligned}$$

One can estimate the parameter \(\beta \) for \(a_*=0.5\) in case of the loop magnetic field \(B_{cl}=10^8\) G (see, [64]) as

$$\begin{aligned} \beta \simeq 3.6\times 10^{-4}\frac{B_8B_2}{M_{10}}\ , \end{aligned}$$
(27)

where \(M_{1}=m_{SBH}/10M_\odot \) is the mass of the stellar-mass black hole normalized to 10\(M_\odot \). \(B_{8}=B_{cl}/(10^{8}\mathrm G)\) and \(B_{2}=B_\textrm{extr}/(10^2 \mathrm G)\). The induced electric charge and \(\omega \) parameter for the considered stellar-mass black hole are

$$\begin{aligned} q_{ind}\simeq & {} 12.3 M_{10}^2 B_8 \ \textrm{cm}\nonumber \\= & {} 1.4\times 10^{15} M_{10}^2 B_8 \ \textrm{Coulomb},\, \end{aligned}$$
(28)

and

$$\begin{aligned} \omega \simeq 4.3\times 10^{-5} M_{10}^2 B_8 B_2, \end{aligned}$$
(29)

respectively.

5.3 Electrons and protons

Our calculations show that the parameter \(\beta \) for electrons in a magnetic field normalized to \(10^2\) G is about \(\beta _e \simeq 2.3 \cdot 10^{-12} B_2\). For protons, \(\beta _p \simeq 8.2 \cdot 10^{-7} \beta _e\), and for neutrons, \(\beta _n \simeq 5.4 \cdot 10^{-7} \beta _e\). The cyclotron frequency \(\omega \) is approximately \(10^{16}\) for electrons and \(10^{13}\) for protons. These \(\beta \) values indicate that the dipole moment interaction is negligible for elementary particles, meaning electrons and protons behave primarily as charged particles in external magnetic fields. Without such fields, their behavior resembles that of neutral particles.

6 Conclusion

The no-hair theorem states that black holes cannot possess a magnetic dipole moment. They can exhibit weak magnetic properties when found in binary systems alongside a neutron star companion and an accretion disc of charged particles. A straightforward model proposed by Petterson suggests that a current loop, as it accretes a Schwarzschild black hole, produces magnetic fields resembling dipoles in the outer part of the loop while maintaining uniformity in the inner region. Thus, our current work aimed to study circular motion and collisions of charged test particles with magnetic dipole moments in both inner and outer regions. To gain insights into the motion of particles and the stability of circular orbits, we derived the effective potential, taking into account the magnetic interactions between external magnetic fields with electric charge and the magnetic dipole of the particles. Moreover, we also investigated the ISCO, angular momentum, and energy of the particles at various values of the magnetic field \(\beta \) and magnetic interaction parameter \(\omega _B\), which correspond to the interactions between the electric charge of the particle and the external magnetic field. Some of our main results are highlighted below:

  • From the analysis, we observed that in the inner region, the maximum effective potential of particles increases for \(\omega >0\), whereas it diminishes for \(\beta \) and \(\omega <0\) situations. On the other hand, in the outer region case, \(\omega >0\) decreases, whereas \(\beta >0\) and \(\omega <0\) contribute to the minima of the effective potential (see right panel of Fig. 1). However, at ISCO, the effective potential reaches its minimum.

  • In the inner region, \(\omega>\) contributes to the angular momentum and energy along the radial distance r, while \(\omega <0\) and \(\beta \) decrease it. Interestingly, \(|\omega |\) and the effect of the magnetic field considerably influence the angular momentum at a larger radial distance.

  • On the other hand, in the outer region case, \(\beta \) influences the angular momentum and energy conversely.

  • The magnetic field enhances the ISCO radius in the inner region while decreasing it along \(\omega \) in the outer region (for details, see the top row of Fig. 4). Without a magnetic field, the ISCO radius reaches its minimum and maximum in the inner and outer regions, respectively.

  • Our analysis shows that the magnetic field enhances energy efficiency in the inner and outer regions.

From the graphical illustration of angular momentum and energy at the ISCO, we found that \(\beta \) diminishes both energy and \(\mathcal{L}\) in the inner region. Interestingly, \(\omega >0\) increases and \(\omega <0\) decreases both of them (see the left columns of Fig. 5). On the other hand, in the outer region case (see the right columns of Fig. 5), these parameters influence the angular momentum and energy of particles at ISCO inversely.

We have also shown that the magnetic interaction parameter (\(\omega \)) contributes to the critical angular momentum, whereas \(\beta \) decreases it. Furthermore, we have investigated the collisional process by considering various cases near the black hole horizon and the implications of magnetic interactions on the critical angular momentum of particles that may collide and the colliding particles’ center of mass energy. From the examination of several collision situations, we can summarize our findings as follows:

  • In neutral and electrically charged particle collisions, \(\omega _1<0\) contributes to the center of mass energy in the inner and outer regions, whereas its positive interactions reduce it. Moreover, it decreases along the radial profile, which shows that the energy release rate is the highest near the black hole horizon.

  • The collision of electrically neutral particles with magnetized particles demonstrated that the magnetic field’s effect decreased the center of mass energy along the radial distance r in the inner and outer regions.

  • In the collision of electrically charged with electrically charged and magnetized particles, our result summarizes that at a small radial distance, we can get less center of mass energy compared to the collision of electrically neutral and magnetized particles (for details, please see the black dotted curves in the left panel of Fig. 11).

  • In the collisions between two magnetized and electrically charged magnetized particles, \(\omega _1<0\) significantly contributes to the center of mass energy in the inner region, while its positive value reduces it. On the contrary, in the outer region, both \(\beta \) and \(\omega _1>0\) rise, whereas, unlike the inner region, \(\omega _1<0\) reduces the center of mass energy. Our finding shows engaging reactions; due to the collisions of magnetized–magnetized particles, the behavior of the center of mass energy is completely different from its behavior in the previous cases, i.e., the collisions between non-magnetized and magnetized particles.

  • In the case of two magnetized and electrically charged particle collisions, the presence of magnetic interactions between the electric charge of the particles and the external magnetic field increases the center of mass energy in both regions.

  • The collision between electrically neutral and magnetized particles, interestingly, reflected that the magnetic field decreases the center of mass energy in both the inner and outer regions.

In the last section, we discussed astrophysical relevant objects with magnetic dipole moment and electric charge: magnetized neutron stars, white dwarfs, rotating stellar-mass black holes, and elementary particles (electrons & protons). It is obtained that the magnetic interaction parameters in neutron stars and white dwarfs are much bigger than the stellar-mass black holes and elementary particles.