1 Introduction

Recent cosmological studies [1,2,3,4,5,6,7] suggest that the Universe evolves with two accelerating phases of expansion, one at early times and one at late times. Although the latter can be explained by the presence of a cosmological constant \(\Lambda \), the inclusion of some modification was necessary due to the associated theoretical issue, the potential for dynamical behavior, and particularly the cosmological constant’s incapacity to explain the early accelerated phase. One possible approach is to stick with general relativity as the basic theory and change the universe’s matter content by adding new fields, like the dark energy sector at later times [8, 9] and/or the inflaton at earlier times [10, 11]. A second option involves altering the gravitational sector itself, creating a theory that, although having general relativity as a specific limit, generally shows more degrees of freedom [12, 13].

A variety of methods construct gravitational modifications, each moderating a different aspect of general relativity. The braneworld theories [14] comes from changing the dimensionality; the F(R) gravity [15, 16], F(G) gravity [17, 18], Lovelock theories [19, 20], etc. come from changing the Einstein-Hilbert Lagrangian; and the Horndeski/Galileon theories [21,22,23] come from adding a scalar field coupled in different ways with curvature. It is also possible to make changes using torsional invariants. This can be done in F(T) gravity [24, 25], \(F(T, T_{G})\) gravity [26], or scalar-torsion theories [27, 28], starting with the similar teleparallel formulation of gravity [29, 30]. Furthermore, we can create a large group of metric-affine theories, each with its own generic linear connection structure [31,32,33]. On the other hand, nonlinear connections can be added, as seen in Finsler and Finsler-like theories [34,35,36,37,38,39].

These affinely connected metric theories, and more specifically the Riemann–Cartan subclass of these theories [40], could be used to make a theory with a certain but not unique connection. This would result in both non-zero curvature and non-zero torsion at the same time, providing the additional degrees of freedom usually required in any gravitational modification [41]. As a result, metric-affine gravity can produce a good phenomenology that can explain both the early and late universe evolution [42,43,44,45,46]. A new paper, [42], looks at the cosmology that comes from using this kind of framework and figures out how things that can be seen change over time, like the density parameters and the effective dark energy equation-of-state parameter. Using the mini-super-space technique, they have studied cosmological behavior, focusing on the effect of the connection and expressing the theory as a deformation from both general relativity and its teleparallel counterpart. Reference [47] has investigated the observational restrictions on metric-affine F(R, T)-gravity. In [48,49,50,51,52,53,54], several metric-affine gravity theories and their applications are covered.

Recently, [55] has investigated observational constraints on some metric-affine gravity models using a wide range of observational datasets. In [56,57,58], we have investigated some exact solutions in metric-affine gravity theories with observational constraints. Recently, we have investigated some exact cosmological models in different scenarios in various modified gravity theories [59,60,61,62,63,64,65]. Recently, [66] have constructed a cosmological model in non-metricity f(Q) gravity using a special connection and statistically analyzed using information criterion AIC, BIC, and DIC to compare its compatibility with \(\Lambda \)CDM model. Recently, using different special affine connections, [67] investigated f(Q, C) gravity cosmology, including non-metricity with boundary terms. Motivated by the above discussions, in this paper, we find some new exact cosmological models in metric-affine gravity.

This paper is organized as follows: Sect. 1 is introductory. Section 2 provides a brief introduction to metric-affine gravity. Section 3 provides field equations and their exact solutions. In Sect. 4, we perform some observational constraints on different parameters using the latest datasets. Section 5 presents a discussion of the results. Section 6 provides the final conclusions.

2 Metric-affine F(R, T) gravity

In the present section, we organize a brief review of metric-affine gravity, also called F(R, T) gravity, with R as curvature and T known as torsion [41, 42]. In this gravity, the choice of a non-special connection is the key factor. Specifically, it is established that enforcing a generic connection \({\omega ^{\alpha }}_{\beta \gamma }\) one defines the torsion tensor and the curvature as [26]

$$\begin{aligned} {R^{\alpha }}_{\beta ij}= & {} {\omega ^{\alpha }}_{\beta j,i}-{\omega ^{\alpha }}_{\beta i,j}+{\omega ^{\alpha }}_{\gamma i}{\omega ^{\gamma }}_{\beta j}-{\omega ^{\alpha }}_{\gamma j}{\omega ^{\gamma }}_{\beta i} \end{aligned}$$
(1)
$$\begin{aligned} {T^{\alpha }}_{ij}= & {} {e^{\alpha }}_{j,i}-{e^{\alpha }}_{i,j}+{\omega ^{\alpha }}_{\beta i}{e^{\beta }}_{j}-{\omega ^{\alpha }}_{\beta j}{e^{\beta }}_{i} \end{aligned}$$
(2)

where \({e_{\alpha }}^{i}\partial _{i}\) is the tetrad field associated with the metric through \(g_{ij}=\eta _{\alpha \beta }{e^{\alpha }}_{i}{e^{\beta }}_{j}\), where \(\eta _{\alpha \beta }=diag(1, -1, -1, -1)\), where the The Latin and Greek indices represent the coordinate and tangent space, respectively, and the comma indicates differentiation.

There are numerous possibilities for connections. The only connection that provides vanishing torsion is the Levi–Civita \(\Gamma _{\alpha \beta \gamma }\). Henceforth, we will refer to the curvature (Riemann) tensor as \({R^{(LC)\alpha }}_{\beta ij}={\Gamma ^{\alpha }}_{\beta j,i}-{\Gamma ^{\alpha }}_{\beta i,j}+{\Gamma ^{\alpha }}_{\gamma i}{\Gamma ^{\gamma }}_{\beta j}-{\Gamma ^{\alpha }}_{\gamma j}{\Gamma ^{\gamma }}_{\beta i}\). The Weitzenböck connection, on the other hand, can be used to obtain the following: \({T^{(W)k}}_{ij}={W^{k}}_{ji}-{W^{k}}_{ij}\). This connection is curvatureless and produces only torsion. Quantities corresponding to \({W^{k}}_{ij}\) are denoted by the label “W”. The previous information suggests that the associated Ricci scalar for the Levi-Civita connection is

$$\begin{aligned} R^{(LC)}= & {} \eta ^{\alpha \beta }{e_{\alpha }}^{i}{e_{\beta }}^{j}\nonumber \\{} & {} \left[ {\Gamma ^{k}}_{ij,k}-{\Gamma ^{k}}_{ik,j}+{\Gamma ^{l}}_{ij}{\Gamma ^{k}}_{kl}-{\Gamma ^{l}}_{ik}{\Gamma ^{k}}_{jl}\right] \end{aligned}$$
(3)

while the torsion scalar corresponding to the Weitzenböck connection is

$$\begin{aligned} T^{(W)}= & {} \frac{1}{4}\left( W^{ikj}-W^{ijk}\right) \left( W_{ikj}-W_{ijk}\right) \nonumber \\{} & {} +\frac{1}{2}\left( W^{ikj}-W^{ijk}\right) \left( W_{kij}-W_{kji}\right) \nonumber \\{} & {} -\left( {W_{j}}^{ij}-{W_{j}}^{ji}\right) \left( {W^{k}}_{ik}-{W^{k}}_{ki}\right) \end{aligned}$$
(4)

The first is utilized in the Lagrangian of general relativity and in all curvature-based modified gravities, such as in F(R) gravity [15], whereas the second is utilized in the Lagrangian of the teleparallel equivalent of general relativity and in all torsion-modified gravities, such as in F(T) gravity [13].

metric-affine gravity uses a non-special connection with simultaneous non-zero curvature and torsion [42]. Since general relativity and its teleparallel counterpart, which both have two degrees of freedom that correspond to the massless graviton, don’t have any extra degrees of freedom, the theory that comes out of them will usually have them, even if the Lagrangian that is used is simple. Here, we consider the action as

$$\begin{aligned} I=\int {d^{4}x~e\left[ \frac{1}{2\kappa ^{2}}F(R,T)+L_{m}\right] } \end{aligned}$$
(5)

where the gravitational constant is \(\kappa ^{2}=8\pi G\), the matter Lagrangian \(L_{m}\) has also been introduced for completeness, and \(e=\det (e^{\alpha }_{i})=\sqrt{-g}\). Take note that the arbitrary function F(R, T) has two variables, R and T, which represent the curvature and torsion scalars, respectively, corresponding to the non-special connection employed [26].

$$\begin{aligned} T=\frac{1}{4}T^{ijk}T_{ijk}+\frac{1}{2}T^{ijk}T_{kji}-{T_{j}}^{ji}{T^{k}}_{ki}, \end{aligned}$$
(6)
$$\begin{aligned} R=R^{(LC)}+T-2{{T_{j}}^{ji}}_{;i} \end{aligned}$$
(7)

where the covariant differentiation with regard to the Levi-Civita connection is indicated by the symbol (;). So, while R depends on the tetrad and its first derivative as well as the connection and its first derivative, it also depends on the second tetrad derivative because of the final term in (7). In contrast, T depends on the tetrad field, its first derivative, and the connection. Therefore, we can finally write using Eqs. (4), (6), and (7).

$$\begin{aligned} R= & {} R^{(LC)}+u, \end{aligned}$$
(8)
$$\begin{aligned} T= & {} T^{(W)}+v. \end{aligned}$$
(9)

The scalar u is contingent upon the tetrad, its first and second derivatives, the connection, and its first derivative, whereas the scalar v is contingent upon the tetrad, its first derivative, and the connection.

The numbers u and v quantify the effect of the specific but non-special imposed connection. If this link turns into the Levi–Civita connection, then \(u = 0\) and \(v = -T^{(W)}\). This makes the above theory the standard F(R) gravity, which, under \(F(R) = R\), coincides with general relativity. Conversely, if the connection is the Weitzenböck one, then \(v = 0\) and \(u = -R^{(LC)}\), and so the theory corresponds with F(T) gravity. For \(F(T) = T\), this gravity thus becomes the teleparallel counterpart of general relativity.

3 Field equations and solutions

We put all of this into a cosmological framework and derive the corresponding field equations that govern the evolution of the universe [42]. We consider the FLRW flat Friedmann homogeneous and isotropic geometry spacetime metric.

$$\begin{aligned} ds^{2}=dt^{2}-a^{2}(t)\delta _{\mu \nu }dx^{\mu }dx^{\nu }, \end{aligned}$$
(10)

which is equivalent to the tetrad \(e^{\alpha }_{i}=diag[1, a(t), a(t), a(t)]\), in which the scale factor is denoted by a(t). In this situation, the torsion and curvature scalars \(T^{(W)}=-6\left( \frac{{\dot{a}}}{a}\right) ^{2}\) and \(R^{(LC)}=6\left( \frac{\ddot{a}}{a}+\left( \frac{{\dot{a}}}{a}\right) ^{2}\right) \) are easily found, respectively. We further consider the conventional substitution \(L_{m}=-\rho _{m}(a)\) [68,69,70]. Ultimately, in light of the previous conversation regarding the interdependence of u and v, we consistently enforce that \(u=u(a, {\dot{a}}, \ddot{a})\) and \(v=v(a, {\dot{a}})\).

In this work, we aim to investigate the cosmic behavior resulting just from the non-special connection in metric-affine gravity. Since the coupling coefficient of R can be absorbed into \(\kappa ^{2}\), we remove it. Instead, we concentrate on the simplest case, where the involved arbitrary function is trivial, which is \(F(R, T) = R + \lambda T\). Be aware that the Lagrangian does not explicitly take into account a cosmological constant term. The spacetime metric (10) is added to the action (5), and we get \(I=\int {Ldt}\) for this Lagrangian selection [55] as

$$\begin{aligned} L= & {} \frac{3}{\kappa ^{2}}[\lambda +1]a{\dot{a}}^{2}-\frac{a^{3}}{2\kappa ^{2}}[u(a, {\dot{a}}, \ddot{a})\nonumber \\{} & {} +\lambda v(a, {\dot{a}})]+a^{3}\rho _{m}(a). \end{aligned}$$
(11)

Taking the Hamiltonian constraint \(H={\dot{a}}\left[ \frac{\partial L}{\partial {\dot{a}}}-\frac{\partial }{\partial t}\frac{\partial L}{\partial \ddot{a}}\right] +\ddot{a}\frac{\partial L}{\partial \ddot{a}}-L=0\) and extracting the equations of motion for a(t), we have the Friedmann equations as [55]

$$\begin{aligned}{} & {} 3(1+\lambda )H^{2}-\frac{1}{2}[Ha(u_{{\dot{a}}}+\lambda v_{{\dot{a}}})-(u+\lambda v)\nonumber \\{} & {} \quad +au_{\ddot{a}}({\dot{H}}-2H^{2})]=\kappa ^{2}\rho _{m} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} (1+\lambda )(2{\dot{H}}+3H^{2})-\frac{1}{6}\left[ 3Ha(u_{{\dot{a}}}+\lambda v_{{\dot{a}}})-3(u+\lambda v)\right. \nonumber \\{} & {} \quad -a(u_{a}+\lambda v_{a}-{\dot{u}}_{{\dot{a}}}-\lambda {\dot{v}}_{{\dot{a}}}) \nonumber \\{} & {} \quad \left. -3a({\dot{H}}+3H^{2})u_{\ddot{a}}-6Ha{\dot{u}}_{\ddot{a}}-a\ddot{u}_{\ddot{a}}\right] =-\kappa ^{2}p_{m} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} {\dot{\rho }}_{m}+3H(\rho _{m}+p_{m})+\frac{1}{2\kappa ^{2}}\nonumber \\{} & {} \quad \times \left[ {\dot{a}}(u_{a}+\lambda v_{a})-({\dot{u}}+\lambda {\dot{v}})+\ddot{a}(u_{{\dot{a}}}+\lambda v_{{\dot{a}}})\right. \nonumber \\{} & {} \quad +(3{\dot{a}}{\dot{H}}+{\dot{a}}H^{2}+a{\ddot{H}})u_{\ddot{a}}\nonumber \\{} & {} \quad \left. +(6{\dot{a}}H+a{\dot{H}}-2a H^{2}){\dot{u}}_{\ddot{a}}+{\dot{a}}\ddot{u}_{\ddot{a}}\right] =0 \end{aligned}$$
(14)

where H is the Hubble parameter defined by \(H=\frac{{\dot{a}}}{a}\), \(p_{m}\) denotes the matter pressure, and the subscripts \(a, {\dot{a}}, \ddot{a}\) indicate the partial derivatives with respect to these arguments.

We now find the solution to the above field equations for two different choices of u and v, which we investigate in the next two sub-sections. As per definitions of u and v, in the first model, we choose \(u=k_{1}H-k_{2}\), \(v=k_{3}aH-k_{4}\), and in the second model, we consider \(u=k_{1}({\dot{H}}+H^{2})-k_{2}\), \(v=k_{3}aH-k_{4}\) with \(k_{i}\)’s \(i=1, 2, 3, 4\) constants.

3.1 Model-I

In this model, we choose \(u=k_{1}H-k_{2}\) and \(v=k_{3}aH-k_{4}\) with \(k_{i}\)’s \(i=1, 2, 3, 4\) constants and \(H=\frac{{\dot{a}}}{a}\), then the above field Eqs. (12) and (13) become

$$\begin{aligned} 3(1+\lambda )H^{2}-\frac{1}{2}(k_{2}+\lambda k_{4})= & {} \kappa ^{2}\rho _{m} \end{aligned}$$
(15)
$$\begin{aligned} (1+\lambda )(2{\dot{H}}+3H^{2})-\frac{1}{2}(k_{2}+\lambda k_{4})= & {} -\kappa ^{2}p_{m} \end{aligned}$$
(16)
$$\begin{aligned} {\dot{\rho }}_{m}+3H(\rho _{m}+p_{m})= & {} 0 \end{aligned}$$
(17)

Taking the non-relativistic matter pressure \(p_{m}\approx 0\) in (16) and rewriting the Eq. (16) as

$$\begin{aligned} 2\frac{\ddot{a}}{a}+\left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{k_{2}+\lambda k_{4}}{2(1+\lambda )}=0,\quad \lambda \ne -1. \end{aligned}$$
(18)

Solving Eq. (18) for the scale factor a(t), we get

$$\begin{aligned} a(t)=\left[ \frac{3\sqrt{3}c_{2}e^{\frac{\sqrt{3n_{1}}}{2}t}-\sqrt{3}c_{1}e^{-\frac{\sqrt{3n_{1}}}{2}t}}{6\sqrt{n_{1}}}\right] ^{\frac{2}{3}}\!\!,\quad n_{1}>0, \end{aligned}$$
(19)

where \(c_{1}, c_{2}\) are arbitrary constants and \(n_{1}=\frac{k_{2}+\lambda k_{4}}{2(1+\lambda )}\), \(\lambda \ne -1\). Without loss of generality, we choose \(c_{1}=k\sqrt{3}, c_{2}=\frac{k}{\sqrt{3}}\) so that we can put the scale factor in the following simplified form (hyperbolic expansion law cosmology).

$$\begin{aligned} a(t)=\left[ \frac{k}{\sqrt{n_{1}}}\sinh {\left( \frac{\sqrt{3n_{1}}}{2}t\right) }\right] ^{\frac{2}{3}},\quad n_{1}>0 \end{aligned}$$
(20)

Alternatively, if we choose \(c_{1}=0\), then we find the exponential expansion law cosmology as \(a(t)=\frac{\sqrt{3}c_{2}}{2\sqrt{n_{1}}}e^{\sqrt{\frac{n_{1}}{3}}t}\) which gives a constant deceleration parameter q that reveals either a decelerating or accelerating expanding universe, but we seek a transit phase (decelerating-accelerating) expanding universe model. To investigate the model, we consider the first choice of \(c_{1}, c_{2}\). Using the scale factor from (20), we found the Hubble parameter (\(H=\frac{{\dot{a}}}{a}\)) and the deceleration parameter (\(q=-\frac{a\ddot{a}}{{\dot{a}}^{2}}\)), which are

$$\begin{aligned} H(t)=\sqrt{\dfrac{n_{1}}{3}}\coth {\left( \frac{\sqrt{3n_{1}}}{2}t\right) }, \end{aligned}$$
(21)
$$\begin{aligned} q(t)=-1+\frac{3}{2}sech^{2}{\left( \frac{\sqrt{3n_{1}}}{2}t\right) }. \end{aligned}$$
(22)

Now we use the relationship \(a(t)=a_{0}(1+z)^{-1}\) [8], in (21), (22), with the present value of scale factor \(a_{0}=1\) in standard convention and z as the redshift, whose positive values show the early evolution of the universe while the negative values of z reveal the future predictions, and \(z=0\) represents the present stage of the universe, we obtain the Hubble parameter H(z) and deceleration parameter q(z) as

$$\begin{aligned} H(z)= & {} \frac{1}{\sqrt{3}}\sqrt{k^{2}(1+z)^{3}+\frac{k_{2}+\lambda k_{4}}{2(1+\lambda )}} \end{aligned}$$
(23)
$$\begin{aligned} q(z)= & {} -1+\frac{3}{2}\frac{k^{2}(1+z)^{3}}{k^{2}(1+z)^{3}+\frac{k_{2}+\lambda k_{4}}{2(1+\lambda )}}. \end{aligned}$$
(24)

Now we’ll talk about two more geometrical parameters, which were suggested in [71]. They are called statefinder parameters r and s, and they show how the universe’s geometry has changed over time and the different stages of dark energy models [71,72,73]. We define these parameters in terms of a scale factor.

$$\begin{aligned} r=\frac{\dddot{a}}{aH^{3}},\quad s=\frac{r-1}{3(q-\frac{1}{2})} \end{aligned}$$
(25)

Using the scale factor (20) in (25), we obtain the statefinder diagnostic parameters r(t) and s(t) as below.

$$\begin{aligned} r(t)= & {} 1-3~sech^{2}{\left( \frac{\sqrt{3n_{1}}}{2}t\right) } \end{aligned}$$
(26)
$$\begin{aligned} s(t)= & {} \frac{2~sech^{2}{\left( \frac{\sqrt{3n_{1}}}{2}t\right) }}{3\left[ 1-sech^{2}{\left( \frac{\sqrt{3n_{1}}}{2}t\right) }\right] } \end{aligned}$$
(27)

Now we define the effective equation of state (EoS) parameter \(\omega _{eff}\) by comparing the Eqs.  (15) and (16) to the standard Friedmann equations in a flat spacetime universe, as

$$\begin{aligned} \omega _{eff}=\frac{p_{eff}}{\rho _{eff}} \end{aligned}$$
(28)

or

$$\begin{aligned} \omega _{eff}=-1+\frac{2n_{1}(\kappa ^{2}\rho _{m0}-\lambda k^{2})}{2n_{1}(\kappa ^{2}\rho _{m0}-\lambda k^{2})+(k_{2}+\lambda k_{4}-2n_{1}\lambda )k^{2}\sinh ^{2}{\left( \frac{\sqrt{3n_{1}}}{2}t\right) }}. \end{aligned}$$
(29)

Also, from Eq. (15), we can derive the total energy density parameter as

$$\begin{aligned} \Omega _{m}+\Omega _{F}=1, \end{aligned}$$
(30)

where

$$\begin{aligned} \Omega _{m}=\frac{\kappa ^{2}\rho _{m}}{3H^{2}},\quad \Omega _{F}=\frac{k_{2}+\lambda k_{4}}{6H^{2}}-\lambda . \end{aligned}$$
(31)

The matter energy density parameter \(\Omega _{m}\) and the dark energy density parameter \(\Omega _{F}\) are named respectively due to the gravity function F(R, T).

In the field Eqs. (15) and (16), for \(\lambda =0\), one can obtain Einstein’s field equations in GR with cosmological constant as \(\Lambda =\frac{k_{2}}{2}\). And in this case, \(\Omega _{F}=\frac{k_{2}}{6H^{2}}=\frac{\Lambda }{3H^{2}}=\Omega _{\Lambda }\). Also, for \(\lambda \ne 0\), we can obtain varying \(\Lambda \)-term as a function of Hubble parameter H, as \(\Lambda (H)=\frac{1}{2}(k_{2}-6\lambda H^{2})\).

3.2 Model-II

In this model, we choose \(u=k_{1}({\dot{H}}+H^{2})-k_{2}\) and \(v=k_{3}aH-k_{4}\) with \(k_{i}\)’s \(i=1, 2, 3, 4\) constants, and \({\dot{H}}+H^{2}=\frac{\ddot{a}}{a}\). In Eqs. (12) and (13), we obtain the following simplified field equations:

$$\begin{aligned}{} & {} \frac{3}{2}(2+2\lambda +k_{1})H^{2}-\frac{1}{2}(k_{2}+\lambda k_{4})=\kappa ^{2}\rho _{m} \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \frac{1}{3}(3+k_{1}+3\lambda )(2{\dot{H}}+3H^{2})-\frac{1}{2}(k_{2}+\lambda k_{4})=-\kappa ^{2}p_{m}\nonumber \\ \end{aligned}$$
(33)

Taking the non-relativistic matter pressure \(p_{m}\approx 0\) in Eq. (33), we rewrite it as

$$\begin{aligned} 2\frac{\ddot{a}}{a}+\left( \frac{{\dot{a}}}{a}\right) ^{2}-\frac{3(k_{2}+\lambda k_{4})}{2(3+k_{1}+3\lambda )}=0 \end{aligned}$$
(34)

Solving Eq. (34) for scale factor a(t), we get

$$\begin{aligned} a(t)=\left[ \frac{3\sqrt{3}c_{4}e^{\frac{\sqrt{3n_{2}}}{2}t}-\sqrt{3}c_{3}e^{-\frac{\sqrt{3n_{2}}}{2}t}}{6\sqrt{n_{2}}}\right] ^{\frac{2}{3}},\quad n_{2}>0 \end{aligned}$$
(35)

where \(c_{3}, c_{4}\) are arbitrary constants and \(n_{2}=\frac{3(k_{2}+\lambda k_{4})}{2(3+k_{1}+3\lambda )}\). Without loss of generality, we choose \(c_{3}=k\sqrt{3}, c_{4}=\frac{k}{\sqrt{3}}\) so that we can write the scale factor as the hyperbolic expansion law.

$$\begin{aligned} a(t)=\left[ \frac{k}{\sqrt{n_{2}}}\sinh {\left( \frac{\sqrt{3n_{2}}}{2}t\right) }\right] ^{\frac{2}{3}} \end{aligned}$$
(36)

Using this scale factor as in Eq. (36), we derive the Hubble parameter H(t) and deceleration parameter q(t) as given below:

$$\begin{aligned} H(t)= & {} \sqrt{\dfrac{n_{2}}{3}}\coth {\left( \frac{\sqrt{3n_{2}}}{2}t\right) } \end{aligned}$$
(37)
$$\begin{aligned} q(t)= & {} -1+\frac{3}{2}sech^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) } \end{aligned}$$
(38)

Again, we can express these in terms of redshift z as

$$\begin{aligned} H(z)= & {} \frac{1}{\sqrt{3}}\sqrt{k^{2}(1+z)^{3}+\frac{3(k_{2}+\lambda k_{4})}{2(3+k_{1}+3\lambda )}} \end{aligned}$$
(39)
$$\begin{aligned} q(z)= & {} -1+\frac{3}{2}\frac{k^{2}(1+z)^{3}}{k^{2}(1+z)^{3}+\frac{3(k_{2}+\lambda k_{4})}{2(3+k_{1}+3\lambda )}} \end{aligned}$$
(40)

In model II, we derive the statefinder diagnostic parameters r(t) and s(t).

$$\begin{aligned} r(t)= & {} 1-3~sech^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) } \end{aligned}$$
(41)
$$\begin{aligned} s(t)= & {} \frac{2~sech^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) }}{3\left[ 1-sech^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) }\right] } \end{aligned}$$
(42)

For model II, we derive the effective EoS parameter as

$$\begin{aligned} \omega _{eff}=-1+\frac{3n_{2}(2\kappa ^{2}\rho _{m0}-k_{1}k^{2}-2\lambda k^{2})-n_{2}k_{1}k^{2}\sinh ^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) }}{3n_{2}(2\kappa ^{2}\rho _{m0}-k_{1}k^{2}-2\lambda k^{2})-3k^{2}(2n_{2}\lambda +n_{2}k_{1}-k_{2}-k_{4}\lambda )\sinh ^{2}{\left( \frac{\sqrt{3n_{2}}}{2}t\right) }} \end{aligned}$$
(43)

Also, from Eq. (32), we can derive the total energy density parameter for model II, as

$$\begin{aligned} \Omega _{m}+\Omega _{F}=1, \end{aligned}$$
(44)

where

$$\begin{aligned} \Omega _{m}=\frac{\kappa ^{2}\rho _{m}}{3H^{2}},\quad \Omega _{F}=\frac{k_{2}+\lambda k_{4}}{6H^{2}}-\lambda -\frac{1}{2}k_{1}. \end{aligned}$$
(45)

Now, we can find the original Einstein’s field equations with cosmological constant \(\Lambda \)-term in GR by substituting \(\lambda =0, k_{1}=0\), with \(\Lambda =\frac{k_{2}}{2}\) otherwise \(\Lambda (H)=\frac{1}{2}[k_{2}-(3k_{1}+6\lambda ) H^{2}]\).

Fig. 1
figure 1

The contour plots of \(H_{0}, \Omega _{m0}, \lambda \) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of H(z) datasets for Model-I

Full size image
Fig. 2
figure 2

The contour plots of \(H_{0}, \Omega _{m0}, \lambda \) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of H(z) datasets for Model-II

Full size image

4 Observational constraints

In this section, we make observational constraints on the model parameters with observational datasets in our derived model. For this, we use the freely available emcee program at [74] to perform an MCMC (Monte Carlo Markov Chain) analysis so that we can compare our derived model with observational datasets. To limit the cosmological and model parameters, the MCMC sampler changes the parameter values in a likely range of priors and looks at the parameter space posteriors. In this section, we evaluate the compatibility of the solution in the model with the cosmic chronometer (CC) data and the Pantheon datasets. These datasets pertain to the observed cosmos during a recent period.

4.1 Hubble datasets H(z)

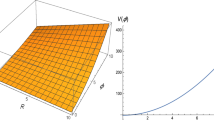
For both theoretical and observational cosmologists, the Hubble parameter is one of the most important cosmological parameters for studying the evolution of the universe. It is possible to find observed values for Hubble datasets H(z) with redshift z. In order to find the best values for model parameters with error bars in the redshift range \(0.07\le z \le 1.965\), we first use the Monte Carlo Markov Chain (MCMC) simulation to compare our derived Hubble function from the field equations with the observed values of the 31 cosmic chronometer data points (Hubble data) [75, 76]. These values were found using the differential ages (DA) of galaxies method. We can get a rough idea of the model parameters \(H_{0}\), \(\Omega _{m0}\), and \(\lambda \) by minimizing the \(\chi ^{2}\) function, which is the same thing as maximizing the likelihood function and is written as

$$\begin{aligned} \chi _{CC}^{2}(\phi )=\sum _{i=1}^{i=N}\frac{[H_{ob}(z_{i})-H_{th}(\phi , z_{i})]^{2}}{\sigma _{H(z_{i})}^{2}}, \end{aligned}$$

where N denotes the total amount of data, \(H_{ob},~H_{th}\), respectively, the observed and hypothesized datasets of H(z) and standard deviations are displayed by \(\sigma _{H(z_{i})}\). Here \(\phi =(H_{0}, \Omega _{m0}, \lambda )\).

In order to calibrate the CC datasets, we utilize Bayesian statistical analysis for Markov chain Monte Carlo (MCMC) simulation. To accomplish this, we utilize the emcee package developed by Foreman-Mackey et al. [74]. We have minimized the chi-squared statistic, \(\chi _{CC}^{2}(\phi )\), to determine the optimal values for the model’s parameters. Table 1 presents these values.

As we can see in Figs. 1 and 2, the contour plots of Model-I and Model-II show how the model parameters compare to Hubble datasets (H(z)) using MCMC analysis. We got the best fit values for the model parameters \(H_{0}, \Omega _{m0}, \lambda \) by using different parameter values in the range (40, 100), (0, 1), and (0, 0.7), with confidence levels of \(1-\sigma \) and \(2-\sigma \), respectively. Table 1 lists the best fit values for each model separately. We have estimated the best fit values of model parameter \(\lambda =0.14_{-0.25}^{+0.49}, 0.38_{-0.16}^{+0.26}\) with \(\Omega _{m0}=0.38\pm 0.15, 0.459_{-0.12}^{+0.096}\) for Model-I and Model-II, respectively. Recently, [55] estimated the value of \(\lambda \) as \(\lambda =0.491_{-0.533}^{+0.387}, 0.537_{-0.550}^{+0.403}\) with \(\Omega _{m0}=0.425_{-0.146}^{+0.107}, 0.339_{-0.122}^{+0.093}\), respectively, in two different models. We have estimated the value of the Hubble constant as \(H_{0}=67.4\pm 3.1, 67.8\pm 2.9 \) Km/s/Mpc, respectively, for two models, Model-I and Model-II, along CC datasets. Recently, the value of the Hubble constant was measured as \(H_{0}=69.8\pm 1.3\) Km s\(^{-1}\) Mpc\(^{-1}\) in [77], and in [78], it was measured as \(H_{0}=69.7\pm 1.2\) Km s\(^{-1}\) Mpc\(^{-1}\). Recently, we measured the value of \(H_{0}\) as \(H_{0}=68.3721\pm 1.7205\) Km/s/Mpc in [61], \(H_{0}=68.3721\pm 1.65678\) Km/s/Mpc in [59] and \(H_{0}=71.66123\pm 0.33061\) in [60].

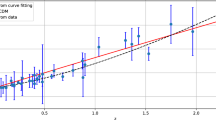
Table 1 The MCMC results in H(z) datasets analysis
Full size table

We have considered the Hubble function for the \(\Lambda \)CDM model as \(H(z)=H_{0}\sqrt{\Omega _{m0}(1+z)^{3}+\Omega _{\Lambda }}\) with \(\Omega _{\Lambda }=1-\Omega _{m0}\) to compare our derived models I and II. That’s Fig. 3, which shows the contour plots of \(H_{0}\) and \(\Omega _{m0}\) at \(1-\sigma \) and \(2-\sigma \) confidence levels in MCMC analysis of H(z) datasets for \(\Lambda \)CDM. We have found the best fit values of the Hubble constant \(H_{0}=67.7\pm 3.1\) Km/s/Mpc and the total matter energy density parameter \(\Omega _{m0}=0.333_{-0.07}^{+0.05}\), which are mentioned in Table 1. The Hubble error bar plots of 31 datasets with a best fit shape of H(z) are shown in Fig. 4. These shapes were found in Models I, II, and \(\Lambda \)CDM, in that order.

4.2 Apparent magnitude m(z)

The relationship between luminosity distance and redshift is one of the main observational techniques used to track the universe’s evolution. The expansion of the cosmos and the redshift of the light from distant brilliant objects are taken into consideration when calculating the luminosity distance (\(D_{L}\)) in terms of the cosmic redshift (z). It is provided as

$$\begin{aligned} D_{L}=a_{0} r (1+z), \end{aligned}$$
(46)

where the radial coordinate of the source r, is established by

$$\begin{aligned} r = \int ^r_{0}dr = \int ^t_{0}\frac{cdt}{a(t)} = \frac{1}{a_{0}}\int ^z_0\frac{cdz'}{H(z')}, \end{aligned}$$
(47)

where we have used \( dt=dz/{\dot{z}}, {\dot{z}}=-H(1+z)\).

Fig. 3
figure 3

The contour plot of \(H_{0}\) and \(\Omega _{m0}\) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of H(z) datasets for \(\Lambda \)CDM

Full size image
Fig. 4
figure 4

The Hubble error bar plots of H(z) datasets (CC datasets) over z, respectively for Model-I, Model-II and \(\Lambda \)CDM

Full size image

Consequently, the following formula determines the luminosity distance:

$$\begin{aligned} D_{L}=c(1+z)\int ^z_0\frac{dz'}{H(z')}. \end{aligned}$$
(48)

Researchers widely use supernovae (SNe) as standard candles to study the cosmic expansion rate with observed apparent magnitude (\(m_{o}\)). The supernovae surveys that found different types of supernovae at different sizes led to the Pantheon sample SNe data set, which has 1048 data points in the range \(0.01\le z \le 2.26\). The theoretical apparent magnitude (m) of these standard candles is defined as [79]

$$\begin{aligned} m(z)=M+ 5~\log _{10}\left( \frac{D_{L}}{Mpc}\right) +25. \end{aligned}$$
(49)

where M is the absolute magnitude. The luminosity distance is measured in terms of length. Based on \(D_{L}\), the Hubble-free luminosity distance (\(d_{L}\)) may be written as \(d_{L}\equiv \frac{H_{0}}{c}D_{L}\), which is a dimensionless quantity. Thus, we can simplify m(z) as given below

$$\begin{aligned} m(z)=M+5\log _{10}{d_{L}}+5\log _{10}\left( \frac{c/H_{0}}{Mpc}\right) +25. \end{aligned}$$
(50)
Fig. 5
figure 5

The contour plot of \(H_{0}\), \(\Omega _{m0}\) and \(\lambda \) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of Pantheon SNe Ia datasets for Model-I

Full size image
Fig. 6
figure 6

The contour plot of \(H_{0}\), \(\Omega _{m0}\) and \(\lambda \) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of Pantheon SNe Ia datasets for Model-II

Full size image

The degeneracy between M and \(H_{0}\) may be observed using the equation above, and it is constant in the \(\Lambda \)CDM background [79, 80]. Redefinition allows us to merge these degenerate parameters.

$$\begin{aligned} {\mathcal {M}}\equiv M+5\log _{10}\left( \frac{c/H_{0}}{Mpc}\right) +25. \end{aligned}$$
(51)

The dimensionless parameter \({\mathcal {M}}\) can be expressed as \({\mathcal {M}}=M-5\log _{10}(h)+42.39\), where \(H_{0}=h\times 100\) Km/s/Mpc. In the Markov Chain Monte Carlo (MCMC) analysis, we employ this parameter along with the corresponding \(\chi ^{2}\) value for the Pantheon data, as given in [80].

$$\begin{aligned} \chi ^{2}_{P}=V_{P}^{i}C_{ij}^{-1}V_{P}^{j} \end{aligned}$$

The expression \(V_{P}^{i}\) is defined as the difference between \(m_{o}(z_{i})\) and m(z). The matrix \(C_{ij}\) is the inverse of the covariance matrix, and the value of m(z) is determined by Eq. (14).

Figures 5 and 6 show the contour plots of model parameters for Model-I and Model-II, respectively. The Pantheon SNe Ia datasets, analyzed using MCMC, display the apparent magnitude m(z). We found the best values for the model parameters \({\mathcal {M}}, \Omega _{m0}, \lambda \) by using values in the range (23, 24) for \({\mathcal {M}}\), (0, 1) for \(\Omega _{m0}\), and (0, 0.7) for \(\lambda \), with confidence levels of \(1-\sigma \) and \(2-\sigma \). Table 2 lists the best fit values for various model parameters in each of the two models. We have estimated the best fit values of model parameter \(\lambda =0.47_{-0.22}^{+0.26}, 0.47_{-0.20}^{+0.22}\) for Model-I and Model-II, respectively, at a fixed value of \(k_{1}=0.2\). Recently, [55] estimated the value of \(\lambda =0.491_{-0.533}^{+0.387}, 0.537_{-0.550}^{+0.403}\), respectively, in two different models. For two different models, we estimated the value of parameter \({\mathcal {M}}=23.807_{-0.013}^{+0.011}, 23.811\pm 0.010\), while for \(\Lambda \)CDM, it is found as \({\mathcal {M}}=23.810\pm 0.011\). Recently, [81] estimated the value of \({\mathcal {M}}=23.809\pm 0.013\). We found that \(\Omega _{m0}\) fits best with the Pantheon SNe Ia datasets for \(\Lambda \)CDM. In the MCMC analysis of the Pantheon SNe Ia datasets for Lambda CDM, the best fit value for the total matter energy density parameter is currently \(\Omega _{m0}=0.300\pm 0.021\) at \(1-\sigma \) and \(2-\sigma \) confidence levels (Fig. 7). Figure 8 shows the apparent magnitude error bar plots with the best fit shape of m(z) derived for the models I, II, and \(\Lambda \)CDM.

5 Result and discussion

We can relate our fitted parameters with derived dimensionless model parameters for model-I as \(k^{2}=\frac{3\Omega _{m0}H_{0}^{2}}{1+\lambda }\) and \(k_{2}+\lambda k_{4}=6(1+\lambda -\Omega _{m0})H_{0}^{2}\) and for model-II as \(k^{2}=3H_{0}^{2}\left[ \frac{3\Omega _{m0}-\frac{1}{2}k_{1}}{3+k_{1}+3\lambda }\right] \) and \(k_{2}+\lambda k_{4}=6(1+\lambda +\frac{1}{2}k_{1}-\Omega _{m0})H_{0}^{2}\). In this paper, we solved the modified field equations for two different cases of u and v in the dust fluid source and found two exact solutions in the form of scale factor a(t), called model-I and model-II. We have found a hyperbolic solution in each case (see (20) and (36)). The scale factor a(t) is the most useful parameter to explore the various properties of an expanding universe, and it is a dimensionless parameter. For the estimated values of model parameters along CC datasets, we have plotted the variation of scale factor over the cosmic time t (measured in \(\times \)978 Gyrs), which is shown in Fig. 9a for models I, II, and \(\Lambda \)CDM model. It can be observed that a(t) is an increasing function of cosmic time t, and as \(t\rightarrow t_{0}\) (present time), then \(a(t)\rightarrow 1\) (i.e., \(a(t_{0})\)). Using this technique, we can estimate the present age of the universe as \(0\le t \le t_{0}\) from Fig. 9a by estimating the cosmic time \(t_{0}\) at which \(a(t_{0})=1\). Therefore, we have found the present age of the universe for both derived universe models, respectively, as \(t_{0}=13.58_{-0.51}^{+1.70}\) Gyrs for model-I and \(t_{0}=13.98_{-0.72}^{+1.51}\) Gyrs for model-II, while for \(\Lambda \)CDM model, it is found as \(t_{0}=13.52\pm 1.61\) Gyrs. In general, the present age of the universe can be expressed as \(t_{0}=978\times \sqrt{\frac{8(1+\lambda )}{3(k_{2}+\lambda k_{4})}}\times \sinh ^{-1}\left( k\sqrt{\frac{k_{2}+\lambda k_{4}}{2k^{2}(1+\lambda )}}\right) \) Gyrs. Moreover, one can find from the derived scale factor a(t) that as \(t\rightarrow \infty \), then \(a(t)\rightarrow \infty \) in the future universe.

A dimensionless parameter q(t), which is called the deceleration parameter, changes over time. This parameter can be found by figuring out the scale factor a(t). This is because the deceleration parameter is defined as \(q(t)=-\frac{a\ddot{a}}{{\dot{a}}^{2}}\). Equation (22) or (24) denotes the deceleration parameter (DP) for the model-I, and Eq. (38) or (40) denotes DP for the model-II. The geometrical evolution of the DP q(z) for both models with \(\Lambda \)CDM model is depicted in Fig. 9b. From Fig. 9b, one can observe that q(z) is an increasing function of redshift z and through the evolution, it shows a signature-flipping (decelerating to accelerating) point for both models. The present value of DP is measured at \(t=t_{0}\) or at \(z=0\) as \(q_{0}=-0.50_{-0.1123}^{+0.0122}\) for the model-I and \(q_{0}=-0.5586_{-0.0851}^{+0.0171}\) for model II, while for \(\Lambda \)CDM model, it is found as \(q_{0}=-0.5005_{-0.1050}^{+0.1750}\), which indicates our derived models are in the accelerating phase of expansion at present (at \(z=0\)). This picture (Fig. 9b) also shows that as \(z\rightarrow -1\), \(q\rightarrow -1\) (late-time acceleration) and as \(z\rightarrow \infty \), \(q\rightarrow 0.5\) (early decelerating phase of an expanding universe) are both taken into account. These models are unable to explain the early accelerating (inflation) scenario of the universe’s evolution. The redshift at which the deceleration parameter q(z) vanishes is called the transition redshift, and it is denoted by \(z_{t}\). The transition redshift is estimated as \(z_{t}=0.5874_{-0.0197}^{+0.2130}\) for the model-I and \(z_{t}=0.6865_{-0.0303}^{+0.1719}\) for the model-II, while for the \(\Lambda \)CDM, it is found as \(z_{t}=0.5882\pm 0.1881\). The redshift z is dimensionless quantity. In general, one can derive the \(z_{t}\) from the expression of the deceleration parameter q(z) for models I and II, as

$$\begin{aligned} z_{t}= & {} \left[ \frac{k_{2}+\lambda k_{4}}{k^{2}(1+\lambda )}\right] ^{\frac{1}{3}}-1,~~\text {and}~~\nonumber \\ z_{t}= & {} \left[ \frac{3(k_{2}+\lambda k_{4})}{k^{2}(3+k_{1}+3\lambda )}\right] ^{\frac{1}{3}}-1.~~~~\lambda \ne -1. \end{aligned}$$
(52)
Table 2 The MCMC results in Pantheon SNe Ia datasets analysis
Full size table
Fig. 7
figure 7

The contour plot of \(H_{0}\) and \(\Omega _{m0}\) at \(1-\sigma \) and \(2-\sigma \) confidence level in MCMC analysis of Pantheon SNe Ia datasets for \(\Lambda \)CDM

Full size image
Fig. 8
figure 8

The apparent magnitude error bar plots with best fit curve of m(z) in the analysis of Pantheon SNe Ia datasets for the Model-I, II and \(\Lambda \)CDM

Full size image

For the \(\Lambda \)CDM model, the general value of the transition redshift is found as \(z_{t}=(2\Omega _{\Lambda 0}/\Omega _{m0})^{1/3}-1\approx 0.6\). This transition value shows that the universe model is in a decelerating phase of expansion for \(z>z_{t}\) and the model is in an accelerating phase of expansion for \(z<z_{t}\). Recently, this transition redshift \(z_{t}=0.74\pm 0.05\) was obtained in [82], and in [83] it was measured as \(z_{t}=0.74\pm 0.04\). In [84], this transition redshift is obtained as \(z_{t}=0.72\pm 0.05\), and in 2018, [85] has suggested that the transition redshift varies over \(0.33< z_{t} < 1.0\). Recently, we have found this transition redshift \(z_{t}\approx 0.7\) in [86, 87]. Thus, the transition redshift \(z_{t}=0.5874_{-0.0197}^{+0.2130}, 0.6865_{-0.0303}^{+0.1719}\) obtained in our derived model is in good agreement with recent observed values in [82,83,84,85,86,87].

The dimensionless, energy density parameters \(\Omega _{m}\) and \(\Omega _{F}\) are derived in Eqs.  (30) and (31) for the model-I, and it is defined in Eqs.  (44) and (45) for the model-II. For the flat spacetime universe, \(\Omega _{m0}+\Omega _{F0}=1\) right now. Taking this into account, we plotted the changes in \(\Omega _{m}\) and \(\Omega _{F}\) versus redshift z for both models with \(\Lambda \)CDM, which can be seen in Fig. 10a, b. From Fig. 10a, b, it can be observed that \(\Omega _{m}\) has a decreasing nature from past to the present, while \(\Omega _{F}\) has an increasing nature from the past to the present, which explores the past matter dominated and late-time dark energy-dominated universe scenarios. Using recent Hubble data points and Pantheon SNe Ia m(z) datasets, we did a statistical analysis of the model and found that the matter energy density parameter is \(\Omega _{m0}=0.38\pm 0.15, 0.438\pm 0.072\) for model-I and \(\Omega _{m0}=0.459_{-0.120}^{+0.096}, 0.495\pm 0.065\) for model-II. For the \(\Lambda \)CDM, it is \(\Omega _{m0}=0.333_{-0.070}^{+0.050}, 0.3\pm 0.021\), based on two datasets, with \(1-\sigma \) and \(2-\sigma \) confidence level of bounds. From Fig. 10a, b, one can see that \(\Omega _{m}\rightarrow 0\) and \(\Omega _{F}\rightarrow 1\) as \(z\rightarrow -1\) (at late-time), which reveals that our model tends to \(\Lambda \)CDM model at the late-time universe, and in the early universe, \(\Omega _{m}\rightarrow 1\) and \(\Omega _{F}\rightarrow -\lambda \) as \(z\rightarrow \infty \) that shows the matter-dominated early universe.

Fig. 9
figure 9

Variation of scale factor over cosmic time t, and deceleration parameter q(z) over z, respectively

Full size image
Fig. 10
figure 10

The plot of total energy density parameters \(\Omega _{m}\) and \(\Omega _{F}\) over redshift z, respectively

Full size image
Fig. 11
figure 11

The plot of effective EoS parameter \(\omega _{eff}\) versus z and \(\Omega _{m}\), respectively

Full size image

Equations (29) and (43) represent the mathematical expressions for the dimensionless effective EoS parameter for models I and II, respectively. Figure 11a shows how \(\omega _{eff}\) changes over time for both models with \(\Lambda \)CDM, and Fig. 11b shows how it changes over time for the matter energy density parameter \(\omega _{m}\). For model-I, it can be observed from Fig. 11a that \(\omega _{eff}\rightarrow -1\) as \(z\rightarrow -1\) (at late-time) and \(\omega _{eff}\rightarrow 0\) as \(z\rightarrow \infty \) (at early universe time) support early matter dominated universes and late-time dark energy-dominated universes, while for model-II, it crosses the cosmological constant value \(-1\) with \(\omega _{eff}\rightarrow -1.0345\) as \(z\rightarrow -1\) that reveals that our model of universe evolves from matter dominated to quintessence, cosmological constant, and then reached the phantom dark energy-dominated phase of the expanding universe. In Fig. 11a, we can see that at the transition line \(z=z_{t}\), the effective EoS parameter \(\omega _{eff}\approx -\frac{1}{3}\) shows how the expanding models of the universe are moving faster. The estimated present value of the effective EoS parameter is obtained as \(\omega _{eff}=-0.6667_{-0.0749}^{+0.0082}\) for model-I and \(\omega _{eff}=-0.7058_{-0.0567}^{+0.0114}\) for model-II, while for \(\Lambda \)CDM model, it is estimated as \(\omega _{eff}=-0.667_{-0.07}^{+0.05}\). The change in \(\omega _{eff}\) over \(\Omega _{m}\) is shown in Fig. 11b. Using math, we can figure out the relationship between \(\omega _{eff}\) and \(\Omega _{m}\) for model-I as \((A-B)k^{2}\Omega _{m}\omega _{eff}+B\rho _{m0}\kappa ^{2}\omega _{eff}-Bk^{2}\Omega _{m}+B\rho _{m0}\kappa ^{2}=0\), where \(A=2n_{1}(\kappa ^{2}\rho _{m0}-\lambda k^{2})\) and \(B=(k_{2}+\lambda k_{4}-2n_{1}\lambda )k^{2}\). It can also be expressed as:

$$\begin{aligned} \omega _{eff}=\frac{Bk^{2}\Omega _{m}-B\rho _{m0}\kappa ^{2}}{(A-B)k^{2}\Omega _{m}+B\rho _{m0}\kappa ^{2}}. \end{aligned}$$
(53)

From Eq. (53) and Fig. 11b, it is clear that the EoS parameter \(\omega _{eff}\rightarrow -1\) for \(\Omega _{m}\rightarrow 0\) and \(\omega _{eff}\rightarrow 0\) for \(\Omega _{m}\rightarrow \frac{\rho _{m0}\kappa ^{2}}{k^{2}}\). From the above relationship, one can obtain the radiation-dominated universe for \(\Omega _{m}>\frac{\rho _{m0}\kappa ^{2}}{k^{2}}\). For model II, this relationship of \(\omega _{eff}\)-\(\Omega _{m}\) is obtained as \((A+B)k^{2}\Omega _{m}\omega _{eff}-B\rho _{m0}\kappa ^{2}\omega _{eff}+(B-n_{2}k_{1}k^{2})k^{2}\Omega _{m}-B\rho _{m0}\kappa ^{2}+n_{2}\rho _{m0}k_{1}k^{2}\kappa ^{2}=0\) where \(A=3n_{2}(2\kappa ^{2}\rho _{m0}-k_{1}k^{2}-2\lambda k^{2})\) and \(B=3k^{2}(2n_{2}\lambda +n_{2}k_{1}-k_{2}-k_{4}\lambda )\). It can also be expressed as

$$\begin{aligned} \omega _{eff}=\frac{B\rho _{m0}\kappa ^{2}-n_{2}\rho _{m0}k_{1}k^{2}\kappa ^{2}-(B-n_{2}k_{1}k^{2})k^{2}\Omega _{m}}{(A+B)k^{2}\Omega _{m}-B\rho _{m0}\kappa ^{2}}\nonumber \\ \end{aligned}$$
(54)

From Eq. (54), we can obtain for \(\Omega _{m}\rightarrow 0\), \(\omega _{eff}\rightarrow -1-\frac{k_{1}}{6-k_{1}}, k_{1}<6\) that gives cosmological constant value. \(\omega _{eff}=-1\) for \(k_{1}=0\), phantom and super-phantom values for \(k_{1}<6\).

5.1 Statefinder analysis:

Now, we discuss two more geometrical dimensionless parameters derived from the scale factor a(t) as the statefinder diagnostic parameters r(t) and s(t), which are defined by the Eq. (25). For the model-I, we have derived these parameters r(t) and s(t) as in Eqs. (26) and (27), respectively, while for the model-II, in Eqs. (41) and (42), respectively. We can find the relation between r and s from these equations as \(3rs+6s+2r-2=0\) for the models I and II. It can be expressed as \(s=\frac{2(1-r)}{3(2+r)}\), which shows that \(s\rightarrow \infty \) for \(r\rightarrow -2\) (singular point) and \(s\rightarrow 0\) for \(r\rightarrow 1\). From Eqs. (22) and (26), we can find the relationship between r & q as \(r+2q+1=0\) for the models. Also, we can rewrite it as \(q=-\frac{1+r}{2}\), which gives \(q>0\) for \(r<-1\) and \(q<0\) for \(r>-1\), and the model undergoes a transition point at \(r=-1\).

5.2 Statistical analysis

In this section, we analyze different cosmological models using the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). In addition, we derive the reduced chi-squared value using the formula (\(\chi _{red}^{2}=\chi ^{2}_{min}/dof\)), where “dof” represents the degrees of freedom. Typically, degrees of freedom are calculated as the difference between the number of data points used and the number of fitted parameters. But we should only use \(\chi ^{2}_{min}/dof\) to explain things, since the degrees of freedom might not be clear for models that aren’t linear with respect to the free parameters [88]. The AIC criterion, derived from information theory, serves as an asymptotically unbiased estimator of Kullback–Leibler information. Assuming Gaussian errors, the AIC criteria can be estimated using the formula mentioned in [89, 90].

$$\begin{aligned} AIC=-2\ln ({\mathcal {L}}_{max})+2n+\frac{2n(n+1)}{N-n-1}, \end{aligned}$$
(55)

where \({\mathcal {L}}_{max}\) represents the maximum likelihood of the dataset(s) being considered, N depicts the total number of data points used in analysis, and n is the number of fitted parameters. Maximizing the likelihood function is equivalent to minimizing the \(\chi ^{2}\) value. For a large value of N, it is evident that this expression yields the original version of AIC, which may be approximated as \(AIC\backsimeq -2\ln ({\mathcal {L}}_{max})+2n\). According to the discussion in [91], it is widely accepted as the most effective approach to utilizing the modified AIC criterion. The BIC criteria is a Bayesian evidence estimator, and it is referenced by [89,90,91].

$$\begin{aligned} BIC=-2\ln ({\mathcal {L}}_{max})+n\ln (N). \end{aligned}$$
(56)

Our task is to arrange the models based on their ability to accurately match the available data, given a collection of scenarios that depict the same type of event. We use the two information criteria (IC) listed above to find the relative difference in the IC value for the given set of models. This is shown as \(\Delta IC_{model}=IC_{model}-IC_{min}\), where \(IC_{min}\) is the model with the lowest IC value. To evaluate the suitability of each model, we utilize the Jeffreys scale [92]. More precisely, when \(\Delta IC\le 2\), it indicates that the data strongly supports the most favored model. When \(2<\Delta IC <6\), it suggests a moderate level of disagreement between the two models. Lastly, when \(\Delta IC\ge 10\), it indicates a significant level of tension between the models [47].

In our analysis, we use two types of datasets: the cosmic chronometer (Hubble data) points and the Pantheon SNe Ia datasets. By minimizing the \(\chi ^{2}\) value, we have fitted the model parameters for our derived models, and the obtained values of \(\chi _{min}^{2}\) and \(\chi _{red}^{2}\) are shown in Tables 1 and 2. For models I and II, we have used \(\chi _{min}^{2}=14.4936\), \(N=31\), and \(n=3\) along CC datasets to obtain the AIC and BIC values, which are mentioned in the below Table 3 with the difference from the best-fitted model \(\Delta IC_{model}=IC_{model}-IC_{min}\).

Table 3 The information criteria AIC and BIC for the examined cosmological models along cosmic chronometer datasets
Full size table

We used \(\chi _{min}^{2}=1026.6706\), \(N=1048\), and \(n=3\) to get the AIC and BIC values for the Pantheon SNe Ia datasets. The AIC and BIC values are shown below in Table 4, along with the difference from the best-fitting model, which is \(\Delta IC_{model}=IC_{model}-IC_{min}\).

Table 4 The information criteria AIC and BIC for the examined cosmological models, along Pantheon SNe Ia datasets
Full size table

From the above Table 3, it is clear that both criterion AIC and BIC for both models come in the second category \(2<\Delta IC <6\) that our derived models are less supportive of the most favored \(\Lambda \)CDM, while from Table 4, we can observe that the AIC criteria suggest that our derived models are less supportive of the \(\Lambda \)CDM model and the BIC criteria suggest strongly disagreement with the \(\Lambda \)CDM most favored model.

6 Conclusions

This study used a flat Friedmann–Lematre–Robertson–Walker (FLRW) spacetime metric to investigate different cosmological scenarios within the framework of metric-affine F(R, T) gravity. The modified Lagrangian function being investigated is defined as \(F(R,T)=R+\lambda T\), where R represents the Ricci curvature scalar, T represents the torsion scalar for the non-special connection, and \(\lambda \) is a parameter specific to the model. \(R=R^{(LC)}+u\) and \(T=T^{(W)}+v\) were used to write the equations. \(R^{(LC)}\) is the Ricci scalar curvature found using the Levi-Civita connection, and \(T^{(W)}\) is the torsion scalar found using the Weitzenbock connection. u and v are functions that depend on the scale factor a(t), connection and its derivatives. We derived two precise solutions to the modified field equations for the scale factor a(t) under two distinct scenarios of u and v. By employing this scale factor, we have derived multiple geometric parameters to examine the cosmological features of the cosmos. We used the Markov chain Monte Carlo (MCMC) simulation to look at two new sets of data: cosmic chronometer (CC) data points (Hubble data) and Pantheon SNe Ia samples. Through this analysis, we determined the model parameters that most accurately matched the observed data within the \(1-\sigma \) and \(2-\sigma \) sectors.

We conducted a comprehensive analysis of geometric and cosmological parameters, taking into account both comparative and relativistic aspects. In model I, we have determined that the effective equation of state (EoS) parameter \(\omega _{eff}\) ranges from \(-1\) to 0, but in model II, it ranges from \(-1.0345\) to 0. The behavior of \(\omega _{eff}\) in both models reveals compatibility with the \(\Lambda \)CDM universe. Model-II progresses from the matter-dominated stage to the quintessence and cosmological constant stages, followed by the phantom and super-phantom stages of the expanding universe. Model-I, on the other hand, moves from the matter-dominated stage to the quintessence stage, getting closer to a cosmological constant value. We have found the values of the Hubble constants \(H_{0}=67.4\pm 3.1, 67.8\pm 2.9\) Km/s/Mpc, respectively, for the two models, while for \(\Lambda \)CDM \(H_{0}=67.7\pm 3.1\) Km/s/Mpc. We have determined that both models represent universes in a transitional phase, where they are transitioning from slowing down to speeding up. For these universes, the transition redshifts are \(z_{t}=0.5874_{-0.0197}^{+0.2130}\) and \(z_{t}=0.6865_{-0.0303}^{+0.1719}\), respectively. Both models show expanding universes in the transit phase, with transition redshifts between 0.3 and 1.0. We have found the present value of DP as \(q_{0}=-0.50_{-0.1123}^{+0.0122}\) for model I and \(q_{0}=-0.5586_{-0.0851}^{+0.0171}\) for model II, while for \(\Lambda \)CDM model, it is found as \(q_{0}=-0.5005_{-0.1050}^{+0.1750}\), which indicates our derived models are in the accelerating phase of expansion at present (at \(z=0\)). The current values of q(z) range from \(-0.6\) to \(-0.5\), which is in good agreement with recent observations [1,2,3,4,5,6,7]. Both models can explain the late-time accelerating and early decelerating scenarios of the universe, but they cannot explain the early-time accelerating (inflation) scenario of the universe. This fits well with recent measurements [82, 87]. Additionally, the present age of these universes is \(t_{0}=13.58_{-0.51}^{+1.70}\) Gyrs and \(t_{0}=13.98_{-0.72}^{+1.51}\) Gyrs, respectively. These findings align with our current understanding of recent universes. Furthermore, we have conducted an analysis of cosmological models obtained using the AIC and BIC information criteria. This analysis aims to assess the compatibility of our derived models with the findings of the most favored model, namely \(\Lambda \)CDM. Finally, from the information criterion AIC and BIC analyses of the models, we have found that our derived models are very close to \(\Lambda \)CDM.

Also, we have found that the dimensionless constants \(k_{1}, k_{2}, k_{3}\), and \(k_{4}\) are not all vanishing together, which confirms the need for investigation of such theories in this context. Thus, we can conclude that the choice of non-special connection (i.e., the choice of u and v) plays an important role in the universe’s dynamical dark energy evolution history. As a result, it requires further investigation, which entices cosmologists to review it.