1 Introduction

So far, many approaches have been introduced for the characterization of quantum chaos ranging from semiclassical methods to random matrix theory to improve this fairly complicated notion [1]. In recent years, the gauge-gravity duality [2,3,4], which relates a d-dimensional quantum field theory (QFT) to some \((d+1)\)-dimensions classical gravitational theory in the bulk, has provided remarkable insights into the nature of quantum chaos.

A distinct feature of quantum chaos is the butterfly effect which is a very common phenomenon in thermal systems. In the context of quantum mechanics, this phenomenon can be characterized using the commutator \(\langle [W(t), V (0)]^2\rangle \) between two generic Hermitian operators V(0) and W(t). This quantity measures how much an early perturbation V(0) affects the later measurements of W(t) or, in other words, how sensitive the system is to an initial perturbation created by acting with V(0). The strength of such measurement is encoded in the following double commutator [5]

$$\begin{aligned} C(t)= - \langle [W(t),V(0)]^{2}\rangle _{\beta }, \end{aligned}$$
(1)

where the expectation value has been taken in a thermal state with \(\beta = 1/T.\) If we assume that V and W are Hermitian and unitary operators, then the double commutator will be written

$$\begin{aligned} C(t)= 2 - 2 \langle W(t) V(0) W(t) V(0) \rangle _{\beta }, \end{aligned}$$
(2)

where the second part, \(\langle W(t) V(0) W(t) V(0) \rangle _{\beta },\) is called Out of Time Ordered Correlation (OTOC) and measures the degree of non-commutativity between W(t) and V(0). It also contains all the information of C(t). OTOC was first introduced by Larkin and Ovchinnikov to quantify the regime of validity of quasi-classical methods in the theory of superconductivity [6]. More recently, the definition of quantum chaos based on OTOC became the focus of much research due to its applicability to many-body quantum systems. This kind of correlator, in the dual gravitational description, is related to the collision of shock waves that takes place close to the black hole horizon [7,8,9,10,11,12,13,14,15,16,17]. Furthermore, there exist experimental proposals for measuring OTOC as a measure of chaos in quantum systems which is found in [18,19,20,21]. There have also been various efforts to connect OTOC and transport and hydrodynamic behavior which we will refer the reader to see [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].

For a chaotic large N theory, C(t) is typically expected to grow exponentially with time

$$\begin{aligned} C(t)\propto \frac{1}{N} e^{\lambda _{L}t},\quad t_d\ll t\ll t_{*} \end{aligned}$$
(3)

where \(\lambda _{L}\) is the Lyapunov exponent. There is the time scale where C(t) becomes of order \( {\mathcal {O}}(1)\) called scrambling time \(t_{*}\sim \frac{1}{N}\log N\) which controls how fast the chaotic system scrambles information. There is another time scale the dissipation time \(t_d\) which characterizes the exponential decay of two-point functions, e.g., \(\langle V(0)W(t)\rangle \sim e^{-\frac{t}{t_d}}\) and also controls the late time behavior of C(t). In quantum field theories when we separate the operators V and W in space, then at large distances the (1) will generalize to

$$\begin{aligned} C(t,{\vec {x}})= - \langle [W(t,{\vec {x}}),V(0,0)]^{2}\rangle _{\beta }. \end{aligned}$$
(4)

The butterfly effect is naturally characterized in terms of such a commutator, which expresses the dependence of later measurements of distant operators \(W(t,{\vec {x}})\) on an earlier perturbation V(0, 0). Note that the above expression is generically divergent and hence it requires regularization by adding imaginary times to the time arguments of the operators V and W,  for example see [39]. The interesting point is that the (4), for a large class of models such as spin chain, higher dimensional Sachdev, Ye and Kitaev (SYK) model, and conformal field theories (CFT’s), is roughly given by [9, 11, 32]

$$\begin{aligned} C(t,{\vec {x}})\propto exp{\bigg [\lambda _{L}\bigg (t-t_{_*}-\frac{\vert x \vert }{v_B}\bigg )\bigg ]}, \end{aligned}$$
(5)

where \(v_B\) is the so-called butterfly velocity which describes the speed at which the information about V(0, 0) will spread among the other degrees of freedom of the system in space. Likewise, the Lyapunov exponent \(\lambda _{L}\) is upper bounded in terms of the Hawking temperature for a generic quantum system by [40]

$$\begin{aligned} \lambda _L \le \frac{2\pi }{\beta }, \end{aligned}$$
(6)

where the bound is saturated in holographic systems with black holes present in the bulk, the nature’s fastest scrambler [41]. Also, this saturation occurs for a variety of systems including two-dimensional CFT’s in the large central charge limit, and strongly coupled SYK models. Moreover, there have been different proposals for the form of the exponential growth \(C(t,{\vec {x}})\) including \(C(t,{\vec {x}}) \sim exp\big [{-\lambda _L\frac{(x-v_B t)^2}{t}}\big ]\) in local random circuit models [42, 43] and \(C(t,{\vec {x}}) \sim exp\big [{\lambda _L t - \frac{\vert x \vert ^2}{D_0 t}}\big ]\) by a diffusive spreading around the exponential growth [44, 45].

Once we study the retarded Green’s functions of the dual field theory in holography, denoted as \(G^{R},\) there exist special points in complex momentum plane \((\omega - k),\) known as pole-skipping points \((\omega _\star ,k_\star ),\) namely \(\omega _\star = i \lambda _{L}\) and \(k_\star = i \frac{\lambda _{L}}{v_B}\) where it will be found that \(G^{R}(\omega ,k)\) becomes non-unique and its behavior is dependent on the slope \(\frac{\delta \omega }{\delta k}\) as we approach \((\omega _\star ,k_\star ).\) From a bulk point of view, this nonuniqueness arises due to the absence of a unique ingoing solutions at the black hole horizon. More generally, the non-uniqueness of Green’s function at \((\omega _\star ,k_\star )\) in complex momentum plane \((\omega - k)\) is explicitly shown in [46, 47] where they perform a near horizon expansion of the equation of motion.

Recent developments have indicated that there exists a sharp manifestation between the retarded Green’s function of energy density, the \(G^{R}_{T^{00}T^{00}}(\omega ,k)\) and chaotic properties of many-body thermal systems at the pole-skipping points \((\omega _\star ,k_\star )\) located in upper-half complex momentum plane, which is referred to as pole-skipping phenomenon [38, 48, 49]. It has also been confirmed that the general pole-skipping points for some models [46, 50,51,52,53,54,55] are located at special points in the lower-half complex momentum plane, namely at negative integer Matsubara frequencies \( \omega _n = - 2\pi i T n\,\, (n \ge 1)\) which are not related to the information of quantum chaos.

The same pole-skipping phenomenon has also been observed in effective field theory (EFT) in two-point functions of energy density and flux [22] and it holds in the context of chaotic two-dimensional CFTs with large central charge limit [26]. Moreover, the pole-skipping can be explored by the near horizon solutions of scalar field perturbations [46, 56, 57]. More investigations have recently been devoted to the relationship between the chaos and energy dynamics in rotating black holes through the pole-skipping phenomenon [58,59,60]. There have been many works studying this phenomenon which we will refer the reader to see [50, 51, 61,62,63,64,65,66,67,68,69].

In this paper, we study the butterfly effect and pole-skipping phenomenon for the 1RCBH model. This model has an analytical top-down string theory construction which is obtained from 5-dimensional maximally supersymmetric gauged supergravity and is holographically dual to a 4-dimensional strongly coupled \({\mathcal {N}}\) = 4 SYM theory at finite chemical potential under a U(1) subgroup of the global SU(4) symmetry of R-charges [70,71,72]. Since the theory is conformal, its phase diagram is a function of a dimensionless parameter \(\frac{\mu }{T},\) where \(\mu \) and T are the U(1) R-charge chemical potential and temperature of the boundary theory, respectively. This model enjoys a second-order phase transition with a critical point at \(\frac{\mu }{T}=\frac{\pi }{\sqrt{2}}\) in its parameter space whose critical exponents were calculated in [73,74,75,76,77,78]. Our primary goal in this paper is to find whether the butterfly velocity \(v_B\) can serve as a measure to probe the critical behavior of this model and if so, what the critical exponents are. Another motivation is to study the appearance of the pole-skipping phenomenon in the 1RCBH model which has a second-order phase transition. To do this, we study the linearized perturbations in scalar sector (spin 0) by two different points of view which are consistent with each other in their results. We also extend our analysis and show that the same phenomenon can also occur at higher Matsubara frequencies \( \omega _n = - 2\pi i T n\,\, (n \ge 1)\) for the gauge perturbations.

The organization of this paper is as follows. In Sect. 2 we focus on the butterfly effect which characterizes chaos by parameters such as butterfly velocity and Lyapunov exponent and study holographically these parameters in the mentioned model. Interestingly, we find that butterfly velocity can probe the critical point of corresponding strongly coupled field theory. Motivated by this, in Sect. 3 the dynamical exponent of this velocity will be obtained near the critical point and the perfect agreement is found with the ones reported in the literature. Additionally, we examine the pole-skipping for higher Matsubara frequencies in differential equation of scalar field perturbations. In particular, we obtain \(\text{ det } \, {\mathcal {M}}(\omega , k^2)\ne 0\) at the points \( \omega _n = - 2\pi i T n\,\, (n \ge 1)\) and \(k = k_\star = i \lambda _{L}/v_B\) regarding the equation \({\mathcal {M}}(\omega , k^2) \cdot \delta {\tilde{\phi }} = {\mathcal {I}}\) in which \({\mathcal {M}}(\omega , k^2)\) is the coefficient matrix for scalar perturbations \(\delta {\tilde{\phi }}\) living near the horizon and \({\mathcal {I}}\) is a complicated vector composed of the other variables. The property \(\text{ det } \, {\mathcal {M}}(\omega , k^2)\ne 0\) states that scalar solutions are unique and the corresponding retarded Green’s functions are not multivalued at \(\omega = \omega _n\) and \(k = k_\star .\) We guess that this feature may come from the presence of finite charge in our model. However, for matrix coefficients of gauge perturbations we get \(\text{ det } {\mathcal {M}}(\omega _n, k_\star ^2) = 0\) and hence the respective retarded correlation functions become multivalued and the poles of Green’s functions skip at the point \(\omega = \omega _n\) and \(k = k_\star .\) In Sect. 4 we study the pole-skipping phenomenon in 1RCBH model. Indeed, we consider a special set of fluctuations in the spin 0 sector and derive the linearized equations for these perturbations. We observe that the \(v-v\) component of Einstein’s equations near the horizon at the \((\omega _\star ,k_\star )\) point becomes equivalent to the shock wave equation and we can read off the information about the chaos. Furthermore, this component of the Einstein equations automatically satisfied at the \((\omega _\star ,k_\star )\) point and one can deduce that there exists one extra regular mode emerging at this point and as a result leads to the pole-skipping in the retarded energy density correlation function. Due to the complicated nature of master equations in the 1RCBH model, we supply MATHEMATICA files containing the linearized equations in the spin zero sector separately. In Sect. 5, we conclude and briefly review our results. To give more details, Appendix A is devoted to more accurate calculations of invariant fluctuations in the Eddington–Finkelstein coordinates. Moreover, in Appendix B we give details of near horizon expansions of scalar fluctuation in Sect. 4.

2 Butterfly effect in the 1RCBH model

We would like to study the butterfly effect in a strongly coupled field theory including a critical point, using the framework of holography. To do so, we first review the 1RCBH model. The bulk theory is a top-down string theory construction which is a consistent truncation of the super-gravity on AdS\(_5 \times \) S\(^5\) geometry in which one scalar field and one gauge field are coupled to the Einstein gravity. The thermal solution is an asymptotically AdS black brane geometry with a nontrivial profile of the scalar and gauge fields, so-called 1RCBH [70,71,72]. This geometry is dual to a four-dimensional strongly coupled gauge theory \({\mathcal {N}}\) = 4 SYM at finite temperature and chemical potential.

2.1 Background

The bulk part of the 1RCBH model is given by the following action [70]

$$\begin{aligned} {{{\mathcal {S}}}}_{\text {bulk}}&=\frac{1}{16 \pi G_5}\int d^5x\sqrt{-g}\left( {{{\mathcal {R}}}}-\frac{f(\phi )}{4}F_{\mu \nu }F^{\mu \nu }\right. \nonumber \\&\quad \left. -\frac{1}{2}(\partial _\mu \phi )^2-V(\phi )\right) , \end{aligned}$$
(7)

where \(G_5\) is the 5-dimensional Newton constant, g and \({{{\mathcal {R}}}}\) are the determinant of the metric and its corresponding Ricci scalar, respectively, and \(F_{\mu \nu }\) is the field strength of the gauge field \(A_{\mu }.\) The self-interacting dilaton potential \(V(\phi )\) and the Maxwell-dilaton coupling \(f(\phi )\) are given by

$$\begin{aligned}&V(\phi )=-\frac{1}{L^{2}}\left( 8e^{\frac{\phi }{\sqrt{6}}}+4 e^{-\sqrt{\frac{2}{3}\phi }}\right) ,\end{aligned}$$
(8)
$$\begin{aligned}&f(\phi )= e^{-2\sqrt{\frac{2}{3}\phi }}. \end{aligned}$$
(9)

where L is the asymptotic \(AdS_5\) radius. For simplicity, in the following we set \(L = 1.\) The equations of motion corresponding to the action (7) are given by

$$\begin{aligned} \varvec{\varphi }&\equiv {1\over \sqrt{-g}} \partial _\mu \left( \sqrt{-g} g^{\mu \nu } \partial _\nu \phi \right) - {f'(\phi ) \over 4} F_{\mu \nu }F^{\mu \nu } - V'(\phi )=0,\nonumber \\ {\mathcal {A}}^\nu&\equiv \partial _\mu \left( \sqrt{-g} f(\phi ) F^{\mu \nu }\right) =0,\nonumber \\ {\mathcal {G}}_{\mu \nu }&\equiv R_{\mu \nu } - {g_{\mu \nu } \over 3} \left( V(\phi ) - {f(\phi ) \over 4} F_{\alpha \beta } F^{\alpha \beta }\right) \nonumber \\&\quad - {1\over 2}\partial _\mu \phi \partial _\nu \phi - {f(\phi ) \over 2} F_{\mu \alpha } F_\nu ^\alpha =0. \end{aligned}$$
(10)

The 1RCBH solution to the equation of motion of the action (7) is described by the following metric

$$\begin{aligned} ds^2=e^{2A(r)}\bigg (-h(r)dt^2+d{\vec {x}}^2\bigg )+\frac{e^{2B(r)}}{h(r)}dr^2 \end{aligned}$$
(11)

where

$$\begin{aligned} A(r)&=\ln \left( r\right) +\frac{1}{6}\ln \left( 1+\frac{Q^2}{r^2}\right) ,\nonumber \\ B(r)&=-\ln \left( r\right) -\frac{1}{3}\ln \left( 1+\frac{Q^2}{r^2}\right) ,\nonumber \\ h(r)&=1-\frac{M^2}{r^2(r^2+Q^2)}, \\\phi (r)&=-\sqrt{\frac{2}{3}} \ln \left( 1+\frac{Q^2}{r^2}\right) ,\nonumber \\ a_t(r)&=\left( \frac{MQ}{r_{H}^2+ Q^2}-\frac{MQ}{r^2 +Q^2} \right) . \end{aligned}$$
(12)

Here, r is the radial bulk coordinate, the holographic direction, and the strongly coupled field theory lives on the boundary at \(r \rightarrow \infty .\) The time component of the gauge field is \(a_t(r)\) which is chosen to be zero on the horizon and is regular on the boundary. M is the black hole mass and Q is its charge. \(r_H\) is the black hole horizon position which is obtained from \(h(r_{H}=0)\) and can be written in terms of the charge Q and mass M of the black hole as follow

$$\begin{aligned} r_H=\sqrt{\frac{\sqrt{Q^4+4M^2}-Q^2}{2}}. \end{aligned}$$
(13)

The Hawking temperature T and the chemical potential \(\mu \) of the dual field theory are also given by

$$\begin{aligned} T&=\frac{\sqrt{-g_{tt}' {g^{rr}}' }}{4\pi }\Bigg \vert _{r=r_{H}}=\left( \frac{Q^2+2r_{H}^{2}}{2\pi \sqrt{Q^2+r_H^2}}\right) , \end{aligned}$$
(14a)
$$\begin{aligned} \mu&=\lim \limits _{r\rightarrow \infty }a_t=\frac{Q r_{H}}{\sqrt{Q^2+r_H^2}}, \end{aligned}$$
(14b)

where “ \(^{/}\) ” denotes a derivative with respect to the r. We can now parametrize the class of solutions corresponding to the 1RCBH model by different values of the dimensionless ratio \(\frac{Q}{r_H}\) which is

$$\begin{aligned} \frac{Q}{r_H}=\sqrt{2} \left( \frac{1\pm \sqrt{1-(\frac{\sqrt{2}}{\pi }\frac{\mu }{T})^2}}{\frac{\sqrt{2}}{\pi }\frac{\mu }{T}} \right) , \end{aligned}$$
(15)

and implying that \(0\le \frac{\mu }{T}\le \frac{\pi }{\sqrt{2}}.\) We point out from above equation that there are two different values of \(\frac{Q}{r_H}\) corresponding to each value of \(\frac{\mu }{T}\) which parametrize two different branches of solutions. Utilizing the relations between entropy s and charge density \(\rho \) in terms of the bulk solution parameters Q and \(r_H,\) we can compute the Jacobian \({\mathcal {J}}=\frac{\partial (s,\rho )}{\partial (T,\mu )}.\) At the critical point \((\frac{\mu }{T})^*=\frac{\pi }{\sqrt{2}}\) \((\frac{Q}{r_H}=\sqrt{2})\) the Jacobian becomes zero and two branches intersect with each other. Thermodynamically stable (unstable) states correspond to the positive (negative) Jacobian branches. The branch with the parameters satisfying \(\frac{Q}{r_H}<\sqrt{2}\) is stable.

2.2 Shock wave geometry

In holographic theories, the butterfly effect corresponds to the blue shift suffered by a probe particle in the bulk, which we call W particle, that falls towards the horizon. W-particle’s energy is blue-shifted by the black hole’s temperature for late times from the point of view of the \(t=0\) slice of the geometry

$$\begin{aligned} E=E_{0}e^{(\frac{2\pi }{\beta })t}, \end{aligned}$$
(16)

where \(E_{0}\) is the asymptotic past energy of the W particle. The back-reaction of this particle on the geometry becomes significant at late times and creates a shock-wave along the horizon. The effect of the shock wave is to produce a shift in the trajectory of W particle. The interesting point is that the shock wave profile contains information about the parameters characterizing the chaotic behavior of the boundary theory [5].

2.2.1 Holographic setup

To study chaos it is convenient to consider a thermofield double state (TFD) which is made out of two identical copies of the CFT

$$\begin{aligned} \vert \psi \rangle =\frac{1}{Z(\beta )^{\frac{1}{2}}}\sum _{{n}}e^{-\beta E_n/2 }\,\vert n\rangle _{L} \,\vert n\rangle _{R}, \end{aligned}$$
(17)

where the subscript L(R) specifies the energy eigenstates of the CFT living on the left (right) asymptotic boundary of geometry. Here, \(Z(\beta )\) is the corresponding CFT partition function. Furthermore, this state is dual to a two-sided black hole with two boundaries which is asymptotically AdS [79]. We now would like to calculate the butterfly effect velocity corresponding to the 1RCBH model (11) by constructing the relevant shock wave geometries. To do so, we assume a general \(d+1\) dimensional metric of the following form

$$\begin{aligned}&ds^2=-f_1(r)dt^2+f_2(r)dr^2+f_3(r)dx_i^2 ,\nonumber \\&i=1,2,\ldots ,d-1, \end{aligned}$$
(18)

whose boundary is located at \(r\rightarrow \infty \) and is assumed to be asymptotically \(AdS_{d+1}.\) We take the horizon as located at \(r=r_H\) on which \(f_1(r)\) vanishes and \(f_2(r)\) has a first-order pole. To describe the shock wave solution of this geometry, it is more useful to re-write the above metric in the Kruskal–Szekeres coordinates. We first define the so-called tortoise coordinate

$$\begin{aligned} dr^*=\sqrt{\frac{f_2(r)}{f_1(r)}}dr, \end{aligned}$$
(19)

which behaves such that \(r^*\rightarrow \infty \) as \(r\rightarrow r_H,\) and then introduce the Kruskal–Szekeres coordinates as follows

$$\begin{aligned} U=e^{\frac{2\pi }{\beta } (r^*-t)},\quad V=-e^{\frac{2\pi }{\beta } (r^*+t)}, \end{aligned}$$
(20)

where \(\beta = \frac{4 \pi }{f_1'(r_H)}.\) In terms of these coordinates, metric (18) can be written

$$\begin{aligned} ds^2=A(UV)dUdV+(f_3)_{ij}(UV)dx^idx^j, \end{aligned}$$
(21)

where \( i,j=1,2,\ldots ,d-1\) run over the \(d-1\) transverse directions, and A(UV) is a function given by the component of the general metric as follows

$$\begin{aligned} A(UV)=\frac{\beta ^2 f_1(UV)}{4\pi ^2 UV}. \end{aligned}$$
(22)

In these coordinates the horizon is located at \(U=0\) or \(V=0,\) and the left and right asymptotic boundaries are positioned in \(UV=-1.\) These coordinates cover the maximally extended eternal black hole solution including two entangled boundaries connected by a wormhole.

As we have mentioned before, the back-reaction of W particle on the geometry becomes significant at late times, (i.e. \(t>\beta ).\) The associated stress energy distribution becomes highly compressed in the V direction and stretched in the U direction and one can approximately read the stress-energy tensor of the W particle as [5, 11]

$$\begin{aligned} T_{VV}\sim \ \beta ^{-1}\,\,\,e^{(\frac{2\pi }{\beta })t} \delta (V) a({\vec {x}}), \end{aligned}$$
(23)

where \(T_{VV}\) is localized at \(V=0\) and \(a({\vec {x}})\) is a generic function whose precise form depends on details of the perturbation in the spatial direction, as well as the propagation to the horizon. The back-reaction of the above matter distribution is a shock wave geometry whose metric is described by [7, 80, 81]

$$\begin{aligned} ds^2&=A(UV)dUdV+(f_3)_{ij}(UV)dx^idx^j\nonumber \\&\quad -A(UV)h(t,{\vec {x}})\delta (V)dV^2, \end{aligned}$$
(24)

where \(h(t,{\vec {x}})\) is the corresponding shift in the U direction, \(U\longrightarrow U+h(t,{\vec {x}}),\) as W-particle crosses the \(V=0\) horizon. Eventually, one can determine the precise form of \(h(t,{\vec {x}})\) by solving the VV component of Einstein equation

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R+\Lambda g_{\mu \nu }=8\pi G_{N} T_{\mu \nu }, \end{aligned}$$
(25)

where \(\Lambda =-\frac{d(d-1)}{2}\) is the cosmological constant, and \(T_{\mu \nu }\) is given by (23). To obtain \(h(t,{\vec {x}})\) one can solve the \(v-v\) component of Einstein’s equations by setting \(\delta '(V)=\frac{-\delta (V)}{V}\) and \(V^{2}\delta (V)^{2}=0.\) For a local perturbation, i.e. \(a({\vec {x}})=\delta ^{d-1}({\vec {x}})\) we get

$$\begin{aligned} \left( \partial _i\partial _i-\chi ^2\right) h({\vec {x}})=\frac{16\pi \, G_{N} f_3(0)}{A(0)}\beta ^{-1}e^{(\frac{2\pi }{\beta })t}\,\, \delta ^{d-1}({\vec {x}}). \end{aligned}$$
(26)

Assuming \((f_3)_{ij}\) to be diagonal and isotropic, the solution to the above differential equation at long distances \(x\gg \chi ^{-1}\) reads

$$\begin{aligned} h(x)\sim \frac{e^{(\frac{2\pi }{\beta })(t-t_{*})-\chi \vert x \vert }}{\vert x \vert ^{\frac{d-1}{2}}}, \end{aligned}$$
(27)

where the screening length \(\chi \) is given by

$$\begin{aligned} \chi ^2=\frac{(d-1)}{A(0)}\frac{\partial f_3(UV)}{\partial (UV)}\bigg \vert _{V=0}, \end{aligned}$$
(28)

and the scrambling time \(t_{*} \sim \frac{\beta }{2\pi } \log \frac{1}{G_{N}}.\) For later convenience, we express \(\chi \) as a function of the coordinates (t, r)

$$\begin{aligned} \chi ^2=\frac{(d-1)\pi f'_3(r)}{\beta \sqrt{f_1(r) f_2(r)}}\bigg \vert _{r=r_H}, \end{aligned}$$
(29)

where “ \(^{/}\) ” takes the radial derivative. For the case of the \(d+1-\)dimensional AdS–Schwarzschild in which \(f_1(r)=r^2-r^{2-d},\) \(f_2(r)=f_1(r)^{-1},\) \(r_H=1\) and \(\beta =\frac{4\pi }{d}\) one finds \(\chi ^2=\frac{d(d-1)}{2}\) as expected [11]. On the other hand, the shock wave profile (27) contains information regarding the parameters such as \(\lambda _{L}\) and \(v_B\) which corresponded to the chaotic behavior of the boundary theory. Hence, one can read off \(\lambda _{L}\) and \(v_B\) holographically as

$$\begin{aligned} \lambda _{L}=\frac{2\pi }{\beta },\quad v_B=\frac{2\pi }{\beta \chi }, \end{aligned}$$
(30)

where \(\lambda _{L}\) is universal in all such theories, while \(v_B\) is model dependent. Now we are in a position to extract butterfly velocity for metric (18). Using (30) and (29) we obtain \(v_B\) as the following form

$$\begin{aligned} v_B=\frac{2\sqrt{\pi }(f_1f_2)^{\frac{1}{4}}}{\sqrt{\beta (d-1)f_3'}}\bigg \vert _{r=r_H}, \end{aligned}$$
(31)

where we simply reach the \(d+1-\) dimensional AdS–Schwarzschild result i.e., \(v_B=\sqrt{\frac{d}{2(d-1)}},\) as reported in [11].

2.3 \(v_B\) in the 1RCBH model

Having discussed the characteristic parameters of chaotic systems such as Lyapunov exponent \(\lambda _{L}\) and butterfly velocity \(v_B\) in detail and obtained the explicit expressions for them, we are now in a position to write \(v_B\) for the 1RCBH model whose metric is given by (11). Using (14a), (14b), (12) and (31) and considering \(f_3(r)=e^{2A(r)},\) \(f_1(r)=h(r) f_3(r)\) and \(f_2(r)=\frac{e^{2B(r)}}{h(r)},\) one can read the butterfly velocity of the 1RCBH model as follows

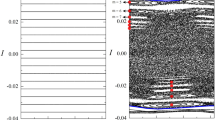
$$\begin{aligned} v_B^2=\frac{4}{7\mp \sqrt{1-\left( \frac{\mu /T}{\pi /\sqrt{2}}\right) ^2}}, \end{aligned}$$
(32)

where \(-(+)\) indicates the stable(unstable) black hole solutions. The above relation has been depicted in Fig. 1 for both stable and unstable black hole solutions for different values of \(\frac{\mu }{T}.\) The circle point has specified the precise location of the critical point which is at \((\frac{\mu }{T})^*=\frac{\pi }{\sqrt{2}}.\) The point is that for all values of \(\frac{\mu }{T},\) we observe that \(v_B^2 > c_s^2 = \frac{1}{3}\) where \(c_s\) is the speed of sound wave propagations. This is the result we obtained for the 1RCBH model in which the conformal symmetry is respected and hence this is not generic in some sense. One can find some models which are not conformal and this bound is violated, see for example [82]. Also, \(v_B\) gets smaller (larger) towards the critical point in stable (unstable) branches solution signaling the fact that the speed of information propagation can be a good diagnostic quantity to pinpoint the location of the critical point.

3 Critical exponent

Fig. 1
figure 1

The square of the butterfly velocity \(v_B^2\) as a function of dimensionless ratio \(\frac{\mu }{T}.\) The solid blue curve corresponds to the stable solutions while the red dashed curve corresponds to the unstable solutions. The green circle point where these branches of solutions merge is called the critical point where \((\frac{\mu }{T})^*=\frac{\pi }{\sqrt{2}}\)

Full size image

As mentioned before, the 1RCBH model we study in this paper enjoys a critical point at \((\frac{\mu }{T})^*=\frac{\pi }{\sqrt{2}}.\) The behavior of different observables near the critical point has been studied in the literature [74, 75, 77, 78, 83,84,85,86] in which the authors have shown that this behavior can be considered as \(\left( (\frac{\mu }{T})^*-\frac{\mu }{T}\right) ^{-\theta }\) where \(\theta \) is the dynamical exponent which is obtained to be \(\frac{1}{2}.\) We also would like to study the behavior of butterfly velocity \(v_B\) near this critical point. To proceed, we expand \(v_B\) and \(\frac{dv_B}{d\left( \frac{\mu }{T}\right) }\) in power of \(\left( (\frac{\mu }{T})^*-\frac{\mu }{T}\right) \) as follows

$$\begin{aligned}&v_B=\frac{2}{\sqrt{7}}+\frac{2^{3/4}}{7\sqrt{7\pi }}\left( \left( \frac{\mu }{T}\right) ^*-\frac{\mu }{T}\right) ^{\frac{1}{2}}+{\mathcal {O}}\left[ \left( \left( \frac{\mu }{T}\right) ^*-\frac{\mu }{T}\right) ^1\right] , \end{aligned}$$
(33)
$$\begin{aligned}&\frac{dv_B}{d\left( \frac{\mu }{T}\right) }=\frac{1}{7\times 2^\frac{1}{4}\sqrt{7\pi }}\left( \left( \frac{\mu }{T}\right) ^*-\frac{\mu }{T}\right) ^{-\frac{1}{2}}+{\mathcal {O}}\left[ \left( \left( \frac{\mu }{T}\right) ^*-\frac{\mu }{T}\right) ^0\right] . \end{aligned}$$
(34)

It has been seen that \(v_B\) remains finite, while \(\frac{dv_B}{d\left( \frac{\mu }{T}\right) }\) diverges near the critical point and one can see that the dynamical exponent is equal to \(\frac{1}{2}.\) This also shows that butterfly velocity can probe the location of the critical point and in other words can be used as a probe to investigate the phase diagram of the 1RCBH model. The reason why we look for \(v_B\) to probe the critical point is that this is a dynamical quantity that has a time scale and seems to have such scaling property.Footnote 1

4 Pole-skipping in the 1RCBH model

As we have pointed out before, OTOCs can be recognized as very useful tools to diagnose many-body quantum chaos. In addition to OTOCs, the chaotic nature of many-body thermal systems is also encoded in the equations of motion for linearized fluctuations in the spin-0 sector. For a general and non-critical background, it has been shown that the vv component of Einstein’s equation near the horizon gets the following form [49]

$$\begin{aligned}&\left( k^2 + k_0^2\frac{\omega }{2 \pi T i}\right) \delta g^{(0)}_{v v}(r_H) + (\omega - 2 i \pi T) \left( \omega \delta g^{(0)}_{x^i x^i}(r_H) \right. \nonumber \\&\quad \left. + 2 k \delta g^{(0)}_{v z}(r_H)\right) = 0, \end{aligned}$$
(35)

where the gravitational and matter perturbations have been expanded near the horizon as

$$\begin{aligned}&\delta g_{\mu \nu }(r) = \delta g_{\mu \nu }^{(0)}\, +\delta g_{\mu \nu }^{(1)} (r -r_H)+\cdots ,\nonumber \\&\delta \phi (r) = \delta \phi ^{(0)}\, + \delta \phi ^{(1)}(r -r_H)+\cdots , \end{aligned}$$
(36)

and the propagations have been parametrize along the z direction. At \(\omega = \omega _\star = 2 \pi T i\) and \(k = k_\star = i k_0\) this equation becomes identically zero. A consequence of this issue is that there exists plenty of linearly independent solutions to the Einstein equations. All these linear solutions approach the \((\omega _\star ,k_\star )\) by different slope

$$\begin{aligned} \frac{\delta \omega }{\delta k} = \frac{2 k_0 \delta g^{0}_{v v}(r_H)}{\frac{k_0^2}{\omega _0} \delta g^{0}_{v v}(r_H) - \omega _0 \delta g^{0}_{x^i x^i}(r_H) - 2 k_0 \delta g^{0}_{v z}(r_H)}, \end{aligned}$$
(37)

where \(\omega _0 = 2 \pi T.\) Another manifestation of having many solutions is that two regular solutions exist in ingoing coordinates, i.e. solutions become \((r -r_H)^{\alpha _1, \alpha _2}\) where both \( (\alpha _1, \alpha _2)\ge 0.\) In this section, we want to examine these features for the 1RCBH model.

4.1 Setup for the 1RCBH model

In this subsection, we would like to study the linearized equations of motion on top of the metric (18) near the following points

$$\begin{aligned} \lambda _{L}=\frac{2\pi }{\beta }=2\pi T, \quad (k_{0})^{2}=\frac{\pi (d-1)f_3'(r_H)}{\beta \sqrt{f_1(r_H)f_2(r_H)}}, \end{aligned}$$
(38)

where \(k_{0}\) has been calculated through (31) and \(k_{0}=\frac{\lambda _{L}}{v_B}.\) The sound mode which corresponds to the retarded hydrodynamic correlators obeys the equations whose solutions satisfy ingoing wave boundary conditions at the horizon. Note also that these solutions in part contain the vv component of Einstein’s equations where v is the ingoing Eddington–Finkelstein (EF) coordinate. It is therefore convenient to introduce ingoing EF coordinates \((v; r; x^{i})\) in terms of which the general metric (18) becomes

$$\begin{aligned} ds^2=-f_1(r)dv^2+2\sqrt{f_1(r)f_2(r)}dvdr+f_3(r)(dx^{i})^2. \end{aligned}$$
(39)

Under infinitesimal diffeomorphism \(x^{\mu }\rightarrow x^{\mu }+\xi ^{\mu }\) and an infinitesimal gauge transformation \(A_{\mu }\rightarrow A_{\mu }+ \nabla _{\mu }\Lambda ,\) the perturbations \(\delta g_{\mu \nu },\) \(\delta A_{\mu }\) and \(\delta \phi \) transform as

$$\begin{aligned}&\delta g_{\mu \nu }\rightarrow \delta g_{\mu \nu }- \nabla _{\mu }\xi _{\nu }-\nabla _{\nu }\xi _{\mu }, \\&\delta A_{\mu }\rightarrow \delta A_{\mu }+ \nabla _{\mu } \Lambda - \xi ^{\nu }\nabla _{\nu } A_{\mu }- A_{\nu }\nabla _{\mu }\xi ^{\nu }, \\&\delta \phi \rightarrow \delta \phi -\xi ^{\nu } \nabla _{\nu } \phi , \end{aligned}$$

where \(\xi _{\mu }\) and \(\Lambda \) are diff and gauge functions, respectively. Due to the symmetry considerations, we set the metric, gauge and scalar field perturbation along the \(x^{3}\equiv z\) direction as follows

$$\begin{aligned}&\delta g_{\mu \nu }(v, r, z) = e^{- i \omega v + i k z} \delta g_{\mu \nu }(r), \nonumber \\&\delta A_{\mu }(v, r, z) = e^{- i \omega v + i k z} \delta A_{\mu }(r),\nonumber \\&\delta \phi (v, r, z) = e^{- i \omega v + i k z} \delta \phi (r). \end{aligned}$$
(40)

The above perturbations can be classified into three sets of sectors named scalar (spin 0), vector (spin 1) and tensor (spin 2) sectors respectively, which are decoupled at the level of equations due to the symmetry [87]. Fluctuations in the spin 0 sector and EF coordinates are given by

$$\begin{aligned} \delta \Phi = \bigg (\delta g_{v v}, \delta g_{r v}, \delta g_{rr}, \delta g_{r z}, \delta g_{v z}, \delta g_{x^{i}x^{i}}, \delta A_{v}, \delta A_{z}, \delta \phi \bigg ), \end{aligned}$$
(41)

which due to the SO(3) invariance, \(\delta g_{y y} = \delta g_{x x}.\) The linearized equations for these perturbations derived from Eq. (10) are very hard to solve. But series solution exists for every single point of the bulk. According to the fluid/gravity conjecture, the small energy (charge) perturbations on top of the living strongly coupled theory on the boundary correspond to equivalent small metric (gauge) field perturbations on the event horizon surface. Therefore, we scrutinize the near horizon points. We make a series assumptions for each perturbing field as

$$\begin{aligned}&\delta g_{\mu \nu }(r) = \sum _{n = 0}^{\infty } \delta g_{\mu \nu }^{n}(r_H)\, (r -r_H)^n,\nonumber \\&\delta A_{\mu }(r) = \sum _{n = 0}^{\infty } \delta A_{\mu }^{n}(r_H)\, (r -r_H)^n,\nonumber \\&\delta \phi (r) = \sum _{n = 0}^{\infty } \delta \phi ^{n}(r_H)\, (r -r_H)^n, \end{aligned}$$
(42)

and plug them into the linearized equations to solve the series order by order in \(\epsilon = r -r_H.\) We observe that the \({\mathcal {G}}_{v v}\) equation for fluctuations near the horizon on top of the 1RCBH background gets the following form

$$\begin{aligned}&\delta g_{v v}^{0}(r_H) \left( k^2 - \frac{i k_{0}^2 \omega }{2 \pi T} \right) + (\omega -2 i \pi T) (2 q \delta g_{z v}^{0}(r_H)\nonumber \\&\quad +2 \omega \delta g_{x x}^{0}(r_H)+\omega \delta g_{z z}^{0}(r_H)) = 0, \end{aligned}$$
(43)

where \(k_{0}^{2} = \frac{\lambda _{L}^2}{v_B^2} = 6 \pi T A'(r_H) e^{A(r_H)-B(r_H)}.\) For general \(\omega \) and k Eq. (43) imposes a non-trivial constraint on the near-horizon expansion components \(\delta g_{v v}^{0}(r_H),\) \(\delta g_{z v}^{0}(r_H),\) \(\delta g_{x x}^{0}(r_H)\) and \(\delta g_{z z}^{0}(r_H).\) However, at the point \(\omega _{*}=i\lambda _{L}=2 \pi Ti\) the metric component \(\delta g_{v v}^{0}(r_H)\) decouples from the other components and Eq. (43) reduces to

$$\begin{aligned} \delta g_{v v}^{0}(r_H) \left( k^2 - \frac{i k_{0}^2 \omega }{2 \pi T} \right) = 0. \end{aligned}$$
(44)

Interestingly, this equation has the same form as the equation that determines the profile of shift corresponding to the shock wave geometry, Eq. (26), with \(\chi ^{2}\equiv \frac{\lambda _{L}^2 }{v_B^2}.\) The other point is that at the point \(k=i k_{0}\) Eq. (44) is automatically satisfied. Put in other words, at \((\omega _\star ,k_\star ),\) Eq. (43) becomes trivial and it does not impose any constraint on the near-horizon expansion components \(\delta g^{0}_{v v}(r_H),\) \(\delta g^{0}_{z v}(r_H),\) \(\delta g^{0}_{x x}(r_H)\) and \(\delta g^{0}_{z z}(r_H).\) Its message is that there exists one extra ingoing mode emerging at this point and as a result lead to the pole-skipping in the retarded energy density correlation function \(G^{R}_{T^{00}T^{00}}(\omega ,k)\) at the \((\omega _\star ,k_\star ).\) To understand this phenomenon more precisely, we can now check what happens as one moves slightly away from the special point. We consider Einstein’s equations with \(\omega =i\lambda +\epsilon \,\delta \omega \) and \(k=i k_{0} + \epsilon \, \delta k\) where \(\vert \epsilon \vert \ll 1\) and hence, at leading order in \(\epsilon ,\) we have a family of different ingoing modes by varying the slope \(\frac{\delta \omega }{\delta k}.\) This slope can be chosen to correspond to the resulting ingoing mode near the \((\omega _\star ,k_\star )\) with different asymptotic solutions at the boundary. If one chooses \(\frac{\delta \omega }{\delta k}\) in the following form

$$\begin{aligned} \frac{\delta \omega }{\delta k} = \frac{2 k_{0} \delta g^{0}_{v v}(r_H)}{\frac{k_{0}^2}{2 \pi T}\delta g^{0}_{v v}(r_H) - 2 k_{0} \delta g^{0}_{z v}(r_H) - 2 \pi T \left( 2\delta g^{0}_{x x}(r_H) + \delta g^{0}_{z z}(r_H)\right) }, \end{aligned}$$
(45)

then we will get an ingoing mode that matches continuously onto the normalizable solution at the boundary. All these lines pass through the \((\omega _\star ,k_\star )\) and if we move away from that point, we see different lines with slopes (45) in the \(T_{v v}\) correlation functions. This can also be described as a line of poles in the energy density correlation function that passes through the special point when we move away from the special point along the slope (45). The point is that one could also choose different \(\frac{\delta \omega }{\delta k}\) such that the ingoing mode matches onto a solution with different asymptotes at the boundary.

Apart from this viewpoint, we can study linearized equations more fashionably. To do this, we have to decouple the linearized equations by choosing the suitable gauge+diff invariant master field variables. In the spin 0 sector, there are 7 combinations of gauge+diff-invariant perturbations [87, 88], but in the on-shell level only three of them are independent. In the following, we write a specific choice of these three combinations for the general metric

$$\begin{aligned}&\psi _1 \equiv \frac{d}{dr}\left[ \frac{2\delta g_{x x}(r) + \delta g_{z z}(r)}{f_3(r)}\right] \nonumber \\&\quad - \frac{i \omega }{f_3(r)} \sqrt{\frac{f_2(r)}{f_1(r)}} \left( 2\delta g_{x x}(r) + \delta g_{z z}(r)\right) \nonumber \\&\quad - \frac{2 i k}{f_3(r)} \left( \delta g_{r z}(r) + \sqrt{\frac{f_2(r)}{f_1(r)}}\delta g_{v z}(r)\right) \nonumber \\&\quad - \frac{3 f_3'(r)}{2 f_3(r) f_2(r)} \left( \delta g_{rr}(r) + 2 \sqrt{\frac{f_2(r)}{f_1(r)}}\delta g_{r v}(r) + \frac{f_2(r)}{f_1(r)} \delta g_{v v}(r)\right) \nonumber \\&\quad - \left( \! 2 k^2\frac{f_2(r)}{f_3(r) f_3'(r)} + \frac{3}{ f_3(r)} \left( \!\frac{f_3''(r)}{f_3'(r)} - \frac{f_3'(r)}{f_3(r)} - \frac{f_2'(r)}{2 f_2(r)}\!\right) \!\right) \delta g_{x x}(r) ,\nonumber \\&\psi _2 \equiv \frac{\delta g_{x x}(r)}{f_3'(r)} \phi '(r) - \delta \phi (r),\nonumber \\&\psi _3 \equiv k \delta A_v(r) + \omega \delta A_z(r) - \frac{k A_t'(r)}{f_3'(r)} \delta g_{x x}(r). \end{aligned}$$
(46)

In Appendix A we discuss the independent combinations of gauge+diff-invariant perturbations in detail. By choosing \((f_1(r), f_2(r), f_3(r)) = (e^{2 A(r)} h(r), \frac{e^{2 B(r)}}{h(r)}, e^{2 A(r)})\) in the Eq. (39), we rewrite the 1RCBH metric in the EF coordinates

$$\begin{aligned} ds^2=-e^{2A(r)}h(r)dv^2+2e^{A(r)+B(r)}dvdr+e^{2A(r)}dx_i^2. \end{aligned}$$
(47)

So, we will get the following gauge-invariant master field variables

$$\begin{aligned}&\psi _1 \equiv \frac{d}{dr}\left[ e^{- 2 A(r)}\left( 2\delta g_{x x}(r)+ \delta g_{z z}(r)\right) \right] \nonumber \\&\quad - \frac{i \omega e^{B(r) - 3 A(r)}}{h(r)} \left( 2\delta g_{x x}(r) + \delta g_{z z}(r)\right) \nonumber \\&\quad - 2 i k e^{- 2 A(r)} \left( \delta g_{r z}(r) + \frac{e^{B(r) - A(r)}}{h(r)}\delta g_{v z}(r)\right) \nonumber \\&\quad - 3 h(r) A'(r) e^{- 2 B(r)}\left( \delta g_{rr}(r) + 2 \frac{e^{B(r) - A(r)}}{h(r)}\delta g_{r v}(r) \right. \nonumber \\&\quad \left. + \frac{e^{2B(r) - 2 A(r)}}{h^2(r)} \delta g_{v v}(r)\right) - \left( k^2\frac{e^{2 B(r) - 4 A(r)}}{A'(r) h(r)} \right. \nonumber \\&\quad \left. + \frac{e^{-2 A(r)} \left( 3 A'(r) h'(r) + h(r) (6 A''(r) - 6 A'(r) B'(r))\right) }{ 2 A'(r) h(r)} \right) \delta g_{x x}(r),\nonumber \\&\psi _2 \equiv e^{- 2 A(r)}\frac{\delta g_{x x}(r)}{2 A'(r)} \phi '(r) - \delta \phi (r),\nonumber \\&\psi _3 \equiv k \delta A_v(r) + \omega \delta A_z(r) - k A_t'(r) e^{- 2 A(r)} \frac{\delta g_{x x}(r)}{ 2 A'(r)}. \end{aligned}$$
(48)

The linearized perturbation equations can be written for these gauge+diff-invariant perturbations. But the choices of metric perturbations in master field variables are not correct, since they are rank (0, 2) tensors and vary under coordinate transformations. We have to convert them to the rank (1, 1) tensors and then plug them into these master equations. To do so, we note that \(\delta g_{\mu \nu } = g^0_{\mu \alpha } \delta g^\alpha _\nu \) where \(g^0_{\mu \alpha }\) are metric components written in (47). Hence, we have

$$\begin{aligned}&\delta g_{r r} = e^{A(r)+B(r)} \delta g^v_r, \nonumber \\&\delta g_{r v} = e^{A(r)+B(r)} \delta g^v_v = - e^{2 A(r)} h(r) \delta g^v_r + e^{A(r)+B(r)} \delta g^r_r, \nonumber \\&\delta g_{v v} = - e^{2 A(r)} h(r) \delta g^v_v + e^{A(r)+B(r)} \delta g^r_v, \nonumber \\&\delta g_{i i} = e^{2 A(r)} \delta g^i_i,\quad i = x, z, \nonumber \\&\delta g_{z j} = e^{2 A(r)} \delta g^z_j,\quad j = r, v. \end{aligned}$$
(49)

These replacements should be inserted in the invariant combinations of Eq. (48). To solve the linearized equations, it is useful to consider the two points. First, from the invariant sets of the Eq. (48) or any combinations, we omit \((\delta g^r_r, \delta A_v, \delta \phi )\) in favor of other fluctuations. Second, the background solutions are used to relate higher derivatives of functions \((A^{(n)}(r), h^{(n)}(r), \phi ^{(n)}(r), \cdots )\) with \(n \ge 2\) to the lower orders \((A^{(n)}(r), h^{(n)}(r), \phi ^{(n)}(r), \cdots )\) with \(n \le 1.\) The Number of independent equations is 11. Four of them are constrained equations that only contain first-order derivative with respect to the “r” coordinate and the rest are dynamical equations with two order of derivatives. To obtain the constrained equations, we define a normal vector \(n_\mu = (0, 1, 0, 0, 0)\) to the \(r= cte\) hypersurfaces. Hence, the constrained equations becomes

$$\begin{aligned}&n^\mu {\mathcal {G}}_{\mu \nu } = g^{\mu \alpha } n_\alpha {\mathcal {G}}_{\mu \nu } = 0, \nonumber \\&n^\mu {\mathcal {A}}_{\mu } = g^{\mu \alpha } n_\alpha {\mathcal {A}}_{\mu } = 0. \end{aligned}$$
(50)

For the 1RCBH background, these equations can be written as follows

$$\begin{aligned}&n^v {\mathcal {G}}_{v v} + n^r {\mathcal {G}}_{r v} = e^{- A(r) - B(r)} {\mathcal {G}}_{v v} + e^{- 2 B(r)} h(r) {\mathcal {G}}_{r v}= 0, \nonumber \\&n^v {\mathcal {G}}_{r v} + n^r {\mathcal {G}}_{r r} = e^{- A(r) - B(r)} {\mathcal {G}}_{v r} + e^{- 2 B(r)} h(r) {\mathcal {G}}_{r r}= 0, \nonumber \\&n^v {\mathcal {G}}_{v z} + n^r {\mathcal {G}}_{r z} = e^{- A(r) - B(r)} {\mathcal {G}}_{v z} + e^{- 2 B(r)} h(r) {\mathcal {G}}_{r z}= 0, \nonumber \\&n^v {\mathcal {A}}_{v} + n^r {\mathcal {A}}_{r} = e^{- A(r) - B(r)} {\mathcal {A}}_{v} + e^{- 2 B(r)} h(r) {\mathcal {A}}_{r}= 0. \end{aligned}$$
(51)

From these equations, the fluctuations \(\big (\delta g'^{z}_v(r), \delta g'^{x}_x(r), \delta g'^z_z(r), \delta A'_z(r)\big )\) are solved in terms of the set \(\big (\delta g^v_r(r), \delta g^r_v(r), \delta g^z_r(r), \delta g^z_v(r), \delta g^x_x(r), \delta g^z_z(r) \big )\) and invariant perturbations

\(\left( \psi _1(r), \psi _2(r), \psi _3(r), \psi '_1(r), \psi '_2(r), \psi '_3(r)\right) .\) On the other hand, the dynamical equations are given by

$$\begin{aligned}&\varvec{\varphi } = 0, \nonumber \\&{\mathcal {A}}_{r} = 0, \quad {\mathcal {A}}_{z} = 0\nonumber \\&{\mathcal {G}}_{r v} = 0, \quad {\mathcal {G}}_{x x} = 0, \quad {\mathcal {G}}_{z z} = 0, \quad {\mathcal {G}}_{v z} = 0. \end{aligned}$$
(52)

To rewrite these dynamical equations in terms of the invariant perturbations, we have to do the following steps:

  1. (1)

    Solving the equations \(\big ( {\mathcal {G}}_{x x} = 0, \,\,\, {\mathcal {G}}_{z z} = 0, \,\,\, {\mathcal {G}}_{v z} = 0, {\mathcal {A}}_{z} = 0\big )\) would give us the results for \((\delta g''^x_x(r), \delta g''^z_z(r), \delta g''^z_v(r), \delta A''_z(r))\) in terms of other perturbations. Remember that from Eq. (51), the perturbations \(\big (\delta g'^{z}_v(r), \delta g'^{x}_x(r), \delta g'^z_z(r), \delta A'_z(r)\big )\) are solved in terms of other non-derivatives perturbations. So the set \((\delta g''^x_x(r), \delta g''^z_z(r), \delta g''^z_v(r), \delta A''_z(r))\) are written solely in terms of non-derivatives fluctuations.

  2. (2)

    The solutions for \((\delta g'''^x_x(r), \delta g'''^z_z(r))\) are derived from derivatives of “r” of the solutions in item one. These are needed for simplifications of the equation \({\mathcal {G}}_{r v} = 0.\)

  3. (3)

    We insert the solutions of \((\delta g''^x_x(r), \delta g''^z_z(r), \delta g''^z_v(r), \delta A''_z(r))\) and \(\left( \delta g'^{z}_v(r), \delta g'^{x}_x(r), \delta g'^z_z(r), \delta A'_z(r)\right) \) into the following equations

    $$\begin{aligned}&\varvec{\varphi } = 0, \nonumber \\&{\mathcal {A}}_{r} = 0,\nonumber \\&{\mathcal {G}}_{r v} = 0, \end{aligned}$$
    (53)

    as well as using zero-order equations. Careful simplifications would give us three dynamical equations for \(\left( \psi _1, \psi _2, \psi _3\right) .\)

Symbolically, the resulting equations are as follows

$$\begin{aligned}&f^1_1(r) \psi _1(r) + f^2_1(r) \psi _2(r) + f^3_1(r) \psi _3(r) +f^1_2(r) \psi _1'(r) \nonumber \\&\quad +f^2_2(r) \psi _2'(r) +f^3_2(r) \psi _3'(r) +f^2_3(r) \psi _2''(r) = 0,\nonumber \\&g^1_1(r) \psi _1(r) + g^2_1(r) \psi _2(r) + g^3_1(r) \psi _3(r) +g^1_2(r) \psi _1'(r) \nonumber \\&\quad +g^2_2(r) \psi _2'(r) +g^3_2(r) \psi _3'(r) +g^3_3(r) \psi _3''(r) = 0,\nonumber \\&m^1_1(r) \psi _1(r) + m^2_1(r) \psi _2(r) + m^3_1(r) \psi _3(r) +m^1_2(r) \psi _1'(r) \nonumber \\&\quad +m^2_2(r) \psi _2'(r) +m^3_2(r) \psi _3'(r) \nonumber \\&m^1_3(r) \psi _1''(r) + m^2_3(r) \psi _2''(r) + m^3_3(r) \psi _3''(r) = 0, \end{aligned}$$
(54)

where \((f^i_j, g^i_j, m^i_j)\) are some coefficients.Footnote 2 This procedure can be applied to any configuration of perturbing fields.

The multivaluedness of boundary retarded Green’s function can also be seen from another point of view. Recently, there have been reported that at higher Matsubara frequencies, i.e. \(\omega = \omega _n = - 2 i n \pi T\) with \(n \ge 1,\) the equations of motion of perturbations exhibit a pole-skipping in the \(G^R_{{\mathcal {O}} {\mathcal {O}}}(\omega , k)\) for the corresponding boundary operator [46, 56, 57]. This is because at these points the equations give no constraints on \(\delta \phi ^n(r_H)\) coefficients of the expansion (42) and these many unknown coefficients reflect many hydrodynamics poles which each of them approaches to that point with a special slope [46].

At \(k = i k_0 = i \lambda _{L}/v_B\) and \(\omega = \omega _n\) the regular solutions are labelled with two independent parameters, since \(\text{ det }\, {\mathcal {M}}(\omega _n, k_0) = 0\) and there exists no non-trivial solution there. To do this, we expand the equations of motion for scalar perturbation around the horizon. The result is as follows

$$\begin{aligned}&{\mathcal {I}}_{1} = M_{1 1}(\omega , k^2) \delta \phi ^0(r_H) + (2 \pi T - i \omega ) \delta \phi ^1(r_H), \nonumber \\&{\mathcal {I}}_{2} = M_{2 1}(\omega , k^2) \delta \phi ^0(r_H) + M_{2 2}(\omega , k^2) \delta \phi ^1(r_H) \nonumber \\&\qquad + (4 \pi T - i \omega ) \delta \phi ^2(r_H),\nonumber \\&\cdots \end{aligned}$$
(55)

where the coefficients \(M_{i j}(\omega , k^2)\) take the following form

$$\begin{aligned} M_{i j}(\omega , k^2) = i \omega a_{i j} + k^2 b_{i j} + c_{i j}, \end{aligned}$$
(56)

with \(a_{i j}, b_{i j}, c_{i j}\) are determined by the background solutions in (12) and their derivatives on the horizon. Expressions \({\mathcal {I}}_{1}, {\mathcal {I}}_{2}, {\mathcal {I}}_{3}\) are combinations of other perturbations with specific coefficients derived from background solutions. Their special form is very complicated and we list them in Appendix B.

We observe from Eq. (55) that at frequencies \(\omega = \omega _n\) it is not possible to read the coefficients iteratively from \(\delta \phi ^0(r_H).\) It means that \(\delta \phi ^n(r_H)\) are no longer dependent parameters and thus are free parameters near the horizon. Also, at the point \(\omega = \omega _n\) the first n equation are decoupled and we can solve a simple matrix equation for \(\delta {\tilde{\phi }} = \left( \delta \phi ^0(r_H), \cdots , \delta \phi ^{n-1}(r_H)\right) \) as it follows

$$\begin{aligned} {\mathcal {M}}(\omega , k^2) \cdot \delta {\tilde{\phi }}= {\mathcal {I}}, \end{aligned}$$
(57)

and \({\mathcal {M}}(\omega , k^2)\) is the coefficient matrix of scalar perturbations living near the horizon. This feature is similar to former observation [46, 56, 57]. However, we observe that at \(k = i k_0\) and \(\omega = \omega _n,\) \(\text{ det }\, {\mathcal {M}}(\omega _n, k_0) \ne 0.\) Therefore, solutions for the linear equations (55) are labelled with just one parameter. This is the novelty of our computations which may be because of the presence of the electric charge. It is worthwhile to mention that equations for gauge field perturbations do not capture such properties.

5 Conclusion

In this paper, we study the chaotic properties of the 1RCBH model. This 5-dimensional Einstein–Maxwell-Dilaton model is dual to a 4-dimensional strongly charged coupled field theory enjoying a critical point in its parameter space. To diagnose these properties, we use the OTOCs and pole-skipping analysis. In the latter, the chaotic properties of many-body thermal systems are encoded in energy density two-point functions \(G^{R}_{T^{00}T^{00}}(\omega ,k)\) and linearized equations of motion. The butterfly velocity \(v_B\) and Lyapunov exponent \( \lambda _{L},\) which are naturally extracted from OTOC, have been studied as the parameters containing the information about chaos. On the other hand, we investigate the pole-skipping phenomenon which concerns the analytic behavior of \(G^{R}_{T^{00}T^{00}}(\omega ,k)\) around the \((\omega _\star ,k_\star )\) in the complex \((\omega -k)\) plane. We also address the chaotic behaviors for AdS-RN background and find that \(v_B^2 \ge c_s^2\) at every point of black hole solutions. This finding is valid for the 1RCBH model as well. We list our main results in the following:

  • We consider a general asymptotically AdS background whose metric is given by Eq. (18) and compute OTOC and then derive holographically explicit expressions for \( \lambda _{L}\) and \(v_B\)

    $$\begin{aligned} \lambda _{L}=\frac{2\pi }{\beta },\quad v_B=\frac{2\sqrt{\pi }(f_1f_2)^{\frac{1}{4}}}{\sqrt{\beta (d-1)f_3'}}\bigg \vert _{r=r_H}, \end{aligned}$$
    (58)

    where \(\beta \) is the inverse of Hawking’s temperature. The above result perfectly matches the previously reported CFT results. In the 1RCBH model, we read

    $$\begin{aligned} v_B^2=\frac{4}{7\mp \sqrt{1-\left( \frac{\mu /T}{\pi /\sqrt{2}}\right) ^2}}, \end{aligned}$$
    (59)

    where \(-(+)\) indicates the stable(unstable) blackhole solutions. Interestingly, we find that the butterfly velocity \(v_B\) can be used as a probe to see the critical point of the corresponding dual field theory. Furthermore, we study the behavior of \(v_B\) near this critical point and observe that the dynamical critical exponent is equal to \(\frac{1}{2}\) which is in complete agreement with the results reported in the literature. Interestingly, we find \(v_B^2 \ge c_s^2\) for every point of \(0 \le \frac{\mu }{T} \le \frac{\pi }{\sqrt{2}}.\)

  • Related to the pole-skipping phenomenon we observe that the metric component \(\delta g_{v v}^{0}(r_H)\) decouples from the other components of the vv component of the linearized equations at special point \(\omega _{*}=i\lambda _{L}=2 \pi Ti\) and reduces to the following form

    $$\begin{aligned} \delta g_{v v}^{0}(r_H) \left( k^2 - \frac{i k_{0}^2 \omega }{2 \pi T} \right) = 0, \end{aligned}$$
    (60)

    which is interestingly identical to the one governing the spatial profile of a gravitational shock wave (26). Hence, one can use the pole-skipping analysis to determine the chaotic properties of the underlying theory including \(v_B\) and \( \lambda _{L}.\) The other point is that at special point \(k=i k_{0}\) Eq. (44) is identically satisfied which means that this equation does not impose any constraint on the near-horizon expansion components \(\delta g_{v v}^{0}(r_H),\) \(\delta g_{z v}^{0}(r_H),\) \(\delta g_{x x}^{0}(r_H)\) and \(\delta g_{z z}^{0}(r_H).\) In other words, there exists an extra linearly independent ingoing solution to Einstein’s equations that leads to the pole-skipping in \(G^{R}_{T^{00}T^{00}}(\omega ,k).\) To find a better understanding of this phenomenon, it is observed that if one moves away from the \((\omega _\star ,k_\star ),\) i.e. \(\omega = 2 \pi T i\) and \(k = i k_0\) along the slope (45), then there will be lines in \(G^{R}_{T^{00}T^{00}}(\omega ,k)\) that passes through that point. As a result, this slope can be considered as an extra parameter in the near-horizon solution and can be used to adjust the ingoing solution onto different asymptotic solutions at the boundary. We study also the pole-skipping phenomenon through the linearized equations from another point of view. Indeed, we decouple the linearized equations by choosing the suitable gauge+diff invariant master field variables focusing on the spin 0 sector. Details of derivations for dynamical equations are given. We provide the exact form of the linearized equations of motion in separate files along with this paper. We investigate pole-skipping of the retarded Green’s function at higher Matsubara points in the equations of motion for scalar field perturbations. It is observed that regular solutions near the horizon are labelled with only one unknown coefficient and point \(k = i k_0\) not to add further constraints on equations. These issues are not seen in the gauge field perturbation equations.

  • We investigate the chaotic behaviors for the AdS-RN background. We obtain \(v_B^2 \ge c_s^2\) for every black hole solution. We obtain the dynamical equations for gauge+diff invariant perturbations given in the (54), by using the general method based on the properties of Einstein equation. Having the regular solutions near the horizon is guaranteed once the Eq. (43) is derived.

Our main concern in this study is to check whether the critical models respond to chaotic conditions. Several questions call which we leave for further investigations. One can investigate the OTOC and pole-skipping for the Non-conformal backgrounds having special critical points. Also examining the chaotic behaviors of the gravitational models having large similarities to the QCD phase diagram deserves further investigation. These works are postponed to our future works. Another interesting work is to look more carefully at the relation \(v_B^2 \ge c_s^2\) by mathematical arguments.