A generalized static spherically symmetric anisotropic compact stellar model

Abstract

We report here a new exact solution of the Einstein field equations that describes a static spherically symmetric, anisotropic compact stellar fluid sphere. A generalized metric form corresponding to the $g_{rr}$ component and a specific anisotropic profile generates the model. The new class of generalized solutions reduces to Finch-Skea, Vaidya Tikekar and Schwarzschild interior solutions for specific cho-ices of the model parameters. The model parameters have been determined from the continuity of the interior and exterior metrics at the surface of the star and setting the radial pressure at the boundary to zero. Recent observed measurements from some pulsars as sources have been utilized to validate our model.

1 Introduction

The general theory of relativity has been pivotal in casting light on gravitational-related phenomena in both astrophysics and cosmology [1]. The validity of classical general relativity (CGR) has been expounded through observations such as the deflection of starlight in the neighbourhood of self-gravitating objects, the observational of gravitational waves, black hole shadows and the precession of Mercury’s orbit, amongst others. On the cosmological scale, observations of fluctuations in the Cosmic Microwave Background Radiation, gravitational lensing, the current expansion rate and acceleration of the Universe have their origins in CGR [2,3,4]. These observations on both the astrophysical and cosmological fronts stand in good stead in support of CGR. However, there have been several shortcomings in the predictive power of CGR in strong gravitational fields and the behaviour of matter at ultra-high densities.

The first attempt at modeling the interior gravitational field of a self-bounded object in CGR was carried out by Schwarzschild [5] in which he assumed spherically symmetry with the interior matter content being characterised by uniform density with isotropic pressure. Over the last century, the interior Schwarzschild solution has been generalised to incorporate more realistic matter distributions including charge, anisotropy, bulk viscous pressure, dark energy and the cosmological constant. Earlier models of compact objects arising from the solutions of the Einstein field displayed various pathologies as was demonstrated by the work of Dev and Glesier [6, 7]. They showed that only a small subset of the vast array of exact solutions describing stellar objects meet the requirements for regularity, causality and stability. Recently, there has been an ‘exponential’ growth in the appearance of stellar models in the literature. These models arise from assumptions on symmetry of the stellar object, Lie analysis, imposition of the Karmarkar condition, complexity-free condition and the use of an equation of state (EOS). The seminal paper by Bowers and Liang [8] which investigated the impact of anisotropic stresses in compact objects has shown that pressure anisotropy impacts on various observable characteristics of stars such as mass-radius values and higher surface redshifts, namely $z_s > 2$. The change in the sign of the anisotropy factor $\varDelta = p_r -p_t$ plays a key role in the stability of the gravitating configuration. The classic stability condition derived by Chandrasekhar for isotropic, static gravitating spheres, $\varGamma > \frac{4}{3}$ is modified in the presence of anisotropy. In the study of dissipative collapse, Herrera, Chan and co-workers studied the problem of dynamical stability of anisotropic, collapsing stars dissipating energy in the form of a radial heat flux. In their work, they employed a perturbative framework to study the evolution of a spherically symmetric gravitating body which loses hydrostatic equilibrium and undergoes dissipative collapse. They derived the adiabatic index in both the Newtonian and Post-Newtonian regimes. In the Newtonian limit for the static model they showed that anisotropy increases $(P_{r0} < P_{t0})$ or decreases $(P_{r0} > P_{t0})$ the instability of the collapsing configuration. In addition, in the post-Newtonian approximation with vanishing dissipation the adiabatic index is modified by contributions from the radial pressure [10,11,12].

In their seminal work on the impact of anisotropy in self-gravitating systems Santos and Herrera [13] carried out a comprehensive investigation of the role played by radial and transverse stresses in non-static and quasi-static stellar objects. They provide a list of possible origins of pressure anisotropy within stellar objects citing phase transitions in dense cores, pion condensation, superconducting phases, rotation, neutrino helicity, amongst others. Sawyer [14] in his work on condensed $\pi ^{-}$ phases at ultra-high densities such as in the core of neutron stars showed that the pressure of the free Fermi gas is drastically altered. In the study of stellar objects with densities in the order of $10^{15}$ g cm$^{-3}$, interactions within the core become relativistic and Ruderman [15] demonstrated the existence of a type-P superfluid which gives rise to pressure anisotropy in these stars. Martinez studied transport processes in radiating stars which dissipate energy to the exterior in the form of a radial heat flux. Thermally generated neutrinos carry energy from the stellar interior to the cooler surface layers. A source of viscosity is neutrino trapping and it was shown that the contributions of shear to the pressure anisotropy is prominent from the centre of the star to a radius of approximately 2 km [16].

The observation of gravitational waves in events such as GW170817 and GW190814 has led researchers to model compact objects which can account for the detected signals by the LIGO-VIRGO collaboration [17,18,19]. For example, the signal observed in the GW190814 event has led to a bigger mystery regarding the nature and components of the binary coalescence. It is believed that the detected signals arose from the merger of a $2.59_{-0.09}^{+0.08}M_{\odot }$ compact object and a $23 M_{\odot }$ black hole [20] (and see references therein). The secondary component of this merger is believed to be a neutron star with a mass greater than the usual $2M_{\odot }$ ‘upper’ bound for neutron stars in CGR. This has led researchers to speculate on the very nature of the coalescence some of which include a triple hierachal system involving a double merger with a tight NS-NS scattering off a massive BH. In order to determine if the GW190814 event was a result of a NS-BH or BH-BH merger, Tews et al. [21] employed the NMMA framework in which they utilised a set of 5000 EOSs that extended beyond 1.5 times the nuclear saturation density. They concluded that GW190814 was a result of a binary black hole merger with a probability of $>99.9\%$.

Researchers have also appealed to modified gravity theories to account for the secondary component of GW190814. In these studies anisotropy plays a key role in the physics of the resulting stellar models. The introduction of anisotropy via Geometric Deformation has been widely exploited and it has been shown that this approach can lead to robust models of compact objects which can account for masses beyond 2 $M_{\odot }$ without resorting to exotic matter distributions [22, 23]. Models of compact stars within the Einstein-Gauss-Bonnet (EGB) gravity have also been fruitful in producing models with higher stellar masses and observed radii in gravitational events [24,25,26]. More recently, researchers have been working in f(Q) gravity theories to model the secondary component of the GW190814 event. They demonstrated that there is an interplay between the EOS parameter, decoupling constant and the f(Q) parameter which sensitives the model’s characteristics such as stability and regularity [27, 28]. Inspired by these observations of gravitational waves and the impact of anisotropy in stars, we model compact objects within the framework of Einstein’s classical general relativity in which the radial and transverse stresses are different. Our model is subjected to stringent tests to ensure that it describes a physically realizable stellar structure.

This paper has been organized as follows: In Sect. 2, the basic Einstein field equations corresponding to the aniso-tropic compact object has been provided. In Sect. 3, we adopt a a generalized metric potential for $g_{rr}$ and a particular anisotropic profile for the interior matter distribution and solve the relevant field equations. All the various relevant physical parameters are derived analytically in this section. The physical criteria necessary for a realistic compact star are stated in Sect. 4. In Sect. 5, the exterior Schwarzschild space-time is matched with the interior solution across the boundary of the star and corresponding boundary conditions have laid down. The analysis of the various physical conditions are discussed in Sect. 6. The recent estimated observed data of some well known pulsars are shown to validate this model in Sect. 7 with some graphical representations and also in tabular form. Stability of the model under different conditions has been discussed in Sect. 8. Finally, some concluding remarks and discussion have been made in Sect. 9.

2 Einstein field equations

The interior space-time geometry of a static, spherically symmetric object is described in standard coordinates $x^0 = t$, $x^1=r$, $x^2 = \theta$, $x^3 = \phi$ by line element as

$$\begin{aligned} ds_{-}^2 = -A_{0}^2(r)dt^2 + B_{0}^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2\theta d\phi ^2), \end{aligned}$$

(1)

where, the gravitational metric potentials $A_{0}(r)$ and $B_{0}(r)$ are dimensionless and functions of the radial coordinate ‘r’ need to be determined. We assume that the compact star composed of matter which is anisotropic in nature with respect to pressure. The assumption that the pressure within the stellar core is anisotropic is a physically reasonable one. Apart from the physical processes which give rise to anisotropy within the stellar fluid, one expects a departure from pressure isotropy in the presence of dissipation, density inhomogeneity and shear viscosity. On the flip-side, for a stellar fluid configuration with an initially isotropic profile to remain isotropic throughout its evolution, the fluid must be nondissipative, shear-free and exhibit homogeneity in the energy-density. It is possible but unlikely for the evolution to maintain isotropy in pressure by demanding that dissipation, inhomogeneity and the Weyl-free stresses cancel each other. Herrera [29] demonstrated that the stability of pressure isotropy in a dynamically evolving fluid can be maintained under the requirements of conformal flatness, homogeneous density and zero dissipative fluxes. To describe the anisotropic fluid system, we use the energy-momentum tensor of the form

$$\begin{aligned} T_{\alpha \beta } = (\rho + p_t)u_{\alpha } {u_\beta } + p_{t} g_{\alpha \beta } + (p_r - p_t)\chi _{\alpha } \chi _{\beta }, \end{aligned}$$

(2)

where $\rho$ represents the energy-density, $p_r$ and $p_t$, respectively denote fluid pressures along the radial and transverse directions respectively. The quantity $u^\alpha$ is the 4-velocity of the fluid and $\chi ^\alpha$ is a unit space-like 4-vector along the radial direction so that the following relations holds: $u^\alpha u_\alpha = -1$, $\chi _\alpha \chi _\beta =-1$ and $u^\alpha \chi _\beta =0$.

The Einstein field equations of the system corresponding to the line element (1) are then obtained as (in natural unit system where we set $G = c = 1$)

$$\begin{aligned} 8\pi \rho= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2 B_0^2}+\frac{2B_0'}{r B_0^3}\right] , \end{aligned}$$

(3)

$$\begin{aligned} 8\pi p_r= & {} \left[ -\frac{1}{r^2}+\frac{1}{B_0^2 r^2}+\frac{2A_0'}{r A_0B_0^2}\right] , \end{aligned}$$

(4)

$$\begin{aligned} 8\pi p_t= & {} \left[ \frac{A_0''}{A_0B_0^2} + \frac{A_0'}{rA_0B_0^2} - \frac{B_0'}{r B_0^3} - \frac{A_0'B_0'}{A_0 B_0^3}\right] . \end{aligned}$$

(5)

In Eqs. (3)–(5), a ‘prime’ denotes differentiation with respect to the radial coordinate r.

Utilizing the Eqs. (4) and (5), we can define the pressure anisotropy of the stellar interior as

$$\begin{aligned} \varDelta (r)= & {} 8\pi (p_t-p_r)\nonumber \\= & {} \left[ \frac{A_0''}{A_0 B_0^2} - \frac{A_0'}{r A_0B_0^2} - \frac{B_0'}{r B_0^3} \frac{A_0'B_0'}{A_0B_0^3} - \frac{1}{r^2B_0^2} + \frac{1}{r^2}\right] .\nonumber \\ \end{aligned}$$

(6)

In principle, $\varDelta$ may be positive as well as negative in nature depending upon whether $p_t>p_r$ or $p_t<p_r$. In our model, we have considered $p_t>p_r$ for the matter distribution to obtain a stable structure of compact objects.

The mass contained within a stellar radius r of is defined as

$$\begin{aligned} m(r)= \frac{1}{2}\int _0^r\omega ^2 \rho (\omega )d\omega . \end{aligned}$$

(7)

Thus we have basically a system of three independent Eqs. (3)–(5) in 5 independent variables, viz. $A_{0}$, $B_{0}$, $\rho$, $p_r$ and $p_t$. Equation (6) representing $\varDelta$ is basically a dependent equation in $p_r$ and $p_t$. To solve the system we must prescribe two of them.

In the present work the two assumptions are as follows: (i) a particular metric ansatz for the $g_{rr}$ metric component, and (ii) a specific form of the anisotropic parameter. With these assumptions we shall solve the set of equations in the next Sect. 3.

3 Generating a new model: analytical solution

To develop a physically reasonable model of the stellar configuration and hence to find exact solutions, any two physical parameters may be freely chosen. Here in this model we assume a particular metric potential and a appropriate form of the anisotropy. The metric potential for the $g_{rr}$ metric is given by

$$\begin{aligned} B_0^2 (r) = \frac{b C r^2+1}{a C r^2+1}, \end{aligned}$$

(8)

where a, b and C are constants and will be determined from the matching conditions. Here C is a scaling factor. This particular metric potential were used by the several authors to construct compact stellar models. Clearly, the metric is regular, finite and continuous within the stellar structure. It is interesting to note that the assumed form of the metric potential is a generalized one and other solutions can be recovered from this with specific choices of the constants as follows:

• $a=0$ and $b\ne 0$, the metric reduces to Finch Skea solution,

• $b=0$ and $a\ne 0$, one can generate the Schwarzschid interior solution,

• $a\ne 0$ and $b\ne 0$, the metric generates Vaidya-Tikekar solution.

With this choice of $B_0(r)$, Eq. (6) then reduces to

$$\begin{aligned} \varDelta (r)= & {} \frac{1}{r A_0\left( b C r^2+1\right) ^2} \times [r \left( a C r^2+1\right) A_0'' \left( b C r^2+1\right) \nonumber \\{} & {} -\left. A0'\left( b C r^2 \left( a C r^2+2\right) +1\right) +b C^2 r^3 (b-a) A_0].\right. \nonumber \\ \end{aligned}$$

(9)

On rearranging Eq. (9) we get

$$\begin{aligned}{} & {} \frac{A_0''}{A_0}-\frac{b C r^2(a C r^2+2)+1)}{r(a C r^2+1)(b C r^2+1)} \frac{A_0'}{A_0}+\frac{(b-a) b C^2 r^2}{(a C r^2+1)(b C r^2+1)} \nonumber \\{} & {} \quad =\frac{\varDelta (r)(b C r^2+1)}{(a C^2+1)}. \end{aligned}$$

(10)

Now the above Eq. (8) can be solved for $A_0(r)$ if $\varDelta (r)$ is specified in particular form. The anisotropy factor has to be chosen in such a way that regularity at the center is satisfied and at the same time easily integrable. Keeping in mind all the conditions imposed on anisotropy it is assumed that

$$\begin{aligned} \varDelta (r)= & {} \frac{b (b-a) C^2 r^2}{(b C r^2+1)^2}. \end{aligned}$$

(11)

The above choice for anisotropy is physically reasonable, as at the center ($r=0$) where both the radial and transverse pressures are equal and hence anisotropy must vanish. Also, this particular choice provides a solution for Eq. (10) in closed analytical form. Substituting Eq. (11) in Eq. (8), we obtain,

$$\begin{aligned} A''_0(r)-\frac{(1+b C r^2(a C r^2+2))}{r(b C r^2+1)(a C r^2+1)} A'_0(r)=0. \end{aligned}$$

(12)

We obtain a simple solution of the Eq. (12)

$$\begin{aligned} A_0(r)= & {} C_2 [\frac{(a-b)}{4 a C \sqrt{ab}} \log (2 a b C r^2+2 \sqrt{a b(a C r^2+1)} \nonumber \\{} & {} \times \sqrt{b C r^2{+}1}{+}a{+}b)\left. {+}\frac{\sqrt{a C r^2{+}1} \sqrt{b C r^2{+}1}}{2 aC} ]{+}C_3,\right. \end{aligned}$$

(13)

where $C_2$ and $C_3$ are constants of integration will be obtained from the boundary conditions. At this juncture, we draw the reader’s attention to the work by Herrera et al. [30] in which they developed a method to derive all static, anisotropic solutions of the field equations. This approach is an extension of the work developed by Lake [31] in which he obtained the most general line element for a spherically symmetric gravitating source with isotropic pressure. The key difference between the works of Herrera et al. and Lake is that in the case of anisotropic fluids two generating functions are required to completely describe the gravitational behaviour of the model. In light of this, we note that our model will be a sub-case of the more general family of solutions obtained by Herrera and co-workers. We are now in a position to determine the physical quantities such as matter density, radial pressure, transverse pressure and mass which can be cast as

$$\begin{aligned} 8\pi \rho&= \frac{C (b-a) \left( b C r^2+3\right) }{\left( b C r^2+1\right) ^2}, \end{aligned}$$

(14)

$$\begin{aligned} 8\pi p_r&= \frac{1}{\phi _1 \phi _2^3\left( 2 a b C r^2+2 \phi _1 \phi _2 \sqrt{a b}+a+b\right) } \nonumber \\&\quad \times \frac{1}{2 \sqrt{a} \sqrt{b} \left( C_2 \phi _1 \phi _2+2 a C C_3\right) +C_2 (a-b) \log \left( 2 a b C r^2+2\sqrt{a} \sqrt{b} \phi _1 \phi _2+a+b\right) } \nonumber \\&\quad \times \left[ C \left( 2 a^{3/2} b^{3/2} \left( C_2 \left( b C r^2 \left( 1-3 b C r^2\right) +4\right) -2 b C C_3 \phi _1\phi _2\right) -2 a^{5/2} \sqrt{b} \right. \right. \nonumber \\&\quad \times \left( 4 b^2 C^2 C_3 r^2 \phi _1\phi _2 +C_2 \phi _2^2\left( 2 b C r^2 \left( b C r^2-7\right) -5\right) \right) \nonumber \\&\quad +2 a^{7/2} \sqrt{b} C \left( 2 bC r^2+1\right) \left( 2 C_3 \phi _1\phi _2+5 C_2 r^2\phi _2^2\right) \nonumber \\&\quad \left. +C_2 (a-b)^2 \left( 2 a^{3/2} \sqrt{b} C r^2 \phi _2^2+ 2\sqrt{a} \sqrt{b} \phi _2^2+a \phi _1 \phi _2 \left( 2 b C r^2+1\right) \right. \right. \nonumber \\&\quad +\left. b \phi _1\phi _2\right) \log \left( 2 a b C r^2+2 \sqrt{a} \sqrt{b} \phi _1\phi _2+a+b\right) \nonumber \\&\quad +8 a^4 b C^2 C_3 r^2\phi _2^2-4 a^3 b C \phi _2^2 \left( 2 C_3 \left( b C r^2-1\right) -5 C_2 r^2 \phi _1 \phi _2 \right) -4 a^2 b \phi _2^2 \left( b C \right. \nonumber \\&\quad \left. \left. \left. \times \left( C_2 r^2 \phi _1 \phi _2+2C_3\right) -5C_2 \phi _1 \phi _2\right) -2 \sqrt{a} b^{5/2} C_2 \phi _2^2-4 a b^2 C_2 \phi _1 \phi _2^3\right) \right] , \end{aligned}$$

(15)

$$\begin{aligned} 8\pi p_t&= \frac{1}{\phi _1 \phi _2^5 \left( 2 a b C r^2+2 \sqrt{a b} \phi _1 \phi _2+a+b\right) } \nonumber \\&\quad \times \frac{1}{2 \sqrt{a b} \left( C_2 \phi _1 \phi _2+2 a C C_3\right) +C_2 (a-b) \log \left( 2 a b C r^2+2\sqrt{ab}\phi _1\phi _2+a+b\right) } \nonumber \\&\quad \times \left[ C \left( 2 a^{3/2} b^{3/2} \left( C_2 \phi _2^2 (\phi _2^2+3)-2 b C C_3 \phi _1 \phi _2\right) \right. \right. \nonumber \\&\quad +2 a^{5/2} \sqrt{b} \left( C_2 \phi _2 \left( 2 b C r^2 \left( 5 b C r^2+9\right) +5\right) -4 b^2 C^2 C_3 r^2 \phi _1\phi _2\right) \nonumber \\&\quad +2 a^{7/2} \sqrt{b} C \left( 2 \phi _2^2-1\right) \left( 2 C_3 \phi _1 \phi _2+C_2 r^2 \phi _2^2 (4 b C r^2+5)\right) +C_2 (a-b)^2\nonumber \\&\quad \times \left( 2 a^{3/2} \sqrt{b} C r^2 \phi _2^2+2 \sqrt{ab}\phi _2^2+a \phi _1 \phi _2 \left( \phi _2^2-1\right) \right. \nonumber \\&\quad \left. +b \phi _1\phi _2\right) \log \left( 2 a b C r^2+ 2 \sqrt{ab} \phi _1\phi _2+a+b\right) +8 a^4 b C^2 C_3 r^2 \phi _2^2+4 a^3 b C \phi _2^2 \nonumber \\&\quad \times \left( C_2 r^2 \phi _1 \phi _2 \left( 4 b C r^2+5\right) + C_3 (2- 2 b C r^2)\right) +4 a^2 b \phi _2^2 \left( b C \left( 3 C_2 r^2 \phi _1\phi _2 -2 C_3\right) \right. \nonumber \\&\quad \left. \left. +5 C_2 \phi _1\phi _2\right) - 2 \sqrt{a} b^{5/2} C_2 \phi _2^2-4 a b^2 C_2 \phi _1 \phi _2^3\right] , \end{aligned}$$

(16)

$$\begin{aligned} m(r)&= \frac{C r^3 (b-a)}{2 b C r^2+2}, \end{aligned}$$

(17)

where $\phi _1=\sqrt{1+a C r^2}$ and $\phi _2=\sqrt{1+b C r^2}$.

4 Physical requirements

The following conditions are required for a physically viable stellar model:

• (i) The gravitational potentials $A_0(r)$, $B_0(r)$ and the physical quantities $\rho$, $p_r$, $p_t$ should be well defined at the center and regular as well as non- singular throughout the interior of the star.

• (ii) The energy density should be positive throughout the interior of the star. Also, its value should monotonically decrease towards the boundary of the star from its maximum value at the centre. Mathematically i.e., $\rho \ge 0$. $\frac{d\rho }{d r}\le 0$.

• (iii) The radial and the tangential pressure must be positive through out the stellar interior i.e., $p_r \ge 0$,     $p_t \ge 0$. The pressures should be monotonically decreasing in nature with the radial parameter. This is ensured by the negative signature of the gradient of the pressures inside the stellar body, i.e., $\frac{dp_r}{dr} < 0$,   $\frac{dp_t}{dr} < 0$. Also, at the boundary $r=R$ of the star the radial pressure should vanish. The condition $p_r(R)=0$ is defines the radius of the star. However, there may be nonzero tangential pressure on its surface. At the centre of the star both the radial and transverse pressures are equal which means the anisotropy should vanish at the centre, $\varDelta (r=0)=0$.

• (iv) For a stable stellar anisotropic compact star, some energy conditions must be satisfied at each interior point of the fluid sphere. Basically, under the framework of general relativity the energy conditions are described in terms of the local inequality relations between energy density and pressures. The energy conditions are the Weak Energy Condition (WEC), Null Energy Condition (NEC), Strong Energy Condition (SEC) and Dominant Energy Condition (DEC) defined by the following inequalities.

  • (1) Weak Energy Condition (WEC): $\rho > 0$,  $p_r + \rho \ge 0$, $p_t + \rho \ge 0$

  • (2) Null Energy Condition (NEC): $p_r + \rho \ge 0$,  $\rho +p_t \ge 0$

  • (3) Strong Energy Condition (SEC): $\rho + p_r + 2 p_t \ge 0$

  • (4) Dominant Energy Conditions (DEC): $\rho - |p_r| \ge 0$ and $\rho -|p_t|\ge 0$

In this context it is interesting to check the trace energy condition (TEC) as suggested by the authors [32, 33]. The Trace of the energy tensor (TEC) should be positive throughout the interior of the star, represented mathematically as: $\rho -p_r -2 p_t \ge 0$.

• (v) The Causality condition, according to which the speed of sound (both radial and transverse) must be smaller than 1 (in the unit of speed of light c = 1) throughout the interior of the star. For a physically acceptable realistic model the causality condition, i.e., $0 \le \frac{dp_r}{d\rho } \le 1$, $0 \le \frac{dp_t}{d\rho } \le 1$ must be satisfied.

• (vi) The interior geometry of the star represented by the metric functions should match smoothly with the exterior Schwarzschild space-time metric across the stellar boundary.

• (vii) Adiabatic index ($\varGamma$), the ratio of two specific heats is related to the stability of an anisotropic stellar configuration. For a stable model, the well known condition for the stability of a Newtonian isotropic sphere is: $\varGamma > 4/3$. For a relativistic anisotropic sphere this condition modified to some extent.

5 Exterior space-time and junction conditions

In general relativity theory, the Schwarzschild metric is the uniquely defined spherically symmetric solution to the vacuum Einstein field equations. The exterior vacuum spacetime for a non radiating star can be described by the Schwarzschild metric which is

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M}{r}\right) dt^{2}+\left( 1 -\frac{2M}{r}\right) ^{-1}dr^{2}\nonumber \\{} & {} \left. +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2} \right) ,\right. \end{aligned}$$

(18)

where $r>2\,M$, M being the total mass of the stellar object. The matching conditions determines the numerical values of the model parameters. The junction conditions demands the continuity of the first and second fundamental forms (intrinsic and extrinsic curvature respectively) across the non-radiating bounding surface. Here we have only imposed the continuity of the first fundamental form developing compact stars by generating only static solutions.The continuity of the second fundamental is not required. For a static Continuity of the first fundamental form at the boundary allows the matching of the interior spacetime metric (1) to the vacuum exterior Schwarzschild solution (18) at the boundary of the star $r=R$. This continuity of the metric functions across the boundary yields:

Continuity of $g_{tt}$

$$\begin{aligned} A^2_0(R) = \left( 1-\frac{2 M}{R}\right) , \end{aligned}$$

(19)

Continuity of $g_{rr}$

$$\begin{aligned} B^2_0(R) = \left( 1-\frac{2 M}{R}\right) ^{-1}. \end{aligned}$$

(20)

Radial pressure vanishes to zero at a finite value of the radial parameter r, defined as the radius of the star. Hence the radius of the star can be obtained by utilizing the condition $p_r(r=R)=0$.

The above boundary conditions determine the model parameters. We have in total 5 constants with three equations. Prescribing any two of them will determine the others. In this case we set the values of a and b to find C, $C_2$ and $C_3$ numerically. These parameters are utilized to represent all the physically relevant quantities graphically in other section.

6 Physical analysis

In this section, we are interested to show that all the physical requirements stated in the previous section (5) are satisfied for our developed model.

• 1. The gravitational potentials at the origin of the star are finite at the center ($r=0$) of the stellar configuration. $A^2_0(0)=\left( \frac{C_2 (a-b) \log \left( \left( \sqrt{a}+\sqrt{b}\right) ^2\right) }{4 a^{3/2} \sqrt{b} C}+\frac{C_2}{2 a C}+C_3\right) ^2$ =constant, $B^2_0(0)=1$. Also we have checked that $(A^2_0(r))'_{r=0}=(B^2_0(r))'_{r=0}=0$. These imply that the metric is regular at the center and regular throughout the stellar interior.

• 2. The value of the density, radial pressure and tangential pressure at the centre in this model are:

  $$\begin{aligned} \rho (0)= & {} 3 C (b-a), \\ p_r(0)= & {} C \left( \frac{8 a^{3/2} \sqrt{b} C_2}{2 \sqrt{a} \sqrt{b} (2 a C C_3+C_2)+C_2 (a-b) \log \left( \left( \sqrt{a}+\sqrt{b}\right) ^2\right) }+a-b\right) , \\ p_t(0)= & {} C \left( \frac{8 a^{3/2} \sqrt{b} C_2}{2 \sqrt{a} \sqrt{b} (2 a C C_3+C_2)+C_2 (a-b) \log \left( \left( \sqrt{a}+\sqrt{b}\right) ^2\right) }+a-b\right) . \end{aligned}$$

  Note that the density is always positive as long as $C>0$ and $b>a$ or $C<0$ and $b<a$. The radial pressure and tangential pressure at the centre are equal which means pressure anisotropy vanishes at the center. Also according to Zeldovich’s condition, $p_r/\rho$ must be $\le 1$ at the centre. Therefore, $\frac{8 a^{3/2} \sqrt{b} C_2}{6 \sqrt{a b} (b-a) (2 a C C_3+C_2)-3 C_2 (a-b)^2 \log \left( \left( \sqrt{a}+\sqrt{b}\right) ^2\right) } \le \frac{4}{3}$.

• 3. The gradient of energy density is obtained as:

  $$\begin{aligned} \frac{d\rho }{dr}= \frac{2 b C^2 r (a-b) \left( b C r^2+5\right) }{\left( b C r^2+1\right) ^3}. \end{aligned}$$

  (21)

However, the analytical expression for the gradient of radial pressure and tangential pressure i.e., $\frac{dp_r}{dr}$ and $\frac{dp_t}{dr}$ are very lengthy and hence we avoided to put the expressions.

The gradient of energy density and pressures could have both positive and negative values in the stellar interior. In our model gradients are negative inside the stellar body are shown graphically in the other section. Also the gradients should vanishes as r goes to $\infty$.

• 4. The radial and transverse velocity of sound ($c=1$) are obtained from the expressions $v^2_{sr}=\frac{dp_r}{d\rho }$ and $v^2_{st}=\frac{dp_t}{d\rho }$. Again the analytical expressions are too big to express here. We estimate the value of sound speeds graphically throughout the interior of the star. In this model the speed of sound are smaller than 1 in the interior of the star, i.e., $0 \le \frac{dp_r}{d\rho } \le 1$, $0 \le \frac{dp_t}{d\rho } \le 1$ which has been shown graphically in the next section.

• 5. Energy Condition: The energy conditions for an anisotropic fluid sphere implies the positive values of the terms $\rho + p_r \ge 0$, $\rho + p_t \ge 0$ and $\rho + p_r + 2 p_t \ge 0$, throughout the stellar interior. These quantities are shown to remain positive throughout the compact sphere graphically in the next section.

• 6. The smooth matching of the interior metric function with that of the Schwarzschild exterior at the boundary is shown graphically in the next section.

• 7. Equation of State(EoS) parameter: Equation of state parameter is given by

  $$\begin{aligned} \omega _r=\frac{p_r}{\rho };~ \omega _t=\frac{p_t}{\rho } \end{aligned}$$

  (22)

  To be non-exotic in nature the value of $\omega$ should lie within 0 and 1. Our model is shown to satisfies the condition $0\le \omega _r\le 1$, $0\le \omega _t\le 1$.

7 Integrating the model with observational data

7.1 A particular pulsar 4U 1608-52

We are now in a position to validate our theoretical model with experimentally observed data from different reliable sources for NS masses and radii. For this purpose plugging the mass and radius of observed pulsars as input parameters the physical acceptability of the model has been checked to validate our model. We have considered the pulsar 4U 1608-52 km [34] with its recent estimated mass $=~1.57^{+0.30}_{-0.29}~M_\odot$ and radius $=~9.8 \pm 1.8$. We have fixed the model parameters using these mass and radius inference of 4U 1608-52 km [34]. With these mass and radius constrains along with other parameter values $a=0.65$ and $b=-0.35$, the junction conditions have been utilized to determine the constants as $C = -0.00589618$, $C2 = 0.00246044$, $C_3 = 1.33505$. The values of these constants thus obtained and plugging the values of G and c in the expressions, various physical quantities have been plotted graphically.

Regular and proper behavioral nature of all the relevant physical quantities and the satisfaction of the required conditions indicate that the model fits with experimental data required for a physically realistic plausible star.

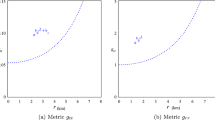
In Fig. 1, the regularity and the non singular nature of the metric potentials considering the pulsar 4U 1608-52 has been shown graphically.

Fig. 1

Metric potential $A_0(r)^2$ and $B_0(r)^2$

Figure 2 shows the nature of the energy density as expected monotonically decreases from its maximum value at the center towards its surface. The density of the compact star is also shown through radial contour plotting in Fig. 3. Variation of radial and tangential pressures have been plotted in Fig. 4, which are also decreases radially towards boundary from its maximum value at the center. It is confirms from the plot that in case of radial pressure it drops to zero at the boundary but having non zero tangential pressure on the surface.

Fig. 2

Density profile

Fig. 3

Density profile (contour)

Fig. 4

Radial and transverse pressure profiles

Radial variation of anisotropy has been depicted in Fig. 5 which is zero at center necessarily and is maximum at the surface. Contour representation of anisotropy variation is shown in Fig. 6.

Fig. 5

Anisotropy profile

Fig. 6

Anisotropy profile (contour)

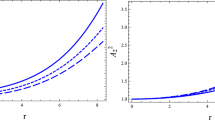
In Fig. 7, the sound speed in radial and transverse directions have been plotted against the radial coordinate. Speeds remain within the required range through out the interior of the star ($c=1$). This feature ensures the non-violations of causality condition.

Fig. 7

Radial and transverse sound speed profile

The energy conditions namely Weak Energy Condition (WEC), Null Energy Condition (NEC), Strong Energy Condition (SEC) and Dominant Energy Condition (DEC) must be satisfied at the every point of the interior of a star which have been plotted in Fig. 8. Figure shows that its value remain positive throughout the stellar interior as required for a relativistic physically acceptable stellar model.

Fig. 8

Energy conditions

We have also examined the trace energy condition graphically. In this model TEC it is found to be satisfied (see Fig. 9).

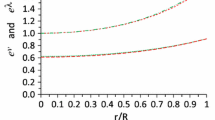
Figure 10 depicted the smooth matching of the interior space time with that of the exterior metric over the bounding surface.

Fig. 9

Energy conditions

Fig. 10

Metric matching

It is to be noted that in developing our model we have not considered any equation of state (EoS). Without prescribing any EoS we graphically presented the relationship between the thermodynamic parameters energy density and pressure hence the nature of the EoS of the matter distribution has been shown in Fig. 11. The almost linear relationship between $\rho$ and $p_r$ reflected from the figure.

The mass function is monotonically increasing the function of r. Also $m(0)=0$ and $m(9.8)=1.58 M\odot$ corresponds to centre and surface as shown in Fig. 12.

Table 1 Values of different model parameters corresponding to known compact star

Fig. 11

EoS profile

Fig. 12

Mass profile

Fig. 13

Mass–Radius (M–R) profile

In Fig. 13 We have derived the mass-radius $(M - R)$ relationship for a fixed surface density of value $4\times 10^{14}$ g cm$^{-3}$. One can observe that the feature of the mass-to-radius relation in this model predicts a maximum mass of about $2~M_\odot$ which is consistent with the observed data.

7.2 Validation with other pulsars

To show that this model has a wide range of applicability for highly compact stars, we have also analyzed the validity of my model by considering some well-known pulsars such as Cen X-3, SAX J1748.9-2021, Vela X-1 and PSR J$0030+0451$.

The estimated masses and radii of these pulsars have been used to determine the corresponding model parameters as given in Table 1. Making use of these values, in Table 2, we have calculated the values of the physically reasonable parameters which are sufficient to justify the requirements of a physically realistic star. Note that we have used $()|_0$ and $()|_R$ to denote the evaluated values of the physical parameters at the center and surface of the star, respectively.

Table 2 Numerical values of the matter variables

8 Stability analysis of the model

8.1 Tolman–Oppenheimer–Volkoff stability condition

The stability of a a star could be described in terms of the well known Tolman–Oppenheimer–Volkoff equilibrium conditions. A star remains in static equilibrium under the forces namely, gravitational force, hydrostatics force and anisotropic force. This condition is formulated mathematically as TOV equation which is

$$\begin{aligned} -\frac{M_G}{r} (\rho +p_r)\frac{A_0(r)}{B_0(r)}-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0, \end{aligned}$$

(23)

where $M_G(r)$ is the gravitational mass of the star having radial distance r. $M_G(r)$ can be derived using the Tolman–Whittaker formula and Einstein’s field equations as

$$\begin{aligned} {M_G}(r)=\frac{r B_0(r) A'_0(r)}{A^2_0(r)}. \end{aligned}$$

(24)

Using the expression of $M_G(r)$ in Eq. (23) we obtain

$$\begin{aligned} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r)-\frac{dp_r}{dr}+\frac{2}{r}(p_t-p_r)=0. \end{aligned}$$

(25)

The above equation is equivalent to

$$\begin{aligned} F_g + F_h + F_a = 0, \end{aligned}$$

(26)

where

$$\begin{aligned} F_g= & {} -\frac{A_0'(r)}{A_0(r)}(\rho +p_r), \end{aligned}$$

(27)

$$\begin{aligned} F_h= & {} -\frac{dp_r}{dr}, \end{aligned}$$

(28)

$$\begin{aligned} F_a= & {} \frac{2}{r}(p_t-p_r), \end{aligned}$$

(29)

represents the gravitational, hydrostatics and anisotropic forces respectively.

Fig. 14

Different forces

Figure 14 depicts the nature of all these forces thus satisfying the TOV equation.

8.2 Adiabatic index

For any stable stellar configuration, one important stability criteria is to check the adiabatic index parameter. The adiabatic index $\varGamma$ is described in terms of the ratio of two specific heats is defined as [10]

$$\begin{aligned} \varGamma =\frac{\rho +p}{p}\frac{dp}{d\rho }. \end{aligned}$$

(30)

The stability of a relativistic anisotropic compact star maintain as long as the value of the adiabatic index $\varGamma >4/3$. This feature is shown to satisfy in Fig. 15.

Fig. 15

Adiabatic index profile

Fig. 16

Difference in sound speeds

8.3 Herrera cracking condition

Another important method to study the stability of anisotropic stars known as cracking condition proposed by Herrera [36]. In this method of cracking, departure or split from the equilibrium configuration to a small degree at a particular point without collapse or expand is applied. The behavior of matter distribution after its departure from equilibrium is studied in cracking method for investigating potentially (un)stable anisotropic configurations. Later Abreu et al. [37] defined the stable region of an anisotropic fluid sphere by imposing restriction on the sound speeds which reads as $-1 \le v^2_{t} - v^2_{r} \le 0$. This condition holds in our model which is shown graphically in Fig. 16.

9 Discussions

In this work, we generated the static, spherically symmetric, and anisotropic fluid analytical solutions to develop and investigate a new stellar structure by assuming a generalized physically reasonable metric potential and a specific form of the anisotropy. With the specific choices of the model parameters some well known solutions e.g., Finch-Skea, Sch-warzschild interior and Vaidya Tikekar solutions can be recovered from our generalized solutions. We have derive physical quantities analytically and numerically solve for some model parameters. The results of this investigation have been shown graphically using a particullar compact star 4U 1608-52. All the physical criterion of a physically well behaved compact object have been shown to satisfy. The model is found to be stable in hydrostatic equilibrium with combined effects of different forces. The developed model has been shown to fit a wide range of recently observed values of masses and radii of pulsars.

Appendix A: Expressions for different forces

The expression for $F_g$, $F_h$ and $F_a$ can be written as,

$$\begin{aligned} F_g&=-\frac{1}{\phi _1^2 \phi _2^4 \left( 2 a b C r^2+2 \sqrt{a} \sqrt{b} \phi _1 \phi _2+a+b\right) }\frac{1}{\left( 2 \sqrt{a} \sqrt{b} \left( C_2 \phi _1 \phi _2+2 a C C_3\right) +C_2 (a-b) \log \left( 2 a b C r^2+2 \sqrt{a} \sqrt{b} \phi _1 \phi _2+a+b\right) \right) ^2} \nonumber \\&\quad \times [8 a^{3/2} \sqrt{b} C^2 C_2 r \left( 2 \sqrt{a} \sqrt{b} \left( -4 a^{7/2} \sqrt{b} C^2 C_3 r^2 \phi _{2}^{2}\right. \right. +2 a^{5/2} \sqrt{b} C \phi _{2}^{2} \left( C_2 r^2 \phi _1 \phi _2 \left( 2 b C r^2+1\right) \right. \left. + 2 C_3 \left( b C r^2-1\right) \right) \nonumber \\&\quad +2 a^{3/2} \sqrt{b} \phi _2^2 \left( b C \left( 3 C_2 r^2 \phi _1 \phi _2\right. \right. \left. \left. +2 C_3\right) +C_2 \phi _1 \phi _2 \right) +a^3 C \left( 2 b C r^2+1\right) \times \left( C_2 \left( 2 b^2 C^2 r^6+3 b C r^4+r^2\right) -2 C_3 \phi _1 \phi _2\right) \nonumber \\&\quad +a^2 \left( 4 b^2 C^2 C_3 r^2\phi _1 \phi _2+C_2 \left( 8 b^3 C^3 r^6+14 b^2 C^2 r^4 \right. \right. \left. +7 b C r^2+1\right) +2 \sqrt{a} b^{3/2} C_2 \phi _1 \phi _2^3+ a b \left( 2 b C C_3 \phi _1 \phi _2 \right. \left. +C_2 \left( 5 b^2 C^2 r^4+7 b C r^2+2\right) \right) \nonumber \\&\quad \left. + b^2 C_2 \phi _2^2\right) -C_2 (a-b)^2 \times \left( 2 a^{3/2} \sqrt{b} C r^2 \phi _2^2\right. \left. +2 \sqrt{a} \sqrt{b} \phi _2^2+a \phi _1 \phi _2 \left( 2 b C r^2+1\right) +b \phi _1 \phi _2\right) \left. \log \left( 2 a b C r^2+ 2 \sqrt{a} \sqrt{b} \phi _1 \phi _2+a+b\right) \right) ], \end{aligned}$$

(A.1)

$$\begin{aligned} F_h&=\frac{1}{\phi _1^3 \phi _2^5 (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})^4}\nonumber \\&\quad \times \frac{1}{\left( 2 \sqrt{a} \sqrt{b} \left( C_2 \phi _1 \phi _2{+}2 a C C_3\right) {+}2 C_2 (a{-}b) \log (\phi _2 \sqrt{a}{+}\phi _1 \sqrt{b})\right) ^2}\nonumber \\&\quad \times [C^2 r \left( 2 \sqrt{a} \sqrt{b} \phi _1 \phi _2 \left( 2 \sqrt{a} \sqrt{b} \left( \phi _1 \phi _2 C_2+2 a C C_3\right) \right. \right. \nonumber \\&\quad \left. +2(a-b) C_2 \log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b}) \right) \nonumber \\&\quad \times \left( 8 b C^2 C_3 r^2 \phi _2^2 a^4+2 \sqrt{b} C \left( 2 b C r^2+1\right) \left( 2 \phi _1 \phi _2 C_3\right. \right. \nonumber \\&\quad \left. + 5 C_2 r^2 \phi _2\right) a^{7/2}-4 b C \phi _2^2 \left( 2 C_3 \left( b C r^2-1\right) \right. \nonumber \\&\quad \left. - 5 C_2 r^2 \phi _1 \phi _2\right) a^3 +2 \sqrt{b} \left( -4 b^2 C^2 C_3 \phi _1 \phi _2 r^2\right. \nonumber \\&\quad \left. -C_2 \phi _2^2 \left( 2 b C r^2 \left( b C r^2-7\right) -5\right) \right) a^{5/2}-4 b \phi _2^2 \left( b C \right. \nonumber \\&\quad \times \left. \left( C_2 \phi _1 \phi _2 r^2+2 C_3\right) -5 C_2 \phi _1 \phi _2\right) a^2 +2 b^{3/2} \nonumber \\&\quad \times \left( C_2 \left( b C \left( 1-3 b C r^2\right) r^2+4\right) -2 b C C_3 \phi _1 \phi _2\right) a^{3/2}\nonumber \\&\quad - 4 b^2 C_2 \phi _1 \phi _2^3 a-2 b^{5/2} C_2 \phi _2^2 \sqrt{a}+(a-b)^2 C_2 \nonumber \\&\quad \times \left. \left( 2 a^{3/2} \sqrt{b} C \phi _2^2 r^2+2 \sqrt{ab}\phi _2^2+a \phi _1 \phi _2 \left( 2 b C r^2+1\right) \right. \right. \nonumber \\&\quad + \left. b \phi _1 \phi _2\right) 2 \log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\left( \sqrt{b} \phi _1+\sqrt{a} \phi _2\right) ^2 \nonumber \\&\quad +4 a^{3/2} \sqrt{b} C_2 \phi _1 \phi _2^3 (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})^2 \left( 8 b C^2 C_3 r^2 \phi _2^2 a^4\right. \nonumber \\&\quad +2 \sqrt{b} C \left( 2 b C +1\right) \left( 2 \phi _1 \phi _2 C_3+5 C_2r^2 \phi _2\right) a^{7/2}\nonumber \\&\quad -4 b C \phi _2^2 \left( 2 C_3 \left( b C r^2-1\right) -5 C_2 r^2 \phi _1 \phi _2\right) a^3 \nonumber \\&\quad +2 \sqrt{b} \left( -4 b^2 C^2 C_3 \phi _1 \phi _2 r^2-C_2 \phi _2^2 \left( 2 b C r^2 \left( b C r^2-7\right) \right. \right. \nonumber \\&\quad \left. \left. -5\right) \right) a^{5/2} -4 b \phi _2^2\left( b C \left( C_2 \phi _1 \phi _2 r^2+2 C_3\right) \right. \nonumber \\&\quad \left. -5 C_2 \phi _1 \phi _2\right) a^2 +2 b^{3/2} \left( C_2 \left( b C \left( 1-3 b C r^2\right) r^2+4\right) \right. \nonumber \\&\quad \left. -2 b C C_3 \phi _1 \phi _2\right) a^{3/2}-4 b^2 C_2 \phi _1 \phi _2^3 a -2 b^{5/2} C_2 \phi _2^2 \sqrt{a}\nonumber \\&\quad + (a-b)^2 C_2 \left( 2 a^{3/2} \sqrt{b} C \phi _2^2 r^2+2 \sqrt{a} \sqrt{b} \phi _2^2+a \phi _1 \phi _2 \right. \nonumber \\&\quad \left. \left. \times \left( 2 b C r^2+1\right) +b \phi _1 \phi _2\right) 2\log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\right) \nonumber \\&\quad +\left. 3 b \phi _1^2 (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})^2 \left( 2 \sqrt{ab} \left( \phi _1 \phi _2 C_2+2 a C C_3\right) \right. \right. \nonumber \\&\quad \left. \left. + 2(a-b) C_2 \log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\right) \left( 8 b C^2 C_3 r^2 \phi _2^2 a^4 \right. \right. \nonumber \\&\quad + 2 \sqrt{b} C \left( 2 b C r^2+1\right) \left( 2 \phi _1 \phi _2 C_3+5 C_2 r^2\phi _2^2\right) a^{7/2}\nonumber \\&\quad -4 b C \phi _2^2 \left( 2 C_3 \left( b C r^2-1\right) -5 C_2 r^2 \phi _1 \phi _2\right) a^3+2 \sqrt{b}\nonumber \\&\quad \times \left( -4 b^2 C^2 C_3 \phi _1 \phi _2 r^2-C_2 \left( b C r^2+1\right) \left( 2 b C r^2 \left( b C r^2-7\right) \right. \right. \nonumber \\&\quad \left. \left. -5\right) \right) a^{5/2}-4 b \phi _2^2\left( b C \left( C_2 \phi _1 \phi _2 r^2+2 C_3\right) \right. \nonumber \\&\quad \left. -5 C_2 \phi _1 \phi _2\right) a^2+2 b^{3/2} \left( C_2 \left( b C \left( 1-3b C r^2\right) r^2+4\right) \right. \nonumber \\&\quad \left. -2 b C C_3 \phi _1 \phi _2\right) a^{3/2}-4 b^2 C_2 \phi _1 \phi _2^3 a-2 b^{5/2} C_2 \phi _2^2\sqrt{a} \nonumber \\&\quad +(a-b)^2 C_2 \left( 2 a^{3/2} \sqrt{b} C \phi _2^2 r^2 +2 \sqrt{a} \sqrt{b}\phi _2^2+a \phi _1 \phi _2 \left( 2 b C r^2\right. \right. \nonumber \\&\quad \left. \left. \left. +1\right) +b \phi _1 \phi _2\right) 2\log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\right) \nonumber \\&\quad \left. +a \phi _2^2 (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\right) ^2 \left( 2 \sqrt{a} \sqrt{b} \left( \phi _1 \phi _2 C_2 +2 a C C_3\right) \right. \nonumber \\&\quad \left. +(a-b) C_22\log (\phi _2 \sqrt{a}+\phi _1 \sqrt{b})\right) \left( 8 b C^2 C_3 r^2 \phi _2^2 a^4 \right. \nonumber \\&\quad + 2 \sqrt{b} C \left( 2 b C r^2+1\right) \left( 2 \phi _1 \phi _2 C_3 +5 C_2 r^2 \phi _2^2\right) a^{7/2}\nonumber \\&\quad \left. -4 b C \phi _2^2 \left( 2 C_3 \left( b C r^2-1\right) -5 C_2 r^2 \phi _1 \phi _2\right) a^3\right. \nonumber \\&\quad + 2 \sqrt{b} \left( -4 b^2 C^2 C_3 \phi _1 \phi _2 r^2 -C_2 \phi _2^2 \left( 2 b C r^2 \left( b C r^2-7\right) -5\right) \right) a^{5/2}\nonumber \\&\quad -4 b \phi _2^2 \left( b C \left( C_2 \phi _1 \phi _2 r^2+2 C_3\right) \right. \nonumber \\&\quad \left. -5 C_2 \phi _1 \phi _2\right) a^2 +2 b^{3/2} \left( C_2 \left( b C \left( 1-3 b C r^2\right) r^2+4\right) \right. \nonumber \\&\quad \left. -2 b C C_3 \phi _1 \phi _2\right) a^{3/2}-4 b^2 C_2 \phi _1 \phi _2^3 a-2 b^{5/2} C_2 \nonumber \\&\quad \times \phi _2^2 \sqrt{a}+2(a-b)^2 C_2 \left( 2 a^{3/2} \sqrt{b} C \phi _2^2 r^2+2 \sqrt{a} \sqrt{b} \phi _2^2\right. \nonumber \\&\quad \left. \left. +a \phi _1\phi _2 \left( 2 b C r^2+1\right) +b \phi _1 \phi _2\right) \log (\sqrt{a}\phi _2+\sqrt{b}\phi _1)\right) \nonumber \\&\quad -\phi _1 \phi _2 (\sqrt{a}\phi _2+\sqrt{b}\phi _1)^2 \left( 2 \sqrt{ab} \left( \phi _1 \phi _2 C_2\right. \right. \nonumber \\&\quad \left. \left. +2 a C C_3\right) +2(a-b) C_2 \log (\sqrt{a}\phi _2+\sqrt{b}\phi _1)\right) \left( C_2 \left( \left( 8 b^2 C^2 r^4\right. \right. \right. \nonumber \\&\quad +\left. 8 b C r^2+1\right) a^2+4 \sqrt{b} \phi _1 \phi _2 \left( 2 b C r^2+1\right) a^{3/2}\nonumber \\&\quad +2 b \left( 4 b C r^2+3\right) a+4 b^{3/2} \phi _1 \phi _2 \sqrt{a}+ 2b^2 \log (\sqrt{a}\phi _2+ \sqrt{b}\phi _1) \nonumber \\&\quad \times (a-b)^2+2 \sqrt{ab}\left( 2 C C_3 \left( 8 b^2 C^2 r^4+8 b C r^2+1\right) a^4\right. \nonumber \\&\quad +4 \sqrt{b} C \left( C2 \left( 15 b^2 C^2 r^4+23 b C r^2+8\right) r^2 \right. \nonumber \\&\quad \left. +2 C_3 \phi _1 \phi _2 \left( 2 b C r^2+1\right) \right) a^{7/2}+\left( -16 b^3 C^3 C_3 r^4\right. \nonumber \\&\quad +60 b^2 C^2 C2 \phi _1 \phi _2 r^4+2 b C \left( 31 C_2 \phi _1 \phi _2 r^2+5 C_3\right) \nonumber \\&\quad \left. +11 C_2 \phi _1 \phi _2\right) a^3-4\sqrt{b} \left( 4 b^2 C^2 C_3 \phi _1 \phi _2 r^2\right. \nonumber \\&\quad \left. +C_2 \left( 3 b^3 C^3 r^6-17 b^2 C^2 r^4-28 b C r^2-8\right) \right) a^{5/2} \nonumber \\&\quad + b \left( -4 b^2 C^2 \left( 3 C2 \phi _1 \phi _2 r^2+4 C_3\right) r^2+b C \left( 44 C2 r^2 \phi _1 \phi _2\right. \right. \nonumber \\&\quad \left. \left. \left. -10 C_3\right) +37 C2 \phi _1 \phi _2\right) a^2-4 b^{3/2} \left( 2 b C \phi _1 \phi _2 C_3\right. \right. \nonumber \\&\quad \left. + C_2 \left( 4 b^2 C^2 r^4-b C r^2-5\right) \right) a^{3/2}+b^2 \left( C_2 \phi _1 \phi _2\right. \nonumber \\&\quad \left. \left. -2 b C \left( 5 C_2 \phi _1 \phi _2 r^2+C_3\right) \right) a-4 b^{5/2} C_2 \phi _2^2 \sqrt{a}- b^3 C_2 \phi _1 \phi _2\right) ],\end{aligned}$$

(A.2)

$$\begin{aligned} F_a&=\frac{2b(b-a)C^2 r}{(1 + b C r^2)^2}. \end{aligned}$$

(A.3)