On dark energy effects on the accretion physics around a Kiselev spinning black hole

Abstract

Kiselev metric in the static and rotating form is widely used to test different aspects of the dark energy (DE) effects. We consider a DE Kiselev spacetime, predicting the reduction to the Kerr black hole (BH) solution under suitable conditions on the DE parameters and in this frame we study the effects of the dark energy on BHs and disks accretion. Elaborating a close comparison with the limiting vacuum Kerr spacetime, we focus on thick accretion disks around the central BH in the Kiselev solution, both co-rotating and counter-rotating with respect the central BH. We examine different aspects of BH accretion energetics by focusing on quantities related to the accretion rates and cusp luminosity, when considered the DE presence, related to the pure Kerr central BH. Our findings show that in these conditions heavy divergences with respect to the vacuum case are expected for the DE metrics. A known effect of the Kiselev metric is to lead to a false estimation the BH spin, we confirm this characteristic from the fluids dynamics analysis. Remarkably our results show that DE is affecting differently the accretion physics, and particularly the accretion rate, according to the fluid rotation orientation with respect to the central spinning attractor, leading in some cases to an under-estimation of the BH spin mass ratio. These contrasting aspects emerging in dependence on the fluids rotational orientation can be a distinguishing general DE feature which could lead to a revised observational paradigm where DE existence is considered.

1 Introduction

We focus on geometrically thick disks around a spinning central black hole (BH) in a dark energy (DE) Kiselev spacetime, having the limiting Kerr BH spacetime for vanishing values of the metric DE parameter [1, 2]. The dark energy DE influence on the BH accretion disk physics is investigated in this frame examining co-rotating and counter-rotating accretion tori orbiting the central spinning BH.

The issue of DE presence in our Universe is all in the ascertainment that the matter and energy content in the current Universe appears into the components of approximately 68 (72)% dark energy, 28 (23)% dark matter DM and less than 4 (4.6)% baryonic matter (according to the standard cosmological model). These percentages often are revised by new observations and alternative analyses (see also  [3] for a recent analysis constraining the fraction of early dark energy, present during the early ages of the Universe). Dark energy in empty space (or vacuum energy) may explain the Universe accelerating expansion. This unknown and undefined component of the observable Universe is usually described by a general relativistic (GR) onset, featuring a repulsive cosmological constant or quintessence (an inhomogeneous, dynamical, canonical scalar field with negative pressure). Dark energy fuels and engineries the Universe expansion, with the velocity of expansion constantly under scrutiny and debated. The new evaluation in  [4] supports prevailing modern cosmological theories with two-thirds (66.2%) of dark energy and one-third matter (33.8%) mostly represented by the dark matter component. There are two main basic issues surrounding the concept of missing energy in our Universe: the identification of the origin and hypothetical form of the missing energy, and how exactly it relates to the cosmological expansion when considered as driver of the accelerated expansion.

There are different DE models currently debated. For example, the so called constrained interacting dark energy (CIDER) model, which consists in a conformally coupled quintessence model mimicking a $\Lambda$CDM expansion, proposed in  [5] – see also [6, 7] for new analysis and cosmological simulations. An interesting actual DE model envisages DE as a quantity with its own evolution that could be different in diverse cosmological eras, in particular during the early Universe, having therefore an early DE (shortly after the Big Bang) form distinct from a late-time DE form. According to [8], an early DE could explain the crisis in cosmology (“Hubble tension”). Interestingly, in [9], the early DE is set in a unified frame with dark matter, focusing on a phase transition in the early Universe where a new form of early DE undergos a phase transition when the Universe expanded (New Early Dark Energy).

Recent study in [10], analyzing observations of Galaxy clusters made by the eROSITA X-ray instrument,¹ shows that DE appears to be distributed uniformly across space and time, i.e. DE energy density is uniform in space and constant in time, suggesting DE could be described by a simple constant–cosmological constant introduced and later abandoned by A. Einstein and related to the vacuum energy by Zeldovich [11]. The same results evaluate the DE component as 76% of Universe total energy density.

There is today no clear interpretation on the DE origin. The missing energy may have a quantum origin, it may be related to the quantum structure of the spacetime, and DE is often modelled as an expression of the so-called vacuum energy. Nevertheless, so far DE calculations from quantum field theory, do not reproduce the observed cosmological constant (“cosmological constant enigma”). Different proposals for a new DE interpretation are therefore constantly investigated, for example in the work [12], basing on the vacuum polarizability of the vacuum from an assumed zero-point fluctuation. Recently, some authors claimed in [13, 14] evidence of BHs as the DE source. One interesting aspect in this proposal is that Einstein’s gravity was ultimately claimed to provide the DE source. The second notable (and more controversial) aspect in this scenario, consists in the details of the DE connection to BHs and the consequent description of the BH nature. The analysis proposes that stellar remnant BHs are the DE astrophysical origin, providing therefore the source for accelerating expansion at $z \sim 0.7$. Black holes gaining mass, growing over time, are a DE source containing vacuum energy blocking also the central singularities to form. From the point of view of our work, it has to be noted that this research connects BHs to DE and above all BHs mass accretion to DE (although it is resolved assuming an interior of the BH devoid of singularity and source of vacuum energy). Today BHs appear 7–20 times larger than nine billion years BHs. Form the comparison between distant young galaxies with local (dormant) giant elliptical galaxies evolving in the early Universe, BHs showed in the past a mass growth much larger than predicted by actual mechanisms of accretion or mergers. Data analysis showed the agreement between the size of the Universe and the BH mass implying, according to this analysis, that vacuum energy “contained in the” BH might be correlated to the amount of DE in the Universe, consequently BHs became coupled to the Universe expansion, and the BHs mass accretion problem would be related to (explained by and explaining) the Universe expansion (cosmological coupling).

In this work we investigate the DE effects on BH accretion disks and BH accretion physics when DE is modeled in the framework of Kiselev spacetime, where GR Kerr metric is deformed by DE, governed by a pair of parameters $(\alpha ,k)$, $\alpha$ for the deformation model,² and parameter k, “DE” parameter, which is interpreted as a measure of the DE effect on the BH³ – [22, 23].

The influence of dark energy as described by the well known Kiselev family of exact solutions has been discussed extensively in the literature. It was first discovered for spherical symmetric BHs (for BHs surrounded by anisotropic fluids⁴) [22], a broad variety of general aspects of these solutions have been already addressed, their features as DE mimickers have been scrutinized, as well as aspects of matter and particles dynamics, for different values of the metric parameters $(\alpha ,k)$, and different extensions of the original metric. More generally, the causal structure and stability, the horizons properties, and the BH thermodynamics of the Kiselev spacetimes have been detailed for the DE case, which is described by certain range of the metric parameter $\alpha$. Geodesic motion, gravitational lensing, BH shadow profiles, fundamental frequencies of motion have been investigated. To our knowledge, our work is the first investigation of orbiting accretion discs in Kiselev spacetimes, highlighting divergences from the standard GR onset that could be inferred from current observations of accretion around spinning attractors (for example, tori energetics and the inner edge location). While in this analysis we will study in depth the structure of horizons, geodesic structure and the stationary limits for all values of the parameter k (and the spacetime dimensionless spin $a>0$), a review of the general aspects of the Kiselev solutions is beyond the scope of our work, and we refer to the extensive literature, partly reported below, on the subject. More in details, there is an extensive literature focusing on different aspects of the DE Kiselev solutions, for metric parameters range we consider here, i.e., parameter of the equation of state (EoS) $\alpha \in ]-1,-1/3[$ (in the literature it is frequent to use also notation $\omega$ for the EoS parameter $\alpha$, the ratio of pressure and energy density of the DE – with $\alpha \in ]-1/3,0[$ for an asymptotically flat solution, $\alpha = 1/3$ for radiation, $\alpha = 0$ for dust and some kind of dark matter for $\alpha = -1/3$). In particular, the case $\alpha =-2/3$ is broadly studied (see also [22] and references below), for the relative simplicity of treatment and the structure of the cosmological horizons (we refer, for comparison and further insights on this case and the general aspects of the DE Kiselev spacetimes, to the present literature, which mostly concentrates on this case).

Hence, a detailed analysis of the Kiselev solution stability for different values of the metric parameters can be found in [24], superradiance and instabilities in the BH spacetime solutions are investigated with the dynamics of a probe scalar field in the BH spacetime. More general issue of Kiselev spacetime stability is also addressed in [25,26,27,28,29,30], with the analysis of the Quasi-Normal Modes (QNMs) spectrum (massless scalar perturbations, the late-time tails structure), and some thermodynamical aspects with superradiance and stability, the massive scalar superradiant scattering. Quasi-Periodic Oscillations (QPOs), QNMs and shadows of (Bardeen–)Kiselev BH are also explored in  [31]. In this analysis discussion of the horizons structure can be also found with a detailed investigation of the dynamics of both neutral and electrically charged test particles (with fundamental Keplerian frequencies and harmonic oscillations), photon spheres, scalars invariants, bolometric luminosity. Orbits and shadows for different parameter ranges are also studied in [26, 30, 32,33,34,35,36,37,38,39,40,41,42,43], with a focus on the BH thermodynamics, phase transitions, causal structure, including the exploration of several extensions of the Kiselev solutions. A focus on the BHs thermodynamics is for example also in [44] and  [45] with an investigation of the thermodynamic stability for Kerr–Newmann–NUT–Kiselev–AdS BH in Rastall gravity – see also [46].

While rotating BHs and “quintessence” (the Kiselev solutions) were studied in depth in  [47], the rotating Kiselev BHs in f(R, T) gravity has been also explored, with the study of Penrose diagrams, in  [48]. In  [49] deflection and gravitational lensing of null and timelike signals in the weak field limit of the Kiselev BH spacetime have been explored with perturbative methods. Analysis in [50] discusses properties of the total stress energy for the generalized Kiselev BHs. In [51] Kerr–Newman–AdS BH in DE has been investigated with a generalized Kiselev rotating BH spacetime. Optical effects, as lensing, or spin precession have been also explored to distinguish BH from naked singularity (NS) solutions in Kiselev spacetimes – see [52,53,54,55,56,57,58,59,60,61]. A study of the state equations for massless spin fields in static spherical spacetime filled with quintessence (Kiselev spacetime) is in [62].

Therefore, following the literature, we explore the Kiselev rotating BH solution for the parameter of state $\alpha =-2/3$, focusing on more complex and general aspects of the Kiselev DE effects in a scenario which is relatively simple to manage analytically. (However, for completeness and comparison we also include in Appendix C an analysis of the Kiselev solution for $\alpha = -1/3$, which has been considered to describe some dark matter effects.). We then proceed exploring the entire range of values of the constant k, which is the metric parameter regulating the DE effects having the Kerr spacetime limit for $k=0$. We shall study the spacetime horizons structure and Lense–Thirring effects, considering the ergosurfaces for all values of the parameter k and BH spin $a>0$ (including $a>M$ describing, in the limit $k=0$, Kerr NSs). The geodesic structure and the fluids specific angular momentum, $\ell (a,k;r)$, regulating the tori behavior (stability and morphology) will be discussed for all values of (a, k). On the basis of these general considerations, traced on the results obtained for any value of k and a, we will focus eventually on three values of (a, k) selecting, without loss of generality, representative values of spin and k for the tori numerical analysis.

More specifically, considering the results on the horizons structure, stationary limits and geodesic structure (analysis of specific angular momentum), for any a and k, we will select three values of k: the limiting case $k=0$ and two other cases which we have considered for the numerical integration. We then study, for any $a\in [0,1]$, both co-rotating and counter-rotating tori with respect to the central attractor. Tori morphological and topological characteristics and tori energetics will be discussed. Finally, for any selected value of k, we will consider a specific value for the spin a, showing examples of the general case, visualizing, in specific cases, the general results discussed from the analysis of the background geodesic structure. Both co-rotating and counter-rotating disks, with respect to the central attractor, have been studied for quiescent and cusped tori, orbiting close and far from the central attractor, and in the spacetime ergoregions, including open structures associated to thick tori, having matter funnels along the spinning BH rotational axis, for any range of tori parameters $(\ell ,K)$. In this way we consider tori for all values of specific angular momentum (given as general function of k and a) and the tori parameter K, regulating the tori stability. From the analysis of the spacetimes geodesics structure, regulating thick tori dynamics, we can trace general considerations (for all values of k and a) on the accretion disk physics, fixing the cusps (tori instability points) and the location of maximum pressure points in the disks. From the observation of these properties we can select specific values of the parameter k, proceeding with the analysis of some exemplificative cases.

General Relativistic Hydrodynamics (GRHD) models of geometrically thick barotropic tori considered in this analysis allow to analyze the energetics associated to tori and their processes, for example the mass accretion rate, as related to the tori morphological characteristics. The adoption of these models, having the limiting case of geometrically thin Keplerian disks, is also advantageous for their notable adaptability to more complex cases, as General Relativistic Magneto-Hydrodynamics (GRMHD) tori. Furthermore, being governed by the geodesic structure of the spacetime, we are able to trace general considerations, from the analysis of the geodesics circular orbits in the background spacetime, also in a multi-parametric metric scenario as we are considering here.

The physics of accretion disks around BHs is capable to engine the most energetic processes of our Universe, with extremely large radiative energy output and ejection of matter in jet-like structures. Here, the orbiting tori are described by fully general relativistic models of stationary toroidal orbiting configurations. Polish Doughnuts (PD) models are characterized by very high (super-Eddington) accretion rates and high optical depth and they are often associated to the background of a central SMBH. The advantages in the adoption of these models, especially in the analytical investigation of the BH accretion physics, are multiple. Despite their relative simplicity, these configurations have been often adopted as the initial conditions in the set up for simulations of the MHD (magnetohydrodynamic) accretion structures [63,64,65,66], showing also predictions on accretion (and jets emission) dynamics that closely adhere, under various aspects, to the GRHD evolution of the tori showing, in several circumstances, the prevalence of the hydrodynamics components of the force balance with respect to the dissipative effects or the influence of magnetic fields especially in thick tori orbiting in the strong gravitational field of the SMBH attractors. A second advantage consists in the relative technical simplicity consisting of two fundamental aspects. Tori symmetries are particularly fitting for the models under investigations in this study. The configurations are axisymmetric and stationary and, where the background spacetime is axisymmetric and stationary, their GRHD equations are fully integrable and governed by an effective potential function governing the pressure gradients in the disks. The model is designed upon the assumption that the gravitational component of the central attractor is predominant in the force balance of the disk with respect to other factors in determining the equilibrium phases as well as the instability leading to accretion. In details, the tori equatorial and symmetry plane coincides with the equatorial plane of the central axisymmetric central attractor [67,68,69]. Tori morphology and stability are essentially governed by the pressure gradients on the equatorial plane, where the thin (Keplerian) disks can be considered as limiting configurations regulated fully by the background geodesic structure. The tori, described by purely hydrodynamic (barotropic) models, are governed by the equipressure (equidensity) surfaces that can be closed, giving stable equilibrium configurations, and open, giving unstable, jet-like (proto-jets) structures caused by the relativistic instability due to the Paczynski mechanism where the effects of strong gravitational fields are dominant with respect to the dissipative ones and predominant to determine the unstable phases of the systems [63, 70,71,72,73,74], see also [65, 66, 75,76,77,78,79]. This implies that the time scale of the dynamical processes (regulated by the gravitational and inertial forces) is much lower than the time scale of the thermal ones (heating and cooling processes, radiation) that is lower than the time scale of the viscous processes. The entropy is constant along the flow and, according to the von Zeipel condition, the surfaces of constant angular velocity $\Omega$ and of constant specific angular momentum $\ell$ coincide [80,81,82,83]. This implies that the rotation law $\ell =\ell (\Omega )$ is independent of the equation of state [84, 85]. The special case of cusped equipotential surfaces is related to the accretion phase onto the central attractor  [67,68,69, 74, 86]. The outflow of matter through the cusp occurs due to an instability in the balance of the gravitational and inertial forces and the pressure gradients in the fluid, i.e., by the so called Paczynski mechanism of violation of mechanical equilibrium of the tori [69].

Many features of the tori dynamics and morphology like their thickness, their stretching in the equatorial plane, and the location of the tori are predominantly determined by the geometric properties of spacetime via a fluid effective potential function. These features make these models particularly suitable in the spacetimes considered in this investigation where DE is geometrized as a metric deformation of the Kerr spacetime. DE has a clear impact in the tori structure. Consequently, DE will influence the energetic characteristics of the BH in accretion and the disk characteristics, as accretion rates or cusp luminosity [87,88,89]. DE affects the cusp formation and cusp location with respect to the central attractor, modifying the disk accretion throat, constraining the thickness of the accretionary flow and the maximum amount of matter swallowed by the central BH, leading to a variation of the central BH energetics, as cusp luminosity, and the accretion rates. In this work we also study the mass-flux, the enthalpy-flux (related to the temperature parameter), the flux thickness, or the cusp luminosity, the disk accretion rate, and the mass flow rate through the cusp.

More in details the plan of the article is as follows: thick disks in axially symmetric spacetimes are discussed in Sect. 2. The Kerr metric is introduced in Sect. 2.1, while the Polish doughnut tori models are examined in Sect. 2.2. The Kerr spacetime extended geodesic structure and tori construction are the subject of Sect. 2.2.1. Notes on tori morphology and energetics follow in Sect. 2.2.2, where we discuss the maximum thickness of a disk accretion throat, and aspects of the accretion tori energetics. The concepts introduced, the considerations outlined and the procedures adopted in this first part of the work are therefore used as the basis analysis and comparison in the following second part of the article, Sect. 3, where we explore tori orbiting around a central spinning DE Kiselev BH. In Sect. 3.1 Kiselev metric is introduced.

In Sect. 3.2, following closely the case of tori orbiting in the Kerr background, we investigate the accretion tori orbiting in the Kiselev spacetime. We split the constant k range of values in positive and negative values and in each of these ranges we select an exemplificative numerical value to fix the ideas and proceed with the numerical integration. Hence the case of DE parameter $k=-0.05$ is considered in Sect. 3.2.1, while in Sect. 3.2.2 the situation for a DE parameter $k=0.0025$ is discussed. Finally, conclusions follow in Sect. 4. In Appendix A are more details on the Kiselev spacetime characteristics. We discuss some general properties as horizons and ergoregions for all values of metric parameters k and $\alpha$, we then concentrate on the case $\alpha =-2/3$ for a DE Universe, and we study in details the horizons structure and the ergoregions for all values of k and spin a (including $a>M$), considering two alterative analysis. Following the analysis of the horizons structure we then investigate the cases of extreme BHs.

In Appendix B, following closely the case of tori orbiting in the Kerr background, discussed in the first part of the analysis, we trace some general considerations on the spacetime geodesics structure and the fluid specific angular momentum regulating tori structure, for all a and k. Some comments on the Kiselev model within a different choice of the state parameter $\alpha$ are in Appendix C. To simplify the reading we also introduced Table 2 containing the main notation and quantities used throughout this paper.

2 Thick disks in axially symmetric spacetimes

We study geometrically thick tori in the axially symmetric DE Kiselev spacetime considered as a DE-induced deformation of the Kerr geometry. Therefore it is useful here to review the properties of the Kerr metric and the construction of tori in this geometry. In Sect. 2.1 the Kerr metric is introduced, while the Polish doughnut tori models are discussed in Sect. 2.2. The Kerr spacetime extended geodesic structure and tori construction are focused in Sect. 2.2.1. Tori morphology and tori energetics are addressed in Sect. 2.2.2, focusing on the maximum thickness of a disk accretion throat, and exploring different aspects of the accretion tori energetics. The concepts introduced in this section will be used also in the second part of this work, outlining the procedures that will be adopted in Sect. 3 where we will explore tori orbiting around a central spinning DE Kiselev BH. Then the case of tori orbiting a central Kerr BH will be taken as comparison, the axially symmetric DE Kiselev spacetime in fact reduces to the Kerr spacetime for some limiting values of the metric parameters.

2.1 The Kerr metric

In the Boyer–Lindquist (BL) coordinates $\{t,r,\vartheta ,\varphi \}$, the Kerr line element reads:

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{2Mr}{\Sigma }\right) dt^2+\frac{\Sigma }{\Delta }dr^2+\Sigma d\vartheta ^2\nonumber \\{} & {} +\left[ (r^2+a^2)+\frac{2M r a^2}{\Sigma }\sin ^2\vartheta \right] \sin ^2\vartheta d\varphi ^2\nonumber \\{} & {} -\frac{4rMa}{\Sigma } \sin ^2\vartheta dt d\varphi , \end{aligned}$$

(1)

where

$$\begin{aligned} \Delta \equiv a^2+r^2-2 rM;\quad \Sigma \equiv a^2(1-\sin ^2\vartheta )+r^2, \end{aligned}$$

(2)

with $r\in [0,+\infty )$, $t\in [0,+\infty )$, $\vartheta \in [0,\pi ]$ and $\varphi \in [0,2\pi ]$. In the following we will consider also the quantity $\sigma \equiv \sin ^2\vartheta \in [0,1]$.

The Kerr solution is a vacuum, asymptotically flat, axially symmetric (and stationary) solution of the Einstein equations, describing the spacetime around a gravitational source, spinning along its symmetry axis, with ADM mass parameter M, and spin parameter $a\equiv J/M$ (the specific angular momentum, the rotational parameter associated to the central object), while J is the total angular momentum.

The Kerr metric describes black holes (BHs) for spin $a\in [0,M]$ and naked singularities (NSs) for $a>M$, with the limiting static solution of the Schwarzschild spacetime for $a=0$ and the extreme Kerr BH solution for $a=M$.

There are two horizons at $r_-<r_+$, solutions of $\Delta =0$, respectively given by

$$\begin{aligned} r_{\pm }\equiv M\pm \sqrt{M^2-a^2}. \end{aligned}$$

(3)

The spacetime has, for $a\ne 0$, an outer and inner stationary limits $r_{\epsilon }^\pm$ (ergosurfaces), which can be found as solutions of $g_{tt}=0$, respectively

$$\begin{aligned} r_{\epsilon }^{\pm }\equiv M\pm \sqrt{M^2- a^2 (1-\sigma )}, \end{aligned}$$

(4)

where $r_+<r_{\epsilon }^+$ on $\vartheta \ne 0$ and $r_{\epsilon }^+=2M$ in the equatorial plane $\vartheta =\pi /2$. Static observers cannot exist inside the ergoregion, however particles crossing the stationary limit and escaping back into the region $r\ge r_{\epsilon }^+$ are possible. In the following we shall consider the motion on the BH equatorial plane ($\sigma =1$), which is a metric symmetry plane and the equatorial (circular) trajectories are confined on the equatorial plane as a consequence of the metric tensor symmetry under reflection through the plane $\vartheta =\pi /2$.

The constants of the equatorial geodesic motion are

$$\begin{aligned}{} & {} \mathcal {E}=-(g_{t\varphi } \dot{\varphi }+g_{tt} \dot{t}),\quad \mathcal {L}=g_{\varphi \varphi } \dot{\varphi }+g_{t\varphi } \dot{t},\nonumber \\{} & {} \quad g_{ab}u^a u^b=-\mu ^2, \end{aligned}$$

(5)

with $u^a\equiv \{ \dot{t},\dot{r},\dot{\vartheta },\dot{\varphi }\}$, where $\dot{q}$ indicates the derivative of any quantity q with respect the proper time (for $\mu =1$) or a properly defined affine parameter for the light-like orbits (for $\mu =0$). In Eq. (5) quantities $\mathcal {E}$ and $\mathcal {L}$ represent the total energy and momentum of the test particle coming from radial infinity, as measured by a static observer at infinity. The relativistic angular velocity and the specific angular momentum are

$$\begin{aligned} \Omega \equiv \frac{u^\varphi }{u^{t}}= & {} -\frac{\mathcal {E}g_{\varphi t}+g_{tt} \mathcal {L}}{\mathcal {E}g_{\varphi \varphi }+g_{\varphi t} \mathcal {L}}= -\frac{g_{t\varphi }+g_{tt} \ell }{g_{\varphi \varphi }+g_{t\varphi } \ell },\nonumber \\ \ell \equiv \frac{\mathcal {L}}{\mathcal {E}}= & {} -\frac{u_\varphi }{u_{t}}=-\frac{g_{\varphi \varphi }u^\varphi +g_{\varphi t} u^t }{g_{tt} u^t +g_{\varphi t} u^\varphi } =-\frac{g_{t\varphi }+g_{\varphi \varphi } \Omega }{g_{tt}+g_{t\varphi } \Omega },\nonumber \\ \end{aligned}$$

(6)

respectively. The particles counter-rotation (co-rotation) is defined by $\mathcal {L}a<0$ ($\mathcal {L}a>0$) and fluid counter-rotation (co-rotation) is defined by $\ell a<0$ ($\ell a>0$).⁵

In the following, where more convenient, we use dimensionless units,⁶ where $M=1$. In Table 2 we also show the main notation and quantities used throughout this paper with links to associated sections or definitions.

2.2 Geometrically thick tori

In this analysis we examine geometrically thick tori, focusing in particular on the Polish doughnut (PD) models. These are analytic and general relativistic toroidal models, well known and used in a variety of situations, especially in axis-symmetric spacetimes.

In particular we specialize on the general relativistic hydrodynamics (GRHD) toroidal configurations, centered on the BH equatorial plane. The orbiting configurations have symmetry plane coincident with the BH equatorial plane. The toroids are constant pressure surfaces composed of perfect fluids with a barotropic equation of state ($p=p(\varrho )$), where the functional form of the angular momentum and entropy distribution, during the evolution of dynamical processes, depends on the initial conditions of the system and not on the details of the dissipative processes [72, 73, 96, 97].

Tori are assumed to have constant fluid specific angular momentum $\ell$. Assuming orbital motion with $u^{\vartheta }=0$ and $u^r=0$, the torus can be parametrized with $\ell =$constant and, because of the symmetries, the continuity equation is identically satisfied, and the toroidal surfaces are defined by the Euler equation only (the tori are stationary and axial-symmetric), which can be expressed in terms of a fluid effective potential $V_{eff}(r;\ell ,a)$ – see Appendix B.

The fluid specific angular momentum $\ell$, fixes pressure gradients (from the Euler equation) and the maximum density points in the disk, which are determined by the gradients of an effective potential function for the fluid. More precisely, the angular momentum distributions $\ell ^\pm :\partial _r V_{eff}=0$, on the equatorial plane $\vartheta =\pi /2$, govern the extremes of the pressure, where $(-)$ is for co-rotating and $(+)$ counter-rotating fluids showed in Fig. 2, left panel.

2.2.1 Extended geodesic structure and tori construction

The boundary of any stationary, barotropic, perfect fluid body is determined by an equipotential surface, i.e., the surface of constant pressure.

The equipotential surfaces can be closed, giving stable equilibrium configurations (quiescent tori), or closed cusped (self-crossed) accreting tori and open cusped solutions, giving unstable, jet-like structures (proto-jets) – (see Fig. 2).

Fig. 1

Kerr spacetime. Gray region is the outer ergoregion. Black region is the BH. All quantities are dimensionless. mbo is for marginally bound circular orbit (blue curves), mco is for marginally circular orbit (cyan curves), mso is for marginally stable circular orbit (darker blue curves). Right panel: Radii of the Kerr geodesic structure $\{r_{mco}^\pm ,r_{mbo}^\pm ,r_{mso}^\pm \}$ and radii $\{r_{(mco)}^\pm ,r_{(mbo)}^\pm \}$, defined in Table 2, for counter-rotating $(+)$ orbits (right panel) and for co-rotating $(-)$ orbits (left panel) as functions of the BH spin a. $\sigma =1$ corresponds to the equatorial plane, where $\sigma \equiv \sin ^2\vartheta \in [0,1]$

Fig. 2

Kerr BH spacetime. Left panel: fluid specific angular momentum $\ell ^\pm (r)$, defined in Eq. (B3) for co-rotating $(-)$ (solid) and counter-rotating $(+)$ orbits (dashed) as function of the radius r for different BH dimensionless spin a signed on the panel. (Blue curves correspond to spin $a=0.999$, black curve corresponds to the Schwarzschild spacetime with $a=0$.) We adopt the notation $\textrm{Q}_\bullet$ for any quantity evaluated at $r_\bullet$. mso is for marginally stable circular orbit, gray curve corresponds to $\ell ^\pm (a_{mso}^\pm )$, where $a_{mso}^\pm (r): r_{mso}^\pm (a)=r$. Right panel: fluid specific angular momentum $\ell _{mbo}^\pm$, on the marginally bound circular orbit (blue curves), $\ell _{mco}^\pm$, on marginally circular orbit (cyan curves), $\ell _{mso}^\pm$, evaluated on the marginally stable circular orbit (darker blue curves) as functions of the BH spin a. Co-rotating fluids momenta $(-)$ are solid curves, and counter-rotating $(+)$ are dashed curves. All quantities are dimensionless

The center, $r_{center}$, is the maximum point of pressure and density in the torus (corresponding to the minimum point of the fluid effective potential with respect to the radius r).

Surfaces cusps $r_\times$ on the equatorial plane are the minimum points of pressure and density in the torus (and the maximum points of the fluid effective potential with respect to the radius r). At the cusps the matter can be considered pressure free, and matter can freely falling into the BH.⁷

The spacetime equatorial circular geodesic structure constrains the accretion disk physics governing the tori cusps and centers locations. In the Kerr geometry the geodesic structure is constituted by the marginally circular orbit for timelike particles $r_{mco}^\pm \equiv r_{\gamma }^{\pm }$, which is also a photon circular orbit, the marginally bound orbit, $r_{mbo}^{\pm }$, and the marginally stable circular orbit, $r_{mso}^{\pm }$ – see Figs. 1 and 2. The situation is detailed in Table 1, where we introduced also the radii $(r_{\mathrm {(mbo)}}^{\pm }, r_{(mco)}^{\pm })$, governing the location of the tori centers, and defined in Table 2 – see Figs. 1 and 2.

Table 1 Kerr BH spacetime. Geodesic structure and orbiting configurations. It refers to the analysis of Sect. 2.2.1. Proto-jets are associated to (not-collimated) open structures, with matter funnels along the BH rotational axis – see [73, 100,101,102,103]. $\ell$ is the fluid specific angular momentum. mbo is for marginally bound circular orbit, mco is for marginally circular orbit, mso is for marginally stable circular orbit. Radii of the Kerr geodesic structure $\{r_{mco}^\pm ,r_{mbo}^\pm ,r_{mso}^\pm \}$ and radii $\{r_{(mco)}^\pm ,r_{(mbo)}^\pm \}$ are in Table 2 for counter-rotating $(+)$ orbits and for co-rotating $(-)$ orbits. (We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$.) Cusp $r_\times$ is the minimum point of pressure and density in the configuration corresponding to the maximum point of the fluid effective potential. The center $r_{center}$ is the maximum point of pressure and density in the configuration, corresponding to the minimum point of the fluid effective potential. At the cusp ($r\le r_\times$) the fluid may be considered pressure-free. Fluid effective potential defines the function $K(r)=V_{eff}(\ell (r))$. Cusped tori have parameter $K=K_\times \equiv K(r_{\times })\in ]K_{center}, 1[\subset ]K_{mso}, 1[$, where $K_{center}\equiv K(r_{center})$. See also Figs. 1 and  2

2.2.2 Notes on tori morphology and energetics

The energetics of the geometrically thick tori (as the accretion rate or the cusps luminosity) orbiting super-massive BHs is constrained by the tori morphology.

In this section we examine the maximum thickness of a disk accretion throat (opening of the cusp) providing information on different aspects of the accretion process energetics.

Table 2 Lookup table containing the main notation and quantities used throughout this paper. Links to associated sections, definitions or figures are also listed. There is $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$

The maximum thickness of a disk accretion throat

In general the accretion throat thickness is maximum for disks with low magnitude of the specific angular momentum $\ell$, that is for $\ell \gtrapprox \mp \ell _{mso}^\pm$ – [93,94,95].

Fig. 3

Kerr spacetime with spin $a=0.9$. All quantities are dimensionless. Tori models: equidensity surfaces and surfaces of constant $\ell$, for co-rotating $(-)$-left panel and counter-rotating $(+)$-right panel, related to the analysis of Sect. 2. Black region is the central BH, gray region is the outer ergoregion, there is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell$ is the fluid specific angular momentum. Right panel: solutions of equation $\ell ^+:\partial _yV_{eff}(a;y,z,\ell )=0$, ($V_{eff}(a;y,z,\ell )$ is the fluids effective potential) coincident with $\ell ^+(x,y,a)=$constant, represented as blue solid curve for $\ell =\ell _{mbo}^+$ and solid black curve for $\ell =\ell _{mso}^+-0.01$. Curves connect the center of maximum density and pressure with the tori geometrical maxima in the range $y=r>r_{mso}^+$, and the cusp $r_\times$ (minimum of pressure), fixed by momentum $\ell ^+=$constant with the minima of the matter throat, providing thus indication of tori (and matter throat) thickness. Gray solid curve are equidensity surfaces for $\ell =\ell _{mso}^+-0.01$, and blue dashed curves are for $\ell =\ell _{mbo}^+$. Left panel: solutions of equation $\ell ^-:\partial _yV_{eff}(a;y,z,\ell )=0$, coincident with $\ell ^-(x,y,a)=$constant, represented as cyan solid curve for $\ell =\ell _{mbo}^-$ and solid black curve for $\ell =\ell _{mso}^-+0.01$. Gray solid curve are equidensity surfaces for $\ell =\ell _{mso}^-+0.01$, and cyan dashed curves are for $\ell =\ell _{mbo}^-$. (Fluid specific angular momentum $\ell _{mbo}^\pm$, is evaluated on the marginally bound circular orbit, $\ell _{mso}^\pm$ is evaluated on the marginally stable circular orbit.)

Fig. 4

Kerr spacetime. Tori models: equidensity surfaces and surfaces of constant $\ell$, for co-rotating $(-)$ and counter-rotating $(+)$ fluids, related to the analysis of Sect. 2. Black region is the central BH, gray region is the outer ergoregion, there is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell$ is the fluid specific angular momentum. All quantities are dimensionless. Left and center panels show the solutions $\ell ^\pm :\partial _yV_{eff}(a;y,z,\ell )=0$, ($V_{eff}(a;y,z,\ell )$ is the fluids effective potential) coincident with $\ell ^\pm (x,y,a)=$constant, for counter-rotating (center panel) and co-rotating tori (left panel) for different $\ell ^\pm$ signed on the curves in a Kerr BH spacetime with spin $a=0.9$. Curves connect the center of maximum density and pressure with the tori geometrical maxima in the range $y=r>r_{mso}^\pm$, and the cusp $r_\times$ (minimum of pressure), fixed by momentum $\ell ^\pm =$constant with the minima of the matter throat, providing thus indication of tori (and matter throat) thickness. Fluid specific angular momentum $\ell _{mbo}^\pm$, is evaluated on the marginally bound circular orbit $r_{mbo}^\pm$, $\ell _{mso}^\pm$ is evaluated on the marginally stable circular orbit $r_{mso}^\pm$. Radii $(r_{mbo}^\pm , r_{mso}^\pm )$ and marginally circular orbit $r_{mco}^\pm$ (which is also a photon orbit $r_{mco}^\pm = r_{\gamma }^\pm$) are shown as vertical lines. Momenta $\ell$ are in the range $\mathbf {L_2^\pm }\equiv [\mp \ell _{mbo}^\pm ,\mp \ell _{mco}^\pm ]$, for proto-jets (dotted-dashed green curves), and range $\mathbf {L_1^\pm }\equiv [\mp \ell _{mso}^\pm , \mp \ell _{mbo}^\pm ]$, for cusped tori (dashed black curves). Right panel: solutions $\ell ^\pm :\partial _yV_{eff}(a;y,z,\ell )=0$, coincident with $\ell ^\pm (x,y,a)=$constant, for counter-rotating (dashed) and co-rotating tori (solid) for $\ell =\ell _{mso}^\pm$, in the Schwarzschild BH ($a=0$) spacetimes (black curve), Kerr BH spacetime with spin $a=0.9$ (blue curves) and $a=0.9991$ (green curves)

Fig. 5

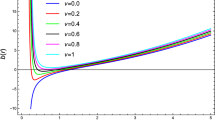
Kerr BH spacetime with spin $a=0.9$. All quantities are dimensionless. Solid (dashed) curves show the situation for the co-rotating – (−) (counter-rotating – ($+$)) fluids with specific angular momentum $\ell =\ell ^-$ ($\ell =\ell ^+$). Black (gray) curves are for momenta $\ell =\ell _{mso}^\pm \mp 0.01$ ($\ell =\ell _{mso}^\pm$), where $\ell _{mso}^\pm$ is the fluid specific angular momentum evaluated on the marginally stable circular orbit $r_{mso}^\pm$ respectively. Left panel shows the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$ related the $\phi$-quantities ($V_{eff}$ is the fluid effective potential here evaluated at the torus cusp r). Right panel shows the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$, related the $\chi$-quantities (r is the torus cusp radius, $\Omega$ is the fluid relativistic angular momentum evaluate at the torus cusp), at different fluid momenta $\ell$ signed close to the curves. Follows the discussion of Sect. 2.2.2. ((While each radius represents a possible cusp, the curves are extended to a larger radial range for graphical convenience.). The $\phi$-quantities regulate the mass-flux, the enthalpy-flux (related to the temperature parameter), and the flux thickness. $\chi$-quantities regulate the cusp luminosity, the disk accretion rate, and the mass flow rate through the cusp i.e., mass loss accretion rate

In Fig. 2 we show the distribution of specific angular momentum $\ell ^\pm$ and in Figs. 3 and 4 we show solutions $\ell ^\pm (x,y,a)$ of $\partial _yV_{eff}(a;z,y,\ell )=0$ (with $r=\sqrt{y^2+z^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$). These curves connect the torus centers to the tori geometrical maxima (at $y=r>r_{mso}^\pm$), and the cusp $r_\times$ to the accretion flow throat geometrical extremes, as shown in the figures. This implies that the curves provide an estimation of the maximum throat thickness – see [93,94,95]. Hence, the amount of matter swallowed by the BH from the accreting torus is constrained by the value $\ell =\ell _{mso}^\pm$. In the Kerr spacetime, $\ell _{mso}^\pm$ depends on the BH dimensionless spin only and, as clear from Fig. 4, the throat thickness increases with the BH spin, reaching its maximum at $a=M$, approaching the BH with increasing spin, for co-rotating fluids.

General considerations on the accretion tori energetics

From the fluid effective potential, the function $K(r)=V_{eff}(\ell (r))$ is defined (where cusped tori have parameter $K=K_\times \equiv K(r_{\times })\in ]K_{center}, 1[\subset ]K_{mso}, 1[$, where $K_{center}\equiv K(r_{center})$) – see Tables 2 and 4.

Some energetic characteristics of the accreiting tori can be related to the geometrical thickness of the super-critical tori flows, that is tori with parameter $K=K_s\in ]K_\times , 1[$, and their accretion throat – [87,88,89, 93,94,95, 104]. Hence, the analysis of tori morphology provides a wide estimation of these characteristics for more refined tori models.

• $\phi$-quantities We can estimate fluid thickness considering introducing quantity $\phi \approx \ln K_s-\ln K_\times$. In the Kerr spacetime $\phi$ has a limiting value, considering $r^\pm _\times \approx r_{mso}^\pm$ (correspondent to slow momenta magnitude $\ell _{mso}^\pm$) and $r_s\approx r_{mbo}^\pm$, where $\phi \approx -\ln K_{mso}^\pm$.

  To make our arguments more precise, we consider polytropic tori having pressure $p=\kappa \varrho ^{1+1/n}$ ($\gamma \equiv 1+1/n$) is the polytropic index and $\kappa$ is a polytropic constant).

  The mass-flux, the enthalpy-flux (related to the temperature parameter), and the flux thickness can be estimated as $\phi$-quantities, having general form $\phi (r_\times ,r_s,n)=\beta _1(n,\kappa )(\ln K_s-\ln K_{\times })^{\beta _2(n)}$, where $\{\beta _1(n,\kappa ),\beta _2(n)\}$ are functions of the polytropic index and constant⁸.

• $\chi$-quantities We examine also the $\chi$-quantities, having general form $\chi =\phi (r_\times ,r_s,n) r_\times /\Omega (r_\times )$; where $\Omega (r_\times )$ is the relativistic angular frequency at the tori cusp $r_\times$ where the pressure vanishes. The $\chi$-quantities regulate the cusp luminosity, measuring the rate of the thermal-energy carried at the cusp, the disk accretion rate, and the mass flow rate through the cusp (i.e., mass loss accretion rate)⁹.

In this analysis we assume $\beta _1=\beta _2=1$, and in the Kerr spacetime we consider the extreme cases, fixing the cusp location at a point $r_\times \approx r_{mso}^\pm$ (i.e. $\ell =\ell _{mso}^\pm$) and we set the maximum throat thickness and location with the limit $K=K_s\approx 1$ correspondent to $r_s\approx r_{mbo}^\pm$ accordingly. Within these assumptions $\phi$-quantities are simply reduced to $\phi =- \ln V_{eff}$ and the $\chi$-quantities are $\chi =-\phi r_\times /\Omega _\times$. It has been convenient to consider in Fig. 5 quantities $\bar{\phi }=-\phi$ and $\bar{\chi }=-\chi$ as for specific angular momentum $\ell \approx \ell _{mso}^\pm$, for co-rotating and counter-rotating fluids orbiting BH spacetimes with spin $a=0.9$. In the following section we consider again $(\bar{\phi },\bar{\chi })$ evaluated the DE effects, as governed by the Kiselev spacetimes with respect to the GR case of Kerr geometry in Figs. 5 and  4.

3 Accretion disks orbiting dark energy Kiselev spinning BHs

In this section we analyze accretion tori orbiting spinning BHs in DE Kiselev spacetime models, where the metrics, for some values of the DE parameters, reduces to the Kerr BH geometry. In Sect. 3.1 we introduce the Kiselev solutions. In Sect. 3.2 we examine the equatorial circular geodesic structures, the specific fluid angular momentum distribution, the tori structure and accretion disks energetics for co-rotating and counter-rotating tori, in the Kiselev spacetime, compared to the dynamics in the Kerr spacetime considered in Sect. 2.2.

Table 3 Dark energy (DE) Kiselev model with parameter with $\alpha =-2/3$. Ergosurfaces radii classification according to the DE parameter k. All quantities are dimensionless. Quantity a is the dimensionless spin. Spin functions $a_\kappa ^\pm$, defined in Eq. (A6), are shown in Fig. 24. Limiting planes $\sigma _E^\pm$ are in Eqs. (A7). (There is $\sigma \equiv \sin ^2\vartheta \in [0,1]$.) Quantities $\{\bar{\bar{r}}\}_{n}$ are the n zeros of quantity $\bar{\bar{r}}$ of Eqs. (A5)

Table 4 Dark energy (DE) Kiselev model with parameter with $\alpha =-2/3$. Ergosurfaces classification according to the spin a. All quantities are dimensionless. Quantity k is the DE parameter. Functions $k_E^\pm$ and limiting planes $\sigma _E^\pm$ are in Eq. (A7). (There is $\sigma \equiv \sin ^2\vartheta \in [0,1]$.) Quantities $\{\bar{\bar{r}}\}_{n}$ is the n zeros of quantity $\bar{\bar{r}}$ of Eqs (A5)

3.1 The Kiselev spacetimes

Kiselev spherically symmetric static geometry has been a popular toy model adopted in different contexts [22]. The Kiselev rotation extension, we consider here, was introduced in [23]. There is

$$\begin{aligned} g_{tt}= & {} \frac{a^2 \sigma -\Delta _K }{\Sigma },\quad g_{t\varphi }=\frac{a \sigma \left[ \Delta _K-\left( a^2+r^2\right) \right] }{\Sigma },\nonumber \\ g_{\varphi \varphi }= & {} \frac{\sigma \left[ \left( a^2+r^2\right) ^2-a^2\sigma \Delta _K \right] }{\Sigma },\nonumber \\ g_{rr}\equiv & {} \frac{\Sigma }{\Delta _K},\quad g_{\vartheta \vartheta }=\Sigma \quad \text{ with }\quad \Delta _K\equiv \Delta -k r^{1-3 \alpha }; \end{aligned}$$

(7)

where $\alpha$ is an EoS parameter for the matter distribution embedding the central BH. The parameter k,“DE-parameter”, is an integration constant regulating the DE effects, where the Kerr limit is for $k=0$.

Table 5 Dark energy (DE) Kiselev spacetime with $\alpha =-2/3$. Horizons analysis according to the spin a. All quantities are dimensionless. k is the DE parameter. Spin functions $\hat{a}_i$, are i-zero of $\hat{a}$ (see Eq. (A6)), shown in Fig.  24 and coincident with spin functions $a_\kappa ^\pm$ of Eqs (A6). Quantity $\{\breve{r}\}_{n}$ is the n zero of quantity $\breve{r}$ of Eqs (A9), coincident with radii $\{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}$ of Fig. 26

Following most of the literature we set the parameter of state $\alpha =-2/3$, which allows to consider the more complex and general aspects of the Kiselev DE spacetimes (as, for example, the horizons structure) in a relatively simple scenario, and we refer to the extensive literature on different aspects of this spacetime family and matter dynamics.

Hence, for a broad analysis of the Kiselev metric and for this choice of metric parameter we refer to Appendix A and for example, to [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47, 49, 51,52,53,54,55,56,57,58,59,60,61,62]. In Appendix A we proceed with the analysis of the spacetime properties within this choice of the $\alpha$ parameter and spin $a>0$ by considering the ergosufaces and detailing the conditions for the horizons existence, then examining the extreme BH Kiselev spacetimes. This analysis constitutes the basis for the investigation of the tori properties in Sect. 3.2.

3.2 Accretion tori around a Kiselev spinning BH

DE affects the orbiting fluids, modifying the Kerr axially symmetric geometry, the geodesic structure and the fluid effective potential. Therefore, following the procedure and considerations outlined in Sect. 2.2, in here we provide an estimate of the DE effects on tori structure, following a two steps analysis:

1.:

In the first step we study the radii limiting the tori construction: the co-rotating and counter-rotating spacetime geodesic equatorial structures as functions of the spin $a\in [0,1]$, and as defined through the fluid effective potential in Eq. (B1) and the angular momentum distribution in Eq. (B2) modified by the DE presence and compared to the case in absence of DE. We then analyze the fluid specific angular momentum $\ell ^\pm$, the tori parameter $K^\pm$ and the test particle (Keplerian) angular momentum $\mathcal {L}^\pm$ as functions of r, (for co-rotating and counter-rotating structures, for $a\in [0,1]$) compared with the Kerr spacetime. This investigation allows to trace the main properties of the orbiting toroids and to proceed with the analysis of the tori and their energetics.

2.:

In the second step, we consider the construction of orbiting tori, discussing their morphology, and in particular the tori geometrical thickness, the distribution of the pressure critical points in the fluids and the tori energetics, following the investigation in Sect. 2.2.2 and distinguishing the co-rotating and counter-rotating cases. We will investigate also the possibility of toroids in the spacetime BH ergoregion.

In Appendix B1 are more details on the geodesics structure and tori construction for $\alpha =-2/3$. Considering the results on the horizons structures of Table 5 and Eq. (A10), and ergoregions in Tables 3 and  4, we split the DE parameter k range in positive and negative values (with the discriminant case $k=0$ corresponding to the Kerr spacetime): in Sect. 3.2.1 we analyze the case with DE parameter $k\le 0$, while in Sect. 3.2.2 the situation for DE parameter $k\ge 0$ is explored.

To fix the ideas, two exemplificative cases are selected:

i):

DE parameter $k=-0.05$, explored in Sect. 3.2.1, and

ii):

DE parameter $k=0.0025$, addressed in Sect. 3.2.2.

Within this choice of the k parameter, the geodesic structure, the fluid specific angular momentum and the tori effective potential are examined for all values of the spin $a\in [0,M]$. However, to clarify our arguments, disks properties as tori thickness, location of the extreme points of pressure in the disks, and tori energetics will be discussed for selected spin. Results for the DE spacetime are compared to the limiting Kerr spacetime occurring at $k=0$.

As the Kiselev metric structure constitutes a multi-parametric scenario, the effective generalization on our parameter choice for the numerical analysis, is ensured by the considerations on the parameter ranges in the study of the horizons structures in Table 5 and Eq. (A10) and ergoregions in Tables 3 and 4, that is close to the Kerr (BH) spacetime case, presenting DE effects which can be possibly detected. (The extreme situations, for the other ranges of the k parameter, emerging from this analysis has been considered in Sect. 3.1, while a deeper analysis of the geodesics structures in these cases goes far from the goals of our analysis.).

In Fig. 27, right panel we show the horizons for $k=0.0025$ and $k=-0.05$. (In the specific case, in details, for $k=-0.05$, there is one horizon at $r=1.832$, for $a=0$ (the static BH), and two horizons for $a\in ]0, 0.977193[$ – see Fig. 27, right panel. There is only one horizon for BH spin $a=0.977193$ at $r=0.934503$. For $k=0.0025$ the situation is more complex: for $a=0$ there are horizons at the radii $r=\{ 2.0101, 397.99\}$. For $a\in ]0, 1.00126[$ there are three horizons. For $a>1.000126$ there is one horizon of cosmic character (located very far from the central attractor) – see Eqs. (A10) and Table 5.

We focus our selection of the k parameter for these two cases on a region of the parameter range close to the limiting value for Kerr spacetimes, i.e. $k\approx 0$ (which numerous observation today tends to confirm), but showing nonetheless clear divergences from the standard GR case either in the horizons structures or in the effects of frame dragging (ergosurfaces) and, as detailed in Sects. 3.2.1 and  3.2.2, in the geodetic structures and therefore in the set of constraints governing the tori morphology and instabilities. (This situation could be seen also through the horizons analysis of Fig. 26 and Table 5, and in Fig. 27 showing also the role of k in the extreme BH cases. The study of the spacetimes ergosurfaces according to the DE parameter k in Fig. 24 and in Table 3 shows that for sufficiently small values of $k> 0$ the situation depends strongly on the BH spin.)

Spacetime horizons structures as in Fig. 25 and Eq. (A10) show that for negative k the situation is regulated by the limiting spin function $a_\kappa ^+$. The positive range of k features the presence of three horizon radii and the situations for the limiting spins is more complex. (In the case of $k>0$ an important limiting case of the positive k parameter range is the value $k=1/8\approx 0.125$).

Physical difference between thick accretion disks in a Kiselev spacetime and in a Kerr spacetime

We discuss here in broad terms the emerging divergences in tori orbiting Kiselev BHs compared to tori of the Kerr BH spacetimes. We close this discussion then with a more specific example illustrating some of these aspects. While next sections detail in deep the physical difference between thick accretion disks in a Kiselev spacetime and in a Kerr spacetime examining, in Sect. 3.2.1 and in Sect. 3.2.2, the specific cases illustrative of the general properties of the accreiting toroids in the Kiselev DE rotating solutions.

Fig. 6

Kiselev spacetime with $\alpha =-2/3$ and spin $a=0.9$, DE parameter $k=0.0025$ (left column) and the Kerr spacetime, case $k=0$ (right column). Black region is the central BH, blue and gray region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^\mp$ are the fluid specific angular momentum for co-rotating (upper row) and counter-rotating (bottom row) fluids respectively. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbit. Dashed and dotted curves are the equipressure surfaces (toroids) at $\ell =\ell _{mso}^\pm$ signed on the panels and different K parameter. Solid curves are solutions with $\ell ^\pm (x,y,a)=$constant of equation $\partial _yV_{eff}(a;y,z,\ell )=0$, connecting toroids centers, surfaces cusps and toroids geometrical extremes. All quantities are dimensionless

• Proto-jets, tori and boundary conditions The toroidal structures are essentially differentiated in the Kiselev case from the Kerr spacetime case by the boundary conditions at infinity of the DE Universe, distinguishing the limit from cusped tori and proto-jets. This effect can be seen in the modification of the geodesic structure which constrains the accretion tori, and in particular for radius $r_{mbo}^\pm$. This implies that, in particular, there can be, for instance, an abundance of proto-jets in orbital regions where accretion disks are expected orbiting the central Kerr BH.

• BHs versus NSs In a situation where value of the spin $a\in [0,1]$ parameter, defining a Kerr BH, defines a Kiselev NS, differences in the accretion physics in presence of DE are obviously many, due to the absence of BHs horizons. This is the case carefully analyzed in Appendix A, where the Kiselev spacetime horizons structures have been studied and compared to the limiting case of Kerr BH spacetimes.

• Cosmological induced excretion The presence of a cosmological horizon, introduced by the DE parameter, induces two main resulting effects. First, there may be excretion tori i.e. orbiting toroids with emission of materials outwardly, due to cosmological repulsive effects. Excretion disks are also effects of the repulsive forces induced, in some cases, by the presence of NSs. However, in our analysis we consider Kiselev BHs only. Excretion is an extreme case when a topological instability, realized with presence of an excretion cusp, is index of a broken gravitational and hydromechanical equilibrium condition due to the combined effects of the cosmological repulsion. Nevertheless, the repulsive effects, associated to the cosmological horizons, can be seen also by a different morphological structure, as presence of double orbiting tori and the existence of an outer limit to the tori formation, which are extraneous to the Kerr BH spacetime.

• Distinguishing tori rotation orientation Significantly, DE may affect differently the orbiting matter according to their rotation orientation with respect to the central spinning BH attractors. These differences will emerge as a significant divergence between the co-rotating and the counter-rotating tori strongly distinguishing this case from that of Kerr BH spacetime. These divergences exist at morphological and topological level, differently affecting also the tori stability and the consequent BH energetics – see for example Fig. 6 and brief discussion below. In this analysis we show that the presence of DE is recognizable, as introduced by the Kiselev model, by the induced change of the accretion physics of the counter-rotating tori with respect to the co-rotating structures with the respect to the central Kerr BH.

• Double accretion toroids Two co-rotating or counter-rotating accretion disks can orbit one Kiselev spinning BH attractor due to the existence of a double limiting radii $r_{mso}^+$ and $r_{mbo}^+$, a situation commonly seen in spacetimes with geometrized repulsive forces (we address this point also in Fig. 6 discussed below).

• Accretion physics and tori energetics in DE universe There may be deviations in the topology and morphology between disks orbiting a Kiselev BH and a Kerr BH. However, as discussed in Sect. 2.2.2, while the topological deviations of disks at constant pressure are linked to differences in the instability processes associated to the cusped toroidal surfaces, the variations in morphology (such as geometric thickness of the disk or its extension on the equatorial plane) manifest in the tori and BH energetics as the accretion rates. Consequently the energetics associated to the unstable phases of the accretion disks result modified in the Kiselev spacetime, with respect to the case of Kerr spacetime, which can lead in some cases, to an increase of accretion rates and luminosities. The relation between morphology, topology and energetics of the BH and accretion disks, has been discussed for the Kerr BH case in Sect. 2.2.2.

• False estimation of the BH spin-mass ratio Distortion of the tori morphology induced by the DE presence in the Kiselev Universe can lead to underestimation or overestimation of the BH accretion rate as well as the BH spin mass ratio. Several methods of evaluation of the BH spin-mass ratio are based on details of accretion physics. A particular relevant approach consists in the evaluation of the accretion rate (that, as discussed above will be modified by the DE effects) and the location of the accretion disk inner edge. Being located in $]r_{mbo}^\pm ,r_{mso}^\pm ]$, which is dependent exclusively on the background property, therefore in the case of Kerr spacetime from the BH spin, this radius is able to provide an estimate of the spin. In the case of DE, the additional metric parameter modifies the geodesic structure, and therefore also the inner edge location, lead hence to a distorted spin evaluation.

These aspects can be clarified focusing on one particular example. Figure 6 concentrate on the Kiselev BH spacetime ($\alpha =-2/3$) with spin $a=0.9$, DE parameter $k=0.0025$ (left column), which will be detailed in Sect. 3.2.2, compared to the case of Kerr spacetime for $k=0$ (right column). (Fig. 6 can be compared also to the Kerr BH case analysed in Fig. 3.) Dotted and dashed curves are the equipressure surfaces (toroids) for fixed $\ell =\ell _{mso}^\pm$ and different values of the K parameter. Solid curves are $\ell ^\pm (x,y,a)=$constant, where $\ell ^\pm (x,y,a)$ are solutions of the equation $\partial _yV_{eff}(a;y,z,\ell )=0$, connecting toroids centers, surfaces cusps and toroids geometrical extremes.

We can observe the different morphologies characterizing the toroids orbiting in DE Universe (left column), compared to the toroids of the Kerr spacetimes (right column). As anticipated, substantial differences appear for the co-rotating (upper row) and counter-rotating (bottom row) tori, emerging with the introduction of the DE parameter.

Upper left panel clearly shows the morphology of the equipressure lines evidencing the repulsive excretion effects, associated to the presence of the outer co-rotating marginally stable orbit $r_{mso}^-$. The bottom left panel shows the presence of two limiting marginally stable orbits, $r_{mso}^+$, for the counter-rotating case. In particular we observe the differences emerging in the distributions of pressure points of fluids the disks, and the excretion effects from the form of the equipressure lines far from the central BH attractor. The possibility of a co-rotating or counter-rotating doubled toroid is a direct consequence of the existence of two marginally stable orbits $r_{mso}^-$ and $r_{mso}^+$, respectively, which has no counterpart in the BH Kerr spacetime. This is particularly clear from the upper left panel of Fig. 6, showing a doubled structure of the co-rotating equidensity lines, even for the limiting case of momentum $\ell =\ell _{mso}^-$. In this case it is expected that the outer orbiting structures will be bounded and modified by the geometry repulsive effects. In the counter-rotating case, nevertheless, the repulsive effects, due to the presence of DE, are more subtle, for both (inner and outer) configurations the toroidal structures are very different from those in the absence of DE. However, in this case the distribution of the pressure points in the counter-rotating toroids is largely different from the Kerr BH spacetime, differentiating therefore also these toroids from the tori rotation orientation.

3.2.1 DE parameter $k\le 0$

In this section we study the case of negative k metric parameter.

Considerations on tori constraints

Fig. 7

Dark energy model. Kiselev spacetime with $\alpha =-2/3$. Circular equatorial geodesic structure of the Kiselev spacetime as function of the spin a, for the DE parameter $k=-0.05$ (cyan and blue curves). Gray curves are the Kerr case ($k=0$) see Fig. 1. Blue (cyan) curves show the counter-rotating (co-rotating) $(+)$ ($(-)$) case. Radii $r_\pm$ (black curves) are the horizons, $r_{\epsilon }^+$ is the outer ergoregion on the equatorial plane, mso is for marginally stable orbit, mco is for marginally circular orbit, mbo is the solution of $V_{eff}=1$ ($V_{eff}$ is the fluid effective potential). All quantities are dimensionless

Fig. 8

Dark energy model. Kiselev spacetime with $\alpha =-2/3$ and DE parameter $k=-0.05$ (green and blue curves). Parameter $k=0$ (gray and black curves) corresponds to the Kerr spacetime. Fluid specific angular momentum $\ell ^\pm$ (right panel), energy parameter $K^\pm$ (left panel), and (test particles) Keplerian angular momentum $\mathcal {L}^\pm$ (center panel), as function of r for co-rotating ($(-)$-plain curves) and counter-rotating ($(+)$-dashed curves) fluids, different spins a according to the notation in the left panel. All quantities are dimensionless

Fig. 9

Kiselev spacetime with $\alpha =-2/3$, and DE parameter $k=-0.05$. All quantities are dimensionless. Gray curves correspond to the case of Kerr BH spacetime (for $k=0$). Cyan (blue) curves show the situation for the co-rotating (counter-rotating) fluids with specific angular momentum $\ell =\ell ^-$ ($\ell =\ell ^+$). Left panel shows the quantities $\mp \ell ^\pm$ evaluated on marginally stable orbits (mso), on the marginally circular orbits (mco), on the marginally bounded orbits (mbo) as functions of the BH spin a, as described on the panel. Follows the discussion of Sect. 3.2.1. Right panel is a close up view of the left panel, and shows $\ell _{mbo}^-$ evaluated on the upper/lower ($(+)/(-)$) marginal bound radius, see Fig. 7

The counter-rotating and co-rotating equatorial geodesic structure of the Kiselev spacetime with $k=-0.05$ is showed in Fig. 7, compared with the Kerr spacetime case ($k=0$) of Fig. 1. Differences between the faster and the slower spinning BHs are clear, particularly with the presence of a doubled co-rotating marginally bound orbit for faster spinning attractors. Remarkably this situation, characterizing only the co-rotating fluids, distinguishes the fluids rotation orientation with respect to the central BH. We can note, from the location of the marginally stable and bound orbits, tori and proto-jets cusps could also be closer to the central attractor in the spacetime with dark energy. This case is addressed also in Fig. 8, with the analysis of the fluid specific angular momentum $\ell ^\pm$ (right panel), the energy parameter $K^\pm$ (left panel), and the (test particles) Keplerian angular momentum $\mathcal {L}^\pm$ (center panel), as functions of r, for co-rotating and counter-rotating fluids, in the spacetimes of faster spinning and slower spinning attractors, and compared with the situation for the Kerr spacetime. Divergences with respect to the Kerr case appear in both the near-horizon and far-horizon regions, at each BHs spin.

Fig. 10

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=-0.05$ and spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell$ is the fluid specific angular momentum. Upper (bottom) row shows the situation for counter-rotating (co-rotating) fluids with momentum $\ell =\ell ^+$ ($\ell =\ell ^-$). Left column panels show surfaces $\ell ^\pm =$constant where the particular case $\ell _{mso}^\pm =$constant (for marginally stable orbits) is signed on the curves. Right column: solutions of equation $\ell ^\pm :\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, respectively, with $\ell ^\pm (x,y,a)=$constant are shown for different $\ell$ signed on the curves, where mco is for marginally circular orbits, mbo for marginally bounded orbits. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$. All quantities are dimensionless

An analysis focused on the different tori structures is in Fig. 9, reflecting the analysis of the geodesic structure. Left panel shows the functions $\mp \ell ^\pm (r)$ evaluated on marginally stable orbits, on the marginally circular orbits and on the marginally bound orbits, as functions of the BH spin a, with respect to the Kerr BH spacetime. Right panel is a close up view of the left panel, with $\ell _{mbo}^-$ evaluated on the upper/lower ($(+)/(-)$) marginal bound radius of Fig. 7. Particularly for faster spinning BH attractors, DE could manifest in the different accretion physics distinguishing co-rotating and counter-rotating tori. The co-rotating and counter rotating specific angular momentum, at almost any spin, is generally lower in magnitude then in the Kerr spacetime. The most evident distinction with respect to the Kerr spacetime rests in the absence of a marginally bounded orbit for slower spinning attractors, and the presence a doubled marginally bound orbit for faster spinning attractors, a (quantitative) deviation from the standard Kerr situation appears also in the location of the radii $(r_{mso}^\pm , r_{mco}^\pm )$ and especially with respect to the location of the marginally stable orbit. DE effect could manifest in the analysis of the mechanics of accreting fluids as false estimate of the BH dimensionlesss spin¹⁰ (as an underestimation or overestimation of the spin-mass ratio of the black hole). In general, radii $(r_{mso}^\pm , r_{mco}^\pm )$ are smaller then in the absence of the DE. This could lead to an underestimation of the BH spin, from the analysis of the counter-rotating fluids, or an overestimation, from the co-rotating fluids analysis. An analogue situation occurs for the momenta $(\ell _{mso}^\pm , \ell _{mco}^\pm )$, lower in magnitude with the respect to the Kerr case, having influence also in an eventual attractor spin shift following accretion. To investigate this situation we consider a Kiselev BH spacetime with spin $a=0.9$.

Tori morphology and critical points

In Fig. 10 we focus on the surfaces $\ell ^\pm =$constant, and in the particular case $\ell _{mso}^\pm =$constant, compared with the solutions $\ell ^\pm :\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, respectively, with $\ell ^\pm (x,y,a)=$constant, at different $\ell$ signed on the curves. The two functions $\ell _{mbo}^-$ are compared with Fig. 4, for the case of Kerr spacetime. The situation for the last stable orbit is similar to the case of Kerr spacetime, and the DE affects mostly the torus inner region and its morphology. (It should be noted that, as discussed in Sect. 2.2.2, $\ell _{mso}^\pm$ provides a constraint to the tori energetics.)

Fig. 11

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=-0.05$ and spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^-$ is the fluid specific angular momentum for co-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbit, mco is for marginally circular orbits, mbo for marginally bounded orbits. Curves are equipotential and equipressure surfaces at different $\ell =$constant signed on the panels. Solutions of equation $\partial _yV_{eff}(a;y,z,\ell )=0$ ($V_{eff}$ is the fluids effective potential), coincident, with $\ell ^-(x,y,a)=$constant are shown, connecting tori centers and tori geometrical maximum, and surfaces cusps and extremes of the accretion throat. All quantities are dimensionless

A detailed analysis is in Fig. 11 for the co-rotating case, showing the solutions of $\ell ^-:\partial _yV_{eff}(a;y,z,\ell )=0$ coincident with $\ell ^-(x,y,a)=$constant, connecting tori centers to the tori geometrical maxima, and surfaces cusps to the extremes of the accretion throats (see Fig. 4 for the Kerr case). It is clear that the tori structure is affected particularly by the presence of two marginally bound orbits. The larger angular momentum is associated to configurations closer to the central attractor. The main differences with the Kerr case are manifest for larger tori, having inner edge close to the marginal bound orbit, and in the region between the marginally bound and marginally stable orbits. In Fig. 12 we repeat the analysis for the counter-rotating case. The situation appears qualitatively similar to the Kerr case.

Fig. 12

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=-0.05$ and spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^+$ is the fluid specific angular momentum for counter-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbit, mco is for marginally circular orbits, mbo for marginally bound orbits. Curves are equipotential and equipressure surfaces at different $\ell =$constant signed on the panels. Solutions of equation $\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, with $\ell ^+(x,y,a)=$constant are shown, connecting tori centers and tori geometrical maximum, and surfaces cusps and extremes of the accretion throat. All quantities are dimensionless

Fig. 13

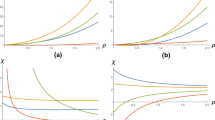
Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=-0.05$ and spin $a=0.9$. All quantities are dimensionless. Black and gray curves correspond to the case of Kerr BH spacetime (for $k=0$), coloured curves are for $k=-0.05$. Bottom (Upper) panels show the situation for the co-rotating (counter-rotating) fluids with specific angular momentum $\ell =\ell ^-$ ($\ell =\ell ^+$). Left column panels show the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$ related the $\phi$-quantities ($V_{eff}$ is the fluid effective potential here evaluated at the torus cusp r). Right column panels show the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$ related the $\chi$-quantities (r is the torus cusp radius, $\Omega$ is the fluid relativistic angular momentum evaluate at the torus cusp), at different fluid momenta $\ell$ signed close to the curves. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbits, mco is for marginally circular orbits, mbo for marginally bound orbits. Follows the discussion of Sect. 3.2.1. (While each radius represents a possible cusp, the curves are extended to a larger radial range for graphical convenience.)The $\phi$-quantities regulate the mass-flux, the enthalpy-flux (related to the temperature parameter), and the flux thickness. $\chi$-quantities regulate the cusp luminosity, the disk accretion rate, and the mass flow rate through the cusp i.e., mass loss accretion rate

Tori energetics

Following the analysis of Sect. 2.2.2 for the Kerr case, Fig. 13 explores the tori energetics, compared with the case of Kerr BH spacetime (black and gray curves), for the co-rotating (bottom panels) and counter-rotating (upper panels) fluids, at different specific momenta $\ell =\ell ^-$ and $\ell =\ell ^+$. Left column panels show the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$, related to the $\phi$-quantities. Right column panels show the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$, related to the $\chi$-quantities. DE effects appear more predominant in the counter rotating case, manifesting differently, however, for the $\phi$ quantities and $\chi$ quantities. In general, DE increases the ($\bar{\phi }$, $\bar{\chi }$) quantities for the co-rotating fluids, with respect to the Kerr case. For the counter-rotating fluids a similar behaviour is clear for the $\bar{\phi }$ quantities. A different situation appears for the $\bar{\chi }$ quantities, decreased by the DE effects. There is a different behaviour with cusp moving away from the attractor and the quantities variation with the magnitude of the fluid specific momentum is more evident for cusps close to the attractors.

3.2.2 DE parameter $k\ge 0$

The analysis of Sect. 3.2.1 is repeated for the case of positive Kiselev spacetime with DE parameter $k=0.0025$.

Considerations on tori constraints

In Fig. 14 is the spacetime geodetic structure on the equatorial plane, compared with the Kerr case ($k=0$) – see Fig. 1 – for counter-rotating and co-rotating fluids. The DE presence induces a robust modification of the co-rotating and counter marginal stable orbits with respect to the Kerr BH spacetime, strongly distinguishing the fluids different rotation orientation with respect to the central spinning attractor. In the counter-rotating case there is no marginal stable orbit in the spacetimes of very fast spinning BH attractors. The different influence of the spin with respect to the Kerr case is clear also from the analysis of Fig. 15, where the fluid specific angular momentum $\ell ^\pm$ (right panel), the energy parameter $K^\pm$ (left panel), and (test particles) Keplerian angular momentum $\mathcal {L}^\pm$ (center panel), are shown as function of r for co-rotating and counter-rotating motion, for different spins a.

In Fig. 16 we consider the quantities $\mp \ell ^\pm$ evaluated on the marginally stable orbits, the marginally circular orbits and on the marginally bound orbits, as functions of the BH spin a, according to the co-rotating and counter-rotating geodesic structures considered in Fig. 14, and compared with the case of Kerr BH spacetimes. Right panel is a close up view of the left panel, showing functions $\mp \ell _{mso}^\pm$ evaluated on the upper/lower ($(+)/(-)$) marginally stable radius for co-rotating and counter-rotating fluids. The existence and location of the marginally stable orbit is crucial for the analysis of numerous accretion disks properties. The main differentiation with respect to the Kerr case appears, for both co-rotating and counter-rotating fluids, for the larger radius $r_{mso}^\pm$, associated to larger values of the specific angular momentum $\ell _{mso}^\pm$ in magnitude. Considering the smaller values of $r_{mso}^\pm$, the (quantitative) divergences of the marginally stable orbits location with respect to the Kerr spacetime, could imply an underestimation of the BH spin, especially for faster spinning attractors in the case of co-rotating fluids, leading on the other hand to a possible overestimation of the BH spin for counter-rotating fluids.¹¹ Conversely, considering the marginally bound orbit, limiting from below the inner edge location of the largest accretion disks (and from above the proto-jets cusps formation), this trend would be reversed, especially for faster spinning attractors implying possibly an overestimation of the BH spin, especially for faster spinning attractors, from the analysis of the co-rotating fluids, and an underestimation of the BH spin from the motion of the counter-rotating fluids. Considering the fluids specific angular momentum, the main quantitative dissimilarities with the Kerr spacetime appear in the counter-rotating case, and in the co-rotating case for the marginally bound orbit values and slow spinning attractors. In general, the strongest DE effects appear for the marginally bound orbit values, independently by the rotation orientation. For momenta $\ell ^\pm _{mbo}$ and $\ell ^\pm _{mco}$, the analysis of counter-rotating fluids may reveal in an overestimation of the BH spin, and the co-rotating fluids a BH spin underestimation. In the case $\ell _{mso}^\pm$, especially for the counter-rotating case, there may be an underestimation of the BH spin, particular for faster spinning spinning attractors.

Fig. 14

Dark energy model. Kiselev spacetime with $\alpha =-2/3$. Circular equatorial geodesic structure of the Kiselev spacetime as function of the spin a, for DE parameter $k=0.0025$ (blue and cyan curves). Gray curves are the Kerr case ($k=0$) see Fig. 1. Blue (cyan) curves show the counter-rotating (co-rotating) $(+)$ ($(-)$) case. Radii $r_\pm$ (black curves) are the horizons, $r_{\epsilon }^+$ is the outer ergoregion on the equatorial plane, mso is for marginally stable orbit, mco is for marginally circular orbit, mbo is the solution of $V_{eff}=1$ ($V_{eff}$ is the fluid effective potential). All quantities are dimensionless

Fig. 15

Dark energy model. Kiselev spacetime with $\alpha =-2/3$ and DE parameter $k=0.0025$ (green and blue curves). Parameter $k=0$ (gray and black curves) corresponds to the Kerr spacetime. Fluid specific angular momentum $\ell ^\pm$ (right panel), energy parameter $K^\pm$ (left panel), and (test particles) Keplerian angular momentum $\mathcal {L}^\pm$ (center panel), as function of r for co-rotating ($(-)$-plain curves) and counter-rotating ($(+)$-dashed curves) fluids, different spins a according to the notation in the left panel. All quantities are dimensionless

Fig. 16

Kiselev spacetime with $\alpha =-2/3$, and DE parameter $k=0.0025$. All quantities are dimensionless. Gray curves correspond to the case of Kerr BH spacetime (for $k=0$). Cyan (blue) curves show the situation for the co-rotating (counter-rotating) fluids with specific angular momentum $\ell =\ell ^-$ ($\ell =\ell ^+$). Left panel shows the quantities $\mp \ell ^\pm$ evaluated on marginally stable orbits (mso), on the marginally circular orbits (mco), on the marginally bound orbits (mbo) as functions of the BH spin a, as described on the panel. Follows the discussion of Sect. 3.2.2. Right panel is a close up view of the left panel, and shows $\mp \ell _{mso}^\pm$ evaluated on the upper/lower ($(+)/(-)$) marginally stable radius, see Fig. 14

Fig. 17

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$ and BH spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell$ is the fluid specific angular momentum. Left (right)panel shows the situation for counter-rotating (co-rotating) fluids with momentum $\ell =\ell ^+$ ($\ell =\ell ^-$). Curves are the surfaces $\ell ^\pm =$constant where the particular cases $\ell _{mso}^\pm =$constant (for marginally stable orbits) is signed on the curves. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$. All quantities are dimensionless

This situation reflects in the tori formation and morphology.

To compare with the case $k=-0.05$, we focus our analysis on the BH attractor with spin $a=0.9$ In Fig. 17, surfaces $\ell ^\pm =$constant, and in particular the surfaces with $\ell ^\pm =\ell _{mso}^\pm =$constant, are shown. Left panel shows the situation for counter-rotating fluids and right panel the co-rotating case. Comparing with the situation in Fig. 4 for the Kerr spacetime and with Fig. 10 for Kiselev spacetime with $k=-0.05$, we note the different roles of the two marginally stable circular orbits appearing in the Kiselev spacetime with $k=0.0025$. In the counter-rotating case, values of the specific angular momentum $\ell _{mso}^+$ are very close, corresponding however to very different surfaces. The situation differs for the co-rotating fluids, with different values of fluids specific angular momenta $\ell _{mso}^-$. In general the larger specific angular momentum confirms the similarity with the Kerr case. In the counter-rotating case the configuration are bound from the outer regions remaining confined in a bound region of the BH spacetime.

To better characterize this different situation we proceed by considering first the co-rotating case, completing with the analysis with the counter-rotating case.

Fig. 18

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$, and BH spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^-$ is the specific angular momentum for co-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbits, mco is for marginally circular orbits, mbo for marginally bound orbits. Solutions of equation $\ell ^-:\partial _yV_{eff}(a;y,z,\ell )=0$, coincident with $\ell ^-(x,y,a)=$constant are shown for different $\ell$ signed on the curves. Left panel is a close-up view of the right panel. All quantities are dimensionless

Tori morphology and critical points

In Fig. 18 solutions of the equation $\ell ^-:\partial _yV_{eff}(a;y,z,\ell )=0$, coincident with $\ell ^-(x,y,a)=$constant, are shown for different constant $\ell$, signed on the curves, where left panel is a close-up view of the right panel. (Curves connect tori centers to tori geometrical maxima, and surfaces cusps to the extremes of the accretion throats.). Tori orbits in a bound region, limiting the location of the tori inner and the outer edge, from the inner and outer marginally stable orbit. The curves of the pressure extremes in the disks, $\ell =$constant, are closed, with the exception of the curves correspondent to the momenta $\ell =\ell _{mso}^-$ (evaluated at the outer radius $r_{mso}^-$). The curve of the extremes bends however towards the central attractor. In this case the presence of DE clearly limits the outer regions for the tori formation and the location of their inner edges, as well as the thick tori vertical structure. In Fig. 19 are the curves of density extremes in the tori. The main differences with respect to the case of Kerr spacetime appear for the larger angular momentum $\ell =\ell _{mso}^-=3.734$. There is no accretion towards BHs.¹² The existence of two limiting specific angular momenta for $\ell _{mso}^-$ and $\ell _{mco}^-$ respectively, has consequences in the mass accretion of the faster spinning BHs following accretion.

Fig. 19

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$ and spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^-$ is the fluid specific angular momentum for co-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbit, mco is for marginally circular orbits, mbo for marginally bound orbits. Curves are equipotential and equipressure surfaces at different $\ell =$constant signed on the panels. Solutions of equation $\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, with $\ell ^-(x,y,a)=$constant are shown, connecting tori centers and tori geometrical maximum, and surfaces cusps and extremes of the accretion throat. All quantities are dimensionless

In Fig. 20, there is the counter-rotating case. In this case the two values for the angular momentum $\ell _{mso}^+$ are very close, corresponding however to different configurations. Analogously to the co-rotating case, the larger value in magnitude is associated to the open curve bending towards the attractor. For different specific angular momentum the curves are open, and there is one only marginally circular orbit. We can see the consequences of this different situation in tori construction and morphology in Fig. 21.

Fig. 20

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$, and BH spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^+$ is the specific angular momentum for counter-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbits, mco is for marginally circular orbits, mbo for marginally bound orbits. Solutions of equation $\ell ^+:\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, respectively, with $\ell ^+(x,y,a)=$constant are shown for different $\ell$ signed on the curves. Left panel is a close-up view of the right panel. All quantities are dimensionless

There are no closed configurations at $\ell _{mco}^+$. The lowest value of $|\ell _{mso}^+|$ is associated to a special morphology of the equidensity lines.

Fig. 21

Dark energy model. Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$ and spin $a=0.9$. Black region is the central BH, blue region is the outer ergoregion. There is $r=\sqrt{z^2+y^2}$ and $\sigma =(\sin \vartheta )^2={y^2}/({z^2+y^2})$, and $\ell ^+$ is the fluid specific angular momentum for counter-rotating fluids. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbit, mco is for marginally circular orbits, mbo for marginally bound orbits. Curves are equipotential and equipressure surfaces at different $\ell =$constant signed on the panels. Solutions of equation $\partial _yV_{eff}(a;y,z,\ell )=0$, coincident, with $\ell ^+(x,y,a)=$constant are shown, connecting tori centers and tori geometrical maximum, and surfaces cusps and extremes of the accretion throat. All quantities are dimensionless

Fig. 22

Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$ and spin $a=0.9$ (colored curves). Black and gray curves correspond to the case of Kerr BH spacetime (for $k=0$). All quantities are dimensionless. Panels show the situation for the counter-rotating fluids with specific angular momentum $\ell =\ell ^+$. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbits, mco is for marginally circular orbits, mbo for marginally bound orbits. Relevant radii of the geodesic structure are also showed as vertical lines. Left panel shows the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$ related the $\phi$-quantities ($V_{eff}$ is the fluid effective potential here evaluated at the torus cusp r), and right panel shows the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$ related the $\chi$-quantities (r is the torus cusp radius, $\Omega$ is the fluid relativistic angular momentum evaluate at the torus cusp), at different fluid momenta $\ell$ signed close to the curves. Follows the discussion of Sect. 3.2.2. (While each radius represents a possible cusp, the curves are extended to a larger radial range for graphical convenience.) The $\phi$-quantities regulate the mass-flux, the enthalpy-flux (related to the temperature parameter), and the flux thickness. $\chi$-quantities regulate the cusp luminosity, the disk accretion rate, and the mass flow rate through the cusp i.e., mass loss accretion rate

Fig. 23

Kiselev spacetime with $\alpha =-2/3$, DE parameter $k=0.0025$ and spin $a=0.9$. All quantities are dimensionless. Panels show the situation for the co-rotating fluids with specific angular momentum $\ell =\ell ^-$. We adopt the notation $q_{\bullet }\equiv q(r_{\bullet })$ for any quantity q evaluated on a radius $r_{\bullet }$, where mso is for marginally stable orbits, mco is for marginally circular orbits, mbo for marginally bound orbits. Relevant radii of the geodesic structure are also showed as vertical lines. Upper left panel shows the co-rotating fluid specific angular momentum as function of r. Radius $r = 25$ is an extreme, with respect to the radius r of the effective potential with $\ell = \ell _{mso}^- = 2.5$ with $r_{mso}^- = 2.238$ (correspondent to the $\bar{\phi }$ blue curve). Dashed curve is the function $\ell ^-(r)$ in the Kerr geometry $(k=0).$ Upper right panel shows the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$ related the $\phi$-quantities ($V_{eff}$ is the fluid effective potential here evaluated at the torus cusp r). Black and gray curves correspond to the case of Kerr BH spacetime (for $k=0$), colored curves are for $k=0.0025$. Bottom panels shows the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$ related the $\chi$-quantities (r is the torus cusp radius, $\Omega$ is the fluid relativistic angular momentum evaluate at the torus cusp), at different fluid momenta $\ell$ signed close to the curves. Black and gray curves correspond to the case of Kerr BH spacetime (for $k=0$), colored curves are for $k=0.0025$. Bottom right panel is an wide view of the bottom left panel. Green curve is a $\bar{\chi }$ quantity evaluated for $r = 25$ (correspondent $\bar{\phi }$-quantity is the blue curves of the upper right panel). Follows the discussion of Sect. 3.2.2. ((While each radius represents a possible cusp, the curves are extended to a larger radial range for graphical convenience.) The $\phi$-quantities regulate the mass-flux, the enthalpy-flux (related to the temperature parameter), and the flux thickness. $\chi$-quantities regulate the cusp luminosity, the disk accretion rate, and the mass flow rate through the cusp i.e., mass loss accretion rate

Tori energetics

For the analysis of the tori energetics it is convenient to consider separately the co-rotating case and the counter-rotating cases. In Fig. 22 there is the analysis for the counter-rotating fluids. Black and gray curves correspond to the case of tori orbiting Kerr BHs, evaluated at $\ell _{mso}^+$ and at a larger momentum in magnitude. Left panel shows the quantity $\bar{\phi }\equiv -\phi \equiv \ln V_{eff}$ related the $\phi$-quantities, while right panel shows the quantity $\bar{\chi }\equiv -\chi =r\bar{\phi }/\Omega$, related the $\chi$-quantities at different fluid momenta $\ell$ signed close to the curves. The effect of the DE appears to the minimal for the $\bar{\phi }$ quantities, the values are smaller with respect to the Kerr case. An opposite situation occurs for the $\bar{\chi }$ quantities, where the DE presence appears to increase the $\bar{\chi }$ quantities. The conditions at infinity reflect the boundary conditions of the metric. The co-rotating case is in Fig. 23. Upper left panel shows the co-rotating fluid specific angular momentum as function of r. Dashed curve is the function $\ell ^-(r)$ in the Kerr geometry. Upper right panel shows the quantity $\bar{\phi }$, compared to the Kerr BH spacetime. Bottom panels show the quantity $\bar{\chi }$, compared to the case $k=0$. Quantity $\bar{\chi }$ is smaller then in the Kerr case and the situation for the two momenta $\ell _{mso}^-$ is strongly distinct. However, it is clear that the smallest momentum presents similarities with the case in absence of dark energy. For cusps close to the central attractor, $\bar{\phi }$ is greater in magnitude then in the Kerr spacetime and closer to the marginally bound orbit case in the absence of DE.¹³

4 Conclusions

In this work we explored the DE effects on the geometrical thick GRHD barotropic accretion disks orbiting around a central Kiselev spinning BH with state parameter $\alpha =-2/3$. DE is treated, in the metric model considered here, as a background deformation, affecting also the BH horizons.

Constraints are imposed on the accretion discs, restricting further the parameter ranges, by pointing to the possible DE marks in some significant accretion features. We have taken as a selection criterion in the space of the DE parameter k, the observation that there are two main expected regimes, for k positive or negative respectively, where $k=0$ is the GR limit of a Kerr BH. Performing a comparative analysis of the accretion tori structure and physics in the Kiselev DE spacetime with respect to the GR case, we addressed the two DE parameters ranges, drawing qualitative and comparative considerations, with the expectations in GR. In the cases analyzed here, there are strongly different horizons structures compared to the reference Kerr solution. (Furthermore, in this work we focused on the analysis of BH spacetimes for the Kiselev solutions with spin $a\in [0,M]$, however it could be possible, for different values of the DE parameter the presence of super-spinning BHs (see Fig. 25).

Significant qualitative detectable variations with respect to the standard Kerr case emerged.¹⁴ The two regimes of the k DE-parameter show appreciable quantitative deformation of the orbiting structures, with qualitatively significant changes of the background geometry defined by the spinning BH. Therefore, results point out possible observational evidences of distinctive DE effects on the accretion disks, which can be traces for the DE presence. Our analysis shows that the DE presence in the Kiselev model, for positive or negative DE parameter, relates to the energetics, therefore to the phenomenology, of BH accretion, but also to the BH evolution following accretion, affecting these aspects with respect to the Kerr predictions. In this context, therefore, DE manifests in both quantitative and qualitative divergences from the Kerr accretion systems, which could lead, in particular, to a false estimation of the BH spin. Remarkably, we found that the DE effects would distinguish, affecting differently, the disks rotation orientation with respect to the central spinning BH attractor. This fact could mean a substantial paradigm shift in the interpretation of the observational data seen up to now, with respect to the evaluation of the BH spin, mass and accretion rates.

The change of the geodesic structure, reflected in the accretion physics, could be interpreted as the DE mimicking an attractor with altered spin, also changing the range for the disk inner edge location, which is a known tracer of the BH spin-mass ratio.¹⁵

DE influence on the tori dimension and the marginally stable and bound orbits in these models can be searched in a variation of the central BH energetics, as cusp luminosity, and the accretion rates. (On the other hand, in this scenario, DE can affect also jets emission: The orbital range locating the proto-jets (the open cusped solutions constraining also the jet emission) cusps can be also very close to the central attractor.)

In some contexts in this analysis it was necessary to focus the investigation on the DE influence on HD pressure gradients in thick discs, and particularly the location of maximum and minimum pressure in the disk, also related to the maximum of accretion throat, a governing feature of the BH energetic characteristics related to accretion. From this analysis (see Figs. 10, 18, 20, significant distortions have emerged compared with the case of Kerr (Fig. 5), as the distinction between fluids with different rotation orientations. In some cases the disks are externally bounded (with respect to the central BH). In other cases accretion is prevented in the close proximity of the BH, with eventually the isolated central BH obscured to the distant observer by the orbiting mass, as an inert attractor by the DE effects.

Below is a brief summary of the steps taken in this analysis.

Overview

The literature on the Kiselev solution as DE mimicker and particularly for the case of $\alpha =-2/3$ considered in this analysis is extensive. To our knowledge our analysis is the first investigation of the effects of DE on orbiting tori in the Kiselev background. More in details in Sect. 3.1 we investigated the horizon structures and ergoregions for all values of Kiselev metric parameters k and $\alpha$. We then focused on the case of DE Universe, considering the case $\alpha =-2/3$ (some further considerations are also is in Appendix C for a different choice of the parameter $\alpha$).

The horizons structure and the ergoregions are detailed in this case for all values of the metric parameter k and spin a (including $a>M$), discussing the results in two alterative analysis – (Figs. 25, 26 – Table 5 and Eq. (A10)). The case of extreme Kiselev BHs was also discussed. This analysis constituted the basis for the investigation on the orbiting toroids in Sect. 3.2 where we investigated the equatorial circular geodesic structures for the fluid effective potential, the specific fluid angular momentum distribution, the tori structure and accretion disks energetics for co-rotating and counter-rotating tori for any spin a and constant k. The geodesic structure and the fluids specific angular momentum, $\ell (a,k;r)$, regulating the behavior (stability and morphology of the tori) has been given analytically for all values of (a, k).

Then, splitting constant k range in positive and negative values, to fix the ideas we proceeded with the numerical integration, selecting two exemplificative numerical values, deepening the case of DE parameter $k=-0.05$ in Sect. 3.2.1, and DE parameter $k=0.0025$ in Sect. 3.2.2.

Results for the DE spacetime are compared to the limiting Kerr spacetime occurring at $k=0$. The geodesic structure and the fluid specific angular momentum and tori effective potential were examined for all values of the spin $a\in [0,M]$. We then studied numerically some disks properties, as tori thickness, the extreme points of pressure in the disks, and tori energetics for selected spin and all values of tori parameters $(\ell ,K)$.

Comparing with the Kerr BH case for both the co-rotating and counter-rotating toroids, we discussed first spacetime geodesic equatorial structures for all $a\in [0,1]$. We then analyzed the fluid specific angular momentum $\ell ^\pm$, the tori parameter $K^\pm$ and the test particle (Keplerian) angular momentum $\mathcal {L}^\pm$ as functions of r, for $a\in [0,1]$ and the limiting fluids angular momentum with respect of the spacetimes geodesics structures. We traced the main properties of the orbiting toroids and proceeded with the analysis of the tori and their energetics also selecting some case for the numerical analysis. Following procedure outlined in Sect. 2.2, we explored the distribution of the pressure critical points in the toroids and the configurations geometrical thickness, including toroids in the BH ergoregions. We concluded the analysis by exploring the tori energetics.

Results of this analysis are detailed in 3.2.2 for negative and Sect. 3.2.1 for positive k. For convenience we sum-up some considerations discussed in these sections below.

• DE parameter $k\le 0$ Divergences with respect to the Kerr case appear in both the near-horizon and far-horizon regions, for each BHs spin – Fig. 8. Notably however, DE could manifest differently for co-rotation or and counter-rotation particularly for faster spinning BH attractors (see Fig. 9). Nevertheless at almost any spin, the specific angular momentum, is generally lower in magnitude then in the Kerr spacetime. A quantitative deviation from the Kerr spacetime emerges in the location of the photon orbit $r_{mco}^\pm$ and especially with respect to the marginally stable orbit $r_{mso}^\pm$. ($(r_{mso}^\pm , r_{mco}^\pm )$ are generally smaller then in the Kerr spacetims). This fact could cause an underestimation of the BH spin, from the analysis of the counter-rotating fluids, or an overestimation, from the co-rotating fluids analysis. Similar situation appears for the fluid momenta $(\ell _{mso}^\pm , \ell _{mco}^\pm )$, which are lower in magnitude with the respect to the Kerr case (having influence also in an eventual attractor spin shift following accretion).

  A remarkable deviation from the GR onset, represented by the Kerr BH spacetime, appears for slower spinning attractors in the absence of a marginally bounded orbit, and for faster spinning attractors in the existence of a doubled marginally bound orbit.

  To investigate further these aspects we focused on the fast spinning Kiselev BHs. Figure 10 showed that the situation for $r_{mso}$ is similar to the Kerr spacetime case in Fig. 4, and more generally we can conclude that the DE affects mostly the torus inner region and its morphology and for larger tori. (In fact in this case inner edge approaches the radius $r_{mbo}$.). The situation for the counter-rotating case is in Fig. 12 and appears qualitatively similar to the Kerr case. A detailed analysis is in Fig. 11 for the co-rotating case: tori structure is affected particularly by the existence of two marginally bound orbits. (The larger angular momentum is associated to configurations closer to the central attractor.). DE incidence in the tori energetics appears more predominant in the counter-rotating case, and differently for the $\phi$ quantities and $\chi$ quantities (see Fig. 13). In general, the presence of DE increases the ($\bar{\phi }$, $\bar{\chi }$) quantities, with respect to the Kerr case for the co-rotating fluids. Viceversa, for the counter-rotating fluids if a similar behaviour characterizes the $\bar{\phi }$ quantities, an opposite situation appears for the $\bar{\chi }$ quantities, which are decreased by the DE presence. (A different behaviour emerges with cusp moving away from the attractor and then the quantities variation with the magnitude of the fluid specific momentum is more evident for cusps close to the attractors.)

• DE parameter $k\ge 0$ In the case of positive DE parameter the situation for the horizons and ergoregion diverges significantly from the Kerr case – see Sect. (3.1 ). The presence of DE affects strongly the marginal stable orbits, distinguishing the fluids different rotation orientation with respect to the spinning BH. For example, in the spacetimes of very fast spinning BH attractors there is no counter-rotating marginal stable orbit – see Fig. 14.

  The main divergences from the GR universe, are for the larger radius $r_{mso}^\pm$, which are associated to larger values of the specific angular momentum $\ell _{mso}^\pm$ in magnitude – see also Fig. 16.

  Influence of the spin on the fluid specific angular momentum $\ell ^\pm$, the energy parameter $K^\pm$, and (test particles) Keplerian angular momentum $\mathcal {L}^\pm$ differs from the Kerr case in the way showed in Fig. 15.

  On the other hand, the quantitative divergences of $r_{mso}^\pm$ location with respect to the Kerr BH spacetime, could lead to an underestimation/overestimation of the BH spin, for particularly the attractors with large spin in the case of co-rotating/counter-rotating fluids. Focusing on radii $r_{mbo}^\pm$ this trend would be reversed (particularly for faster spinning attractors) originating a possible overestimation/underestimation of the BH spin from the analysis of the co-rotating/counter-rotating fluids.

  In general, the strongest DE effects appear for the marginally bound orbit values, independently by the rotation orientation. Considering the fluids specific angular momentum, DE appears to affect mostly the counter-rotating fluids and in the co-rotating case for the marginally bound orbit values and slow spinning attractors. In the case of $\ell _{mso}^\pm$, there may be an underestimation of the BH spin, particular for faster spinning spinning attractors and the counter-rotating fluids. From ($\ell ^\pm _{mbo}$, $\ell ^\pm _{mco}$), in the counter-rotating/co-rotating case DE may reveal in an overestimation/underestimation of the BH spin.

  Focusing on the fast spinning BHs we stressed the different roles of the two marginally stable circular orbits – see also Fig. 17. In general the larger specific angular momentum is similar to the Kerr case. In the counter-rotating case the configuration are bound from the outer regions remaining confined in a bound region of the BH spacetime. Values of the specific angular momenta $\ell _{mso}^+$ are very narrow, corresponding however to very different surfaces. The main differences with respect to the case of Kerr spacetime appear for the larger angular momentum $\ell =\ell _{mso}^-=3.734$ – Fig. 19. There is no accretion towards BHs.

  In co-rotating case the presence of DE clearly limits the outer regions for the tori formation, the location of their inner edges and the thick tori vertical structure. The curves of the pressure extremes in the disks are closed (a part for $\ell$ evaluated at the outer radius $r_{mso}^-$) and bend towards the central attractor. Co-rotating tori can orbit a bound region, limiting the location of the tori inner and the outer edges, from the inner and outer marginally stable orbit – Fig. 18

  Similarly in counter-rotating case shown in Fig. 20, the two close values for the angular momentum $\ell _{mso}^+$ correspond to different configurations. For different specific angular momentum the curves are open, and there is one only marginally circular orbit. The larger value in magnitude is associated to the open curve bending towards the attractor-see also Fig. 21.

  The lowest value of $|\ell _{mso}^+|$ is associated to a special morphology of the equidensity lines, while there are no closed configurations at $\ell _{mco}^+$.

  For the energetics of the counter-rotating tori we can say that the effect of the DE appears to the minimal for the $\bar{\phi }$ quantities (with values smaller than in the Kerr case), conversely DE presence appears to increase the $\bar{\chi }$ quantities. The conditions at infinity reflect the boundary conditions of the metric – Fig. 22.

  For the co-rotating case, the smallest momentum presents similarities with the case in absence of dark energy, but $\bar{\chi }$ quantities are smaller then in the Kerr case and the situation for the two momenta $\ell _{mso}^-$ is strongly distinct – Fig. 23 – also for cusps close to the central attractor, $\bar{\phi }$ quantities are greater in magnitude and closer to the marginally bound orbit case than in the GR case.

These findings therefore prove accretion to be a good indicator of the divergences induced by the DE presence with the accretion disks in DE spacetime as valid DE models discriminant. The differentiation by rotation orientation stands as a remarkable and intriguing key aspect. The underestimation (overestimation) of the BH spin, depends on positive or negative DE parameter as well as the tori rotation orientation with respect to the spinning BH. A comparative evaluation of tori morphology, and particularly the accretion throat and inner edge orbital range, the fluid angular specific momentum, and the tori energetics quantities, can lead to different and contrasting false esteems of the BH dimensionless spin. These puzzling aspects could be a distinctive general mark of the DE affecting BHs and we believe, requiring further investigation, should be considered more generally in the context where DE presence is considered.

Appendices

Appendix A: Kiselev spacetime characteristics

We can define the horizons, for a general solutions of $\Delta _K=0$, in terms of the spin-function:

$$\begin{aligned} a_{h}\equiv \sqrt{r \left( 2-r\right) +k r^{1-3 \alpha }}, \end{aligned}$$

(A1)

analogously to the Kerr case in Eq. (A3), or equivalently in terms of the k parameter as the functions $k_{h}(r;a)\equiv \Delta r^{3 \alpha -1}$ Similarly the ergosurfaces, from the solution of $g_{tt}=0$, in terms of the functions

$$\begin{aligned} a_\epsilon \equiv \frac{a_{h}}{\sqrt{1-\sigma }}, \end{aligned}$$

(A2)

analogously to the Kerr case¹⁶ in Eq. (4), or equivalently in terms of the k parameter¹⁷ as the function $k_\epsilon ^\pm \equiv r^{3 \alpha -1} \left( \Sigma -2 r\right)$, where, for $\sigma =1$ (the equatorial plane), there is $k_\epsilon ^\pm = (r-2) r^{3 \alpha }$. Note, the solutions $g_{tt}=0$, in the spherical symmetric case ($a=0$), determines (for some value of the DE parameter k) the horizons of the metric.

The ergosurfaces

Definition in Eq. (A2) can be express in terms of ergosurfaces radii, analogously to the Kerr case in Eq. (4), as the functions $r_\epsilon ^\pm \equiv \{\bar{\bar{r}}\}_{n}$, which are the n zeros of the quantity $\bar{\bar{r}}$

$$\begin{aligned} \bar{\bar{r}}:r^3 k-r^2+2 r+a^2 (\sigma -1)=0 \end{aligned}$$

(A5)

shown in Fig. 24. Conditions for the ergosurfaces existence are classified in Table 3, according to the spin a, for different ranges values of the DE parameter k and in Table 4, according to the DE parameter k. for different ranges of the spin a, introducing the following spin functions:

$$\begin{aligned} (a_\kappa ^\pm )^2\equiv \pm \frac{2 \left[ k \left( k \sqrt{-\frac{(6 k-1)^3}{k^4}}\pm 9\right) \mp 1\right] }{27 k^2}, \end{aligned}$$

(A6)

giving zeros of the polynomial $\hat{a}\equiv 27 k^2 a^4+4(1-9 k) a^2 +32 k-4$, shown in Fig. 24, and the function $k_E^\pm (a):a^2=(a_\kappa ^\pm )^2$, where

$$\begin{aligned} k_E^\mp \equiv \mp \frac{2 \left[ a^2 \left( a^2 \sqrt{-\frac{(3 a^2-4)^3}{a^8}}\mp 9\right) \pm 8\right] }{27 a^4}, \end{aligned}$$

(A7)

with the poloidal angle $\vartheta$ constrained by the functions $\sigma _E^\pm (a,k)\in [0,1]$, defined as

$$\begin{aligned} \sigma _E^\mp \equiv \frac{1}{27} \left[ 27\mp 2 \sqrt{-\frac{(6 k-1)^3}{a^4 k^4}}+\frac{2(1-9 k)}{a^2 k^2}\right] . \end{aligned}$$

(A8)

Fig. 24

Dark energy (DE) model. Kiselev spacetime with $\alpha =-2/3$. Left panel: Spin functions $a_\kappa ^\pm$ of Eq. (A6) as function of the DE parameter k. Limiting values are also shown as vertical or horizonthal lines-see also Tables 3 and 4. Center panel: the spin $\hat{a}_i$, i-zero of $\hat{a}$ in Eqs. (A6), as functions of the DE parameter, coincident with spin functions $a_\kappa ^\pm$. Right panel: ergosurfaces $r_\epsilon ^\pm$ as functions of k for different spins a and plane $\sigma \equiv \sin ^2\vartheta \in [0,1]$ as signed on the panel. All quantities are dimensionless

From the analysis in Tables 4 and  3, and from Fig. 24, the existence of limiting values of the DE parameter and the BH spin is evidenced. In particular, we shall consider separately in this analysis the case $k<0$ and $k>0$ (Fig. 25).

Fig. 25

Dark energy (DE) model. Kiselev spacetime with $\alpha =-2/3$. Horizons $r_\pm$ as function of the DE parameter k for different spins as signed on the panel (left panel) and spins a for different k as signed on the panel (right panel). There is $\sigma =\sin ^2\vartheta$, where the equatorial plane is for $\sigma =1$. The case $k=0$ corresponds to the Kerr spacetime. All quantities are dimensionless

The horizons The horizons, defined in Eqs (A1), can be expressed, for in the Kiselev spacetimes¹⁸ with $\alpha =-2/3$, analogously to the Kerr spacetime in Eq. (3) in terms of radii $r_\pm =\{r_{\kappa _1},r_{ \kappa _2},r_{\kappa _3}\}$, where explicitly:

$$\begin{aligned} r_{\kappa _1}\equiv & {} \frac{2 \nu \cos \left( \frac{\xi }{3}\right) +1}{3 k},\quad r_{\kappa _2}\equiv \frac{1-2 \nu \sin \left( \frac{2 \xi +\pi }{6} \right) }{3 k},\nonumber \\ r_{\kappa _3}\equiv & {} \frac{1-2\nu \cos \left( \frac{\xi +\pi }{3} \right) }{3 k}, \quad \text{ with }\nonumber \\ \xi\equiv & {} \cos ^{-1}\left[ \frac{\nu [9 k (3 a k\!-\!2)+2]}{2 (1-6 k)^2}\right] ,\quad \text{ and }\quad \nu \!\equiv \! k \sqrt{\frac{1-6 k}{k^2}}\nonumber \\ \end{aligned}$$

(A9)

zeros of the polynomial $\breve{r}\equiv k r^3-r^2+2 r-a^2$ – see Fig. 26. The horizons exist under the following conditions (see also Table 5)

$$\begin{aligned}{} & {} k<0: (a\!=\!0, r_{\kappa _1}), (a\in ]0,a_\kappa ^+[, \{r_{\kappa _1},r_{\kappa _3}\}), (a\!=\!a_\kappa ^+, r_{\kappa _3}),\nonumber \\{} & {} \left. k\in \right] 0,\frac{1}{8}\left[ : (a\!=\!0, \{r_{\kappa _1},r_{\kappa _3}\}), (a\in ]0,a_\kappa ^+[, \{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}),\right. (a\ge a_\kappa ^+, r_{\kappa _1}), \nonumber \\{} & {} k=\frac{1}{8}: (a=0, r=4), \left. \left( a\in \right] 0,\frac{32}{27}\left[ , \{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}\right) ,\right. \nonumber \\{} & {} \qquad \left( a=\frac{32}{27}, \left( r=\left\{ \frac{4}{3},\frac{16}{3}\right\} \right) \right) ,\left( a>\frac{32}{27}, r_{\kappa _1}\right) ,\nonumber \\{} & {} \left. k\in \right] \frac{1}{8},\frac{1}{6}\left[ : (a\in ]0,a_\kappa ^-], r_{\kappa _2}), (a\in ]a_\kappa ^-,\right. a_\kappa ^+[, \{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}), (a\ge a_\kappa ^+, r_{\kappa _1}),\nonumber \\{} & {} k\ge \frac{1}{6}: (a>0, r_{\kappa _3}). \end{aligned}$$

(A10)

In Table 5 conditions in Eq. (A10) are expressed alternatively for faster and slower spinning BH attractors, where it has been convenient to consider functions $a_\kappa ^\pm$ of Eq. (A6) as the i-zero, $\hat{a}_i$, of the polynomial $\hat{a}$, shown in Fig. 24, and radii $\{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}$ of Eq. (A9) as the n zeros, $\{\breve{r}\}_{n}$, of the polynomial $\breve{r}$ – see Fig. 26. Note, there is $\breve{r}=\left. \bar{\bar{r}}\right| _{\sigma =0}$, similarly to the case of Kerr geometry, where, for $k=0$, there is $\breve{r}=-\Delta$.

Fig. 26

Dark energy (DE) Kiselev model with parameter with $\alpha =-2/3$. Horizons radii as functions of the DE parameter k. All quantities are dimensionless. Right panel show functions $\{\breve{r}\}_{n}$, which are n zeros of quantity $\breve{r}$ of Eqs (A9), for different spins signed on the curves. Dashed vertical lines are limiting values of the k parameter – see also Table 5. Inside panel shows an enlarged view. Left panel shows horizons radii $\{r_{\kappa _1},r_{\kappa _2},r_{\kappa _3}\}$, coincident with radii $\{\breve{r}\}_{n}$, for different values of the spin a as signed on the panel

The extreme solutions

The DE Kiselev rotating BH spacetime has some extreme BH solutions, for special values of the spin a and the DE parameter k, corresponding, for $k=0$, to the extreme Kerr BH spacetime with $a=1$.

For a general (k, a), we evaluate the extremes of the spin function $a_{h}(r; a,k)$, as function of the radius r, having the two radii

$$\begin{aligned} r_{\max }^\pm (k)\equiv \frac{1\pm \sqrt{1-6 k}}{3 k} \end{aligned}$$

(A11)

showed in Fig. 27, left panel, where $k\le 1/6$ (and $k\ne 0$), with the limiting value $r_{\max }^\pm =2$ for $k=1/6$.

Fig. 27

Dark energy model. Kiselev spacetime with $\alpha =-2/3$. Horizontal lines are $r=1$ and $r=2$. All quantities are dimensionless. Left panel: Radii $r_{max}^\pm (k):\partial _r a_{h}=0$ in Eq. (A11), as function of the DE parameter k, where $a_{h}$ are the BH horizons spin functions Eqs (A1). The limiting case $k=1/6$, where $r_{max}^\pm =2$, is shown as a vertical orange curve. Center panel: radius $r_{\max }^\pm (a): a_{\max }^\pm =a$, of Eq. (A13) as function of the spin a, the limiting spin $a=2/\sqrt{3}$, where $r_{\max }^\pm =2$, is also signed. Right panel: horizons $r_\pm (a)$ as functions of the spin, for $k=0.0025$ (blue curve), $k=-0.05$ (cyan curve) and $k=0$ (black-dashed curve) correspondent to the Kerr spacetime. Gray curve is the radius $r_{\max }^-$

Then, there is

$$\begin{aligned} a_{\max }^\mp (k)\equiv a_{h}(r_{\max }^\mp )=a_\kappa ^\pm (k). \end{aligned}$$

(A12)

Using function $a_{\max }^\pm (k)$, and solving for $k: a_{\max }^\pm (k)=a$, we obtain the radii $r_{\max }^\pm (a): a_{\max }^\pm (k)=a$

$$\begin{aligned}{} & {} \left. \text{ with }:\quad a\in \right] 0,\frac{2}{\sqrt{3}}\left[ :\quad \right. \nonumber \\{} & {} \quad r_{\max }^\pm (a)\equiv \frac{6 a^2}{3 a^2\mp \sqrt{\left( 3 a^2-4\right) \left( 3 a^2\pm 4 \sqrt{4-3 a^2}-8\right) }} \end{aligned}$$

(A13)

shown in Fig. 27, center panel. Radius $r_{\max }^-(a)$ provides the horizons $r_\pm (a)$ of the extreme BH cases with respect to the spin parameter a – see Fig. 27-right panel. (Note, for $a=1$, there is $r_{\max }^+=3$, while $r_{\max }^-=1$.)

From condition (A13) it is clear that such radius exists for $a<2/\sqrt{3}$ and for $k<1/6$ (with the limiting condition $(k=0,a=0,r=2)$ – see Fig. 27, left panel and Eqs (A10).

The axis-symmetric and stationary DE models considered here describe BHs and NSs spacetimes and, focusing on the BHs DE solutions, we define similarly to the Kerr spacetime case the notion of co-rotating and counter-rotating motions as defined by the relations $\mathcal {L}a\gtrless 0$ and $\mathcal {\ell }a\gtrless 0$ (with $a>0$) respectively.¹⁹

Appendix B: Tori construction

The fluid effective potential is

$$\begin{aligned} V_{eff}^2={\frac{g_{t\varphi }^2-g_{\varphi \varphi } g_{tt}}{g_{\varphi \varphi }+2 g_{t\varphi } \ell +g_{tt} \ell ^2}}. \end{aligned}$$

(B1)

and the angular momentum function is

$$\begin{aligned}{} & {} \ell \equiv \frac{\Lambda _5\pm \sqrt{\Lambda _1^2 \Lambda _2}-\Lambda _3}{\Lambda _4}\quad \text{ where }\nonumber \\{} & {} \Lambda _1\equiv g_{t\varphi }^2-g_{\varphi \varphi } g_{tt}; \quad \Lambda _2\equiv g_{t\varphi }'^2-g_{\varphi \varphi }' g_{tt}';\nonumber \\{} & {} \Lambda _3\equiv g_{t\varphi } \left( g_{tt} g_{\varphi \varphi }'+g_{\varphi \varphi } g_{tt}'\right) ; \nonumber \\ {}{} & {} \Lambda _4\equiv g_{tt}^2 g_{\varphi \varphi }'-2 g_{t\varphi } g_{tt} g_{t\varphi }'+g_{t\varphi }^2 g_{tt}';\nonumber \\{} & {} \Lambda _5\equiv g_{\varphi \varphi } g_{tt} g_{t\varphi }'+g_{t\varphi }^2 g_{t\varphi }' \end{aligned}$$

(B2)

(for $\vartheta =\pi /2$, where $(')$ is for the derivative with respect to r). For the Kerr spacetime, Eq. (B2) is

$$\begin{aligned} \ell ^\mp (r)=\frac{a [r (4-3 r)-a^2]\pm \sqrt{r^3 \left( a^2+(r-2) r\right) ^2}}{(r-2)^2 r-a^2}. \end{aligned}$$

(B3)

1.1 Appendix B1: The geodesics structure and tori construction for $\varvec{\alpha }\mathbf {=-2/3}$

Let us start by first considering a spacetime with general (a, k) parameters, and then, by taking into account also the spacetimes properties outlined in Sect. 3.1, to fix our arguments, we will concentrate on some fixed values of the parameter k, studying co-rotating and counter-rotating tori for all values of tori parameters $(\ell ,K)$ and attractor spin $a>0$.

We introduce below the fluids specific angular momentum $\ell ^\pm (a,k;r)$:

$$\begin{aligned}{} & {} \ell ^\mp \equiv \frac{\nu _1\pm \sqrt{2} \sqrt{r^3 \left( 2-k r^2\right) \left( a^2+r \left[ r(1-k r)-2\right] \right) ^2}}{a^2 \left( k r^2-2\right) +2 r [r (k r-1)+2]^2}, \nonumber \\{} & {} \text{ where }\quad \nu _1\equiv a^3 \left( k r^2-2\right) +a r [r (k r [r (2 k r-1)+8]-6)+8]\nonumber \\ \end{aligned}$$

(B4)

for co-rotating and counter-rotating fluids respectively, coincident with the functions Eq. (B3) for the Kerr spacetimes at $k=0$.

More precisely, we focus on the radii constraining the orbiting configurations in accordance with the analysis of Sect. 2.2.1, therefore we do not study the geodesic structure as such, but define the radii governing the pressure gradients in the disk according to the effective potential and the distributions of constant angular momentum (It is also clear that these radii define the structures also in the limit of very thin rings of matter orbiting at the “disk” centers, with very small radial extension on the equatorial plane). However, for the sake of brevity, in the following we refer to these radii defined by the spacetime geodesic structure and we use the similar notation conventions adopted for the Kerr case.

Therefore, we identify the “marginally circular orbit”, $r_{mco}^\pm$, as the radius $r_{mco}^\pm \equiv r_\gamma ^\pm :K^\pm (r)=\infty$, the “marginally bound orbit” defined by $r_{mbo}^\pm :K^\pm (r)=1$ (asymptotically flat spacetimes) and the “marginally stable orbits” $r_{mso}^\pm : \partial _r\ell ^\pm =0$. We proceed by discussing first the spacetimes “geodesic” structure on the equatorial plane, then we analyze the quantities $(L,K,\ell )$ determining the fluids and particles dynamics (see also [114]). Analogously to the Kerr case discussed in Fig. 2, we analyze the fluid specific angular momentum $\ell ^\pm$ of Eq. (B4) on the geodesic orbits, constraining different topologies of the orbiting structures.

Appendix C: Kiselev spacetime with $\alpha =-1/3$

For $\alpha =-{1}/{3}$ the horizons are

$$\begin{aligned} r_\pm =\frac{1}{1-k}\pm \sqrt{\frac{a^2 (k-1)+1}{(k-1)^2}}, \end{aligned}$$

(C1)

and the ergosurfaces can be written as²⁰

$$\begin{aligned} r_\epsilon ^\pm =\pm \frac{\sqrt{a^2 (k-1)(1-\sigma )+1}\mp 1}{k-1}, \end{aligned}$$

(C2)

where, on the equatorial plane, there is

$$\begin{aligned} r_\epsilon ^\pm =r_{k_0}\equiv \frac{2}{1-k},\quad (\sigma =1), \end{aligned}$$

(C3)

see Fig. 28.

Fig. 28

Kiselev spacetime with $\alpha =-1/3$. Horizons $r_\pm$ and ergosurfaces $r_{\epsilon }^\pm$ of the Kiselev metric, for different parameter k and spins a. In left panel black surface is the Kerr case. Gray curves of the right panel show the relative quantities for the Kerr geometry $k=0$. There is $\sigma =\sin ^2\theta$, where the equatorial plane is for $\sigma =1$. All quantities are dimensionless

Fig. 29

Kiselev spacetime with $\alpha =-1/3$. Equatorial circular geodesic structure for different k and spins a. Gray curves are for the Kerr geometry ($k=0$). Radii $r_\pm$ (dotted-dashed curves) is the horizons, $r_{\epsilon }^+$ is the outer ergoregion on the equatorial plane, $r_{mso}^\pm$ is for marginally stable orbit, $r_{mco}^\pm$ is for marginally circular orbit, $r_{mbo}^\pm$ is the solution of $V_{eff}=1$ (solution $V_{eff}=\sqrt{1-k}$ is also shown in long-dashed curves). $\ell ^\pm$ is the fluid specific angular momentum. ± is for counter-rotating and co-rotating fluids respectively. All quantities are dimensionless

Then the horizons of the static geometry, $a=0$, exist for

$$\begin{aligned} a= & {} 0:\quad \left( k\in [0,1[, r\in \{0, r_{k_0}\}\right) ,\quad \left( k\ge 1,r=0\right) ,\nonumber \\{} & {} \left( k<0,r=\{0, r_{k_0}\}\right) \end{aligned}$$

(C4)

• Fig. 28. For $a>1$ the horizons are for

  $$\begin{aligned}{} & {} k\in [0,1[: (a\in [1,a_k[,r=r_\pm ),\quad (a=a_k,r=r_-);\nonumber \\{} & {} k=1: (a\ge 1,r= r_{\circledast });\nonumber \\{} & {} k>1: (a\ge 1,r=r_+), \end{aligned}$$

  (C5)

where $r_{\circledast }\equiv a^2/2$, and the spin function $a_k$ is

$$\begin{aligned} a_k\equiv \sqrt{\frac{1}{1-k}}. \end{aligned}$$

(C6)

For $a\in ]0,1]$ the horizons are for

$$\begin{aligned}{} & {} k\le 0:(a\in [0,a_k[,r=r_\pm ),\quad (a=a_k,r=r_-);\\{} & {} k\in ]0,1[:(a\in [0,1],r=r_\pm ); \\{} & {} k=1: (a\in [0,1],r= r_{\circledast }); \quad k>1:(a\in [0,1],r=r_+). \end{aligned}$$

The BH metric horizon is generally located of a larger radius to the Kerr metric horizon in the $a-r$ plane, although for some values of k this condition changes – Fig. 28. We consider $k=\pm 0.81$. The geodesic structure regulating the fluid dynamics is plotted in Fig. 29. The Kiselev metric, seen as deformation of the Kerr spacetime, regulated by the $(\alpha ,k)$ parameters, appears to affect quantitatively the orbiting tori structure. with respect to the reference Kerr metric, allowing accretion tori located considerably far from the central attractor, with the shift of the location of the BH horizons and the geodesic structure radii outwardly.