1 Introduction

The theory of general relativity (GR) has been proven to be one of the most spellbinding achievements of the last century. This theory has explained enormous difficult issues at the solar system scale as well as cosmological scales with great observational support. It has portrayed various enchanting discoveries incorporating gravity and also manifested different challenging revolutions to various astrophysical phenomena in the arena of modern cosmology. Currently, black holes (BHs) are recognized as the most fascinating astronomical objects possessing the captivating attributes of strong gravitational fields. The intense gravitational field of the BH prevents anything from escaping, while anything interacting in its environment is absorbed. Relating the physical properties of BH geometries, there have always been remarkable effects of quantum fluctuations. In the structural properties of BH, the occurrence of singularity is one of the fundamental issues. The singularity is a central era of spacetime where the curvature as well as the density diverges and the physical laws become abolished.

Moreover, despite these remarkable findings, there is still no proof supporting the existence of quantum gravity or quantum particle interaction in the occurrence of an intense gravitational field of astronomical objects. The BH evaporation via Hawking radiation is one of the key hypotheses of the quantum field theory in the curved framework [1]. By astronomical criteria, this impact is very weak because the Hawking temperature of BHs is significantly lower than the Cosmic Microwave Background at about \(10^{-7}\) K. Furthermore, the theory of BH states that it requires around \(10^{67}\) years to completely vanish through the Hawking radiation. Later, Unruh [2] presented a comparison between a light wave passing through a BH’s event horizon and a sound wave crossing a supersonic fluid to elaborate the effects of quantum gravity around the BHs. This acoustic analog is characterized as an acoustic BH sonic hole or dumb hole.

In the field of astrophysics, the acoustic BH manifests the notion acquired from the field of acoustics that exhibits the alternative to BHs. Acoustic BHs can be compared to light waves passing through a BH’s event horizon and sound waves traveling through the supersonic fluid. Analogous to the astrophysical BH illustration, the event horizon is the border of an acoustic BH where the flow speed alters from being more than the speed of sound to less than the speed of sound. Even though acoustic BHs are not the solutions of the Einstein field equations, they still retain all the characteristics of the general relativistic BHs. For this reason, the acoustic BH is a priceless instrument for lab research on gravitational phenomena. One can learn important details about the fundamentals of wave propagation, scattering, and dispersion around astronomical objects by examining how sound waves propagate in these systems. In turn, this can help us to comprehend wave physics more accurately providing new theoretical foundations for a variety of wave phenomena across disciplines and even allowing us to test some relativistic effects. Because of this, researchers have been more interested in acoustic BHs and have looked into novel similar solutions as well as a variety of phenomena concerning these objects [3,4,5,6,7,8,9]. Inspired by the Navier–Stokes equation in classical Newtonian fluids, an acoustic BH with a spiral vortex shape is developed in [10]. An alternative to acoustic BHs that use the Josephson effect theory is laid out in [11]. The study of thermodynamical properties of d-dimensional acoustic BH is presented in [12]. Further, the holographic description of usual acoustic BHs is explained in [13] and the appearance of analogous Minkowski spacetime and acoustic BHs in curved spacetime is studied in [14]. The orbits of test vertices and sound wave of (2+1)-dimensional acoustic BHs are explained in [15]. As a unique feature of the retarded Green’s function of BH disturbances, the pole-skipping phenomena may have experimental relevance when applied to acoustic BHs [16]. By taking into account the relativistic Gross–Pitaevskii theory in the fixed background spacetime geometry, Ge et al. [17] developed the Schwarzschild acoustic BH solution. Vieira and Kokkotas [18] discussed the massless scalar field corresponding to the Schwarzschild acoustic BH and analyzed its salient characteristics. Toshmatov et al. [19] inspected the influences of electromagnetic as well as the massive scalar oscillations for Schwarzschild acoustic BH and calculated their quasinormal modes.

The occurrence of timelike thin-shell within static spherical configurations represents a remarkable cosmological structure that helps to examine many cosmic conjectures. An extremely slender layer of matter that functions as a connector between two areas of spacetime is known as a thin-shell. As thin-shell includes a specific fluid configuration, it must meet specified energy bounds that confirm the viability of the corresponding geometry. These bounds can be linked with the extrinsic curvature of considered geometry via matter-energy tensor. General relativity makes use of the cut-and-paste procedure, often called the Israel junction conditions, to seamlessly link different spacetimes at the boundary [20]. The study of matter and energy behavior at the interface between two separate areas of spacetime is an area where this technique shines. Research into the dynamics of complicated geometries, including wormholes (WHs) and BHs, within the framework of analog gravity, can be efficiently accomplished through the use of the cut and paste approach [21, 22]. The layer that connects the Schwarzschild and Minkowski metrics as external and internal configurations, respectively, is the most basic example of a thin-shell structure. Through the connecting of two distinct manifolds at thin-shell intersections, Israel’s groundbreaking work established a valuable framework for the hypothetical building of time-like thin-shells [20]. A thin-shell can shed light on the physics of spacetime and the cosmos as a whole by allowing travel and communication over enormous distances in space [21]. Their importance stems from the fact that they can link different parts of spacetime, which might lead to discoveries in cosmology and astrophysics as well as a better knowledge of the complexities of cosmic phenomena. Various applications have been explored, including BHs matter accretion, spherical WHs, bubble universes, and cosmic domain walls [21, 22]. Supernova explosions and gravitational collapse are only two of the astrophysical events that have been studied using these cosmological structure models [23,24,25]. After that, several researchers [26,27,28,29] modified this study for the dynamical portrayal of bubbles within BH, spinning BH as well as the strings by incorporating the Israel formalism. It is of huge importance to inspect the stability of such thin-shell structures both thermodynamically and dynamically.

The idea of hypothetical structures comprising topological geometries, known as WHs, is illustrated through the study of various cosmic conjectures. A WH facilitates travel to distant places by creating a minor bridge across any two points in the cosmos. This theoretical property was first described as a non-traversable WH by Flamm [30]. Morris and Thorne [31] developed the structure of a traversable WH that joins distant eras with the help of a throat. This substance keeps the throat open but defies the null energy bound that should be minimized for the physical occurrence of WHs. To obtain physically consistent solutions of the WHs, the quantity of exotic substances must be limited at the throat. This quantity is minimized by Visser [32] with the help of a feasible WH structure producing a thin-shell WH. There exists a huge literature to explore the various structural attributes of WHs obtained through BH metrics [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52].

Several investigations include the behavior of thin-shell and WHs with thin-shell using radial oscillations by considering the various possibilities of the matter ingredients. The stability analysis of a thin-shell joining an internal flat metric to the Schwarzschild BH is examined by Brady et al. [53]. Martinez [54] discussed the stability of such objects on thermodynamical grounds. By taking into account the variable equation of state (EoS), the stability of thin-shell is observed by Mazharimousavi et al. [55]. The thermodynamical as well as linear stable structure of thin-shell geometries has also been examined by employing barotropic/non-barotropic EoSs [56]. To check the stability of WHs via radial oscillations, Eiroa and Simeone [57] adopted distinct BHs solutions and found the enhancement in the stable eras for some particular ranges of physical factors. Halilsoy et al. [58] presented the behavior of Chaplygin gas, linear as well as logarithmic configurations as candidates of exotic matter by considering spherical systems. The stable thin-shell WH geometry under the influence of barotropic and non-barotropic fluids has also been determined by Varela [59]. Jusufi and Ovgun [60] obtained the stable geometry of the canonical acoustic thin-shell WHs corresponding to the different physical parameters. In the realm of neo-Newtonian context, Ovgun and Salako [61] examined the acoustic thin-shell WH and inspected its stable structure by changing neo-Newtonian factors. Ovgun and Jusufi [62] displayed some fascinating results in examining the stability of thin-shell WHs associated with the string theory. The geometry of thin-shell WHs having stable solutions that are obtained from various spherical BHs using variable EoS have also been determined in literature [63,64,65,66,67].

Mazur and Mottola [68] proposed a novel description of the compact celestial body, known as gravastars, by modifying the Bose-Einstein concept to the gravitational structures isolated by a thin surface in which matter is restricted. Such geometries have crucial significance as they can interpret two basic issues for BHs, i.e., the information loss paradox and the singularity issue. In BH geometries, gravastars forbid the core singularity and event horizon from existing. Geometrical constructions like these are produced within the framework of diverse BH spacetimes, and their stability can be analyzed through the use of different EoS [69,70,71,72,73,74,75]. The various aspects of prototype gravastar structures by incorporating the de-Sitter and Schwarzschild BH metric [76, 77] and with phantom energy [78] have been discussed that provide various interesting facts. Corresponding to various fluid choices at thin-shell, it is found that the created structure can be either unstable, stable, or bounded excursion gravastar [79]. The gravastar structures associated with the noncommutative impact [80, 81], higher-dimensional metric [82], Kuchowicz type of metric function [83], charged and quintessence regular BHs using distinct EoS [84,85,86,87] have been studied presenting the outcomes of stable structures.

Recently, Javed [88] obtained the geometry of a thin-shell by using the flat interior and renormalization group improved Schwarzschild BH as an outer geometry. He discussed the dynamics of thin-shell filled with a massive as well as massless scalar field using the dynamical equation and Klein–Gordon (KG) equation. He also determined the stable structure of thin-shell via linearized radial perturbation for a phantomlike EoS, i.e., the dark energy, quintessence, and phantom energy. Following the above-mentioned articles, in this manuscript, our main goal is to explore the thin-shell configuration with external flat and internal acoustic Schwarzschild BH. We also analyze the dynamics as well as the stability of the obtained structures. The paper is organized as follows. Section 2 deals with the fundamentals thin-shell for Schwarzschild acoustic BH. In Sect. 3, we discuss the dynamics of thin-shell with massless and massive scalar fields. Section 4 is devoted to analyzing the stable/unstable solutions by employing distinct possibilities of matter contents. Finally, the concluding section provides a summary of our results.

2 Thin-Shell in Schwarzschild acoustic black hole

This section concentrates on the construction of a \((2+1)\)-dimensional thin-shell (a boundary separating the interior spacetime from the exterior) specified by \(\Sigma \) with a radius of \(r=y(\tau )\) with \(\tau \) being the proper time. As the thin-shell joins the separate manifolds, we designate the outer domain (\(r>y\)) as the acoustic Schwarzschild metric, and the inner domain (\(r<y\)) is characterized as a flat geometric configuration. The metric for the interior geometry is specified as follows

$$\begin{aligned} ds^2_{-}=-\mathcal {H}(r)dt^2+\frac{dr^2}{\mathcal {H}(r)} +r^2d\Omega ^2, \end{aligned}$$
(1)

with \(\mathcal {H}(r)=1\) and \(d\Omega ^2=d\theta ^2+\sin ^2\theta d\phi ^2\). For an outer manifold, the line element for an acoustic Schwarzschild BH can be expressed as

$$\begin{aligned} ds^2_{+}=-\mathcal {A}(r)dt^2+\frac{dr^2}{\mathcal {A}(r)} +r^2d\Omega ^2, \end{aligned}$$
(2)

where the metric function \(\mathcal {A}(r)\) is given as

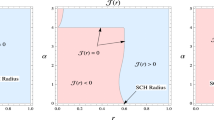
$$\begin{aligned} \mathcal {A}(r)=\left\{ 1-\gamma \frac{2 m}{r} \left( 1-\frac{2 m}{r}\right) \right\} \left( 1-\frac{2 m}{r}\right) . \end{aligned}$$
(3)

Here, m symbolizes the Schwarzschild BH mass while \(\gamma \) denotes the real constant. The metric function \(\mathcal {A}(r)\) reduces to the Schwarzschild solution in GR for \(\gamma \)=0. Notice that the place where the event horizon is located and the position where the metric function reaches zero value coincide. By adopting \(\mathcal {A}(r)=0\), the relevant event horizon of the acoustic Schwarzschild BH is determined as

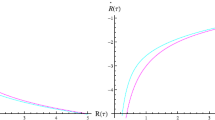
$$\begin{aligned} r=2m,\quad \quad r=\gamma m\pm \sqrt{\gamma ^2 m^2-4 \gamma m^2}. \end{aligned}$$
(4)

When \(\gamma \ge 4\wedge m>0\), we obtain the constraints about the event horizon as \(r>0\). We compare the event horizons of Schwarzschild and acoustic Schwarzschild BHs for different values of the mass of BH as shown in Fig. 1. We investigate how the metric function (\(\mathcal {A}(r)\)) behaves for specific values of physical parameters in Fig. 1. The light blue region indicates \(\mathcal {A}(r)>0\) and the pink region demonstrates that \(\mathcal {A}(r)<0\). The boundary between these regions is represented by a straight line (\(r=2m\)), i.e., \(\mathcal {A}(r)=0\). It is noteworthy to emphasize that the location of the event horizon is established as \(\gamma \ge 4\). For massive BH, the position of the event horizon moves away from the center of BH. The location of an acoustic Schwarzschild BH’s event horizon must be larger than that of a Schwarzschild BH. The event horizon of Schwarzschild BH is significantly influenced by the physical parameters.

Fig. 1
figure 1

The graphical representation of the metric function of acoustic Schwarzschild BH by considering \( m=0.1\) (1st), \(m=0.25\) (2nd) and \(m=0.5\) (3rd) against r and \(\gamma \)

Full size image

Visser [32] proposed a popular method for creating thin-shell gravastars by combining two spacetimes to remove the event horizon and singularity. We define a subset (\(\Upsilon ^\pm \)) of the inner and outer manifolds \((\Pi ^\pm )\) by using a cut and paste technique to ensure they do not include any event horizon or singularity, i.e., \(\Upsilon ^\pm \subset \Pi ^\pm \). Here, \(\Upsilon ^\pm \) is defined as the set of points \(x^\nu \) where \(r_\pm \ge y(\tau ) > r_h\), with \(x^\nu \), \(\tau \), and \(y(\tau )\) denoting coordinates on the manifold, proper time on the shell, and shell radius, respectively. The subsets \(\Upsilon ^\pm \) are connected at their shared timelike hypersurface \(\partial \Upsilon \), meaning that \(\partial \Upsilon \) is a subset of both \(\Upsilon ^\pm \). The matching of \(\Upsilon ^+\) and \(\Upsilon ^-\) at the shell radius establishes a link between the inner and exterior spacetimes (\(\partial \Upsilon \equiv \Upsilon ^+\cup \Upsilon ^- \)) by the radial flare-out condition. The manifold (\(\partial \Upsilon \)) represents a geodesically complete thin-shell. A timelike 2-sphere characterized by coordinates \(z^i=(\tau ,\theta ,\phi )\) represents the geometry of a thin-shell, with the line element given as

$$\begin{aligned} ds^2=h_{ij}dz^{i}dz^j=-d\tau ^2+y^2d\Omega ^2, \end{aligned}$$
(5)

Also, the components of unit normals at \(\Upsilon _{\pm }\) is computed as

$$\begin{aligned} n_{\pm }^{\mu }=\left( \frac{\dot{y}}{\Phi _\pm (y)},\sqrt{\Phi _\pm (y) +\dot{y}^2},0,0\right) , \end{aligned}$$
(6)

where \(\dot{y}=dy/d\tau \) and \(\Phi _\pm \) denotes the lapse function of inner as well as outer manifolds. The components of extrinsic curvature are defined as

$$\begin{aligned}{} & {} K_{ij}^{\pm }=-n_{\mu }^{\pm }\left( \Gamma ^\mu _{\alpha \beta }\frac{ dx^{\alpha }_{\pm }}{dz^{i}}\frac{ dx^{\beta }_{\pm }}{ dz^{j}}+\frac{d^2x_{\pm }^\mu }{dz^i dz^j}\right) ,\nonumber \\{} & {} \alpha ,\beta =0,1,2,3,\quad i,j=0,2,3. \end{aligned}$$
(7)

By using Eqs. (5), (6) in Eq. (7), we have

$$\begin{aligned} K_{\tau }^{\tau \pm }= & {} \frac{\Phi '_\pm (y)+2\ddot{y}}{\sqrt{\Phi _\pm (y)+\dot{y}^2}}, \quad K_{\theta }^{\theta \pm }= \frac{\sqrt{ \Phi _\pm (y)+\dot{y}^2}}{y},\nonumber \\ K^{\phi \pm }_{\phi }= & {} \sin ^2\theta K_{\theta }^{\theta \pm }, \end{aligned}$$
(8)

where \(\Phi '_\pm (y)=\frac{d\Phi _\pm (y)}{dy}\). The discontinuity in extrinsic curvature at a hypersurface is due to the matter present on its surface, which can be studied using the Israel formalism. If the difference between the extrinsic curvatures on each side of the surface is not zero, i.e. \((K_{ij}^{+}-K_{ij}^{-}\ne 0)\), it can be mathematically observed. The characteristics of matter surfaces on thin-shells are defined by the Lanczos equations, which serve as the field equations for the hypersurface as

$$\begin{aligned} S^{i}_{j}=-\frac{1}{8\pi }\{[K^{i}_{j}]-\delta ^{i}_{j}K\}, \end{aligned}$$
(9)

where \(S^{i}_{j}\) is used to explain the characteristics of matter contents located at the shell \(\partial \Upsilon \), \([K^{i}_{j}]=K^{+i}_{j}-K^{-i}_{j}\) and \(K=tr[K_{ij}]=[K^{i}_{j}]\). We get the following form of \(S^{i}_{j}\) for ideal fluid distribution

$$\begin{aligned} S^{i}_{j}=\left( \rho +\mathfrak {P}\right) u^i u_j+\mathfrak {P}\delta ^{i}_{j}, \end{aligned}$$
(10)

here shell’s velocity is denoted with \(u_i\), the energy density is explained by using term \(\rho \) and \(\mathfrak {P}\) is used for the pressure. From Eqs. (8), (9) and (10), we get

$$\begin{aligned} S^{\tau }_{\tau }\equiv & {} \rho (y)=-\frac{[K^\theta _\theta ]}{4\pi }=-\frac{1}{4\pi y}\{\chi _e(y)-\chi _i(y)\},\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} S^{\theta }_{\theta }=S^{\phi }_{\phi }\equiv & {} \mathfrak {P}(y)=\frac{[K^\theta _\theta ]+[K_{\tau }^{\tau }]}{8\pi } =\frac{-\chi _i(y)+\chi _e(y)}{8\pi y}\nonumber \\{} & {} +\frac{2\ddot{y}+\mathcal {A}'(y)}{16\pi \chi _e(y)}- \frac{2\ddot{y}+\mathcal {H}'(y)}{16\pi \chi _i(y)}, \end{aligned}$$
(12)

where

$$\begin{aligned} \chi _i(y)=\sqrt{\mathcal {H}(y)+\dot{y}^2}, \quad \chi _e(y)=\sqrt{\mathcal {A}(y)+\dot{y}^2}, \end{aligned}$$
(13)

the derivatives concerning the proper time and radial coordinate are denoted by the overdot and dash, respectively. Therefore, we have

$$\begin{aligned} \rho= & {} -\frac{\sqrt{\mathcal {A}(y)+\dot{y}^2}-\sqrt{\mathcal {H}(y)+\dot{y}^2}}{4 \pi y}, \end{aligned}$$
(14)
$$\begin{aligned} \mathfrak {P}= & {} \frac{1}{8 \pi }\left( \frac{2 \ddot{y}+\mathcal {A}'(y)}{2 \sqrt{\dot{y}^2+\mathcal {A}(y)}}-\frac{2 \ddot{y}+\mathcal {H}'(y)}{2 \sqrt{\dot{y}^2+\mathcal {H}(y)}}\right. \nonumber \\{} & {} \left. +\frac{\sqrt{\dot{y}^2+\mathcal {A}(y)}- \sqrt{\dot{y}^2+\mathcal {H}(y)}}{y}\right) , \end{aligned}$$
(15)

In a state of equilibrium, \(\dot{y}_{0}=\ddot{y}_{0}=0\) (where zero in the sub-index indicates values of the physical quantities at the state of equilibrium of the shell, i.e., \(y=y_0\)) and the corresponding values of surface stresses turn out to be

$$\begin{aligned} \rho _0= & {} \frac{1}{4 \pi y_0}-\frac{\sqrt{\left( 1-\frac{2 m}{y_0}\right) \left( 1-\frac{\gamma (2 m) \left( 1-\frac{2 m}{y_0}\right) }{y_0}\right) }}{4 \pi y_0}, \end{aligned}$$
(16)
$$\begin{aligned} \mathfrak {P}_0= & {} \frac{m \left( 12 \gamma m^2+y_0 (-8 \gamma m+\gamma y_0+y_0)\right) }{8 \pi y_0^4 \sqrt{\frac{(y_0-2 m) \left( y_0^2-2 \gamma m (y_0-2 m)\right) }{y_0^3}}}\nonumber \\{} & {} +\frac{\sqrt{\frac{(y_0-2 m) \left( y_0^2-2 \gamma m (y_0-2 m)\right) }{y_0^3}}-1}{8 \pi y_0}, \end{aligned}$$
(17)

For Minkowski spacetime, within the shell, there is an absence of gravity because the matter does not exist in the internal domain. Likewise, the external segment is considered a vacuum, yet the gravity effects persist as specified by the BH. The factor m present in the metric function (3) is correlated with the shell’s gravitational mass which governs the kinetic energy, gravitational potential energy along with the rest-mass energy. The mass of a shell can be defined as \(M=4\pi k^2\rho \). Additionally, it is obtained that matter density and surface pressure adhere to the conservation equation as

$$\begin{aligned} \mathfrak {P}\frac{d}{d\tau }(y^{2})+\frac{d}{d\tau }(\rho y^{2})=0, \end{aligned}$$
(18)

yielding

$$\begin{aligned} \rho '=-\frac{2}{y}\left( \mathfrak {P}(\rho ,y)+\rho \right) . \end{aligned}$$
(19)

Equations of motion are crucial for evaluating the dynamics of particles and fields in analog gravity geometries since they define how physical systems evolve. Researchers can explore the impact of gravity analogs on the behavior of matter and energy by examining the equations of motion for various fields and particles in curved spacetime backdrops. This research can offer useful insights into the emergence of gravitational events in systems that simulate features of general relativity [89,90,91]. An equation of motion is explicitly obtained from the surface energy density given in Eq. (14) as

$$\begin{aligned} \dot{y}^2+ \Omega (y,\rho (y))=0. \end{aligned}$$
(20)

Here, \(\Omega (y,\rho (y))\) stands for the effective potential of the thin-shell expressed as

$$\begin{aligned}{} & {} \Omega (y,\rho (y))\nonumber \\ {}{} & {} \quad =1-\frac{m^2}{16 \pi ^2 y^4 \rho ^2}\nonumber \\ {}{} & {} \qquad -\frac{\gamma m^2 (y-2 m)^2 \left\{ 4 \gamma m^2-4 \gamma m y+(\gamma +2) y^2\right\} }{16 \pi ^2 y^8 \rho ^2}\nonumber \\{} & {} \qquad -\frac{\gamma m (y-2 m)^2}{y^3}-\frac{m}{y}-4 \pi ^2 y^2 \rho ^2. \end{aligned}$$
(21)

The potential function is very useful to explain the dynamical behavior of the shell composed of different types of matter contents. It is very advantageous to examine the dynamical configuration of the shell. In the next section, we examine the dynamical properties of constructed thin-shell.

3 Scalar field and dynamics of thin-shell

At thin-shell, the presence of matter has a significant impact on both the stability and dynamics of the configuration. At this point, we are curious to see how the scalar field affects the thin-shell dynamical evolution. Scalar particles’ behavior can be described by the KG equation, a basic equation of quantum field theory. The KG equation is frequently employed to investigate the propagation of scalar fields in curved spacetime backdrops within the framework of analog gravity geometries [92,93,94,95,96,97,98]. The behavior of quantum fields in gravitational analogs, including Hawking radiation and BH thermodynamics, can be better understood by solving the KG equation in different analog gravity configurations [99,100,101]. To this end, we employ the transformation, i.e., \(u_{a}=\frac{\Upsilon _{,a}}{\sqrt{\Upsilon _{,b}\Upsilon ^{,b}}}\), where \(\Upsilon \) describes the scalar field [96,97,98]. This transformation links the surface pressure and energy density of the ideal fluid to the derivative of the scalar field and the potential function of the scalar field (\(\Pi (\Upsilon )\)). In a scalar field, the surface pressure and energy density are defined to have the following relationships [96,97,98]

$$\begin{aligned} \mathfrak {P}=\frac{1}{2}\left[ \Upsilon _{,b}\Upsilon ^{,b}-2\Pi (\Upsilon )\right] ,\quad \rho =\frac{1}{2}\left[ \Upsilon _{,b}\Upsilon ^{,b}+2\Pi (\Upsilon )\right] . \end{aligned}$$
(22)

For such type of scalar field, the stress-energy tensor provides [96,97,98]

$$\begin{aligned} S_{ij}=\nabla _{i}\Upsilon \nabla _{j}\Upsilon -\eta _{ij}\left[ \frac{1}{2}(\nabla \Upsilon )^2-\Pi (\Upsilon )\right] . \end{aligned}$$

The scalar field solely depends on \(\tau \) since the hypersurface is a function of \(\tau \) only. Therefore

$$\begin{aligned} \mathfrak {P}=\frac{1}{2}\left[ \dot{\Upsilon }^2-2\Pi (\Upsilon )\right] , \quad \rho =\frac{1}{2}\left[ \dot{\Upsilon }^2+2\Pi (\Upsilon )\right] . \end{aligned}$$
(23)

In the present case, the first and second components of the aforementioned equation reflect the kinetic and potential energies of the scalar field, respectively. The mass of the thin-shell is determined through the scalar field expression as follows

$$\begin{aligned} \mathcal {M}=4\pi y^{2} \rho = 2\pi y^{2}(\dot{\Upsilon }^2+2\Pi (\Upsilon )). \end{aligned}$$
(24)

By substituting Eqs. (23) and (24) into (19), we obtain

$$\begin{aligned} \ddot{\Upsilon }+2\frac{\dot{y}\dot{\Upsilon }}{y}+\frac{\partial }{\partial \Upsilon }\Pi (\Upsilon )=0, \end{aligned}$$
(25)

which is dubbed as the KG equation. In the vicinity of considered acoustic Schwarzschild BH having a scalar field, the corresponding potential function of the constructed thin-shell is provided as

$$\begin{aligned}{} & {} \Omega (y) {=}{-}\frac{m^2 y^4{+}\gamma m^2 (y-2 m)^2 \left( \gamma (y-2 m)^2+2y^2\right) {+}4 \pi ^4 y^{10} \left( 2 \Pi (\Upsilon ){+}\dot{\Upsilon } ^2\right) ^4}{4 \pi ^2 y^8 \left( 2 \Pi (\Upsilon ){+}\dot{\Upsilon } ^2\right) ^2}{-}\frac{m \left( \gamma (y-2 m)^2+y^2\right) }{y^3}+1. \end{aligned}$$
(26)

The specific matter contents of the scalar field are not explicitly defined by the EoS. The fact that the energy density of the scalar field is divided into potential and kinetic energies, makes it impractical to precisely manifest the energy density with a single value of p. To establish a relation amongst the stress-energy tensor’s components, we use a specialized form of the potential function expressed in terms of some parameter which may aid in determining the effective mass and interaction strength of the scalar field. Subsequently, we explore two disparate values of the potential function described as

  • \(\Pi (\Upsilon )=0\), i.e., the massless scalar field

  • \(\Pi (\Upsilon )=m^2\Upsilon ^2\), i.e., the massive scalar field:

The conservation equation and the KG equation govern the dynamical structure of a thin-shell composed of massive and massless scalar fields. Considering their masses and interactions, the KG equation explains how the scalar fields on the thin-shell evolve. Constraints on the thin-shell dynamics are provided by the conservation equation, which provides that momentum and energy are conserved throughout the system. The propagation and interaction of the scalar fields inside the thin-shell, which effects its stability and behaviour as a whole, is defined by the KG equation. In the KG equation, the mass term dictates how the massive scalar field behaves, whereas the massless scalar field adds to the system’s entire energy distribution. For the thin-shell to remain stable and coherent as a whole, the conservation equation is of paramount importance. It prevents the system from behaving in an unphysical or unstable way by limiting its evolution and configuration options through the application of momentum and energy conservation laws. The general dynamics and evolution of the thin-shell can be better understood with the help of this equation, which directs future research and interpretation. To sum up, when studying the dynamical structure of a thin-shell with massive and massless scalar fields, the KG equation and the conservation equation are crucial components. By outlining the interplay and development of the system’s scalar fields, they clarify the system’s general behaviour and stability. In the following subsections, we briefly discuss the dynamical structure for both cases of scalar field.

Fig. 2
figure 2

The graphical representation of the dynamical evolution of shell through effective potential corresponding to the massless scalar field using \(\gamma =4\) (left graph) and \(\xi =0.1\) (right graph) against y for \(m =0.2\)

Full size image

3.1 Thin-shell with massless scalar field

In this case, i.e., by considering \(\Pi (\Upsilon )=0\) in Eq. (23), the energy-momentum tensor components are connected by the EoS \(\mathfrak {P}=\rho \). The corresponding KG equation can be expressed as

$$\begin{aligned} y\ddot{\Upsilon }+2\dot{y}\dot{\Upsilon }=0, \end{aligned}$$
(27)

which yields

$$\begin{aligned} \xi =y^2\dot{\Upsilon }, \end{aligned}$$
(28)

where \(\xi \) specifies the integrating constant. By setting \(\Pi (\Upsilon )=0\) and incorporating Eq. (28) in (26), we derive the dynamical equations governing thin-shell’s structure in the realm of a massless scalar field as

$$\begin{aligned} \dot{y}=\pm \sqrt{\frac{m^2 y^4}{4 \pi ^2 \xi ^4}+\frac{\gamma m^2 (y-2 m)^2 \left( 4 \gamma m^2-4 \gamma m y+(\gamma +2) y^2\right) }{4 \pi ^2 \xi ^4}+\frac{\gamma m (y-2 m)^2}{y^3}+\frac{m}{y}+\frac{\pi ^2 \xi ^4}{y^6}-1}. \end{aligned}$$
(29)

The effective potential of scalar shell takes on the following form

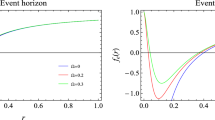
$$\begin{aligned} \Omega (y)= & {} -\frac{m^2 y^4}{4 \pi ^2 \xi ^4}\nonumber \\ {}{} & {} -\frac{\gamma m^2 (y-2 m)^2 \left( 4 \gamma m^2-4 \gamma m y+(\gamma +2) y^2\right) }{4 \pi ^2 \xi ^4}\nonumber \\ {}{} & {} -\frac{\gamma m (y-2 m)^2}{y^3}-\frac{m}{y}-\frac{\pi ^2 \xi ^4}{y^6}+1, \end{aligned}$$
(30)

To get a better understanding of how the thin-shell acts under the influence of a scalar field, the dynamical characteristics of a thin-shell are revealed through a graphical representation. This analysis originates from an advanced adaptation of the Schwarzschild BH. The progressive behavior of the thin-shell is best comprehended by exploring the behavior of effective potential associated with the scalar shell. Figure 2 serves as a visual representation to illustrate the dynamical evolution of thin-shell comprised of a massless scalar field through varying the parameters \(\xi \) and \(\gamma \). We noticed that the thin-shell tends to collapse, i.e., \(\Omega (y)<0\) for a specific choice of physical parameters. Interestingly, when we increase \(\xi \), the collapse happens more slowly. It is interesting to mention that the massless scalar shell collapse rate increases as the shell radius increases. Similarly, we observe the behavior of the scalar shell for different values of \(\gamma \) as shown in the right plot of Fig. 2. By increasing the values of \(\gamma \), the scalar shell expresses more collapsing behavior for higher values of shell radius. As shell radius decreases, the collapsing behavior of the shell also decreases.

Fig. 3
figure 3

The graphical representation of the dynamical evolution of shell through effective potential corresponding to massive scalar field by considering \(p_{0}=1\) (left plot) and \(\gamma =4\) (right plot) against y with \(B_0 =1, m=0.2\)

Full size image

3.2 Thin-shell with massive scalar field

In the subsequent analysis, our aim is to comprehend the dynamics of a scalar shell undergoing evolution in the vicinity of a massive scalar field characterized by the form \(\Pi (\Upsilon ) = m^2\Upsilon ^2\). Consequently, the expression in Eq.(23) for massive scalar field becomes

$$\begin{aligned} 2m^2\Upsilon ^2=\rho -\mathfrak {P}, \quad \dot{\Upsilon }^2=\rho +\mathfrak {P}. \end{aligned}$$
(31)

We establish a crucial link between the mass of the surface matter at thin-shell and the surface energy density to develop the dynamical equations about the observer in a static position. To approach this, we put forward a relationship governing the surface matter at the shell. This relationship takes the form of a linear relation between surface energy density and pressure as \(\mathfrak {P}=B_{0}e^{-\gamma y}\), where \(\gamma \) and \(B_{0}\) stand as constants. In essence, this proposed linear relationship provides a valuable framework for understanding how surface matter properties (prescribed by energy density and pressure) influence the overall dynamics of the thin-shell. By incorporating such considerations, we can gain a comprehensive understanding of how these surface properties contribute to the dynamic evolution of the system especially when observed from a static viewpoint. Making use of Eq. (19) with the specific choice of \(\mathfrak {P}\), we have

$$\begin{aligned} \rho =\frac{h}{y^{2}}+\frac{2B_0}{(y\gamma )^{2}} \Gamma (2,y\gamma ), \end{aligned}$$
(32)

where \(\Gamma (2,y\gamma )=\int _{y\gamma }^{\infty }t^{3}e^{-t}dt\) and h represents the integrating constant. Using the values of energy density and surface pressure in Eq. (31), we obtain

$$\begin{aligned} \dot{\Upsilon }^2= & {} \frac{h}{y^{2}}+B_0\left\{ e^{-\gamma y}-\frac{2}{(y\gamma )^{2}}\Gamma (2,y\gamma )\right\} , \end{aligned}$$
(33)
$$\begin{aligned} \Upsilon ^2= & {} \frac{h}{2m^2y^{2}}-\frac{B_0}{2m^2}\left\{ e^{-\gamma y}+\frac{2}{(y\gamma )^{2}}\Gamma (2,y\gamma )\right\} . \end{aligned}$$
(34)

Additionally, we have

$$\begin{aligned} \mathcal {M}=4\pi y^{2}\rho =4\pi h-\frac{8\pi B_{0}}{\gamma ^{2}}\Gamma (2,y\gamma ). \end{aligned}$$
(35)

We explore the dynamics of a massive scalar shell by using the expression \(\Pi (\Upsilon )=m^2\Upsilon ^2\), and substituting Eq. (33) in (26) while considering specific values for physical parameters as graphically represented in Fig. 3. The analysis of effective potential unfolds a captivating result, i.e., the massive scalar shell undergoes an initial phase of collapsing behavior, transitioning thereafter into an expanding state as illustrated in the left plot of Fig. 3. Moreover, the expanding behavior tends to decrease with an increase in the acoustic parameter. This signifies a delicate interplay between the shell’s dynamics and the acoustic parameter adding depth to our understanding of its behavior. The dynamical evolution is also affected due to the presence of other parameters. This comprehensive analysis allows us to appreciate not only the primary trends but also the subtle dependencies and interactions that characterize the dynamics of the massive scalar shell. In Fig. 3, it is found that the effective potential of a massive scalar shell approaches zero as the shell radius increases which leads to the expansion of the shell. In the left plot of Fig. 3, it is interesting to mention that the massive scalar shell expresses less collapsing and more expanding behavior for the choice of Schwarzschild BH comparatively acoustic Schwarzschild BH. Also, the parameter \(p_0\) greatly effects the dynamical behavior of the massive scalar shell. For smaller values of shell radius, we find maximum collapsing behavior and collapsing rate decreases as shell radius increases.

4 Stability analysis

This section focuses on the stability analysis of thin-shell. Initially, our approach involves examining the changing process of a thin-shell by investigating the equation of motion which establishes a connection between kinetic energy and potential energy. Notably, it is difficult to solve Eq. (20) due to its highly non-linear nature. Consequently, we opt for a linearized representation of the equation after the perturbation. To do this, we employ a Taylor series expansion for the second order to expand the potential function at the equilibrium radius. This linearization aids in simplifying the analysis and provides a more tractable framework for examining the stability of the thin shell. The potential function is then obtained as

$$\begin{aligned} \Omega (\rho ,y)= & {} \Omega (y_0)+\frac{d\Omega }{dy}|_{y=y_0} (y_0-y)\\{} & {} +\frac{d^2\Omega }{dy^2}|_{y=y_0}\frac{(y_0-y)^2}{2}+O((y_0-y)^3). \end{aligned}$$

In this context, a significant observation is made as \(\Omega (\rho _0,y_0)=0=\frac{d^2\Omega }{dy^2}|_{y=y_0}\). By introducing the variable transformation \(x=y-y_0\), we find

$$\begin{aligned} \dot{x}^2+\omega _{ts}^2x^2\simeq 0, \end{aligned}$$
(36)

where \(\omega _{ts}^2=\frac{1}{2}\frac{d^2\Omega }{db^2}|_{y=y_0}.\) Taking the derivative of Eq. (36) w.r.t proper time, the following representation is established

$$\begin{aligned} \ddot{x}+\omega _{ts}^2x\simeq 0. \end{aligned}$$
(37)

This equation determines whether the thin-shell is stable or unstable depending on how \(\omega _{ts}^2\) behaves. The stability condition can be expressed as \(\frac{d^2\Omega }{dy^2}\Big |{y=y_0}>0 \Rightarrow \omega _{ts}^2>0\). If \(\frac{d^2\Omega }{dy^2}\Big |{y=y_0}<0\) indicating \(\omega _{ts}^2 < 0\), the shell’s radius exhibits an exponential trend resulting in an unstable configuration. Thus, we derive an expression for \(\omega _{ts}^2\) given by

$$\begin{aligned} \omega _{ts}^2= & {} -\frac{\left( \mathcal {A}(y_0)-\mathcal {H}(y_0)\right) {}^2-256 \pi ^4 y_0^4 \rho _0^4}{32 \pi ^2 y_0^3 \rho _0^3}\Omega _{10}\nonumber \\{} & {} -\frac{(\mathfrak {P}_0+\rho _0) \left( 256 \pi ^4 y_0^4 \rho _0^4-\left( \mathcal {A}(y_0)-\mathcal {H}(y_0)\right) {}^2\right) }{16 \pi ^2 y_0^4 \rho _0^3}\Omega _{20}\nonumber \\{} & {} +\frac{1}{64 \pi ^2 y_0^4 \rho _0^4}\left( 2 \mathfrak {P}_0 \rho _0 \left( -\left( \mathcal {A}(y_0){-}\mathcal {H}(y_0)\right) \left( {-}4 y_0 \mathcal {H}'(y_0)\right. \right. \right. \nonumber \\{} & {} -\, \left. \left. \left. 5 \mathcal {H}(y_0){+}4 y_0 \mathcal {A}'(y_0){+}5 \mathcal {A}(y_0)\right) {-}768 \pi ^4 y_0^4 \rho _0^4\right) \right. \nonumber \\{} & {} -\left. 4 \mathfrak {P}_0^2 \left( 3 \left( \mathcal {A}(y_0)-\mathcal {H}(y_0)\right) {}^2+256 \pi ^4 y_0^4 \rho _0^4\right) \right. \nonumber \\{} & {} \left. +\rho _0^2 \left( y_0 \left( y_0 \left( 16 \pi ^2 y_0^2 \rho _0^2 \left( \mathcal {H}''(y_0)+\mathcal {A}''(y_0)\right) \right. \right. \right. \right. \nonumber \\{} & {} -\left. \left. \left. \left. \left( \mathcal {A}'(y_0)-\mathcal {H}'(y_0)\right) {}^2-\left( \mathcal {A}(y_0)-\mathcal {H}(y_0)\right) \right. \right. \right. \right. \nonumber \\{} & {} \times \left. \left. \left. \left. \left( \mathcal {A}''(y_0)-\mathcal {H}''(y_0)\right) -768 \pi ^4 y_0^2 \rho _0^4\right) \right. \right. \right. \nonumber \\{} & {} -\left. \left. \left. 4\left( \mathcal {A}(y_0)-\mathcal {H}(y_0)\right) \left( \mathcal {A}'(y_0)-\mathcal {H}'(y_0)\right) \right) \right. \right. \nonumber \\{} & {} -\left. \left. \left( \mathcal {A}(y_0)-\mathcal {H}(y_0) \right) {}^2\right) \right) , \end{aligned}$$
(38)

where

$$\begin{aligned} \Omega _{10}=\frac{d\mathfrak {P}}{dy}|_{y=y_0},\quad \Omega _{20}=\frac{d\mathfrak {P}}{d\rho }|_{y=y_0}. \end{aligned}$$

The stable or unstable thin-shell structures can be inspected by examining the negative or positive role of \(\omega _{ts}^2\). When \(\omega _{ts}^2=0\), the critical values of \(\Omega _{20}\) can be derived indicating specific parameter values where the system undergoes a transition between stable and unstable configurations. The critical values are found to be

$$\begin{aligned} \Omega _{20cts}=\frac{\mathcal {D}_1\Omega _{10c}+\mathcal {D}_2}{\mathcal {D}_3}, \end{aligned}$$
(39)

where

$$\begin{aligned} \mathcal {D}_1= & {} -y_0 \rho _0 \left( -m^2 y_0^4-2 \gamma m^2 y_0^2 (y_0-2 m)^2-\gamma ^2 m^2 \right. \\ {}{} & {} \times \left. (y_0-2 m)^4+64 \pi ^4 y_0^{10} \rho _0^4\right) ,\\ \mathcal {D}_2= & {} \gamma ^2 m^2 (y_0-2 m)^2 \left( \mathfrak {P}_0 \rho _0 \left( -28 m^2+12 m y_0+y_0^2\right) \right. \\{} & {} \left. +6 \mathfrak {P}_0^2 (y_0-2 m)^2+4 m \rho _0^2 (5 m-y_0)\right) \\ {}{} & {} +2 \gamma m y_0^2 \left( m \mathfrak {P}_0 \rho _0 \left( -12 m^2+4 m y_0+y_0^2\right) \right. \\{} & {} \left. {+}4 \pi ^2 y_0^3 \rho _0^4 \left( 24 m^2{-}12 m y_0{+}y_0^2\right) {+}2 m^2 \rho _0^2 (3 m-y_0)\right. \\ {}{} & {} +\left. 6 m \mathfrak {P}_0^2 (y_0-2 m)^2\right) +y_0^4 \left( m^2 \mathfrak {P}_0 (6 \mathfrak {P}_0+\rho _0)\right. \\{} & {} \left. +8 \pi ^2 m y_0^3 \rho _0^4+32 \pi ^4 y_0^6 \rho _0^4 \left( 4 \mathfrak {P}_0^2+6 \mathfrak {P}_0 \rho _0+3 \rho _0^2\right) \right) , \\ \mathcal {D}_3= & {} 2 \rho _0 (\mathfrak {P}_0+\rho _0) \left( m^2 y_0^4+2 \gamma m^2 y_0^2 (y_0-2 m)^2\right. \\{} & {} \left. +\gamma ^2 m^2 (y_0-2 m)^4-64 \pi ^4 y_0^{10} \rho _0^4\right) . \end{aligned}$$

The critical value \(\Omega _{20c}\) is directly related to the stability of the shell just like \(\omega _{ts}^2\). Also, it depends on \(\Omega _{10}\) which explains its dependence on the EoS. Different choices of matter contents located in the shell effects the stability as well as the dynamical configuration of thin-shell. Hence, we observe the graphical behavior of the \(\Omega _{20c}\) to determine the stability of the developed structure for different values of physical parameters. It is worth noting that the thin-shell structure is stable when \(\Omega _{20cts}>0\), i.e., the positive behavior of \(\Omega _{20cts}\). Conversely, an unstable configuration arises when \(\Omega _{20cts}\) exhibits negative characteristics.

Fig. 4
figure 4

The graphical representation of \(\Omega _{20cts}\) by considering \(\omega =-0.1\) (left plot) and \(\omega =-0.2\) (right plot) and \( m=1\) against \(\gamma \) and \(\mathcal {E}\)

Full size image

4.1 Stable/unstable configuration for phantom-like EoS

Fig. 5
figure 5

The graphical representation of \(\Omega _{20cts}\) by considering \(\omega =-0.4\) (left plot) and \(\omega =-0.5\) (right plot) and \( m=1\) against \(\gamma \) and \(\mathcal {E}\)

Full size image
Fig. 6
figure 6

The graphical representation of \(\Omega _{20cts}\) by considering \(\omega =-1.5\) (left plot) and \(\omega =-2\) (right plot) and \( m=1\) against \(\gamma \) and \(\mathcal {E}\)

Full size image

The stable configuration of a thin shell holds significant importance in both cosmology and astrophysics, particularly in the exploration of viable WH solutions. The EoS is a crucial factor in assessing the impact of different types of matter distributed across the \(\Sigma \) on the stability of the thin-shell. Various models for exotic matter exist with one example being a phantom-like EoS expressed as

$$\begin{aligned} \mathfrak {P}(y)=\omega \rho (y). \end{aligned}$$
(40)

Here, the notation \(\omega <0\) manifests the EoS parameter. This parameter signifies various types of matter contents for distinct ranges characterized as

  • When \(\omega <-1\), it specifies the state of phantom energy.

  • When \(0>\omega >-1/3\), it illustrates quintessence like matter composition.

  • When \(\omega <-1/3\), it indicates the state of dark energy.

Presently, our focus lies in investigating the unstable/stable characteristics of the thin-shell within the context of an acoustic Schwarzschild BH. This exploration uses \(\Omega _{20cts}\) for a phantom-like EoS and is graphically depicted in Figs. 4, 5, and 6. Notably, the intriguing observation is that the unstable/stable nature of the thin shell adheres to the fundamental condition in thin-shell dynamics, i.e., the radius of the shell must exceed the radius of the event horizon (Fig. 1) for the event horizon and Figs. 4, 5, and 6 for representations of the thin-shell structure). As a result, our anticipated findings regarding stability of the thin-shell emerge after the position of the event horizon. It is observed that the thin-shell exhibits stable behavior for acoustic Schwarzschild BHs filled with quintessence-like matter contents near the position of the event horizon as depicted in Fig.(4). However, for \(\gamma <4\), the thin-shell becomes unstable regardless of the chosen matter content. When the parameter m is increased, the thin-shell demonstrates more stable behavior for smaller values of \(\gamma \) as illustrated in the right plot of Fig. 4. Additionally, the stability of the shell rises for higher values of \(\gamma \) when \(\gamma >4\) (as shown in Fig. 5). Notably, the configurations with dark energy-type matter exhibit a more stable structure than those with a quintessence-type matter distribution. Conversely, for phantom energy-type EoS, the thin-shell displays unstable behavior for every choice of physical parameters (Fig. 6). In summary, the thin-shell exhibits a stable configuration when governed by quintessence and the EoS for dark energy whereas it demonstrates instability under the influence of phantom energy-type EoS.

5 Final remarks

The presence of a timelike thin-shell within static spherical systems stands out as a noteworthy cosmic configuration offering valuable insights into various cosmic hypotheses. The thin-shell is an extremely thin layer of matter functioning as a bridge connecting two distinct regions of spacetime and it holds significance in the exploration of cosmic phenomena. In the present article, we endeavor to employ a cut-and-paste approach to elucidate the geometric evolution of a thin-shell situated between an outer acoustic Schwarzschild BH and an inner flat spacetime. To govern the dynamic behavior of the shell and maintain its stability, a minimal layer of matter is essential within its structure. The dynamical equations dictating such constructed geometries are derived from a simplified version of Einstein’s equations at the hypersurface that gives rise to the stress-energy tensor components. By analyzing the graphical behavior of the metric potential (provided in Fig. 1), we have determined that the event horizon of the acoustic Schwarzschild BH is either larger than or equal to that of the Schwarzschild BH. Next, we have used the KG equation and conservation equation to investigate the dynamical structure of the thin-shell comprised of both massive and massless scalar fields. Additionally, we have studied the stable configuration of the thin-shell under linearized radial perturbations via critical values of \(\Omega _{20cts}\), endorsed with matter components according to EoS of dark energy, quintessence, and phantom energy.

The evolutionary conduct of a thin-shell with a massless scalar field for a variety of the values of \(\xi \) as well as \(\gamma \) is depicted in Fig. 2. Under appropriately chosen physical parameters, the results have revealed a collapsing tendency of the thin-shell (\(\Omega (y)<0\)). It is observed that when the parameter \(\xi \) increases, the rate of collapse diminishes. Moreover, for larger values of \(\gamma \), we have found that the effective potential demonstrates a stronger collapsing characteristic. Nevertheless, the behavior of effective potential has revealed that the scalar shell initially exhibits a collapsing behavior before transitioning to an expanding state. With an increase in the acoustic parameter, the extent of expansion decreases. It is crucial to note that the dynamic behavior of the shell is influenced by additional factors (Fig. 3). Interestingly, by considering Schwarzschild BH over acoustic Schwarzschild BH, the massive scalar shell exhibited less collapsing and more expanding behavior. Furthermore, the enormous scalar shell’s dynamical behavior is significantly influenced by the parameter \(p_0\). We examined the maximal collapsing behavior for smaller values of shell radius and a reduction in collapsing rate with increasing shell radius.

In addition to studying the dynamic evolution of the thin-shell, we have delved into a comprehensive analysis of its stability. This investigation involves a detailed examination of the factors that contribute to the stability or instability of the developed thin-shell configuration. For the thin-shell to maintain its stability, its size must surpass that of the event horizon. Consequently, the stability of the thin-shell is directly influenced by the location of the event horizon providing us the crucial insights. Our findings have revealed that when matter is introduced into the acoustic Schwarzschild BH via quintessence-type EoS, the thin-shell maintains stability, particularly near the event horizon (Fig. 4). Conversely, the thin-shell becomes unstable for all possible options of matter content when \(\gamma >4\). This distinction in behavior sheds light on the intricate relationship between matter composition, the event horizon, and the stability of the thin-shell.

Through this analysis, we have concluded that the stability of the thin-shell is enhanced when considering the acoustic Schwarzschild BH in comparison to the standard Schwarzschild BH.