1 Introduction

Recent advancements in general relativity (GR) have brought challenging revolutions to several astrophysical phenomena in the cosmic setup, and have also led to several fascinating experiments using gravity. In the modern era of study, black holes (BHs) are considered to be one of the most remarkable features of powerful gravitational fields. A BH’s powerful gravitational zone prevents anything from escaping its event horizon, but it also swallows anything that becomes entangled in its surroundings. There have always been astonishing consequences of quantum fluctuations related to the physical characteristics of BH geometries. Singularity is a core region of spacetime where density and spacetime curvature diverges and physical laws are rendered invalid. The presence of singularity is one of the fundamental problems in BH physics. Particularly, the Hawking evaporation process, entanglement, and the information loss paradox are all results of the quantum gravitational processes in BHs, which have a rich history and deep results. The BH singularities are solved by the quantum gravity effects that stem from loop quantum gravity and the renormalization-group-improvement (RGI) technique, which either prevent or eliminate the emergence of a singularity during the gravitational collapse of a dying star [1, 2]. As the BH dissipates during the Hawking evaporation process, the naked singularity of the spacetime curve is revealed. The RGI theory, on the other hand, postulates that the evaporation process stops when critical mass is reached, such that there is no singularity in the final state. The Schwarzschild singularity at \(r = 0\) is also replaced by a de Sitter core in this theory. Thermodynamics of horizons, gravitational lensing, and accretion dynamics are just a few of the broader contexts in which the RGI Schwarzschild BH has been researched in the literature [2, 3].

A timelike thin-shell in a static spherical geometry is one of the fascinating cosmological configurations that can be used to analyze a wide range of cosmological scenarios. A thin-shell is referred to as an infinitesimally thin layer of a substance that serves as a spacetime junction. Since thin-shell integrates a certain matter distribution, it must satisfy certain energy constraints that validate the validity of the respective spacetime. These conditions can be related to the extrinsic curvature of the geometrical structure through stress–energy tensor. The surface that combines the Minkowski spacetime and the Schwarzschild spacetime, which are referred to as the inner and exterior geometries, respectively, is the manifestation of the thin-shell configuration that is the simplest possible form. The primal work of Israel introduced a useful system in the theoretical construction of time-like shells, by joining two different manifolds at thin-shell [4]. Later on, researchers extended this work for a dynamical description of bubbles in BH, spinning BH, and strings as [5,6,7] by employing Israel junction conditions. It is important to investigate the stability of thin-shell arrangements, either from a dynamic or a thermodynamic point of view.

Numerous researchers have investigated the dynamics of thin-shell and thin-shell wormholes (WHs) (by the joining of two equivalent copies of BH spacetimes) through the use of radial perturbation in the context of several choices for the matter contents. Brady et al. [8] studied the stable/unstable configuration of thin-shell which is constructed from the match of inner flat spacetime to the outer Schwarzschild BH. Later, the thermodynamical stability of the such geometrical structure is explored by Martinez [9]. Later, Mazharimousavi et al. [10] presented stable thin-shell configuration by applying a variable equation of state (EoS). Bergliaffa et al. [11] analyzed the linear and thermodynamical stability of these thin-shell structures by assuming both barotropic and non-barotropic EoS at thin-shell. The stability of thin-shell WH can be studied either by assuming radial perturbations or an EoS for the exotic matter at thin-shell. Eiroa and Simeone [12] studied this analysis for thin-shell WHs from various BHs solutions with enhancement in the stability regions taking some specific choices of the physical parameters. Halilsoy et al. [13] discussed the role of linear, logarithmic, and Chaplygin gas models as alternatives of exotic matter for spherical configurations. Varela [14] found stable thin-shell WH solutions by assuming barotropic and non-barotropic fluids. Jusufi and Ovgun [15] studied the stability of canonical acoustic thin-shell WHs and Ovgun and Salako [16] investigated an acoustic thin-shell WH within the context of neo-Newtonian theory and found that changing the parameters of neo-Newtonian theory led to stable states of the developed solution. Ovgun and Jusufi uncovered several intriguing findings while researching the stable configuration of dyonic thin-shell WHs within the context of low-energy string theory [17]. Thin-shell WH stability with regular Hayward BH is explored in [18] and rotating thin-shell discussed in [19], also stability of thin-shell WH with dark energy and dark matter with Lorentz symmetry breaking is studied in [20]. Stable thin-shell WHs are also presented from different spherical BH spacetimes for variable EoS [21,22,23].

Another well-known geometrical structure of thin-shell is referred as gravastar which is developed from de-Sitter (interior) and BH geometry (exterior) through cut and paste approach [24]. These structures are highly relevant because they can solve two key issues, namely the singularity problem and the information loss paradox for BHs. These geometrical structures are built within the context of various BH spacetimes, the stabilities of which may be evaluated using various EoS [25,26,27,28,29]. The physical characteristics of a prototype gravastar model by taking de-Sitter and Schwarzschild BH spacetimes [30, 31] as well as gravastar with phantom energy [32] have been studied yielding some useful consequences. It turns out that the constructed geometry can either be a stable, unstable, or bounded excursion gravastar in the vicinity of different choices of fluids at thin-shell. In the background of noncommutative geometry, the stable configuration of charged gravastar is analyzed in [33]. The gravastar models by considering noncommutative effects [34, 35], higher-dimensional spacetimes [36], Kuchowicz metric potential [37], regular and charged quintessence BHs with variable EoS [38,39,40,41] have been explored with appearance of stable configurations.

There is significant interest in investigating the dynamics and the geometrical structure of boson stars (compact objects composed with massless and massive scalar field). Without any choice of EoS, the stability of self-gravitating compact stars in the background of a scalar field is investigated by Ruffini and Bonazzola [42]. Seidel and Suen [43] found some results to understand the formation as well as the existence of boson stars since they focused on the dynamics of boson stars and discovered some precise values of a scalar field that indicates the equilibrium configuration. Boson stars are discussed by Jetzer [44], along with their genesis from gravitational instability and the discovery that their size and mass is affected by the mass of the associated scalar field. By analyzing the compact stars with a massless scalar field, Siebel et al. [45] found that they exhibit oscillation or collapse behavior. Núñez [46] presented a cosmic model as a compact object surrounded by a spherical shell and discovered that the effect of self-gravitating and gravitational forces are canceled out by the inner tangential pressure. Núñez et al. [47] investigated the thin-shell composed of massless and massive scalar field developed from two Schwarzschild BH. They also explore the expanding and collapsing behavior of the shell through the equation of motion of the scalar shell. Sharif and Abbas [48] extended this work for the charged BH and found the dynamical behavior of the shell through the massless and massive scalar field. Later, Sharif and his collaborators extend this work for BTZ, charged BTZ, rotating and regular BHs [49,50,51,52].

In this paper, we develop a thin-shell by taking the inner flat and outer renormalization group improved Schwarzschild BH and explore the dynamics composed with scalar field and stability thin-shell. The paper is arranged in the following manner. Section 2 is devoted to presenting a generic thin-shell through the matching of inner and outer manifolds through a cut and paste approach. In Sect. 3, we explore the dynamical configuration of thin-shell using the massless and massive scalar field. Section 4 deals with the stability of thin-shell through linearized radial perturbation about equilibrium shell radius with phantomlike EoS. Finally, the last section summarizes our results.

2 Generic thin-shell formalism

This section is devoted to developing a \((2+1)-D\) thin-shell represented by \(\Sigma \) with radius \(r=w(\tau )\), where \(\tau \) is the proper time. This shell connects two different manifolds, i.e., the exterior region \((r>w)\) is chosen as a BH spacetime while the interior region \((r<w)\) is defined by a flat geometry. The line element for these geometries can be written as

$$\begin{aligned} ds^2_{\pm }=-f_{n}(r)dt^2+(f_n(r))^{-1}dr^2 +r^2(d\theta ^2+\sin ^2\theta d\phi ^2), \end{aligned}$$
(1)

where \(n=i,e\) correspond to the interior and exterior regions, respectively.

At thin-shell, the metric function \(h_{ij}\) represents a timelike 2-sphere with coordinates \(y^i=(\tau ,\theta ,\phi )\) which can be expressed as

$$\begin{aligned} ds^2=h_{ij}dy^{i}dy^j=-d\tau ^2+w^2d\theta ^2+w^2\sin ^2\theta d\phi ^2. \end{aligned}$$
(2)

A thin-shell refers to a boundary that separates interior spacetime from the exterior one. For the physical viability of thin-shell, junction conditions like the continuity of the induced metric at thin-shell and extrinsic curvature discontinuity are required [4]. We also derive the surface stresses for these geometries through the field equations of thin-shell named Lanczos equations. We can compute physical features at the shell (causing extrinsic curvature discontinuity) by using stress–energy tensor \(S^{i}_{j}\) [4]. The matter components at thin-shell can be written as

$$\begin{aligned} S^{\tau }_{\tau }\equiv & {} \rho (w)=-\frac{1}{4\pi w}(\chi _e(w)-\chi _i(w)), \end{aligned}$$
(3)
$$\begin{aligned} S^{\theta }_{\theta }=S^{\phi }_{\phi }\equiv & {} {\mathfrak {P}}(w)=\frac{-\chi _i(w)+\chi _e(w)}{8\pi w}+\frac{2\ddot{w}+f_e'(w)}{16\pi \chi _e(w)}\nonumber \\{} & {} - \frac{2\ddot{w}+f_i'(w)}{16\pi \chi _i(w)}, \end{aligned}$$
(4)

where

$$\begin{aligned} \chi _i(w)=\sqrt{f_i(w)+\dot{w}^2}, \quad \chi _e(w)=\sqrt{f_e(w)+\dot{w}^2}, \end{aligned}$$
(5)

\(\rho (w)\) and \({\mathfrak {P}}(w)\) represent energy density and tangential pressure while overdot and dash correspond to the derivatives w.r.t proper time and radial coordinate, respectively. Hence, we have

$$\begin{aligned} \rho= & {} -\frac{\sqrt{\dot{w}^2+f_e(w)}-\sqrt{\dot{w}^2+f_i(w)}}{4 \pi w}, \end{aligned}$$
(6)
$$\begin{aligned} {\mathfrak {P}}= & {} \frac{1}{8 \pi }\left( \frac{2 \ddot{w}+f_e'(w)}{2 \sqrt{\dot{w}^2+f_e(w)}}-\frac{2 \ddot{w}+f_i'(w)}{2\sqrt{\dot{w}^2+f_i(w)}}\right. \nonumber \\{} & {} \left. +\frac{\sqrt{\dot{w}^2+f_e(w)}-\sqrt{\dot{w}^2+f_i(w)}}{w}\right) . \end{aligned}$$
(7)

At equilibrium shell radius \(\dot{w}_{0}=\ddot{w}_{0}=0\). Hence, we get

$$\begin{aligned} \rho _0=\rho (w_0)= & {} -\frac{\sqrt{f_e(w_0)}-\sqrt{f_i(w_0)}}{4 \pi w_0}, \end{aligned}$$
(8)
$$\begin{aligned} {\mathfrak {P}}_0={\mathfrak {P}}(w_0)= & {} \frac{1}{8 \pi }\left( \frac{\sqrt{f_e(w_0)}-\sqrt{f_i(w_0)}}{w_0}+\frac{f_e'(w_0)}{2 \sqrt{f_e(w_0)}}\right. \nonumber \\{} & {} \left. -\frac{f_i'(w_0)}{2 \sqrt{f_i(w_0)}}\right) . \end{aligned}$$
(9)

For Minkowski spacetime, gravity does not exist inside the shell due to the absence of matter contents in the interior geometry. The exterior part is also taken as a vacuum but the gravitational field exists as it is defined by BH. The mass parameter m in this metric can be related to the gravitational mass of the shell which governs the gravitational potential energy, kinetic energy as well as the rest-mass energy of the spacetime. We can define the mass of the shell as \(M=4\pi w^2\rho \). Additionally, the conservation equation yields

$$\begin{aligned} {\mathfrak {P}}\frac{d}{d\tau }(w^{2})+\frac{d}{d\tau }(\rho w^{2})=0, \end{aligned}$$
(10)

which yields

$$\begin{aligned} \rho '=-\frac{2}{w}\left( {\mathfrak {P}}(\rho ,w)+\rho \right) . \end{aligned}$$
(11)

The surface energy density (6) explicitly yields an equation of motion as

$$\begin{aligned} \dot{w}^2+\Pi (\rho (w),w)=0, \end{aligned}$$
(12)

where \(\Pi (\rho (w),w)\) shows effective potential of the shell given by

$$\begin{aligned} \Pi (\rho (w),w)= & {} \frac{f_e f_i}{32 \pi ^2 w^2 \rho ^2}-\frac{f_i^2}{64 \pi ^2 w^2 \rho ^2}+\frac{f_i}{2}\nonumber \\{} & {} -\frac{f_e^2}{64 \pi ^2 w^2 \rho ^2}+\frac{f_e}{2}-4 \pi ^2 w^2 \rho ^2. \end{aligned}$$
(13)
Fig. 1
figure 1

Plots of metric function for \( m=0.1\) (left) and \(m=0.2\) (right) verses r with \(\gamma =0.05\)

Full size image

2.1 Thin-shell: inner flat and outer RGI Schwarzschild BH

The renormalization group methods are used to incorporate the quantum effects into the Schwarzschild BH geometry. Since spacetime singularities are eliminated as a result of this modification, the respective manifold can have zero, one, or two horizons. Here, we are interested to develop a thin-shell by using an inner flat and outer RGI Schwarzschild BH through cut and paste technique. The corresponding metric functions interior flat and exterior improved Schwarzschild BH is expressed as [1]

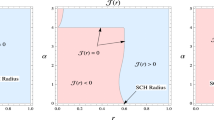
$$\begin{aligned} f_{i}(r)=1,\quad f_e(r)=1-\frac{2 m}{r} \left( \frac{\gamma m^3 \Omega }{r^3}+\frac{m^2 \Omega }{r^2}+1\right) ^{-1}, \end{aligned}$$
(14)

where m is the mass of Schwarzschild BH with real constants \(\Omega \) and \(\gamma \). For \(\Omega =0\), it is reduced to a Schwarzschild solution in GR. The position of the BH event horizon coincides with the radial position at which the metric function become zero. Hence, we can determine the position of the event horizon using \(f_e(r)=0\) as follows

$$\begin{aligned} r_{h}=\frac{1}{6} \left( \frac{8 \root 3 \of {2} m^2}{\root 3 \of {h(r)}}+2^{2/3} \root 3 \of {h(r)}+4 m\right) , \end{aligned}$$
(15)

where

$$\begin{aligned} h(r)= & {} m^3 (16-9 (3 \gamma +2) \Omega ) \\{} & {} +3 \sqrt{3}\sqrt{\Omega m^6 \left( (9 \gamma (3 \gamma +4)-4) \Omega -32 \gamma +4 \Omega ^2\right) }. \end{aligned}$$

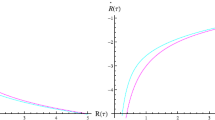
In Fig. 1, we discuss the behavior of the metric function for suitable values of physical parameters. The position of the event horizon decreases for RGI Schwarzschild BH (\(r_h\) decreases as \(\Omega \) increases). It found that \(r_h\) becomes large for higher values of mass for both Schwarzschild and improved Schwarzschild BHs.

The respective stress–energy tensor components at the equilibrium shell radius become

$$\begin{aligned} \rho _0= & {} \frac{1}{4 \pi w_0}\left( 1-\sqrt{1-\frac{2 m}{w_0}{ \left( \frac{\gamma m^3 \Omega }{w^3_0}+\frac{m^2 \Omega }{w^2_0}+1\right) }^{-1}}\right) , \nonumber \\\end{aligned}$$
(16)
$$\begin{aligned} {\mathfrak {P}}_0= & {} \frac{1}{8 \pi w_0}\left( \sqrt{1-\frac{2 m w^2_0}{m^2 \Omega (\gamma m+w_0)+w^3_0}}-1\right) \nonumber \\{} & {} {+}\frac{m w^4_0{-}m^3 w_0 \Omega (2 \gamma m{+}w_0)}{8 \pi \left( m^2 \Omega (\gamma m{+}w_0){+}w^3_0\right) ^2 \sqrt{1{-}\frac{2 m w^2_0}{m^2 \Omega (\gamma m{+}w_0){+}w^3_0}}}.\nonumber \\ \end{aligned}$$
(17)

It is interesting to mention that the “mass of BH” refers to the actual mass contained within the event horizon of a BH, where gravity is so strong that nothing, not even light, can escape. On the other hand, the “gravitational mass” of the shell refers to the mass that contributes to the gravitational force felt by objects outside of the event horizon. Using Eqs. (5) and (14), we find relations between the gravitational mass and mass of the shell as

$$\begin{aligned}{} & {} \chi _e(w)-\chi _i(w)=-M/w, \nonumber \\{} & {} \chi _e(w)+\chi _i(w)=\frac{2 w^3 m}{M \left( w^3+m^2 \Omega (w+\gamma m)\right) }. \end{aligned}$$
(18)

By solving these equations simultaneously, we obtain the following form of mass of BH in terms of mass of the shell as

$$\begin{aligned} m= & {} \frac{1}{6 \gamma M \Omega (M-2 w_0)}\\{} & {} {\times }\left( \frac{2 \root 3 \of {2} w^2_0 M \Omega (2 w_0{-}M) \left( 6 w^2_0 \gamma {+}M \Omega (2 w_0{-}M)\right) }{h(w_0)}\right. \\{} & {} \left. +2^{2/3} h(w_0)+2 w_0 M \Omega (2 w_0-M)\right) . \end{aligned}$$

The corresponding effective potential function yields

$$\begin{aligned} \Pi (\rho (w),w)= & {} \frac{1}{16} w^2 \left( -\frac{16 m}{m^2 \Omega (\gamma m+w)+w^3}\right. \\{} & {} \left. {-}\frac{m^2}{\pi ^2 \rho ^2 \left( m^2 \Omega (\gamma m{+}w){+}w^3\right) ^2}{-}64 \pi ^2 \rho ^2\right) \\{} & {} +1. \end{aligned}$$

3 Scalar shell dynamics

The matter contents located at thin-shell play a remarkable role to discuss dynamical as well as stable configuration. Now, we are interested to observe the effects of the scalar field over the dynamical evaluation of thin-shell. In this regard, we use the following formal transformation i.e., \(\left( u_{a}=\frac{\Upsilon _{,a}}{\sqrt{\Upsilon _{,b}\Upsilon ^{,b}}}\right) \), where \(\Upsilon \) represents the scalar field [46,47,48]. With the help of this transformation, the potential function of scalar field \((V(\Upsilon ))\) and the derivative of the scalar field is connected to the surface pressure and energy density of the ideal fluid. We consider the following relation to defining the surface pressure (P) and energy density \((\sigma )\) for scalar field as [47]:

$$\begin{aligned} P=\frac{1}{2}\left[ \Upsilon _{,b}\Upsilon ^{,b}-2V(\Upsilon )\right] ,\quad \sigma =\frac{1}{2}\left[ \Upsilon _{,b}\Upsilon ^{,b}+2V(\Upsilon )\right] .\nonumber \\ \end{aligned}$$
(19)

The stress–energy tensor such as a type of scalar field yields

$$\begin{aligned} S_{ij}=\nabla _{i}\Upsilon \nabla _{j}\Upsilon -\eta _{ij}\left[ \frac{1}{2}(\nabla \Upsilon )^2-V(\Upsilon )\right] . \end{aligned}$$

As the proper time is the only parameter that deals with the evolutionary behavior of the shell as the hypersurface depends on \(\tau \). Therefore, the scalar field only depends on \(\tau \). Thus

$$\begin{aligned} P=\frac{1}{2}\left[ \dot{\Upsilon }^2-2V(\Upsilon )\right] , \quad \sigma =\frac{1}{2}\left[ \dot{\Upsilon }^2+2V(\Upsilon )\right] . \end{aligned}$$
(20)

In this case, the first expression (\(\dot{\Upsilon }^2\)) represents the kinetic energy and \(V(\Upsilon )\) indicates the potential energies of the scalar field. Thin-shell mass is described by the following scalar field formula:

$$\begin{aligned} {\mathcal {M}}=4\pi w^{2} \sigma = 2\pi w^{2}[\dot{\Upsilon }^2+2V(\Upsilon )]. \end{aligned}$$
(21)

By plugging Eqs. (20) and (21) in (11), we obtain

$$\begin{aligned} \ddot{\Upsilon }+2\left( \frac{\dot{w}}{w}\right) \dot{\Upsilon }+\frac{\partial }{\partial \Upsilon }V(\Upsilon )=0. \end{aligned}$$
(22)

The above equation is a well-known Klein–Gordon (KG) equation. It is very useful to explore the dynamic configuration of the shell. The potential function of thin-shell from RGI Schwarzschild BH with scalar field is given as

$$\begin{aligned} \Pi (w)= & {} -\frac{m w^2}{m^2 \Omega (\gamma m+w)+w^3}\nonumber \\{} & {} -\frac{m^2 w^2}{4 \pi ^2 \left( 2 V(\Upsilon )+\dot{\Upsilon } ^2\right) ^2 \left( m^2 \Omega (\gamma m+w)+w^3\right) ^2}\nonumber \\{} & {} -\pi ^2 w^2 \left( 2 V(\Upsilon )+\dot{\Upsilon } ^2\right) ^2+1. \end{aligned}$$
(23)

The matter contents of the scalar field are not connected in any particular way by the EoS. Because the scalar field’s energy density is split into potential and kinetic energies, no single value of P can accurately represent the energy density. To construct a link between components of the stress–energy tensor, we employ a special form of \(V(\Upsilon )\) to determine the effective mass. Following this, we will investigate two distinct values of the potential function, which are named as:

  • Massless scalar field: \(V(\Upsilon )=0\),

  • Massive scalar field: \(V(\Upsilon )=m^2\Upsilon ^2\).

Fig. 2
figure 2

Dynamics of shell via effective potential of massless scalar field \(m=0.2\) (left plot) and \(m=0.5\) (right plot) verses w with different values of \(\xi \) and \(\gamma =0.5, \Omega =0.5\)

Full size image
Fig. 3
figure 3

Massless scalar shell radius versus proper time for \(\Omega =0.1\) (left plot) and \(\Omega =0.5\) (right plot) with initial condition \(w[0]=0.5\) and \(\dot{w}>0\) for \(\lambda =0.2,m=0.3,\gamma =0.5\)

Full size image

In this paper, we study the dynamics of a shell composed of a scalar field by analyzing its equations of motion. It is demonstrated that there are two ways to integrate the equations of motion \((\dot{w}^2+\Pi (w)=0).\) The first involves taking into account the shell’s pressure as an explicit function of its radius, whereas the second involves supposing the existence of an equation of state connecting the shell’s pressure and energy density. As we mentioned, the equation \(\dot{w}^2+\Pi (w)=0\) corresponds to the energy conservation law which states that the sum of the “kinetic component” \(\dot{w}^2\) and “potential component” \(\Pi (w)\) equals zero at any time. This is more a constraint than a dynamical equation in the sense that one cannot give arbitrary initial conditions to evolve the system, but only those conditions that satisfy the conservation equation. It follows that the solutions allowed are only those for which the effective potential is negative or zero, i.e., \(\Pi (w)<0\) or \(\Pi (w)=0\). The second case \((\Pi (w)=0)\) will correspond either to a static configuration or to the turning points which lead to \(\dot{w}^2=0\), i.e., orbits of extremal radius w. The term \(\Pi (w)>0\) does not permit the propagation of the shell. First, we consider the first case \((\dot{w}\ne 0)\) for both massless and massive scalar fields and observe the dynamics of the scalar shell. The numerical integration of the coupled system of differential equations like conservation equation and Klein–Gordon (KG) equation is carried out by specifying, for example, an initial radius \(w(\tau )\), and the initial values of \(\dot{\Upsilon }(\tau )\) and \(\Upsilon (\tau )\).

3.1 Massless scalar thin-shell

By considering \(V(\Upsilon )=0\) in Eq. (20), this case the components of the stress–energy tensor are related through EoS \((P=\rho ).\) The respective KG equation can be written as

$$\begin{aligned} w\ddot{\Upsilon }+2\dot{w}\dot{\Upsilon }=0, \end{aligned}$$
(24)

which yields

$$\begin{aligned} \xi =w^2\dot{\Upsilon }, \end{aligned}$$
(25)

where the integrating constant is represented with \(\xi \). By using \(V(\Upsilon )=0\) and Eq. (25) in Eq. (23), we obtain the respected effective potential of the massless scalar shell becomes

$$\begin{aligned} \Pi (w)= & {} -\frac{m^2 w^{10}}{4 \pi ^2 \xi ^4 \left( m^2 \Omega (\gamma m+w)+w^3\right) ^2}\nonumber \\{} & {} -\frac{m w^2}{m^2 \Omega (\gamma m+w)+w^3}-\frac{\pi ^2 \xi ^4}{w^6}+1. \end{aligned}$$
(26)

For a massless scalar field, we analyze the effective potential and shell radius by using the initial condition as (\(\dot{w}\ne 0\)) shown in Figs. 2 and 3. The behavior of effective potential of the massless scalar field corresponds to a monotonic expanding shell (Figs. 2 and 3), that is, a shell which, starting from a specific radius with positive initial velocity  away from the center \(w=0\), will expand forever see Fig. 3.

3.2 Massive scalar thin-shell

Now, we investigate the behavior of the scalar shell as it evolves in the presence of a massive scalar field, denoted by the equation \(V(\Upsilon )=m^2\Upsilon ^2\). Hence, Eq. (20) for the massive scalar shell becomes

$$\begin{aligned} 2m^2\Upsilon ^2=\sigma -P, \quad \dot{\Upsilon }^2=\sigma +P. \end{aligned}$$
(27)

We create a link between the mass of the surface matter at thin-shell and \(\sigma \) to build the dynamical equations concerning the static observer. To do this, we propose that the surface matter at the shell complies with the linear relationship among surface energy density and pressure as, i.e., \(P=B_{0}e^{-z w}\), where z and \(B_{0}\) are constants. Using Eq. (11) with the particular choice of P, we have

$$\begin{aligned} \sigma =\frac{\chi }{w^{2}}+\frac{2B_0}{(wz)^{2}} \Gamma (2,wz), \end{aligned}$$
(28)

here \(\chi \) represents the integrating constant and \(\Gamma (2,wz)=\int _{wz}^{\infty }\nu ^{3}e^{-\nu }d\nu \). By considering the expression of \(\sigma \) and P in Eq. (27), we get

$$\begin{aligned} \dot{\Upsilon }^2= & {} \frac{\chi }{w^{2}}+B_0\left\{ e^{-z w}+\frac{2}{(wz)^{2}}\Gamma (2,wz)\right\} , \end{aligned}$$
(29)
$$\begin{aligned} \Upsilon ^2= & {} \frac{\chi }{2m^2w^{2}}+\frac{B_0}{2m^2}\left\{ \frac{2}{(wz)^{2}}\Gamma (2,wz)-e^{-z w}\right\} , \end{aligned}$$
(30)
Fig. 4
figure 4

Dynamics of shell via effective potential of massive scalar field for different values of \(B_{0}\) (left plot) and z (right plot) verses w with \(\gamma =0.5, \chi =1, m=0.2, \Omega =0.5\)

Full size image
Fig. 5
figure 5

Massive scalar field versus the proper time \(\tau \) for \(m=0.2\) (left plot) and \(m=1\) (right plot) with initial conditions \(\dot{w}(0)=0.5,\dot{\Upsilon } [0]=1.5,\Upsilon [0]=1.5\) for \(\gamma =0.5,\Omega =0.5\). The oscillations are highly damped at the beginning when \( \dot{w}>0\) is large due to the expansion of the shell

Full size image

which follows the KG equation. Also, we have

$$\begin{aligned} {\mathcal {M}}=4\pi w^{2}\sigma =4\pi \chi +\frac{8\pi B_{0}}{z^{2}}\Gamma (2,wz). \end{aligned}$$
(31)

The dynamical evaluation of a massive scalar shell is explored by using \(V(\Upsilon )=m^2\Upsilon ^2\) and Eq. (29) in Eq. (23) with suitable values of physical parameters as shown in Fig. 4.

For massive scalar fields, this procedure of integration is shown in Figs. 4 and 5 which depict the effective potential, and the scalar field, respectively, for solutions of the equations (conservation and KG equations) describing an expanding shell with a quadratic scalar potential. In Fig. 4, we notice that the behavior of effective potential \(\Pi (w)\) depends on the scalar field due to its explicit dependence on the scalar field. We also remark that as the shell expands, \(\Pi (w)\) tends to zero, and so the expansion slows down. This affects the behavior of \(\Upsilon \) in the sense that the amplitude is highly damped at the beginning of the motion when \(\dot{w}\) is large, but then it becomes like an ordinary harmonic oscillator when \(\dot{w}\) is smaller as shown in Fig. 5.

Further, we explore the behavior of scalar shell for the static configuration as \(\dot{w}=0\).

3.3 Static configuration

For any time \(\tau \), a static orbit indicates that the gravitational and stress forces cancel each other, hence the condition \(\dot{w}=0\) must hold. From the KG, with \(\dot{w}=0\), we obtain

$$\begin{aligned} \ddot{\Upsilon }+\frac{\partial }{\partial \Upsilon }V(\Upsilon )=0, \end{aligned}$$
(32)

which leads to

$$\begin{aligned} \dot{\Upsilon }^2+2V(\Upsilon )=\mathcal {J}, \end{aligned}$$
(33)

where \({\mathcal {J}}\) denotes the integration constant. The equation of motion requires in this case the vanishing of the effective potential as well as its first derivative. The fact that \(\partial \Pi (w)/\partial w<0\) for \(w>w_0\), where \(w_0\) represents the position of the static shell, we conclude that the radius \(w=w_0\) gives the maximum of the effective potential, and so an unstable configuration. Such a radius depends on the remaining parameters in the form of \(w_0( \gamma ,\Omega ,m,{\mathcal {J}})\) which is found when solving simultaneously the two algebraic equations \(\Pi (w_0)=0\) and \(\frac{d\Pi (w)}{dw}|_{w=w_0}=0\), which can be reduced to a fourth-order algebraic equation for \(w_0\) given as

$$\begin{aligned}{} & {} \frac{ w_0^3 \Omega +3 m^2 w_0^5}{m^{-4}\pi ^2 {\mathcal {J}}^2}-2 \left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) \nonumber \\{} & {} \qquad {\times }\left( 2 m^4 \Omega ^2 (\gamma m{+}w_0)^2{+}m^2 w_0^3 \Omega ((4 \gamma {-}1) m{+}4 w_0)\right. \nonumber \\{} & {} \qquad \left. +w_0^5 (2 w_0-3 m)\right) =0. \end{aligned}$$
(34)

The static radius is shown to be real and positive by the explicit roots of this equation for certain values of the parameters. In the absence of \(\Omega =0\), our results reduce for the Schwarzschild BH as [47]

$$\begin{aligned} -\frac{3 m^2}{4 \pi ^2 {\mathcal {J}}^2}-\frac{3 m w_0^3}{2}+w_0^4=0. \end{aligned}$$
(35)

In the static case, the equation of motion of the scalar field decouples from the dynamical behavior of the shell, and the scalar field presents its dynamics. For the massive scalar field \(V(\Upsilon )=m^2\Upsilon ^2\), the KG equation takes the form

$$\begin{aligned} \dot{\Upsilon }^2+2m^2\Upsilon ^2=\mathcal {J}. \end{aligned}$$
(36)

Its solutions with initial condition \(\Upsilon [0]=1\) can be expressed as a

$$\begin{aligned} \Upsilon (\tau )=\frac{\sqrt{{\mathcal {J}}}}{m} \tanh \left( \sqrt{J} m \tau -\cosh ^{-1}\left( -\frac{\sqrt{{\mathcal {J}}}}{\sqrt{{\mathcal {J}}-m^2}}\right) \right) .\nonumber \\ \end{aligned}$$
(37)

4 Stability analysis with phantom-like EoS

This section deals with the stable configurations of thin-shell at equilibrium shell radius through linearized radial perturbation which plays a remarkable role to linearized the complex expression of the potential function. The equation of motion of thin-shell provides a relation between the kinetic and potential energies. It is noted that we cannot find the exact solution of Eq. (12) as it is highly non-linear thus choosing a linearized form for this equation after the perturbation. In this context, we expand the potential function at \(w=w_0\) through Taylor series expansion as

$$\begin{aligned} \Pi (\rho ,w)= & {} \Pi (\rho _0,w_0)+\frac{d\Pi }{dw}|_{w=w_0}(w-w_0)\\{} & {} +\frac{d^2\Pi }{dw^2}|_{w=w_0}\frac{(w-w_0)^2}{2}+O((w-w_0)^3). \end{aligned}$$

At equilibrium shell radius \((w=w_0),\) it is found that the potential function and its first derivative are vanished, i.e., \(\Pi (\rho _0,w_0)=0=\frac{d\Pi }{dw}|_{w=w_0}\). Taking \(x=w-w_0\), we get

$$\begin{aligned} \dot{x}^2+\omega _{ts}^2x^2\simeq 0, \end{aligned}$$
(38)

where \(\omega _{ts}^2=\frac{1}{2}\frac{d^2\Pi }{dw^2}|_{w=w_0}.\) Differentiating Eq. (38) w.r.t proper time, we get

$$\begin{aligned} \ddot{x}+\omega _{ts}^2x\simeq 0. \end{aligned}$$
(39)

This equation indicates stable/unstable thin-shell configurations depending on the behavior of \(\omega _{ts}^2\). The stable condition can be written as \(\frac{d^2\Pi }{dw^2}|_{w=w_0}>0\Rightarrow \omega _{ts}^2>0.\) For \(\frac{d^2\Pi }{dw^2}|_{w=w_0}<0\Rightarrow \omega _{ts}^2<0\), the radius of the shell depicts an exponential behavior leading to an unstable configuration.

Hence, we get an expression for \(\omega _{ts}^2\) as follows

$$\begin{aligned} \omega _{ts}^2= & {} -\frac{\left( f_e(w_0)-f_i(w_0)\right) {}^2-256 \pi ^4 w_0^4 \rho _0^4}{32 \pi ^2 w_0^3 \rho _0^3}\Pi _{10}\nonumber \\{} & {} {-}\frac{({\mathfrak {P}}_0{+}\rho _0) \left( 256 \pi ^4 w_0^4 \rho _0^4{-}\left( f_e(w_0){-}f_i(w_0)\right) {}^2\right) }{16 \pi ^2 w_0^4 \rho _0^3}\Pi _{20}\nonumber \\{} & {} +\frac{1}{64 \pi ^2 w_0^4 \rho _0^4}\left( 2 {\mathfrak {P}}_0 \rho _0 \left( -\left( f_e(w_0)-f_i(w_0)\right) \right. \right. \nonumber \\{} & {} \left. \left. \times \left( -4 w_0 f_i'(w_0) \right. \right. \right. \nonumber \\{} & {} \left. \left. {-}5 f_i(w_0){+}4 w_0 f_e'(w_0){+}5 f_e(w_0)\right) {-}768 \pi ^4 w_0^4 \rho _0^4\right) \nonumber \\{} & {} -4 {\mathfrak {P}}_0^2 \left( 3 \left( f_e(w_0)-f_i(w_0)\right) {}^2+256 \pi ^4 w_0^4 \rho _0^4\right) \nonumber \\{} & {} +\rho _0^2 \left( w_0 \left( w_0 \left( 16 \pi ^2 w_0^2 \rho _0^2 \left( f_i''(w_0)+f_e''(w_0)\right) \right. \right. \right. \nonumber \\{} & {} \left. -\left( f_e'(w_0)-f_i'(w_0)\right) {}^2\right. \nonumber \\{} & {} {-}\left. \left( f_e(w_0){-}f_i(w_0)\right) \left( f_e''(w_0){-}f_i''(w_0)\right) \right. \nonumber \\{} & {} \left. {-}768 \pi ^4 w_0^2 \rho _0^4\right) \nonumber \\{} & {} \left. -4 \left( f_e(w_0)-f_i(w_0)\right) \left( f_e'(w_0)-f_i'(w_0)\right) \right) \nonumber \\{} & {} -\left. \left. \left( f_e(w_0)-f_i(w_0) \right) {}^2\right) \right) , \end{aligned}$$
(40)

where

$$\begin{aligned} \Pi _{10}=\frac{d{\mathfrak {P}}}{dw}|_{w=w_0},\quad \Pi _{20}=\frac{d{\mathfrak {P}}}{d\rho }|_{w=w_0}. \end{aligned}$$

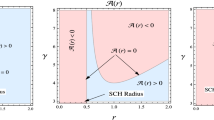
The stability/instability of thin-shell geometries can be observed through positive/negative behavior of \(\omega _{ts}^2\), respectively. Taking \(\omega _{ts}^2=0\), we can derive the critical values of \(\Pi _{20}\) as

$$\begin{aligned} \Pi _{20cts}=\frac{{\mathcal {A}}_1\Pi _{10c}+{\mathcal {A}}_2}{{\mathcal {A}}_3}, \end{aligned}$$
(41)

where

$$\begin{aligned}{} & {} {\mathcal {A}}_1 =2 w_0 \rho _0 \left( 64 \pi ^4 \rho _0^4-\frac{m^2}{\left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) ^2}\right) ,\\{} & {} {\mathcal {A}}_2 =24 {\mathfrak {P}}_0^2 \left( -\frac{3 m^2}{\left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) ^2}-64 \pi ^4 \rho _0^4\right) \\{} & {} +2 {\mathfrak {P}}_0 \rho _0 \left( -\frac{m^2 \left( m^2 \Omega (13 \gamma m+9 w_0)+w_0^3\right) }{\left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) ^3}-192 \pi ^4 \rho _0^4\right) \\{} & {} +\rho _0^2 \left( \frac{6 m^4 w_0^3 \Omega (2 \gamma m+w_0)-3 m^6 \Omega ^2 \left( 5 \gamma ^2 m^2+6 \gamma m w_0+2 w_0^2\right) }{\left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) ^4}\right. \\{} & {} -\frac{16 \pi ^2 m \rho _0^2 \left( \gamma ^2 m^6 \Omega ^2{-}m^2 w_0^3 \Omega (7 \gamma m+3 w_0){+}w_0^6\right) }{\left( m^2 \Omega (\gamma m{+}w_0){+}w_0^3\right) ^3}{-}\left. 192 \pi ^4 \rho _0^4\right) , \\{} & {} {\mathcal {A}}_3 =4 \rho _0 ({\mathfrak {P}}_0+\rho _0) \left( 64 \pi ^4 \rho _0^4-\frac{m^2}{\left( m^2 \Omega (\gamma m+w_0)+w_0^3\right) ^2}\right) . \end{aligned}$$

It is noted that the respective structure of the thin-shell is stable for \(\Pi _{20cts}>0\), otherwise unstable configuration exists for its negative behavior.

Fig. 6
figure 6

Stability analysis of thin-shell filled with quintessence type matter contents for \( m=0.1\) (left plot) and \(m=0.2\) (right plot) verses \(w_0\) with \(\gamma =0.05\)

Full size image
Fig. 7
figure 7

Stability analysis of thin-shell filled with dark energy type matter contents for \( m=0.1\) (left plot) and \(m=0.2\) (right plot) verses \(w_0\) with \(\gamma =0.05\)

Full size image

4.1 Phantom-like EoS

The equation of state is an extremely important concept to understand to explain the impacts of various kinds of matter contents placed at the hypersurface on the stable/unstable characteristics of thin-shell structures. Here, we consider a specific type of EoS state named phantom-like EoS expressed as

$$\begin{aligned} {\mathfrak {P}}(w)=\beta \rho (w), \end{aligned}$$
(42)

where \(\beta <0\) denotes the EoS parameter. The different ranges of equation state parameter denotes the different types of matter contents expressed as:

  • If \(\beta <-1\) then it represents phantom energy state.

  • If \(0>\beta >-1/3\) then it represents quintessence type matter contents.

  • If \(\beta <-1/3\) then it represents dark energy state.

Now, we explore the stable and unstable characteristics of thin-shell in the background of improved Schwarzschild BH by using \(\Pi _{20cts}\) for phantomlike EoS graphically as shown in Figs. 6, 7 and 8. It is very interesting to mention that the stable/unstable behavior of thin-shell follows the basic condition of thin-shell that shell radius must be greater than the radius of event horizon (see Fig. 1 for event horizon and Figs. 6, 7 and 8 for thin-shell configuration). Hence, our desired results related to the stability of thin-shell are formed after the position of the event horizon. It is found that thin-shell shows stable behavior for both Schwarzschild and improved Schwarzschild BHs filled with quintessence type matter contents (Fig. 6). It is noted that thin-shell stability is decreased for the choice of improved Schwarzschild BH as compared to Schwarzschild BH. Thin-shell stability increases for higher values of mass. Similarly, we obtain the same results for the choice of dark energy type matter contents (Fig. 7). The dark energy type matter contents show a more stable configuration than the quintessence type matter distribution. For phantom energy type EoS, thin-shell shows unstable behavior for every choice of physical parameters (Fig. 8). Hence, thin-shell expressed stable configuration for the choice of quintessence and dark energy type EoS shows unstable behavior for phantom energy type EoS.

Fig. 8
figure 8

Stability analysis of thin-shell filled with phantom energy type matter contents for \( m=0.1\) (left plot) and \(m=0.2\) (right plot) verses \(w_0\) with \(\gamma =0.05\)

Full size image

5 Final remarks

This paper is devoted to explaining the geometrical construction of thin-shell with inner flat spacetime and outer RGI Schwarzschild BH through a cut and paste approach. The thin layer of matter contents plays a vital role in the dynamics as well as the stable configuration of thin-shell. The components of the stress–energy tensor are calculated from the reduced form of Einstein field equations at the hypersurface which develop the dynamical equations of these constructed geometries. We observed the graphical behavior of the metric function and found that the position of the event horizon of RGI Schwarzschild is less than the Schwarzschild BH (see Fig. 1). Then, we are interested to explore the dynamical configuration of thin-shell composed of the massless and massive scalar field by using KG and conservation equations. Further, we explored the stable configuration of thin-shell filled with matter distribution which follows quintessence, dark energy, and phantom energy type EoS with linearized radial perturbation about equilibrium shell radius through critical values of \(\Pi _{20}\). The results are mentioned in detail as follows:

Firstly, thin-shell dynamics in the context of scalar field are discussed by using the effective potential and shell radius of thin-shell without considering the equilibrium position of shell radius. In this regard, we consider conservation equation and KG equation to explore the behavior of effective potential, shell radius, and scalar field in the background of proper time. The analysis of effective potential and shell radius with initial condition \(\dot{w}>0\) with particular values parameters are shown in Figs. 2 and 3. Figures 4 and 5 explained the behavior of massive scalar shells and massive scalar fields, respectively. Despite the lack of general knowledge about the collapse of a massive scalar field, we conducted a numerical study of various scenarios to uncover key characteristics of the dynamic equations. Notably, certain parameter selections resulting in a massive scalar shell structure exhibited an oscillatory configuration. This configuration featured a continual exchange of potential and kinetic energy, which was made possible by the fluctuating surface pressure of the shell and the pull of gravity (Fig. 5).

Secondly, the stable configuration of developed structure explored by using linearized radial perturbation about equilibrium shell radius in the background of phantomlike EoS. It is very interesting to mention that the graphical analysis of thin-shell follows the basic condition of thin-shell that the shell radius must be greater than the radius of event horizon \(w>r_h\) (see Figs. 1, 6, 7 and 8). The stability of thin-shell is observed by considering \(\Pi _{20cts}\) for phantomlike EoS graphically as shown in Figs. 6, 7 and 8. It is noted that thin-shell expressed stable behavior for both quintessence and dark energy type matter contents. Thin-shell represented unstable configuration for every choice of physical parameters for phantom energy type EoS (Fig. 8). It is found that the dark energy type matter contents show a more stable configuration than the quintessence type matter distribution.

It is concluded that the stability of thin-shell is decreased for the choice of RGI Schwarzschild BH as compared to Schwarzschild BH.