1 Introduction

In 1973, Ablowitz, Kaup, Newell and Segur (AKNS) generalized the linear operators based on the results from Zakharov and Shabat [1], they obtained nonlinear Schrödinger (NLS), sine-Gordon, Korteweg-de Vries (KdV), modified KdV equations and so on [2,3,4,5]. It follows that

$$\begin{aligned} v_{x}=Xv,~X=\left( \begin{array}{cc} -ik &{} q(x,t) \\ r(x,t) &{} ik \\ \end{array} \right) , \end{aligned}$$
(1.1)

which is the space evolution equation, where q(x, t), r(x, t) are two complex-valued functions, k is the spectral parameter and \(v(x,t)=\left( \begin{array}{c} v_{1}(x,t) \\ v_{2}(x,t)\\ \end{array} \right) \). On the other hand, the time evolution equation of the AKNS system is given by

$$\begin{aligned} v_{t}=Yv,~Y=\left( \begin{array}{cc} A &{} B \\ C &{} -A \\ \end{array} \right) , \end{aligned}$$
(1.2)

where A, B, C can be defined with the polynomials of k. It can be expressed as

$$\begin{aligned} A=\sum \limits _{j=0}^{3}A_{j}k^{j},~B=\sum \limits _{j=0}^{3}B_{j}k^{j},~C=\sum \limits _{j=0}^{3}C_{j}k^{j}. \end{aligned}$$
(1.3)

According to the compatibility condition \(v_{xt}=v_{tx}\), it reads

$$\begin{aligned} {\left\{ \begin{array}{ll} A_{x}=qC-rB,\\ q_{t}=B_{x}+2ikB+2qA,\\ r_{t}=C_{x}+2ikC+2rA. \end{array}\right. } \end{aligned}$$
(1.4)

Assume that \(A=-\frac{i\cos u}{4k}\), \(B=\frac{i\sin u}{4k}=C\) and, \(q(x,t)=-r(x,t)=-\frac{u_{x}}{2}\), ones obtained the local sine-Gordon equation

$$\begin{aligned} u_{xt}=\sin u. \end{aligned}$$
(1.5)

Based on a symmetric constraint condition

$$\begin{aligned} r(x,t)=q(-x,-t), \end{aligned}$$
(1.6)

the Eq. (1.5) can be transformed into the nonlocal sine-Gordon case,

$$\begin{aligned} \left( \frac{i}{4k}\cos u\right) _{x}=\frac{i}{2}\big (q(x,t)q(-x,-t)\big )_{t}. \end{aligned}$$
(1.7)

In other words, the Eq. (1.7) is also a conservation law equation. It also indirectly indicates that the nonlocal sine-Gordon equation has real physical significance and can be applied to classical mechanics and dynamic systems [6].

What’s more, the nonlocal symmetry is a very important research field [7]. In 1998, Bender and Boettcher obtained the nonlocal symmetry through replacing the Hermiticity of the Hamiltonians in quantum theory, and fully proved that the nonlocal symmetry also maintains more basic properties in quantum Physics. Thus, the nonlocal symmetry has been successfully applied to optics, electricity and so on [8,9,10,11,12,13,14]. Then, Ablowitz proposed the nonlocal nonlinear Schrödinger equation and shown an integrable infinite dimensional Hamiltonian equation by the PT symmetric [15]. PT symmetry has been applied in fields such as single-mode laser, optoelectronic oscillators, sensing, and unidirectional transmission. For the nonlocal nonlinear Schrödinger equation, it was applied in a physical application of magnetics and physical intuition differ from local case. And a large number of models of the nonlocal integrable systems were proposed and studied [16,17,18,19,20]. Therefore, according to the construction of Darboux transformation for the local integrable systems, lots of the nonlocal integrable equations have also been studied by the method of Darboux transformation [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Based on this, we apply the Darboux transformation to the quantum sine-Gordon equation.

This article is organized as follows. In Sect. 2, based on a gauge transformation, we deform the space and time evolution Eqs. (1.1) and (1.2) into the new linear equations (2.2). Then, we obtain the relation between the new potentials and the old cases via 1-fold Darboux transformation. And, the N-fold Darboux transformation for the nonlocal sine-Gordon equation is given by the Proposition 1. In Sect. 3, we give the forms of 1-soliton solution, 2-soliton solutions, kink solution and mixed solutions via a seed solution. In fact, by taking different values of \(a_{i}\) and \(b_{i}\), other forms of the solutions for the nonlocal sine-Gordon equation can be obtained.

2 The construction of Darboux transformation for the nonlocal sine-Gordon equation

Based on the procedures of the Darboux transformation for the classical local integrable systems, ones obtain the Darboux transformation for the nonlocal sine-Gordon equation (1.7). Assuming that the seed solution is \(q(x,t)=0\), many solutions different from the classical local case are obtained due to the constraint condition (1.6). Firstly, we introduce a gauge transformation,

$$\begin{aligned} v^{(1)}=T^{(1)}v. \end{aligned}$$
(2.1)

Thus, the space and time evolution equations (1.1) and (1.2) can be deduced to

$$\begin{aligned} {\left\{ \begin{array}{ll} v_{x}^{(1)}=(T^{(1)}_{x}+T^{(1)}X)(T^{(1)})^{-1}v^{(1)}\equiv X^{(1)}v^{(1)},\\ v_{t}^{(1)}=(T^{(1)}_{t}+T^{(1)}Y)(T^{(1)})^{-1}v^{(1)}\equiv Y^{(1)}v^{(1)}. \end{array}\right. } \end{aligned}$$
(2.2)

It is worth mentioning that \(X^{(1)}\) and \(Y^{(1)}\) have the same forms as X and Y, and these two references have been proven through calculations [16, 33], at the same time, we also provided the corresponding calculation process later. It means that

$$\begin{aligned}{} & {} X^{(1)}=\left( \begin{array}{cc} -ik &{} q^{(1)}(x,t) \\ r^{(1)}(x,t)&{} ik \\ \end{array} \right) , \nonumber \\{} & {} \quad Y^{(1)}=\left( \begin{array}{cc} \frac{i}{4k}\cos u &{} \frac{i}{4k}\sin u \\ \frac{i}{4k}\sin u &{} \frac{-i}{4k}\cos u \\ \end{array} \right) . \end{aligned}$$
(2.3)

Given the form of 1-fold Darboux transformation for the nonlocal sine-Gordon equation has a form,

$$\begin{aligned} T^{(1)}=I_{2\times 2}k+g^{(1)},~g^{(1)}=\left( \begin{array}{cc} g^{(1)}_{11}(x,t) &{} g^{(1)}_{12}(x,t)\\ g^{(1)}_{21}(x,t) &{} g^{(1)}_{22}(x,t) \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(2.4)

where \(I_{2\times 2}\) is a \(2\times 2\) identity matrix. Substitute the Eq. (2.4) into the Eq. (2.2), ones obtain the relations between the new potentials and the old potentials, which is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} q^{(1)}(x,t)=q(x,t)-2ig^{(1)}_{12}(x,t),\\ r^{(1)}(x,t)=r(x,t)-2ig^{(1)}_{21}(x,t). \end{array}\right. } \end{aligned}$$
(2.5)

Combine with the constraint condition (1.6) and the Eq. (2.5), we have

$$\begin{aligned} g^{(1)}_{12}(x,t)=g^{(1)}_{21}(-x,-t). \end{aligned}$$
(2.6)

Let \(\alpha =\left( \begin{array}{c} \alpha _{1}(k_{j}) \\ \alpha _{2}(k_{j}) \\ \end{array} \right) \), and \(\beta =\left( \begin{array}{c} \beta _{1}(k_{j}) \\ \beta _{2}(k_{j}) \\ \end{array} \right) \) are the eigenvectors of the linear equations (1.1) and (1.2), \(k_{j} (j=1,2)\) are the eigenvalues corresponding to \(\alpha \) and \(\beta \). Then we have

$$\begin{aligned} T^{(1)}(\alpha (k_{j})+\sigma _{j}\beta (k_{j}))=0,~j=1,2, \end{aligned}$$
(2.7)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} k_{j}+g_{11}^{(1)}+\gamma _{j}g_{12}^{(1)}=0, \\ g_{21}^{(1)}+\gamma _{j}(k_{j}+g_{22}^{(1)})=0, \end{array}\right. } \end{aligned}$$
(2.8)

where the specific forms of \(\gamma _{j}\) are given by \(\gamma _{j}=\frac{\alpha _{2}(k_{j})+\sigma _{j}\beta _{2}(k_{j})}{\alpha _{1}(k_{j})+\sigma _{j}\beta _{1}(k_{j})}\) and \(\sigma _{j}\) are constants. Solving the Eq. (2.8), \((g^{(1)}_{ij})_{1\le i,j\le 2}\) are given as

$$\begin{aligned} g^{(1)}_{11}=\frac{\det \left( \begin{array}{cc} -k_{1} &{} \gamma _{1} \\ -k_{2} &{} \gamma _{2} \end{array}\right) }{\det \left( \begin{array}{cc} 1 &{} \gamma _{1} \\ 1 &{} \gamma _{2} \end{array}\right) },~ g^{(1)}_{12}=\frac{\det \left( \begin{array}{cc} 1&{}-k_{1} \\ 1&{}-k_{2} \end{array}\right) }{\det \left( \begin{array}{cc} 1 &{} \gamma _{1} \\ 1 &{} \gamma _{2} \end{array}\right) }, \end{aligned}$$
(2.9)
$$\begin{aligned} g^{(1)}_{21}=\frac{\det \left( \begin{array}{cc} -k_{1}\gamma _{1} &{} \gamma _{1} \\ -k_{2}\gamma _{2} &{} \gamma _{2} \end{array}\right) }{\det \left( \begin{array}{cc} 1 &{} \gamma _{1} \\ 1 &{} \gamma _{2} \end{array}\right) },~ g^{(1)}_{22}=\frac{\det \left( \begin{array}{cc} 1&{}-k_{1}\gamma _{1} \\ 1&{}-k_{2}\gamma _{2} \end{array}\right) }{\det \left( \begin{array}{cc} 1 &{} \gamma _{1} \\ 1 &{} \gamma _{2} \end{array}\right) }. \end{aligned}$$
(2.10)

Thus, the Eq. (2.4) can be rewritten into

$$\begin{aligned} T^{(1)}{=}\left( \begin{array}{cc} k &{} 0 \\ 0 &{} k\\ \end{array} \right) +\frac{1}{\gamma _{2}-\gamma _{1}} \left( \begin{array}{cc} k_{2}\gamma _{1}-k_{1}\gamma _{2} &{} k_{1}-k_{2} \\ \gamma _{1}\gamma _{2}(k_{2}-k_{1}) &{} k_{1}\gamma _{1}-k_{2}\gamma _{2} \\ \end{array} \right) .\nonumber \\ \end{aligned}$$
(2.11)

Based on the formulations

$$\begin{aligned} {\left\{ \begin{array}{ll} T^{-1}=\frac{T^{\star }}{\det (T)},\\ (T_{x}+TX)T^{\star }=\det (T)A(k), \end{array}\right. } \end{aligned}$$
(2.12)

where \(A(k)=\left( \begin{array}{cc} a^{(1)}_{11}k+a^{(0)}_{11} &{} a^{(1)}_{12}k \\ a^{(1)}_{21}k &{} a^{(1)}_{22}k+a^{(0)}_{22}\\ \end{array} \right) \), and \(T^{\star }\) represents the adjoint matrix of T. It shows that

$$\begin{aligned} T^{(1)}_{x}+T^{(1)}X^{(1)}=A(k)T^{(1)}, \end{aligned}$$
(2.13)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} g_{11,x}^{(1)}-ik^{2}-ikg^{(1)}_{11}+g^{(1)}_{12}q^{(1)}(-x,-t)=a^{(1)}_{11}k^{2}\\ +(a^{(1)}_{11}g^{(1)}_{11}+g^{(1)}_{21}a^{(1)}_{12} +a^{(0)}_{11})k+g^{(1)}_{11}a^{(0)}_{11},\\ g_{12,x}^{(1)}+kq^{(1)}+g^{(1)}_{11}q^{(1)}+ikg^{(1)}_{12} \\ =a^{(1)}_{11}g^{(1)}_{12}k+a^{(1)}_{12}k^{2}+g^{(1)}_{12}a^{(0)}_{11}+g^{(1)}_{22}a^{(1)}_{12}k,\\ g_{21,x}^{(1)}-ikg^{(1)}_{21}+g^{(1)}_{22}q^{(1)}(-x,-t) +kq^{(1)}(-x,-t)\\ =a^{(1)}_{21}k^{2}+(a^{(1)}_{21}g^{(1)}_{11} +g^{(1)}_{21}a^{(1)}_{22})k+a^{(0)}_{22}g^{(1)}_{21},\\ g_{22,x}^{(1)}+q^{(1)}g^{(1)}_{21}+ik^{2} +ikg^{(1)}_{22}=a^{(1)}_{21}g^{(1)}_{12}k+a^{(1)}_{22}k^{2} \\ +(a^{(1)}_{22}g^{(1)}_{22}+a^{(0)}_{22})k+a^{(0)}_{22}g^{(1)}_{22}. \end{array}\right. }\nonumber \\ \end{aligned}$$
(2.14)

Comparing the order of k on both sides of the Eq. (2.14), we have

$$\begin{aligned}{} & {} a^{(1)}_{11}=-i,~a^{(0)}_{11}=0, \nonumber \\{} & {} \quad ~a^{(1)}_{12}=q^{(1)},~a^{(1)}_{21}=q^{(1)}(-x,-t), \nonumber \\{} & {} \quad ~a^{(1)}_{22}=i,~a^{(0)}_{22}=0. \end{aligned}$$
(2.15)

Thus, \(X^{(1)}=\left( \begin{array}{cc} -ik &{} q^{(1)}(x,t) \\ q^{(1)}(-x,-t)&{} ik \\ \end{array} \right) \), where \(q^{(1)}(x,t)\) and q(x, t) are connected by the Eq. (2.5).

Proposition 1

The N-fold Darboux transformation for the nonlocal sine-Gordon equation (1.7) can be given by

$$\begin{aligned}{} & {} v^{(N)}=T_{N}(k)v, \nonumber \\{} & {} \quad ~T_{N}(k)=T^{(N)}(k)T^{(N-1)}(k)\cdots T^{(p)}(k)\cdots T^{(1)}(k),\nonumber \\ \end{aligned}$$
(2.16)

and

$$\begin{aligned}{} & {} T^{(p)}(k)=\left( \begin{array}{cc} k &{} 0 \\ 0 &{} k \\ \end{array} \right) +\frac{1}{\gamma _{2p}-\gamma _{2p-1}} \nonumber \\{} & {} \left( \begin{array}{cc} k_{2p}\gamma _{2p-1}-k_{2p-1}\gamma _{2p} &{} k_{2p-1}-k_{2p} \\ \gamma _{2p-1}\gamma _{2p}(k_{2p}-k_{2p-1}) &{} k_{2p-1}\gamma _{2p-1}-k_{2p}\gamma _{2p} \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(2.17)

where \(\gamma _{j}=\frac{\alpha _{2}^{(p-1)}(k_{j})+\sigma _{j}\beta _{2}^{(p-1)}(k_{j})}{\alpha _{1}^{(p-1)}(k_{j}) +\sigma _{j}\beta _{1}^{(p-1)}(k_{j})}\), \(j=2p, 2p-1\), \(p=1, 2,\ldots , N\),

\(\alpha ^{(p)}(k)=\left( \begin{array}{c} \alpha ^{(p)}_{1}(k)\\ \alpha ^{(p)}_{2}(k) \\ \end{array} \right) =T^{(p)}\alpha ^{(p-1)}(k_{1}, k_{2},\ldots , k_{2p}) \),

\(\beta ^{(p)}(k)=\left( \begin{array}{c} \beta ^{(p)}_{1}(k)\\ \beta ^{(p)}_{2}(k) \\ \end{array} \right) =T^{(p)}\beta ^{(p-1)}(k_{1}, k_{2},\ldots , k_{2p}) \),

$$\begin{aligned} g^{(p)}_{12}(x,t)=g^{(p)}_{21}(-x,-t). \end{aligned}$$
(2.18)

Thus, we can get the relations between the old and new solutions,

$$\begin{aligned} q^{(N)}(x,t)=q(x,t)-2i\sum \limits _{p=1}^{N}g_{12}^{(p)},~p=1,2,\ldots ,N. \nonumber \\ \end{aligned}$$
(2.19)

It is worth mentioning that the Darboux transformation of the nonlocal sine-Gordon equation (1.7) is different from the local case, because the constraints are added to the nonlocal case, this is also the innovation of this article.

3 Exact solutions for the nonlocal sine-Gordon equation

According to the Proposition 1, we can obtain a new solution for the nonlocal sine-Gordon equation (1.7) via a seed solution \(q(x,t)=0\). Follow from the the space and time evolution equations (1.1) and (1.2), we have

\(\alpha (x,t;k)=\left( \begin{array}{c} \text {e}^{-ikx-\frac{it}{4k}} \\ 0 \\ \end{array} \right) , \)

\(\beta (x,t;k)=\left( \begin{array}{c} 0 \\ \text {e}^{ikx+\frac{it}{4k}} \\ \end{array} \right) , \)

and

Fig. 1
figure 1

Where \(a_{1}=-1, b_{1}=1\)

Full size image
Fig. 2
figure 2

Where \(a_{1}=-1, b_{1}=1\)

Full size image
Fig. 3
figure 3

Where \(a_{1}=0.3, b_{1}=-1\)

Full size image
Fig. 4
figure 4

Where \(a_{1}=0.3, b_{1}=-1\)

Full size image
Fig. 5
figure 5

Where \(a_{1}=0.1, b_{1}=1, a_{3}=1, b_{3}=0.2 \)

Full size image
Fig. 6
figure 6

Where \(a_{1}=0, b_{1}=1, a_{2}=-1, b_{1}=0, a_{3}=0.1, b_{3}=1\)

Full size image
Fig. 7
figure 7

Mixed solutions with soliton and periodic wave with \(a_{1}=0, b_{1}=1, a_{2}=-1, b_{1}=0, a_{3}=0.1, b_{3}=1\)

Full size image
$$\begin{aligned} \gamma _{j}=\sigma _{j}\text {e}^{2ik_{j}x+\frac{it}{2k_{j}}},~j=1,2, \end{aligned}$$
(3.1)
$$\begin{aligned} g^{(1)}_{12}=\frac{k_{1}-k_{2}}{\sigma _{2}\text {e}^{2ik_{2}x+\frac{it}{2k_{2}}} -\sigma _{1}\text {e}^{2ik_{1}x+\frac{it}{2k_{1}}}}, \end{aligned}$$
(3.2)
$$\begin{aligned} g^{(1)}_{21}=(k_{2}-k_{1})\frac{\sigma _{1}\sigma _{2}\text {e}^{2i(k_{1}+k_{2})x +(\frac{i}{2k_{1}}+\frac{i}{2k_{2}})t}}{\sigma _{2}\text {e}^{2ik_{2}x+\frac{it}{2k_{2}}} -\sigma _{1}\text {e}^{2ik_{1}x+\frac{it}{2k_{1}}}}. \end{aligned}$$
(3.3)

Based on the equation (2.18), we have

$$\begin{aligned} \sigma ^{2}_{1}=1,~\sigma ^{2}_{2}=1. \end{aligned}$$
(3.4)

It is obvious that there are many values for \(\sigma _{1}\) and \(\sigma _{2}\) in the Eq. (3.4), in fact, \(q^{(1)}(x,t)\) is the solution to the classical sine-Gordon equation as \(\sigma _{1}=1\), \(\sigma _{2}=1\). It is obvious that \(\sigma _{1}^{2}=1\), \(\sigma _{2}^{2}=1\) not only contain solutions for the classical case but also provide solutions for other cases. From the subsequent analysis, this undoubtedly enriches the types of understanding and is also more conducive to analyzing the dynamic behavior of the solutions. Here we emphasis on the solution for the nonlocal sine-Gordon equation as \(\sigma _{1}=1\), \(\sigma _{2}=-1\). Under the condition of providing some special parameter values, we can get the various figures of complex solutions but are different from the local cases. Then, the new solution of the nonlocal sine-Gordon equation is given by means of the first-order Darboux transformation,

$$\begin{aligned} q^{(1)}(x,t)=2i\frac{k_{1}-k_{2}}{\text {e}^{2ik_{2}x+\frac{it}{2k_{2}}}+\text {e}^{2ik_{1}x+\frac{it}{2k_{1}}}}. \end{aligned}$$
(3.5)

Case 1,

Let \(k_{1}=a_{1}+ib_{1}\), \(k_{2}=a_{1}-ib_{1}\), where \(a_{1}, b_{1}\) are real. we can obtain the soliton solution for the nonlocal sine-Gordon equation, which is given by

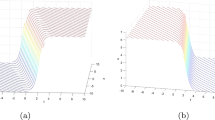
$$\begin{aligned}{} & {} q^{(1)}(x,t) \nonumber \\{} & {} =-2b_{1}\text {e}^{-2ia_{1}\left( x+\frac{t}{4(a^{2}_{1}+b^{2}_{1})}\right) } \text {sech}\left( 2b_{1}(x-\frac{t}{4(a^{2}_{1}+b^{2}_{1})})\right) .\nonumber \\ \end{aligned}$$
(3.6)

And, the Fig. 1 shows the three-dimensional diagram of one-soliton, Fig. 2 shows the trajectory and density of one-soliton. It is worth mentioning that the propagation direction of solitons is single due to \(\frac{1}{4(a^{2}_{1}+b^{2}_{1})}>0\).

Case 2,

Let \(k_{1}=a_{1}+ib_{1}\), \(k_{2}=2a_{1}-i0\), we have

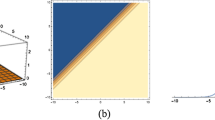
$$\begin{aligned} q^{(1)}(x,t)=\frac{(6ia_{1}-2b_{1})\text {e}^{4ia_{1}(x+\frac{t}{16a^{2}_{1}})}}{1+\text {e}^{-2b_{1}x+\frac{b_{1}t}{2(a^{2}_{1}+b^{2}_{1})}+4ia_{1}x+\frac{it}{4a_{1}}+\frac{ia_{1}}{2(a^{2}_{1}+b^{2}_{1})}}}. \end{aligned}$$
(3.7)

If \(b_{1}>0\), the complexiton propagates like a kink wave, \(b_{1}<0\), it might be the anti-kink waves. And Fig. 3 shows the three-dimensional diagram of the kink solutions. Although it can not be seen intuitively from the shape of the solution that this is a kink wave. Given the trajectory of the solution at different times, the kink wave can be perfectly displayed in Fig. 4.

Case 3,

And, we can obtain multiple mixed solutions via the two-order Darboux transformation (2.16). By giving different spectral parameters, we can get completely different solutions from the classical sine-Gordon equation, such as periodic solutions, rogue wave solutions. Let \(\lambda _{1}=\lambda ^{*}_{2}\), \(\lambda _{3}=\lambda ^{*}_{4}\), the two soliton solutions of the Eq. (1.7) can be given, thus we have

$$\begin{aligned} q^{(2)}(x,t)=-2i(g^{(1)}_{12}(x,t)+g^{(2)}_{12}(x,t)), \end{aligned}$$
(3.8)

where

$$\begin{aligned} g^{(2)}_{12}(x,t)=\frac{k_{3}-k_{4}}{\gamma _{4}-\gamma _{3}}, \end{aligned}$$
(3.9)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma _{3}=\frac{\alpha ^{(1)}_{2}(k_{3})+\sigma _{3}\beta ^{(1)}_{2}(k_{3})}{\alpha ^{(1)}_{1}(k_{3}) +\sigma _{3}\beta ^{(1)}_{1}(k_{3})},\\ \gamma _{4}=\frac{\alpha ^{(1)}_{2}(k_{4})+\sigma _{4}\beta ^{(1)}_{2}(k_{4})}{\alpha ^{(1)}_{1}(k_{4}) +\sigma _{4}\beta ^{(1)}_{1}(k_{4})}, \end{array}\right. }\sigma _{3}=1, \sigma _{4}=-1, \nonumber \\ \end{aligned}$$
(3.10)
$$\begin{aligned} \alpha ^{(1)}(k_{j})=\left( \begin{array}{c} \alpha ^{(1)}_{1}(k_{j}) \\ \alpha ^{(1)}_{2}(k_{j}) \\ \end{array} \right) =T^{(1)}\left( \begin{array}{c} e^{-ik_{j}t-\frac{it}{k_{j}}} \\ 0 \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(3.11)
$$\begin{aligned} \beta ^{(1)}(k_{j})=\left( \begin{array}{c} \beta ^{(1)}_{1}(k_{j}) \\ \beta ^{(1)}_{2}(k_{j}) \\ \end{array} \right) =T^{(1)}\left( \begin{array}{c} 0\\ e^{ik_{j}t+\frac{it}{k_{j}}} \\ \end{array} \right) , j=3,4.\nonumber \\ \end{aligned}$$
(3.12)

Here is the density diagram of two solitons, see the Fig. 5.

Case 4,

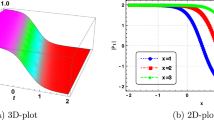
In order to demonstrate the mixed solutions with soliton and periodic rogue wave of the Eq. (1.7), we let the spectral parameters as \({\text {Re}}(\lambda _{1})=0, {\text {Im}}(\lambda _{2})=0\), \(\lambda _{3}=\lambda ^{*}_{4}\), so the mixed solutions can be given by Figs. 6 and 7.

It is worth noting that the second figure in Fig. 7 shows that when we give different times and have a certain spatial location, the three lines all tend to the same constant.

4 Conclusions

As one of the most classical methods, Darboux transformation can successfully give various solutions of this kind of nonlocal integrable systems. At the same time, nonlocal model is also widely used in nonlinear optics. Therefore, the study of nonlocal integrable systems is also very important and meaningful. The main contribution of this paper is to propose the nonlocal sine-Gordon equation based on the symmetric relation. At the same time, it can be clearly seen that the nonlocal sine-Gordon equation satisfies the conservation law relationship, which means it has strict physical significance. Meanwhile, we give several kinds of analytical solutions of this equation through mathematical methods, and analyze the asymptotic properties of these solutions.