Symmetry-based study and dynamics of casual bulk viscous matter-dominated universe

Abstract

The dynamics of cosmological expansion is studied for a spatially flat matter-dominated universe filled with barotropic casual bulk viscous fluid. The evolution equation for the Hubble parameter is derived using Friedmann equations and conservation law for the viscous fluid, in which the viscous pressure is modeled by truncated version of the full Israel-Stewart theory of bulk viscosity. We use a Lie symmetry-based approach to study the evolution of the expansion rate of the Universe. The model equation possesses eight-parameter Lie symmetry generators and gives two different analytic group invariant solutions for the Hubble parameter. Expressions for various important cosmological parameters are obtained and values are estimated analytically for the explanation of the evolution dynamics of the Universe. The interesting features of the obtained symmetry-based solutions are that, one satisfies the present acceleration of the Universe, while the other could not support present accelerating phase, rather represents a universe dominated by non-viscous stiff fluid. We make useful checks on the observational constraints on the model parameters from the latest released observational data. The accelerating phase of the current universe is investigated using observational bounds and compared the model under investigation with the $\Lambda$CDM model. The evolutionary cosmic phases obtained from the analysis of the Lie symmetry-based solutions correspond to the association with the critical points in the equivalent phase space. These interesting features are investigated and analyzed using dynamical systems approach.

1 Introduction

Observation data from type Ia supernovae [1,2,3,4,5,6,7], as well as cosmic microwave background (CMB) [8] led to the discovery that the expansion of the present universe is accelerating. It is well known that the present accelerated expansion of our universe cannot be explained only with matter-dominated universe. It is a fact from the measurements of cosmic microwave anisotropy [9] and WMAP data [10], that most of the energy of the universe is some sort of dark energy (cosmic matter with negative pressure), with a ratio of pressure to density $\omega \le -\frac{1}{3}$ [11, 12]. The dark energy is gravitationally repulsive. The main property for the dark energy fluid lies on the negativity of its pressure in order to achieve an accelerating expansion. The most natural dark energy candidate is a cosmological constant ($\Lambda$) which arises as the result of a combination of quantum field theory and general relativity. Although the dark energy can be explained by introducing ($\Lambda$) into general relativity, it has two severe problems [13]. First, its theoretical value is between 60 and 120 orders of magnitude, greater than the observed value for the dark energy and the second problem is the so-called cosmic coincidence problem [14]. An alternative to the cosmological constant ($\Lambda$) is a self-interacting scalar field, known as quintessence [15]. In this context, a generalized Chaplygin gas (GCG) model, an alternative to quintessence model, can also explains the acceleration of the Universe via an exotic equation of state [15,16,17]. But, in spite of many attractive features of GCG model, this model also suffers from a major drawback as it predicts strong small scale oscillations or instabilities in the matter power spectrum [13, 15].

The astrophysical as well as cosmological observations indicate that the content of our universe cannot be modeled by the energy-momentum tensor only using the perfect fluid, but dissipative effects should be considered in studying the evolution of the Universe [18,19,20,21]. Dissipative processes are certainly to be present in any realistic theory of evolution of our universe. The evolution of the Universe contains a sequence of important dissipative processes [21]. In this context, the observed physical phenomena such as the remarkable degree of isotropy of the cosmic microwave background radiation and large entropy per baryon, the evolution of cosmic string due to their interaction with each other and the surrounding matter, interaction between matter and radiation, particle creation process and formation of galaxies and interaction between different components of dark matter and dark energies, which not yet been fully discovered, suggest analysis of dissipative effects in cosmology [22,23,24]. In isotopic and homogeneous universe, the dissipative processes are usually characterized by the bulk viscosity, neglecting heat dissipation and shear viscosity which are incompatible with the cosmological principle [25]. The rich viscosity effects in cosmos may be considered as an assemblage of a variety of dynamical and kinematics effects of locally cosmic motion and globally cosmological large-scale evolution, which may show different features when observed on different scales and/or in different evolutional stages [25]. Bulk viscosity exists intrinsically in the observational cosmic evolution with various effects for different evolutionary phases endowed with complicated cosmic media [25]. Bulk viscosity can reduce the effect of the kinetic pressure and makes the effective pressure negative [26]. This creates a repulsive gravity and contributes to the accelerating expansion of the Universe. To maintain the fluid hypothesis to dark energy and ensure thermodynamic compatibility, one should consider dissipative processes like bulk viscosity [22]. Here, it is important to note that a plausible scenario for the accelerating expansion is provided by a viscous imperfect fluid that keeps the energy conditions satisfied and possesses an effective negative pressure [27]. Consequently, it is argued that an effective bulk viscous pressure can play the role of an agent i.e. dark energy that drives the present acceleration of the Universe and could be a good model for the present accelerated universe. Interestingly, the well known $\Lambda$CDM model and the GCG models can be reproduced as special cases of this imperfect viscous fluid description. Thus like other forms of dark energy components, viscous imperfect fluid plays an important role in explaining the accelerated expansion of the universe [26, 28]. The possibility that the present acceleration of the Universe is driven by a kind of viscous fluid, is exploited in [29].

It is well known that thermodynamics of our early universe was far from equilibrium. In this context, it is to be noted that from the thermodynamics point of view bulk viscosity in a physical system is due to its deviation from local thermodynamic equilibrium [30]. In a cosmological fluid the viscosity arises when the fluid expands to fast so that the system does not have enough time to restore the local equilibrium and it appears as an effective pressure restoring the system to its local thermodynamic equilibrium [31]. When the fluid reaches again the thermal equilibrium then the bulk viscosity pressure vanishes [30, 32,33,34]. In an expanding universe the expansion process is likely to be collection of states that lose their thermal equilibrium in a small fraction of time giving rise to the existence of bulk viscosity and bulk viscosity is a measure of the pressure required to restore equilibrium of the expanding system [35]. In dissipative fluid dynamics, the connection between the macroscopic theory and microscopic theory enters through the transport coefficients of the matter. Qualitatively, one can interpret the bulk viscosity as a macroscopic consequence coming from the frictional effects within the fluid that originate from microphysical molecular-like interaction. The interaction between galaxies or baryon clumps and other thermal interactions occurred in local area could be effectively depicted by molecular-like interactions that are seen on large-scale [25].

Interest in viscous theories in cosmology has increased in recent years because bulk viscosity is the only possible dissipative mechanism in homogeneous and isotropic spacetimes. Isotropic spatially-flat homogeneous viscous cosmological models have been investigated through causal and non-causal theories. The thermodynamics of viscous dark matter fluid can be described using different formalisms. In the first-order theories due to Eckart – the so-called Eckart’s formalism [36], which supposes that the viscous fluid reaches instantaneously the equilibrium at each momentum; on the other hand, in the causal second-order theory – the Israel-Stewart formalism, which includes a relaxation time [21, 37]. The non-causal theory are proposed by Eckart [36]. Eckart’s theory has got the shortcoming that bulk viscous pressure perturbations travel infinitely fast and violate causality, and all its equilibrium states are unstable [38, 39]. This problem arises as it considered only first-order deviation from the equilibrium leading to the parabolic differential equation [40]. Later, Israel and Stewart proposed a more general stable and causal physical theory [41], so called the Israel-Stewart theory which avoids this problem. The implication of second-order theory in cosmology was first considered by Belinskii et. al. [42] and later Pavón et. al. [43]. Particularly, the evolution of a homogeneous isotropic spatially-flat universe filled with a causal viscous fluid has been investigated thoroughly in [42, 43]. The possibility of exponential inflationary solutions driven by bulk viscosity were studied in [21, 44]. In the context of full causal theory that characteristic of evolution equation is so complicated to treat analytically, that several are using Eckart’s formalism because of its simple form and it illustrates a linear relationship between the bulk viscous pressure and the rate of expansion of the Universe [45]. Eckart’s approaches has been used in models explaining the acceleration of the Universe with a bulk viscous fluid. The Israel-Stewart theory, as well as other versions of extended thermodynamics and also Eckart’s standard thermodynamics are all based on near-equilibrium conditions, and cannot be applied to inflationary expansion [21, 46]. But recently, the feasibility of the model has been checked by contrasting with models based on the full Israel-Stewart and the Eckart viscous theories [47]. It has also been shown that the truncated viscous model appears more compatible with astronomical observations than the Eckart and full causal viscous models [47]. In one of our recent articles we have chosen to work with the viscous pressure obtained from a truncated causal transport theory [11, 12] in order to study the late time accelerated expansion of the Universe and provided an in-depth study of viscous effect that supports the transition from early deceleration to present acceleration phase of the universe without any dark energy. The nonlinear terms of full Israel-Stewart (FIS) theory are often neglected in the theory so-called truncated version of viscous theory [47]. Although the truncated theory may lead to a different behavior as compared with the full theory, we shall for simplicity base our analysis on the truncated version of the FIS approach. In this context it is to be noted that close to thermodynamic equilibrium [11, 12, 21, 47], the hydrodynamic equation for viscous pressure can be approximated by the truncated equation and obtained from dynamical equation of bulk viscous pressure of the full causal Israel-Stewart theory [21]. For analysis in situations like expanding universe, such a truncated version is equivalent to the full causal theory due to Israel and Stewart because it also retains stability and causality condition [44, 48]. Therefore, it is reasonable to consider the truncated Israel-Stewart theory, so called the Maxwell-Cattaneo theory [49].

It is well known that the present accelerated expansion of our universe cannot be explained only with matter-dominated universe. In this article we study viscous effect that supports the transition from early matter dominated deceleration phase to present acceleration phase of the Universe without any other forms of dark energy. In view of this, we consider spatially-flat FLRW matter-dominated universe filled with barotropic causal bulk viscous fluid. Several models have been proposed to explain the present accelerating phase of the universe including the viscous unified model [22, 26, 50]. Here, the approach sought by us, is the so-called time-honored Lie symmetry formulation. The approach has its origin in the classic work of Sophus Lie, who pioneered this modern approach for studying and finding special solutions of systems of nonlinear partial differential equations (PDEs) [51]. The method introduced by Lie (1891) considers the invariance of the form of the differential equation itself under a set of point transformations of dependent and independent variables. In the many branches of mathematics, physics and engineering, solving a set of partial as well as ordinary differential equations rely on symmetries [52, 53]. Some most important ones are reduction of variables of differential equations, reduction of order of differential equations, conservation laws, mapping one solution curve to another solution curve and construction of the group-invariant solutions [52, 53]. In this context, we should note that symmetries of space-time have been the guiding principle for formulations of all the new fundamental laws of nature [54]. Symmetries are a very important subject to study in many branches of physics for many reasons. Recently, ever increasing interest in studying the Lie point symmetries of differential equations that model physical systems and wide applicability of Lie symmetries [52, 53] has motivated us to employ Lie symmetries method and find symmetry-based solution for bulk-viscous model of the universe. The most important point of a realistic cosmological model is to check the viability of the given model through the known solution of the cosmological equations or by seeking physically plausible new solution that are observationally relevant. An alternative way to extract useful information about the asymptotic behavior of the model rather than searching for a exact analytical solution of the complicated model equation. Here the knowledge of the critical points in the phase space corresponding to a given model is sometime very useful. In this context the presence of the equilibrium points can be correlated with generic cosmological solutions in order to understand the physical nature of cosmic evolution of the realistic universe. Motivated with the idea we also have checked that the dynamical behaviour of the solutions of the present model equation obtained from the symmetries has not been explored yet. In this context, we should note that a different form other than the symmetry analysis and more powerful approach so-called dynamical systems technique is used to analyze the asymptotic behavior of the governing field equations by studying the fixed points of the field equations. This theory helps us to study various phases of the expansion that are coming out from the current cosmological model.

We organize the paper as follows: the basic equation describing the dynamics of expansion rate of spatially-flat FLRW matter dominated universe filled with barotropic causal bulk viscous fluid is obtained in Sect. 2. In Sect. 3 we present the Lie symmetries for the equation and then use these symmetries to find the exact analytical group invariant solutions from invariant curve condition. The nature of evolution of cosmological parameters such as the deceleration parameter, the EoS parameter, the statefinder pair, the density parameter and curvature scalar parameter are studied from the obtained analytical results that agree with the present astronomical observational data in Sect. 4. Section 5 deals with the best estimation of values the free parameters of the bulk viscous model and thereby obtain the values for various cosmological parameters. The obtained results are also compared with the results in $\Lambda$CDM model. Section 6 is devoted to provide dynamical systems analysis of the present model. Finally, we make some concluding remarks in Sect. 7.

2 Cosmological model equation: bulk viscous matter-dominated universe

Almost $96\%$ of the energy density of the universe today consists of an unknown component called dark matter and dark energy. In the standard $\Lambda$CDM model, two mixed fluids (dark matter and dark energy) are assumed. These two fluids influence the cosmic evolution separately. Since both cold dark matter (CDM) and dark energy are invisible and origins of these are yet unknown and even at present the gravitational probe is still unable to differentiate between these two fluids, the so-called dark degeneracy problem [55]. Thus it is considered that the dark components of the Universe are manifestations of a single viscous fluid [15]. Naturally, they are just different aspects of a single fluid, frequently dubbed as the unified dark matter (UDM) model [13, 55, 56]. This formalism is also valid for a cosmological model containing only pressureless fluid with constant bulk viscosity in a flat universe [31]. A spatially flat, homogeneous and isotropic universe can be described by the Friedmann–Lemaître–Robertson–Walker (FLRW) line element,

$$\begin{aligned} ds^{2}=-dt^{2}+S(t)^{2}(dr^{2}+r^{2}d\theta ^{2}+r^{2}\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$

(1)

where $(r,\theta , \phi )$ are the co-moving coordinates, t denotes the cosmic time and S(t) is the scale factor of the Universe. In deriving the model equation we shall restrict ourselves to a FLRW matter-dominated universe filled with a bulk viscous fluid. In the context of consideration of cosmological fluids, the well-known assumption to be dominant along various cosmological epochs belongs to the barotropic class. We have considered the barotropic equation of state for the one component fluid that filled the Universe is

$$\begin{aligned} p=(\gamma -1)\rho , \end{aligned}$$

(2)

where p, $\gamma$ and $\rho$ are the barotropic pressure, barotropic index and the energy density of the fluid respectively. The range of $\gamma$ is $1\le \gamma \le 2$ and for matter $\gamma =1$ implies $p=0$ from (2). Following [20] we get a simple relation among the bulk viscous coefficient $\zeta$, the energy density $\rho$ of the cosmological fluid and the relaxation time for transient bulk viscous effect $\tau$ as

$$\begin{aligned} \tau =\frac{\zeta }{\rho }. \end{aligned}$$

(3)

The relaxation time $\tau (\ge 0)$ is the time the system takes in going back to equilibrium once the divergence of 4-velocity has been switched off. But here we can use a more general form of relaxation time, given by [21]

$$\begin{aligned} \tau =\frac{\zeta }{(\rho +p)c_{b}^{2}}, \end{aligned}$$

(4)

where $c_{b}$ is the speed of the bulk viscous perturbation, i.e., the non-adiabatic contribution to the speed of sound $v_s$ in a dissipative fluid without heat flux or shear viscosity. Generally the speed of sound in dissipative fluid medium can be written as

$$\begin{aligned} v_s^{2}=c_{s}^{2}+c_{b}^{2}, \end{aligned}$$

(5)

where $c_{s}$ and $c_{b}$ are constant and $c_{s}^2=(\frac{\partial p}{\partial \rho })_s$ is the adiabatic contribution. In this context $v_{s}^2 \le 0$ assures the causality condition. As a consequence $c_{s}=0$, the bulk viscous perturbation propagates with speed $c_{b}^{2}=\frac{\zeta }{\rho \tau }$. For bulk viscous universe, the dissipative speed of sound follows the limit of causality $c_b^2\le 1$. As the bulk viscous pressure represents only a small correction to the thermodynamical pressure, it is a reasonable assumption that the inclusion of viscous term in the energy-momentum tensor does not change fundamentally the dynamics of the cosmic evolution and that has been successfully applied for solving problems in astronomical scale of length and time, such as the formulation of the cosmological models. It is well known, in the framework of FLRW metric the shear viscosity has no contribution in the energy-momentum tensor, and the bulk viscosity behaves like an effective pressure. Here we have considered cosmological model in a flat universe filled with two unified fluids in a unified manner. One of them is a bulk viscous fluid characterized by the coefficient of bulk viscosity proportional to the energy density of the form in (2) and the second one is a pressureless matter fluid so that $P_{\textrm{eff}}={\Pi }$ [11, 12]. The expression for pressure of the Universe filled with single bulk viscous fluid is now modified from that of perfect thermodynamical fluid pressure and is given by $P_{\textrm{eff}}=p+\Pi$, i.e. we can consider a splitting into the equilibrium part p plus the contribution of the non-equilibrium part, so-called bulk viscous pressure $\Pi$. In the presence of bulk viscous contribution, the energy–momentum tensor is now modified from that of the isotropic perfect fluid, and for a model containing only imperfect fluid with constant bulk viscosity it takes the form [30]

$$\begin{aligned} T_{\mu \nu } = (\rho +P_{\textrm{eff}})u_\mu u_\nu + P_{\textrm{eff}} g_{\mu \nu }, \end{aligned}$$

(6)

where $u^\mu$ is the 4-velocity. In this context, the presence of viscous fluid modifies the conservation equation accordingly as

$$\begin{aligned} {\dot{\rho }}+3H(\rho +P_{\textrm{eff}})=0. \end{aligned}$$

(7)

It is to be noted that for a perfect fluid we have $\Pi =0$, i.e., $P_{\textrm{eff}}>0$. But $\Pi <0$ is valid for a conventional viscous fluid during expansion. In this context, we have the bulk viscous pressure $\Pi =-3\zeta H$ in the case of first-order Eckart’s theory [57, 58], were, $H=\frac{{\dot{S}}}{S}$ is the Hubble parameter. While, in more realistic second-order causal theories of bulk viscosity, viscous pressure $\Pi$ behaves as a dynamical degree of freedom [59]. Both first- and second-order theories are valid under the condition $\vert \Pi \vert <p$, such that the effective pressure $P_{\textrm{eff}}$ of a viscous fluid or gas is positive. As we have discussed earlier that unlike the first-order Eckart theory, the Israel-Stewart thermodynamics is causal and stable under a wide range of conditions. Therefore, in obtaining the best thermo-hydrodynamic model with the available physical theories, the causal Israel-Stewart theory of bulk viscosity is preferable [21]. According to full casual FIS theory of nonequilibrium thermodynamics, the bulk viscous pressure $\Pi$ follows the transport equation [11, 12]

$$\begin{aligned} \Pi +\tau {\dot{\Pi }}=-3\zeta H-\frac{\epsilon \tau \Pi }{2}\left( 3H+\frac{{\dot{\tau }}}{\tau }-\frac{{\dot{\xi }}}{\xi }-\frac{{\dot{T}}}{T}\right) . \end{aligned}$$

(8)

In this context, it is to be noted that for $\tau =0$, it returns to Eckart’s theory, and we get back the Maxwell–Cattaneo equation for $\epsilon =0$ for truncated causal theory [11, 12, 21]. Considering that the temperature is following barotropic law and having power-law relation $T\propto \rho ^{\frac{(\gamma -1)}{\gamma }}$, it is easy to show that using Gibbs integrability condition [21] for near equilibrium condition $\Pi<<\rho$, the FIS transport equation (8) can be recast in the following truncated form

$$\begin{aligned} \Pi +\tau ^{*}{\dot{\Pi }}=-3\zeta ^{*} H, \end{aligned}$$

(9)

where the reduced relaxation time is $\tau ^{*}=\frac{\tau }{1+3\gamma \tau H}$, and $\zeta ^{*}=\frac{\zeta }{1+3\gamma \tau H}$, is called reduced bulk viscosity [11, 12, 21]. We can account the amount of reduction that depends on the size of $\tau$ relative to H. If $\tau$ represents the order of mean interaction time, then the required condition for the hydrodynamical description is $\tau H<1$. Again, if $\tau H<<1$, then we have $\tau ^{*}\approx \tau$ and $\zeta ^{*}\approx \zeta$. It is also important to note that the term $\tau ^{*}{\dot{\Pi }}$ of (9) describes the relaxation of $\Pi$ towards its standard value $-3\zeta H$, and the conventional Eckart’s treatment is reduced if it is absent.

The Friedmann equations describing the evolution of the flat matter-dominated universe filled with bulk viscous matter are

$$\begin{aligned} H^{2}=\frac{\rho }{3} \end{aligned}$$

(10)

and

$$\begin{aligned} {\dot{H}}+H^{2}=-\frac{1}{6}(\rho +3P_{\textrm{eff}}). \end{aligned}$$

(11)

The overdot on H in (11) represents the derivative with respect to cosmic time t and we have taken $c=8\pi G=1$. In order to model the late time acceleration of the Universe, that is compatible with the recent observations, we study a model of matter-dominated universe taking into consideration the bulk viscous fluid. Now using (7), (9), (10) and (11), we can find

$$\begin{aligned} {\ddot{H}}+\left( 6 H+\frac{1}{\mathcal{\tau } }\right) {\dot{H}}+\frac{3 H^2}{2 \mathcal{\tau } }+\frac{9}{2} H^3 \left( 1-c_b^2\right) =0. \end{aligned}$$

(12)

Equation (12) can be simplified in the form

$$\begin{aligned} {\ddot{H}}+\alpha H{\dot{H}}+\beta H^{3}=0, \end{aligned}$$

(13)

where

$$\begin{aligned} \alpha =6+{{\mathcal {N}}} \end{aligned}$$

(14)

and

$$\begin{aligned} \beta =\frac{3}{2} \left( -3 c_b^2+{{\mathcal {N}}}+3\right) . \end{aligned}$$

(15)

Interestingly, H in (13) satisfies the well known modified Painleve-Ince equation. In writing (13) we have used ${{\mathcal {N}}}$ for ${(\mathcal{\tau } H)}^{-1}$. When ${{\mathcal {N}}}>>1$, the fluid behaves almost perfect and dissipative effects are significant for ${{\mathcal {N}}}\simeq 1$. By changing the variable from cosmic time to $x=ln S$; the differential equation in (13) can be recast to the following form

$$\begin{aligned} \frac{d^{2}H}{d x^{2}}+\frac{1}{H}\left( \frac{dH}{dx}\right) ^{2}+\alpha \frac{dH}{dx}+\beta H=0. \end{aligned}$$

(16)

In the next section, we shall follow the scheme for Lie symmetry analysis for second-order differential equation presented in Appendix A and use the technique to find the symmetries of (16) and obtain the group invariant solution from invariant curve condition.

3 Lie symmetries and group invariant solution of Eq. (16)

Following the methodology of finding Lie symmetry presented in Appendix A, Eq. (16) can be written as

$$\begin{aligned} M(x,\,H,\,\dot{H},\,{\ddot{H}})={\ddot{H}} + \frac{1}{H}{\dot{H}}^2+ \alpha \dot{H} + \beta H=0. \end{aligned}$$

(17)

Here, overdot represents the derivative with respect to x. Using (A4), (A8) and applying the condition in (7) on (17) we get a set of determining linear partial differential equations for $\xi (x,\,H)$ and $\eta (x,\,H)$. Computing the solutions for $\xi (x,\,H)$ and $\eta (x,\,H)$ from the set of determining equations, we obtain the following eight-parameter Lie symmetries given by

$$\begin{aligned} G_{1}&= \partial _{x},&\end{aligned}$$

(18)

$$\begin{aligned} G_{2}&= -\frac{\alpha }{\beta }\partial _{x}+2H\partial _{H},&\end{aligned}$$

(19)

$$\begin{aligned} G_{3}&= \frac{e^{-\frac{1}{2} \left( \alpha +\sqrt{\alpha ^2-8\beta }\right) x}}{H}\partial _{H},&\end{aligned}$$

(20)

$$\begin{aligned} G_{4}&= \frac{e^{\frac{1}{2} \left( -\alpha +\sqrt{\alpha ^2-8\beta }\right) x}}{H}\partial _{H},&\end{aligned}$$

(21)

$$\begin{aligned} G_{5}&= -\frac{1}{\beta }\left( 1+\frac{\alpha }{ \sqrt{\alpha ^2-8 \beta }}\right) e^{ \sqrt{\alpha ^2-8 \beta }\,x}\partial _{x}\nonumber \\ {}&\quad +\frac{2 e^{ \sqrt{\alpha ^2-8 \beta }\,x}}{\sqrt{\alpha ^2-8 \beta }}H\partial _{H},&\end{aligned}$$

(22)

$$\begin{aligned} G_{6}&= -\frac{1}{\beta }\left( 1-\frac{\alpha }{\sqrt{\alpha ^2-8 \beta }}\right) \nonumber \\ {}&\quad \times e^{ -\sqrt{\alpha ^2-8 \beta }\,x}\partial _{x}-\frac{2 e^{-\sqrt{\alpha ^2-8 \beta }\,x}}{\sqrt{\alpha ^2-8 \beta }}H\partial _{H},&\end{aligned}$$

(23)

$$\begin{aligned} G_{7}&=4 H^2 e^{\frac{1}{2} \left( \alpha +\sqrt{\alpha ^2-8 \beta }\right) x}\partial _{x} \nonumber \\ {}&\quad -\bigg (\alpha -\sqrt{\alpha ^2-8 \beta }\bigg )H^3 e^{\frac{1}{2} \left( \alpha +\sqrt{\alpha ^2-8 \beta }\right) x}\partial _{H}&\end{aligned}$$

(24)

$$\begin{aligned}&\quad and \nonumber \\ G_{8}&=4 H^2 e^{\frac{1}{2} \left( \alpha -\sqrt{\alpha ^2-8 \beta }\right) x}\partial _{x}-\bigg (\alpha +\sqrt{\alpha ^2-8 \beta }\bigg )\nonumber \\ {}&\quad \times H^3 e^{\frac{1}{2} \left( \alpha -\sqrt{\alpha ^2-8 \beta }\right) x}\partial _{H}.&\end{aligned}$$

(25)

The first symmetry generator $G_1$ represents the generator similar to the time translation operator. The interesting point of equation (16) is that as it possesses eight-parameter Lie symmetry, the maximum number of generators for a second order differential equation, it is linearizable by a point transformation.

Solution using Lie symmetry: We find the group invariant solution of (16) using the symmetries presented above. Following the discussion of the methodology for finding the group-invariant solution in Appendix A, we consider any curve C and find the group invariant solution generated by a particular generator G. It is an invariant curve if and only if the tangent to C at each point (x, H) is parallel to the tangent vector ($\xi (x,H),\, \eta (x,H)$). Mathematically this is expressed with the characteristic $Q = \eta (x,H) - {\dot{H}}\xi (x,H)$. Every curve C on the (x, H) plane that is invariant under the group generated by G satisfies (A10) and consequently, in this case we have

$$\begin{aligned} Q \equiv \eta (x,H) - {\dot{H}} \xi (x,H)= 0. \end{aligned}$$

(26)

on $C$. We have used all the symmetry generators presented in Sect. 3 to check whether the symmetry generator provides the group invariant solution of Eq. (16) or not. Fortunately, the group generators $G_5$ in (22), $G_6$ in (23), $G_7$ in (24) and $G_8$ in (25) could generate the group invariant solutions of Eq. (16) from the invariant curve condition in (26). Interestingly both the generators $G_5$ in (22) and $G_7$ in (24) give the same solution

$$\begin{aligned} H_1(x) =H_0 e^{-\frac{1}{4}\left( \alpha -\sqrt{\alpha ^2-8\beta }\right) x}, \end{aligned}$$

(27)

while we have obtain another solution from $G_6$ in (23) and $G_8$ in (25)

$$\begin{aligned} H_2(x) =H_0 e^{-\frac{1}{4}\left( a+\sqrt{\alpha ^2-8\beta }\right) x}. \end{aligned}$$

(28)

Here $H_0$ is a integration constant, the present Hubble parameter. $\alpha$ and $\beta$ are given in (14) and (15) respectively. By changing the variable from cosmic time to $x=\ln S$; the forms of solutions in (27) and (28) in terms of scale factor now become

$$\begin{aligned} H_1 = H_0 S^{-\frac{1}{4}\left( \alpha -\sqrt{\alpha ^2-8\beta }\right) } \end{aligned}$$

(29)

and

$$\begin{aligned} H_2 = H_0 S^{-\frac{1}{4}\left( \alpha +\sqrt{\alpha ^2-8\beta }\right) }. \end{aligned}$$

(30)

4 Results and discussion

At present we know that the Universe is going through an accelerating phase after long consecutive decelerating radiation- and matter-dominated phases followed by a primordial stiff matter era. In the following, we now proceed for the investigation and analyzed various observational cosmological parameters that are coming out from the model supporting particular cosmological era.

4.1 The behaviour of deceleration parameter

The deceleration parameter q in cosmology is a dimensionless measure of the cosmic acceleration of the expansion of space in FLRW universe, defined by

$$\begin{aligned} q=-\frac{{\ddot{S}}S}{{\dot{S}}^{2}}=-\frac{{\ddot{S}}}{S{H}^{2}}=-1-\frac{{\dot{H}}}{H^{2}}. \end{aligned}$$

(31)

For accelerating expansion we have ${\ddot{S}}>0$ and in this case the deceleration parameter will be negative and vice versa. Substituting the Hubble parameters in (29), (30) and its time derivatives, the deceleration parameter in (31) takes the following forms

$$\begin{aligned} q_1=\frac{1}{4} \left( 2+{{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) , \end{aligned}$$

(32)

and

$$\begin{aligned} q_2=\frac{1}{4} \left( 2+{{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) . \end{aligned}$$

(33)

In writing (32) and (33) we have made use of (14) and (15). For accelerating expansion of our present universe, the deceleration parameter should be negative. Variation of deceleration parameter with ${{\mathcal {N}}}$ for different $c_b$ is shown in Fig. 1.

Fig. 1

Variation of deceleration parameter (a) $q_1$ and (b) $q_2$ as a function of ${{\mathcal {N}}}$ from Eq. (32) and (33) for $c_b=0,\,\,\, 0.904778$

If there is no bulk viscosity, $c_b=0$, the deceleration parameter is always positive, implies decelerating phase. As we know a purely matter-dominated universe (Einstein-de Sitter universe) cannot be accounted for by the accelerated expansion. In the case of Einstein-de Sitter model of the universe dominated by non-relativistic matter, the deceleration parameter for the flat universe is $q=\frac{1}{2}$. From (32) it can be checked that we can reach this value of q i.e., $q_1=\frac{1}{2}$ for null viscosity regardless of any value of ${{\mathcal {N}}}$. If we tune the effect of bulk viscosity $c_b>0$, we can see from Fig. 1a a transition from decelerating phase to accelerating phase as we decrease the values of ${{\mathcal {N}}}$, i. e. by tuning the bulk viscosity on. It is interesting to note that when ${{\mathcal {N}}}$ is close to 1, the dissipative effects are significant [21]. From Fig. 1b it is clear that for ${{\mathcal {N}}}=1$ and $c_b=0.904778$, we can reach the present value of deceleration parameter $q_{10} =-0.63$ [60,61,62]. Here interestingly the causality condition $0\le c_b\le 1$ automatically holds. But, on the other hand, we cannot reach $q_2=\frac{1}{2}$ for $c_b=0$ and any value of ${{\mathcal {N}}}$ from (33). This only can be made possible for both $c_b={{\mathcal {N}}}=0$, indicating a purely matter dominated Universe. Figure 1b shows that Eq. (33) always gives positive value of q for any $c_b$ and ${\mathcal {N}}$. We have checked that for ${{\mathcal {N}}}=1$ and $c_b=0.904778$, the value of deceleration parameter $q_{20} =2.13$. This represents a stiff matter era (prior radiation era) because q lies in the range $2< q < \infty$ [63, 64]. Thus (33) represents the model solution in which bulk viscous fluid behaves like a fluid similar to that of a non-viscous stiff fluid. In this context, it is the first suggestion by Zel’dovich that a stiff matter era may have occurred in the very early universe, before the matter and radiation eras [64]. The corresponding behaviour is shown in Fig. 1b.

Fig. 2

The evolution of the Hubble parameter (a) $H_1$ and (b) $H_2$ with scale factor S from Eqs. (34) and (35) respectively for $c_b=0,\,\,\, 0.904778$

4.2 The behaviour of Hubble parameter and scale factor

Using (14) and (15), the solutions in (29) and (30) take the forms

$$\begin{aligned} H_1=H_0 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) } \end{aligned}$$

(34)

and

$$\begin{aligned} H_2=H_0 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }. \end{aligned}$$

(35)

The solutions in (34) and in (35) of the model Eq. (16) give interesting results. We have seen the first solution represents the acceleration of the Universe, while the later gives decelerating phase for the value of ${{\mathcal {N}}}=1$ and $c_b=0.904778$. For $c_b=0$, the Hubble parameter (34) reduces to $H_1 \thickapprox S^{-3/2}$, which is a purely matter-dominated (Einstein-de Sitter) phase. In Fig. 2, the behaviors of Hubble parameter with scale factor are shown. It is clearly seen that Hubble parameter becomes infinity as $S \rightarrow 0$ i.e., the density by virtue of Friedmann equation (10) also becomes infinity, which suggests initial singularity at the origin.

From the definition of Hubble parameter $H \equiv \frac{{\dot{S}}}{S}$ we can write (34) and (35) as

$$\begin{aligned} \frac{1}{S}\frac{dS}{dt}=H_0 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) } \end{aligned}$$

(36)

and

$$\begin{aligned} \frac{1}{S}\frac{dS}{dt}=H_0 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }. \end{aligned}$$

(37)

Integrating Eq. (36),

$$\begin{aligned} \int _{1}^{S}\frac{dS'}{S'^{-\frac{1}{4} \left( {{\mathcal {N}}}+2-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }} = \int _{t_0}^{t} H_0 dt'=H_0 \left( t-t_0\right) ,\nonumber \\ \end{aligned}$$

(38)

we obtain

$$\begin{aligned} S_1(t)= & {} \left( 1+\frac{1}{4} \bigg ({{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36c_b^2}\right) \nonumber \\ {}{} & {} \quad \times H_0 \left( t-t_0\right) \bigg ){}^{\frac{4}{{{\mathcal {N}}}+6-\sqrt{36 c_b^2+{{\mathcal {N}}}^2}}}. \end{aligned}$$

(39)

Again integrating Eq. (37),

$$\begin{aligned} \int _{1}^{S}\frac{dS'}{S'^{-\frac{1}{4} \left( {{\mathcal {N}}}+2+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }} = \int _{t_0}^{t} H_0 dt' =H_0 \left( t-t_0\right) ,\nonumber \\ \end{aligned}$$

(40)

we obtain

$$\begin{aligned} S_2(t)= & {} \left( 1+\frac{1}{4} \bigg ({{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36c_b^2}\right) \nonumber \\ {}{} & {} \quad \times H_0 \left( t-t_0\right) \bigg ){}^{\frac{4}{{{\mathcal {N}}}+6+\sqrt{36 c_b^2+{{\mathcal {N}}}^2}}}. \end{aligned}$$

(41)

The evolution behaviour of the scale factor with $H_0 \left( t-t_0\right)$ is shown in Fig. 3.

Fig. 3

The evolution of the scale factors (a) $S_1$ and (b) $S_2$ from Eq. (39) and (41) with $H_{0}(t-t_0)$ for $c_b=0,\,\,\, 0.904778$

When $H_0(t-t_0)\rightarrow \infty$ the scale factor increases to infinity, and becomes 1 for $H_0(t-t_0)= 0$, i.e. as expected the scale factor becomes 1 at the present time $t=t_0$.

4.3 The age of the universe

Just now we have seen that there is a Big-Bang at the origin of the Universe. Hence in this scenario the age of the Universe can be properly defined. On equating $S(t_{BB})=0$ for $t=t_{BB}$, we obtain the cosmic time $t_{BB}$ when the Big-Bang happens

$$\begin{aligned} t_{BB_1}=t_0-\frac{4}{\bigg (6+{{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36c_b^2}\bigg ) H_0} \end{aligned}$$

(42)

and

$$\begin{aligned} t_{BB_2}=t_0-\frac{4}{\bigg (6+{{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36c_b^2}\bigg ) H_0} \end{aligned}$$

(43)

respectively from the Eqs. (39) and (41). Now we define the age of the Universe as the elapsed time between the time $t_{BB}$ until the present time $t_{0}$. Therefore using the above expression in (42) and (43), the age of the Universe can be defined and we obtain

$$\begin{aligned} Age_1 \equiv t_{0}-t_{BB_1}=\frac{4}{\bigg (6+{{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36c_b^2}\bigg ) H_0} \end{aligned}$$

(44)

and

$$\begin{aligned} Age_2 \equiv t_{0}-t_{BB_2}=\frac{4}{\bigg (6+{{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36c_b^2}\bigg ) H_0}. \end{aligned}$$

(45)

For a matter-dominated universe i.e., the Einstein-de Sitter universe ($c_b=0$), the age of the Universe can be obtained as from (44) is $\frac{2}{3H_0}=9.68$ Gyr, where we have used $H_{0}=67.36$ km $s^{-1}$ $Mpc^{-1}$, which is lower that of the age 12.9± 2.9 Gyr obtained for the oldest globular clusters [65] and age $15.8 \pm 2.1$ Gyr of the oldest star (HD 140,283) [66]. The present age should not be less than the age of the oldest globular clusters and oldest stars given above. The conflict between the age of the oldest star and age 13.69 Gyr, deduced from CMB anisotropy data [8] of the present universe is disappeared in our model. From expression (44) using the values (${{\mathcal {N}}}=1$, $c_{b}=0.904778$), that fit the present deceleration parameter $q_0=-0.63$, we have calculated the age of the Universe and obtained around 39.25 Gyr. This is larger than the standard value of the age. In this context, it is also to be noted that the calculated age of the Universe becomes 13.69 Gyr for $({{\mathcal {N}}}=1,\,c_b = 0.428006)$, which is good agreement with the observational results, but this cannot explain the present accelerating phase as $q_1=0.061003$. For $({{\mathcal {N}}}=1, c_{b}=0.904778)$, on the other hand, from the expression (45) we find the age of the Universe is 4.64 Gyr.

4.4 Evolution of equation of state parameter

The expansion profile of the Universe can also be studied and verified by introducing an important parameter called the equation of state (EoS) parameter. The EoS parameter is defined by the ratio between its pressure and energy density

$$\begin{aligned} \omega =\frac{p}{\rho }. \end{aligned}$$

(46)

In this context, the Universe experiences an accelerating expansion is strongly confirmed by the Cosmic Microwave Background (CMB) data that restricts the value of EoS parameter for $\omega < -\frac{1}{3}$. One can also obtain the EoS parameter from the relation [67, 68]

$$\begin{aligned} \omega =-1-\frac{1}{3}\frac{d\ln h^2 }{dx}, \end{aligned}$$

(47)

where $h=\frac{H}{H_0}$, is the weighted Hubble parameter. Using (34) and (35), from (47) it is easy to obtain

$$\begin{aligned} \omega _1 = \frac{1}{6} \left( {{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) \end{aligned}$$

(48)

and

$$\begin{aligned} \omega _2 = \frac{1}{6} \left( {{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) . \end{aligned}$$

(49)

The evolution of the equation of state parameter with ${{\mathcal {N}}}$ is shown in the Fig. 4. Interestingly, the values $({{\mathcal {N}}}=1,\,c_b=0.904778)$, for which we have obtained the present deceleration parameter $q_{10}=-0.63$, one can easily check the present value of the EoS parameter $\omega _{10} = -0.753334$ from the Eq. (48). This value of $\omega _{10}$ is slightly higher than the experimental value $-0.93$ obtained in the combined analysis of WMAP + BAO + SN data [69, 70]. For $c_b=0$, we get a matter dominated ($\omega =0$) Einstein-de Sitter model and resembles cosmological constant dominated universe ($\omega =-1$) for the value of ${{\mathcal {N}}}=0$ and $c_b=1$ which is unphysical in this model (violates causality condition), and hence de Sitter phase cannot be realized. From (49), using ${{\mathcal {N}}}=1,\, \textrm{and} ~c_b=0.904778$ we have calculated the value of the EoS parameter $\omega _2$ =1.08667. This corresponds to the stiff fluid character [63]. In this context, it is to be noted that the stiff matter era appears in the cosmological model of Zel’dovich [71] in which the universe is made of a cold gas of baryons, and in certain models of relativistic BECs with a stiff equation of state [64].

Fig. 4

The evolution of equation of state parameters (a) $\omega _1$ and (b) $\omega _2$ with ${{\mathcal {N}}}$ from Eq. (48) and (49) for $c_b=0,\,\,\, 0.904778$

4.5 Statefinder analysis

It has been established that the expansion of the Universe is accelerating and the most well-known geometric variables are the Hubble parameter and the deceleration parameter and a discussion on the Hubble parameter and the deceleration parameters are given in context of our model in this section. But the accuracy of cosmological observational data compels us to advance beyond these parameters. In this context, Sahni et al. [72] introduced a new cosmological diagnostic pair $\{r,\,s\}$, so-called the Statefinder. These are constructed from the scale factor of the Universe and its time derivatives only. The statefinder diagnostic can effectively differentiate among different forms of dark energy and can provide an excellent diagnostic for describing the properties of dark energy [73,74,75,76]. The statefinder pair $\{r,s\}$ depends on third derivative of the scale factor and are usually defined by

$$\begin{aligned} r=\frac{\dddot{S}}{SH^3}, \; s=\frac{r-1}{3(q-\frac{1}{2})}, \end{aligned}$$

(50)

where q is defined in (31). It is to be noted that the characteristic property of the statefinder parameter pair is that the $\Lambda$CDM model and the Standard CDM (SCDM) have fixed point values of statefinder parameter $\{r,s\}=\{1,0\}$ and $\{r,s\}=\{1,1\}$ respectively. Using (32), (33), (34) and (35), the statefinder pair parameters in (50) can be expressed as

$$\begin{aligned} r_1 =\frac{1}{4} \left( 4+{{\mathcal {N}}}^2+18 c_b^2+3{{\mathcal {N}}} -({{\mathcal {N}}}+3)\sqrt{{{\mathcal {N}}}^2+36 c_b^2} \right) ,\nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned} s_1 = \frac{2 \left( 3+{{\mathcal {N}}}-3 c_b^2\right) }{6+{{\mathcal {N}}}+\sqrt{36 c_b^2+{{\mathcal {N}}}^2}}, \end{aligned}$$

(52)

and

$$\begin{aligned} r_2= & {} \frac{1}{4} \left( 4+{{\mathcal {N}}}^2+18 c_b^2+3{{\mathcal {N}}} +({{\mathcal {N}}}+3)\sqrt{{{\mathcal {N}}}^2+36 c_b^2} \right) ,\nonumber \\ \end{aligned}$$

(53)

$$\begin{aligned} s_2= & {} \frac{2 \left( 3+{{\mathcal {N}}}-3 c_b^2\right) }{6+{{\mathcal {N}}}-\sqrt{36 c_b^2+{{\mathcal {N}}}^2}}. \end{aligned}$$

(54)

Putting the values ${{\mathcal {N}}}=1, c_b=0$ in Eqs. (51) and (52) give pair for Standard CDM (SCDM) model $\{r_1,\, s_1\}=\{1,1\}$, and whereas we obtain $\{r_1,\,s_1\}=\{1,0\}$, which corresponds $\Lambda$CDM model for the values of ${{\mathcal {N}}}=1$,  $c_b=\frac{2}{\sqrt{3}}$. But at this value of ${{\mathcal {N}}}=1$ and $c_b=0$ Eqs. (53) and (54) give $\{r_2,\, s_2\}=\{3,\,4/3\}$. For (${{\mathcal {N}}}=1$,   $c_{b}=0.904778$), from (51) and (52), we have found the present values of statefinder parameters are {$r_{10}$,  $s_{10}$} = $\{0.163801, \, 0.246667\}$ while from (53) and (54) we obtain {$r_{20}$, $s_{20}$} = $\{11.2038,\, 2.086667\}$. These indicate the present matter-dominated bulk viscous model is distinguishably different from SCDM and $\Lambda$CDM model.

4.6 Evolution of the matter density parameter

We have also studied the evolution of the matter density. From the definition of matter density parameter, we can write

$$\begin{aligned} \Omega _m =\frac{\rho _m}{\rho _c}, \end{aligned}$$

(55)

where $(\rho _c=3H_{0}^{2})$ is the critical density. Using Eqs. (10), (34) and (35) in (55) we can obtain

$$\begin{aligned} \Omega _{m1} (S)=S^{-\frac{1}{2} \left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) } \end{aligned}$$

(56)

and

$$\begin{aligned} \Omega _{m2} (S)=S^{-\frac{1}{2} \left( {{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) } \end{aligned}$$

(57)

respectively. Interestingly from Eq. (56), for zero bulk viscosity ($c_b=0$), viscous pressure $\sigma \rightarrow 0$, $\Omega _{m1} (S)=S^{-3}$, corresponds to the usual matter dominated universe. The evolution of matter density parameter with scale factor is shown in Fig. 5. The figures show that the matter density goes to infinity when the scale factor is equal to zero ($S \rightarrow 0$). This supports the assumption of a Big-Bang as the beginning of the Universe. The decreasing nature of density parameter in the future delineates the absence of big rip [77].

Fig. 5

The variations of matter density parameter (a) $\Omega _{m1}$ and (b) $\Omega _{m2}$ with scale factor S from Eq. (56) and (57) respectively. Here we have used ${{\mathcal {N}}}=1$ and $c_b=0,\,\,\, 0.904778$

4.7 Evolution of the curvature scalar

The evolution of the curvature scalar of the Universe confirms that there is not any particular singularity other than Big Bang. The curvature scalar R for a spatially flat universe is given by [78]

$$\begin{aligned} R=6({\dot{H}}+2H^2). \end{aligned}$$

(58)

On substituting the Hubble parameters from (34), (35) and its time derivative in (58), we have found the expressions of curvature scalar R as

$$\begin{aligned} R_1= & {} \frac{3}{2}H_0^2\left( -{{\mathcal {N}}}+2+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) \nonumber \\ {}{} & {} \quad \times S^{-\frac{1}{2}\left( {{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) } \end{aligned}$$

(59)

and

$$\begin{aligned} R_2= & {} \frac{3}{2} H_0^2 \left( -{{\mathcal {N}}}+2-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) \nonumber \\ {}{} & {} \quad \times S^{-\frac{1}{2} \left( {{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }. \end{aligned}$$

(60)

Fig. 6

The variations of curvature scalar (a) $R_1$ and (b) $R_2$ with scale factor S from Eqs. (59) and (60) for ${{\mathcal {N}}}=1$ and $c_b=0, \,\,\, 0.904778$

For a matter dominated universe, it can be easily obtained the value of curvature scalar is $R_m=\frac{3 H_0^2}{S^3}$ from (58). One can easily check this from (59) for $c_b=0$, any value of ${{\mathcal {N}}}$, and from (60) for both $c_b={{\mathcal {N}}}=0$, as expected. The variations of curvature scalar with scale factor are shown in Fig. 6. From these figures we can see that the curvature scalar diverges when scale factor $S \rightarrow 0$. This supports the existence of a Big Bang in the past of the Universe.

4.8 Thermodynamics and the local entropy

In the FLRW space time, following the formulation presented in [79,80,81], the law of production of local entropy can be expressed as

$$\begin{aligned} T\nabla _\nu S^\nu =\zeta (\nabla _\nu u^\nu )^2=9H^2\zeta , \end{aligned}$$

(61)

where T is the temperature and $\nabla _\nu S^\nu$ is the rate of entropy generation in a unit volume. Therefore, the condition for the validity of second law of thermodynamics can be expressed as

$$\begin{aligned} T\nabla _\nu S^\nu \ge 0, \end{aligned}$$

(62)

and this implies

$$\begin{aligned} \zeta \ge 0. \end{aligned}$$

(63)

Using (4) and the expressions of Hubble parameters from (34) and (35), we can write the expression of bulk viscosity $\zeta (S)$ as

$$\begin{aligned} \zeta _1(S) =\frac{3 H_0 c_b^2 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }}{\mathcal {N}} \end{aligned}$$

(64)

and

$$\begin{aligned} \zeta _2(S) =\frac{3 H_0 c_b^2 S^{-\frac{1}{4} \left( {{\mathcal {N}}}+6+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) }}{{{\mathcal {N}}}}. \end{aligned}$$

(65)

Figure 7 shows that bulk viscosity coefficient is always positive throughout the evolution of the Universe. So, the condition in (63) always holds and there is no violation of the second law of thermodynamics [54, 82, 83]. In this context, we should note that in a universe, models dominated by negative viscosity, one can find that the fluid’s entropy decreases with time [81].

5 Model analysis using observational data

In this section, we try to constrain the model parameters and check the viability of the model using the released observational datasets obtained from the type Ia supernova (SN Ia) data survey [84]. In this context it is to be noted that the data survey has played a key role in the discovery of the expansion profile of the universe. Cosmology using Type Ia supernovae (SNe Ia) has become a very successful and important field over the last 15 years, with SNe Ia playing a central role in studying viable models of dark energy, responsible for the late-time accelerated expansion of the universe. Over the years, several compilations of SNe Ia data have been released. To constrain the model parameters, here, in particular, we have used the latest Pantheon sample, composed of 1048 data points in the redshift range $0.1 \le z \le 2.3$ [84]. The Pantheon sample is a compilation of 279 SNe Ia discovered by the Pan-STARRS1 medium deep survey, the distance estimates from the Sloan Digital Sky Survey (SDSS), Supernova Legacy Survey (SNLS) and from various low redshift and Hubble Space Telescope (HST) samples [85, 86]. To validate our approach, we must constrain these model parameters with some observational datasets to yield the best fit values for these model parameters. For completeness, at first, following [85,86,87] we briefly summarize the data analysis method. The luminosity distance $D_L(z, {{\mathcal {N}}}, c_b, H_0)$ is defined as the integral expression

$$\begin{aligned} D_L(z, {{\mathcal {N}}}, c_b, H_0)=c(1+z)\int _0^{z}\frac{\textrm{d}z'}{H(z', {{\mathcal {N}}}, c_b, H_0)}, \end{aligned}$$

(66)

where c is the speed of the light and $H(z, {{\mathcal {N}}}, c_b, H_0)$ is the Hubble parameter.

The theoretical distance moduli for the i-th supernova with red shift z is expressed as

$$\begin{aligned} \mu _{th}(z, {{\mathcal {N}}}, c_b, H_0)=5\log _{10}\left[ \frac{D_L(z, {{\mathcal {N}}}, c_b, H_0)}{Mpc}\right] +25.\nonumber \\ \end{aligned}$$

(67)

Fig. 7

The evolution of the bulk viscosity coefficient $\zeta$ with scale factor S from Eqs. (64) and (65). Here we have used ${{\mathcal {N}}}=1,\,\,\,c_b= 0.904778$

The observational distance modulus is given by

$$\begin{aligned} \mu _{obs}(z_i)=m-M, \end{aligned}$$

(68)

where m and M are the apparent and absolute magnitudes of the supernovae respectively. In this way $\chi ^2$ is defined as [88,89,90,91]

$$\begin{aligned} \chi ^2 = \sum _{i=1}^{N} \frac{[\mu _{th}(z_i,{{\mathcal {N}}}, c_b, H_0)-\mu _{obs}(z_i)]^2}{\sigma _i^2}, \end{aligned}$$

(69)

here N is the total number of data points of the Pantheon sample and $\sigma _i^2$ represents the variance of the i-th measurement. Here N is the total number of data points and $\sigma _i^2$ represents the variance of the i-th measurement. The reduced $\chi ^2$ function $\chi _{red}^2$ is defined by

$$\begin{aligned} \chi _{red}^2=\frac{\chi ^2}{N_d}, \end{aligned}$$

(70)

where $N_d = N-n$ is the number of degrees of freedom and n is the number of parameter of the model. In general, the fit is reasonably good if $\chi _{red}^2 \approx 1$, and if $\chi _{red}^2>> 1$ the fit is a poor one.

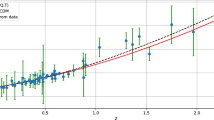
In our model, we have three model parameters: ${{\mathcal {N}}}, c_b$ and present Hubble parameter $H_0$. We obtain these parameters value with the help of latest Pantheon sample using $\chi ^2$ minimization technique given in Eq. (69). We also obtain the parameter values of $\Lambda CDM$ model using the same data. For comparison, parameter values obtained from theoretical analysis and also for our model using pantheon data sets and compare our model with $\Lambda CDM$ in tabular form. From the table we can see that the data analysis provides goodness of $\chi _{red}^2$ around one. Figure 8 shows the evolution of the $\mu$ function versus z for our model and also for the $\Lambda CDM$. The present value of Hubble parameter is almost comparable with the $\Lambda CDM$ model. Thus data table and Fig. 8 suggest that the model consider here is closely matches the observed values as well as the $\Lambda CDM$.

Param.	Bulk viscous model
	Th. result	Obs. result	$\Lambda CDM$
$c_b$	0.904778	0.7	$\times$
${{\mathcal {N}}}$	1	0.939734	$\times$
$\Omega$	1	1	0.285
$H_0$	67.36	68.99	68.99
M	$\times$	$-19.35$	$-19.38$
$\chi _{min}^2$	$\times$	1066.61	1035.59
$\chi _{red}^2$	$\times$	1.02	0.99
q	$-0.63$	$-0.34$	$-0.57$
$\omega$	$-0.75$	$-0.56$	$-0.71$
$\{r, \, s\}$	$\{0.16, \, 0.24\}$	$\{-0.10, \, 0.43\}$	$\{1, \, 0\}$
Age(Gyr)	39.2	21.5	13.8

Fig. 8

The evolution of the $\mu$ function versus z. The green curve is our bulk viscous model and black dash curve represents $\Lambda CDM$ model. The red dots with errors bars are the Pantheon 1048 data points

6 Dynamical systems analysis

In this section, we have analyzed the dynamical system behaviour of a matter-dominated universe filled with causally bulk viscous fluid by using methods of dynamical systems theory [92, 93]. The dynamical systems theory can be used to extract very useful information about the asymptotic properties of the model by calculating the eigenvalues of the linearized system at critical points. The phase-space and stability examination allow us to bypass the nonlinearities of the equations, and a description of the global dynamics can easily be obtained without knowing its initial condition [94, 95]. In the phase space analysis, thus knowledge of the critical points corresponding to a given cosmological model is very important. The another important features of dynamical system analysis is that the nature of critical points from phase plane analysis can provide the information that can be used to identify various cosmological eras [96]. Here the connection between critical points and epoch of the evolution history of the Universe are of particular relevance. The stability of those cosmological eras are determined by calculating the eigenvalues of the linearized systems at the critical point. In this regards to study the dynamical systems analysis of the model let us define proper dimensionless variables to rewrite the field equations as a system of autonomous differential equations so that our analysis can be universal. Following [92, 97], here we choose the normalized dimensionless variables u and v as

$$\begin{aligned} u=\frac{\rho }{3H^2} \end{aligned}$$

(71)

and

$$\begin{aligned} v=\frac{\Pi }{3H^2}, \end{aligned}$$

(72)

in order to build the required autonomous system of differential equation to study the dynamical system behaviour of the present model.

Using Friedmann equations in (10) and (11), the conservation equation (7) for matter and truncated form of transport equation (FIS) (9), it is easy to obtain the first order system of equations in terms of the above normalized variables as

$$\begin{aligned}{} & {} u^\prime =3(u-1)v=f(u,\,v), \end{aligned}$$

(73)

$$\begin{aligned}{} & {} v^\prime =v (3 v-n)-3 c_b^2=g(u,\,v), \end{aligned}$$

(74)

and

$$\begin{aligned} H^\prime =-\frac{1}{2} H (u+3 v+2). \end{aligned}$$

(75)

Here, prime denotes derivative with respect to $\ln S$. Interestingly, the above set of first-order differential equations (73), (74) and (75) do not depend explicitly on the independent variable. The system now can be analyzed quantitatively using dynamical system technique. Using the conditions for equilibrium or stationary state $u^\prime = 0$ and $v^\prime = 0$, we obtain the equilibrium point $(u_c, v_c)$ from Eqs. (73) and (74). In order to study the linear stability, following the methodology of the dynamical systems theory, we linearize the system by considering small perturbations around the critical point $u\rightarrow u_c+\delta u, v \rightarrow v_c+\delta v$, which satisfy the following matrix equation

$$\begin{aligned} \left( \begin{array}{c} u' \\ v' \end{array} \right) =\left( \begin{array}{cc} \frac{\partial f}{\partial u} &{} \frac{\partial f}{\partial v} \\ \frac{\partial g}{\partial u} &{} \frac{\partial g}{\partial v} \end{array} \right) _0 \left( \begin{array}{c} u \\ v \end{array} \right) =J\left( \begin{array}{c} u \\ v \end{array} \right) , \end{aligned}$$

(76)

where suffix 0 at Jacobian matrix J in (76) represents that all the matrix elements are evaluated at the equilibrium point or critical point $(u_c, v_c)$. In the theory of dynamical system, the eigenvalues of the Jacobian matrix play an important role for linear stability analysis. From the conditions of the eigenvalues one can judge about the nature of the stability of the critical points. Depending on the signs of the real parts of the eigenvalues of Jacobian matrix, the equilibrium point can be classified into [98]: (i) source point or past attractor if the real parts of all of the eigenvalues are positive, (ii) saddle point if at least one of the real parts of the eigenvalues is of a different sign and (iii) future attractor if the real parts of all of the eigenvalues are negative.

Here for the system of Eqs. (73) and (74), we have calculated two critical points $(u_{c1}, v_{c1})=\bigg (1, \frac{1}{6} \bigg ({{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2\,{+}\,36 c_b^2}\bigg )\bigg )$ and $(u_{c2}, v_{c2})\,{=}\,\bigg (1, \frac{1}{6}\bigg ({{\mathcal {N}}}\,{+}\,\sqrt{{{\mathcal {N}}}^2\,{+}\,36 c_b^2}\bigg )\bigg )$. Now, in the following, we are interested to investigate the dynamics of the system and present detailed discussion on the behavior of the critical points of the system corresponding to different stages of cosmological evolution.

In terms of the normalized dimensionless variables, the deceleration parameter (31) and EoS parameter (47) can be written as

$$\begin{aligned} q=\frac{1}{2} (1+3 v) \end{aligned}$$

(77)

and

$$\begin{aligned} \omega =v. \end{aligned}$$

(78)

Now we begin with the critical point located at $(u_{c1}, v_{c1})=\bigg (1, \frac{1}{6} \bigg ({{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\bigg )\bigg )$. The Jacobian matrix corresponding to this critical point is

$$\begin{aligned} J_1=\left( \begin{array}{cc} \frac{1}{2} \left( {{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) &{} 0 \\ 0 &{} -\sqrt{{{\mathcal {N}}}^2+36 c_b^2} \end{array} \right) \end{aligned}$$

(79)

and eigenvalues corresponding to this Jacobian matrix are given by

$$\begin{aligned} \lambda _{11}=-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}, \,\lambda _{12}=\frac{1}{2} \left( {{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) .\nonumber \\ \end{aligned}$$

(80)

The deceleration parameter and the EoS parameter from Eqs. (77) and (78) corresponding to this critical point is

$$\begin{aligned} q_1=\frac{1}{4} \left( 2+{{\mathcal {N}}}-\sqrt{36 c_b^2+{{\mathcal {N}}}^2}\right) \end{aligned}$$

(81)

and

$$\begin{aligned} \omega _1=\frac{1}{6}({{\mathcal {N}}}-\sqrt{{{\mathcal {N}}}^2+36c_b^2}) \end{aligned}$$

(82)

It is interesting to see that from (81) and (82) we obtain the values of deceleration parameter $q_1=\frac{1}{2}$ and EoS parameter $\omega _1=0$ respectively for $c_b=0$. This indicates a purely Einstein-de Sitter decelerating universe. When ${{\mathcal {N}}}(=\frac{1}{\mathcal{\tau } H })$ is close to 1, i.e., dissipative effect is significant, the deceleration parameter and EoS parameter becomes $q_{10}=-0.63$ and $\omega _{10}=-0.753334$ respectively for the value of $c_b=0.904778$. The values of these parameters suggest present accelerated phase of the Universe. For ${{\mathcal {N}}}=1$ and $c_b=0.904778$, the critical point is $(1, -0.753334)$ and the corresponding eigenvalues are $(\lambda _{11}, \lambda _{12})=(-5.52, -2.26)$. Since both eigenvalues are negative, the critical point is a stable node and represents a future attractor or sink. This indicates any trajectory in the neighbourhood of the critical point will converge to it irrespective of the initial conditions. This fact is diagrammatically represented in phase plane in Fig. 13. Interestingly, the critical point $A(1, -0.753334)$ in phase space diagram represents a future attractor [98].

Integrating Eq. (75), one can easily obtain the expression for the Hubble parameter and scale factor corresponding this critical point as

$$\begin{aligned} H_1=\frac{ H_0}{1+\frac{H_0}{4} \left( t-t_0\right) \left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) }, \end{aligned}$$

(83)

and

$$\begin{aligned} \begin{aligned} S_1&=(1+\frac{{H_0}^2}{4} \left( t-t_0\right) \\&\quad \times \left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) )^{\frac{4}{\left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) }}. \end{aligned} \end{aligned}$$

(84)

Here we use the integration limit at $t=t_0$, $H=H_0$ and $S=1$.

The expression of $H_1$ from (83) is a positive quantity as $\left( {{\mathcal {N}}}+6-\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) > 0$. The behaviour of scale factor at this critical point is shown in Fig. 9a and this indicates an accelerated expansion of the Universe. From (84) it is clear that when bulk viscosity is zero i.e. $c_b=0$ the scale factor reduces to $S \approx t^{\frac{2}{3}}$ as expected. The second derivative of scale factor with respect to time can be expressed as

$$\begin{aligned} \begin{aligned} \frac{d^2S_1}{dt^2}&=\frac{{H_0}^2}{4} \left( -\mathcal {N}-2+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \\&\quad \times (1+ \frac{H_0}{4} (t-t_0)\\&\quad \times \left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) )^{\left( \frac{2\mathcal {N}+8-2\sqrt{\mathcal {N}^2+36 c_b^2}}{-\mathcal {N}-6+\sqrt{\mathcal {N}^2+36 c_b^2}}\right) }. \end{aligned}\nonumber \\ \end{aligned}$$

(85)

From Eq. (85) it is seen that $\frac{d^2S}{dt^2}$ is a positive quantity, therefore suggests acceleration of the Universe as expected. Its evolution is shown in Fig. 9b. The density and bulk viscous pressure are

$$\begin{aligned} \rho _1 =\frac{3 H_0^2}{\left( 1+\frac{H_0}{4} \left( t-t_0\right) \left( \mathcal {N}+6-\sqrt{\mathcal {N}^2+36 c_b^2}\right) \right) ^2} \end{aligned}$$

(86)

and

$$\begin{aligned} \sigma _1 =\frac{H_0^2 \left( \mathcal {N}-\sqrt{\mathcal {N}^2+36 c_b^2}\right) }{2\left( -1+\frac{H_0}{4} \left( t-t_0\right) \left( -\mathcal {N}-6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \right) ^2}.\nonumber \\ \end{aligned}$$

(87)

The behaviour of both density and bulk viscous pressure is shown in Fig. 10a and b. From Fig. 10a it is clear that when time goes to zero, density becomes high. This signifies Big bang at the origin. Figure 10b shows that the bulk viscous pressure is negative and this negative pressure is responsible for acceleration of the universe.

Fig. 9

The variations of scale factor (a) $S_1$ and (b) $\frac{1}{H_0^2}\frac{d^2S_1}{dt^2}$ with $H_0 \left( t-t_0\right)$ from Eqs. (84) and (85) for ${\mathcal {N}}=1$ and $c_b=0.904778$

Fig. 10

The evolution of energy density (a) $\frac{\rho _1}{H_0^2}$ and bulk viscous pressure (b) $\frac{\sigma _1}{H_0^2}$ with $H_0 \left( t-t_0\right)$ from Eqs. (86) and (87) for ${{\mathcal {N}}}=1$ and $c_b=0.904778$

Next we consider the second critical point $(u_{c2}, v_{c2})=(1,\frac{1}{6} \left( {{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) )$. The Jacobian matrix corresponding to this critical point is

$$\begin{aligned} J_2=\left( \begin{array}{cc} \frac{1}{2} \left( {{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) &{} 0 \\ 0 &{} \sqrt{{{\mathcal {N}}}^2+36 c_b^2} \end{array} \right) \end{aligned}$$

(88)

and eigenvalues are given by

$$\begin{aligned} \lambda _{21}=\sqrt{{{\mathcal {N}}}^2+36 c_b^2}, \,\lambda _{22}=\frac{1}{2} \left( {{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36 c_b^2}\right) \end{aligned}$$

(89)

The deceleration parameter and the equation of state parameter from Eqs. (77) and (78) corresponding to this critical point is

$$\begin{aligned} q_2=\frac{1}{4} \left( 2+{{\mathcal {N}}}+\sqrt{36 c_b^2+{{\mathcal {N}}}^2}\right) \end{aligned}$$

(90)

and

$$\begin{aligned} \omega _2=\frac{1}{6}({{\mathcal {N}}}+\sqrt{{{\mathcal {N}}}^2+36c_b^2}). \end{aligned}$$

(91)

From the expressions (90) and (91) we obtain the values of deceleration parameter $q_2=\frac{1}{2}$ and EoS parameter $\omega _2=0$ respectively for ${{\mathcal {N}}}=0$ and $c_b=0$. This indicates the decelerating phase of the purely matter-dominated Einstein-de Sitter universe. While for ${{\mathcal {N}}}=1$ and $c_b=0.904778$, we have found the $q_{20}=2.13$ and $\omega _{20}= 1.08667$ respectively. These values obtained lie in the ranges $2<q<\infty$ and $1<\omega <\infty$, and characterize a cosmological phase, the so called stiff matter era (prior radiation era). This is the case in which bulk viscous fluid behaves almost like stiff fluid.

For (${{\mathcal {N}}}=1$ and $c_b=0.9064778$ ) the critical point is (1, 1.08667) and the corresponding eigenvalues are $(\lambda _{21}, \lambda _{22}) =(5.52, 3.26)$. Since the two eigenvalues are positive, this critical point is a unstable node and represents a past attractor or source. This fact is also shown in Fig. 13. The critical point corresponds to the point B(1, 1.08667) shown in phase space diagram in Fig. 13 where from the trajectories are diverging is a unstable past attractor [98].

The Hubble parameter and scale factor corresponding this critical point becomes

$$\begin{aligned} H_2=\frac{H_0}{1+\frac{H_0}{4} \left( t-t_0\right) \left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) } \end{aligned}$$

(92)

and

$$\begin{aligned} \begin{aligned} S_2&=\Bigg (1+\frac{H_0}{4} \left( t-t_0\right) \\&\quad \times \left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \Bigg )^{\frac{4}{\left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) }} \end{aligned} \end{aligned}$$

(93)

From (93) one can obtain corresponding matter dominated Universe i.e. $S \approx t^{\frac{2}{3}}$ when both ${{\mathcal {N}}}=c_b=0$. The behaviour of scale factor at this critical point is shown in Fig. 11a and indicates a decelerated expansion. The second derivative of scale factor with respect to time can be expressed as

$$\begin{aligned} \begin{aligned} \frac{d^2S_2}{dt^2}&=-\frac{ {H_0}^2}{4} \left( \mathcal {N}+2+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \\&\quad \times \Bigg (1+ \frac{H_0}{4} (t-t_0)\\&\quad \times \left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \Bigg )^{\left( \frac{2\mathcal {N}+8+2\sqrt{\mathcal {N}^2+36 c_b^2}}{-\mathcal {N}-6-\sqrt{\mathcal {N}^2+36 c_b^2}}\right) }. \end{aligned}\nonumber \\ \end{aligned}$$

(94)

Fig. 11

The evolution of scale factor (a) $S_2(t)$ and (b) $\frac{1}{H_0^2}\frac{d^2S_2}{dt^2}$ with $H_0 \left( t-t_0\right)$from Eqs. (93) and (94) for ${{\mathcal {N}}}=1$ and $c_b= 0.904778$

Fig. 12

The evolution of energy density (a) $\frac{\rho _2}{H_0^2}$ and bulk viscous pressure (b) $\frac{\sigma _2}{H_0^2}$ with $H_0 \left( t-t_0\right)$ from Eqs. (95) and (96) for $\mathcal {N}=1$ and $c_b= 0.904778$

Equation (94) shows that $\frac{d^2S_2}{dt^2}$ is a negative quantity, therefore, indicates deceleration of the Universe. Its evolution is shown in Fig. 11b. The density and bulk viscous pressure are calculated as

Fig. 13

Phase space diagram for the dynamical system (71) and (72). The critical point B(1, 1.08667) in the upper right corner is a unstable past attractor and the point $A(1,-0.75333)$, below the first critical point, is a future attractor. The direction of the trajectories is shown by the arrow head

$$\begin{aligned} \rho _2 =\frac{3 H_0^2}{\left( 1+\frac{H_0}{4} \left( t-t_0\right) \left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \right) ^2} \end{aligned}$$

(95)

and

$$\begin{aligned} \sigma _2 =\frac{H_0^2 \left( \mathcal {N}+\sqrt{\mathcal {N}^2+36 c_b^2}\right) }{2\left( 1+\frac{H_0}{4} \left( t-t_0\right) \left( \mathcal {N}+6+\sqrt{\mathcal {N}^2+36 c_b^2}\right) \right) ^2}.\nonumber \\ \end{aligned}$$

(96)

The behaviour of both density and bulk viscous pressure are shown in Fig. 12a and b. From Fig. 12a it is clear that when time goes to zero, density becomes high, suggest Big Bang at the origin while Fig. 12b suggests that the bulk viscous pressure is positive and therefore confirming deceleration of the Universe. The evolution of the phase space trajectories in the (u, v) plane is shown in the Fig. 13. In the phase space diagram B(1, 1.08667) and $A(1,-0.753334)$ are two critical points. The critical point B(1, 1.08667) is a unstable past attractor as the phase space trajectories are originating from this critical point and these emerging trajectories finally converges to the critical point $A(1,-0.753334)$, which is the future attractor.

7 Conclusion

After matter domination decelerating phase, the epoch in which the Universe becomes dark energy dominated, it started accelerating. In this phase the dynamics is governed by the dark energy, which is characterized by the negative pressure. There exists a number of dark energy models which generate late-time acceleration of the Universe. It is now well known fact that the late-time accelerated universe can be modelled with pressureless cold dark matter and dark energy that could in principle considered to be different manifestations of the same physical phenomenon whose dynamics is provided by a single unified viscous fluid. The bulk viscous pressure of the cosmic fluid arises as a consequence of self-interactions within the fluid matter and interactions turn out to be equivalent to effective one-particle forces, which are self-consistently exerted by the cosmic medium on each of its individual particles. The cosmological principle restricts these forces to act like ‘friction’ or ‘anti-friction’, and The generalized equilibrium theory relates those forces to temperature and chemical potential. It is to be noted that for a non-relativistic substratum only cosmic anti-friction generates a negative fluid bulk pressure [26]. In viscous fluid flow the dissipation due to bulk viscosity converts kinetic energy of the particles into heat and transform it into internal energy of the fluid. According to the second law of thermodynamics, this dissipative process will generate entropy. The entropy generation can be related to the expansion rate or the local fluid velocity through a bulk viscosity term [82, 82, 83]. A simple mechanism for producing of bulk viscosity in cosmological view point is due to the decay of a dark matter particle into relativistic products. Such decay resulting heat in the cosmic fluid leads to an increase in entropy and are inherently dissipative in nature. The increase in entropy produced by the particle decay leads to a cosmic fluid out of pressure and temperature equilibrium and can therefore be represented by a bulk viscosity. In this article we have presented our investigation by studying the basic scenario of a late-time viscous cosmology using a model of casual bulk viscous matter-dominated universe with the viscous pressure obtained from a truncated causal transport theory [11, 12, 21, 47]. The purposes of this study are the Lie symmetry analysis of the model equation and phase plane analysis by treating the model equation in terms of dynamical system theory with a view to confront with the observed acceleration and various phases of the Universe.

First by employing Lie symmetry approach we have found eight-parameter Lie symmetry generators and obtained two different group invariant solutions given in (27) and (28) for Hubble parameter using invariant curve condition. From these we have calculated expressions for various cosmological parameters that are important for the explanation of late time evolution dynamics of the Universe. Interestingly, the deceleration parameter q in (32) obtained from (29) satisfies the present acceleration of the Universe for ${{\mathcal {N}}}=1$ and $c_b=0.904778$, while other solution in (30) couldn’t support the accelerating phase of the Universe, but could represent the solution of the model equation that corresponds to a universe dominated by a non-viscous stiff fluid. For zero bulk viscosity $c_b=0$ present model reduce to the Einstein-de Sitter model.

We have also established a relationship between the Hubble parameter and the scale factor in this model. Without the bulk viscous coefficient the model transforms to ordinary matter dominated Universe, $H \approx S^{-3/2}$. The behaviour of scale factor with time suggests that there is a Big Bang at the beginning of the Universe. Therefore age of the Universe is defined and for the values of model parameters ${{\mathcal {N}}} = 1$ and $c_b = 0.904778$, we have found that the age of the Universe is 39.25 Gyr. Indeed, the age value is much higher than the presently accepted age 13.69 Gyr. of the Universe. Obviously, although there is an age problem in the present model unless a higher value of $H_0$ is observationally established in the future, the obtained model parameters could not only explain the present acceleration $q=-0.63$, but also successfully overcomes the conflict between the age of the oldest star and the present age. Also if we neglect bulk viscosity $(c_b=0)$, the age of the matter dominated universe becomes 9.68 Gyr which is good agreement with the observations.

We also have studied the equation of state parameter and its evolution from two sets of symmetry-based solutions given in (29) and (30) and interestingly the results obtained by us confirm the same as that of the results indicated by the obtained deceleration parameter. We also have obtained the expressions for the statefinder pair from the above two solutions and results are given in (51)–(54). For both cases, the present values of statefinder pair are obtained for (${{\mathcal {N}}}=1,\,\,\, c_b=0.904778$) and the result indicates that the bulk viscous model is certainly differ from SCDM and $\Lambda$CDM model.

From the study of cosmic matter density parameter and evolution of curvature scalar, it is seen that when scale factor $S\rightarrow 0$, density goes to infinity that supports Big-Bang in the past of the Universe.

Here the Universe, modeled by a flat causally bulk viscous unified fluid and bulk viscosity dominates the dynamics of our universe. Phase space analysis is presented for this model of the Universe in which the viscous pressure is obtained from a truncated version of full causal transport theory [11, 12, 21, 47]. An autonomous system of equations has been derived by using an appropriate set of dimensionless phase space variables which plays a remarkable role to study the stability of dynamical system. The corresponding autonomous system is studied by means of the dynamical systems tools. In the theory of dynamical system as in the text we have discussed that the eigenvalues of the Jacobian matrix play an important role for linear stability analysis. From the conditions of the eigenvalues one can judge about the nature of the stability of the critical points. When ${{\mathcal {N}}}(=\frac{1}{\mathcal{\tau } H })$ is close to 1, i.e., dissipative effect is significant, and $c_b=0.904778$, the critical point is $(1, -0.753334)$ and the corresponding eigenvalues are $(\lambda _{11}, \lambda _{12})=(-5.52, -2.26)$. For ${{\mathcal {N}}}=1$ the deceleration parameter and EoS parameter becomes $q=-0.63$ and $\omega =-0.753334$ respectively for the value of $c_b=0.904778$. While on the other hand, for same (${{\mathcal {N}}}=1$ and $c_b=0.9064778$ ) we have found other critical point is (1, 1.08667). In this case the corresponding eigenvalues are $(\lambda _{21}, \lambda _{22}) =(5.52, 3.26)$ and we have the values of deceleration parameter and equation of state parameter at this critical point are $q_2=2.13$ and $\omega _2= 1.08667$ respectively. In our study the critical point B(1, 1.08667) is an unstable past attractor or source as trajectories emerge from this point and these emerging trajectories are finally converging to the critical point $A(1,-0.753334)$, which is the future attractor.

Here one important thing should be mentioned that our model requires a very large bulk viscosity to make models consistent with cosmological observations and what will be the microphysical mechanism that could be responsible for producing such large viscosities? In this context, it is well known that the our universe underwent various cosmological phases immediate after inflationary phase. At the time of last scattering during evolution, the universal temperature of our universe was of about $3000\, K$ and gradually approaches to almost zero corresponding to the dilution of cosmic-fluid through late-stage expansion. We set the approximate effective temperature as $2.73\, K$, equaling to the CMB black-body temperature at present day universe. Regarding microphysical mechanism of the generation of bulk viscosity, one can adopt two appropriate molecular-like collision and or interaction models for cosmological study, from which the viscosity is physically generated: one is based on the Chapman-Enskog equation [99] for dilute multi-component gas mixtures, which assumes that molecules possess only translational kinetic energy and energy and momentum can be transferred by direct interaction as well as by actual molecular movement [100]. The other is Sutherland’s formula [99], that assumes molecules are smooth rigid elastic spheres surrounded by fields of attractive force. At low temperature $(T<< 300 K)$, a general equation which can approximately represent the main feature of Chapman’s and Sutherland’s formulae [99] represents the expression for the bulk viscous coefficient in terms of the temperature [25]. Finally, it is important to note that the system of equations studied in this paper not only describes the evolution of a dissipative fluid with bulk viscosity, but also the evolution of a different kind of non-viscous matter. Particularly, the theoretical values obtained for model parameters is used to estimate the values of cosmological parameters that not only support present accelerating phase but also are in good agreement with the early non-viscous stiff matter phase. The free model parameters as well as the cosmological parameters obtained form cosmological data analysis are compared with the results that in $\Lambda$CDM model. In the phase space diagram we obtain two critical points. One of them is a unstable past attractor as the phase space trajectories are originating from this critical point and these emerging trajectories finally converge to the another critical point, which is the future attractor. Here, fortunately and interestingly, we have seen that the cosmological parameters obtained analytically using the analysis of Lie symmetry-based solutions result two dynamical phases of cosmic evolution and they are associated with the critical points in the equivalent phase space correlating the physical nature of cosmic evolution of the realistic universe. Thus the Lie symmetry-based analysis and the dynamical systems analysis certainly provide an elegant theoretical platform toward describing the various phases of the cosmic expansion that are coming out from the study of present model equation with homogeneous EoS. It will be a interesting future work considering inhomogeneous EoS of the bulk viscous model of the dark energy [101,102,103].

Appendices

Appendix

Appendix A: Lie point symmetry and group invariant solution

The key point of Lie’s approach for finding the symmetry of an ordinary differential equation considers the invariance of the form of the differential equation itself under the infinitesimal transformations that depend on the independent variable (t) and the dependent variable (x(t)) given by

$$\begin{aligned} t'=t+ \delta t\,,\,\,\,\,\,\,\delta t=\epsilon \,\xi (t,\,x) \end{aligned}$$

(A1)

and

$$\begin{aligned} x'=x+ \delta x\,,\,\,\,\,\,\,\delta x=\epsilon \,\eta (t,\,x). \end{aligned}$$

(A2)

Here $\epsilon$ is an arbitrary small quantity, and the functions $\xi (t,\,x)$ and $\eta (t,\,x)$ are the coefficient functions of a finite differential operator, when coupled with infinitesimal parameter $\epsilon$, gives the generator of the infinitesimal transformations. For an arbitrary analytic function $g=g(t,\,x)$, it is easy to show

$$\begin{aligned} \delta g=\epsilon X g, \end{aligned}$$

(A3)

where

$$\begin{aligned} X=\xi (t,\,x)\frac{\partial }{{\partial t}} + \eta (t,\,x)\frac{\partial }{{\partial x}}, \end{aligned}$$

(A4)

is the generator of the infinitesimal transformations in (A1) and (A2). A similar consideration when applied to $h=h(t,\,x,\,\dot{x})$ gives

$$\begin{aligned} \delta h=\epsilon X^{(1)} h \end{aligned}$$

(A5)

with

$$\begin{aligned} X^{(1)}=X+\left[ {{\dot{\eta }}}(t,\,x)- {{\dot{\xi }}}(t,\,x){\dot{x}}\right] \frac{\partial }{\partial \dot{x}}. \end{aligned}$$

(A6)

Understandably, $X^{(1)}$ stands for the first-order prolongation of X to the extended space of the variables $(t,\,x,\,\dot{x})$. Similarly in the extended space of variables $(t,\,x,\,\dot{x},\,\ddot{x})$, we can find $X^{(2)}$, the second-order prolongation of the generator X given by [53]

$$\begin{aligned} X^{(2)}=X+\left[ {{\dot{\eta }}}(t,\,x)- {{\dot{\xi }}}(t,\,x){\dot{x}}\right] \frac{\partial }{\partial \dot{x}}+\eta ^{''}\frac{\partial }{\partial \ddot{x}}, \end{aligned}$$

(A7)

with

$$\begin{aligned} \eta {''}=\left[ \ddot{\eta }(t,\,x)-2{{\dot{\xi }}}(t,\,x)\ddot{x}- \ddot{\xi }(t,\,x)\dot{x}\right] . \end{aligned}$$

(A8)

A second-order ordinary differential equation of the form $M(t,\,x,\,\dot{x},\,\ddot{x})=0$ possesses Lie point symmetry generator of the form (A4) provided [11, 12, 51, 52, 104,105,106]

$$\begin{aligned} X^{(2)}M(t,\,x,\,\dot{x},\,\ddot{x})=0. \end{aligned}$$

(A9)

To find the group invariant solution generated by a particular generator X, we follow the approach: Any curve C, is an invariant curve if and only if the tangent to C at each point $(t,\,x)$ is parallel to the tangent vector $(\xi (t,\,x),\,\eta (t,\,x))$. This condition can be expressed mathematically by introducing the characteristic $Q = \eta (t,\,x) - \dot{x}\xi (t,\,x)$ [107]. Every curve C on the $(t,\,x)$ plane that is invariant under the group generated by X satisfies

$$\begin{aligned} Q \equiv \eta (t,\,x) - \dot{x}\xi (t,\,x) = 0 \end{aligned}$$

(A10)

on C. From this invariant curve condition we can find out the solution for a differential equation from symmetry. Equation (7) provides a natural basis to carry out the Lie symmetry analysis for finding the symmetry of second-order ordinary differential equations, whereas the invariant curve condition in (A10) can be used to find the group invariant solutions generated by the symmetry generators in (A4).