The $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays within BHLS$_2$ and the muon HVP

Abstract

The departure of the latest FNAL experimental average for the muon anomalous magnetic moment $a_\mu =(g_\mu -2)/2$ measurements, having increased from $4.2 \sigma$ (Abi et al. in Measurement of the positive muon anomalous magnetic moment to 0.46 ppm, arXiv:2104.03281, 2021) to $5.0 \sigma$ (Muon g-2, D.P. Aguillard et al. in Measurement of the positive muon anomalous magnetic moment to 0.20 ppm, arXiv:2308.06230, 2023) with respect to the white paper (WP) consensus (Aoyama et al. in Phys Rep 887:1, arXiv:2006.04822, 2020), may indicate a hint for new physics. As the most delicate piece of $a_\mu$ is its leading-order hadronic vacuum polarization (HVP) part $a_\mu ^{HVP-LO}$, methods to ascertain its theoretical value are crucial to appropriately interpreting this departure from the measurement. We, therefore, propose to closely examine the dipion spectra from the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays in the hidden local symmetry (HLS) context using its BHLS$_2$ broken variant. We thus have at our disposal a framework where the close relationship of the dipion spectra from the $\eta /{\eta ^\prime }$ and $\tau$ decays and of the $e^+e^- \rightarrow \pi ^+\pi ^-$ annihilation can be simultaneously considered. A special focus is given to the high-statistics dipion spectra from the $\eta$ decay collected by the KLOE/KLOE2 Collaboration and ${\eta ^\prime }$ decay collected by the BESIII Collaboration, and it is shown that the BHLS$_2$ framework provides a fair account of their dipion spectra. More precisely, it is first proven that a single Omnès representation real polynomial is required, common to both the $\eta$ and ${\eta ^\prime }$ dipion spectra. Moreover, it is shown that fits involving the $\eta /{\eta ^\prime }/\tau$ dipion spectra, and excluding the $e^+e^- \rightarrow \pi ^+\pi ^-$ annihilation data, allow for a prediction of the pion vector form factor data $F_\pi (s)$ which agrees fairly well with the usual dipion spectra collected in the $e^+e^- \rightarrow \pi ^+\pi ^-$ annihilation channel. Even if more precise $\eta /{\eta ^\prime }/\tau$ dipion spectra would help to be fully conclusive, this confirms the dispersive approach results for $a_\mu ^{HVP-LO}$ and points toward a common non-experimentally dependent origin to this tension with the now well-accepted LQCD result.

1 Preamble: various aspects of the dispersive approach to the muon HVP

The hadronic vacuum polarization (HVP) $a_\mu \equiv (g_\mu - 2)/2$ plays a central role in precision physics, in particular in the Standard Model prediction of the muon anomalous magnetic moment, but equally importantly for a precise calculation of the running electromagnetic fine structure constant $\alpha _{em}(s)$ and the electroweak mixing parameter $\sin ^2 \theta _W(s)$. Therefore, accurate predictions suffer from the non-perturbative contributions from low-lying hadron physics that are difficult to address precisely from first principles.

Recently [2], the Fermi National Accelerator Laboratory (FNAL) Muon $g-2$ experiment re-estimated the previous average value of their run 1 data sample [2] and the latest Brookhaven National Laboratory (BNL) measurement [4] by also considering their run 2 and 3 data samples; this turns out to increase the statistics by a factor of $\simeq 4$. Moreover, the Muon $g-2$ FNAL Collaboration achieved an improvement in their systematic uncertainty by about a factor of 2. The derived updated average

$$\begin{aligned} a_\mu ^{exp.} = 116 592 059(22) \times 10^{-11} (0.19 \textrm{ppm}) \end{aligned}$$

increases the deviation from the white paper (WP) Standard Model consensus [3] from $4.2~ \sigma$ [1] to $5.0 ~\sigma$ [2]. The difference $\delta _a =a_\mu ^{exp.}-a_\mu ^{th.}$ is now $\delta _a= 24.4 \pm 4.5$ in units of $10^{-10}$, dominated by the uncertainty agreed upon by the WP theory consensus [3]. Of course, this departure from theoretical expectations deserves to be explored, as the overall pattern reflected by the various model/theoretical approaches is indeed unclear, even contradictory.

The WP Standard Model consensus for $a_\mu ^{th.}$ resorts to a data-driven dispersion relation (DR) approach, where the experimental low-energy hadron production cross sections provide the non-perturbative input to calculate the HVP effects. Fortunately, the problem can be restricted to precise knowledge of the process $e^+e^- \rightarrow \gamma ^* \rightarrow \text{ hadrons }$, and for what concerns the muon $g-2$, the $e^+e^- \rightarrow \pi ^+\pi ^-$ channel provides the dominant contribution to the model uncertainty.

Regarding its non-perturbative hadronic content, the standard dispersion-based (DR) evaluation of the HVP consists of deriving the contribution of each $e^+e^- \rightarrow \gamma ^* \rightarrow \text{ hadrons }$ annihilation channel by combining the different spectra collected by the different experiments in the hadronic channel considered, employing algorithms of different levels of sophistication. The full HVP value is then defined, for what concerns its non-perturbative content, by the sum of these different contributions. The WP Standard Model consensus [3] is based on a combination of two such evaluations [5, 6].

Although the main challenge is then, seemingly, the simple $\pi \pi$ production process, the experimental challenge is highly complex, depending on a precise understanding of the detectors and, on the theory side, the radiative corrections required to disentangle hadronic effects from electromagnetic contamination. Unfortunately, the data samples provided by the different experiments do not exhibit satisfactory consistency—and some can even be in strong contradiction [7] with the others. The use of the $\tau \rightarrow \pi ^-\pi ^0 \nu _\tau$ decay information, first proposed by [8], has been considered to discriminate among the $\pi ^+ \pi ^-$ spectra, but it did not lead to convincing enough conclusions.

It is widely considered that all low-energy hadronic processes derive from quantum chromodynamics (QCD), even though in the non-perturbative low-energy regime, tools to make valid predictions of real-time hadronic cross sections are missing. Nevertheless, as hadron physics is accepted to derive from QCD, it follows that the various specific hadronic decay processes are highly correlated with each other. This motivates the need to address these correlations, especially in order to constrain the non-perturbative sector of the $e^+e^- \rightarrow \gamma ^* \rightarrow \text{ hadrons }$ annihilations.

Although we lack methods to predict a process like $e^+e^- \rightarrow \pi ^+\pi ^-$, we know that QCD implies well-defined symmetry patterns such as approximate chiral symmetry, and gives rise to chiral perturbation theory (ChPT), a systematic expansion about the chiral symmetry point. It allows one to work out reliable predictions from first principles for the low-energy tail of the QCD hadron spectrum (up to about the $\eta$ meson mass).

With this in mind, an attempt to consider the $e^+e^- \rightarrow \pi ^+\pi ^-$ annihilation not only in relation to the $\tau ^\pm \rightarrow \pi ^\pm \pi ^0 \nu _\tau$ decay but also in relation to other related spectra is important; it motivates a unified modeling¹ by a version of the resonance Lagrangian approach (RLA) [9, 10]—we adopted the hidden local symmetry (HLS) version² [12, 13]—needed to extend the chiral perturbation theory toward higher energy to cover the $\rho$, $\omega$, and $\phi$ energy range.³ To practically succeed in such a program, the original HLS model (see, for instance, [16] for a review) has been supplied with appropriate symmetry-breaking mechanisms with various levels of sophistication to derive the earlier versions of the BHLS model in [17,18,19], or the more refined BHLS$_2$ version [20], updated in [21].

One thus achieved a simultaneous consistent fit of the $e^+e^- \rightarrow \pi ^+\pi ^-$ data from CMD-2 [22], SND [23], KLOE [24,25,26], BaBar [27, 28], BESIII [29, 30], and CLEO-c [31], and the $\tau \rightarrow \pi ^-\pi ^0 \nu _\tau$ decay spectral functions collected by ALEPH [32], CLEO [33], and Belle [34] (see [17, 18, 20, 21]). This updated BHLS$_2$ fairly recovers the known properties of the $[\pi ^0,\eta ,{\eta ^\prime }]$ system thanks to its kinetic breaking mechanism [21].

Besides keeping the neutral vector current conserved, this breaking mechanism also generates a violation of the charged vector current conservation and a departure of $F_\pi ^\tau (s=0) =1$ by a few per mil. Such an option finds support in [34] in Belle own in their own fit results reported in their Table VII; additional $\tau$ spectra are needed to conclude—see the discussion in Section 3 of [21]—as such a breaking mechanism might affect $\tau$-based predictions for the muon HVP.

Alongside the $\pi ^+\pi ^-$ annihilation channel and the $\tau \rightarrow \pi ^-\pi ^0 \nu _\tau$ decay spectra, BHLS$_2$ [20, 21] also successfully addressed the $\pi ^+\pi ^-\pi ^0, (\pi ^0/\eta ) \gamma$ and $K \overline{K}$ final states in a fully correlated way represented by a single Lagrangian. A few additional radiative partial width decays are also considered, notably those for $\pi ^0/\eta /{\eta ^\prime }\rightarrow \gamma \gamma$, and some more $VP\gamma$ radiative decays.

In view of the significant inconsistencies in the data samples collected by some experiments, the global fit approach has two advantages: first, the additional data are expected to reduce the uncertainties of the HVP evaluations, and second, it provides consistency checks of each $e^+e^- \rightarrow \gamma ^* \rightarrow \text{ hadrons }$ data set versus the other samples collected in the same annihilation channel or in another one.

In the present work, we go a step further by also involving the $\eta /{\eta ^\prime }\rightarrow \pi ^+\pi ^- \gamma$ decay modes in order to obtain additional $\pi \pi$ dipion spectra from experiments with systematics quite different from those encountered in $e^+e^-$ annihilations. As will be seen below, these decays allow for a new test of the self-consistency of the DR-based estimates of $a_\mu$. Indeed, the $\eta /\eta '$ decay spectra can provide a DR evaluation for $a_\mu (\pi ^+\pi ^-, \sqrt{s} < 1~\textrm{GeV})$, which can be fruitfully compared with those directly derived by directly integrating the $e^+e^- \rightarrow \pi ^+\pi ^-$ annihilation data. One may expect that the $\eta /{\eta ^\prime }$ dipion spectra benefit from systematics largely independent of those in the $e^+e^-$ annihilation.

Besides the DR approach which gave rise to several evaluations of the muon HVP $a_\mu$ listed in the white paper [3], the challenging lattice QCD (LQCD) approach has been used by several groups and produced results with relatively poor precision at the time of the white paper. They were not used to define the so-called WP Standard Model consensus reported in [3] which, based on some DR estimates, provided the leading-order (HVP-LO) consensus $a_\mu ^\textrm{LO}[\mathrm{th.}] = 693.1(4.0)\times 10^{-10}$. Using the LQCD approach, the BMW Collaboration, which first got [3, 35] $a_\mu ^\textrm{LO}=(711.1 \pm 7.5 \pm 17.4) \times 10^{-10}$, later improved their calculation and got $a_\mu ^\textrm{LO}=(707.5 \pm 5.5) \times 10^{-10}$ [36], at clear variance with the WP consensus just mentioned. This evaluation finds support from the new evaluations by other LQCD groups: $a_\mu ^\textrm{LO}=(720.0 \pm 12.4_\textrm{stat} \pm 9.9_\textrm{syst}) \times 10^{-10}$ (Mainz/CLS 19) [37, 38] and $a_\mu ^\textrm{LO}=(715.4 \pm 16.3_\textrm{stat}\pm 9.2_\textrm{syst}) \times 10^{-10}$ (RBC/UKQCD18) [39].

The lattice calculation of $a_\mu ^\textrm{LO}$ thus brings the SM prediction of $a_\mu$ into acceptable agreement with the experiment but generates significant disagreement between the LQCD results and the different data-driven dispersive results; this now looks well established. It adds to the former puzzle from data versus predictions a puzzle between LQCD and the DR approaches, which deserves clarification.

2 Introduction

In this article, we focus on the traditional way of estimating the contribution of the non-perturbative energy region to the photon HVP which relies on dispersive methods using as basic ingredients the $e^+e^-$ annihilation cross sections to all the possible exclusive hadronic final states collected up to $\sqrt{s} \simeq 2$ GeV.

The different successive broken variants of the HLS model, especially BHLS$_2$ [20, 21], provide a well-adapted framework to address the most relevant $e^+e^-$ annihilations to hadronic channels in the crucial part of the low-energy region ($\sqrt{s} \le 1.05$ GeV), namely the $e^+ e^-$ annihilations to the $\pi ^+ \pi ^-, K \overline{K}/\pi ^+ \pi ^- \pi ^0 /\pi ^0 \gamma /\eta \gamma$ final states; these already provide more than 80% of the muon HVP, when integrated up to the $\phi$ meson mass.

A BHLS$_2$-based computer code was used for this analysis which considered the large number of available data samples (several dozen), more than 1400 data points and, thus, practically the whole set of the available data samples has been exhausted. They have been listed, analyzed, and discussed in full detail previously, especially in the recent articles [20, 21], where a large number of previous references can be found.⁴ This computer code faithfully takes into account all the uncertainty information provided together with these data samples, and therefore, yielding satisfactory global fit probabilities turns out to simultaneously have a satisfactory model, satisfactory handling of data of the samples collected in several physics channels, and also satisfactory dealing with their reported uncertainty information.

In this perspective, the given data samples exhibiting contradictory aspects compared to most of the others either may lead to discarding them or, when meaningful, may motivate several solutions that avoid mixing up contradictory spectra; this has led us in our previous studies [20, 21] to provide different HVP evaluations based on some of the reported dipion KLOE samples—namely [24,25,26]—on the one hand, and separately on their BaBar analog [27, 28] on the other hand.

Regarding the various dipion spectra, the studies found strong contradictions between the so-called KLOE8 data sample [40] or the recently published SND spectrum [41], and the bulk of the other considered data samples have been discarded.

Comparing our own evaluations with those based on dispersion relations collected in [3], one does not observe any loss in precision with any of the various reported values of the muon $g-2$; however, differences between central values can be observed, clearly related to the contradictory properties of some data samples, especially KLOE [24, 25] versus BaBar [27, 28], reported long ago [18, 19, 42].

As noted above, the contribution of the listed HLS channels to the HVP is large; however, it is also worth mentioning that their contribution to the HVP uncertainty is almost negligible compared to that of the rest of the non-perturbative region. Moreover, as the HLS approach implies tight connections between the various annihilation channels, it allows one to perform stringent consistency checks on the different data samples involving the same physics channels or the other channels addressed by the HLS Lagrangian. It is worthwhile pointing out this important property specific to global models like the BHLS$_2$ model and also stressing that, by far, most of the available data samples fulfill this stringent constraint.

On the other hand, as indicated in the previous section, the updated version BHLS$_2$ variant [21] of the broken HLS model [20] allows us to fairly address the physics of the [$\pi ^0,~\eta ,~{\eta ^\prime }$] system within the HLS corpus. Indeed, besides the $e^+ e^- \rightarrow (\pi ^0/\eta ) \gamma$ annihilations, the PS decays to $\gamma \gamma$, and the $VP\gamma$ couplings, the pseudoscalar meson (PS) mixing properties in the octet-singlet [43,44,45] and quark flavor [46,47,48] basis parameterizations have been analyzed, leading to a satisfactory comparison with expectations.

Among the other processes involving the properties of the [$\pi ^0,~\eta ,~{\eta ^\prime }$] system, the ${\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decay spectrum deserves special attention. The measurements of this decay process started long ago—as early as 1975 [49]—and several experiments have collected samples of limited statistics [50,51,52,53,54,55,56,57], motivated by a reported 20 MeV mass shift of the $\rho$ peak compared to its observed value in the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation.

This effect was soon attributed to an interference between the ${\eta ^\prime }\rightarrow \rho \gamma$ ($\rho \rightarrow \pi ^+ \pi ^-$) resonant amplitude and the Wess–Zumino–Witten (WZW) anomalous ${\eta ^\prime }\pi ^+ \pi ^- \gamma$ contact term [58, 59]; this so-called box anomaly was expected to occur alongside the triangle anomaly responsible for the two-photon decays of the $\pi ^0,~\eta$ and ${\eta ^\prime }$ mesons. A basic HLS approach including this anomalous interaction term alongside the dominant ${\eta ^\prime }\rho ^0 \gamma$ coupling [60] confirmed this guess.

However, the dipion ${\eta ^\prime }$ spectrum from the BESIII Collaboration [61] published much later, thanks to its large statistics (970,000 events), modified the picture: It led to the conclusion that supplementing the ($\rho ^0,\omega$) resonance contributions by only a contact term is insufficient to reach a satisfactory description of the dipion spectrum.

On the other hand, the reported dipion spectrum observed in the parent $\eta \rightarrow \pi ^+ \pi ^- \gamma$ decay has undergone many fewer measurements. Besides former spectra⁵ from Layter et al. [62] and Gormley et al. [63], WASA-at-COSY reported for a 14,000-event spectrum [64], whereas the KLOE/KLOE2 Collaboration collected a 205,000-event spectrum [65].

As the dipion spectra reported from the recent measurements of the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays carry high statistics, it thus becomes relevant to re-examine whether (and how) they fit within the recently defined BHLS$_2$ framework of the HLS model, especially thanks to its kinetic breaking (see Appendix A.5), which has already allowed for a satisfactory description of the [$\pi ^0,~\eta ,~{\eta ^\prime }$] system properties [21]. Moreover, even if the physics of the $\eta /{\eta ^\prime }$ mesons is interesting per se, a better understanding of their properties is important, given their important role in the light-by-light (LbL) contribution to the muon anomalous magnetic moment.

The paper is organized as follows. Section 3 recalls the Kroll conditions [66] which reduce the number of free parameters of the kinetic breaking mechanism from 3 to 1; it also recalls and corrects Lagrangian pieces relevant for the present study. Section 4 identifies the Lagrangian pieces contributing to the considered $\eta$ and ${\eta ^\prime }$ radiative decays and displays the involved diagrams; the BHLS$_2$ amplitudes for these are constructed in Sect. 5 for the $\eta \rightarrow \pi ^+ \pi ^- \gamma$ decay and in Sect. 6 for the ${\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ one. The relation between the anomalous HLS amplitudes and their WZW [58, 59] analogs is given in Sect. 7. The derivation of the dipion mass spectrum in the $\eta /{\eta ^\prime }$ radiative decays is done in Sect. 8, and the role of the additional polynomial factor in the $\eta /{\eta ^\prime }$ radiative decays is thoroughly examined in Sect. 9. The polynomial factors accompanying the pion form factor parameterize an approximation to higher inelastic effects (beyond the two-pion channel) and are associated with the production vertex.⁶

Section 10 constitutes the central part of the present study. Section 10.1 provides an exhaustive presentation of the available $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ data samples; for this purpose it is important to note that all the available spectra carry an arbitrary absolute normalization, and that accounting for the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ partial widths also implies using an external piece of (PDG [70]) information. A detailed study of the additional polynomial degrees is the subject of Sect. 10.2, which reports on the fits performed separately with the $\eta$ and ${\eta ^\prime }$ spectra to find the appropriate degrees of the requested polynomials. This allows us to perform the fits of the dipion spectra reported in Sect. 10.3, where it is proved that a unique polynomial can satisfactorily account for both the $\eta$ and ${\eta ^\prime }$ dipion spectra simultaneously.

Section 10.4 is devoted to comparing our polynomial results with those reported in the literature. The role of intermediate $\rho ^\pm$ exchanges is emphasized in Sect. 10.6. The global BHLS$_2$ fits performed to simultaneously describe the dipion spectral line shapes examined in the previous subsections and the PDG information for the partial widths $\Gamma (\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma )$ are worked out in Sect. 10.7. A brief numerical analysis of some parameter values returned by the fits of the $\eta /{\eta ^\prime }$ dipion spectra is the subject of Sect. 10.5. Finally, in Sect. 11, we examine the issues relative to the connection between the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays (and also the $\tau$ decay data) and the hadronic contribution to the muon anomalous magnetic moment $a_\mu$. Section 12 summarizes the conclusions reached in the present study.

For ease of reading, the main pieces of information regarding the HLS model are briefly revisited in Appendix A.1, whereas its symmetry-breaking mechanisms are briefly summarized in Appendices A.2 to A.5. An erratum to the previous broken version of the BHLS$_2$ version is the subject of Appendix B. Also for ease of reading in the present work, it is appropriate to give the most relevant parts of the non-anomalous and anomalous BHLS$_2$ pieces under the Kroll conditions—mentioned just below—in Appendices C and D.

3 The Kroll conditions and VPP Lagrangian pieces

In the Feldmann–Kroll–Stech (FKS) approach [46,47,48] to the [$\pi ^0,~\eta ,~{\eta ^\prime }$] system, it has been found appropriate to impose the Kroll conditions [66] to axial current matrix elements. Applied to the BHLS$_2$ axial currents, these conditions,

$$\begin{aligned}{} & {} \displaystyle \langle 0|J^a_\mu | \eta _b(p)\rangle =ip_\mu f_a \delta _{ab}, \displaystyle |\eta _b(p)\rangle =| b \overline{b}(p)\rangle ,\nonumber \\{} & {} \quad \displaystyle J^a_\mu =\overline{a} \gamma _\mu \gamma _5 a, \displaystyle \{a,b =u,d,s\}, \end{aligned}$$

(1)

lead to two nontrivial relations [21]—referred to below as $A_\pm$ solutions—among the $\lambda _i$ parameters of the generalized ’t Hooft term [45, 71] (see Appendix B); one gets

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle { \mathrm Solutions} ~~A_\pm ~ \Longleftrightarrow&\displaystyle \lambda _0= \sqrt{2} \lambda _8 = \pm \sqrt{\frac{3}{2}} \lambda _3 \end{array} \right\} , \end{aligned}$$

(2)

which reduces the actual parameter freedom of the kinetic breaking from three to only one.

One thus should note that the Kroll conditions tightly couple the breaking in the BHLS$_2$ Lagrangian of the original U(3) symmetry to SU(3)$\times$U(1) and a particular isospin-breaking piece (via $\lambda _3 \ne 0$); it also leads to $F_\pi ^\tau (s=0)=1-\lambda _3^2/2$.

The $\pm 1$ factor in Eq. (2) is propagated below as $d_\pm$; thus, $A_+$ corresponds to $d_+$ and $A_-$ to $d_-$. The non-anomalous pieces ${{\mathcal {L}}}_{\eta ^\prime \pi ^\pm }$ and ${{\mathcal {L}}}_{\eta \pi ^\pm }$ of the BHLS$_2$ Lagrangian acquire simplified expressions compared to [21]:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {{\mathcal {L}}}_{\pi ^0 \pi ^\pm }= &{} \displaystyle \frac{iag}{2} (1+\Sigma _V) \left( 1-\frac{\lambda _0^2}{3}\right) \left[ ~ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^0 - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^0 \right] \\ \displaystyle {{\mathcal {L}}}_{\eta \pi ^\pm }= &{} \displaystyle - \frac{iag}{2} \left[ 1+ \Sigma _V \right] \left[ \epsilon - \frac{A_\pm }{2} \sin {\delta _P} \right] \left[ ~ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\eta - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\eta \right] \\ \displaystyle {{\mathcal {L}}}_{\eta ^\prime \pi ^\pm }= &{} \displaystyle -\frac{iag}{2} \left[ 1+ \Sigma _V \right] \left[ \epsilon ^\prime + \frac{A_\pm }{2} \cos {\delta _P}\right] \left[ ~ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\eta ^\prime - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\eta ^\prime \right] \end{array} \right. \end{aligned}$$

(3)

where

$$\begin{aligned} A_\pm = \Delta _A+d_\pm \lambda _0^2, \end{aligned}$$

(4)

exhibiting the Bando–Kugo–Yamawaki (BKY) $\Delta _A$, and $\delta _P$ is defined by

$$\begin{aligned} \displaystyle \cos {\delta _P}= & {} \frac{1}{\sqrt{3}} \left[ \sin {\theta _P} + \sqrt{2}\cos {\theta _P} \right] ,\nonumber \\ \sin {\delta _P}= & {} - \frac{1}{\sqrt{3}} \left[ \cos {\theta _P} - \sqrt{2}\sin {\theta _P} \right] \end{aligned}$$

(5)

in terms of $\theta _P$, the third mixing angle [72] which is one of the BHLS$_2$ fit parameters. It was shown in [21] that the BKY parameter $\Sigma _V$ can be dropped out without any loss in generality.

One should note that if ${{\mathcal {L}}}_{\pi ^0 \pi ^\pm }$ is the leading order, both ${{\mathcal {L}}}_{\eta \pi ^\pm }$ and ${{\mathcal {L}}}_{{\eta ^\prime }\pi ^\pm }$ are manifestly ${{\mathcal {O}}}(\delta )$, i.e., first order in breakings. Finally, it is worthwhile to recall that terms of order ${{\mathcal {O}}}(\delta ^2)$ or higher in amplitudes are discarded.

4 The $\eta /{\eta ^\prime }\rightarrow \pi ^- \pi ^+ \gamma$ decays in the BHLS$_2$ framework

The amplitudes for the $\eta /{\eta ^\prime }\rightarrow \pi ^- \pi ^+ \gamma$ decays a priori involve the APPP, VPPP, and AVP sectors of the full BHLS$_2$ Lagrangian [20, 21]. The interaction terms involved are displayed in Appendices C and D in terms of the physical pseudoscalar fields and ideal vector fields which should be replaced by their physical partners following the method developed in [20]. The $V -\gamma$ transition couplings can be found in [20], Appendix A, and the relevant non-anomalous VPP couplings have been displayed for convenience in Sect. 3 just above.

Fig. 1

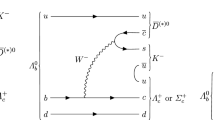
The classes of tree diagrams. P stands for either of $\eta$ and $\eta ^\prime$. In diagrams a and b, the double lines stand for the neutral vector mesons (subject to mixing). In the c diagrams, the intermediate vector meson is $\rho ^\pm$, whereas the external one is neutral. The pions are charged. The vanishing of the AVP couplings (see text) implies that diagrams (b2) and (c1) do not contribute to the decay amplitudes

The classes of diagrams involved a priori in the $\eta /{\eta ^\prime }$ decays to $\pi ^- \pi ^+ \gamma$ are displayed in Fig. 1. Namely, diagram (a1) illustrates the APPP interaction, whereas diagram (a2) sketches the VPPP contributions with $V -\gamma$ transitions ($V=\rho ^0,~\omega ,~\phi$) provided by the non-anomalous BHLS$_2$ Lagrangian ([20], Appendix A). These two kinds of diagrams are generally named box anomaly terms.

Diagram (b1) sketches the diagram class involving VVP couplings; these diagrams provide the major contribution to the $\eta /{\eta ^\prime }$ dipion spectra. As one assumes that $c_3=c_4$ thanks to former works [18], all contributions involving AVP couplings, such as those depicted in Figs. (b2) and (c1), identically vanish. Finally, the (c2) diagram class illustrates the diagrams reflecting the two possible choices for the $\pi ^\pm \pi ^\mp$ pair, each involving an intermediate $\rho ^\pm$ exchange.

In the following, for the $\eta$ and ${\eta ^\prime }$ decays, the non-resonant (a1) and (a2) contributions are gathered into the $T^{NR}$ partial amplitude, whereas the (b1) and (c2) resonant contributions are given by the $T^{R1}$ and $T^{R2}$ terms, respectively.

5 The $\eta \rightarrow \pi ^+ \pi ^- \gamma$ amplitude within BHLS$_2$

As three kinds of diagrams contribute, the full $T(\eta )$ amplitude for the $\eta \rightarrow \pi ^+ \pi ^- \gamma$ decay is written as

$$\begin{aligned} \displaystyle T(\eta ) = T^{NR}(\eta ) + T^{R1}(\eta ) + T^{R2}(\eta ), \end{aligned}$$

(6)

and they include the common tensor object

$$\begin{aligned} \displaystyle F= \epsilon ^{\mu \nu \alpha \beta } \varepsilon _\mu (\gamma , q) q_\nu p^-_\alpha p^+_\beta \end{aligned}$$

(7)

typical of the anomalous Lagrangian piece expressions; F exhibits the obvious momentum notations. This factor is understood in the $T(\eta /{\eta ^\prime })$ amplitude expressions here and below to lighten the writing; it is restored in the final expressions involving the differential decay widths.

As already stated, the first term in the expansion (6) gathers the non-resonant (APPP/VPPP) contributions, whereas the second and third terms collect the resonant contributions of different structures generated via the VVP Lagrangian as noted in the section just above.

The $T^\eta _{NR}$ term can be written ($A_\pm =\Delta _A+d_\pm \lambda _0^2$):

$$\begin{aligned} T^{NR}(\eta )= & {} \displaystyle - \frac{ie}{4\pi ^2 f_\pi ^3} \left[ 1-\frac{3 c_3}{2} \right] g_{\eta \pi ^+\pi ^-\gamma } ~~\textrm{with}\nonumber \\ g_{\eta \pi ^+\pi ^-\gamma }= & {} \epsilon + \left\{ 1 -\frac{A_\pm }{2} - \frac{3\lambda _0^2}{4} \right\} \sin {\delta _P}. \end{aligned}$$

(8)

It is worth noting that (i) the dependence upon $c_1-c_2$ drops out when summing up the APPP and VPPP contributions, and (ii) if one cancels out the symmetry-breaking contributions, $T^{NR}(\eta )$ remains nonzero and corresponds to the WZW term [58, 59].

On the other hand, the $T^{R1}(\eta )$ contributions to the $T(\eta )$ amplitude can be written ($m^2=a g^2 f_\pi ^2$):

$$\begin{aligned} \left\{ \begin{array}{ll} T^{R1}(\eta )= \displaystyle c_3~\frac{ie m^2}{8 \pi ^2 f_\pi ^3} \left[ \frac{T^0_\rho (\eta )}{D_\rho (s)} + \frac{T^0_\omega (\eta )}{D_\omega (s)} + \frac{T^0_\phi (\eta )}{D_\phi (s)} \right] \\ \displaystyle T^0_\rho (\eta )=\epsilon + \frac{2\beta (s)}{z_A} \cos {\delta _P}\\ \qquad \qquad + 3 \left[ 1 -\frac{3\lambda _0^2}{4} - \frac{A_\pm }{6} + \frac{\alpha (s)}{3} +2 \xi _3\right] \sin {\delta _P} \\ \displaystyle T^0_\phi (\eta )= -\left[ \frac{2 \beta (s)}{z_A} \right] \cos {\delta _P} \\ \displaystyle T^0_\omega (\eta ) = -~\alpha (s) \sin {\delta _P} \end{array} \right. , \end{aligned}$$

(9)

where $D_\rho (s)$, $D_\omega (s)$, and $D_\phi (s)$ are the indicated inverse vector meson propagators; they are parameterized as defined in Section 9 of [20]. Equation (9) displays the dependency upon the angles $\alpha (s)$ and $\beta (s)$ defining the dynamical vector meson mixing (see Appendix A.4) and upon the parameter defined by the kinetic breaking mechanism (see Appendix A.5) once the Kroll conditions [66] are applied. It is worth remarking that $\rho ^0$ is the only resonant contribution which survives when symmetry-breaking terms are turned off. Moreover, the $\omega$ and $\phi$ contributions are outside the phase space actually available in the $\eta$ decay.

$T^{R2}(\eta )$, the second resonant contribution, is produced by the non-anomalous $\rho ^\pm \eta \pi ^\mp$ coupling purely generated by our breaking procedures (see Eq. (3)) and by the $\omega \rho ^\pm \pi ^\mp$ term of the $VV\eta$ Lagrangian piece (see Appendix C.2.2). Setting

$$\begin{aligned} s_{\pm 0}=(p_\pm +q)^2,~~q= \mathrm{photon ~momentum}, \end{aligned}$$

we write:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{R2}(\eta )= \displaystyle c_3~ \frac{ie m^2}{8 \pi ^2 f_\pi ^3} ~ T^\pm _\rho (\eta ) \left[ \frac{1}{D_\pm (s_{+0}) } + \frac{1}{D_\pm (s_{-0})} \right] \\ \displaystyle T^\pm _\rho (\eta )=\epsilon - \frac{A_\pm }{2}\sin {\delta _P}. \end{array} \right. \nonumber \\ \end{aligned}$$

(10)

The $D_\pm (s_{\pm 0})$s denote the inverse $\rho ^\pm$ propagators; the $T^{R2}$ contribution, a pure product of symmetry breakings, cancels out when all symmetries are restored. Finally, the three amplitude pieces just defined depend on the HLS parameter $c_3$.

At the chiral point 

$$\begin{aligned} s=s_{+0}=s_{-0}=0, \end{aligned}$$

the vector meson inverse propagators fulfill [20] $D_V(0)=-m_V^2$, with

$$\begin{aligned}{} & {} m_{\rho _\pm }^2=m^2,\,\, m_{\rho _0}^2=m^2(1+\xi _3)^2,\,\, m_\omega ^2=m^2(1+\xi _0)^2,\,\,\nonumber \\{} & {} m_\phi ^2=m^2 z_V(1+\xi _0)^2, \end{aligned}$$

(11)

where $m^2=ag^2 f_\pi ^2$, the conditions $\alpha (0)=\beta (0)=0$ being exactly fulfilled.

6 The $\eta ^\prime \rightarrow \pi ^+ \pi ^- \gamma$ amplitude within BHLS$_2$

The decay process $\eta ^\prime \rightarrow \pi ^+ \pi ^- \gamma$ undergoes a quite similar treatment to those performed for the $\eta \rightarrow \pi ^+ \pi ^- \gamma$ decay in the preceding section, and so one will avoid duplicating the comments on the ${\eta ^\prime }$ amplitude already stated on the $\eta$ amplitude. The three different kinds of contributions to the ${\eta ^\prime }$ decay amplitude are

$$\begin{aligned} \displaystyle T({\eta ^\prime }) = T^{NR}({\eta ^\prime })+ T^{R1}({\eta ^\prime }) + T^{R2}({\eta ^\prime }). \end{aligned}$$

(12)

The first term, which gathers the APPP and VPPP contributions to the full amplitude $T^{\eta ^\prime }$, is given by

$$\begin{aligned} T^{NR}({\eta ^\prime })= & {} \displaystyle - \frac{ie}{4 \pi ^2 f_\pi ^3} \left[ 1-\frac{3 c_3}{2} \right] g_{\eta ^\prime \pi ^+\pi ^-\gamma } ~~~\textrm{with}\nonumber \\ \displaystyle g_{\eta ^\prime \pi ^+\pi ^-\gamma }= & {} \epsilon ^\prime - \left\{ 1 -\frac{A_\pm }{2} - \frac{3\lambda _0^2}{4} \right\} \cos {\delta _P} \end{aligned}$$

(13)

and does not depend on $c_1-c_2$. On the other hand, the contributions gathered in $T^{R1}({\eta ^\prime })$ are given by

$$\begin{aligned} \left\{ \begin{array}{ll} T^{R1}({\eta ^\prime })= \displaystyle c_3 \frac{ie m^2}{8 \pi ^2 f_\pi ^3} \left[ \frac{T^0_\rho (\eta ^\prime )}{D_\rho (s)} + \frac{T^0_\omega (\eta ^\prime )}{D_\omega (s)} + \frac{T^0_\phi (\eta ^\prime )}{D_\phi (s)} \right] \\ \displaystyle T^0_\rho ({\eta ^\prime })=\epsilon ^\prime + \frac{2\beta (s)}{z_A} \sin {\delta _P}\\ \qquad \qquad - 3 \left[ 1 -\frac{3\lambda _0^2}{4} - \frac{A_\pm }{6} +\frac{\alpha (s)}{3} +2 \xi _3\right] \cos {\delta _P} \\ \displaystyle T^0_\phi ({\eta ^\prime })= -\left[ \frac{2 \beta (s)}{z_A} \right] \sin {\delta _P} \\ \displaystyle T^0_\omega ({\eta ^\prime }) = +~\alpha (s) \cos {\delta _P} \end{array} \right. , \end{aligned}$$

(14)

where, as for the $\eta$ decay, only the $\rho ^0$ term is ${{\mathcal {O}}} (\delta ^0=1)$ in breakings. Finally,

$$\begin{aligned} \left\{ \begin{array}{ll} T^{R2}({\eta ^\prime })= \displaystyle c_3~ \frac{ie m^2}{8 \pi ^2 f_\pi ^3} ~T^\pm _\rho ({\eta ^\prime }) \left[ \frac{1}{D_\pm (s_{+0}) } + \frac{1}{D_\pm (s_{-0})} \right] \\ \displaystyle T^\pm _\rho ({\eta ^\prime })=\epsilon ^\prime + \frac{A_\pm }{2}\cos {\delta _P} \end{array} \right. , \nonumber \\ \end{aligned}$$

(15)

which is purely ${{\mathcal {O}}} (\delta )$.

The $\omega$ contribution in the ${\eta ^\prime }$ decay must be visible in high-statistics data samples (like [61]) and is worth comparing with its line shape in the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation. Regarding the $\phi$ contribution, it is somewhat outside the allowed phase space—by $\simeq 60$ MeV. Finally, the influence of higher vector mesons, especially the first radial excitation $\rho ^\prime$, is outside the HLS scope; global fit properties may reveal their actual influence w.r.t. the broken HLS context.

7 BHLS$_2$ and the WZW box anomalies

Traditionally, the amplitudes associated with the box anomalies are derived from the Wess–Zumino–Witten (WZW) Lagrangian [58, 59]:

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{WZW}= -i\frac{N_c e}{3 \pi ^2 f_\pi ^3} ~\epsilon ^{\mu \nu \alpha \beta } A_\mu \textrm{Tr} \left[ Q \partial _\nu P \partial _\alpha P \partial _\beta P\right] , \end{aligned}$$

(16)

where P is the bare pseudoscalar meson U(3) matrix. This Lagrangian differs from the anomalous APPP Lagrangian piece of the HLS model (see Eq. (86)) by the factor

$$\begin{aligned} \left[ 1-\frac{3}{4}(c_1-c_2+c_4)\right] \end{aligned}$$

.

The BHLS$_2$ $\eta /{\eta ^\prime }$ decay amplitudes just defined are expected to coincide with their WZW analogs at the chiral point, where the HLS $c_i$’s dependencies of the decay amplitudes should cancel out. Their expressions at the chiral point ($s=s_{+0}=s_{-0}=0$) are given by⁷:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle T(\eta )= \displaystyle - \frac{ie}{4\pi ^2 f_\pi ^3} \left[ \epsilon + \left\{ 1 -\frac{A_\pm }{2} - \frac{3\lambda _0^2}{4} \right\} \sin {\delta _P} \right] , \\ T({\eta ^\prime })= \displaystyle - \frac{ie}{4 \pi ^2 f_\pi ^3} \left[ \epsilon ^\prime - \left\{ 1 -\frac{A_\pm }{2} - \frac{3\lambda _0^2}{4} \right\} \cos {\delta _P} \right] , \\ T(\pi ^0)= \displaystyle + \frac{ie}{4\pi ^2 f_\pi ^3} \\ \qquad \qquad \times \left[ \left\{ 1 -\frac{A_\pm }{2} - \frac{\lambda _0^2}{3}\right\} - \epsilon \sin {\delta _P}+ \epsilon ^\prime \cos {\delta _P}\right] \end{array} \right. \nonumber \\ \end{aligned}$$

(17)

and coincide with those which can be directly derived from the WZW Lagrangian equation (16) after applying the breaking procedures mentioned in the Appendices.

8 $\eta /\eta ^\prime$ radiative decays: the BHLS$_2$ dipion mass spectra

The amplitudes $T(\eta )$ and $T({\eta ^\prime })$ allow us to describe—within the full EBHLS$_2$ framework [20, 21]– the dipion mass spectra observed in the $\eta /\eta ^\prime$ radiative decays have been derived in Sects. 5 and 6, respectively; both should be multiplied by the function⁸$F(s,s_{0+})$ (see Eq. (7)). The differential decay widths can be written as

$$\begin{aligned} \displaystyle \frac{d^2\Gamma _X}{ds ds_{0+}}= \frac{1}{(2 \pi )^3} \frac{1}{32 M_X^3} |T_X~F(s,s_{0+})|^2,~X=\eta ,\eta ^\prime \end{aligned}$$

(18)

in terms of, respectively, s, the ($\pi ^+ \pi ^-$), and $s_{0+}$, the ($\pi ^+ \gamma$) pair invariant masses squared of the $\eta /\eta ^\prime$ decay products. The accessible invariant mass spectra being functions of only s, this expression should be integrated over $s_{0+}$:

$$\begin{aligned}{} & {} \displaystyle \frac{d\Gamma _X}{ds}= \frac{1}{(2 \pi )^3} \frac{1}{32 M_X^3} \int _{s_{min}}^{s_{max}}|T_X~F(s,s_{0+})|^2 ds_{0+},~\nonumber \\ {}{} & {} X=\eta ,\eta ^\prime \end{aligned}$$

(19)

where

$$\begin{aligned}{} & {} \displaystyle s_{min/max}=\frac{M_X^2+2 m_\pi ^2-s}{2} \mp p_\pi \frac{M_X^2-s}{\sqrt{s}}\quad \mathrm{and~~}\nonumber \\{} & {} \displaystyle p_\pi =\frac{\sqrt{s-4 m_\pi ^2}}{2}. \end{aligned}$$

(20)

Both amplitudes $T(\eta )$ and $T({\eta ^\prime })$, generically referred to as $T_X$, can be written

$$\begin{aligned} T_X(s,s_{0+})= & {} \displaystyle R_X(s)+C_X G(s,s_{0+}) {\ \mathrm with~~}\nonumber \\ G (s,s_{0+})= & {} \displaystyle \frac{1}{D_\rho (s_{0-})}+ \frac{1}{D_\rho (s_{0+})}, \end{aligned}$$

(21)

having defined $s_{0\pm }=(q + p^\pm )^2$ related by

$$\begin{aligned} s_{0-}-m_\pi ^2=(M_X^2-s)-(s_{0+}-m_\pi ^2). \end{aligned}$$

$R_X(s)$ collects the contributions previously named $T^{NR}(X)$ and $T^{R1}(X)$ and is (by far) the dominant term, whereas⁹$T^{R2}(X) = C_X G(s,s_{0+})$ is only ${{\mathcal {O}}}(\delta )$ in breakings.

On the other hand, the $[F(s,s_{0+})]^2$ factor in Eq. (19) is

$$\begin{aligned} \displaystyle [F(s,s_{0+})]^2= & {} \frac{s}{4} (s_{0+}-m_\pi ^2)(s_{0-}-m_\pi ^2)\nonumber \\{} & {} - \frac{m_\pi ^2}{4} (M_X^2-s)^2 \end{aligned}$$

(22)

and can be solely expressed in terms of s and $s_{0+}$ to perform the integration shown in Eq. (19). This leads to pre-defining within the fitting code the following integrals:

$$\begin{aligned} \displaystyle I_1(s)= & {} \int _{s_{min}}^{s_{max}}|F(s,s_{0+})|^2 ds_{0+},\nonumber \\ I_2(s)= & {} \int _{s_{min}}^{s_{max}}|F(s,s_{0+})|^2|G (s,s_{0+})|^2ds_{0+} \nonumber \\ \displaystyle I_3(s)= & {} \int _{s_{min}}^{s_{max}}|F(s,s_{0+})|^2 \textbf{Re} \left[ G (s,s_{0+}) \right] ds_{0+},\nonumber \\ I_4(s)= & {} \int _{s_{min}}^{s_{max}}|F(s,s_{0+})|^2 \textbf{Im} \left[ G (s,s_{0+}) \right] ds_{0+}. \end{aligned}$$

(23)

Actually, $I_1(s)$ can be integrated in closed form:

$$\begin{aligned} \displaystyle I_1(s)= \frac{(M_X^2-s)^3}{3}\frac{p_\pi ^3}{\sqrt{s}}~ \end{aligned}$$

(24)

with $p_\pi$ given in Eq. (20). The three other functions should be integrated numerically within the iterative procedure context already running to address the $e^+ e^- \rightarrow \pi ^+ \pi ^- \pi ^0$ annihilation data within the BHLS [18] or BHLS$_2$ [20, 21] frameworks. One then gets

$$\begin{aligned} \displaystyle \frac{d\Gamma _X}{ds}= & {} \frac{1}{(2 \pi )^3} \frac{1}{32M_X^3}\nonumber \\{} & {} \times \left[ |R_X (s)|^2~I_1(s)+C_X^2 I_2(s) + 2 C_X ~(\textbf{Re} \left[ R_X(s) \right] \right. \nonumber \\{} & {} \left. I_3(s) + \textbf{Im} \left[ R_X(s) \right] ~I_4(s)) \right] \end{aligned}$$

(25)

In the BHLS$_2$ approach, only leading-order terms in the breaking parameters ${{\mathcal {O}}}(\delta )$ (as the $C_X$ term) are addressed, and then terms of order ${{\mathcal {O}}}(\delta ^2)$—like the $C_X^2$ contribution—can be neglected.

The $I_1(s)$ term in Eq. (25) can be rewritten, for subsequent use in the text:

$$\begin{aligned} \displaystyle \frac{d\widetilde{\Gamma }_X}{ds}= & {} \Gamma _0(s) |R_X (s)|^2, \displaystyle \mathrm{with~~}\nonumber \\ \Gamma _0(s)= & {} \frac{s (M_X^2-s)^3 [\sigma _\pi (s)]^3}{3 \cdot 2^{11} \pi ^3 M_X ^3}~ \displaystyle \mathrm{and~~}\nonumber \\ \sigma _\pi (s)= & {} \sqrt{1-\frac{4 m_\pi ^2}{s}}. \end{aligned}$$

(26)

9 Pion form factor in the $\eta /{\eta ^\prime }$ radiative decays

The study in [73], also referred to hereafter as SHKMW, has placed a valuable emphasis on the connection between the pion vector form factor $F_\pi (s)$—as it comes out of the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation process—and the dipion spectra from the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ radiative decays. Further works have followed (see, for instance, [74,75,76,77,78] for further reference), generally motivated by a better understanding of the $\eta$ and ${\eta ^\prime }$ meson properties regarding their contributions to the light-by-light (LbL) fraction of the muon anomalous magnetic moment $a_\mu$.

(i) It is worthwhile to briefly outline how this connection is established [73]. The pion vector form factor $F_\pi (s)$ and the P-wave $\pi ^+ \pi ^-$ scattering amplitude $T_{\pi \pi }(s)$ are related by

$$\begin{aligned} \displaystyle \textrm{Im } \left[ F_\pi (s) \right] = \sigma _\pi (s) \left[ T_{\pi \pi }(s) \right] ^* F_\pi (s) \Theta (s-4 m_\pi ^2), \end{aligned}$$

(27)

valid along the energy region where the $\pi ^+ \pi ^-$ scattering is elastic; $\sigma _\pi (s)$ has been defined just above. Therefore, in this energy region, the pion vector form factor $F_\pi (s)$ and the elastic scattering amplitude $T_{\pi \pi }(s)$ should carry equal phases. The Heaviside function indicates that $F_\pi (s)$ is real below the $2\pi$ threshold; the first significant inelastic channel being $\omega \pi$, the validity range of Eq. (27) practically extends up to $\simeq 922$ MeV, substantially above the $\eta$ mass and slightly below the ${\eta ^\prime }$ mass (by only 36 MeV). Stated another way, the phase-equality property holds over almost the whole HLS energy range of validity ($\sqrt{s}\le 1.05$ GeV).

On the other hand, assuming the $\pi ^+\pi ^-$ scattering is elastic for all $s \ge 4 m_\pi ^2$, the P-wave amplitude $T_{\pi \pi }(s)$ is written as

$$\begin{aligned} \displaystyle T_{\pi \pi }(s) =\frac{\sin {\delta _{11}(s)} e^{i\delta _{11}(s)}}{\sigma _\pi (s)} \end{aligned}$$

(28)

in terms of the P-wave phase shift $\delta _{11}(s)$, and the solution to Eq. (27) can be expressed in terms of the Omnès function $\Omega (s)$ by

$$\begin{aligned}{} & {} \displaystyle F_\pi (s)= K(s) \Omega (s),~\textrm{where}~~~ \nonumber \\ {}{} & {} \Omega (s)=\exp { \left( \frac{s}{\pi } \int _{4 m_\pi ^2}^\infty \frac{dz}{z} \frac{\delta _{11}(z)}{z-s-i\epsilon } \right) }, \end{aligned}$$

(29)

K(s) being some appropriate real analytic function, required to be free of singularities over the physical region $s\ge 4 m_\pi ^2$. This expression intends to factor out the non-perturbative contribution to $F_\pi (s)$ contained in the $\Omega (s)$ function, and so the remaining part K(s) (perturbative in the sense of ChPT, at low energy) is expected to behave smoothly and can be well approximated by a polynomial [73] along our region of interest (up to $\simeq m_\phi$). This smooth function K(s) is process-dependent, whereas $\Omega (s)$, being determined by the $\pi \pi$ final state re-scattering phase shifts, represents a more universal part of the vector form factor. It is shown in [74] that a first-degree polynomial $K(s)=1+\alpha _\Omega s$ allows us to reach a nice (linear) correlation up to $s\simeq 1$ GeV$^{2}$ between the dipion spectrum from Belle [34] and the $\Omega (s)$ functions derived from the phase shift data from [79], see also [67,68,69]; a value $\alpha _\Omega \simeq 0.1$ GeV$^{-2}$ can be inferred from Figure 1 in [74]. The deterioration of the linear behavior above $s \simeq m_\phi ^2$ is actually not unexpected because of rising inelasticities and of the high-mass vector meson influence.

(ii) Assuming the pion pair emerging from the $\eta /{\eta ^\prime }$ radiative decays is purely isospin 1 and a P-wave [61, 64], its amplitude should carry the same analytic properties as $F_\pi (s)$, i.e., they may only differ by a real analytic function, free of right-hand side singularities. Reference [73] thus proposes to write the differential dipion spectra as

$$\begin{aligned} \begin{array}{llll} \displaystyle \frac{d\overline{\Gamma }_X}{ds}= \Gamma _0(s) |A_X P_X(s) F_\pi (s)|^2, ~~(X=\eta /{\eta ^\prime }), \end{array} \end{aligned}$$

(30)

where $\Gamma _0(s)$ has already been defined in Eq. (26), and the $A_X$’s being appropriate normalization constants. The $P_X(s)$ functions ($P_X(0)=1$) are remaining correction factors specific to the $\eta$ and ${\eta ^\prime }$ radiative decays (in the present case, but are more generally dependent on higher inelastic effects existing at any $\pi \pi$ production vertex), which could both be analyzed within the extended ChPT context [43, 45] (see also [80]) and are free of right-hand side singularities.

As just argued regarding the pion vector form factor and its K(s) factor, the $P_X(s)$ functions should satisfactorily be approximated by low-degree polynomials [73]. This is what is shown by the bottom panel in Figure 1 of [74], which moreover indicates that $P_\eta (s)=P_{\eta ^\prime }(s)$ should likely hold. Of course, procedures to complement this approach by symmetry-breaking effects also have to be invoked, prominently—but not only—the $\rho ^0-\omega$ mixing for the ${\eta ^\prime }$ decay process.

(iii) The issue is now to relate $d\overline{\Gamma }_X$ (Eq. (30)) and $d\widetilde{\Gamma }_X$ (Eq. (26)) within the HLS framework when no breaking is at work. Equivalently, this turns out to check whether the $R_X(s)$’s and $F_\pi (s)$ (can) carry the same phase in this case.

Let us consider the pion vector form factor $F_\pi (s)$ as given in [20], discarding terms of order ${{\mathcal {O}}}(\delta )$ or higher in breaking parameters; keeping only tree contributions (loop corrections, like the $\rho ^0-\gamma$ transition amplitude, are counted as ${{\mathcal {O}}}(\delta )$), and dropping out the ${{\mathcal {L}}}_{p^4}$ contributions, one derives ($m^2=a g^2 f_\pi ^2$, the unbroken $\rho ^0$ HK mass.):

$$\begin{aligned} \displaystyle F_\pi (s)= \left( 1 - \frac{a}{2} \left[ 1 + \frac{m^2}{D_\rho (s)} \right] \right) + {{\mathcal {O}}}(\delta ). \end{aligned}$$

(31)

Similarly, the $R_X(s)$ functions in Eq. (26) reduce to

$$\begin{aligned} \displaystyle R_\eta= & {} - \frac{ie \sin {\delta _P}}{4 \pi ^2 f_\pi ^3} \left( 1-\frac{3}{2} c_3 \left[ 1 + \frac{m^2}{D_\rho (s)} \right] \right) , \nonumber \\ R_{\eta ^\prime }= & {} + \frac{ie \cos {\delta _P}}{4 \pi ^2 f_\pi ^3} \left( 1-\frac{3}{2} c_3 \left[ 1 + \frac{m^2}{D_\rho (s)} \right] \right) \end{aligned}$$

(32)

up to terms of ${{\mathcal {O}}}(\delta )$ in breaking parameters.

These equations lead us to define a no-breaking reference by requiring the following:

(1) Holding of the vector meson dominance assumption, which implies $a \equiv a_{VMD}=2$ within the generic HLS model [12, 16], it is worth recalling here (see Section 2 in [21] for details) that the HLS parameter a is not reachable by fit, once the BKY breaking (see Appendix A.2) is at work. Indeed, all Lagrangian terms of interest for our physics depend on the product $a^\prime =a(1+\Sigma _V)$ and not on each of these parameters separately; therefore, one can freely fix $a=2$, and then the term $\delta a= a_{VMD} \Sigma _V$ is clearly¹⁰${{\mathcal {O}}}(\delta )$.

(2) The universality of the $\rho$ phase implies that $R_\eta (s)$, $R_{\eta ^\prime }(s)$, and $F_\pi (s)$ share the same phase, and therefore it requires the existence of an “unbroken” value for $c_3$. Indeed, imposing $c_3^{ref}=2/3$ alongside $a_{VMD}=2$, one can derive a satisfactory no-breaking reference as

$$\begin{aligned} \displaystyle F_\pi (s)= & {} - \frac{m^2}{D_\rho (s)}, \displaystyle R_\eta = + \frac{ie \sin {\delta _P}}{4 \pi ^2 f_\pi ^3} \frac{m^2}{D_\rho (s)},\nonumber \\ \displaystyle R_{\eta ^\prime }= & {} - \frac{ie \cos {\delta _P}}{4 \pi ^2 f_\pi ^3} \frac{m^2}{D_\rho (s)}, \end{aligned}$$

(33)

which should be complemented by ${{\mathcal {O}}}(\delta )$ contributions to account for real data.

The issue becomes whether the values returned for a and $c_3$ from fits to the (real) data differ little enough from $a_{VMD}$ and $c_3^{ref}$ that their differences can be considered ${{\mathcal {O}}}(\delta )$ effects. For this purpose, one can refer to the latest published BHLS$_2$ standard fit results collected in Table 10 of [21], in particular, one finds the following:

• $a=1.766 \pm 0.001$, which shows a deviation $\delta a=0.244$ from $a_{VMD}=2$ corresponding to having $\Sigma _V=0.122$; and

• $c_3= 0.742 \pm 0.003$ which deviates by $\delta c_3= 0.076$ from $c_3^{ref}=0.667$,

focusing on the favored solution $A_-$ [21] to the Kroll conditions (see Sect. 3)—the $A_+$ solution actually provides similar values. Thus, $\delta a$ and $\delta c_3$ look small enough to be viewed as departures from, respectively, $a_{VMD}$ and $c_3^{ref}$ and treated as ${{\mathcal {O}}}(\delta )$ corrections, on the same footing as the manifest breaking parameters. To our knowledge, it is the first time that an identified physics condition can propose a constraint on one of the FKTUY [13] parameters, namely¹¹$c_3$.

Fig. 2

The $\delta _{11}$ phase shift plotted as a function of $\sqrt{s}$. Besides the data points of [81, 82], the dashed black curve is the solution to the Roy equations [83], the green full line shows the phase reconstructed in [84], and the red full line shows the BHLS$_2$ phase shift exhibiting the $\omega$ and $\phi$ signals. The black stars show the smeared BHLS$_2$ spectrum (e.g., the red curve)

(iv) From what has been just argued, it is clear that within the BHLS$_2$ context, the $\eta /{\eta ^\prime }\rightarrow \pi ^+\pi ^- \gamma$ decay amplitudes $T_X(s)$ reported in Sects. 5 and 6 above can actually be written as

$$\begin{aligned} T_X(s)=B_X F_\pi (s) + {{\mathcal {O}}}(\delta ) \mathrm{,~~ X=\eta /{\eta ^\prime },} \end{aligned}$$

(34)

the $B_X$’s being definite constants depending on the breaking parameters. $F_\pi (s)$ contains already manifest breaking terms like the $\omega$ and $\phi$ signals with, however, different weights from their analogs in the $T_X(s)$ amplitudes.¹²

On the other hand, as shown in [20], yielding a fair description of the data samples for $|F_\pi (s)|$ (see Figure 2 and Table 3 in [20]), BHLS$_2$ also leads to a fair account of the phase shift $\delta _{11}(s)$ over its whole range of validity without involving any phase shift data sample in its derivation. This is illustrated by¹³ Fig. 2, which reflects the fair accord reached by the BHLS$_2$ prediction with the phase derived from the Roy equations [83] or the pion form factor phase of Ref. [84] on the one hand, and the experimental phase shift data from [81, 82] on the other hand. Moreover, the same BHLS$_2$ spectrum was smeared over 10 MeV bins, to mimic the CERN-Munich spectrum [81] (black star symbols), to clearly show that the $\omega$ and $\phi$ signals cannot be manifestly observed in the existing data.

All this leads to the conclusion that the SHKMW modification [73] shown in Eq. (30),

$$\begin{aligned} F_\pi (s) \rightarrow A_X P_X(s)F_\pi (s), \end{aligned}$$

also applies in the global BHLS$_2$ context. In this case, this turns out to perform the change

$$\begin{aligned} T_X(s) \Longrightarrow H_X P_X(s) T_X(s) \end{aligned}$$

when using the amplitudes constructed in Sects. 5 and 6. Our notations are connected with those in Ref. [73] by writing the following¹⁴:

$$\begin{aligned} A_X=A_X^0 H_X,~~ H_X \equiv 1+\delta _X,~~X=\eta ,{\eta ^\prime } \end{aligned}$$

(35)

as the $A_X^0$ factors are already accounted for in the $T_X$ amplitudes derived from the BHLS$_2$ Lagrangian as shown below.

Then the global character of the BHLS$_2$ fitting context¹⁵ ensures that the non-perturbative effects are suitably accounted for as reflected by Fig. 2.

From now on, the $P_X(s)$ functions are chosen polynomials of the lowest possible degree consistent with a satisfactory fitting. Being beyond the BHLS$_2$ scope, these functions are supplemented within the fit procedure by performing the change

$$\begin{aligned} \displaystyle T_X(s) \Longrightarrow H_X P_X(s) T_X(s),~\mathrm{with~~} P_X(0)=1,~X=\eta ,{\eta ^\prime }\nonumber \\ \end{aligned}$$

(36)

in Eq. (25) above. Practically, each term in the right-hand side of Eq. (25) gets a factor of $|H_X P_X(s)|^2$, the coefficients of which have to be derived by the global fit, where the $[C_X]^2$ term can be discarded as it is manifestly ${{\mathcal {O}}}(\delta ^2)$.

10 Fits of the $\eta /{\eta ^\prime }$ radiative decay spectra within BHLS$_2$

The reference set of data samples ${{\mathcal {H}}}_R$ included within the BHLS$_2$ framework has been presented several times and recently in [20, 21]; it covers the six $e^+ e^-$ annihilation channels to $\pi ^+ \pi ^-$, $K^+ K^-$, $K_L K_S$, $\pi ^+ \pi ^- \pi ^0$, $\pi ^0 \gamma$, and $\eta \gamma$, some more decay widths (in particular $\pi ^0/\eta /{\eta ^\prime }\rightarrow \gamma \gamma$), and, finally, the dipion mass spectrum in the $\tau \rightarrow \pi \pi \nu$ decay. These represent already the largest set of data (altogether 1366 data points) successfully submitted to a global fit, as reflected by Table 9 in [21]; they will not be discussed here further. It is nevertheless relevant to remember that ${{\mathcal {H}}}_R$ encompasses almost all existing samples except for the recent CMD-3 dipion data as already argued in footnote 4, the KLOE08 [40], BaBar [27, 28], and the recent SND [85] dipion spectra because of the strong tension they exhibit with respect to the rest of the (more than 60) ${{\mathcal {H}}}_R$ samples. This issue has been thoroughly reexamined in [21].

The present study aims to include also the dipion spectra measured in the $\eta /{\eta ^\prime }$ radiative decays within the global BHLS$_2$ framework. However, it is certainly cautious to avoid using simultaneously the $\eta /{\eta ^\prime }$ dipion spectra and the $\pi ^+ \pi ^- \pi ^0$ annihilation data within global fits as long as a specific study has not assessed some clear statement about process-specific corrections (accounted for by a polynomial) in the latter channel¹⁶ and data.

For the general model dependence of BHLS/BHLS$_2$ models and also the magnitude of possible biases in the fits, we rely on our previous studies (notably [20] and also [89]) that demonstrated those are limited with respect to other sources of systematics.

More recently, our 2022 publication [21] (see, for example, Section 11.3 therein), which extends BHLS$_2$ and introduced a comprehensive treatment of the $[\pi ^0,\eta ,\eta ']$ system, includes also a detailed discussion on model dependencies in the new framework (partly by studying model variants)¹⁷. This 2022 study, which in fact prefigured and allowed the present work, reached again the conclusion that model dependence exists but is not a strong source of systematics. It confirmed previous studies which explored systematic differences between BHLS and BHLS$_2$ types of models (and various subvariants); see, for example, Section 17 in [20].

We explore below eventual new sources of (model and others) systematics, again by studying the fit result dependencies when using model and hypotheses variations (in particular, but not only, for the $P_X$ polynomials), in the same spirit as in our previous works.

It is worthwhile to stress that all the published dipion spectra of the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays carry an arbitrary normalization; so they only provide the spectrum line shapes measured by the various experiments. It follows from this peculiarity that they allow fitting only the $P_X(s)$ polynomials, and they are totally insensitive to the $H_X$ parameter values; this issue will be addressed by performing global fits where the corresponding partial widths [taken from the “Review of Particle Properties” (RPP) [70]] are also considered inside the fitting procedure.

10.1 Available dipion spectra from the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays

Measurements of the dipion spectrum in the ${\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decay started long ago, as early as 1975 [49], and several experiments have collected samples of various (but low) statistics motivated by the $\simeq 20$-MeV shift reported for the $\rho ^0$ peak location compared to its value in $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilations: JADE [50], CELLO [51], TASSO [52], PLUTO [53], TPC-2$\gamma$ [54], ARGUS [55], and Lepton F [56]; the Crystal Barrel Collaboration published in 1997 is the most precise spectrum [57], carrying 7400 events. The breakthrough has come from the BESIII Collaboration [61] which published a 970 ,000-event spectrum in 2017.

The formerly collected samples have been examined, and their behavior is briefly reported below. Dealing with the uncertainty information provided with these ${\eta ^\prime }$ samples is generally straightforward, except for the BESIII dipion spectrum [61], for which a spectrum for the energy resolution is provided. It is accounted for by replacing within the minimization procedure the genuine model function value by that of its convolution with the resolution function, assuming the provided resolutions are the standard deviations of Gaussians; the net effect of the BESIII energy resolution information deserves to be shown (see below).

The BESIII data [65] are provided as two 112-data-point spectra, the former giving the numbers of ${\eta ^\prime }$ event candidates in 10 MeV bins ($N_{evt}^i$), the latter the estimated numbers of background events ($N_{bkg}^i$) within the same bins. One has provided our global fitting code with the $N_{signal}^i= N_{evt}^i-N_{bkg}^i$ spectrum; we have assumed the original distributions to be Poissonian and fully correlated by attributing to $N_{signal}^i$ an uncertainty $\sigma _i=\sqrt{N_{evt}^i}+ \sqrt{N_{bkg}^i}$; it is shown below that these specific assumptions allow a fair dealing with the BESIII spectrum [61].

On the other hand, the reported dipion spectrum observed in the parent $\eta \rightarrow \pi ^+ \pi ^- \gamma$ decay has undergone much less measurement. Besides former spectra¹⁸ from Layter et al. [62] and Gormley et al. [63], WASA-at-COSY reported for a 14 ,000-event spectrum [64], whereas the KLOE/KLOE2 Collaboration has collected a 205 ,000-event spectrum [65]; it should be noted that the WASA dipion spectrum is given with only statistical errors.

It is worth stressing again that the normalization of all these spectra being arbitrary, the theoretical (absolute) distribution scales provided by the BHLS$_2$ Lagrangian are lost when normalizing to the specific scale of each data set when fitting; stated otherwise, these data samples only allow addressing the fit of the $P_X(s)$ functions ($X=\eta ,{\eta ^\prime }$) and not of the $H_X$ constants which are canceled out when normalizing the model functions to the experimental spectra.

10.2 $\eta /{\eta ^\prime }$ experimental spectra: fits in isolation

The first exercise is thus to explore the degree issue for the $P_X(s)$ polynomials and so does not need to deal with complications due to keeping the constant $H_X$ within the fit procedure. Therefore, fits have been performed, supplementing the reference data set of samples ${{\mathcal {H}}}_R$ by either of the experimental ${\eta ^\prime }$ or $\eta$ spectra. In this section, one only reports on using the $A_-$ BHLS$_2$ variant,¹⁹ [21] which will be our working BHLS$_2$ version.

Regarding the $P_{\eta ^\prime }(s)$ polynomial, the results given in the Table just below²⁰ focus on only the BESIII ${\eta ^\prime }$ sample (112 data points) [61]; indeed, because of their statistics, all the other ${\eta ^\prime }$ dipion spectra, including the Crystal Barrel one [57], do not exhibit any clear sensitivity to the $P_{\eta ^\prime }$ degree and may easily accommodate $P_{\eta ^\prime }\equiv 1$:

$$\begin{aligned} \begin{array}{ ||c||c|c|c| } \hline \quad P_{\eta ^\prime }(s) \,\,{\hbox {degree}}\,\, &{} 1 &{} 2 &{} 3\\ \hline \quad \chi ^2_{BESIII}~(N=112) &{} 160 &{} 99 &{} 98 \\ \quad \chi ^2_{TOT}~(N=1187) &{} 1167 &{} 1097 &{} 1096 \\ \quad \,\,{\hbox {Probability}} \,\, &{} 44.7\% &{} 90.6\% &{} 90.8 \% \\ \hline \end{array} \end{aligned}$$

This clearly points out that, thanks to the statistics reached by the BESIII Collaboration, the first degree for $P_{\eta ^\prime }(s)$ can be excluded ($\langle \chi ^2\rangle = 1.43$), and the third degree is obviously useless.

Regarding the $\eta$ data, complementing ${{\mathcal {H}}}_R$ with the KLOE/KLOE2 sample (59 data points) [65] alone or together with the WASA sample (37 data points) [64], the picture returned by the fits is much less conclusive, as a first-degree $P_\eta (s)$ provides²¹$\chi ^2(KLOE/KLOE2)=55$ and $\chi ^2$(WASA)$=45$, and a second-degree $P_\eta (s)$ yields $\chi ^2(KLOE)=51$ and $\chi ^2$(WASA)$=51$ with similar fit probabilities, both at the 90% level, as just above. The choice of a minimal degree has been preferred for $P_\eta (s)$.

Therefore, in the following, when different, the polynomials $P_\eta (s)$ and $P_{\eta ^\prime }(s)$ are definitely chosen, the former first degree, the latter second degree. The polynomial coefficients returned by the global fits performed with the $A_-$ BHLS$_2$ variant are discussed below and given in Table 2.

It is worthwhile noting that the degradation of the fit quality observed when assuming a first-degree $P_{\eta ^\prime }(s)$ is essentially carried by the the BESIII ${\eta ^\prime }(s)$ data sample itself, with a quite marginal influence on the standard channels of the BHLS$_2$ framework and on the $\eta$ dipion spectra. This emphasizes the robustness of the BHLS$_2$ Lagrangian.

In order to lighten the forthcoming discussion, let us comment on the formerly collected $(\eta /{\eta ^\prime })$ dipion spectra listed in the subsection above, which have also been analyzed within the BHLS$_2$ context; they quite generally yield stable $\chi ^2/N$ values. Some of them return large $\chi ^2/N$ values from the global fit procedure, namely, those from TPC-2$\gamma$ (69/13), LEPTON-F (45/20), and Layter et al. (60/15). Most of these former samples, however, achieve reasonable $\chi ^2/N$ values, typically 8/12 (TASSO), 15/21 (CELLO), 23/18 (PLUTO), 20/15 (ARGUS), 11/17 (CRYSTAL BARREL²²), and 13/14 (Gormley et al.) but have a quite negligible impact on the issues examined in the present study. Therefore, one focuses on the high-statistics data samples from BESIII and KLOE/ KLOE2; the case for the WASA data set may be nevertheless commented on$^{21}$.

10.3 The $\eta /{\eta ^\prime }$ experimental spectra: analysis within the BHLS$_2$ context

Table 1 collects the relevant fit quality information derived when running global fits within the $A_-$ BHLS$_2$ variant. The first data column gives the fit information in a global fit performed²³ by discarding the $\eta /{\eta ^\prime }$ to provide the BHLS$_2$ reference fit pattern; using the full ${{\mathcal {H}}}_R$, one would have found the numbers given in the last data column of Table 9 in [21]. The second and third data columns report on the fits performed by including $\eta /{\eta ^\prime }$ dipion spectra within the fit data set ${{\mathcal {H}}}_R$ under the conditions indicated in the top line of Table 1.

The fit information concerning the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation data collected in scan mode (with different detectors at the various Novosibirsk facilities) is displayed in the first data line (the exact sample content behind the wording NSK is explained in [21], for instance). The line KLOE stands for the merging of the KLOE10 [24] and KLOE12 [25] data samples. The spacelike vector pion form factor data merges the NA7 and Fermilab samples [91, 92].

Taking the first data column of Table 1 as a reference, one can clearly conclude that the fit quality obtained when using the $\eta /{\eta ^\prime }$ dipion spectra is unchanged and fairly good. Indeed, the $\chi ^2$ increase of the NSK set of scan data samples is obviously negligible, and those of the ISR data collected under the name KLOE and spacelike data are unchanged. The description of the data samples in the other channels from BHLS$_2$ (not shown) is also unchanged.²⁴

Regarding the triangle anomaly sector, the $\chi ^2$ information for the $\pi ^0/\eta /{\eta ^\prime }\rightarrow \gamma \gamma$ decays are

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \textrm{BHLS}_2~~A_- ~~\mathrm{variant~with~} P_\eta (s) \ne P_{\eta ^\prime }(s):&{} (\chi ^2_{\pi ^0},\chi ^2_{\eta },\chi ^2_{{\eta ^\prime }}) \\ \quad =( 1.08,0.01,3,33) \\ \displaystyle \textrm{BHLS}_2~~A_- ~~\mathrm{variant~with~} P_\eta (s) \equiv P_{\eta ^\prime }(s):&{} (\chi ^2_{\pi ^0},\chi ^2_{\eta },\chi ^2_{{\eta ^\prime }})\\ \quad =( 0.73,0.03,4.77). \end{array} \right. \nonumber \\ \end{aligned}$$

(37)

Thus, the RPP width [70] for $\pi ^0 \rightarrow \gamma \gamma$ is reproduced at the $(0.9\div 1)~\sigma$ level, and the one for $\eta \rightarrow \gamma \gamma$ is reconstructed at nearly its RPP value; the width for ${\eta ^\prime }\rightarrow \gamma \gamma$ is found in the range $(1.8\div 2.2)~\sigma$, somewhat larger but still acceptable.

Table 1 Fit properties of selected dipion data sample sets using the $A_-$ BHLS$_2$ variant. The fit reported in the first data column is free of $\eta /{\eta ^\prime }$ dipion influence. The second data column corresponds to fitting with independent $P_\eta (s)$ and $P_{\eta ^\prime }(s)$, whereas the third data column reports on the fit where $P_\eta (s) \equiv P_{\eta ^\prime }(s)$ has been imposed. The $\chi ^2/N_\textrm{pts}$ value for the WASA sample, fitted or not, is in the range$^{21}$ $(44--47)$ for 37 data points

On the other hand, and more importantly, comparing the second and third data columns of Table 1 obviously substantiates the SHKMW conjecture [73] about the uniqueness of the $P_X(s)$ function, e.g., $P_\eta (s) \equiv P_{\eta ^\prime }(s)$. One may also note the slight improvement generated by having stated $P_\eta (s) \equiv P_{\eta ^\prime }(s)$; this should be due to having provided its curvature to $P_\eta (s)$ which in turn lessens the (already marginal) tension between the KLOE/KLOE2 and BESIII data samples.

Fig. 3

The dipion invariant mass spectrum in the $\eta \rightarrow \pi ^+ \pi ^-\gamma$ decay. The blue data points are the KLOE/KLOE2 spectrum, and the green ones display the WASA spectrum. The red curve is the BHLS$_2$ fit leaving free the $P_\eta (s)$ polynomial. Vertical units are arbitrary

Before going on with solely using the $A_-$ variant of the BHLS$_2$ Lagrangian, it is worthwhile reporting on its $A_+$ variant behavior. Let us limit this to reporting on the $A_+$ variant best fit performed assuming $P_\eta (s) \equiv P_{\eta ^\prime }(s)$ is of the second degree; one obtains $\chi ^2/N({BESIII})=110/112$, and the $\eta$ dipion spectrum from the KLOE/KLOE2 Collaboration yields this ratio at 54/59; for its part, the unfitted WASA sample yields 49/37. The global fit probability is 51.5% only, to be compared to 90.6 % for the global fit performed under the $A_-$ variant reported in Table 1.

This drop in probability is noticeable, and the cause deserves to be identified; indeed, the $\chi ^2({BESIII})$ increases by “only” eight units, whereas the $\chi ^2$ for the $\eta$ dipion spectra are almost unchanged compared to Table 1. Moreover, the usual BHLS$_2$ channels also benefit from $\chi ^2$’s comparable in magnitude to their $A_-$ analogs. Surprisingly, the single place where the disagreement blows up is in the $\gamma \gamma$ decays, as

$$\begin{aligned} (\chi ^2_{\pi ^0},\chi ^2_{\eta },\chi ^2_{{\eta ^\prime }}) =(29.92,0.34, 0.08); \end{aligned}$$

e.g., the $\pi ^0 \rightarrow \gamma \gamma$ partial width is at more than $5 \sigma$ from its accepted value [70], which is by far too large to be acceptable. Indeed, this implies that the $A_+$ fit central value for the $\pi ^0 \rightarrow \gamma \gamma$ partial width is reconstructed at 70% of its present RPP value [70]; this should be brought into balance with the $A_-$ variant, which yields this partial width reconstructed 5% larger than the expected value (7.8 eV).

Therefore, the $A_+$ variant unexpectedly exhibits a strong tension between the triangle and box anomaly sectors of the BHLS$_2$ Lagrangian, whereas the $A_-$ variant behaves smoothly in both sectors. Therefore, from now on, we will focus on the $A_-$ variant of BHLS$_2$ which becomes our reference model; results derived using the $A_+$ variant are no longer reported except when explicitly stated.

Regarding the $\eta$ spectra, Fig. 3 shows an almost perfect account of the KLOE/KLOE2 spectrum: the BHLS$_2$ spectrum matches the dipion spectrum from KLOE/KLOE2 [65] on the whole energy range, except for a marginal issue in the 0.45-GeV energy region. Even if its $\chi ^2$ value is acceptable, the WASA spectrum [64] may look somewhat distorted with respect to its KLOE/KLOE2 partner, clearly favored by BHLS$_2$ expectations$^{21}$.

Fig. 4

The dipion invariant mass spectrum in the ${\eta ^\prime }\rightarrow \pi ^+ \pi ^-\gamma$ decay. The blue data points are the BESIII spectrum, and the green ones are those from Crystal Barrel. The red curve is the fit function, i.e., the convolution of the BHLS$_2$ model function with the energy resolution function assumed Gaussian; the blue curve is the underlying BHLS$_2$ model function itself. Both curves superimpose over the whole energy range except for the $\rho -\omega$ drop-off region. Vertical units are arbitrary

Fig. 5

The $\overline{P}_{\eta ^\prime }(s)$ and, in the inset, the $\overline{P}_\eta (s)$ spectra (Eq. 38). The full red curve and full black curve superimposed to, respectively, $\overline{P}_{\eta ^\prime }(s)$ and $\overline{P}_\eta (s)$ are, respectively, the $P_{\eta ^\prime }(s)$ and $P_\eta (s)$ polynomials returned by the fits. The dashed red curve in the inset is also $P_{\eta ^\prime }(s)$ but superimposed to the $\overline{P}_\eta (s)$ spectrum. Some pieces of fit information are also displayed

Regarding the ${\eta ^\prime }$ spectrum, Fig. 4 shows a noticeably fair accord between the BHLS$_2$ modeling and the BESIII spectrum [61] all along the energy range. The vertical green dotted lines locate the $\omega$ mass and thus the $\rho -\omega$ drop-off region, otherwise magnified in the inset. Here, one can observe the effect of convoluting the BHLS$_2$ model function with energy resolution Gaussians as provided by the BESIII Collaboration: It does perfectly what it is supposed to do, i.e., soften the drop-off to its right line shape with, moreover, a noticeable accuracy. On the rest of the spectrum, the convoluted curve and the underlying model curve superimpose on each other within the thickness of the curves. One should also state that no tension in the $\rho -\omega$ drop-off region is observed in the fits with any of the other dipion spectra submitted to the fit.

It is useful to consider the spectra²⁵

$$\begin{aligned} \displaystyle \overline{P}_X(s)= \left[ \frac{d\Gamma _{exp}(s)}{d \sqrt{s}}/ \frac{d\Gamma _{theor}(s)}{d \sqrt{s}} \right] _X ~ P_X(s), ~~ X=\eta ,{\eta ^\prime }\nonumber \\ \end{aligned}$$

(38)

to illustrate the behavior of the $P_X(s)$ polynomials under the two assumptions discussed above. As the bracketed term in Eq. (38) fluctuates around 1 and reflects the experimental uncertainty spectrum, the $\overline{P}_X(s)$ spectrum looks to be an appropriate experimentally based evaluation of its corresponding model function $P_X(s)$.

Fig. 6

The $\overline{P}_{\eta ^\prime }(s)$ and, in the inset, the $\overline{P}_\eta (s)$ spectra (Eq. 38). The full red curve is superimposed on the $\overline{P}_{\eta ^\prime }(s)$ and, in the inset, the $\overline{P}_\eta (s)$ spectra is their common fit function $P_X(s)$. The $\omega$ pole location is indicated. Some pieces of fit information are also displayed

Figure 5 displays the $\overline{P}_{\eta ^\prime }(s)$ and $\overline{P}_\eta (s)$ spectra defined just above for the BESIII, KLOE/KLOE2, and WASA spectra together with their model partners $P_{\eta ^\prime }(s)$ (second degree) and $P_\eta (s)$ (first degree). As could be inferred from the fit properties shown in Table 1, $P_{\eta ^\prime }(s)$ (the red dashed curve in the inset) is also a good evaluation for $\overline{P}_\eta (s)$.

Figure 6 also displays the $\overline{P}_{\eta ^\prime }(s)$ and $\overline{P}_\eta (s)$ spectra for the BESIII, KLOE/KLOE2, and WASA data samples but together with their common model fit function denoted $P_X(s)$, a second-degree polynomial. As reflected by the fit information mentioned in the body of the figure, a fair simultaneous parameterization of the $\eta$ and ${\eta ^\prime }$ dipion spectra is reached by only supplying the BHLS$_2$ model amplitudes with a single second-degree polynomial $P_X(s)$ fulfilling $P_X(0)=1$.

10.4 $P_X(s)$: BHLS$_2$ fit results versus others

The top bunch in Table 2 displays the values returned for the polynomial coefficients of

$$\begin{aligned} \displaystyle P_\eta (s) = 1 + \alpha _1 s~~~\textrm{and}~~ P_{\eta ^\prime }(s) = 1 + \alpha _1^\prime s + \alpha _2^\prime s^2. \end{aligned}$$

(39)

When using the same polynomial for the $\eta$ and ${\eta ^\prime }$ spectra, it is second degree and denoted $P_X(s)$. It should be noted that the coefficients for $P_{\eta ^\prime }(s)$ (second data column) and $P_X(s)$ (third data column) carry numerical values close to each other, i.e., at $\simeq 1~\sigma$ from each other for both the first- and second-degree coefficients.²⁶ In the case of having a (single) common function $P_X(s)$, the covariance is $\langle \delta \alpha _1^\prime ~\delta \alpha _2^\prime \rangle =-0.746$.

Regarding the systematics: In the BHLS$_2$ approach, the statistical and systematic uncertainties provided by the experiments together with their spectra are carefully embodied within the fitting code without any modification; so our reported uncertainties automatically merge both kinds of experimental errors.

On the other hand, the last two data lines in Table 2 clearly illustrate that $\delta a= a-2$ and $\delta c_3= c_3-2/3$ remain consistent with expectations, i.e., they can be regarded as $\textbf{O}(\delta )$ breaking parameters. The other fit parameter values are given in Table 3 displayed in the next Sect. 10.5; they are scrutinized in order to detect eventual hints of effects spoiling the BHLS$_2$ model fit in the $3 \pi$ channel—where correction polynomials are not implemented by now.

• (j) Regarding the $P_\eta (s)$ polynomial, it is worth comparing our numerical value for $\alpha _1$ with those available in the literature. The first published evaluation (GeV$^{-2}$) of $\alpha _1$ is the one from the WASA-at-COSY Collaboration ($\alpha _1 = 1.89 \pm 0.25_{stat} \pm 0.59_{syst} \pm 0.02_{th}$) [64], soon followed by $\alpha _1 = 1.96 \pm 0.27_{fit} \pm 0.02_{F_\pi }$ [73]; more precise evaluations have been proposed²⁷ since (GeV$^{-2}$):

  $$\begin{aligned}{} & {} \displaystyle \alpha _1 =1.32\pm 0.08_{stat} \pm 0.10_{syst} \pm 0.02_{th} [65],\nonumber \\ {}{} & {} \displaystyle \alpha _1 =1.52\pm 0.06_{stat} \quad [75]. \end{aligned}$$

  (40)

  Our own evaluation (reported in Table 2) is in good agreement ($\simeq 1 \sigma$) with the KLOE/KLOE2 Collaboration result [65].

• (jj) As far as we know, there are only two evaluations for the $P_{\eta ^\prime }(s)$ coefficients available in the literature, the former from the BESIII Collaboration [61]:

  $$\begin{aligned}{} & {} \displaystyle \mathrm{BESIII:}\nonumber \\{} & {} \left\{ \begin{array}{lll} \displaystyle \alpha _1^\prime (\mathrm{~~GeV}^{-2})\,{=} &{}\,0.992 {\pm } 0.039_{stat} \\ &{}\pm 0.067_{syst} {\pm } 0.163_{th}\\ \displaystyle \alpha _2^\prime (\mathrm{~~GeV}^{-4})\,{=}&{} {-}0.523 \pm 0.039_{stat}\\ &{} \pm 0.066_{syst} \pm 0.181_{th} \end{array} \right\} , \end{aligned}$$

  (41)

  the latter from the HHHK group [77, 78]. In their Addendum Table 1, the HHHK group proposes quite comparable values (we quote here the values obtained by the likelihood method):

  $$\begin{aligned}{} & {} \displaystyle \mathrm{HHHK:} \left\{ \displaystyle \alpha _1^\prime = ~~0.714 \pm 0.055~~\textrm{GeV}^{-2},\right. \nonumber \\ {}{} & {} \qquad \left. \displaystyle \alpha _2^\prime = -0.412 \pm 0.055 ~~\textrm{GeV}^{-4} \right\} . \end{aligned}$$

  (42)

  Here, one is faced with a surprising pattern: While the BESIII parameterization for $P_X(s)$ is far from the favored $A_-$ variant reported in Table 2, it is in quite remarkable accord with the $A_+$ solution displayed in the last data column of Table 2; as BESIII does not deal with the intrinsic relationship between the box and the triangle anomalies, their modeling is not influenced by the $\pi ^0 \rightarrow \gamma \gamma$ partial width issue identified in Sect. 10.3 just above.

Table 2 The parameter values from the $A_-$ BHLS$_2$ variant fit. The first data column reports on the fit using the usual set of data samples ${{\mathcal {H}}}_R$, excluding the $e^+ e^-$ annihilation to $3 \pi$ data. The second and third data columns report on the fits performed on the same amputated ${{\mathcal {H}}}_R$ sample set, completed with the $\eta /{\eta ^\prime }$ dipion spectra under the conditions indicated in the top line of the table ($P_X(s)=P_\eta (s) \equiv P_{\eta ^\prime }(s)$). The fair probability values can be emphasized. The last data column displays the fit results when using the $A_+$ variant

Table 3 Fit parameter values based on the $A_-$ BHLS$_2$ variant: The first data column presents the parameter values when including the $3 \pi$ spectra only, and the second column provides the same information when the $3 \pi$ spectra are discarded from the fit procedure. The third and fourth data columns display the fit results when the $\eta /{\eta ^\prime }$ spectra are included and the $3 \pi$ spectra excluded

Table 4 Main global fit results involving the KLOE+NSK and BaBar+NSK samples collected in $e^+ e^- \rightarrow \pi ^+ \pi ^-$ annihilations. On top are displayed the parameters involved in the correction polynomials (see text for details) followed by the contribution to $a_\mu (\pi \pi )$ of the $[2 m_\pi , 1.0$-GeV] energy range. The lowest bunch provides statistical information relative to the corresponding global fits

As a matter of conclusion, within the BHLS$_2$ framework, it has been shown that the conjecture $P_{\eta ^\prime }(s)=P_\eta (s)$ is a valid statement at the (high) degree of precision permitted by the spectra from the BESIII and KLOE/KLOE2 Collaborations. Moreover, Table 1 exhibits fair fit probabilities and does not reveal any noticeable tension among the dipion spectra from KLOE/KLOE2 and BESIII on the one hand and, on the other hand, the other channels embodied within the BHLS$_2$ fit procedure and their data, especially the dipion spectra collected in $e^+ e^-$ annihilations.²⁸

10.5 Brief analysis of the BHLS$_2$ parameter values

Table 3 collects the model parameter values of the BHLS$_2$ Lagrangian. In order to figure out the effect of the $e^+ e^- \rightarrow \pi ^+ \pi ^- \pi ^0$ annihilation data on the numerical results, its first data column²⁹ displays the fit parameter values derived when they are considered, whereas the second data column provides the same information when they are excluded from the fit procedure. The third and fourth data columns report the fit results when the $\eta /{\eta ^\prime }$ dipion spectra are included within the set of data samples ${{\mathcal {H}}}_R$ amputated from the 3-pion data.

Besides providing the parameter values themselves, the issue here is to reach an educated guess about unaccounted-for effects in the fit (like $P_X$ polynomial equivalent corrections) in the $e^+ e^- \rightarrow \pi ^+ \pi ^- \pi ^0$ annihilation process: some effects in this channel could be numerically invisible or be absorbed effectively by the other model parameters.

First of all, the last line in Table 4 clearly shows that one always reaches fair accounts of the spectra submitted to the BHLS$_2$ global fit. Regarding the parameters collected in the top rows of the table, one observes value differences beyond the reported fit uncertainty, however, with magnitudes consistent with reasonable systematic effects.

The parameters in the lower section of the table look less well behaved. Indeed, regarding $\epsilon$, $\epsilon ^\prime$, and $\xi _3$, the pieces of information derived by the three fits excluding the 3-pion data are consistent with each other but not with the first column result. The values for $\xi _0$ look confusing and may only indicate large systematics.

This is in fact reproducing an enduring situation since our previous 2022 publication [21]: there, we also noticed such variations in the isospin-breaking parameters, and also shifts from those same parameter estimations based on meson mass differences (see Sects. 17 and 21 in [21]).³⁰ This was not the case for the mixing parameters (Section 20 in [21]) which behaved more robustly and were close to other groups’ results.

While this situation is not pleasing, we have not investigated yet what could be the origin of these variations, because we feel that (a) their understanding probably needs long investigations; (b) they seem to have little influence on the central subject matter of the present work, which is focused primarily on our first shot at global fitting the $\eta /\eta '$ data in the HLS framework, and secondarily on the implications for the $a_\mu$ estimation, especially concerning the DR-LQCD discrepancy; and (c) the limited number of independent evaluations of these isospin-breaking parameters from other groups.

Good candidate explanations for this situation could be the effect of higher-order corrections, which may in part be accounted for by the fit and absorbed in these parameters; parametric ambiguities in the fit representation of the model³¹, particularly in the case of parameters which are more indirectly connected to fitted physics observables, or only in combination with other parameters.³²

In this context, the question of the 3-pion data (see the first column), which is not used in the present work, is still open, and is complicated by the fact that no correction polynomial (à la $P_X$) was used in [21].

Nevertheless, there is no obvious hint of significant fit probability spoiling effects in the $e^+ e^- \rightarrow \pi ^+ \pi ^- \pi ^0$ annihilation process, but it is clear that this process and the way it could be integrated into the fit certainly deserve more scrutiny in future work [88].

10.6 The $T^{R2}(\eta /{\eta ^\prime })$ terms in BHLS$_2$: the role of $\rho ^\pm$ exchanges

Thanks to the breaking mechanisms [20, 21] which lead to the BHLS$_2$ Lagrangian, the derived $\eta /{\eta ^\prime }$ decay amplitudes involve $\rho ^\pm$ exchanges as depicted in Fig. 1 by the diagram classes (c1) and (c2). Relying on previous works in the HLS context which have shown that $c_3=c_4$ is fairly well accepted by the data, this constraint is assumed; as a straightforward consequence [12, 16], all diagrams involving direct AVP couplings—all proportional to ($c_3-c_4$)—identically vanish, and therefore, the diagram class (c1) contributions also vanish. Nevertheless, the (c2) diagram class, also ${{\mathcal {O}}}(\delta )$ in breakings, survives and participates to the decay amplitudes $T_{\eta ^\prime }$ and $T_\eta$ at $\textbf{O}(\delta$). Such contributions are not involved in the BHLS$_2$ vector pion form factor $F_\pi (s)$ expression [20]; they come naturally in the derivation of the amplitude $T(\eta /{\eta ^\prime })$ and are not governed by an additional ad hoc parameter.

Even with $\textbf{O}(\delta )$ corrections, the $T^{R2}(\eta /{\eta ^\prime })$ amplitudes play a noticeable role within the BHLS$_2$ context:

• (i) They are necessary in order for the full amplitudes $T(\eta /{\eta ^\prime })=T^{NR}(\eta /{\eta ^\prime })+T^{R1}(\eta /{\eta ^\prime })+T^{R2}(\eta /{\eta ^\prime })$ to coincide with their analogs directly derived from the WZW Lagrangian [58, 59] at the chiral point³³$s=s_{0+}=s_{0-}=0$. Indeed, at the chiral point, the intensities $T^{\pm }(\eta /{\eta ^\prime })$ of the $T^{R2}(\eta /{\eta ^\prime })$ amplitudes defined in Sects. 5 and 6 are written as

  $$\begin{aligned} \displaystyle T^{R2}(\eta )= & {} -\frac{ie c_3}{4 \pi ^2 f_\pi ^3} \left[ \epsilon -\frac{A_\pm }{2}\sin {\delta _P} \right] ~~~ \mathrm{and~~~}\nonumber \\ \displaystyle T^{R2}({\eta ^\prime })= & {} -\frac{ie c_3}{4 \pi ^2 f_\pi ^3} \left[ \epsilon ^\prime +\frac{A_\pm }{2}\cos {\delta _P} \right] \end{aligned}$$

  (43)

  and manifestly depend on the FKTUY parameter [13] $c_3$. The condition for the amplitudes $T({\eta ^\prime })$ and $T(\eta )$ to coincide with those derived from the WZW Lagrangian (see Eq. 17) is that all dependencies upon the FKTUY parameters vanish at $s=s_{0+}=s_{0-}=0$; this condition cannot be fulfilled if dropping out (artificially) the $T^{R2}(\eta /{\eta ^\prime })$ terms from the full-amplitude expressions $T(\eta /{\eta ^\prime })$.

• (ii) To identify the effects of the $T^{R2}(\eta /{\eta ^\prime })$ terms, fits have been performed by discarding them in the full amplitudes and rather fit using $T(\eta /{\eta ^\prime })=T^{NR}(\eta /{\eta ^\prime })+T^{R1}(\eta /{\eta ^\prime })$. The fits have been performed by imposing the constraint $P_\eta (s)=P_{\eta ^\prime }(s)$ and return the results collected in the next table.

  $$\begin{aligned} \qquad \begin{array}{||c||c|c|c| } \hline \quad T^{R2}(\eta /{\eta ^\prime }) \,\,{\hbox {(off/on)}}\,\, &{} off &{} on \\ \hline \quad \chi ^2_{BESIII}~(N=112) &{} 122 &{} 102 \\ \qquad \qquad \quad \chi ^2_{KLOE/KLOE2}~(N=59) &{} 57 &{} 55 \\ \hline \quad \chi ^2_{TOTAL}~(N=1246) &{} 1187 &{} 1154 \\ \qquad \qquad \quad \,\,{\hbox {Probability} (\%)}\,\, &{} 73.0 &{} 90.6 \\ \hline \end{array} \end{aligned}$$

  The $\chi ^2$ values indicate that $T^{R2}(\eta )$ can be safely neglected, but also that discarding $T^{R2}({\eta ^\prime })$ is not safe. The $P_X(s)$ parameterization returned by the fit is

  $$\begin{aligned}{} & {} \left\{ \displaystyle \textrm{A}_-/\mathrm{no~TR2~}: \displaystyle \alpha _1^\prime = ~~0.437 \pm 0.039~~\textrm{GeV}^{-2},\right. \nonumber \\ {}{} & {} \left. \displaystyle \alpha _2^\prime = -0.573 \pm 0.007 ~~\textrm{GeV}^{-4} \right\} , \end{aligned}$$

  (44)

  closer to the HHHK results [77, 78] recalled in Expressions (42) than to those in Table 2. Therefore, the following is clear from the results collected in Table 2 and the other presented results: (1) The $\eta$ dipion spectrum is essentially insensitive to using or discarding the $T^{R2}$ term in its parameterization; whereas (2) the ${\eta ^\prime }$ dipion spectrum parameterization is significantly degraded if its $T^{R2}$ component is dropped out. This absence may explain the reported failure of the so-called “model-dependent” fit in [61].

In summary, one may conclude that once the polynomial correction and the ${{\mathcal {O}}}(\delta )$ $T^{R2}$ contribution predicted by the kinetic breaking of BHLS$_2$ [21] are considered, the average $\chi ^2$ per data point for the $\eta /{\eta ^\prime }$ dipion spectra can be considered optimum ($\langle \chi ^2\rangle \simeq 1$). Thus, at the level of precision permitted by the presently available $\eta$ [65] and ${\eta ^\prime }$ [61] dipion spectra, additional contributions beyond those of the basic vector meson nonet—like the higher-mass vector mesons [61] or the $a_2(1320)$ exchanges [75]—need not be invoked.

10.7 Dealing with the absolute scale of the $\eta /{\eta ^\prime }$ dipion spectra

Having determined the $\eta /{\eta ^\prime }$ dipion spectrum line shapes by fitting their common factor $P_X(s)$ ($X=\eta /{\eta ^\prime }$), it remains to derive the value of the $H_X$’s ($X=\eta /{\eta ^\prime }$) to also have their absolute magnitudes. As already noted, the value of the $H_X$ constants can be derived by introducing the accepted values [70] for the $\Gamma (\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma )$ partial widths into the fitting procedure. This can be (and has been) done, and global fits have been performed in order to get the optimum values for the $\{H_\eta , ~H_{\eta ^\prime },~P_X(s)\}$ triplets.

However, regarding the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays, each of the published dipion spectra is solely given by its line shape; concerning their normalization, they are tightly related to their partial widths. It happens that the single available “measurement” for each of these decays is the corresponding RPP piece of information [70]. In this case, as just argued, the values for $H_X$ ($X=\eta /{\eta ^\prime }$) can be derived through the fitting code appropriately modified to take the partial widths into account, but also algebraically once the fit to determine the $P_X(s)$ ($X=\eta /{\eta ^\prime }$) function has been performed. In this case, one has, using obvious notations,

$$\begin{aligned}{} & {} \left[ \Gamma (\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma ) \right] _{RPP}\nonumber \\ {}{} & {} \quad \equiv \int \left[ \frac{d\Gamma _X(s)}{d\sqrt{s}} \right] _{exp.} d\sqrt{s}\nonumber \\ {}{} & {} \quad = H_X^2 \int \left[ \frac{d\Gamma _X(s)}{d\sqrt{s}} \right] _{BHLS2} [P_X(s)]^2 d\sqrt{s}, \end{aligned}$$

(45)

the integrals being performed over the whole energy range of the $X=\eta /{\eta ^\prime }$ decays, and the fit values for the $\Gamma (\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma )$ partial widths coincide with the RPP pieces of information.

Two cases have been considered regarding the specific $e^+ e^- \rightarrow \pi ^+ \pi ^-$ annihilation sample combinations involved; the first one is $\{{{\mathcal {H}}}_R + \eta /{\eta ^\prime }\}$, which corresponds to global fitting with the {KLOE, NSK, BESIII, CLEO-c} combination. Correspondingly, the second case involves the {BaBar, NSK, BESIII, CLEO-c} sample combination. The relevant fit results regarding the correction polynomials are summarized in Table 4.

The average $\chi ^2$ per point of the $\eta$ and ${\eta ^\prime }$ dipion spectra are clearly insensitive to using either of the KLOE or BaBar $e^+ e^- \rightarrow \pi ^+ \pi ^-$ annihilation data within the global fit procedure. The global fit probabilities are instead quite different and correspond to our previous BHLS$_2$ results [20, 21]. This insensitivity to the KLOE versus BaBaR issue is well reflected by the fit results collected in the top part of Table 4: None of the $P_X$ and $H_X$ parameter central values are observed to differ by more than $1 \sigma$ in the various fit configurations.

Similarly, as the different $P_X(s)$ parameter values derived from fitting with the various sample combinations look like statistical fluctuations, differences observed between fitting only $P_X(s)$ or the $(P_X(s) and H_{\eta /{\eta ^\prime }})$ triplet look like statistical fluctuations. Moreover, defining $\delta _X=H_X-1$ and focusing, for instance, on the KLOE+NSK combination, one gets

$$\begin{aligned} \delta _\eta = -0.211 \pm 0.017, \delta _{\eta ^\prime }= -0.329 \pm 0.017, \end{aligned}$$

(46)

which corresponds to, respectively, $\delta$ and $\delta ^\prime$ as defined by Stollenwerk et al. [73], for which these authors derived the values $\delta =-0.22 \pm 0.04$ and $\delta ^\prime =-0.40 \pm 0.09$; these are clearly identical to our $\delta _\eta$ and $\delta _{\eta ^\prime }$, respectively. As a last remark, it should be noted that once $P_X(s)$ is determined, which implies that both $\frac{d\Gamma _X(s)}{d\sqrt{s}}$ and both BHLS$_2$ functions are known, Eq. (45) implies that both $H_X$ are not free but are algebraically related.

11 $\eta /{\eta ^\prime }$ decays: the muon anomalous magnetic moment

The renewed interest³⁴ in the $\eta /{\eta ^\prime }$ physics is intimately related to dealing with the light-by-light contribution to the anomalous magnetic moment (AMM) of the muon. As shown above and previously in [21], the BHLS$_2$ approach can address accurately several topics related to the $\eta /{\eta ^\prime }$ physics, and its results are supported by fair probabilities; these probabilities faithfully reflect the actual behavior of each of the data samples within the global framework, as the error information provided with it is embodied without any ad hoc enlargement inside the fitting code.

11.1 Accuracy of the $P_X(s)$ parameterization

It has been shown above that a single polynomial $P_X(s)$ allows us to address simultaneously both the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays within the BHLS$_2$ framework and that the second degree is quite satisfactory. The $P_X(s)$ parameterizations derived using the $A_\pm$ variants of BHLS$_2$ displayed in Table 2 are based on the choice of the largest set of data samples collected in almost all physics channels covering the HLS energy region (e.g., up to the $\simeq \phi$ mass region) and are consistent with each other. It was also shown that the $A_-$ parameterization is the best favored, but nevertheless, one found it relevant to also provide the $A_+$ parameterization despite its (sole real) identified failure with the $\pi ^0$ lifetime (or partial width) that $A_+$ reconstructs at more than $5\sigma$ from its commonly accepted value [70].

In this section, one aims to emphasize the reliability of the $A_-$ parameterization by examining carefully how the $P_X(s)$ parameter values evolve while using the various dipion spectra collected in $e^+e^-$ annihilations which are known to exhibit—sometimes severe—inconsistencies among themselves.

A possible fit bias in the parameterizations reported in Table 2 is the choice of the dipion data samples because of their mutual consistency; this issue is examined first. For this purpose, it is useful to define and name some sets of data samples in order to ease the reading.

Basically, the data samples$^{23}$ common to the sets of data samples presently embodied within the BHLS$_2$-based fit procedure are the {$(\pi ^0/\eta )\gamma$, $K_L K_S$, $K^+K^-$} $e^+e^-$ annihilation channels, the dipion spectra from the $\tau$ decay provided by the ALEPH, CLEO, and BELLE Collaborations, and the pion and kaon spacelike spectra from NA7 [91] and Fermilab [92]; let us, for clarity, name this basic set ${{\mathcal {X}}}_\tau$.

Table 5 The $P_X(s)$ parameter values from the $A_-$ BHLS$_2$ variant fit. The first column indicates which data set combination is submitted to the global fit. $\langle \chi ^2_{\pi \pi }\rangle$ indicates the average $\chi ^2$ of the timelike $F_\pi (s)$ data points of the sample named in the first column. $\alpha ^\prime _1$ and $\alpha ^\prime _2$ are the coefficients of the first- and second-degree terms of $P_X(s)$, respectively. The last data column displays the probability of the corresponding global fit

Regarding the available $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation spectra, one has distinguished four groups³⁵ (two of which being, actually, a one sample “group”): (1) the scan data collected under the name NSK (see [19] for its content), (2) the KLOE ($\equiv$ KLOE10+KLOE12) [24, 25] ISR data sample group, (3) the KLOE08 ISR sample [40], and (4) the BaBar one [27, 28]. For definiteness, the largest set of data samples found consistent with each other and referred to here and before [20, 21] as ${{\mathcal {H}}}_R$ gathers the sets ${{\mathcal {X}}}_\tau$, NSK, and KLOE just listed. Finally, the set of dipion spectra from the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays [61, 65] is referred to as $\eta /{\eta ^\prime }$.

Fig. 7

The curve displayed in the left panel a is the pion form factor predicted by fitting the data sample set $\{{{\mathcal {X}}}_\tau +\eta /{\eta ^\prime }\}$ and, superimposed, the unfitted pion form factor spectra (including those from BaBar). The right panel b shows the pion form factor derived from fitting the full $\{{{\mathcal {H}}}_R+\eta /{\eta ^\prime }\}$ data sample set which includes the KLOE and NSK pion form factors (but not the BaBar spectrum). See the text for comments

The four top lines in Table 5 display the coefficient values of the first- ($\alpha ^\prime _1$) and second-degree ($\alpha ^\prime _2$) terms of the polynomial $P_X(s)$; as indicated in its first column, the corresponding fits differ from each other only by the exact content of the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation spectra sample set submitted to the minimization procedure. Whatever the fit quality, reflected by its corresponding $\langle \chi ^2_{\pi \pi }\rangle$ value and its probability, the different values derived for $\alpha ^\prime _1$ as for $\alpha ^\prime _2$ are not distant by more than $(1\div 2) \sigma$ from each other. It should also be remarked that the parameter values derived in the fit for {${{\mathcal {H}}}_R$ + $\eta /{\eta ^\prime }$ }—which includes the KLOE and NSK data sets together—are intermediate between those involving the KLOE and NSK sample sets separately. Therefore, the large spread of probabilities between the fits involving NSK and/or KLOE, and those involving BaBar or KLOE08, does not produce a significant change in the determination of the common $\eta /{\eta ^\prime }$ function $P_X(s)$.

The last line in Table 5 displays the $P_X(s)$ coefficients returned by a fit excluding the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation spectra. The linear term coefficient $\alpha ^\prime _1$ is never found distant by more than $\simeq 2 \sigma$ from the other corresponding values displayed in the same Table. In contrast, the curvature coefficient $\alpha ^\prime _2$ exhibits a $\simeq (4 \div 5) \sigma$ departure regarding the other reported fit values. Relying on Figs. 5 and 6, one expects the second-degree term ($\alpha ^\prime _2$) to mostly affect the $\rho ^0-\omega$ energy region. This piece of information renders it interesting to compare the pion form factor predicted by the fit of the $\{ {{\mathcal {X}}}_\tau +\eta /{\eta ^\prime }\}$ set³⁶ with the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation data and the fit results derived when fitting the $\{ {{\mathcal {H}}}_R+\eta /{\eta ^\prime }\}$ set. This is the purpose of Fig. 7.

Comparing the curve in both panels of Fig. 7, the overall agreement between both fits is fairly good, except for the magnitude at the very $\rho ^0$ peak location which may look somewhat underestimated³⁷ by the ${\eta ^\prime }$ dipion spectrum. Instead, the drop-off location and its intensity are fairly well predicted by the $\{ {{\mathcal {X}}}_\tau +\eta /{\eta ^\prime }\}$ sample set. This behavior deserves to be confirmed by new precise ${\eta ^\prime }$ dipion spectra, complementing [61]. So, while within the BHLS$_2$ framework, the ${\eta ^\prime }$ decay is accounted for largely independently of the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation process, but this does not prevent its prediction for $F_\pi (s)$ to exhibit a relatively fair accord with the (fully independent) $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation spectra.

Still, this accord is not perfect, and one has to contrast the good compatibility of the $\eta /\eta '$ samples with the rest of the reference data set (as reflected in the high corresponding fit probability), and also the high probability of the $\{ {{\mathcal {X}}}_\tau +\eta /{\eta ^\prime }\}$ fit (without the annihilation data contribution), and the visible pion form factor deviation causing the $a_\mu$ shift. It is difficult to be categorical at the moment about the nature of this effect on the form factor, which could be due to a variety of causes,³⁸ also because, as discussed in Sect. 11.3 below, it is sometimes difficult to interpret restricted data set fits, which have a more exploratory and confirmatory nature than “full” fits, and in principle, one should trust more our full data set fits, which indeed have no difficulty using the usual data sets in association with the $\eta /\eta '$ data.

In any case, it seems that the $a_\mu$ value from valid fits where the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation data are, to some extent, replaced by the $\eta /\eta '$ data are much closer to the dispersive estimations than to the LQCD ones. This could indicate that part of the DR-LQCD discrepancy may not depend on experimental or analysis artifacts in the various experiments, since we witness a similar effect for the newly HLS fitted $\eta /\eta '$. If the present study is taken at face value, the DR-LQCD puzzle seems in fact bolstered, but on the other hand, tentative solutions based on potential purely experimental-level problems could appear less favored (to be clear, we also trust LQCD results).

Based on the current knowledge, other specific interpretations for the DR-LQCD conundrum are speculative (possible effects beyond the Standard Model? $\pi \pi$ loop differences in $e^+e^-$ annihilation channel? See also 11.3.2 below), and in this light, the same can be stated about the FNAL measurement discrepancy [2] (and even more speculative are eventual causal links between the three $a_\mu$ determinations).

Fig. 8

$a_\mu (\pi \pi , \sqrt{s} < 1.0$ GeV) in units of $10^{-10}$ for various data sample combinations. The top two data points display the values derived by a direct integration of all the dipion spectra (when including BaBar, KLOE is excluded) [94]. The point tagged by KNT19 [6] is a usual (external) reference; the following point is derived using BHLS$_2$ with the indicated (largest) content of $e^+e^- \rightarrow \pi ^+ \pi ^-$ spectra. The two following points show our fit results for two indicated combinations of data samples; within parentheses, one also displays the results obtained by also including the $\eta /{\eta ^\prime }$ samples within the global fit procedure. The small magnitude of the BHLS$_2$-derived uncertainties should be noted (see text). The bottom entry in this figure exhibits the prediction derived for $a_\mu (\pi \pi , \sqrt{s} < 1.0$ GeV) when all annihilation to dipion data are discarded from the fit. The growth of its uncertainty reflects the drastic reduction of the statistics involved in the corresponding fit

Regarding the function $P_X(s)$, awaiting for other theoretical estimates of it, one can conclude that our favored $P_X(s)$ parameterization³⁹ derived from fitting (${{\mathcal {H}}}_R$ + $\eta /{\eta ^\prime }$) provides already a reliable one and benefits from, respectively, a $\simeq 3 \%$ and $\simeq 10 \%$ precision for, respectively, the linear and the curvature terms.

11.2 The $\eta /{\eta ^\prime }$ spectra and HVP estimates

The purpose of Fig. 8 is to elucidate the overall picture of the estimates for $a_\mu (\pi \pi ,\sqrt{s}<1.0$ GeV) which emerges from the present work. The top bunch of data points display the values for $a_\mu (\pi \pi , \sqrt{s} \le 1 ~\textrm{GeV})$ in units of $10^{-10}$ derived by direct integration of the dipion data taking all dipion spectra, but either excluding the BaBar spectrum or excluding the KLOE spectra; the reason to proceed this way is related to inconsistencies occurring when fitting the pion form factors [21] as reported years prior [42].

The point showing the KNT19 result [6], the usual reference [3], is followed by the evaluation derived from the BHLS$_2$ global fit involving the ${{\mathcal {X}}}_\tau +KLOE+NSK+BABAR$ sample set which contains the same $e^+ e^- \rightarrow \pi ^+ \pi ^-$ dipion spectra⁴⁰ as KNT19. The central values derived for $a_\mu (\pi \pi , \sqrt{s} \le 1 ~\textrm{GeV})$ are substantially identical, reflecting the fact that the normalization uncertainty treatment used to derive the KNT19 evaluation is similar to our own [89]. The BHLS$_2$ uncertainty is however much improved (by a factor of $\simeq$2), as can be expected from having performed a (more constraining) global fit; indeed, within a global context, in contrast with KNT19 and others who treat the dipion spectra in a standalone mode, one benefits from also involving the $\tau$ dipion spectra and all non-$\pi \pi$ final-state spectra, which play as an increased statistics for all the channels involved by the underlying HLS context, in particular the $\pi \pi$ one. Therefore, comparing KNT19 and our evaluation illustrates that the BHLS$_2$ Lagrangian approach does not generate biases and that the difference in the central values is essentially due to the data samples chosen to derive motivated physical conclusions.

The top two data points of the lowest bunch substantiate numerically the amplitude of the tension between using ${{\mathcal {X}}}_\tau +KLOE+NSK$ and ${{\mathcal {X}}}_\tau +BABAR+NSK$; both agree with the direct integration results and exhibit a $\simeq 5.4 \times 10^{-10}$ distance between their evaluations of $a_\mu (\pi \pi , \sqrt{s} \le 1 ~\textrm{GeV})$. In both cases, the first number displayed is the evaluation derived by a standard BHLS$_2$ fit and is 100% consistent with the results published in [21].

The number within parentheses instead displays the result obtained when adding the $\eta /{\eta ^\prime }$ data set defined above according to, respectively, ${{\mathcal {X}}}_\tau +KLOE+NSK$ and ${{\mathcal {X}}}_\tau +BABAR+NSK$. One should note that the fit probabilities are unchanged when adding the $\eta /{\eta ^\prime }$ data set and reflect fairly good fits: $88.7\% \rightarrow 90.6\%$ for ${{\mathcal {X}}}_\tau +KLOE+NSK (+\eta /{\eta ^\prime })$ and $47.2\% \rightarrow 55.9\%$ for ${{\mathcal {X}}}_\tau +BABAR+NSK (+\eta /{\eta ^\prime })$. This illustrates that there is no tension between the $e^+ e^- \rightarrow \pi ^+ \pi ^-$ dipion spectra and those derived from the $(\eta /{\eta ^\prime })$ decays, as the probability difference between the fits involving the two data sample sets is not degraded by including the $(\eta /{\eta ^\prime })$ samples. The corresponding central values are very similar too, confirming that there are no bad surprises with the $\eta /{\eta ^\prime }$ data and the new Lagrangian terms describing them, at least in the ${{\mathcal {X}}}_\tau +KLOE+NSK$ and ${{\mathcal {X}}}_\tau +BABAR+NSK$ cases.

11.3 The case for the $\tau$ data

11.3.1 Fitting the $\tau$ data

Among the data set combinations that look interesting to explore and fit, and in addition to the ones mentioned above, the quasi “standalone” fitting of the $\tau$ decay-specific data, in the spirit of what was achieved in our previous works [18, 19], and [89]⁴¹ for the BHLS model, seems in order.

Since the inception of the BHLS$_2$ type of models [20], we are unable to reach a satisfactory convergence (and good global probability) for such a fit, using the same type of complementary simple ($\pi \pi$-independent) RPP data that was used for BHLS (with some tentative variations in these data choices, and also in the MINUIT fit handling). We made additional tries⁴² by adding in the fitted data set spacelike $\pi \pi$ data (the idea being to constrain the fit behavior around $s=0$, while mostly preserving independence from the annihilation $\pi \pi$ information, due also to the limited statistical weight of the spacelike data sets), but to no avail. So, whereas the working quasi “standalone” $\tau$ fit in the BHLS framework allowed us to nicely reconstruct the full pion vector form factor⁴³ (including in the near spacelike region), and vice versa for the dipion spectra in $\tau$ decays, using only the $\tau$ data for the former and only the annihilation $\pi \pi$ data for the latter, BHLS$_2$ does not seem to behave in the same way.

While this could seem disappointing, the importance of not being able to fit the $\tau$ data in “standalone” form should be put into perspective. Indeed, several considerations are relevant:

• (i) Compared to BHLS, in BHLS$_2$ more general methods are employed to break symmetries (covariant derivative, kinetic breaking, for example); while those allow for a more consistent and more powerful way to parameterize the breakings, it seems that BHLS$_2$ is differently constrained in the $\tau$ sector. This could have the unfortunate effect of spoiling the BHLS$_2$ standalone $\tau$ fit convergence (due to secondary false minima, for example).

• (ii) While the standalone $\tau$ fit does not work in BHLS$_2$, we stress that the global fit, involving the full range of usual data sets (plus the $\tau$ and the new $\eta /\eta '$ data), is well behaved and returns good probabilities, as reported above. This means BHLS$_2$, when correctly constrained, describes adequately the data, and that the involved data sets, including the $\tau$, are statistically compatible⁴⁴

• (iii) While it is advisable to perform partial data fits (like the $\tau$ one, and also the ${{\mathcal {X}}}_\tau + \eta /\eta '$ fit), there is no guarantee that fits will continue to converge while discarding data sets (without changing the model). It is difficult with relatively complicated and parametrically intricate models like BHLS$_2$ to predict the minimal set of data allowing sound convergence, and in practice, one resorts to the empirical method of trying to fit, hoping for good convergence and probability.⁴⁵ So while many workers use partial fits to explore sensitivities (of $a_\mu$, for example) relative to the data set composition, in some cases, the meaning of those fits should be pondered. The minimal acceptability requirement is of course that partial fits behave correctly and yield probabilities comparable to the full data set fits.

Apart from the well-known variations in the fitted data sets (like replacing KLOE by BaBar data, Fig. 8), in this work, we explored two interesting partial fits: the ${{\mathcal {X}}}_\tau + \eta /\eta '$ fit and the standalone $\tau$ fit. The former fit has good convergence and good probability, which is not the case for the latter (here, we confirmed our previous observations). This is why we kept the ${{\mathcal {X}}}_\tau + \eta /\eta '$ fit and discarded the incomplete $\tau$ fit, and give no $a_\mu$ estimation from this last fit.

Again, we emphasize that the role of these partial fits should not be overestimated: the real benchmarks for data compatibility and model adequacy are the full fits.

A worry could be that in full fits, data sets with lower statistical weight may be of little influence when fitted together with large and precise data sets (BaBar, KLOE, etc.). In these regards and in the $a_\mu$ determination case at least, we can think of two reasons to be reassured: (a) we consider only fits with high probability, meaning high global $\chi ^2$ probability which practically guarantees that the fitted pion form factor will be close to the data, and hence to the usual dispersive estimations; (b) we require also good local (partial) $\chi ^2$ probability in the various sectors/data sets in the function to be minimized, which de facto eliminates full fits which describe poorly a particular data set, and also allows sometimes to detect discrepancies between data sets.

Still, in view also of the recent renewed interest for the $\tau$ decay data, we have not completely abandoned the idea of demonstrating a $\tau$ quasi-standalone BHLS$_2$ fit, but the present lack of success in this endeavor certainly indicates an unknown level of difficulty.

11.3.2 $\tau$ data and $a_\mu$

To broaden the discussion on the $\tau$ decay data, we repeat the comment conveyed in Subsection 21.3 of [20], where we put forward the idea that the QCD-QED interference at work in the neutral current (NC) $\pi ^+\pi ^-$ channel may cause a shift of the data with respect to the LQCD result. While in the neutral channel (NC) process $e^+e^- \rightarrow \pi ^+\pi ^-$, experiments measure the photon propagator, at leading order in lattice QCD one is calculating the pure QCD hadronic current two-point correlator, free of external QED corrections. In the charged current (CC) $\tau ^\pm \rightarrow \pi ^\pm \pi ^0 \nu _\tau$ decay, in contrast, one measures the W propagator in the quasi-static limit, and the $\rho ^+$ meson does not mix with a photon exchange (also, no HVP subtraction correction needs to be applied), and the hadronic blob exhibited in the $\tau$ data is naturally much more directly related to the LQCD HVP than the one in the NC data. Actually, some recent $\tau$ data-driven analyses [95,96,97] find results such as $a_\mu ^{HVP-LO}[\tau ] = 704.1^{+4.1}_{4.0}\,\times 10^{-10}$, which also is close to the dispersive results [98] of $a_\mu ^{HVP-LO}[\tau ] = 705.3\pm 4.5 [689.8\pm 5.2]\,\times 10^{-10}$ (result excluding $\tau$ data in brackets).

When combining $e^+e^-$ and $\tau$ data in HVP calculations, usually, the $\tau$ data are corrected towards matching the $e^+e^-$ ones, where in the latter the QCD-QED mixing is inherent. A part of the QCD-QED mix-up is the $\rho ^0-\gamma$ [84] mixing. Besides having corrected the $\tau$ spectra by the commonly accepted isospin-breaking effects, other corrections like the $\rho ^0-\gamma$ mixing or the mass and width shift between $\rho ^0$ and $\rho ^\pm$ can be applied to the I=1 component of $\pi ^+\pi ^-$ data in order to reduce the QED contamination of the latter.⁴⁶ In 2008, Belle [34] already, after applying standard (commonly accepted) isospin-breaking corrections, obtained the $\tau$ data-driven result $a_\mu ^{\pi \pi }[2 m_\pi , 1.8~\textrm{GeV}]=(523.5\pm 1.5(\mathrm{exp.})\pm 2.6(\mathrm{Br.})\pm 2.5(\textrm{isospin}))\times 10^{-10}\, (\tau$ data from $\textrm{Belle})$, which was compared to the $e^+e^-$ data-driven NSK result $a_\mu ^{\pi \pi }[2 m_\pi , 1.8~\textrm{GeV}]=(504.6\pm 3.1(\mathrm{exp.})\pm 0.9.6(\textrm{rad}))\times 10^{-10}\, (e^+e^-:\,\mathrm{CMD2,\,SND})$. The difference is $18.9 \times 10^{-10}$, and if applied to dispersive result $a_\mu ^{HVP-LO}[e^+e^-] = (694.79 \pm 4.18)\,\times 10^{-10}$ [94], one gets $713.7 \times 10^{-10}$, and we note that with $a_\mu ^{HVP-LO} = 718.2 \times 10^{-10}$, we would have the coincidence of theory and experiment in the muon $g-2$: $a_\mu ^{exp.}=a_\mu ^{th.}$. Recently, the CMD-3 Collaboration [99], for the range 0.327 to 1.2 GeV, obtained $a_\mu ^{had;LO}(2\pi ,\,\textrm{CMD3}=(526.0\pm 4.2)\,\times 10^{-10}$, to be compared to $(506.0\pm 3.4)\,\times 10^{-10}$ reported in the white paper document. Again, the difference shifts the WP value $a_\mu ^{HVP-LO}[e^+e^-] = (693.1\pm 4.0)\times 10^{-10}$ to $(713.1\pm 4.7)\times 10^{-10}$. We note that the CMD-3 result, clearly at variance with all previous $e^+e^- \rightarrow \pi ^+\pi ^-$ results, has been obtained by applying a new RLA-based generalized vector dominance model (GVDM) correction [100], whereas other experiments apply scalar QED to perform QED corrections. Using older $\pi \pi$ data, our HLS global fits (standalone or not) showed no incompatibility between the $\tau$ data and the annihilation $\pi \pi$ data, which seems to shift the problem away from a pure $\tau$ data incompatibility with other main data sets but rather towards a questioning of the relation between $a_\mu$ and the pion form factor as we know it.

11.4 $\eta /{\eta ^\prime }$-based evaluations of the HVP

If, as conjectured long ago [73], an accurate enough determination of the function $P_X(s)$ can be provided (by extended ChPT [43,44,45], possibly), dipion spectra from the ${\eta ^\prime }$ decay may provide a new way to estimate the dipion contribution to the muon HVP up to $\simeq 1$ GeV. The present work has shown that phenomenology is able to provide already a function $P_X(s)$ carrying a noticeable precision, and moreover, it has also been shown that a unique function accommodates easily the available $\eta$ and ${\eta ^\prime }$ high-precision dipion spectra simultaneously.

Indeed, within the BHLS$_2$ context [20, 21], the amplitudes for the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays and for the $e^+e^- \rightarrow \pi ^+ \pi ^-$ annihilation proceed from the same Lagrangian and do not call for a special treatment of their common dominant neutral $\rho$ meson signal. Moreover, once the $P_X(s)$ effects are factored out, the derivation of both amplitudes from the same Lagrangian is unchanged.

On the other hand, discrepancies revealed by comparing with each other the dipion spectra collected in scan mode (NSK) and the various samples collected in ISR mode by KLOE [24, 25, 40] and BaBar [27, 28] has not resulted in a really satisfactory solution; the recent SND20 [41]—and even more, presumably, the new CMD3 [7] data—seems rather to darken the picture.

Therefore, getting high-statistics dipion spectra independent of the $e^+ e^-$ annihilation mechanism, carrying different kinds of systematics, may helpfully contribute to a more satisfactory understanding of the crucial $\pi ^+ \pi ^-$ contribution to the muon HVP.

For the time being, the limited number of high-statistics $\eta$ [65] and ${\eta ^\prime }$ [61] dipion spectra allow us to already derive the prediction for $a_\mu (\pi \pi , \sqrt{s} < 1.0$ GeV) displayed in the bottom of Fig. 8, namely,

$$\begin{aligned} a_\mu (\pi \pi , \sqrt{s} \le 1 ~\textrm{GeV}) = (484.98 \pm 1.93) \times 10^{-10} \end{aligned}$$

(47)

with a 96.3% fit probability, and is distant from its estimate based on fitting the ${{\mathcal {H}}}_R$ data sample set⁴⁷ by $2.6 \sigma$ (conservatively). Therefore, additional high-statistics $\eta /{\eta ^\prime }$ data samples can put more light on the issue, clearly located in the $\rho ^0-\omega$ invariant mass region.

12 Concluding remarks

The present work has shown that besides the already reported $e^-e^+$ annihilation spectra, some decay modes (especially the $P \rightarrow \gamma \gamma$ modes) or $\tau$ dipion spectra [20, 21], BHLS$_2$ can encompass the dipion spectra from the $\eta$ and ${\eta ^\prime }$ decays; however, to reach this result, one has to invoke a (common) correction polynomial—not a part of the HLS model—as inferred by the SHKMW group in [73].

In this context, BHLS$_2$ offers a fairly good simultaneous fit of the $\eta$ and ${\eta ^\prime }$ dipion spectra together with the $e^+ e^-$ annihilations into $\pi ^+ \pi ^-/K \overline{K}/\pi ^0 \gamma /\eta \gamma$ final states and the $\tau ^\pm \rightarrow \pi ^\pm \pi ^0 \nu _\tau$ decay also addressed by the BHLS$_2$ framework in our previous [20, 21].

This proves that once the $P_X(s)$ correction is accounted for, the BESIII ${\eta ^\prime }$ spectrum [61] does not need more information that that already present in BHLS$_2$ to get a satisfactory picture; the picture is found as fair for the $\eta$ spectrum reported in [65]—and, actually, even for those in [64]. The role of the charged $\rho$ meson—a natural feature of BHLS$_2$, [21], never considered elsewhere—has been shown to provide a fair treatment of the ${\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ dipion spectrum.

This turns out to state that most of the parameters needed to write out the relevant decay amplitudes are not free but are numerically shared with the other channels embodied within the same BHLS$_2$ framework. This is an additional step in the proof in which a unified effective Lagrangian can fairly describe the low-energy physics up to and including the $\phi$ mass region.

One has first shown that the $\eta$ and ${\eta ^\prime }$ dipion spectra are well fitted with specific low-degree polynomials supplementing the amplitudes derived from the BHLS$_2$ Lagrangian. In a second step, it has been proved that, actually, the same second-degree polynomial $P_X(s)$ is involved in the considered $\eta$ and ${\eta ^\prime }$ decays, as inferred in [73]. As already noted, the $\rho ^\pm$ exchange implied by the kinetic breaking defined in [21] is shown to enhance the global fit quality. The polynomial coefficients have been derived from our fits with fair precision and found that they remain stable when varying the fit conditions (see Table 5).

It should be noted that the picture revealed by comparing both panels of Fig. 7 suggests that the traditionally used dipion spectra carry a line shape compatible with the ${\eta ^\prime }$ dipion spectrum. Thus, higher statistics on this can be a helpful tool in the present controversy concerning the dispersive approaches and LQCD, due to the different systematics affecting the ${\eta ^\prime }$ dipion spectrum, certainly independent of those involved in the $e^-e^+ \rightarrow \pi ^+ \pi ^-$ annihilation. At its level of accuracy, the present ${\eta ^\prime }$ dipion spectrum [61] rather favors the DR prediction, as shown in Fig. 8; this could indicate that the DR-LQCD $a_\mu$ discrepancy is not entirely related to experimental biases, since it appears also in the independent $\eta /\eta '$ data, but could rather be a misunderstood effect in dispersive estimations for processes involving pion pairs.⁴⁸ However, better statistics and a finer binning in the $\rho ^0-\omega$ energy region look mandatory for a competing estimate of the muon $a_\mu (\pi ^+ \pi ^-, \sqrt{s} < 1.0~\textrm{GeV})$. This may motivate our colleagues to enlarge the available ${\eta ^\prime }$ dipion sample by analyzing the already existing data or by collecting new samples at other detectors.

Appendices

Appendices

Brief outline of the HLS/BHLS$_2$ approach

For the reader’s convenience, it appears worthwhile to avoid too much cross-references and briefly collect here the various ingredients which participate in the definition and working of our symmetry-broken hidden local symmetry (HLS) model which is spread out into several references. The HLS model admits a non-anomalous sector [12] and also an anomalous sector [13]—see also [16]. To make this approach a successful tool in its physical realm, the HLS model should undergo symmetry-breaking mechanisms. The salient features of the broken version named BHLS$_2$ which underlie the present study can be found, recalled, or defined, in⁴⁹ [20, 21]. As it grounds the present study, the anomalous sector of the HLS model [13, 16] is mostly discussed in the body of the text.

1.1 The unbroken non-anomalous HLS Lagrangian

The non-anomalous HLS Lagrangian is a generalization of the ChPT Lagrangian [101, 102] which can be written [16] as

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_\textrm{chiral}= & {} \frac{f_\pi ^2}{4} \textrm{Tr} \left[ \partial _\mu U~ \partial ^\mu U^\dagger \right] \nonumber \\= & {} -\frac{f_\pi ^2}{4} \textrm{Tr} \left[ \partial _\mu \xi _L ~ \xi _L^\dagger - \partial _\mu \xi _R ~ \xi _R^\dagger \right] ^2, \end{aligned}$$

(48)

where $f_\pi$ (= 92.42 MeV) is the pion decay constant, and

$$\begin{aligned} \displaystyle \xi _{R/L}(x)=\exp {\left[ \pm iP(x)/f_\pi \right] }~~\Longrightarrow U(x)=\xi _L^\dagger (x) \xi _R(x),\nonumber \\ \end{aligned}$$

(49)

when working in the so-called unitary gauge, which removes a scalar field term in the definition of $\xi _{R/L}(x)$; P(x) is the usual pseudoscalar (PS) field matrix. Ignoring in this reminder the weak sector [16, 20], the HLS approach turns out to replace in Eq. (48) the usual derivative by the covariant derivative:

$$\begin{aligned} \displaystyle D_\mu \xi _{R/L} =\partial _\mu \xi _{R/L} -ig V_\mu \xi _{R/L} +ie \xi _{R/L} A_\mu Q, \end{aligned}$$

(50)

where $A_\mu$ is the photon field, $Q=\textrm{Diag}[2/3,-1/3,-1/3]$ is the quark charge matrix, and $V_\mu$ is the vector field matrix; the expressions for P and⁵⁰V are the usual ones—fulfilling the U(3) flavor symmetry—and can be found in [16, 18, 103], for example. In this way, the first HLS Lagrangian piece named ${{\mathcal {L}}}_A$ is derived from Eq. (49). However, a second piece—${{\mathcal {L}}}_V$—can be defined, which vanishes in the inverse substitution $D_\mu \rightarrow \partial _\mu$. The two pieces are written as

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_A= & {} -\frac{f_\pi ^2}{4} \textrm{Tr} \left[ D_\mu \xi _L ~ \xi _L^\dagger - D_\mu \xi _R ~ \xi _R^\dagger \right] ^2,\nonumber \\ {{\mathcal {L}}}_V= & {} -\frac{f_\pi ^2}{4} \textrm{Tr} \left[ D_\mu \xi _L ~ \xi _L^\dagger + D_\mu \xi _R ~ \xi _R^\dagger \right] ^2\;., \end{aligned}$$

(51)

and the full non-anomalous HLS Lagrangian is written as

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_\textrm{HLS}={{\mathcal {L}}}_A +a {{\mathcal {L}}}_V, \end{aligned}$$

(52)

where a is a free parameter specific to the HLS approach [16]. This (unbroken) HLS Lagrangian can be found expanded in [103].

1.2 Breaking the HLS Lagrangian I: the BKY mechanism

The first breaking mechanism for the HLS Lagrangian has been proposed in [104]; one uses a modified version of it given in [103] in order to avoid identified undesirable properties of the original proposal [105]. Originally, the BKY mechanism was intended to only break the U(3) symmetry of the HLS Lagrangian; it has been extended following the lines of [106] to also cover isospin-breaking effects.

Defining $L=D_\mu \xi _L ~ \xi _L^\dagger$ and $R=D_\mu \xi _R ~ \xi _R^\dagger$, the (modified and extended) BKY breaking is implemented in the BHLS$_2$ framework by modifying Eq. (51) as follows:

$$\begin{aligned}{} & {} \displaystyle {{\mathcal {L}}}_A=-\frac{f_\pi ^2}{4} \textrm{Tr} \left[ (L - R) X_A\right] ^2,\nonumber \\ {}{} & {} \displaystyle {{\mathcal {L}}}_V=-\frac{f_\pi ^2}{4} \textrm{Tr} \left[ (L + R) X_V\right] ^2, \end{aligned}$$

(53)

where the constant matrices $X_{A/V}$ provide departures from the unit matrix; they have been parameterized as $X_{A/V} =$ Diag$(q_{A/V},y_{A/V},z_{A/V})$. In practice, one prefers setting $q_{A/V}=1+(\Sigma _{A/V}+ \Delta _{A/V})/2$ and $y_{A/V}=1+(\Sigma _{A/V}- \Delta _{A/V})/2$. As $z_{A}$ and $z_{V}$ are affecting the $s\overline{s}$ entries, their departure from 1 can be (and are found) large compared to $q_{A/V}$ and $y_{A/V}$—which refer to, respectively, the $u\overline{u}$ and $d\overline{d}$ entries [18, 20, 21].

Within the BHLS$_2$ context opened in [20], it has been shown that the diagonalization of the vector meson mass term implies $\Delta _{V}=0$; on the other hand, it has also been proved [20] that $\Sigma _{V}$ is actually out of reach and can be fixed to zero without any loss of generality. Therefore, the BKY-breaking mechanism introduces three free parameters: $z_A$ and $\Delta _A$ tightly related with the ratio $f_K/f_\pi$ and $z_V$ with the Higgs–Kibble $\phi$ meson mass.

1.3 Breaking the HLS Lagrangian II: the covariant derivative (CD) breaking

The main ingredient in the HLS approach is the covariant derivative as displayed in Eq. (50), complemented when relevant by W and $Z^0$ terms [16]. Thus, a relevant breaking mechanism can be chosen affecting the covariant derivative itself; this can be done by replacing Eq. (50) by

$$\begin{aligned} \displaystyle D_\mu \xi _{R/L} =\partial _\mu \xi _{R/L} -ig \left[ V_\mu ^I +\delta V_\mu \right] \xi _{R/L} +ie \xi _{R/L} A_\mu Q, \nonumber \\ \end{aligned}$$

(54)

where $\delta V_\mu$ can be chosen to break the $U(3)_V$ symmetry in a controlled way. Breaking the universality of the vector coupling g is an interesting tool; a priori one may think that breaking nonet symmetry (i.e., along the Gell–Mann matrix $T^0$) can be performed independently of breaking the $SU(3)_V$ symmetry (i.e., along the Gell–Mann matrix $T^8$); the diagonalization of the vector meson mass term and the expected values of the pion and kaon form factors at the chiral point prevent such a freedom of choice [20].

Identifying the field combinations associated with each of the canonical Gell–Mann $T_a$ U(3) matrix basis, one is led to define the following components which can participate to $\delta V_\mu$ separately or together:

$$\begin{aligned} \left\{ \displaystyle \begin{array}{l} \displaystyle \delta V_\mu ^0 =\frac{\xi _0}{\sqrt{2}} \left[ \frac{\sqrt{2} \omega _\mu ^{I} + \Phi _\mu ^{I}}{3}\right] \textrm{Diag} [1,1,1] ,\\ \displaystyle \delta V_\mu ^8 =\frac{\xi _8}{\sqrt{2}} \left[ \frac{\omega _\mu ^{I} - \sqrt{2} \Phi _\mu ^{I}}{3\sqrt{2}}\right] \textrm{Diag} [1,1,-2] ,\\ \displaystyle \delta V_\mu ^3 =\frac{\xi _3}{\sqrt{2}} \left[ \frac{\rho _I^0}{\sqrt{2}} \right] \textrm{Diag} [1,-1,0], \end{array} \right. \end{aligned}$$

(55)

in terms of the usual ideal field combinations; the CD-breaking term is

$$\begin{aligned} \delta V_\mu =\delta V_\mu ^0+\delta V_\mu ^8+\delta V_\mu ^3. \end{aligned}$$

The (free) breaking parameters $\xi _0$, $\xi _8$, and $\xi _3$ are only requested to be real in order that $\delta V_\mu$ is hermitian as $V_\mu ^I$ itself. Clearly, $\delta V_\mu ^0$ defines a breaking of the nonet symmetry down to $SU(3)_V \times U(1)_V$, $\delta V_\mu ^8$ rather expresses the breaking of the $SU(3)_V$ symmetry, while $\delta V_\mu ^3$ is related to a direct breaking of isospin symmetry in the vector sector.

As mentioned above, it happens that the $\xi$ parameters introduced by Eq. (55) should fulfill [20] $\xi _0=\xi _8$, and so that the CD breaking only involves two new free parameters. This means that within BHLS$_2$, one cannot solely break nonet symmetry, which should be accompanied by a SU(3) breaking of similar intensity.

1.4 Breaking the HLS Lagrangian III: dynamical vector meson mixing

The unbroken HLS Lagrangian already exhibits couplings for $\rho _I/\omega _I/\phi _I \rightarrow K^+K^-/K^0 \overline{K}^0$ transitions; this property is naturally transferred to all its broken versions. This implies that at one-loop order, the $\rho ^0/\omega /\phi$ squared mass matrix exhibits non-diagonal entries, and thus, the ideal vector fields are no longer mass eigenstates.

At one-loop order, the squared mass matrix of the $\rho ^0/\omega /\phi$ system can be written as

$$\begin{aligned} \displaystyle M^2(s)=M_0^2(s)+\delta M^2(s), \end{aligned}$$

(56)

where the dependence upon the momentum squared s flowing through the vector lines is made explicit. After the BKY and CD breakings just sketched, the vector meson masses are written⁵¹ as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle m_{\rho ^0}^2= \displaystyle m^2 \left[ 1+\Sigma _V + 2 ~\xi _3\right] ,\\ \displaystyle m_{\omega }^2= \displaystyle m^2 \left[ 1+\Sigma _V + \frac{4}{3} ~\xi _0 + \frac{2 }{3} ~\xi _8\right] \\ \qquad \qquad =m^2 \left[ 1+\Sigma _V +2 ~\xi _0\right] ,\\ \displaystyle m_{\Phi }^2 = \displaystyle m^2 ~z_V \left[ 1+\frac{2}{3}~\xi _0 + \frac{4}{3}~\xi _8 \right] = m^2 ~z_V \left[ 1+2~\xi _0 \right] \;.\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(57)

in terms of the various breaking parameters; $\Sigma _V$ has been kept for convenience. The $M_0^2(s)$ matrix occurring in Eq. (56) is thus written as

$$\begin{aligned} \displaystyle M_0^2(s)=\textrm{Diag} (m_{\rho ^0}^2+ \Pi _{\pi \pi }(s),m_\omega ^2,m_\phi ^2)\;. \end{aligned}$$

(58)

and is diagonal; $\Pi _{\pi \pi }(s)$ is the pion loop and includes the $\rho \pi ^+ \pi ^-$ coupling squared.

The expression for $\delta M^2(s)$ is slightly more involved. Having defined the ($\rho ^0,~\omega ,~\phi$) renormalized fields, generally indexed by R (i.e., those which diagonalize the vector meson mass term), one can derive the ${{\mathcal {V}}}_R^i \rightarrow {{\mathcal {V}}}_R^j$ transitions ($i,j=\rho ^0,~\omega ,~\phi$). For this purpose, having defined $\Pi _\pm (s)$ and $\Pi _0(s)$, respectively, the amputated charged and neutral kaon loops, the transition amplitudes ($i,j=\rho ^0,~\omega ,~\phi$) are written as

$$\begin{aligned} \displaystyle \delta M^2_{i, j}(s)=g^i_{K^+ K^-}g^j_{K^+ K^-}\Pi _\pm (s)+ g^i_{K^0 \overline{K}^0}g^j_{K^0 \overline{K}^0}\Pi _0(s), \nonumber \\ \end{aligned}$$

(59)

where the $g_{K \overline{K}}$ coupling constants are displayed in Section 10 of [20].

The physical $\rho ^0,~\omega ,~\phi$ are the eigenvectors of the full squared mass matrix $M^2(s)$; they are related to their renormalized partners by

$$\begin{aligned} \left( \begin{array}{ll} \rho _{R}\\ \omega _{R}\\ \Phi _{R}\\ \end{array} \right) = \left( \begin{array}{ccc} \displaystyle 1 &{}\displaystyle -\alpha (s) &{} \beta (s) \\ \displaystyle \alpha (s) &{} \displaystyle 1 &{} \displaystyle \gamma (s) \\ \displaystyle -\beta (s) &{} \displaystyle -\gamma (s) &{} \displaystyle 1 \end{array} \right) \left( \begin{array}{ll} \rho _{Phys}\\ \omega _{Phys}\\ \Phi _{Phys}\\ \end{array} \right) \end{aligned}$$

(60)

The three complex angles occurring here are combinations of the $\delta M^2(s)$ matrix elements and of the eigenvalues of the full $M^2(s)$ matrix, as displayed in Subsection 10.2 of [20].

It is worth remarking that the dynamical mixing just sketched has provided the first solution [17, 18] to the long-standing puzzle “$e^+e^-$ versus $\tau$” [98, 107, 108], as it generates a s-dependent difference between the $\rho ^\pm - W^\pm$ and $\rho ^0 - \gamma$ transition amplitudes.

1.5 The kinetic breaking and the [$\pi ^0,~\eta ,~{\eta ^\prime }$] system

This section is mostly aimed at reviewing the notations used in the body of the paper; these essentially deal with the pseudoscalar meson (PS) sector of the HLS model.

The full pseudoscalar meson kinetic energy term of the BHLS$_2$ Lagrangian [21] is written as

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{kin}^\prime = \textrm{Tr} \left[ \partial P_{bare} X_A \partial P_{bare} X_A\right] + 2 ~ \{ \textrm{Tr} \left[ X_H \partial P_{bare} \right] \}^2, \nonumber \\ \end{aligned}$$

(61)

where $P_{bare}$ is the PS bare field matrix. The first term is already broken by the BKY mechanism applied to the ${{\mathcal {L}}}_{A}$ HLS Lagrangian piece (see Eq. 53 in Appendix A), and the second one expresses the so-called kinetic breaking generalizing the ’tHooft mechanism [71]. It has been shown in [21] that an appropriate choice for the $X_H$ matrix is

$$\begin{aligned} \displaystyle X_H = \lambda _0 T_0 +\lambda _3 T_3+\lambda _8 T_8 \end{aligned}$$

(62)

in terms of the canonical U(3) Gell–Mann matrices ($T_0=I/\sqrt{6}$, $\textrm{Tr} [T_aT_b] = \delta _{ab}/2$) with real $\lambda _i$ coefficients in close correspondence with the CD breaking term $\delta V$ affecting the vector sector (see Appendix A.3). This choice manifestly allows for isospin symmetry breaking, nonet symmetry breaking (the so-called ’t Hooft term [71]), and SU(3) breaking.

It is useful to introduce the vector of PS fields as

$$\begin{aligned} \begin{array}{lll} \displaystyle { {\mathcal {V}}}_{any}=(\pi ^3_{any},\eta ^0_{any},\eta ^8_{any})~~&\mathrm{where~~} any=(bare,~R1,~R) \end{array} \nonumber \\ \end{aligned}$$

(63)

to clarify the component indexing.

The diagonalization of the kinetic energy Eq. (61) which leads from the bare PS fields to their renormalized partners (hereafter indexed by R) is performed in two steps. The intermediate step (from bare to to R1 fields) turns out to diagonalize $\textrm{Tr} \left[ \partial P_{bare} X_A \partial P_{bare} X_A\right]$ and to define the W transformation matrix as

$$\begin{aligned} \displaystyle W = \left( \begin{array}{ccc} \displaystyle 1 &{} \displaystyle -\frac{\Delta _A}{\sqrt{6}} &{} \displaystyle -\frac{\Delta _A}{2\sqrt{3}} \\ \displaystyle - \frac{\Delta _A}{\sqrt{6}} &{} \displaystyle B &{} \displaystyle A \\ \displaystyle -\frac{\Delta _A}{2\sqrt{3}} &{} \displaystyle A&{} \displaystyle C \end{array} \right) \end{aligned}$$

(64)

which depends on the BKY breaking parameter $\Delta _A$ and via

$$\begin{aligned} \begin{array}{lll} \displaystyle A=\sqrt{2} \frac{z_A-1}{3z_A},&B= \displaystyle \frac{2 z_A+1}{3z_A},&C=\displaystyle \frac{z_A+2}{3z_A} \end{array} \end{aligned}$$

(65)

on the other BKY breaking parameter $z_A$ (see Appendix A.2 above).

In order to achieve the diagonalization of the (full) kinetic energy term of the BHLS$_2$ Lagrangian, one still has to define the linear transform which relates the intermediate R1 and final R renormalized PS fields (see Eq. (28) in [21]). Given the (co-)vector

$$\begin{aligned} \displaystyle a^t = \left( ~\lambda _3, \lambda _0 B + \lambda _8 A, \lambda _0 A + \lambda _8 C \right) , \end{aligned}$$

(66)

one can then prove [21] that Eq. (61) becomes canonical (at first order in breakings) when expressed in terms of the ${ {\mathcal {V}}}_R$ fields defined by

$$\begin{aligned} \displaystyle {{\mathcal {V}}}_{bare} = W \cdot \left[ 1- \frac{1}{2}a \cdot a^t \right] \cdot \mathcal{V}_{R}. \end{aligned}$$

(67)

However, the ${{\mathcal {V}}}_{R}$ fields are not still the PS mass eigenstates denoted by the triplet ($\pi ^0,~\eta ,~{\eta ^\prime }$). One expects these physical states to be related with the ${ {\mathcal {V}}}_R$ fields via a three-dimensional rotation and thus three angles. Adopting the Leutwyler parameterization [109], one has

$$\begin{aligned} \left( \begin{array}{l} \displaystyle \pi ^3_R \\ \displaystyle \eta ^8_R \\ \displaystyle \eta ^0_R \end{array} \right)= & {} \left( \begin{array}{ccc} \displaystyle 1 &{} \displaystyle -\epsilon &{} \displaystyle -\epsilon ^\prime \\ \displaystyle \epsilon \cos {\theta _P}+\epsilon ^\prime \sin {\theta _P} &{} \displaystyle \cos {\theta _P} &{}\displaystyle \sin {\theta _P} \\ \displaystyle -\epsilon \sin {\theta _P}+\epsilon ^\prime \cos {\theta _P} &{} \displaystyle -\sin {\theta _P} &{}\displaystyle \cos {\theta _P} \end{array} \right) \left( \begin{array}{l} \displaystyle \pi ^0 \\ \displaystyle \eta \\ \displaystyle {\eta ^\prime }\end{array} \right) \nonumber \\ \end{aligned}$$

(68)

to relate the R fields which diagonalize the kinetic energy to the physical (i.e., mass eigenstates) neutral PS fields. The three angles ($\epsilon$, $\epsilon ^\prime$, and even $\theta _P$) are assumed ${{\mathcal {O}}}(\delta )$ perturbations; nevertheless, for clarity, the so-called third mixing angle [72] is not treated as manifestly small.

On the other hand, the “angles” $\epsilon$ and $\epsilon ^\prime$ are related with the light quark masses, and it is worth stating that they are expected to have like signs (see the discussion in [21]).

Erratum: the VPP/APP interaction pieces in BHLS$_2$

It is worthwhile to list the VPP and APP interaction terms of the BHLS$_2$ Lagrangian, corrected when needed, related with the present study, i.e., the charged and neutral pion fields, the $\eta$ and ${\eta ^\prime }$ mesons. We have

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{\pi ^-\pi ^+}&= \displaystyle ie \left[ 1 -\frac{a}{2} (1+ \Sigma _V) \right] A \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^+\nonumber \\ {}&\quad + \frac{i a g}{2} (1+ \Sigma _V) \left[ 1+\xi _3 \right] \rho ^0_I \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^+ \nonumber \\ \displaystyle {{\mathcal {L}}}_{\pi ^0 \pi ^\pm }&= \displaystyle \frac{iag}{2} (1+\Sigma _V) (1-\frac{\lambda _3^2}{2})\nonumber \\ {}&\quad \left[ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^0 - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\pi ^0 \right] \nonumber \\ \displaystyle {{\mathcal {L}}}_{\eta \pi ^\pm }&= \displaystyle - \frac{iag}{2} \left[ \left\{ \frac{1}{2\sqrt{3}} \Delta _A + \frac{\lambda _3 \widetilde{\lambda }_8}{2} \right\} \cos {\theta _P} \right. \nonumber \\ {}&\left. \quad -\left\{ \frac{1}{\sqrt{6}} \Delta _A + \frac{\lambda _3 \widetilde{\lambda }_0}{2} \right\} \sin {\theta _P} +\epsilon \right] \nonumber \\&\quad \displaystyle \left[ 1+ \Sigma _V \right] \left[ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\eta - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\eta \right] \nonumber \\ \displaystyle {{\mathcal {L}}}_{\eta ^\prime \pi ^\pm }&= \displaystyle -\frac{iag}{2} \left[ \left\{ \frac{1}{\sqrt{6}} \Delta _A + \frac{\lambda _3 \widetilde{\lambda }_0}{2} \right\} \cos {\theta _P}\right. \nonumber \\ {}&\left. \quad + \left\{ \frac{1}{2\sqrt{3}} \Delta _A + \frac{\lambda _3 \widetilde{\lambda }_8}{2} \right\} \sin {\theta _P} +\epsilon ^\prime \right] \nonumber \\&\quad \displaystyle \left[ 1+ \Sigma _V \right] \left[ \rho ^- \cdot \pi ^+ {\mathop {\partial }\limits ^{\leftrightarrow }}\eta ^\prime - \rho ^+ \cdot \pi ^- {\mathop {\partial }\limits ^{\leftrightarrow }}\eta ^\prime \right] \end{aligned}$$

(69)

The last two Lagrangian pieces supersede the corresponding formulae displayed in Eq. (45) of [21]; they were given for completeness but unused. In the present study, they should be considered.

In the expressions above, the kinetic breaking parameters occur; besides $\lambda _3$, one also has

$$\begin{aligned} \begin{array}{ll} \displaystyle \widetilde{\lambda }_0= \lambda _0 B + \lambda _8 A,&\displaystyle \widetilde{\lambda }_8= \lambda _0 A + \lambda _8 C, \end{array} \end{aligned}$$

(70)

where A, B, and C have also been mentioned in the Appendix A.5 just above. On the other hand, we have chosen here to keep the $\Sigma _V$ parameter for clarity. However, it has been shown in [21] that it is out of reach and can be fixed to zero without any loss of generality.

$A_\pm$ solutions: the AAP and VVP Lagrangians

It is worthwhile displaying the anomalous BHLS$_2$ Lagrangian pieces associated with the so-called triangle anomalies, having imposed the Kroll conditions [66], examined in full details in [21] and briefly sketched in Sect. 3. Using obvious notations, these anomalous pieces are derived from the following [13, 16]:

$$\begin{aligned} \left\{ \begin{array}{lll} {{\mathcal {L}}}_{VVP}=&{} \displaystyle - \frac{N_c g^2}{4 \pi ^2 f_\pi } ~c_3 \epsilon ^{\mu \nu \alpha \beta }\textrm{Tr}[ \partial _\mu V_\nu \partial _\alpha V_\beta P] \\ {{\mathcal {L}}}_{AAP}=&{} \displaystyle - \frac{N_c e^2 }{4 \pi ^2 f_\pi } ~(1- c_4) \epsilon ^{\mu \nu \alpha \beta }\partial _\mu A_\nu \partial _\alpha A_\beta \textrm{Tr}[Q^2 P]\\ {{\mathcal {L}}}_{AVP}=&{} \displaystyle - \frac{N_c ge }{8 \pi ^2 f_\pi } ~(c_4- c_3) \epsilon ^{\mu \nu \alpha \beta }\partial _\mu A_\nu \textrm{Tr}[ \{ \partial _\alpha V_\beta , Q \} P]. \end{array} \right. \nonumber \\ \end{aligned}$$

(71)

The phenomenology examined so far with the broken variants of the HLS model never led to us consider a nonzero $c_3-c_4$; therefore, one assumes $c_3=c_4$, which turns out to discard the ${{\mathcal {L}}}_{AVP}$ Lagrangian piece.

Unless otherwise stated, the neutral vector fields displayed here are the so-called ideal combinations generally named $\rho ^I$, $\omega ^I$, and $\phi ^I$. The transformation which connects the bare vector fields to their physical partners is treated in [20] and briefly mentioned in Appendix A above.

We also recall here the definition for $\delta _P$:

$$\begin{aligned}{} & {} \left\{ \displaystyle \sin {\delta _P} = \frac{1}{\sqrt{3}} \left( \sqrt{2} \sin {\theta _P}- \cos {\theta _P} \right) ,\right. \nonumber \\ {}{} & {} \qquad \left. \cos {\delta _P}= \displaystyle \frac{1}{\sqrt{3}} \left( \sqrt{2} \cos {\theta _P} + \sin {\theta _P}\right) \right. \end{aligned}$$

(72)

and ($d_\pm \equiv \pm 1$)

$$\begin{aligned} A_\pm = \Delta _A+ d_\pm \lambda _0^2. \end{aligned}$$

(73)

used below.

1.1 The AAP Lagrangian

The AAP Lagrangian defined in the header just above where Q is the quark charge matrix and P the U(3) symmetric matrix of the bare pseudoscalar fields is given for definiteness:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle g_{\pi ^0\gamma \gamma }&{}=\displaystyle ~~\frac{1}{6} \left\{ 1 - \frac{5}{6}A_\pm - \frac{\lambda _0^2}{3} \right\} \\ &{}\quad \displaystyle -\displaystyle \frac{\epsilon }{18 z_A} \left\{ 5 z_A\sin {\delta _P}+\sqrt{2}\cos {\delta _P} \right\} \\ {} &{}\quad -\displaystyle \frac{\epsilon ^\prime }{18 z_A} \left\{ \sqrt{2}\sin {\delta _P}- 5 z_A\cos {\delta _P} \right\} ,\\ \displaystyle g_{\eta \gamma \gamma }&{}=\displaystyle -\frac{\epsilon }{6} -\frac{\sqrt{2}}{18 z_A} \cos {\delta _P}\\ {} &{}\quad +\frac{1}{12} \left\{ A_\pm + \frac{5}{6} (3\lambda _0^2 -4) \right\} \sin {\delta _P} \\ \displaystyle g_{{\eta ^\prime }\gamma \gamma }&{}=\displaystyle -\frac{\epsilon ^\prime }{6} -\frac{\sqrt{2}}{18 z_A} \sin {\delta _P}\\ &{}\quad -\frac{1}{12} \left\{ A_\pm + \frac{5}{6} (3\lambda _0^2 -4) \right\} \cos {\delta _P}. \end{array} \right. \end{aligned}$$

(74)

The coupling constants for the physical mesons $P_0 \gamma \gamma$ ($P_0=\pi ^0,\eta ,{\eta ^\prime }$) are given by

$$\begin{aligned} \displaystyle G_{P_0 \gamma \gamma }= -\frac{3 \alpha _{em}}{\pi f_\pi } (1-c_4) g_{P_0\gamma \gamma }, \end{aligned}$$

(75)

and the AAP Lagrangian can also be written as

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{AAP_0}= & {} G_{P_0 \gamma \gamma }~~ P_0 ~ \epsilon ^{\mu \nu \alpha \beta } \partial _\mu A_\nu \partial _\alpha A_\beta ~~ \mathrm{for~each~of}~~\nonumber \\{} & {} P_0 = \pi ^0,\eta ,{\eta ^\prime }. \end{aligned}$$

(76)

1.2 The VVP Lagrangian

The VVP Lagrangian is given by

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{VVP}= & {} -\frac{3 g^2}{4 \pi ^2 f_\pi }~c_3 ~\epsilon ^{\mu \nu \alpha \beta } \textrm{Tr} \left[ \partial _\mu V_\nu \partial _\alpha V_\beta P \right] , ~~~~\nonumber \\ \displaystyle C= & {} -\frac{N_c g^2 c_3}{4 \pi ^2 f_\pi }. \end{aligned}$$

(77)

1.2.1 The $VV\pi$ Lagrangians

The $VV\pi$ Lagrangians relevant for our phenomenology are given by

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{VVP}(\pi ^\pm ){} & {} = \displaystyle \frac{C}{2} \epsilon ^{\mu \nu \alpha \beta } \Biggl \{ \left[ \left( 1+\frac{2 \xi _0+\xi _8}{3} \right) \partial _\mu \omega _\nu ^I\right. \nonumber \\ {}{} & {} \quad \left. +\frac{\sqrt{2}}{3} (\xi _0-\xi _8) \partial _\mu \phi ^I_\nu \right] \nonumber \\ {}{} & {} \quad \times \left[ \partial _\alpha \rho ^+_\beta \pi ^- +\partial _\alpha \rho ^-_\beta \pi ^+ \right] \Biggr \} \end{aligned}$$

(78)

and:

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{VVP}(\pi ^0){} & {} = \displaystyle \frac{C}{2} \epsilon ^{\mu \nu \alpha \beta } \Biggl \{ G_0 \partial _\mu \rho ^I_\nu \partial _\alpha \omega ^I_\beta +G_1 \left[ 2 \partial _\mu \rho ^-_\nu \partial _\alpha \rho ^+_\beta \right. \nonumber \\ {}{} & {} \left. \quad + \partial _\mu \rho ^I_\nu \partial _\alpha \rho ^I_\beta + \partial _\mu \omega ^I_\nu \partial _\alpha \omega ^I_\beta \right] \Biggr . \nonumber \\{} & {} \quad \displaystyle \Biggl . + G_2 \partial _\mu \phi ^I_\nu \partial _\alpha \phi ^I_\beta + G_3 \partial _\mu \rho ^I_\nu \partial _\alpha \phi ^I_\beta \Biggr \}~\pi ^0 \end{aligned}$$

(79)

where:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle G_0=\left[ 1-\frac{\lambda _0^2}{3} + \frac{2 \xi _0+\xi _8}{3} +\xi _3 \right] \\ \displaystyle G_1 = -\frac{A_\pm }{4} +\frac{1}{2} \left[ \epsilon ^\prime \cos {\delta _P} - \epsilon \sin {\delta _P} \right] \\ \displaystyle G_2 = -\frac{1}{z_A \sqrt{2}} \left[ \epsilon ^\prime \sin {\delta _P} + \epsilon \cos {\delta _P} \right] \\ \displaystyle G_3 = \frac{\sqrt{2}}{3} (\xi _0-\xi _8). \end{array} \right. \end{aligned}$$

(80)

Actually, one imposes $\xi _0=\xi _8$, so that, always, $G_3 =0$.

1.2.2 The $VV\eta$ Lagrangian

The $VV\eta$ Lagrangian is given by

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{VVP}(\eta ){} & {} = \displaystyle \frac{C}{2} \epsilon ^{\mu \nu \alpha \beta } \Biggl \{ K_1 \partial _\mu \rho ^-_\nu \partial _\alpha \rho ^+_\beta + K_2 \partial _\mu \rho ^I_\nu \partial _\alpha \rho ^I_\beta \nonumber \\ {}{} & {} \quad + K_3 \partial _\mu \omega ^I_\nu \partial _\alpha \omega ^I_\beta + K_4 \partial _\mu \phi ^I_\nu \partial _\alpha \phi ^I_\beta \Biggr . \nonumber \\{} & {} \quad \displaystyle \Biggl . + K_5 \partial _\mu \omega ^I_\nu \partial _\alpha \phi ^I_\beta + K_6 \partial _\mu \rho ^I_\nu \partial _\alpha \omega ^I_\beta \Biggr \}~\eta . \end{aligned}$$

(81)

Having defined⁵²

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle H_2 = \frac{1}{8} \left[ 3\lambda _0^2 -4 \right] ,&\displaystyle H_3 = -\frac{\sqrt{2}}{6 z_A} \left[ (3+2 \xi _0+4 \xi _8) \right] \end{array} \right\} \nonumber \\ \end{aligned}$$

(82)

the $VV\eta$ couplings become:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle K_1= 2 H_2 \sin {\delta _P},\qquad \qquad \quad \displaystyle K_2 = (H_2 - \xi _3) \sin {\delta _P} \\ \displaystyle K_3 = \left[ H_2 - \frac{2 \xi _0+\xi _8}{3} \right] \sin {\delta _P},\quad \displaystyle K_4 = H_3 \cos {\delta _P} \\ \displaystyle K_5 = -\frac{(\xi _0 -\xi _8)}{3 z_A}\left[ 2 \cos {\delta _P} + z_A \sqrt{2} \sin {\delta _P} \right] ,\\ \displaystyle K_6 = \frac{A_\pm }{2} \sin {\delta _P} - \epsilon \end{array} \right. \end{aligned}$$

(83)

Actually, similarly to just above, the $K_5$ term drops out in the practical BHLS$_2$ context.

1.2.3 The $VV{\eta ^\prime }$ Lagrangian

The $VV{\eta ^\prime }$ Lagrangian is given by

$$\begin{aligned} \begin{array}{ll} \displaystyle {{\mathcal {L}}}_{VVP}({\eta ^\prime })&{}= \displaystyle \frac{C}{2} \epsilon ^{\mu \nu \alpha \beta } \Biggl \{ K^\prime _1 \partial _\mu \rho ^-_\nu \partial _\alpha \rho ^+_\beta + K^\prime _2 \partial _\mu \rho ^I_\nu \partial _\alpha \rho ^I_\beta \\ &{}\quad + K^\prime _3 \partial _\mu \omega ^I_\nu \partial _\alpha \omega ^I_\beta + K^\prime _4 \partial _\mu \phi ^I_\nu \partial _\alpha \phi ^I_\beta \Biggr . \\ &{}\quad \displaystyle \Biggl . + K^\prime _5 \partial _\mu \omega ^I_\nu \partial _\alpha \phi ^I_\beta + K^\prime _6 \partial _\mu \rho ^I_\nu \partial _\alpha \omega ^I_\beta \Biggr \}~{\eta ^\prime }\end{array}\nonumber \\ \end{aligned}$$

(84)

the $VV{\eta ^\prime }$ couplings being

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle K^\prime _1= -2 H_2 \cos {\delta _P},\qquad \qquad \displaystyle K^\prime _2 = -(H_2 - \xi _3)\cos {\delta _P} \\ \displaystyle K^\prime _3 = -\left[ H_2 - \frac{2 \xi _0+\xi _8}{3} \right] \cos {\delta _P},\quad \displaystyle K^\prime _4 = H_3 \sin {\delta _P} \\ \displaystyle K^\prime _5 = -\frac{(\xi _0 -\xi _8)}{3 z_A}\left[ - z_A \sqrt{2} \cos {\delta _P} +2 \sin {\delta _P} \right] ,\\ \displaystyle K^\prime _6 = -\frac{A_\pm }{2} \cos {\delta _P} -\epsilon ^\prime \end{array}\right. \nonumber \\ \end{aligned}$$

(85)

where also the $K^\prime _5$ term drops out in the practical BHLS$_2$ context, where $\xi _0 =\xi _8$. The $H_i$ functions occurring here have been defined in our previous paper and have been mentioned in the subsection just above—$H_1$ vanishes thanks to having requested the Kroll conditions.

One should also note that the $VV{\eta ^\prime }$ couplings are related to the $VV\eta$ couplings and can be derived by making in the $VV\eta$ couplings

$$\begin{aligned} \{\sin {\delta _P} \rightarrow -\cos {\delta _P} ~~\textrm{and} ~~~\cos {\delta _P} \rightarrow \sin {\delta _P}\}. \end{aligned}$$

$A_\pm$ solutions: the APPP and VPPP Lagrangians

Besides the Lagrangian pieces associated with the triangle anomalies mentioned in the Appendix just above, those associated with the so-called box anomalies play an important role in the $\eta /{\eta ^\prime }\rightarrow \pi ^+ \pi ^- \gamma$ decays and in the $e^+ e^- \rightarrow \pi ^+ \pi ^-\pi ^0$ annihilation thoroughly considered in our [21]. We find it helpful to provide their expressions while the Kroll conditions are applied. The APPP and VPPP Lagrangian pieces introduce a new HLS parameter ($c_1-c_2$) which is not fixed by the model and should be derived from fits.

As for the VVP interactions mentioned in Appendix C, the neutral vector fields occurring in the VPPP interaction Lagrangian are their ideal combinations; they should be expressed in terms of physical vector fields as developed in [20] in practical applications.

1.1 The APPP Lagrangian

The APPP Lagrangian is given by

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{APPP}= & {} D ~\epsilon ^{\mu \nu \alpha \beta } A_\mu \textrm{Tr} \left[ Q \partial _\nu P \partial _\alpha P \partial _\beta P\right] , ~~\nonumber \\ \displaystyle D= & {} -i\frac{N_c e}{3 \pi ^2 f_\pi ^3} \left[ 1-\frac{3}{4}(c_1-c_2+c_4)\right] . \end{aligned}$$

(86)

Regarding the phenology we address, the relevant APPP Lagrangian piece to be considered is

$$\begin{aligned} \displaystyle {{\mathcal {L}}}_{APPP}^1= & {} D \epsilon ^{\mu \nu \alpha \beta } A_\mu \left\{ g_{\gamma \pi ^0} \partial _\nu \pi ^0 + g_{\gamma \eta } \partial _\nu \eta + g_{\gamma {\eta ^\prime }} \partial _\nu {\eta ^\prime }\right\} ~\nonumber \\{} & {} \partial _\alpha \pi ^- \partial _\beta \pi ^+ , \end{aligned}$$

(87)

in terms of fully renormalized PS fields. Requiring the $A_\pm$ Kroll conditions, these $g_{\gamma P}$ couplings can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle g_{\gamma \pi ^0} = -\frac{1}{4} \left[ 1 - \frac{A_\pm }{2} -\frac{\lambda _0^2}{3} -\epsilon \sin {\delta _P} +\epsilon ^\prime \cos {\delta _P} \right] \\ \displaystyle g_{\gamma \eta } =~~~~ \left[ 1 -\frac{A_\pm }{2} -\frac{3 \lambda _0^2}{4} \right] \frac{\sin {\delta _P}}{4} + \frac{\epsilon }{4}\\ \displaystyle g_{\gamma {\eta ^\prime }} = - \left[ 1 -\frac{A_\pm }{2} -\frac{3 \lambda _0^2}{4} \right] \frac{\cos {\delta _P}}{4} + \frac{\epsilon ^\prime }{4}, \end{array} \right. \end{aligned}$$

(88)

keeping only the leading-order terms in the breakings.

1.2 The VPPP Lagrangian

The VPPP anomalous HLS Lagrangian is

$$\begin{aligned} {{\mathcal {L}}}_{VPPP}= & {} \displaystyle - i \frac{N_c g }{4 \pi ^2 f_\pi ^3} (c_1-c_2-c_3) \epsilon ^{\mu \nu \alpha \beta }\nonumber \\ {}{} & {} \textrm{Tr}[V_\mu \partial _\nu P \partial _\alpha P \partial _\beta P] \end{aligned}$$

(89)

where the $c_i$ are the FKTUY parameters not fixed by the model. $N_c$ is the number of colors fixed to 3.The V and P field matrices are the bare ones.

The relevant part of ${{\mathcal {L}}}_{VPPP}$ within the present context is

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\displaystyle {{\mathcal {L}}}_{VP_0 \pi ^+ \pi ^-}\\ &{}=E\epsilon ^{\mu \nu \alpha \beta } \left\{ \left[ g_{\rho \pi }^0 \partial _\nu \pi ^0+g_{\rho \eta }^0 \partial _\nu \eta +g_{\rho \eta ^\prime }^0 \partial _\nu \eta ^\prime \right] ~\rho ^{I}_\mu \right. \\ &{}\quad \left. \displaystyle +\left[ g_{\omega \pi }^0 \partial _\nu \pi ^0+g_{\omega \eta }^0 \partial _\nu \eta + +g_{\omega \eta ^\prime }^0 \partial _\nu \eta ^\prime \right] ~\omega _\mu ^{I}\right. \\ &{}\left. \quad + g_{\phi \pi }^0\partial _\nu \pi ^0 ~\phi _\mu ^{I} \right\} \partial _\alpha \pi ^- \partial _\beta \pi ^+ \\ &{}\displaystyle \mathrm{~~with~~} E=-i \frac{ 3 g (c_1-c_2-c_3)}{4 \pi ^2 f_\pi ^3} \end{array} \right. \end{aligned}$$

(90)

in terms of the physical pseudoscalar fields. Keeping only the $A_\pm$ solutions and the leading-order breaking terms, the couplings just defined are

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle g_{\rho \pi ^0}^0= \frac{1}{4} \left[ \frac{A_\pm }{2} + \epsilon \sin {\delta }_P - \epsilon ^\prime \cos {\delta }_P \right] \\ \displaystyle g_{\rho \eta }^0=\frac{1}{4} \left[ 1 +\xi _3 - \frac{3}{4} \lambda _0^2 \right] \sin {\delta }_P \\ \displaystyle g_{\rho \eta ^\prime }^0= -\frac{1}{4} \left[ 1 +\xi _3 - \frac{3}{4} \lambda _0^2 \right] \cos {\delta }_P \end{array} \right. \end{aligned}$$

(91)

and:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle g_{\omega \pi ^0}^0= -\frac{3}{4} \left[ 1 + \frac{2 \xi _0+\xi _8}{3} - \frac{1}{3}\lambda _0^2 \right] \\ \displaystyle g_{\omega \eta }^0= \frac{3}{4} \left\{ \epsilon - \frac{A_\pm }{2} \sin {\delta _P} \right\} \\ \displaystyle g_{\omega \eta ^\prime }^0= \frac{3 }{4} \left\{ \epsilon ^\prime +\frac{A_\pm }{2} \cos {\delta _P} \right\} \\ \displaystyle g_{\phi \pi }^0= -\frac{\sqrt{2}}{4}\left[ \xi _0-\xi _8 \right] ,~~g_{\phi \eta }^0= 0,~~g_{\phi \eta ^\prime }^0= 0. \end{array} \right. \end{aligned}$$

(92)

As pseudoscalar meson form factor values at origin imply [20] $\xi _0=\xi _8$, one observes that no term involving $\phi ^I$ survives at leading order in breakings.