Observation of $${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $$ and $${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $$ decays

doi:10.1140/epjc/s10052-024-12752-3

Observation of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{()0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{-}_{s}} $ decays

Regular Article - Experimental Physics
Open access
Published: 05 June 2024

Volume 84, article number 575, (2024)
Cite this article

Download PDF

You have full access to this open access article

The European Physical Journal C Aims and scope Submit manuscript

Observation of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays

Download PDF

LHCb Collaboration

297 Accesses
2 Altmetric
Explore all metrics

A preprint version of the article is available at arXiv.

Abstract

The decays ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ are observed for the first time, in proton-proton collision data at $\sqrt{s} =13\text {Te\hspace{-1.00006pt}V} $, corresponding to an integrated luminosity of 5.4$\text {fb} ^{-1}$ collected with the LHCb detector. Their ratios of branching fractions with respect to the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ mode are measured to be

$$\begin{aligned} \begin{aligned} \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 0.1908 {}_{-0.0034}^{+0.0036} {}_{-0.0018}^{+0.0016} \pm 0.0038,\\ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 0.589 {}_{-0.017}^{+0.018} {}_{-0.018}^{+0.017} \pm 0.012,\\ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 1.668 \pm 0.022 {}_{-0.055}^{+0.061}, \end{aligned} \end{aligned}$$

where the first uncertainties are statistical, the second systematic, and the third, for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays, are due to the uncertainties on the branching fractions of the ${{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} $ and ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} $ decay modes. The measured branching fractions probe factorization assumptions in effective theories and provide the normalization for future pentaquark searches in ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decay channels.

Observation of $${{\varXi } ^0_{b}} \rightarrow {{\varXi } ^+_{c}} {{D} ^-_{s}} $$ and $${{\varXi } ^-_{b}} \rightarrow {{\varXi } ^0_{c}} {{D} ^-_{s}} $$ decays

Article Open access 07 March 2024

First observation and branching fraction measurement of the $$ {\Lambda}_b^0\to {D}_s^{-}p $$ decay

Article Open access 10 July 2023

Observation of $${{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} 3{{\uppi } ^+} 2{{\uppi } ^-} $$ and $${{\mathrm {B}} ^+} \rightarrow {\uppsi {(2\mathrm {S})}} {{\uppi } ^+} {{\uppi } ^+} {{\uppi } ^-} $$ decays

Article Open access 06 February 2017

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

1 Introduction

Hadrons are systems of quarks bound by the strong interaction, described at the fundamental level by quantum chromodynamics (QCD). Decays of heavy hadrons containing at least one b quark provide clean signatures to test new emergent phenomena in the realms of QCD and physics beyond the Standard Model. Effective theories testing these signatures are based on the fact that the heavy-quark mass $m_Q$ (e.g. $m_{b} \sim 4\text {Ge\hspace{-1.00006pt}V} $) is much larger than the QCD scale $\varLambda _\text {QCD}\sim 100\text {Me\hspace{-1.00006pt}V} $.^{Footnote 1} Processes that occur at the scale of $m_Q$ can be described by perturbative QCD, while nonperturbative effects, including the formation of light hadrons, are suppressed by powers of $\varLambda _\text {QCD}/m_Q$. This factorization of high-energy and low-energy processes is widely used in effective theories describing decays of heavy hadrons, such as the heavy quark effective theory (HQET) [1,2,3,4].

Beauty hadron decays to two charmed hadrons probe factorization assumptions in HQET in a regime where their application is contestable due to the presence of two charm quarks ($m_{c} \sim 1.3\text {Ge\hspace{-1.00006pt}V} $) in the final state. In particular, decays of the ${{\varLambda } ^0_{b}} $ baryon, which has quark content udb, are interesting as the $({u} {d})$ diquark is in a spin-zero state, which gives rise to additional symmetries of HQET. In that sense, the ${{\varLambda } ^0_{b}} $ baryon is a simpler object than a B meson.

This article reports the measurement of the branching fraction of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $, ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ double-open-charm decays, relative to that of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ decay. The dominant Feynman diagrams of these decays are shown in Fig. 1, where the left and middle diagrams contribute to ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays, while the right diagram corresponds to ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} ^{(*)-}_{s} $ decays. The color-suppressed, internal ${W} $-emission diagram, as shown in the middle, does not exist for ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} ^{(*)-}_{s} $ decays. The isospin of the light diquark in the left and right diagrams is conserved, such that ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays are suppressed, and ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{D} ^{(*)-}_{s} $ decays are forbidden up to nonfactorizing contributions [5, 6].

Two-body beauty to double-open-charm decays have been theoretically studied for over three decades, and several models predict the ratio of branching fractions $\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \right) /\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) $ in the range 0.75–2.2 [7,8,9,10,11,12,13,14,15,16,17,18,19]. Due to the complexity of the three-body system, there are no predictions for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ channels. However, the contribution of color-suppressed amplitudes in ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ can be qualitatively assessed by comparing the relative branching fractions to those of mesons, when exchanging the ud diquark in the ${{\varLambda } ^0_{b}} $ with an antiquark [20]. For this comparison, it is convenient to define the double ratio

$$\begin{aligned} \mathcal{D}\mathcal{R}^{(*)}(M_b){} & {} \equiv \left[ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }\right] \Big /\nonumber \\{} & {} \quad \times \left[ \frac{\mathcal {B}\left( M_b\rightarrow M_c {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \right) }{\mathcal {B}\left( M_b\rightarrow M_c {{D} ^-_{s}} \right) }\right] , \end{aligned}$$

(1)

where $M_b$ or $M_c$ is a beauty or charm meson, and the star in $\mathcal{D}\mathcal{R}^{(*)}$ denotes the ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ ground state or the ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} ^{*}(2007)^{0}} $ vector state. Additionally, there is a large interest in exploring the resonance structure of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays. The reason is that the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ and ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} $ systems are the open-charm equivalent of the ${{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} ({c} {\overline{{c}}}){p} ({u} {u} {d})$ final state, where $P _{c} ^+({c} {\overline{{c}}} {u} {u} {d})$ pentaquark resonances have been observed [21,22,23,24]. Decays of these pentaquarks to ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ and ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} $ states are anticipated in many models, yet the predicted branching fractions relative to that into ${{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} $ vary by orders of magnitude [19, 25,26,27,28,29,30,31,32,33,34,35]. To test those predictions experimentally, two more ingredients are needed, namely the pentaquark fit fractions coming from ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ amplitude analyses $f_{{{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}}(P _{c} ^+)$, and the branching fractions of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays relative to that of the ${{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} $ mode [36]. Assuming that the production mechanism for ${{\varLambda } ^0_{b}} \!\rightarrow P _{c} ^+{{K} ^-} $ is the same as for ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} $ decays, the fit fraction in the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ final states is given by

$$\begin{aligned} f_{{{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}}(P _{c} ^+)= & {} f_{{{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p}}(P _{c} ^+) \cdot \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \right) } \nonumber \\{} & {} \cdot \frac{\mathcal {B}\left( P _{c} ^+\!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0} \right) }{\mathcal {B}\left( P _{c} ^+\!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} \right) }. \end{aligned}$$

(2)

Thus, the values of $\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \right) }$ that will be derived in this article, can be used to calculate sensitivities for observing $P _{c} ^+$ in the ${{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}$ system for a given theoretical prediction of $\frac{\mathcal {B}\left( P _{c} ^+\!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0} \right) }{\mathcal {B}\left( P _{c} ^+\!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} \right) }$.

Using 5.4$\text {fb} ^{-1}$ of proton-proton (pp) collision data collected at $\sqrt{s} =13\text {Te\hspace{-1.00006pt}V} $ by the LHCb detector in 2015–2018, the branching fractions of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $, ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $, and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays are measured relative to that of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ decays. The latter is chosen as a normalization channel because it has large signal yield, and its branching fraction has been previously measured [37]. The ${{\varLambda } ^0_{b}} $ decays proceed through different intermediate charm hadron decays, namely ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $, ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} $ and/or ${{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} $. All decays are reconstructed with the same particles in the final state, ${p} {{K} ^-} {{K} ^-} {{K} ^+} {{\pi } ^-} {{\pi } ^+} $, which reduces or cancels various uncertainties related to the ${{\varLambda } ^0_{b}} $ production and the determination of absolute reconstruction and selection efficiencies. Neutral objects or electron-positron pairs, in the decays of ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} $ or ${{D} ^{*-}_{s}} $ mesons are not reconstructed. Therefore, the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays are referred to as partially reconstructed signal.

The expressions for the ratio of branching fractions for ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays are

$$\begin{aligned}&\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }\\&\quad = \frac{N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} }}{N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }} \frac{\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }}{\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} }} \frac{\mathcal {B}\left( {{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} \right) }{\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} \right) }, \\&\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) } \quad = \frac{N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} }}{N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }} \frac{\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }}{\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} }}, \end{aligned}$$

where $N^X$ are the observed yields and $\epsilon ^X$ the efficiency for the decay mode X. The ratio of branching fractions $\mathcal {B}\left( {{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} \right) /\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} \right) $ is taken from Ref. [38].

2 LHCb detector

The LHCb detector [39, 40] is a single-arm forward spectrometer covering the pseudorapidity range $2<\eta <5$ at the LHC, designed for the study of particles containing $b $ or $c $ quarks. The detector includes a high-precision tracking system consisting of a silicon-strip vertex detector surrounding the pp interaction region [41], a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about $4{\mathrm {\,Tm}}$, and three stations of silicon-strip detectors and straw drift tubes [42, 43] placed downstream of the magnet. The tracking system provides a measurement of the momentum, $p$, of charged particles with a relative uncertainty that varies from about 0.5% below 20$\text {Ge\hspace{-1.00006pt}V}$ to 1.0% at 200$\text {Ge\hspace{-1.00006pt}V}$. The minimum distance of a track to a primary vertex (PV), the impact parameter (IP), is measured with a resolution of $(15+29/p_{\textrm{T}})\,\upmu \text {m} $, where $p_{\textrm{T}}$ is the component of the momentum transverse to the beam, in $\text {Ge\hspace{-1.00006pt}V}$. Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov (RICH) detectors [44]. Hadrons are identified by a calorimeter system consisting of scintillating-pad and preshower detectors, an electromagnetic and a hadronic calorimeter. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers [45].

The online event selection is performed by a trigger [46, 47], which consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, which applies a full event reconstruction.

Simulation is required to calculate reconstruction and selection efficiencies, and to determine the shapes of partially reconstructed components in the invariant mass distributions. Some of these components are modeled by the fast simulation package RapidSim [48] and the AmpGen generator [49]. In the full detector simulation, pp collisions are generated using Pythia [50] with a specific LHCb configuration [51]. Decays of unstable particles are described by EvtGen [52], in which final-state radiation is generated using Photos [53]. The interaction of the generated particles with the detector, and its response, are implemented using the Geant4 toolkit [54, 55] as described in Ref. [56]. The underlying pp interaction is reused multiple times, with an independently generated signal decay for each simulated event [57].

3 Dataset and selection

Data are selected first by an online trigger system, consisting of a hardware- and two software stages, further filtered in an offline selection. Online, data are selected by a sequence of inclusive trigger decisions. The majority of candidates are selected by criteria based on the topology of b-hadron decays [58, 59]. In the offline selection, candidates that fulfill characteristics of the exclusive ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ or ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ decay are selected using tracks with hits in at least the vertex tracker and the three downstream tracking stations. Further selection is applied on momentum, transverse momentum, track quality and displacement from any PV. Intermediate charm hadrons are selected using the distance of closest approach of their decay products, the decay vertex fit $\chi ^2$, and the displacement of the decay vertex from any PV. Combined information from particle identification (PID) detectors is used to reject topologically similar background contributions. The ${{\varLambda } ^0_{b}} $ candidates are reconstructed by combining a ${{\varLambda } ^+_{c}} $ candidate with either a ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ candidate and a companion kaon or a ${{D} ^-_{s}} $ candidate. Kinematic and topological variables are used to suppress combinatorial background: namely the sum of transverse momenta of all the final-state particles, the presence of at least one track with large displacement from any PV and high momentum and high transverse momentum, the angle between the reconstructed momentum direction of the ${{\varLambda } ^0_{b}} $ candidate and its flight direction and distance, determined from the production and decay vertices.

A clean sample of ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ and ${{D} ^-_{s}} $ mesons is selected using topological and kinematic criteria, and a requirement on the product of the probabilities of final-state kaons and pions to be correctly identified. These probabilities correspond to the response of a neural network combining PID information from the full detector [40]. Even though the ${{\varLambda } ^+_{c}} $ decays produce high-momentum protons that can be cleanly reconstructed and identified, the shorter lifetime compared to ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ and ${{D} ^-_{s}} $ mesons makes it more difficult to suppress background contributions in the reconstruction of ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ decays. Consequently, a dedicated gradient boosted decision tree (BDT) algorithm [60] for secondary ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ decays is trained and calibrated on ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\pi } ^-} $ data, similar to the ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ BDT classifier used in Ref. [37]. An optimization procedure is carried out, that determines a working point for for the following variables: the ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ BDT output, the $\chi ^2_{\text {IP}} $ of the ${{\varLambda } ^0_{b}} $ candidate, where $\chi ^2_{\text {IP}} $ is defined as the difference in the vertex-fit $\chi ^2$ of a given PV reconstructed with and without the ${{\varLambda } ^0_{b}} $ candidate, and the probability of the companion kaon to be correctly identified in the ${\varLambda } ^+_{c} $ ${\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0$ ${K} ^-$ channel. The optimization is carried out in form of a grid search, maximizing the approximate signal significance ($S/\sqrt{S+B}$) multiplied by the purity ($S/(S+B)$). Here, S and B represent the signal and background yields in a 2 $\sigma $ window around the exclusive ${{\varLambda } ^0_{b}} $ signal mass peak. This optimization is done independently for signal and normalization channels.

Candidates for which the opening angle between any track pair is smaller than 0.2 mrad are rejected, which removes artifacts from matching track segments reconstructed with the downstream tracking stations and the vertex locator. Fiducial regions are selected in the phase-space later used for weighting simulated events, see Sect. 5. This concerns the transverse momentum and pseudorapidity of the ${{\varLambda } ^0_{b}} $ candidate, as well as the total number of tracks in the event.

Sources of peaking background candidates from particle misidentification are studied by statistically subtracting the combinatorial background contribution [61], identified in a preliminary fit to the invariant mass of the reconstructed system, described in Sect. 4. For the background-subtracted sample, invariant-mass distributions with swapped particle hypotheses are investigated to identify and remove candidates with misidentified particles. To increase selection efficiencies, only those candidates that also fail at least one tighter particle identification requirement, are removed as summarized in Table 1.

Table 1 Explicitly rejected physics backgrounds. Some background contributions are present only in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ or ${{\varLambda } ^+_{c}} {{D} ^-_{s}} $ systems, while others in both. A particle, $M_\textrm{misID}$, that decays through a real particle a, which is reconstructed as a particle with different mass hypothesis b, is denoted as $M_\textrm{misID}\!\rightarrow \{a \leftarrow b\}X $, where X corresponds to the rest of the decay. As there are two ${{K} ^-} $ mesons in the final state, the subscripts “${{\varLambda } ^+_{c}} $” and “com” (for companion) or “${{D} ^-_{s}} $” denote the assignment in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ or ${{\varLambda } ^+_{c}} {{D} ^-_{s}} $ reconstruction chain. Cases where the proton is misidentified as a pion or kaon and combined into a ${{D} ^0} $ candidate, are marked with the ${{D} ^0} $ subscript

Full size table

Background events from a wrong combination of candidates in the sample of ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ decays, such as ${{\varLambda } ^0_{b}} \!\rightarrow {p} {{D} ^0} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {K} _{{{\varLambda } ^+_{c}}}^{-} $, with ${{D} ^0} \!\rightarrow K^-_\textrm{com}{{\pi } ^+} ({{\pi } ^0}) $, where the subscripts “${{\varLambda } ^+_{c}} $” and “com” denote the nominal assignment in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ reconstruction chain. are suppressed by requiring a small IP and $\chi ^2_{\text {IP}} $ of the companion kaon $K^-_\textrm{com}$, with respect to the ${{\varLambda } ^0_{b}} $ decay vertex.

For each species of charm hadron, an invariant-mass requirement is defined such that the central 95% of the individual charm-candidate signal is retained. These are determined from a three-dimensional fit to the invariant masses of the ${{\varLambda } ^0_{b}} $ candidate and the two intermediate charm-hadron candidates. To select at most one ${{\varLambda } ^0_{b}} $ candidate for a given LHC bunch crossing, a final selection step randomly removes all but one candidate from each event. This concerns 2.4% of the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ candidates and 1.1% of the ${{\varLambda } ^+_{c}} {{D} ^-_{s}} $ candidates.

4 Invariant-mass fits

Unbinned maximum-likelihood fits are first carried out in three mass dimensions, given by the invariant mass of ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ or ${{\varLambda } ^+_{c}} {{D} ^-_{s}} $ decays, and the two charm hadrons. The invariant masses of beauty candidates are defined as $m({{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-})\equiv m({p} {{K} ^-} {{\pi } ^+} {{K} ^+} {{\pi } ^-} {{K} ^-})-m({p} {{K} ^-} {{\pi } ^+})-m({{K} ^+} {{\pi } ^-})+M_{{{\varLambda } ^+_{c}}}+M_{{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0}}$ and $m({{\varLambda } ^+_{c}} {{D} ^-_{s}})\equiv m({p} {{K} ^-} {{\pi } ^+} {{K} ^-} {{K} ^+} {{\pi } ^-})-m({p} {{K} ^-} {{\pi } ^+})-m({{K} ^-} {{K} ^+} {{\pi } ^-})+M_{{{\varLambda } ^+_{c}}}+M_{{{D} ^-_{s}}}$, where $M_X$ is the known value of the mass of particle X from Ref. [38].

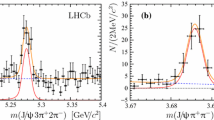
This fit is restricted to narrow regions around the exclusively reconstructed ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ signals in any of the three mass dimensions as shown in Fig. 2. The figures illustrate that the three-dimensional fit directly measures the normalization of single-charm and charmless backgrounds. The central interval containing 95% of the signal component determines the mass selection of the charm candidates, which removes backgrounds of different origin that would complicate model building in a three-dimensional fit in the full mass range.

Exclusive signal contributions in all mass dimensions are modeled by two-sided Hypatia functions, which are convolved with a Gaussian function [62]. The core width of the Hypatia and the mass parameter are free in the fits, the parameters which determine the transitioning points from the generalized hyperbolic resolution model to the exponential tails are constrained and the remaining parameters of the signal models are fixed. Constraining and fixing parameters in the signal model and other components is validated with simulation and pseudoexperiments to ensure unbiased parameter estimation and ensure valid coverage properties. Combinatorial backgrounds are described by Chebychev polynomial functions up to order three; their coefficients allowed to float free in the fit. The order chosen for an individual fit is the one minimizing a likelihood that has been corrected for the number of degrees of freedom in the fit model, accounting for constraints and the number of parameters [63]. This likelihood is also used to select a baseline fit model among the various possibilities discussed in Sect. 6.

The only significant single-charm or charmless background contribution comes from the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{K} ^+} {{\pi } ^-} {{K} ^-} $ decay. Its three-dimensional probability density function (PDF) is composed of a signal component in $m({p} {{K} ^-} {{\pi } ^+})$, a dedicated linear background in $m({{K} ^+} {{\pi } ^-})$ or $m({{K} ^-} {{K} ^+} {{\pi } ^-})$, and a conditional Gaussian PDF in $m({{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-})$ or $m({{\varLambda } ^+_{c}} {{D} ^-_{s}})$. The mean of the conditional Gaussian PDF depends linearly on $m({{K} ^+} {{\pi } ^-})$ or $m({{K} ^-} {{K} ^+} {{\pi } ^-})$, since a ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ or ${{D} ^-_{s}} $ mass constraint is used in the definition of $m({{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-})$ or $m({{\varLambda } ^+_{c}} {{D} ^-_{s}})$. In total, $84\pm 13$ ($990\pm 50$) ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{K} ^+} {{\pi } ^-} {{K} ^-} $ candidates remain in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ (${{\varLambda } ^+_{c}} {{D} ^-_{s}} $) dataset used for the one-dimensional baseline fit. A subsequent one-dimensional fit, referred to as the baseline fit, which is independent from the three-dimensional fit, is used to determine the exclusive and partially reconstructed signal yields, that are needed for measuring the branching fractions. In the baseline fit, the models of signal and combinatorial background are the same as in the three-dimensional fit, following the same strategy of floating, fixed and constrained parameters described earlier. The yields of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{K} ^+} {{\pi } ^-} {{K} ^-} $ decays are fixed in the baseline fit, and their uncertainties, including the anti-correlation with the signal yields, are propagated from the fit result of the three-dimensional fit to the statistical uncertainty of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ branching fraction.

The partially reconstructed quasi-two-body decays ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $, ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} ^*_{{s} 0}(2317)^- $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} _{{s} 1}(2460)^- $ are described analytically. Their kinematic endpoints, which define the domain of the corresponding PDF, are fully determined by the masses of the decay products [38]. Each PDF is a superposition of Gaussian functions convolved with a two-sided step-function with a sloped plateau (box-like), and an upward- or downward-open parabola [64, 65]. These PDFs model the spin structure of the respective decays, and additionally describe a linear drop of efficiency towards lower invariant masses, which is constrained to the value extracted from simulation.

In particular, the quasi-two-body decays through vector mesons, ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {\gamma } \right] _{{{D} ^{*-}_{s}}} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {{\pi } ^0} \right] _{{{D} ^{*-}_{s}}} $ are modeled by parabolic shapes facing downward and upward respectively, and due to the spin-1/2 initial state also involve a box-like component. Their relative normalization is constrained by the branching fraction of $\mathcal {B}({{D} ^{*-}_{s}} \!\rightarrow {{D} ^-_{s}} {{\pi } ^0} )$. Quasi-two-body decays through the spin-0 meson ${D} ^*_{{s} 0}(2317)^-\!\rightarrow {{D} ^-_{s}} {{\pi } ^0} $, and the spin-1 meson ${D} _{{s} 1}(2460)^-\!\rightarrow {{D} ^-_{s}} {\gamma } $ are fully described by a box-like PDF. The latter is an effective description, since only about 20% of the high mass tail of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {\gamma } \right] _{{D} _{{s} 1}(2460)^-} $ decay can be reconstructed in the chosen mass range, and variations of the spin structure in simulation do not significantly alter the shape. The normalization of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {{\pi } ^0} \right] _{{D} ^*_{{s} 0}(2317)^-} $ and also ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {\gamma } \right] _{{D} _{{s} 1}(2460)^-} $ decays is loosely constrained relative to that of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ component by means of the average of branching fraction measurements from the corresponding meson decays, their simulated integral in the chosen invariant-mass range, and a correction accounting for the additional degrees of freedom in the spin structure of baryon decays [6]. Further decays to excited ${{D} ^-_{s}} $ mesons are either kinematically forbidden or contribute at a significantly lower rate.

The shapes of partially reconstructed multibody decays, i.e. ${{\varLambda } ^0_{b}} \!\rightarrow \left[ {{\varLambda } ^+_{c}} \pi \pi \right] _{{\varLambda } _{c} ^{*+}}{{D} ^-_{s}} $ and partially reconstructed decays in $m({{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-})$ cannot be modelled analytically unless their corresponding three-body dynamics is known and modeled. Shapes of those decays are thus derived from simulation in terms of a nonparametric PDF using a kernel density estimation method (KDE) [66]. Fast simulation samples, either generated with AmpGen [49] or RapidSim [48], are used to model and cross-validate the shapes of ${{\varLambda } ^0_{b}} \!\rightarrow \left[ {{\varLambda } ^+_{c}} \pi \pi \right] _{{\varLambda } _{c} ^{*+}}{{D} ^-_{s}} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ decays. As the shape of the partially reconstructed ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ decay depends on the three-body dynamics, a dedicated simulation sample including the most prominent ${{D} ^+_{s}} $ resonances, ${D} _{{s} 1}(2536)^-$ and ${D} ^*_{{s} 1}(2700)^-$, as well as a small contribution from ${\varXi } _{c} (2790)^0$ is used. The same sample is employed for the efficiency correction described in Sect. 5. The composition of simulated resonances is adapted to what is observed in the data. An effective correction for unconsidered three-body dynamics or efficiency effects is obtained by multiplying the KDE template for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ contribution with a first order polynomial function with a freely varying coefficient. That coefficient is anticorrelated ($-0.38$) to the leading coefficient of the polynomial describing the combinatorial background, and shared between the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{\pi } ^0} \right] _{{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}}}{{K} ^-} $ and the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {\gamma } \right] _{{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}}}{{K} ^-} $ components. The normalization of those components is a free parameter in the fit, found to be consistent with the world-average value of $\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{\pi } ^0} \right) /\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {\gamma } \right) $ [38].

The baseline fits for the signal and normalization channel are shown in Fig. 3. The measured signal yields are

$$\begin{aligned}&N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} } = 4010\pm 70,\quad N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} } = 10\,560^{+310}_{-290}, \\&N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} } = 35\,450 \pm 200,\quad N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} } = 46\,400 \pm 500, \end{aligned}$$

where the uncertainties are statistical, and the asymmetric uncertainties of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ signal yield are driven by an anticorrelation with the ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ component.

5 Efficiency correction

Efficiency ratios are calculated as the product of four factorizing terms:

Efficiencies of selections before the GEANT4 step of the simulation, referred to as generator level efficiencies hereafter.
Trigger, reconstruction, and selection efficiencies are taken from simulation, up to but excluding the final selection step.
Selection efficiencies of the final step are computed from simulation that has been weighted to match data.
${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ BDT efficiencies are evaluated using ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\pi } ^-} $ data.

Generator level efficiency ratios comprise the angular coverage of LHCb, as well as loose kinematic and geometric selections of the generated candidates. Efficiencies are calculated only from those events for which a new underlying pp interaction has been simulated.

The efficiency correction of the final selection step handles variables that are more difficult to model, like those that combine PID information [67]. These variables depend on detector multiplicity, production and decay kinematics, hereafter referred to as calibration variables.

Simulated events are weighted to match signal distributions in the phase-space of the calibration variables. The set of 5 or 7 variables chosen for calibration are the track multiplicity, transverse momentum and pseudorapidity of the ${{\varLambda } ^0_{b}} $ candidate for the production kinematics and the two square Dalitz variables of ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $, as well as those of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ for ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ candidates. It is not necessary to weight the simulated kinematics of the ${{D} ^+_{s}} \!\rightarrow {{K} ^+} {{K} ^-} {{\pi } ^+} $ decay in ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} ^{(*)-}_{s} $, due to the good agreement of the EvtGen model with the data [68]. The convention used for the square Dalitz variables follows that of Ref. [69]:

$$\begin{aligned} m'\equiv \frac{1}{\pi } \arccos \left( 2\frac{m_{12}-m_{12}^\textrm{min}}{m^\textrm{max}_{12}-m_{12}^\textrm{min}}-1\right) \quad \textrm{and} \quad \theta '\equiv \frac{1}{\pi } \theta _{12} \, \end{aligned}$$

where $m^\textrm{max}_{12}=m_P-m_{c_3}$ and $m_{12}^\textrm{min}=m_{c_1}+m_{c_2}$ are the kinematic limits of $m_{12}$ in the $P\!\rightarrow c_1 c_2 c_3 $ decay, while $\theta _{12}$ is the helicity angle between $c_1$ and $c_3$ in the rest frame of $c_1 c_2$. In the squared Dalitz plot of the ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $, P corresponds to ${{\varLambda } ^+_{c}} $, $c_1$ to the proton, $c_2$ to the kaon and $c_3$ to the pion; while P corresponds to ${{\varLambda } ^0_{b}} $, $c_1$ to ${{\varLambda } ^+_{c}} $, $c_2$ to ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ and $c_3$ to the companion kaon in the square Dalitz plot for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $.

In the weighting, the 7 (5) dimensional calibration variable space is factorized into one 1D and three (two) 2D spaces for ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $(${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {D} ^{(*)-}_{s} $). This speeds up the weighting algorithm and allows for finer bins/partitions. For weighting, the Meerkat library [70] is used to create kernel density profiles of calibration variable distributions from reconstructed simulation and signal data. This method is validated against an adaptive binning algorithm, that split the calibration spaces in equally populated bins. Several configurations of the adaptive binning returned negligible differences with respect to the nominal kernel density method. The assumption of factorization is verified with control plots that show that weighting in a certain subspace does not affect the other calibration variables. It is further validated by testing the weighting procedure with a method that does not factorize the space of calibration variables, but partitions the full phase space using gradient boosted decision trees [71]. Without weighting, individual efficiencies are found to be larger across all studied decays, up to 2.5%. In the ratio, the difference with respect to the weighted evaluation is between 0.6 and 1.8%.

The efficiency ratio for the ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ BDT response is obtained in a data-driven manner using the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\pi } ^-} $ calibration channel. Efficiencies are obtained by fitting the calibration samples, weighted to match ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ or ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ data, simultaneously in “pass” and “fail” categories. For validation tests, the requirements on the BDT response are equalized between signal and normalization channels. The systematic uncertainty associated with the ${{\varLambda } ^+_{c}} \!\rightarrow {p} {{K} ^-} {{\pi } ^+} $ BDT efficiency correction is negligible due to the large size of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\pi } ^-} $ samples, but also due to the similarity of selection requirements between this channel and the signal.

The overall efficiency ratios are found to be

$$\begin{aligned} \epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} }/\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 0.809\pm 0.006, \\ \epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} }/\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 0.689\pm 0.005, \\ \epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} }/\epsilon ^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 0.785\pm 0.005, \end{aligned}$$

where the uncertainties are statistical.

6 Systematic uncertainties

6.1 Invariant-mass fits

As described in Sect. 4, the baseline model is the one that minimizes the likelihood corrected for the number of degrees of freedom in the fit model. Nine alternative models, returning comparable corrected likelihood values, are used in a discrete profiling method [63] to evaluate systematic uncertainties of the fit model. Each of these alternative models concerns a single aspect of the baseline model. For example an exponential instead of a linear function is used as the combinatorial background description. For each alternative, all other variations are tested in conjunction with the given variation, and the model that minimizes the corrected likelihood is taken into consideration for the discrete profiling. Changes to the baseline model are described below:

For signal, the baseline Gaussian-convolved Hypatia function is replaced with a double-sided Crystal Ball function [72] with common mean. The double-sided Crystal Ball model improves the corrected likelihood in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ channel, but not in the normalization channel. For consistency, the Hypatia model is quoted as the baseline result, while the uncertainty calculation uses the alternative model as best fit to calculate the likelihood envelope of the discrete profiling method.
Combinatorial background models are either Chebychev polynomials or exponential functions. It is found that either a first or second order polynomial function describes the combinatorial background best, even though higher-order functions can improve the uncorrected likelihood.
In the baseline fit, the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ decays are modeled with a KDE approach, in which the ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} $ decay modes are separated. An alternative model is a KDE template of the combined ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ decay where the relative normalization of individual ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} $ decay modes is fixed at the level of event generation.
The ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ decays are modeled with KDE templates from AmpGen simulation, numerically convolved with a Gaussian function. One variation multiplies the shape with a first-order polynomial, to effectively correct for unconsidered three-body dynamics or efficiency effects, another one adds contributions from ${\varSigma } _{c} (2520)^+$ decays. When allowing the normalization of this component to float free in the fit, it is compatible with zero yield. A model is employed, that loosely constrains the ratio of yields of the components modeling the decays through ${\varSigma } _{c} (2520)^+$ and ${\varSigma } _{c} (2455)^+$ states. The value of the constraint is based on the approximate ratios observed in ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{K} ^-} {{K} ^+} {{\pi } ^-} $ [73] and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\pi } ^-} {{\pi } ^+} {{\pi } ^-} $ [74] decays.
The normalization fraction of box-like shapes with respect to parabolic shapes are separated for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {{\pi } ^0} \right] _{{{D} ^{*-}_{s}}} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} \left[ {{D} ^-_{s}} {\gamma } \right] _{{{D} ^{*-}_{s}}} $ components. In addition, the slope parameter that models the efficiency gradient and the ${{D} ^{*-}_{s}} $ branching fractions is fixed, instead of constrained, to values obtained from simulation.
The ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \pi \pi $ decays are effectively modeled by a KDE template derived from an AmpGen simulation sample where the decay occurs through the ${\varLambda } _{c} (2625)^+$ resonance. An alternative model is the decay through the ${\varLambda } _{c} (2595)^+$ state.

To compute the envelope for the discrete profiling method analytically, likelihoods are approximated with bifurcated parabolas, which account for asymmetric uncertainties. From this method, the yield ratios obtained, including their statistical and systematic uncertainties due to the fit model, are

$$\begin{aligned} \begin{aligned} N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} }/N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 0.1132 {}_{-0.0020}^{+0.0021} {}_{-0.0007}^{+0.0006}, \\ N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} }/N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 0.298 {}_{-0.008}^{+0.009} {}_{-0.009}^{+0.008}, \\ N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} }/N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} }&= 1.309 \pm 0.017 {}_{-0.043}^{+0.047}\ . \end{aligned} \end{aligned}$$

The dominating systematic effect comes from the signal shape variation in the determination of the exclusive ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ yields. For the measurement of $N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} }$, the dominant source of uncertainty is the multiplication of the ${{\varLambda } ^0_{b}} \!\rightarrow {\varSigma } _{c} ^+{{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ component by a first-order polynomial function. Changing the combinatorial background description, and separating the normalization fraction of the contributions in the description of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays, are the largest contributions to the uncertainty on $N^{{{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} }$.

6.2 Parameters of the simulation weighting

Efficiency ratios are calculated using five different settings of the initial phase-space binning to generate the adaptive KDE profiles. The results are found to be very stable against changing this parameter from the default 80 bins to 20, 40, 160 and 320 bins. Their standard deviation with respect to the baseline result is taken as the systematic uncertainty.

6.3 Multiple candidates

Multiple candidates are randomly removed from the sample, as they are mainly composed of candidates where a signal track has been swapped with a combinatorial track that happens to have similar kinematics. In the case of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $, another source of multiple candidates exists, swapping the companion ${{K} ^-} $ with that from the ${{\varLambda } ^+_{c}} $ decay. Removing this background entirely is inefficient, but since the fraction of multiple candidates in the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ channel is larger (2.4% compared to 1.1% in ${\varLambda } ^+_{c} $ ${D} ^-_{s} $), further methods to remove multiple candidates are studied: namely using the minimal $\chi ^2/$ndf of a kinematic fit of the decay chain [75], or the maximum sum of PID variables to select the best out of the multiple candidates. The resulting maximum deviation from the baseline result is small, but assigned as systematic uncertainty.

6.4 Simulation and control sample sizes

Statistical uncertainties of the generator level efficiency ratios, and simulation and calibration sample sizes are propagated to the branching ratio measurement, as summarized in Table 2. For generator level efficiencies, only those events for which a new underlying pp interaction has been simulated can be taken into account for the uncertainty calculation. As the underlying pp interaction is reused 100 times [57], with an independently generated signal decay for each simulated event, the uncertainty on the generator level efficiency ratio is treated independently of the statistical uncertainty of the final simulation sample size.

6.5 Summary

Table 2 summarizes the systematic uncertainties for the three measured ratios of branching fractions.

Table 2 Systematic uncertainties relative to the branching fraction ratio measurements. The relative statistical uncertainty is shown as a reference. Values are given in percent

Full size table

The choice of the fit model is found to dominate the uncertainty for partially reconstructed decays, while the systematic uncertainties for ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ are small compared to their corresponding statistical uncertainty.

7 Conclusion

The ratio of branching fractions for the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $, ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays, relative to that of the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} $ decay, are measured in ${p} {p} $ collisions at $\sqrt{s} =13\text {Te\hspace{-1.00006pt}V} $ corresponding to an integrated luminosity of 5.4$\text {fb} ^{-1}$ collected with the LHCb detector. The results are found to be

$$\begin{aligned} \begin{aligned}&\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }\cdot \frac{\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} \right) }{\mathcal {B}\left( {{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} \right) }\\&= 0.1400 {}_{-0.0025}^{+0.0026} {}_{-0.0013}^{+0.0012}, \\&\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }\cdot \frac{\mathcal {B}\left( {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} \right) }{\mathcal {B}\left( {{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} \right) }\\&= 0.432 {}_{-0.012}^{+0.013} \pm 0.013, \end{aligned} \end{aligned}$$

where the first uncertainties are statistical and the second systematic. In the ${{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} $ channel, the ratio of branching fractions of ${{\varLambda } ^0_{b}} $ decays proceeding through the excited compared to the ground state ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} $ is measured to be

$$\begin{aligned} \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} \right) }=3.09^{+0.11}_{-0.10}{}^{+0.09}_{-0.10}, \end{aligned}$$

where correlations between uncertainties are taken into account, but are found to be small. Including the known values of the ${D} $ meson branching fractions from Ref. [38], the ratios of branching fractions are

$$\begin{aligned} \begin{aligned} \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 0.1908 {}_{-0.0034}^{+0.0036} {}_{-0.0018}^{+0.0016} \pm 0.0038, \\ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 0.589 {}_{-0.017}^{+0.018} {}_{-0.018}^{+0.017} \pm 0.012, \\ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }&= 1.668 \pm 0.022 {}_{-0.055}^{+0.061}, \end{aligned} \end{aligned}$$

where the third uncertainties are due to the uncertainty of the branching fractions of ${{D} ^-_{s}} \!\rightarrow {{K} ^-} {{K} ^+} {{\pi } ^-} $ and ${{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} \!\rightarrow {{K} ^+} {{\pi } ^-} $ decays.

The result obtained for $\frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^-_{s}} \right) }$ is compatible with several predictions [9,10,11, 13, 15,16,17].

To probe factorization approaches in the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays, the following values for the double ratios $\mathcal{D}\mathcal{R}^{(*)}$, defined in Eq. (1), are obtained

$$\begin{aligned} \mathcal{D}\mathcal{R}({{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}B}} {}^0})&=1.29\pm 0.20,&\mathcal{D}\mathcal{R}^{*}({{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}B}} {}^0})&=1.28\pm 0.19,\\ \mathcal{D}\mathcal{R}({{{B} ^-}})&=1.20\pm 0.30,&\mathcal{D}\mathcal{R}^{*}({{{B} ^-}})&=0.87\pm 0.12,\\ \mathcal{D}\mathcal{R}({{B} _{c} ^-})&=1.3\pm 0.5,&\mathcal{D}\mathcal{R}^{*}({{B} _{c} ^-})&=0.8\pm 0.4, \end{aligned}$$

assuming uncorrelated uncertainties, and taking known values for the mesonic branching fractions from Ref. [38]. Larger baryonic branching fractions are expected, because of an additional color-suppressed amplitude (see Fig. 1) in the ${{\varLambda } ^0_{b}} $ decay, which does not exist for mesons, however the measured ratios are still inconclusive.

The ratios of branching fractions that are relevant for pentaquark searches, see Eq. (2), are

$$\begin{aligned} \begin{aligned} \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^0} {{K} ^-} \right) }&=0.152^{+0.032}_{-0.028}, \\ \frac{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} {{K} ^-} \right) }{\mathcal {B}\left( {{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{*0}} {{K} ^-} \right) }&=0.049^{+0.011}_{-0.009}, \end{aligned} \end{aligned}$$

using results from Ref. [36], and assuming that uncertainties are uncorrelated. A future search for pentaquarks in the ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ decays will be able to determine the fit fractions $f_{{{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}}(P _{c} ^+)$, which can be used to test model predictions of the ratio of $P _{c} ^+$ branching fractions $\mathcal {B}(P _{c} ^+\!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0})/\mathcal {B}(P _{c} ^+\!\rightarrow {{J \hspace{-1.66656pt}/\hspace{-1.111pt}\psi }} {p} )$.

Data Availability Statement

Data cannot be made available for reasons disclosed in the data availability statement. [Authors’ comment: The LHCb experiment has agreed to the CERN open data policy that is summarised in https://opendata.cern.ch/docs/about. In particular, Level 1 data associated with this publication are made available on the CERN document server at http://cdsweb.cern.ch/record/2882052. These data contain material related to the paper that allows a reinterpretation of the results in the context of new theoretical models. Level 3 data are also available from the CERN open data portal, but due to the large amount of data, only the Run1 dataset has been made public up to now.]

Code Availability Statement

This manuscript has no associated code/software. [Author’s comment: Software/Code that is associated with this publication and that is publicly available is referenced within the publication content. Specific analysis software/code used to produce the results shown in the publication is preserved within the LHCb collaboration internally and can be provided on reasonable request, provided it doesn’t contain information that can be associated with unpublished results.]

Notes

The inclusion of charge conjugate processes and the use of natural units are implicit throughout this article.

References

N. Isgur, M.B. Wise, Weak decays of heavy mesons in the static quark approximation. Phys. Lett. B 232, 113 (1989). https://doi.org/10.1016/0370-2693(89)90566-2
Article ADS Google Scholar
N. Isgur, M.B. Wise, Weak transition form-factors between heavy mesons. Phys. Lett. B 237, 527 (1990). https://doi.org/10.1016/0370-2693(90)91219-2
Article ADS Google Scholar
E. Eichten, B.R. Hill, An effective field theory for the calculation of matrix elements involving heavy quarks. Phys. Lett. B 234, 511 (1990). https://doi.org/10.1016/0370-2693(90)92049-O
Article ADS Google Scholar
M. Neubert, Heavy quark symmetry. Phys. Rep. 245, 259 (1994). https://doi.org/10.1016/0370-1573(94)90091-4. arXiv:hep-ph/9306320
Article ADS Google Scholar
A. Datta, H.J. Lipkin, P.J. O’Donnell, Implications of isospin conservation in ${\Lambda }^0_{{b}}$ decays and lifetime. Phys. Lett. B 450, 250 (1999). https://doi.org/10.1016/S0370-2693(99)00139-2. arXiv:hep-ph/9809294
Article ADS Google Scholar
A. Datta, H.J. Lipkin, P.J. O’Donnell, Nonleptonic ${\Lambda }^0_{{b}}$ decays to ${D}^*_{{s} 0}(2317)$, ${D}_{{s} 1}(2460)$ and other final states in factorization. Phys. Rev. D 69, 094002 (2004). https://doi.org/10.1103/PhysRevD.69.094002. arXiv:hep-ph/0312160
Article ADS Google Scholar
T. Mannel, W. Roberts, Nonleptonic ${\Lambda }^0_{{b}}$ decays at colliders. Z. Phys. C 59, 179 (1993). https://doi.org/10.1007/BF01555853
Article ADS Google Scholar
H.-Y. Cheng, Nonleptonic weak decays of bottom baryons. Phys. Rev. D 56, 2799 (1997). https://doi.org/10.1103/PhysRevD.56.2799. [Erratum: Phys. Rev. D 99, 079901 (2019)]. arXiv:hep-ph/9612223
A.K. Giri, L. Maharana, R. Mohanta, Two-body nonleptonic ${\Lambda }^0_{{b}}$ decays with $1/M^Q$ corrections. Mod. Phys. Lett. A 13, 23 (1998). https://doi.org/10.1142/S021773239800005X
Article ADS Google Scholar
Fayyazuddin, Riazuddin, Two-body nonleptonic ${\Lambda }^0_{{b}}$ decays in quark model with factorization ansatz. Phys. Rev. D 58, 014016 (1998). https://doi.org/10.1103/PhysRevD.58.014016. arXiv:hep-ph/9802326
Article ADS Google Scholar
R. Mohanta et al., Hadronic weak decays of ${\Lambda }^0_{{b}}$ baryon in the covariant oscillator quark model. Prog. Theor. Phys. 101, 959 (1999). https://doi.org/10.1143/PTP.101.959. arXiv:hep-ph/9904324
Article ADS Google Scholar
J. Zhu, Z.-T. Wei, H.-W. Ke, Semileptonic and nonleptonic weak decays of ${\Lambda }^0_{{b}}$. Phys. Rev. D 99, 054020 (2019). https://doi.org/10.1103/PhysRevD.99.054020. arXiv:1803.01297
Article ADS Google Scholar
Z.-X. Zhao, Weak decays of heavy baryons in the light-front approach. Chin. Phys. C 42, 093101 (2018). https://doi.org/10.1088/1674-1137/42/9/093101. arXiv:1803.02292
Article ADS Google Scholar
W.-H. Liang, E. Oset, Pseudoscalar or vector meson production in non-leptonic decays of heavy hadrons. Eur. Phys. J. C 78, 528 (2018). https://doi.org/10.1140/epjc/s10052-018-5997-4. arXiv:1804.00938
Article ADS Google Scholar
T. Gutsche, M.A. Ivanov, J.G. Körner, V.E. Lyubovitskij, Nonleptonic two-body decays of single heavy baryons $\Lambda _Q$, $\Xi _Q$, and $\Omega _Q$$(Q=b, c)$ induced by $W$ emission in the covariant confined quark model. Phys. Rev. D 98, 074011 (2018). https://doi.org/10.1103/PhysRevD.98.074011. arXiv:1806.11549
Article ADS Google Scholar
H.-W. Ke, N. Hao, X.-Q. Li, Revisiting ${\Lambda }^0_{{b}}\rightarrow {\Lambda }^c_{{+}}$ and $\Sigma _{b}\rightarrow \Sigma _{c}$ weak decays in the light-front quark model. Eur. Phys. J. C 79, 540 (2019). https://doi.org/10.1140/epjc/s10052-019-7048-1. arXiv:1904.05705
Article ADS Google Scholar
C.-K. Chua, Color-allowed bottom baryon to $s$-wave and $p$-wave charmed baryon nonleptonic decays. Phys. Rev. D 100, 034025 (2019). https://doi.org/10.1103/PhysRevD.100.034025. arXiv:1905.00153
Article ADS Google Scholar
S. Rahmani, H. Hassanabadi, J. Kříž, Nonleptonic and semileptonic ${\Lambda }^0_{{b}} \rightarrow {\Lambda }^+_{{c}}$ transitions in a potential quark model. Eur. Phys. J. C 80, 636 (2020). https://doi.org/10.1140/epjc/s10052-020-8214-1
Article ADS Google Scholar
Y.-W. Pan, M.-Z. Liu, L.-S. Geng, Production rates of hidden-charm pentaquark molecules in $\Lambda _b$decays. arXiv:2309.12050
T.J. Burns, E.S. Swanson, Production of $P_c$ states in ${\Lambda }^0_{{b}}$ decays. Phys. Rev. D 106, 054029 (2022). https://doi.org/10.1103/PhysRevD.106.054029. arXiv:2207.00511
Article ADS Google Scholar
LHCb collaboration, R. Aaij et al., Observation of ${J}/\psi {p}$ resonances consistent with pentaquark states in ${{\Lambda }^0_{{b}}}\rightarrow {{J}/\psi {p}{K}^-}$ decays. Phys. Rev. Lett. 115, 072001 (2015). https://doi.org/10.1103/PhysRevLett.115.072001. arXiv:1507.03414
LHCb collaboration, R. Aaij et al., Model-independent evidence for ${J}/\psi {p}$ contributions to ${{\Lambda }^0_{{b}}}\rightarrow {{J}/\psi {p}{K}^-}$ decays. Phys. Rev. Lett. 117, 082002 (2016). https://doi.org/10.1103/PhysRevLett.117.082002. arXiv:1604.05708
LHCb collaboration, R. Aaij et al., Evidence for exotic hadron contributions to ${{\Lambda }^0_{{b}}}\rightarrow {{J}/\psi {p}\pi ^-}$ decays. Phys. Rev. Lett. 117, 082003 (2016). https://doi.org/10.1103/PhysRevLett.117.082003. arXiv:1606.06999
LHCb collaboration, R. Aaij et al., Observation of a narrow pentaquark state, $P_c(4312)^+$, and of two-peak structure of the $P_c(4450)^+$. Phys. Rev. Lett. 122, 222001 (2019). https://doi.org/10.1103/PhysRevLett.122.222001. arXiv:1904.03947
Z.-H. Guo, J.A. Oller, Anatomy of the newly observed hidden-charm pentaquark states: $P_c(4312)$, $P_c(4440)$ and $P_c(4457)$. Phys. Lett. B 793, 144 (2019). https://doi.org/10.1016/j.physletb.2019.04.053. arXiv:1904.00851
Article ADS Google Scholar
C.W. Xiao, J. Nieves, E. Oset, Heavy quark spin symmetric molecular states from $\overline{D}^{(*)}\Sigma _c^{(*)}$ and other coupled channels in the light of the recent LHCb pentaquarks. Phys. Rev. D 100, 014021 (2019). https://doi.org/10.1103/PhysRevD.100.014021. arXiv:1904.01296
Article ADS Google Scholar
X.-Z. Weng, X.-L. Chen, W.-Z. Deng, S.-L. Zhu, Hidden-charm pentaquarks and $P_c$ states. Phys. Rev. D 100, 016014 (2019). https://doi.org/10.1103/PhysRevD.100.016014. arXiv:1904.09891
Article ADS Google Scholar
M.B. Voloshin, Some decay properties of hidden-charm pentaquarks as baryon-meson molecules. Phys. Rev. D 100, 034020 (2019). https://doi.org/10.1103/PhysRevD.100.034020. arXiv:1907.01476
Article ADS Google Scholar
Y.-H. Lin, B.-S. Zou, Strong decays of the latest LHCb pentaquark candidates in hadronic molecule pictures. Phys. Rev. D 100, 056005 (2019). https://doi.org/10.1103/PhysRevD.100.056005. arXiv:1908.05309
Article ADS Google Scholar
A.N. Semenova, V.V. Anisovich, A.V. Sarantsev, New narrow LHCb pentaquarks as lowest antiquark-diquark-diquark systems. Eur. Phys. J. A 56, 142 (2020). https://doi.org/10.1140/epja/s10050-020-00151-7. arXiv:1911.11994
Article ADS Google Scholar
H.-X. Chen, Decay properties of $P_c$ states through the Fierz rearrangement. Eur. Phys. J. C 80, 945 (2020). https://doi.org/10.1140/epjc/s10052-020-08519-1. arXiv:2001.09563
Article ADS Google Scholar
Y. Dong, P. Shen, F. Huang, Z. Zhang, Selected strong decays of pentaquark State $P_c(4312)$ in a chiral constituent quark model. Eur. Phys. J. C 80, 341 (2020). https://doi.org/10.1140/epjc/s10052-020-7890-1. arXiv:2002.08051
Article ADS Google Scholar
Z.-G. Wang, H.-J. Wang, Q. Xin, The hadronic coupling constants of the lowest hidden-charm pentaquark state with the QCD sum rules in rigorous quark-hadron duality. Chin. Phys. C 45, 063104 (2021). https://doi.org/10.1088/1674-1137/abf13b. arXiv:2005.00535
Article ADS Google Scholar
C.W. Xiao, J.X. Lu, J.J. Wu, L.S. Geng, How to reveal the nature of three or more pentaquark states. Phys. Rev. D 102, 056018 (2020). https://doi.org/10.1103/PhysRevD.102.056018. arXiv:2007.12106
Article ADS Google Scholar
S.-Y. Li et al., Hidden-charm pentaquark states in a mass splitting model. Phys. Rev. D 108, 056015 (2023). https://doi.org/10.1103/PhysRevD.108.056015. arXiv:2307.00539
Article ADS Google Scholar
LHCb collaboration, R. Aaij et al., Study of the productions of ${\Lambda }^0_{{b}}$ and $\overline{{B}}^0$ hadrons in ${p}{p}$ collisions and first measurement of the ${{\Lambda }^0_{{b}}}\rightarrow {{J}/\psi {p}{K}^-}$ branching fraction. Chin. Phys. C 40, 011001 (2016). https://doi.org/10.1088/1674-1137/40/1/011001. arXiv:1509.00292
LHCb collaboration, R. Aaij et al., Study of beauty hadron decays into pairs of charm hadrons. Phys. Rev. Lett. 112, 202001 (2014). https://doi.org/10.1103/PhysRevLett.112.202001. arXiv:1403.3606
Particle Data Group, R.L. Workman et al., Review of particle physics. Prog. Theor. Exp. Phys. 2022, 083C01 (2022). https://doi.org/10.1093/ptep/ptac097. http://pdg.lbl.gov/
LHCb collaboration, A.A. Alves Jr. et al., The LHCb detector at the LHC. JINST 3, S08005 (2008). https://doi.org/10.1088/1748-0221/3/08/S08005
LHCb collaboration, R. Aaij et al., LHCb detector performance. Int. J. Mod. Phys. A 30, 1530022 (2015). https://doi.org/10.1142/S0217751X15300227. arXiv:1412.6352
R. Aaij et al., Performance of the LHCb vertex locator. JINST 9, P09007 (2014). https://doi.org/10.1088/1748-0221/9/09/P09007. arXiv:1405.7808
Article Google Scholar
R. Arink et al., Performance of the LHCb outer tracker. JINST 9, P01002 (2014). https://doi.org/10.1088/1748-0221/9/01/P01002. arXiv:1311.3893
Article Google Scholar
P. d’Argent et al., Improved performance of the LHCb outer tracker in LHC Run 2. JINST 12, P11016 (2017). https://doi.org/10.1088/1748-0221/12/11/P11016. arXiv:1708.00819
Article Google Scholar
M. Adinolfi et al., Performance of the LHCB RICH detector at the LHC. Eur. Phys. J. C 73, 2431 (2013). https://doi.org/10.1140/epjc/s10052-013-2431-9. arXiv:1211.6759
Article ADS Google Scholar
A.A. Alves Jr. et al., Performance of the LHCb muon system. JINST 8, P02022 (2013). https://doi.org/10.1088/1748-0221/8/02/P02022. arXiv:1211.1346
Article Google Scholar
R. Aaij et al., Performance of the LHCb trigger and full real-time reconstruction in Run 2 of the LHC. JINST 14, P04013 (2019). https://doi.org/10.1088/1748-0221/14/04/P04013. arXiv:1812.10790
Article Google Scholar
R. Aaij et al., A comprehensive real-time analysis model at the LHCb experiment. JINST 14, P04006 (2019). https://doi.org/10.1088/1748-0221/14/04/P04006. arXiv:1903.01360
Article Google Scholar
G.A. Cowan, D.C. Craik, M.D. Needham, RapidSim: an application for the fast simulation of heavy-quark hadron decays. Comput. Phys. Commun. 214, 239 (2017). https://doi.org/10.1016/j.cpc.2017.01.029. arXiv:1612.07489
Article ADS Google Scholar
T. Evans, AmpGen. https://github.com/GooFit/AmpGen(in preparation)
T. Sjöstrand, S. Mrenna, P. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852 (2008). https://doi.org/10.1016/j.cpc.2008.01.036. arXiv:0710.3820
I. Belyaev et al., Handling of the generation of primary events in Gauss, the LHCb simulation framework. J. Phys. Conf. Ser. 331, 032047 (2011). https://doi.org/10.1088/1742-6596/331/3/032047
Article Google Scholar
D.J. Lange, The EvtGen particle decay simulation package. Nucl. Instrum. Methods A 462, 152 (2001). https://doi.org/10.1016/S0168-9002(01)00089-4
Article ADS Google Scholar
P. Golonka, Z. Was, PHOTOS Monte Carlo: a precision tool for QED corrections in $Z$ and $W$ decays. Eur. Phys. J. C 45, 97 (2006). https://doi.org/10.1140/epjc/s2005-02396-4. arXiv:hep-ph/0506026
Article ADS Google Scholar
Geant4 collaboration, J. Allison et al., Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006). https://doi.org/10.1109/TNS.2006.869826
Geant4 collaboration, S. Agostinelli et al., Geant4: a simulation toolkit. Nucl. Instrum. Methods A 506, 250 (2003). https://doi.org/10.1016/S0168-9002(03)01368-8
M. Clemencic et al., The LHCB simulation application, Gauss: design, evolution and experience. J. Phys. Conf. Ser. 331, 032023 (2011). https://doi.org/10.1088/1742-6596/331/3/032023
Article Google Scholar
D. Müller, M. Clemencic, G. Corti, M. Gersabeck, ReDecay: a novel approach to speed up the simulation at LHCb. Eur. Phys. J. C 78, 1009 (2018). https://doi.org/10.1140/epjc/s10052-018-6469-6. arXiv:1810.10362
Article ADS Google Scholar
V.V. Gligorov, M. Williams, Efficient, reliable and fast high-level triggering using a bonsai boosted decision tree. JINST 8, P02013 (2013). https://doi.org/10.1088/1748-0221/8/02/P02013. arXiv:1210.6861
Article ADS Google Scholar
T. Likhomanenko et al., LHCb topological trigger reoptimization. J. Phys. Conf. Ser. 664, 082025 (2015). https://doi.org/10.1088/1742-6596/664/8/082025
Article Google Scholar
H. Voss, A. Hoecker, J. Stelzer, F. Tegenfeldt, TMVA-toolkit for multivariate data analysis with ROOT. PoS ACAT, 040 (2007). https://doi.org/10.22323/1.050.0040
M. Pivk, F.R. Le Diberder, sPlot: a statistical tool to unfold data distributions. Nucl. Instrum. Methods A 555, 356 (2005). https://doi.org/10.1016/j.nima.2005.08.106. arXiv:physics/0402083
Article ADS Google Scholar
D. Martínez Santos, F. Dupertuis, Mass distributions marginalized over per-event errors. Nucl. Instrum. Methods A 764, 150 (2014). https://doi.org/10.1016/j.nima.2014.06.081. arXiv:1312.5000
P.D. Dauncey, M. Kenzie, N. Wardle, G.J. Davies, Handling uncertainties in background shapes: the discrete profiling method. JINST 10, P04015 (2015). https://doi.org/10.1088/1748-0221/10/04/P04015. arXiv:1408.6865
Article ADS Google Scholar
LHCb collaboration, R. Aaij et al., Observation of the doubly charmed baryon decay $\Xi _{cc}^{++} \rightarrow \Xi _{c}^{\prime +} \pi ^{+}$. JHEP 05, 038 (2022). https://doi.org/10.1007/JHEP05(2022)038. arXiv:2202.05648
LHCb collaboration, R. Aaij et al., Measurement of CP observables in ${B}^\pm \rightarrow {D^{(\ast )}{K}^\pm }$and${B}^\pm \rightarrow {D^{(\ast )}\pi ^\pm }$ decays. Phys. Lett. B 777, 16 (2018). https://doi.org/10.1016/j.physletb.2017.11.070. arXiv:1708.06370
K.S. Cranmer, Kernel estimation in high-energy physics. Comput. Phys. Commun. 136, 198 (2001). https://doi.org/10.1016/S0010-4655(00)00243-5. arXiv:hep-ex/0011057
Article ADS Google Scholar
R. Aaij et al., Selection and processing of calibration samples to measure the particle identification performance of the LHCb experiment in Run 2. Eur. Phys. J. Tech. Instrum. 6, 1 (2019). https://doi.org/10.1140/epjti/s40485-019-0050-z. arXiv:1803.00824
Article Google Scholar
BaBar collaboration, P. del Amo Sanchez et al., Dalitz plot analysis of ${{D}^+_{s}}\rightarrow {{K}^+{K}^-\pi ^+}$. Phys. Rev. D 83, 052001 (2011). https://doi.org/10.1103/PhysRevD.83.052001. arXiv:1011.4190
J. Back et al., Laura$^{++}$: a Dalitz plot fitter. Comput. Phys. Commun. 231, 198 (2018). https://doi.org/10.1016/j.cpc.2018.04.017. arXiv:1711.09854
Article ADS Google Scholar
A. Poluektov, Kernel density estimation of a multidimensional efficiency profile. JINST 10, P02011 (2015). https://doi.org/10.1088/1748-0221/10/02/P02011. arXiv:1411.5528
Article ADS Google Scholar
A. Rogozhnikov, Reweighting with boosted decision trees. J. Phys. Conf. Ser. 762, 012036 (2016). https://doi.org/10.1088/1742-6596/762/1/012036. arXiv:1608.05806. https://github.com/arogozhnikov/hep_ml
T. Skwarnicki, A study of the radiative cascade transitions between the Upsilon-prime and Upsilon resonances. PhD thesis, Institute of Nuclear Physics, Krakow. http://inspirehep.net/record/230779/DESY-F31-86-02 (1986)
LHCb collaboration, R. Aaij et al.,textitObservation of the ${\Lambda }^0_{{b}} \rightarrow \Lambda ^+_{c} {K}^+ {K}^- \pi ^-$ decay. Phys. Lett. B 815, 136172 (2021). https://doi.org/10.1016/j.physletb.2021.136172. arXiv:2011.13738
LHCb collaboration, R. Aaij et al., Measurements of the branching fractions for ${{B}_{({s})}^0}\rightarrow {D_{(s)}\pi \pi \pi }$ and ${{\Lambda }^0_{{b}}}\rightarrow {\Lambda ^+_{c}\pi \pi \pi }$. Phys. Rev. D 84, 092001 (2011). https://doi.org/10.1103/PhysRevD.84.092001. arXiv:1109.6831. [Erratum: ibid. 85, 039904 (2012). https://doi.org/10.1103/PhysRevD.85.039904]
W.D. Hulsbergen, Decay chain fitting with a Kalman filter. Nucl. Instrum. Methods A 552, 566 (2005). https://doi.org/10.1016/j.nima.2005.06.078. arXiv:physics/0503191
Article ADS Google Scholar

Download references

Acknowledgements

We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes. We acknowledge support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); MOST and NSFC (China); CNRS/IN2P3 (France); BMBF, DFG and MPG (Germany); INFN (Italy); NWO (Netherlands); MNiSW and NCN (Poland); MCID/IFA (Romania); MICINN (Spain); SNSF and SER (Switzerland); NASU (Ukraine); STFC (United Kingdom); DOE NP and NSF (USA). We acknowledge the computing resources that are provided by CERN, IN2P3 (France), KIT and DESY (Germany), INFN (Italy), SURF (Netherlands), PIC (Spain), GridPP (United Kingdom), CSCS (Switzerland), IFIN-HH (Romania), CBPF (Brazil), and Polish WLCG (Poland). We are indebted to the communities behind the multiple open-source software packages on which we depend. Individual groups or members have received support from ARC and ARDC (Australia); Key Research Program of Frontier Sciences of CAS, CAS PIFI, CAS CCEPP, Fundamental Research Funds for the Central Universities, and Sci. & Tech. Program of Guangzhou (China); Minciencias (Colombia); EPLANET, Marie Skłodowska-Curie Actions, ERC and NextGenerationEU (European Union); A*MIDEX, ANR, IPhU and Labex P2IO, and Région Auvergne-Rhône-Alpes (France); AvH Foundation (Germany); ICSC (Italy); GVA, XuntaGal, GENCAT, Inditex, InTalent and Prog. Atracción Talento, CM (Spain); SRC (Sweden); the Leverhulme Trust, the Royal Society and UKRI (United Kingdom).

Author information

A. Gomes, M. Stahl.

Authors and Affiliations

School of Physics and Astronomy, Monash University, Melbourne, Australia
U. Egede, Y. Fujii, T. Hadavizadeh, R. D. L. Henderson, J. J. Lane, M. Monk, R. Song, E. J. Walton & J. A. Ward
Centro Brasileiro de Pesquisas Físicas (CBPF), Rio de Janeiro, Brazil
J. Baptista de Souza Leite, I. B. Bediaga, M. Cruz Torres, U. De Freitas Carneiro Da Graca, J. M. De Miranda, A. C. dos Reis, L. N. Falcao, A. Gomes, A. Massafferri, L. Santoro & D. Torres Machado
Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
S. Amato, L. De Paula, F. Ferreira Rodrigues, M. Gandelman, A. Hicheur, J. H. Lopes, L. Meyer Garcia, I. Nasteva, J. M. Otalora Goicochea, E. Polycarpo, M. S. Rangel & B. Souza De Paula
Center for High Energy Physics, Tsinghua University, Beijing, China
C. Dong, G. Gong, X. Hu, Y. Kang, A. Li, Z. Lian, G. M. Ma, H. Mu, N. Qin, S. Qu, Y. Song, Y. Tan, D. Y. Tou, J. Wang, Z. Wang, L. Xu, L. Xu, D. Yang, M. Zeng, L. Zhang, Y. Z. Zhang, X. Z. Zheng & X. Zhu
Institute Of High Energy Physics (IHEP), Beijing, China
B. Batsukh, S. Chen, M. Feng, X. Jiang, T. Li, Y. Li, S. Liu, D. Miao, S. Sheng, M. Tobin, J. Wang, Z. Xiang, Z. Xu, X. Yuan & Q. Zou
School of Physics State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
L. An, X. Dai, Y. Gao, Y. Guz, W. Hu, Y. J. Jiang, Y. Luo, Z. M. Mu, M. Saur, Y. Shang, Z. Shen, Y. S. Song, X. Tong, G. Wan, J. Wang, Y. Wei, Y. Wu, X. Yang, Z. Yang, C. Y. Yu, C. Zhang, S. Zhang, Y. Zhang & T. Zhou
University of Chinese Academy of Sciences, Beijing, China
D. Ao, A. F. Campoverde Quezada, Z. Chen, Y. Fan, M. Feng, J. Fu, H. Gao, L. Hao, J. He, W. Huang, X. Jiang, Y. Jiang, C. Lin, H. Liu, Q. Liu, S. Liu, X.-R. Lyu, R. Ma, D. Miao, H. Miao, D. Popov, W. Qian, Z. Ren, S. Sheng, B. Shi, Y. Su, N. W. Wang, Z. Wang, J. Xu, Z. Xu, S. Yang, J. Zhang, Y. Zheng, Y. Zhou, L. Z. Zhu, Z. Zhu & Q. Zou
Institute of Particle Physics, Central China Normal University, Wuhan, Hubei, China
J. Deng, Y. Gao, Y. Gao, K. G. Garg, Q. Han, R. Hou, K. Li, S. Li, Y. Li, G. Wang, Y. Wang, J. Wu, Y. Xie, H. Yin, D. Zhang, X. Zhou & X. Zhu
Consejo Nacional de Rectores (CONARE), San Jose, Costa Rica
S. Arguedas Cuendis, R. Caravaca-Mora, J. Castro Godinez & F. Mũnoz-Rojas
CNRS, IN2P3-LAPP, Université Savoie Mont Blanc, Annecy, France
I. Bachiller Perea, F. C. R. Bishop, M. Chefdeville, D. Decamp, A. G. Downes, Y. Hou, J. F. Marchand, C. Normand, B. Pietrzyk, S. T’Jampens & G. Vouters
CNRS/IN2P3, LPC, Université Clermont Auvergne, Clermont-Ferrand, France
Z. Ajaltouni, E. Cogneras, J. Daniel, O. Deschamps, R. Lefèvre, T. Miralles, S. Monteil, P. Perret, H. Sazak, V. Tisserand & Z. Xu
CNRS/IN2P3, CPPM, Aix Marseille Univ, Marseille, France
E. Aslanides, G. Benane, J. Cerasoli, C. Chen, J. Cogan, V. Dedu, B. K. Kutsenko, R. Le Gac, O. Leroy, G. Mancinelli, A. G. Morris, A. Poluektov & D. vom Bruch
CNRS/IN2P3, IJCLab, Université Paris-Saclay, Orsay, France
Y. Amhis, S. Barsuk, B. Fang, F. C. Glaser, M. Guittiere, M. Hartmann, G. Khreich, F. Machefert, C. Mancuso, J. Nicolini, G. Pietrzyk, P. Robbe, M. H. Schune, Y. Shimizu, F. C. Volle, Z. Wang, G. Wormser & V. Yeroshenko
Laboratoire Leprince-Ringuet, CNRS/IN2P3, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau, France
B. Audurier, V. Balagura, O. Boente Garcia, F. Fleuret, C. Gu, K. R. Mattioli, E. Maurice, G. R. Ricart & R. Sadek
LPNHE, CNRS/IN2P3, Sorbonne Université, Paris Diderot Sorbonne Paris Cité, Paris, France
R. Amalric, E. Ben-Haim, P. Billoir, M. Charles, A. Correia, L. Del Buono, T. Fulghesu, F. I. Giasemis, V. V. Gligorov, F. Polci, A. Scarabotto & P. Vincent
I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
J. M. Basels, S. Escher, J. Heuel, H. Jage, T. Kirn, S. Kretzschmar, M. Materok, R. D. Moise, T. Oeser, S. Schael, S. Schmitt, G. Schwering & V. Zhukov
Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
J. Albrecht, A. Battig, M. Becker, M. S. Bieker, J. E. Blank, J. A. Boelhauve, N. Breer, L. Calefice, E. Dall’Occo, F. De Vellis, H.-P. Dembinski, J. Ellbracht, Q. Fuehring, L. L. Gerken, J. A. Gooding, S. E. Hollitt, V. Jevtic, L. Kolk, J. Langer, S. Maccolini, G. Meier, B. Mitreska, D. S. Mitzel, A. Mödden, J. Nicolini, M. Olocco, N. Schulte, A. Seuthe, J. G. Speer, H. Stevens, L. Toscano & D. Wiedner
Max-Planck-Institut für Kernphysik (MPIK), Heidelberg, Germany
M. Schmelling & M. Zavertyaev
Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
S. Bachmann, L. Carus, R. Caspary, C. Cocha Toapaxi, M. De Cian, G. Frau, F. C. Glaser, P. A. Günther, X. Han, S. Hansmann-Menzemer, P. Herrero Gascon, J. Hu, J. Kubat, C. Langenbruch, B. Leverington, J. Marks, M. P. Morgenthaler, P. R. Pais, S. R. Roy, M. Ruiz Diaz, R. Skuza, G. Tuci, L. H. Uecker, D. J. Unverzagt, U. Uwer, C. Wang, L. Witola, Y. Zhao & A. Zhelezov
School of Physics, University College Dublin, Dublin, Ireland
A. M. Donohoe, K. Lynch, L. Mcconnell & R. McNulty
INFN Sezione di Bari, Bari, Italy
L. Congedo, P. d’Argent, M. De Serio, F. Debernardis, R. A. Fini, G. Galati, A. Palano, M. Pappagallo, A. Pastore & S. Simone
INFN Sezione di Bologna, Bologna, Italy
A. Carbone, F. Ferrari, M. Fontana, D. Galli, D. Manuzzi, U. Marconi, C. Patrignani, S. Perazzini, E. Spedicato, V. Vagnoni, G. Valenti & A. Villa
INFN Sezione di Ferrara, Ferrara, Italy
M. Andreotti, M. Argenton, W. Baldini, N. V. Biesuz, R. Bolzonella, C. Bozzi, R. Calabrese, L. Capriotti, G. Cavallero, V. Cavallini, M. Fiorini, E. Franzoso, C. Giugliano, M. Guarise, E. Luppi, S. Okamura, L. L. Pappalardo, B. Passalacqua, G. Romolini, A. Saputi, L. Tomassetti & S. Vecchi
INFN Sezione di Firenze, Firenze, Italy
L. Anderlini, M. Barbetti, C. Lucarelli, G. Passaleva & M. Veltri
INFN Laboratori Nazionali di Frascati, Frascati, Italy
P. Albicocco, G. Bencivenni, S. Cali, P. Campana, P. Ciambrone, E. De Lucia, P. De Simone, P. Di Nezza, M. Giovannetti, G. Morello, M. Palutan, M. Pepe Altarelli, M. Poli Lener, M. Rotondo, M. Santimaria & B. Sciascia
INFN Sezione di Genova, Genoa, Italy
I. Belov, R. Cardinale, F. Fontanelli, A. Petrolini, A. Sergi & Y. Yang
INFN Sezione di Milano, Milan, Italy
S. Cesare, L. Frontini, P. Gandini, C. Mancuso, D. Marangotto, A. Merli, N. Neri, E. Spadaro Norella, G. Tonani & M. Wang
INFN Sezione di Milano-Bicocca, Milan, Italy
A. Anelli, M. Borsato, M. Calvi, S. Capelli, P. Carniti, D. Fazzini, C. Gotti, M. Martinelli, A. Minotti, M. Pizzichemi, M. Salomoni & E. B. Shields
INFN Sezione di Cagliari, Monserrato, Italy
D. Brundu, S. Cadeddu, A. Cardini, A. Contu, C. De Angelis, F. Dettori, F. Dordei, F. Fabiano, M. Garau, A. Lai, A. Lampis, R. Litvinov, A. Loi, G. Manca, C. Normand, R. Oldeman, B. Saitta & J. Sun
Università degli Studi di Padova, Università e INFN, Padova, Padua, Italy
A. Bertolin, F. Borgato, L. Buonincontri, L. Giambastiani, D. Lucchesi, A. Lupato, L. Sestini, G. Simi & D. Zuliani
INFN Sezione di Perugia, Perugia, Italy
V. Duk, L. Fantini, G. Martelli & M. Piccini
INFN Sezione di Pisa, Pisa, Italy
G. Bassi, F. Bedeschi, S. Kholodenko, N. Kleijne, F. Lazzari, M. J. Morello, D. Passaro, L. Pica, G. Punzi, M. Rama, R. Ribatti, D. Riccardi, F. Terzuoli, J. Walsh & A. Xu
INFN Sezione di Roma La Sapienza, Rome, Italy
G. Martellotti, D. Pinci, R. Santacesaria, A. Sarti & C. Satriano
INFN Sezione di Roma Tor Vergata, Rome, Italy
F. Archilli, E. Santovetti & A. Satta
Nikhef National Institute for Subatomic Physics, Amsterdam, Netherlands
R. Aaij, K. Akiba, A. Biolchini, J. de Boer, S. Ferreres Sole, E. Gabriel, M. D. Galati, R. E. Geertsema, L. M. Greeven, K. Heijhoff, W. Hulsbergen, E. Jans, T. Ketel, P. Koppenburg, I. Kostiuk, V. Lukashenko, D. Magdalinski, M. Merk, A. Pellegrino, C. Sanchez Gras, A. Snoch, N. Tuning & M. van Veghel
Nikhef National Institute for Subatomic Physics and VU University Amsterdam, Amsterdam, Netherlands
S. Klaver, G. Raven, M. Senghi Soares & A. Usachov
Faculty of Physics and Applied Computer Science, AGH-University of Science and Technology, Kraków, Poland
M. Firlej, T. Fiutowski, M. Idzik, P. Kopciewicz, M. W. Majewski, J. Moron, A. Oblakowska-Mucha, B. Rachwal, J. Ryzka, K. Swientek, T. Szumlak & A. Ukleja
Henryk Niewodniczanski Institute of Nuclear Physics Polish Academy of Sciences, Kraków, Poland
J. Bhom, J. T. Borsuk, J. Brodzicka, A. Chernov, M. Chrzaszcz, M. W. Dudek, A. Dziurda, M. A. Giza, M. Goncerz, I. Juszczak, W. Kucewicz, M. Kucharczyk, T. Lesiak, J. J. Malczewski, B. Malecki, K. Prasanth, M. Witek & M. Zdybal
National Center for Nuclear Research (NCBJ), Warsaw, Poland
H. K. Giemza, S. Joshi, K. Klimaszewski, M. R. Kmiec, W. Krzemien, D. Melnychuk, A. Szabelski & W. Wislicki
Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest-Magurele, Romania
L. Cojocariu, A. Ene, A. T. Grecu, F. Maciuc & V. Placinta
Affiliated with an Institute Covered by a Cooperation Agreement with CERN, Geneva, Switzerland
A. Andreianov, A. Artamonov, F. Baryshnikov, K. Belous, I. Belyaev, A. Berezhnoy, V. Bocharnikov, A. Boldyrev, N. Bondar, A. Butkevich, A. Chubykin, V. Chulikov, S. Dadabaev, A. Danilina, I. Diachkov, S. Didenko, A. Dolmatov, A. Dzyuba, A. Egorychev, V. Egorychev, S. Filippov, D. Golubkov, A. Golutvin, I. V. Gorelov, S. Gromov, V. Guliaeva, A.-K. Guseinov, E. Gushchin, Y. Guz, M. Hushchyn, D. Ilin, A. Inglessi, A. Iniukhin, A. Ishteev, K. Ivshin, D. Karpenkov, M. Karpov, A. Kharisova, A. Konoplyannikov, M. Korolev, A. Kozachuk, P. Kravchenko, L. Kravchuk, P. Krokovny, V. Kudryavtsev, E. Kulikova, O. Lantwin, A. Leflat, S. Legotin, S. Luchuk, A. Maevskiy, D. Maisuzenko, A. Malinin, T. Maltsev, V. Matiunin, S. Mokhnenko, P. Neustroev, N. Nikitin, V. Obraztsov, T. Ovsiannikova, G. Panshin, D. Pereima, N. Polukhina, S. Poslavskii, F. Ratnikov, V. Romanovskiy, A. Ryzhikov, N. Sagidova, D. Saranin, D. Savrina, A. Semennikov, M. Shapkin, I. Shchemerov, L. Shekhtman, V. Shevchenko, E. Shmanin, R. Shorkin, A. Solomin, A. Solovev, I. Solovyev, E. Spiridenkov, O. Stenyakin, D. Strekalina, E. Ursov, A. Ustyuzhanin, V. Vorobyev, N. Voropaev, A. Zharkova & V. Zhukov
DS4DS, La Salle, Universitat Ramon Llull, Barcelona, Spain
S. Bernet Andres, M. Calvo Gomez, E. Golobardes, C. Trippl, N. Valls Canudas & X. Vilasis-Cardona
ICCUB, Universitat de Barcelona, Barcelona, Spain
A. Alfonso Albero, A. Comerma-Montells, P. Garcia Moreno, L. Garrido, A. Gioventù, P. Gironella Gironell, S. Gomez Fernandez, E. Graugés, A. Lobo Salvia, A. Lopez Huertas, R. Manera Escalero, C. Marin Benito, J. Mauricio & R. Vazquez Gomez
Instituto Galego de Física de Altas Enerxías (IGFAE), Universidade de Santiago de Compostela, Santiago de Compostela, Spain
B. Adeva, P. Baladron Rodriguez, S. Belin, A. Brea Rodriguez, A. Brossa Gonzalo, J. Cambon Bouzas, L. Carcedo Salgado, V. Chobanova, X. Cid Vidal, I. Corredoira, J. Dalseno, C. Eirea Orro, M. Fernandez Gomez, A. Gallas Torreira, B. Garcia Plana, C. Landesa Gomez, J. Lomba Castro, S. L.ópez Soliño, D. Martinez Santos, A. Morcillo Gomez, J. Novoa Fernandez, A. Pereiro Castro, M. Plo Casasus, C. Prouve, E. Rodriguez Fernandez, E. Rodriguez Rodriguez, M. Romero Lamas, A. Romero Vidal, R. A. Ruiz Fernandez, J. J. Saborido Silva, C. Santamarina Rios, S. Sellam, C. B. Van Hulse, P. Vazquez Regueiro & C. V.ázquez Sierra
Instituto de Fisica Corpuscular, Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
S. J. Jaimes Elles, B. K. Jashal, F. Martinez Vidal, A. Oyanguren, M. Rebollo De Miguel, I. Sanderswood & J. Zhuo
European Organization for Nuclear Research (CERN), Geneva, Switzerland
C. Agapopoulou, F. Alessio, Y. Amhis, F. Borgato, A. Boyer, C. Burr, J. Buytaert, W. Byczynski, M. Cattaneo, Ph. Charpentier, G. Ciezarek, P. Cifra, M. Clemencic, J. Closier, V. Coco, P. Collins, T. Colombo, G. Corti, B. Couturier, C. D’Ambrosio, M. De Cian, L. Dufour, P. Durante, S. Easo, F. Fabiano, M. Feo, M. Ferro-Luzzi, R. Forty, M. Frank, C. Frei, S. Gambetta, J. García Pardiñas, C. Gaspar, A. Golutvin, L. A. Granado Cardoso, Y. Guz, T. Gys, C. Haen, J. Haimberger, M. Hajheidari, M. M. Halvorsen, C. Hasse, F. Hemmer, A. M. Hennequin, R. Jacobsson, S. Jakobsen, B. Jost, N. Jurik, M. Karacson, F. Keizer, P. Kopciewicz, D. Lacarrere, P. Li, R. Lindner, B. Malecki, L. Malentacca, S. Mariani, C. Marin Benito, L. Martinazzoli, R. Matev, M. Mazurek, T. Mombächer, A. B. Morris, T. Nanut, N. Neufeld, S. Okamura, A. Perro, F. Pisani, F. Polci, I. Polyakov, S. Ponce, F. Redi, E. Rodrigues, D. L. Rolf, P. Roloff, T. Ruf, A. Saputi, H. Schindler, B. Schmidt, A. Schopper, R. Schwemmer, A. Sciuccati, N. Serra, V. Sriskaran, F. Stagni, M. Stahl, S. Stahl, E. N. Stein, M. Szymanski, F. Teubert, E. Thomas, A. Valassi, M. Vieites Diaz & K. Wyllie
Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
M. Bachmayer, A. Bay, F. Blanc, S. A. Bouchiba, S. Celani, S. Cholak, S. Ek-In, M. Faria, L. M. Garcia Martin, E. Graverini, G. Haefeli, L. Henry, D. Hill, D. Kaminaris, A. M. Kauniskangas, V. S. Kirsebom, V. Lisovskyi, R. Marchevski, P. Mayencourt, T. Nakada, E. M. Niel, R. Quagliani, F. Ronchetti, O. Schneider, S. Schulte, L. Shchutska, Y. Song, R. Van Laak, A. Venkateswaran & E. Zaffaroni
Physik-Institut, Universität Zürich, Zurich, Switzerland
C. Abellan Beteta, M. Andersson, P. Andreola, V. Bellee, R. Bernet, C. Betancourt, Ia. Bezshyiko, A. Buonaura, D. C. Craik, D. De Simone, V. Denysenko, J. Eschle, S. Esen, M. Ferrillo, D. Lancierini, A. Mathad, K. Müller, P. Owen, N. Serra, O. Steinkamp & A. Terentev
NSC Kharkiv Institute of Physics and Technology (NSC KIPT), Kharkiv, Ukraine
S. Kandybei
Institute for Nuclear Research of the National Academy of Sciences (KINR), Kyiv, Ukraine
S. Chernyshenko, V. Dobishuk, S. Koliiev, O. Kot, V. Lukashenko & V. Pugatch
University of Birmingham, Birmingham, UK
D. Johnson, C. Lazzeroni, M. M. Madurai, N. Sahoo, M. W. Slater, P. N. Swallow, D. J. D. Thompson & N. K. Watson
H.H. Wills Physics Laboratory, University of Bristol, Bristol, UK
M. Adinolfi, J. L. Amey, J. J. Cottee Meldrum, Z. Ghorbanimoghaddam, R. Lane, A. M. Marshall, K. Petridis, J. H. Rademacker, J. Reich, A. Solomin, J. J. Velthuis, R. Wang & B. D. C. Westhenry
Cavendish Laboratory, University of Cambridge, Cambridge, UK
P. Alvarez Cartelle, M. Bartolini, J. Bex, M. P. Blago, J. S. Butter, H. V. Cliff, D. Foulds-Holt, V. Gibson, C. R. Jones, M. Kenzie, T. Long, G. H. Lovell, L. R. Madhan Mohan, R. Williams & S. A. Wotton
Department of Physics, University of Warwick, Coventry, UK
A. S. W. Abdelmotteleb, F. Abudinén, J. J. Back, A. Beck, T. Blake, M. F. Cicala, A. Davidson, T. Gershon, L. Grazette, R. D. L. Henderson, R. J. Hunter, T. P. Jones, M. Kreps, T. Latham, M. Lehuraux, M. Monk, E. Muhammad, B. Pagare, L. Paolucci, R. I. Rabadan Trejo, M. Ramos Pernas, F. Swystun, M. Vesterinen, J. A. Ward, A. R. Wiederhold, M. Xu & V. Zhovkovska
STFC Rutherford Appleton Laboratory, Didcot, UK
S. Easo, T. Lin, A. Modak, R. Nandakumar, A. Papanestis, S. Ricciardi, A. Rogovskiy & F. F. Wilson
School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
W. Barter, F. Betti, A. Bohare, P. E. L. Clarke, R. Currie, S. Eisenhardt, K. Farmer, S. Gambetta, Y. Liu, S. E. Mitchell, F. Muheim, M. Needham, F. Oliva, R. H. O’Neil, O. Ozcelik, S. Petrucci, M. Richardson-Slipper, G. Sarpis, L. Soares Lavra, C. Vrahas & M. R. J. Williams
School of Physics and Astronomy, University of Glasgow, Glasgow, UK
M. Alexander, D. Bobulska, N. Cooke, A. D. Docheva, L. Douglas, L. Grillo, N. T. McHugh, H. N. Nur, G. Robertson, M. Schiller, F. J. P. Soler, P. Spradlin & M. Whitehead
Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
T. Ackernley, T. J. V. Bowcock, J. Brown, G. Casse, A. J. Chadwick, C. A. Chavez Barajas, T. Halewood-leagas, J. Hammerich, T. Harrison, K. Hennessy, N. Howarth, D. Hutchcroft, P. J. Marshall, P. Naik, K. Rinnert, E. Rodrigues, S. Scherl, T. Shears & E. Vilella Figueras
Imperial College London, London, UK
M. Birch, M. J. Bradley, S. Ely, E. L. Gkougkousis, A. Golutvin, J. Herd, Y. L. Liu, A. Mauri, M. McCann, R. Murta, R. Newcombe, M. Patel, M. Smith, H. Tilquin, E. van Herwijnen, X. W. Wang & D. Websdale
Department of Physics and Astronomy, University of Manchester, Manchester, UK
Z. Aliouche, R. J. Barlow, C. Bertella, A. Bitadze, S. Borghi, A. T. Burke, J. L. Cobbledick, J. E. Davies, A. Davis, O. De Aguiar Francisco, S. De Capua, E. Ejopu, T. Evans, C. Fitzpatrick, L. F. Foreman, D. A. Friday, E. Gersabeck, M. Gersabeck, J. Horswill, L. Li, T. H. McGrath, A. McNab, C. Parkes, F. Reiss, N. Skidmore, S. Taneja, D. J. White, H. Yeung & G. Zunica
Department of Physics, University of Oxford, Oxford, UK
D. Bacher, D. Cervenkov, K. M. Fischer, R. Gao, A. L. Gilman, F. Goncalves Abrantes, N. Harnew, M. John, I. Mackay, S. Malde, R. A. Mohammed, T. Pajero, J. Patoc, P. K. Resmi, A. Rollings, L. G. Scantlebury Smead, J. C. Smallwood, S. Stanislaus, F. Suljik, M. D. Tat, G. Wilkinson & Y. Zhang
Massachusetts Institute of Technology, Cambridge, MA, USA
M. Atzeni, A. Casais Vidal, B. Delaney, O. Kitouni, N. S. Nolte, K. Richardson, E. Smith & M. Williams
University of Cincinnati, Cincinnati, OH, USA
S. Akar, T. Boettcher, M. Elashri, E. Epple, N. A. Grieser, C. Henderson, P. Ilten, J. W. Kautz, B. Meadows, G. Nowak, C. Pappenheimer, M. D. Sokoloff & M. K. Wilkinson
University of Maryland, College Park, MD, USA
S. Braun, A. D. Fernez, M. Franco Sevilla, C. Hadjivasiliou, P. M. Hamilton, A. Jawahery, E. Jiang, Y. Sun & Z. Yang
Los Alamos National Laboratory (LANL), Los Alamos, NM, USA
C. L. Da Silva, J. M. Durham, K. Smith, H. Van Hecke & C. P. Wong
Syracuse University, Syracuse, NY, USA
D. Andreou, M. Artuso, J. Bartz, A. Beiter, H. C. Bernstein, S. Blusk, S. Ding, D. M. Keller, B. Khanji, W. Krupa, Z. Li, X. Liang, C. Matteuzzi, E. Minucci, R. Mountain, H. Pham, M. S. Rudolph, R. S. Sharma, J. D. Shupperd, R. Silva Coutinho, T. Skwarnicki, F. L. Souza De Almeida & H. Wu
Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Rio de Janeiro, Brazil
I. R. Barbosa & C. Göbel
School of Physics and Electronics, Hunan University, Changsha City, China
L. Dai, J. Yu & S. Zhang
Guangdong Provincial Key Laboratory of Nuclear Science, Guangdong-Hong Kong Joint Laboratory of Quantum Matter, Institute of Quantum Matter, South China Normal University, Guangzhou, China
A. Bursche, W. Duan, J. Hu, H. Li, T. Li, G. Liu, X. Wang & S. Xian
Lanzhou University, Lanzhou, China
P.-R. Li, K. Liu & Y. Liu
School of Physics and Technology, Wuhan University, Wuhan, China
H. Cai, B. Fang, L. Sun & J. Wang
Departamento de Fisica, Universidad Nacional de Colombia, Bogota, Colombia
S. J. Jaimes Elles, D. A. Milanes, I. A. Monroy & J. A. Rodriguez Lopez
Universität Bonn-Helmholtz-Institut für Strahlen und Kernphysik, Bonn, Germany
E. Eckstein, J. P. Grabowski, M. Mikhasenko, S. Neubert, P. Nogga, K. O. Padeken, M. Sarpis & H. Schmitz
Eotvos Lorand University, Budapest, Hungary
B. Dey & A. M. Schertz
Van Swinderen Institute, University of Groningen, Groningen, Netherlands
K. De Bruyn & M. Mulder
Universiteit Maastricht, Maastricht, Netherlands
C. S. Bolognani, D. H. Campora Perez, J. A. de Vries, M. Lucio Martinez, M. Merk, D. Nicotra, C. J. G. Onderwater, C. J. Pawley & K. Vos
Tadeusz Kosciuszko Cracow University of Technology, Cracow, Poland
P. Duda, M. M. Duras, L. Felkowski & S. Kubis
Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden
P. Adlarson, L. Eklund, A. Kupsc & J. Ruiz Vidal
University of Michigan, Ann Arbor, MI, USA
C. A. Aidala, I. Chahrour, D. S. Fitzgerald, S. H. Lee, C. Nunez, M. Ramírez García & D. M. Shangase
Departement de Physique Nucleaire (SPhN), Gif-Sur-Yvette, France
G. R. Ricart
Universidade de Brasília, Brasília, Brazil
A. Gomes
Centro Federal de Educacão Tecnológica Celso Suckow da Fonseca, Rio De Janeiro, Brazil
U. De Freitas Carneiro Da Graca
Hangzhou Institute for Advanced Study, UCAS, Hangzhou, China
J. He
School of Physics and Electronics, Henan University, Kaifeng, China
T. Li
LIP6, Sorbonne Universite, Paris, France
F. I. Giasemis
Excellence Cluster ORIGINS, Munich, Germany
M. Mikhasenko
Universidad Nacional Autónoma de Honduras, Tegucigalpa, Honduras
M. Cruz Torres
Università di Bari, Bari, Italy
M. De Serio, F. Debernardis, G. Galati, M. Pappagallo & S. Simone
Università di Bologna, Bologna, Italy
A. Carbone, D. Galli & C. Patrignani
Università di Cagliari, Cagliari, Italy
C. De Angelis, F. Dettori, F. Fabiano, M. Garau, R. Litvinov, G. Manca, C. Normand, R. Oldeman & B. Saitta
Università di Ferrara, Ferrara, Italy
R. Bolzonella, R. Calabrese, V. Cavallini, M. Fiorini, E. Franzoso, C. Giugliano, E. Luppi, S. Okamura, L. L. Pappalardo, B. Passalacqua & L. Tomassetti
Università di Firenze, Firenze, Italy
M. Barbetti & C. Lucarelli
Università di Genova, Genoa, Italy
R. Cardinale, F. Fontanelli, A. Petrolini, A. Sergi & Y. Yang
Università degli Studi di Milano, Milan, Italy
S. Cesare, L. Frontini, C. Mancuso, D. Marangotto, A. Merli, N. Neri, E. Spadaro Norella & G. Tonani
Università di Milano Bicocca, Milan, Italy
A. Anelli, M. Borsato, M. Calvi, S. Capelli, P. Carniti, D. Fazzini, M. Martinelli, A. Minotti, M. Pizzichemi, M. Salomoni & E. B. Shields
Università di Padova, Padua, Italy
D. Lucchesi
Università di Perugia, Perugia, Italy
L. Fantini & G. Martelli
Scuola Normale Superiore, Pisa, Italy
G. Bassi, N. Kleijne, M. J. Morello, D. Passaro, L. Pica, R. Ribatti & D. Riccardi
Università di Pisa, Pisa, Italy
F. Lazzari & G. Punzi
Università della Basilicata, Potenza, Italy
C. Satriano
Università di Roma Tor Vergata, Rome, Italy
F. Archilli
Università di Siena, Siena, Italy
F. Terzuoli
Università di Urbino, Urbino, Italy
M. Veltri
Universidad de Alcalá, Alcalá de Henares, Spain
C. B. Van Hulse
Universidade da Coruña, Coruña, Spain
V. Chobanova
Department of Physics/Division of Particle Physics, Lund, Sweden
J. Ruiz Vidal

Consortia

LHCb Collaboration

R. Aaij
, A. S. W. Abdelmotteleb
, C. Abellan Beteta
, F. Abudinén
, T. Ackernley
, B. Adeva
, M. Adinolfi
, P. Adlarson
, C. Agapopoulou
, C. A. Aidala
, Z. Ajaltouni
, S. Akar
, K. Akiba
, P. Albicocco
, J. Albrecht
, F. Alessio
, M. Alexander
, A. Alfonso Albero
, Z. Aliouche
, P. Alvarez Cartelle
, R. Amalric
, S. Amato
, J. L. Amey
, Y. Amhis
, L. An
, L. Anderlini
, M. Andersson
, A. Andreianov
, P. Andreola
, M. Andreotti
, D. Andreou
, A. Anelli
, D. Ao
, F. Archilli
, M. Argenton
, S. Arguedas Cuendis
, A. Artamonov
, M. Artuso
, E. Aslanides
, M. Atzeni
, B. Audurier
, D. Bacher
, I. Bachiller Perea
, S. Bachmann
, M. Bachmayer
, J. J. Back
, P. Baladron Rodriguez
, V. Balagura
, W. Baldini
, J. Baptista de Souza Leite
, M. Barbetti
, I. R. Barbosa
, R. J. Barlow
, S. Barsuk
, W. Barter
, M. Bartolini
, J. Bartz
, F. Baryshnikov
, J. M. Basels
, G. Bassi
, B. Batsukh
, A. Battig
, A. Bay
, A. Beck
, M. Becker
, F. Bedeschi
, I. B. Bediaga
, A. Beiter
, S. Belin
, V. Bellee
, K. Belous
, I. Belov
, I. Belyaev
, G. Benane
, G. Bencivenni
, E. Ben-Haim
, A. Berezhnoy
, R. Bernet
, S. Bernet Andres
, H. C. Bernstein
, C. Bertella
, A. Bertolin
, C. Betancourt
, F. Betti
, J. Bex
, Ia. Bezshyiko
, J. Bhom
, M. S. Bieker
, N. V. Biesuz
, P. Billoir
, A. Biolchini
, M. Birch
, F. C. R. Bishop
, A. Bitadze
, A. Bizzeti
, M. P. Blago
, T. Blake
, F. Blanc
, J. E. Blank
, S. Blusk
, D. Bobulska
, V. Bocharnikov
, J. A. Boelhauve
, O. Boente Garcia
, T. Boettcher
, A. Bohare
, A. Boldyrev
, C. S. Bolognani
, R. Bolzonella
, N. Bondar
, F. Borgato
, S. Borghi
, M. Borsato
, J. T. Borsuk
, S. A. Bouchiba
, T. J. V. Bowcock
, A. Boyer
, C. Bozzi
, M. J. Bradley
, S. Braun
, A. Brea Rodriguez
, N. Breer
, J. Brodzicka
, A. Brossa Gonzalo
, J. Brown
, D. Brundu
, A. Buonaura
, L. Buonincontri
, A. T. Burke
, C. Burr
, A. Bursche
, A. Butkevich
, J. S. Butter
, J. Buytaert
, W. Byczynski
, S. Cadeddu
, H. Cai
, R. Calabrese
, L. Calefice
, S. Cali
, M. Calvi
, M. Calvo Gomez
, J. Cambon Bouzas
, P. Campana
, D. H. Campora Perez
, A. F. Campoverde Quezada
, S. Capelli
, L. Capriotti
, R. Caravaca-Mora
, A. Carbone
, L. Carcedo Salgado
, R. Cardinale
, A. Cardini
, P. Carniti
, L. Carus
, A. Casais Vidal
, R. Caspary
, G. Casse
, J. Castro Godinez
, M. Cattaneo
, G. Cavallero
, V. Cavallini
, S. Celani
, J. Cerasoli
, D. Cervenkov
, S. Cesare
, A. J. Chadwick
, I. Chahrour
, M. Charles
, Ph. Charpentier
, C. A. Chavez Barajas
, M. Chefdeville
, C. Chen
, S. Chen
, Z. Chen
, A. Chernov
, S. Chernyshenko
, V. Chobanova
, S. Cholak
, M. Chrzaszcz
, A. Chubykin
, V. Chulikov
, P. Ciambrone
, M. F. Cicala
, X. Cid Vidal
, G. Ciezarek
, P. Cifra
, P. E. L. Clarke
, M. Clemencic
, H. V. Cliff
, J. Closier
, J. L. Cobbledick
, C. Cocha Toapaxi
, V. Coco
, J. Cogan
, E. Cogneras
, L. Cojocariu
, P. Collins
, T. Colombo
, A. Comerma-Montells
, L. Congedo
, A. Contu
, N. Cooke
, I. Corredoira
, A. Correia
, G. Corti
, J. J. Cottee Meldrum
, B. Couturier
, D. C. Craik
, M. Cruz Torres
, R. Currie
, C. L. Da Silva
, S. Dadabaev
, L. Dai
, X. Dai
, E. Dall’Occo
, J. Dalseno
, C. D’Ambrosio
, J. Daniel
, A. Danilina
, P. d’Argent
, A. Davidson
, J. E. Davies
, A. Davis
, O. De Aguiar Francisco
, C. De Angelis
, J. de Boer
, K. De Bruyn
, S. De Capua
, M. De Cian
, U. De Freitas Carneiro Da Graca
, E. De Lucia
, J. M. De Miranda
, L. De Paula
, M. De Serio
, D. De Simone
, P. De Simone
, F. De Vellis
, J. A. de Vries
, F. Debernardis
, D. Decamp
, V. Dedu
, L. Del Buono
, B. Delaney
, H.-P. Dembinski
, J. Deng
, V. Denysenko
, O. Deschamps
, F. Dettori
, B. Dey
, P. Di Nezza
, I. Diachkov
, S. Didenko
, S. Ding
, V. Dobishuk
, A. D. Docheva
, A. Dolmatov
, C. Dong
, A. M. Donohoe
, F. Dordei
, A. C. dos Reis
, L. Douglas
, A. G. Downes
, W. Duan
, P. Duda
, M. W. Dudek
, L. Dufour
, V. Duk
, P. Durante
, M. M. Duras
, J. M. Durham
, A. Dziurda
, A. Dzyuba
, S. Easo
, E. Eckstein
, U. Egede
, A. Egorychev
, V. Egorychev
, C. Eirea Orro
, S. Eisenhardt
, E. Ejopu
, S. Ek-In
, L. Eklund
, M. Elashri
, J. Ellbracht
, S. Ely
, A. Ene
, E. Epple
, S. Escher
, J. Eschle
, S. Esen
, T. Evans
, F. Fabiano
, L. N. Falcao
, Y. Fan
, B. Fang
, L. Fantini
, M. Faria
, K. Farmer
, D. Fazzini
, L. Felkowski
, M. Feng
, M. Feo
, M. Fernandez Gomez
, A. D. Fernez
, F. Ferrari
, F. Ferreira Rodrigues
, S. Ferreres Sole
, M. Ferrillo
, M. Ferro-Luzzi
, S. Filippov
, R. A. Fini
, M. Fiorini
, M. Firlej
, K. M. Fischer
, D. S. Fitzgerald
, C. Fitzpatrick
, T. Fiutowski
, F. Fleuret
, M. Fontana
, F. Fontanelli
, L. F. Foreman
, R. Forty
, D. Foulds-Holt
, M. Franco Sevilla
, M. Frank
, E. Franzoso
, G. Frau
, C. Frei
, D. A. Friday
, L. Frontini
, J. Fu
, Q. Fuehring
, Y. Fujii
, T. Fulghesu
, E. Gabriel
, G. Galati
, M. D. Galati
, A. Gallas Torreira
, D. Galli
, S. Gambetta
, M. Gandelman
, P. Gandini
, H. Gao
, R. Gao
, Y. Gao
, Y. Gao
, Y. Gao
, M. Garau
, L. M. Garcia Martin
, P. Garcia Moreno
, J. García Pardiñas
, B. Garcia Plana
, K. G. Garg
, L. Garrido
, C. Gaspar
, R. E. Geertsema
, L. L. Gerken
, E. Gersabeck
, M. Gersabeck
, T. Gershon
, Z. Ghorbanimoghaddam
, L. Giambastiani
, F. I. Giasemis
, V. Gibson
, H. K. Giemza
, A. L. Gilman
, M. Giovannetti
, A. Gioventù
, P. Gironella Gironell
, C. Giugliano
, M. A. Giza
, E. L. Gkougkousis
, F. C. Glaser
, V. V. Gligorov
, C. Göbel
, E. Golobardes
, D. Golubkov
, A. Golutvin
, A. Gomes
, S. Gomez Fernandez
, F. Goncalves Abrantes
, M. Goncerz
, G. Gong
, J. A. Gooding
, I. V. Gorelov
, C. Gotti
, J. P. Grabowski
, L. A. Granado Cardoso
, E. Graugés
, E. Graverini
, L. Grazette
, G. Graziani
, A. T. Grecu
, L. M. Greeven
, N. A. Grieser
, L. Grillo
, S. Gromov
, C. Gu
, M. Guarise
, M. Guittiere
, V. Guliaeva
, P. A. Günther
, A.-K. Guseinov
, E. Gushchin
, Y. Guz
, T. Gys
, T. Hadavizadeh
, C. Hadjivasiliou
, G. Haefeli
, C. Haen
, J. Haimberger
, M. Hajheidari
, T. Halewood-leagas
, M. M. Halvorsen
, P. M. Hamilton
, J. Hammerich
, Q. Han
, X. Han
, S. Hansmann-Menzemer
, L. Hao
, N. Harnew
, T. Harrison
, M. Hartmann
, C. Hasse
, J. He
, K. Heijhoff
, F. Hemmer
, C. Henderson
, R. D. L. Henderson
, A. M. Hennequin
, K. Hennessy
, L. Henry
, J. Herd
, P. Herrero Gascon
, J. Heuel
, A. Hicheur
, D. Hill
, S. E. Hollitt
, J. Horswill
, R. Hou
, Y. Hou
, N. Howarth
, J. Hu
, J. Hu
, W. Hu
, X. Hu
, W. Huang
, W. Hulsbergen
, R. J. Hunter
, M. Hushchyn
, D. Hutchcroft
, M. Idzik
, D. Ilin
, P. Ilten
, A. Inglessi
, A. Iniukhin
, A. Ishteev
, K. Ivshin
, R. Jacobsson
, H. Jage
, S. J. Jaimes Elles
, S. Jakobsen
, E. Jans
, B. K. Jashal
, A. Jawahery
, V. Jevtic
, E. Jiang
, X. Jiang
, Y. Jiang
, Y. J. Jiang
, M. John
, D. Johnson
, C. R. Jones
, T. P. Jones
, S. Joshi
, B. Jost
, N. Jurik
, I. Juszczak
, D. Kaminaris
, S. Kandybei
, Y. Kang
, M. Karacson
, D. Karpenkov
, M. Karpov
, A. M. Kauniskangas
, J. W. Kautz
, F. Keizer
, D. M. Keller
, M. Kenzie
, T. Ketel
, B. Khanji
, A. Kharisova
, S. Kholodenko
, G. Khreich
, T. Kirn
, V. S. Kirsebom
, O. Kitouni
, S. Klaver
, N. Kleijne
, K. Klimaszewski
, M. R. Kmiec
, S. Koliiev
, L. Kolk
, A. Konoplyannikov
, P. Kopciewicz
, P. Koppenburg
, M. Korolev
, I. Kostiuk
, O. Kot
, S. Kotriakhova
, A. Kozachuk
, P. Kravchenko
, L. Kravchuk
, M. Kreps
, S. Kretzschmar
, P. Krokovny
, W. Krupa
, W. Krzemien
, J. Kubat
, S. Kubis
, W. Kucewicz
, M. Kucharczyk
, V. Kudryavtsev
, E. Kulikova
, A. Kupsc
, B. K. Kutsenko
, D. Lacarrere
, A. Lai
, A. Lampis
, D. Lancierini
, C. Landesa Gomez
, J. J. Lane
, R. Lane
, C. Langenbruch
, J. Langer
, O. Lantwin
, T. Latham
, F. Lazzari
, C. Lazzeroni
, R. Le Gac
, S. H. Lee
, R. Lefèvre
, A. Leflat
, S. Legotin
, M. Lehuraux
, O. Leroy
, T. Lesiak
, B. Leverington
, A. Li
, H. Li
, K. Li
, L. Li
, P. Li
, P.-R. Li
, S. Li
, T. Li
, T. Li
, Y. Li
, Y. Li
, Z. Li
, Z. Lian
, X. Liang
, C. Lin
, T. Lin
, R. Lindner
, V. Lisovskyi
, R. Litvinov
, G. Liu
, H. Liu
, K. Liu
, Q. Liu
, S. Liu
, Y. Liu
, Y. Liu
, Y. L. Liu
, A. Lobo Salvia
, A. Loi
, J. Lomba Castro
, T. Long
, J. H. Lopes
, A. Lopez Huertas
, S. L.ópez Soliño
, G. H. Lovell
, C. Lucarelli
, D. Lucchesi
, S. Luchuk
, M. Lucio Martinez
, V. Lukashenko
, Y. Luo
, A. Lupato
, E. Luppi
, K. Lynch
, X.-R. Lyu
, G. M. Ma
, R. Ma
, S. Maccolini
, F. Machefert
, F. Maciuc
, I. Mackay
, L. R. Madhan Mohan
, M. M. Madurai
, A. Maevskiy
, D. Magdalinski
, D. Maisuzenko
, M. W. Majewski
, J. J. Malczewski
, S. Malde
, B. Malecki
, L. Malentacca
, A. Malinin
, T. Maltsev
, G. Manca
, G. Mancinelli
, C. Mancuso
, R. Manera Escalero
, D. Manuzzi
, D. Marangotto
, J. F. Marchand
, R. Marchevski
, U. Marconi
, S. Mariani
, C. Marin Benito
, J. Marks
, A. M. Marshall
, P. J. Marshall
, G. Martelli
, G. Martellotti
, L. Martinazzoli
, M. Martinelli
, D. Martinez Santos
, F. Martinez Vidal
, A. Massafferri
, M. Materok
, R. Matev
, A. Mathad
, V. Matiunin
, C. Matteuzzi
, K. R. Mattioli
, A. Mauri
, E. Maurice
, J. Mauricio
, P. Mayencourt
, M. Mazurek
, M. McCann
, L. Mcconnell
, T. H. McGrath
, N. T. McHugh
, A. McNab
, R. McNulty
, B. Meadows
, G. Meier
, D. Melnychuk
, M. Merk
, A. Merli
, L. Meyer Garcia
, D. Miao
, H. Miao
, M. Mikhasenko
, D. A. Milanes
, A. Minotti
, E. Minucci
, T. Miralles
, S. E. Mitchell
, B. Mitreska
, D. S. Mitzel
, A. Modak
, A. Mödden
, R. A. Mohammed
, R. D. Moise
, S. Mokhnenko
, T. Mombächer
, M. Monk
, I. A. Monroy
, S. Monteil
, A. Morcillo Gomez
, G. Morello
, M. J. Morello
, M. P. Morgenthaler
, J. Moron
, A. B. Morris
, A. G. Morris
, R. Mountain
, H. Mu
, Z. M. Mu
, E. Muhammad
, F. Muheim
, M. Mulder
, K. Müller
, F. Mũnoz-Rojas
, R. Murta
, P. Naik
, T. Nakada
, R. Nandakumar
, T. Nanut
, I. Nasteva
, M. Needham
, N. Neri
, S. Neubert
, N. Neufeld
, P. Neustroev
, R. Newcombe
, J. Nicolini
, D. Nicotra
, E. M. Niel
, N. Nikitin
, P. Nogga
, N. S. Nolte
, C. Normand
, J. Novoa Fernandez
, G. Nowak
, C. Nunez
, H. N. Nur
, A. Oblakowska-Mucha
, V. Obraztsov
, T. Oeser
, S. Okamura
, R. Oldeman
, F. Oliva
, M. Olocco
, C. J. G. Onderwater
, R. H. O’Neil
, J. M. Otalora Goicochea
, T. Ovsiannikova
, P. Owen
, A. Oyanguren
, O. Ozcelik
, K. O. Padeken
, B. Pagare
, P. R. Pais
, T. Pajero
, A. Palano
, M. Palutan
, G. Panshin
, L. Paolucci
, A. Papanestis
, M. Pappagallo
, L. L. Pappalardo
, C. Pappenheimer
, C. Parkes
, B. Passalacqua
, G. Passaleva
, D. Passaro
, A. Pastore
, M. Patel
, J. Patoc
, C. Patrignani
, C. J. Pawley
, A. Pellegrino
, M. Pepe Altarelli
, S. Perazzini
, D. Pereima
, A. Pereiro Castro
, P. Perret
, A. Perro
, K. Petridis
, A. Petrolini
, S. Petrucci
, H. Pham
, L. Pica
, M. Piccini
, B. Pietrzyk
, G. Pietrzyk
, D. Pinci
, F. Pisani
, M. Pizzichemi
, V. Placinta
, M. Plo Casasus
, F. Polci
, M. Poli Lener
, A. Poluektov
, N. Polukhina
, I. Polyakov
, E. Polycarpo
, S. Ponce
, D. Popov
, S. Poslavskii
, K. Prasanth
, C. Prouve
, V. Pugatch
, G. Punzi
, W. Qian
, N. Qin
, S. Qu
, R. Quagliani
, R. I. Rabadan Trejo
, B. Rachwal
, J. H. Rademacker
, M. Rama
, M. Ramírez García
, M. Ramos Pernas
, M. S. Rangel
, F. Ratnikov
, G. Raven
, M. Rebollo De Miguel
, F. Redi
, J. Reich
, F. Reiss
, Z. Ren
, P. K. Resmi
, R. Ribatti
, G. R. Ricart
, D. Riccardi
, S. Ricciardi
, K. Richardson
, M. Richardson-Slipper
, K. Rinnert
, P. Robbe
, G. Robertson
, E. Rodrigues
, E. Rodriguez Fernandez
, J. A. Rodriguez Lopez
, E. Rodriguez Rodriguez
, A. Rogovskiy
, D. L. Rolf
, A. Rollings
, P. Roloff
, V. Romanovskiy
, M. Romero Lamas
, A. Romero Vidal
, G. Romolini
, F. Ronchetti
, M. Rotondo
, S. R. Roy
, M. S. Rudolph
, T. Ruf
, M. Ruiz Diaz
, R. A. Ruiz Fernandez
, J. Ruiz Vidal
, A. Ryzhikov
, J. Ryzka
, J. J. Saborido Silva
, R. Sadek
, N. Sagidova
, N. Sahoo
, B. Saitta
, M. Salomoni
, C. Sanchez Gras
, I. Sanderswood
, R. Santacesaria
, C. Santamarina Rios
, M. Santimaria
, L. Santoro
, E. Santovetti
, A. Saputi
, D. Saranin
, G. Sarpis
, M. Sarpis
, A. Sarti
, C. Satriano
, A. Satta
, M. Saur
, D. Savrina
, H. Sazak
, L. G. Scantlebury Smead
, A. Scarabotto
, S. Schael
, S. Scherl
, A. M. Schertz
, M. Schiller
, H. Schindler
, M. Schmelling
, B. Schmidt
, S. Schmitt
, H. Schmitz
, O. Schneider
, A. Schopper
, N. Schulte
, S. Schulte
, M. H. Schune
, R. Schwemmer
, G. Schwering
, B. Sciascia
, A. Sciuccati
, S. Sellam
, A. Semennikov
, M. Senghi Soares
, A. Sergi
, N. Serra
, L. Sestini
, A. Seuthe
, Y. Shang
, D. M. Shangase
, M. Shapkin
, R. S. Sharma
, I. Shchemerov
, L. Shchutska
, T. Shears
, L. Shekhtman
, Z. Shen
, S. Sheng
, V. Shevchenko
, B. Shi
, E. B. Shields
, Y. Shimizu
, E. Shmanin
, R. Shorkin
, J. D. Shupperd
, R. Silva Coutinho
, G. Simi
, S. Simone
, N. Skidmore
, R. Skuza
, T. Skwarnicki
, M. W. Slater
, J. C. Smallwood
, E. Smith
, K. Smith
, M. Smith
, A. Snoch
, L. Soares Lavra
, M. D. Sokoloff
, F. J. P. Soler
, A. Solomin
, A. Solovev
, I. Solovyev
, R. Song
, Y. Song
, Y. Song
, Y. S. Song
, F. L. Souza De Almeida
, B. Souza De Paula
, E. Spadaro Norella
, E. Spedicato
, J. G. Speer
, E. Spiridenkov
, P. Spradlin
, V. Sriskaran
, F. Stagni
, M. Stahl
, S. Stahl
, S. Stanislaus
, E. N. Stein
, O. Steinkamp
, O. Stenyakin
, H. Stevens
, D. Strekalina
, Y. Su
, F. Suljik
, J. Sun
, L. Sun
, Y. Sun
, P. N. Swallow
, K. Swientek
, F. Swystun
, A. Szabelski
, T. Szumlak
, M. Szymanski
, Y. Tan
, S. Taneja
, M. D. Tat
, A. Terentev
, F. Terzuoli
, F. Teubert
, E. Thomas
, D. J. D. Thompson
, H. Tilquin
, V. Tisserand
, S. T’Jampens
, M. Tobin
, L. Tomassetti
, G. Tonani
, X. Tong
, D. Torres Machado
, L. Toscano
, D. Y. Tou
, C. Trippl
, G. Tuci
, N. Tuning
, L. H. Uecker
, A. Ukleja
, D. J. Unverzagt
, E. Ursov
, A. Usachov
, A. Ustyuzhanin
, U. Uwer
, V. Vagnoni
, A. Valassi
, G. Valenti
, N. Valls Canudas
, H. Van Hecke
, E. van Herwijnen
, C. B. Van Hulse
, R. Van Laak
, M. van Veghel
, R. Vazquez Gomez
, P. Vazquez Regueiro
, C. V.ázquez Sierra
, S. Vecchi
, J. J. Velthuis
, M. Veltri
, A. Venkateswaran
, M. Vesterinen
, M. Vieites Diaz
, X. Vilasis-Cardona
, E. Vilella Figueras
, A. Villa
, P. Vincent
, F. C. Volle
, D. vom Bruch
, V. Vorobyev
, N. Voropaev
, K. Vos
, G. Vouters
, C. Vrahas
, J. Walsh
, E. J. Walton
, G. Wan
, C. Wang
, G. Wang
, J. Wang
, J. Wang
, J. Wang
, J. Wang
, M. Wang
, N. W. Wang
, R. Wang
, X. Wang
, X. W. Wang
, Y. Wang
, Z. Wang
, Z. Wang
, Z. Wang
, J. A. Ward
, N. K. Watson
, D. Websdale
, Y. Wei
, B. D. C. Westhenry
, D. J. White
, M. Whitehead
, A. R. Wiederhold
, D. Wiedner
, G. Wilkinson
, M. K. Wilkinson
, M. Williams
, M. R. J. Williams
, R. Williams
, F. F. Wilson
, W. Wislicki
, M. Witek
, L. Witola
, C. P. Wong
, G. Wormser
, S. A. Wotton
, H. Wu
, J. Wu
, Y. Wu
, K. Wyllie
, S. Xian
, Z. Xiang
, Y. Xie
, A. Xu
, J. Xu
, L. Xu
, L. Xu
, M. Xu
, Z. Xu
, Z. Xu
, Z. Xu
, D. Yang
, S. Yang
, X. Yang
, Y. Yang
, Z. Yang
, Z. Yang
, V. Yeroshenko
, H. Yeung
, H. Yin
, C. Y. Yu
, J. Yu
, X. Yuan
, E. Zaffaroni
, M. Zavertyaev
, M. Zdybal
, M. Zeng
, C. Zhang
, D. Zhang
, J. Zhang
, L. Zhang
, S. Zhang
, S. Zhang
, Y. Zhang
, Y. Zhang
, Y. Z. Zhang
, Y. Zhao
, A. Zharkova
, A. Zhelezov
, X. Z. Zheng
, Y. Zheng
, T. Zhou
, X. Zhou
, Y. Zhou
, V. Zhovkovska
, L. Z. Zhu
, X. Zhu
, X. Zhu
, Z. Zhu
, V. Zhukov
, J. Zhuo
, Q. Zou
, D. Zuliani
& G. Zunica

Corresponding author

Correspondence to M. Stahl.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Funded by SCOAP³.

Reprints and permissions

About this article

Cite this article

LHCb Collaboration. Observation of ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} $ and ${{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} $ decays. Eur. Phys. J. C 84, 575 (2024). https://doi.org/10.1140/epjc/s10052-024-12752-3

Download citation

Received: 23 November 2023
Accepted: 30 March 2024
Published: 05 June 2024
DOI: https://doi.org/10.1140/epjc/s10052-024-12752-3

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Observation of \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{()0}{{K} ^-} \) and \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{-}_{s}} \) decays

Abstract

Similar content being viewed by others

Observation of $${{\varXi } ^0_{b}} \rightarrow {{\varXi } ^+_{c}} {{D} ^-_{s}} $$ and $${{\varXi } ^-_{b}} \rightarrow {{\varXi } ^0_{c}} {{D} ^-_{s}} $$ decays

First observation and branching fraction measurement of the $$ {\Lambda}_b^0\to {D}_s^{-}p $$ decay

Observation of $${{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} 3{{\uppi } ^+} 2{{\uppi } ^-} $$ and $${{\mathrm {B}} ^+} \rightarrow {\uppsi {(2\mathrm {S})}} {{\uppi } ^+} {{\uppi } ^+} {{\uppi } ^-} $$ decays

1 Introduction

2 LHCb detector

3 Dataset and selection

4 Invariant-mass fits

5 Efficiency correction

6 Systematic uncertainties

6.1 Invariant-mass fits

6.2 Parameters of the simulation weighting

6.3 Multiple candidates

6.4 Simulation and control sample sizes

6.5 Summary

7 Conclusion

Data Availability Statement

Code Availability Statement

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Consortia

LHCb Collaboration

Corresponding author

Rights and permissions

About this article

Cite this article

Navigation

Observation of \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{(*)0}{{K} ^-} \) and \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{*-}_{s}} \) decays

Abstract

Similar content being viewed by others

Observation of $${{\varXi } ^0_{b}} \rightarrow {{\varXi } ^+_{c}} {{D} ^-_{s}} $$ and $${{\varXi } ^-_{b}} \rightarrow {{\varXi } ^0_{c}} {{D} ^-_{s}} $$ decays

First observation and branching fraction measurement of the $$ {\Lambda}_b^0\to {D}_s^{-}p $$ decay

Observation of $${{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} 3{{\uppi } ^+} 2{{\uppi } ^-} $$ and $${{\mathrm {B}} ^+} \rightarrow {\uppsi {(2\mathrm {S})}} {{\uppi } ^+} {{\uppi } ^+} {{\uppi } ^-} $$ decays

1 Introduction

2 LHCb detector

3 Dataset and selection

4 Invariant-mass fits

5 Efficiency correction

6 Systematic uncertainties

6.1 Invariant-mass fits

6.2 Parameters of the simulation weighting

6.3 Multiple candidates

6.4 Simulation and control sample sizes

6.5 Summary

7 Conclusion

Data Availability Statement

Code Availability Statement

Notes

References

Acknowledgements

Author information

Authors and Affiliations

Consortia

LHCb Collaboration

Corresponding author

Rights and permissions

About this article

Cite this article

Share this article

Search

Navigation

Observation of \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {\hspace{1.79993pt}\overline{\hspace{-1.79993pt}D}} {}^{()0}{{K} ^-} \) and \({{\varLambda } ^0_{b}} \!\rightarrow {{\varLambda } ^+_{c}} {{D} ^{-}_{s}} \) decays