1 Introduction

Thermonuclear fusion research started in the 1950s after the development of the hydrogen bomb. The development of the peaceful research counterpart appeared a few years later, with the first pinch experiments [1]. The first two attempts were made using the simple schemes of \(\theta \)-pinch and z-pinch. To clarify, \(\theta \) and z refer to the direction of the plasma current in terms of a cylindrical coordinate system r, \(\theta \), z. In addition to historical factors, from the point of view of technological development, both systems present simplicity in experimental implementation and theoretical treatment when compared to more complex, but more effective, forms of confinement, such as stellerators and tokamaks [2, 3]. Both models rest on cylindrical approximations, however, in the Z-pinch case the coiling of the confinement coils occurs in the z direction of the cylinder, and in the \(\theta \)-pinch case it happens along the \(\theta \) direction of the cylinder, that is, at various points of the cylindrical column. The plasma confinement configurations in an infinite Z-pinch theoretical model resemble the approximations used in large aspect ratio tokamak reactors. Among several approaches to plasma modeling in z-pinch, Weibel’s work from 1959 [4] brings one of these simple and practical approaches, which was recently revised [5].

It is simple to produce plasma by ionizing hydrogen gas in a tube, and a conductive fluid is obtained by a strong current induced by discharging a capacitor bank over an external coil surrounding the gas tube. From these studies, problems related to the equilibrium of plasma columns confining using complex configurations of magnetostatic fields reported by [6, 7], bicuspid arrangements investigated by [8], or self-organizing structuring as observed by [9] have been extensively studied in the literature [4, 10,11,12,13,14]. An investigation point of these investigations was related to the magnetic confinement of the fusion plasma [15]. On the other hand, an investigation point that we intend to open up with this work is to use plasma to obtain background fields that can provide us with physics different from the Standard Model of Particle Physics.

The Weinberg–Salam–Glashow Standard Model (SM) results from an intense search to understand the origin and behavior of elementary particles. The large hadron collider (LHC) has made the discovery missing for the acceptance of the model, the experimental verification of the Higgs boson. Also, physics out of the Standard Model, such as the pentaquark [16], has started to emerge at LHC.

Despite its success, the Standard Model ignores gravitational interaction and the problems related to it. So the SM has nothing to clarify about the dark Matter [17,18,19] and Energy problems. Thus, it is interesting to investigate possible extensions of the SM, and this line of research is known as Physics Beyond the Standard Model. With this goal, Kostelecký and Samuel [20] have shown that the Lorentz symmetry (LS) can be broken spontaneously. The development of this proposal by the works [21, 22] has established what we today know as the Standard Model Extended (SME).

In the context of electrodynamics, Carroll et al. [23,24,25] have investigated the presence of a background vector field, \(\xi ^{\nu }\), coupled to a Chern-Simons-like lagrangean in \( (3+1)\)-dimensions, \(\epsilon _{\mu \nu \alpha \beta }\,\xi ^{\nu }F^{\alpha \beta }\), the dual electromagnetic tensor, which violates Lorentz symmetry [26,27,28,29,30,31]. This term violates CPT-symmetry and presents interesting modified electromagnetism, such that vacuum birefringence. Thus, we propose a non-minimal coupling

$$\begin{aligned} D_\mu= & {} \,\partial _{\mu }-i e A_{\mu } \\{} & {} \quad \longrightarrow \quad {{{\mathcal {D}}}}_\mu =\, \partial _{\mu }-i e A_{\mu }-g \epsilon _{\mu \nu \kappa \lambda }\,\xi ^{\nu }F^{\kappa \lambda }, \end{aligned}$$

[24], where \(\epsilon _{\mu \nu \kappa \lambda }\) is a Levi-Civita pseudo-tensor, and the 4-vector \(\xi ^{\nu }\) is a fixed vector and acts on a vector field that violates the Lorentz symmetry, in the Lagrangian,

$$\begin{aligned} {{\mathcal {L}}}_{CPT-odd} = - \frac{1}{4}F_{\mu \nu }F^{\mu \nu } + \sum _f {\bar{\Psi }}_f(i \gamma ^\mu {{\mathcal {D}}}_\mu - m_f)\Psi _f, \end{aligned}$$
(1)

such that f represents the fermions in the theory, \(A_{non-min}^\mu \sim A^\mu + g\epsilon _{\mu \nu \kappa \lambda }\,\xi ^{\nu }F^{\kappa \lambda }\) and \(A_{non-min}^\mu J_\mu = A_{non-min}^\mu {\bar{\Psi }}\gamma _\mu \Psi \) is the current matter term, where the new covariant derivative is \({{\mathcal {D}}}_\mu \), with g as a Lorentz breaking parameter, and the current \(J^\mu \) carries the presence of matter.

It is studied in various branches of physics, such that in magnetic moment generation [24], in Rashba spin-orbit interaction, in Maxwell–Chern–Simons vortices [32], on vortexlike configurations [33], in Casimir effect [34, 35], in cosmological constraints in electrodynamic [36, 37] and on an analogy of the quantum hall conductivity [38]. In the non-relativistic limit, there are studies in an Aharonov–Bohm–Casher system, in quantum holonomies, in a Dirac neutral particle inside a two-dimensional quantum ring, on a spin-orbit coupling for a neutral particle. In the relativistic case, there are studies on Einstein–Podolsky–Rosen correlations, geometric quantum phases, Landau–He–McKellar–Wilkens quantization, and bound state solutions for a Coulomb-like potential, quantum scattering [39] and in a scalar field [40,41,42,43,44,45,46].

In this article, we investigate the effective electromagnetism that a plasma undergoes in the presence of a quadrivector that violates the Lorentz symmetry coming from the non-minimum coupling. The structure of this paper is as follows: in Sect. 2 we study the influence of space-time anisotropies under a plasma environment by our non-minimal coupling, in the Sect. 3 we study the modification in electromagnetism, caused by the Lorentz breaking sector in the effects of the z-pinch model, in the Sect. 4 we present our conclusions.

2 Plasma with Lorentz symmetry violation

In this section, we investigated the influence of the spacetime anisotropies under a Plasma environment by our non-minimal coupling. For this, we take the Lagrangian and analyze the term where we have LSV, and then we have the modified mechanical momenta

$$\begin{aligned} \vec {\Pi } _{\pm }=\vec {p}{\mp } e\vec {A}{\mp } g\left[ \xi ^{0}\vec {B}-\vec {\xi }\times \vec {E}\right] , \end{aligned}$$

with \((g\xi ^{0},g\vec {\xi })\) being a perturbation quadrivector parameter \(\xi ^\mu \). Under that consideration, the main Hamiltonian associated with low-energy plasma particle motions can be depicted as \({\mathcal {H}}_{\pm } = \frac{1}{2m_\pm }\left( \Pi _{\pm } \right) ^2 \pm e \phi \). Using the connection between the Electromagnetic fields and the potentials we observe that \(\vec {E} = -\nabla \phi - \frac{\partial {\vec {A}} }{\partial t}, \,\,\,\,\,\, {\vec {B}} = \nabla \times {\vec {A}} \), and given that we are interested in stationary configurations \(\frac{\partial {\vec {A}}}{\partial t}=0 \). Again, one may see that \( \vec {E} (\vec {r}) = - \nabla \phi (\vec {r}),\,\,\,\,\,\, {\vec {B}}(\vec {r}) = \nabla \times {\vec {A}}(\vec {r}) \). Then, the Hamiltonian becomes

$$\begin{aligned} {\mathcal {H}}_{\pm }= & {} \frac{1}{2m_\pm }\left( \vec p {\mp } e {\vec {A}} {\mp } g \left[ \xi ^0 (\nabla \times {\vec {A}}) + {\vec {\xi }} \times (\nabla \phi )\right] \right) ^2 \pm e \phi . \end{aligned}$$

Given the axial symmetries imposed by the Weibel model, we can observe that \({\vec {A}} = A_z {\hat{e}}_z\), and in a similar way we can put \(\phi =\phi (r)\), then we encounter the following equations

$$\begin{aligned} {\mathcal {H}}_{\pm }= & {} \frac{1}{2m_\pm }\left( \vec p {\mp } e {\vec {A}} {\mp } g \left[ \xi ^0 \left( -\frac{d A_z}{d r} {\hat{e}}_r\right) \right. \right. \\{} & {} \left. \left. + {\vec {\xi }} \times \left( \frac{d \phi }{d r} {\hat{e}}_r\right) \right] \right) ^2 \pm e \phi . \end{aligned}$$

Looking more explicitly for the components obtained inside the momentum term at the Hamiltonian, we observe that \({\vec {\xi }} = \xi _r {\hat{e}}_r + \xi _\phi {\hat{e}}_\phi + \xi _z {\hat{e}}_z\), and considering that we are able to attribute any value to the proposed perturbation quadrivector \((\xi ^0,\xi ^1, \xi ^2, \xi ^3)\) only using the condition that the spatial part of it maintains its norm equal to the unity.

Considering that the E.M. equations associated with the potentials for the new proposition can be written as (restricting our analysis for stationary cases)

$$\begin{aligned} - \nabla ^2 \phi= & {} 4\pi \rho - g {\vec {\xi }} \cdot \left( \nabla \times \vec J \right) , \end{aligned}$$
(2)
$$\begin{aligned} - \nabla ^2 {\vec {A}}= & {} \frac{4\pi }{c}\vec J + g \left[ \xi ^0 \nabla \times \vec J + {\vec {\xi }} \times \nabla \rho \right] . \end{aligned}$$
(3)

3 Non-neutral Plasma pinch effect with CPT-odd coupling

Now, we will apply the considerations of the modification in electromagnetism, caused by the Lorentz breaking sector in the effects of the z-pinch model, initially described by Weibel in his paper [4], to recover this theory and verify the new effects of a given parameter g.

In other to evaluate some conclusions about \(\vec J\), we take the constant temperature parameter \(\beta = (k_B T)^{-1}\), in canonical Ensemble to describes Plasma fluids \(\mathcal {F}_{\pm } = a_{\pm }exp\left( -\beta \mathcal {H}_{\pm }\right) \delta (p_z) \), such that,

$$\begin{aligned}{} & {} n_{+} = \int \mathcal {F}_{+} (\vec p, \vec q) d^3 \vec p,\nonumber \\{} & {} \vec J_{+}(\vec q) = \frac{e}{m_{+}} \int ({\vec {\Pi }}_+) \mathcal {F}_{+}(\vec p,\vec q) d^3 \vec p,~ \end{aligned}$$
(4)
$$\begin{aligned}{} & {} n_{-} = \int \mathcal {F}_{-} (\vec p, \vec q) d^3 \vec p,\nonumber \\{} & {} \vec J_{-}(\vec q) = \frac{e}{m_{-}} \int ({\vec {\Pi }}_-) \mathcal {F}_{-}(\vec p,\vec q) d^3 \vec p, \end{aligned}$$
(5)

where \(a_\pm \) are integration constants.

Introducing the space-like condition from the Lorentz vector \(\xi ^\mu = (0,\vec {\xi })\), where \(\vec {\xi } = \hat{e}_{\phi }\), and then we choose \((\xi ^{0},\xi ^{1},\xi ^{2},\xi ^{3})=(0,0,1,0)\), which produce

$$\begin{aligned} \vec {\xi }\cdot \left( \nabla \times \vec {J}\right) =\left( \nabla \times \vec {J}\right) _{\phi }=-\frac{dJ_{z}}{dr}, \end{aligned}$$

and

$$\begin{aligned} \xi ^{0}\nabla \times \vec {J}+\vec {\xi }\times \nabla \rho =\hat{e}_{\phi }\times \nabla \rho =-\frac{d\rho }{dr}\hat{e}_{z}, \end{aligned}$$

where we use \(\vec {J}=J(r)\hat{e}_z\), and \(\rho =\rho (r)\) as proposed by [4], such that \(\rho = e n_{0} (n_{+} - n_{-})\) and \(J_z = J_{+} + J_{-}\). The potential equations can be written as

$$\begin{aligned} \frac{1}{r}\frac{d}{dr}\left( r\frac{d\phi }{dr}\right) =-4\pi \rho -{ { g \left( \frac{dJ_z}{dr}\right) }}, \end{aligned}$$
(6)

for the electric sector, and

$$\begin{aligned} \frac{1}{r}\frac{d}{dr}\left( r\frac{dA_{z}}{dr}\right) =-\frac{4\pi }{c} J_{z}+ g \left( \frac{d\rho }{dr} \right) , \end{aligned}$$
(7)

for the magnetic sector. Now, using the following parameterization based on Weibel’s paper parameterization [4] and considering that terms with \(e^2\), \(g^2\) and \(e\,g\) we can neglect, due to their orders of magnitude, knowing that they usually appear multiplying the potential function, generating terms of negligible values.

$$\begin{aligned} \frac{1}{m_+}= & {} \frac{1}{2M}(1- b),\quad \frac{1}{m_-}= \frac{1}{2M}(1+ b),\\{} & {} (a_+a_-)^{\frac{1}{2}}=n_0,\quad r=\left( \frac{M}{{e}^{2}n_0}\right) ^{\frac{1}{2}}x, \end{aligned}$$

and the fields

$$\begin{aligned} \frac{eA(r) }{2(Mk_BT)^{\frac{1}{2}}}= u (x),\quad \frac{e{\phi }(r)}{k_B T} - \frac{1}{2} \ln \left( \frac{a_+}{a_-}\right) = v(x). \end{aligned}$$
(8)

Being \(a_{\pm }\) represents the normalization constant of each distribution \(F_{\pm }\). Here, y and u represent, respectively, the dimensionless electric potential and the magnetic vector potential. x is a dimensionless radial coordinate. \(n_{0}\) is a typical plasma particle density in the center of the cylinder, taking into account ion and electrons, \(M = \frac{m_{+}m_{-}}{m_{+}+ m_{-}}\) is a reduced mass for the species analyzed, and \(\beta = \frac{1 - \frac{m_{-}}{m_{+}}}{1 + \frac{m_{-}}{m_{+}}}\) is the dimensionless difference of mass between the ions and electrons [4, 5]. There is a need to redefine the derivatives depending on the new parameters \(dr = \sqrt{\frac{M}{e^{2}n_{0}}} dx\) and \(\frac{d}{dr}=\sqrt{\frac{e^{2}n_{0}}{M}} \frac{d}{dx}\).The densities expressions became,

$$\begin{aligned} \rho= & {} e n_{0} \exp \left( -{u}^{2}\right) \left[ \exp \left( -{u}^{2}{\beta }+v\right) - \exp \left( {u}^{2}{\beta }-v\right) \right] \nonumber \\{} & {} + u v'\exp \left( g \sqrt{\frac{n_{0}}{\beta }} \frac{1}{M}(1-\beta ) u v'\right) , \end{aligned}$$
(9)

and

$$\begin{aligned} J= & {} \frac{e^{2} n_{0}}{2M} \frac{2 \sqrt{Mk_{B}T}}{e} u \exp \left( -{u}^{2}\right) \left[ \exp \left( -{u}^{2}{\beta }+v\right) \nonumber \right. \\{} & {} \left. - \exp \left( {u}^{2}{\beta }-v\right) \right] + u v'\exp \left( g \sqrt{\frac{n_{0}}{\beta }} \frac{1}{M}(1-\beta ) u v' \right) .\nonumber \\ \end{aligned}$$
(10)

Then, replacing these expressions of densities in the differential equations that we have before, we achieve this new equation system that allows us to find the fields equations

$$\begin{aligned} v''+\frac{v'}{x}= & {} \frac{M}{k_{B}T} \exp \left( -{u}^{2}\right) \left[ \exp \left( -{u}^{2}{\beta }+v\right) \nonumber \right. \\{} & {} \left. - \exp \left( {u}^{2}{\beta }-v\right) \right] \nonumber \\{} & {} \times \, \exp \left[ g (n_{0}\,k_{B}T)^{\frac{1}{2}} \frac{1}{2M} (1-b)\,u\,v'\right] , \end{aligned}$$
(11)

and

$$\begin{aligned} u''+\frac{u'}{x}= & {} u \exp \left( -{u}^{2}\right) \left[ \frac{(1-{\beta })}{2}\exp \left( {u}^{2}{\beta }-y\right) \nonumber \right. \\{} & {} \left. \,+ \, \frac{(1+{\beta })}{2} \exp \left( -{u}^{2}{\beta }+y\right) \right] \nonumber \\{} & {} \times \, \exp \left[ g (n_{0}\,k_B T)^{\frac{1}{2}} \frac{1}{2M} (1-b)\,u\,v'\right] . \end{aligned}$$
(12)

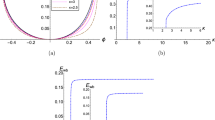
To find v(x) and u(x), we use algorithms for numeric methods to solve this ordinary differential equations system, using the Runge–Kutta (RK) method, in the Fortran-90 language, exploring the distinct values of the parameter g. In order to run the RK code, we use a computer with 2 processors Intel Quad Core Xeon E5540, 2.53 GHz, 8 M L3 cache, 5.86GT/s, and 24GB of memory, DDR3 ECC SDRAM, 1066 MHz. Note that if we take the parameter \(g=0\) we recover the expressions of the classic model explored in the papers [4, 5]. Thus, using \(g=10^{-15}\) and the same initial conditions in an algorithm, we achieve similar results for the fields and densities in Fig. 1. Considering the dimensionless terms associated with the arguments of exponential functions, it can be noted that the parameter g can be associated with the ratio between the magnetic interaction (magnetic pressure) and the electrostatic interaction (electrostatic potential energy) merged. See the demand for dimensionlessness of the product \(\frac{[eB_0R_0^2]}{[V_0]}= \frac{[q] [B_0][R_0]^2}{[V_0]}=[g]\) Using the input parameters from Weibel’s [4] original article, g would be on the order of \(10^{-10}\).

Fig. 1
figure 1

The fields and densities curves as a function of the plasma column radius (\(u(0)=0.05,y(0)=0.00279376, v(12)=17.9961, u(12)=5.83457\)), \((\beta =0.999455, M/k_B T=10\)), (\(g=10^{-15}\))

Full size image

By changing the values of the coupling constant g, varying by one order of magnitude at a time, between the values of \(g=10^{-15}\) and \(g=10^{-7}\), the profiles are of the same form. Although, when we achieve the value of \(g=10^{-6}\) we observe an alteration in the form of the profiles, as we see in the Fig. 2.

Fig. 2
figure 2

The fields and densities curves as a function of the plasma column radius (\(u(0)=0.05,y(0)=0.00279376, v(12)=17.9961, u(12)=5.83457\)), \((\beta =0.999455, M/k_B T=10\)), (\(g=10^{-15}\) and \(g=10^{-6}\))

Full size image

For the values of “g” between \(g=10^{-6}\) and \(g= 6\times 10^{-6}\), it was possible to see different alterations in the curves that present the field intensities and particle densities, as we see in the Fig. 3.

Fig. 3
figure 3

The fields and densities curves as a function of the plasma column radius (\(u(0)=0.05,y(0)=0.00279376, v(12)=17.9961, u(12)=5.83457\)), \((\beta =0.999455, M/k_B T=10\)), varying between (\(g=10^{-15}\) and \(g=6 \times 10^{-6}\))

Full size image

Analyzing the densities graphs is possible to see that in the same way that the column radius grows up, the densities of particles go to zero. This means that, in that parameter configuration, the plasma column is confined. Furthermore, it is possible to note that the parameter g can alter the profile of particle densities. As far as the coupling constant value increase, the densities of the electrons became more concentrated, assuming a profile similar to a Dirac’s delta distribution function, evidencing even more the profile of skin effect [47]. The phenomenological effect of electron condensation at the plasma edge, directly points to a reinforcement of the conductive properties of non-neutral plasma without collisions. These characteristics may be associated with critical conditions. For the values of “g” above that we used in the algorithm, larger than \(g= 6\times 10^{-6}\), the algorithm was unable to complete the resolution.

Exploring more possibilities related to the preferential direction of the background field vector, we investigate the perturbation contribution if the background vector had the preferential direction in \((0,0,0,\xi ^3=1)\) and \((0,\xi ^2=1,0,0)\). However, in these scenarios, the contribution of the perturbation factor is negligible, returning to the results presented in [4] and [5].

To improve our analysis, we calculate the ratio between electromagnetic energy and thermal energy, following the method used in [5]. The electromagnetic energy is given by

$$\begin{aligned} E_{E M}=\frac{1}{8 \pi } \int \left[ (-\nabla \Phi )^{2}+(\nabla \times \vec {A})^{2}\right] r L d r d \phi . \end{aligned}$$
(13)

Using thermal energy as the integration of an ideal gas approximated energy.

$$\begin{aligned} E_{T}=\frac{3}{2} \int \left( n_{+}+n_{-}\right) k_B T r L d r d \phi . \end{aligned}$$
(14)

Using the same change of variables proposed by [4], we achieve the following expressions.

$$\begin{aligned} E_{E M}= & {} \frac{L(k_B T)^{2}}{4 e^{2}} \int _{0}^{R 0\left( \frac{e^{2} n 0}{M}\right) ^{\frac{1}{2}}}\nonumber \\{} & {} \times \left[ \left( \frac{\partial y}{\partial x}\right) ^{2}+\frac{4 M}{k_B T}\left( \frac{\partial u}{\partial x}\right) ^{2}\right] x d x, \end{aligned}$$
(15)
$$\begin{aligned} E_{T}= & {} 3 k_B T \pi {\text {Ln}}_{0}\left( \frac{M}{e^{2} n 0}\right) \int _{0}^{R 0\left( \frac{e^{2} n 0}{M}\right) ^{\frac{1}{2}}}\nonumber \\{} & {} \times \left( \frac{n_{+}}{n_{0}}+\frac{n_{-}}{n_{0}}\right) x d x. \end{aligned}$$
(16)

As a result, of analysing the confinement configurations, the ratio between the electromagnetic energy and the thermal energy indicates a value bigger than unit \(E_{E M} / E_{T}>1\), meaning the electromagnetic field had energy enough to contain the expansion of the plasma column. Calculating this energy ratio for the different confinement configurations that we analyze and for the different values of the “g” parameter that we analyze the plasma column, the ratio \(E_{E M} / E_{T}>1\) is satisfied. It means that the behavior of thermal expansion emulating an ideal gas is suppressed by the electrostatic and magnetostatic field pressure.

4 Conclusions

In this paper we investigate how the Lorentz symmetry violation (LSV) would disturb the electromagnetic field in a plasma electromagnetic confinement scenario known as z-pinch. Initially, we reproduced the results of the classical model, developed by Weibel [4] and [5], using a Fortran-90 code, to solve the differential equation system from the development of the new model, considering that the values of the coupling constant “g” were null or very small (Fig. 1).

Increasing values to the coupling constant “g”, we introduce the perturbation effect from the term of Carrol, Field, and Jackiw that appears in the graphs of field intensities and electronic densities. For values of the order \(g=10^{-6}\), the fields and electronic densities begin to suffer the influence of the anisotropy caused by the LSV, modifying the aspect of the fields and electronic densities curves (Fig. 2). In the range of \(g=1.10^{-6}\) and \(g=6.10^{-6}\), was possible to detect more modifications in the intensities of the fields e electronic densities (Fig. 3).

For values in the order of \(\gtrsim 6 \times 10^{-6}\), we note an instability region, that collapses the intensity of the field, electronic densities, and the confinement configuration of the plasma column.

According to these results, in a scenario of LSV, a background field vector would couple with the electromagnetic field, disturbing the classical electromagnetic field and consequently, disturbing particle densities as well.