Invariant mass reconstruction of heavy gauge bosons decaying to $\tau$ leptons using machine learning techniques

Abstract

Many analyses are performed by the LHC experiments to search for heavy gauge bosons, which appear in several new physics models. The invariant mass reconstruction of heavy gauge bosons is difficult when they decay to $\tau$ leptons due to missing neutrinos in the final state. Machine learning techniques are widely utilized in experimental high-energy physics, in particular in analyzing the large amount of data produced at the LHC. In this paper, we study various machine learning techniques to reconstruct the invariant mass of $Z^{\prime }~\rightarrow ~\tau \tau$ and $W^{\prime }~\rightarrow ~\tau \nu$ decays, which can improve the sensitivity of these searches.

1 Introduction

After the discovery of a standard model (SM) like Higgs boson by the ATLAS and CMS experiments at the CERN-LHC [1, 2], a major focus of the current physics program at the LHC is to search for beyond standard model (BSM) signatures. Many analyses are performed at the LHC to search for the production of heavy gauge bosons, $Z^{\prime }$ and $W^{\prime }$, which are predicted by several BSM models. In certain BSM scenarios, the $Z^{\prime }$ and $W^{\prime }$ bosons can preferentially decay to third-generation fermions, which motivates the search for $Z^{\prime }~\rightarrow ~\tau \tau$ and $W^{\prime }~\rightarrow ~\tau \nu$ decays. Both ATLAS and CMS experiments have performed searches for $Z^{\prime }$ and $W^{\prime }$ bosons in the final states with $\tau$ leptons [3,4,5]. The $\tau$ lepton, being the heaviest among the three leptons, decays after a short time to electron, muon, or hadrons, accompanied by neutrinos. The charged leptons, charged hadrons, and neutral hadrons (mostly $\pi ^{0}$s, which further decay to a pair of photons) can be observed in the detector and are referred to as visible decay products. Neutrinos, being very weakly interacting particles, escape the detector undetected. However, at the ATLAS and CMS experiment, the sum of the transverse momentum of neutrinos is indirectly inferred from the momentum imbalance in the transverse plane. So, the missing transverse momentum ($\vec {p}_{T}^{miss}$) is defined as the negative vector sum of all visible particles in the transverse plane. But, the z-component of the neutrino momentum can not be measured since the momentum of the colliding partons is not known. Therefore, it is difficult to reconstruct the invariant mass of the $Z^{\prime }~\rightarrow ~\tau \tau$ and $W^{\prime }~\rightarrow ~\ell \nu$ ($\ell ~=\textrm{e},~\mu ,~\textrm{or}~\tau$) decays. The ATLAS and CMS experiments have used visible di-$\tau$ mass ($m^{vis}_{\tau \tau }$, reconstructed from the visible component of the $\tau$ lepton momentum) or $m(\tau _1, \tau _2, \vec {p}_{T}^{miss})$ [4] in searches for $Z^{\prime }~\rightarrow ~\tau \tau$ and $m_{T}(\ell , \vec {p}_{T}^{miss})$ in searches for $W^{\prime }~\rightarrow ~\ell \nu$, respectively [3,4,5]. Recently, machine learning (ML) techniques have been widely applied in high energy physics data analyses, especially at the LHC, providing remarkable improvements in particle identification, jet classification, event classification, energy regression, etc. In this article, we study the application of ML in the context of reconstructing the full invariant mass of the $Z^{\prime }~\rightarrow ~\tau \tau$ and $W^{\prime }~\rightarrow ~\tau \nu$ decays, which can help in improving the sensitivity of these searches at the LHC due to better separation of signal from the SM backgrounds. We study the reconstruction of $Z^{\prime }~\rightarrow ~\tau \tau$ invariant mass using an artificial neural network (NN), which is implemented with the Python deep learning library Keras [6]. We compare the performance of our results to that of $m^{vis}_{\tau \tau }$ and the invariant mass computed using SVfit [7], which is based on the likelihood method and used by the CMS collaboration to compute the invariant mass of $Z~\rightarrow ~\tau \tau$ and $H~\rightarrow ~\tau \tau$ decays. To reconstruct the invariant mass of $W^{\prime }~\rightarrow ~\tau \nu$ we study a modified adversarial network. The method can also be applicable for $W^{\prime }~\rightarrow ~\textrm{e}\nu$ and $W^{\prime }~\rightarrow ~\mu \nu$ searches. The rest of the paper is structured as follows. The details of BSM and SM simulated samples and the control regions are described in Sect. 2. Sections 3 and  4 provide the details about the ML techniques used for the reconstruction of the invariant mass of $Z'\rightarrow \tau \tau$ and $W'\rightarrow \tau \nu _{\tau }$ final states. The results are presented in terms of improvement in mass resolution. No effort is made to provide any signal significance since a full search analysis is beyond the scope of this paper.

2 Event generation

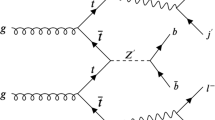
Monte Carlo simulation is used to generate event samples with single $\tau$ and di-$\tau$ in the final states and originating from $W'$, and $Z'$ decays, respectively, as well as $Z/\gamma ^*\rightarrow \tau \tau$ and $W\rightarrow \tau \nu _{\tau }$ background processes. The parton level events are generated using the MadGraph_aMC@NLO 2.9.9 [8] and Pythia8 [9] is used for fragmentation and hadronization. The detector simulation and object reconstruction are performed using the fast simulation package Delphes 3.5 [10], with the CMS detector configuration, taking into account the acceptance and expected performance of the detector. The heavy gauge bosons are generated by following a simplified model, which extends the SM field content by introducing the massive vector fields $W^{\prime \pm }$ and $Z^{\prime }$ [11]. The sensitivity to searches of new heavy bosons is usually explored using a reference model, in which $Z'$($W'$) interacts with the leptons with the same left-handed couplings as the counterpart Z(W) bosons in the SM. The signal samples are produced for the various resonant masses in the 1–6 TeV range with the 250 GeV interval. The decay width and the cross section of some of the signal samples are given in the Table 1. The main backgrounds considered for the $Z'\rightarrow \tau \tau$ and $W'\rightarrow \tau \nu _{\tau }$ are the $Z/\gamma ^* \rightarrow \tau \tau$ and $W\rightarrow \tau \nu _{\tau }$, respectively. The final states with $\tau$-leptons decaying to hadrons are considered. The sum of the visible components of the tau lepton is required to have the $p^{\tau }_{T} > 80$ GeV and $-2.3< \eta < 2.3$. The identification efficiencies of the $\tau$ leptons are considered according to [12]. Figure 1 shows the visible invariant mass and transverse mass distributions of $Z^{\prime }$ and $W^{\prime }$, respectively, comparing with their own generated invariant mass. In the heavy gauge boson search, the invariant mass can provide a better separation between the signal and the background compared to the visible mass distribution [13]. For the di-$\tau$ final states, we study a supervised learning technique, which is a regression method using a deep neural network (DNN) [14]. To evaluate the expected improvement in the performance, the ML reconstructed invariant mass is compared to the invariant mass reconstructed using the SVfit algorithm [7]. The single $\tau$ final states have enriched $p^{miss}_{T}$ contribution, where there are two types of neutrino contributions originating from $W'$ and the hadronic $\tau$ decays, respectively. In this case, we study the invariant mass reconstruction by proposing a new network architecture which has similar network architecture as that of generative adversarial network called modified adversarial network (mAN), discussed in Sect. 4.2.

Table 1 The cross section and mass decay width of the signal samples

Fig. 1

The visible ($M_{vis}$) and generated invariant mass (M) of $\tau \tau$ final states (Top). The transverse ($M_{T}$) and generated mass (M) of $\tau \nu _{\tau }$ final states (Bottom)

3 Invariant mass of $Z'\rightarrow \tau \tau$

In this section, we study the reconstruction of the invariant mass of $Z'\rightarrow \tau \tau$ using a deep neural network architecture and compare its performance to that of the SVfit algorithm.

3.1 DNN regression

High-level keras API gives the architecture for constructing the DNN. The NN used in this study comprises four hidden layers and 110 fully connected neurons. The network architectural details are shown in the Table 2. Each layer is re-weighted according to the gradient value of the mean squared loss function. The commonly employed “rectified linear unit (ReLU)” activation function is used.

The DNN model is trained using thirteen input variables: Four components of the visible momenta and visible $\tau$ lepton mass from each $\tau$ leptons, the $p_{T}^{miss}$ components, and the visible invariant mass of the di-$\tau$ system. Figure 2 shows the training performance of the DNN regression in terms of the loss vs the epoch. The model is trained with the batch size of 128 over an epoch until the loss is saturated. The training samples consist of events with double $\tau$ final states which includes Drell–Yan events and $Z^{\prime }\rightarrow \tau \tau$ events with mass ranging from 1 to 6 TeV with 250 GeV interval. For training and validation we have produced 10 thousands events for each sample. The 1000 events are used for testing the model. Once the regression model is well trained, the performance of the model is tested by obtaining the invariant mass distribution from the test samples that consists of $Z^{\prime }\rightarrow \tau \tau$ events at 3, 4, 5 and 6 TeV and the $Z\rightarrow \tau \tau$ events.

3.2 Mass reconstruction using SVfit

To evaluate the performance of the neural network, the NN reconstructed mass is compared to that of other methods, such as SVfit [7]. SVfit reconstructs the mass of the di-$\tau$ system using a dynamical likelihood technique. The term dynamical likelihood techniques refer to likelihood-based methods used for the reconstruction of kinematic quantities on an event-by-event basis. The inputs to SVfit are the visible decay products of the $\tau$-leptons, x, and y components of $p_{T}^{miss}$ as well as its covariance matrix. The $p_{T}^{miss}$ covariance matrix represents the expected resolution of the $p_{T}^{miss}$ reconstruction in the detector.

Table 2 The DNN architecture for $Z'\rightarrow \tau \tau$ mass regression

Fig. 2

The training of DNN for $Z^{\prime }$ samples. The validation and training loss values are close for higher epochs, which ensures the training is not over or under-fitted

3.3 Results

The reconstructed invariant mass for the $m_{Z} =90$ GeV and for different $m_{Z'}$ are shown in Figs. 3 and 4, respectively. The distribution of the relative difference of the reconstructed mass and the true mass, $(M_{\text {reco}}-M_{\text {gen}})/M_{\text {gen}}$ distributions obtained from the SVfit and DNN algorithm for different $m_{Z'}$ are shown in Fig. 5. It is observed that the resolution of the $Z^{\prime }\rightarrow \tau \tau$ invariant mass improves significantly by DNN regression. The DNN regression is also able to interpolate for in-between mass points, which are not used in the training. Figure 6 shows that the DNN regression is able to predict the mass distribution for the samples generated at 4.1 and 4.9 TeV, which are not used in the training. Furthermore, it is to be noted that the reconstruction using DNN regression is faster than the SVfit algorithm. The training of neural networks depends on the CPU and GPU performance of the computational system. In the current training, with 210,000 events, we have used an 8 core CPU with 3.2 GHz clock speed which computed each epoch in 0.3 s, for 4000 epochs it is around 20 min. After training, to evaluate 10,000 events it takes less than a minute. On the other hand, the SVfit algorithm in the same architecture takes approximately 1.22 s for one event. Therefore the total time taken for a sample with 10,000 events is approximately 3 h 23 min.

Fig. 3

The invariant mass distributions of Z boson obtained from the DNN regression and SVfit method

Fig. 4

The distribution of $Z'\rightarrow \tau \tau$ invariant mass obtained from the DNN regression and SVfit method

Fig. 5

The comparison of the distributions of $(M_{\text {reco}}-M_{\text {gen}})/M_{\text {gen}}$ for $Z^{\prime }\rightarrow \tau \tau$ decays obtained from DNN and SVfit methods

4 Invariant mass of $W'\rightarrow \tau \nu _{\tau }$

Unlike the $Z'\rightarrow \tau \tau$ process where we have thirteen variables, such as the 4-momenta and visible mass of each tau, the components of missing transverse energy and the invariant mass of visible di-$\tau$ system to fit the DNN regression model, there are lesser variables available for single tau final state. Therefore, DNN may not be an optimal model for such a regression problem. So in this case we also studied a neural network architecture like adversarial network model, since it can learn the invariant mass distribution from the given data and help to reproduce the same distribution. As discussed in Sect. 4.2 we modify the adversarial network into a regression network by learning from the simulated mass, which helps to improve the reconstructed invariant mass resolution. Note that mAN was also studied for $Z'\rightarrow \tau \tau$ mass regression, however, it doesn’t show significant improvement with respect to the DNN model. Therefore, it is not reported in this article.

4.1 DNN regression

To compare the results of the adversarial networks, we perform regression using a deep neural network as discussed in the Sect. 3.1. The best-optimized model for $W'$ is shown in Table 3. The DNN model is trained using seven input variables: Four components of the visible momenta of the $\tau$ lepton, the $p_{T}^{miss}$ components, and the transverse mass. Figure 7 shows the training performance of the DNN regression in terms of the loss vs the epoch. After 4000 epochs, the loss is saturated by obtaining the optimized NN model. Once the DNN regression model is trained, the invariant mass distribution is obtained from the test samples which consists of $W'\rightarrow \tau \nu _{\tau }$ events at 3, 4, 5 and 6 TeV and the $W\rightarrow \tau \nu$ events.

4.2 Adversarial network regression

The modified adversarial network consists of two neural network components, generator (G) and discriminator (D), as shown in Fig. 8. A generator neural network component, which is the same as the DNN model used in the previous section, has the input layer with the components of the visible momentum of the $\tau$ lepton, $p_{T}^{miss}$ components, and the transverse mass as input variables and one output node. The discriminator is a classification network, having the input as the simulated mass of $W'$ and the output value of the generator network. The architectures of these two networks are described in Table 4. Unlike the DNN regression, the generator learns from the output value of the discriminator. However, the output of the generator and the true simulated mass of the $W'$ boson are fed to the discriminator, which learns to discriminate the true simulated mass of the $W'$ boson from that of the mass obtained by the generator. After a certain iteration of training, both the generator and the discriminator find Nash’s equilibrium [15] when the output of the generator matches that of the true simulated value and the discriminator output is approximately 0.5. The discriminator has the input of simulated mass distribution ($\mu _M$) and the generated mass distribution from generator network ($\mu _G$). The value D(x) is the discriminator’s estimate of the probability that real data ($\mu _M$) instance x is real and $G(x_{input})$ is the generator’s output with the training feature ($x_{input}$). The loss function of the adversarial network is defined similar to the generative adversarial network (GAN) [16, 17], except we modify the network by adding mean square error loss term which is the third term in Eq. 1. This helps to train the generator with the input variables.

$$\begin{aligned} L(D,G)&= \mathop {{\mathbb {E}}}_{x\sim \mu _M}\log {D(x)} + \mathop {{\mathbb {E}}}_{x_{input}\sim \mu _G}\log \left( 1-D(G(x_{input}))\right) \nonumber \\&\quad + \lambda \frac{(G(x_{input}) - x)^2}{2} \end{aligned}$$

(1)

Fig. 6

The distribution of $Z'\rightarrow \tau \tau$ invariant mass obtained from the DNN regression. The mass points 4.1 and 4.9 TeV are not used in the training but tested to verify whether the NN model interpolates well for in-between mass points

All the hyper-parameter such as the number of neurons, learning rate and $\lambda$ are tuned using the GridsearchCV method. The training performance of adversarial neural network is obtained from the generator and discriminator loss functions. Figure 9 shows the values of the loss over iterations for both generator and discriminator, which are saturated and coinciding with each other after sufficient number of iterations. This ensures that the model is fitted properly. Once the mAN model is trained well, the invariant mass distribution obtained from the test sample which consists of $W'\rightarrow \tau \nu _{\tau }$ events at 3, 4, 5 and 6 TeV and the $W\rightarrow \tau \nu$ events.

Table 3 DNN architecture for $W'\rightarrow \tau \nu _{\tau }$ mass regression

4.3 Results

The reconstructed invariant mass for the $m_{W}=80$ GeV and for different $m_{W'}$ are shown in Figs. 10 and 11, respectively. The comparisons of resolutions are presented for different $m_{W'}$ values in Fig. 12. From the Figs. 11 and 12, it is observed that the mass regression using the mAN model not only reconstructs the full invariant mass of $W'\rightarrow \tau \nu$ system, where a part of the energy is missing due to neutrinos, but also improves its resolution significantly in comparison to that of the regression using a DNN model. The mAN regression is also able to interpolate for in-between mass points, which are not used in the training. Figure 13 shows that the mAN regression is able to predict the mass distribution for the samples generated at 4.1 and 5.6 TeV, which are not used in the training.

Fig. 7

The training of DNN for $W^{\prime }$ samples. The validation and training loss values are close for higher epochs, which ensures the training is not over or under-fitted

Fig. 8

A schematic diagram of the adversarial neural network used for performing mass regression of $W'\rightarrow \tau \nu$

Table 4 The detailed architecture of the modified adversarial network model

Fig. 9

The training performances of mAN for different $W^{\prime }$ mass are shown. The plots show the loss values for discriminator and generator

Fig. 10

The invariant mass distributions of W boson obtained from the DNN regression and modified adversarial network

Fig. 11

The invariant mass distributions of $W'$ obtained from the DNN regression and modified adversarial network

Fig. 12

The comparison of the distributions of $(M_{\text {reco}}-M_{\text {gen}})/M_{\text {gen}}$ for $W^{\prime }\rightarrow \tau \nu$ decays obtained from DNN and mAN methods

Fig. 13

The distribution of $W'\rightarrow \tau \nu$ invariant mass obtained from the mAN regression. The mass points 4.1 and 5.6 TeV are not used in the training but tested to verify whether the mAN model interpolates well for in-between mass points

5 Summary

We studied different ML-based algorithms to reconstruct invariant mass of high mass resonances decaying to $\tau$-lepton final states. It is found that a DNN-based mass regression provides better performance, in terms of mass resolution, in reconstructing the invariant mass of the $Z'\rightarrow \tau \tau$ system in comparison to traditional likelihood-based algorithms, such as SVfit. It is also relatively faster in terms of computing time. We also studied a modified adversarial network model, to reconstruct the full invariant mass of the $W'\rightarrow \tau \nu$ decays, where the $\tau$ decays to hadrons and neutrino. The performance of the adversarial model is compared to that of the mass regression obtained using a DNN model with the same set of input variables. The invariant mass obtained with the adversarial model not only restores the mass peak but also significantly improves its resolution in comparison to that of the DNN model. We expect that such a reconstruction of the invariant mass will provide well-separated distributions against the standard model backgrounds and will significantly improve the search capacity of the $W'\rightarrow \tau \nu$ processes. Furthermore, this technique can also be applicable for reconstructing the invariant mass of $W'\rightarrow e\nu$, $\mu \nu$ processes as well as that of the charged Higgs boson ($H^+\rightarrow \tau \nu$), significantly enhancing their search capabilities.