No scalar-haired Cauchy horizon theorem in charged Gauss–Bonnet black holes

Abstract

Recently, a “no inner (Cauchy) horizon theorem” for static black holes with non-trivial scalar hairs has been proved in Einstein–Maxwell–scalar theories and also in Einstein–Maxwell–Horndeski theories with the non-minimal coupling of a charged (complex) scalar field to Einstein tensor. In this paper, we study an extension of the theorem to the static black holes in Einstein–Maxwell–Gauss–Bonnet-scalar theories, or simply, charged Gauss–Bonnet (GB) black holes. We find that no inner horizon with charged scalar hairs is allowed for the planar ($k=0$) black holes, as in the case without GB term. On the other hand, for the non-planar ($k=\pm 1$) black holes, we find that the haired inner horizon can not be excluded due to GB effect generally, though we can not find a simple condition for its existence. As some explicit examples of the theorem, we study numerical GB black hole solutions with charged scalar hairs and Cauchy horizons in asymptotically anti-de Sitter space, and find good agreements with the theorem. Additionally, in an Appendix, we prove a “no-go theorem” for charged de Sitter black holes (with or without GB terms) with charged scalar hairs in arbitrary dimensions.

1 Introduction

It is an important question in general relativity (GR) whether the predictability is lost due to an inner (Cauchy) horizon or not. Recently, Cai et al. established [1,2,3,4] a “no inner (Cauchy) horizon theorem” for both planar and spherical static black holes with charged (complex) scalar hairs in Einstein–Maxwell–scalar (EMS) theories that suggests unstable Cauchy horizons in the presence of charged scalar hairs. A remarkable thing in the proof is its simplicity and quite generic results which do not depend on the details of the scalar potentials and so it’s applicability would be quite far-reaching.

As the first step towards the classification of all possible extensions of the theorem, we extended the theorem to black holes in Einstein–Maxwell–Horndeski (EMH) theories, with the non-minimal coupling of a charged scalar field to Einstein tensor as well as the usual minimal gauge coupling [5]. Actually, since the Horndeski term is a four-derivative term via the Einstein coupling, it generalizes the recent set-up in [1,2,3,4] into higher-derivative theories. There have been also several other generalizations of the theorem [6,7,8].

In this paper, we will consider an extension of the theorem in another important higher-derivative gravity, Einstein–Maxwell–Gauss–Bonnet-scalar (EMGBS) theories with the coupling of a charged scalar hair and the Gauss–Bonnet (GB) term [9], whose equations of motion remain second order as in the Horndeski case. The organization of this paper is as follows. In Sect. 2, we consider the set-up for EMGBS theories in arbitrary dimensions and obtain the equations of motion for a static and spherically symmetric ansatz. In Sect. 3, we consider the radially conserved scaling charge and “no scalar-haired Cauchy horizon theorem” for charged GB black holes. In Sect. 4, we consider the near horizon relations for the fields and the condition of scalar field at the horizons. In Sect. 5, we consider numerical black hole solutions with a Cauchy horizon in asymptotically anti-de Sitter (AdS) space and find good agreements with the theorem. In Sect. 6, we conclude with several remarks. In Appendix D, in addition, we prove a no-go theorem for charged de Sitter black holes (with or without GB terms) with charged scalar hairs in arbitrary dimensions.

2 The action and equations of motion

As the set-up, we start by considering the D-dimensional Einstein–Maxwell–Gauss–Bonnet–scalar (EMGBS) action, up to boundary terms, with a U(1) gauge field $A_{\mu }$ and a charged (complex) scalar field $\varphi$,

$$\begin{aligned} I= & {} \int d^D x \sqrt{-g} \left[ \frac{1}{\kappa } R +\mathcal{L}_m \right] , \end{aligned}$$

(1)

$$\begin{aligned} \mathcal{L}_m= & {} -\frac{Z(|\varphi |^2)}{4 \kappa } F_{\mu \nu } F^{\mu \nu }-{\alpha }(D_{\mu } \varphi )^* (D^{\mu } \varphi )-V(|\varphi |^2) \nonumber \\{} & {} +{\beta }(|\varphi |^2) \left( R_{\mu \nu {\alpha }{\beta }} R^{\mu \nu {\alpha }{\beta }} -{4 R_{ {\alpha }{\beta }} R^{{\alpha }{\beta }}}+R^2\right) , \end{aligned}$$

(2)

where $F_{\mu \nu } \equiv \nabla _{\mu } A_{\nu }-\nabla _{\nu } A_{\mu }$, $D_{\mu } \equiv \nabla _{\mu }-i q A_{\mu }$ with the scalar field’s charge q, and $\kappa \equiv 16 \pi G$. Here, we have introduced Z, V, and ${\beta }$ as arbitrary functions of $|\varphi |^2$, as well as the usual minimal coupling ${\alpha }$. Note that the last term is the (quadratic) Gauss–Bonnet (GB) term [9], which is a topological, i.e., total-derivative, term in $D=4$ for a constant coupling ${\beta }$ so that it does not affect equations of motion and the local structure of spacetime.

Let us now consider the general maximally symmetric and static ansatz,

$$\begin{aligned} ds^2= & {} -h(r)dt^2+\frac{1}{f(r)}dr^2+r^2 d \Omega _{D-2,k}, \nonumber \\ \varphi= & {} \varphi (r),~A=A_t(r)dt, \end{aligned}$$

(3)

where $d \Omega _{D-2,k}$ is the metric of $(D-2)$-dimensional unit sphere with the spatial curvatures which are normalized as $k=1,0,-1$ for the spherical, planar, hyperbolic topologies, respectively. The equations of motion [Here, we consider $D=4$ case for simplicity but we will discuss about higher-dimensional cases later, which are straightforward (for the details, see Appendix A)] are given by,

$$\begin{aligned} E_{A_t}\equiv & {} \frac{1}{{\kappa }} \left( Z(|\varphi |^2) \sqrt{\frac{f}{h}}~ r^{2} A_t' \right) ' -\frac{2 q^2 {\alpha }r^2 |\varphi |^2 A_t }{f} \sqrt{\frac{f}{h}} =0,\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} E_{\varphi }\equiv & {} \left( \sqrt{\frac{h}{f}}f {\alpha }r^2 \varphi ' \right) ' +\frac{ q^2 {\alpha }r^2 A_t^2 \varphi }{h}\sqrt{\frac{h}{f}} \nonumber \\{} & {} +r^{2} \left( \frac{1}{2 {\kappa }} \sqrt{\frac{f}{h}} {\dot{Z}} {A_t'}^2-\sqrt{\frac{h}{f}}~ {\dot{V}} \right) \varphi + {\dot{{\beta }}} \varphi \mathcal{G}=0, \end{aligned}$$

(5)

$$\begin{aligned} E_{h}\equiv & {} \frac{2}{{\kappa }} \left( f-k+r f' \right) +r^2 V (|\varphi |^2) +f {\alpha }r^2 |\varphi '|^2 \nonumber \\{} & {} +\frac{r^2}{2 h} \left( \frac{1}{{\kappa }} {Z}f {A_t'}^2 +2 {\alpha }q^2 |\varphi |^2 A_t^2 \right) \nonumber \\{} & {} +8{\dot{{\beta }}} \left[ (k-3f) f' |\varphi \varphi '| +2 f(k-f) ( |\varphi '|^2\right. \nonumber \\{} & {} \left. +|\varphi \varphi ''|) \right] +32 \ddot{{\beta }} f(k-f) |\varphi \varphi '|^2=0, \end{aligned}$$

(6)

$$\begin{aligned} E_f\equiv & {} \frac{2}{{\kappa }} \left( f-k+r f' \left( \frac{h'}{h} \right) \right) +r^2 V (|\varphi |^2) -f {\alpha }r^2 |\varphi '|^2 \nonumber \\{} & {} +\frac{r^2}{2 h} \left( \frac{1}{{\kappa }} {Z}f {A_t'}^2 -2 {\alpha }q^2 |\varphi |^2 A_t^2 \right) \nonumber \\{} & {} +8{\dot{{\beta }}} \frac{f}{h}(k-3f) h' |\varphi \varphi '|=0, \end{aligned}$$

(7)

where $\mathcal{G}$ is the GB density in $D=4$,

$$\begin{aligned} \mathcal{G}\equiv & {} \frac{2}{\sqrt{f} h^{3/2}} \left[ (k-f) f h'^2\right. \nonumber \\ {}{} & {} \left. -h \left( (k-3f) f' h'+2(k-f) f h''\right) \right] . \end{aligned}$$

(8)

[The prime $(')$ and dot $(\dot{~})$ denote the derivatives with respect to r and $|\varphi |^2$, respectively] Here, (4), (5) are the equations for the gauge field $A_t$ and the scalar field $\varphi$, and (6), (7) are for the metric functions h, f, respectively. As far as we know, there is no exact solution for the charged GB black holes (i.e., with a gauge field $A_t$) with the scalar field’s charge q and the field-dependent coupling ${\beta }(|\varphi |^2)$. In this paper, we will consider numerical solutions of the above non-linear ODE (4) $\sim$ (7) by shooting method and study the black hole’s interior space-time, as well as the exterior space-time. But before that, in the next section we first study the “no scalar-haired Cauchy horizon theorem” to see whether it can be extended to the case with the GB coupling also.

3 No scalar-haired Cauchy horizon theorem

In this section, we consider the “no scalar-haired Cauchy horizon theorem” for charged GB black holes with a charged (complex) scalar hair. One of the key ingredients in the proof of the theorem is the existence of the radially conserved scaling charge,

$$\begin{aligned} \mathcal{Q}= & {} (D-2) r^{D-3} \sqrt{\frac{f}{h}} \left[ \frac{1}{{\kappa }} \left( r {h}'-2h -r {Z} A_t {A_t}' \right) \right. \nonumber \\{} & {} \left. -\frac{2 (D-3)}{r^2} f (r {h}'-2h) \left( (D-4) {\beta }+4 r |\varphi \varphi '| {\dot{{\beta }}} \right) \right] \nonumber \\{} & {} +k \int ^r dr~ r^{D-4} \left\{ 2(D-2) (D-3) \sqrt{\frac{h}{f}} \right. \nonumber \\{} & {} \times \Bigg [\frac{1}{{\kappa }} -4{\dot{{\beta }}} \left( |\varphi (f' \varphi '+2 f \varphi '')| +2 f |\varphi '|^2 \right) \nonumber \\{} & {} \quad -16 \ddot{{\beta }} f |\varphi \varphi '|^2 \Bigg ] \nonumber \\{} & {} +\frac{(D-4)(D-3)(D-2)}{r \sqrt{f} h^{3/2}} \nonumber \\{} & {} \times \Bigg [{\beta }\left( r h (f'h'+2 f h'')-6 f' h^2-r f h'^2 \right) \nonumber \\{} & {} +4 {\dot{{\beta }}}f h (r h'-6h) |\varphi \varphi '|\Bigg ] \nonumber \\ {}{} & {} +\frac{\sum ^D_{n=5} (n-5) (n-4) (n-3)}{r^2 \sqrt{f h}}~ \nonumber \\{} & {} \times \left. 8 {\beta }\left[ r f h'+2 (k-2f) h \right] \right\} , \end{aligned}$$

(9)

where we have recovered the full dimensional dependencies.¹ From the equations of motion (4)–(7), one can prove that $\mathcal{Q}$ is radially conserved, i.e., r-independent, due to a remarkable relation,

$$\begin{aligned} \mathcal{Q}'= & {} 2 \sqrt{\frac{f}{h}} \left[ r \left( \frac{h}{f} {\mathcal{E}_f}'+\frac{1}{2} \frac{{h}'}{f} \mathcal{E}_f \right) \right. \nonumber \\{} & {} \left. +\left( (D-2) \frac{h}{f} +\frac{r}{2} \frac{{h}'}{f}\right) \mathcal{E}_h \right. \nonumber \\{} & {} \left. +\frac{r}{2} h |\varphi '~ \mathcal{E}_\varphi |+\frac{1}{2} \left( (D-2) A_t + r A_t' \right) \mathcal{E}_{A_t} \right] =0, \end{aligned}$$

(10)

where $\mathcal{E}_f =E_f r^{D-4}/2,~\mathcal{E}_h =-E_h r^{D-4}/2,~ \mathcal{E}_\varphi =2 E_\varphi /\sqrt{f h}, ~ \mathcal{E}_{A_t} =- E_{A_t}\sqrt{h/f}$ represent the (rescaled) equations of motion for the fields $f,h,\varphi$, and $A_t$, respectively.

For the planar topology, i.e., $k=0$, the local charge $\mathcal{Q}$ is the Noether charge associated with a scaling symmetry (for the details, see Appendix B) [10]. For non-planar topologies, i.e., $k=+1$ (spherical topology), or $k=-1$ (hyperbolic topology), one can still construct a radially conserved charge $\mathcal{Q}$ by including the non-local parts with space integrals so that the non-conserved terms from the local parts are exactly canceled [4,5,6].

Now, due to the r-independence of the scaling charge $\mathcal{Q}$, one can consider the charges at the horizons, in particular, the outer event horizon $r_+$ and the inner Cauchy horizon $r_-$, if exists, so that we have

$$\begin{aligned}{} & {} \frac{(D-2)}{{\kappa }} \left[ r_+^{D-2} \left. \sqrt{\frac{f}{h}} \left( {h}'-Z A_t A_t' \right) \right| _{r_+} \right. \nonumber \\{} & {} \qquad \left. -r_-^{D-2} \left. \sqrt{\frac{f}{h}}\left( {h}'-Z A_t A_t' \right) \right| _{r_-} \right] \nonumber \\{} & {} \quad =-k \int ^{r_+}_{r_{-}} dr~ r^{D-4} \left\{ 2(D-2) (D-3) \sqrt{\frac{h}{f}} \right. \nonumber \\{} & {} \qquad \times \left. \left[ \frac{1}{{\kappa }} -4{\dot{{\beta }}} \left( |\varphi (f' \varphi '+2 f \varphi '')| +2 f |\varphi '|^2 \right) \right. \right. \nonumber \\ {}{} & {} \left. \left. \qquad -16 \ddot{{\beta }} f |\varphi \varphi '|^2 \right] \right. \nonumber \\{} & {} \qquad +\frac{(D-4)(D-3)(D-2)}{r\sqrt{f} h^{3/2}} \nonumber \\{} & {} \qquad \times \left[ {\beta }\left( r h (f'h'+2 f h'')-6 f' h^2-r f h'^2 \right) \right. \nonumber \\ {}{} & {} \qquad \left. +4 {\dot{{\beta }}}f h(r h'-6h) |\varphi \varphi '|\right] \nonumber \\{} & {} \qquad \left. +\frac{\sum ^D_{n=5} (n-5) (n-4) (n-3)}{r^2 \sqrt{f h}}~ \right. \nonumber \\{} & {} \times \left. 8 {\beta }\left[ r f h'+2 (k-2f) h \right] \right\} . \end{aligned}$$

(11)

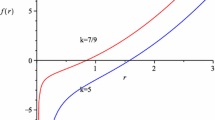
From the property ${h}'\sqrt{{f}/{h}} |_{r_-} \le 0$ at the assumed inner horizon $r_-$ and for non-extremal black holes with the finite Hawking temperature or surface gravity $\sim {h}' \sqrt{{f}/{h}}|_{r_+} >0$ at the outer horizon $r_+$ with $f|_{r_{\pm }}\sim h|_{r_{\pm }}=0$, the purely metric-dependent terms in the left-hand side of (11) are positive , i.e., non-negative (Fig. 1). Moreover, one can prove that $A_t$ needs to be zero at the horizons,

$$\begin{aligned} A_t (r_+)=A_t (r_-)=0, \end{aligned}$$

(12)

from the regularity at the horizons with “charged” (complex) scalar fields [4, 5] so that the gauge field terms in the left-hand side of (11) vanish at the horizons. This regularity condition is another key ingredient for the proof of the theorem (see Appendix C for the proof of (12)).

Fig. 1

Typical plots of f(r) and h(r) for a non-extremal charged black hole with the inner (Cauchy) horizon $r_-$ and the outer (event) horizon $r_+$. Due to the non-vanishing Hawking temperature at the Killing horizon $r_{\pm }$ with $f|_{r_{\pm }}\sim h|_{r_{\pm }}=0$, we have $f'\sim {h}'>0$ at the outer horizon $r_+$, but $f'\sim {h}' \le 0$ at the inner horizon generally, if exists (orange, solid line). In the absence of the inner horizon, $f'$ and ${h}'$ can have arbitrary values but there is no inner point of $f\sim h=0$ (blue, dashed line)

Hence, the left-hand side of (11) is always positive if the two horizons exist, which is consistent with the relation (11) only if the right-hand side is also positive: This is a necessary condition (but not sufficient) for the existence of the inner horizon with the outer horizon (or the existence of the outer horizon with the inner horizon), from the radial conservation of the scaling charge $\mathcal{Q}$. Otherwise, the assumption of existence of the inner (or outer) horizon with charged scalar hairs will not be true, which results in a no-go theorem for the scalar-haired Cauchy horizon. This is a powerful theorem since it does not depend on the details of scalar potential $V(|\varphi |^2)$, contrary to the usual no-hair theorems.

In addition, if there is another horizon, exterior to the outer horizon $r_+$, i.e., the cosmological horizon $r_{++}$ in asymptotically de Sitter space, one can prove also a no-go theorem for charged de Sitter black holes (with or without GB terms) with charged scalar hairs, since (12) can not be satisfied for both the outer horizon and the cosmological horizon (see Appendix D for the proof).

Then, for $k=0$, one can easily find that (11) can not be satisfied since the right-hand side is zero which is in contradiction to the non-vanishing (positive) left-hand side. This means “no smooth inner (Cauchy) horizon with the outer horizon” can be formed for black planes.

However, for $k\ne 0$, the right-hand side does not have a definite sign generally with the GB terms (${\beta }\ne 0$), and so there is no simple condition for the (non) existence of the inner (or outer) horizon associated with non-planar topologies. This implies that, for $k=+1$ (black holes with spherical topology) or $k=-1$ (topological black holes with hyperbolic topology), we may have a Cauchy horizon due to GB terms, depending on the solutions. For example, if we consider the $D=4$ case, for simplicity, where only the first integral in the right-hand side of (11) remains, all the GB terms, except $|\varphi (f' \varphi '+2 f \varphi '')|$, are positive for ${\dot{{\beta }}}(|\varphi |^2), \ddot{{\beta }}(|\varphi |^2)>0$ so that the no-inner-horizon theorem in EMS theories could apply. However, the excepted term can cause a problem in applying the theorem because of the sign-changing behaviors of $f'$ at the two horizons with $f|_{r_{\pm }}\sim h|_{r_{\pm }}=0$, i.e., $f'|_{r_+}>0, f'|_{r_-}<0$, unless compensated by $\varphi$, i.e., $\varphi \varphi '|_{r_+}<0,~\varphi \varphi '|_{r_-}>0$, but $\varphi \varphi ''|_{r_+}, \varphi \varphi ''|_{r_-}>0$. In higher dimensions, we might need more complicated conditions.

This is in contrast to the EMS (Einstein–Maxwell–scalar) theories (${\beta }=0$) [4] or EMH (Einstein–Maxwell–Horndeski) theories with a positive coupling ${\gamma }>0$ to Einstein tensor [5], where (11) is inconsistent unless $k=-1$ so that “no smooth inner (Cauchy) horizon with an outer horizon” can be formed for $k=0$ or $k=+1$.

However, even with GB terms, we have the general criterion as follows, depending on the integral parts of (11): (a) if the right-hand side (RHS) of (11) is zero or negative, the inner (or outer) horizon can not be formed, (b) if RHS of (11) is positive, the inner (or outer) horizon can be formed but not necessarily always. We will see that this general criterion is satisfied by the numerical solutions in Sect. 5.

4 Near horizon relations

In order to find numerical solutions for charged GB black holes, it is useful to study behaviors of metric functions, scalar and gauge fields near the horizons. To this end, we first solve the equation for f (7), which is a quadratic polynomial of f, and obtain

$$\begin{aligned} f^{-1} \equiv e^B= \frac{-\mu (r) {\pm } \sqrt{{\mu }(r)^2-4 {\nu }(r)}}{2}, \end{aligned}$$

(13)

where²

$$\begin{aligned}{} & {} {\mu }(r)\nonumber \\ {}{} & {} = \frac{2 \left( 4 k |\varphi \varphi '| {\dot{{\beta }}} +{r}/{{\kappa }} \right) A' +\left( {r^2} e^{-A} Z A_t'^2+{4} \right) /{2{\kappa }} -{\alpha }r^2 |\varphi '|^2 }{-{\alpha }q^2 r^2 e^{-A} |\varphi |^2 A_t^2-2k/{\kappa }+r^2 V}, \nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned}{} & {} {\nu }(r)= \frac{-24 |\varphi \varphi '| {\dot{{\beta }}} A'}{-{\alpha }q^2 r^2 e^{-A} |\varphi |^2 A_t^2-2k/{\kappa }+r^2 V } \end{aligned}$$

(15)

by introducing $e^A\equiv h(r)$ and $e^{B} \equiv f^{-1}(r)$ for convenience³. Here, we note that the first term in the denominator $\sim e^{-A} |\varphi |^2 A_t^2$ is finite and may not be neglected at the horizons generally, with $e^{-A}\rightarrow \pm \infty , A_t \rightarrow 0, \varphi =finite$. Once the solutions for $A(r),\varphi (r)$, and $A_t(r)$ are obtained, the metric function B(r) can be also obtained by (13). The ± roots depend on the topology parameter k and the region we consider, i.e., the black hole interior $r \in [r_-,r_+]$ or the black hole exterior $r \in [r_+, \infty ]$ or deep interior $r \in [0, r_-]$.

By substituting $e^B$ from (13), the remaining Eqs. (4), (5), and (6) with the three independent fields $A,\varphi , A_t$ can be written as

$$\begin{aligned} {A''=\frac{P}{S}, ~\varphi ''=\frac{U}{W}, ~A_t''=\frac{R}{Y},} \end{aligned}$$

(16)

while $B'$ can be written as

$$\begin{aligned} B'(r)=-\frac{{\nu }' +e^B {\mu }'}{2 e^{2B}+e^B {\mu }} \end{aligned}$$

(17)

for both ± roots of $e^B$. Here, P, S, U, W, R, Y are complicated functions of ($r, e^B,e^{A}, A', \varphi ', A_t', {\dot{{\beta }}}, \ddot{{\beta }}$) whose explicit expressions are not shown here (for the computational details, see Appendix E). Since $A''$ diverges already at the horizons and $A_t''$ is finite for regular solutions with a finite $A_t'$ and the condition of $A_t=0$ (12) at the horizons, $\varphi ''$ gives the most information at the horizons. For the solvability of the information, we consider the case where the term $\sim e^{-A} |\varphi |^2 A_t^2$ in the denominator of (14) and (15) can be neglected by considering a rapidly-decaying gauge field at the horizons, $A_t^2 \sim h^{\delta }~({\delta }>1)$, whilst satisfying (12) also. Then, one can find that

$$\begin{aligned} \varphi ''=C(\varphi , \varphi ', A_t',T)A' +\mathcal{O}(1) \end{aligned}$$

(18)

and so, in order to have a regular scalar field with a finite $\varphi ''$ at the horizons, we need

$$\begin{aligned} C(\varphi , \varphi ', A_t',T)=0 \end{aligned}$$

(19)

at the horizons $r_H$, i.e., $A\rightarrow \infty , A' \rightarrow \pm \infty$ ($+\infty$ for $r_+$, $-\infty$ for $r_{-}$). Here, $T \equiv h'=e^A A'$ corresponds to Hawking temperature (up to a finite factor) and given by

$$\begin{aligned} T =\left. \frac{{\kappa }r^2 Z A_t'^2 \left[ 2 {\kappa }r^2 Z \left( {\alpha }q^2 r^2 e^{-A} |\varphi |^2A_t^2+2 {\kappa }{k}-r^2 V\right) -\widetilde{Q}^2 (r) \right] }{4 \widetilde{Q}^2 (r)(4k |\varphi \varphi '| {\dot{{\beta }}}+{\kappa }r)} \right| _{r_H}, \nonumber \!\!\! \\ \end{aligned}$$

(20)

by keeping $e^{-A} |\varphi |^2A_t^2$ term for the sake of completeness, which will be neglected in the next section for numerical solutions, for simplicity. (See Appendix E for some relevant computations and the explicit form of $C(\varphi , \varphi ', A_t',T)$) $\widetilde{Q}(r)$ is the black hole charge function by integrating the gauge field equation (4),

$$\begin{aligned}{} & {} \frac{Z}{{\kappa }} e^{-(A+B)/2} r^2 A_t'={\widetilde{Q}(r)}, \end{aligned}$$

(21)

$$\begin{aligned}{} & {} {\widetilde{Q}(r)}=2 {\alpha }q^2 \int ^r_{r_H} dr r^2 e^{(B-A)/2} |\varphi |^2 A_t + \widetilde{Q}(r_H) \end{aligned}$$

(22)

so that we obtain, from (21),

$$\begin{aligned} e^B=\frac{{\kappa }^2 Z^2 r_H^4}{\widetilde{Q}^2(r_H)}{A_t'}^2 e^{-A} \end{aligned}$$

(23)

at the black hole horizons $r_H$: By comparing (23) and the near horizon expansion of (13) with $T=e^A A'$, one can find the temperature formula (20).

Then, solving the condition (19), we obtain the condition of $\varphi '|_{r_H}$ at the horizons from a finiteness of $\varphi ''|_{r_H}$. We note that the condition of $\varphi '|_{r_H}$ is important in obtaining numerical solutions in the next section because it gives the proper initial condition at the horizons. As we have noted above, we will consider the rapidly vanishing gauge field $A_t$ at the horizons so that $e^{-A} |\varphi |^2 A_t^2$ term in (14), (15), and (20) are neglected for the solvability of (19).

5 Numerical solutions

In Sect. 3, we have proved that, for the planar topology $(k=0)$ of charged GB black holes, the Cauchy horizon with charged scalar fields can not be formed. However, for non-planar topologies, i.e., spherical ($k=1$) or hyperbolic ($k=-1$) black holes, there is no simple condition for the existence of the haired Cauchy horizons due to the GB term, except a general criterion on the integral parts of the scaling charge. In this section, we consider numerical solutions with the scalar-haired Cauchy horizon for the hyperbolic case as some explicit examples of our theorem.

Fig. 2

Numerical solutions of the $D=4$ hyperbolic charged GB black hole ($k=-1$) with the model (24) and initial conditions (25) in asymptotically AdS space. In the left panel, we plot f (orange), h (blue), $\varphi$ (green), $A_t$ (purple), and they show the inner Cauchy horizon at $r_-\approx 0.240558232$ as well as the outer event horizon at $r_+ \approx 0.837565833$, where all the solutions are smooth. We find $A_t=0$ at the two horizons, in consistent with the condition (12). In the right panel, we plot $r^2 /f,10 r^2/h, {\varphi , A_t/70}$, and the solutions reveal the asymptotically AdS-like behaviors $f \sim h \sim r^{2}$ with $\varphi \sim 0$ and a finite $A_t$

In Fig. 2, we first present numerical solutions of the four-dimensional ($D=4$) hyperbolic charged GB black hole in EMGBS gravity for the choice of the model

$$\begin{aligned} {\beta }(|\varphi |^2)={\lambda }|\varphi |^2,~V(|\varphi |^2) =-6 +m^2 |\varphi |^2, ~ Z(|\varphi |^2)=1 \nonumber \\ \end{aligned}$$

(24)

with ${\lambda }=10^{-10}$, $m^2=-0.18388$⁴, and $q=1.5$. We choose the outer horizon $r_+ \approx 0.837565833$ and the initial conditions at $r_+$ as follows (we have set ${\kappa }\equiv {\alpha }\equiv 1)$:

$$\begin{aligned}{} & {} h(r_+)=-10^{-10},~h'(r_+)=1.23278,\nonumber \\{} & {} A_t(r_+)=10^{-10},~A_t'(r_+)\approx -0.927989424, \nonumber \\ ~{} & {} \varphi (r_+)=1.106834110,~ \varphi '(r_+)=-0.165094, ~\nonumber \\ {}{} & {} \widetilde{Q}(r_+)=0.650999915. \end{aligned}$$

(25)

Here, $\varphi '(r_+)$ and $A_t'(r_+)$ are determined by (19) and (20) by $T=h'(r_+)$, respectively. By rewriting the second-order equations of motion (4), (5), (6) into the first-order forms via new variables $H(r)\equiv h'(r),~ \Phi (r)\equiv \varphi '(r),~ E(r) \equiv A_t' (r)$ (after replacing f(r) and $f'(r)$ by (13) and (17), respectively), we numerically solve the six differential equations (with $k=-1$) by shooting method, for the variables $(h, H, \varphi , \Phi , A_t, E)$ from $r=r_+ +{\epsilon }$ to $r=10^4$ for the black hole exterior solution (we set ${\epsilon }=10^{-9}$), and from $r=r_+ -{\epsilon }$ to $r=10^{-8}$ for the black hole interior solution. We use NDSolve of MATHEMATICA with PrecisionGoal $\rightarrow 26$ and WorkingPrecision $\rightarrow 27$.

The code for the black hole interior solution solves the differential equations up to the inner Cauchy horizon at $r_-\approx 0.240558232$ but does not solve beyond the inner horizon, due to increasing numerical errors at $r_-$. In order to obtain the deep interior solution beyond the inner horizon, we need to consider another set up of the code with now the initial conditions at $r_-$ as follows, which can be determined from the obtained numerical interior solutions:

$$\begin{aligned}{} & {} h(r_-)=10^{-10},\!~h'(r_-)=-2.33135,\nonumber \\{} & {} A_t(r_-)\!=\!-10^{-10},~A_t'(r_-)\approx 1.868563472, \nonumber \\ ~{} & {} \varphi (r_-)=1.140835529,~ \varphi '(r_-)=-0.0560344,\nonumber \\ {}{} & {} ~\widetilde{Q}(r_-)=-0.137024. \end{aligned}$$

(26)

Fig. 3

Plots of the scaling charge $\mathcal{Q}$ (purple) together with its local (blue) and integrand (orange) parts for the numerical solutions in Fig. 2. The local and integrand parts are smooth at the horizons. We can see also the radial conservation, i.e., constancy, of the charge $\mathcal{Q}$, across the horizons

Here, in order to obtain the proper initial conditions of $h'(r_-)$ and $\varphi '(r_-)$, we first determine the black hole charge $\widetilde{Q}$ from $h'(r_-)=-2.328970925, \varphi '(r_-)=-537884.8323$ which can be read naively from the interior solution, and use (19) and (20). It is important to note that $\widetilde{Q}$ is a quite stable parameter in the numerical solutions and its first determination gives the reasonable initial conditions of $\varphi '(r_-)$ which matches well with the interior solution, even with the high values of naively-read $\varphi '(r_-)$ due to numerical errors at $r_-$.

By combining all the solutions in three different regions, we obtain the whole region solution as in Fig. 2 (left panel), which shows the smooth matchings at the inner and outer horizons. Here, note that we need to use the ‘$+$’ root of $f^{-1}=e^B$ in (13) for the black hole interior solution, and the ‘−’ root of for the deep interior and black hole exterior solutions, respectively. The exterior solutions in Fig. 2 (right panel) show the asymptotically AdS-like behaviors $f \sim h \sim r^{2}$ with $\varphi \sim 0$ and finite $A_t$. Figure 3 shows the radially conserved (i.e., constancy) of scaling charge, and its local and integrand parts which show smooth matchings at the horizons and so supports well our numerical solutions.

Fig. 4

Numerical solutions of a $D=4$ hyperbolic charged black hole in EMS gravity with the same model (24) and initial conditions (25) in asymptotically AdS space. This agrees well with Fig. 2 and also the earlier result in [4], but without the complexified integration to avoid the coordinate singularity problem at the inner horizon

In Figs. 4 and 5, for a comparison, we present numerical solutions of the corresponding hyperbolic charged black hole in the EMS case (${\beta }=0$) for the same choice of the model (24) and initial conditions (25), as in [4]. Figure 4 shows quite good agreements with Fig. 2 which can be considered as EMS limit (${{\beta }} \rightarrow 0$) so that it can be a consistency check of our numerical method. Actually, we reproduce the numerical solutions in [4] (Fig. 3) but without using the complexified integration to avoid the coordinate singularity at the inner horizon which can not be applied to our case with GB term, due to different roots of $f^{-1}=e^B$ (13) in different regions: There is only one root of $e^B$ in (13) without GB term (${\beta }=0$) and one has the same field equations for the whole region. One difference is the last point of the deep interior solution where the numerical computation stops, $r\approx 0.0000262$, which is smaller than $r\approx 0.0038097$ for Fig. 2 and might indicate a possible GB effect near $r=0$.

In Fig. 6, we present another numerical solution of the $D=4$ hyperbolic charged GB black hole in EMGBS gravity for the model with

$$\begin{aligned} {\lambda }=10^{-3},~m^2=-0.18,~q=2.5. \end{aligned}$$

(27)

We choose initial conditions

$$\begin{aligned}{} & {} r_+=0.91, h(r_+)=-10^{-10},~h'(r_+)=2.48104 \times 10^{-8},\nonumber \\ {}{} & {} ~A_t(r_+)=10^{-10},~A_t'(r_+)=10^{-4}, \nonumber \\ ~{} & {} \varphi (r_+)=0.682,~ \varphi '(r_+)=-0.0918761, ~\widetilde{Q}(r_+)=0.65.\nonumber \\ \end{aligned}$$

(28)

Using the same method as in Fig. 2, we obtain the numerical solutions for the black hole interior and exterior as shown in Fig. 6. But, in this case no deep interior solution is found due to higher numerical errors at the inner horizon $r_-\approx 0.132916515$. For the exterior solution, we can see the similar AdS-like behaviors in f(r), h(r), $\varphi \sim 0$ and finite $A_t$ as in Fig. 2. Figure 7 shows the radial conservation of $\mathcal{Q}$ as well as its local and integrand parts with smooth matchings at the horizons and so supporting our numerical solutions.

In all the numerical solutions, we find that (a) the vanishing gauge field condition (12), $A_t (r_H)=0$ and (b) the general criterion for the existence of an inner Cauchy horizon, i.e., negativeness of RHS in (11) (or integrand of $\mathcal{Q}$ in Figs. 2, 5, and 7) are satisfied. On the other hand, at the asymptotic boundary ($r=10^4$ in our analysis), we find that $r^2/f \approx 1, \varphi \approx 0$, $r^2/h$ and $A_t$ approach to finite values with vanishing derivatives. This indicates the AdS-like behaviors of $f, h \sim r^2, A_t \sim 1/r, \varphi \sim 1/r^a$ with $a>0$⁵.

Fig. 5

Plots of the scaling charge $\mathcal{Q}$ (dots) and its local (solid line), integrand (dashed line) parts for the numerical solutions in Fig. 4

Fig. 6

Numerical solutions of a $D=4$ hyperbolic charged GB black hole with the model (27) and initial condition (28). In the left panel, we plot f (orange), $10^8 h$ (blue), $\varphi$ (green), $10^4 A_t$ (purple), and no solution is found for the deep interior region due to high numerical errors at the inner horizon $r_-\approx 0.132916515$. In the right panel, we plot $r^2/f,r^2/(10^8 h),{2 \varphi }, 10^4 A_t/45$, and they show the AdS-like behaviors in f, h, $\varphi \sim 0$ and finite $A_t$ as in Fig. 2

6 Concluding remarks

In conclusion, we have studied an extension of the “no scalar-haired inner (Cauchy) horizon theorem” to the electrically charged Gauss–Bonnet (GB) black holes in Einstein–Maxwell–Gauss–Bonnet–scalar (EMGBS) theories with charged (complex) scalar fields. We have found that the condition of vanishing gauge field $A_t=0$ at the horizons from the regularity of equations of motion is unchanged even with GB coupling. We have computed the radially conserved scaling charge $\mathcal{Q}$ for GB coupling ${\beta }(|\varphi |^2)$ in arbitrary dimensions D.

From the constancy of scaling charge $\mathcal{Q}$ at the outer and inner horizons, we have obtained the no scalar-haired Cauchy horizon theorem for $k=0$, i.e., “no scalar-haired inner (Cauchy) horizon for planar ($k=0$) black holes”. For $k=1$ (spherical) or $k=-1$ (hyperbolic) black hole, a simple condition for the no scalar-haired theorem is not available due to some terms in the integral part of $\mathcal{Q}$ which do not have definite signs in the black hole interior region, but one can still consider a general criterion for applying the theorem, depending on the resulting sign of the integral part. This means that a Cauchy horizon with non-trivial, charged scalar hairs might exist even for $k=1$, contrary to Einstein–Maxwell–scalar (EMS) or Einstein–Maxwell–Horndeski (EMH) theories, as a genuine GB effect.

Fig. 7

Plots of the scaling charge $\mathcal{Q}$ (purple) and its local (blue), integrand (orange) parts for the numerical solution in Fig. 6

We have obtained numerical solutions with the inner horizon for $k=-1$ and in the asymptotically anti-de Sitter space. For a very small GB coupling parameter ${\lambda }=10^{-10}$, we have obtained a solution covering the whole region of $r \in [0, \infty ]$, which agrees with EMS solution of [4], but without the “complexification” method to obtain the deep interior solution of $r \in [0, r_-]$. On the other hand, for ${\lambda }= 10^{-3}$, we have obtained solutions for the inner and exterior regions, i.e., $r \in [r_-, \infty ]$ from the initial conditions at the outer horizon $r_+$, but no solution is found for the deep interior region of $r \in [0, r_-]$ due to increased errors in finding initial conditions at the inner horizon. We have checked the radial conservation, i.e., constancy of the scaling charge $\mathcal{Q}$ and the general criterion of the scalar-haired Cauchy horizon in the obtained numerical solutions.

However, we were not able to find numerical solutions with the inner horizon for $k=1$, which might exist due to a GB effect. From the no-go theorem for $k=1$ in EMS theories [1,2,3,4], we expect that the solution may exist in the non-GR branch, where the GB coupling is not small. On the other hand, in Appendix D, we have shown a no-go theorem for charged de Sitter black holes (with or without GB terms) with charged scalar hairs.

It would be a challenging problem to obtain the whole range solutions including the deep interior solutions for a sizable coupling ${\lambda }\sim \mathcal{O} (1)$ also, by controlling the numerical errors at the inner horizons more efficiently. There is no known exact charged GB black hole solution with complex scalar hairs as far as we know. It would be interesting to see whether some exact haired solutions can be found by considering some special potential and to study the GB effect on the interior and deep interior spaces.

Appendices

Full equations of motion in arbitrary dimensions

In this Appendix, we present the reduced action for the general static ansatz (3) and full equations of motion in arbitrary dimensions D, generalizing the $D=4$ case (4)–(7) in the text. First, the reduced action reads, up to boundary terms,

$$\begin{aligned} I{} & {} =\int d^D x \sqrt{-g}\left( \frac{1}{\kappa }R+{\mathcal {L}}_{m}\right) \nonumber \\{} & {} ={\Omega }_{D-2,k} \int dt dr \nonumber \\{} & {} \quad \times \Bigg [ \frac{r^{D-3}}{\sqrt{f h}} \Bigg \{ \frac{(D-2) h}{{\kappa }r} \left( (D-3) (k-f)-r f'\right) \nonumber \\{} & {} \quad +\frac{r f Z(|\varphi |^2)}{2 \kappa } A_{t}'^2 \nonumber \\{} & {} \quad + \alpha q^2 r |\varphi |^2 A_{t}^2 -\alpha r f h |\varphi '|^2-r h V(|\varphi |^2) \Bigg \}\nonumber \\{} & {} \quad + \beta (|\varphi |^2)~ {\mathcal {G}}_{1}+ |\varphi \varphi '| {{\dot{\beta }}}(|\varphi |^2)~ {\mathcal {G}}_{2} \Bigg ], \end{aligned}$$

(A1)

where

$$\begin{aligned} {\mathcal {G}}_{1}{} & {} \equiv (D-4)(D-3)(D-2) \nonumber \\{} & {} \quad \times \sqrt{\frac{ h}{f}} r^{D-6} (f-k) \left[ (D-5) (f-k)+2 rf'\right] ,\end{aligned}$$

(A2)

$$\begin{aligned} {\mathcal {G}}_{2}{} & {} \equiv 4 (D-3) (D-2) \sqrt{\frac{f}{h}} r^{D-4} (k-f) h' \end{aligned}$$

(A3)

are the contributions from the GB term and ${\Omega }_{D-2,k}$ is the volume of $(D-2)$-dimensional hypersurface for a curvature parameter k. Varying the above action leads to the following equations for $A_{t},\varphi ,h$, and f

$$\begin{aligned} E_{A_t}{} & {} \equiv \frac{1}{{\kappa }} \left( Z(|\varphi |^2) \sqrt{\frac{f}{h}}~ r^{D-2} A_t' \right) ' \nonumber \\{} & {} \quad -\frac{2 q^2 {\alpha }r^{D-2} |\varphi |^2 A_t }{f} \sqrt{\frac{f}{h}} =0, \end{aligned}$$

(A4)

$$\begin{aligned} E_{\varphi }{} & {} \equiv \left( {\alpha }r^{D-2} \varphi ' f \sqrt{\frac{h}{f}} \right) '+ \frac{ q^2 {\alpha }r^{D-2} A_t^2 \varphi }{h} \sqrt{\frac{h}{f}} \nonumber \\{} & {} \quad +r^{D-2} \left( \frac{1}{2 {\kappa }} \sqrt{\frac{f}{h}} {\dot{Z}}(|\varphi |^{2}) {A_t'}^2-\sqrt{\frac{h}{f}}~ {\dot{V}}(|\varphi |^{2}) \right) \varphi \nonumber \\{} & {} \quad + \varphi {{\dot{\beta }}}(|\varphi |^2) \left( {\mathcal {G}}_{1}-\frac{1}{2} {{\mathcal {G}}_{2}'}\right) =0, \end{aligned}$$

(A5)

$$\begin{aligned} E_{h}{} & {} \equiv \frac{(D-2)(D-3)}{{\kappa }} \left( f-k+\frac{r f'}{D-3}\right) \nonumber \\{} & {} \quad +r^2 V (|\varphi |^2) +{\alpha }f r^2|\varphi '|^2 \nonumber \\{} & {} \quad +\frac{r^2}{2 h}\left( \frac{1}{{\kappa }} {Z(|\varphi |^{2})}f {A_t'}^2 +2 {\alpha }q^2 |\varphi |^2 A_t^2 \right) \nonumber \\{} & {} \quad +\frac{2 \sqrt{fh}}{r^{D-4}} \left( \frac{|\varphi \varphi '| {\dot{\beta }}(|\varphi |^2)}{h'(r)}{\mathcal {G}}_{2} \right) ^{\prime }\nonumber \\{} & {} \quad -\frac{1}{r^{D-4}} \sqrt{\frac{f}{h}} \left( \beta (|\varphi |^2){\mathcal {G}}_{1} -|\varphi \varphi '| {\dot{\beta }}(|\varphi |^2){\mathcal {G}}_{2} \right) =0, \nonumber \\ \end{aligned}$$

(A6)

$$\begin{aligned} E_f{} & {} \equiv \frac{(D-2)(D-3)}{{\kappa }} \left( f-k+\frac{r f}{D-3} \left( \frac{{h}'}{h}\right) \right) \nonumber \\{} & {} \quad +r^2 V (|\varphi |^2)-{\alpha }f r^2 |\varphi '|^2 \nonumber \\{} & {} \quad +\frac{r^2}{2 h}\left( \frac{1}{{\kappa }} {Z(|\varphi |^{2})}f {A_t'}^2 -2{\alpha }q^2 |\varphi |^2 A_t^2 \right) \nonumber \\{} & {} \quad +\left( |\varphi \varphi '| {\dot{\beta }}(|\varphi |^2) \mathcal{H}_1+ \beta (|\varphi |^2) \mathcal{H}_2 \right) {\mathcal {G}}_{2}=0, \end{aligned}$$

(A7)

where

$$\begin{aligned} \mathcal{H}_1\equiv & {} \sqrt{\frac{f}{h}} \frac{ \left[ 2 (D-4) h (k-f)+r (k-3 f) h'\right] }{r^{D-3} (k-f) h'},\end{aligned}$$

(A8)

$$\begin{aligned} \mathcal{H}_2\equiv & {} \frac{(D-4) }{4 r^{D-2} h'}\left[ \sqrt{\frac{h}{f}}(D-5) \left( f-k\right) +\sqrt{\frac{f}{h}}2 r h'\right] . \end{aligned}$$

(A9)

We note that, for $D=4$, there is only the $\mathcal{G}_2$ term with a non-vanishing coefficient ${\dot{\beta }} (|\varphi |^2)$, whereas for higher dimensions $D>4$, there are both $\mathcal{G}_1$ and $\mathcal{G}_2$ terms with an arbitrary $\beta (|\varphi |^2)$. On the other hand, there is no GB contribution for the lower dimensions, i.e. $D=3, 2$.

Computational details of scaling charge formulas (9) and (10)

In this Appendix, we present computational details of the scaling charge formula (9) and its radial conservation equation (10). Let us first start with the action (12) and, for the sake of computational simplicity, consider the planar metric with the following coordinate choice,

$$\begin{aligned} ds^{2}=-a(\rho )^{2}dt^{2}+d\rho ^{2}+b(\rho )^{2}d\textbf{x}_{D-2}^{2} \end{aligned}$$

(B1)

with $(D-2)$-dimensional planar metric $d \textbf{x}^2_{D-2}$. Employing the same ansatz (3) for the scalar and gauge fields’, it is straightforward to show that the action (12) is invariant under the following finite scaling transformations

$$\begin{aligned} a(\rho )\rightarrow & {} \lambda ^{2-D}a(\rho ),\end{aligned}$$

(B2)

$$\begin{aligned} b(\rho )\rightarrow & {} \lambda b(\rho ),\end{aligned}$$

(B3)

$$\begin{aligned} A_{t}(\rho )\rightarrow & {} \lambda ^{2-D}A_{t}(\rho ) \end{aligned}$$

(B4)

with an arbitrary constant parameter ${\lambda }>0$. Here, we note that the radial coordinate $\rho$ as well as the scalar field $\varphi$ is not transformed and this makes our computation simpler: If we need a scaling transformation for $\rho$ also, the radial derivatives for the fields do not simply transform as (B2)-(B4) and this makes the computation more complicated. Then, to find the Noether charge we use a field theory trick where the global symmetry parameter $\lambda$ is localized as ${\lambda }(\rho )$ and then the Noether charge is the coefficient of $\lambda ^{\prime }(\rho )$ in the variation of the action. The validity of this trick with higher derivatives and “higher-level” analogs of Noether’s theorem were proved in [15] and the corresponding Noether charge $\mathcal{Q}$ reads from the coefficient of $\lambda ^{\prime \prime }(\rho )$ in the variation of the action.

Computing the transformation of action, we find the conserved scaling Noether charge [16]

$$\begin{aligned} \mathcal{Q}= & {} \frac{2}{\kappa } (D-2) \left( a' b^{D-2}-a b^{D-3} b' \right) \nonumber \\ {}{} & {} -\frac{(D-2)b^{D-2} A_{t} A_{t}'Z\left( |\varphi |^2\right) }{\kappa a}\nonumber \\{} & {} +4 \beta (|\varphi |^{2}) (D-4) (D-3) (D-2) b^{D-5}\nonumber \\ {}{} & {} \times \left( a b'^3-a'b b'^2\right) \nonumber \\{} & {} +16 {\dot{{\beta }}}(|\varphi |^{2}) |\varphi \varphi '| b^{D-4} b' (ab'-a'b). \end{aligned}$$

(B5)

The radial derivative of (B5) is combination of field equations which indicates that it is conserved “on-shell”

$$\begin{aligned} \mathcal{Q}^{\prime }= & {} (D-2) \left( a E_{a} -\frac{b E_{b} }{(D-2)}+ A_{t} E_{A_{t}} \right) , \end{aligned}$$

(B6)

where $E_{a}, E_{b}, E_{A_{t}}$ are the field equations of $a, b, A_{t}$, respectively.

Here, it is important to note that the scaling symmetry and its associated local charge (B5) is valid only for the planar topology [10]. In other words, if we move onto the spherical (or hyperbolic) topology with the corresponding metric

$$\begin{aligned} ds^{2}=-a(\rho )^{2}dt^{2}+d\rho ^{2}+b(\rho )^{2}d\Omega _{D-2} \end{aligned}$$

(B7)

and $(D-2)$-dimensional spherical (or hyperbolic) metric $d\Omega _{D-2}$, one finds that the action (12) is not invariant under the finite transformations (B2)–(B4) by the k-dependent terms. However, one can still construct a conserved charge by simply adding the space integral of all the non-conservation terms in (B6) with a minus sign [4, 5] so that all the non-conservation terms are canceled. But in this case, the conserved charge has non-local (i.e. integral) terms as well as the usual local terms, and so it seems that there is no relation to the action invariance and it is beyond the Noether’s theorem. Following this idea and a coordinate transformation to our main metric (3), we find the conserved charge formula (9) with the radial conservation Eq. (10).

Proof of $A_t=0$ at the horizons for charged GB black holes with charged (complex) scalar hairs

In this Appendix, we present a proof of the condition (12), $A_t=0$ at the horizons $r_H$ for charged GB black holes with charged (i.e., complex) scalar hairs. This is one of the key ingredients in our “no scalar-haired Cauchy horizon theorem”.

To this end, we first note that ‘$q \varphi A_t|_{r_H}=0$’ from the regularity (i.e., no singularities) of the equations of motion (4)–(7) at the horizons $r_{H}$. [Here, we consider $D=4$ case for simplicity but the result is unchanged for arbitrary higher dimensions also] Then, in order to avoid the horizon singularities in (4)–(7) for the charged scalar field ($q \ne 0$), we need to consider either (a) $A_t|_{r_H}=0$ or (b) $\varphi |_{r_H}=0$ with $A_t|_{r_H} \ne 0$. We will prove that the case (a) is the only possible condition for hairy black holes with a smooth scalar field $\varphi$.

Aiming for the proof by contradiction [4], let us first suppose that the case (b) is true. From the smoothness of $\varphi$, one can consider the Taylor expansion near the horizons $r_H$,

$$\begin{aligned} \varphi (r)=\varphi _m {\delta }^m + \varphi _{m+1} {\delta }^{m+1} +\cdots \end{aligned}$$

(C1)

with $\varphi _m \equiv \frac{1}{m !} \varphi ^{(m)}|_{r_H} \ne 0$ ($m \ge 1$) and ${\delta }\equiv r-r_H$. Similarly, from the smoothness of $\sqrt{g} \sim \sqrt{f/h}$ at the horizons, one can consider the metric functions’ expansions,

$$\begin{aligned} h(r)= & {} h_{n}{\delta }^n + h_{n+1} {\delta }^{n+1} +\cdots , \end{aligned}$$

(C2)

$$\begin{aligned} f(r)= & {} f_{n}{\delta }^n +f_{n+1} {\delta }^{n+1} +\cdots \end{aligned}$$

(C3)

with $h_{n}, f_{n} \ne 0$ ($n \ge 1$). From the smoothness of the scalar equation (5), we need $m \ge n$ and then (5) becomes

$$\begin{aligned} 2 \alpha r^2_{H} \varphi _m \left( q^2 A_t^2|_{r_H}+m^2 f_1 h_{1} \right) +\mathcal{O}({\delta })=0, \end{aligned}$$

(C4)

by considering the non-extremal black hole, i.e., $n=1$, for simplicity. Then, it is easy to see that there is no way to satisfy (C4) for the case (b) with $\varphi _m \ne 0$ at the leading order and for the Killing horizons with $f_1 \sim h_1$, up to a positive factor, from the surface gravity ${\kappa }_H \sim f'|_{r_H}\sim h'|_{r_H}$. Actually, the resulting leading terms in (C4) are the same as in EMS theories, even though there are GB corrections in the subleading terms. This proves that the case (b) can not be correct and the case (a) is the only correct condition.⁶ All these proofs are unchanged for any higher value of $m \ge n$ and arbitrary higher dimensions $D \ge 4$, where (A5) becomes

$$\begin{aligned}{} & {} 2 \alpha r^2_{H} r^{D-4}_{H} \varphi _n \left[ q^2 A_t^2|_{r_H} +m(m+n-1) f_n h_n {\delta }^{2m-2} \right] \nonumber \\ {}{} & {} +\mathcal{O}({\delta }^n)=0. \end{aligned}$$

(C5)

Proof on general behaviors of $A_t(r)$ with $A_t|_{r_H}=0$

Fig. 8

In the left panel, we plot the behaviors of $A_t(r)$ with extremum points $r_*$ and $A_t|_{r_H}=0$ at the horizons $r_H$. In the right panel, we consider the generic case with the inner horizon $r_-$ and the cosmological horizon $r_{++}$, as well as the outer horizon $r_+$. When there is a cosmological horizon in de Sitter black holes, $A_t(r)$ can not be zero due to the monotonicity property in the black hole exterior region $r \in [r_+,r_{++}]$ from (D1). But this is in contradiction to the property of $A_t|_{r_H}=0$ at the horizons $r_H$

In this Appendix, we present a proof on general behaviors of $A_t (r)$ when the property of $A_t|_{r_H}=0$ (12) is satisfied for charged scalar hairs with $q\ne 0$.

We first prove that “there is no local extremum of $A_t(r)$ for the time-like region with $f,h >0$”. In order to prove this, we first consider a maximum point $r_*$ where $A_t'|_{r_*}=0,~A_t''|_{r_*}<0$ are satisfied. Then, the gauge field equation (4) becomes

$$\begin{aligned} A_t''|_{r_*}=\left. \frac{2 \alpha q^2 A_t^2 |\varphi |^2 }{f Z}\right| _{r_*} \end{aligned}$$

(D1)

at the extremum point $r_*$ in arbitrary dimensions.⁷ If we consider a positive $A_t(r)$ in the region starting from $r_H$ (Fig. 8 (left), upper curve) with $A_t|_{r_H}=0$ (12) (Appendix C), then it is easy to find that the maximum point $r_*$ with $A_t''|_{r_*}<0 ~( A_t>0)$ is not possible unless $f,h<0$, i.e., the space-like region since we have assumed charged scalar fields with $q \ne 0$ and a non-minimal coupling factor $Z(|\varphi |^2)>0.$

Similarly, one can also prove that there is no local minimum point $r_*$ with $A_t'|_{r_*}=0,~A_t''|_{r_*}>0$ for a negative $A_t(r)$ in the region starting from $r_H$ with $A_t|_{r_H}=0$, unless $f,h<0$ (Fig. 8 (left), lower curve). Our proof is essentially the same as that of [4] but with a simple manner in our context.

So, we have proved that $A_t$ can have a local extremum only in the black hole interior region $r \in [r_-,r_+]$ (Fig. 8 (right)), in order to be consistent with the condition of $A_t|_{r_H}=0$ (12) for charged scalar hairs. We have confirmed this property in the numerical solutions for asymptotically anti-de Sitter space in Sect. 5.

One remarkable corollary is, as noted in Sect. 3, that “there is no de Sitter (dS) black holes with charged scalar hairs in EMS or EMGBS theories in arbitrary dimensions” and it can be simply proved as follows. First, suppose that we apply the above property on the extremum of $A_t$ to the black hole exterior region $r \in [r_+,r_{++}]$ for the black hole horizon $r_+$ and the cosmological horizon $r_{++}$, then one easily find that $A_t$ needs to be monotonically increasing or decreasing, depending on its value in the interior region $r \in [r_-,r_{+}]$ (see Fig. 8 (right)). Then, $A_t$ at the cosmological horizon $r_{++}$ will not be vanished but this is in contradiction to the property of $A_t|_{r_H}=0$ (12) for charged scalar hairs. This proves the above no-go theorem for charged dS black holes with charged scalar hairs.⁸ Of course, this does not exclude the neutral, i.e., real scalar hairs for charged dS or charged scalar hairs for neutral dS black holes. Another interesting possibility of evasion of the no-go theorem is the case with Einstein coupling in Horndeski theories (see footnote No. 4) if $[\alpha r^2+{\gamma }(k-f)-{\gamma }f f']<0$ is satisfied in the region $r \in [r_+,r_{++}]$.

Relevant computations on (19)

In this Appendix, we present the computational details on the relation (19) in Sect. 4. Here, for the sake of computational simplicity and practical purpose in the numerical solutions, we consider the $D=4$ case. Let us begin by considering the functions P, S, U, W, R, Y given in (16)

$$\begin{aligned} P{} & {} \equiv -2 \alpha r^2 e^{A+4 B} \left( r^2 \kappa \left( 2 e^{B}+\mu \right) V-4 \left( k e^{B}-1\right) \right) \nonumber \\{} & {} \quad +2 r^2 e^{3 B } \Bigg \{-2 \alpha q^2 \kappa e^{B} \varphi ^2 A_{t}^2 \left( \alpha r^2 e^{B}\!-\!16 \left( k e^{B}\!-\!1\right) {\dot{\beta }}\!\right) \nonumber \\{} & {} \quad - A_{t}'^2 \left( \alpha r^2 e^{B} Z-16 \varphi ^2 \left( k e^{B}-1\right) {\dot{\beta }} {\dot{Z}}\right) \Bigg \}+\nonumber \\{} & {} \quad -4 e^{A} \Bigg \{16 \kappa \varphi ^2 \left( k e^{B}-1\right) \Bigg (A' \left( k e^{B}-3\right) \nu ' {\dot{\beta }}^2 \nonumber \\{} & {} \quad +2 e^{2 B} A'^2 \left( k e^{B}-1\right) {\dot{\beta }}^2+2 \alpha r^2 e^{3 B} \varphi '^2 \ddot{\beta }+r^2 e^{4 B} {{\dot{\beta }}} \dot{V}\Bigg )\nonumber \\{} & {} \quad -e^{B} \mu ' \left[ {\alpha r^3 e^{2 B}}\right. \nonumber \\{} & {} \quad \left. +8 \kappa \varphi {{\dot{\beta }}} \left( 2 \varphi A' \left( k e^{B}-3\right) \left( k e^{B}-1\right) {{\dot{\beta }}}-\alpha r^2 e^{B} \varphi '\right) \right] \nonumber \\{} & {} \quad -8 \alpha \kappa r \varphi \varphi ' {{\dot{\beta }}} \left( {e^{2B} (k e^B-1)\left( r A'+4\right) }+r \nu '\right) \nonumber \\{} & {} \quad +\alpha r^2 e^{2 B} \left[ \kappa e^{B} \varphi '^2 \left( 16 \left( k e^{B}-1\right) {{\dot{\beta }}} +\alpha r^2 e^{B}\right) +r \nu '\right] \Bigg \}\nonumber \\{} & {} \quad +e^{B} \mu \Bigg \{2 \kappa e^{A} \Bigg [-16 \varphi ^2 \left( k e^{B}-1\right) \left( 2 A'^2 \left( k e^{B}-1\right) {{\dot{\beta }}}^2\right. \nonumber \\{} & {} \quad \left. +2 \alpha r^2 e^{B} \varphi '^2 \ddot{\beta }+r^2 e^{2 B} {{\dot{\beta }}} \dot{V}\right) \nonumber \\{} & {} \quad +8 \alpha r e^{B} \varphi \left( r A'+4\right) \left( k e^{B}-1\right) \varphi '{{\dot{\beta }}} \nonumber \\{} & {} \quad -\alpha r^2 e^{B} \varphi '^2 \left( 16 \left( k e^{B}-1\right) {{\dot{\beta }}}+\alpha r^2 e^{B}\right) \Bigg ]\nonumber \\{} & {} \quad +4 \alpha r^2 e^{A+2 B} \left( k e^{B}-1\right) +r^2 e^{B} \nonumber \\{} & {} \quad \times \Bigg [-2 \alpha \kappa q^2 e^{B} \varphi ^2 A_{t}^2 \left( \alpha r^2 e^{B}-16 \left( k e^{B}-1\right) {{\dot{\beta }}}\right) \nonumber \\{} & {} \quad -A_{t}'^2 \left( \alpha r^2 e^{B} Z-16 \varphi ^2 \left( k e^{B}-1\right) {{\dot{\beta }}} \dot{Z}\right) \Bigg ]\Bigg \},\end{aligned}$$

(E1)

$$\begin{aligned} S{} & {} \equiv 128 \kappa \varphi ^2 e^{A+B} \left( k e^{B}-1\right) ^2 \left( 2 e^{B}+\mu \right) {{\dot{\beta }}}^2, \end{aligned}$$

(E2)

$$\begin{aligned} U{} & {} \equiv -2 \kappa r^2 e^{A+3 B} \left( 2 e^{B}+\mu \right) V-r^2 e^{2 B} \left( 2 e^{B}+\mu \right) \nonumber \\{} & {} \quad \times \left( 2 \alpha \kappa q^2 e^{B} \varphi ^2 A_{t}^2+Z A_{t}'^2\right) \nonumber \\{} & {} \quad +2 e^{A} \Bigg \{e^{B} \mu \left[ \kappa \varphi '^2 \left( -32 \varphi ^2 \left( k e^{B}-1\right) \ddot{\beta }\right. \right. \nonumber \\ {}{} & {} \left. \left. -16 \left( k e^{B}-1\right) {{\dot{\beta }}}-\alpha r^2 e^{B}\right) \right. \nonumber \\{} & {} \quad \left. +2 e^{B} \left( k e^{B}-1\right) \right] \nonumber \\{} & {} \quad -2 e^{3 B} \left[ \kappa \varphi '^2 \left( 16 k \left( 2 \varphi ^2 \ddot{\beta }+{{\dot{\beta }}} \right) +\alpha r^2\right) +2\right] \nonumber \\{} & {} \quad -2 e^{B} \mu ' \left( 4 \kappa \varphi \left( k e^{B}-3\right) \varphi ' {{\dot{\beta }}}+r e^{B}\right) \nonumber \\{} & {} \quad -2 e^{B} \nu ' \left( 4 \kappa k \varphi \varphi ' {{\dot{\beta }}} +r\right) +4 k e^{4 B}\nonumber \\ {}{} & {} \quad +32 \kappa e^{2 B} \varphi '^2 \left( 2 \varphi ^2 \ddot{\beta }+{{\dot{\beta }}} \right) +24 \kappa \varphi \nu ' \varphi ' {{\dot{\beta }}} \Bigg \},\end{aligned}$$

(E3)

$$\begin{aligned} W{} & {} \equiv 32 \kappa \varphi e^{A+B} \left( k e^{B}-1\right) \left( 2 e^{B}+\mu \right) {{\dot{\beta }}},\end{aligned}$$

(E4)

$$\begin{aligned} R{} & {} \equiv 4 \alpha \kappa q^2 r e^{2 B} \varphi ^2 A_{t} \left( 2 e^{B}+\mu \right) \nonumber \\{} & {} \quad +A_{t}'\Bigg \{Z \left[ e^{B} \left( \mu \left( r A'\!-\!4\right) \!-\!r \mu '\right) \!+\!2 e^{2 B} \left( r A'\!-\!4\right) \!-\!r \nu '\right] \nonumber \\{} & {} \quad -4 r e^{B} \varphi \left( 2 e^{B}+\mu \right) \varphi ' {\dot{Z}}\Bigg \},\end{aligned}$$

(E5)

$$\begin{aligned} Y{} & {} \equiv 2 r e^{B} \left( 2 e^{B}+\mu \right) Z, \end{aligned}$$

(E6)

where $e^B,\mu ,\nu$ are functions of $A,\varphi ,A_t$ and their first radial derivatives as given in (13)–(15), and (17). Without the gauge field $A_t$, i.e., for neutral GB black holes $(\widetilde{Q}=0)$, the above results correspond to those of [12] for a real scalar field $\phi$ and the coupling parameter ${\beta }=f(\phi )$.

By expanding all the above functions and equations in (16) near the horizons, i.e. taking $A\rightarrow \infty , A'\rightarrow \pm \infty$ for $r_{\pm }$, we find the aforementioned constraint (19), $C(\varphi ,\varphi ^\prime ,A_{t}^{\prime },T) \equiv C_{1}/C_{2}=0$ with

$$\begin{aligned} C_{1}{} & {} \equiv \left( 4 \kappa k \varphi \varphi ' {{\dot{\beta }}} \!+\!r\right) \Bigg \{ 256 \kappa ^3 T^2 \varphi ^3 \varphi '^2 {{\dot{\beta }}}^2 \left( r^2 \dot{V}\!-\!4 \kappa k V {\dot{\beta }}\! \right) \nonumber \\{} & {} \quad +16 \kappa k T \varphi ^2 \varphi ' {{\dot{\beta }}} \Bigg [8 \kappa r T \left( \kappa V {{\dot{\beta }}} \left( \kappa r^2 V-6 k\right) +r^2 {\dot{V}}\right) \nonumber \\{} & {} \quad +A_{t}'^2 \left( r^2 {\dot{Z}} \left( \kappa r^2 V-2 k\right) \right. \nonumber \\{} & {} \quad \left. +2 \kappa Z \left( 2 {{\dot{\beta }}} \left( 2-3 \kappa k r^2 V\right) +r^4 {\dot{V}}\right) \right) \Bigg ]\nonumber \\{} & {} \quad +2 \alpha \kappa r^3 T \varphi ' \left( \kappa r^2 V-2 k\right) \left( r Z A_{t}'^2+4 T\right) \nonumber \\{} & {} \quad +\varphi \Bigg (-8 \kappa {\dot{\beta }}\Bigg [r^2 \Bigg (\kappa k V \left( -4 T^2 \left( \alpha \kappa r^2 \varphi '^2+2\right) \right. \nonumber \\{} & {} \quad \left. +r^2 Z^2 A_{t}'^4+4 r T Z A_{t}'^2\right) +2 \kappa ^2 r^2 T^2 V^2\nonumber \\{} & {} \quad +8 \alpha \kappa T^2 {\varphi '}^2-Z^2 A_{t}'^4\Bigg )+24 T^2\Bigg ] \nonumber \\{} & {} \quad +r^3 A_{t}'^2 \dot{Z} \left( \kappa r^2 V-2 k\right) \left( r Z A_{t}'^2 +4 T\right) \nonumber \\{} & {} \quad +\kappa r^4 \dot{V} \left( r Z A_{t} '^2+4 T\right) ^2\Bigg ) \Bigg \}\nonumber \\ C_{2}{} & {} \equiv 2 \kappa T \Bigg \{-2 \alpha k r^4 \left( r Z A_{t}'^2+4 T\right) \nonumber \\{} & {} \quad +128 \kappa ^3 r^3 T \varphi ^2 V^2 {{\dot{\beta }}}^2 \left( k r-2 \kappa \varphi \varphi ' {{\dot{\beta }}} \right) \nonumber \\{} & {} \quad +\kappa r V \left( 16 \kappa k T \varphi \varphi ' {{\dot{\beta }}} \left( \alpha r^4+32 \kappa \varphi ^2 {{\dot{\beta }}}^2\right) \right. \nonumber \\{} & {} \quad \left. +\alpha r^5 \left( r Z A_{t}'^2+4 T\right) -32 \kappa r \varphi ^2 {{\dot{\beta }}}^2 \left( r Z A_{t} '^2+20 T\right) \right) \nonumber \\{} & {} \quad +64 \kappa k \varphi ^2 {{\dot{\beta }}}^2 \left( r Z A_{t}'^2+12 T\right) -32 \alpha \kappa r^3 T \varphi \varphi ' {{\dot{\beta }}} \Bigg \} \end{aligned}$$

(E7)

from the finite $\varphi ''$ at the horizons. Here, we note that the results on $C_1$ and $C_2$ depends on the value of the topology parameter k and where we evaluate, as $e^B$ does in (13). In the above, we showed the negative root case for the $k=-1$ case and the outer horizon of the black hole interior. Now, by solving the constraint $C_1=0$ ($C_2\ne 0$ generically) in terms of $\varphi '$, we find three roots

$$\begin{aligned}{} & {} \varphi '_{\pm }\equiv D_{\pm }/{{\tilde{D}}},\end{aligned}$$

(E8)

$$\begin{aligned}{} & {} D_{\pm }\equiv 4 \kappa r T^2 \left[ \kappa \left( 16 k r^2 \varphi ^2 {{\dot{\beta }}} \dot{V} +16 \kappa k \varphi ^2 V {{\dot{\beta }}}^2 \right. \right. \nonumber \\{} & {} \quad \left. \left. \times \left( \kappa r^2 V-6 k\right) +\alpha r^4 V \right) -2 \alpha k r^2\right] \nonumber \\{} & {} \quad +\kappa T A_{t}'^2 \Bigg [8 k r^2 \varphi ^2 {{\dot{\beta }}} \left( \dot{Z} \left( \kappa r^2 V-2 k\right) +2 \kappa r^2 Z \dot{V} \right) \nonumber \\{} & {} \quad +32 \kappa k \varphi ^2 Z {{\dot{\beta }}}^2 \left( 2-3 \kappa k r^2 V \right) \nonumber \\{} & {} \quad +\alpha r^4 Z \left( \kappa r^2 V -2 k\right) \Bigg ]\nonumber \\ {}{} & {} \pm \Bigg \{\kappa ^2 T^2 \Bigg [\Bigg (-8 \alpha k r^3 T+4 \kappa r T \Bigg ( 16 k r^2 \varphi ^2 {{\dot{\beta }}} \dot{V} \nonumber \\{} & {} \quad +16 \kappa k \varphi ^2 V {{\dot{\beta }}}^2\times \left( \kappa r^2 V-6 k\right) \nonumber \\{} & {} \quad +\alpha r^4 V \Bigg )+A_{t}'^2 \Bigg [8 k r^2 \varphi ^2 {{\dot{\beta }}} \left( \dot{Z}\left( \kappa r^2 V-2 k\right) \right. \nonumber \\{} & {} \quad \left. +2 \kappa r^2 Z \dot{V}\right) +32 \kappa k \varphi ^2 Z {{\dot{\beta }}}^2 \left( 2-3 \kappa k r^2 V\right) \nonumber \\{} & {} \quad +\alpha r^4 Z \left( \kappa r^2 V-2 k\right) \Bigg ]\Bigg )^2\nonumber \\ {}{} & {} -32 \varphi ^2 {{\dot{\beta }}} \Bigg (\kappa k V \left( \alpha r^4-32 \kappa \varphi ^2 {{\dot{\beta }}}^2\right) \nonumber \\{} & {} \quad -2 r^2 \left( \alpha -4 \kappa \varphi ^2 {{\dot{\beta }}} \dot{V} \right) \Bigg )\nonumber \\{} & {} \quad {\times }\Bigg [-8 \kappa {{\dot{\beta }}} \left[ r^2 \left( 2 \kappa T^2 V \left( \kappa r^2 V-4 k\right) \right. \right. \nonumber \\{} & {} \left. \left. \quad +Z^2 A_{t}'^4 \left( \kappa k r^2 V-1\right) \right. \right. \nonumber \\{} & {} \quad \left. \left. +4 \kappa k r T V Z A_{t} '^2\right) +24 T^2\right] \nonumber \\{} & {} \quad +r^3 A_{t} '^2 \dot{Z} \left( \kappa r^2 V-2 k\right) \left( r Z A_{t}'^2+4 T\right) \nonumber \\{} & {} \quad +\kappa r^4 \dot{V} \left( r Z A_{t}'^2+4 T\right) ^2\Bigg ]\Bigg ]\Bigg \}^{1/2},\end{aligned}$$

(E9)

$$\begin{aligned} \tilde{D}\equiv & {} 32 \kappa ^2 T^2 \varphi {{\dot{\beta }}} \left( \kappa k V \left( 32 \kappa \varphi ^2 {{\dot{\beta }}}^2-\alpha r^4\right) \right. \nonumber \\{} & {} \quad \left. +2 r^2 \left( \alpha -4 \kappa \varphi ^2 {{\dot{\beta }}} \dot{V}\right) \right) ,\end{aligned}$$

(E10)

$$\begin{aligned} \varphi '_{3}= & {} -\frac{r}{4 \kappa k \varphi {{\dot{\beta }}}}. \end{aligned}$$

(E11)

Here, we have considered a rapidly vanishing gauge field $A_t$ at the horizons so that $e^{-A} |\varphi |^2 A_t^2$ term can be neglected to solve the condition $C_1=0$, which is quite involved when we keep the mentioned term. Note that these solutions are valid only at the horizons $r_H$, i.e., the outer event horizon $r_+$ or the inner Cauchy horizon $r_-$ and so they can be used as the initial conditions for the numerical solutions. In our numerical solutions, we have considered only the positive root $\varphi '_{+}$ because it only shows a smooth Einstein limit as $\beta \rightarrow 0$.