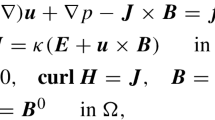1 Introduction

Post-Newtonian (PN) approximation is an effective approach to modeling the relativistic gravitational problems, which has been the major analytic tool to study the dynamics and waveforms of the system of compact objects (neutron stars and/or black holes) in the early stage of the inspiral. In particular, the consistency of PN waveforms with numerical relativity [1] greatly support the effectiveness of PN approximation.

The PN Hamiltonian approximation and the PN Lagrangian approximation are the two major PN approaches and used in many problems, such as the compact binaries [2,3,4,5], the relativistic restricted three-body problem [6,7,8], and the general relativistic N-body problem [9,10,11]. However, the research on the dynamics of PN systems mainly depends on effective numerical integrations for such systems. For example, the chaoticity of the system needs the calculation of chaotic indicators such as the Lyapunov characteristic exponent [12,13,14], the fast Lyapunov indicator [15, 16], and the generalized alignment index [17] by numerically solving the system.

Although there exist some discrepancies between the PN Hamiltonian and the PN Lagrangian, the authors of [18] show that structure-preserving (symplectic or energy-preserving) integrators of PN Lagrangian systems still have to be constructed with the help of Hamiltonian frame. This point further highlights the importance of efficiently solving for PN Hamiltonian systems. Therefore, the aim of this paper is just to establish accurately efficient explicit methods that possess some good properties such as the symplecticity for the PN Hamiltonian systems.

In Hamiltonian systems, the phase flow of the system is a symplectic mapping from the state at one point to another due to the presence of the symplectic structure. Therefore, the symplectic method becomes the natural and sometimes the default candidate for Hamiltonian systems [19, 20]. Theoretical analyses in the literature show that the global error of symplectic methods increases linearly with time for (near) integrable Hamiltonian systems, while the energy error does not have a secular long-term increase with time but oscillates in a bounded region of a small magnitude [19, 21]. This confirms the superiority of symplectic methods over traditional methods such as the Runge–Kutta methods whose global error and energy error respectively grow quadratically and linearly.

Among all the symplectic methods, explicit symplectic methods are more favoured because of the high efficiency that consumes less CPU time to obtain numerical solutions of given precision in comparison with implicit ones. For the Hamiltonian system of Newtonian N-body problems, explicit methods have been well developed based on the feasible separation of integrable sub-Hamiltonians, such as the standard \(T+V\) splitting methods [22, 23], the \(H_0+\varepsilon H_1\) splitting methods [24], the force gradient methods [25,26,27], and the pseudo-high-order methods [28,29,30,31]. In particular, the group of Wu proposed some explicit symplectic methods in Schwarzschild- and Kerr-type black hole spacetimes via an integrable multiple-part separation [32,33,34,35,36].

However, different from the Newtonian Hamiltonian system, the PN Hamiltonian system at least contains the interaction terms of the generalized position and the generalized momentum. This interaction disables the explicit solving for the corresponding sub-Hamiltonian. That is, even for the PN Hamiltonian system of compact binaries that only involves orbital term and thus is integrable, explicit symplectic methods are hardly constructed except for some particular separable Hamiltonian [37]. In addition, the consideration of the spinning effect that contains interaction terms of the generalized position, the generalized momentum, and the spin variables further makes it impossible to establish explicit symplectic methods for general PN Hamiltonian systems. The existing symplectic methods for PN Hamiltonian systems are either fully implicit like the Gauss collocation method [38, 39] or semi-implicit like the mixed methods [40,41,42] that mix the explicit solving for the Newtonian term and the implicit symplectic solving for the PN term.

In fact, efforts for explicit symplectic methods have existed for many years. For example, the explicit extended phase space method is symplectic in the sense of extended phase space [43,44,45,46]. Although this class of methods is no longer symplectic in the original phase space of the Hamiltonian, its symmetry still ensures a nonsecular growth of energy errors. We also note that the author of [44] proved the linear global error growth of the explicit extended phase space method for integrable Hamiltonian systems. However, the linear global error growth for near-integrable or nonintegrable Hamiltonian systems is still uncertain. That is, the application of extended phase space methods to PN Hamiltonian systems may lose the most important property of linear global error growth.

In this paper, by observing the presence of the small parameter \(\varepsilon \) in the PN Hamiltonian, we consider replacing the implicit symplectic solver for the PN term with explicit ones in the mixed symplectic method. Then, the derived methods are certainly explicit. Furthermore, we present a theoretical analysis that the new method is \({\mathscr {O}}(\varepsilon ^{p+1}h^{p+1})\) close to symplectic methods. That is, the proposed methods are really explicit and near-symplectic. The numerical experiments with the spinning compact binaries show that the proposed methods behave very like symplectic methods so that their discrepancy are indistinguishable in the same plot, while the CPU time consumed by the proposed methods are much less than the corresponding mixed symplectic methods. This strongly supports the good near-symplecticity and high efficiency of the new methods.

The rest of this paper is organized as follows. In Sect. 2, we introduce the PN Hamiltonian of spinning compact binaries and then present a brief discussion on the canonical conjugate spin variables and integrability of the system. We derive the formulation of explicit near-symplectic methods and provide the theoretical analysis in Sect. 3. Numerical experiments with the spinning compact binaries are presented in Sect. 4 by showing the comparison of energy errors, orbital errors, and CPU time between the proposed methods and the mixed symplectic methods. Conclusions are drawn in the last section.

2 Post-Newtonian Hamiltonian formulation

In comparison with the Newtonian term, the PN term is usually small, regardless of the number of bodies in the system. Without loss of generality, we consider the conservative PN Hamiltonian of spinning compact binaries in Arnowitt–Deser–Misner (ADM) coordinates and in the center-of-mass frame, in which chaos may occur due to the high nonlinearity.

To describe the Hamiltonian, the following notations are used throughout this paper. Let \({\varvec{P}}\) be the momenta of body 1 relative to the center, \({\varvec{Q}}\) be the position coordinates of body 1 relative to body 2, \({\varvec{N}}={\varvec{Q}}/r\) be the unit vector, \(r=|{\varvec{Q}}|=\sqrt{q_1^2+q_2^2+q_3^2}\) be the distance of body 1 relative to body 2, and \({\varvec{S}}_i(i=1,2)\) be the spins of the two compact bodies. The mass of the two compact bodied are respectively denoted by \(m_1\) and \(m_2~(m_1\le m_2).\) Then, we have the total mass \(M=m_1+m_2,\) the reduced mass \(\mu =m_{1}m_{2}/M\) and the mass ratio \(\beta =m_1/m_2.\) Another frequently used parameter is \(\eta =\mu /M=\beta /(1+\beta )^{2}.\) It is also noted that \({\varvec{S}}_i~(i=1,2)\) are usually expressed by \({\varvec{S}}_i=\Lambda _i\hat{{\varvec{S}}}_i,\) where \(\hat{{\varvec{S}}}_i\) are the unit vectors, and \(\Lambda _i=\chi _{i}m_{i}^{2}/M^{2}\) \((\chi _i\in [0, 1])\) are spin magnitudes. Finally, the time t,  space \({\varvec{Q}},\) momentum \({\varvec{P}},\) and spin \({\varvec{S}}_i\) are respectively rescaled and measured in GM,  GM,  \(\mu ,\) and \(M^2\) (see, e.g. [6, 8, 47,48,49]).

With the above notations, the PN Hamiltonian considered in this paper is written as follows:

$$\begin{aligned}{} & {} H({\varvec{Q}},{\varvec{P}},{\varvec{S}}_1,{\varvec{S}}_2) = H_{N} + \frac{1}{c^2}H_{1PN} + \frac{1}{c^4}H_{2PN}\nonumber \\{} & {} \qquad + \frac{1}{c^6}H_{3PN} + \frac{1}{c^3}H_{1.5PN}^{SO} + \frac{1}{c^5}H_{2.5PN}^{SO}\nonumber \\{} & {} \qquad + \frac{1}{c^7}H_{3.5PN}^{SO} + \frac{1}{c^4}H_{2PN}^{SS}. \end{aligned}$$
(1)

In this formulation, \(H_{N},\) \(H_{1PN},\) \(H_{2PN}\) and \(H_{3PN}\) are respectively the Newtonian term (i.e., the Kepler flow), the 1PN-, 2PN-, and 3PN-order orbital contributions. The spin-orbit couplings, i.e., the leading-order term \(H_{1.5PN}^{SO},\) the next-to-leading-order term \(H_{2.5PN}^{SO},\) and the next-to-next-to-leading-order term \(H_{3.5PN}^{SO},\) are respectively accurate up to 1.5PN, 2.5PN, and 3.5PN order by adopting the assumption that the rotational speed of the compact object is in the same magnitude of c. The last term \(H_{SS}\) is the spin-spin couplings and accurate up to 2PN order.

Following [50], the orbital terms can be expressed as follows

$$\begin{aligned}{} & {} H_{N}=\frac{{\varvec{P}}^2}{2}-\frac{1}{r}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} H_{1PN}=\frac{1}{8}(3\eta -1){\varvec{P}}^4-\frac{1}{2}\big [(3+\eta ){\varvec{P}}^2 +\eta ({\varvec{N}}\cdot {\varvec{P}})^2\big ]\frac{1}{r}\nonumber \\{} & {} \quad +\frac{1}{2r^{2}}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} H_{2PN}= \frac{1}{16}(1-5\eta +5\eta ^2){\varvec{P}}^6 +\frac{1}{8}\big [(5-20\eta -3\eta ^2){\varvec{P}}^4 \nonumber \\{} & {} \quad -2\eta ^2{({\varvec{N}}\cdot {\varvec{P}})^2}{\varvec{P}}^2 -3\eta ^2{({\varvec{N}}\cdot {\varvec{P}})^4}\big ]\frac{1}{r}\nonumber \\{} & {} \quad +\frac{1}{2}\big [(5+8\eta ){\varvec{P}}^2 +3\eta ({\varvec{N}}\cdot {\varvec{P}})^2\big ]\frac{1}{r^2}\nonumber \\{} & {} \quad -\frac{1}{4}(1+3\eta )\frac{1}{r^3}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} H_{3PN}=\frac{1}{128}(-5+35\eta -70\eta ^2+35\eta ^3) {\varvec{P}}^8+\frac{1}{16}\big [(-7 \nonumber \\{} & {} \quad +42\eta -53\eta ^2-5\eta ^3){\varvec{P}}^6 +(2-3\eta )\eta ^2\cdot ({\varvec{N}}\nonumber \\{} & {} \quad \cdot {\varvec{P}})^2{\varvec{P}}^4 +3(1-\eta )\eta ^2({\varvec{N}}\cdot {\varvec{P}})^4 {\varvec{P}}^2-5\eta ^3({\varvec{N}} \nonumber \\{} & {} \quad \cdot {\varvec{P}})^6\big ]\frac{1}{r}+\Bigg [\frac{1}{16}(-27+136\eta +109\eta ^2) {\varvec{P}}^4 \nonumber \\{} & {} \quad +\frac{1}{16}(17+30\eta )\eta ({\varvec{N}}\cdot {\varvec{P}})^2{\varvec{P}}^2 +\frac{1}{12}(5+43\eta ) \nonumber \\{} & {} \quad \cdot \eta ({\varvec{N}}\cdot {\varvec{P}})^4\Bigg ]\frac{1}{r^2} +\Bigg \{\Bigg [-\frac{25}{8}+\Bigg (\frac{1}{64}\pi ^2-\frac{335}{48}\Bigg )\eta \nonumber \\{} & {} \quad -\frac{23}{8}\eta ^2\Bigg ]{\varvec{P}}^2 +\Bigg (-\frac{85}{16}- \frac{3}{64}\pi ^2-\frac{7}{4}\eta \Bigg ) \eta ({\varvec{N}} \nonumber \\{} & {} \quad \cdot {\varvec{P}})^2\Bigg \}\frac{1}{r^3}+\Bigg [\frac{1}{8}+\Bigg (\frac{109}{12} -\frac{21}{32}\pi ^2\Bigg )\eta \Bigg ]\frac{1}{r^4}. \end{aligned}$$
(5)

Let \({\varvec{S}}= {\varvec{S}}_1 + {\varvec{S}}_2,\) \({\varvec{S}}^{*}=\frac{1}{\beta }{\varvec{S}}_1+\beta {\varvec{S}}_2,\) and \({\varvec{L}}\) be the orbital angular momentum vector \({\varvec{L}}={\varvec{Q}} \times {\varvec{P}}.\) According to [51], the Hamiltonian of spin-orbit coupling terms are respectively written as

$$\begin{aligned} H_{1.5PN}^{SO}= & {} \frac{1}{r^{3}} \Bigg (2{\varvec{S}} +\frac{3}{2}{\varvec{S}}^{*}\Bigg )\cdot {\varvec{L}}, \end{aligned}$$
(6)
$$\begin{aligned} H_{2.5PN}^{SO}= & {} \frac{1}{r^{3}} \Bigg [\Bigg (\frac{19}{8}\eta {\varvec{P}}^{2}+\frac{3}{2}\eta ({\varvec{N}}\cdot {\varvec{P}})^{2} -(6+2\eta )\frac{1}{r}\Bigg ){\varvec{S}}\nonumber \\{} & {} \quad +\Bigg (-\Bigg (\frac{5}{8}+2\eta \Bigg ){\varvec{P}}^{2}+\frac{3}{4}\eta ({\varvec{N}} \cdot {\varvec{P}})^{2}-(5\nonumber \\{} & {} \quad +2\eta )\frac{1}{r}\Bigg ){\varvec{S}}^{*}\Bigg ]\cdot {\varvec{L}}, \end{aligned}$$
(7)
$$\begin{aligned} H_{3.5PN}^{SO}= & {} \frac{1}{r^{3}} \Bigg \{\Bigg [-\frac{9}{8}\eta \Bigg (1-\frac{22}{9}\eta \Bigg ){\varvec{P}}^{4} -\frac{3}{4}\eta \Bigg (1-\frac{9}{4}\eta \Bigg ){\varvec{P}}^{2}\nonumber \\{} & {} \cdot ({\varvec{N}}\cdot {\varvec{P}})^{2} +\frac{5}{16}\eta ^{2}({\varvec{N}}\cdot {\varvec{P}})^{4} +\frac{1}{r}\Bigg [-\frac{157}{8}\eta \Bigg (1 \nonumber \\{} & {} +\frac{39}{314}\eta \Bigg ){\varvec{P}}^{2}-16\eta \Bigg (1+\frac{45}{256}\eta \Bigg )({\varvec{N}}\cdot {\varvec{P}})^{2} \nonumber \\{} & {} +\frac{1}{r}\frac{21}{2}(1+\eta )\Bigg ]\Bigg ]{\varvec{S}} +\Bigg [\frac{1}{16}(7-37\eta +39\eta ^{2}) \nonumber \\{} & {} \cdot {\varvec{P}}^{4}+\frac{9}{16}\eta (2\eta -1){\varvec{P}}^{2} \cdot ({\varvec{N}}\cdot {\varvec{P}})^{2} +\frac{1}{r}\Bigg [\frac{1}{8}(27 \nonumber \\{} & {} -129\eta -\frac{39}{2}\eta ^{2}){\varvec{P}}^{2} -6\eta \Bigg (1+\frac{15}{32}\eta \Bigg )({\varvec{N}} \nonumber \\{} & {} {\cdot {\varvec{P}})^{2}+}\frac{1}{r}\Bigg (\frac{75}{8}+\frac{41}{4}\eta \Bigg ) \Bigg ]\Bigg ]{\varvec{S}}^{*}\Bigg \}\cdot {\varvec{L}}. \end{aligned}$$
(8)

Finally, the spin-spin Hamiltonian \(H_{SS}\) is quadratic in the two spins and has the following formulation

$$\begin{aligned} H_{2PN}^{SS}({\varvec{Q}},{\varvec{S}}_1,{\varvec{S}}_2)=\frac{1}{2r^3} \big [3({\varvec{S}}_0\cdot {\varvec{N}})^2-{\varvec{S}}_0^2\big ], \end{aligned}$$
(9)

where

$$\begin{aligned} {\varvec{S}}_{0} = {\varvec{S}} + {\varvec{S}}^{*} = \Bigg (1+\frac{1}{\beta }\Bigg ){\varvec{S}}_1 +(1+\beta ){\varvec{S}}_2. \end{aligned}$$

As explained in [7, 8, 52, 53], to conveniently describe specific physical phenomena whose quantities are measured in the International System of Units, we should readjust the parameter c once the geometric unit \(G=M=1\) is employed. For example, the parameter c should be readjusted to \(c\approx 1.0067\times 10^4\) for the solar system. In general, we can roughly say that a smaller value of c for (1) indicates a stronger PN effect.

Note that the PN Hamiltonian (1) is not expressed by completely canonical conjugate variables, because its evolution equations read [50]

$$\begin{aligned}{} & {} \frac{d{\varvec{Q}}}{dt}=\frac{\partial {H}}{\partial {\varvec{P}}}, \quad \frac{d{\varvec{P}}}{dt}=-\frac{\partial {H}}{\partial {\varvec{Q}}},\nonumber \\{} & {} \frac{d{\varvec{S}}_i}{dt}=\frac{\partial {H}}{\partial {\varvec{S}}_i}\times {\varvec{S}}_i,\quad i=1,2, \end{aligned}$$
(10)

which clearly indicate that the spin variables \({\varvec{S}}_i\) are not conjugate to each other. Fortunately, the authors of [54] introduced the canonical conjugate spin variables \({\varvec{\theta }}=(\theta _1,\theta _2)\) and \({\varvec{\xi }}=(\xi _1,\xi _2)\):

$$\begin{aligned} {\varvec{S}}_i=\left( \begin{aligned}&\rho _{i}\cos (\theta _{i})\\&\rho _{i}\sin (\theta _{i})\\&\quad \xi _{i} \end{aligned} \right) ,\quad i=1,2, \end{aligned}$$
(11)

where \(\rho _{i}^2+\xi _{i}^2=\Lambda _i^2\) and \(\rho _{i}>0.\) According to (10), it is yielded that the spin magnitudes \(\Lambda _i=|{\varvec{S}}_i|\) are conserved for the system. Then, the usage of new variables makes the original 12-dimensional system \(H({\varvec{Q}},{\varvec{P}},{\varvec{S}}_1,{\varvec{S}}_2)\) of (1) reduce to a 10-dimensional canonical Hamiltonian system \(H({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}),\) whose evolution equations read

$$\begin{aligned}{} & {} \frac{d{\varvec{Q}}}{dt}=\frac{\partial {H}}{\partial {\varvec{P}}}, \quad \frac{d{\varvec{P}}}{dt}=-\frac{\partial {H}}{\partial {\varvec{Q}}},\nonumber \\{} & {} \frac{d{\varvec{\theta }}}{dt}=\frac{\partial {H}}{\partial {\varvec{\xi }}}, \quad \frac{d{\varvec{\xi }}}{dt}=-\frac{\partial {H}}{\partial {\varvec{\theta }}}. \end{aligned}$$
(12)

It should be noticed that the variables \(\rho _i\) defined in (11) differ slightly from that [54] by a factor of \(\Lambda _i.\)

For the 10-dimensional canonical Hamiltonian system \(H({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}),\) there exists only four independent constants, i.e., the total angular momentum vector

$$\begin{aligned} {\varvec{J}}={\varvec{L}}+{\varvec{S}}_1+{\varvec{S}}_2, \end{aligned}$$
(13)

and the total energy

$$\begin{aligned} E={H}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}). \end{aligned}$$
(14)

This means that the spinning Hamiltonian (1) is nonintegrable, and hence chaos may occur in this system. We also note that once the spin-spin term \(H_{SS}\) is excluded from (1), there exists an additional constant, i.e., the length of the orbital angular momentum vector

$$\begin{aligned} |{\textbf{L}}|=\sqrt{{\textbf{L}}^2}. \end{aligned}$$
(15)

In this case, the system will be completely integrable according to the integrability theory of canonical Hamiltonian systems.

3 Explicit near-symplectic methods

According to the formulation of (1), it is yielded that the Hamiltonian \({H}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }})\) is nonseparable because of the nonlinear interactions between \({\varvec{Q}}\) and \({\varvec{P}},\) and that between \({\varvec{\theta }}\) and \({\varvec{\xi }}.\) This point means that the construction of explicit symplectic methods is impossible for the Hamiltonian \({H}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}).\) Given that the integrable separation cannot be applied, implicit symplectic methods, such as the Gauss Runge–Kutta collocation methods, are the inevitable choice for \({H}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}).\)

3.1 Mixed symplectic methods

Since fully implicit symplectic methods such as the Gauss collocation methods are usually expensive for the consumed CPU time, an effective approach to increase the computational efficiency is to explicitly solve the Hamiltonian as much as possible. This idea is followed by the mixed symplectic methods for PN Hamiltonian systems [40,41,42], which combine the explicit exact solver for the Newtonian part and the implicit numerical solver for the nonseparable PN part.

To illustrate the idea, by letting \(\varepsilon =\frac{1}{c^2}\) we separate the Hamiltonian (1) with the canonical conjugate spin variables \(({\varvec{\theta }},{\varvec{\xi }})\) into two typical parts as follows:

$$\begin{aligned} H({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }})=H_N({\varvec{Q}},{\varvec{P}}) + \varepsilon H_{PN}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}), \end{aligned}$$
(16)

where \(H_N({\varvec{Q}},{\varvec{P}})\) is just the Newtonian term (2) and \(H_{PN}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }})\) represents the PN term that includes the PN orbital terms (3)(4)(5), the spin-orbit terms (6)(7)(8), and the spin-spin term (9). Because \(H_N\) is integrable and an exact analytical solution exists in principle, one can exactly solve this part by an exact operator \(S_0(h)\) that is naturally symplectic. However, the PN part \(H_{PN}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }})\) can only be solved by implicit symplectic operator M(h). Then, the combination of \(S_0(\alpha h)\) and \(M(\gamma h)\) with different coefficients \(\alpha \) and \(\gamma \) yields symplectic methods for the Hamiltonian (16).

Once the symplectic implicit midpoint method IRK2 with the stepsize h is used as M(h) to numerically solve \(H_{PN},\) the typical second-order mixed symplectic method \(S_2(h)\) [40,41,42] is given as follows:

$$\begin{aligned} S_2(h)\equiv \text {IRK2}\Big (\frac{1}{2}h\Big )\circ S_0(h) \circ \text {IRK2}\Big (\frac{1}{2}h\Big ). \end{aligned}$$
(17)

Then a fourth-order mixed symplectic method by Yoshida’s triple product of \(S_2(h)\) can be derived as follows:

$$\begin{aligned}{} & {} S_4(h) =\text {IRK2}\Big (\frac{\lambda }{2}h\Big )\circ S_0(\lambda h)\circ \text {IRK2}\Big (\frac{\lambda }{2}h\Big )\nonumber \\{} & {} \quad \circ \text {IRK2}\Big (\frac{1-2\lambda }{2}h\Big ) \circ S_0\big ((1-2\lambda )h\big )\circ \text {IRK2}\Big (\frac{1-2\lambda }{2}h\Big )\nonumber \\{} & {} \quad \circ \text {IRK2}\Big (\frac{\lambda }{2}h\Big ) \circ S_0(\lambda h)\circ \text {IRK2}\Big (\frac{\lambda }{2}h\Big ), \end{aligned}$$
(18)

where \(\lambda =\frac{1}{2-2^{1/3}}.\) The fourth-order method \(S_4(h)\) is essentially a nine-operator method. It is noted that the collection of neighboring operators \(\text {IRK2}(\gamma h)\) in (18) results in a seven-operator method in Forest–Ruth formula as follows:

$$\begin{aligned} \text {FR}(h)= & {} \text {IRK2}\Big (\frac{\lambda }{2}h\Big )\circ S_0(\lambda h)\circ \text {IRK2}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0\big ((1-2\lambda )h\big ) \circ \text {IRK2}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0(\lambda h)\circ \text {IRK2}\Big (\frac{\lambda }{2}h\Big ). \end{aligned}$$
(19)

However, the numerical solutions of \(\text {IRK2}(h)\) for \(H_{PN}\) only have second-order accuracy, this leads to that the symplectic method (19) is also of order two for (16).

The mixed symplectic methods take two advantages over the fully implicit symplectic methods for PN Hamiltonian systems. First, the mixed method always consumes less CPU time since the dominant part of the Hamiltonian is explicitly solved. Second, according to the particular formulation of the separation (16), the small parameter \(\varepsilon =\frac{1}{c^2}\) will appear in the dominant local truncation error of the mixed symplectic method, i.e., \({\mathscr {O}}(\varepsilon h^{p+1})\) for a pth-order method, while the local error is \({\mathscr {O}}(h^{p+1})\) for fully implicit symplectic methods. On account of the small magnitude of \(\varepsilon ,\) the mixed symplectic method always has a smaller truncation error than the same order fully implicit symplectic method. Details on the mixed symplectic method can be referred to [8, 42].

3.2 Near-symplectic methods

Suppose that \(\Phi :~{\varvec{Z}}_{n}\rightarrow {\varvec{Z}}_{n+1}\) is a numerical method of the 2d-dimensional Hamiltonian system \(H({\varvec{Z}}).\) We introduce the following definition concerning near-symplectic methods.

Definition 1

A numerical method of the Hamiltonian system \(H({\varvec{Z}})\) is called near-symplectic, if there exists an integer r such that the condition

$$\begin{aligned} \Big (\frac{\partial {\varvec{Z}}_{n+1}}{\partial {\varvec{Z}}_{n}}\Big )^{\intercal }J_{2d} \Big (\frac{\partial {\varvec{Z}}_{n+1}}{\partial {\varvec{Z}}_{n}}\Big ) = J_{2d} + {\mathscr {O}}(h^r) \end{aligned}$$

holds for all n,  where \(J_{2d}= \left( \begin{array}{cc} O &{} I_d \\ -I_d &{} O \\ \end{array}\right) ,\) \(I_d\) is the identity matrix of size d,  and h is the stepsize.

Before the construction of near-symplectic methods, we present the Butcher tableau of the implicit midpoint method IRK2, the explicit second-order method RK2, and the conventional fourth-order method RK4 [19] as follows:

Now, we turn to the adaption of the mixed symplectic method. Due to the small parameter \(\varepsilon \) appearing in the PN term, we consider using explicit methods as M(h) to numerically solve \(H_{PN}.\) If replacing the implicit midpoint method IRK2 with the explicit second-order Runge–Kutta method RK2, we then derive the counterpart of \(S_2(h)\) as follows:

$$\begin{aligned} S^*_2(h)\equiv \text {RK2}\Big (\frac{1}{2}h\Big )\circ S_0(h) \circ \text {RK2}\Big (\frac{1}{2}h\Big ). \end{aligned}$$
(20)

For the fourth-order symplectic method \(S_4(h),\) replacing \(\text {IRK2}(h)\) with the explicit fourth-order method \(\text {RK4}(h)\) in (18) yields

$$\begin{aligned}{} & {} \text {RK4}\Big (\frac{\lambda }{2}h\Big )\circ S_0(\lambda h)\circ \text {RK4}\Big (\frac{\lambda }{2}h\Big )\circ \text {RK4}\Big (\frac{1-2\lambda }{2}h\Big )\\{} & {} \quad \circ S_0\big ((1-2\lambda )h\big ) \circ \text {RK4}\Big (\frac{1-2\lambda }{2}h\Big )\circ \text {RK4}\Big (\frac{\lambda }{2}h\Big )\\{} & {} \quad \circ S_0(\lambda h)\circ \text {RK4}\Big (\frac{\lambda }{2}h\Big ). \end{aligned}$$

Given that RK4 has the same order with \(S_4(h),\) collecting the neighbouring operators \(\text {RK4}\big (\frac{\lambda }{2}h\big )\) and \(\text {RK4}\big (\frac{1-2\lambda }{2}h\big )\) finally yields a Forest–Ruth-type integrator similar to (19) as follows

$$\begin{aligned} S^*_4(h)\equiv & {} \text {RK4}\Big (\frac{\lambda }{2}h\Big )\circ S_0(\lambda h)\circ \text {RK4}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0\big ((1-2\lambda )h\big ) \circ \text {RK4}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0(\lambda h)\circ \text {RK4}\Big (\frac{\lambda }{2}h\Big ). \end{aligned}$$
(21)

Unlike (19) which only has second-order accuracy, the usage of \(\text {RK4}\) allows \(S^*_4(h)\) to retain fourth-order accuracy. This fact will be illustrated in the remaining content.

A further improvement for (21) is to replace \(\text {RK4}\) with \(\text {RK2},\) which reads

$$\begin{aligned} {\widetilde{S}}^*_4(h)\equiv & {} \text {RK2}\Big (\frac{\lambda }{2}h\Big )\circ S_0(\lambda h)\circ \text {RK2}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0\big ((1-2\lambda )h\big ) \circ \text {RK2}\Big (\frac{1-\lambda }{2}h\Big )\nonumber \\{} & {} \circ S_0(\lambda h)\circ \text {RK2}\Big (\frac{\lambda }{2}h\Big ). \end{aligned}$$
(22)

This improvement is based on the two following facts. First, the second-order method \(\text {RK2}\) has fewer stages than \(\text {RK4},\) thus the less computation amount of \({\widetilde{S}}^*_4(h)\) makes it consume less CPU time than \({S}^*_4(h).\) Second, since \(\text {RK2}\) is used to numerically solve the perturbed PN term \(\varepsilon H_{PN}({\varvec{Q}},{\varvec{P}},{\varvec{\theta }},{\varvec{\xi }}),\) the presence of \(\varepsilon \) makes the local truncation error of \(\text {RK2}\) have the particular form \({\mathscr {O}}(\varepsilon ^3 h^3),\) which leads to \({\widetilde{S}}^*_4(h)\) being a pseudo-fourth-order method whose local truncation error reads \({\mathscr {O}}(\varepsilon ^3 h^3 + \varepsilon h^5).\) Both theoretical analysis and numerical comparison in the remaining content show that for a small \(\varepsilon \) and large h,  the two methods \({S}^*_4(h)\) and \({\widetilde{S}}^*_4(h)\) nearly behave the same, and the difference between them will be very small until it disappears for a threshold value of \(\varepsilon .\)

3.3 Property of near-symplectic methods

To analyze the property of the new methods \(S^*_2(h),\) \(S^*_4(h),\) and \({\widetilde{S}}^*_4(h),\) we introduce the following Lie derivative operators defined by the Poisson brackets \(\{\cdot ,\cdot \}\) as follows

$$\begin{aligned} X=\{\cdot ,H\}=\frac{\partial H}{\partial {\varvec{P}}}\frac{\partial }{\partial {\varvec{Q}}} -\frac{\partial H}{\partial {\varvec{Q}}}\frac{\partial }{\partial {\varvec{P}}} +\frac{\partial H}{\partial {\varvec{\xi }}}\frac{\partial }{\partial {\varvec{\theta }}} -\frac{\partial H}{\partial {\varvec{\theta }}}\frac{\partial }{\partial {\varvec{\xi }}}, \end{aligned}$$

which corresponds to the Hamiltonian H. Then, the operators corresponding to \(H_N\) and \(H_{PN}\) are respectively denoted by

$$\begin{aligned} A=\{\cdot ,H_N\}=\frac{\partial H_N}{\partial {\varvec{P}}}\frac{\partial }{\partial {\varvec{Q}}} -\frac{\partial H_N}{\partial {\varvec{Q}}}\frac{\partial }{\partial {\varvec{P}}}, \end{aligned}$$

and

$$\begin{aligned} B=\{\cdot ,H_{PN}\}= & {} \frac{\partial H_{PN}}{\partial {\varvec{P}}}\frac{\partial }{\partial {\varvec{Q}}} -\frac{\partial H_{PN}}{\partial {\varvec{Q}}}\frac{\partial }{\partial {\varvec{P}}}\\{} & {} +\frac{\partial H_{PN}}{\partial {\varvec{\xi }}}\frac{\partial }{\partial {\varvec{\theta }}} -\frac{\partial H_{PN}}{\partial {\varvec{\theta }}}\frac{\partial }{\partial {\varvec{\xi }}}. \end{aligned}$$

The partial derivative operators regarding \({\varvec{\xi }}\) and \({\varvec{\theta }}\) disappear in the operator A because \(H_N\) only involves the variables \({\varvec{P}}\) and \({\varvec{Q}}.\) This definition derives \(X=A+\varepsilon B.\)

Using the exponential map \(\exp (\tau X)\) to denote the phase flow of the Hamiltonian H,  we then express the standard leapfrog method as

$$\begin{aligned} \exp \Big (\frac{1}{2}\varepsilon hB\Big )\exp (hA) \exp \Big (\frac{1}{2}\varepsilon hB\Big ). \end{aligned}$$
(23)

Note that the phase flows \(\exp (\tau X),\) \(\exp (\tau A),\) and \(\exp (\tau \varepsilon B)\) are all symplectic maps. In addition, the integrability of \(H_N\) enables an explicit solving for \(\exp (\tau A).\) However, since \(H_{PN}\) is nonintegrable as discussed in Sect. 2, we cannot explicitly express \(\exp (\tau B)\) to get the exact solution of \(H_{PN}.\) Even so, with the Baker–Campbell–Hausdorff (BCH) formula, we can derive the following theoretical expression

$$\begin{aligned}{} & {} \exp \Big (\frac{1}{2}\varepsilon hB\Big )\exp (hA) \exp \Big (\frac{1}{2}\varepsilon hB\Big )\nonumber \\{} & {} \quad =\exp \big (h(A+\varepsilon B) +\varepsilon h^3S_3 +\cdots \big ), \end{aligned}$$
(24)

where \(S_3=-\frac{1}{24}[A,[A,B]] + \frac{1}{12}\varepsilon [B,[B,A]],\) \([A,B]=AB-BA,\) and the dots \(\cdots \) in the formula indicates higher-order odd-power terms of h. The formula (24) explains that the leapfrog method is second-order, symmetric, and symplectic because the composition of symplectic phase flows is still symplectic.

Suppose that the numerical method M(h) is of order q. Applying M(h) to solve the PN term \(\varepsilon H_{PN}\) derives that the local truncation error possesses the particular form \(O(\varepsilon ^{q+1}h^{q+1})\) due to the presence of \(\varepsilon \) in the differential equations of the Hamiltonian \(\varepsilon H_{PN}.\) Then, we further have

$$\begin{aligned} M(h)=\exp (\varepsilon h B+\varepsilon ^{q+1}h^{q+1} B_{q+1}+\cdots ) \end{aligned}$$
(25)

for some vector fields \(B_{q+i}~(i=1,2,\ldots ).\) Note that even though the method M(h) could be expressed by an exponential map, the properties of M(h) will depend on \(B_{q+i}\) and thus M(h) cannot always be symplectic for arbitrary \(B_{q+i}.\) For the special symmetric case of M(h),  there only exist the terms involving odd powers of \(\varepsilon h.\)

If M(s) is selected as the second-order symplectic implicit midpoint method IRK2, we then have

$$\begin{aligned} \text {IRK2}(h)= & {} \exp (\varepsilon h B+\varepsilon ^{3}h^{3} B_{3}+ \varepsilon ^{5}h^{5} B_{5}\nonumber \\{} & {} +{\mathscr {O}}(\varepsilon ^{7}h^{7})+\cdots ). \end{aligned}$$
(26)

On noting that \(\exp (hA)\) exactly solves \(H_{N}\) and can act as \(S_0(h),\) replacing \(\exp (\varepsilon h B)\) with (26) in the leapfrog formula (24) derives

$$\begin{aligned} S_2(h)= & {} \exp \big (h(A+\varepsilon B)+\varepsilon h^3S_3 +\varepsilon ^{3}h^{3} B_{3}\nonumber \\{} & {} +{\mathscr {O}}(\varepsilon h^5 +\varepsilon ^{5}h^{5})+\cdots \big ), \end{aligned}$$
(27)

which only contains odd-power terms of h. A comparison between the formula (27) and the exact phase flow \(\exp (hX)=\exp \big (h(A+\varepsilon B)\big )\) yields that the mixed method \(S_2(h)\) is really second-order. The symplecticity and symmetry of \(S_2(h)\) follow from that of the phase flow \(\exp (hA)\) and the midpoint method IRK2. This result has been discussed in [42]. Readers can find more details therein.

Consider the explicit nonsymmetric second-order method RK2. Similarly, applying RK2 to \(\varepsilon H_{PN}\) yields

$$\begin{aligned} \text {RK2}(h)= & {} \exp (\varepsilon h B+\varepsilon ^{3}h^{3} {\bar{B}}_{3}+ \varepsilon ^{4}h^{4} {\bar{B}}_{4}\nonumber \\{} & {} + {\mathscr {O}}(\varepsilon ^{5}h^{5})+\cdots ). \end{aligned}$$
(28)

Incorporating this formula into (20) gives

$$\begin{aligned} S_2^*(h)= & {} \exp \big (h(A+\varepsilon B)+\varepsilon h^3S_3 +\varepsilon ^{3}h^{3} {\bar{B}}_{3}\nonumber \\{} & {} +\varepsilon ^{4}h^{4} {\bar{B}}_{4} +{\mathscr {O}}(\varepsilon h^5 +\varepsilon ^{5}h^{5})+\cdots \big ). \end{aligned}$$
(29)

This shows that the new method \(S_2^*(h)\) is certainly of second order as the dominant truncation part regarding h is \({\mathscr {O}}(\varepsilon h^3 +\varepsilon ^{3}h^{3}).\) Moreover, the difference between \(S_2^*(h)\) and \(S_2(h)\) (or the leapfrog method (24)) is \({\mathscr {O}}(\varepsilon ^{3}h^{3}),\) which represents the closeness of \(S_2^*(h)\) to a symplectic method. That is, for a certain stepsize h,  with the decrease of the parameter \(\varepsilon ,\) the explicit method \(S_2^*(h)\) becomes closer to a symplectic method. In this sense, \(S_2^*(h)\) can be called a near-symplectic method for the Hamiltonian (16). For \(S_2^*(h),\) we finally point out that it is not symmetric due to the presence of the term \(\varepsilon ^{4}h^{4} {\bar{B}}_{4}.\) In conclusion, \(S_2^*(h)\) is an explicit second-order near-symplectic method.

For the standard fourth-order Forest–Ruth method

$$\begin{aligned}{} & {} \exp \Big (\frac{\lambda }{2}\varepsilon hB \Big )\exp (\lambda hA) \exp \Big (\frac{1-\lambda }{2}\varepsilon hB\Big )\exp \big ((1-2\lambda )hA\big )\\{} & {} \quad \circ \exp \Big (\frac{1-\lambda }{2}\varepsilon hB\Big ) \exp (\lambda hA) \exp \Big (\frac{\lambda }{2}\varepsilon hB \Big ), \end{aligned}$$

if we denote the dominant term of its local truncation error by \(\varepsilon h^5 D,\) it can be derived the following expression for the mixed symplectic method \(S_4(h)\):

$$\begin{aligned} S_4(h)= & {} \exp \big (h(A+\varepsilon B)+\varepsilon h^5D +\varepsilon ^{5}h^{5} {B}_{5}\nonumber \\{} & {} +{\mathscr {O}}(\varepsilon h^7 +\varepsilon ^{7}h^{7})+\cdots \big ), \end{aligned}$$
(30)

whose even-power terms of h vanish. In a similar way, we express the fourth-order method RK4 applying to \(\varepsilon H_{PN}\) as follows:

$$\begin{aligned} \text {RK4}(h)= & {} \exp (\varepsilon h B+\varepsilon ^{5}h^{5} {\widehat{B}}_{5}+ \varepsilon ^{6}h^{6} {\widehat{B}}_{6}\nonumber \\{} & {} + {\mathscr {O}}(\varepsilon ^{7}h^{7})+\cdots ). \end{aligned}$$
(31)

Then, RK4 introduce the additional error terms \(\varepsilon ^{5+i}h^{5+i} {\widehat{B}}_{5+i}\) \((i=0,1,\ldots )\) into the new method \(S_4^*(h)\) as

$$\begin{aligned} S_4^*(h)= & {} \exp \big (h(A+\varepsilon B)+\varepsilon h^5D+\varepsilon ^{5}h^{5} {\widehat{B}}_{5}\nonumber \\{} & {} +\varepsilon ^{6}h^{6} {\widehat{B}}_{6}+{\mathscr {O}}(\varepsilon h^7 +\varepsilon ^{7}h^{7})+\cdots \big ). \end{aligned}$$
(32)

A comparison between (30) and (32) shows that the new method \(S_4^*(h)\) is also of order four, and that the difference between \(S_4^*(h)\) and a symplectic method (such as \(S_4(h)\) or the standard Fourth–Ruth method) is about \({\mathscr {O}}(\varepsilon ^{5}h^{5})\) which tends to zero with the decrease of \(\varepsilon .\) Hence, \(S_4^*(h)\) is an explicit fourth-order near-symplectic method.

For the improved method \({\widetilde{S}}_4^*(h)\) obtained by replacing RK4 with RK2 in \(S_4^*(h),\) we can similarly derive

$$\begin{aligned} {\widetilde{S}}_4^*(h)= & {} \exp \big (h(A+\varepsilon B)+\varepsilon h^5D+(\varepsilon ^{3}h^{3} {\bar{B}}_{3}\nonumber \\{} & {} +\varepsilon ^{4}h^{4} {\bar{B}}_{4}+\cdots )+{\mathscr {O}}(\varepsilon h^7)+\cdots \big ). \end{aligned}$$
(33)

Unlike \(S_4^*(h),\) this formula shows that \({\widetilde{S}}_4^*(h)\) is essentially not fourth-order as the lowest power of h in the dominant error term \({\mathscr {O}}(\varepsilon ^{3}h^{3}+\varepsilon h^5)\) is 3. In fact, the method \({\widetilde{S}}_4^*(h)\) is pseudo-fourth-order in the sense of pseudo-high-order method [28,29,30,31]. In the case \(\varepsilon \ll \tau \) (at least \(\varepsilon \approx \tau \)), this method behaves the same as a fourth-order method. Only in the case \(\varepsilon >\tau ,\) this method reduces to second order.

As considered in this paper that the parameter \(\varepsilon \) always takes a small value, the method \({\widetilde{S}}_4^*(h)\) can be regarded as a fourth-order method once \({\mathscr {O}}(\varepsilon h^5)\) dominates the error terms. In this case, the difference between \({\widetilde{S}}_4^*(h)\) and \({S}_4(h)\) (or the standard Forest–Ruth method) is \({\mathscr {O}}(\varepsilon ^{3}h^{3}),\) which has a larger magnitude than that between \({S}_4^*(h)\) and \({S}_4(h),\) i.e., \({\mathscr {O}}(\varepsilon ^{5}h^{5}).\) This point will be stressed by numerical experiments in the following section.

Although the proposed explicit near-symplectic methods up to (pseudo) fourth-order are designed for the system of spinning compact binaries, they are valid for any Hamiltonian that admits the separation of a dominant integrable part and a perturbed nonintegrable part. Meanwhile, the construction of (pseudo) higher-order explicit near-symplectic methods can be conducted in a similar way by composition or splitting approach.

4 Numerical experiments

Fig. 1
figure 1

Orbital evolution of the reference solutions: a \(c=10^{1/2};\) b \(c=10^{3/2}\)

Full size image
Fig. 2
figure 2

Energy errors \(|\Delta H|\) of the reference solutions corresponding to Fig. 1: a \(c=10^{1/2};\) b \(c=10^{3/2}\)

Full size image
Fig. 3
figure 3

Energy errors \(|\Delta H|\) and orbital errors \(|\Delta X|\) of different methods with different c: a \(S_2^*(h)\) with \(c=10^{1/2};\) b \(S_2^*(h)\) with \(c=10^{3/2};\) c \(S_4^*(h)\) with \(c=10^{1/2};\) d \(S_4^*(h)\) with \(c=10^{3/2};\) e \({\widetilde{S}}_4^*(h)\) with \(c=10^{1/2};\) f \({\widetilde{S}}_4^*(h)\) with \(c=10^{3/2}\)

Full size image
Fig. 4
figure 4

Energy errors \(|\Delta H|\) and orbital errors \(|\Delta X|\) between different methods with different c: a \(S_2^*(h)\) and \(S_2(h)\) with \(c=10^{1/2};\) b \(S_2^*(h)\) and \(S_2(h)\) with \(c=10^{3/2};\) c \(S_4^*(h)\) and \(S_4(h)\) with \(c=10^{1/2};\) d \(S_4^*(h)\) and \(S_4(h)\) with \(c=10^{3/2};\) e \({\widetilde{S}}_4^*(h)\) and \(S_4(h)\) with \(c=10^{1/2};\) f \({\widetilde{S}}_4^*(h)\) and \(S_4(h)\) with \(c=10^{3/2}\)

Full size image
Fig. 5
figure 5

Dependence of energy errors \(|\Delta H|\) and orbital errors \(|\Delta X|\) on the parameter c

Full size image
Fig. 6
figure 6

The discrepancy between: a \(S_2^*(h)\) and \(S_2(h);\) b \(S_4^*(h)\) and \(S_4(h);\) c \({\widetilde{S}}_4^*(h)\) and \(S_4(h)\)

Full size image

During our numerical experiments, the initial conditions are selected as \({\varvec{Q}}=(25.34,0,0),\) \({\varvec{P}}=(0,0.18,0),\) \({\varvec{\theta }}=(71.57^\circ ,35.54^\circ ),\) and \({\varvec{\xi }}=(0.0445,0.0705)\) with the spin magnitudes \(\Lambda _1=0.0479\) and \(\Lambda _2=0.6104.\) The mass ratio is set to \(\beta =0.28.\) As we mentioned in Sect. 2 and discussed in [7, 8, 52, 53], the parameter c should be readjusted to match different PN effects under the setting \(G=M=1.\) In this case, a larger readjusted c thus a smaller \(\varepsilon \) as \(\varepsilon =\frac{1}{c^2}\) indicates a weaker PN effect.

During our test, a fully implicit symplectic method, i.e., the eighth-order Gauss collocation method is used with a tiny stepsize to obtain the reference solutions. We mention here that this method is very expensive and the CPU time up to the integration time \(T=10^5\) is about 8 min (480 s), which is much larger than the new methods proposed in this paper. The orbit evolution for two different cases \(c=10^{1/2}\) and \(c=10^{3/2}\) are presented in Fig. 1. As the initial z-component is set to zero, the orbit of the Newtonian term \(H_N\) will be an ellipse restricted to the x–y plane. It can be seen from Fig. 1 that the larger the value of c,  the smaller z-component of the orbit will be. This point coincides with the fact that a larger c makes the whole Hamiltonian H closer to the Newtonian term \(H_N\) thus the z-component is closer to zero. The energy errors of the reference solutions are shown in Fig. 2. The magnitude of about \(10^{-15}\) in Fig. 2 indicates the high accuracy of the reference solutions.

The energy errors and orbital errors of the proposed explicit near-symplectic methods \(S_2^*(h),\) \(S_4^*(h),\) and \({\widetilde{S}}_4^*(h)\) are presented in Fig. 3, where the stepsize for \(S_2^*(h)\) is set to \(h=5\) while \(h=20\) for \(S_4^*(h)\) and \({\widetilde{S}}_4^*(h).\) We first see that the results of \({\widetilde{S}}_4^*(h)\) are nearly the same as \(S_4^*(h),\) which confirms that the pseudo-fourth-order method \({\widetilde{S}}_4^*(h)\) performs nearly the same as a real fourth-order method. From this figure, it can be derived that all the energy errors do not have a secular increase with time, while the orbital errors linearly increase with time (i.e., the slope of the red orbital error curves is near to 1). The numerical results show that the newly proposed methods are very close to symplectic methods whose energy errors oscillate in a bounded region and global errors linearly increase with time.

We do not show the energy errors and orbital errors of the corresponding mixed symplectic methods, because they overlap the near-symplectic methods. Figure 4 gives more details on the difference between the proposed explicit near-symplectic methods and the corresponding mixed symplectic methods. A comparison between Fig. 4 and Fig. 3 shows that the difference between explicit near-symplectic methods and mixed symplectic methods are much smaller than the errors of the former in both the two cases \(c=10^{1/2}\) and \(c=10^{3/2}.\) In particular, the difference error between \(S_4^*(h)\) and \(S_4(h)\) in the case \(c=10^{1/2}\) is smaller than that between \({\widetilde{S}}_4^*(h)\) and \(S_4(h).\) This point supports our analysis in Sect. 3 that their theoretical difference are respectively \({\mathscr {O}}(\varepsilon ^{5}h^{5})\) and \({\mathscr {O}}(\varepsilon ^{3}h^{3}).\) In the case \(c=10^{3/2},\) the difference error between \(S_4^*(h)\) and \(S_4(h)\) is nearly the same as that between \({\widetilde{S}}_4^*(h)\) and \(S_4(h),\) as we consider that the secondary error term \({\mathscr {O}}(\varepsilon h^{7})\) in the standard Forest–Ruth method will be larger than \({\mathscr {O}}(\varepsilon ^{3}h^{3})\) and \({\mathscr {O}}(\varepsilon ^{5}h^{5}),\) and thus dominates the difference errors. Furthermore, the case \(c=10^{3/2}\) in Fig. 4 has a smaller difference error than the case \(c=10^{1/2},\) which supports our analysis that the proposed near-symplectic methods become closer to symplectic methods with the decrease of the small parameter \(\varepsilon \) (i.e., the increase of c as \(\varepsilon =\frac{1}{c^2}\)).

Figures 3 and 4 show that the proposed explicit near-symplectic methods behave extremely like the mixed symplectic methods. To compare their efficiency, Table 1 lists the CPU time (in seconds) consumed by all the mentioned methods that are written in Fortran and run on the Lenovo desktop Qitian M437 with 3.10 GHz CPU i5-10500. For the case \(c=10^{1/2},\) the CPU time of \(S_2^*(h)\) is about 44.33% of \(S_2(h);\) the CPU time of \(S_4^*(h)\) is about 52.98% of \(S_4(h),\) while the CPU time of \({\widetilde{S}}_4^*(h)\) is 26.41% of \(S_4(h).\) For the weaker PN effect case \(c=10^{3/2},\) these values become 68.23%, 86.55%, and 43.71%. That is, in the two different cases, the proposed near-symplectic methods are more efficient than the corresponding mixed symplectic methods. Meanwhile, the stronger PN effect (a smaller value of c) increases the computation amount of the mixed methods, while the CPU time is almost unchanged for the explicit near-symplectic methods. In particular, the pseudo-fourth-order method \({\widetilde{S}}_4^*(h)\) consumes about half the time of \(S_4^*(h),\) even though the two methods behave almost the same. From the point of view of efficiency, we recommend the explicit near-symplectic methods \(S_2^*(h)\) and \({\widetilde{S}}_4^*(h)\) as substitutions of \(S_2(h)\) and \(S_4(h).\)

We further display the dependence of the energy errors and orbital errors on the readjusted parameter c in Fig. 5. As shown in Fig. 5a and c, except for several small values (indicating strong PN effect), the energy error curves of all the presented methods \((S_2(h),\) \(S_2^*(h),\) \(S_4(h),\) and \(S_4^*(h))\) exhibit a quadratic decrease with the increase of c as the slope is \(-2.\) The case for the orbital errors has a slightly different performance, where a clear inflection point whose different sides have different slopes is shown in both Fig. 5b and d. The c values of the inflection points are about 2.8 and 15.6 respectively for Fig. 5b and d, which are nearly in the same magnitudes as \(h=5\) and \(h=20\) that are used respectively for second-order methods and (pseudo) fourth-order methods. Moreover, the slopes of the orbital error curves on the right side of the inflection points are both about \(-2.\) This is also consistent with our theoretical analysis that once \(\epsilon < h\) the term \({\mathscr {O}}(\varepsilon h^{3})\) or \({\mathscr {O}}(\varepsilon h^{5})\) will dominate the truncation error, which leads to a linear decrease of the global error with the decrease of \(\varepsilon \) (thus a quadratic decrease of the global error with the increase of c as \(\varepsilon =\frac{1}{c^2}\)). In this figure, we do not display the result of \({\widetilde{S}}_4^*(h),\) because its curves overlap the curves of \(S_4^*(h).\)

We finally display the dependence of the discrepancies between the proposed explicit near-symplectic methods and the mixed symplectic methods on the readjusted parameter c in Fig. 6. It can be seen that once c is smaller than some certain value, the discrepancies decrease with the increase of c. Afterward, the discrepancies approximately reach a stable value whose magnitudes are respectively about \({\mathscr {O}}(10^{-9})\) for orbital errors and \({\mathscr {O}}(10^{-15})\) for energy errors. Especially for that between \(S_2^*(h)\) and \(S_2(h),\) the discrepancy becomes zero once \(c>144.5\) (since the discrepancy is plotted in logarithmic scale, we technically set \(10^{-17}\) to represent the zero value in Fig. 6a). We consider that the stabilization of the discrepancy is caused by the term \({\mathscr {O}}(\varepsilon h^{5})\) that dominates the difference once \(\varepsilon =\frac{1}{c^2}\) is too small. Overall, the much smaller discrepancies in Fig. 6 than the global (energy or orbital) errors in Fig. 5 sufficiently confirm the good near symplecticity of the proposed explicit methods.

Table 1 CPU time (seconds) for each method with \(T=10^5\)
Full size table

5 Conclusion

In the numerical simulation for Hamiltonian systems, explicit symplectic methods are more favoured than implicit ones due to their higher efficiency. However, the PN Hamiltonian involving the interactions of the generalized position, the generalized momentum, and the spin variables in the PN approximation approach is usually nonseparable. This disables the explicit symplectic solving for the PN Hamiltonian, and the available symplectic methods are either fully implicit or semi-implicit.

To take advantage of both the high efficiency of explicit methods and the good long-term performance of symplectic methods, we explored the construction of explicit near-symplectic methods for PN Hamiltonian systems. On account of the small parameter \(\varepsilon \) in the PN term, we considered replacing the implicit symplectic solvers in the mixed symplectic methods with conventional explicit nonsymplectic solvers and derived three explicit methods. Then, the error analysis based on the BCH formula showed that the three proposed methods are respectively second-order, fourth-order, and pseudo-fourth-order. Numerical results with the spinning compact binaries showed that the proposed explicit near-symplectic methods nearly have the same error behavior as the corresponding semi-implicit mixed symplectic methods that the energy error oscillates in a bounded region and the orbital error has a linear growth with time. Meanwhile, the proposed explicit methods are more efficient than their implicit counterparts by comparing the consumed CPU time. Finally, the pseudo-fourth-order method \({\widetilde{S}}^*_4(h)\) consume much less CPU time than the fourth-order \(S^*_4(h),\) and thus we recommend the explicit near-symplectic methods \(S_2^*(h)\) and \({\widetilde{S}}_4^*(h)\) as substitutions of \(S_2(h)\) and \(S_4(h).\)

In summary, we proposed three explicit near-symplectic methods that almost preserve the property of symplectic methods and possess the high efficiency of explicit methods. The new methods can be applied to PN Hamiltonians that admit a dominant integrable part and a perturbed nonintegrable part. Following the idea in this paper, (pseudo) higher-order explicit near-symplectic methods can be constructed in a similar way.