Relic gravitons and pulsar timing arrays: a theoretical viewpoint

Abstract

During the last 3 years the pulsar timing arrays reported a series of repeated evidences of gravitational radiation (with stochastically distributed Fourier amplitudes) at a benchmark frequency of the order of 30 nHz and characterized by spectral energy densities (in critical units) ranging between $10^{-8}$ and $10^{-9}$. While it is still unclear whether or not these effects are just a consequence of the pristine variation of the space-time curvature, the nature of the underlying physical processes would suggest that the spectral energy density of the relic gravitons in the nHz domain may only depend on the evolution of the comoving horizon at late, intermediate and early times. Along this systematic perspective we first consider the most conventional option, namely a post-inflationary modification of the expansion rate. Given the present constraints on the relic graviton backgrounds, we then show that such a late-time effect is unable to produce the desired hump in the nHz region. We then analyze a modified exit of the relevant wavelengths as it may happen when the gravitons inherit an effective refractive index from the interactions with the geometry. A relatively short inflationary phase leads, in this case, to an excess in the nHz region even if the observational data coming from competing experiments do not pin down exactly the same regions in the parameter space. We finally examine an early stage of increasing curvature and argue that it is not compatible with the observed spectral energy density unless the wavelengths crossing the comoving horizon at early times reenter in a decelerated stage not dominated by radiation.

1 Introduction

The low-frequency gravitons notoriously affect the the propagation of electromagnetic signals so that the temperature and the polarization anisotropies of the cosmic microwave background (CMB) are in fact detectors of relic gravitational waves in the aHz range¹ (see, for instance, [1]). Even though the physical nature of the effects remains practically the same, the nHz range exceeds the Cosmic Microwave Background (CMB) frequencies by roughly 10 orders of magnitude and, as suggested long ago [2,3,4], the millisecond pulsars can be employed as effective detectors of random gravitational waves for a typical domain that corresponds to the inverse of the observation time during which the pulsar timing has been monitored. More specifically, Sazhin [2] suggested that the arrival times of pulsar’s pulses could be used for direct searches of gravitational radiation and shortly after Detweiler [3] made a similar point by deriving one of the first upper limits on the relic gravitational waves in the nHz range. This aspect has been more accurately reinstated in Ref. [4] where the authors also derived an important property of the isotropic backgrounds of gravitational radiation stipulating that the signal coming, in our context, from relic gravitons should be correlated across the baselines while that from others noises will not. This effect depends on the angle between a pair of Earth-pulsars baselines and it is often dubbed by saying that the correlation signature of an isotropic and random gravitational wave background follows the so-called Hellings–Downs curve [4]. If the gravitational waves are not characterized by stochastically distributed Fourier amplitudes the corresponding signal does not necessarily follow the Hellings–Downs correlation.

By using this logic, since the mid 1990s a series upper limits on the spectral energy density of the relic gravitons in the nHz range has been obtained [5,6,7,8] and during the last 3 years the pulsar timing arrays (PTA) reported an evidence that could be attributed to isotropic backgrounds of gravitational radiation [9,10,11,12]. The PTA collaborations² customarily assign the chirp amplitude at a reference frequency $\nu _{ref} = 31.68\,\, \textrm{nHz}$ that corresponds to $\textrm{yr}^{-1}$:

$$\begin{aligned} h_{c}(\nu ,\tau _{0}) = \,Q \,\biggl (\frac{\nu }{\nu _{ref}}\biggr )^{\beta }, \qquad \qquad \nu _{ref} = \frac{1}{\textrm{yr}}= 31.68\,\, \textrm{nHz}. \end{aligned}$$

(1.1)

The pivotal models analyzed in Refs. [9,10,11,12] assumed $\beta = -2/3$ or, which is the same,³$\overline{\gamma } = 13/3$. In Eq. (1.1) the value of Q inferred from the observational data should be ${\mathcal O}(10^{-15})$ so that we find it natural to parametrize the amplitude at $\nu _{ref}$ as $Q= q_{0} \times 10^{-15}$. In the previous data releases the $q_{0}$ ranged between 1.92 and 5.13 depending on the values of $\beta$ [9,10,11,12]. Even more recently the new data of the PTA collaborations have been released [13,14,15] together with the first determinations of the Chinese Pulsar Timing array (CPTA) [16]. The Parkes PTA collaboration considered 30 millisecond pulsars spanning 18 years of observations; they estimated $q_{0}= 3.1^{1.3}_{-0.9}$ with a spectral index $\beta = -0.45\,\pm \, 0.20$ [13]; for a spectral index $\beta =-2/3$ the collaboration obtains instead $q_{0} =2.04_{-0.22}^{0.25}$ which is compatible with the determinations of the previous data releases [10]. The Parkes PTA collaboration did not claim the detection of the Hellings–Downs correlation [13] and carefully considered the issues related to time-dependence of the common noise. The conclusions of the Parkes PTA seem significantly more conservative than the one of the NANOgrav collaboration examining 67 millisecond pulsars in the last 15 years. The NANOgrav experiment claimed the detection of the Hellings–Downs correlation [14] but the inferred values of the spectral parameters are slightly different from the ones of PPTA since $q_{0} = 6.4^{+4.2}_{-2.7}$ and $\beta = -0.10 \pm 0.30$ [14]. The chirp amplitude of Eq. (1.1) can be related to the spectral energy density evaluated for typical frequencies larger than the Hubble rate at the present time [17]

$$\begin{aligned} h_{0}^2 \, \Omega _{gw}(\nu _{ref},\tau _{0}) = 6.287 \times 10^{-10} \, \, q_{0}^2, \end{aligned}$$

(1.2)

implying $h_{0}^2 \, \Omega _{gw}(\nu _{ref},\tau _{0}) = {\mathcal O}(2.57) \times 10^{-8}$ in the case of Ref. [14] (for $q_{0} =6.4$) and $h_{0}^2 \, \Omega _{gw}(\nu _{ref},\tau _{0}) = {\mathcal O}(6.04)\times 10^{-9}$ for Ref. [13] (for $q_{0} =3.1$). The connection between $h_{0}^2 \, \Omega _{gw}(\nu _{ref},\tau _{0})$ and $h_{c}(\nu ,\tau _{0})$ has been explicitly discussed in Eqs. (A.18)–(A.19) and (A.20) of Appendix A.

Even if the interpretation of various collaborations preferentially focuses on a background produced by diffuse astrophysical sources at the present time,⁴ in this paper we are going to examine the qualitatively different hypothesis that the excesses summarized by Eqs. (1.1)–(1.2) are caused by the parametric amplification of the quantum fluctuations of the tensor modes of the geometry. Since the relic gravitons are only coupled to the evolution of the space-time curvature Grishchuk [18, 19], Ford and Parker [20] and some others first outlined that the formation of a diffuse backgrounds of gravitational radiation are a generic consequence of quantum mechanics in cosmological space-times. Depending on the early variation the space-time curvature, relic gravitons are then expected in different dynamical situations and, in particular, during a stage of de Sitter and quasi-de Sitter expansion [21].

Considering that, at early times, the conventional expanding stages of the concordance paradigm are complemented by an inflationary epoch, $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ is a monotonically decreasing function of the comoving frequency from the aHz range to the MHz domain. More precisely between few aHz and 100 aHz the spectral energy density in critical units scales approximately as $\nu ^{-2}$ [25,26,27]; for higher frequencies $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ exhibits a quasi-flat plateau whose precise slope depends in fact upon the parameter $r_{T}$ measuring the ratio between the tensor power spectrum and its scalar counterpart. In the case of single-field inflationary scenarios (often taken as the benchmark class of models by some observers [22,23,24]) the consistency relations stipulate that the tensor spectral index $m_{T}$ and the slow-roll parameter $\epsilon _{k}$ are both determined by the value of $r_{T}$ according to the following (approximate) chain of equalities $m_{T} \simeq - r_{T}/8 \simeq - 2 \epsilon _{k}$ that are customarily referred to as the consistency conditions. The simplest version of the concordance scenario includes only one further free parameter, namely the ratio $r_{T}(k_{p})$ describing the tensor component of the large-scale inhomogeneity at a conventional pivot scale that coincides, in what follows, with $k_{p} = 0.002\,\, \textrm{Mpc}^{-1}$. The addition of a single tensor component (only described by $r_{T}$) allows for an accurate set of limits implying that $r_{T} \le 0.06$ or even $r_{T}\le 0.03$ [22,23,24]. Moreover, the pivot wavenumber $k_{p}$ corresponds to $\nu _{p} = k_{p}/(2\pi ) = 3.09\,\,\textrm{aHz}$ and this is why the limits on $r_{T}(k_{p})$ may be translated into constraints on the spectral energy density of the relic gravitons in the aHz range.

For typical comoving frequencies of the order of the nHz the current bounds on $r_{T}$ suggest that in the concordance paradigm $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ must be ${\mathcal O}(10^{-17})$ (or smaller); in this case all the relevant wavelengths exit in the inflationary stage and reenter during the radiation phase. Furthermore, the accurate estimate of $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ in the nHz region involves a number of late-time effects that may reduce even further the overall amplitude of the spectral energy density: the corrections due to neutrino free-streaming [28] (see also, for instance, [29,30,31]) suppress $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ for $\nu <\nu _{bbn}$ where $\nu _{bbn} = {\mathcal O}(10^{-2})\,\, \textrm{nHz}$ is the typical frequency associated with big-bang nucleosynthesis. Thus in the nHz range the relic gravitons produced within the conventional lore are nine or ten orders of magnitude smaller than the figures reported in Eq. (1.2). This means that if the nHz excess is caused by relic gravitons amplified by the evolution of the space-time curvature the relevant time-scale of the problem is primarily given by $\tau _{k}$ defining the moment at which the wavelength associated with $\nu _{ref}$ crossed the comoving Hubble radius after the end of inflation. A simple estimate suggests that $\tau _{k}$ is just a fraction of the time-scale of big-bang nucleosynthesis⁵

$$\begin{aligned} \frac{\tau _{k}}{\tau _{bbn}}&= 3.40 \times 10^{-2} \biggl (\frac{\nu _{PTA}}{31.68 \, \textrm{nHz}}\biggr )^{-1}\, \biggl (\frac{T_{bbn}}{\textrm{MeV}}\biggr ) \, \nonumber \\ {}&\quad \times \biggl (\frac{h_{0}^2 \Omega _{R0}}{4.15 \times 10^{-5}}\biggr )^{1/4}. \end{aligned}$$

(1.3)

In what follows $\nu _{PTA}$ denote the frequency of the PTA and it can be either slightly larger or smaller than $\nu _{ref}$; when $\nu _{PTA} > \nu _{ref}$ the corresponding wavelength crossed the comoving horizon even earlier. The second relevant scale of the problem is given by the ratio between $\nu _{PTA}$ and the expansion rate at the end of inflation:

$$\begin{aligned} \frac{\nu _{PTA}}{a_{1} \, H_{1}}= & {} 2.05 \times 10^{-17} \biggl (\frac{\nu _{PTA}}{31.68 \, \textrm{nHz}}\biggr )\,\biggl (\frac{h_{0}^2 \Omega _{R0}}{4.15 \times 10^{-5}}\biggr )^{-1/4} \, \nonumber \\{} & {} \times \biggl (\frac{r_{T}}{0.03}\biggr )^{-1/4} \, \biggl (\frac{{\mathcal A}_{{\mathcal R}}}{2.41\times 10^{-9}}\biggr )^{-1/4}, \end{aligned}$$

(1.4)

where ${\mathcal A}_{{\mathcal R}}$ denotes the amplitude of the curvature inhomogeneities at the pivot scale $k_{p}$. From Eqs. (1.3)–(1.4) it follows that any modification of the post-inflationary evolution is unlikely to produce a hump for frequencies ${\mathcal O}(\nu _{ref})$; interesting enhancements may arise for $\nu > \textrm{mHz} \gg \nu _{ref}$ implying that the post-inflationary evolution is indeed able to increase the spectral energy density between the mHz and the MHz [32,33,34] but not in the nHz range. As we shall see Eqs. (1.3)–(1.4) ultimately imply that an excess comparable with Eq. (1.2) cannot be related to a post-inflationary modification of the comoving horizon.

Before plunging into the analysis it is probably useful to stress that already after the first data releases of the PTA a large number of different (and sometimes opposite) explanations for the nHz excess have been proposed. A common characteristic distinguishing the hypothesis pursued in this paper and the ones propounded in the current literature is that the nHz excess is typically due the presence of late-time sources of anisotropic stress. An example along this direction is represented by cosmic strings whose oscillating loops may emit gravitational waves at different epochs ultimately producing a stochastic background [35] with quasi-flat spectral energy density which is typically larger than the inflationary signal. For the largest values of the string tension in Planck units there is the possibility of an excess in the nHz region (see e.g. [36, 37]). Various subsequent analyses based on these observations have been proposed more recently with various degrees of success. Another late-time source of gravitational radiation is represented by strongly first-order phase transitions that are known to produce spikes at low and intermediate frequencies because of the partial breaking of homogeneity due to the nucleation of bubbles of the new phase. The amount of gravitational radiation produced by the phase transition depends chiefly on the difference between the energy density in the broken and in the symmetric phase. This energy density may be comparable with the energy density of the ambient plasma (and in this case the phase transition experiences a strong supercooling) or smaller than the energy density of the surrounding radiation (and in this case the phase transition is mildly supercooled). When the gravitational radiation is produced from the collisions of the bubbles of the new phase [38,39,40] the spectral energy density scales like $\nu ^3$, reaches a maximum and then decreases with a power that may be faster than $\nu ^{-1}$. The spectral energy density inherits also contribution from the sound waves of the plasma [41] and this second component may be even larger than the one due to bubble collisions. There are two points that make this explanation difficult. The first one is that the powers of the hump are typically steeper than the ones suggested by the PTA observations. The second observation concerns the physics of the phase transition. The bursts of gravitational radiation coming from the TeV are absent at frequencies much lower than the $\mu$Hz also because the electroweak phase transition is not strongly first-order given the values of the Higgs mass. This implies the necessity of more contrived explanations (see e.g. [42] and references therein). There exist also more exotic possibilities where the nHz excess is caused by modifications of gravity in alternative cosmological scenarios; see, in this respect, [43] and references therein.

The layout of this investigation is the following. In Sect. 2 the post-inflationary modifications of the expansion rate (related to the reentry of $\lambda _{PTA} \simeq 1/\nu _{PTA}$) are analyzed and confronted with the nHz excesses. In Sect. 3 we instead examine the exit of the PTA scale during inflation and focus on the possibility of a refractive index coming from the interactions of the relic gravitons with the background geometry. In Sect. 4 the general features of the bouncing scenarios (modifying both the exit and the reentry of $\lambda _{PTA}$) are specifically examined in the light of a potential nHz signal. Section 5 contains our concluding remarks. Appendix A covers the main notations employed in the paper and Appendix B is instead focussed on the general form of the effective action of the relic gravitons and on its different parametrizations.

2 The comoving horizon after inflation

2.1 General considerations

When all the wavelengths of the relic gravitons are shorter than the comoving Hubble radius at the present time, the spectral energy density in critical units can be expressed as:

$$\begin{aligned}{} & {} \Omega _{gw}(k, \tau ) = \frac{ 2\, k^4 }{3 \,\pi \, M_{P}^2\, H^2 \, a^4 } \biggl (\frac{a_{re}}{a_{ex}}\biggr )^2 \bigl |{\mathcal Q}_{k}(\tau _{ex}, \tau _{re})\bigr |^2 \nonumber \\{} & {} \quad \times \biggl [ 1 + \biggl (\frac{{\mathcal H}_{re}}{k}\biggr )^2 + {\mathcal O}({\mathcal H}/k) + {\mathcal O}({\mathcal H}^2/k^2) \biggr ], \end{aligned}$$

(2.1)

where ${\mathcal H} = a \, H$ and ${\mathcal H}= a^{\prime }/a$; the notations employed here are summarized in Appendix A and, in particular, in Eqs. (A.2) and (A.10)–(A.11). Equation (2.1) has been deduced in the limit $a_{re} \gg a_{ex}$ which is valid for all conventional and unconventional inflationary scenarios even if, in some cases, $\Omega _{gw}(k,\tau )$ may also depend on the intermediate evolution between $\tau _{ex}$ and $\tau _{re}$ since ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re})$ (whose square modulus enters Eq. (2.1)) contains an integral over the conformal time coordinate $\tau$:

$$\begin{aligned} {\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) = 1 - ({\mathcal H}_{ex} + i k) \int _{\tau _{ex}}^{\tau _{re}} \frac{a_{ex}^2}{a^2(\tau )} \, \,d\tau . \end{aligned}$$

(2.2)

From the evolution of the mode functions of Eq. (A.15), $\tau _{ex}$ and $\tau _{re}$ are the roots of the equation

$$\begin{aligned} k^2 = a^2 \, H^2 [ 2 - \epsilon (a)], \qquad \qquad \epsilon = - \dot{H}/H^2, \end{aligned}$$

(2.3)

that ultimately defines the different regimes of the evolution of the mode functions. In a stricter mathematical perspective, $\tau _{re}$ and $\tau _{ex}$ define the turning points where the solutions of Eq. (A.15) change their asymptotic behaviour. Defining, for the sake of simplicity, $\epsilon _{re}= \epsilon (\tau _{re})$ and $\epsilon _{ex} = \epsilon (\tau _{ex})$, the turning points are regular whenever $\epsilon _{re} \ne 2$ and $\epsilon _{ex} \ne 2$. For instance, if the exit occurs during a conventional stage of inflationary expansion (i.e. $\epsilon _{ex} \ll 1$) we have that, by definition, $k \simeq a_{ex} \, H_{ex}$ and $\tau _{ex} \simeq 1/k$. Conversely, if the reentry takes place close to the radiation-dominated stage of expansion we should have $\epsilon _{re} \rightarrow 2$ in Eq. (2.3) so that $k \ll a_{re}\, H_{re}$.

The corrections appearing inside the squared bracket of Eq. (2.1) (of the order ${\mathcal H}/k$ and ${\mathcal H}^2/k^2$) are both negligible in the limit $k \tau \gg 1$ when all the relevant wavelengths are inside the comoving horizon. Therefore, if all the wavelengths exit during inflation and reenter in a stage dominated by radiation (as it happens in the concordance paradigm and in Fig. 1) Eq. (2.2) implies that ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) \rightarrow 1$. There can be however physical contingencies where the contribution of the integral in Eq. (2.2) gets larger than 1 and, as long as the exit is a regular turning point that the integrals appearing in Eq. (2.2) can be estimated as:

$$\begin{aligned} {\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) = 1 - \int _{\tau _{ex}}^{-\tau _{1}} \frac{a_{ex}^2}{a_{inf}^2(x)} \, d\, x - \int _{\tau _{-1}}^{\tau _{re}} \frac{a_{ex}^2}{a_{post}^2(x)} \, d\, x, \end{aligned}$$

(2.4)

where $x = \tau /\tau _{ex}$ and ${\mathcal H}_{ex} = a_{ex} \, H_{ex} \simeq k$. In Eq. (2.4) we also included two subscripts in the integrand with the purpose of stressing that the corresponding contributions may arise during the inflationary and in the post-inflationary stage; we also conventionally assumed, for the sake of concreteness, that the accelerated stage lasts up to $-\tau _{1}$ and it is replaced for $\tau > - \tau _{1}$ by a decelerated evolution.

2.2 The post-inflationary evolution of the comoving horizon

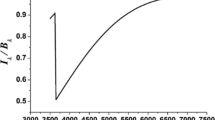
The ratio between the comoving horizon and $\lambda _{PTA}$ is illustrated in Fig. 1 when the relevant bunch of wavelengths exits the comoving horizon during inflation (i.e. $\epsilon _{ex} \ll 1$) and reenters in a radiation-dominated stage of expansion (i.e. $\epsilon _{re} \rightarrow 2$); in this case the spectral slope of $\Omega _{gw}(\nu , \tau _{0})$ follows from Eqs. (2.1)–(2.4) and by just focussing, for simplicity, on the k-dependence we can deduce the spectral slope

$$\begin{aligned}{} & {} \frac{k^4}{a_{1}^4 \, H_{1}^4} \biggl (\frac{a_{re}}{a_{ex}}\biggr )^2 \biggl (\frac{k}{a_{re}\, H_{re}}\biggr )^{-2} \bigl |{\mathcal Q}_{k}(\tau _{ex}, \tau _{re})\bigr |^2 \nonumber \\{} & {} \quad = \frac{a_{re}^4 \, H_{re}^2}{a^4 \, H^2} \, \biggl (\frac{k}{a_{1} \, H_{1}}\biggr )^{m_{T}}. \end{aligned}$$

(2.5)

Fig. 1

The ratio between the comoving horizon and the wavelength $\lambda _{PTA} = {\mathcal O}(0.30) \, \textrm{pc}$ is illustrated; as already mentioned $\lambda _{PTA}$ corresponds to the comoving frequency $\nu _{PTA} = 31.68 \, \textrm{nHz}$. Common logarithms are employed on both axes and the two blobs indicate the exit and to the reentry of the corresponding wavelength. The full line is associated with $\nu _{PTA}$ while the dot-dashed and the dashed lines illustrate, respectively, the situations where the frequency is slightly larger (i.e. $10\, \nu _{PTA}$) or slightly smaller (i.e. $0.1\, \nu _{PTA}$) than the benchmark value provided by $\nu _{ref}$. The timeline reported in this cartoon is characteristic of the concordance paradigm where all the wavelengths (including $\lambda _{PTA}$) do their first crossing during inflation (i.e. for $a< a_{1}$) and reenter in the radiation-dominated stage

In Eq. (2.5) we used that $a_{ex}\, H_{ex} = - 1/[(1 -\epsilon _{ex}) \tau _{ex}]$ and $k \tau _{re} \ll 1$; moreover, by enforcing the validity of the consistency relations (i.e. $r_{T} = 16 \epsilon _{k}$), the spectral index $m_{T}$ is given by⁶

$$\begin{aligned} m_{T} = - \frac{2 \epsilon _{k}}{1 - \epsilon _{k}} = - 2 \epsilon _{k} + {\mathcal O}(\epsilon _{k}^2) \simeq - \frac{r_{T}}{8} + {\mathcal O}(r_{T}^2) \ll 1. \end{aligned}$$

(2.6)

Equation (2.6) is a consequence of Fig. 1 where the first crossing of $\lambda _{PTA}$ occurs during inflation and the reentry takes place for $\epsilon _{re} \rightarrow 2$; this is however not the most general situation even assuming that the left portion of Fig. 1 (i.e. $a< \,a_{1}$) is not modified. Indeed for $a\,>\,a_{1}$, the post-inflationary expansion rate can be modified as $(a\, H)^{-1} \propto a^{1/\delta }$ with $\delta \ne 1$ and this case is illustrated in Fig. 2 when the usual radiation epoch (with $\delta \rightarrow 1$) is either preceded by a stage expanding faster than radiation (i.e. $\delta > 1$) or by one expanding at a rate slower than radiation (i.e. $\delta <1$). While more complicated possibilities are swiftly examined at the end of the present section, already these two opposite situations lead to a modified $\Omega _{gw}(k,\tau )$ above $\nu _{bbn}$ [32,33,34] and may potentially lead to an excess in the nHz range.

The dashed curve of Fig. 2 corresponds to the comoving horizon in the limit $\delta \rightarrow 1$ while for the two remaining profiles the radiation phase is preceded by a stage where $\delta \ne 1$. In the three cases the minima depend both on the length of the post-inflationary stage and on its expansion rate:

$$\begin{aligned} \frac{(a_{1} \, H_{1})^{-1}}{\lambda _{PTA}} = 2.05 \times 10^{-17} \, \, \xi ^{(1 - \delta )/[ 2 (\delta +1)]}, \quad \xi = H_{r}/H_{1}, \end{aligned}$$

(2.7)

where $H_{r}$ and $H_{1}$ denote, respectively, the Hubble rates at the onset of the radiation stage and at the end of inflation (see e.g. Eq. (A.2)). Since, by definition, $\xi < 1$ the comoving horizon at its minimum is comparatively larger for $\delta > 1$ than for $\delta \rightarrow 1$. For the same reason the opposite is true when $\delta < 1$ and $(a_{1}\, H_{1})^{-1}/\lambda _{PTA}$ gets smaller than in the limit $\delta \rightarrow 1$. In Fig. 2 the $\lambda _{PTA}$ crosses the comoving Hubble radius when the expansion rate is different from radiation and this is why, according to Eq. (2.1) the spectral energy density gets modified.

Fig. 2

As in the case of Fig. 1 the ratio between the comoving horizon and $\lambda _{PTA}$ is illustrated with the difference that, in the present cartoon, the post-inflationary evolution is not immediately dominated by radiation; the curve $\delta \rightarrow 1$ (dashed line) is also reported for comparison. The post-inflationary stage with $\delta \ne 1$ lasts until the crossing time of $\lambda _{PTA}$. On the one hand this choice maximizes the deviations from the standard form of the spectral energy density, on the other hand the modified post-inflationary evolution cannot last much longer; this is because the crossing time of $\lambda _{PTA}$ is just a fraction of $\tau _{bbn}$ (see Eq. (1.3) and discussion therein)

If the $\lambda _{PTA}$ reenters the Hubble radius when $\delta \ne 1$ (as it may happen in Fig. 2) $\epsilon _{re} = {\mathcal O}(1)$ while, as before, $\epsilon _{ex} \ll 1$. For this reason, unlike the standard case illustrated in Fig. 1, $|k \tau _{re}|^{-2}= {\mathcal O}(1)$ in Eq. (2.1) and the spectral slope is not given by $m_{T}$ (as in Eq. (2.6)) but rather by the intermediate spectral index $n_{T}$:

$$\begin{aligned} n_{T} = \frac{1 - 3 \epsilon _{k}}{1 - \epsilon _{k}} - 2 \biggl |\delta -\frac{1}{2}\biggr | \simeq \frac{16 - 3 r_{T}}{16 - r_{T}} - 2 \,\biggl |\delta -\frac{1}{2}\biggr |. \end{aligned}$$

(2.8)

The consistency relations remain valid since, for $a< a_{1}$, Figs. 1 and 2 share the same inflationary evolution. We note however that for $\delta > 1/2$ the integral appearing in Eq. (2.4) gives a subleading contribution and ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) \rightarrow 1$. Conversely, when $\delta < 1/2$, we have instead ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) \simeq 1 + |k\,\tau _{1}|^{ 1 - 2\delta }$ so that the second contribution dominates for all the frequencies of the spectrum (i.e. for $k \tau _{1} < 1$). Finally, when $\delta \rightarrow 1/2$ the integral of Eq. (2.4) inherits a logarithmic correction which is relevant in specific models [32,33,34].

2.3 Enhanced spectrum at intermediate frequencies

It is useful to remark that, for conventional sources driving the background geometry (e.g. perfect irrotational fluids or scalar fields), the condition $\delta \ge 1/2$ is generally verified and when the wavelengths $\lambda = {\mathcal O}(\lambda _{PTA})$ cross the comoving Hubble radius the spectral slope of $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ can be deduced from Eq. (2.8):

$$\begin{aligned} n_{T} = \frac{32 - 4 \, r_{T}}{16 - r_{T}} - 2 \delta , \qquad \qquad r_{T} \le 0.03. \end{aligned}$$

(2.9)

It then follows from Eq. (2.9) that $n_{T} = 2 ( 1 - \delta ) + {\mathcal O}(r_{T})$. Thus $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ increases for $\delta < 1$ while it decreases for $\delta >1$; when $\delta \rightarrow 1$, Eq. (2.9) reduces to Eq. (2.6). To compare the slopes of Eq. (2.9) with the potential signals suggested by the PTA we recall that the relation between the chirp amplitude $h_{c}(\nu , \tau _{0})$ of Eq. (1.1) follows from Eqs. (A.18)–(A.19) of Appendix A and the final result is

$$\begin{aligned}{} & {} h_{0}^2 \Omega _{gw}(\nu , \tau _{0}) = 6.287 \times 10^{-10} \, q_{0}^2 \, \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{2 + 2 \beta }, \qquad \nonumber \\{} & {} \nu _{ref} = 31.68\, \, \textrm{nHz}. \end{aligned}$$

(2.10)

For $\nu = \nu _{ref}$ Eq. (2.10) coincides with Eq. (1.2) and since the values of $q_{0}$ and $\beta$ are determined observationally [13, 14] (see also Refs. [9, 10] for the preceding data releases) we can preliminarily identify the slopes of Eqs. (2.9) and (2.10). Therefore, when $\delta > 1/2$, the relation between $\delta$, $\beta$ and $r_{T}$ is simply given by:

$$\begin{aligned} \delta = - \beta - \frac{r_{T}}{r_{T} +1} >\frac{1}{2}, \qquad \beta < 0. \end{aligned}$$

(2.11)

Both in the previous [9, 10] and in the most recent [13, 14] data releases the value of $2 (1 + \beta )$ is always positive definite (i.e. $1 + \beta >0$) while $\beta$ itself is generally smaller than 1. In the special case $\beta \rightarrow -2/3$, Eq. (2.11) implies $\delta = 2/3 + {\mathcal O}(r_{T})$. If we would now assume that the post-inflationary evolution is driven by a relativistic and irrotational fluid we would have $\delta = 2/(3 w+1)$ implying that $\beta \rightarrow - 2/3$ for $w \rightarrow 2/3$. Another possibility would be that the effective expansion rate is dictated by an oscillating scalar field (like the inflaton) with potential $V(\varphi ) = V_{0} (\varphi /\overline{M}_{P})^{2 q}$; in this case the expansion rate during the oscillating phase would be given by $\delta = (q+1)/(2q -1)$ [44,45,46,47,48,49,50] suggesting that $q = {\mathcal O}(5)$ for $\beta = {\mathcal O}(-2/3)$.

Unless the relic gravitons would lead exactly to the same slope of the astrophysical foregrounds associated with black-hole binary systems, the value $\beta =-2/3$ is not particularly compelling in a cosmological setting. In the general case (i.e. when the special value $\beta = -2/3$ is not preliminarily selected) the Parkes PTA collaboration [13] suggests that $\beta = - 0.45\, \pm \, 0.20$. This determination is only marginally compatible with the value of Eq. (2.11) in the limit $\delta \ge 1/2$. The discrepancy between the observational determination of $\beta$ and the values predicted by Eq. (2.11) becomes even more significant if we look at that NANOgrav data suggesting [14] $\beta = -0.10 \pm 0.30$. Thus if we stick to the general situation suggested by the observational collaborations the limit $\delta <1/2$ should also be adequately considered in Eq. (2.8) so that Eq. (2.11) is ultimately replaced by:

$$\begin{aligned} \delta = \beta + \frac{16}{16 - r_{T}}< \frac{1}{2}, \qquad \beta < 0. \end{aligned}$$

(2.12)

From Eq. (2.11) we have $\delta = -\beta + {\mathcal O}(r_{T})$ while in the case $\delta < 1/2$ Eq. (2.12) implies $\delta = 1 + \beta + {\mathcal O}(r_{T})$. From the profile of Fig. 2 with the help of Eqs. (2.1)–(2.2) and (2.8) the spectral energy density at high-frequencies becomes:

$$\begin{aligned} h_{0}^2 \, \Omega _{gw}(\nu , \tau _{0}) = {\mathcal N}(r_{T})\, \biggl (\frac{\nu }{\nu _{r}}\biggr )^{n_{T}}, \qquad \nu > \nu _{r}, \end{aligned}$$

(2.13)

where ${\mathcal N}(r_{T})$ includes the effect of the suppressions associated with the low-frequency transfer function, with the neutrino free-streaming [28,29,30] and with the other late-time sources of damping (like the one associated with the dark-energy dominance [17]). For $r_{T} =0.03$ we can numerically estimate that ${\mathcal N}(r_{T})= 10^{-16.8}$ [51]; we then safely consider⁷ for the present ends ${\mathcal N}= {\mathcal O}(10^{-17})$ with a theoretical amplitude at $\nu _{ref}$ that ultimately depends upon $\nu _{r}$ (see Eq. (2.13))

$$\begin{aligned} \nu _{r} = \overline{\nu }_{max} \sqrt{\xi } = 271.88 \biggl (\frac{g_{s,\, eq}}{g_{s\,r}}\biggr )^{1/3} \biggl (\frac{g_{\rho ,\, r}}{g_{\rho \,eq}}\biggr )^{1/4} \,\, \sqrt{\xi } \,\, \textrm{MHz}, \end{aligned}$$

(2.14)

where the ratio $\xi = H_{r}/H_{1}$ has been already introduced in Eq. (2.7) while $\overline{\nu }_{max}$ given by:

$$\begin{aligned} \overline{\nu }_{max}= & {} 271.88 \biggl (\frac{g_{s,\, eq}}{g_{s\,r}}\biggr )^{1/3} \biggl (\frac{g_{\rho ,\, r}}{g_{\rho \,eq}}\biggr )^{1/4} \biggl (\frac{h_{0}^2 \Omega _{R0}}{4.15 \times 10^{-5}}\biggr )^{1/4} \,\nonumber \\{} & {} \times \biggl (\frac{r_{T}}{0.03}\biggr )^{1/4} \, \biggl (\frac{{\mathcal A}_{{\mathcal R}}}{2.41\times 10^{-9}}\biggr )^{1/4}\, \, \textrm{MHz}. \end{aligned}$$

(2.15)

In spite of the specific value given in Eq. (2.14), $\nu _{r}$ cannot be smaller than $\nu _{bbn}$ and this remark turns out to be quite relevant for the comparison between the observed excesses and the theoretical expectations. Note that ${\mathcal A}_{\mathcal R}$ is the amplitude of curvature inhomogeneities at the pivot scale $k_{p}$ (see also Eq. (1.4) and discussion thereafter).

2.4 Theoretical expectations and observed excesses

Fig. 3

The two straight lines illustrate Eq. (2.18) for ${\mathcal N}(r_{T}) =10^{-17}$ (full line) and for ${\mathcal N}(r_{T}) =10^{-16}$ (dashed line). The two filled rectangles represent the regions probed by the Parkes PTA and by NANOgrav in the plane $(\log {q_{0}}, \, \beta )$. Since the two diagonal lines do not overlap with the shaded areas appearing in the lower portion of the plot, the amplitudes and the slopes of the theoretical signal cannot be simultaneously matched with the corresponding observational determinations. Common logarithms have been employed on the horizontal axis since the range of the observational determinations of $q_{0}$ spans nearly one order of magnitude

Even if the theoretical and the observed slopes can be compatible for specific values of $\delta$, the corresponding amplitudes involve rather different orders of magnitude and to analyze this essential aspect we may impose that Eqs. (2.10) and (2.13) coincide at $\nu _{ref}$

$$\begin{aligned} {\mathcal N}(r_{T}) \bigl (\nu _{ref}/\nu _{r}\bigr )^{n_{T}}= 6.287\,\times 10^{-10}\, q_{0}^2. \end{aligned}$$

(2.16)

In spite of the equality sign, the left-hand side of Eq. (2.16) turns out to be systematically smaller than the right-hand side and the two sides of the equation are in agreement only if $\nu _{r}$ is much smaller than $\nu _{ref}$ while, at the same time, $n_{T}= 2 + 2 \beta$ is sufficiently large and positive. A large enough value of $n_{T}$ guarantees a sharp increase of the spectral energy density while the condition $\nu _{r}\ll \nu _{ref}$ makes wider the frequency range of the potential growth. Since the minimal value of $\nu _{r}$ is provided by $\nu _{bbn}$

$$\begin{aligned} \nu _{bbn} = 0.35\,\, \biggl (\frac{T_{bbn}}{10\,\textrm{MeV}}\biggr ) \, \biggl (\frac{h_{0}^2 \, \Omega _{R\,0}}{4.15\times 10^{-5}}\biggr )^{-1/4} \, \, \textrm{nHz},\qquad \end{aligned}$$

(2.17)

we can select the most favourable situation and posit $\nu _{r} = {\mathcal O}(\nu _{bbn})$. For different values of ${\mathcal N}(r_{T})$ (see Eq. (2.13) and discussion thereafter) Eq. (2.16) leads therefore to a specific relation between $\beta$ and $\log {q_{0}}$:

$$\begin{aligned} \beta = -1 + \frac{ 2 \log {q_{0}} - \log {{\mathcal N}(r_{T})} - 9.201}{2 \log {(\nu _{ref}/\nu _{bbn})}}. \end{aligned}$$

(2.18)

To close the circle, the result of Eq. (2.18) must then be compared in the plane $(\log {q_{0}}, \, \beta )$ with the ranges of $\beta$ and $q_{0}$ determined by the PTA collaborations [13, 14]. The two filled rectangles in Fig. 3 correspond, in this respect, to the observational ranges of $q_{0}$ and $\beta$; in the same plot the relation between $\beta$ and $\log {q_{0}}$ has been illustrated as it follows from Eq. (2.18) for two neighbouring values of ${\mathcal N}(r_{T})$. The two diagonal lines in Fig. 3 imply that the values of $\beta$ required to obtain $h_{0}^2 \Omega _{gw}(\nu _{ref}, \tau _{0})$ of the order of $10^{-8}$ or $10^{-9}$ should be much larger than the ones determined observationally and represented by the two shaded regions. Since the full and dashed lines of Fig. 3 do not overlap with the two rectangles in the lower part of the cartoon, we can conclude that the excess observed by the PTA collaborations cannot be explained by the modified post-inflationary evolution suggested of Fig. 2. For the sake of accuracy we may separately analyze the case $\beta = -2/3$ and, in this situation, Eq. (2.16) becomes

$$\begin{aligned} {\mathcal N}(r_{T}) \bigl (\nu _{ref}/\nu _{r}\bigr )^{2/3}= 6.287\,\times 10^{-10}\, q_{0}^2. \end{aligned}$$

(2.19)

Again to maximize the potential growth of the spectral energy density we set $\nu _{r} = {\mathcal O}(\nu _{bbn})$ and obtain that the left-hand side of Eq. (2.19) is $2.015\times 10^{-15}$ whereas the right-hand side is always larger than ${\mathcal O}(10^{-9})$. As in the previous case, larger values of $\nu _{r}$ only reduce the left-hand side of Eq. (2.19) and ultimately increase the mismatch between Eqs. (2.10) and (2.13).

The argument leading to Eqs. (2.18) and (2.19) follows from the profile of Fig. 2 when the post-inflationary expansion rate is slower than radiation since only in this case the slope of $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ increases, as required by Eq. (2.10). There is however a complementary possibility stipulating that the comoving horizon prior to radiation dominance consists of two successive stages expanding at different rates and this situation is illustrated in Fig. 4 where the two consecutive post-inflationary stages (characterized by the rates $\delta _{1}$ and $\delta _{2}$) precede the ordinary radiation-dominated epoch. Even the standard sources considered before (satisfying $\delta _{i} \ge 1/2$ for $i =1,\,2$) imply that when $\delta _{1}< 1$ and $\delta _{2} > 1$ (see the left plot of Fig. 4) the spectral energy density $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ develops a trough at the intermediate frequency $\nu _{2} \gg \nu _{r} \ge \nu _{bbn}$. In other words for $\nu < \nu _{2}$ the spectral energy density decreases while it increases above $\nu _{2}$. The presence of a trough in $h_{0}^2\, \Omega _{gw}(\nu ,\tau _{0})$ corresponds to an expansion rate that is first slower (i.e. $\delta _{1} <1)$ and then faster (i.e. $\delta _{2} >1$) than radiation. In this case, however, $\lambda _{PTA}$ crosses the comoving horizon when $\delta _{2} > 1$ and the spectral index for the corresponding bunch of wavelengths is negative whereas Eq. (2.10) suggests it should be positive. Instead of a single spectral index $n_{T}$ there will now be two different spectral indices $n_{1}$ and $n_{2}$. For the profile appearing in the left plot of Fig. 4 the spectral index $n_{1}$ is positive

$$\begin{aligned} n_{1} = \frac{32 - 4 \, r_{T}}{16 - r_{T}} - 2 \delta _{1} = 2( 1 - \delta _{1}) + {\mathcal O}(r_{T}) > 0, \end{aligned}$$

(2.20)

since $\delta _{1} <1$. However for $\nu < \nu _{2}$ the spectral index will be instead given by:

$$\begin{aligned} n_{2} = \frac{32 - 4 \, r_{T}}{16 - r_{T}} - 2 \delta _{2} = 2( 1 - \delta _{2}) + {\mathcal O}(r_{T}) < 0, \end{aligned}$$

(2.21)

since $\delta _{2} >1$. This means that the spectral index is positive for $\nu > \nu _{2}$ and negative when $\nu < \nu _{2}$ with a trough in $\nu = {\mathcal O}(\nu _{2})$. Consequently the spectral energy density is even more suppressed than in the case of the concordance paradigm and the corresponding timeline of the comoving horizon is not relevant for the present discussion where would instead aim at a large signal in the nHz range.

Fig. 4

The evolution of the comoving horizon is again illustrated in units of $\lambda _{PTA}$ but the post-inflationary evolution is now characterized by two different expansion rates prior to the radiation-dominated phase. In the plot at the left we have that the expansion rate is initially slower than radiation (i.e. $\delta _{1} <1$) and then faster than radiation (i.e. $\delta _{2} > 1$). In the right plot the timeline is inverted and $\delta _{1} >1$ while $\delta _{2}< 1$. In the left plot $\lambda _{PTA}$ crosses the comoving horizon when the plasma expands faster than radiation and this is why, for $\nu = {\mathcal O}(\nu _{ref})$ the spectral energy density decreases in frequency. Conversely, in the right plot, the expansion rate is slower than radiation when $\lambda _{PTA}$ crosses the comoving horizon and, in this case, $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ inherits a growing frequency spectrum

For the present ends the relevant timeline is illustrated in the right plot in Fig. 4 where $\delta _{1} > 1$ and $\delta _{2} < 1$: the expansion rate is initially faster than radiation and then it gets slower so that $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ decreases above $\nu _{2}$ while it increases for $\nu < \nu _{2}$. This means that the spectral energy density in critical units develops a hump for $\nu = {\mathcal O}(\nu _{2})$; the signs of the spectral indices appearing in Eqs. (2.20) and (2.21) are exchanged: since $\delta _{1}> 1$ we have that $n_{1}< 0$ while $n_{2} >0$ because $\delta _{2}< 1$ (see always the right plot of Fig. 4). In this case the wavelengths smaller than $\lambda _{PTA}$ cross the comoving horizon when the the expansion rate is controlled by $\delta _{2} < 1$ and, for frequencies $\nu = {\mathcal O}(\nu _{ref})$, the spectral energy density increases as:

$$\begin{aligned} h_{0}^2 \, \Omega _{gw}(\nu , \tau _{0}) = {\mathcal N}(r_{T}) (\nu /\nu _{r})^{n_{2}}, \qquad \qquad \nu _{r}< \nu < \nu _{2} \end{aligned}$$

(2.22)

where, as already stressed, $n_{2} > 0$. The frequency $\nu _{2}$ follows from profile of the comoving horizon and it is given by

$$\begin{aligned} \nu _{2} = \sqrt{\xi _{1}} \, \,\xi _{2}^{\frac{(\delta _{2} -1)}{2 (\delta _{2}+1)}}\,\,\overline{\nu }_{max}, \qquad \xi _{1} = H_{2}/H_{1}, \qquad \xi _{2} = H_{r}/H_{2}, \end{aligned}$$

(2.23)

where, by definition, $\xi _{1} <1$ and $\xi _{2} <1$ denote the ratios of the curvature scales at the end and at the beginning of each expanding stage that precedes the ordinary radiation phase. The expressions of $\nu _{r}$ and $\overline{\nu }_{max}$ coincide, respectively, with Eqs. (2.14) and (2.15) since, by definition, $\xi = \xi _{1}\, \xi _{2} = H_{1}/H_{r} <1$. As before the analytic expression of $\nu _{2}$ is not essential for the present purposes. Indeed, in spite of the expression of $\nu _{2}$ the largest signal will be obtained when $\nu _{2} = \nu _{ref}$ since for $\nu > \nu _{2}$ the spectral energy density decreases as:

$$\begin{aligned}{} & {} h_{0}^2 \, \Omega _{gw}(\nu , \tau _{0}) = {\mathcal N}(r_{T},\nu ) (\nu _{2}/\nu _{r})^{n_{2}}\,\, \nonumber \\{} & {} (\nu /\nu _{2})^{- |n_1|}, \qquad \qquad \nu _{2}< \nu < \nu _{max}, \end{aligned}$$

(2.24)

where we introduced the absolute value of the spectral index $n_{1}$ to stress that $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ is suppressed for $\nu > \nu _{2}$ with a negative spectral index $n_{1} = 2 (1 - \delta _{1}) < 0$ (i.e. $\delta _{1} > 1$). We can now try to match the amplitude and the slope of Eq. (2.22) with Eq. (2.10). If we set $\nu _{2}= \nu _{ref}$ and $n_{2} = 2 ( 1 - \delta _{2}) + {\mathcal O}(r_{T}) = 2 + 2 \beta$ the condition on the amplitude becomes:

$$\begin{aligned} {\mathcal N}(r_{T}) (\nu _{ref}/\nu _{r})^{n_{2}} = 6.287 \times 10^{-10} \, q_{0}^2. \end{aligned}$$

(2.25)

Again the widest frequency range corresponds to the case when $\nu _{r} \rightarrow \nu _{bbn}$ and after some algebra we get back exactly to the same condition of Eq. (2.18). Due to the smallness of the potential signal, the direct bounds coming from wide-band interferometers [52, 53] and the indirect constraints from big-bang nucleosynthesis [55,56,57] do not play a relevant rôle in the argument of this section.⁸ The results obtained so far can then be summarized in the following manner:

• if the post-inflationary evolution is modified prior to radiation dominance $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ may increase in comparison with the concordance paradigm for typical frequencies $\nu = {\mathcal O}(\nu _{ref})$; this happens only if the wavelengths ${\mathcal O}(0.3)$ pc (roughly corresponding to comoving frequencies ${\mathcal O}(30)$ nHz) cross the comoving horizon when the expansion rate is slower than radiation;

• the PTA signals imply a growing spectral energy density (i.e. $2 + 2 \beta >0$) and this is consistent with an expansion rate that is slower than radiation at least when the wavelengths ${\mathcal O}(\lambda _{PTA})$ reenter the comoving horizon;

• however the amplitudes and the slopes of the theoretical signal do not match simultaneously the observational determinations of the PTA in the $(\log {q_{0}}, \, \beta )$ plane.

A hump in $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ for $\nu = {\mathcal O}(\nu _{ref})$ indeed follows when the post-inflationary expansion rate is slower than radiation but the theoretical signal is not consistent with the slope and with the amplitude of the observational spectrum. In specific cases the theoretical and the observed slopes are compatible but the corresponding amplitudes differ by 9 or even 10 orders of magnitude. As usual the agreement between theoretical and observed slopes is just a mere indication that is, per se, irrelevant for the final conclusion.

3 The comoving horizon during inflation

3.1 Modified evolution of the comoving horizon

If the refractive index n(a) of the relic gravitons is dynamical the condition of Eq. (2.3) defining the exit of a given wavelength is now replaced by:

$$\begin{aligned} k^2 = n^3 \, b^2 \, F^2 \biggl [ 2 - \overline{\epsilon }+ \frac{3\, \dot{n}}{2 \,n \,F}\biggr ], \qquad F = \frac{\dot{b}}{b}, \qquad \overline{\epsilon } = - \frac{\dot{F}}{F^2}, \end{aligned}$$

(3.1)

where the overdot denotes, as usual, a derivation with respect to the cosmic time coordinate; in Eq. (3.1) $a(\tau )$ is actually rescaled as $b = a/\sqrt{n}$ and $\overline{\epsilon }$ is, in practice, the generalization of the slow-roll parameter $\epsilon$ already introduced in the previous section and in the appendices. The details on the connection between F and H are also discussed in Eqs. (B.5)–(B.6) of Appendix B and the analog of $(a\, H)^{-1}$ is now represented by $(b\, F)^{-1}$ whose evolution in units of $\lambda _{PTA}$ is illustrated in Fig. 5. By looking at the profiles of Fig. 5 there are in fact two complementary possibilities:

• if $\lambda _{PTA}$ crosses the comoving horizon when the refractive index is dynamical $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ may inherit a growing spectrum comparable with the PTA excess and in Fig. 5 the two curves (labeled, respectively, by 1 and 2) illustrate this possibility; while in the case 2 the first crossing occurs during the refractive phase, for the curve labeled by 1 the crossing occurs nearly at the end of it;

• if the first crossing takes place after the end of the refractive phase (see the curve labeled by 3 in Fig. 5) the spectral energy density does not show any appreciable excess and the resulting spectral energy density is quasi-flat.

Even if the curve 3 in Fig. 5 does not lead to a growing spectrum for $\lambda _{PTA}$ it is anyway relevant for shorter wavelengths $\lambda \ll \lambda _{PTA}$; for the corresponding frequencies $h_{0}^2 \Omega _{gw}(\nu , \tau _{0})$ may have a flatter slope but also further spikes caused by the post-inflationary evolution. Both structures are significantly constrained in the audio and in the MHz bands.

Fig. 5

The comoving horizon is illustrated in units of $\lambda _{PTA}$ when its early evolution is modified during the inflationary stage; as usual common logarithms are employed on both axes. The dynamics of the refractive index of the relic gravitons is responsible for the modified evolution illustrated in this cartoon. If the crossing of $\lambda _{PTA}$ occurs during the refractive phase (or at the end of it) the spectral energy density inherits a blue or violet spectrum that may eventually explain, under very specific conditions, the PTA excess

3.2 Refractive index and effective action

When the refractive index of the relic gravitons increases during a conventional stage of inflationary expansion the spectral energy density is blue at intermediate frequencies (typically above the fHz) and then flattens out after a knee that is generally smaller than the mHz [58]. The general shapes of $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ suggest that this possibility is particularly interesting in the light of the PTA excesses. When the refractive index is dynamical the action of the relic gravitons (see e.g. Eq. (A.3) and discussion therein) is modified as described in Appendix B and it can be written as:

$$\begin{aligned} S&= \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x\, \int d\tau \,\, a^2(\tau ) \,\nonumber \\ {}&\quad \times \biggl [ \partial _{\tau } h_{i\, j} \partial _{\tau } h^{i\, j} - \frac{1}{n^2(\tau )} \partial _{k} h_{i\, j} \partial ^{k} h^{i\, j} \biggr ]. \end{aligned}$$

(3.2)

The analysis of Eq. (3.2) is greatly simplified if the conformal time coordinate is redefined from $\tau$ to $\eta$ where the relation between the new and the old time parametrizations implicitly follows from $n(\eta ) \, d\eta = d \tau$. Equation (3.2) becomes then canonical in terms of a redefined scale factor conventionally denoted by $b(\eta )$ [58]:

$$\begin{aligned}&S = \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x\, \int d\eta \, b^2(\eta )\, \biggl [ \partial _{\eta } h_{i\, j} \partial _{\eta } h^{i\, j} - \partial _{k} h_{i\, j} \partial ^{k} h^{i\, j} \biggr ], \qquad \nonumber \\&b(\eta ) = a(\eta )/\sqrt{n(\eta )}. \end{aligned}$$

(3.3)

The result of Eq. (3.3) generalizes the standard Ford-Parker action discussed in Appendix A to the case of a dynamical refractive index and it explains how and why the evolution of the tensor modes is modified even during a conventional stage of inflationary expansion. A number of different physical reasons may lead to an effective index of refraction of gravitational waves in curved space-times [58,59,60]. For instance the effective action of single-field inflationary models involves all the terms that include four derivatives⁹ and are suppressed by the negative powers of a large mass scale [61]. Another possible origin of a refractive index are non-generic models of inflation where the higher-order corrections assume a specific form since the inflaton has some particular symmetry (like a shift symmetry $\varphi \rightarrow \varphi + c$) or because the rate of inflaton roll remains constant (and possibly larger than 1), as it happens in certain fast-roll scenarios [65,66,67]. There are also the cases where the higher-order curvature corrections are given in terms of the Gauss-Bonnet combination weighted by some inflaton dependent-coupling [68,69,70]. In [58] (see also [71,72,73]) it has been argued that in all these situations the effective action of the relic gravitons can be modified and ultimately assumes the general form discussed in Appendix B.

For the present purposes what matters is not so much the origin of the refractive index but rather the possibility that its dynamical evolution could lead to a nHz excess. We then assign n(a) and even if the phase velocity of the relic gravitons is not required to be sub-luminal we impose, for consistency, that $n(a) \ge 1$. Moreover, since the contributions to n(a) arise from diverse physical considerations we prefer to reverse the problem by focussing the attention on those profiles that eventually lead to potential excesses in the nHz range. Along this perspective we are led to consider an appreciable change of the refractive index during inflation with the concurrent requirement that n(a) reaches 1 in the standard decelerated stage of expansion¹⁰:

$$\begin{aligned}&n(a) = n_{*} \frac{ (a/a_{*})^{\alpha } \,\,e^{- \overline{d}\,(a/a_{1})}}{(a/a_{*})^{\alpha } + 1} + 1, \quad \nonumber \\&n_{*} = n_{i} (a_{*}/a_{i})^{\alpha } = n_{i} e^{\alpha \, N_{*}}, \end{aligned}$$

(3.4)

where $a_{i}$ and $a_{1}$ denote, respectively, the beginning and the end of the inflationary epoch; $a_{*}$ indicates the boundary of the refractive stage. The three successive physical regimes described by Eq. (3.4) are, in some sense, more relevant than the specific analytic form that is however quite useful for numerical estimates. When $a\gg a_{1}$ we have that $n(a) \rightarrow 1$ and the sharpness of the transition is controlled by the parameter $\overline{d} \ge 1$. In the range $a_{*}< a < a_{1}$ n(a) is constant but still larger than 1 (i.e. $n(a)\simeq n_{*} > 1$) and, finally, when $a< a_{*}$ the refractive index is truly dynamical since $n (a) \simeq n_{*} (a/a_{*})^{\alpha }$.

3.3 The spectral energy density in critical units

We start by examining the spectral energy density for typical wavenumbers $k < a_{*}\, H_{*}$ where $\Omega _{gw}(k,\tau )$ is actually increasing. Using Eqs. (3.3)–(3.4) the spectral energy density in critical units can be obtained from Eqs. (2.1)–(2.2) with few relevant modifications:

$$\begin{aligned} \Omega _{gw}(k,\tau )&= \frac{k^4}{12 \,\pi ^2\, H^2\, \overline{M}_{P}^2\, a^{4}}\,\,\nonumber \\ {}&\quad \times \bigl |{\mathcal Q}_{k}(\eta _{ex}, \eta _{re})\bigr |^2 \,\, \biggl (\frac{b_{re}}{b_{ex}}\biggr )^2 \biggl ( 1 + \frac{1}{k^2 \tau _{re}^2} \biggr ). \end{aligned}$$

(3.5)

Equation (3.5) is valid under the assumption that $\eta _{re} = \tau _{re}$ so that the reentry of the relevant wavelengths occurs when the refractive index is not dynamical; furthermore if $\tau _{re}$ falls within the radiation phase (i.e. $a^{\prime \prime } \rightarrow 0$) we also have $k \tau _{re}\ll 1$ in Eq. (3.5). Since any wavelength exiting for $\eta < - \eta _{*}$ does its first crossing during the inflationary phase, the corresponding refractive index is $n = n_{*} (a/a_{*})^{\alpha }$; moreover the explicit expression of ${\mathcal Q}_{k}(\eta _{ex}, \eta _{re})$ is also slightly more general than in the case of Eq. (2.2)

$$\begin{aligned} {\mathcal Q}_{k}(\eta _{ex}, \eta _{re}) = 1 - ({\mathcal F}_{ex} + i k) \int _{\eta _{ex}}^{\eta _{re}} \frac{b_{ex}^2}{b^2(\tau )} \, d\eta , \quad {\mathcal F}= \partial _{\eta }b/b. \end{aligned}$$

(3.6)

Finally, from Eq. (3.3) $b(\eta )$ can be expressed in the following manner:

$$\begin{aligned} b(\eta ) = b_{*} (- \eta /\eta _{*})^{-\zeta }, \ b_{*} = a_{*}/\sqrt{n_{*}}, \ \zeta = \frac{ 2 - \alpha }{2 ( 1 - \epsilon + \alpha )}. \end{aligned}$$

(3.7)

The result of Eq. (3.7) is valid if all the wavelengths ${\mathcal O}(\lambda _{PTA})$ exit while the refractive index is still dynamical (as illustrated in the curves 1 and 2 of Fig. 5). Inserting now Eq. (3.7) into Eq. (3.5) a more explicit form of the spectral energy density can be deduced:

$$\begin{aligned}{} & {} h_{0}^2 \,\Omega _{gw}(\nu ,\tau _{0})\nonumber \\ {}{} & {} \quad = \biggl (\frac{H_{1}}{M_{P}}\biggr )^2 \,{\mathcal D}_{*}(\alpha ,n_{T}) \biggl (\frac{\nu }{\nu _{*}}\biggr )^{n_{T}}, \quad \nu _{eq}< \nu < \nu _{*}, \end{aligned}$$

(3.8)

$$\begin{aligned}{} & {} {\mathcal D}_{*}(\alpha ,n_{T}) = \frac{4 n_{*}^3\, h_{0}^2 \Omega _{R0} }{3 \pi } \, \biggl (1 + \frac{\alpha }{1-\epsilon _{k}}\biggr )^2 \, \biggl (\frac{g_{\rho , \, r}}{g_{\rho , \, eq}}\biggr ) \nonumber \\{} & {} \qquad \qquad \qquad \ \times \biggl (\frac{g_{s,\, eq}}{g_{s,\, r}}\biggr )^{4/3} \, \biggl (\frac{\Omega _{M0}}{\Omega _{\Lambda }}\biggr )^2,\, \, \end{aligned}$$

(3.9)

where $g_{\rho }$ and $g_{s}$ are, respectively, the effective number of relativistic species associated with the energy and with the entropy density. As usual $\Omega _{M0}$ and $\Omega _{\Lambda }$ denote the present critical fractions of matter and dark energy. It is well known that the dominance of dark energy suppresses the spectrum by a factor $(\Omega _{M0}/\Omega _{\Lambda })^2 = {\mathcal O}(0.1)$ (see, for instance, [17]). In Eq. (3.8) $\nu _{*}$ denotes the frequency of the spectrum associated with $\eta _{*}$ and since $k_{*} = 1/\eta _{*}$ the corresponding comoving frequency is:

$$\begin{aligned} \nu < \nu _{*} = \biggl (1 + \frac{\alpha }{1 - \epsilon _{k}}\biggr ) e^{\alpha N_{*} - \Delta N} \, \overline{\nu }_{max},\qquad \Delta N= N_{t} - N_{*}. \end{aligned}$$

(3.10)

In Eq. (3.10) $N_{*} = \ln {(a_{*}/a_{i})}$ is the number of e-folds during the refractive stage while $N_{t} = \ln {(a_{1}/a_{i})}$ denotes the total number of e-folds; finally $\overline{\nu }_{max}$ indicates the maximal frequency of the spectrum and it coincides with Eq. (2.15) since, so far, the radiation dominance starts right after the end of inflation. The spectral index $n_{T}$ appearing in Eq. (3.8) depends on $\alpha$ and on $\epsilon _{k}$ and it is:

$$\begin{aligned} n_{T} = 2 - 2 \zeta= & {} \frac{3 \alpha - 2\epsilon _{k}}{(1 + \alpha - \epsilon _{k})} \nonumber \\= & {} \frac{3 \alpha }{1 + \alpha } + \frac{\epsilon _{k}\, (\alpha - 2)}{(1 + \alpha )^2} + {\mathcal O}(\epsilon _{k}^2). \end{aligned}$$

(3.11)

The tensor spectral index of Eq. (3.11) applies in the intermediate frequency range when the corresponding wavelengths exit during inflation and reenter in the radiation phase; in Eq. (3.11) $\alpha$ is always much larger than $\epsilon _{k}\simeq r_{T}/16 \le 0.03/16 \ll 1$ so that the exact result can be accurately evaluated in the limit $\epsilon _{k} \ll 1$. While Eqs. (3.8) and (3.11) hold for $\nu <\nu _{*}$, the spectral energy density can also be evaluated in the range $\nu _{*}< \nu < \overline{\nu }_{max}$ (i.e. $a_{*} \, H_{*}< k < a_{1}\, H_{1}$) corresponding to wavelengths that exited the comoving horizon when the refractive index was already constant (see the curve 3 in Fig. 5). Since the corresponding wavelengths do their first crossing when the refractive index is already constant (i.e. $n\rightarrow n_{*}$) we have that $\eta _{ex} = \tau _{*}/n_{*}$ and the spectral energy density becomes:

$$\begin{aligned} h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})= & {} \biggl (\frac{H_{1}}{M_{P}}\biggr )^2\, {\mathcal D}_{max}(\alpha , m_{T}) \, \, \nonumber \\{} & {} \times \biggl (\frac{\nu }{\overline{\nu }_{max}}\biggr )^{m_{T}}, \qquad \nu _{*}< \nu < \overline{\nu }_{max}, \end{aligned}$$

(3.12)

where the spectral index is given by $m_{T} = - 2 \epsilon _{k} = - r_{T}/8$ and

$$\begin{aligned} {\mathcal D}_{max}(\alpha , m_{T})= & {} \frac{4 \,h_{0}^2 \Omega _{R0} }{3 \pi } \, e^{(3 -m_{T})\alpha \,N_{*}} e^{ m_{T} \Delta N} \nonumber \\{} & {} \times \biggl (1 + \frac{\alpha }{1-\epsilon _{k}}\biggr )^{2-m_{T}}\,\ \, \, \nonumber \\{} & {} \times \biggl (\frac{g_{\rho , \, r}}{g_{\rho , \, eq}}\biggr ) \biggl (\frac{g_{s,\, eq}}{g_{s,\, r}}\biggr )^{4/3} \, \biggl (\frac{\Omega _{M0}}{\Omega _{\Lambda }}\biggr )^2. \end{aligned}$$

(3.13)

Equation (3.12) evaluated for $\nu = \nu _{*}$ corresponds exactly to Eq. (3.8) computed at the same reference frequency and the equivalence of the two expressions ultimately follows from Eq. (3.10). Furthermore, in Eqs. (3.8) and (3.11) $(H_{1}/M_{P})^2$ can be traded for $\pi \, \epsilon _{k}\, {\mathcal A}_{{\mathcal R}}$ where ${\mathcal A}_{{\mathcal R}}$ is the amplitude of curvature inhomogeneities at the pivot scale $k_{p}$ (see also Eqs. (1.4) and (2.15)). It is finally worth recalling that, for a standard thermal history, $g_{s,\,eq} = 3.94$ while $g_{\rho ,\, r} = g_{s,\, r}=106.75$ in Eqs. (3.9) and (3.13).

Before proceeding further it is useful to comment on the possible range of variation of $N_{t}$ and $N_{*}$ appearing in Eq. (3.10). The value of $N_{*}$ measures the range of variation of the refractive index during inflation and, for this reason, $N_{*} < N_{t}$. The total number of e-folds is, in principle, arbitrary but a useful benchmark value is notoriously given by $N_{t} = {\mathcal O}(60)$. This figure coincides, approximately, with the number of e-folds elapsed from the moment where the CMB wavelengths crossed the Hubble radius during inflation. If we estimate these wavelengths with $k_{p}^{-1}$ (where $k_{p} = 0.002\,\, \textrm{Mpc}^{-1}$) then we have that $N_{k}$ (i.e. the number of e-folds elapsed since the crossing of $k_{p}^{-1}$) is, approximately, ${\mathcal O}(60)$ for $r_{T}= 0.06$; more precisely it can be shown that

$$\begin{aligned} N_{k} = 59.4 + \frac{1}{4}\ln {\biggl (\frac{\epsilon _{k}}{0.001}\biggr )} - \ln {\biggl (\frac{k}{0.002 \,\, \textrm{Mpc}^{-1}}\biggr )} \end{aligned}$$

(3.14)

where, as before, $\ln {}$ denotes the natural logarithm and $\epsilon _{k}$ is the value of the slow-roll parameter at the crossing of the given set of wavelengths. Equation (3.14) assumes that after inflation the evolution is always dominated by radiation even if in Fig. 12 this assumption will be relaxed. The value of $N_{k}$ is also of the order of $N_{max}$ (i.e. the maximal number of e-folds presently accessible to large-scale observations); see in this respect the appendices of Ref. [54]. This value follows by requiring that the redshifted inflationary event horizon fits within the present Hubble patch; in practice this means that $H_{i}^{-1} (a_{0}/a_{i}) \simeq H_{0}^{-1}$ where $H_{i}$ denotes the expansion rated during the initial stages of inflation. Neglecting for simplicity the evolution of the relativistic species of the plasma we get that $N_{max} = 61.55$ for the same fiducial set of parameters employed in Eq. (3.14). Typical values of $N_{t}$ of the order of $N_{k}$ and $N_{max}$ define, in practice, the minimal duration of the inflationary stage. Conversely values of $N_{t}$ smaller than $N_{k}$ (or $N_{max}$) characterize the durations of inflationary stages that are comparatively shorter than the benchmark value of Eq. (3.14). As we shall see in a moment, the relatively short inflationary stages (where $N_{t} \le {\mathcal O}(61)$) seem to be preferred for a potential explanations of the PTA excesses.

Fig. 6

The regions pinned down by the Parkes PTA are illustrated in the left plot in terms of the parameters appearing in Eqs. (3.8) and (3.12). The shaded areas follow by imposing the range of Eq. (3.16) for different values of $N_{t}$ (denoting, as repeatedly mentioned, the total number of e-folds). We also remind that $N_{*}$ controls the length of the phase where the refractive index is effectively dynamical. In both plots we traded $\alpha$ for $\beta$ at a fixed value of $\epsilon _{k}=0.0018$ (see Eq. (3.15) and discussion therein); the value of $\epsilon _{k}$ is related to $r_{T}=0.03$ by the consistency relations. While in the left plot we illustrated $q_{0}(\beta , \,N_{*})$ for different values of $N_{t}$, in the right plot $\beta$ has been fixed to $-2/3$; in this case the allowed range of $q_{0}(N_{t}, N_{*})$ is slightly different from the one of Eq. (3.16) and it is given by $1.82< q_{0}(N_{t}, N_{*}) < 2.29$. Finally, the shaded regions in both plots are consistent with the higher-frequency bounds coming from the audio band

3.4 Accounting for the PTA excesses?

Equations (3.5), (3.8) and (3.12) are now compared with the parametrizations of the PTA signal given in Eqs. (1.2) and (2.10). Since, by definition, the intermediate spectral index is given as $2 + 2\beta = n_{T}$ Eq. (3.11) implies a relation that determines $\alpha$ as a function of $\epsilon _{k}$ (or $r_{T}$) and $\beta$:

$$\begin{aligned} \alpha = \frac{2 [\beta (\epsilon _{k} -1)-1]}{2 \beta -1}. \end{aligned}$$

(3.15)

Moreover, given that $q_{0}$ depends on all the other parameters determining the amplitude of $\Omega _{gw}(\nu ,\tau _{0})$ (see Eqs. (3.8) and (3.12)), we can demand that $\beta$ and $q_{0}$ fall within the phenomenologically allowed ranges and check if the results of Eqs. (3.8) and (3.12) are compatible with the empirical determinations of the PTA. According to the Parkes PTA the values of $\beta$ and $q_{0}$ fall, respectively, in the following intervals:

$$\begin{aligned} -0.65 \le \beta \le -0.25, \qquad \qquad 2.2< q_{0} < 4.4. \end{aligned}$$

(3.16)

Equation (3.16) constrains the spectral energy density and the corresponding region of the theoretical parameters is illustrated in the left plot of Fig. 6 where we report $q_{0}(\beta ,\, N_{*})$ for different values of $N_{t}$; the shape of each shaded region directly follows by requiring $2.2< q_{0}(\beta ,\,N_{*}) < 4.4$ for the various $N_{t}$ mentioned in the plot. On a technical side we note that Eq. (3.15) has been used with the purpose of trading directly $\alpha$ for $\beta$ at a fixed value of $\epsilon _{k}$. In the right plot of Fig. 6$\beta$ is however fixed (i.e. $\beta \rightarrow -2/3$) and, for such a choice, also the range of $q_{0}$ must be adapted following the observational determinations (i.e. $q_{0}= 2.04_{-0.22}^{+0.25}$ [13]). For this reason in the right plot of Fig. 6 the constraints can be directly examined in the plane $(N_{t}, \, N_{*})$. For the sake of accuracy, in Fig. 7 we illustrated the region pinned down in the plane ($\alpha$, $\log {r_{T}}$) by the different values of $\beta$. The same analysis illustrated in the case of the Parkes PTA can be repeated for the NANOgrav determinations with slightly different results; the analog of Eq. (3.16) is now given by [14]

$$\begin{aligned} -0.40 \le \beta \le -0.20, \qquad \qquad 3.7< q_{0} < 10.6. \end{aligned}$$

(3.17)

Fig. 7

The shaded region follows by requiring $-0.65< \beta < -0.25$ (as implied by Eq. (3.16)) and by imposing the relation of Eq. (3.15). The thick line outside the shaded region corresponds to $\beta = -2/3$. If the consistency relations are imposed $\beta$ is determined in the $(\alpha , r_{T})$ plane. However, as the plot shows, the smallness of $r_{T}$ implies that $\epsilon _{k}$ can be neglected for the determination of the spectral index in the region $\nu <\nu _{*}$

Fig. 8

In the left plot we illustrate the region pinned down by the NANOgrav PTA in the plane $(\beta ,\, N_{*})$ for different values of $N_{t}$. Both plots can be compared with the ones of Fig. 6 where we discussed the case of the Parkes PTA. The shaded regions in the left plot follow by imposing Eq. (3.17) for different values of $N_{t}$. The right plot is obtained by fixing $\beta \rightarrow -2/3$ and the shaded region corresponds to the range $1.8< q_{0}(N_{t},N_{*}) < 3.1$; this is because for $\beta \rightarrow -2/3$ the NANOgrav collaboration suggests $q_{0}= 2.4_{-0.6}^{0.7}$. As in Fig. 6 the high-frequency bounds from the audio band have been also imposed

While the range of $\beta$ given in Eq. (3.17) is narrower than in Eq. (3.16), in the case of $q_{0}$ we observe the opposite: the allowed values of $q_{0}$ of Eq. (3.17) are comparatively larger than the ones of Eq. (3.16). These differences slightly modify the shaded regions of Figs. 6 and 8 and the related parameters: both the ranges of $N_{t}$ and $N_{*}$ get narrower and $N_{t}$ is at most ${\mathcal O}(55)$ while $N_{*} \le {\mathcal O}(10)$.

A second class of constraints determining the shaded regions of Figs. 6 and 8 is related to the direct bounds from the operating wide-band detectors. In particular we remind that the LIGO, Virgo and Kagra collaborations (LVK) reported a constraint [52] implying:

$$\begin{aligned} \Omega _{gw}(\nu , \tau _{0})< 5.8 \times 10^{-9}, \qquad \qquad 20 \,\, \textrm{Hz}< \nu _{L} < 76.6 \,\, \textrm{Hz}, \end{aligned}$$

(3.18)

in the case of a flat spectral energy density; in the present notations $\nu _{L}$ indicates the LIGO-Virgo-Kagra frequency. The limit of Eq. (3.18) improves on a series of bounds previously deduced by the wide-band interferometers (see Ref. [17] for a review of the older results); in particular in Ref. [53] the analog of Eq. (3.18) implied $\Omega _{gw}(\nu , \tau _{0}) < 6 \times 10^{-8}$ for a comparable frequency interval and always in the case of a flat spectral energy density. The bound of Eq. (3.18) can be used also in Eq. (3.8) since at high-frequency the spectral energy density is nearly scale-invariant. The results of Ref. [52] report however a threefold bound for a handful of spectral slopes; in particular, if the spectral energy density is parametrized as

$$\begin{aligned} \Omega _{gw}(\nu , \tau _{0}) = \overline{\Omega }(\sigma ) \biggl (\frac{\nu }{\nu _{L}}\biggr )^{\sigma }, \qquad \qquad \nu _{L} = 25 \,\, \textrm{Hz}, \end{aligned}$$

(3.19)

the limits of Ref. [52] read $\overline{\Omega }(0) < 5.8 \times 10^{-9}$ (valid in the case $\sigma =0$), $\overline{\Omega }(2/3) < 3.4 \times 10^{-9}$ (when $\sigma = 2/3$) and $\overline{\Omega }(3) < 3.9 \times 10^{-10}$ (when $\sigma = 3$). As the value of $\sigma$ increases the bound becomes more restrictive for a fixed reference frequency and the three previous results are summarized by the following interpolating formula:

$$\begin{aligned} \log {\overline{\Omega }}(\sigma ) < -\,8.236 -\, 0.335\, \sigma - 0.018\, \sigma ^2. \end{aligned}$$

(3.20)

Since in the present case the bound (3.20) should be applied at high-frequencies we will have $\sigma =- 2 \epsilon _{k}/ (1- \epsilon _{k})$ with $\epsilon \ll 0.1$; to leading order in $\epsilon _{k}$, Eq. (3.20) implies that $\log {\overline{\Omega }}(\epsilon _{k}) < -\,8.236 -\, 0.335\, \epsilon _{k} -0.393 \epsilon _{k}^2$.

3.5 Shapes of the spectra and further possibilities

Instead of using the approximations employed above it is instructive to compute numerically the spectral energy density from the exact form of the mode functions¹¹.

As an example in the two plots of Fig. 9 we considered two different values of $\beta$ (i.e. $\beta = -0.65$ and $\beta = -0.55$). Given a specific value of $\beta$ within the observational range, the previous results (see, in particular, Figs. 6 and 8) lead directly to the allowed values of $N_{*}$ and $N_{t}$. If $N_{*}$ and $N_{t}$ are of the same order the refractive index stops evolving when inflation approximately ends and, in this case, it is impossible to get a large signal in the nHz range without jeopardizing the big-bang nucleosynthesis constraint [58, 73].

Fig. 9

We illustrate the common logarithm of the spectral energy density in critical units as a function of the common logarithm of the comoving frequency. In both plots $N_{t} =61$ but the values of $\beta$ and $r_{T}$ do not coincide and they are indicated above each of the two cartoons. The arrows indicate the PTA signal for the spectral indices corresponding to the ones selected in each of the plots. The high-frequency region labeled by LVK refers to the Ligo–Virgo–Kagra bound that applies in the audio band. The increasing branch and the flat plateau corresponds, respectively, to the analytic estimate of Eqs. (3.5) and (3.8)

Conversely, when $N_{*} <N_{t}$ the refractive index stops evolving well before the onset of the post-inflationary stage, i.e. when the background is still inflating deep inside the quasi-de Sitter stage of expansion. In both plots of Fig. 9, to ease the comparison, we selected $N_{t} = 61$ while different values of $N_{*}$ are illustrated. In both plots, for the same choice of the parameters, we also illustrated (with an arrow) the PTA excess and the Ligo–Virgo–Kagra bound [52, 53]. The PTA signal occurs for typical frequencies ${\mathcal O}(\nu _{ref})$ while the LVK bound applies approximately between 25 and 100 Hz.

The discussion of Sect. 2 does not exclude the possibility of two concurrent modifications of the comoving horizon operating before and after the end of inflation [71, 72]. This viewpoint is explored in Fig. 10 where we consider the possibility that the refractive index stops its evolution well before the end of inflation (i.e. $N_{*} \ll N_{t}$); however, unlike the case of Fig. 9, the post-inflationary evolution includes a long phase expanding at a rate slower than radiation. The spectral energy density in critical units will therefore have three different slopes for $\nu > \nu _{eq}$. In both plots of Fig. 10, at intermediate frequencies $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ has the same intermediate slopes appearing in Fig. 9 (see also Eqs. (3.11) and (3.15)). However, after the quasi-flat plateau, the spectral energy density exhibits a further increasing branch before the maximal frequency. The corresponding wavelengths left the comoving Hubble radius during inflation and reentered in the post-inflationary stage before radiation dominance. In Fig. 10 the high-frequency spectral slope is ${\mathcal O}(1)$ since during the post-inflationary stage the evolution is described by a stiff fluid with $\delta \simeq 1/2$ implying that $(a\, H)^{-1} \propto a^2$. The main difference between the plots of Figs. 9 and 10 ultimately comes from the high-frequency shape. While in the case of Fig. 9 the most relevant constraint comes from the operating interferometers [52, 53], in the case of Fig. 10 the bounds coming from big-bang nucleosynthesis [55,56,57] must be taken into account since they imply:

$$\begin{aligned}{} & {} h_{0}^2 \int _{\nu _{bbn}}^{\nu _{max}} \Omega _{\textrm{gw}}(\nu ,\tau _{0}) d\ln {\nu }\nonumber \\{} & {} \quad = 5.61 \times 10^{-6} \Delta N_{\nu } \biggl (\frac{h_{0}^2 \Omega _{\gamma 0}}{2.47 \times 10^{-5}}\biggr ), \end{aligned}$$

(3.21)

where $\Omega _{\gamma 0}$ is the (present) critical fraction of CMB photons. As it is well known, the limit of Eq. (3.21) also sets an indirect constraint on all the extra-relativistic species (and, among others, on the relic gravitons). If applied to massless fermionic species, the limit is often expressed for practical reasons in terms of $\Delta N_{\nu }$ representing the contribution of supplementary neutrino species. The actual bounds on $\Delta N_{\nu }$ range from $\Delta N_{\nu } \le 0.2$ to $\Delta N_{\nu } \le 1$; the integrated spectral density in Eq. (3.21) is thus between $10^{-6}$ and $10^{-5}$. It is interesting to point out that the spectra of Fig. 10 are sensitive both to the interferometric bounds [52, 53] and to the the limits of Eq. (3.21): the wide-band detectors constrain the height of the intermediate plateau while Eq. (3.21) sets a bound on the integrated $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ and, ultimately, on the (global) maximum of the spectral energy density.

Fig. 10

As in Fig. 9 we illustrate the common logarithm of the spectral energy density as a function of the common logarithm of the comoving frequency. In the two plots the value of $r_{T}$ is the same but the values of $N_{t}$ are slightly dissimilar. In the plot at the left $N_{*}= 14$ while the three spectra correspond slightly different values of $\beta$. In the plot at the right $\beta = -0.63$ and the three curves illustrate the variation of $N_{*}$. Since the effect of neutrino free-streaming has been included, in both plots $R_{\nu }$ denotes the neutrino fraction

4 Bounces of the scale factor and curvature bounces

4.1 Basic considerations

In bouncing scenarios the spectral index can be positive between the fHz and the Hz [17] as it happens in the presence of a dynamical refractive index. However, while in the previous section both the amplitudes and the slopes could be predicted with reasonable accuracy thanks to the underlying inflationary dynamics, for the bouncing case it is comparatively easier to estimate $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ in the intermediate frequency region rather than in the high-frequency domain which is often associated with a regime of strong curvatures. Even in the absence of a detailed theoretical derivation of the corresponding slopes, the high-frequency normalization can be disambiguated by employing the constraints of the audio band [52, 53] and the big-bang nucleosynthesis limits [55,56,57].

The bouncing dynamics is sometimes associated with a contracting stage (i.e. $\dot{a} <\,0$ and $H<0$), as historically suggested, along slightly different perspectives, by Tolman and Lemaître [74, 75] (see also [76, 77]). For the present purposes it is useful to distinguish (at a purely kinematical level) the bounces of the scale factor from the ones involving the extrinsic (Hubble) curvature. While H and $\dot{H}$ change sign (at least) once in the bounces of the scale factor, for the curvature bounces H is always positive but $\dot{H}$ changes sign (at least) once. Broadly speaking the spectral slope at intermediate frequencies (which is the relevant one for the discussion of the PTA excesses) is related to the wavelengths that crossed the comoving Hubble radius before either H or $\dot{H}$ changed their sign the first time.¹² In both situations we can express the spectral energy density in terms of a common template

$$\begin{aligned} h_{0}^2 \,\Omega _{gw}(\nu , \tau _{0}) = \overline{\Omega }_{*} \,\, (\nu /\nu _{*})^{m_{T}}, \qquad \qquad \nu _{*}< \nu <\nu _{max}, \end{aligned}$$

(4.1)

where $m_{T}$ is the high-frequency spectral index and $\overline{\Omega }_{*}$ accounts for the corresponding normalization. The notations employed in Eq. (4.1) are purposely similar to the ones of the previous section since, in both cases, $\overline{\Omega }_{*}$ controls the high-frequency normalization. The physical meaning of the two quantities is however slightly different since $\overline{\Omega }_{*}$ now depends on the maximal curvature scale at the bounce (of the order of $H_{1}$) and on a number of other late-times parameters; in the simplest situation (where all the wavelengths reenter during a radiation dominated stage) the value of $\overline{\Omega }_{*}$ is given by

$$\begin{aligned} \overline{\Omega }_{*} = \frac{4 \, h_{0}^2 \Omega _{R0}}{3 \pi } \, \biggl (\frac{H_{1}}{M_{P}}\biggr )^2\, \biggl (\frac{g_{\rho , \, r}}{g_{\rho , \, eq}}\biggr ) \biggl (\frac{g_{s,\, eq}}{g_{s,\, r}}\biggr )^{4/3} \, \biggl (\frac{\Omega _{M0}}{\Omega _{\Lambda }}\biggr )^2. \end{aligned}$$

(4.2)

In inflationary scenarios the analog of $(H_{1}/M_{P})$ is fixed by the amplitude of the (adiabatic and Guassian) curvature inhomogeneities whereas in the case of Eq. (4.2) it is more productive to determine $\overline{\Omega }_{*}$ directly from the available phenomenological constraints and to confront the obtained templates with the PTA observations. In this respect the most relevant limits are the ones coming from the audio band (see Eqs. (3.19)–(3.20)) and the big-bang nucleosynthesis constraint (see Eq. (3.21) and discussion thereafter).

4.2 Growing spectral slopes at intermediate frequencies

While Eq. (4.2) applies in the high-frequency regime where the amplitude of $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ is constrained by the current phenomenological bounds, in the intermediate frequency range (i.e. for $\nu < \nu _{*}$) the slope of the spectral energy density is instead denoted by $n_{T}= n_{T}(\gamma , \delta )$:

$$\begin{aligned} h_{0}^2\, \Omega _{gw}(\nu ,\tau _{0}) = \overline{\Omega }_{*} \,\, (\nu /\nu _{*})^{n_{T}(\gamma , \delta )},\quad \nu _{eq}< \nu <\nu _{*}. \end{aligned}$$

(4.3)

In Eq. (4.3) $\gamma$ and $\delta$ control, respectively, the expansion (or contraction) rates at early and late times; the general form of the spectral index can be expressed as:

$$\begin{aligned} n_{T}(\gamma , \delta ) = 4 - 2 \biggl |\delta - \frac{1}{2}\biggr | - 2\biggl |\frac{\gamma }{1 - \gamma } - \frac{1}{2} \biggr |. \end{aligned}$$

(4.4)

where the value of $\gamma$ is related to the expansion (or contraction) rate in the cosmic time coordinate as $a(t) = a_{1}(- t/t_{1})^{\gamma }$ and this parametrization is valid before the first zero of H or $\dot{H}$. As in the previous sections also in Eq. (4.4) $\delta$ denotes the expansion rate in the conformal time coordinate during the decelerated stage after the bounce. For $0< \gamma < 1$ Eq. (4.4) gives the spectral slope when, prior to the bouncing regime (taking place for $|t | < t_{1}$), the background experiences a stage of accelerated contraction (i.e. $\dot{a} < 0$ and $\ddot{a} <0$). Conversely when $\gamma < 0$ the background expands and accelerates (i.e. $\dot{a} >0$ and $\ddot{a} >0$) with growing Hubble rate (i.e. $\dot{H} >0$). If $\delta > 1/2$ the contribution to $n_{T}(\gamma ,\delta )$ only comes from the term $k^4\, |a_{re}/a_{ex}|^2$ in Eq. (2.1) while ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re})\rightarrow 1$. Conversely, when $\delta < 1/2$, ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re})\propto 1 + |k \, \tau _{1}|^{-1 + 2 \delta }$ which is much larger than 1 for all the amplified modes of the spectrum (i.e. for $k \tau _{1} \ll 1$). Since the second term in ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re})$ dominates for $\delta <1/2$ and for $k \tau _{1} < 1$ we have that the spectral energy density $\Omega _{gw}(k, \tau ) \propto k^4\, |a_{re}/a_{ex}|^2 \bigl |{\mathcal Q}_{k}(\tau _{ex}, \tau _{re})\bigr |^2$ has overall a spectral slope (valid for a generic value of $\delta$) proportional to $| \delta -1/2|$. After matter-radiation equality the same analysis implies:

$$\begin{aligned} h_{0}^2 \, \Omega _{gw}(\nu , \tau _{0}) = \overline{\Omega }_{*} \,\, (\nu /\nu _{*})^{n_{T}(\gamma , \delta )}\,\,(\nu /\nu _{eq})^{-2},\quad \nu <\nu _{eq}. \end{aligned}$$

(4.5)

Fig. 11

We illustrate the intermediate spectral index $n_{T}(\gamma ,\delta )$ appearing in Eqs. (4.3)–(4.4). In both plots $\gamma$ indicates the expansion (or contraction) rates before the bounce; $\delta$ denotes instead the expansion rate at late times (after the bounce) when the intermediate wavelengths of the spectrum reenter the Hubble radius. In the left plot $0\le \gamma < 1$ and the evolution before the bouncing regime is characterized by an accelerated contraction. In the right plot $\gamma < 0$ implying a phase of accelerated expansion (with growing Hubble rate) before the bouncing regime

Below ${\mathcal O}(100)$ aHz $h_{0}^2 \, \Omega _{gw}(\nu , \tau _{0})$ is much smaller than in the case of the concordance paradigm. In particular for typical frequencies $\nu = {\mathcal O}(\nu _{p})$ (where $\nu _{p} =k_{p}/(2\pi ) = 3.092 \, \textrm{aHz}$) the spectral energy density of Eq. (4.5) is further suppressed by the term $(\nu _{p}/\nu _{*})^{n_{T}(\gamma , \delta )}$ in comparison with the case of the concordance paradigm where this contribution is ${\mathcal O}(1)$.

Fig. 12

The values of $\beta (\gamma ,\delta )$ are illustrated together with the observational constraints derived from the Parkes PTA data. The shaded region denotes, in both plots, the range $-0.65< \beta (\gamma ,\delta ) < -0.25$ which is pinned down by the Parkes PTA [13]. In the left plot $0\le \gamma <1$ and this values describe a stage of accelerated contraction, as it happens for the bounces of the scale factor. In the right plot we discuss the case $\gamma <0$ (i.e. accelerated expansion with growing expansion rate) that occurs for the bounces of the scale factor

4.3 The slopes and amplitudes of the PTA excesses

If all the wavelengths of the order of $\lambda _{PTA}$ do the second crossing in a radiation-dominated stage (i.e. when $\delta \rightarrow 1$) the spectral index of Eq. (4.4) becomes:

$$\begin{aligned} \lim _{\delta \rightarrow 1} n_{T}(\gamma , \delta ) = 3 - 2 \biggl |\frac{\gamma }{1- \gamma } - \frac{1}{2} \biggr |. \end{aligned}$$

(4.6)

When $\gamma \rightarrow 1/3$ in Eq. (4.6) the spectral index $n_{T}(1/3, 1) \rightarrow 3$; in this case the stage of accelerated contraction may be driven, in the simplest situation, by the kinetic energy of a scalar field as it happens, for instance, in the dilaton-driven phase of pre-big bang scenarios [78,79,80,81]. Similarly when $\gamma \rightarrow 0$ we would have, from Eq. (4.6), that $n_{T}(\gamma , 1) \rightarrow 2$; this is the situation preferred in the context of ekpyrotic models [82, 83]. Whenever the expansion rate at the second crossing is eventually different from radiation (i.e. $\delta \ne 1$) also the form of Eq. (4.6) is different. For this reason it is relevant to illustrate the general situation and this has been done in Fig. 11 for the two complementary ranges $0< \gamma < 1$ and $\gamma <0$. Grossly speaking the results of Fig. 11 imply that the spectral slopes suggested by the PTA collaborations can be reproduced either when $\delta >1$ (if $0 \le \gamma < 1$) or when $0< \delta < 1$ (provided $\gamma < 0$). To scrutinize this point in further detail it is easier to express $\beta$ directly as a function of $\gamma$ and $\delta$:

$$\begin{aligned} \beta (\gamma , \delta ) = 1 - \biggl |\delta - \frac{1}{2}\biggr | - \biggl |\frac{\gamma }{1 -\gamma } - \frac{1}{2} \biggr |. \end{aligned}$$

(4.7)

Using Eq. (4.7) we can therefore limit the range of variation of $\beta (\gamma ,\delta )$ and deduce the allowed domain of the parameters. Along this perspective, the shaded areas of Fig. 12 are determined by requiring $-0.65< \beta (\gamma ,\delta ) <- 0.25$ as suggested by the Parkes PTA [13]. In Fig. 12 the line $\delta = 1$ intersects the allowed region only if $\gamma > {\mathcal O}(0.6)$. A similar conclusion follows from Fig. 13 where we examine the NANOgrav observations [14]; in this case, as already stressed in the previous sections, the allowed range of $\beta$ is narrower (even if the corresponding range of $q_{0}$ is larger). The shaded area in both plots of Fig. 13 correspond to the interval $-0.40< \beta < -0.20$ and the correct values of $\beta$ seem to be reproduced for $0< \gamma < 1$ but only when $\delta > 1$. The opposite is true in the case $\gamma < 0$ where the region $\delta < 1$ seems comparatively wider.

Fig. 13

The contours are determined exactly as in the case of Fig. 12 but in the present situation we consider the NANOgrav intervals [14] for $\beta$ rather than the ones of the Parkes PTA. Since the interval of $\beta$ is narrower in the case of Ref. [14], the shaded regions of both plots are narrower than the ones illustrated in Fig. 12. As usual, in both figures the values of $\beta (\gamma ,\delta )$ remains the same on each contour

So far we discussed the spectral slopes and we must now consider the corresponding amplitudes. For this purpose we then examine Eq. (4.1) and express it in terms of the parametrization of Eq. (1.1):

$$\begin{aligned} 6.287\times 10^{-10} q_{0}^2 (\nu /\nu _{ref})^{2 + 2 \beta } = \overline{\Omega }_{*} \, (\nu /\nu _{*})^{n_{T}}. \end{aligned}$$

(4.8)

Since the slope $n_{T}(\gamma ,\delta )$ coincides with $2 + 2 \beta (\gamma ,\delta )$ the amplitude $q_{0}$ (which is determined experimentally) not only depends on $\beta$ but also on $(\nu _{*}/\nu _{ref})$ and $\overline{\Omega }_{*}$. The high-frequency amplitude of the spectral energy density appearing in Eqs. (4.1)–(4.3) can then be fixed to the largest value compatible with the limits of wide-band interferometers in the audio band [52, 53]. From the theoretical viewpoint $q_{0}$ becomes a function of $\beta$ and of $(\nu _{*}/\nu _{ref})$:

$$\begin{aligned} q_{0}(\beta , \nu _{*}) = 1.97 (\nu _{ref}/\nu _{*})^{1 + \beta }. \end{aligned}$$

(4.9)

Since we know from Figs. 11 and 12 that there exist regions in the $(\gamma ,\,\delta )$ plane where $\beta$ falls within the observed range, from Eq. (4.9) we can determine the range of variation of $\nu _{*}$. A careful analysis reported in Fig. 14 shows that $\nu _{*}$ must be slightly smaller than $\nu _{ref}$. More specifically in Fig. 14 we illustrate the different contours of $q_{0}(\beta , \nu _{*})$ and the shaded areas correspond, respectively, to the regions pinned down, respectively, by the Parkes PTA (i.e. $3.7\le q_{0} \le 10.6$ in the left plot of Fig. 14) and by the NANOgrav PTA (i.e. $2.2\le q_{0} \le 4.4$ in the right plot of Fig. 14).

4.4 Excluding a single blue slope

The allowed region of the parameter space pins down a range $\nu _{*} = {\mathcal O}(\nu _{ref})$ but there are theoretical models where the transition to the decelerated regime is very short (i.e. $\nu _{*} \gg \nu _{ref}$) so that $\nu _{*}$ can eventually be of the order of $\nu _{max}$. To investigate this situation we can therefore write the spectral energy density in the following form:

$$\begin{aligned}&h_{0}^2 \Omega _{gw}(\nu , \tau _{0}) = \overline{\Omega }_{max} \, \biggl (\frac{\nu }{\nu _{max}}\biggr )^{n_{T}(\gamma , \delta )}, \qquad \qquad \nonumber \\&\nu _{eq} < \nu \le \nu _{max}, \end{aligned}$$

(4.10)

and demand that $n_{T}(\gamma , \delta )$ falls in the interval of slopes associated with the PTA; if this is the case, then $n_{T}(\gamma , \delta ) = 2 (1 + \beta ) >0$. If we combine Eq. (4.10) with the requirements of Eq. (3.21) we also have that $\overline{\Omega }_{max}$ is constrained as:

$$\begin{aligned}{} & {} \overline{\Omega }_{max} \biggl [ 1 - \biggl (\frac{\nu _{bbn}}{\nu _{max}}\biggr )^{2 (1 + \beta )}\biggr ] \le 2 ( 1 + \beta )\, \overline{\Omega }_{bbn}, \nonumber \\{} & {} \overline{\Omega }_{bbn}= {\mathcal O}(10^{-7}). \end{aligned}$$

(4.11)

Thanks to Eq. (4.11) we can first trade $\overline{\Omega }_{max}$ for $\overline{\Omega }_{bbn}$ and then we can also express $q_{0}$ in terms of $\beta$ and $y = (\nu _{ref}/\nu _{max})$:

$$\begin{aligned}&q_{0}(y, \beta )= 17.83 \, \biggl (\frac{\overline{\Omega }_{bbn}}{10^{-7}}\biggr )^{1/2} \frac{ y^{\beta +1}}{ \sqrt{1 - w_{bbn} \,\,y^{ 2 \beta + 2}}}, \qquad \qquad \nonumber \\&w_{bbn} = (\nu _{bbn}/\nu _{ref}) = 0.011. \end{aligned}$$

(4.12)

Fig. 14

We illustrate the contours of constant $q_{0}(\nu _{*},\beta )$ for a fixed value of $\overline{\Omega }_{*}$. The labels appearing on the various contours correspond to the common logarithms of $q_{0}(\nu _{*},\beta )$. The intervals of $\beta$ match the ones of the corresponding observations. The shaded regions correspond, as indicated in each of the plots, to the ranges of $q_{0}$ determined by the Parkes [13] and by the NANOgrav [14] PTA

Equation (4.12) is illustrated in Fig. 15 where $q_{0}$ is viewed as a function of $\beta$ and $\nu _{max}$; on the vertical axis of both plots we report the range of $\beta$ compatible with each of the corresponding experiment (i.e. the Parkes [13] and the NANOgrav [14] PTA). The shaded regions define the allowed range of $q_{0}$ for each of the two experiments. The results of Fig. 15 are incompatible with Eq. (4.10) since, grossly speaking, we can expect $\nu _{max}$ between few MHz and the THz [17]. In the parametrization of Eq. (4.10) the common logarithm of $(\nu _{ref}/\nu _{max})$ (reported on the horizontal axes of the plots of Fig. 15) should be between $-20$ and $-15$. On the contrary the allowed region in Fig. 15 is located for $y = {\mathcal O}(10^{-2})$.

Fig. 15

After imposing the big-bang nucleosynthesis constraints (see Eq. (4.11)) we illustrate the contours of constant $q_{0}(\beta ,\nu _{ref}/\nu _{max})$. The intervals of $\beta$ match the ones of the corresponding observations and the shaded regions correspond, as indicated in each of the plots, to the ranges of $q_{0}$ determined by the Parkes [13] and by the NANOgrav [14] PTA

If the PTA excesses are the result of a bouncing stage it is necessary that the wavelengths of the order of $\lambda _{PTA}$ do their second crossing during a decelerated stage not dominated by radiation. Moreover a bouncing model leading to a spectral energy density with a single blue slope (possibly ranging between the equality frequency and $\nu _{max}$) is unable to account for the PTA excesses if all the phenomenological bounds are concurrently satisfied. Various bouncing scenarios have been constructed with the aim of either complementing or even challenging the conventional inflationary ideas. Bouncing scenarios appear by physical premises that are quite different and various reviews are currently available (see, for instance, [84,85,86,87,88]). It is not uncommon that the solutions obtained in a given framework are recycled in an entirely different situation. Recently it has been argued that conventional inflationary models are generically in tension with the swampland criteria [89] and this is often seen as a further motivation for bouncing dynamics. The indications of the PTA can be very precious in this context and they might even contribute to the long standing problem of bouncing scenarios, i.e. the origin of a Gaussian and adiabatic mode of large-scale curvature inhomogeneities [17].

5 Concluding remarks

During the last two decades a series of significant limits from the millisecond pulsars at intermediate frequencies (roughly corresponding to the inverse of the time-scale along which the various pulsars have been monitored) severely constrained the isotropic and random backgrounds of gravitational radiation. More recently different ensembles of millisecond pulsars have been scrutinized with regular cadence by the pulsar timing arrays (PTA in the bulk of the paper). Despite the different conclusions on the expected correlations in the pulse arrival times between pairs of pulsars (and despite the slightly dissimilar determinations of the spectral parameters), the competing experiments seem to suggest concurrent evidences of gravitational radiation with stochastically distributed Fourier amplitudes at a benchmark frequency ${\mathcal O}(30)$ nHz and with $h_{0}^2 \Omega _{gw}(\nu ,\tau _{0})$ ranging between $10^{-8}$ and $10^{-9}$. While the origins of the PTA excesses are still perplexing, in this paper we speculate that the relic gravitons are responsible of the observed signal. Even if a collection of late-time sources may eventually lead to a diffuse background of gravitational radiation, the relic gravitons are instead produced, by definition, at much earlier times and solely because the rapid variation of the space-time curvature.

The theoretical perspective explored in this investigation strongly suggests that the problem is not yet to fit (more or less reliably) the existing data in terms of a series of preferred scenarios but to understand preliminarily whether or not the observed excesses in the nHz range are compatible with a modified evolution of the comoving horizon since this is the only way the spectrum of relic gravitons at intermediate frequencies can be affected. The goal of this study is therefore not to endorse a specific model (or to pin down the likely values of a hypothetical spectral index) but to see, more modestly, if and how the relic gravitons could be associated with the nHz excesses. All in all the systematic approach developed in this paper propounds three complementary physical possibilities that have been carefully perused and that should be further analyzed in the near future.

• The most conventional option stipulates that the timeline of the comoving horizon is not modified during inflation so that the nHz excess is caused by the drastic change of the post-inflationary expansion rate prior to big-bang nucleosynthesis.

• A second alternative implies a modified evolution of the tensor modes during a conventional inflationary stage as it happens, for instance, when the gravitons inherit an effective refractive index from the interactions with the geometry.

• We finally consider the possibility of an epoch of increasing curvature prior to the conventional decelerated stage of expansion and argue that this option is only reconcilable with the observed excesses provided the wavelengths crossing the comoving horizon at early times do not reenter in an epoch dominated by radiation.

In connection with these three complementary options the results obtained in this analysis are, in short, the following.

• A late-time modification of the comoving horizon may indeed alter the spectral energy density of the relic gravitons in the nHz range but the observed amplitudes and slopes are unfortunately neither compatible nor comparable with this minimal explanation.

• Conversely, if a dynamical refractive index evolves during a conventional inflationary phase of nearly minimal duration the corresponding $h_{0}^2 \, \Omega _{gw}(\nu ,\tau _{0})$ compares well with the nHz hump even if the observational data coming from competing experiments pin down slightly different regions of the parameter space.

• In the context of the bouncing scenarios, it is finally possible to exclude a nHz excess associated with a single slope of the spectral energy density between 100 aHz and the GHz range. However, if the spectral energy density has a break in the nHz region the direct limits of the wide-band detectors constrain the high-frequency amplitude and, in this case, we could account for the hump provided the bunch of PTA wavelengths reenter the comoving horizon during a decelerated stage not yet dominated by radiation.

The three possibilities discussed here are therefore not mutually exclusive: in the bouncing case, the simplest way to match the amplitudes and the slopes of the spectra is to modify the comoving horizon also at late times. The potential nHz excesses make even more relevant the high-frequency determinations of the spectral energy density. In particular the direct bounds in the audio band are essential even if the largest signal of the relic gravitons is expected in the MHz and GHz domains where smaller detectors may play a crucial rôle, as repeatedly suggested in the past. While the observational aspects of the problem cannot be addressed with the theoretical approach reported here, it is nonetheless true that the physical interpretation of the results probably demands a conceptual framework (such as the one pursued in this analysis) that could clarify (and even exclude) the primeval origin of the nHz excesses.

Appendices

Basic conventions and notations

With the purpose of making the presentation self-contained, in this and in the following appendix we illustrate the main notations employed in the bulk of the paper. We start by reminding that the tensor modes of the geometry are related to the first-order traceless and solenoidal fluctuations of the four-dimensional metric

$$\begin{aligned}{} & {} g_{\mu \nu }(\vec {x},\tau ) = a^2(\tau ) \eta _{\mu \nu } + \delta _{t}^{(1)} g_{\mu \nu }(\vec {x}, \tau ), \nonumber \\{} & {} \delta _{t}^{(1)} g_{i\,j}(\vec {x}, \tau ) = - a^2(\tau ) h_{ij}(\vec {x},\tau ), \end{aligned}$$

(A.1)

where $a(\tau )$ denotes the scale factor of a conformally flat background geometry, $\tau$ is the conformal time coordinate and $\eta _{\mu \nu }$ is the Minkowski metric with signature $(+,\, -,\,-,\, -)$; Greek indices are four-dimensional while the Latin (lowercase) indices are three-dimensional; in Eq. (A.1) the first-order (tensor) fluctuations $h_{i\,j}(\vec {x}, \tau )$ are, by definition, solenoidal and traceless. As a general rule throughout the text the prime denotes a derivation with respect to $\tau$ while the overdot denotes a derivation with respect to the cosmic time coordinate t. Since the relation between the two is given by $a(\tau ) d \tau = d\,t$ it also follows, as usual, that

$$\begin{aligned} a \, H = {\mathcal H} = a^{\prime }/a, \qquad \qquad H= \dot{a}/a. \end{aligned}$$

(A.2)

Different parametrizations of the time coordinate are also discussed in Appendix B and are relevant in the discussion of Sect. 3. Within these notations the effective action of the tensor modes of the geometry, originally due to Ford and Parker [20] can be written as:

$$\begin{aligned}{} & {} S = \frac{\overline{M}_{P}^2}{8} \int d^{4} x \, \, \sqrt{- \overline{g}} \,\,\overline{g}^{\alpha \beta } \partial _{\alpha } h_{i\,j} \, \partial _{\beta } h^{i\,j}, \nonumber \\{} & {} \overline{M}_{P} = M_{P}/\sqrt{8\, \pi }. \end{aligned}$$

(A.3)

In the framework of a specific scenario Eq. (A.3) may be complemented by other terms. For instance, in the case single-field inflationary models the effective action contains all the terms that contain four space-time derivatives and that are suppressed by the inverse power of a large mass scale M [61]; among all these terms there are combinations that break parity and that are neglected here even if their inclusion does not substantially alter the conclusions of the discussion given the smallness of the corresponding effects [64]. From Eq. (A.3) the effective energy-momentum pseudo-tensor is given by:

$$\begin{aligned} {\mathcal T}_{\mu }^{\nu } = \frac{\overline{M}_{P}^2}{4} \biggl ( \partial _{\mu } h_{i\, j} \partial ^{\nu } h^{i\, j} - \delta _{\mu }^{\,\,\, \nu } \overline{g}^{\alpha \beta } \partial _{\alpha } h_{i\,j} \partial _{\beta } h^{i\, j} \biggr ), \end{aligned}$$

(A.4)

where the indices are raised and lowered by means of the background metric $\overline{g}_{\mu \nu }(\tau )$. While there exist different strategies to assign the energy-momentum pseudo-tensor, the one obtained from the functional variation (with respect to the background metric) of the effective action (A.3) leads to a positive semi-definite energy density both inside and outside the Hubble radius [90]; from the temporal components of Eq. (A.4) we obtain the explicit expression of the energy density:

$$\begin{aligned} \rho _{gw} = \frac{\overline{M}_{P}^2}{8\, a^2} \biggl (\partial _{\tau } h_{i\,j} \partial _{\tau } \, h^{i\,j} + \partial _{k} h_{i\,j} \partial _{k} \, h^{i\,j}\biggr ). \end{aligned}$$

(A.5)

In the present investigation the tensor amplitude in Fourier space is defined as:

$$\begin{aligned}{} & {} h_{i\,j}(\vec {x},\tau )= \frac{1}{(2\pi )^{3/2}} \, \int d^{3} k \, e^{-i \vec {k}\cdot \vec {x}} \, h_{i\, j}(\vec {k}, \tau ), \nonumber \\{} & {} h_{i\, j}^{*}(\vec {k}, \tau ) = h_{i\, j}(- \vec {k}, \tau ), \end{aligned}$$

(A.6)

where $k^{i} \, h_{i\,j} = k^{j} \,h_{i\,j} =0$ and $h_{i}^{i} =0$. For a stochastic random field the Fourier amplitudes of Eq. (A.6) and their time derivatives are associated, respectively, with the two tensor power spectra $P_{T}(k,\tau )$ and $Q_{T}(k,\tau )$

$$\begin{aligned}{} & {} \langle h_{i\,j}(\vec {k},\tau ) \, h_{m\, n}(\vec {p}, \, \tau ) \rangle \nonumber \\{} & {} \quad = \frac{2 \pi ^2}{k^3} \,\,P_{T}(k,\tau ) \,\, \delta ^{(3)}(\vec {k} + \vec {p}) \,\,S_{i\,j\,m\,n}(\hat{k}), \end{aligned}$$

(A.7)

$$\begin{aligned}{} & {} \langle \partial _{\tau } h_{i\,j}(\vec {k},\tau ) \, \partial _{\tau } h_{m\, n}(\vec {p}, \, \tau ) \rangle \nonumber \\{} & {} \quad = \frac{2 \pi ^2}{k^3} \,\,Q_{T}(k,\tau ) \,\, \delta ^{(3)}(\vec {k} + \vec {p}) \,\,S_{i\,j\,m\,n}(\hat{k}), \end{aligned}$$

(A.8)

where $S_{i\,j\,m\,n}(\hat{k}) = [p_{i\,m}(\hat{k})\, p_{j\,n}(\hat{k}) + p_{j\,m}(\hat{k})\, p_{i\,n}(\hat{k}) - p_{i\, j}(\hat{k}) p_{m\, n}(\hat{k})]/4$ is given in terms of the transverse projectors $p_{i\,j}(\hat{k}) = (\delta _{i\, j} - \hat{k}_{i} \, \hat{k}_{j})$. After inserting Eq. (A.6) into Eq. (A.5) we can average the obtained result term by term and deduce:

$$\begin{aligned} \langle \rho _{gw} \rangle = \frac{\overline{M}_{P}^2}{8\,\, a^2 } \int \frac{d k}{k} \biggl [ k^2 P_{T}(k,\tau ) + Q_{T}(k,\tau )\biggr ]. \end{aligned}$$

(A.9)

If the result of Eq. (A.9) is divided by the critical energy density $\rho _{crit} = 3 \, H^2\, \overline{M}_{P}^2$ we obtain the spectral energy density in critical units conventionally denoted by $\Omega _{gw}(k,\tau )$:

$$\begin{aligned} \Omega _{gw}(k,\tau )&= \frac{1}{\rho _{crit}} \, \frac{ d \, \langle \rho _{gw} \rangle }{d \ln {k}}\nonumber \\ {}&= \frac{1}{24 \, H^2 \, a^2} \biggl [ k^2 \, P_{T}(k,\tau ) + Q_{T}(k,\tau )\biggr ]. \end{aligned}$$

(A.10)

When the wavelengths are shorter than the comoving horizon the corresponding wavenumbers exceed the expansion rate and, in this regime, $Q_{T}(k,\tau )$ and $k^2 \, P_{T}(k,\tau )$ are roughly comparable so that Eq. (A.10) can also be written as:

$$\begin{aligned} \Omega _{gw}(k,\tau ) = \frac{k^2}{12 \, H^2 \, a^2} \, P_{T}(k, \tau ), \qquad \frac{k}{{\mathcal H}} = \frac{k}{a\, H} >1. \end{aligned}$$

(A.11)

The tensor power spectra $P_{T}(k,\tau )$ and $Q_{T}(k,\tau )$ depend on the evolution of the mode functions $F_{k}(\tau )$ and $G_{k}(\tau ) = F_{k}^{\prime }(\tau )$ where, as already mentioned above, the prime denotes throughout a derivation with respect to the cosmic time coordinate $\tau$:

$$\begin{aligned} P_{T}(k, \tau )= & {} \frac{4 k^3 }{\overline{M}_{P}^2\,\pi ^2} \bigl | F_{k}(\tau ) \bigr |^2 = \frac{4 k^3}{\pi ^2\,\overline{M}_{P}^2\, a^2} \bigl | f_{k}(\tau ) \bigr |^2,\nonumber \\ \end{aligned}$$

(A.12)

$$\begin{aligned} Q_{T}(k, \tau )= & {} \frac{4 k^3}{\overline{M}_{P}^2 \, \pi ^2} \bigl | G_{k}(\tau ) \bigr |^2 = \frac{4 k^3}{\pi ^2\, \overline{M}_{P}^2 a^2} \bigl | g_{k}(\tau ) \bigr |^2,\nonumber \\ \end{aligned}$$

(A.13)

In Eqs. (A.12)–(A.13) the rescaled mode functions $f_{k}(\tau )$ and $g_{k}(\tau )$ obey:

$$\begin{aligned} f_{k}^{\prime } = g_{k} + {\mathcal H} f_{k}, \qquad \qquad g_{k}^{\prime } = - k^2 \, f_{k} - {\mathcal H} f_{k}. \end{aligned}$$

(A.14)

The evolution of the mode functions can be solved in various regimes and a detailed discussion on these issues can be found elsewhere. If we eliminate $g_{k}(\tau )$ from Eq. (A.14) the evolution of $f_{k}(\tau )$ can be expressed as

$$\begin{aligned} f_{k}^{\prime \prime } + \bigl \{ k^2 - a^2 \, H^2 [ 2 - \epsilon (a)]\bigr \} f_{k}=0, \qquad \qquad \epsilon = - \dot{H}/H^2. \end{aligned}$$

(A.15)

As stressed in the bulk of the paper, the condition $k^2 = a^2 \, H^2 [ 2 - \epsilon (a)]$ defines two complementary turning points where the analytical evolution of the mode functions gets modified; moreover, since $(a\, H)^{-1}$ gives approximately the comoving horizon, they are associated, respectively, to the exit and to the reentry of a given wavelength. The use of the term horizon to identify the inverse of the Hubble rate (and its comoving counterpart) is rather common even if potentially inaccurate; we shall not try to correct here this terminology. When the wavelengths are shorter than the comoving horizon the expressions of $F_{k}(\tau )$ and $G_{k}(\tau )$ are:

$$\begin{aligned} F_{k}(\tau )= & {} \frac{e^{- i k \tau _{ex}}}{\sqrt{2 k}\, a} \biggl (\frac{a_{re}}{a_{ex}}\biggr ) {\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) \nonumber \\{} & {} \times \biggl [ \frac{{\mathcal H}_{re}}{k} \sin { k \Delta \tau } + \cos {k \Delta \tau } \biggr ], \end{aligned}$$

(A.16)

$$\begin{aligned} G_{k}(\tau )= & {} \frac{e^{- i k \tau _{ex}}}{a} \,\sqrt{\frac{k}{2}}\, \biggl (\frac{a_{re}}{a_{ex}}\biggr ) {\mathcal Q}_{k}(\tau _{ex}, \tau _{re}) \nonumber \\{} & {} \times \biggl \{ \biggl [ \frac{{\mathcal H}_{re}}{k} \cos { k \Delta \tau } - \sin {k \Delta \tau } \biggr ] \nonumber \\{} & {} - \frac{{\mathcal H}}{k} \biggr [\frac{{\mathcal H}_{re}}{k} \sin { k \Delta \tau } + \cos {k \Delta \tau } \biggr ]\biggr \}, \end{aligned}$$

(A.17)

where ${\mathcal Q}_{k}(\tau _{ex}, \tau _{re})$ has been already introduced in Eq. (2.2) and $\Delta \tau = (\tau - \tau _{re})$. If Eqs. (A.16)–(A.17) are inserted first into Eqs. (A.12)–(A.13) and then into Eq. (A.10) we can obtain the expression of Eq. (2.1). To match the notations of the present paper with the ones of the PTA collaborations we recall that the relation between the chirp amplitude $h_{c}(\nu ,\tau )$ and the tensor power spectrum $P_{T}(k,\tau )$ is $2 \, h_{c}^2(\nu ,\tau ) = P_{T}(\nu , \tau )$. Similarly the connection between the spectral amplitude $S_{h}(\nu ,\tau )$ and the chirp amplitude is given by $\nu \, S_{h}(\nu , \tau ) = h_{c}^2(\nu , \tau )$. Putting everything together we then have

$$\begin{aligned} \Omega _{gw}(k,\tau _{0}) = \frac{2 \pi ^2 \nu ^2}{3 \, H_{0}^2 } \,h_{c}^2(\nu , \tau _{0}), \end{aligned}$$

(A.18)

where we used $a_{0} =1$; this means, within our conventions, that the comoving and the physical frequencies coincide at the present time. If we now parametrize the signal as in Eq. (1.1) a more explicit relations can be obtained from Eq. (A.1) and it is given by:

$$\begin{aligned} \Omega _{gw}(\nu ,\tau _{0}) = \frac{2 \pi ^2}{3} \, Q^2 \, \biggl (\frac{\nu _{ref}}{H_{0}}\biggr )^2 \,\, \biggl (\frac{\nu }{\nu _{ref}}\biggr )^{2 + 2 \beta }. \end{aligned}$$

(A.19)

If we now multiply Eq. (A.19) by $h_{0}^2$ (where $h_{0}$ denotes the indetermination in the present value of the Hubble rate), take into account the explicit value of $\nu _{ref}$ and parametrize Q as $Q= q_{0} \times 10^{-15}$ we obtain the relations already discussed in Eq. (1.2) (for $\nu \rightarrow \nu _{ref}$) and, more generally, in Eq. (2.10). With the same logic we can also deduce the explicit relation between the spectral amplitude and the chirp amplitude:

$$\begin{aligned} S_{h}(\nu , \tau _{0}) = 3.15 \, \times 10^{-23} \, \, q_{0}^2\,\,\bigl (\nu /\nu _{ref}\bigr )^{2 \beta -1} \, \, \textrm{Hz}^{-1}. \end{aligned}$$

(A.20)

It is often customary to employ the square root of Eq. (A.20) so that $\sqrt{S_{h}(\nu , \tau _{0})}$ is measured in units $1/\sqrt{\textrm{Hz}}$, i.e. $\sqrt{S_{h}(\nu , \tau _{0})} =5.61\times 10^{-12} \, \, q_{0} (\nu /\nu _{ref})^{\beta -1/2} \,\, 1/\sqrt{\textrm{Hz}}$.

The general form of the effective action

A more general form of the effective action of the tensor modes of the geometry suggests to weight the various terms of Eq. (A.3) with time-dependent coefficients:

$$\begin{aligned} S_{g}= & {} \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x \int \, d \tau \biggl [ c_{1}(\tau ) \,\partial _{\tau } h_{i\, j}\, \partial _{\tau } h^{i\, j} \nonumber \\{} & {} - c_{2}(\tau ) \, \partial _{k} h_{i \, j} \,\partial ^{k}h^{i\, j}- c_{3}(\tau )\, m_{c}^2\, h_{i \, j} \, \partial h^{i \, j} \biggr ]. \end{aligned}$$

(B.1)

As before, in Eq. (B.1) the parity-breaking terms associated with quadratic combinations involving either the dual Riemann or the dual Weyl tensors have been neglected; both terms would appear in the effective action and can polarize the backgrounds of relic gravitons [64] (see also [91]). Among the three function $c_{i}(\tau )$ (with $i =1,\, 2,\, 3$) we have that $c_{1}(\tau )$ and $c_{2}(\tau )$ are related to the expanding dimensions while $c_{3}(\tau )$ may appear in the case of compact extra-dimensions [92]. If we factor $c_{1}(\tau )$ in Eq. (B.1) the resulting expression will be given by:

$$\begin{aligned} S_{g}&= \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x \int \, d \tau \,c_{1}(\tau )\nonumber \\ {}&\quad \times \biggl [\partial _{\tau } h_{i\, j} \partial _{\tau } h^{i\, j} - \frac{1}{n^2(\tau )} \,\partial _{k} h_{i \, j} \partial ^{k} h^{i\, j} - \frac{1}{\overline{n}^2(\tau )} m_{c}^2 h_{i \, j} h^{i \, j} \biggr ], \end{aligned}$$

(B.2)

where $n(\tau )$ and $\overline{n}(\tau )$ denote, respectively, the refractive indices associated with the expanding and with the compact dimensions [92], i.e. $n(\tau ) = \sqrt{c_{1}(\tau )/c_{2}(\tau )}$ and $\overline{n}(\tau ) = \sqrt{c_{1}(\tau )/c_{3}(\tau )}$. Equation (B.2) simplifies after a rescaling of the background dependence and its final form becomes¹³:

$$\begin{aligned} S_{g}&= \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x \int \, d \eta \, \, b^2(\eta )\nonumber \\ {}&\quad \times \biggl [\partial _{\eta } h_{i\, j} \partial _{\eta } h^{i\, j} - \, \, \partial _{k} h_{i \, j} \partial ^{k} h^{i\, j} - r_{c}^2(\eta ) m_{c}^2 \, h_{i \, j} h^{i \, j} \biggr ]. \end{aligned}$$

(B.3)

Equation (B.3) follows from Eq. (B.2) by first changing the time parametrization from $\tau$ (the conformal time coordinate) to $\eta$; the relation between the two time parametrizations is simply given by$n(\eta ) d\eta = d\tau$. Let us therefore consider the simplest situation where the refractive index increases during inflation as suggested in Eq. (3.4); in this case for $a< a_{*}$ we would have $n(a) = n_{*} (a/a_{*})^{\alpha }$ (with $\alpha >0$) so that the relation between the conformal time coordinate $\tau$ and the $\eta$-time can be swiftly worked since $d \eta = d\tau /n(a)$. From the definition of $\eta$ we therefore have:

$$\begin{aligned} \eta = \int \frac{da}{a^2 \, H\, n} = - \frac{1}{a\, H\, n} + (\epsilon - \alpha )\int \frac{d a}{a^2 \, H\, n}, \end{aligned}$$

(B.4)

where, as in Eq. (A.2), $H = \dot{a}/a$ and the overdot denotes a derivation with respect to the cosmic time coordinate. The second equality in Eq. (B.4) follows after integration by parts since $\dot{\epsilon } \ll 1$ and $\dot{\alpha } =0$. Equation (B.4) also implies that $a \, H\, n= - 1/[(1 -\epsilon + \alpha ) \eta ]$; note once more that when $n \rightarrow 1$ we also have $\alpha \rightarrow 0$ and the standard relation $a \, H= -1/[(1-\epsilon )\tau ]$ is immediately recovered. In the $\eta$-time parametrization the evolution of the mode functions simplifies and it is given by

$$\begin{aligned} \partial _{\eta }^2 f_{k} + \biggl [ k^2 - \frac{\partial _{\eta }^2 b}{b}\biggr ] f_{k} =0, \qquad g_{k} = \partial _{\eta } f_{k} - \frac{\partial _{\eta }b}{b} f_{k}. \end{aligned}$$

(B.5)

From Eq. (B.5) it follows that the crossing of a given wavelength occurs when $k^2 = (\partial _{\eta }^2 b)/b$. This expression generalizes therefore the notion of the comoving horizon during the refractive phase. More specifically we may recall the connection between the derivations in the various time parametrizations introduced so far, namely

$$\begin{aligned} \partial _{\eta } = n \, \partial _{\tau } = n\, a\,\partial _{t}, \qquad \partial _{X} = \frac{\partial }{\partial X}, \end{aligned}$$

(B.6)

where $\eta$, $\tau$ and t denote, once more, the $\eta$-time, the conformal time and the cosmic time coordinates. By using Eq. (B.6) in the condition $k^2 = (\partial _{\eta }^2 b)/b$ we obtain, after simple algebra, a condition similar to Eq. (3.1):

$$\begin{aligned} k^2 = n^3 \, b^2 \, F^2 \biggl [ 2 - \overline{\epsilon }+ \frac{3 \dot{n}}{2 n F}\biggr ], \qquad F = \frac{\dot{b}}{b}, \qquad \overline{\epsilon } = - \frac{\dot{F}}{F^2}. \end{aligned}$$

(B.7)

In the limit $n\rightarrow 1$ we get $b \rightarrow a$, $F\rightarrow H$ and $\overline{\epsilon }\rightarrow \epsilon$. This is why it is appropriate to consider $(b\, F)^{-1}$ as the generalization of the comoving horizon during inflation. Different choices in Eq. (B.1) are in fact artificial since they are ultimately equivalent to the one of Eq. (B.2). For instance instead of factoring $c_{1}(\tau )$ we may factor $c_{2}(\tau )$. If we rescale $c_{2}(\tau )$ we simply get the analog of Eq. (B.2):

$$\begin{aligned} S_{g}= & {} \frac{\overline{M}_{P}^2}{8} \int \, d^{3} x \int \, d \tau \,\,c_{2}(\tau )\, \nonumber \\ {}{} & {} \times \biggl [ n^2(\tau )\, \partial _{\tau } h_{i\, j} \partial _{\tau } h^{i\, j} - \, \partial _{k} h_{i \, j} \partial ^{k} h^{i\, j} \nonumber \\{} & {} - m_{c}^2 \frac{c_{3}(\tau )}{c_{2}(\tau )}\,h_{i \, j} h^{i \, j} \biggr ]. \end{aligned}$$

(B.8)

We may now introduce the $\eta$-time defined as $n(\eta ) \, d\eta = d\tau$; Eq. (B.8) then takes the same form of Eq. (B.2) with the difference that $b^2(\eta )$ is now replaced by $\overline{b}^2(\eta )$ where $\overline{b}(\eta ) = \sqrt{c_{2}(\eta )\, n(\eta )}$. It turns out, however, that $\overline{b}(\eta )$ and $b(\eta )$ coincide since, ultimately, $\overline{b}(\eta ) = b(\eta ) = [ c_{1}(\eta )\, c_{2}(\eta )]^{1/4}$. In the $\eta$-time parametrization the evolution of the mode functions of Eq. (B.5) is exactly solvable in various situations of practical interest. For instance if $b(\eta )$ is given by Eq. (3.7) the solution of Eq. (B.5) is simply given by

$$\begin{aligned}{} & {} f_{k}(\eta ) = \frac{{\mathcal M}}{\sqrt{ 2 k}} \, \sqrt{- k \eta } \, H_{\mu }^{(1)}(- k\, \eta ), \nonumber \\{} & {} g_{k}(\eta ) = - {\mathcal M}\,\sqrt{\frac{k}{2}} \,\sqrt{- k\,\eta } \, H_{\mu -1}^{(1)}(- k \eta ), \end{aligned}$$

(B.9)

where $\mu = \zeta +1/2$ and $H_{\mu }^{(1)}(-k\eta )$ is the Hankel function of first kind [93] and $|{\mathcal M}| = \sqrt{\pi /2}$. From Eq. (B.9) the tensor power spectrum becomes:

$$\begin{aligned} P_{T}(k, \eta )= & {} \frac{4\, k^{3}}{\pi ^2 \, \overline{M}_{P}^2\,b^2(\eta )} \bigl | f_{k}(\eta ) \bigr |^2 \nonumber \\= & {} \biggl (\frac{H_{1}}{M_{P}}\biggr )^2\,\, {\mathcal B}(n_{T}, N_{*}, N_{t}, \epsilon ) \,\, \biggl (\frac{k}{a_{1} H_{1}}\biggr )^{n_{T}}, \end{aligned}$$

(B.10)

where we remind that $\overline{M}_{P} = M_{P}/\sqrt{8 \,\pi }$; in Eq. (B.10) we also introduced, for practical reasons, the following rescaled amplitude

$$\begin{aligned} {\mathcal B}(n_{T}, N_{*}, N_{t}, \epsilon )= & {} \frac{ 2^{6 - n_{T}}}{\pi ^2} \biggl | 1 + \frac{\alpha }{1 -\epsilon }\biggr |^{2 - n_{T}}\, \nonumber \\{} & {} \times \Gamma ^2\biggl (\frac{3 -n_{T}}{2}\biggr )e^{\alpha \, N_{*}( 3 - n_{T}) - n_{T} (N_{*} - N_{t})}. \nonumber \\ \end{aligned}$$

(B.11)

The result of Eq. (B.10) corresponds to the limit $| k \eta | \ll 1$ where $P_{T}(k, \eta )$ becomes constant in the $\eta$-time with $r_{T}(\nu )$ given by

$$\begin{aligned}{} & {} r_{T}(\nu ) = \frac{\epsilon }{\pi } \, {\mathcal B}(n_{T}, N_{*}, N_{t}, \epsilon ) \biggl (\frac{\nu }{\nu _{max}}\biggr )^{n_{T}}, \nonumber \\{} & {} \lim _{\alpha \rightarrow 0} {\mathcal C}(n_{T}, N_{*}, N_{t}, \epsilon ) = 16\pi . \end{aligned}$$

(B.12)

For $\alpha \rightarrow 0$ we have that $r_{T}\rightarrow 16 \epsilon$ and the standard consistency relation is recovered; note that $n_T$ is given exactly by the expression already mentioned in Eq. (3.11); therefore in the limit $\alpha \rightarrow 0$ we have that $n_{T}\rightarrow - 2\epsilon$. The notations employed here imply that the definition of the power spectrum $P_{T}(k,\eta )$ (and equally for $P_{T}(k,\tau )$) directly follow from the quantum mechanical normalization of the corresponding field operators. In particular we have that

$$\begin{aligned} \widehat{h}_{i\,j}(\vec {x}, \, \eta )= & {} \frac{\sqrt{2}}{\overline{M}_{P}(2\,\pi )^{3/2}\,b^2(\eta )} \sum _{\alpha = \oplus ,\otimes } e^{(\alpha )}_{i\, j}(\hat{k}) \int \, d^{3} k\, \nonumber \\{} & {} \times \biggl [ \widehat{a}_{\vec {k},\,\alpha }\, f_{k,\alpha }(\eta ) e^{- i \vec {k}\cdot \vec {x}} + \widehat{a}_{\vec {k},\,\alpha }^{\dagger }\, f_{k,\alpha }^{*}(\eta ) e^{ i \vec {k}\cdot \vec {x}} \biggr ],\nonumber \\ \end{aligned}$$

(B.13)

where $[ \widehat{a}_{\vec {k},\, \alpha }, \widehat{a}_{\vec {p},\, \beta }^{\dagger } ] = \delta ^{(3)}(\vec {k}- \vec {p})$; the two tensor polarizations are $e^{\oplus }(\hat{k}) = (\hat{m}_{i}\, \hat{m}_{j} - \hat{n}_{i} \hat{n}_{j})$ and $e^{\otimes }(\hat{k}) = (\hat{m}_{i}\, \hat{n}_{j} + \hat{n}_{i} \hat{m}_{j})$ where $\hat{m}$, $\hat{n}$ and $\hat{k}$ form a triplet of mutually orthogonal unit vectors. From Eq. (B.13) we can compute

$$\begin{aligned}&\langle \widehat{h}_{i\,j}(\vec {x}, \, \eta )\, \widehat{h}_{i\,j}(\vec {x} + \vec {r}, \, \eta )\rangle \nonumber \\&\quad = \int d \ln {k}\,\, P_{T}(k,\eta )\, j_{0}(k\, r),\qquad j_{0}(k\, r) = \sin {k\, r}/(k\, r). \end{aligned}$$

(B.14)

As anticipated, the tensor power spectrum of Eq. (B.14) is defined as in Eq. (B.10). For a full quantum mechanical discussion of this class of problems problem see, for instance, Ref. [90].