1 Introduction

The ‘\(\mu \) from \(\nu \)’ Supersymmetric Standard Model (\(\mu \nu \textrm{SSM}\)) [1, 2] (for a recent review, see Ref. [3]) is a predictive model alternative to the Minimal Supersymmetric Standard Model (MSSM) [4,5,6,7,8] and the Next-to-MSSM (NMSSM) [9, 10]. It solves the \(\mu \)-problem and the \(\nu \)-problem (neutrino masses) simultaneously, without the need to introduce additional energy scales beyond the supersymmetry (SUSY)-breaking scale. In contrast to the MSSM, and the NMSSM, R-parity and lepton number are not conserved, leading to a completely different phenomenology characterized by distinct prompt or displaced decays of the lightest supersymmetric particle (LSP), producing multi-leptons/jets/photons with small/moderate missing transverse energy (MET) from neutrinos [11,12,13,14,15,16,17]. The smallness of neutrino masses is directly related with the low decay width of the LSP. Actually, it is also related to the existence of possible candidates for decaying dark matter in the model. This is the case of the gravitino [18,19,20,21,22], or the axino [23], with lifetimes greater than the age of the Universe. It is also worth mentioning concerning cosmology, that baryon asymmetry might be realized in the \(\mu \nu \textrm{SSM}\) through electroweak (EW) baryogenesis [24]. The EW sector of the \(\mu \nu \textrm{SSM}\) can also explain [15, 16] the longstanding discrepancy between the experimental result for the anomalous magnetic moment of the muon [25, 26] and its SM prediction [27].Footnote 1

Because of R-parity violation (RPV) in the \(\mu \nu \textrm{SSM}\), basically all SUSY particles are candidates for the LSP, and therefore analyses of the LHC phenomenology associated to each candidate are necessary to test them. This crucial task, given the current experimental results on SUSY searches, has been mainly concentrated on the EW sector of the \(\mu \nu \textrm{SSM}\), analyzing left sneutrinos, the right smuon and the bino as candidates for the LSP [11,12,13,14,15,16]. More recently, the color sector of the \(\mu \nu \textrm{SSM}\) has started to be analyzed. In particular, in Ref. [17] the SUSY partners of the top quark as LSP candidates, i.e. the left and right stops, were considered. The aim of this work is to continue with the systematic analysis of the color sector of the \(\mu \nu \textrm{SSM}\), focusing now on the right sbottom as the LSP. As we will discuss, although the left sbottom can also be light, the D-term contribution makes the left stop lighter.

Thus, we will study the constraints on the parameter space of the model by sampling it to get the right sbottom as the LSP in a wide range of masses. We will pay special attention to reproduce neutrino masses and mixing angles [28,29,30,31,32,33]. In addition, we will impose on the resulting parameters agreement with Higgs data as well as with flavor observables.

The paper is organized as follows. In Sect. 2, we will review the \(\mu \nu \textrm{SSM}\) and its relevant parameters for our analysis of neutrino, neutral Higgs and sbottom sectors. In Sect. 3, we will introduce the phenomenology of the sbottom LSP, studying its pair production channels at the LHC and its signals. The latter consist of displaced vertices with a lepton and a top quark or a neutrino and a bottom quark. In Sect. 4, we will discuss the strategy that we will employ to perform scans searching for points of the parameter space of our scenario compatible with current experimental data on neutrino and Higgs physics, as well as flavor observables such as B and \(\mu \) decays. The results of these scans will be presented in Sect. 5, and applied to show the current reach of the LHC search on the parameter space of the sbottom LSP based on ATLAS and CMS results [34,35,36,37]. Finally, our conclusions are left for Sect. 6.

2 The \(\mu \nu \)SSM

In the \(\mu \nu \textrm{SSM}\) [1,2,3], the particle content of the MSSM is extended by RH neutrino superfields \({\hat{\nu }}^c_i\). The simplest superpotential of the model is the following [1, 2, 11]:

$$\begin{aligned} W&= \epsilon _{ab} \left( Y_{e_{ij}} \, {\hat{H}}_d^a\, {\hat{L}}^b_i \, {\hat{e}}_j^c + Y_{d_{ij}} \, {\hat{H}}_d^a\, {\hat{Q}}^{b}_{i} \, {\hat{d}}_{j}^{c} + Y_{u_{ij}} \, {\hat{H}}_u^b\, {\hat{Q}}^{a} \, {\hat{u}}_{j}^{c} \right) \nonumber \\&\quad + \epsilon _{ab} \left( Y_{{\nu }_{ij}} \, {\hat{H}}_u^b\, {\hat{L}}^a_i \, {\hat{\nu }}^c_j - \lambda _i \, {\hat{\nu }}^c_i\, {\hat{H}}_u^b {\hat{H}}_d^a \right) + \frac{1}{3} \kappa _{ijk} {\hat{\nu }}^c_i{\hat{\nu }}^c_j{\hat{\nu }}^c_k, \end{aligned}$$
(1)

where the summation convention is implied on repeated indices, with \(i,j,k=1,2,3\) the usual family indices of the SM and \(a,b=1,2\) \(SU(2)_L\) indices with \(\epsilon _{ab}\) the totally antisymmetric tensor, \(\epsilon _{12}= 1\).

Working in the framework of a typical low-energy SUSY, the Lagrangian containing the soft SUSY-breaking terms related to W is given by:

$$\begin{aligned}{} & {} -\mathcal {L}_{\text {soft}} = \epsilon _{ab} \left( T_{e_{ij}} \, H_d^a \, {\widetilde{L}}^b_{iL} \, {\widetilde{e}}_{jR}^* + T_{d_{ij}} \, H_d^a\, {\widetilde{Q}}^b_{iL} \, {\widetilde{d}}_{jR}^{*} \right. \nonumber \\{} & {} \quad \left. +T_{u_{ij}} \, H_u^b {\widetilde{Q}}^a_{iL} {\widetilde{u}}_{jR}^* + \text {h.c.} \right) \nonumber \\{} & {} \quad + \epsilon _{ab} \left( T_{{\nu }_{ij}} \, H_u^b \, {\widetilde{L}}^a_{iL} {\widetilde{\nu }}_{jR}^* - T_{{\lambda }_{i}} \, {\widetilde{\nu }}_{iR}^* \, H_d^a H_u^b\right. \nonumber \\{} & {} \quad \left. + \frac{1}{3} T_{{\kappa }_{ijk}} \, {\widetilde{\nu }}_{iR}^* {\widetilde{\nu }}_{jR}^* {\widetilde{\nu }}_{kR}^* \ + \text {h.c.}\right) \nonumber \\{} & {} \quad + m_{\widetilde{Q}_{ijL}}^2 \widetilde{Q}_{iL}^{a*} \widetilde{Q}^a_{jL} {+} m_{\widetilde{u}_{ijR}}^{2} \widetilde{u}_{iR}^* {\widetilde{u}}_{jR}\nonumber \\{} & {} \quad + m_{\widetilde{d}_{ijR}}^2 \widetilde{d}_{iR}^* {\widetilde{d}}_{jR} + m_{\widetilde{L}_{ijL}}^2 \widetilde{L}_{iL}^{a*} \widetilde{L}^a_{jL} \nonumber \\{} & {} \quad + m_{\widetilde{\nu }_{ijR}}^2 \widetilde{\nu }_{iR}^* {\widetilde{\nu }}_{jR} + m_{\widetilde{e}_{ijR}}^2 \widetilde{e}_{iR}^* {\widetilde{e}}_{jR} \nonumber \\{} & {} \quad + m_{H_d}^2 {H^a_d}^* H^a_d + m_{H_u}^2 {H^a_u}^* H^a_u \nonumber \\{} & {} \quad + \frac{1}{2}\, \left( M_3\, {{\widetilde{g}}}\, {{\widetilde{g}}} + M_2\, {\widetilde{W}}\, {\widetilde{W}} +M_1\, {{\widetilde{B}}}^0 \, {{\widetilde{B}}}^0 + \text {h.c.} \right) . \end{aligned}$$
(2)

In the early universe not only the EW symmetry is broken, but in addition to the neutral components of the Higgs doublet fields \(H_d\) and \(H_u\) also the left and right sneutrinos \({\widetilde{\nu }}_{iL}\) and \({\widetilde{\nu }}_{iR}\) acquire a vacuum expectation value (VEV). With the choice of CP conservation, they develop real VEVs denoted by:

$$\begin{aligned} \langle H_{d}^0\rangle= & {} \frac{v_{d}}{\sqrt{2}},\quad \langle H_{u}^0\rangle = \frac{v_{u}}{\sqrt{2}},\nonumber \\ \quad \langle {\widetilde{\nu }}_{iR}\rangle= & {} \frac{v_{iR}}{\sqrt{2}},\quad \langle {\widetilde{\nu }}_{iL}\rangle = \frac{v_{iL}}{\sqrt{2}}. \end{aligned}$$
(3)

The EW symmetry breaking is induced by the soft SUSY-breaking terms producing \(v_{iR}\sim {{{\mathcal {O}}}(1 \,\text {TeV})}\) as a consequence of the right sneutrino minimization equations in the scalar potential [1, 2, 11]. Since \({\widetilde{\nu }}_{iR}\) are gauge-singlet fields, the \(\mu \)-problem can be solved in total analogy to the NMSSM through the presence in the superpotential (1) of the trilinear terms \(\lambda _{i} \, {\hat{\nu }}^c_i\,{\hat{H}}_u {\hat{H}}_d\). Then, the value of the effective \(\mu \)-parameter is given by \(\mu = \lambda _i v_{iR}/\sqrt{2}\). These trilinear terms also relate the origin of the \(\mu \)-term to the origin of neutrino masses and mixing angles, since neutrino Yukawa couplings \(Y_{{\nu }_{ij}} {\hat{H}}_u\, {\hat{L}}_i \, {\hat{\nu }}^c_j\) are present in the superpotential generating Dirac masses for neutrinos, \(m_{{\mathcal {D}_{ij}}}\equiv Y_{{\nu }_{ij}} {v_u}/{\sqrt{2}}\). Remarkably, in the \(\mu \nu \)SSM it is possible to accommodate neutrino masses and mixings in agreement with experiments [28,29,30,31] via an EW seesaw mechanism dynamically generated during the EW symmetry breaking [1, 2, 38,39,40,41,42]. The latter takes place through the couplings \(\kappa {_{ijk}} \hat{\nu }^c_i{\hat{\nu }}^c_j{\hat{\nu }}^c_k\), giving rise to effective Majorana masses for RH neutrinos \({{\mathcal {M}}}_{ij} = {2}\kappa _{ijk} {v_{kR}}/{\sqrt{2}}\). Actually, this is possible at tree level even with diagonal Yukawa couplings [38, 40]. It is worth noticing here that the neutrino Yukawas discussed above also generate the effective bilinear terms \(\mu _i {\hat{H}}_u\, {\hat{L}}_i \) with \(\mu _i=Y_{{\nu }_{ij}} {v_{jR}}/{\sqrt{2}}\), used in the bilinear RPV model (BRPV) [43].

We conclude therefore, that the \(\mu \nu \textrm{SSM}\) solves not only the \(\mu \)-problem, but also the \(\nu \)-problem, without the need to introduce energy scales beyond the SUSY-breaking one.

The parameter space of the \(\mu \nu \textrm{SSM}\), and in particular the neutrino, neutral Higgs and sbottom sectors are relevant for our analysis in order to reproduce neutrino and Higgs data, and to obtain in the spectrum a sbottom as the LSP. In particular, neutrino and Higgs sectors were discussed in Refs. [14,15,16, 44], and we refer the reader to those works for details, although we will summarize the results below. First, we discuss here several simplifications that are convenient to take into account given the large number of parameters of the model. Using diagonal mass matrices for the scalar fermions, in order to avoid the strong upper bounds upon the intergenerational scalar mixing (see e.g. Ref. [45]), from the eight minimization conditions with respect to \(v_d\), \(v_u\), \(v_{iR}\) and \(v_{iL}\) to facilitate the computation we prefer to eliminate the soft masses \(m_{H_{d}}^{2}\), \(m_{H_{u}}^{2}\), \(m_{\widetilde{\nu }_{iR}}^2\) and \(m_{\widetilde{L}_{iL}}^2\) in favor of the VEVs. Also, we assume for simplicity in what follows the flavour-independent couplings and VEVs \(\lambda _i = \lambda \), \(\kappa _{ijk}=\kappa \delta _{ij}\delta _{jk}\), and \(v_{iR}= v_{R}\). Then, the higgsino mass parameter \(\mu \), bilinear couplings \(\mu _i\) and Dirac and Majorana masses discussed above are given by:

$$\begin{aligned} \mu= & {} 3\lambda \frac{v_{R}}{\sqrt{2}}, \;\;\;\; \mu _i=Y_{{\nu }_{i}} \frac{v_{R}}{\sqrt{2}}, \;\;\;\; m_{{\mathcal {D}_i}}= Y_{{\nu }_{i}} \frac{v_u}{\sqrt{2}}, \nonumber \\ {{\mathcal {M}}}= & {} {2}\kappa \frac{v_{R}}{\sqrt{2}}, \end{aligned}$$
(4)

where we have already used the possibility of having diagonal neutrino Yukawa couplings \(Y_{{\nu }_{ij}}=Y_{{\nu }_{i}}\delta _{ij}\) in the \(\mu \nu \textrm{SSM}\) in order to reproduce neutrino physics.

2.1 The neutrino sector

For light neutrinos, under the above assumptions, one can obtain the following simplified formula for the effective mass matrix [40]:

$$\begin{aligned} (m_{\nu })_{ij}\approx & {} \frac{m_{{\mathcal {D}_i}} m_{{\mathcal {D}_j}} }{3{\mathcal {M}}} \left( 1-3 \delta _{ij}\right) -\frac{v_{iL}v_{jL}}{4M}, \nonumber \\ \frac{1}{M}\equiv & {} \frac{g'^2}{M_1} + \frac{g^2}{M_2}, \end{aligned}$$
(5)

where \(g'\), g are the EW gauge couplings, and \(M_1\), \(M_2\) the bino and wino soft SUSY-breaking masses, respectively. This expression arises from the generalized EW seesaw of the \(\mu \nu \textrm{SSM}\), where due to RPV the neutral fermions have the flavor composition \((\nu _{iL},{\widetilde{B}}^0,{\widetilde{W}}^0,\widetilde{H}_{d}^0,{\widetilde{H}}_{u}^0,\nu _{iR})\). The first two terms in Eq. (5) are generated through the mixing of \(\nu _{iL}\) with \(\nu _{iR}\)-Higgsinos, and the third one also include the mixing with the gauginos. These are the so-called \(\nu _{R}\)-Higgsino seesaw and gaugino seesaw, respectively [40]. One can see from this equation that once \({{\mathcal {M}}}\) is fixed, as will be done in the parameter analysis of Sect. 4.2, the most crucial independent parameters determining neutrino physics are:

$$\begin{aligned} Y_{\nu _i}, \, v_{iL}, \, M_1, \, M_2. \end{aligned}$$
(6)

Note that this EW scale seesaw implies \(Y_{\nu _i}\lesssim 10^{-6}\) driving \(v_{iL}\) to small values because of the proportional contributions to \(Y_{\nu _i}\) appearing in their minimization equations. A rough estimation gives \(v_{iL}\lesssim m_{{\mathcal {D}_i}}\lesssim 10^{-4}\).

Considering the normal ordering for the neutrino mass spectrum, and taking advantage of the dominance of the gaugino seesaw for some of the three neutrino families, three representative type of solutions for neutrino physics using diagonal neutrino Yukawas were obtained in Ref. [14]. In our analysis we will use the so-called type 2 solutions, which have the structure

$$\begin{aligned} M>0, \, \text {with}\, Y_{\nu _3}< Y_{\nu _1}< Y_{\nu _2}, \, \text {and} \, v_{1L}<v_{2L}\sim v_{3L}, \end{aligned}$$
(7)

In this case of type 2, it is easy to find solutions with the gaugino seesaw as the dominant one for the third family. Then, \(v_{3L}\) determines the corresponding neutrino mass and \(Y_{\nu _3}\) can be small. On the other hand, the normal ordering for neutrinos determines that the first family dominates the lightest mass eigenstate implying that \(Y_{\nu _{1}}< Y_{\nu _{2}}\) and \(v_{1\,L} < v_{2\,L},v_{3\,L}\), with both \(\nu _{R}\)-Higgsino and gaugino seesaws contributing significantly to the masses of the first and second family. Taking also into account that the composition of the second and third families in the second mass eigenstate is similar, we expect \(v_{2L} \sim v_{3L}\). In Ref. [14], a quantitative analysis of the neutrino sector was carried out, with the result that the hierarchy qualitatively discussed above for Yukawas and VEVs works properly. See in particular Fig. 4 of Ref. [14], where \(\delta m^2=m^2_2-m^2_1\) versus \(Y_{\nu _{i}}\) and \(v_{iL}\) is shown for the scans carried out in that work, using the results for normal ordering from Ref. [33].

We will argue in Sect. 5 that the other two type of solutions of normal ordering for neutrino physics are not going to modify our results. The same conclusion is obtained in the case of working with the inverted ordering for the neutrino mass spectrum. The structure of the solutions is more involved for this case, because the two heaviest eigenstates are close in mass and the lightest of them has a dominant contribution from the first family. Thus, to choose \(Y_{\nu _1}\) as the largest of the neutrino Yukawas helps to satisfy these relations. For the second and third family, a delicate balance between the contributions of \(\nu _{R}\)-higgsino and gaugino seesaws is needed in order to obtain the correct mixing angles. In particular, a representative type of solutions for the case of inverted ordering has the structure \(M>0\), with \(Y_{\nu _3} \sim Y_{\nu _2} < Y_{\nu _1}\), and \(v_{1\,L}<v_{2\,L}\sim v_{3\,L}\).

2.2 The Higgs sector

The neutral Higgses are mixed with right and left sneutrinos, since the neutral scalars and pseudoscalars in the \(\mu \nu \textrm{SSM}\) have the flavor composition \((H_{d}^0, H_{u}^0, {\widetilde{\nu }}_{iR}, {\widetilde{\nu }}_{iL}) \). Nevertheless, the left sneutrinos are basically decoupled from the other states, since the off-diagonal terms of the mass matrix are suppressed by the small \(Y_{\nu _{ij}}\) and \(v_{iL}\). Unlike the latter states, the other neutral scalars can be substantially mixed. Neglecting this mixing between the doublet-like Higgses and the three right sneutrinos, the expression of the tree-level mass of the SM-like Higgs is [2]:

$$\begin{aligned} m_h^2 \approx m^2_Z \left( \cos ^2 2\beta + 10.9\ {\lambda }^2 \sin ^2 2\beta \right) , \end{aligned}$$
(8)

where \(\tan \beta = v_u/v_d\), and \(m_Z\) denotes the mass of the Z boson. Effects lowering (raising) this mass appear when the SM-like Higgs mixes with heavier (lighter) right sneutrinos. The one-loop corrections are basically determined by the third-generation soft SUSY-breaking parameters \(m_{\widetilde{u}_{3R}}\), \(m_{{\widetilde{Q}}_{3\,L}}\) and \(T_{u_3}\) (where we have assumed for simplicity that for all soft trilinear parameters \(T_{ij}=T_{i}\delta _{ij}\)). These three parameters together with the coupling \(\lambda \) and \(\tan \beta \), are the crucial ones for Higgs physics. Their values can ensure that the model contains a scalar boson with a mass around \(\sim 125 \,\text {GeV}\) and properties similar to the ones of the SM Higgs boson [44, 46,47,48].

In addition, \(\kappa \), \(v_R\) and the trilinear parameter \(T_{\kappa }\) in the soft Lagrangian (2), are the key ingredients to determine the mass scale of the right sneutrinos [2, 38]. For example, for \(\lambda \lesssim 0.01\) they are basically free from any doublet admixture, and using their minimization equations in the scalar potential the scalar and pseudoscalar masses can be approximated respectively by [11, 49]:

$$\begin{aligned} m^2_{\widetilde{\nu }^{\mathcal {R}}_{iR}} \approx \frac{v_R}{\sqrt{2}} \left( T_{\kappa } + \frac{v_R}{\sqrt{2}}\ 4\kappa ^2 \right) , \quad m^2_{\widetilde{\nu }^{\mathcal {I}}_{iR}}\approx - \frac{v_R}{\sqrt{2}}\ 3T_{\kappa }. \end{aligned}$$
(9)

Finally, \(\lambda \) and the trilinear parameter \(T_{\lambda }\) not only contribute to these masses for larger values of \(\lambda \), but also control the mixing between the singlet and the doublet states and hence, they contribute in determining their mass scales as discussed in detail in Ref. [44]. We conclude that the relevant parameters in the Higgs (-right sneutrino) sector are:

$$\begin{aligned} \lambda , \, \kappa , \, \tan \beta , \, v_R, \, T_\kappa , \, T_\lambda , \, T_{u_3}, \, m_{{\widetilde{u}}_{3R}}, \, m_{{\widetilde{Q}}_{3L}}. \end{aligned}$$
(10)

Note that the most crucial parameters for the neutrino sector (6) are basically decoupled from these parameters controlling Higgs physics. This simplifies the analysis of the parameter space of the model, as will be discussed in Sect. 4.2.

2.3 The sbottom sector

The mass matrix of the sbottoms includes new terms with respect to the one of the MSSM [2, 11], similar to other squarks in the \(\mu \nu \textrm{SSM}\). However, these terms are negligible given that they are proportional to the small parameters \(v_{iL}\). Thus, the sbottom eigenstates of the \(\mu \nu \)SSM coincide basically with those of the MSSM, and one has the following tree-level mass matrix in the flavor basis (\({\widetilde{b}}_L\), \({\widetilde{b}}_R\)):

$$\begin{aligned} m_{\widetilde{b}}^2=\begin{pmatrix} m_b^2+m_{\widetilde{Q}_{3L}}^2+\Delta \widetilde{d}_L &{} m_b X_b \\ m_b X_b &{} m_b^2+m_{\widetilde{d}_{3R}}^2+\Delta \widetilde{d}_R \end{pmatrix}, \end{aligned}$$
(11)

where \(m_b\) is the bottom-quark mass, \(\Delta \widetilde{d}_{L,R}\) denote the D-term contributions

$$\begin{aligned} \Delta {\widetilde{d}}_L= & {} - m^2_Z \left( \frac{1}{2} - \frac{1}{3} \sin ^2\theta _W \right) \cos 2\beta , \nonumber \\ \Delta {\widetilde{d}}_R= & {} - \frac{1}{3} m^2_Z \sin ^2\theta _W \cos 2\beta , \end{aligned}$$
(12)

with \(\theta _W\) the weak-mixing angle, and \(X_b\) the left-right sbottom mixing term

$$\begin{aligned} X_b= \frac{T_{d_3}}{Y_{d_3}}- \mu \tan \beta . \end{aligned}$$
(13)

As can easily be deduced from Eq. (11), the physical sbottom masses are controlled mainly by the value of the soft SUSY-breaking parameters:

$$\begin{aligned} m_{{\widetilde{Q}}_{3L}}, \, m_{{\widetilde{d}}_{3R}}, \, T_{d_3}. \end{aligned}$$
(14)

However, the trilinear parameter is typically less relevant than the two mass parameters because it contributes to sbottom masses through the mixing term, which is suppressed by the bottom-quark mass. Playing with the values of these parameters, it is straightforward to obtain the lightest eigenvalue dominated either by the left sbottom composition (\({\widetilde{b}}_L\)) or by the right sbottom composition (\({\widetilde{b}}_R\)). Note that in the case of the lightest sbottom mainly \({\widetilde{b}}_L\), a small value of the common soft mass \(m_{{\widetilde{Q}}_{3L}}\) makes \({\widetilde{t}}_L\) slightly lighter than \({\widetilde{b}}_L\) at tree level due to the D-term contribution, \(m_{{\widetilde{t}}_L}^{2} = m_{\widetilde{b}_{L}}^2 +m_W^2 \cos 2\beta \) with \(\cos 2\beta <0\). Thus, in what follows we will focus on the right sbottom LSP, for which a low value of \(m_{{\widetilde{d}}_{3R}}\) is crucial.

In our analysis of Sect. 5, we will sample the relevant parameter space of the \(\mu \nu \textrm{SSM}\), which contains the independent parameters determining neutrino and Higgs physics in Eqs. (6) and (10). Nevertheless, the parameters for neutrino physics \(Y_{\nu _i}\), \(v_{iL}\), \(M_1\) and \(M_2\) are essentially decoupled from the parameters controlling Higgs physics. Thus, for a suitable choice of the former parameters reproducing neutrino physics, there is still enough freedom to reproduce in addition Higgs data by playing with \(\lambda \), \(\kappa \), \(v_R\), \(\tan \beta \), \(T_{u_3}\), etc., as shown in Refs. [14,15,16]. As a consequence, we will not need to scan over most of the latter parameters, relaxing our computing task. For this task we have employed the Multinest [50] algorithm as optimizer. To compute the spectrum and the observables we have used SARAH [51] to generate a SPheno [52, 53] version for the model.

3 Sbottom LSP phenomenology

The production of sbottoms at colliders is dominated by QCD processes, since the RPV contributions to their production are strongly suppressed in the \(\mu \nu \textrm{SSM}\). The pair production of colored SUSY particles at large hadron colliders has been extensively studied. Since we do not expect a significant difference from the values predicted in the MSSM, we make use of NNLL-fast-3.0 [54,55,56,57] to calculate the number of sbottom pair events produced. In particular, for our range of interest of sbottom masses between about 200 GeV and 2000 GeV, the production cross section is in the range between 74.4 pb and 2\(\times 10^{-5}\) pb.

3.1 Decay modes

Fig. 1
figure 1

Dominant decay channels in the \(\mu \nu \textrm{SSM}\) for a sbottom LSP. (left) Decay to top quark and leptons; (right) Decay to bottom quark and neutrinos

Full size image

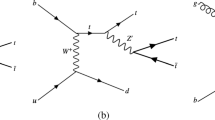
There are two dominant channels for the decay of the right sbottom LSP to standard model particles. Similarly to the stop LSP case [17], the sbottom LSP mainly decays to a quark and a lepton/neutrino. In the case of the decay to quark and leptons, the dominant contribution arises from the top quark, while for the decay to quark and neutrinos it arises from the bottom quark. Both cases are shown in Fig. 1.

The relevant interactions for our analysis are given in Appendix A. There, one can identify the most important contributions for the decays. In particular, the relevant diagram shown in Fig. 1 left corresponds to the second term multiplying the projector \(P_{R}\) in Eq. (A.1.1). Thus it occurs mainly through the Yukawa coupling \(Y_{b}\) of \({\widetilde{b}}\) with t and charged higgsinos, via the mixing between the latter and \(\ell \). The diagram in Fig. 1 right corresponds to the second term multiplying the projector \(P_{L}\) (and the first term multiplying the projector \(P_{R}\)) in Eq. (A.2.1). It occurs through the gauge coupling \(g'\) of \({\widetilde{b}}\) with b and neutral bino (Yukawa coupling \(Y_{b}\) of \({\widetilde{b}}\) with b and neutral higgsinos), via the mixing between bino (higgsinos) and \(\nu \).

In the case of (pure) right sbottom LSP, the values of the partial decay widths can be approximated, as:

$$\begin{aligned}{} & {} \Gamma (\widetilde{b}_R \rightarrow t \ell _i) \sim \frac{(m_{\widetilde{b}}^2-m_t^2)^2}{16 \pi m_{\widetilde{b}}^3}\left( Y_b \frac{\mu _i}{ \mu }\right) ^2, \nonumber \\{} & {} \sum _i \Gamma (\widetilde{b}_R \rightarrow b \nu _i)\sim \frac{m_{\widetilde{b}}}{16 \pi } \sum _{i}\nonumber \\{} & {} \quad \left[ \left( \frac{\sqrt{2}}{3}g'U_{i4}^V\right) ^2+\left( Y_b U_{i6}^V \right) ^2\right] \end{aligned}$$
(15)

As discussed in Appendix A, \(U^V\) is the matrix which diagonalizes the mass matrix for the neutral fermions, and the above entries \(U^V_{i4}\) and \(U^V_{i6}\), corresponding to the mixing between neutrinos and bino and neutrinos and neutral higgsino \({\widetilde{H}}^0_d\), respectively, can be approximated as

$$\begin{aligned} U^V_{i4}\approx \frac{{-}g'}{M_1}\sum _{l}{\frac{v_{lL}}{\sqrt{2}}U^{\tiny \text {PMNS}}_{il}},\quad \quad {U^V_{i6}\approx \ \frac{1}{\mu }\sum _l \frac{\mu _l}{\sqrt{2}} U^{\tiny \text {PMNS}}_{il}}, \end{aligned}$$
(16)

where \(U^{\text {\tiny {PMNS}}}_{il}\) are the entries of the PMNS matrix, with i and l neutrino physical and flavor indices, respectively. We also approximate other entries of the matrices involved in the computation (see Appendix A), as follows: \(Z_{16}^{D}\approx 1\) (pure right sbottom), \(U_{L, 33}^{d} \approx 1\) and \(U_{R, 33}^{d} \approx 1\) (pure LH and RH bottom quarks), \(U_{L, 33}^{u} \approx 1\) (pure LH top quark), \(U_{R, j 5}^{e}\approx {\mu _i}/{\mu }\). In addition, we use \(m_{\widetilde{b}}\gg m_b, m_{\ell }\). Let us remark nevertheless that the results of Sect. 5 have been obtained using the full tree-level numerical computation of decay widths implemented in SPheno, taking also into account the small contamination between left and right sbottoms, \(|Z^D_{36}|^2\). Loop corrections for sbottom decays are negligible since the dominant ones are two body decays. We have checked it numerically.

As can be easily deduced from Eq. (15), the decay width of \(\widetilde{b}_R\) to leptons is smaller than the one to neutrinos for sbottom masses close to the top mass. This is qualitatively different from the case of the stop LSP, where the decay width to leptons is larger that the one to neutrinos for stop masses close to the top mass, as can be seen in Fig. 5 of Ref. [17]. In our computation we will use a lower bound for the sbottom mass of 200 GeV.

3.2 LHC searches

The event topologies originated from the sbottom LSP decaying as described in Sect. 3.1 will produce signals at hadron colliders detectable with diverse LHC searches. As it is shown in Fig. 1, the possible decays include: the production of a lepton (e, \(\mu \) or \(\tau \)) and a top quark or the production of a neutrino and a bottom quark. Consequently, the production of a pair of sbottoms will lead to events of the form: \(\bar{t}t\bar{l}l\), \(\bar{b}b\bar{\nu }\nu \) or \(\bar{t}b\bar{\nu }l\). In addition, the decay length of the sbottom LSP ranges from sub-mm scale up to \(\sim 30\) mm. Therefore, there are different LHC searches that will have the highest sensitivity for each case. We will classify the signals according to the lifetime scale and apply to each one different searches.

Case (i) Non-prompt jets

The timing capabilities of the CMS electromagnetic calorimeter allow to discriminate jets arriving at times significantly larger than the traveling times expected for light hadrons, which are moving at velocities close to the speed of light. This time delay can be associated with two effects: First, the larger indirect path formed by the initial trajectory of a long-lived particle plus the subsequent trajectories of the child particles. Secondly, the slower velocity of the long-lived particle due to the high mass compared to light hadrons. Such analysis is performed by the CMS collaboration in the work [34] in the context of long-lived gluinos decaying to gluons and stable gravitinos, excluding gluinos with masses of \(\sim 2500\) GeV for lifetimes of \(\sim 1\) m.

The case where the sbottom LSP decays producing a neutrino and a bottom quark with proper decay lengths above \(\sim 30\) cm will produce a signal similar to the one analyzed in [34]. For each point analyzed in this search we compare the 95% observed upper limit on cross section, corresponding to the signal of two delayed jets for a given parent particle mass and \(c\tau \), with the prediction of the signal cross section calculated as \(\sigma (pp\rightarrow \tilde{b}\tilde{b}^*)\times BR(\tilde{b}\rightarrow b \nu )^2\).

Case (ii) Displaced vertices

For shorter lifetimes, one can confront the points of the model with the limits from events with displaced vertices including jets. The ATLAS search [35] targets final states with at least one displaced vertex (DV) with a high reconstructed mass and a large track multiplicity in events with large missing transverse momentum. The search originally targets long-lived massive particles with lifetimes in the range 1–100 mm. Thus, this search can be sensitive to the sbottom LSP when \(c\tau \) is in this range. However, the signal topologies analyzed in the search do not match the ones originated from the decays shown in Fig. 1.

To have a reasonable estimate of the exclusion power of this search, we use a recast version of the analysis within CheckMATE-LLP [58]. CheckMATE [59, 60] is a universal tool for the recasting of LHC searches in the context of arbitrary new physics models. It uses the fast detector simulation framework Delphes [61] with customized ATLAS detector card and additional built-in tuning for a more accurate reproduction of experimental efficiencies. The validation of the recasted search is discussed in [58]. We generate signal Monte Carlo (MC) samples of sbottom pair production with MadGraph5_aMC@NLO-v3.4.2 [62,63,64] at leading order (LO). The hard event corresponds to tree-level production of sbottom pairs and includes the emission of up to two additional partons, the NNPDF23LO [65, 66] PDF set is used. Simulated signal events were passed to Pythia-8.306 [67] for parton showering (PS) and hadronization. Jet matching and merging to parton-shower calculations is accomplished by the MLM algorithm [68]. Sbottom pair-production nominal cross sections are derived at NNLO+NNLL using NNLL-fast-3.0 [54,55,56,57]. Finally, we process the events generated trough CheckMATE. The results are used to calculate the efficiency (\(\epsilon \)) of the search, defined as the number of events predicted in the signal region divided by the total number generated events.

We generate samples for values of the mass equal to [250, 500, 750, 1000, 1500, 2000] GeV, \(c\tau \) equal to \([1,3,5,10,15,20,40,60]\) mm and for all of the different combinations of decays shown in Fig. 1, and calculate \(\epsilon \) for each case. For each point tested in this work, we calculate the \(\epsilon \) interpolating from each channel and value of mass and \(c\tau \), within the set of \(\epsilon \) obtained as described above.

Finally, the point is considered excluded if the total number of events predicted in the signal region of the search [35], calculated as the sum of \(\mathcal {L}\times \sigma (pp\rightarrow \tilde{b}\tilde{b}^*)\times BR_{channel}\times \epsilon _{channel}\) over all channels, is greater than the 95% upper limit on signal events, which correspond to approximately 3 events.

Case (iii) Prompt and nearly-prompt b-jets

If the proper decay length of the sbottom LSP is sufficiently short, the LHC searches designed to look for b-tagged jets originated from the decay of short-lived particles will be sensitive to the sbottom signal.

The ATLAS collaboration has shown, in a reanalysis of a selection of searches targeting RPV and RPC SUSY models [69], that the impact of the parent particle lifetime over the distribution of the observables used as discriminants in the searches for b-jets+missing transverse energy (MET) [70], such as the number of jets, the missing transverse energy (MET), or the effective mass (meff), is unaffected for values of \(c\tau < 3\) mm. Moreover, the b-tagging efficiency is improved for decay lengths of the order of millimeters. The same considerations can be made for the ATLAS search for sbottoms in events with b-jets+MET [36]. However, this search includes an additional restriction with respect to [70]: Jet candidates are reconstructed from charged-particle tracks matched to the hard-scatter vertex with the requirement \(|z_0\sin \theta |<\) 2.0 mm, where \(z_0\) is their longitudinal impact parameter. To check the compatibility of the signal of the decay of the sbottom LSP with this requirement, we have generated events corresponding to a pair of 1000 GeV sbottoms decaying to bottom quarks and neutrinos, with different values of \(c\tau \). In Fig. 2 we show the distribution of \(|z_0\sin \theta |\) of the charged tracks at truth level. For values of \(c\tau =1\) mm, more than 90% of the charged tracks satisfy the requirement. A conservative estimate of the sensitivity of this search to slightly displaced sbottoms can be obtained applying the limits from this search only to points where \(c\tau \lesssim 1\) mm.Footnote 2

Fig. 2
figure 2

Distribution of the impact parameter of charged tracks for simulated events

Full size image

We test the points where the sbottom satisfies the requirement on \(c\tau \) by comparing the 95% observed cross-section upper limit, corresponding to sbottom pair production decaying to bottom quarks plus massless neutralinos, in the search [36] with the prediction of the signal cross section, calculated as \(\sigma (pp\rightarrow \tilde{b}\tilde{b}^*)\times BR(\tilde{b}\rightarrow b \nu )^2\).

Some of the points explored in this work, with masses between 200 GeV and 400 GeV fall outside of the range of masses analyzed in the ATLAS search [36]. An alternative ATLAS search for sbottoms in final states with MET and two b-jets, made with data of accumulated 20.1 \(\textrm{fb}^{-1}\) of pp collisions at \(\sqrt{s}=8\) TeV [37], is sensitive to masses between 100 and 800 GeV. Thus, complementing the previous constraints over higher sbottom masses. We assume that the same considerations made about the impact of the parent particle lifetime over the kinematic observables based on hadronic activity still hold for this ATLAS analysis. There is an additional requirement, that all jets with \(p_T<50\ \textrm{GeV}\) and \(|\eta |<2.5\) are required to have at least one track identified as coming from the primary vertex, otherwise the event is discarded. We expect this requirement to not be sensitive to the jets originated from sbottom LSP decays, since their decays are 2-body processes to 2 nearly massless particles which will carry an energy \(\sim m_{\tilde{b}}/2\), much larger than the 50 GeV threshold.

We check those points comparing the prediction of the signal cross section, calculated as \(\sigma (pp\rightarrow \tilde{b}\tilde{b}^*)\times BR(\tilde{b}\rightarrow b \nu )^2\), with the 95% observed cross section upper limit, corresponding to sbottom pair production decaying to bottom quarks plus massless neutralinos.

Finally, is worth noting that there are LHC searches looking for events with displaced leptons that can be sensitive to the leptons produced in the decay of a long-lived sbottom LSP. That is the case of the ATLAS search for displaced leptons [71], whose main discriminant is the presence of leptonic tracks with an impact parameter greater than 3 mm. There are other LHC searches that look for displaced signals including leptons, but they target topologies which do not match the decays of the sbottom LSP. We have tested the sensitivity of the search for displaced leptons trough a recasting strategy similarly to the case of displaced vertices and we found that no additional point is excluded.

4 Strategy for the scanning

In this section, we describe the methodology that we have employed to search for points of our parameter space that are compatible with the current experimental data on neutrino and Higgs physics, as well as ensuring that the sbottom is the LSP. In addition, we have demanded the compatibility with some flavor observables, such as B and \(\mu \) decays. To this end, we have performed scans on the parameter space of the model, with the input parameters optimally chosen.

4.1 Experimental constraints

All experimental constraints (except the LHC searches which are discussed in the previous section) are taken into account as follows:

  • Neutrino observables We have imposed the results for normal ordering from Ref. [31], selecting points from the scan that lie within \(\pm 3 \sigma \) of all neutrino observables. On the viable obtained points we have imposed the cosmological upper bound on the sum of the masses of the light active neutrinos given by \(\sum m_{\nu _i} < 0.12\) eV [72].

  • Higgs observables The Higgs sector of the \(\mu \nu \textrm{SSM}\) is extended with respect to the (N)MSSM. For constraining the predictions in that sector of the model, we have interfaced HiggsBounds v5.10.2  [73,74,75,76,77,78] with Multinest, using a conservative \(\pm 3 \,\text {GeV}\) theoretical uncertainty on the SM-like Higgs boson in the \(\mu \nu \textrm{SSM}\) as obtained with SPheno. Also, in order to address whether a given Higgs scalar of the \(\mu \nu \textrm{SSM}\) is in agreement with the signal observed by ATLAS and CMS, we have interfaced HiggsSignals v2.6.2  [79, 80] with Multinest. Our requirement is that the p-value reported by HiggsSignals be larger than 2%, which is equivalent to impose \(\chi ^2 < 159\) for the 111 relevant degrees of freedom taken into account in our numerical calculation. It is worth noting here that HiggsTools [81] was released a year ago, including exotic final states or scalar searches that do not explicitly target Higgs bosons. The inclusion of these computations is not expected to change our current results, thus the implementation of HiggsTools is left for future works.

  • B decays \(b \rightarrow s \gamma \) occurs in the SM at leading order through loop diagrams. We have constrained the effects of new physics on the rate of this process using the average experimental value of BR\((b \rightarrow s \gamma )\) \(= (3.55 \pm 0.24) \times 10^{-4}\) provided in Ref. [82]. Similarly to the previous process, \(B_s \rightarrow \mu ^+\mu ^-\) and \(B_d \rightarrow \mu ^+\mu ^-\) occur radiatively. We have used the combined results of LHCb and CMS [83], \( \text {BR} (B_s \rightarrow \mu ^+ \mu ^-) = (2.9 \pm 0.7) \times 10^{-9}\) and \( \text {BR} (B_d \rightarrow \mu ^+ \mu ^-) = (3.6 \pm 1.6) \times 10^{-10}\). We put \(\pm 3\sigma \) cuts from \(b \rightarrow s \gamma \), \(B_s \rightarrow \mu ^+\mu ^-\) and \(B_d \rightarrow \mu ^+\mu ^-\), as obtained with SPheno. We have also checked that the values obtained are compatible with the \(\pm 3 \sigma \) of the recent results from the LHCb collaboration [84].

  • \(\mu \rightarrow e \gamma \) and \(\mu \rightarrow e e e\) We have also included in our analysis the constraints from BR\((\mu \rightarrow e\gamma ) < 4.2\times 10^{-13}\) [85] and BR\((\mu \rightarrow eee) < 1.0 \times 10^{-12}\) [86], as obtained with SPheno.

  • Chargino mass bound Charginos have been searched at LEP with the result of a lower limit on the lightest chargino mass of 103.5 GeV in RPC MSSM, assuming universal gaugino and sfermion masses at the GUT scale and electron sneutrino mass larger than 300 GeV [87]. This limit is affected if the mass difference between chargino and neutralino is small, and the lower bound turns out to be in this case 92 GeV [88]. LHC limits can be stronger but for very specific mass relations [89,90,91,92]. Although in our framework there is RPV and therefore these constraints do not apply automatically, we typically choose in our analyses of the \(\mu \nu \textrm{SSM}\) a conservative limit of \(m_{\widetilde{\chi }^\pm _1} > 92 \,\text {GeV}\). However, since in this work we are analysing the sbottom as the LSP, the chargino mass is always well above the mentioned bound.

  • Electroweak precision measurements There have been recently several improvements in EW measurements such as \(M_W\), \(g-2\), S, T, U, etc. (see e.g. Refs. [93,94,95]). Thus the confrontation of the theory predictions and experimental results might be timely for SUSY models. However, in our framework electroweak precision measurements are not given significant contributions. This is because the SUSY mass spectrum turns out to be above 1.1 TeV, where the latter value is the lower bound that we obtain in Sect. 5 for the mass of the sbottom LSP.

4.2 Parameter analysis

Table 1 Pair of low-energy values of the input parameters \(\lambda \) and \(\tan \beta \) determining the eight scans carried out. For all the cases, the input parameters \(T_{u_3}\), \(m_{{\widetilde{d}}_{3R}}\) are varied in the ranges shown in Eqs. (17), (18), and \(v_{iL}\), \(Y_{\nu _i}\) in the ranges shown in Table 3
Full size table
Table 2 Low-energy values of the input parameters that are fixed in the eight scans of Table 1, with the VEVs \(v_R\) and the soft SUSY-breaking parameters given in GeV
Full size table

The parameters \(\lambda \) and \(\tan \beta \) are crucial for our analysis. First, they contribute to reproduce Higgs data, as discussed in Sect. 2.2. Second, they determine the values of the sbottom decay widths, which depend on the higgsino mass parameter \(\mu \) and the bottom Yukawa coupling \(Y_b\) (15). Note in this sense that \(\lambda \) contributes to \(\mu \) (see Eq. (4)), and that \(Y_b\) increases with \(\tan \beta \). As it is shown in Table 1, we chose a range of moderate/large values of \(\lambda \in (0.15, 0.50)\), thus we are in a similar situation as in the NMSSM (see Ref. [96] and references therein) and small/moderate values of \(\tan \beta \), \(|T_{u_{3}}|\), and soft stop masses are necessary to obtain through loop effects the correct SM-like Higgs mass  [44, 46,47,48]. In particular, the corresponding values of \(\tan \beta \) are also shown in Table 1, it is sufficient for our analysis to fix \(m_{{\widetilde{Q}}_{3\,L}}\) and \(m_{{\widetilde{u}}_{3R}}\) to a reasonable value of 2000 GeV, as can be seen in Table 2, and finally for all the cases we scanned over the low-energy values of \(T_{u_3}\) in the range:

$$\begin{aligned} -T_{u_3} = 900-4000\ \text {GeV}. \end{aligned}$$
(17)

It is worth noting here that the entire mass spectrum has been obtained using the full one-loop numerical computation implemented in SPheno.

Table 3 Range of low-energy values of the input parameters related to neutrino physics that are varied in the eight scans of Table 1, with the VEVs \(v_{iL}\) given in GeV
Full size table

In Table 2, we also show the low-energy values of other input parameters. Reproducing Higgs data requires suitable additional parameters such as \(\kappa \), \(v_R\), \(T_\kappa \), \(T_\lambda \) (see Eq. (10)). Thus, we fixed to appropriate values \(T_\lambda \), which is relevant for obtaining the correct values of the off-diagonal terms of the mass matrix mixing the right sneutrinos with Higgses, and \(\kappa \), \(T_\kappa \), \(v_R\) which basically control the right sneutrino sector. To ensure that chargino is heavier than sbottom, the lower value of \(\lambda \) forces us to choose a large value for \(v_R\) in order to obtain a large enough value of \(\mu \) (see Eq. (4)). The parameters \(\kappa \) and \(T_{\kappa }\) are crucial to determine the mass scale of the right sneutrinos. We choose the value of \(-T_{\kappa }\) to have heavy pseudoscalar right sneutrinos, and therefore the value of \(\kappa \) has to be large enough in order to avoid too light (even tachyonic) scalar right sneutrinos. Working with the values of \(\lambda \) of Table 1, we can keep perturbativity up to an intermediate scale of new physics around \(10^{11}\) GeV, as discussed in detail in Ref. [44].

Fig. 3
figure 3

Proper decay length \(c\tau _{{\widetilde{b}}_{R}}\) versus the right sbottom mass \(m_{\widetilde{b}_{R}} \; [ \text {GeV} ]\), corresponding to the scans discussed in Sect. 4.2 with \(\lambda =0.15, 0.20, 0.25, 0.30, 0.35\) (lower plot) and \(\lambda =0.40, 0.45, 0.50\) (upper plot). All points fulfill the experimental constraints discussed in Sect. 4.1. (Light) Dark points (do not) fulfill the LHC constraints

Full size image

The values of other parameters shown in Table 2 concern slepton, squark and gluino masses, as well as quark and lepton trilinear parameters, which are not specially relevant for our analysis. The values chosen for the latter are reasonable within the supergravity framework, where the trilinear parameters are proportional to the corresponding Yukawa couplings. Concerning neutrino physics, as discussed in Sect. 2.1 the most crucial parameters (6) are basically decoupled from those controlling Higgs physics (10). Thus, for the concrete values of \(\lambda \), \(\kappa \), \(\tan \beta \), \(v_R\), etc., chosen to reproduce Higgs data, there is still enough freedom to reproduce in addition neutrino data by playing with appropriate values of \(M_1\), \(M_2\) and \(Y_{\nu _i}\), \(v_{iL}\), as shown in the last row of Table 2, and in Table 3.

Fig. 4
figure 4

Points of Fig. 3 but showing for them the sum of branching ratios of right sbottom LSP decaying to \(t \ell \) (lower plots) and \(b \nu \) (upper plots) versus the right sbottom mass \(m_{\widetilde{b}_{R}} \; [ \text {GeV} ]\). (Light) Dark points (do not) fulfill the LHC constraints

Full size image

Finally, the soft mass of the right sbottom, \(m_{\widetilde{d}_{3R}}\), is obviously a crucial parameter in our analysis, since it controls the physical sbottom mass, as discussed in Sect. 2.3. Thus, for obtaining a right sbottom LSP we scanned this parameter in the low-energy range:

$$\begin{aligned} m_{{\widetilde{d}}_{3R}} = 200-2000\ \text {GeV}. \end{aligned}$$
(18)

Summarizing, we performed eight scans over the 8 parameters \(m_{{\widetilde{d}}_{3R}}\), \(T_{u_3}\), \(v_{iL}\) and \(Y_{\nu _i}\) corresponding to the pair of values (\(\lambda \), \(\tan \beta \)) shown in Table 1.

5 Results

Following the methods described in the previous sections, in order to find regions consistent with experimental observations we performed scans of the parameter space, and our results are presented here. To carry this analysis out, we selected first points from the scans that lie within \(\pm 3\sigma \) of all neutrino physics observables [31]. Second, we put \(\pm 3\sigma \) cuts from \(b \rightarrow s \gamma \), \(B_s \rightarrow \mu ^+\mu ^-\) and \(B_d \rightarrow \mu ^+\mu ^-\) and require the points to satisfy also the upper limits of \(\mu \rightarrow e \gamma \) and \(\mu \rightarrow eee\). In the third step, we imposed that Higgs physics is realized. In particular, we require that the p-value reported by HiggsSignals be larger than 2%. Also, since we are interested in the right sbottom as LSP, of the allowed points we selected those satisfying this condition.

We show in Fig. 3 the proper decay length of the right sbottom LSP for the points of the parameter space studied fulfilling the above experimental constraints. As expected, for a fixed value of \(\lambda \) the decay length increases with decreasing sbottom mass. On the other hand, the decay length depends strongly on \(\lambda \) (and tan\(\beta \)). In particular, for a fixed sbottom mass \(c\tau \) increases with increasing \(\lambda \). This is because \(\lambda \) contributes to \(\mu \) and therefore the total decay width (see Eq. (15)) decreases with increasing \(\lambda \), as discussed in Sect. 4.2. This dependence becomes relevant when applying the LHC constraints discussed in Sect. 3.2. For \(\lambda = 0.15\), 0.20 all points of our scan have prompt decays since \(c \tau < 1\) mm, whereas for \(\lambda = 0.25\)–0.4 there are also points with displaced decays, depending on the value of \(m_{{\widetilde{b}}_{R}}\). As shown in the upper plot of the figure, all points with \(\lambda = 0.45\), 0.50 have displaced decays.

As can be seen from Fig. 3, for the cases \(\lambda = 0.25\)–0.50 the maximum value of the sbottom mass as LSP is \(\sim 1900\) GeV for the chosen scan range in Eq. (18). The slight shift in the upper bound is because for masses close to 2000 GeV the impact of \(\tan \beta \) in the stop mass is relevant. In particular, when increasing \(\lambda \) smaller values of \(\tan \beta \) are necessary to reproduce the Higgs mass implying in turn smaller values for the stop mass, resulting at the end of the day in a stop LSP. On the other hand, for \(\lambda =0.15, 0.20\), the maximum values of the sbottom LSP masses are \(\sim 1200\), 1500 GeV, respectively. This is because for these masses and values of \(\lambda \) and \(v_R\) the \(\mu \) parameter becomes sufficiently small as to give rise to neutral higgsino LSPs. For \(\lambda <0.15\) the neutral higgsino is the LSP unless the sbottom is very light, and, as a consequence experimentally excluded. It is true that choosing larger values of \(v_R\) would allow larger higgsino masses, modifying this lower bound for \(\lambda \). Nevertheless, given the contribution of both parameters to \(\mu \), this would be equivalent to increase \(\lambda \), and, as will be clear from the discussion below, the relevant lower bounds for the sbottom LSP mass found would not change.

In Fig. 4, the branching ratios (BRs) of both decay modes corresponding to each \(\lambda \) are shown, i.e. sbottom LSP decaying to a top and leptons (lower plots) and decaying to a bottom and neutrinos (upper plots). First, we see that the BR of \(\widetilde{b}_R\) to leptons is smaller than the one to neutrinos for sbottom masses close to the top mass. As discussed in Sect. 3.1, this is an obvious consequence of Eq. (15) for the partial decay widths. Second, for a fixed \(m_{{\widetilde{b}}_{R}}\) the BR of \(\widetilde{b}_R\) to leptons (neutrinos) decrease (increase) with increasing (decreasing) \(\lambda \). This is because the decay width to leptons is inversely proportional to \(\lambda \), while the total decay width is slightly dominated by the term proportional to \(U^V_{i4}\) in the decay width to neutrinos. The latter occurs because even though neutrino-higgsino mixing is slightly bigger than the neutrino-bino one, the couplings multiplying them make \(\sqrt{2}g'U^V_{i4}/3\gtrsim Y_b U^V_{i6}\). In addition, this term makes that the decay width to neutrinos slightly dominates with respect to the one to leptons. As can be seen from Fig. 4, for each decay channel the variation of BRs with \(\lambda \) is less than 10\(\%\).

In these figures, for the points of our scans with displaced decay lengths we applied the LHC constraints discussed in Case (ii) of Sect. 3.2. As we can see from Fig. 3, \(c\tau \) is well below 300 mm for all points, therefore Case (i) is not used to constrain any of them. For the points of our scans with prompt decay lengths we applied the constraints discussed in Case (iii). As a result of our analysis, points with dark (light) colours in the figures are allowed (forbidden) by LHC data. In particular, in the lower plot of Fig. 3 allowed (dark) points start to appear for \(m_{\tilde{b}_R}\approx 1070\) GeV, corresponding to prompt decay lengths of 0.97 mm for \(\lambda =0.35\), 0.73 mm for \(\lambda =0.30\), 0.26 mm for \(\lambda =0.25\), 0.06 mm for \(\lambda =0.20\), and 0.02 mm for \(\lambda =0.15\). In the upper plot, for \(\lambda =0.40\) the allowed points start to appear for \(m_{\tilde{b}_R}\approx 1041\) GeV, corresponding to a decay length of 1.7 mm. For \(\lambda =0.45\), they appear for \(m_{\tilde{b}_R}\approx 1130\) GeV, with decay length of 2.6 mm. Finally, in the case of \(\lambda =0.5\), this happens for \(m_{\tilde{b}_R}\approx 1235\) GeV, corresponding to a decay length of 3.5 mm. It is worth noting that for \(\lambda =0.40\) the decay length becomes smaller than 1 mm for masses \(m_{\tilde{b}_R}\approx 1685\) GeV, so for the analysis we combined the constraints of Cases (ii) and (iii).

Let us finally remark that the use of other type of solutions for neutrino physics different from the one presented in Eq. (7), would not modify the results obtained. This can be understood from the summation over leptons present in Eqs. 15 and 16, since for the most restrictive searches, for instance [35] [71], the results are independent of the lepton family or integrate over it.

6 Conclusions

We analyzed the signals expected at the LHC for a right sbottom LSP in the framework of the \(\mu \nu \textrm{SSM}\), imposing on the parameter space the experimental constraints on neutrino and Higgs physics, as well as flavour observables such as B and \(\mu \) decays. The sbottoms are pair produced and have two different decay channels producing a lepton and a top quark, or a neutrino and a bottom quark. We studied these channels and the corresponding decay length for different representative values of the trilinear coupling \(\lambda \) between right sneutrinos and Higgses, comparing the predictions with ATLAS and CMS results [34,35,36,37]. As shown in Fig. 3, for \(\lambda \in (0.15-0.35)\) the allowed points have prompt decays, and we obtained a lower limit on the sbottom mass of about 1070 GeV. On the other hand, for \(\lambda \in (0.40-0.50)\) we found that the allowed points have displaced decays, and a lower limit on the sbottom mass of about 1041 GeV was obtained. The largest value for the decay length found is about 3.5 mm.