1 Introduction

Fisher–Janis–Newman–Winicour (FJNW) metric is the exact solution of Einstein’s equations in the theory of gravity coupled minimally with a massless scalar field. The solution is a two-parameter asymptotically flat, static, and spherically symmetric with a naked singularity. It was first introduced by Fisher in 1948 [1] and somehow was rediscovered by Janis, Newman, and Winicour in 1968 [2]. The instability under radial perturbations of the Fisher’s solution was studied by Bronnikov and Khodunov in 1979 [3]. Furthermore, Wyman in 1981 introduced implicitly and independently the same spacetime [4] in completing the early attempt of Bergmann and Leipnik [5] to obtain the spherically symmetric solution of Einstein’s equations with a special form of the energy-momentum tensor. In [4] the uniqueness of the solution was also proved. The solution introduced by Wyman in his original paper doesn’t contain the FJNW metric and it was shown by Virbhadra in 1997 that these solutions are the same [6]. Their solution was also reported in some other works [7,8,9,10,11]. This solution was generalized by Xanthapoulos and Zannias to arbitrary spacetime dimensions in 1989 in [10] where the fact that the spacetime is naked singular in 3+1 dimensions was generalized to any arbitrary dimensions. A deep analysis of the d-dimensional FJNW spacetime was carried out by Abdolrahimi and Shoom in [12]. In 1993, Robert obtained the same solution in null coordinates and showed that the asymptotic flatness of the static spherically-symmetric solution of the Einstein equations in this theory is not a required pre-assumption but it is intrinsic to the solution [11]. In other words, the FJNW solution is the most general static and spherically symmetric solution of the theory. In [9], FJNW was studied in the Newman-Penrose formalism. The naked singularity of FJNW spacetime made it a good candidate to examine its observational characteristic properties and compare them with the correspondence black hole i.e., the Schwarzschild spacetime [13,14,15,16,17,18,19,20,21,22,23,24,25]. A good introduction to this theory can be found in [26]. The gravitational collapse of a massless scalar field was also studied in [27,28,29,30,31]. Particularly, we should mention the recent works on Einstein’s gravity coupled with a massless scalar field by Turimov, et al [32, 33] as well as [34] where in the latter one the electromagnetic field has also been considered.

Keeping in mind the impact of the FJNW metric in the evolution of our understanding about the formation of singularities in general relativity and their physical effects, we aim in this Letter to present a new solution in the same context whose spherically symmetric feature is broken. In this regard, we introduce a nonspherically-symmetric compact black hole solution in Einstein’s theory coupled with a nonspherically-symmetric massless scalar field.

2 The action and the solution

We start with the action of Einstein’s theory coupled with a massless scalar field (\(8\pi G=1\))

$$\begin{aligned} I=\frac{1}{2}\int d^{4}x\sqrt{-g}\left( {\mathcal {R}}-\left( \nabla \phi \right) ^{2}\right) , \end{aligned}$$
(1)

where \({\mathcal {R}}\) is the Ricci scalar and \(\phi \) is a massless scalar field. Variation of the action w.r.t the metric tensor and the scalar field yields, respectively, the Einstein and scalar field equations given by

$$\begin{aligned} R_{\mu \nu }=\partial _{\mu }\phi \partial _{\nu }\phi , \end{aligned}$$
(2)

and

$$\begin{aligned} \nabla _{\mu }\nabla ^{\mu }\phi =0. \end{aligned}$$
(3)

Moreover, we consider the spacetime to be axially symmetric with the line element

$$\begin{aligned} ds^{2}= & {} -f\left( r\right) dt^{2}+K\left( r,\theta \right) \left( \frac{dr^{2} }{f\left( r\right) }+r^{2}d\theta ^{2}\right) \nonumber \\{} & {} +r^{2}\sin ^{2}\theta d\varphi ^{2}, \end{aligned}$$
(4)

in which \(f\left( r\right) \) and \(K\left( r,\theta \right) \) are two metric functions to be found. Herein, \(\left\{ t\in \left( -\infty ,+\infty \right) ,r\in \left[ 0,\infty \right) ,\theta \in \left( 0,\pi \right) ,\right. \)\(\left. \varphi \in \left[ 0,2\pi \right) \right\} \) are the standard spherical coordinates such that with \(f\left( r\right) \) and \(K\left( r,\theta \right) \) equal to unity, (4) reduces to the flat Minkowski spacetime in the spherical coordinates representation. Concerning the line element (4) the nonzero components of the Ricci tensor are given by

$$\begin{aligned} R_{tt}= & {} \frac{f\left( rf^{\prime \prime }+2f^{\prime }\right) }{2K}, \end{aligned}$$
(5)
$$\begin{aligned} R_{rr}= & {} -\frac{f^{\prime \prime }}{2f}+\frac{1}{2r^{2}f}\left( \left( \frac{ K_{,\theta }}{K}\right) ^{2}-\frac{K_{,\theta \theta }}{K}-\frac{K_{,\theta } }{K\tan \theta }\right) \nonumber \\{} & {} +\frac{1}{2}\left( \left( \frac{K_{,r}}{K}\right) ^{2}-\frac{K_{,rr}}{K}\right) , \end{aligned}$$
(6)
$$\begin{aligned} R_{r\theta }= & {} \frac{K_{,\theta }}{4K}\left( \frac{f^{\prime }}{f}+\frac{2}{r} \right) +\frac{K_{,r}}{2K\tan \theta }, \end{aligned}$$
(7)
$$\begin{aligned} R_{\theta \theta }= & {} 1-f-rf^{\prime }-\frac{K_{,r}}{2K}\left( r^{2}f^{\prime }+2rf\right) \nonumber \\{} & {} +\frac{r^{2}f}{2}\left( \left( \frac{K_{,r}}{K}\right) ^{2}- \frac{K_{,rr}}{K}\right) \nonumber \\{} & {} +\frac{1}{2}\left( \frac{K_{,\theta }}{K}\right) ^{2}-\frac{K_{,\theta \theta }}{2K}+\frac{K_{,\theta }}{2K\tan \theta }, \end{aligned}$$
(8)

and

$$\begin{aligned} R_{\varphi \varphi }=-\frac{\sin ^{2}\theta }{K}\left( rf^{\prime }-1+f\right) , \end{aligned}$$
(9)

where \(^{\prime }=\frac{d}{dr},\) \(^{\prime \prime }=\frac{d^{2}}{dr^{2}}\), \( K_{,r}=\frac{\partial K}{\partial r},K_{,\theta }=\frac{\partial K}{\partial \theta },\) \(K_{,rr}=\frac{\partial ^{2}K}{\partial r^{2}}\) and \(K_{,\theta \theta }=\frac{\partial ^{2}K}{\partial \theta ^{2}}.\) By assuming a nonspherically-symmetric scalar field \(\phi =\phi \left( \theta \right) \) i.e., the scalar potential depends only on the polar coordinate \(\theta ,\) one obtains exact solutions of the field equations expressed by

$$\begin{aligned}{} & {} f\left( r\right) =1-\frac{2m}{r}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} K\left( r,\theta \right) =\frac{\left( \frac{m^{2}\sin ^{2}\theta }{r^{2}} \right) ^{2\beta ^{2}}}{\left( 1-\frac{2m}{r}+\frac{m^{2}\sin ^{2}\theta }{ r^{2}}\right) ^{2\beta ^{2}}}, \end{aligned}$$
(11)

and

$$\begin{aligned} \phi \left( \theta \right) =\pm \beta \ln \left( \frac{1-\cos \theta }{ 1+\cos \theta }\right) , \end{aligned}$$
(12)

in which m and \(\beta \) are two integration constants representing the gravitational mass and the scalar field, respectively. Since the sign of \( \pm \beta \) doesn’t change the physical properties of the solution without loss of generality we consider the positive branch and \(\beta \ge 0.\) The line element, hence, reads

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2m}{r}\right) dt^{2}\nonumber \\{} & {} +\frac{\left( \frac{m^{2}\sin ^{2}\theta }{r^{2}}\right) ^{2\beta ^{2}}}{\left( 1-\frac{2m}{r}+\frac{ m^{2}\sin ^{2}\theta }{r^{2}}\right) ^{2\beta ^{2}}}\left( \frac{dr^{2}}{1- \frac{2m}{r}}+r^{2}d\theta ^{2}\right) \nonumber \\{} & {} +r^{2}\sin ^{2}\theta d\varphi ^{2} \end{aligned}$$
(13)

which clearly is a 2-parameter, namely m,  and \(\beta \), metric that reduces to the standard Schwarzschild black hole in the absence of the scalar field i.e., \(\beta \rightarrow 0\). The Kretschmann scalar is calculated to be

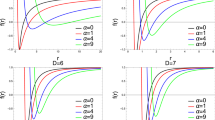
$$\begin{aligned} {\mathcal {K}}= & {} \frac{48\left( r^{2}-2mr+m^{2}\sin ^{2}\theta \right) ^{4\beta ^{2}-1}}{\left( \sin \theta \right) ^{4\left( 2\beta ^{2}+1\right) }m^{8\beta ^{2}}r^{6}}\left( m^{4}\sin ^{6}\theta \right. \nonumber \\{} & {} +\frac{2rm^{3}\left( 4\beta ^{2}-3\right) \sin ^{4}\theta }{3} \nonumber \\{} & {} + \frac{r^{2}m^{2}\sin ^{2}\theta \left( \left( 6\beta ^{2}-3\right) \cos ^{2}\theta +11\beta ^{4}-10\beta ^{2}+3\right) }{3}\nonumber \\{} & {} \left. +\frac{2r^{3}m\beta ^{2}\left( \left( 2\beta ^{2}-1\right) \cos ^{2}\theta -5\beta ^{2}+1\right) }{3}+\beta ^{4}r^{4}\right) .\nonumber \\ \end{aligned}$$
(14)

The latter expression reveals that for \(4\beta ^{2}-1\ge 0\) or equivalently \(\beta \ge \frac{1}{2},\) the Kretschmann scalar diverges at \(\theta =0,\pi , \) and \(r=0\) which are located on the axis of symmetry, namely, the z -axis in the corresponding cylindrical coordinates. On the other hand, with \( 4\beta ^{2}-1<0\) or equivalently \(\beta <\frac{1}{2}\), the spacetime is singular not only at \(\theta =0,\pi ,\) and \(r=0\) but also at the surface of \( r^{2}-2mr+m^{2}\sin ^{2}\theta =0\) which is plotted in Fig. 1.

Fig. 1
figure 1

The plots of the singular hypersurfaces for \(4\beta ^{2}-1<0 \) which are the inner surfaces. The outer spherical surface is defined by \(r=2m\) which is nothing but the surface of the event horizon. The singular hypersurfaces are hidden behind the event horizon. Furthermore, the axis of symmetry is also a singular line

Full size image

Having the singularities located on the axis of symmetry and hidden by the hypersurface \(r=2m\), Eq. (13) admits a spherical event horizon located at \( r=2m\) which is practically the same as the event horizon of the black hole in the absence of the massless scalar field. This is worth noting that

$$\begin{aligned} \lim _{r\rightarrow 2m}\frac{\left( \frac{m^{2}\sin ^{2}\theta }{r^{2}} \right) ^{2\beta ^{2}}}{\left( 1-\frac{2m}{r}+\frac{m^{2}\sin ^{2}\theta }{ r^{2}}\right) ^{2\beta ^{2}}}=1, \end{aligned}$$
(15)

indicating that the area of the black hole is the same as the corresponding Schwarzschild black hole.

Introducing the prolate spheroidal coordinates given by \(X=\frac{r}{m}-1\in \left[ -1,\infty \right) ,\) \(Y=\cos \theta \in \left[ -1,1\right) ,\) \( \varphi =\varphi \in \left[ 0,2\pi \right) \), and \(t=t\in \left( -\infty ,\infty \right) ,\) Eq. (13) becomes

$$\begin{aligned} ds^{2}= & {} -\left( \frac{X-1}{X+1}\right) dt^{2}+m^{2}\left( \frac{X+1}{X-1} \right) \nonumber \\{} & {} \times \Bigg \{ \left( X^{2}-1\right) \left( \frac{1-Y^{2}}{X^{2}-Y^{2}} \right) ^{2\beta ^{2}}\left( \frac{dX^{2}}{X^{2}-1}\right. \nonumber \\{} & {} \left. +\frac{dY^{2}}{1-Y^{2}} \right) +\left( X^{2}-1\right) \left( 1-Y^{2}\right) d\varphi ^{2}\Bigg \}. \end{aligned}$$
(16)

Calculating the Kretschmann scalar in this coordinates system reveals

$$\begin{aligned} {\mathcal {K}}= & {} \frac{48}{m^{4}}\left( \frac{X^{2}-Y^{2}}{1-Y^{2}}\right) ^{4\beta ^{2}}\nonumber \\{} & {} \times \left( \frac{\beta ^{4}\left( X^{2}+\frac{4}{3}\left( XY^{2}-X+1\right) -\frac{7}{3}Y^{2}\right) }{\left( X^{2}-Y^{2}\right) \left( 1-Y^{2}\right) ^{2}\left( 1+X\right) ^{4}}\right. \nonumber \\{} & {} \left. +\frac{\frac{2}{3}\beta ^{2}\left( X^{2}-Y^{2}+3XY^{2}-3X\right) }{\left( X^{2}-Y^{2}\right) \left( 1-Y^{2}\right) \left( 1+X\right) ^{5}}+\frac{1}{\left( 1+X\right) ^{6}} \right) \end{aligned}$$
(17)

which shows the singularities at \(X=-1\) corresponding to \(r=0\), \(Y^{2}=1\) corresponding the poles, \(X^{2}=Y^{2}\) corresponding to \(\left( \frac{r}{m} -1\right) ^{2}=\cos ^{2}\theta \) provided \(4\beta ^{2}<1.\) The scalar potential is also transformed to be

$$\begin{aligned} \phi \left( Y\right) =\beta \ln \left( \frac{1-Y}{1+Y}\right) , \end{aligned}$$
(18)

which is clearly singular at \(Y=\pm 1\) which is the boundary of the domain of Y.

3 The energy conditions

The black hole introduced in the previous section is supported by a nonspherically symmetric scalar field. In this section, we investigate the energy conditions, namely the null, weak, strong, and dominant energy conditions, abbreviated by NEC, WEC, SEC, and DEC, respectively. To do so we calculate the energy-momentum of the scalar field given by

$$\begin{aligned} T_{\mu }^{\nu }=\partial _{\mu }\phi \partial ^{\nu }\phi -\frac{1}{2}\delta _{\mu }^{\nu }\partial _{\alpha }\phi \partial ^{\alpha }\phi \end{aligned}$$
(19)

which knowing that \(\phi \left( Y\right) \), Eq. (18) explicitly reads

$$\begin{aligned} T_{\mu }^{\nu }=-\frac{1}{2}\left( \partial _{Y}\phi \partial ^{Y}\phi \right) diag\left[ 1,1,-1,1\right] \end{aligned}$$
(20)

where

$$\begin{aligned} \partial _{Y}\phi \partial ^{Y}\phi =g^{YY}\left( \partial _{Y}\phi \right) ^{2}=\frac{4\beta ^{2}}{m^{2}}\frac{1}{\left( X+1\right) ^{2}}\frac{\left( X^{2}-Y^{2}\right) ^{2\beta ^{2}}}{\left( 1-Y^{2}\right) ^{2\beta ^{2}+1}}.\nonumber \\ \end{aligned}$$
(21)

Hence, introducing \(T_{\mu }^{\nu }=diag\left[ -\rho ,p_{X},p_{Y},p_{\varphi }\right] ,\) we implicitly find the energy density and the pressures in different directions to be given by

$$\begin{aligned} \rho =-p_{X}=p_{Y}=-p_{\varphi }=\frac{2\beta ^{2}}{m^{2}}\frac{1}{\left( X+1\right) ^{2}}\frac{\left( X^{2}-Y^{2}\right) ^{2\beta ^{2}}}{\left( 1-Y^{2}\right) ^{2\beta ^{2}+1}}. \nonumber \\ \end{aligned}$$
(22)

The NEC implies \(\rho +p_{i}\ge 0\) which clearly satisfied. Furthermore, the WEC is the union of NEC and \(\rho \ge 0\) which is also perfectly satisfied. Next is the SEC which is the union of NEC and \(\rho +p_{X}+p_{Y}+p_{\varphi }\ge 0\) which is certainly satisfied. Finally the DEC implies \(\rho \ge 0,\) and \(\rho -\left| p_{i}\right| \ge 0\) in which \(i=X,Y,\varphi .\) With (22) one can easily see that DEC is also satisfied. Therefore, all energy conditions are perfectly satisfied by the energy-momentum tensor of the scalar field that indicates the black hole is supported by a physical scalar field. This is also important to mention that the energy-momentum tensor is singular at \(X=-1\) and \(Y=\pm 1.\) The former singular point is the center of the black hole corresponding to \(r=0\) in the spherical coordinates system. The latter implies the north and the south poles which effectively addresses the axis of symmetry. On the surface of singularity i.e., \(X^{2}=Y^{2}\), the energy-momentum tensor vanishes which indicates the nature of this singularity is not the energy-momentum tensor or the scalar field but it is due to the geometry of the spacetime. It is in analogy with the \(\gamma \) metric [35, 36].

4 The photon orbit

In this section, we investigate the effect of the scalar field on the photon orbit around the black hole. The Lagrangian of a null particle moving in the vicinity of the black hole (13) is given by

$$\begin{aligned} 2{\mathcal {L}}= & {} -\left( 1-\frac{2m}{r}\right) \dot{t}^{2}\nonumber \\{} & {} +\frac{\left( \frac{ m^{2}\sin ^{2}\theta }{r^{2}}\right) ^{2\beta ^{2}}}{\left( 1-\frac{2m}{r}+ \frac{m^{2}\sin ^{2}\theta }{r^{2}}\right) ^{2\beta ^{2}}}\left( \frac{\dot{r }^{2}}{1-\frac{2m}{r}}+r^{2}{\dot{\theta }}^{2}\right) \nonumber \\{} & {} +r^{2}\sin ^{2}\theta {\dot{\varphi }}^{2}, \end{aligned}$$
(23)

where a dot stands for the derivative with respect to an affine parameter. The energy of the particle as well as its angular momentum about the axis of symmetry are conserved such that

$$\begin{aligned} E=-\frac{\partial {\mathcal {L}}}{\partial \dot{t}}=1-\frac{2m}{r}, \end{aligned}$$
(24)

and

$$\begin{aligned} \ell =\frac{\partial {\mathcal {L}}}{\partial {\dot{\varphi }}}=r^{2}\sin ^{2}\theta {\dot{\varphi }}. \end{aligned}$$
(25)

The equation of motion in \(\theta \) direction is rather far from being trivially satisfied simply by \(\theta =\theta _{0}\) unless \(\theta _{0}= \frac{\pi }{2}.\) Applying the constraint of the null geodesics i.e., \(\dot{x} _{\mu }\dot{x}^{\mu }=0,\) on the equatorial plane where \(\theta _{0}=\frac{ \pi }{2}\) the main radial equation is obtained to be

$$\begin{aligned} \left( \frac{r}{m}-1\right) ^{-4\beta ^{2}}\dot{r}^{2}+V_{eff}\left( r\right) =E^{2}, \end{aligned}$$
(26)

where the effective potential is given by

$$\begin{aligned} V_{eff}\left( r\right) =\frac{\ell ^{2}}{r^{2}}\left( 1-\frac{2m}{r}\right) . \end{aligned}$$
(27)

We observe from the effective potential that the circular orbit where \(\dot{r }=0\) and \(\ddot{r}=0\) is possible at \(r_{c}=3m\) where \(V_{eff}^{\prime }\left( r_{c}\right) =0\) however since \(V^{\prime \prime }\left( r_{c}\right) <0\) this circular orbit is unstable. The situation is the same as the Schwarzschild black hole. Although the circular orbit of the null particle is \(\beta \)-independent, the actual general motion of a null as well as a massive particle very much depends on \(\beta \) which is clearly observed from (26).

5 Conclusion

In this Letter, we introduced an exact black hole solution in the theory of gravity coupled with a massless scalar field. The solution contains two integration parameters which are m and \(\beta .\) These parameters are related to the mass of the black hole and the charge of the scalar field. In particular, \(\beta \ge 0\) may be called the charge of the scalar field and it plays a crucial role in the global configuration of the solution. The contribution of \(\beta \) is in analogy with the parameter \(\gamma \) in \( \gamma \)-metric which is also known as Zipoy-Voorhees metric [35, 36]. For \(\beta =0\) the solution becomes the Schwarzschild black hole with a timelike singularity at \(r=0.\) For \(0<\beta \) the solution is axially symmetric and geometrically the spacetime is deformed such that \(\beta = \frac{1}{2}\) seems to play a topological phase transition point such that for \(\beta \ge \frac{1}{2}\) the surfaces of singularities disappear. Hence, topologically one defines three regions: (i) \(\beta =0\), ii. \(0<\beta <\frac{1 }{2}\) and (ii) \(\frac{1}{2}\le \beta \). In all three cases, the event horizon is formed at \(r=2m\) although for \(\beta >0\) the horizon surface is singular at the poles. The scalar field depends only on the polar angle \( \theta \) and is singular at the poles. Unlike, the well-known FJNW metric which is spherically symmetric, asymptotically flat, and naked singular, the solution we presented here is non-spherical, non-asymptotically flat with an event horizon. The main singularity is the axis of symmetry of the black hole in analogy with the Levi-Civita spacetime [37], however, the event horizon is spherical and covers the singularity, except on the axis of symmetry. Except for the poles, which are singular, the event horizon in other directions is regular. We have also shown explicitly that the energy conditions are all satisfied unconditionally. The photon orbit on the equatorial plane is exactly the same as the Schwarzschild black hole.